Age-related differences in the structural complexity of subcortical and ventricular structures

Abstract

It has been well established that the volume of several subcortical structures decreases in relation to age. Different metrics of cortical structure (e.g., volume, thickness, surface area, gyrification) have been shown to index distinct characteristics of inter-individual differences; thus, it is important to consider the relation of age to multiple structural measures. Here we compare age-related differences in subcortical and ventricular volume to those differences revealed with a measure of structural complexity, quantified as fractal dimensionality. Across three large datasets, totalling nearly 900 individuals across the adult lifespan (18–94 years old), we found greater age-related differences in complexity than volume for the subcortical structures, particularly in the caudate and thalamus. The structural complexity of ventricular structures was not more strongly related to age than volume. These results demonstrate that considering shape-related characteristics improves sensitivity to detect age-related differences in subcortical structures.

Graphical Abstract

1. Introduction

The structure of the brain changes with age, and these changes can be measured in vivo using magnetic resonance imaging (MRI) (Creasey & Rapoport, 1985; Drayer, 1988; Kemper, 1994; Raz & Rodrigue, 2006). While age-related differences are apparent throughout the brain, differences are particularly evident in the volume of subcortical structures (Allen et al., 2005; Goodro et al., 2012; Greenberg et al., 2008; Gunning-Dixon et al., 1998; Inano et al., 2013; Jernigan et al., 2001; Long et al., 2012; Potvin et al., 2016; Raz et al., 2004, 2005; Tamnes et al., 2013; Walhovd et al., 2005, 2011; Yang et al., 2016). Accompanying these changes, the ventricles also enlarge with age (Apostolova et al., 2012; Barron et al., 1976; Kaye et al., 1992; LeMay, 1984; Walhovd et al., 2011; Nestor et al., 2008). Here we investigated age-related changes in the shape of these same subcortical structures and tested if this additional information could explain variance beyond that explained by volumetric changes.

Walhovd et al. (2011) conducted a comprehensive review of the literature examining age-related differences in subcortical structures. In their review, along with their own multi-sample analyses, they found strong age-related differences in the volume of the putamen, thalamus, and accumbens; other regions, including the caudate and amygdala, were relatively unaffected by aging. Walhovd et al. also found volumetric differences in the lateral ventricles and third ventricle to also be strongly related to age, but no age-related differences in the fourth ventricle. In a supplemental figure (Walhovd et al., 2011, Figure S2), the authors additionally illustrated age differences in the shape of these subcortical structures, though there was no accompanying quantitative analysis of shape.

While it is known that there are age-related differences in cortical thickness and gyrification (Hogstrom et al., 2013; Fjell et al., 2009; McKay et al., 2014; Salat et al., 2004), many other morphological measures can also be examined (e.g., sulcal depth, span, and variability [Kochunov et al., 2008; Im et al., 2006; Thompson et al., 1996; Yun et al., 2013]; curvature [Fischl et al., 1999; Pienaar et al., 2008]). Recently we demonstrated that age-related differences in the shape, i.e., structural complexity, of cortical regions were more pronounced than in cortical thickness or gyrification (Madan & Kensinger, 2016). Moreover, we found that complexity statistically accounted for all of the age-related differences associated with cortical thickness and gyrification. Although it is currently unclear what features of brain morphology are captured by this metric of complexity, the results underscore that—at least for cortical regions—complexity is a particularly robust metric for assessing age-associated differences. Of course, explaining the ‘most’ age-related variability is not always desired, as this may leave less remaining variance to account for other sources of inter-individual variability (e.g., cognitive abilities); but the extant research suggests that if the goal is to estimate effects of age on brain morphology, metrics of structural complexity may be of particular utility.

Here we sought to extend this research by assessing the extent by which complexity can improve the characterization of age-related differences in brain structure beyond the cortex, by examining subcortical and ventricular structures. A number of studies have demonstrated that the shape of subcortical structures can differ between patients and healthy controls. For instance, autism has been associated with differences in the shape of the amygdala (Chung et al., 2008), Alzheimer’s disease has been related to differences in several structures, particularly the hippocampus, amygdala, and lateral ventricles (Tang et al., 2014), and schizophrenic patients have shown differences in hippocampal and thalamus shape (Zhao et al., 2016; also see Smith et al., 2011, and Qiu et al., 2009). Though these studies provide evidence that shape characteristics can be a relevant measure for subcortical structures, it is possible that these systematic differences only occur in the presence of neurological or psychiatric disorders. Furthermore, increased explained variance may not always be desired, instead, we propose that the use of multiple metrics can lead to better characterization of inter-individual differences.

Here we used fractal dimensionality to measure the structural complexity of the investigated subcortical and ventricular structures. This approach was inspired by the innovative work of Mandelbrot (1967), where fractal geometry principles were applied to quantify the complexity of complex natural structures. While Mandelbrot initially applied fractal dimensionality to geographic data (coast lines), neuroimagers have previously considered the notion of using fractal dimensionality to quantify the complexity of the brain (e.g., Free et al., 1996; Hofman, 1991; Kiselev et al., 2003). More broadly, fractal dimensionality have been used in neuroscience from the scale of individual neurons to the whole brain (see Di Ieva et al., 2014, 2015, for a review).

Using three large datasets, here we first replicated the age-related differences in volume of subcortical and ventricular structures, then further calculated age-related differences in their structural complexity. The present study addressed two primary questions: (1) are there systematic age-related differences in the shape of subcortical structures, as indexed by structural complexity, using the same approach as in Madan and Kensinger (2016) and (2) how do these differences compare to volumetric age-related differences in these structures. Different structural measures may also serve complimentary roles—where different measures may index distinct population-level characteristics; as such we additionally assessed the collinearity of the measures and the unique variance they can explain with respect to age-related variability.

2. Procedure

2.1. Datasets

Three datasets were used to evaluate age-related differences in subcortical and ventricular structure.

Sample 1 (OASIS) consisted of 314 healthy adults (196 females), aged 18–94, from the publicly available Open Access Series of Imaging Studies (OASIS) cross-sectional dataset (Marcus et al., 2007; http://www.oasis-brains.org). Participants were recruited from a database of individuals who had (a) previously participated in MRI studies at Washington University, (b) were part of the Washington University Comminity, or (c) were from the longitudinal pool of the Washington University Alzheimer Disease Research Center. Participants were screened for neurological and psychiatric issues; the Mini-Mental State Examination (MMSE) and Clinical Dementia Rating (CDR) were administered to participants aged 60 and older. In the current sample, participants with a CDR above zero were excluded; all remaining participants scored 25 or above on the MMSE. Multiple T₁ volumes were acquired using a Siemens Vision 1.5 T with a MPRAGE sequence; only the first volume was used here. Scan parameters were: TR=9.7 ms; TE=4.0 ms; flip angle=10°; voxel size=1.25×1×1 mm.

Sample 2 (IXI) consisted of 427 healthy adults (260 females), aged 20–86, from the publicly available Information eXtraction from Images (IXI) dataset (http://brain-development.org/ixi-dataset/). This is the same set of individuals we used previously to investigate age-related differences in the cortex (Madan & Kensinger, 2016). These individuals were scanned at one of three hospitals in the London, UK (Guy’s Hospital, Hammersmith Hospital, and Institute of Psychiatry) in 2005–2006. Details on how these individuals were recruited is unavailable, nor are details on how mental health was assessed. See Madan and Kensinger (2016) for further details.

Sample 3 (BC) consisted of 176 healthy adults (89 females), aged 18–83, recruited by the Cognitive and Affective Laboratory at Boston College (BC) in 2012–2015. All participants were screened for neurological and psychiatric issues, and to have scored above 26 on the MMSE. T₁ volumes were acquired using a Siemens Trio 3 T with a MEMPRAGE sequence optimized for morphometry studies (van der Kouwe et al., 2008; Wonderluck et al., 2009). Scan parameters were: TR=2530 ms; TE=1.64, 3.50, 5.36, 7.22 ms; flip angle=7°; voxel size=1×1×1 mm.

2.2. Segmentation and volumetric analyses

All structural MRIs were processed using FreeSurfer 5.3.0 on a machine running CentOS 6.6 (Fischl, 2012; Fischl & Dale, 2000; Fischl et al., 2002). FreeSurfer’s standard pipeline was used (i.e., recon-all). FreeSurfer’s segmentation procedure produces labels for seven subcortical structures (thalamus, hippocampus, amygdala, caudate, putamen, accumbens, palladium) and four ventricular structures (lateral, inferior lateral, third, fourth) all within a common segmentation volume (Fischl et al., 2002, 2004). Figure 1 shows the subcortical structures investigated here. Volumes for subcortical and ventricular structures were obtained directly from FreeSurfer.

Figure 1. Coronal slices, 3D reconstruction, and 2D illustration of the seven subcortical structures examined.

Coronal slices, with anterior slices on the left, are shown at 5-mm spacing from a representative participant; positions of the displayed coronal slices are marked on the inset sagittal slice. The 3D reconstruction is based on the same participant’s MRI as the coronal slices (following from Madan, 2015). The 2D illustration was adapted from Toro et al. (2014).

Validation studies have shown that this automated segmentation procedure corresponds well with manual tracing (e.g., Fischl et al., 2002; Jovicich et al., 2009; Keller et al., 2012; Lehmann et al., 2010; Mulder et al., 2014; Pardoe et al., 2009; Tae et al., 2008; Wenger et al., 2014). FreeSurfer has been used in a large number of studies investigating age-differences in subcortical structures (e.g., Inano et al., 2013; Jovicich et al., 2009; Long et al., 2012; Potvin et al., 2016; Tamnes et al., 2013; Walhovd et al., 2005, 2011; Wenger et al., 2014; Yang et al., 2016).

Intracranial volume (ICV) was also estimated using FreeSurfer (Buckner et al., 2004), which has also been shown to correspond well with manual tracing (Sargolzaei et al., 2015).

2.3 Fractal dimensionality analyses

The complexity of each structure was calculated using the calcFD toolbox (Madan & Kensinger, 2016; http://cmadan.github.io/calcFD/). This toolbox calculates the ‘fractal dimensionality’ of a 3D structure, and is specifically designed to use intermediate files from the standard FreeSurfer analysis pipeline, here aparc.a2009s+aseg.mgz. The toolbox has previously been used with parcellated cortical structure, as well as validated using several benchmark volumes (Madan & Kensinger, 2016).

We use fractal dimensionality as a measure of the complexity of a 3D structure, i.e., a subcortical structure. Unlike volume, which corresponds to the ‘size’ of any 3D structure, fractal dimensionality measures shape information and is scale invariant (Madan & Kensinger, 2016). In fractal geometry, several approaches have been proposed to quantify the ‘dimensionality’ or complexity of a fractal; the approach here calculates the Minkowski–Bouligand or Hausdorff dimension (see Mandelbrot, 1967). This structural property can be measured by considering the 3D structure within a grid space and counting the number of boxes that overlap with the edge of the structure, referred to as the ‘box-counting algorithm’ (Caserta et al., 1995; Mandelbrot, 1982). By then using another grid size (i.e., changing the box width), the relationship between the grid size and number of counted boxes can be determined. Here we used box sizes (in mm) corresponding to powers of 2, ranging from 0 to 4 (i.e., 2^k [k = 0, 1, 2, 3, 4] = 1, 2, 4, 8, 16 mm). The slope of this relationship in log-log space is the fractal dimensionality of the structure. Thus, the corresponding equation is:

$$FD=-\frac{\mathrm{\Delta }lo{g}_2(\text{Count})}{\mathrm{\Delta }lo{g}_2(\text{Size})}$$

There are two distinct fractal dimensionality values that can be calculated: If only the boxes overlapping with the edge/surface of the structure are counted, this slope represents the fractal dimensionality of the surface, denoted as FD_s. If the boxes within the structure are also counted, the resulting slope represents the fractal dimensionality of the filled volume, denoted as FD_f.

As the relative alignment of the grid space and the structure can influence the obtained fractal dimensionality value using the box-counting algorithm, we instead used a dilation algorithm that is equivalent to using a sliding grid space and calculating the fractal dimensionality at each alignment (Madan & Kensinger, 2016), but can be calculated much faster as it is less computationally demanding. This was implemented using a 3D-convolution operation (convn in MATLAB). As an example, Figure 2 illustrates the calculation of fractal dimensionality for a complex 2D structure.

Figure 2. Illustration of how fractal dimensionality is measured from a 2D structure.

Reprinted from Madan and Kensinger (2016) with permission. Copyright 2016, Elsevier.

2.4. Data Analysis

All volume measurements were ICV-corrected prior to conducting the regression analyses. Specifically, ICV-corrected volumes were calculated as the residual after the volume data was regressed for ICV (as in Walhovd et al., 2011). Formal comparisons of procedures used to adjust for ICV suggest that results generalize across differing procedures (Greenberg et al., 2008).

Age differences in the subcortical and ventricular structures was first assessed using regression models examining the linear and quadratic relationships between age and volume (or fractal dimensionality) of the structure, with the amount of variance explained (i.e., R²) as the statistic. All of the regression models reported controlled for effects of sex (and site, in the case of the IXI dataset).

To directly assess if fractal dimensionality explained more age-related variability than volume, we formally compared model fits based on either measure, for each structure, using the Bayesian Information Criterion (BIC). This approach allows us to compare different regression models and determine which model fits the data best, or if models perform comparably. Additionally, models with more parameters are penalized for these additional degrees of freedom. As a rule of thumb, if the difference in BIC between two models is less than two, neither of the models’ fit to the data is significantly better (Burnham & Anderson, 2002, 2004). As absolute BIC values are arbitrary, we subtract the BIC value for the best model considered from all BIC values and report ΔBIC for each of the models, as is common practice. As a result, the best model considered is ΔBIC=0.00 by definition.

3. Results

3.1. Age-related differences in subcortical structures

We used the OASIS dataset as our primary sample because Walhovd et al. (2011) previously examined age-related differences in volumetric measures in this sample (Samples 4a and 4b in their analyses). As such, the volumetric analyses here were intended to serve as a replication of their findings.

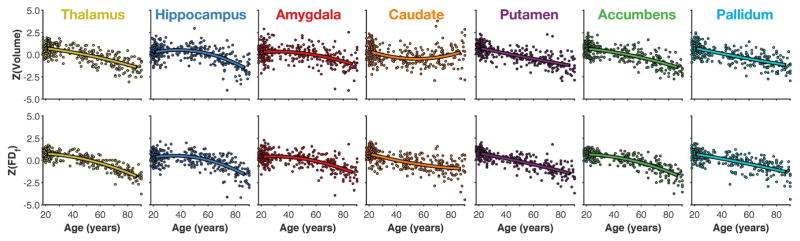
The subcortical structures investigated here were the thalamus, hippocampus, amygdala, caudate, putamen, accumbens, and pallidum; a representative reconstruction of the structures from a participant’s MRI is shown in Figure 1. As shown in Table 1, linear and quadratic relationships between age and volumes of subcortical structures closely matched the amount of variance explained (i.e., R²) reported by Walhovd et al. for the same sample. Briefly, age-related differences were most pronounced in the thalamus, putamen, accumbens, and pallidum—each with R² values near 50% or above (Figure 3A). Age explained a moderate amount of variability in the volume of the hippocampus and amygdala, whereas caudate volume was the least related to age-related differences. The upper half of Figure 4 shows the quadratic fits for each structure.

Table 1. Effects of age on volume and fractal dimensionality for the structures examined.

Volume measures were ICV-corrected; effects of site were regressed out for the IXI sample. Values in the Age² columns indicate amount of explained variance (R²) for the model consisting of Age+Age² and are printed in bold/italic+underline only if the addition of the quadratic term significantly increased the amount of explained variance. Bold: p<.01; Italic+Underline: p<.05.

	Volume						FDf
	1		2		3		1		2		3
	OASIS		IXI		BC		OASIS		IXI		BC
	Age	Age2	Age	Age2	Age	Age2	Age	Age2	Age	Age2	Age	Age2
Thalamus	.55	.55	.28	.30	.28	.37	.71	.74	.52	.54	.51	.56
Hippocampus	.26	.38	.14	.20	.38	.47	.31	.43	.10	.13	.26	.32
Amygdala	.18	.21	.10	.12	.35	.42	.28	.33	.23	.24	.42	.48
Caudate	.03	.12	.05	.06	.04	.10	.39	.40	.26	.26	.29	.31
Putamen	.51	.51	.28	.28	.50	.51	.62	.62	.32	.32	.44	.46
Accumbens	.53	.54	.23	.23	.44	.45	.61	.65	.31	.31	.47	.49
Pallidum	.47	.48	.06	.06	.33	.34	.49	.49	.10	.11	.30	.31
Ventricles
Lateral	.53	.60	.32	.38	.44	.48	.51	.53	.26	.28	.48	.48
Inferior Lateral	.39	.57	.19	.28	.28	.32	.30	.41	.07	.09	.25	.28
3rd	.52	.63	.30	.34	.44	.49	.52	.59	.28	.30	.43	.47
4th	.02	.08	.01	.02	.00	.00	.00	.08	.00	.01	.01	.01

Figure 3.

Amount of variance explained (R²) by quadratic models of age in volume and structural complexity for each subcortical structure (Panel A). Panel B shows the amount of variance common to both volume and complexity (i.e., collinearity), as well as combined variance explained by including both volume and complexity.

Figure 4.

Scatter plots of age-related differences in volume and structural complexity for each subcortical structure along with best-fitting quadratic models.

We calculated the fractal dimensionality, both FD_s and FD_f, of the structures for each individual to additionally measure age-related differences in their structural complexity. Fractal dimensionality of the surface (FD_s) captured more variability than volume for some of the structures; for instance, 64% for the thalamus and 66% for the accumbens. There was a smaller increase in variability explained by FD_s relative to volume in the amygdala (31%) and there was effectively no additional age-related differences explained in the caudate (16%). However, less variability was explained by FD_s than by volume in other structures, such as the hippocampus (20%), putamen (31%), and pallidum (36%). Importantly, FD_s captures shape-related, but not volumetric, characteristics of the surface structure. In contrast, FD_f, while scale invariant, is influenced by a combination of shape- and volumetric-related characteristics of the structure. Age-related differences in FD_f were larger than those for volume across all seven subcortical structures, as shown in Table 1 and Figure 3A; differences were also larger than for FD_s for all but one structure, though that comparison was only nominally smaller [accumbens, quadratic R²: FD_s = 66%; FD_f = 65%]. Relative to volume, the amount of variability explained in FD_f was much higher for the thalamus and caudate (74% and 40% variance explained with the quadratic model, respectively; versus 55% and 12% with volume, respectively). More moderate increases (of approximately 10% more variance explained) were found for the amygdala, putamen, and accumbens. The lower half of Figure 4 shows the quadratic fits for the structures; relationships are generally consistent as those with volume, though generally there is less unexplained variability (i.e., the residual).

Figure 3B illustrates that volume and structural complexity are highly collinear. Volume and structural complexity were the most distinct for the caudate, with 59% shared variance. Apart from the caudate, the amount of shared variance ranged from 73–86%. Including both volume and structural complexity within the same model marginally increased the total amount of variance explained (Figure 3B) relative to the FD_f models, with increases ranging from 1–4% for six of the structures. However, the inclusion of volume led to a 12% additional variance explained for the caudate, suggesting that age-related differences in volume and complexity were distinct for this region.

The two fractal dimensionality measures were slightly more collinear, with shared variances of: thalamus (77%), hippocampus (71%), amygdala (85%), caudate (76%), putamen (63%), accumbens (99%), and pallidum (72%). In almost all cases, the combined variance explained by the two fractal dimensionality measures was increased by less than 5% relative to the FD_f-only regression model; the only exception to this was the caudate, where the combined model explained 56% of age-related variability.

Formal model comparisons are reported in Table 2. In contrast to the analyses presented in Figures 3–4 and Table 1, where the structural measures were used as the dependant variable (DV), here we used age as the DV such that we could compare how well the various structural measures were able to explain variability in this common DV. Here we found that fractal dimensionality explained more age-related variability than volume for all of the subcortical structures.

Table 2. Model fitness in comparing the effects of volume and fractal dimensionality in explaining age, for each of the structures examined, based on the OASIS dataset.

Values in the Quadratic columns indicate model fitness (ΔBIC) for the regression model consisting of both linear and quadratic terms. Models with BIC values with a difference greater than two suggest that the model with the lower BIC value is a significantly better fit than the other models. Best fitting models for each structure are denoted in bold.

	Volume		FDf
	Linear	Quadratic	Linear	Quadratic
Thalamus	138.81	144.04	0.00	1.97
Hippocampus	294.06	292.48	268.43	274.18
Amygdala	325.39	328.65	282.02	285.23
Caudate	378.02	374.80	230.20	234.18
Putamen	166.08	166.43	87.17	91.08
Accumbens	148.45	146.21	88.52	85.10
Pallidum	185.06	188.54	178.19	177.54
Ventricles
Lateral	151.21	111.27	160.55	148.52
Inferior Lateral	229.71	212.61	274.11	260.23
3rd	156.98	123.98	154.28	144.76
4th	380.47	385.83	386.21	387.84

3.2. Limitations to scale invariance of fractal dimensionality

While fractal dimensionality is mathematically scale invariant, constraints of MRI data acquisition may introduce a lower limit to this theoretical property. Specifically, smaller structures are inherently more ‘rectangular’ due to voxel resolution constraints and thus will have lower structural complexity as a result. A lower limit on the scale invariance of fractal dimensionality would appear as a steep relationship with volume, indicating that the resolution of the 3D structure’s shape was insufficient to yield additional contributions from shape-related properties.

Here we examined the relationship between total volume (without ICV-correction) and FD_f and found some evidence of a limitation in scale invariance (Figure 5). Specifically, smaller subcortical structures (e.g., accumbens, pallidum) had steeper relationships between volume and FD_f and less ‘off-axis’ variability than larger structures (e.g., thalamus, caudate). This indicates that (1) FD_f for smaller structures was influenced more by volumetric characteristics than in the larger structures, and (2) FD_f for smaller structures was more correlated with volume, while FD_f for larger structures additionally indexed other sources of variability (i.e., shape-related characteristics). This increase in off-axis variability was not true of all larger structures, specifically the putamen, though this could be related to biological constraints in the variability in shape of the structure.

Figure 5.

Scatter plot of total volume and structural complexity along with best-fitting power-function models.

These results indicate that future applications of structural complexity will be limited for structures that are inherently small (e.g., hippocampal subfields), though this limitation can be attenuated by acquiring MRI data with higher-resolution imaging protocols (i.e., decreasing the voxel size during acquisition). As noted in the Methods section, the MRI data in the datasets analyzed here were acquired with a voxel size of 1 mm3-isotropic or slightly larger. However, when anatomical fidelity is critical, current neuroimaging protocols can acquire high-resolution images with voxel dimensions on the scale of 0.5 mm in-plane (e.g., Hrybouski et al., 2016; La Joie et al., 2010; Palombo et al., 2013; Reagh & Yassa, 2014; Yushkevich et al. 2015).

3.3. Age-related differences in the ventricles

We also examined age-related differences in the volume and structural complexity of the ventricles, as shown in Figure 6. The amount of variability in volume explained by age-related differences was consistent with Walhovd et al. (2011). Interestingly, variability in the fractal dimensionality (FD_f) of the structures was more weakly associated with age-related differences than volume, unlike the subcortical structures (see Table 1). When formally compared (see below), volume explained more age-related variability than fractal dimensionality for all of the ventricular structures (Table 2).

Figure 6. Age-related differences in volume and structural complexity of ventricular structures.

(A) Bar plot of amount of variance explained (R²) by quadratic models of age. (B) Scatter plots of age-related differences in either measure.

3.4. Replication in independent samples

To assess the reproducibility of our findings of age-related differences in the structural complexity of the subcortical and ventricular structures, we conducted similar analyses in two additional samples.

In the IXI sample, we generally found less age-related differences in both volume and fractal dimensionality; however, the volumetric differences observed here were within the inter-sample variability observed in Walhovd et al. (2011). Importantly, the same regions were found to show the strongest age-related differences in volume (e.g., thalamus, putamen, lateral ventricles; though not the pallidum). Fractal dimensionality (FD_f) was again more closely related to age-related differences. Results in the BC sample were consistent with those observed in the OASIS and IXI samples, and magnitudes of explained variance on age-related differences in volume and fractal dimensionality were generally in-between those observed in each of the other datasets.

4. Discussion

When examining age-related differences in brain structure, it is important to consider the most appropriate measure. With cortical structure, it has been established that age-related differences are reflected most in cortical thickness, rather than surface area or volume (Hogstrom et al., 2013; Fjell et al., 2009; McKay et al., 2014; Salat et al., 2004); however, we recently demonstrated that structural complexity of the cortex is more sensitive to age-related differences than thickness (Madan & Kensinger, 2016). In the present study, we found systematic age-related differences in the structural complexity of subcortical regions that was not captured by volumetric measures. Additionally, we found that structural complexity was not more closely related to age-related differences across all brain structures: this measure showed a weaker association with age for the ventricular regions than did other metrics. Thus, it is clear that considering the shape of subcortical structures provides additional information about age-related atrophy beyond ICV-corrected volume, but only when the ‘contents’ of the structure are themselves meaningful—i.e., neural tissue, rather than CSF.

Evidence of age-related differences in fractal dimensionality in subcortical structures (as well as cortical structures; Madan & Kensinger, 2016) demonstrates that current approaches of measuring age-related differences in volume (and cortical thickness) only partially characterize how the structural properties of the brain relate to age. While the neurobiological basis (i.e., cellular through systems level) of these differences is unclear, these differences are demonstrably evident at the macro-level of brain structures that is measured using structural MRIs. Further research is needed to establish how these shape-related differences manifest in more precise measures of neural structure (e.g., differences in neuronal composition or density). Indeed, the use of fractal dimensionality to measure complexity at the micro- and meso-level structures within neuroscience has already been established (Di Ieva et al., 2014, 2015) and may prove useful in examining age-related differences within these subcortical structures, such as in the composition of neurons. Nonetheless, the present results provide evidence of an additional metric for evaluating inter-individual differences in physiological brain age.

Prior work in young and older adults has demonstrated that fractal dimensionality can index inter-individual differences in brain morphology that relate to cognition and differs between healthy adults and patient populations. While the current work applies fractal dimensionality analyses to subcortical structures, others have used fractal dimensionality to characterize the structural complexity of segmented grey or white matter structure (e.g., King et al., 2009; Madan & Kensinger, 2016; Mustafa et al., 2012; Sandu et al., 2008). Using these approaches, fractal dimensionality has been related to inter-individual differences in measures of fluid intelligence (Mustafa et al., 2012; Sandu et al., 2014), IQ (Im et al., 2006), and performance on the cognitive subscale of the Alzheimer’s Disease Assessment Scale (King et al., 2010). Fractal dimensionality has also been shown to differ between healthy adults and a number of patient populations, particularly in Alzheimer’s disease (King et al., 2009, 2010; Thompson et al., 1998) and schizophrenia (Ha et al., 2005; Narr et al., 2004; Nenadic et al., 2014; Sandu et al., 2008; Yotter et al., 2011; Zhao et al., 2016). Thus, while we have demonstrated the benefits of using fractal dimensionality to index age-related differences in subcortical structure, as well as cortical structure (Madan & Kensinger, 2016), the variability of this morphological measure also is related to inter-individual differences in cognitive measures and may hold promise as a biomarker for some neurological disorders. However, it is important to consider that more inter-individual variability explained by age may not always be desired, as this leaves less variance available to be related to other factors, e.g., performance on cognitive measures, so volume may still be a preferable measure depending on the research question. As such, we advocate for the use of multiple brain morphology measures when examining inter-individual differences.

Though we measured structural complexity here using fractal dimensionality, this is not the only approach to quantify these shape-related properties; other related approaches such as spherical harmonics (Chung et al., 2008, 2010; Yotter et al., 2011) and Laplace-Beltrami spectra (Reuter et al., 2006; Wachinger et al., 2015) may similarly be able to capture these structural differences. Seo and Chung (2011) demonstrated that Laplace-Beltrami eigenfunctions can yield better fits to the original structure than spherical harmonics, when reconstructing cortical and subcortical surfaces. This difference was attributed to Laplace-Beltrami spectra not necessitating spherical parameterization. As of yet, no comparison has been done between Laplace-Beltrami spectra and the current approach of using fractal dimensionality.

In summary, the present results reveal that metrics of fractal dimensionality can capture age-associated variance within subcortical structures that is missed when using only volumetric measures. This result represents an important extension of prior research examining cortical structure (Madan & Kensinger, 2016), revealing that fractal dimensionality is strongly associated with age even in relatively small, subcortical structures. Moreover, these results emphasize the benefits of including metrics of fractal dimensionality in assessments of structural differences associated with aging and of assessing both subcortical and cortical structures.

Highlights.

• Compared age-related differences in subcortical volume to differences in structural complexity

• Structural complexity was quantified as fractal dimensionality

• Three datasets, totaling nearly 900 individuals across adult lifespan (18–94 years old)

• Greater age-related differences in complexity than volume for subcortical structures

• Complexity of ventricular structures was not improved relative to volume differences