Abstract
Libraries of 16S rRNA genes provide insight into the membership of microbial communities. Statistical methods help to determine whether differences in library composition are artifacts of sampling or are due to underlying differences in the communities from which they are derived. To contribute to a growing statistical framework for comparing 16S rRNA libraries, we present a computer program, ∫-LIBSHUFF, which calculates the integral form of the Cramér-von Mises statistic. This implementation builds upon the LIBSHUFF program, which uses an approximation of the statistic and makes a number of modifications that improve precision and accuracy. Once ∫-LIBSHUFF calculates the P values, when pairwise comparisons are tested at the 0.05 level, the probability of falsely identifying a significant P value is 0.098 for a study with two libraries, 0.265 for three libraries, and 0.460 for four libraries. The potential negative effects of making the multiple pairwise comparisons necessitate correcting for the increased likelihood that differences between treatments are due to chance and do not reflect biological differences. Using ∫-LIBSHUFF, we found that previously published 16S rRNA gene libraries constructed from Scottish and Wisconsin soils contained different bacterial lineages. We also analyzed the published libraries constructed for the zebrafish gut microflora and found statistically significant changes in the community during development of the host. These analyses illustrate the power of ∫-LIBSHUFF to detect differences between communities, providing the basis for ecological inference about the association of soil productivity or host gene expression and microbial community composition.
The use of 16S rRNA gene libraries to describe microbial communities continues to provide powerful insights into microbial ecology. Traditionally, clone libraries have been compared by describing differences in phylogenetic distributions and diversity indices (e.g., see references 3, 10, 18, and 20). However, the results of these studies were dependent on arbitrary definitions of the operational taxonomic unit. Furthermore, without rigorous statistical analysis it is not possible to differentiate between differences that are due to an ecological phenomenon and those that are due to chance.
Since its publication in 2001, LIBSHUFF (27) has become an increasingly popular tool for making statistical comparisons of the diversity of taxonomic lineages represented in 16S rRNA gene libraries (1, 4, 5, 11, 13, 15, 21, 23, 28, 30). LIBSHUFF applies the approximation form of the Cramér-von Mises statistic, and other studies have recently described other statistical methods for making similar comparisons (8, 9, 14, 19). These tools provide a foundation for the analysis of libraries of gene sequences using quantitative and statistical methods. As environmental microbiologists attempt to understand the ecological mechanisms that underlie differences between 16S rRNA gene libraries, robust statistical tools will be necessary.
Here we describe ∫-LIBSHUFF, a computer program that uses the exact and integral form of the Cramer-von Mises statistic but also enables the user to choose the approximation form of the statistic as implemented in LIBSHUFF. In addition, the program analyzes more than two libraries with a single input file and single execution of the program, measures the probability of falsely identifying differences as being statistically significant, selects the number of randomizations to perform, and has accelerated execution times compared to LIBSHUFF.
MATERIALS AND METHODS
Test statistic.
The Cramér-von Mises statistic is traditionally used to test the quality of a curve fit (22). When applied to 16S rRNA gene libraries, the statistic measures the number of sequences that are unique to one library when two libraries are compared (27). More precisely, the exact and integral form of the statistic is the following:
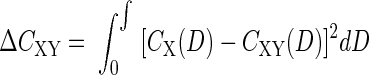 |
where CX(D) and CXY(D) are measures of library coverage, and D is the size of the distance window that is used to determine the level of coverage.
The genetic distance between two sequences is the percentage of nucleotides in one sequence that are different from those in another after correcting for multiple substitutions, for example, by computing the maximum-likelihood distance with the Jukes-Cantor nucleotide substitution model (16). Library coverage is the percentage of sequences in a library that is not comprised of singletons. A singleton is any sequence whose distance to all other sequences in some set is at least as large as some specified distance. As an analogy, we could represent each sequence as a point in some space such that all of the pairwise distances between points agreed with the maximum-likelihood distances. If we placed a circle of a given radius, D, around each point, singletons are points with no other points within their circle. As we increase the radius of each circle, ΔD, the coverage of the library increases. As a function of the distance, the coverage for a library is a nondecreasing step function that jumps at each realized pairwise distance between sequences in the library. LIBSHUFF essentially uses an approximation of this coverage function where all jumps occur at regular intervals, while ∫-LIBSHUFF does not make this approximation and uses the exact values of the coverage functions.
Both LIBSHUFF and ∫-LIBSHUFF calculate library coverage by using the method of Good (12). The coverage of library X, CX, is calculated using the formula CX(D) = 1 − [NX(D)/nX], where NX(D) is the number of singleton sequences in library X for individual values of D, and nX is the total number of sequences in library X. The coverage of library X by library Y or the percentage of sequences in library X with a similar sequence in library Y, CXY, is calculated using the formula CXY(D) = 1 − [NXY(D)/nX]. NXY(D) is the number of sequences in library X that are a distance D or greater from every sequence in Y. The value of CX(D) − CXY(D) represents the percentage of sequences in X that are not singletons in X and are not found in Y for an individual value of D. When the square of CX(D) − CXY(D) is integrated over all possible values of D, the square of the differences between the two libraries is evaluated over all phylogenetic levels.
Significance testing.
LIBSHUFF and ∫-LIBSHUFF use a Monte Carlo procedure to calculate the probability that the observed differences between the two libraries are due to chance. These programs implement the procedure by constructing two new libraries by randomly dividing the original sequences in libraries X and Y into two new libraries equal in size to X and Y. Then they calculate ΔCXY values for the randomized library. The programs construct a random distribution of ΔCXY by repeating the randomization and ΔCXY calculation many times. Both programs determine the proportion of the random distribution that has ΔCXY values larger than the ΔCXY value from the original data. This proportion is the probability that the observed differences between the two libraries are due to chance if they are actually the same (the P value). The random ΔCXY distribution and P value become more precise with more randomizations. The P value for the reverse comparison, ΔCYX, is useful as well. To calculate this statistic, the program repeats the analysis and switches the perspective of the comparison.
Small P values for both comparisons indicate strong evidence that neither library is a subset of the other. A small P value for ΔCXY coupled with a high P value for ΔCYX indicates that the sequences in library Y are a subsample of the sequences in library X. Likewise, a small P value for ΔCYX, coupled with a small P value for ΔCXY, indicates that the sequences in library X are a subsample of the sequences in library Y. Since the P values only help to determine whether two collections of sequences were sampled from the same population, it is not possible to infer a degree of relatedness between the two libraries using ∫-LIBSHUFF. In general, small P values indicate that observed differences are more likely due to how the clone libraries were constructed or underlying differences in the communities from which they were derived than to chance.
Differences in implementation.
The primary conceptual difference between LIBSHUFF and ∫-LIBSHUFF is the version of the Cramér-von Mises statistic that the program calculates. LIBSHUFF uses an approximation form of the statistic:
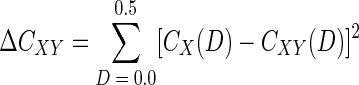 |
LIBSHUFF increases the value of D by an increment, ΔD, of 0.01 and evaluates values of D between 0.0 and 0.5. In the Monte Carlo procedure, LIBSHUFF performs 1,000 randomizations. ∫-LIBSHUFF calculates the approximation form of the statistic with any desired value of ΔD and any number of randomizations.
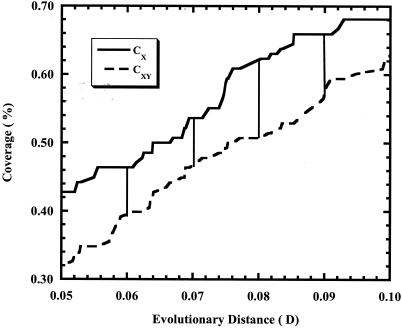
We call this form of the statistic an approximation because the value of ΔCXY is dependent on the size of ΔD. Since distance matrices are typically precise to 0.0001, using a ΔD value greater than 0.0001 results in method-induced round-off error. While it is possible to use ΔD values of 0.0001, this would require making 10,000 comparisons between coverage values for each calculation of the statistic when there may be only 300 sequences in the comparison. However, ∫-LIBSHUFF also implements the integral form of the statistic, which only requires comparing coverage values for, at most, the number of sequences in the analysis (Fig. 1). For most cases, the integral form of the calculation should run faster than the approximation form of the calculation using a ΔD value of 0.0001.
FIG. 1.
A partial plot of CX and CXY that shows the differences found using the integral form and approximation form of Cramér-von Mises statistic as a function of the size of the distance window used to identify singleton sequences. Plot was generated by using comparison between soil 16S rRNA gene libraries of McCaig et al. (20). Vertical bars denote the locations where the approximation form calculates CX and CXY as implemented in LIBSHUFF with a ΔD value of 0.01. The integral form implemented in ∫-LIBSHUFF calculates CX and CXY continuously over the entire range of observed distance values.
Our work builds on the important contribution that LIBSHUFF made to the field of environmental microbiology. We have added the prefix “∫” to its name to indicate the modification using the integral form of the Cramér-von Mises statistic. ∫-LIBSHUFF uses a distance matrix generated by the DNADIST program in the PHYLIP package (http://evolution.genetics.washington.edu/phylip.html) as the input file, which contains distances for comparisons between two or more libraries. ∫-LIBSHUFF calculates P values between two or more libraries in a single execution of the program. Finally, because we wrote ∫-LIBSHUFF in the C++ programming language instead of the Perl programming language, execution times for the same analysis are substantially faster than with LIBSHUFF. The ∫-LIBSHUFF source code is currently available from the ∫-LIBSHUFF website (http://www.plantpath.wisc.edu/fac/joh/S-LIBSHUFF.html), and the executables for Microsoft Windows are available as well.
Datasets.
To validate and evaluate ∫-LIBSHUFF, we obtained 16S rRNA gene sequence collections that were published and then deposited as a complete collection in GenBank (3, 10, 18, 20). Since manual alignments are not typically reproducible by others, we aligned sequences from 16S rRNA gene libraries by using ClustalW (ftp://ftp.ebi.ac.uk/pub/software/unix/clustalw/) under the default settings with a gap-opening penalty of 10.0 and a gap-extension penalty of 0.1 for pairwise and multiple alignments.
We also obtained sequences from the Ribosomal Database Project II (RDP-II) (7). RDP-II aligns sequences using a modified version of RNACAD, which implements a stochastic context-free grammar based on 16S rRNA secondary structure (6). Using a Perl script that we wrote, we selected the 14,653 accessions from the September 2003 release, which contained the conserved oligonucleotide sequences ACNCCTACGGGNGGCNGC (Escherichia coli position 338) and TGNACACCGCCCGT (E. coli position 1405). We trimmed each sequence so that these oligonucleotides marked the beginning and end of each accession. For the multiple-comparisons simulation, the Perl script randomly drew sequences from these accessions.
While there is no obvious choice for correcting evolutionary distances for multiple substitutions, we calculated all distance matrices by using the DNADIST program within the PHYLIP software package, using the Jukes-Cantor correction for multiple substitutions. Use of other correction models did not change P values beyond their 95% confidence interval when using the Jukes-Cantor correction (data not shown). FASTA files, alignments, and distance files from simulations performed in this study are available from the ∫-LIBSHUFF website. Unless otherwise stated, all LIBSHUFF analyses used version 1.1 as made available before 15 December 2003 from the LIBSHUFF website (http://www.arches.uga.edu/∼whitman/libshuff.html). A corrected form of LIBSHUFF has been made available as version 1.2.
We ran all simulations within the Linux Mandrake 9.2 operating system on a Dell Inspiron 5100 laptop with a Pentium 4 2.4-GHz processor and 500 MB of RAM.
RESULTS
Program validation.
We observed that LIBSHUFF and ∫-LIBSHUFF calculated the same test statistic using the same input distance matrix. However, the random distributions calculated by ∫-LIBSHUFF resulted in lower P values than those calculated by LIBSHUFF. After comparing the values of internal variables used to calculate the random ΔCXY distribution, we identified two typographical errors on lines 264 and 265 of LIBSHUFF. These lines are involved in calculating CXY for the randomized libraries. However, the indices used to access elements of the randomized distance matrix were reversed. When libraries X and Y were the same size, LIBSHUFF calculated CYX(D) instead of CXY(D). When the libraries were not the same size, it calculated an incorrect value for CYX. Once we exchanged the indices on lines 260 and 261, the two programs produced similar P values (Table 1). Although we were unable to obtain sequence files from all of the studies that used LIBSHUFF, reanalysis of some with ∫-LIBSHUFF resulted in lower P values. It is unclear what conditions, if any, would have resulted in higher P values.
TABLE 1.
Validation and evaluation of P values from comparisons using 16S rRNA gene libraries from the studies of Bond et al. (3), Dunbar et al. (10), and McCaig et al. (20), using various testing conditionsa
| Site (reference) | Library name (no. of sequences) | Published LIBSHUFF P valueb | Our P value, using LIBSHUFFb | Corrected LIBSHUFF P valueb |
P value, using ∫-LIBSHUFF for ΔD value ofb:
|
P value for integral form | ||
|---|---|---|---|---|---|---|---|---|
| 10−2 | 10−3 | 10−4 | ||||||
| Sequencing batch | SBR1 (97) | 0.308 | 0.300 | 0.087 | 0.076 | 0.066 | 0.065 | 0.065 |
| reactors (3) | SBR2 (92) | 0.824 | 0.951 | 0.798 | 0.808 | 0.744 | 0.747 | 0.747 |
| Arid soils (10) | C0 (59) | 0.042 | 0.043 | 0.011 | 0.011 | 0.012 | 0.012 | 0.012 |
| S0 (53) | 0.398 | 0.290 | 0.171 | 0.177 | 0.188 | 0.187 | 0.187 | |
| Scottish soil (20) | SAF (138) | 0.120 | 0.139 | 0.035 | 0.032 | 0.032 | 0.030 | 0.030 |
| SL (137) | 0.135 | 0.256 | 0.074 | 0.076 | 0.074 | 0.073 | 0.073 | |
For each pair of libraries, the first row of P values indicates when results when the first library is the homologous library, and the second row indicates results when the second library is the homologous library. The margin of error for the P value's 95% confidence interval when P values are near 0.05 for the comparison between the published P values of Singleton et al. (27) and our implementation of the uncorrected and corrected LIBSHUFF was approximately 0.014 (1,000 randomizations). For the simulations performed using ∫-LIBSHUFF, it was approximately 0.004 (10,000 randomizations).
The range of summation was between 0.00 and 0.50.
Improved accuracy of ΔCXY.
Taxonomic placement of 16S rRNA sequences is often approximated based on its distance value when compared to a sequence of known origin. Although controversial and admittedly crude (31), distance values ranging between 0.00 and 0.03 group sequences at the species level, distance values smaller than 0.05 group sequences at the genus level, and distance values smaller than 0.20 group sequences at the phylum level (14, 25). Therefore, the size of ΔD describes the level of resolution used to differentiate between these distances. Since the precise breakpoint between taxonomic divisions is unknown, the most cautious approach is to incorporate as much precision as possible by using a small ΔD value and a wide range of values for D given the available computing power.
The most widely used distance-calculating program is DNADIST, a program in the free PHYLIP software package. The distances calculated in DNADIST are precise to 0.0001 distance units, although a preferred degree of precision may be closer to 0.001, since 16S rRNA genes are 1,500 bp long. To evaluate the effects of ΔD in the approximation form of ΔCXY, we evaluated ΔD values of 0.01, 0.001, and 0.0001, using 10,000 randomizations with a summation range between distances of 0.0 and 0.5, using ∫-LIBSHUFF (Table 1). The P values showed sensitivity to the magnitude of ΔD for each of the datasets we analyzed, demonstrating that round-off errors were significant for any ΔD values greater than 0.0001.
When we used the integral form of the statistic over all possible values of D with 10,000 randomizations, we found P values identical to those observed with a ΔD value of 0.0001. For comparisons between more disparate libraries, P values obtained using the integral form and the approximation form of the statistic may be different if there are distances between sequences in libraries X and Y greater than 0.5, which is the upper bound of the summation for the approximation form of the statistic. When we executed ∫-LIBSHUFF using the approximation form of the statistic with a ΔD value of 0.01, the program ran 100 times faster than LIBSHUFF. Using the integral form of the statistic, execution times were 50 times faster than running LIBSHUFF. ∫-LIBSHUFF execution times using the integral form of the statistic were two to six times faster than using the approximation form with a ΔD value of 0.0001.
Improved precision of P values.
The actual P value for any comparison would be calculated by constructing the test distribution by considering every possible permutation of the sequences in each library. ∫-LIBSHUFF and LIBSHUFF implement a Monte Carlo method that approximates the test distribution by performing a large number of random samplings. Therefore, P values obtained from each of these programs have some error due to the randomization procedure. The standard error for this error can be approximated by the square root of [(P)(1 − P)]/(number of randomizations) (29). For a P value of 0.05, we approximate margins of error for a P value's 95% confidence interval of 0.014, 0.004, 0.001, and 0.0004 for 103, 104, 105, and 106 randomizations, respectively.
The improved execution times with ∫-LIBSHUFF make it possible to use more randomizations to obtain an acceptable degree of precision without exceeding the amount of time that LIBSHUFF would have taken to run. When the McCaig et al. (20) sequence collection (n = 275 sequences) was analyzed using the integral form of the Cramér-von Mises statistic and 10,000 randomizations, the analysis took 23 s. By comparison, the corrected version of LIBSHUFF took 103 s to execute 1,000 randomizations with a ΔD value of 0.01. The net result of using ∫-LIBSHUFF was a fivefold improvement in execution times with maximum possible ΔCXY accuracy and a margin of error for the P value's 95% confidence interval of 0.004 for P values near 0.05.
Case study: Scottish soil.
McCaig et al. (20) constructed three clone libraries from an unimproved grassland soil (SAF) and three libraries from an improved grassland soil (SL) collected in Scotland to compare the effects of fertilization and grazing on soil microbial diversity. This data set has also become the standard data set for studies investigating the efficacy of various statistical procedures (8, 14, 19, 27). Based on the diversity indices calculated by McCaig et al. (20), there was not a meaningful difference in diversity between their pooled improved and unimproved soil libraries. However, by analyzing phylogenetic trees, they found that the two libraries differed in the diversity of the α-proteobacteria populations each library contained. Later, Martin (19) found that the two libraries each exhibited a high level of diversity, but they contained different phylogenetic lineages, indicated by a parsimony-based statistical analysis. Using a corrected version of the LIBSHUFF program, we found the libraries had P values of 0.035 (SAF [X] versus SL [Y]) and 0.074 (SL [X] versus SAF [Y]; margin of error for the P value's 95% confidence interval of 0.014). However, using the integral form of the statistic with 10,000 randomizations in ∫-LIBSHUFF, we calculated P values of 0.030 and 0.073 (SL [X] versus SAF [Y], margin of error for the P value's 95% confidence interval of 0.004). After applying the Bonferroni correction (29) or the false discovery rate correction (2) to account for two pairwise comparisons, we were unable to identify a significant difference with an experimentwise error rate of 0.05.
Case study: Scottish versus Wisconsin soil.
∫-LIBSHUFF can compare more than two libraries simultaneously by using a single input file and execution. To test this capability, we compared the clone libraries from improved and unimproved grassland of McCaig et al. (20) to the clone libraries constructed by Liles et al. (18) in 1997 and 2000 from a Wisconsin soil (Table 2). Although the libraries were constructed using different “universal” bacterial primers, the Scottish soil DNA was obtained by using a freeze-thaw lysis method, and the Wisconsin soil DNA was obtained by using a bead-beating method, comparison of the four libraries still demonstrates the usefulness of ∫-LIBSHUFF. Using the integral form of the statistic in ∫-LIBSHUFF with 10,000 randomizations, we found that the P values for all of the comparisons except those between the unimproved (SAF) and improved (SL) soils were very small (all P values were <0.001 [Table 2]). This would suggest that there is a high probability that the 16S rRNA gene libraries constructed by McCaig et al. (20) and Liles et al. (18) contained different taxonomic lineages.
TABLE 2.
Comparison of 16S rRNA gene librariesa
| Source (reference) | Homologous library (X) |
P value of ΔCxy heterologous library (Y)
|
|||
|---|---|---|---|---|---|
| Scottish soil
|
Wisconsin soil
|
||||
| SAF | SL | 1997 | 2000 | ||
| Scottish soil (20) | SAF | 0.014 | <0.001 | <0.001 | |
| SL | 0.099 | <0.001 | <0.001 | ||
| Wisconsin soil (18) | 1997 | <0.001 | <0.001 | <0.001 | |
| 2000 | <0.001 | <0.001 | <0.001 | ||
Libraries were constructed from unimproved (SAF, n = 138 sequences) and improved (SL, n = 137) Scottish soils and libraries constructed using soils collected in 1997 (n = 139) and 2000 (n = 129) from a Wisconsin agricultural soil. Comparisons were made using the integral form of the Cramér-von Mises statistic as implemented in ∫-LIBSHUFF with 10,000 randomizations and an upper integration bound of infinity. The margin of error for the P value's 95% confidence interval for the P values near 0.05 was 0.004.
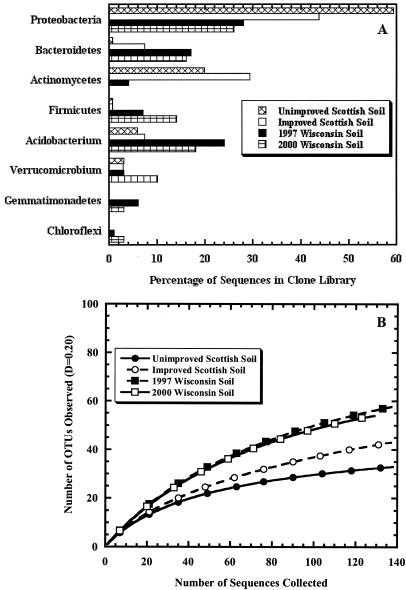
To determine whether this was a reasonable result based on taxonomic representation in the libraries, we compared the taxonomic distribution of the four libraries (Fig. 2A). There were large differences between the libraries in the relative abundance of the most common phyla. We also constructed collector's curves at a pseudo-phylum level using a distance value of 0.20 (Fig. 2B). Although the curves for the two Scottish soil clone libraries were very different from each other, the curves from the two Wisconsin soil clone libraries were similar. These two lines of evidence provide further support for the conclusions we drew from the ∫-LIBSHUFF analysis that the clone libraries constructed from Wisconsin and Scottish soils contain different taxonomic lineages. Construction of additional clone libraries is necessary to determine whether the differences between libraries are due to soil sampling, library construction, or biological differences between the soils.
FIG. 2.
Comparison of the taxonomic diversity in Wisconsin from 1997 (n = 139) and 2000 (n = 128) and improved (n = 138) and unimproved (n = 137) Scottish soil clone libraries as reported in original publications for most abundant phyla (A) and using collector's curves for a distance of 0.20 (B). OTUs, operational taxonomic units.
Case study: zebrafish development.
Rawls et al. (24) recently investigated the change in the microbial community in the gut of zebrafish (Danio rerio). They constructed 16S rRNA clone libraries from the gut community of conventionally raised zebrafish 6, 10, 20, and 30 days postfertilization (dpf) and from adult fish. They found that sequences similar to those from Aeromonas and Pseudomonas spp. were found at all time points, and those similar to sequences from Vibrio and Lactococcus spp. were commonly found throughout the zebrafish life cycle. Our goal was to determine the statistical significance of the differences they observed between each time point.
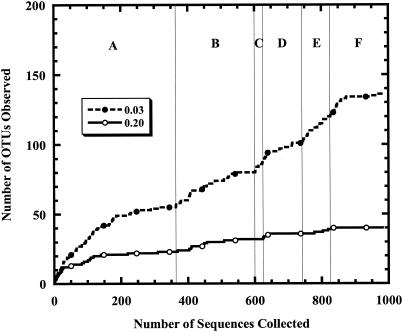
We obtained 1,179 accessions from GenBank that were deposited by the authors of the previous study. Some of these sequences were from mitochondrial genomic DNA, and others were from the 3′ end of the 16S rRNA gene. The majority of the sequences (n = 982) were from the 5′ end of the bacterial 16S rRNA gene. Using the distance-based OTU and richness analysis (Fig. 3), we found that the collector's curves constructed by using distances of 0.03 and 0.20 continued to increase as additional libraries were sequenced, suggesting that the libraries contained different phylogenetic lineages. With ∫-LIBSHUFF, we found that all possible comparisons between libraries constructed using guts from conventionally raised zebrafish at 6 (n = 362), 20 (n = 103), and 30 (n = 76) dpf and adults (n = 167) indicated significant differences (all P values were <0.001). The library constructed using guts from zebrafish that were 10 dpf (n = 35) were not significantly different from any other developmental stage (smallest P value, 0.011) when used as the homologous library and correcting for multiple comparisons. Finally, guts of 6-dpf gnotobiotic fish colonized with bacteria with water from a conventional zebrafish aquaculture facility (n = 239) were significantly different from guts obtained from the conventionally raised zebrafish at each developmental stage (all P values were <0.001) except when the 10-dpf library was used as the homologous library (P = 0.26).
FIG. 3.
Collector's curves constructed using distance-based OTU and richness for distances of 0.03 and 0.20, assuming that GenBank accession numbers represent the order in which the sequences were collected. The collector's curves are divided into six sections, representing the six libraries that Rawls et al. constructed: 6 dpf, conventionally raised (A; n = 362), 6 dpf, conventionally raised (B, n = 239), 10 dpf, conventionally raised (C; n = 35), 20 dpf, conventionally raised (D; n = 103), 30 dpf, conventionally raised (E; n = 76), and adult, conventionally raised (F; n = 167). OTUs, operational taxonomic units.
Rawls et al.'s 16S rRNA analysis (24) was part of a larger gene expression study where they compared the expression of zebrafish genes in the fish gut containing various microbial communities. Using ∫-LIBSHUFF, we have shown that although there may be some overlap in the microbial communities across developmental stages, the gut microflora changes dramatically throughout development. Rawls et al. (24) noted several differences in the composition of the clone libraries constructed from conventionally raised and conventionalized 6-dpf guts, such as the relative abundance of Vibrio and Aeromonas sp. sequences in the two libraries. However, our analysis shows that the phylogenetic lineages in the two libraries are significantly different. It is possible that differences in relative abundance in certain phylogenetic groups are responsible for the differences in the fish's gene expression; it seems more likely that the presence or absence of certain species had a considerable effect. Finally, the zebrafish gut microbial community could be a model system for assigning biological relevance to statistical differences.
Sequence alignments.
The P values for the comparison between the McCaig et al. (20) sequences in the Scottish versus Wisconsin soil case study (Table 2) were outside of the margin of error for the P value's 95% confidence interval for the precision of the P values observed in the comparison between the improved and unimproved soils from the first case study (Table 1). This difference is due to differences in sequence alignment. The alignments used in each case study were different, because the alignments used different numbers and types of sequences. When we repeated the Scottish soil case study using the Scottish soil sequences from the four-library alignment, the P values for the comparison between the improved and unimproved soils were the same as those we observed for the four-library comparison in Table 2.
To test the sensitivity of P values to alignment quality, we repeated the two-library case study, using a gap-opening penalty of 15.0 and a gap extension penalty of 5.0 for pairwise and multiple comparisons in ClustalW. The P values were 0.026 and 0.105 for the comparisons SAF (X) versus SL (Y) and SL (X) versus SAF (Y), respectively, when using the integral form of the statistic with 10,000 randomizations.
Multiple comparisons.
The application of the Cramér-von Mises statistic to a pair of sequence libraries requires two comparisons to determine whether libraries are a subset or independent of each other. The number of possible comparisons between any number of libraries or treatments, k, is k(k − 1). For example, in the Scottish versus Wisconsin soil case study there were 4 treatments and 12 possible pairwise comparisons. This type of analysis is analogous to performing 12 t tests instead of a single analysis of variance. Making these 12 comparisons increased the probability of detecting a statistically significant difference by chance. The probability of finding a difference between any two treatments based on chance when there is no actual difference is the pairwise error rate, α. A conventional choice for α is 0.05. If there were multiple independent comparisons and there was no actual difference between the treatments, then the probability of having found one small P value less than α, by chance, can be determined by the formula 1 − (1 − α)k(k − 1) (29). This probability is the experimentwise error rate. A study with two treatments that tested each comparison at the 0.05 level would have an experimentwise error rate of 0.098, and a study with four treatments would have an experimentwise error rate of 0.460, if the P values for each comparison were independent. This means that the studies would have a 9.8 and 46.0% chance, respectively, of finding a P value between the two libraries that was below 0.05 based on chance alone. A study is highly likely to find a P value below 0.05, by chance, when there are at least 10 treatments (experimentwise error = 0.99).
To test the independence of P values and the effect of multiple comparisons on the experimentwise error rate, we performed several simulations using randomly generated 16S rRNA gene libraries. We constructed simulated studies with various numbers of libraries and sizes of libraries by randomly selecting accessions from the RDP-II as described in the Materials and Methods section above. Because our Perl program randomly placed accessions into each library, we assumed that the libraries were not statistically or biologically different. The analysis of the simulated studies used the integral form of the statistic with 10,000 randomizations. The proportion of randomizations where the minimum ΔCXY value for any comparison had a P value below 0.05 represented the expected experimentwise error rate when testing at the pairwise error rate of 0.05, and there were no actual differences between the libraries. When considering two treatments, the experimentwise error rate was 0.098; for three treatments, it was 0.265; and for 10 treatments, it was 0.999. From these simulations, the experimentwise error rates we compute in the test with the random sample data agree closely with predictions made assuming that all tests were independent. Although the experimentwise error rate increases with the number of treatments, there are several options for correcting the error rate to reach a statistically based conclusion (see Discussion).
DISCUSSION
∫-LIBSHUFF is an improved implementation of the Cramér-von Mises statistic for making comparisons between 16S rRNA gene libraries. ∫-LIBSHUFF provides more accurate and precise P values, shorter execution times, and improved flexibility and ease of use compared to LIBSHUFF. Moreover, ∫-LIBSHUFF can account for the experimentwise error rate.
Each of the improvements incorporated into ∫-LIBSHUFF allowed us to show easily that there is a high probability that biological differences are responsible for the differences observed between libraries constructed from Scottish and Wisconsin soil libraries or among those communities in the guts of zebrafish at different developmental stages. A similar analysis using LIBSHUFF for the zebrafish analysis would have required constructing 15 separate distance matrix files, converting each of those into a form that was compatible with LIBSHUFF, and then executing the program 15 times, obtaining P values that were not as accurate or precise as those calculated with ∫-LIBSHUFF (Table 2). Instead, we made one alignment and distance matrix, which we used as the input file for ∫-LIBSHUFF, and had a result in less than 5 min. Without considering the extra time required to construct additional alignments, distance matrices, and input files, it would have taken longer to execute LIBSHUFF to make two sets of comparisons than it took us to make 15.
∫-LIBSHUFF calculates accurate and precise P values. The programming flaw in LIBSHUFF leads to miscalculation of P values, and the artificially high P values may have resulted in abandonment of a hypothesis that was, in fact, supported by the data. The first improvement we incorporated was to allow the increment size, ΔD, to be altered when using the approximation form of the statistic to improve the accuracy of the statistic. Next, the integral form of the statistic can be calculated, which is a more elegant implementation of the Cramér-von Mises statistic. Because of the accelerated execution times, 100,000 randomizations can be performed in the same time it would have taken LIBSHUFF to run 1,000 using the same increment size. The net effect of the increased number of randomizations is a P value that is 10 times more precise than that generated with LIBSHUFF. Each of these improvements provides greater confidence that the P values describing the difference between two libraries are accurate and precise.
The increased execution speeds of ∫-LIBSHUFF result from using the integral form of the statistic and writing the program in the C++ programming language. Free versions of Perl are available for any operating system, thereby making Perl programs highly portable, but Perl is very slow in performing numerical calculations for various reasons. Since not all potential users use a single operating system, we will make ∫-LIBSHUFF available for use on as many operating systems as possible. Executable versions of the program and instructions are available from the ∫-LIBSHUFF website http://www.plantpath.wisc.edu/fac/joh/S-LIBSHFF.html).
∫-LIBSHUFF has the capacity to make all possible pairwise comparisons between any number of sequence libraries. In addition, the input file is a distance matrix that is produced by the freely available DNADIST program in the PHYLIP package. The most difficult step in performing the analysis using LIBSHUFF was the process of formatting the input file to be compatible with the program. We have eliminated the formatting steps, making the analysis process simple.
The final significant improvement incorporated in ∫-LIBSHUFF is the calculation of the experimentwise error rates. None of the studies that used LIBSHUFF have accounted for the increased experimentwise error rate (1, 4, 5, 11, 13, 15, 21, 23, 27, 28, 30). Our simulations demonstrate the substantial effect of multiple comparisons on the experimentwise error rates. Several methods are available to correct the experimentwise error for multiple comparisons, including the Bonferroni correction and the false discovery rate-controlling procedure (2, 29). The purpose of correcting for the experimentwise error rate is to account for the increased probability of detecting small P values due to chance when making multiple comparisons.
It is possible that biologically meaningful differences exist where they were not statistically significant. As in the Scottish soil case study, the inability to detect differences between libraries may be due to a lack of statistical power, as discussed in the original paper introducing LIBSHUFF (27). In the zebrafish analysis, there were only 35 sequences in the 10-dpf 16S rRNA library, and it was not possible to identify any statistically significant differences using this as the homologous library. We suspect that if more sequences were collected, a statistically significant difference might have been detected. The biological significance of a difference cannot be anticipated by the numerical size or statistical significance of the difference.
The resources available to obtain increased statistical power must be balanced against the resources available for long, high-quality sequences. While DNADIST provides precision to 0.0001 (i.e., one base change every 10 kb), a more realistic degree of precision for full-length sequences would be 0.0006 (1 per 1.5 kb), and 0.0012 for half-length sequences (1 per 750 bp). Any ambiguous nucleotides will decrease the degree of precision. However, ∫-LIBSHUFF provides the flexibility to calculate P values based on the data contained within the distance matrix without making further assumptions. Since at least five sequencing reads are necessary to obtain double coverage of an entire 16S rRNA gene and only two are necessary for double coverage of 700 bp, it is preferable to obtain more partial-length sequences rather than fewer, full-length sequences. This approach will provide the greatest amount of statistical power for the resources available instead of additional precision below the level of accuracy of the Monte Carlo procedure itself.
There is a sentiment and suspicion expressed in the microbial ecology literature that soil microbial communities are too diverse to quantify and compare (14, 17). One concern that has been expressed is that if too few sequences are sampled from a clone library, it will be too easy to detect differences between libraries that represent random differences, not sample differences. However, in such a scenario we would expect the coverage within a library, CX or CY, to be low. If the coverage within both libraries is low, then the coverage between both libraries, CXY and CYX, will also be low. Since all four coverage values would be low, ∫-LIBSHUFF would find the P value for either comparison to be high because there is insufficient information to make a comparison. Finally, all statistical analyses are based on the premise that it is impossible to sample the entire community to reach a conclusion. In a statistical analysis, the power to test a hypothesis does not depend on the size of the community but on the size of the sample.
While the focus of this study has been on the comparison of 16S rRNA gene libraries, ∫-LIBSHUFF should be able to make comparisons between other types of gene libraries. There are many exciting challenges that require the application of computational methods to environmental microbiology: defining a biologically relevant difference based on 16S rRNA gene sequences (31), determining the minimum number of sequences needed to detect differences (14), and making comparisons between metagenomic libraries (26) are some of the knotty quantitative problems remaining to be solved.
Acknowledgments
We thank W. B. Whitman and D. R. Singleton for their thoughtful comments on the manuscript.
A USDA postdoctoral fellowship in soil biology to P.D.S., an NIH grant to B.R.L., the NSF Microbial Observatory program (MCB-0132085), the Howard Hughes Medical Institute, and the University of Wisconsin—Madison College of Agricultural and Life Sciences provided funding for this project.
REFERENCES
- 1.Alain, K., M. Olagnon, D. Desbruyeres, A. Page, G. Barbier, S. K. Juniper, J. Querellou, and M. A. Cambon-Bonavita. 2002. Phylogenetic characterization of the bacterial assemblage associated with mucous secretions of the hydrothermal vent polychaete Paralvinella palmiformis. FEMS Microbiol. Ecol. 42:463-476. [DOI] [PubMed] [Google Scholar]
- 2.Benjamini, Y., and Y. Hochberg. 1995. Controlling the false discovery rate—a practical and powerful approach to multiple testing. J. R. Stat. Soc. B Methodol. 57:289-300. [Google Scholar]
- 3.Bond, P. L., P. Hugenholtz, J. Keller, and L. L. Blackall. 1995. Bacterial community structures of phosphate-removing and non-phosphate-removing activated sludges from sequencing batch reactors. Appl. Environ. Microbiol. 61:1910-1916. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 4.Bowman, J. P., and R. D. McCuaig. 2003. Biodiversity, community structural shifts, and biogeography of prokaryotes within Antarctic continental shelf sediment. Appl. Environ. Microbiol. 69:2463-2483. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 5.Brofft, J. E., J. V. McArthur, and L. J. Shimkets. 2002. Recovery of novel bacterial diversity from a forested wetland impacted by reject coal. Environ. Microbiol. 4:764-769. [DOI] [PubMed] [Google Scholar]
- 6.Brown, M. P. S. 2000. Small subunit ribosomal RNA modeling using stochastic context-free grammar, p. 57-66. In P. Bourne, M. Gribskov, R. Altman, N. Jensen, D. Hope, T. Lengauer, J. Mitchell, E. Scheeff, C. Smith, S. Strande, and H. Weissig (ed.), Proceedings of the Eighth International Conference on Intelligent Systems for Molecular Biology. AAAI Press, Menlo Park, Calif. [PubMed]
- 7.Cole, J. R., B. Chai, T. L. Marsh, R. J. Farris, Q. Wang, S. A. Kulam, S. Chandra, D. M. McGarrell, T. M. Schmidt, G. M. Garrity, and J. M. Tiedje. 2003. The Ribosomal Database Project (RDP-II): previewing a new autoaligner that allows regular updates and the new prokaryotic taxonomy. Nucleic Acids Res. 31:442-443. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 8.Curtis, T. P., W. T. Sloan, and J. W. Scannell. 2002. Estimating prokaryotic diversity and its limits. Proc. Natl. Acad. Sci. USA 99:10494-10499. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 9.Dunbar, J., S. M. Barns, L. O. Ticknor, and C. R. Kuske. 2002. Empirical and theoretical bacterial diversity in four Arizona soils. Appl. Environ. Microbiol. 68:3035-3045. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 10.Dunbar, J., S. Takala, S. M. Barns, J. A. Davis, and C. R. Kuske. 1999. Levels of bacterial community diversity in four arid soils compared by cultivation and 16S rRNA gene cloning. Appl. Environ. Microbiol. 65:1662-1669. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 11.Furlong, M. A., D. R. Singleton, D. C. Coleman, and W. B. Whitman. 2002. Molecular and culture-based analyses of prokaryotic communities from an agricultural soil and the burrows and casts of the earthworm Lumbricus rubellus. Appl. Environ. Microbiol. 68:1265-1279. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 12.Good, I. J. 1953. The population frequencies of species and the estimation of population parameters. Biometrika 40:237-264. [Google Scholar]
- 13.Hongoh, Y., M. Ohkuma, and T. Kudo. 2003. Molecular analysis of bacterial microbiota in the gut of the termite Reticulitermes speratus (Isoptera; Rhinotermitidae). FEMS Microbiol. Ecol. 44:231-242. [DOI] [PubMed] [Google Scholar]
- 14.Hughes, J. B., J. J. Hellmann, T. H. Ricketts, and B. J. M. Bohannan. 2001. Counting the uncountable: statistical approaches to estimating microbial diversity. Appl. Environ. Microbiol. 67:4399-4406. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 15.Humayoun, S. B., N. Bano, and J. T. Hollibaugh. 2003. Depth distribution of microbial diversity in Mono Lake, a meromictic soda lake in California. Appl. Environ. Microbiol. 69:1030-1042. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 16.Jukes, T. H., and C. R. Cantor. 1969. Evolution of protein molecules, p. 21-132. In H. N. Munro (ed.), Mammalian protein metabolism. Academic Press, New York, N.Y.
- 17.Kent, A. D., D. J. Smith, B. J. Benson, and E. W. Triplett. 2003. Web-based phylogenetic assignment tool for analysis of terminal restriction fragment length polymorphism profiles of microbial communities. Appl. Environ. Microbiol. 69:6768-6776. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 18.Liles, M. R., B. F. Manske, S. B. Bintrim, J. Handelsman, and R. M. Goodman. 2003. A census of rRNA genes and linked genomic sequences within a soil metagenomic library. Appl. Environ. Microbiol. 69:2684-2691. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 19.Martin, A. P. 2002. Phylogenetic approaches for describing and comparing the diversity of microbial communities. Appl. Environ. Microbiol. 68:3673-3682. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 20.McCaig, A. E., L. A. Glover, and J. I. Prosser. 1999. Molecular analysis of bacterial community structure and diversity in unimproved and improved upland grass pastures. Appl. Environ. Microbiol. 65:1721-1730. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 21.Pantos, O., R. P. Cooney, M. D. A. Le Tissier, M. R. Barer, A. G. O'Donnell, and J. C. Bythell. 2003. The bacterial ecology of a plague-like disease affecting the Caribbean coral Montastrea annularis. Environ. Microbiol. 5:370-382. [DOI] [PubMed] [Google Scholar]
- 22.Pettitt, A. N. 1982. Cramér-von Mises statistic, p. 220-221. In S. Kotz, N. L. Johnson, and C. B. Read (ed.), Encyclopedia of statistical sciences. Wiley, New York, N.Y.
- 23.Powell, S. M., J. P. Bowman, I. Snape, and J. S. Stark. 2003. Microbial community variation in pristine and polluted nearshore Antarctic sediments. FEMS Microbiol. Ecol. 45:135-145. [DOI] [PubMed] [Google Scholar]
- 24.Rawls, J. F., B. S. Samuel, and J. I. Gordon. 2004. Gnotobiotic zebrafish reveal evolutionarily conserved responses to the gut microbiota. Proc. Natl. Acad. Sci. USA 101:4596-4601. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 25.Sait, M., P. Hugenholtz, and P. H. Janssen. 2002. Cultivation of globally distributed soil bacteria from phylogenetic lineages previously only detected in cultivation-independent surveys. Environ. Microbiol. 4:654-666. [DOI] [PubMed] [Google Scholar]
- 26.Sebat, J. L., F. S. Colwell, and R. L. Crawford. 2003. Metagenomic profiling: microarray analysis of an environmental genomic library. Appl. Environ. Microbiol. 69:4927-4934. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 27.Singleton, D. R., M. A. Furlong, S. L. Rathbun, and W. B. Whitman. 2001. Quantitative comparisons of 16S rRNA gene sequence libraries from environmental samples. Appl. Environ. Microbiol. 67:4374-4376. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 28.Singleton, D. R., P. F. Hendrix, D. C. Coleman, and W. B. Whitman. 2003. Identification of uncultured bacteria tightly associated with the intestine of the earthworm Lumbricus rubellus (Lumbricidae; Oligochaeta). Soil Biol. Biochem. 35:1547-1555. [Google Scholar]
- 29.Sokal, R. R., and F. J. Rohlf. 1995. Biometry: the principles and practice of statistics in biological research, 3rd ed. Freeman, New York, N.Y.
- 30.Stach, J. E. M., L. A. Maldonado, D. G. Masson, A. C. Ward, M. Goodfellow, and A. T. Bull. 2003. Statistical approaches for estimating actinobacterial diversity in marine sediments. Appl. Environ. Microbiol. 69:6189-6200. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 31.Ward, D. M. 1998. A natural species concept for prokaryotes. Curr. Opin. Microbiol. 1:271-277. [DOI] [PubMed] [Google Scholar]