Comparison of Adaptive Treatment Strategies Based on Longitudinal Outcomes in Sequential Multiple Assignment Randomized Trials

Abstract

In sequential multiple assignment randomized trials, longitudinal outcomes may be the most important outcomes of interest since this type of trials are usually conducted in areas of chronic diseases or conditions. We propose to use a weighted generalized estimating equation (GEE) approach to analyzing data from such type of trials for comparing two adaptive treatment strategies based on generalized linear models. Although the randomization probabilities are known, we consider estimated weights in which the randomization probabilities are replaced by their empirical estimates, and prove that the resulting weighted GEE estimator is more efficient than the estimators with true weights. The variance of the weighted GEE estimator is estimated by an empirical sandwich estimator. The time variable in the model can be linear, piece-wise linear, or more complicated forms. This provides more flexibility which is important because in the adaptive treatment setting the treatment changes over time and hence a single linear trend over the whole period of study may not be practical. Simulation results show that the weighted GEE estimators of regression coefficients are consistent regardless of the specification of the correlation structure of the longitudinal outcomes. The weighted GEE method is then applied in analyzing data from the Clinical Antipsychotic Trials of Intervention Effectiveness (CATIE).

1 Introduction

The sequential multiple assignment randomized trial (SMART) [1-2] has been developed to obtain data to make inference about adaptive treatment strategies. An adaptive treatment strategy [2-4], also called a treatment strategy or simply a strategy, is a sequence of decision rules that specifies the treatment a patient receives at each stage based on patient baseline characteristics and performance on previous treatments. It arises often in treating chronic diseases or conditions since in these situations the treatment is an ongoing process involving multiple decisions over time. These decisions may include, but are not restricted to, change of treatment type or dosage, according to patient response to previous treatments in terms of efficacy, tolerance, burden and so on. For example, in treating attention deficit hyperactivity disorder (ADHD) in children, one possible adaptive treatment strategy is to start with low dose medication, and if the child responds well then stay on low dose medication, but if there is inadequate response then the treatment is switched to low dose behavioral therapy. In a SMART, subjects may be randomized multiple times during the trial. One example of SMART is a trial conducted to assess different treatment options for ADHD [5]. In this trial, children with ADHD were initially randomly assigned to low dose behavioral therapy or medication. The response was monitored after the initiation of the treatments. If at some time during the study, which lasted 36 weeks, the predefined nonresponse criterion was met, then the child was rerandomized to either an intensification of the current treatment or the combination of the two types of treatment. In this trial, 4 embedded adaptive treatment strategies can be studied, one of which is the example adaptive treatment strategy described above. There are at most two decision points in this trial and thus two ramdomizations. A graphical illustration of the randomization scheme is provided, for example, in Li and Murphy [6]. Trials with more than two randomizations, an example of which is the STAR*D trial for treatment of depression [7], exist but are uncommon. In this article, we focus on trials with at most two randomizations, which are also called two-stage randomized trials. Generalization to trials with more than two stages is straightforward in principle.

Almost all of the previous work on the design and analysis of two-stage randomized trials has been focused on cases in which the primary outcome is either a single continuous outcome or a survival type outcome. For example, the work on analysis include [2] and [8-15]. The work focusing on the design of such trials include [2], [6], and [16-18]. Orellana et al. [19] proposed an estimating equation that can be used to estimate the mean outcomes under different DTRs using observational data for the single outcome case. Recently, Ertefaie et. al. [20] adopted the methodology in [19] to estimate the best embedded treatment strategy using SMART data. In [21], Moodie et al. focus on inference about adaptive treatment strategies with discrete outcomes but under the Q-learning setting. Earlier work before the name SMART appeared exists, examples of which include [22-23]. However, in the area of chronic diseases or conditions in which the focus is mainly on symptoms rather than survival, longitudinal outcomes arise very often and may be more important than survival outcomes or single continuous outcomes. For example, in the ADHD trial mentioned above, a behavioral score is measured on each child weekly for 36 weeks after the initial treatment. It is an indicator of the severity of the disorder and is the basis on which the efficacy of a treatment is assessed. Another example is the Clinical Antipsychotic Trials in Intervention Effectiveness (CATIE) [24], which also involved two randomizations. In this trial, a first-generation antiphychotic, perhenazine, was compared to several atypical antipsychotics. The patients were initially randomized to perhenazine or one of four atypical antipsychotics. The initial drug may be switched due to either low efficacy or bad tolerance. Those who decided to switch treatment were further randomized to one of several antipsychotics different from the initial drug. The positive and negative syndrome scale (PANSS), a primary assessment instrument for psychopathology, was measured at month 0 (baseline), 1, and 3, and then every three months afterwards. Change of the PANSS scores signifies the change in severity of the symptoms. The drug is deemed efficacious if the PANSS scores drop significantly after taking the drug; otherwise there is no reason to believe the drug is efficacious. Hence, the change in PANSS scores after taking the drug is a direct way of measuring the efficacy of the drug. Lieberman et al. [24] used the time to all cause discontinuation as the outcome when they compared the drugs. However, longer time to discontinuation may only be due to better tolerance which does not necessarily imply higher efficacy. If the focus is more on efficacy, the trend of change in longitudinal PANSS scores would be more relevant. Analysis of longitudinal data in SMART trials has not been well studied in the literature, except that authors in [25-26] proposed methods for estimating mean responses of treatment strategies based on longitudinal data in observational studies.

In this paper we focus on the analysis of two-stage randomized trials for comparing two adaptive treatment strategies when the outcome is longitudinal. We propose to use a weighted generalized estimating equation (GEE) approach for the inference of unknown parameters in generalized linear models for the counterfactual outcomes under the two strategies. The weights are used to take into account the fact that different subjects may be consistent with a strategy with different probabilities and the same subject may be consistent with more than one strategy (see, e.g., [6] and [8]). As the standard GEE, the weighted GEE can handle both continuous and discrete longitudinal data. Also, the weighted GEE yields consistent estimators of unknown parameters regardless of whether the correlation structure among the longitudinal outcomes is correctly specified or not. The asymptotic variance of the weighted GEE estimator is consistently estimated by an empirical sandwich estimator. Although the randomization probabilities are known in SMART trials, we consider estimated weights in which the randomization probabilities are estimated by observed proportions, resulting in more efficient estimators. The inverse probability weighting method has been used in most of the literature in SMART trials, while estimation with estimated weights has never been considered before. Moreover, in our model, the time variable can appear as linear, piece-wise linear, or more complicated forms such as polynomial. This provides more flexibility which is important because in the adaptive treatment setting the treatment changes over time and hence the rate of change of mean outcomes may also change over time. Consequently a linear model over the whole period of study may not be adequate to describe the trend of change over time. This work is novel in several aspects. At first, it is the first to consider the generalized estimating equation approach for analyzing longitudinal data in SMART studies, an area where existing work is very scarce. Second, in order to adapt the methodology to our special setting, we propose both linear models and piece-wise linear models for the longitudinal trajectories, and propose different methods for comparing treatment strategies, e.g., comparing rates of change and more importantly, the areas under curve for the two strategies compared.

The following content is arranged as follows. Section 2 describes the weighted GEE method for comparing two treatment strategies using generalized linear models. Section 3 presents results of a simulation study and in Section 4 we apply the proposed method in analyzing data from the CATIE. We conclude with a discussion in Section 5. A sketch of the proof of asymptotic results is put in the Appendix.

2 The weighted generalized estimating equation

2.1 The general method

In the typical two-stage randomized trials we consider, subjects are initially randomized to one of two treatments, denoted by A₁ = 1 and A₁ = 2. After the initial treatment, some subjects are rerandomized to one of two second-stage treatments and some subjects are not rerandomized. Suppose the subjects who are rerandomized are randomly assigned one of two second-stage treatments, denoted by A₂ = 1 and A₂ = 2. Denote p₁ = P(A₁ = 1), p₂₁ = P(A₂ = 1|A₁ = 1) and p₂₂ = P (A₂ = 1|A₁ = 2). Here the rerandomization criterion can be different in different situations. For example, in the ADHD trial mentioned above, nonresponders to the initial treatments are rerandomized to either intensification of the initial treatment or the addition of another type of treatment. In some cases, responders to the initial treatment are further randomized to one of several maintenance treatments, which is common in cancer trials. Moreover, those who are not rerandomized may stay on the initial treatment or are assigned a different treatment. For example, in some cancer trials, nonresponders to the induction therapy are not rerandomized and are all put on salvage treatment. For definiteness, we assume that only nonresponders to the initial treatment are rerandomized, and denote R to be the rerandomization indicator, i.e., R = 1 if the subject is rerandomized and R = 0 otherwise. In this type of trials, there are four embedded adaptive treatment strategies, denoted by strategy “11”, “12”, “21” and “22”, respectively. Here strategy “jk” means a subject starts with A₁ = j, and if the subject does not respond well then he or she switches to A₂ = k as the second-stage treatment, for j, k = 1, 2.

The goal of two-stage randomized trials is to assess different treatment strategies. Specifically, we assume the purpose is to compare two strategies “st” and “s′t′”, where s, t, s′, t′ can take values 1 or 2. Suppose we observe i.i.d. data for n subjects, and the longitudinal outcome of the ith subject is observed at M_i time points. Denote y_i = (y_i1, · · · , y_iMi)^T as the vector of longitudinal outcomes for subject i, for 1 ≤ i ≤ n. As usual, we adopt the counterfactual outcome framework [27]. Denote $y_i^{st}={(y_{i1}^{st},\cdots ,y_{i{M}_i}^{st})}^T$ as the vector of counterfactual longitudinal outcomes for subject i if the subject, possibly contrary to the fact, followed strategy “st”, for 1 ≤ i ≤ n and s, t = 1, 2. We make the consistency assumption [3] that, if subject i actually followed strategy “st”, then $y_i=y_i^{st}$. Denote ${\mu }_{im}^{st}=E(y_{im}^{st}\mid d_{im}^{st})$. Denote x_i to be a vector of covariates and t_im to be the mth measurement time, both for subject i, for 1 ≤ m ≤ M_i and 1 ≤ i ≤ n. Let $d_{im}^{st}$ and $d_{im}^{s^{\prime }{t}^{\prime }}$ be d-dimensional design vectors which may include x_i and t_im as components. In order to compare the two strategies, we assume a generalized linear model

$$h\left({\mu }_{im}^{st}\right)={\left(d_{im}^{st}\right)}^T\beta ,\text{and}h\left({\mu }_{im}^{s^{\prime }{t}^{\prime }}\right)={\left(d_{im}^{s^{\prime }{t}^{\prime }}\right)}^T\beta$$ (1)

for 1 ≤ m ≤ M_i, where h(·) is a known link function. Here different choices for $d_{im}^{st}$ and $d_{im}^{s^{\prime }{t}^{\prime }}$ correspond to different models and different tests for the equivalence of the two strategies. Specific choices are discussed below.

Use of weights to adjust for the unique design of two-stage randomized trials is standard (see, e.g., [6], [8] and [10]). As in [6], we define weight

$$W_{jk}=\frac{I(A_1=j)}{p_1^{2-j}{(1-p_1)}^{j-1}}\left\{1-R+\frac{I(A_2=k)}{p_{2j}^{2-k}{(1-p_{2j})}^{k-1}}R\right\}$$

for strategy “jk”, where j, k = 1, 2. These weights are essentially the inverse of the proportions of subjects being consistent with the strategies. Analogous to the usual GEE [29], we use the following estimating equation to estimate the parameter β in model (1) based on the observed data:

$$\sum _{(j,k)\in \{(s,t),(s^{\prime },t^{\prime })\}}\sum _{i=1}^n{W}_{jk,i}\frac{\partial {\left({\mu }_i^{jk}\right)}^T}{\partial \beta }{\left(V_i^{jk}\left[{\widehat{\alpha }}_{jk}\{\beta ,\widehat{\varphi }\left(\beta \right)\}\right]\right)}^{-1}(y_i-{\mu }_i^{jk})=0,$$ (2)

where ${\mu }_i^{jk}={({\mu }_{i1}^{jk},\cdots ,{\mu }_{i{K}_i}^{jk})}^T$. In the above estimating equation, the “working” covariance matrix $V_i^{jk}\left({\alpha }_{jk}\right)$ is defined as

$$V_i^{jk}\left({\alpha }_{jk}\right)={\left(A_i^{jk}\right)}^{1∕2}{R}_{jk}\left({\alpha }_{jk}\right){\left(A_i^{jk}\right)}^{1∕2}∕\varphi$$

where R_jk(α_jk) is a “working” correlation matrix for $W_{jk,i}(y_i-{\mu }_i^{jk})$, and the lth diagonal element of the diagonal matrix $A_i^{jk}∕\varphi$ equals the variance of $W_{jk,i}(y_{il}^{jk}-{\mu }_{il}^{jk})$ which is a function of ${\mu }_{il}^{jk}$ and ϕ. If R_jk(α_jk) is the true correlation matrix for $W_{jk,i}(y_i-{\mu }_i^{jk})$, then $V_i^{jk}\left({\alpha }_{jk}\right)=\mathrm{var}\left\{W_{jk,i}(y_i-{\mu }_i^{jk})\right\}$. In the above estimating equation, the parameter α_jk in the matrix $V_i^{jk}\left({\alpha }_{jk}\right)$ is estimated first with ${\widehat{\alpha }}_{jk}\{\beta ,\widehat{\varphi }\left(\beta \right)\}$ for fixed β, where $\widehat{\varphi }\left(\beta \right)$ is an estimator for ϕ for fixed β. As in the standard GEE, different “working” correlation structures can be used. In more general situations, the consistency of the resulting GEE estimator depends on the specification of the correlation matrix (see, e.g., [28] and references cited therein). However, in our case it is true that the above estimator for β does not depend on the specification of the correlation matrix, and the estimator is the most efficient when the correlation structure is correctly specified. The equation given above is in its most general form. In many cases, it may be reasonable to assume that $V_i^{jk}\left({\alpha }_{jk}\right)=V_i^{j^{\prime }{k}^{\prime }}\left({\alpha }_{j^{\prime }{k}^{\prime }}\right)=V_i\left(\alpha \right)$. For computation, the iterative algorithm of [29] which iterates between β and the nuisance parameters can be used to find the solution to (2). Finally, it is worth mentioning that in the above estimating equation, the two treatment strategies “st” and “s′t′” can be any two strategies embedded in the trial, including strategies with different initial treatments such as “11” and “22” and strategies with the same initial treatment such as “11” and “12”.

Although the randomization probabilities are known, using estimated weights in which p₁, p₂₁ and p₂₂ are replaced by their estimates, can improve the efficiency of the weighted GEE estimator, if the estimator for p = (p₁, p₂₁, p₂₂)^T is efficient (see, e.g., [30]). Let p̂₁ be the proportion of subjects randomized to A₁ = 1 and let p̂_2j be the proportion of subjects rerandomized to A₂ = 1 among all subjects who receive A₁ = j and who are rerandomized, for j = 1, 2. Denote p̂ = (p̂₁, p̂₂₁, p̂₂₂)^T. Replace p in the definition of W_st by p̂, and denote the resulting weight as W_st(p̂), for s, t = 1, 2. The weighted GEE with estimated weights is

$$\sum _{(j,k)\in \{(s,t),(s^{\prime },t^{\prime })\}}\sum _{i=1}^n{W}_{jk,i}\left(\widehat{p}\right)\frac{\partial {\left({\mu }_i^{jk}\right)}^T}{\partial \beta }{\left(V_i^{jk}\left[{\widehat{\alpha }}_{jk}\{\beta ,\widehat{\varphi }\left(\beta \right)\}\right]\right)}^{-1}(y_i-{\mu }_i^{jk})=0.$$ (3)

Denote the solutions to (2) and (3) as $(\widehat{\beta },{\widehat{\alpha }}_1,{\widehat{\alpha }}_2)$ and $({\widehat{\beta }}^{\ast },{\widehat{\alpha }}_1^{\ast },{\widehat{\alpha }}_2^{\ast })$, respectively. Let ${\epsilon }_i^{st}=y_i-{\mu }_i^{st}$. Let ${\stackrel{.}{W}}_{st,i}\left(p\right)=\partial W_{st,i}\left(p\right)∕\partial p$. In addition, denote p_rj = P (R = 1|A₁ = j), which is the probability of being rerandomized given that the initial treatment is A₁ = j, for j = 1, 2. The following theorem states the asymptotic properties of the estimators $\widehat{\beta }$ and ${\widehat{\beta }}^{\ast }$ and shows that the latter is more efficient. The necessary regularity conditions are stated in the Appendix.

Proposition 1

Under some regularity conditions, we have

$$\sqrt{n}(\widehat{\beta }-\beta ){\to }_{d}N(0,U^{-1}\Sigma U^{-1}),$$

and

$$\sqrt{n}({\widehat{\beta }}^{\ast }-\beta ){\to }_{d}N(0,U^{-1}\Sigma U^{-1}-U^{-1}BP{B}^T{U}^{-1}),$$

as n → ∞, where

$$U=E\sum _{(j,k)\in \{(s,t),(s^{\prime },t^{\prime })\}}\frac{\partial {\mu }_i^{jk}}{\partial \beta }{\left\{V_i^{jk}\left({\alpha }_{jk}\right)\right\}}^{-1}\frac{\partial {\left({\mu }_i^{jk}\right)}^T}{\partial \beta },$$

$$\Sigma =\mathrm{cov}\left[\sum _{(j,k)\in \{(s,t),(s^{\prime },t^{\prime })\}}{W}_{jk,i}\frac{\partial {\left({\mu }_i^{jk}\right)}^T}{\partial \beta }{\left\{V_i^{jk}\left({\alpha }_{jk}\right)\right\}}^{-1}{\epsilon }_i^{jk}\right].$$

$$B=E\sum _{(j,k)\in \{(s,t),(s^{\prime },t^{\prime })\}}\frac{\partial {\mu }_i^{jk}}{\partial \beta }{\left\{V_i^{jk}\left({\alpha }_{jk}\right)\right\}}^{-1}{\epsilon }_i^{jk}{\stackrel{.}{W}}_{jk,i}^T\left(p\right),$$

and P = diag(p₁(1 – p₁), p₂₁ (1 – p₂₁)/p₁p_r1, p₂₂(1 – p₂₂)/(1 – p₁)p_r2).

Denote ${\widehat{D}}_i^{jk}={\partial {\mu }_i^{jk}∕\partial \beta \mid }_{\beta =\widehat{\beta }}$, ${\widehat{D}}_i^{\ast jk}={\partial {\mu }_i^{jk}∕\partial \beta \mid }_{\beta ={\widehat{\beta }}^{\ast }}$, ${\widehat{\epsilon }}_i^{jk}=y_i-{\widehat{\mu }}_i^{jk}$, and ${\widehat{\epsilon }}_i^{\ast jk}=y_i-{\widehat{\mu }}_i^{\ast jk}$, where ${\widehat{\mu }}_i^{jk}$ and ${\widehat{\mu }}_i^{\ast jk}$ are calculated by model (1) with the unknown parameters replaced by $(\widehat{\beta },{\widehat{\alpha }}_1,{\widehat{\alpha }}_2)$ and $({\widehat{\beta }}^{\ast },{\widehat{\alpha }}_1^{\ast },{\widehat{\alpha }}_2^{\ast })$, respectively. Denote ${\widehat{V}}_i^{jk}$ and ${\widehat{V}}_i^{\ast jk}$ to be $V_i\left[{\widehat{\alpha }}_{jk}\{\beta ,\widehat{\varphi }\left(\beta \right)\}\right]$ with β replaced by $\widehat{\beta }$ and ${\widehat{\beta }}^{\ast }$, respectively. The asymptotic covariance matrix for $\widehat{\beta }$ can be consistently estimated by the empirical sandwich estimator ${\widehat{U}}_n^{-1}{\widehat{\Sigma }}_n{\widehat{U}}_n^{-1}$, where

$${\widehat{U}}_n=\frac{1}{n}\sum _{i=1}^n\sum _{(j,k)\in \{(s,t),(s^{\prime },t^{\prime })\}}{W}_{jk,i}{\left({\widehat{D}}_i^{jk}\right)}^T{\left({\widehat{V}}_i^{jk}\right)}^{-1}{\widehat{D}}_i^{jk}$$

and

$${\widehat{\Sigma }}_n=\frac{1}{n}\sum _{i=1}^n{\left[\sum _{(j,k)\in \{(s,t),(s^{\prime },t^{\prime })\}}{W}_{jk,i}\frac{\partial {\left({\mu }_i^{jk}\right)}^T}{\partial \beta }{\left\{V_i^{jk}\left({\alpha }_{jk}\right)\right\}}^{-1}{\epsilon }_i^{jk}\right]}^{\otimes 2},$$

where $A^{\otimes 2}=A^{T}A$ for a matrix A. To estimate the asymptotic covariance matrix for ${\widehat{\beta }}^{\ast }$, we estimate U and Σ similarly as above but with $(\widehat{\beta },{\widehat{\alpha }}_1,{\widehat{\alpha }}_2)$ replaced by $({\widehat{\beta }}^{\ast },{\widehat{\alpha }}_1^{\ast },{\widehat{\alpha }}_2^{\ast })$. We denote the estimators by ${\widehat{U}}_n^{\ast }$ and ${\widehat{\Sigma }}_n^{\ast }$, respectively. Then estimate B by

$${\widehat{B}}_n=\frac{1}{n}\sum _{i=1}^n\sum _{(j,k)\in \{(s,t),(s^{\prime },t^{\prime })\}}{\widehat{D}}_i^{\ast jk}{\left({\widehat{V}}_i^{\ast jk}\right)}^{-1}{\widehat{\epsilon }}_i^{\ast jk}{\stackrel{.}{W}}_{jk,i}\left(p\right).$$

Denote the number of subjects who receive A₁ = j and who are further rerandomized to be n_rj, for j = 1, 2. The asymptotic variance of ${\widehat{\beta }}^{\ast }$ is consistently estimated by ${\widehat{U}}_n^{\ast -1}{\widehat{\Sigma }}_n^{\ast }{\widehat{U}}_n^{\ast -1}-{\widehat{U}}_n^{\ast -1}{\widehat{B}}_n\widehat{P}{\widehat{B}}_n^T{\widehat{U}}_n^{\ast -1}$, where P̂ = diag(p₁(1 – p₁), p₂₁(1 – p₂₁)/(n_r1/n), p₂₂(1 – p₂₂)/(n_r2/n)).

2.2 Specific models

The model we consider is linear or generalized linear model. Here “linear” means the transformed mean outcome is a linear function in the unknown parameters. Under this framework, however, the trajectory of the longitudinal outcomes over time can be modeled as either a linear or a nonlinear function, as described in detail below. Without loss of generality, we assume that the two strategies compared are either “11” and “22” or “11” and “12”.

2.2.1 Linear model

At first, the simplest model for the trajectory is a linear model. This is a plausible model for comparing two strategies with different initial treatments. To be specific, assume that the interest is in comparing strategies “11” and “22”. This corresponds to

$$d_{im}^{gg}={(1,g-1,t_{im},(g-1)t_{im},x_i^T)}^T$$ (4)

for g = 1, 2, and $\beta ={({\beta }_1,\cdots ,{\beta }_4,{\beta }_5^T)}^T$ in the general formulation $h\left({\mu }_{im}^{gg}\right)={\left(d_{im}^{gg}\right)}^T\beta$. Although in randomized studies the effect of baseline covariate x_i is not of primary interest, there is the possibility and advantage to estimate it in these studies [31]. In this model, since β₄ is the interaction between the group indicator and time, i.e., the difference in the rates of change of the longitudinal outcomes over time under the two strategies, the comparison of the two strategies reduces to the test of the hypothesis of H₀ : β₄ = 0. Denote the (4,4)th elements of ${\widehat{U}}_n^{-1}{\widehat{\Sigma }}_n{\widehat{U}}_n^{-1}$ and ${\widehat{U}}_n^{\ast -1}({\widehat{\Sigma }}_n^{\ast }-{\widehat{B}}_n\widehat{P}{\widehat{B}}_n^T){\widehat{U}}_n^{\ast -1}$ by ${\widehat{\sigma }}_{4,4}^2$ and ${\widehat{\sigma }}_{4,4}^{\ast 2}$, respectively. In order to test for H₀ : β₄ = 0, we use the test statistics

$$T_n=\frac{\sqrt{n}{\widehat{\beta }}_4}{{\widehat{\sigma }}_{4,4}},\text{or}{T}_n^{\ast }=\frac{\sqrt{n}{\widehat{\beta }}_4^{\ast }}{{\widehat{\sigma }}_{4,4}^{\ast }},$$

for the test with true weights and estimated weights, respectively. By Theorem 1 and the consistency of ${\widehat{\sigma }}_{4,4}$ and ${\widehat{\sigma }}_{4,4}^{\ast }$, T_n and $T_n^{\ast }$ both have a standard normal asymptotic distribution under H₀. Hence, we reject H₀ when |T_n| > z_1–α/2 (or when $\mid T_n^{\ast }\mid >z_{1-\alpha ∕2}$ if estimated weights are used) at a two-sided significance level α, where z_q denotes the upper 100q% percentile of the standard normal distribution.

2.2.2 Piece-wise linear model

In adaptive treatment strategies, the treatment may change over time, and the change of treatment is usually triggered by patient response to previous treatments. It may be expected that the rates of change of longitudinal outcomes may be different when the patient is on different treatments. This motivates a piece-wise linear model for the trajectory of the longitudinal outcomes. Specifically, suppose that for all subjects who are rerandomized to a second-stage treatment, the second-stage treatment starts at the same time, which is denoted by t*. Suppose that the mean longitudinal outcome changes linearly before time t* at a rate r₁ for those who start with A₁ = j and who are rerandomized to A₂ = k, and after time t*, the rate of change becomes r₂. Also, suppose that for those who start with A₁ = j but are not rerandomized, the rate of change is r₃ over the whole study period. Under these assumptions, the mean counterfactual outcome for strategy “jk” is still a piece-wise linear function of time with a change point t*. For comparing strategies “11” and “22”, this piece-wise linear model corresponds to

$$d_{im}^{gg}={(1,g-1,a\left(t_{im}\right),(g-1)a\left(t_{im}\right),b\left(t_{im}\right),(g-1)b\left(t_{im}\right)x_{im}^T)}^T,\text{for}g=1,2,$$ (5)

In (1) where a(t) = t*I(t ≥ t*)+tI(t < t*), b(t) = (t – t*)I(t ≥ t*), and $\beta ={({\beta }_1,\cdots ,{\beta }_6,{\beta }_7^T)}^T$. Here β₂ is the difference in intercepts, β₄ is the difference in slopes before time t*, and β₆ is the difference in slopes after time t*, between the two strategies compared.

The above model is of particular interest in comparing two strategies with the same initial treatment, specifically, strategies “11” and “12”, when the start time for the second-stage treatments is the same for all subjects, since in that case, the linear model is impossible if there is any difference between the two strategies, while the piece-wise linear model remains a plausible model. In this case, we have to set

$$d_{im}^{1g}={(1,g-1,a\left(t_{im}\right),b\left(t_{im}\right),(g-1)b\left(t_{im}\right),x_{im}^T)}^T,\text{for}g=1,2,$$ (6)

in (1), where $\beta ={({\beta }_1,\cdots ,{\beta }_5,{\beta }_6^T)}^T$. Here β₂ is the difference in intercepts at time 0, and β₅ is the difference in slopes after time t*, which is the parameter of interest. Note that in this model there is no interaction term (g – 1)a(t_im) because the slopes must be the same before time t* when the treatments before time t* coincide for the two treatment strategies “11” and “12”.

For comparison of the two strategies under model (5), one possibility is to compare the mean outcomes at a fixed time point, e.g., at the end of study. Another possibility is to compare the areas under the curve (from time 0 to, say, the end of study) for the two trajectories of the mean longitudinal outcomes. First, suppose we want to test for the difference in the mean outcomes at time T which is usually the end of study period. By simple algebra, the difference in the means of the counterfactual outcomes at T between the two strategies is β₂ + t* β₄ + (T – t*)β₆. Ignoring β₂, the difference resulting from difference at baseline, we test for the hypothesis $H_0^{\left(1\right)}:{\lambda }_1^T\beta =0$, where λ₁ = (0,0,0, t*, 0, T – t*)^T. This amounts to comparing the differences in mean outcomes from time 0 to time T between the two strategies. We use the test statistic

$$T_{1n}=\frac{\sqrt{n}{\lambda }_1^T\widehat{\beta }}{\sqrt{{\lambda }_1^T{\widehat{U}}_n^{-1}{\widehat{\Sigma }}_n{\widehat{U}}_n^{-1}{\lambda }_1}}\text{or}{T}_{1n}^{\ast }=\frac{\sqrt{n}{\lambda }_1^T{\widehat{\beta }}^{\ast }}{\sqrt{{\lambda }_1^T{\widehat{U}}_n^{\ast -1}({\widehat{\Sigma }}_n^{\ast }-{\widehat{B}}_n\widehat{P}{\widehat{B}}_n^T){\widehat{U}}_n^{\ast -1}{\lambda }_1}}$$

for the test with true weights and estimated weights, respectively, and reject $H_0^{\left(1\right)}$ when |T_1n| > z_1–α/2 (or when $\mid T_{1n}^{\ast }\mid >z_{1-\alpha ∕2}$ if estimated weights are used) at a two-sided significance level α. Second, suppose we want to test for the difference in the areas under curve from time 0 to T between the two strategies. The difference in the areas under curve can be calculated as

$$T{\beta }_2+\frac{1}{2}{t}^{\ast }(2T-t^{\ast }){\beta }_4+\frac{1}{2}{(T-t^{\ast })}^2{\beta }_6.$$

We also ignore the difference resulting from the difference at baseline and test for the hypothesis $H_0^{\left(2\right)}:{\lambda }_2^T\beta =0$, where λ₂ = (0, 0, 0, t* (2T – t*), 0, (T – t*²)^T. We use the test statistic

$$T_{2n}=\frac{\sqrt{n}{\lambda }_2^T\widehat{\beta }}{\sqrt{{\lambda }_2^T{\widehat{U}}_n^{-1}{\widehat{\Sigma }}_n{\widehat{U}}_n^{-1}{\lambda }_2}}\text{or}{T}_{2n}^{\ast }=\frac{\sqrt{n}{\lambda }_2^T{\widehat{\beta }}^{\ast }}{\sqrt{{\lambda }_2^T{\widehat{U}}_n^{\ast -1}({\widehat{\Sigma }}_n^{\ast }-{\widehat{B}}_n\widehat{P}{\widehat{B}}_n^T){\widehat{U}}_n^{\ast -1}{\lambda }_2}}$$

for the tests with true weights and estimated weights, respectively, and reject $H_0^{\left(2\right)}$ when |T_2n| > z_1–α/2 (or when $\mid T_{2n}^{\ast }\mid >z_{1-\alpha ∕2}$ if estimated weights are used) at a two-sided significance level α.

Since in model (6), the only parameter of interest is β₅, to compare strategies “11” and “12” under this model, we test for the hypothesis H₀ : β₅ = 0. This is similar to testing for H₀ : β₄ = 0 in the linear model (4) thus the details are omitted.

2.2.3 Polynomial model

Another alternative model that can be considered is the polynomial model. As a starting point, the quadratic polynomial can be applied, and if higher flexibility is necessary, a cubic model may be considered. As an example, for comparing strategies “11” and “22”, to formulate a quadratic model, we let

$$d_{im}^{gg}={(1,g-1,t_{im},(g-1)t_{im},t_{im}^2,(g-1)t_{im}^2,x_{im}^T)}^T,\text{for}g=1,2,$$

where $\beta ={({\beta }_1,\cdots ,{\beta }_6,{\beta }_7^T)}^T$. This type of models is of particular interest in cases where the start time of the second-stage treatment is random, which makes the piece-wise linear model less applicable because there is no logically meaningful change point. To compare two strategies under this type of models, we can compare the mean outcomes at a fixed time point (T) or compare the areas under the curve in the interval (0, T), with the corresponding null hypothesis being $H_0^{\left(1\right)}:{\lambda }_1^T\beta$ and $H_0^{\left(2\right)}:{\lambda }_2^T\beta$, respectively, where λ₁ = (0, 0, 0, T, 0, T², 0)^T and λ₂ = (0, 0, 0, T²/2, T³/3, 0)^T. The test statistics and the rejection regions are constructed in the same way as those in Section 2.2.2 and thus the details are omitted.

3 Simulation

We conduct a simulation study to assess the performance of the weighted GEE method for data analysis. The simulation is performed to compare strategies “11” and “22”. At first, we generate data from model (1), where s = t = 1 and s′ = t′ = 2. The link function h(·) is chosen to be the identity function and the measurement error is assumed to be normally distributed. The choice for $d_{im}^{gg}$ is (4) in one simulation and (5) in another simulation, corresponding to a linear model and a piece-wise linear model, respectively. Suppose the outcome of interest is measured at 6 time points t_im = m, for 0 ≤ m ≤ 5. The change point in the piece-wise linear model is supposed to be t* = 2. First, A₁ is generated from a Bernoulli distribution with probability 0.5. In the piece-wise linear model, we first generate the longitudinal outcomes up to time 2 using a linear trajectory model with a positive slope. If the measurement at t = 2 is greater than twice of the measurement at time t = 0, then R is set to be 0 and the measurements after time t = 2 are still generated using the same linear model as for t ≤ 2. Otherwise, R is set to be 1 and we generate A₂ from a Bernoulli distribution with probability 0.5, and the measurements after t = 2 are generated using a linear model with a slope that is different from the slope before time t = 2, where the intercepts of the linear models are chosen to make the trajectories continuous at time t = 2. The one-dimensional covariate X in the model is generated from a standard normal distribution, independently from the other variables. The parameters are chosen such that the resulting β is β = (2.5, −0.25, 2, 1. 5, 1)^T for the linear model and β = (2, 0, 0.5, 0.2, 0.47, 0.2, 0.5)^T for the piece-wise linear model. The vector of measurement errors ε_i is generated from a multivariate normal distribution where the correlation coefficient between ${\epsilon }_{il}^g$ and ${\epsilon }_{im}^g$ follows an AR(1) correlation structure: 0.6^{|t_il–t_im|}, where t_il and t_im are the lth and mth measurement times for subject i, respectively, for 0 ≤ l, m ≤ 5 and 1 ≤ i ≤ n. The common variance of the components of ${\epsilon }_i^g$ is set to be 5. For the working correlation structure in the weighed GEE, we try both the “independence” correlation structure and the “true” correlation structure. Here the “independence” and “true” correlation structure mean that we replace R_gg(α_g) in the expression for $V_i^{gg}\left({\alpha }_{gg}\right)$ with the identity matrix and the AR(1) correlation structure, respectively. They are not really the “independence” and the “true” correlation structures because here the true correlation structure refers to that of $W_{gg,i}(y_i-{\mu }_i^g)$ instead of $y_i-{\mu }_i^g$. The correct specification of the correlation of $W_{gg,i}(y_i-{\mu }_i^g)$ is difficult because in simulation we generate the y_is using a specific correlation structure but the correlation structure of $W_{gg,i}(y_i-{\mu }_i^g)$ is different and complicated. We run the simulation for sample sizes 50, 100 and 300, and in each simulation scenario, 1000 replications are run.

Tables 1 and 2 below present the results of this simulation. We list the biases, mean estimated variances, empirical variances, and the empirical coverage rates of the 95% confidence intervals of selected parameters of the most interest. These results show that the weighted GEE method works well, yielding low biases and consistent estimates of variances and confidence intervals with expected coverage rates. The consistency of the estimators is achieved under both of the correlation structures. Moreover, the estimators based on estimated weights are slightly more efficient than those with true weights in this simulation.

Table 1.

Simulation results for selected parameters in the linear trajectory model.

	true weights				estimated weights
	bias	V1	V2	coverage	bias	V1	V2	coverage
“independence” working correlation structure
n = 50
β 2	−0.02	0.92	0.99	0.93	−0.01	0.93	0.94	0.93
β 4	0.01	0.14	0.15	0.92	0.01	0.12	0.13	0.92
β 5	0.01	0.20	0.23	0.91	0.00	0.22	0.24	0.91
n = 100
β 2	−0.03	0.47	0.47	0.95	−0.03	0.48	0.48	0.95
β 4	0.01	0.08	0.08	0.95	0.01	0.06	0.06	0.95
β 5	0.02	0.11	0.12	0.92	0.02	0.12	0.12	0.92
n = 300
β 2	−0.02	0.16	0.16	0.95	−0.02	0.16	0.16	0.95
β 4	0.00	0.023	0.023	0.95	−0.00	0.018	0.019	0.95
β 5	0.01	0.04	0.04	0.94	0.01	0.03	0.03	0.94
“true” working correlation structure
n = 50
β 2	−0.01	0.89	0.94	0.93	−0.01	0.88	0.92	0.92
β 4	0.00	0.13	0.15	0.92	0.01	0.12	0.14	0.93
β 5	0.00	0.20	0.22	0.91	0.00	0.20	0.21	0.93
n = 100
β 2	−0.03	0.45	0.45	0.95	−0.03	0.43	0.43	0.94
β 4	0.01	0.07	0.07	0.95	0.01	0.07	0.07	0.95
β 5	0.02	0.11	0.12	0.92	0.02	0.11	0.11	0.93
n = 300
β 2	−0.02	0.15	0.15	0.95	−0.02	0.14	0.14	0.95
β 4	−0.00	0.022	0.023	0.95	−0.00	0.016	0.017	0.94
β 5	0.01	0.04	0.04	0.94	0.01	0.04	0.04	0.94

V1: mean estimated variance; V2: empirical variance; coverage: empirical coverage rate for the 95% confidence interval.

Table 2.

Simulation results for selected parameters in the piece-wise linear trajectory model.

	true weights				estimated weights
	bias	V1	V2	coverage	bias	V1	V2	coverage
“independence” working correlation structure
n = 50
β 2	0.01	0.89	0.90	0.93	−0.01	0.89	0.87	0.97
β 4	0.00	0.13	0.14	0.93	0.01	0.15	0.13	0.97
β 6	−0.01	0.15	0.16	0.94	−0.01	0.16	0.15	0.96
β 7	0.01	0.05	0.06	0.93	0.01	0.07	0.06	0.96
n = 100
β 2	−0.03	0.47	0.46	0.95	−0.03	0.46	0.44	0.96
β 4	0.01	0.071	0.073	0.94	0.01	0.072	0.069	0.97
β 6	0.01	0.078	0.080	0.93	0.01	0.077	0.075	0.96
β 7	0.02	0.027	0.030	0.92	0.02	0.029	0.028	0.95
n = 300
β 2	−0.02	0.16	0.16	0.95	−0.02	0.16	0.15	0.96
β 4	0.00	0.024	0.024	0.95	−0.00	0.023	0.022	0.96
β 6	0.01	0.026	0.025	0.95	0.01	0.024	0.023	0.96
β 7	0.01	0.01	0.01	0.94	0.01	0.01	0.01	0.94
“true” working correlation structure
n = 50
β 2	−0.01	0.86	0.88	0.93	−0.01	0.87	0.84	0.97
β 4	0.00	0.12	0.13	0.92	0.01	0.13	0.12	0.96
β 6	0.01	0.14	0.15	0.92	0.01	0.15	0.14	0.97
β 7	0.00	0.05	0.06	0.91	0.00	0.06	0.06	0.93
n = 100
β 2	−0.03	0.45	0.45	0.95	−0.03	0.43	0.43	0.96
β 4	0.01	0.072	0.071	0.95	0.01	0.069	0.067	0.96
β 6	0.01	0.075	0.077	0.92	0.01	0.076	0.074	0.96
β 7	0.02	0.027	0.028	0.93	0.02	0.029	0.028	0.95
n = 300
β 2	−0.02	0.15	0.15	0.95	−0.02	0.14	0.14	0.96
β 4	−0.00	0.023	0.024	0.94	−0.00	0.024	0.023	0.96
β 6	0.01	0.025	0.026	0.93	0.01	0.025	0.024	0.96
β 7	0.01	0.01	0.01	0.94	0.01	0.01	0.01	0.94

V1: mean estimated variance; V2: empirical variance; coverage: empirical coverage rate for the 95% confidence interval.

4 An Application

In this section we apply the weighted GEE method in analyzing data from the CATIE. The CATIE was conducted to determine the long-term effects and usefulness of antipsychotic medications in persons with schizophrenia [24]. In this trial, 1500 schizophrenia patients were initially randomized to receive one of 5 antipsychotic drugs including olanzapine, perphenazine, quetiapine, risperidone, and ziprasidone. Patients may discontinue or switch treatment at some time after the initial treatment. Patients who chose to switch treatment can choose one of two further randomization pathways. In one of the pathways, patients were randomized to receive either clozapine or one of olanzapine, quetiapine or risperidone; and in the other pathway patients were randomized to receive either ziprasidone or one of olanzapine, questiapine, and risperidone. In both pathways no one is assigned to the same drug as the initial drug. It was pointed out by [24] that, usually those who chose to switch treatment due to low efficacy were likely to choose the first randomization pathway and those who switched due to bad tolerance were likely to choose the second randomization pathway.

Results of data analysis [24] showed that olanzapine is the best treatment with respect to patient adherence among the 5 drugs. A natural further question to ask is that which treatment should a patient switch to if he or she starts with olanzapine and chooses to switch treatment. This is a problem of assessing adaptive treatment strategies. For this purpose we consider only patients who started with olanzapine. Denote the two randomization pathways as “E” and “T” (corresponding to efficacy and tolerance, respectively). For those who chose the “E” randomization pathway, denote the two options they were randomized to as A₁ = 1 and A₁ = 2, where A₁ = 1 means clozapine and A₁ = 2 means choosing one from olanzapine, quetiapine or risperidone. For those who chose the “T” randomization pathway, denote the two options as A₂ = 1 and A₂ = 2, where A₂ = 1 means ziprasidone and A₂ = 2 is the same as A₁ = 2. For our purpose we assume that the outcome of interest is the longitudinal PANSS scores, which were measured at months 0, 1, and 3, and then every three months afterwards up to month 18. This trial can be analyzed similarly as the typical two-stage randomization trials in the previous section. However, the weights will be different because of the difference in the trial design. Denote strategy “jk” to be the strategy in which a subject starts with olanzapine, and then switches to A₁ = j if he or she chooses to switch treatment because of “E” and switches to A₂ = k if it is because of “T”, for j, k = 1, 2. In the CATIE trial, 333 patients started with olanzapine, among whom 214 patients did not switch treatment during the following 18 month period and thus are consistent with all 4 treatment strategies. The remaining 119 patients switched treatment in that time period and each of them is consistent with two of the 4 treatment strategies. Denote p₁ = P (A₁ = 1|E = 1) and p₂ = P (A₂ = 1|T = 1) to be the randomization probabilities. Denote R to be the indicator for switching treatment in the study period. Let E to be the indicator for switching treatment due to “E” and T to be the indicator for switching treatment due to “T”. Then the weight function for strategy “jk” is:

$${\tilde{W}}_{jk}=1-R+\frac{EI(A_1=j)}{p_1^{2-j}{(1-p_1)}^{j-1}}+\frac{TI(A_2=k)}{p_2^{2-k}{(1-p_1)}^{k-1}},\text{for}j,k=1,2.$$

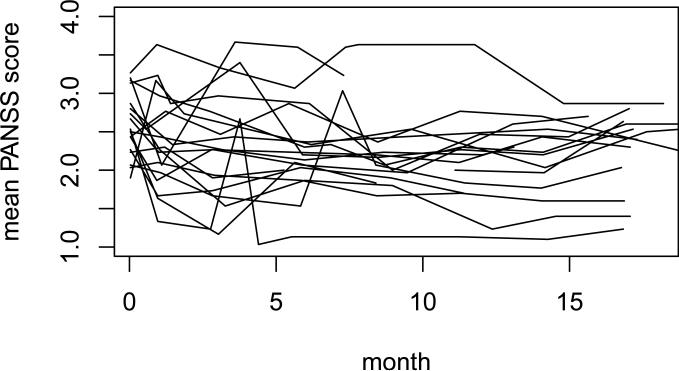
Figure 1 shows the trajectories of the mean PANSS score for a number of randomly selected patients in CATIE. There seems to be little difference in the rates of change among patients. The same is expected for different treatment strategies but formal statistical analyses need to be carried out to confirm this. Since the start time of the second-stage treatment can be different for different patients in this trial, we use the quadratic polynomial model instead of the linear or piece-wise linear model. Based on the data from all the subjects who started with olanzapine, and using the method in Section 2.2.3, we compare the mean outcomes at month 18 as well as the areas under the curve from time 0 to month 18 for each pair of the 4 adaptive treatment strategies. The results of this analysis show that the differences between strategies are very small, with the absolute values of the estimated coefficients in the quadratic model being close to 0.01 and the p values ranging from 0.29 to 0.75 when the true weights or estimated weights are used. Obviously these differences are too small to be interesting.

Figure 1.

Plot of longitudinal mean PANSS scores for a number of randomly selected patients in the CATIE.

5 Discussion

In the above, we mainly focused on a typical two-stage randomized trials in which only responders or nonresponders to the first-stage treatments are rerandomized to second-stage treatments. The proposed method generalizes easily to more general SMART trials, for example, trials with more than two stages, trials in which only responders to one of the two initial treatments are rerandomized, trials in which both responders and nonresponders to the initial treatments are rerandomized, and so on. The only difference is the formulae for the weights. Specific weights for some examples are illustrated in [6].

When the second-stage treatment initiates at different (random) times for different subjects, the comparison of two treatment strategies is more challenging than the other cases. In this case, the linear model is still a possible approximation of the trajectories but it is likely to fail. The piece-wise linear model may be used, but the change point is not known priori and can be different for different strategies. Hence, the piece-wise linear assumption as well as the change point (if the assumption is supported by preliminary data) need to be ascertained by preliminary data.

Although it is not the focus of this article, the proposed method can be used to estimate the best treatment strategy among all embedded strategies, for which the method in [21] can be applied as well. To use our method, we first impose an appropriate model for the longitudinal outcomes under each strategy. Then use the proposed methods and the models to estimate a summary quantity for each strategy, and the estimate of the best strategy is based on this quantity. For example, this summary quantity can be the mean outcome at a specific time point or the area under the curve, as described in Section 2.2.2.

Finally, missing data may be a problem in longitudinal studies, and for any GEE approach to yield unbiased results the missing mechanism need to be missing completely at random [32]. Some modifications (e.g., [32]), have been proposed to guarantee unbiasedness estimation under the more general missing at random mechanism. Extension of our proposed method for this purpose is a potential topic for future research.

Appendix: proofs of asymptotic results

For simplicity, assume α₁ = α₂ = and R₁(α) = R₂(α) = R(α). The following are the assumptions that are used in the proof:

• A1 The parameter space for β, $\mathcal{B}$, is a compact set in R^p where p is the dimension of β.

• A2 The parameter space for α, $\mathcal{A}$, is a compact set in R^q where q is the dimension for α.

• A4 $\widehat{\alpha }(\widehat{\beta },\widehat{\varphi }\left(\beta \right))$ is uniformly consistent for α.

• A5 The derivative of the components of R⁻¹(α) is continuous in $\mathcal{A}$, and the first and second derivative of μ_ig with respect to β is continuous in $\mathcal{B}$.

• A6 For any β₁, β₂ ∈ $\mathcal{B}$, Eμ_ig (,d_ig, β₁) = Eμ_ig(d_ig, β₂) if and only if β₁ = β₂.

At first, we assume that the true weights are used. Denote ${\alpha }^{\ast }\left(\beta \right)=\widehat{\alpha }(\beta ,\widehat{\varphi }\left(\beta \right))$, and

$$S_i(\beta ,\alpha )=\sum _{g=1}^2{W}_{gg,i}\frac{\partial {\mu }_{ig}^T}{\partial \beta }{V}_{ig}^{-1}\left(\alpha \right)(y_i-{\mu }_{ig}).$$

Then $\widehat{\beta }$ is the solution to ${\sum }_{i=1}^n{S}_i\{\beta ,{\alpha }^{\ast }\left(\beta \right)\}=0$. Taylor expansion and rearranging terms yield

$$\sqrt{n}(\widehat{\beta }-\beta )=U_{1n}^{-1}\frac{1}{\sqrt{n}}\sum _{i=1}^n{S}_i\{\beta ,{\alpha }^{\ast }\left(\beta \right)\}+o_p\left(1\right)=0,$$

where

$$\begin{array}{cc}\hfill U_{1n}& =\frac{1}{n}\sum _{i=1}^n\frac{d{S}_i\{\beta ,{\alpha }^{\ast }\left(\beta \right)\}}{d\beta }\hfill \\ \hfill & =\frac{1}{n}\sum _{i=1}^n\left[\frac{\partial S_i\{\beta ,{\alpha }^{\ast }\left(\beta \right)\}}{\partial \beta }+\frac{\partial S_i\{\beta ,{\alpha }^{\ast }(\beta ,)\}}{\partial {\alpha }^{\ast }}\frac{\partial {\alpha }^{\ast }\left(\beta \right)}{\partial \beta }\right]\hfill \\ \hfill & =E\sum _{g=1}^2\frac{\partial {\mu }_{ig}^T}{\partial \beta }{V}^{-1}\left(\alpha \right)\frac{\partial {\mu }_{ig}}{\partial \beta }+o_p\left(1\right)\hfill \\ \hfill & =U_1+o_p\left(1\right).\hfill \end{array}$$

Furthermore,

$$\begin{array}{cc}\hfill \frac{1}{\sqrt{n}}\sum _{i=1}^n{S}_i\{\beta ,{\alpha }^{\ast }\left(\beta \right)\}& =\frac{1}{\sqrt{n}}\sum _{i=1}^n{S}_i(\beta ,\alpha )+\frac{1}{n}\sum _{i=1}^n\frac{\partial S_i(\beta ,\alpha )}{\partial \alpha }\sqrt{n}\{{\alpha }^{\ast }\left(\beta \right)-\alpha )\}\hfill \\ \hfill & =\frac{1}{\sqrt{n}}\sum _{i=1}^n{S}_i(\beta ,\alpha )+o_p\left(1\right),\hfill \end{array}$$

where we used the facts that ${\sum }_{i=1}^n\partial S_i(\beta ,\alpha )∕\partial \alpha ∕n=o_p\left(1\right)$ by the law of large numbers and that $\sqrt{n}\{{\alpha }^{\ast }\left(\beta \right)-\alpha )\}=O_p\left(1\right)$ [29]. It follows that

$$\sqrt{n}(\widehat{\beta }-\beta )=U_1^{-1}\frac{1}{\sqrt{n}}\sum _{i=1}^n{S}_i(\beta ,\alpha )+o_p\left(1\right)=0,$$

which yields the desired result when true weights are used.

When p is estimated in the weights, Taylor expansion with arguments similar as above yields that

$$\sqrt{n}({\widehat{\beta }}^{\ast }-\beta )=U_1^{-1}\frac{1}{\sqrt{n}}\sum _{i=1}^n{S}_i(\beta ,\alpha )+U_1^{-1}B\sqrt{n}(\widehat{p}-p)+o_p\left(1\right)=0.$$

Denote the number of subjects who are randomized to A₁ = j and who are further rerandomized to be n_2j, for j = 1, 2. Straightforwardly, we have

$$\sqrt{n}(\widehat{p}-p)=\left(\begin{array}{c}\hfill \sqrt{n}({\widehat{p}}_1-p_1)\hfill \\ \hfill \sqrt{n∕n_{21}}\sqrt{n_{21}}({\widehat{p}}_{21}-p_{21})\hfill \\ \hfill \sqrt{n∕n_{22}}\sqrt{n_{22}}({\widehat{p}}_{22}-p_{22})\hfill \end{array}\right){\to }_{d}N(0,P).$$

Since p̂ is an efficient estimator for p, the three conditions in [33] are satisfied and the conclusion follows from (1.3) therein.