The Role of Long-Term Memory in a Test of Visual Working Memory: Proactive Facilitation but no Proactive Interference

Abstract

We report four experiments examining whether associations in visual working memory are subject to proactive interference from long term memory (LTM). Following a long-term learning phase in which participants learned the colors of 120 unique objects, a working memory (WM) test was administered in which participants recalled the precise colors of three concrete objects in an array. Each array in the WM test consisted of one old (previously learned) object with a new color (old-mismatch), one old object with its old color (old-match), and one new object. Experiments 1 to 3 showed that WM performance was better in the old-match condition than in the new condition, reflecting a beneficial contribution from long term memory. In the old mismatch condition, participants sometimes reported colors associated with the relevant shape in LTM, but the probability of successful recall was equivalent to that in the new condition. Thus, information from LTM only intruded in the absence of reportable information in WM. Experiment 4 tested for, and failed to find, proactive interference from the preceding trial in the WM test: Performance in the old-mismatch condition, presenting an object from the preceding trial with a new color, was equal to performance with new objects. Experiment 5 showed that long-term memory for object-color associations is subject to proactive interference. We conclude that the exchange of information between LTM and WM appears to be controlled by a gating mechanism that protects the contents of WM from proactive interference but admits LTM information when it is useful.

The relation between working memory (WM) and long-term memory (LTM) has been a matter of long and sometimes heated debate. On the one end of the spectrum of theoretical positions are models assuming that WM and LTM are separable systems of memory: WM is conceptualized as a limited-capacity system for maintaining a small set of currently relevant representations, potentially through persistent neural firing. In contrast, LTM is assumed to be a virtually unlimited memory for events and general knowledge, neurally implemented through long-term synaptic changes (Atkinson & Shiffrin, 1968; Davelaar, Goshen-Gottstein, Ashkenazi, Haarmann, & Usher, 2005; Jeneson & Squire, 2012). On the other end of the theoretical spectrum are models of a unitary memory system rendering the distinction between WM and LTM void (Brown, Neath, & Chater, 2007). Several intermediate theories of various flavors have also been proposed that treat WM as a subset of LTM representations that temporarily assume a qualitatively distinct state of heightened accessibility (Cowan, 1995; Farrell, 2012; Oberauer, 2009).

The present article will not adjudicate between these theoretical alternatives. Rather, we pursue the more modest aim of illuminating the contribution of LTM to performance in tests of WM. This question is motivated by a functional view of WM (Oberauer, 2009). We use the concept of WM for the set of mechanisms that enables us to hold some mental representations available for processing. These representations can be rapidly accessed and flexibly manipulated, updated, or discarded. WM serves as a medium for building new representations, so that people can entertain new thoughts, create new images, formulate new sentences, and consider new courses of action. The malleability of representations in WM contrasts with the relative stability of LTM, which serves to maintain our knowledge of what happened (episodic), what is the case (semantic), and how to do things (procedural). We remain neutral as to how the mechanisms of WM are implemented – as a separate store (Atkinson & Shiffrin, 1968; Baddeley, 2001), as a distinct cognitive or neural state of representations (Cowan, 2005), or as a special context to which representations are bound that renders them particularly accessible (Farrell, 2012) – but we maintain that they must establish some form of separation between contents of WM and representations in LTM to reflect their different functions. On this premise we can ask under which circumstances information from LTM enters WM.

Consideration of the function of WM for cognition reveals a dilemma: On the one hand, WM serves as a workspace for reasoning and action planning that can be rapidly and seamlessly updated, and that can be used to construct new representations detached from knowledge and habit (e.g., when considering a hypothetical, counterfactual state of affairs, or when planning an action that departs from a learned routine). To serve this function, the contents of WM need to be decoupled from those of LTM. On the other hand, WM needs to be able to draw on knowledge in LTM, and it must be possible to store new contents of WM over the long term. To that end a two-way information channel between LTM and WM is necessary. Ideally, a well-designed WM system could have a flexible gate to LTM that can be opened or closed depending on the current cognitive needs, analogous to the hypothetical gate between WM and the outside world (Awh & Vogel, 2008; Chatham, Frank, & Badre, 2014; Kessler & Oberauer, 2014; O'Reilly & Frank, 2005). To examine this issue, we tested under which conditions shape/color associations encoded into LTM contribute to responses in a subsequent WM test on which participants were asked to store distinct combinations of shapes and color for immediate reproduction.

If the flow of information between WM and LTM is controlled to serve current cognitive goals, we should expect a stronger contribution of LTM to performance on a WM test when that contribution is helpful than when it is harmful. To test this prediction, we need to distinguish between helpful and harmful influences of LTM on tests of WM, relative to a baseline without any influence of LTM. We will refer to harmful influences as proactive interference, and to helpful effects as proactive facilitation. In the following we review the evidence for effects of LTM on performance in WM tests. Whereas there is ample evidence for a beneficial effect of LTM, the evidence for an interfering effect of LTM on WM task performance is much less compelling.

Long-Term Memory Supporting Working Memory

WM is usually investigated through tests of immediate memory in which people are asked to remember small random sets of items (e.g., lists of digits or words, or sets of visual objects) over brief retention intervals (in the order of seconds). For many of these tests it has been shown that performance is better when the memory set matches knowledge in LTM. For instance, immediate serial recall of verbal materials is better when the materials are known words than when they are artificial pseudowords (Hulme, Maughan, & Brown, 1991), and better when the words are highly familiar than when they are less familiar (Hulme et al., 1997). Serial recall of word lists is also improved if the list agrees with grammatical constraints of the participants' native language (Gerver, 1969; Perham, Marsh, & Jones, 2009). Lists of pseudowords are recalled better the more frequent their phoneme transitions occur in the participants' language (Thorn & Frankish, 2005).

Immediate serial recall is also substantially improved by learning during the experiment: In the Hebb repetition paradigm, one list is repeated on multiple trials, interspersed with new lists. People's immediate recall of repeated lists – but not of new lists – improves across repetitions (Hebb, 1961; Hitch, Fastame, & Flude, 2005; Page, Cumming, Norris, McNeil, & Hitch, 2013). This so-called Hebb effect has been demonstrated not only with verbal materials but also with lists of faces (Horton, Hay, & Smyth, 2008) and of visually presented spatial locations (Couture & Tremblay, 2006). The Hebb effect reflects the acquisition of long-term memory about the repeated list because the repetition benefit occurs with two or more trials intervening between the repetitions. A limited-capacity WM cannot be expected to retain outdated information across several trials. Further evidence that immediate recall of verbal lists benefits from long-term knowledge comes from studies showing better recall for lists consisting of word pairs that have been learned in an earlier phase of the experiment, compared to lists with novel pairings of words (Chen & Cowan, 2005, 2009). Similarly, lists of verbal elements are better recalled when they match previously acquired probabilistic transition rules between elements (Botvinick & Bylsma, 2005; Majerus, Martinez Perez, & Oberauer, 2012; Majerus, van der Linden, Mulder, Meulemans, & Peters, 2004).

Whereas the evidence of a supporting effect of LTM on WM tests for sequentially presented lists of (mostly verbal) items is pervasive, tests of visual WM using simultaneously presented arrays have often been surprisingly impervious to long-term learning. Olson and Jiang (2004) asked participants to remember arrays of spatial locations or shapes. Immediate memory was tested by an item-recognition test. Olson and Jiang found no improvement of immediate recognition on arrays that were repeated every 12 trials. Yet, at the end of the experiment participants were able to recognize the repeated arrays with above-chance accuracy, showing that some long-term learning must have occurred. Logie, Brockmole, and Vandenbroucke (2009) repeated arrays of colored shapes every three trials and found no improvement in a change-detection test compared to non-repeated arrays. Only when they repeated the same array on every trial did they observe a small beneficial effect of repetition in a change-detection test, and a more robust beneficial effect in a probed-recall test. A benefit of repeating a memory set from one trial to the next is not unambiguous evidence for a contribution of LTM because it is plausible that residual traces of the previous memory set remain in WM after the response to the preceding trial and carry over into the next trial. That said, the gradual improvement of performance across blocks that Logie et al. (2009) observed for repeated arrays with probed recall – but not with change detection – speaks in favor of cumulative learning in LTM.

Additional support for a beneficial effect of LTM to visual WM comes from the study of Brady, Konkle, and Alvarez (2009) who tested memory for arrays of colors. The colors were arranged into pairs by spatial proximity, and performance was found to improve over blocks when the paired colors co-occurred frequently throughout the experiment.

In sum, there is compelling evidence that knowledge in LTM assists performance on WM tests of immediate serial recall, with the majority of studies using verbal materials. Analogous evidence for a beneficial effect of LTM on WM tests for simultaneously presented visual arrays is comparatively sparse, but at least under some conditions such benefits can be demonstrated.

Long-Term Memory Interfering with Working Memory

The evidence reviewed in the previous section shows the bright side of long-term learning – here we look at evidence for a complementary dark side, proactive interference (PI). PI refers to adverse effects of previously learned material on memory acquired later, and it has been well documented in LTM (Crowder, 1976). Here we ask whether there is PI from LTM to a subsequent WM test, reflecting an impairment of WM caused by the obligatory intrusion of LTM.

It has been suggested that WM is immune to PI (Cowan, 2005), based on findings showing no PI in tests of immediate memory (Cowan, Johnson, & Saults, 2005; Halford, Maybery, & Bain, 1988; Wickens, Born, & Allen, 1963; Wickens, Moody, & Dow, 1981). Against this generalization, a recent review by Beaudry, Neath, Surprenant, and Tehan (2014) showed that there are at least as many published findings in support of PI in immediate memory as there are failures to find PI.

Evidence for PI in tests of WM comes from five paradigms. The first one follows the traditional paradigm for studying the build-up and release from PI in LTM: Trials are organized into mini-blocks of three to five using the same class of materials. After each mini-block the class of materials is changed (e.g., from words to digits, or from one semantic category to another). Build-up of PI is observed as the gradual decline of performance across trials within a mini-block, and release from PI is evidenced by the resurgence of performance at the first trial of each mini-block. This pattern has been observed with the complex-span paradigm for testing WM, in which encoding of a list alternates with a distracting task such as evaluating arithmetic equations (Bunting, 2006; Emery, Hale, & Myerson, 2008). Build-up and release from PI has also been shown with a probed-recall paradigm (Jones & Oberauer, 2013; Sanders & Willemsen, 1978). Of two studies with a visual-array recognition paradigm, one found evidence for build-up of and release from PI (Hartshorne, 2008), whereas the other did not (Lin & Luck, 2012). One possible explanation for these effects is that the WM tests draw in part on LTM (i.e., a record of the current trial in episodic LTM), and PI impairs the contribution of LTM to performance. If that is the case, the build-up of PI would reflect a reduction of the facilitatory contribution of LTM, not an interfering effect of LTM that suppresses WM performance below a hypothetical baseline without any contribution from LTM.

A second paradigm for inducing PI in immediate memory is the two-list paradigm developed by Tehan and Humphreys (1995): Immediately after encoding a first list of words, participants are instructed to forget that list and encode a second list instead. (On a subset of trials, the first list is tested to motivate encoding of that list). Memory for the second list is tested by probed recall, using a semantic category (e.g., “animal”) as the retrieval cue. PI is induced by including a word that matches the retrieval cue in the first list (e.g., “dog” appears in the first list, and “cat” in the second list). When the first list was read aloud and the second list was read silently, memory for the second list was worse in the PI condition than the control condition, and this effect was driven mostly by erroneously recalling the word from the first list that matched the cue (e.g., recalling “dog” instead of “cat”). Later work extended this finding to serial recall of the second list (Ralph et al., 2011). One limitation of the two-list paradigm is that it does not unambiguously demonstrate that LTM is the source of the PI effect: The source of PI precedes the target list by just about one second – the same interval that separated items within lists -- leaving open the possibility that representations of the first list were not entirely cleared from WM until the second list was tested. In that case, the PI effect could be due to interference within WM rather than between LTM and WM.

A third source of evidence for PI comes from manipulations of temporal distinctiveness between successive trials. Increasing the interval between successive trials has been found to improve performance in the Brown-Peterson paradigm with verbal materials (Unsworth, Heitz, & Parks, 2008) and in immediate-memory tests with visual material (Mercer, 2014; Ricker, Spiegel, & Cowan, 2014; Shipstead & Engle, 2013; Souza & Oberauer, 2015). These findings provide evidence for PI from previous trials, which is reduced by longer inter-trial intervals. This effect could reflect a contribution of episodic LTM to performance on the WM task, which is reduced by PI when temporal distinctiveness is poor (Brown et al., 2007). Such an explanation is particularly plausible for the Brown-Peterson task, in which participants recall a list after 10 or more second of a demanding distractor task that must be expected to interfere heavily with the contents of WM. The studies reporting temporal-distinctiveness effects for visual WM used comparatively rapid sequences of brief trials, with the shorter inter-trial intervals barely more than 1 s, raising the possibility that residual traces of the previous trial remain in WM, creating PI within WM. Therefore, temporal-distinctiveness effects do not provide unambiguous evidence for an obligatory intrusion of LTM representations into WM.

The fourth demonstration of PI comes from studies showing that gradual learning across trials, as in the Hebb paradigm, leads not only to improved performance but also to learning of errors. Lafond, Tremblay, and Parmentier (2010) re-analyzed recall sequences from a Hebb-learning experiment with lists of spatial locations (Parmentier, Maybery, Huitson, & Jones, 2008). They found that, across trials with the repeated list, participants not only reproduced correct responses more often, but also errors they had committed on earlier trials with the same list. This shows that Hebb repetition learning involves learning of one's previous response, including errors. Yet, performance on the repeated lists was not worse than on non-repeated lists for which no LTM learning was possible (Parmentier et al., 2008). Thus, the net effect of drawing on information in LTM for recall of the repeated lists was not detrimental. Botvinick and Bylsma (2005) had participants learn the probabilistic transition rules between items before transferring them to an immediate serial-recall test using those items. People tended to “regularize” lists that did not follow the rules, reproducing sequences that were in better accordance with the rules. Unfortunately, Botvinick and Bylsma did not include a baseline condition of lists unrelated to the pre-learned transition probabilities, so it is not clear whether the regularization errors reflect a detrimental effect of LTM. It could be that people drew on their knowledge of transition probabilities only as a best guess in cases when they had no useful information about the next item in WM, so that regularization errors merely stood in for random guesses that participants would have produced in the absence of LTM knowledge. The fifth paradigm showing PI in tests of immediate memory is the recent-negative-probes paradigm, a variant of the Sternberg recognition paradigm: When negative recognition probes – which match no item in the current memory set – match an item in a recent previous trial, false-alarm rates increase and response times for correct rejections are slower compared to negative probes not coming from any recent trial (Atkinson, Herrmann, & Wescourt, 1974; Jonides, Smith, Marshuetz, Koeppe, & Reuter-Lorenz, 1998; Monsell, 1978). The recent-negative-probes effect has also been observed with visual materials (Hartshorne, 2008). This effect shows that irrelevant memories of previous trials contribute to the recognition decision on the current trial, impairing performance. It is not entirely clear that the interfering effect comes from LTM. One study with words found that the effect is limited to probes coming from the immediately preceding trial (Berman, Jonides, & Lewis, 2009), leaving open the possibility that it reflects PI within WM arising from residual traces of the preceding memory set carrying over into the current trial. Against this possibility, Hartshorne (2008) showed a gradual decline of false-alarm rates with increasing number of trials intervening between the source of a recent negative probe and the current trial. It is very unlikely that a limited-capacity WM keeps residual representations across several trials. Thus, these studies provide some evidence that LTM representations can intrude on performance in a subsequent WM task, but important questions remain regarding the nature of this interference. One possibility is that PI arises at encoding, reducing the probability that an association is successfully stored in WM. For example, prior learning of color/shape associations might reduce the probability that subjects can successfully encode new associations with the same shapes. Alternatively, PI could arise at test through a competition for retrieval between representations in WM and representations in LTM. A third alternative is that PI arises at the decision process, at which a familiarity signal from LTM competes with information retrieved from WM for determining the recognition decision.

Evidence for the third possibility comes from studies investigating the time course of retrieval through a response-deadline method (McElree & Dosher, 1989; Öztekin & McElree, 2007). These studies show a surge in false-alarm rates to recent negative probes early during retrieval (i.e., at short deadlines), followed by a decline at later deadlines. This time course is well explained by the competition between a fast-accruing familiarity signal and a slower recollection process (McElree & Dosher, 1989). The familiarity signal arises from temporary activation of representations in LTM (Oberauer, 2001): Attending to a stimulus activates its representation in LTM, so that when the same, or a very similar, stimulus is experienced again later, an internal familiarity signal is automatically generated. The recognition decision process uses the familiarity signal as one source of evidence in favor of a positive response to a probe. Doing so is misleading when the probe is a recent negative one, but it is helpful on both positive probes (which are highly familiar) and non-recent negative probes (which are very unfamiliar). Hence, across all trial types in a recognition experiment, drawing on the familiarity signal from LTM is arguably beneficial, and the performance decrement on recent negative probes is a fairly modest price to pay for that benefit. The usefulness of familiarity can be demonstrated by testing short-term recognition with trial-unique stimuli, such that there are no recent-negative probes. Endress and Potter (2014) demonstrated that, under these conditions, performance on an item-recognition test for visual stimuli was doubled, compared to a condition in which the same small set of stimuli was used throughout.

Based on these findings we argue that the recent-negative-probes effect may reflect interference with recognition decisions rather than a deficit in working memory storage per se. Thus, this empirical pattern does not rule out our hypothesis that the gate between WM and LTM is opened only when using information from LTM is beneficial. Evidence in favor of this hypothesis comes from a study by Öztekin and McElree (2007), who combined a release-from-PI paradigm with recent negative probes: The semantic category of stimuli in a short-term recognition task was changed every three trials. Release from PI was evident in faster and more accurate recognition decisions on the first trial than on subsequent trials using the same semantic category. Over the three successive trials using the same semantic category, the elevated false-alarm rate to recent negative probes at short deadlines was dampened, suggesting that the influence of familiarity on the decision process was reduced as PI built up. This is what would be expected if the cognitive system relied on familiarity to the degree that doing so is helpful for performance.

To conclude, there is compelling evidence for PI in WM, but none of that evidence unambiguously shows that information from LTM intrudes into WM in an obligatory way. Some of the instances of PI reviewed above can either be explained as an overall beneficial contribution of LTM that is reduced in the conditions of high PI, or as reflecting interference between representations within WM. Other demonstrations that LTM information can influence WM performance might be specific to cases in which there was no competing representation in WM. Thus, the goal of the present work was to provide a sensitive test of whether prior associations in LTM have an obligatory negative impact on WM storage when new associations must be stored using the same stimulus materials. To anticipate our conclusions, our findings support the assumption of a flexible gate between WM and LTM that can be opened when information from LTM can be expected to be helpful (such as when there is no useful information in WM), but that remains closed otherwise to protect representations in WM from proactive interference (Oberauer, 2009). In the General Discussion we discuss ways in which such a flexible gate could be implemented without assuming that the WM system has clairvoyant powers of knowing when information from LTM will be helpful before even retrieving it.

The Present Experiments

In the present experiments we tested for both facilitatory and interfering effects of LTM on a test of WM. Doing so requires a neutral baseline in which the LTM effect in question is zero. To that end we used a paired-associates WM paradigm using images of concrete objects: On each trial, participants encoded three object-color pairs. At test they were given an object as a retrieval cue and reproduced that object's color on a continuous response scale (Brady, Konkle, Gill, Oliva, & Alvarez, 2013). The WM test was preceded by a long-term learning phase in which participants learned a large number of object-color associations. This two-phase protocol enabled us to realize three conditions in the WM test, characterized by the object that served as retrieval cue: In the old-match condition, an old object that had been involved in the LTM learning phase was presented in a WM trial, paired with the same color that had been associated with it in the LTM learning phase. In the old-mismatch condition, an old object was presented in a WM trial, paired with a new, randomly selected color. In the new condition, a new object is used in the WM trial with a randomly selected color. The new condition serves as baseline because there is no knowledge in LTM about the object's color.¹ The old-match condition serves to measure a potential facilitatory effect of LTM: To the extent that people draw on their knowledge from the LTM learning phase they can improve their WM test performance in the old-match condition relative to the new condition. The old-mismatch condition serves to measure the interfering effect of LTM: To the extent that knowledge acquired in the LTM learning phase obligatorily contributes to WM performance, it should interfere with reproducing the object's novel color, leading to performance below baseline.

In Experiments 1 and 2, using the design described above, we obtained evidence for proactive facilitation but against proactive interference. Experiment 3 replicates the absence of proactive interference in a variant of the design omitting the old-match condition. Failing to find PI from previously acquired long-term knowledge, in Experiment 4 we searched for PI from one WM trial to the next, and failed to find that, too. Finally, in Experiment 5 we replaced the WM test by an LTM test of object-color associations, and observed proactive interference from previously acquired knowledge.

Experiment 1

The experiment consisted of two phases. In the first, LTM learning phase participants learned 120 object-color associations. We followed the procedure of Brady et al. (2013) who showed that people can learn large numbers of object-color associations reasonably well. To further boost long-term learning we interspersed study phases with test phases to capitalize on the testing effect (Roediger III & Karpicke, 2006; Sutterer & Awh, in press). The second phase tested WM for object-color bindings. The memory set of each trial included one object from the LTM-learning phase in its original color (old-match), one object from the LTM-learning phase in a new color (old-mismatch), and one novel object (new). Memory for all three objects was tested in random order. If participants use LTM to improve performance in the WM test, they should benefit from it in the old-match trials. If LTM intrudes in an obligatory manner into retrieval from WM, performance on the old-mismatch objects should be impaired relative to new objects. In addition, PI from LTM should lead to a tendency to erroneously recall the color learned in the LTM-learning phase when tested on an old-mismatch object in the WM phase.

Method

Participants

Nineteen students of the University of Zurich took part in a single session lasting between two and three hours. They were reimbursed with partial course credit or 40 Swiss Francs (about 40 USD).

Materials

We obtained 385 silhouette images of concrete nameable objects by conducting a web search for royalty-free clip art. Images were combined with one of 360 colors from a color wheel in the CIE L × a × b color space, centered on L = 70, a = 20, and b = 38, with a radius of 60. This is the color wheel most commonly used in continuous-reproduction tests of visual WM, because it consists of colors that are approximately equidistant in psychological similarity space, and approximately equally bright (for a critical discussion see Bae, Olkkonen, Allred, Wilson, & Flombaum, 2014). The silhouette images were presented uniformly in the chosen color against a grey background.

Procedure: LTM Learning

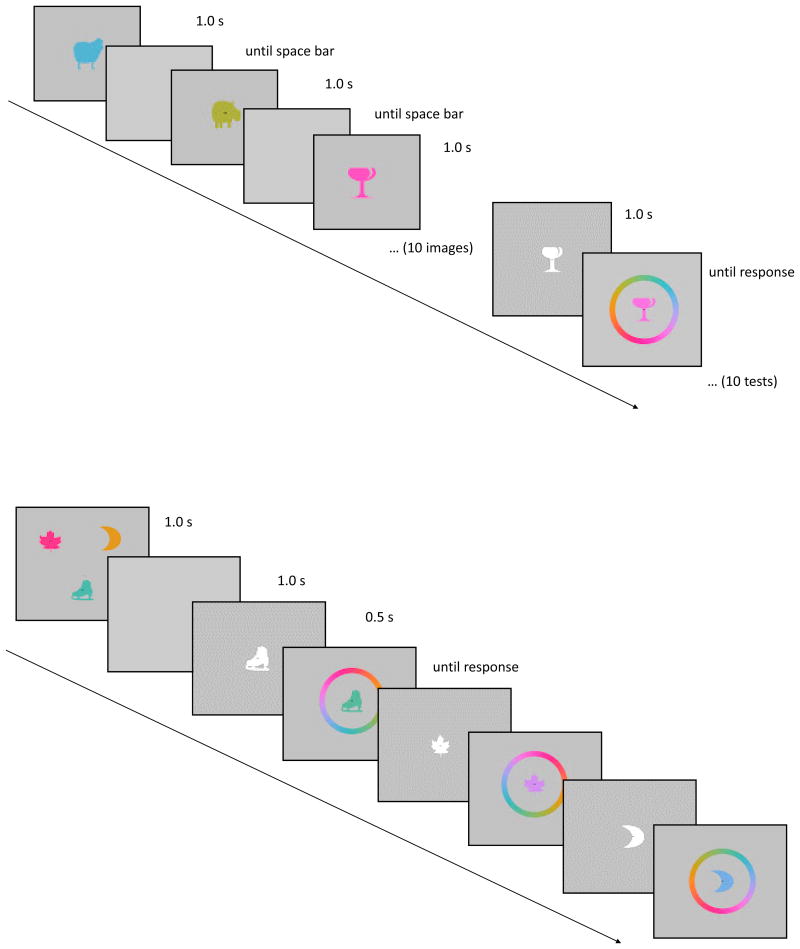
Participants studied each of 120 object-color combinations once. They started each study trial by pressing the space bar, upon which the object was displayed centrally on the screen for 1 s in a color chosen at random from the color wheel. The image size was scaled to 200 × 200 pixel square. After every 10 study trials, memory for the last 10 stimuli was tested in random order. These testing phases interspersed with study were intended to boost memory through the testing effect (Sutterer & Awh, in press). Participants initiated each of the 10 test trials by pressing the space bar. Each test trial began with the presentation of one of the 10 objects studied in the preceding set in white in the screen center. After 1 s, a color wheel was displayed around the object, rotated into a random orientation from trial to trial, and a mouse arrow appeared in the object's center. Once participants moved the mouse away from the center in the direction of one of the colors of the color wheel, the object assumed that color. Thus, by moving the mouse the participants continuously adapted the object's color. They were instructed to reproduce the color they remembered for the object as accurately as possible. Once they were satisfied with their reproduction of the remembered color, they entered their response by a mouse click. After that, feedback was provided for 1 s by displaying the object in its true color at study, together with a number between -180 and 180 indicating the angular deviation between the true color and the response.

After the 12 cycles of studying and subsequent testing of 10 object-color combinations, the entire set was tested again in random order. This LTM test proceeded in the same way as the shorter tests interspersed with study, except that all 120 objects were tested in random order in an uninterrupted sequence. At the end of this LTM test participants received feedback on their probability of recalling the correct color and the precision of reproduction (expressed as standard deviation in degrees), which were estimated from their responses using a mixture model (described below).

Procedure: WM Test

Following the LTM test, participants worked through 180 trials of a WM test, split into 3 blocks of 60 trials. Each trial used an array including two old objects chosen at random from the 120 learned objects, and one new object chosen at random from the remaining objects. One of the old objects was presented with its color learned in the LTM learning phase (old-match), and the other with a new randomly chosen color (old-mismatch). The color of the new object was also chosen at random. Within each block of 60 WM trials sampling of objects was without replacement, so that each of the 120 old objects was used exactly once per block, and new objects never repeated within a block.

Each trial began with a central fixation dot, together with a text informing participants about the number of the upcoming trial. Participants started the trial by pressing the space bar, upon which the screen went grey for 500 ms before the three-object array was shown for 1 s. The three objects were scaled to 200 × 200 pixels each, and arranged equidistantly on a virtual circle centered on the screen center, with a diameter set to the vertical screen extension minus 280 pixels. Offset of the array and onset of the test display were separated by a 1 s retention interval during which the screen went grey. The first test display showed one randomly selected object from the array in white in the center, which was 500 ms later surrounded by a color wheel in a random orientation. Participants reproduced the object's color in the same way as during the LTM tests, but received no feedback. All three objects of each array were tested in this way in random order. Thus, each participant contributed 180 responses for each of the three conditions.

Results

For each memory test we calculated the deviation of the response from the true color by subtracting the true color's angle on the color wheel from the angle of the response. The primary dependent variable, response error, was defined as the absolute value of that deviation.

In addition, we used a measurement model to obtain more detailed information about the sources of error in each condition. Our basic measurement model was a two-parameter mixture model (Zhang & Luck, 2008), which represents the observed distribution as a weighted mixture of two distributions, a circular-normal (von-Mises) distribution centered on the target (i.e., on the correct color of the tested object), and a uniform distribution reflecting responses carrying no information about the target. The first component reflects memory for the target color with a given precision, estimated by the standard deviation of the von-Mises distribution. The second component captures responses from binding errors (i.e., erroneously retrieving the color of one of the non-targets) and responses reflecting no information from memory, such as random guesses. Whereas these two sources can be teased apart with a more complex mixture model (Bays, Catalao, & Husain, 2009), here we are not concerned with the distinction between non-target responses and other responses, and therefore use the simpler measurement model. The model has two free parameters, the standard deviation of the von-Mises distributions, SD, and the proportion of responses attributed to the target distributions, P(mem). In the context of discrete-capacity models of visual WM, P(mem) is interpreted as the probability that an item in the array is represented in WM at all, whereas SD reflects the precision with which an item is represented (Zhang & Luck, 2008). We fit this measurement model to the data of each participant in each condition separately and used the parameter estimates as dependent variables for statistical analysis. We had no hypotheses about which parameter of the mixture model would be affected by proactive interference or facilitation, so the analyses of experimental effects on the parameters are exploratory. In addition, we used an extended mixture model to measure the contribution of LTM to responses in the WM test directly, as explained below. Technical details about the mixture models are provided in the Appendix.

Long-Term Memory

We first assessed how well participants acquired long-term knowledge of object-color associations in the LTM-learning phase. Table 1 presents the mean errors as well as the parameter estimates of the mixture model for the interleaved memory tests (averaged over all 12 tests) and the final LTM test. These data reflect substantial success of learning – after studying 120 object-color combinations, people were able to recall the colors of more than half of the objects with a standard deviation of about 25 degrees.

Table 1. Mean Response Errors and Mixture-Model Parameters of Tests of Long-Term Memory in LTM-Learning Phase.

Test	Error (deg.)	P(mem)	SD
Exp. 1, interleaved	39.6 (15.1)	0.71 (0.18)	24.9 (5.3)
Exp. 1, final	52.9 (14.8)	0.55 (0.24)	26.6 (10.2)
Exp. 2, final	42.5 (20.1)	.65 (0.26)	18.6 (7.6)
Exp. 3, interleaved	30.8 (13.6)	0.80 (0.15)	21.5 (5.5)
Exp. 3, final	44.7 (17.1)	0.65 (0.21)	26.1 (13.3)
Exp. 5, interleaved	33.4 (15.1)	0.77 (0.18)	21.7 (7.6)
Exp. 5, final	45.3 (16.9)	0.64 (0.24)	24.2 (7.9)

Note: Values in parentheses are standard deviations over subjects; “interleaved” refers to the tests following every 10 study trials, and “final” refers to the final test after all study trials.

Working Memory: Performance

We analyzed the errors of the WM test, and the mixture-model parameters P(mem) and SD, with a Bayesian ANOVA (Rouder, Morey, Speckman, & Province, 2012) using the BayesFactor package (Morey & Rouder, 2015) for R (R-Development-Core-Team, 2015). Each analysis returned a Bayes Factor (BF) reflecting the strength of evidence in the data in favor of a model with the main effect of condition (old-match, old-mismatch, or new) compared to a Null model without that main effect. The BF expresses the Bayesian likelihood ratio of a model including the effect of condition over one excluding it. The BF is the factor by which our ratio of prior probabilities of the two models should be updated to obtain the ratio of posterior probabilities. For instance, if we start with equal prior probabilities in favor and against the effect in question, a BF of 10 should lead us to believe that the effect is 10 times more probable than its absence in light of the data. Conversely, a BF of 0.1 should lead us to believe that the absence of the effect is 10 times more likely than its presence. Hence, a Bayesian analysis can provide evidence in favor of the Null hypothesis as much as in favor of the alternative hypothesis.

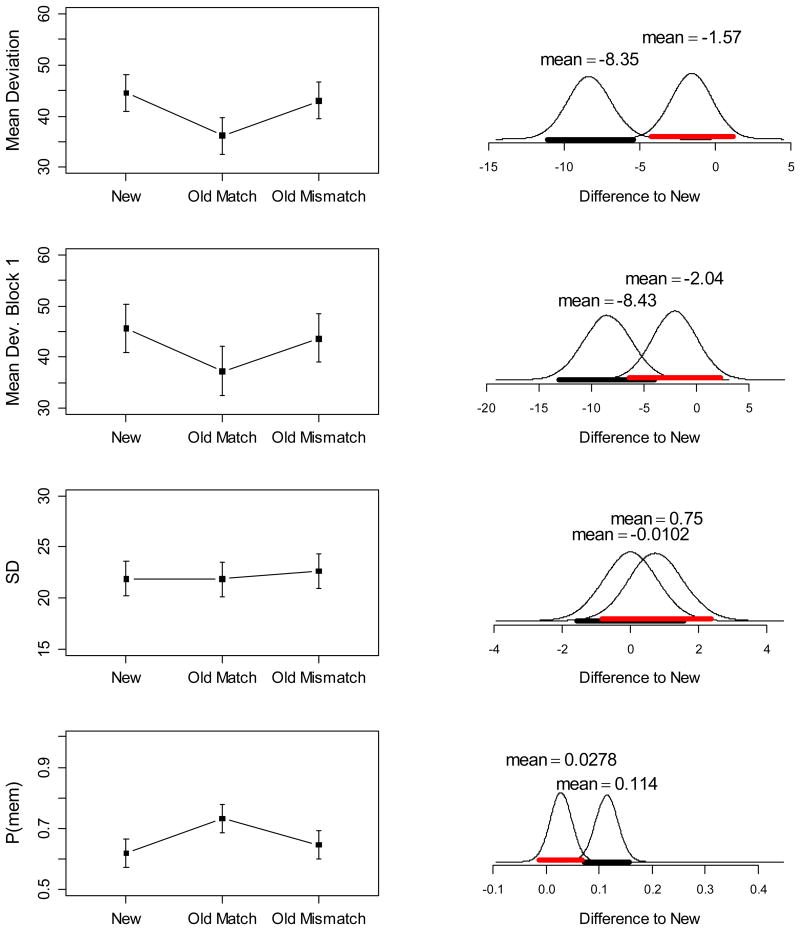
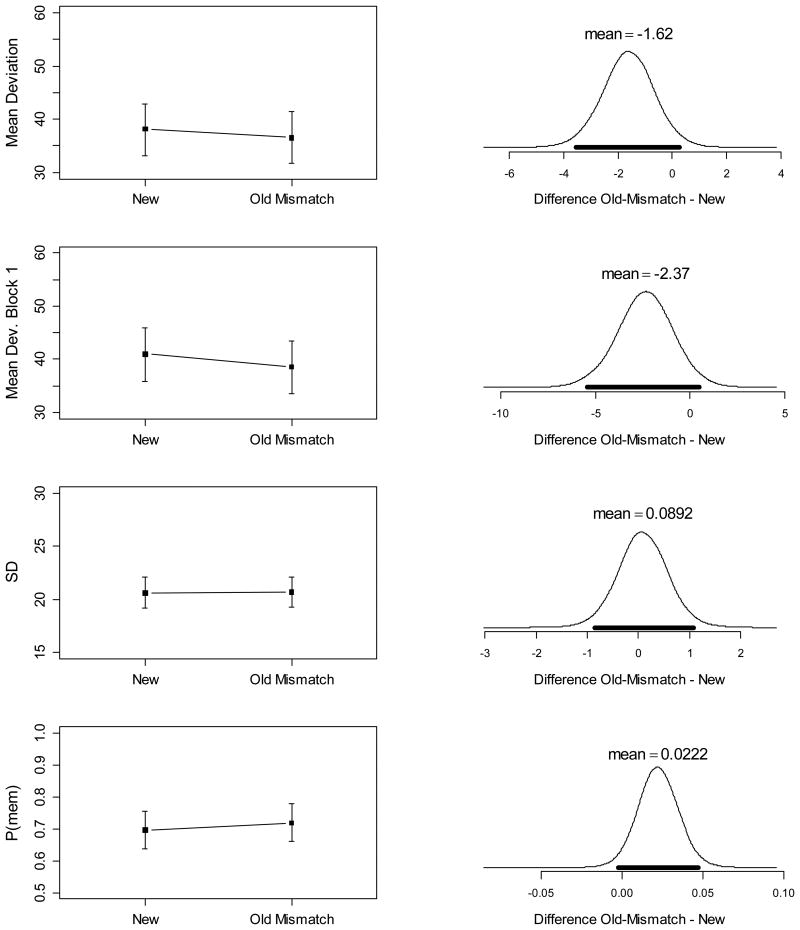
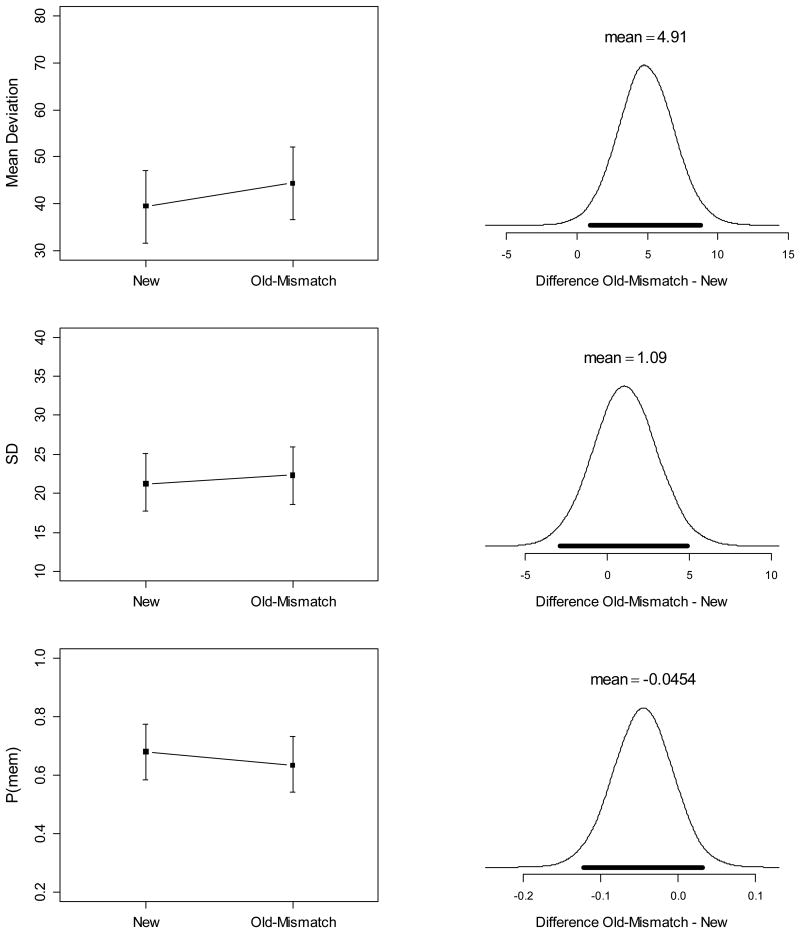
Table 2 presents the BFs for Experiment 1, and the left-side panels of Figure 2 shows the means of the dependent variables in each condition. The first column of Table 2 presents the BFs in favor of the main effect of condition. There was strong evidence for an effect of condition on mean errors (first row of Table 2). Because we repeated the objects up to three times across the three blocks of the WM test we also ran the analysis on the errors from only the first block to rule out any distortion of the effects through learning from one block to the next. The results (second row of Table 2 and of Figure 2) are qualitatively the same as for the complete data.

Table 2. Bayes Factors for Effects of Condition on Working Memory Test, Experiment 1.

Dependent Variable	Main Effect Condition	New vs. Old-Match	New vs. Old-Mismatch	New vs. Old-Mismatch (one-sided)
Mean Error	52545	19258	0.49	0.11
Mean Error (1st block)	70	205	0.37	0.13
SD	0.15	0.23	0.48	0.85
P(mem)	11388	5066	0.75	0.10

Figure 2.

Left: Condition means of dependent variables from the WM test of Experiment 1: Mean error for all blocks (top row) and for the first block only (second row); P(mem) parameter (third row) and SD parameter (fourth row) of the mixture model. Error bars cover the 95% highest-density interval computed from the ANOVA model including the main effect of condition (Kruschke, 2011), meaning that the true value of the dependent variable lies within that interval with a posterior probability of .95. Right: Posterior densities of pairwise differences of the old-match condition (black) and the old-mismatch condition (red) relative to the new condition. The thick black bar covers the 95% highest-density interval of the posterior difference; if that interval excludes zero, the absolute effect size exceeds zero with a probability of at least .95.

ANOVAs for the parameters of the mixture model showed that condition had a main effect on P(mem) but not on SD. The ANOVA for SD returned a BF = 0.15 for the model including the effect of condition, which implies a BF of 1/0.15 = 6.66 in favor of the Null model without such an effect. Hence, the data provide evidence for the Null hypothesis that condition had no effect on SD.

We decomposed the main effect of condition into two pairwise comparisons of the old-object conditions to the baseline (new): Performance in the old-match condition was superior to the baseline, confirming a facilitatory effect of LTM knowledge when it matched the object-color binding to be held in WM (BFs in the second column of Table 2)In contrast, there was no hint of a performance decrement in the old-mismatch condition. The BFs for comparing old-mismatch vs. new (third column of Table 2) all favored the Null hypothesis, though only weakly. For instance, the BF = 0.47 with errors as dependent variable implies BF = 1/0.47 = 2.1 in favor of the Null. This result is for the comparison of a Null model to an unconstrained alternative model that allows for both positive and negative effects of condition. The substantive hypothesis under investigation is more constrained: We predicted a decrement of performance – an increase in errors and in SD, and a decrease in P(mem) – in the old-mismatch condition relative to baseline. To test this hypothesis, we can compare a one-sided model including the directed effect we predict to a Null model in which the effect is either zero or opposite to the prediction. The results of these tests (Morey & Wagenmakers, 2014) are shown in the right-most column of Table 2. These BFs provide substantial evidence against the directed alternative and in favor of the Null hypothesis for errors and P(mem) as dependent variables, and ambiguous evidence for SD. Thus, the data provide positive evidence against proactive interference from LTM. When an object had been previously associated with a different color, working memory for the new color was no worse than for objects that had no prior associations with a color.

The right-side panels of Figure 2 present the posterior densities of the two pairwise comparisons of interest (i.e., the difference of old-match vs. new, and of old-mismatch vs. new). These densities reflect how, in light of the data and the default priors used in the Bayesian ANOVA, we should distribute our degrees of belief over the continuous scale of the effect in question. For instance, the top-right panel in Figure 2 shows the posterior density for the difference in the error measure between the new condition and the old-match condition, 95% of which covers an interval from about -12 to -6, marked by the thick black horizontal bar. This means that, in light of the data, we can be 95% certain that the true difference lies between -12 and -6 degrees. The same panel also shows the posterior density for the difference in the error measure between the new and the old-mismatch condition, 95% of which covers the interval between approximately -4 and 2 (thick red bar). Hence, the true error difference between these two conditions is most likely small, and although it is more probable to be negative than positive, both possibilities retain non-negligible posterior probabilities.

Working Memory: Responses from LTM

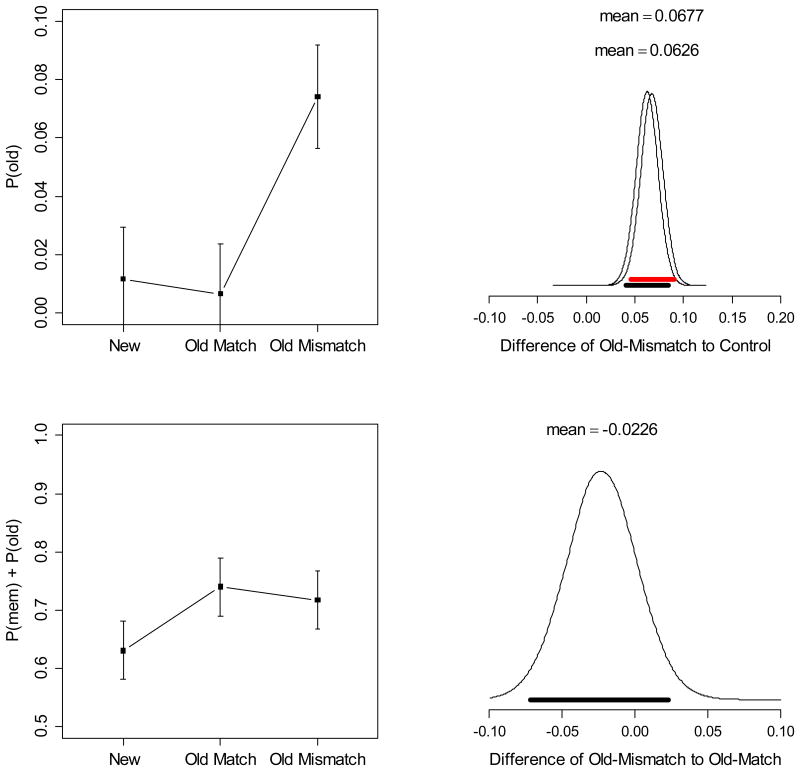
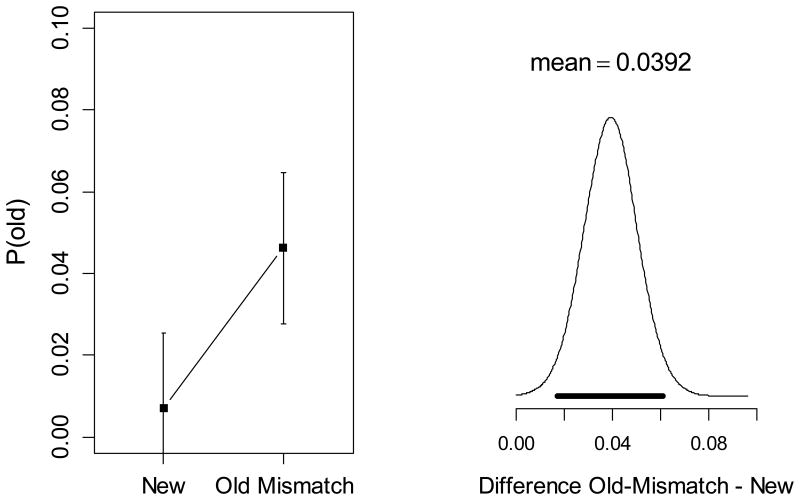
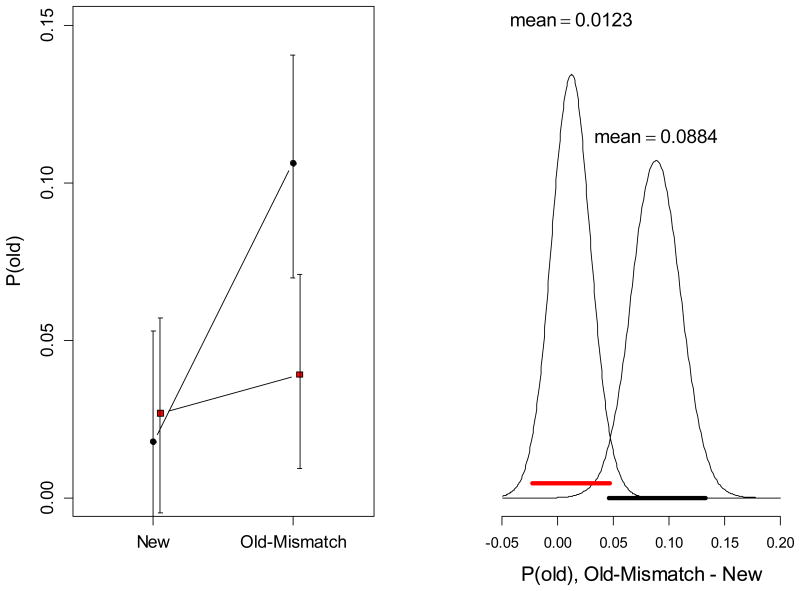
If LTM contributes to behavior in the WM test, we should detect its influence as a tendency to respond to old objects with their old color (i.e., the color learned for them in the LTM-learning phase). Old-mismatch items provide an opportunity to distinguish responses with the old color from responses with their new color in the WM test. To measure the contribution of LTM to these responses we extended the mixture model by a third component, a von-Mises distribution centered on the object's old color. A third parameter, P(old), estimated the proportion of trials coming from this distribution (see the Appendix for details).

We applied this model to the deviations from the old-mismatch condition. For comparison we also applied the model to the other two conditions, for which there was no separate set of old colors. For these conditions we created a phantom set of old colors by shuffling the old colors of the old-mismatch condition. Because participants did not experience these phantom old colors, the P(old) estimates in these conditions should be close to zero – we used them as a baseline against which to compare P(old) in the old-mismatch condition. The top left panel of Figure 3 shows the means of these estimates. As expected, P(old) was indistinguishable from zero in the old-match and the new condition, but it was clearly larger than zero in the old-mismatch condition. This observation was confirmed by a Bayesian ANOVA, returning a BF = 1.2 × 10⁶ in favor of a main effect of condition on P(old). Pairwise comparisons showed no evidence for a difference between old-match and new (BF = 0.42), but unambiguous evidence for a difference between old-mismatch and new (BF = 2194) and between old-mismatch and old-match (BF = 10270); the posterior densities of the old-mismatch condition to the two control conditions are shown in the top right panel of Figure 3. Clearly, participants did respond with the color they associated with the object in LTM on about 7% of trials in the old-mismatch condition.

Figure 3.

Left: Means and 95% highest-density intervals of P(old) (top) and of the sum of P(mem) and P(old) (bottom) from the extended mixture model applied to response distributions from the WM test of Experiment 1. Top right: Posterior densities of pairwise condition differences of P(old), comparing the old-mismatch condition to the new (black) and to the old-match condition (red). Bottom right: Posterior density of the difference in P(mem) + P(old) between old-match and old-mismatch condition. The thick black bars in the right panels cover the 95% highest-density intervals of the posteriors (Kruschke, 2011).

The estimate of about 7% for P(old) in the old-mismatch condition is numerically close to the 10% gain of P(mem) in the old-match condition over the baseline (new). That gain could therefore be explained by assuming an equal proportion of responses from LTM in the old-match condition, which the mixture model would attribute to the target in WM. To test this assumption, we added P(old) to P(mem) to simulated the proportion of target-related responses that would be obtained in the old-mismatch condition if all responses from LTM were counted as coming from the target. The means of this parameter sum are shown in the bottom row of Figure 3. P(mem) + P(old) was numerically larger in the old-match than the old-mismatch condition, but that difference was not supported statistically (BF = 0.46); its posterior density, shown in the bottom right panel of Figure 3, straddles zero. Hence, the data are compatible with the notion that participants respond with the old color from LTM to old objects to an equal degree in the old-match and the old-mismatch condition.

Discussion

Experiment 1 provided clear evidence for a facilitatory effect of LTM when it matched the content of WM. It was equally clear that WM performance was not impaired by interference from LTM when the object-color association in LTM mismatched the object-color conjunction in WM. At the same time, people did draw on LTM on a substantial proportion of trials of the old-mismatch condition. Why did this contribution from LTM not impair performance in that condition relative to baseline?

The pattern of findings cannot be explained by an obligatory contribution of LTM to behavior in the WM test. If information from LTM were added to information in WM with a constant (perhaps small) weight on each trial, or if the old color from LTM replaced an object's current color in WM on a random subset of trials, that would result in an increase of errors in the old-mismatch condition compared to the new condition. No such increase of errors was observed. We are forced to conclude that the WM system draws on LTM in an adaptive way, using it only when it is helpful or at least not damaging to performance. This could mean that people deliberately choose to retrieve the object's old color from LTM only on the subset of trials on which they find no useful information in WM. Alternatively, it could mean that a given object's old color in LTM is always retrieved, together with its current color from WM. In most cases the retrieved information from WM is stronger (i.e., more active, or less noisy). The two retrieved color representations compete with each other, and the representation from LTM wins the competition only on the small set of trials in which the representation from WM is very weak or absent, so that replacing it by the LTM representation does not incur any loss of performance. Both variants of the adaptive use of LTM can operate without access to any knowledge about the quality or accuracy of information in LTM – in fact, in the old-mismatch trials the information from LTM is always inaccurate, and yet it is occasionally used. All the adaptive mechanism needs is information about the existence and the quality of information in WM.

Experiment 2

In Experiment 1 we used the testing effect to boost acquisition of long-term knowledge. Studies with word lists have shown that testing reduces the PI effect of tested lists on subsequently learned lists (Pastötter, Schicker, Niedernhuber, & Bäuml, 2011; Szpunar, McDermott, & Roediger III, 2008). This raises the possibility that the interleaved tests during the LTM learning phase eliminated PI from the learned object representations on the subsequent WM test. To test this possibility, we replicated Experiment 1 without interleaved tests. In the LTM learning phase participants learned 150 object-color associations. Objects were presented in blocks of 10 as in Experiment 1, but blocks were not followed by a test; rather participants simply moved on to the next block. To ensure sufficient learning, learning of the entire set was repeated 4 times. Thus, the LTM learning phase consisted of 60 blocks of 10 objects each; every sub-sequence of 15 blocks presented the entire set in a new random order.

After the 60 blocks of learning, a random subset of 30 objects was selected for an LTM test to gauge the degree of learning. Each of the 30 objects was tested once. The remaining 120 objects were used for the WM test, which was exactly as in Experiment 1.

Results and Discussion

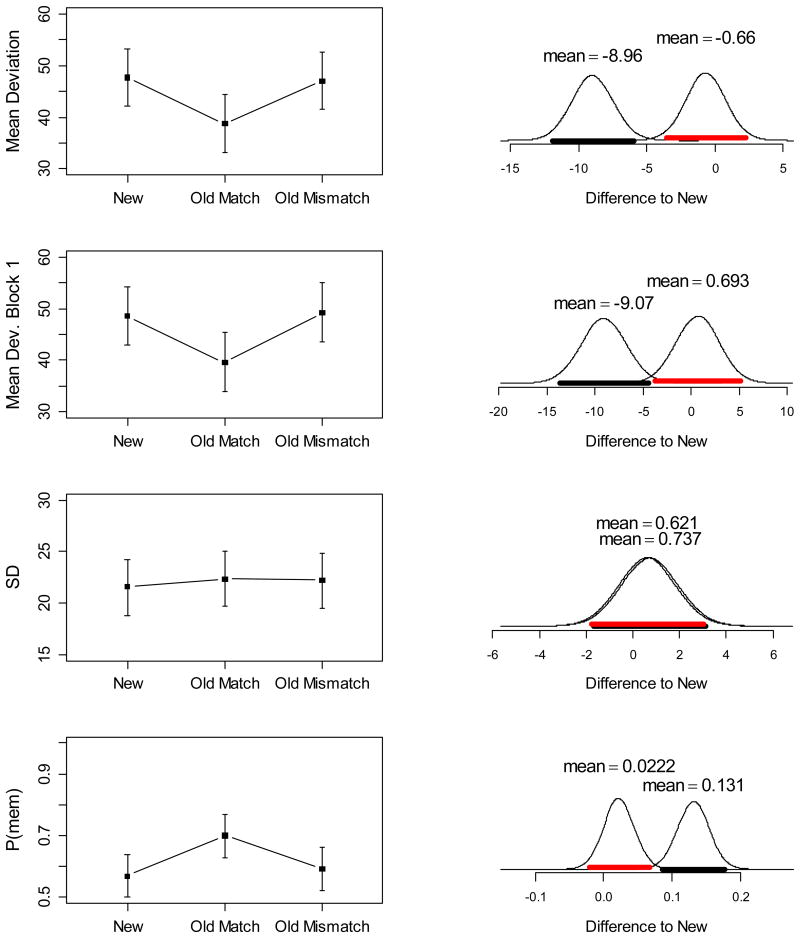
Long-term learning, assessed by the mean error, was comparable to Experiment 1 (see Table 1). The table also reports parameter estimates from the mixture model although with only 30 trials per participant these estimates might not be robust.

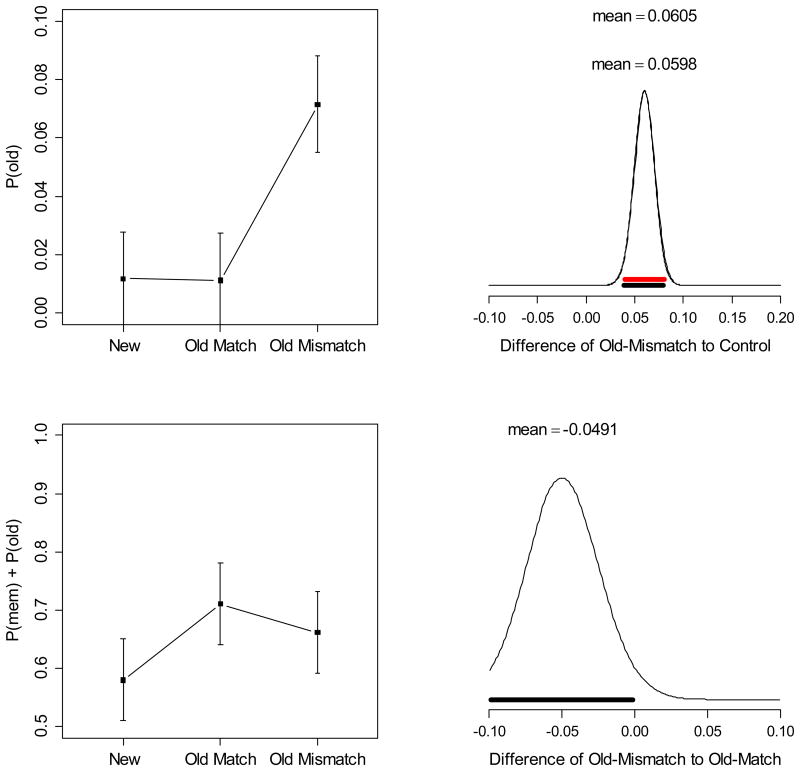
The results from the WM test are presented in Table 3 and in Figures 4 and 5 in the same format as for Experiment 1. They replicate every aspect of Experiment 1: There was proactive facilitation in the old-match condition, but no proactive interference in the old-mismatch condition. At the same time, participants reported the old color from the LTM learning phase on about 7% of trials in the old-mismatch condition. Because none of the old objects used in the WM test has ever been submitted to a test of LTM, we can rule out that testing has reduced their chance to interfere proactively with WM.

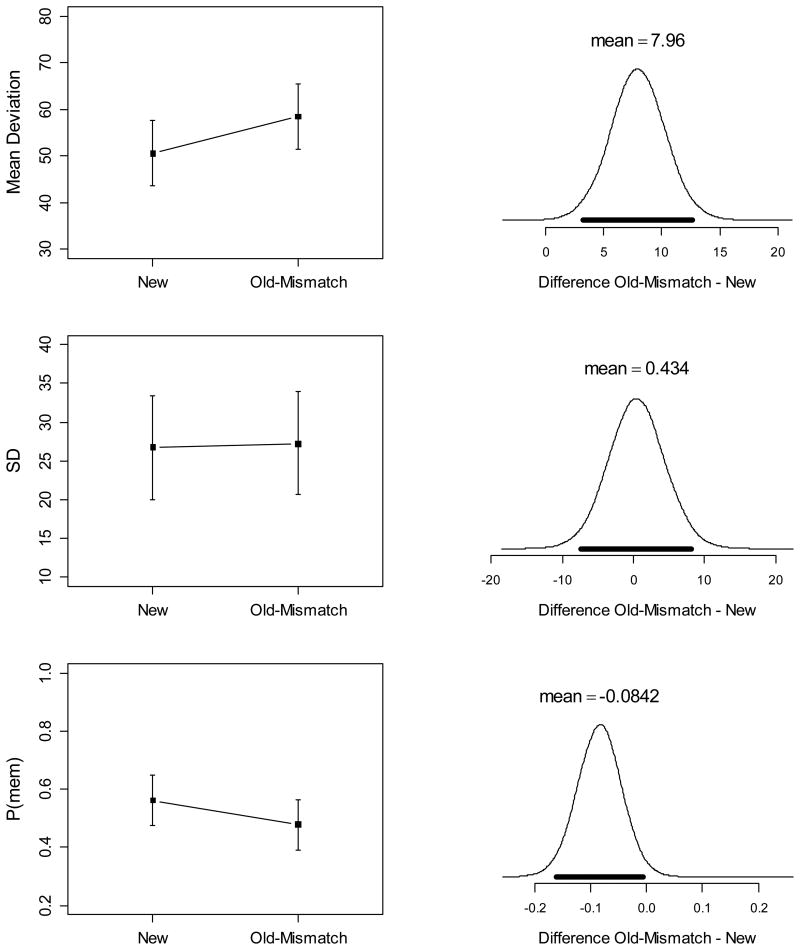
Table 3. Bayes Factors for Effects of Condition on Working Memory Test, Experiment 2.

Dependent Variable	Main Effect Condition	New vs. Old-Match	New vs. Old-Mismatch	New vs. Old-Mismatch (one-sided)
Mean Error	206021	741.3	0.28	0.15
Mean Error (1st block)	635	45.0	0.25	0.32
SD	0.01	0.30	0.27	0.39
P(mem)	51326	4587	0.42	0.11

Figure 4.

Left: Condition means of dependent variables from the WM test of Experiment 2; error bars cover the 95% highest-density interval computed from the ANOVA model including the main effect of condition (Kruschke, 2011). Right: Posterior densities of pairwise differences of the old-match condition (black) and the old-mismatch condition (red) relative to the new condition. The thick black bar covers the 95% highest-density interval of the posterior difference.

Figure 5.

Left: Means and 95% highest-density intervals of P(old) (top) and of the sum of P(mem) and P(old) (bottom) from the extended mixture model applied to response deviation distributions from the WM test of Experiment 2. Top right: Posterior densities of pairwise condition differences of P(old), comparing the old-mismatch condition to the new (black) and to the old-match condition (red). Bottom right: Posterior density of the difference in P(mem) + P(old) between old-match and old-mismatch condition. The thick black bars in the right panels cover the 95% highest-density intervals of the posteriors (Kruschke, 2011).

Experiment 3

Our third experiment replicated the first with one difference: We omitted the old-match condition. The old-match object in each WM array was replaced by a second new object. We made this change to test the possibility that participants in Experiments 1 and 2 became aware of the fact that one third of all WM objects had the same color as they had during the LTM-learning phase, and therefore strategically decided to draw on LTM to supplement WM. In Experiment 3 the environment did not encourage drawing on what people learned in the LTM-learning phase. We were interested in whether people still occasionally responded with the old color from LTM.

Method

Participants

Seventeen students of the University of Zurich took part in exchange for partial course credit or 40 Swiss Francs.

Materials and Procedure

The experiment was identical to Experiment 1, except that the old-match object in each WM array was replaced by a second new object drawn at random from the pool of images.

Results

The results are presented in the same format as for Experiment 1: Table 1 summarizes memory performance from the LTM tests, confirming that participants learned the object-color associations quite successfully. Table 4 contains the BFs for the main effect of condition (old-mismatch vs. new) on the dependent variables of the WM test, and Figure 6 shows the condition means (left) and the posterior densities of the condition differences (right). The BFs comparing the unconstrained alternative model to the Null model are ambiguous (i.e., close to 1), leaving uncertain whether or not the dependent variables differ between conditions. This uncertainty arises because performance was numerically better in the old-mismatch than the new condition – contrary to what is predicted from PI. The BFs from the one-sided tests returned clear evidence in favor of the Null, and against the model assuming worse performance in the old-mismatch than the new condition.

Table 4. Bayes Factors for Effects of Condition on Working Memory Test, Experiment 3.

Dependent Variable	New vs. Old-Mismatch	New vs. Old-Mismatch (one-sided)
Mean Error	1.11	0.09
Mean Error (1st block)	0.94	0.10
SD	0.26	0.30
P(mem)	1.30	0.09

Figure 6.

Left: Condition means of dependent variables from the WM test of Experiment 3, with 95% highest-density intervals. Right: Posterior densities of the differences between old-mismatch and new condition. The thick black bar covers the 95% highest-density interval (Kruschke, 2011).

The left panel of Figure 7 plots the means of P(old) from the extended mixture model. For the old-mismatch condition P(old) was again unambiguously positive, demonstrating that participants responded with the old color from LTM on about 5% of trials. The difference between conditions in P(old) was confirmed statistically (BF = 70.7); its posterior density is shown on the right of Figure 7.

Figure 7.

Left: Mean and 95% highest-density interval of P(old) from the extended mixture model applied to response deviation distributions from the WM test of Experiment 3. Right: Posterior of the effect of condition (old-mismatch vs. new) on P(old). The thick black bar covers the 95% highest-density interval (Kruschke, 2011).

Discussion

Experiment 3 replicated the absence of PI from previously acquired associations in LTM. At the same time, it replicated the tendency of participants to occasionally respond with the old color from LTM. This tendency could not reflect a strategic decision because the environment of Experiment 3 gave no incentive to use LTM strategically. It could still be that participants decided to draw on LTM when they had no better source for their response, perhaps because they erroneously believed that the colors in the WM test were related to those learned in the LTM-learning phase, or because the information in LTM provided an easily available guessing option. Alternatively, retrieval of information from LTM could be automatic but its influence on performance restricted to trials in which competing WM representations are either weak or absent.

Experiment 4

So far we found no evidence for PI from previously acquired LTM in a test of visual WM. This stands in contrast to the results of Hartshorne (2008), who observed PI from preceding trials in a test of visual WM (see also Makovski & Jiang, 2008). Therefore, in Experiment 4 we applied our experimental design – suited for distinguishing proactive facilitation and proactive interference – to the question whether information from previous WM trials creates PI in WM.

Method

Participants

Twenty-four students from the University of Zurich participated in a session of about 90 minutes in exchange for partial course credit or 20 Swiss Francs. Data from three participants were not used because their P(mem) values were exceptionally poor (< .20).

Materials and Procedure

The experiment consisted only of a WM test with 180 trials presented in three blocks of 60 trials. The three test blocks were preceded by a practice block with 10 trials. The WM task was exactly like that used in the preceding experiments, with one exception: Each array consisted of two new objects and one old-mismatch object. The old-mismatch object was one of the two new objects of the immediately preceding trial, chosen at random, and combined with a new randomly selected color. New objects were used only once, and old objects only twice, throughout the experiment.

Results and Discussion

Table 5 presents the BFs for the effect of condition (old-mismatch vs. new) on the three dependent variables. All BFs were < 1, reflecting evidence in favor of the Null. This evidence was moderately strong for the one-sided tests on errors and on P(mem), with BF = 6.7 and 6.2 in favor of the Null, respectively. The condition means and the posteriors of effects in Figure 8 confirm that there was no performance decrement for old-mismatch objects relative to new objects.

Table 5. Bayes Factors for Effects of Condition on Working Memory Test, Experiment 4.

Dependent Variable	New vs. Old-Mismatch	New vs. Old-Mismatch (one-sided)
Mean Error	0.27	0.15
SD	0.44	0.77
P(mem)	0.24	0.16

Figure 8.

Left: Condition means of dependent variables from the WM test of Experiment 4, with 95% highest-density intervals. Right: Posterior densities of the differences between old-mismatch and new condition. The thick black bar covers the 95% highest-density interval (Kruschke, 2011).

Figure 9 shows the means of P(old). There was again a tendency, albeit tiny, to respond with the old color to an old-mismatch object. A comparison with the baseline level of P(old) returned moderate evidence for an elevated P(old) in the old-mismatch condition, BF = 5.5. The 95% highest-density interval of the posterior of that effect (Figure 9, right panel) just excluded zero.

Figure 9.

Left: Mean and 95% highest-density interval of P(old) from the extended mixture model applied to response deviation distributions from the WM test of Experiment 4. Right: Posterior of the effect of condition (old-mismatch vs. new) on P(old). The thick black bar covers the 95% highest-density interval (Kruschke, 2011).

The pattern of results matches that of the preceding experiments: There was no PI from one WM trial to the next. Again we found a small tendency to respond with an object's old color. This effect could reflect a carry-over of residual traces in WM into the next trial, or a contribution of a representation of the preceding trial in LTM. We think that a carry-over of WM representations across trials is an unlikely explanation, because it would imply that the residual representations from the previous trials contributed in a mandatory, uncontrolled manner to performance on the current trial, and that would be detrimental for old-mismatch objects: Bindings of these objects with their old colors remaining in WM would interfere with bindings of the same objects to new colors. The alternative interpretation, that people occasionally retrieve the repeated object's color from the previous trial from LTM, is more attractive as it converges with the conclusions from the previous experiments: The WM system uses LTM information about a tested object only if it has no useful information in WM. The small signal of the object's old color in the response distribution reflects the rare occasions on which the tested object's representation in LTM from the previous trial is stronger than its representation in WM from the current trial.

Experiment 5

After four consecutive failures to find PI in a test of visual WM we began to wonder whether there might be something to our paradigm for testing memory that renders it insensitive to PI. In the final experiment we used the same paradigm to test for PI in LTM. The experiment consisted of two LTM-learning phases. In the first phase participants learned 80 unique object-color associations. In the second phase they learned another 160 object-color associations. Among the 160 objects 80 were new, and 80 were the objects of the first phase, now paired with a new color. PI in LTM would be shown by worse memory in the second phase for the old objects, paired with new colors, than for the new objects.

Method

Participants

Twenty-four students of the University of Zurich were enrolled in a single session that lasted approximately 2 hours. They received partial course credit or 30 Swiss Francs as reimbursement.

Materials and Procedure

Both phases of the experiment worked exactly like the LTM-learning phases of Experiments 1 and 3: Participants studied the stimuli one by one and were tested after every 10 study trials on the preceding 10 objects. At the end of each phase they were tested on all objects of that phase in random order. The first phase consisted of 80 different objects, each paired with a randomly chosen color. The second phase consisted of 160 objects, 80 of which were new, and 80 of which were the objects of the first phase, paired with new randomly chosen colors. These 80 old-mismatch stimuli were inserted into the sequence of 160 stimuli as follows: Of the 160 study events in the second phase, a random half was reserved for the old-mismatch objects. The order of those 80 objects in the first phase was shuffled within sets of 10, and then they were inserted into the reserved events of the second phase in their new order. In this way the sequence of studied objects in the second phase was an unpredictable mix of new and old-mismatch objects, and the old-mismatch objects were repeated in roughly, but not exactly, the same order in which they were studied in the first phase, thereby keeping the repetition lag between 71 and 169 study trials.

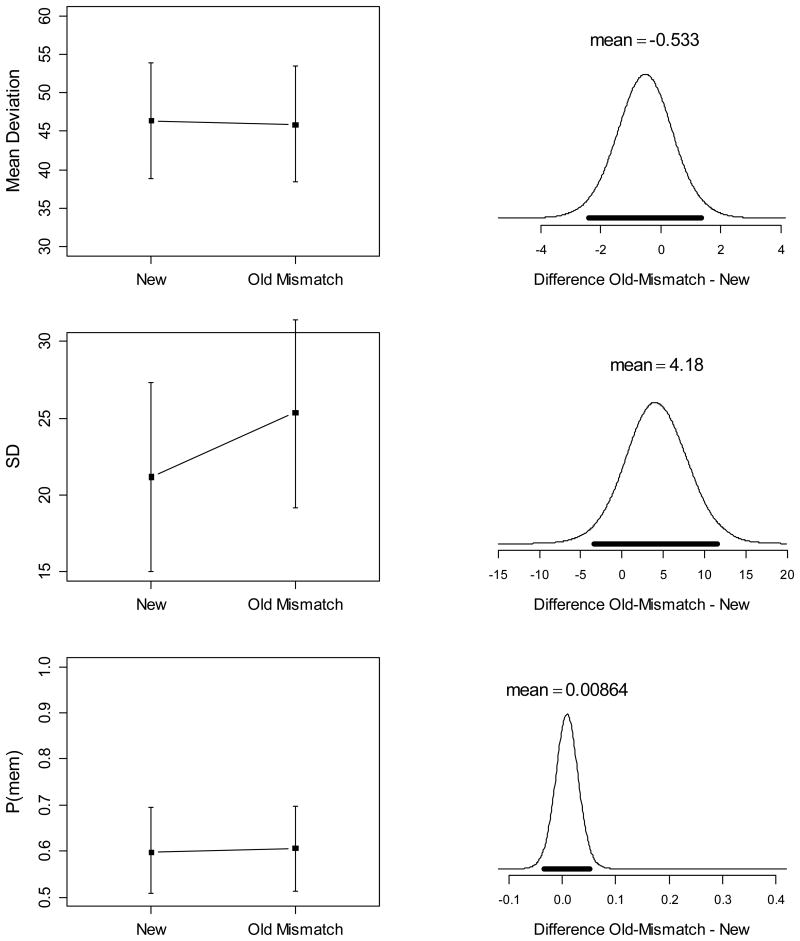
Results and Discussion

Learning in the first phase was again satisfactory (see Table 1). Of primary interest was memory in the two conditions of the second phase. We analyzed data from the interleaved tests and the final tests separately. Table 6 shows the BFs for the effects of condition (old-mismatch vs. new) on the mean errors and the parameters of the mixture model. In the data from the interleaved tests (Figure 10), there was moderate evidence for PI on the mean error, but not on any of the mixture-model parameters. In the data from the final test (Figure 11) there was unambiguous evidence for PI on mean error, and tentative evidence for PI on P(mem). At both test occasions the evidence went against any effect of condition on the precision parameter SD.

Table 6. Bayes Factors for Effects of Condition on Second Long-Term Memory Test, Experiment 5.

Dependent Variable	New vs. Old-Mismatch	New vs. Old-Mismatch (one-sided)
Interleaved Tests
Mean Error	4.3	8.5
SD	0.25	0.36
P(mem)	0.46	0.81
Final Test
Mean Error	33.1	66.2
SD	0.21	0.24
P(mem)	2.22	4.38

Figure 10.

Left: Condition means of dependent variables from the interleaved test of the second LTM-learning phase in Experiment 5, with 95% highest-density intervals. Right: Posterior densities of the differences between old-mismatch and new condition. The thick black bar covers the 95% highest-density interval (Kruschke, 2011).

Figure 11.

Left: Condition means of dependent variables from the final test of the second LTM-learning phase in Experiment 5, with 95% highest-density intervals. Right: Posterior densities of the differences between old-mismatch and new condition. The thick black bar covers the 95% highest-density interval (Kruschke, 2011).

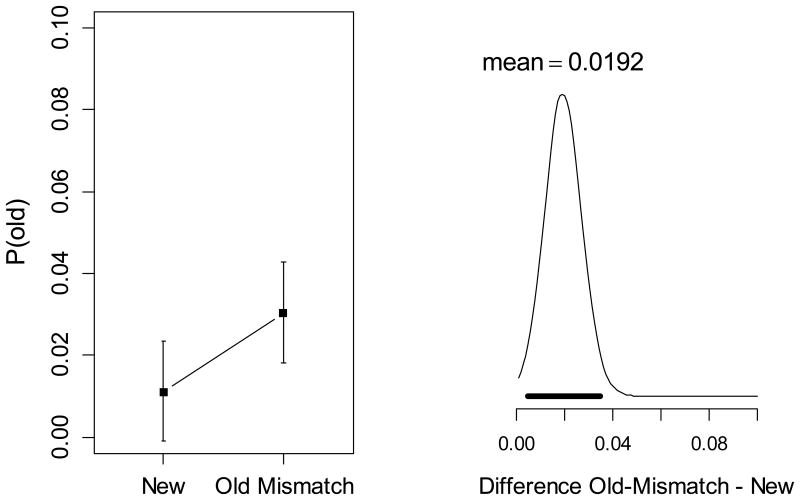
Figure 12 shows the mean estimates of P(old) from the extended mixture model. At the interleaved tests there was clear evidence for a tendency to report the old color in the old-mismatch condition, which exceeded the baseline, BF = 335.8. At the final test, there was only a slight numerical tendency in the same direction, which was not supported by statistical evidence, BF = 0.28.

Figure 12.

Left: Mean and 95% highest-density interval of P(old) from the extended mixture model applied to response deviation distributions from the intermediate (black) and the final test (red) of the second LTM-learning phase of Experiment 5. Right: Posterior of the effect of condition (old-mismatch vs. new) on P(old) in the intermediate (black) and final test (red). The thick black bar covers the 95% highest-density interval (Kruschke, 2011).

In contrast to the first three experiments, which found evidence against PI in a test of WM, here we obtained evidence for PI in an analogous test of LTM. The detrimental effect of PI on old-mismatch objects relative to new objects was most pronounced at the final test, at which there was no noticeable tendency to erroneously report the object's old color. Such a tendency was observed quite strongly at the interleaved tests, which suffered less severe PI.

The results from the interleaved tests – relatively weak PI, and a robustly positive estimate of P(old) – look like a mixture of the results of the WM tests in the previous experiments and the present results from the final LTM test. In fact, it is plausible that the interleaved tests represent a mixture of retrievals from LTM and from WM. The interleaved tests tested the 10 objects from the preceding study set in random order. If people hold several of these objects in WM, and some of these objects happen to be tested early, then responses in the interleaved test could in part draw on information in WM. In contrast, the final test of 160 objects is a relatively pure test of LTM. That test showed clear signs of PI but not of intrusions of old colors. Clearly, the detrimental PI effect is not a direct function of P(old), in line with our previous conclusion that reports of old colors do not reflect an uncontrolled intrusion of old memories but rather the controlled use of LTM.

General Discussion

Across four experiments we found that a test of visual WM was not affected by PI from LTM. In contrast, an analogous test of visual LTM suffered from PI. Together these findings support the assumption that the contents of WM are protected against interference from LTM. At the same time, we found that behavior in a WM test does reflect information in LTM. Experiments 1 and 2 showed proactive facilitation when previously learned object-color associations converged with the object-color bindings to be held in WM. Moreover, in each study, WM responses reflected a small contribution of information about previously learned colors of the tested objects, which came either from the long-term learning phase (Experiments 1 to 3) or from the preceding WM trial (Experiment 4). Of course we cannot rule out that other methods of inducing long-term learning, potentially creating stronger knowledge in LTM, would produce PI in WM. What we can say is that our method induced knowledge strong enough to show a systematic, replicable impact on WM test performance, and that that impact was exclusively beneficial or neutral, never harmful.

How could LTM influence performance on a WM test without generating PI? Clearly, the contribution of LTM is not an obligatory one that intrudes into recall from WM in a non-selective manner. An obligatory contribution of LTM would mean that the information retrieved from LTM is combined with the information retrieved from WM, or that LTM information replaces WM information on a proportion of trials. Because in the old-mismatch condition the object's current color and its old color are uncorrelated, this would be tantamount to adding uniformly distributed noise to the responses in the old-mismatch condition. This would necessarily result in a decrement of performance in the old-mismatch condition relative to baseline. Our results support the conclusion that LTM has an impact in the WM test when it is helpful, but that this influence is blocked when it would be harmful to performance. How is this possible without a homunculus at the levers of the gate that knows what is good for WM? We can think of two ways to implement the flexible gate without having to make assumptions about a control mechanism equipped with implausible knowledge.

One possible scenario is that the person, when tested on an object, assesses the goodness of information in WM about that object's feature, and decides to try and retrieve information about the object from LTM if, and only if, the information in WM is deemed very poor. Rademaker, Tredway, and Tong (2012) have found that participants' confidence ratings were strongly correlated with their accuracy of reproducing orientation in a visual WM task, rendering it plausible that people have knowledge about how good their representations in WM are on a given trial, and could base their decision to retrieve from LTM on it.

Alternatively, the gating mechanism could be a by-product of the competition at test between information retrieved from WM and information retrieved from LTM. In this scenario, the target object presented at test serves as a retrieval cue for associated information in LTM, as well as for information bound to it in WM. The two retrieval processes proceed in parallel, and when they return incongruent information, such as two different colors, the two pieces of information are not simply added or averaged. Instead, they compete in a winner-takes-all fashion, so that the stronger of the two retrieved color representations determines the response exclusively. In most cases, the representation in WM will win the competition. In a minority of cases, the representation retrieved from LTM is stronger than that retrieved from WM, and these cases account for the responses reflecting LTM information in the old-mismatch conditions. In this scenario, LTM representations influence responses only when WM representations are virtually useless, so LTM representations never damage performance. They either result in a response that is as poor as one based purely on WM would be (in the old-mismatch condition) or a response that is better (in the old-match condition).

Our results support the assumption that the information exchange between LTM and WM is controlled by a flexible gate that, when shut, protects the contents of WM from PI (Oberauer, 2009). This enables the cognitive system to represent new information in WM even if it contradicts well-learned information in LTM – for instance, when experiencing or imagining a new feature of an object that deviates from its typical feature (e.g., “think of a pink banana”), or when considering a new action that departs from a routine. This hypothesis is akin to the classic assumption that WM (or the short-term store) is immune to PI (Cowan et al., 2005; Halford et al., 1988), but it differs from it in two regards. First, it leaves open the possibility of PI between multiple representations in WM: Information encoded earlier into WM interferes with information encoded later as long as the earlier-encoded information is not completely removed. Second, our hypothesis leaves open the possibility that information from LTM contributes to responses in a WM task in a beneficial way, and that benefit is reduced by PI in LTM. Hence, our hypothesis makes a prediction about the circumstances under which PI is observed in a WM test: PI should be observed when the interfering information is still in WM, and when performance in the WM test benefits from information in LTM. As we reviewed in the introduction, all cases of PI in tests of WM observed so far (Beaudry et al., 2014) can be explained in this way.

One possible objection against this argument is that it entails the risk of circularity: Whenever evidence for PI in a test of WM is obtained, it can be explained by assuming that LTM contributes to performance in that test, and the PI effect reflects a reduction of that contribution through PI within LTM. It is true that, as long as there is no independent method for gauging the contribution of LTM to a given WM test, this circularity exists. In our defense we say that, unfortunately, this is the lay of the logical land – we are merely spelling it out. It is simply the case that any empirical evidence for PI in a WM test does not demonstrate the vulnerability of the hypothetical WM system to PI from LTM as long as the alternative explanation – a contribution of LTM to performance in the WM test – cannot be ruled out. We point this out to explain why extant evidence for PI in WM tests does not contradict our hypothesis of a flexible gate between LTM and WM. Positive evidence for that hypothesis must come from tests that carry the risk of falsification. Merely testing for PI does not meet that criterion, but our paradigm, measuring PI and proactive facilitation at the same time, does: The flexible-gate hypothesis predicts a selective effect of LTM on WM performance, such that information in LTM can be used to improve WM performance while the same information does not impair performance. Had we found evidence for PI alongside evidence for proactive facilitation, or no evidence for either effect, it would have falsified the hypothesis.

Obviously, the evidence we present here is very limited in that it pertains to only one test of WM with one kind of material. The experimental paradigm can be generalized to other tests of WM. For instance, participants could acquire LTM knowledge of serial order by learning transition probabilities between items (Botvinick & Bylsma, 2005; Majerus et al., 2004) or entire lists (Hebb, 1961; Hitch et al., 2005), and subsequently be tested on immediate serial recall in three conditions: An old-match condition in which the list matches what they had learned; an old-mismatch condition in which the list consists of the items from the learning phase, but in an order mismatching what has been learned; and a new condition using items for which no order information has been acquired in the LTM test. We predict that, as in the present series of experiments, performance in the old-match condition will exceed that in the new condition, showing proactive facilitation, but performance in the old-mismatch condition will not be worse than in the new condition, reflecting the absence of PI.

Figure 1.

Top: Flow of events in the LTM test; bottom: Flow of events in the WM test.

Appendix: The Mixture Models

The 2-parameter mixture model describes the distribution of responses x̂ as a mixture of a von-Mises distribution centered on the true target feature x, and a uniform distribution.

$$P(\widehat{x}|x)=P(\mathit{\text{mem}})\cdot v\mathit{\text{Mises}}(\widehat{x}|,x,\kappa )+[1-P(\mathit{\text{mem}})]\frac{1}{2\pi }$$

The von-Mises distribution – the normal distribution on the circle – is given by:

$$v\mathit{\text{Mises}}(\widehat{x},x,\kappa )=\frac{exp(\kappa \cdot cos(\widehat{x}-x))}{2\pi \cdot I_0(\kappa )}$$

where I₀(κ) is the modified Bessel function of order 0. The two parameters of the mixture model are P(mem), the proportion of responses attributed to the von-Mises distribution, and κ, the precision of the von-Mises distribution. The precision parameter is related to the standard deviation of the von-Mises, SD, by

$$SD=\sqrt{1-\frac{I_1(\kappa )}{I_0(\kappa )}}$$

The extended mixture model includes a third component, a von-Mises distribution centered on the old feature of the target, x_old.

$$P(\widehat{x}|x)=P(\mathit{\text{mem}})\cdot v\mathit{\text{Mises}}(\widehat{x}|,x,\kappa )+P(\mathit{\text{old}})\cdot v\mathit{\text{Mises}}(\widehat{x}|,x_{\mathit{\text{old}}},\kappa )+\left[1-P(\mathit{\text{mem}})-P(\mathit{\text{old}})\right]\frac{1}{2\pi }$$

We fit the model separately to data from each participant in each condition, minimizing the negative log(Likelihood) with the fminsearch function of Matlab, which implements the Simplex algorithm. The model equations above provide the likelihood of each response; their natural logarithms were added across all trials to obtain the log(Likelihood) of the model. The parameter values providing the best fit were used as parameter estimates.