Overlap of movement planning and movement execution reduces reaction time

In the planning of a movement, the brain has the opportunity to delay the incorporation of accuracy requirements of the motor plan in order to reduce the reaction time by up to 100 ms (average: 32 ms). Such shortening of reaction time is observed here when the first phase of the movement consists of a transport phase. This forces us to reconsider the hypothesis that motor plans are fully defined before movement onset.

Abstract

Motor planning is the process of preparing the appropriate motor commands in order to achieve a goal. This process has largely been thought to occur before movement onset and traditionally has been associated with reaction time. However, in a virtual line bisection task we observed an overlap between movement planning and execution. In this task performed with a robotic manipulandum, we observed that participants (n = 30) made straight movements when the line was in front of them (near target) but often made curved movements when the same target was moved sideways (far target, which had the same orientation) in such a way that they crossed the line perpendicular to its orientation. Unexpectedly, movements to the far targets had shorter reaction times than movements to the near targets (mean difference: 32 ms, SE: 5 ms, max: 104 ms). In addition, the curvature of the movement modulated reaction time. A larger increase in movement curvature from the near to the far target was associated with a larger reduction in reaction time. These highly curved movements started with a transport phase during which accuracy demands were not taken into account. We conclude that an accuracy demand imposes a reaction time penalty if processed before movement onset. This penalty is reduced if the start of the movement consists of a transport phase and if the movement plan can be refined with respect to accuracy demands later in the movement, hence demonstrating an overlap between movement planning and execution.

NEW & NOTEWORTHY In the planning of a movement, the brain has the opportunity to delay the incorporation of accuracy requirements of the motor plan in order to reduce the reaction time by up to 100 ms (average: 32 ms). Such shortening of reaction time is observed here when the first phase of the movement consists of a transport phase. This forces us to reconsider the hypothesis that motor plans are fully defined before movement onset.

motor planning is the process of selecting a goal and the appropriate motor commands to achieve this goal. This process has largely been considered part of a single building block that specifies all the characteristics of the ensuing movement. For instance, the latest theories of motor planning suggest that the “complete specification of the motor command” occurs before movement start (Wong et al. 2015). Optimal control theory (Harris and Wolpert 1998; Scott 2004; Todorov and Jordan 2002) also suggests that the control policy is defined before movement onset. In case of multiple possible motor plans, the average of these control policies is used early on and the appropriate motor plan is selected later (Gallivan et al. 2016a, 2016b; Stewart et al. 2014).

The idea that a movement should be completely preplanned before its execution is reminiscent of the work of Henry and Rogers in the 1960s (Henry and Rogers 1960). In their memory drum theory of movement preparation, they suggested that planning took longer for more complex movements, which was reflected in the movement reaction time. More precisely, Henry and Rogers (1960) found that reaction time was shorter when simply lifting a finger than when reaching to a goal with a single movement or with a more complicated sequence of movements. However, in these experiments, distance to the target or accuracy demands (i.e., how accurate the movements must be, which depends on target size, etc.) are confounded with movement complexity. These factors nonetheless influence movement reaction time. For instance, Laszlo and Livesey (1977) found that reaction times were 100 ms shorter for non-goal-directed movements (when accuracy requirements were removed) than for goal-directed movements with strict accuracy demands (while movement complexity was matched). In contrast, loosening accuracy requirements by increasing the width of the target does not influence reaction time (Orban de Xivry 2013; Orban de Xivry and Lefèvre 2016; Quinn et al. 1980). Considering that non-goal-directed movements are movements with minimal accuracy requirements, there seems to be a conflict between the effect of loosening or completely removing accuracy demands on reaction time (i.e., only the latter influences reaction time). The aim of this study was to resolve this apparent contradiction by looking at the actual influence of accuracy demands on movement reaction time.

To do this, we set up a line bisection task in which the position of the lines forced the participants to adopt different strategies for different conditions but accuracy demands were identical across conditions. As a result, we observed that when the movement began with a transport phase (requiring less accuracy) the reaction time was much shorter than when the participants moved directly toward the center of the line. In other words, delaying the influence of accuracy demands on movement kinematics (because of the transport phase) led to shorter reaction times, which were up to 100 ms shorter than in the control condition. That is, delaying the planning for movement accuracy during execution led to a substantial decrease in reaction time. These data suggest that increasing the overlap between movement planning and movement execution leads to a reduction in reaction time.

METHODS

Participants.

Thirty-one healthy young participants were recruited to participate in our experiment. All participants had no known history of neurological disorders and no recent or residual consequences of upper limb trauma, were right-handed and between 20 and 38 yr old (mean: 24 yr), and had normal or corrected-to-normal vision. All of them gave written informed consent. The procedures were approved by the Université catholique de Louvain Ethics Committee and were in accordance with the latest version of the Declaration of Helsinki.

Experimental setup.

Participants sat in front of a robotic arm (Endpoint Kinarm, BKin Technologies, Kingston, ON, Canada). They controlled the handle of the robot with their right hand in order to move a white cursor (disk with diameter of 0.5 cm) that was displayed on a horizontal mirror positioned above the arm. The cursor and targets of interest were displayed on a screen placed tangentially above the mirror and were reflected by it. Because the mirror was halfway between the handle and the screen [52-in. monitor (16-to-9 ratio) with refresh rate at 75 Hz], the cursor appeared to be positioned at the same position in space as the hand after horizontal positions were properly calibrated. With this setup, subjects could not see their hand and the displayed cursor was the only available visual feedback of their arm position.

The robot controlled the display through custom-made MATLAB (R2007) programs uploaded to a real-time computer. It also monitored hand position, velocity, and acceleration at 1,000 Hz. Kinematic and dynamic data were stored on a PC for off-line analysis.

Protocol.

In this experiment, participants were instructed to perform a line bisection task by moving the cursor and crossing lines projected on the horizontal mirror at their middle point (Fig. 1). At the start of each trial, participants were required to bring the hand cursor inside a 2-cm × 2-cm orange square that was located on the lower right part of the workspace. When the cursor was inside the square, an orange line appeared at one of four possible positions. There were three possible line lengths (10, 15, or 20 cm). The participants were instructed to drive the cursor through the middle of the line with a continuous and smooth movement. For each position, the line was presented either horizontally or vertically (see Fig. 1). The center of horizontal lines was either 5 cm or 22.5 cm to the left of the starting point and 10 cm above it. The center of the vertical lines was 10 cm to the left of the starting point and either 5 cm or 22.5 cm above it. With this design, each line position was associated with only one line orientation. Lines were presented after a random time interval once the hand cursor was inside the starting position (1,000-1,500 ms) so that the participants could not anticipate where and when the next line would appear. Once the participants crossed the line they were required to go back to the starting position, and the next trial was initiated after an intertrial time interval of 200 ms. Participants were instructed to move at a comfortable speed. Each block consisted of five subblocks of 12 trials (2 line orientations × 2 distances × 3 lengths) that were randomly presented. Participants performed two blocks for a total of 120 trials.

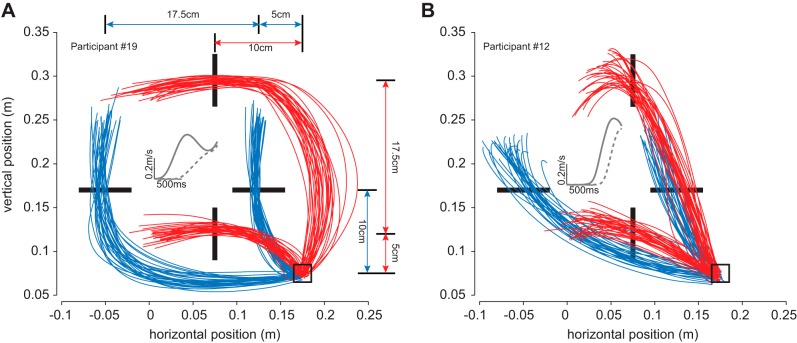
Fig. 1.

During the line bisection task, participants adopted very different behaviors as illustrated by the hand trajectories from 2 typical subjects. Participant 19 (A) exhibited curved movements for the far targets, while participant 12 (B) reached straight to the center of the line for both near and far targets. For each subject, the starting position is represented by the square and the target lines are represented as black bars. For clarity, the lines are shorter in the illustration than in reality (10, 15, or 20 cm). Hand trajectories of all the trials for these participants are given for horizontal lines (blue traces) and for vertical lines (red traces). The distances between the different targets and the starting position are given in A. For each subject, the inset in the center of the panel represents the average vectorial velocity trace (aligned on time of reaching to the target) for horizontal near and far targets (dashed and solid lines, respectively). Body midline was aligned with 0 on the horizontal axis.

Movement curvature was measured as the average distance between the actual hand trajectory and a straight line linking movement onset and offset. Reaction time was defined as the time between the line appearance and the start of the movement, which corresponded to the time at which the vectorial velocity reached 2 cm/s. Trials in which movement onset was detected before target appearance or >750 ms after target appearance were rejected from the analysis (8% of the trials). Movement duration was computed as the time between movement onset and when the hand cursor crossed the line (i.e., offset). The absolute position error was computed as the distance between the hand cursor and the middle of the line at the time of line bisection. Finally, to quantify movement variability of these two-dimensional movements, we first normalized the time of movement (0% is the movement onset and 100% is line bisection) and resampled each movement in 0.4% time intervals (250 samples) using spline functions (as in Orban de Xivry et al. 2011). For each of the 250 samples, we computed the minimum distance between the two-dimensional cursor position and the average movement trajectory. Across-movement variability was equal to the average distance across movements. This measure of variability was normalized by its value on the first sample (at movement onset) in order to account for intersubject variability.

Changes in line length and in line position ensured that the participants were not aware that they had to reach the exact same point. However, the influence of the line length parameter on the behavior was not analyzed. Data were therefore merged according to the remaining conditions.

For each participant, median reaction time (instead of mean given the skewness of reaction time data) and mean curvature, absolute position error, movement duration, and normalized variability were computed. They were used as dependent variables in two repeated-measure ANOVAs with two within-subject factors: orientation of the line (horizontal or vertical) and distance of the line (near or far). Tukey's post hoc tests were used for one-to-one comparisons. Changes in the variables of interest were obtained by subtracting their value for the near target from the same measure for the far target independently for each line orientation.

Statistical tests were performed with Statistica (Dell). Level of significance was 0.05. Effect sizes were evaluated through partial η². The effect of period (1st or 2nd half of the experiment) was never found to be significant, either as main effect or in an interaction (absence of learning effect). This effect is thus not reported in results.

One participant was excluded from the analysis because he failed to comply with the task instructions and did not aim at the center of the lines.

RESULTS

We asked participants to bisect lines of different length with a cursor. In this task, the directionality of the target led to a wide between-participant variety of hand paths. This variety of strategies is illustrated in Fig. 1 for two participants. The first participant presented in Fig. 1 (participant 19, Fig. 1A) exhibited simple and slightly curved movements toward the near targets. The velocity profile of these movements to the near targets exhibited a single peak. In contrast, the movements to the far targets were highly curved and the corresponding average velocity profiles exhibited a local minimum (Fig. 1A, inset). In other words, this participant chose a curved hand trajectory in such a way that it crossed the line perpendicular to it. However, there was a lot of variability across participants in terms of movement curvature. Some participants, such as the one illustrated in Fig. 1B, did not exhibit highly curved movements for the far targets, and the velocity profiles for both targets only exhibited a single peak (Fig. 1B, inset).

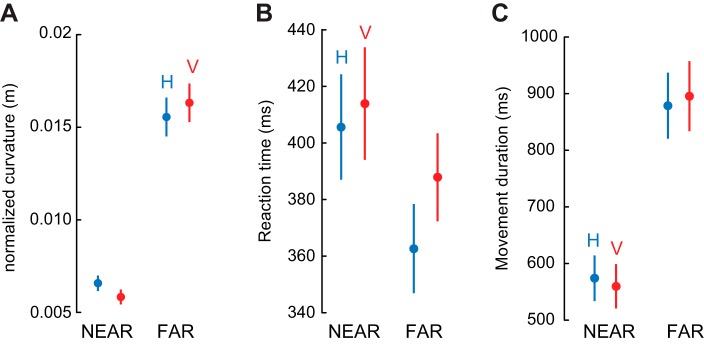
This feature of the movements was characterized by the movement curvature, which was much higher for movements to the far than to the near targets [main effect of target distance: F(1,29) = 150.69, P < 0.001, partial η²: 0.84; Fig. 2A]. In addition, the change in movement curvature was slightly larger for vertical than horizontal lines [interaction between orientation and distance: F(1,29) = 5.94, P = 0.02, partial η²: 0.17]. Nonetheless, the effect of target distance on movement curvature was highly significant for both line orientations (Tukey's post hoc tests: P < 0.001 for both).

Fig. 2.

Target distance influenced normalized movement curvature (A), reaction time (B), and movement duration (C) for both line orientations. Blue represents horizontal lines (H) and red vertical lines (V). Error bars represent SE.

Despite being more curved, movements to the far targets had shorter reaction times than movements to the near targets (Fig. 2B). This effect gave rise to a main effect of target distance on reaction time [F(1,29) = 46.36, P < 0.001, partial η²: 0.61] but also to an interaction between line direction and target distance [F(1,29) = 8.62, P = 0.006, partial η²: 0.23], which was due to the fact that the decrease in reaction time with target distance was more pronounced for horizontal lines than for vertical lines. However, this effect remained significant for both line orientations [post hoc test: P < 0.001 for both orientations; change in reaction time (ΔRT) horizontal targets (H): 40 ± 5.8 ms (mean ± SE); ΔRT vertical targets (V): 24 ± 5.5 ms]. That is, it took less time to start a more curved movement toward a farther target. Nonetheless, accuracy to near and far targets were essentially identical [absolute position error: main effect of target distance: F(1,29) = 0.55, P = 0.46, partial η²: 0.018]. However, this change in reaction time was insufficient to compensate for the longer movement duration (from movement onset to movement offset) for the far target compared with the near target. Indeed, the movements toward the far targets were, on average, 320 ms (SE: 24 ms) longer than the movements toward the near target [main effect of target distance: F(1,29) = 183.22, P < 0.001, partial η²: 0.86]. Participants that reduced their reaction time by 80–100 ms from near to far targets had a corresponding increase in movement duration of 300–400 ms.

Similar to movement curvature, the pattern of within-subject variability across movements was different for the near and far targets. While across-movement variability only slightly increased for movements to the near target, there was a marked transient increase in across-movement variability for movements to the far target. Movement variability peaked around the middle of movement before decreasing to levels similar to those for the near target as the participants approached the target (Fig. 3). At the time of line bisection, variability was higher for the far target than for the near target [main effect of target distance: F(1,29) = 19.4, P < 0.001, partial η²: 0.4]. This effect was present for the horizontal lines but not for the vertical lines [interaction between line orientation and target distance: F(1,29) = 8.32, P = 0.007; post hoc Tukey test: H: P < 0.001, V: P = 0.3].

Fig. 3.

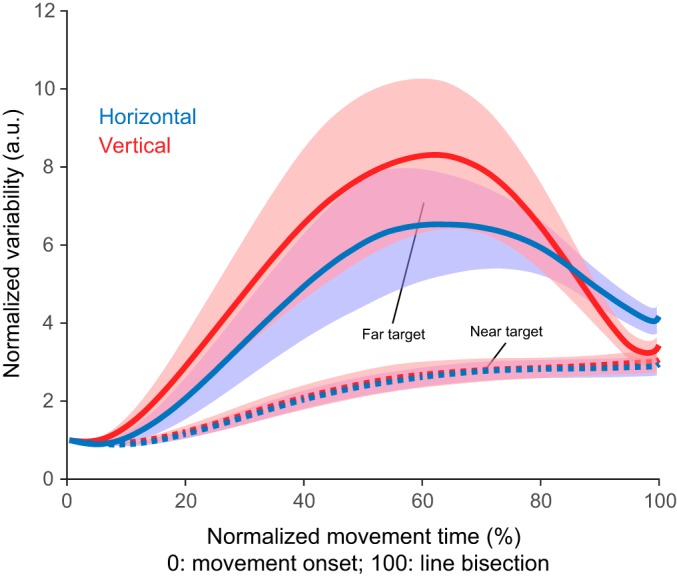
Target distance influenced the normalized within-subject variability along the movements for both line orientations. Blue represents horizontal lines (H) and red vertical lines (V). Solid lines represent the far targets and dashed lines the near targets. Error bars represent 95% confidence interval. a.u., Arbitrary units.

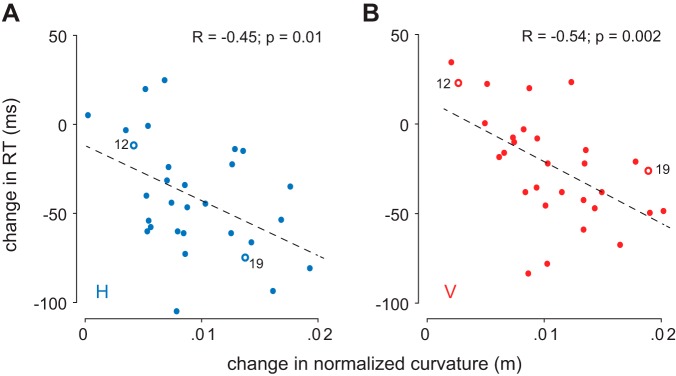
There was a lot of variability in how the curvature of movements changed with target distance (compare Fig. 1, A and B). Therefore, we tested whether participants who exhibited large changes in movement curvature had a larger change in reaction time with target distance than people who performed straight movements toward the target independent of target distance (Fig. 1B). To do this, we correlated the change in median reaction time from near to far targets with the change in movement curvature from near to far targets. This was performed independently for each line orientation (Fig. 4). We found that the changes in curvature with movement distance were correlated with the change in reaction time with movement distance across subjects (H: r = −0.45, P = 0.01; V: r = −0.54, P = 0.002). It should be noted that reaction time and curvature for each distance and line orientation were not correlated, probably because of the large interindividual differences in average reaction time. Similarly, the change in reaction time was uncorrelated with the change in absolute error at the end of the movement (H: r = −0.23, P = 0.23; V: r = 0.03, P = 0.86) or the change in end-point movement variability (H: r = −0.08, P = 0.66; V: r = 0.2, P = 0.28).

Fig. 4.

Participants who exhibited a larger increase in movement curvature from near to far targets also exhibited a larger decrease in reaction time (RT) with target distance. This was true for both line orientations. A: movements toward horizontal lines. B: movements toward vertical lines. In each panel, the 2 points indicated by open circles and numbers correspond to the values for the 2 subjects illustrated in Fig. 1.

The change in target distance influenced not only movement curvature but also movement speed [main effect of target distance on movement peak velocity: F(1,29) = 137.9, P < 0.0001; mean ± SE: near targets: 0.44 ± 0.053 m/s, far targets: 0.56 ± 0.061 m/s]. In addition, peak velocity of the movement was correlated with reaction time. We observed that an increase in movement speed was coupled with an increase in reaction time (H: r = 0.54, P = 0.02; V: r = 0.35, P = 0.057). To make sure that the effect of movement curvature on reaction time was independent of movement speed, we performed a partial correlation analysis and found that, even when the change in movement speed was taken into account, changes in movement curvature and changes in movement reaction time were still correlated (H: r = −0.38, P = 0.038; V: r = −0.48, P = 0.007).

DISCUSSION

In this study, we showed that the reaction time of a reaching movement was affected by the chosen hand trajectory. Curved movements made toward a more distant target had, on average, a shorter reaction time than straighter movements made toward a nearer target. Furthermore, this effect depended on the curvature of the movement. A larger increase in movement curvature for the far compared with the near target was accompanied by a larger decrease in movement reaction time. This decrease in reaction time was not correlated with movement accuracy or variability.

Confounding factors.

Movement complexity, movement extent, or the presence or absence of a sequence of submovements differs between movements to near and far targets. Interestingly, all these possible confounding factors would result in an increase in reaction time for movements toward the far targets compared with the near targets (i.e., opposite to what was observed). For instance, several studies have shown that an increase in movement complexity is accompanied by longer reaction times (Christina and Rose 1985; Henry and Rogers 1960; Klapp et al. 1974). Similarly, larger movements are traditionally associated with longer reaction times (Falco et al. 2013; Munro et al. 2007). Finally, an increased number of movement phases, such as the ones we sometimes observed toward the far target, has been associated with an increase in reaction time (Klapp 1995).

Taking accuracy demands into account later.

In contrast to Laszlo and Livesey (1977), who showed that the presence or absence of accuracy demands had a substantial impact on reaction time, we observed a modulation of reaction time with target distance despite matched accuracy demands across conditions. On the basis of our results, we hypothesize that, while movements to the near targets had to take the accuracy demand into account before movement onset, the influence of accuracy demands for movements to the farther target could be delayed to later during the movement. As a result, reaction times were shorter for the farther target.

This hypothesis is consistent with the fact that movement variability increased during the first phase of the movements toward the far target (a sign that accuracy demands are not so important early in the movement) but was reduced during the second phase of the movement (Fig. 3). This is also compatible with the existence of two movement phases: a transport phase during which across-movement variability increased and a second phase during which movement variability was reduced. In contrast, movement variability remained much smaller during movements toward the near target (Fig. 3), which suggests that the existence of these two phases is specific to movements to the farther targets.

This hypothesis can also account for the correlation between movement curvature and reaction time (Fig. 4). Following this hypothesis, highly curved movements (e.g., Fig. 1A), which often consisted of two velocity peaks, are composed of two submovement parts: a first submovement aimed at transporting the hand to an intermediate location, while the second submovement was responsible for bringing the hand to bisect the target line as accurately as possible. In contrast, participants who moved their hand directly toward the far target (e.g., Fig. 1B) did not exhibit such a transport phase and directly aimed at the center of the line. Therefore, for these movements, accuracy demands were taken into account before movement initiation. This suggests that participants who postponed the processing of accuracy demands had a shorter reaction time for far targets compared with near targets whereas participants who did not postpone accuracy demands exhibited similar reaction times for both target distances. Similar effects of accuracy demands on reaction time have been found for catch-up saccades that are executed during visual tracking of moving targets (Orban de Xivry and Lefèvre 2007). Saccadic eye movements have been thought to be ballistic because of the limited visual inputs during their execution, yet when saccades were made toward a moving target, some of these movements exhibited clear changes in direction (i.e., curvature) during their execution (Schreiber et al. 2006). Similar to the reaching movements in this study, curved saccades had a shorter reaction time than straight saccades. That is, saccades that were updated online to integrate new information had a shorter reaction time than the straighter saccades that were not modified during the movements (Schreiber et al. 2006). Together with our results, this suggests that the brain either can decide to start a movement early and modify it later on the basis of new incoming information or can delay the onset of a movement and make it more straight (i.e., no change in goal during movement execution).

Importantly, our data highlight that taking accuracy demands into account in the planning of movement trajectory is not a black or white process as suggested by the study of Laszlo and Livesey (1977). Rather, we observed a continuum of change in reaction times. For straight hand trajectories to the far targets, accuracy demands are taken into account before movement onset. For such straight movements toward the target, reaction time is not influenced by the loosening of accuracy demands (as in Orban de Xivry 2013; Orban de Xivry and Lefèvre 2016) but just by their presence. Alternatively, delaying the effect of accuracy demands on hand trajectory (by refining movement plan during its execution) resulted in a gradual decrease in reaction time.

Impact of these results on theories of motor planning.

Reaction time is widely considered an important variable in understanding motor planning, as it is considered that all the processes related to motor planning take place during that interval (Haith et al. 2016; Wong et al. 2015). Indeed, there is a widely accepted hypothesis that motor commands are assembled before movement execution during the motor planning stage. However, the present data suggest that this might only be true for pure ballistic movements and reveal a different picture. Incorporating accuracy demands into motor planning seems to be a dynamic process, with the amount of accuracy demands taken into account increasing over time. Independent of how loose they are, taking into account accuracy demands imposes a reaction time penalty. This penalty is reduced if the start of the movement consists of a transport phase and therefore the accuracy demands can be incorporated into motor commands later in the movements, hence reducing the cost of accuracy on reaction time.

The incorporation of accuracy demands into the control policy can be achieved by the tuning of feedback gains (Scott 2004; Todorov and Jordan 2002; Wong et al. 2015), which control the response of the motor system to any perturbations. The tuning of these feedback gains is considered to be achieved at the planning stage for most movements (Crevecoeur et al. 2014; Nashed et al. 2012) but can be performed during the movements if relevant information has changed (position of target: Dimitriou et al. 2013; choice of target: Gallivan et al. 2016b). Here we provide an example in which the motor system deliberately chose to tune the feedback gains later in the movement, even in the absence of any external changes/perturbation.

Such specification of motor commands before movement onset is also a hallmark of the state-space theory of motor planning in which neurons in the motor cortex are thought to reach a given neural state before the movement is actually started (Ames et al. 2014; Kaufman et al. 2014; Shenoy et al. 2013). One can then wonder what the neural state looks like when motor preparation is not complete before movement onset but is further refined early during the movement. One prediction is that preparatory activity (in the null space following Kaufman et al. 2014) should be observed during movement execution. Our paradigm can provide information about how delaying the influence of accuracy demands on movement trajectory can influence the neural state of the motor cortex prior to and during movement.

Conclusions.

In this study, we demonstrate that the presence of accuracy demands for reaching movements greatly impacts reaction time. That is, reaction time can be up to 100 ms longer in movements for which accuracy demands are immediately taken into account compared with movements for which the influence of accuracy demands on movement kinematics is delayed. In contrast to what current theories of motor planning suggest, these results show that movement kinematics can be refined during movement execution in order to reduce reaction time at movement initiation.

GRANTS

This work was supported by the Belgian Program on Interuniversity Attraction Poles and PRODEX initiated by the Belgian Federal Science Policy Office, Actions de Recherche Concertée (French community, Belgium), and the European Space Agency (ESA) of the European Union. V. Legrain is supported by the Research Fund of the French-Speaking Community of Belgium (F.R.S.-FNRS).

DISCLOSURES

No conflicts of interest, financial or otherwise, are declared by the author(s).

AUTHOR CONTRIBUTIONS

J.-J.O.d.X. and V.L. conceived and designed research; J.-J.O.d.X. performed experiments; J.-J.O.d.X. analyzed data; J.-J.O.d.X. interpreted results of experiments; J.-J.O.d.X. prepared figures; J.-J.O.d.X. drafted manuscript; J.-J.O.d.X., V.L., and P.L. edited and revised manuscript; J.-J.O.d.X., V.L., and P.L. approved final version of manuscript.