Optimizing computer models of corticospinal neurons to replicate in vitro dynamics

We developed models of motor cortex corticospinal neurons that replicate in vitro dynamics, including hyperpolarization-induced sag and realistic firing patterns. Models demonstrated resonance in response to synaptic stimulation, with resonance frequency increasing in apical dendrites with increasing distance from soma, matching the increasing oscillation frequencies spanning deep to superficial cortical layers. This gradient may enable specific corticospinal neuron dendrites to entrain to relevant oscillations in different cortical layers, contributing to appropriate motor output commands.

Abstract

Corticospinal neurons (SPI), thick-tufted pyramidal neurons in motor cortex layer 5B that project caudally via the medullary pyramids, display distinct class-specific electrophysiological properties in vitro: strong sag with hyperpolarization, lack of adaptation, and a nearly linear frequency-current (F–I) relationship. We used our electrophysiological data to produce a pair of large archives of SPI neuron computer models in two model classes: 1) detailed models with full reconstruction; and 2) simplified models with six compartments. We used a PRAXIS and an evolutionary multiobjective optimization (EMO) in sequence to determine ion channel conductances. EMO selected good models from each of the two model classes to form the two model archives. Archived models showed tradeoffs across fitness functions. For example, parameters that produced excellent F–I fit produced a less-optimal fit for interspike voltage trajectory. Because of these tradeoffs, there was no single best model but rather models that would be best for particular usages for either single neuron or network explorations. Further exploration of exemplar models with strong F–I fit demonstrated that both the detailed and simple models produced excellent matches to the experimental data. Although dendritic ion identities and densities cannot yet be fully determined experimentally, we explored the consequences of a demonstrated proximal to distal density gradient of I_h, demonstrating that this would lead to a gradient of resonance properties with increased resonant frequencies more distally. We suggest that this dynamical feature could serve to make the cell particularly responsive to major frequency bands that differ by cortical layer.

NEW & NOTEWORTHY We developed models of motor cortex corticospinal neurons that replicate in vitro dynamics, including hyperpolarization-induced sag and realistic firing patterns. Models demonstrated resonance in response to synaptic stimulation, with resonance frequency increasing in apical dendrites with increasing distance from soma, matching the increasing oscillation frequencies spanning deep to superficial cortical layers. This gradient may enable specific corticospinal neuron dendrites to entrain to relevant oscillations in different cortical layers, contributing to appropriate motor output commands.

corticospinal neurons (SPI) are the large pyramidal neurons in motor cortex layer 5B (L5B) that project caudally via the medullary pyramids to brainstem centers or directly to the spinal cord (Suter et al. 2013). In the primary motor cortex, these cells will provide output that may define or at least influence motor commands. SPI neurons display distinct class-specific electrophysiological properties in in vitro recordings. The subthreshold properties are notable for strong sag with hyperpolarization, providing evidence for high levels of I_h, the anomalous rectifier (Sheets et al. 2011). SPI neurons also show relatively brief action potentials (APs), with a lack of adaptation with firing in response to current clamp and a nearly linear frequency-current (F–I) relationship (Suter et al. 2013). These physiological properties distinguish SPIs from the other excitatory cell population of L5, the corticostriatal cells, which also differ anatomically by having smaller apical tufts. Along with other excitatory cell types in neocortex, corticostriatal neurons are involved in various loops via other telencephalic structures: thalamus, striatum, cerebellum, and contralateral cortex. Understanding of the functional organization of motor cortex will require knowledge of both corticospinal and corticostriatal populations (Anderson et al. 2010; Kiritani et al. 2012; Apicella et al. 2012; Suter and Shepherd 2015; Yamawaki and Shepherd 2015).

In addition to playing a critical role in projection out of the motor cortex circuit, SPI neurons are remarkable in their size and dendritic appearance. The large apical dendrite will play an important role in determining input-output properties of this cell type, with evidence pointing to a major role for I_h in modulating the efficacy of synaptic integration in the dendrites (Sheets et al. 2011). Further evaluation of these properties will require better understanding of the interplay of dendritic and somatic voltage-sensitive ion channels in producing local membrane potentials and converting them to somatic and axon-initial-segment depolarizations leading to APs. However, dendritic localization and isomer identity of the voltage-sensitive channel densities within dendrites cannot yet be determined with precision experimentally. Immunohistochemical techniques show channel locations but give only a gross estimate of density and do not show functional state. Dual impalement of apical dendrite (at ∼500 μm) and soma (Kole et al. 2006) gives limited information on oblique dendrites and is very difficult due to small dendrite size. Physiological and pharmacological manipulations are not generally able to isolate particular channel types with precision even when these are accessible. Current-source density (CSD) assessments use extracellular electrodes that record signals from dendrites but these then mix response from apical and oblique dendrites, from multiple cells, and from different channel types. Voltage-sensitive dye imaging technologies are also not sensitive enough to obtain this type of data at the required resolution.

Computational modeling provides a complementary approach for exploring the integrative properties of SPI neurons and predicting the set of ion channels and biophysical mechanisms that contribute to their dynamics and function. Despite the availability of numerous models that capture specific aspects of layer 5 pyramidal neuron electrical behavior (Hay et al. 2011; Hu et al. 2009; Bahl et al. 2012; Almog and Korngreen 2014), none of these models have captured the multiple features that we have explored experimentally: I_h-dependent sag and resonance, linear F–I curve, nonadapting firing rates, and fast APs (Suter et al. 2013). We therefore started afresh, using optimization procedures to constrain model dynamics to match the dynamics observed in our electrophysiological data. In this way, we created a set of models exhibiting optimality across one or more out of a set of fitness functions. We used these functions to create publicly available searchable archives of both detailed and simplified (6-compartment) multicompartment models, giving users flexibility in selecting which SPI models one might want to use in different contexts.

Our approach to optimization was to use a two-step sequence consisting of an adaptive coordinate descent algorithm (PRAXIS) (Brent 1973; Carnevale and Hines 2006) for fitting the passive properties (capacitance, resistivity, leak, etc.) and the densities of channels contributing to subthreshold responses, followed by evolutionary multiobjective optimization (EMO) (Deb 2001; Deb et al. 2002; Garrett 2014a,b) to fit densities of other active channels to optimize particular firing features. The first step in our approach produces a resting membrane potential. The second step then more easily molds firing patterns atop this stable resting membrane potential.

Our models demonstrated several forms of I_h-dependent resonance as emergent dynamical features that were not specifically targeted by optimization. Subthreshold response to somatic stimulation showed resonance between 4 and 6 Hz, consistent with experiment (Sheets et al. 2011). Synaptic resonance frequency in the apical dendrite varied from about 7–20 Hz with a gradual increase up the apical dendrite (Silva et al. 1991), paralleling the increase in hyperpolarization-activated cyclic nucleotide-gated (HCN) channel density with distance from the soma. This resonance could allow the apical dendrites to parse out primary activation frequencies that differ by cortical layer.

MATERIALS AND METHODS

Animals and Slice Preparation

Animal studies were approved by the Animal Care and Use Committee of Northwestern University. Mice (strain: C57Bl/6J; Jackson Laboratories) underwent stereotaxic injections of retrograde tracers (fluorescent microspheres) at postnatal day (P) 21, following previously described methods. Animals were euthanized by anesthetic overdose and decapitation, and brain slices (300 μm) containing motor cortex were prepared one or more days after tracer injections (P23-32). Slices were transferred to artificial cerebrospinal fluid (ACSF, in mM: 127 NaCl, 25 NaHCO₃, 25 d-glucose, 2.5 KCl, 1 MgCl₂, 2 CaCl₂, and 1.25 NaH₂PO₃; aerated with 95% O₂-5% CO₂), maintained at 34°C for 30 min, and returned to room temperature for at least 30 min before recording.

Electrophysiology

Brain slices were transferred to the recording chamber of an upright microscope (Olympus BX51WI) and superfused with recirculating aerated ACSF warmed to 34°C. Fluorescently labeled SPI neurons were targeted for somatic whole cell recordings using borosilicate patch pipettes (tip resistance 2–4 MΩ) and a patch-clamp amplifier (Multiclamp 700B; Axon Instruments). Pipette capacitance was compensated before breaking in, and in current-clamp mode the bridge was balanced periodically using the auto-adjust feature. Series resistance was monitored periodically in voltage-clamp mode by brief negative steps, and recordings were terminated if it exceeded ∼25 MΩ.

Recordings were made in current-clamp mode with a potassium-based internal solution (in mM: 128 KMeSO₄, 10 HEPES, 1 K₂-EGTA, 4 MgCl₂, 4 Na₂-ATP, 0.4 Na-GTP, 10 Na₂-phosphocreatine, and 3 ascorbate; pH 7.3). The intracellular concentration of sodium ion was 28.4 mM, and the calculated reversal potential for sodium was 44.6 mV. In some experiments biocytin (2–4 mg/ml) was added to the internal solution. Traces were filtered online with the amplifier's 10 kHz Bessel filter and digitized (16-bit resolution, USB-6259; National Instruments) at 40 kHz. The modeled neuron's recordings were filtered at 4 kHz and sampled at 10 kHz; these data were excluded from AP waveform analysis but included in firing rate analyses. Experiments were controlled by open-source (www.ephus.org) Ephus software on a workstation running Microsoft Windows (Suter et al. 2010). All data are reported after subtracting 10.5 mV from the recorded membrane potential to compensate for a calculated liquid junction potential.

Intrinsic properties were characterized by presenting families of current steps (−200 to 600 pA in 50-pA increments, duration 1.0 s), unless indicated otherwise. A holding potential (V_h) of about −80 mV was maintained by constant current injection. A parallel data set was collected at the resting membrane potential (V_r). Because V_r tended to be close to V_h and because results from the two data sets were highly consistent, the data presented are mostly from the V_h data set, except where indicated.

Sag of the membrane potential was calculated as the percentage difference between the peak amplitude of the initial response (0–0.1 s after step onset) relative to the peak amplitude of the steady-state response (0.9–1.0 s), both measured with respect to the baseline averaged over 0.3 s before step onset. We averaged a 5-ms window around the initial and the steady-state peak.

To quantify the shape of individual AP waveforms, we first identified the threshold (in mV) as the point when dV/dt exceeded 10% of its maximum value, relative to a dV/dt baseline measured 2 ms before the AP peak. The AP peak was taken as the maximum membrane potential reached after threshold, and AP amplitude as the difference between threshold and peak. The AP width was measured at half- and quarter-amplitudes with linear interpolation between samples. The minimum and maximum dV/dt slopes were also used to quantify AP shape.

Pharmacology

Synaptic blockers were added to the bath solution (10 μM NBQX, 5 μM CPP, and 10 μM gabazine; Tocris), except where noted. Additional drugs to block voltage-gated ion channels were added during the recordings from the modeled neuron, as noted: TTX (1 μM; Tocris), TEA (15 mM; Sigma), 4-AP (2.5 mM; Sigma), XE991 (10 μM; Tocris), and ZD7288 (25 μM; Tocris).

Morphological Reconstruction

After recordings were completed, brain slices containing biocytin-filled neurons were returned to a holding chamber for 1–2 h at room temperature, before fixing in 4% PFA-phosphate buffer (8% aqueous paraformaldehyde diluted 1:1 with 0.2 M phosphate buffer) for ∼16 h at 22°C (Fig. 1). After fixation, slices were rinsed thoroughly and maintained in phosphate buffer, with daily solution changes until further processing. To stain the recorded neurons for two-photon fluorescence microscopy, slices were rinsed in Tris-buffered saline (TBS, 7×, 5 min each), permeabilized in TBS-Triton (3%, 1 h), blocked in normal goat serum (NGS; 10%) and BSA (bovine serum albumin, 0.5%) in TBS for 30 min, rinsed in TBS (2×, 5 min each), and stained with streptavidin-Alexa-488 conjugate (1:200; Invitrogen) in TBS with NGS (1%) and BSA (0.5%) for ∼16 h at 4°C. After being stained, slices were rinsed in TBS (4×, 5 min each) and mounted on a #1 glass cover slip (0.17-mm thickness) in mounting medium (Dako), using additional coverslips as spacers to avoid compression of the tissue. Slides were sealed with nail polish. Samples were shielded from light throughout these procedures.

Fig. 1.

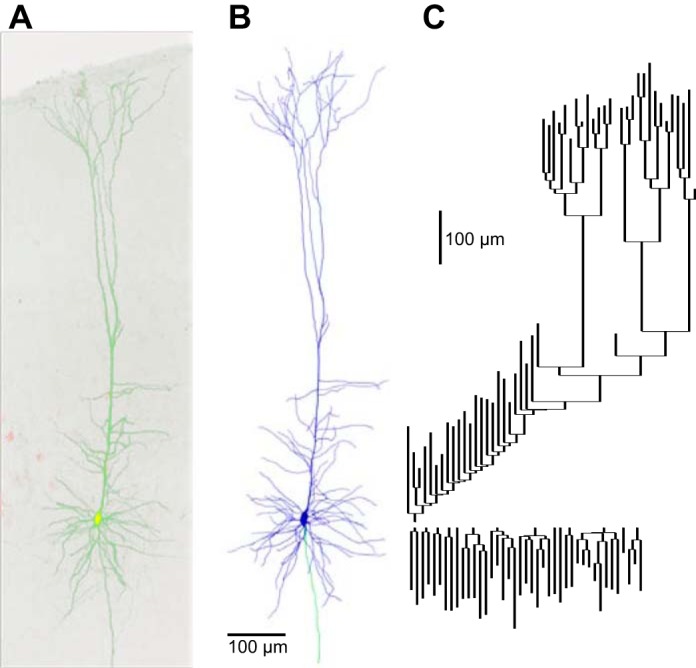
Morphological reconstruction of the representative corticospinal neuron. A: 2-photon fluorescence image (maximum intensity projection) of a corticospinal neuron filled intracellularly with fluorescent dye (green); the red channel shows numerous corticospinal neurons retrogradely labeled with fluorescent beads (red). B: 3-dimensional reconstruction of the same neuron. Blue, dendrites; green, axon. C: dendrogram representation of the dendritic arbor topology of the reconstructed neuron. Apical branches point upwards and basal branches point downward. Vertical distance represents dendritic path length; horizontal connectors are dimensionless.

Fluorescent neurons were imaged on a custom-built two-photon laser-scanning microscope equipped with a ×25 objective lens (numerical aperture, 0.8; Zeiss), using the lens collar to compensate for differences in index of refraction between the immersion medium (glycerol), cover slip, and mounting medium. The laser was tuned to 810 nm to excite both the dye in the filled neuron and the retrograde tracer for emission in separate channels. Pixels were 0.2 μm (x and y dimensions), and z-steps were 0.84 μm. Image stack contained ∼1.3 billion voxels, with typically three to four stacks required per neuron for the entire dendritic arbor. For visualization, custom software macros (ImageJ; Fiji) automatically flattened the image stacks by maximal intensity z-projection and stitched the resulting tiles starting from stack coordinates recorded during image acquisition, with an automatic optimization step for fine alignment. The stitching step made use of a freely available algorithm (Preibisch et al. 2009). To calibrate the scale of the resulting high-resolution image stacks, epifluorescence images were taken with a ×4 objective lens of the live slice and of the fixed slice once mounted, and the x-y distance between landmarks was compared.

Neuronal morphology was digitally reconstructed using Neurolucida software (MBF Bioscience). Multiple image stacks were aligned in three dimensions, the software was configured for the appropriate voxel size, and the neuron was reconstructed manually. Dendrites and the axon were reconstructed as a connected tree of tapered cylinders, and the soma was reconstructed as a series of contours. Spines were not reconstructed. All dendrites were reconstructed; the axonal reconstruction was limited to the proximal intracortical portion of the main stem.

Modeling

Simulations were run in the NEURON (version 7.4) simulation environment (Carnevale and Hines 2006).

Model Units

Throughout the paper, the following units are used for the different model parameters and variables: voltages are given in millivolts (mV); currents are given in nanoamps (nA); diameters (diam) and lengths (L) are given in micrometers (μm); conductance densities are given in S/cm² unless indicated otherwise; capacitance density (cap) is given in μF/cm²; permeability is given in cm/s; axial resistivity is given in Ω-cm; time-constants (τs) are given in milliseconds (ms); and temperatures are given in °C.

Detailed Model

A representative SPI neuron was selected for detailed reconstruction and biophysical simulation. The morphological reconstruction was exported from Neurolucida to an MBF ASC format file and then imported into NEURON using the Import3D tool, which converted the soma from contour lines to series of tapered cylinders and established connections from each dendritic process to the center of the soma. We confirmed the absence of any topologically or electrically isolated sections and grouped the resulting morphology into somatic, axonal, basal dendritic, and apical dendritic sections. Apical dendrites were further subdivided into the following sections: main-trunk (proximal to soma), oblique, uppertrunk (distal from soma), tuft, before-branchpoint, and after-branchpoint. Here branchpoint is the first main branch in the apical dendrite main trunk when moving from soma towards tuft. Based on inspection of the two-photon images, all dendritic sections except the proximal apical trunk (0–32 μm) were classified as spiny. The effect of spines was approximated by increasing the membrane capacitance and the membrane leak conductance (in all spiny sections) by a factor >1 that was among the passive properties optimized during development of the model. In all other respects passive properties were evenly distributed in all compartments. The model neuron was composed of compartments. We have made the morphological reconstruction available at http://neuromorpho.org/neuron_info.jsp?neuron_name=BS0284, part of a larger set of SPI neuron reconstructions (http://neuromorpho.org/KeywordResult.jsp?str=suter_shepherd,corticospinal).

Simplified Model

A simplified (simple) model consisting of 6 compartments was also developed for use in large network simulations. The six compartments consisted of three apical dendrites (equivalent properties in each compartment), one basal dendrite, one soma, and one axon.

Ion Channels and Ca²⁺ Handling Mechanisms

Model neurons contained a passive leak channel, fast sodium channel (Na_f) for producing APs, three potassium channels (K_D-R, K_a, and K_D) for repolarization after AP and regulation of firing dynamics, and two voltage-gated calcium channels (VGCC; L-type: CaL, N-type: CaN) (Neymotin et al. 2016b) for further regulation of firing dynamics and neuronal excitability. Model neurons contained an HCN channel based on (Kole et al. 2006) (adjusted reversal potential E_h to −37 mV), which contributed to sag, subthreshold dynamics, and resonance. Model neurons also contained large-conductance BK calcium-activated potassium currents based on (Stadler et al. 2014; Reetz et al. 2014) for regulating AP shape.

Leak, Na⁺, and K⁺ currents were represented by the conductance approximation: I_ion = g_ion·(V − E_ion) (g conductance; E reversal potential) using E_Na of 42 mV and E_k of −104 mV, calculated from concentrations of ions in solution, and E_leak optimized (described below). The Goldman-Hodgkin-Katz (GHK) flux equation was used for Ca²⁺ currents: I_Ca = p_Ca·GHK_Ca (p permeability). Channel dynamics were corrected for temperature by a Q₁₀ using the factor of qt = Q₁₀^(T−25)/10with T = 34°C and 25° was taken to be the temperature at which the experiment for fitting original ion channel models was done (unless noted otherwise). Conductances and activation curves were not corrected for temperature (Iftinca et al. 2006). Voltage-sensitive channels largely followed variants on the Hodgkin-Huxley formalism, whereby $\frac{dx}{dt}=\frac{x_{\infty }-x}{{\tau }_x}$ using steady-state value $x_{\infty }=\frac{{\alpha }_{\infty }}{{\alpha }_{\infty }+{\beta }_{\infty }}$, the τ_x forms were either

$${\tau }_{\mathrm{E}\mathrm{Q}\mathrm{N}1}:{\tau }_x=\frac{1}{qt\cdot ({\alpha }_{\tau }+{\beta }_{\tau })}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\text{or}\hspace{0.17em}\hspace{0.17em}{\tau }_{\mathrm{E}\mathrm{Q}\mathrm{N}2}:{\tau }_x=\frac{{\beta }_{\tau }}{qt\cdot a_0\cdot (1+{\alpha }_{\tau })}$$

where x is m or n for an activation variable and h for an inactivation variable. F is Faraday's constant; R is the gas constant. Variations on this scheme are noted below.

L-type Ca²⁺ channel (Ca_L).

The Ca_L variation is p_L = p̄_L·m_L²·h_L; with h_L (inactivation) was Ca²⁺ dependent: h_L(Ca_cyt²⁺) = $\frac{k_i}{k_i+\mathrm{C}{\mathrm{a}}_{\mathrm{c}\mathrm{y}\mathrm{t}}^{\mathrm{2}\mathrm{+}}}$ with k_i = 0.001 mM; m_L: α_∞ = $\frac{15.69\cdot (-V+81.5)}{\exp ((-V+81.5)\hspace{0.17em}/\hspace{0.17em}10.0)-1.0}$; β_∞ = 0.29·exp(−V/10.86); τ_EQN2 with α_τ = exp(0.0378·2·(V − 4)), β_τ = exp(0.0378·2·0.1·(V − 4)); α₀ = 0.1; Q₁₀ = 5.

N-type Ca²⁺ channel (Ca_N).

The Ca_N variation is p_N = p̄_N·m_N²·h_N·h2_N; m_N used α_∞ = 0.1967·(−V + 19.88)/(exp((−V + 19.88)/10.0) − 1.0); β_∞ = 0.046·exp(−V/20.73); τ_EQN2 with α_τ = exp(0.0378·2·(V − (−14))); h_N following: α_∞ = 1.6·10⁻⁴·exp(−V/48.4); β_∞ = 1/(exp((−V + 39.0)/10) + 1); constant τ_h = 80; with h2_N = {0.001}/{0.001 + Ca_cyt²⁺}; α₀ = 0.03; Q₁₀ = 5.

Na channel.

The Na channel variation is g_Na = ḡ_Na·m_Na³·h_Na; m_Na using τ_EQN1 with: α = 0.4·(V + 30)/(1 − exp(− (V + 30)/7.2)) β = 0.124·(−V − 30)/(1 − exp((V + 30)/7.2)) h_Na with special form h_∞ = $\frac{1}{1+\exp ((V+50)/4)}$ and using τ_EQN1 with α_τ = 0.03·(V + 45)/(1 − exp(−(V + 45)/1.5)) and β_τ = 0.01·(−V − 45)/(1 − exp(−(V − 45)/1.5)); Q₁₀ = 2; experimental temperature = 24°C.

K_dr channel.

The K_dr channel variation is g_Kdr = ḡ_Kdr·n_Kdr; n_Kdr following an atypical steady state: n_∞ = $\frac{1}{1+\alpha }$ with α = exp(10⁻³·−3·(V − l_KdrV_1/2)·9.648·10⁴/(8.315·(273.16 + T))) using the same α in τ_EQN2 with β = exp(10⁻³·−3·0.7·(V − n_KdrV_1/2)·9.648·10⁴/(8.315·(273.16 + T))); α₀ = 0.0075; Q₁₀ = 1; experimental temperature = 24°C; n_KdrV_1/2 = 13 unless indicated otherwise.

K_A channel.

The K_A channel variation is g_KA = ḡ_KA·n_KA·l_KA; n_KA with τ_EQN2 and an atypical steady-state value: n_∞ = $\frac{1}{1+\alpha }$ with α = exp(10⁻³·ζ(V)·(V − n_KAV_1/2)·9.648·10⁴/(8.315·(273.16 + T))); ζ(V) = −1.5 + (−1/(1 + exp((V − tq_KA)/5))); β_n(V) = exp(10⁻³·ζ(V)·0.55 (V − n_KAV_1/2)·9.648·10⁴/(8.315·(273.16 + T))); a₀ = 0.05; Q₁₀ = 5. l_KA: with steady state: l_∞ = $\frac{1}{1+\alpha }$; α = exp(10⁻³·−3·(V − l_KAV_1/2)·9.648·10⁴/(8.315·(273.16 + T))); time constant: τ = 0.26·(V + 50)·qt; Q₁₀ = 1; experimental temperature = 24°C; n_KAV_1/2= 35, l_KAV_1/2= −56, tq_KA = −45 unless indicated otherwise.

K_D channel.

The K_D channel variation is g_KD = ḡ_KD·m_KD·h_KD; m_KD with special form m_∞ = $\frac{1}{(1+\exp (-(V+25)\hspace{0.17em}/\hspace{0.17em}14))}$ and constant τ_m = 1; h_KD with special form h_∞ = $\frac{1}{(1+\exp ((V+100)\hspace{0.17em}/\hspace{0.17em}8))}$ and τ_h = $\frac{\exp (0.004\cdot (V+5))}{qt\cdot 0.00058\cdot (1+\exp (0.02\cdot (V+5)))}$ with Q₁₀ = 3; experimental temperature = 34°C.

BK channel.

The BK channel variation is g_BK = ḡ_BK·m_BK; m_∞ with special form m_∞ = $\frac{P0\mathrm{c}\mathrm{a}}{1+\exp ((V\mathrm{h}\mathrm{c}\mathrm{a}-V)\hspace{0.17em}/\hspace{0.17em}17)}$, with P0ca = $\frac{1}{1+0.00002\hspace{0.17em}/\hspace{0.17em}[Ca]}$ and Vhca = Shift_BK − 46.08 + $\frac{201.75-Shif{t}_{BK}}{1+{(0.00002\hspace{0.17em}/\hspace{0.17em}[Ca])}^{-0.94208}}$ .

The passive parameters (capacitive density, axial resistivity, ḡ_leak, E_leak) were equal in all compartments of the detailed model. For simplified models, ḡ_leak and capacitive density in each compartment type (apical dendrite, basal dendrite, soma, axon) were set independently. Spiny capacitance factor (SCF) was used to increase the capacitance and leak density in the spiny dendrite compartments of the detailed model above the values in other compartments.

Ion channels were distributed within neuronal compartments based on the experimental literature. K_A, Na, K_dr channels were present with uniform density in all compartments but increased by five times in the axon to allow AP initiation. Somatic and dendritic compartments additionally contained Ca_L, Ca_N, BK, and HCN channels. K_D was present in the soma and at 20 times somatic density in the axon. The axon contained only leak, Na, K_A, K_dr, and K_D ion channels. Basal dendrites contained uniform density of all their channels. Apical dendrite HCN channel density increased exponentially with distance from soma until reaching the nexus with apical dendrite tufts, where the HCN channel density plateaus at 0.00565 S/cm² (Harnett et al. 2015). This exponential increase of HCN channel density within the main apical trunk was set to ḡ_h·exp(d/λ_h), where d is distance of the apical dendrite compartment from soma and λ_h is the length constant, defined as d_nexus/log(0.00565/ḡ_h), d_nexus is distance from soma to nexus (∼300 μm), and ḡ_h is somatic HCN channel density.

Intracellular calcium concentration ([Ca], in mM) was linked to voltage-gated calcium channel (VGCC) currents (Ca_L, Ca_N) and decayed exponentially with the following equation (Neymotin et al. 2015): $\frac{d[\mathrm{C}\mathrm{a}]}{dt}$ = − (10000)·i_Ca/((2·F·depth_Ca) + ([Ca]_∞ − [Ca])/τ_Ca), i_Ca is transmembrane calcium current (nA), F is Faraday's constant, [Ca]_∞ is steady-state calcium concentration (0.0002 mM), depth_Ca is depth of calcium shell (μm), and τ_Ca is the Ca²⁺ decay time constant (ms).

Optimization

A two-step optimization procedure was used to produce model dynamics comparable to those seen in vitro under somatic whole cell current clamp experiments (−0.15 to 0.6 nA in 0.05-nA steps).

PRAXIS optimization.

NEURON's PRAXIS algorithm (Brent 1973, Carnevale and Hines 2006) was used in a preliminary step to fit the following passive parameters: 1) capacitive density; 2) axial resistivity; 3) ḡ_leak; 4) E_leak; 5) ḡ_KD; 6) ḡ_h at soma; and 7) initialization voltage (V_init). For the detailed model, PRAXIS also optimized SCF, which scaled spiny compartment capacitance and leak conductance. When optimizing the simplified models, which lacked realistic geometry, we also allowed PRAXIS to modify diameter and length of individual compartments. Sum of squared error between simulated somatic voltage and in vitro somatic voltage was used as the fitness function for all subthreshold current steps.

Evolutionary multiobjective optimization.

In the second optimization step, the inspyred Python library (Garrett 2014a,b) was used for evolutionary multiobjective optimization (EMO) with the nondominated sorting genetic algorithm (NSGA2) (Deb 2001; Deb et al. 2002). NSGA2 uses crowding for replacement with binary tournament selection to create population size (100) offspring and the Pareto archival strategy (Garrett 2014a). NSGA2 aims to find a Pareto optimal archive, consisting of the best solutions in the high-dimensional fitness space. In a Pareto optimal set of models, an individual model is better than another model if it is better than or equal to the other model in all fitness functions and strictly better in at least one fitness function (Konak et al. 2006; Garrett 2014a). This criterion is used to determine whether an individual model is selected for entry into the final archive, which only occurs if the model is at least as good as the other models in the archive. For all runs of EMO, the mutation rate was set to 0.2 and crossover rate was set to 1.0.

The same fitness functions were used in EMO for both simplified and detailed models: 1) firing-rate vs. current injection (F–I) curve with sum of squared error of differences between experimental and simulated curves; 2) interspike-interval (ISI) voltage: squared error between experimental and simulated responses from corresponding ISI voltage snippets, defined as voltage in between corresponding APs in a train; 3) instantaneous firing rate: sum of squared differences between time-series of inverse periods between successive APs; 4) AP shape: weighted sum of absolute difference in 0.1·AP threshold + 0.1·maximum AP slope + 0.15·minimum AP slope + 0.15·AP duration at 25% maximum amplitude + 0.25·AP duration at 50% maximum amplitude + 0.25·AP peak. Sum takes absolute differences in features between corresponding experimental and simulated APs. The full measure takes average across all spikes in a train; 5) subthreshold voltage: squared error between experimental and simulated somatic voltages for subthreshold steps. These additional fitness functions were used in EMO for the simplified model, to allow EMO to have more flexibility in finding optimal fits for different AP shape features: 6) AP peak voltage; 7) AP duration: absolute difference at 25 and 50% maximum amplitude; 8) AP slope (sum of absolute difference between maximum/minimum 1st derivative of corresponding simulated and experimental APs); and 9) AP threshold (absolute difference between thresholds of corresponding simulated and experimental APs).

The following model parameters were optimized for both types of model: 1) ḡ_Naf; 2) ḡ_Kdr; 3) ḡ_KA; 4) ḡ_KD; 5) p̄_L; 6) p̄_N; 7) ḡ_BK; 8) Shift_BK; 9) depth_Ca; 10) τ_Ca. When optimizing the simplified models, we also allowed evolution to modify n_KdrV_1/2, l_KAV_1/2, n_KAV_1/2, and tq_KA for the greater flexibility needed to regulate the simplified neuron's excitability and AP shape. All parameter ranges used in evolution were constrained within prespecified boundaries, which expanded automatically during evolution when a good model had values near the boundaries. Shift_BK was optimized to adjust the BK channel's voltage dependence to limit BK's role in dynamics to only modulating AP shape.

We used the Neuroscience Gateway Portal high-performance computers (HPC) (Sivagnanam et al. 2013) and our own HPC cluster to run evolution over thousands of generations parallelized over 100–200 cores. Simplified model neurons evolved over ∼30,000 generations (1–3 min per generation) while detailed model neurons evolved over 6,276 generations (15–20 min per generation). Populations within a given generation consisted of 100 individuals (models).

Final Model Sets for Analysis

EMO evaluated 627,600 detailed models and over 2,998,900 simple models. As evolution progressed, the number of individuals in the EMO archive increased with selection into the archive using the Pareto archival strategy described above. Final evolutionary archives of the detailed and simple models are included on ModelDB. Each model in the archive includes its parameter values and fitness function errors. Models in the archives were further analyzed and compared using an overall scalar error. This error was measured as the vector length in the high-dimensional fitness space determined by the error for each of the individual fitness functions, after normalization by division by the mean for that error.

Resonance

We tested neuronal resonance using two methods: 1) impedance amplitude profile (ZAP) using chirp current injections at soma; and 2) ratio of somatic excitatory postsynaptic potentials (EPSP) output under apical dendrite AMPA stimulation. Chirp stimulation was a time-varying sinusoidal current injection with increasing frequency over time. The frequencies ranged continuously from 1 to 15 Hz over a 15-s duration and were applied at the soma (Sheets et al. 2011). To calculate resonance, we computed the ratio of fast Fourier transform (FFT) amplitude of somatic voltage (output) to FFT amplitude of chirp input. This quantified how well the input frequencies were represented in somatic voltage output. The synaptic stimulation protocol applied subthreshold AMPA stimulation (exponential rise, decay: 0.05, 5.3 ms) at each apical dendrite independently over a range of frequencies (1–30 Hz). We then calculated the EPSP response in soma as the output. The frequency of AMPA stimulation which produced the maximum EPSP response at the soma was defined as the resonant frequency.

Software, Models, Morphologies, and Electrophysiology

All files comprising our models and final model sets, including morphological and electrophysiological data, are available online. The exemplar model, model archives, and somatic whole cell current clamp recordings are available in ModelDB (Peterson et al. 1996; Migliore et al. 2003; Hines et al. 2004): http://senselab.med.yale.edu/modeldb/ShowModel.cshtml?model=195615. The evolutionary optimization code and fitness functions are available in SimtoolDB: https://senselab.med.yale.edu/SimToolDB/ShowTool.cshtml?tool=195665. The corticospinal reconstruction used in this paper is available at NeuroMorpho (Ascoli et al. 2007) http://neuromorpho.org/neuron_info.jsp?neuron_name=BS0284 with a full set of associated mouse M1 and S2 corticospinal morphologies available using the following search: http://neuromorpho.org/KeywordResult.jsp?str=suter_shepherd,corticospinal.

RESULTS

We used a two-step optimization procedure consisting of adaptive coordinate descent (PRAXIS algorithm) followed by evolutionary multiobjective optimization (EMO) with the NSGA2 algorithm to create and assess over 625,000 multicompartment (706-compartment) models that were culled to produce a detailed-model archive of 9,804 useful models with different degrees of fitness for the different fitness functions. Similarly, 3,000,000 simplified (6-compartment) models were culled to produce a simple model archive of 9724 models. We have made these archives available on ModelDB (http://senselab.med.yale.edu/modeldb/ShowModel.cshtml?model=195615). The larger number of simple models evaluated reflects both the greater difficulty of getting fits with lesser modulation from dendrites and the relative ease of running large numbers due to the faster compute time for these smaller models (0.5-s clocktime for simple, 17 s for complex model for 1 s at 7 Hz; 0.02 s, 2.5 s for subthreshold simulation). Optimization of both models produced parameter values within physiological ranges.

Diversity of Models in Final Archives

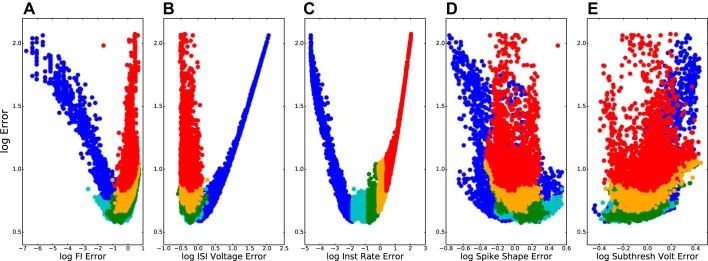
The archives included models that were optimized according to five criteria, chosen so as to represent major aspects of cell dynamics relevant to the activation of a cell in a network (Fig. 2). Firing rate as a function of current injection (called F–I here rather than I–F to distinguish from integrate-and-fire acronym) is perhaps the most widely used “classical” measure of excitability. Interspike interval voltage trajectory (ISI voltage, largely due to effects of K⁺ currents on afterhyperpolarization) complemented F–I. By taking account of voltage variation between spikes, ISI voltage regulates neuronal responsiveness to synaptic inputs at different phases with ongoing spiking activity. Instantaneous firing rate (IFR) is a measure closely related to overall firing rate but one that takes account of a spiking adaptation. Spike shape (SpSh), while not immediately connected with cell responsiveness, is another indicator of the adequacy of parameterization because it reflects major ionic currents, particularly the ḡ_Na and ḡ_Kdr of the original Hodgkin-Huxley equations. Finally, subthreshold stimulation voltage trajectories (SubTh), consequent on passive parameters of leak conductance and capacitance as well as I_h, were revisited as part of the EMO after being initially set by the PRAXIS algorithm. This final fitness function was included to make sure that passive properties did not deviate greatly through the setting of the first four functions. In this paper, we primarily focus on two examples from the archives with excellent F–I fitness, which allows us to demonstrate robustness of the model across different levels of current injection.

Fig. 2.

Models of the detailed models archive (n = 9,804) are optimized across all 5 fitness functions but demonstrate tradeoffs between full 5-dimensional error (y-axis) and individual error (individual x-axes). Frequency-current relation (F–I; A), interspike interval voltage (ISI voltage; B), instantaneous firing rate (IFR; C); spike shape (SpSh; D), and subthreshold activation voltage (SubTh; E). Log-log plots; color code based on the 5 error percentiles in C in order of increasing percentiles (dark blue, light blue, green, orange, and red) causing overdrawing of some points in A, B, D, and E.

Models accepted into the archive showed adequate fit across all measures, but some were more optimized for one or more particular measures, whereas others had similar fitness across all measures. Figure 2C is used here to provide the color code for all five panels, showing a set of models that have high IFR fitness (blue) and a set with poor IFR fitness (red). Some models show excellent overall fitness (low values on y-axis) and some models show relatively poor overall fitness (high y-values). The U-shaped distributions seen in Fig. 2, A–C, reflect the bimodal distribution of error in each of these single measures. Figure 2A shows individual models that are highly specialized for a particular measure; these are likely to not be as good across all measures. Figure 2B shows models that are particularly poor on a particular fitness function; these will end up with a poor overall fitness score due to the poor individual score. Figure 2C shows models that will be generally good across all fitness scores and end up with best overall score, at the nadir of these U-curves.

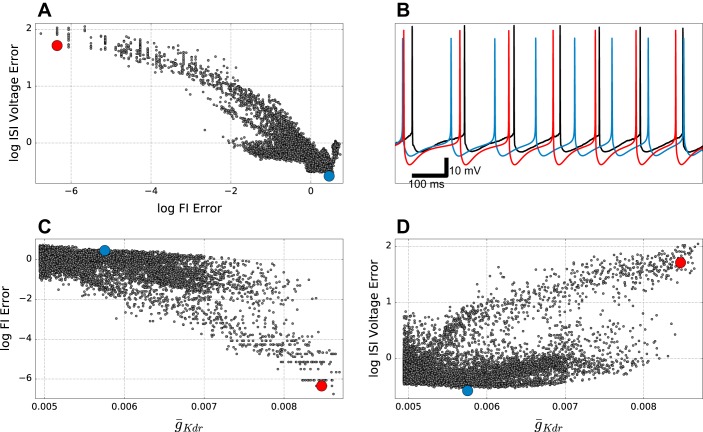
Figure 2, A and C, show increasing error in the same direction (blue to red in color code). This similarity between F–I (Fig. 2A) and IFR reflects the fact that both are based on interspike interval duration. By contrast, error for fitting ISI voltage trajectory (Fig. 2B) also shows a U-shaped curve, but the error goes in the opposite direction. This is due to the fact that closer fitting of the interval between spikes is done most easily by manipulating currents, mostly using K⁺ channels, whose time constants most closely match the desired period. These K⁺ currents will then directly alter the voltage trajectory. The opposition of these two fitness functions in our model suggests that we are missing one or more channels, or channel influences (e.g., the details of Ca²⁺ handling for Ca²⁺-sensitive K⁺ channels), that determine this trajectory (see discussion). There was no clear association of order error with spike shape and subthreshold voltage (Fig. 2, D and E), both of which occupied a narrower range of error values. The interspike interval fitness tradeoff was due to K⁺ currents, including I_Kdr (Fig. 3). Increasing ḡ_Kdr increased the ISI depth beyond what was seen physiologically (red dot in Fig. 3, A and D, and red trace in Fig. 3B), while augmenting duration providing better fits to frequency across different amounts of current clamp (Fig. 3, A and C). By contrast, the blue dot and blue trace in Fig. 3 show good ISI voltage trajectory with worse F–I fit. ISI voltage trajectory was not only affected by ḡ_Kdr but also by other K⁺ channels, explaining the large number of models with low ISI voltage error across a broad range of ḡ_Kdr values (bottom of Fig. 3D). Tradeoffs similar to that seen here were also observed in the simple model archive, but overall errors were slightly higher (not shown).

Fig. 3.

Tradeoffs between firing rate (F–I) and interspike-interval (ISI) voltage errors in detailed model archive. A: F–I and ISI voltage error show inverse relationship. B: somatic membrane potential in response to 0.3-nA current clamp corresponding to red and blue points in other panels. Black trace is experimental data. C: F–I error decreases with increasing ḡ_Kdr (r = −0.68; P < 0.001). D: subthreshold ISI Voltage error increases with ḡ_Kdr (r = 0.54; P < 0.001).

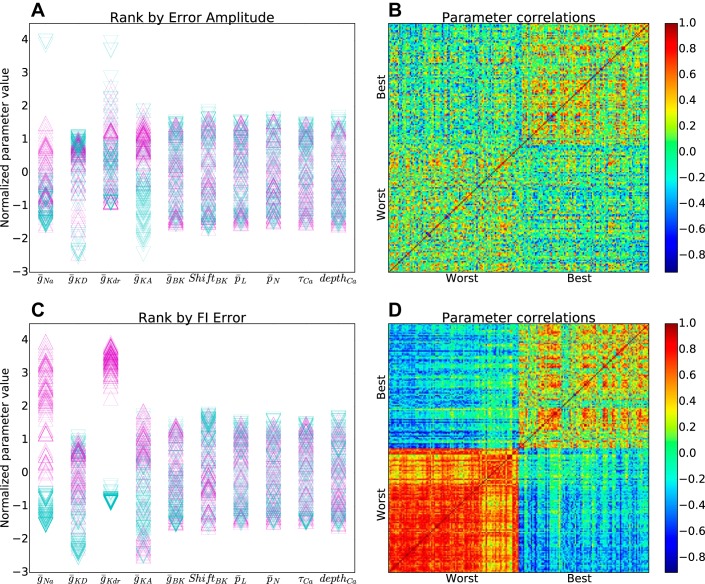
Final model parameters were highly variable, demonstrating the principle of parameter degeneracy (Edelman and Gally 2001; Golowasch et al. 2002; Prinz et al. 2004; Neymotin et al. 2016a): many different parameter combinations could produce a given neural dynamics. Parameters acted in combination, such that no one parameter was a good predictor of the dynamics (Fig. 4). For any individual parameter, parameter magnitude was not predictive for the overall quality of fitness, assessed by comparing highest to lowest one percentile of the archive for overall fitness quality (Fig. 4A, purple-up vs. blue-down triangles). Furthermore, the top and bottom percentiles, identified as a vector of parameter values across all of the parameters, did not show much overlap (Fig. 4B), suggesting that these locations did not form independent distinct clouds in parameter space. By contrast, individual parameters did have predictive power when looking at a single fitness function, here F–I (Fig. 4, C and D). In addition to the influence of ḡ_Kdr (Fig. 4C, 1st column, compare to Fig. 3C), ḡ_Na also had major influence on this measure (Fig. 4C, 2nd column). These two parameters were both bimodal for F–I, with segregation between the top and bottom percentiles. The models with highest overall F–I fitness were associated with high values of ḡ_Na and ḡ_Kdr. High values provided a balance of strong positive and strong negative feedback on spike production, permitting the system to accelerate rapidly in either direction. The bottom percentile from the archive had low ḡ_Na and low ḡ_Kdr. For similar reasons, the best models also tended to have high values of other conductances, but without segregation of top and bottom (Fig. 4C, columns 2, 4, and 5). Self-similarity for the F–I fitness function top and bottom parameter sets was pronounced, particularly for the bottom one percentile (bottom left square in Fig. 4D).

Fig. 4.

Distinct parameter values for top and bottom one percentile in detailed models archive. A: normalized parameter values for top (purple-up triangles) and bottom (blue-down triangles) based on overall fitness across all measures. B: Pearson correlations between parameter vectors in A show weak intraclass similarity (best-best: 0.18; worst-worst: 0.11; best-worst: −0.05). C: normalized parameter values for top (purple-up triangles) and bottom (blue-down triangles) based on F–I fitness. D: Pearson correlations between parameter vectors in C show strong intraclass similarity with strong interclass dissimilarity (best-best: 0.56; worst-worst: 0.86; best-worst: −0.62). (Parameter normalization by subtraction of mean and division by SD.)

Exemplar Models Show Good F-I Fit

Selecting from each final-model archive, we focus now on two exemplars, one detailed and one simple model, with minimal F–I error to show quality of fit across different current injections. The detailed model exemplar is that shown by a red dot in Fig. 3; we selected a similar F–I -optimized model from the simple-model archive for comparison. Parameter values for these two models are provided in Table 1.

Table 1.

Parameters of exemplar models optimized for F-I

Parameter	Simple	Detailed
Axial resistivity, Ω-cm	114.51	137.49
Capacitance density, μF/cm2	—	0.7
Spiny capacitance factor (SCF; unitless)	—	1.48
Vinit, mV	−75.04	−70.04
Eleak, mV	−88.54	−90.22
ḡleak, S/cm2	—	0.0260 · 10−3
Apical dend diam, μm	1.58	—
Apical dend L, μm	261.90	—
Apical dend cap, μF/cm2	1.03	—
Apical dend ḡleak, S/cm2	0.93 · 10−3	—
Basal dend diam, μm	2.28	—
Basal dend L, μm	299.81	—
Basal dend cap, μF/cm2	1.90	—
Basal dend ḡleak, S/cm2	0.76 · 10−3	—
Soma diam, μm	28.21	—
Soma L, μm	48.41	—
Soma cap, μF/cm2	1.79	—
Soma ḡleak, S/cm2	0.54 · 10−3	—
Axon diam, μm	1.41	—
Axon L, μm	594.29	—
Axon cap, μF/cm2	1.01	—
Axon ḡleak, S/cm2	0.25 · 10−3	—
ḡNa, S/cm2	34.5117 · 10−3	15.3130 · 10−3
ḡh, S/cm2	0.1410 · 10−3	0.0661 · 10−3
ḡKD, S/cm2	0.4474 · 10−3	1.1091 · 10−3
ḡKdr, S/cm2	13.1104 · 10−3	8.4716 · 10−3
nKdrV1/2, mV	11.64	—
ḡKA, S/cm2	89.8600 · 10−3	61.4003 · 10−3
lKAV1/2, mV	−59.79	—
nKAV1/2, mV	32.79	—
tqKA, mV	−52.10	—
ḡBK, S/cm2	0.0510 · 10−3	0.0725 · 10−3
ShiftBK, mV	43.89	46.97
p̄L, cm/s	4.4 · 10−6	5.7 · 10−6
p̄N, cm/s	4.6 · 10−6	4.7 · 10−6
τCa, ms	99.11	16.02
depthCa, μm	0.12	0.10

Voltages are given in mV; diameters (diam) and lengths (L) are given in μm; conductance densities are given in S/cm² unless indicated otherwise; capacitance density (cap) is given in μF/cm²; permeability is given in cm/s; - indicates parameter value not optimized or not applicable. F–I, frequency-current; dend, dendritic; cap, capacitance density.

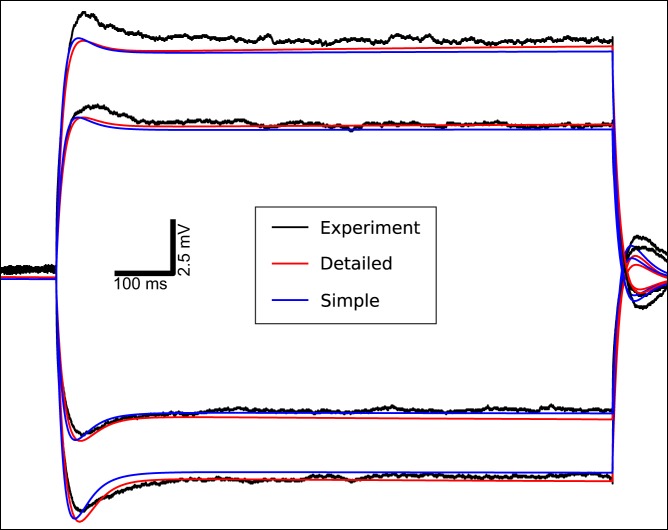
Both the simple and detailed models accurately followed the subthreshold voltage trajectories seen in the in vitro experiments, replicating the noticeable I_h-dependent sag (Fig. 5). Before the current injection the models had stable somatic resting membrane potentials near −80 mV. Current injection produced a sharp transition in membrane potential followed by a sag due to I_h (HCN channel). I_h opposed hyperpolarization by opening and creating an inward current and opposed depolarization by closing and thereby reducing net inward current. After the current injection was turned off membrane potential showed overshoot, again due to I_h. The detailed model (red) had better overall fits to the subthreshold data, compared to the simplified model (blue). Subthreshold fit in this F–I-optimized model was not as good with depolarization due to the effects of high K_v currents, which were increased in the F–I optimization (Fig. 4C, columns 2–5).

Fig. 5.

Corticospinal neuron (SPI) models replicate in vitro subthreshold responses to current injections, including bidirectional I_h-dependent sag in somatic membrane potential. The 1-s subthreshold somatic current injection starts at 500 ms (−0.1, −0.05, 0.05, and 0.1-nA current injections arrayed from bottom to top). Black: experiment; red: detailed SPI neuron model; blue: simplified SPI neuron model.

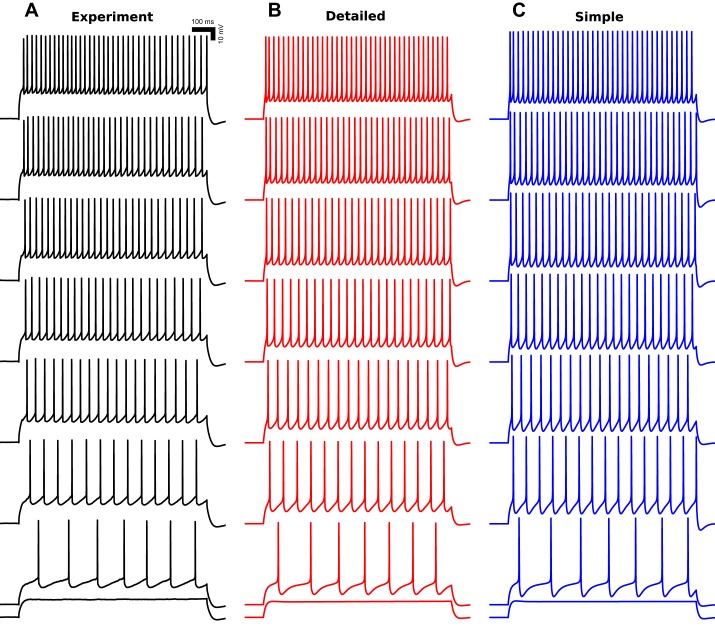
Exemplar model neurons displayed similar firing patterns to those observed in vitro (Fig. 6). All model neurons had AP threshold at 0.3-nA current injection, which produced a 7-Hz firing, identical to experiment. Spike trains were weakly adapting at high current injections, showing some adaptation after the first one to two spikes with nearly constant ISIs thereafter. Model neurons displayed nearly linear increases in firing rates, from 7 to 38 Hz, with increasing current injection from 0.3 to 0.6 nA (Fig. 7).

Fig. 6.

SPI model neurons replicate in vitro firing patterns. Detailed (B) and simplified (C) model neurons replicate in vitro (A) firing patterns (1-s somatic current injections from 0.25–0.60 nA in 0.05-nA increments from bottom to top). Action potential threshold is at 0.30-nA somatic current injection (2nd trace from bottom). Black: experiment; red: detailed SPI neuron model; blue: simplified SPI neuron model.

Fig. 7.

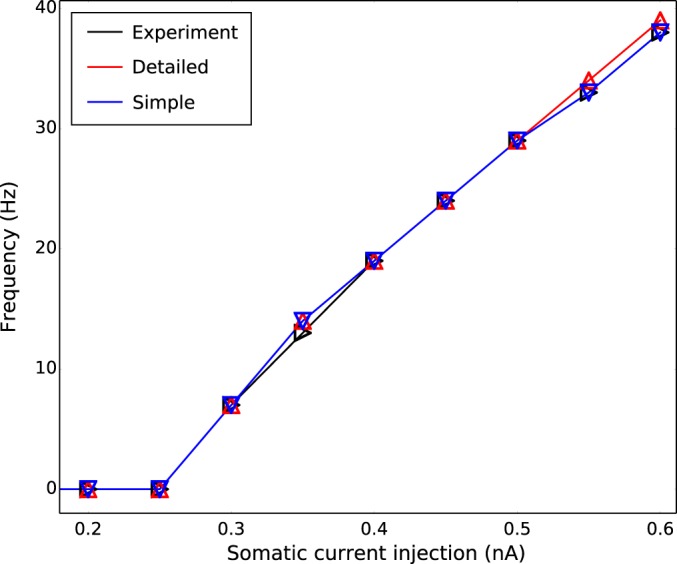
Exemplar models showed linear firing frequency-current (F–I) relationship with firing threshold at 0.3-nA somatic current injection.

Somatic and Synaptic Resonance

Although the models were not optimized for resonance dynamics, the exemplar models displayed resonance with subthreshold chirp stimulation at the soma (Fig. 8). Peak resonance was at 4.7 Hz for the detailed model and 5.8 Hz for the simple model, comparable to the 4.2 Hz value seen experimentally (Sheets et al. 2011). With I_h turned off, this resonance was abolished.

Fig. 8.

Exemplar neurons show somatic and dendritic resonance. A: subthreshold chirp somatic current input produces peak voltage resonance between ∼4 and 6 Hz in models and experiment (impedance Z measured as ratio of oscillatory V/I power; see materials and methods). Vertical dotted lines indicate resonant peak frequencies. B: synaptic resonance based on apical dendrite distance from soma measured as apical dendrite AMPA stimulation that produces maximal excitatory postsynaptic potentials (EPSP) amplitude in soma for I_h on (●) vs. I_h off (×).

Variable frequency subthreshold synaptic stimulation in individual apical dendrites demonstrated how this resonance could have functional implications for transformation of synaptic inputs (Fig. 8B). Exemplar models showed an increase in resonant frequency from ∼8–17 Hz with distance from the soma. The resonance gradient corresponded to the HCN channel density gradient up the apical dendrites, which reaches a maximum at the nexus before the apical tuft (Harnett et al. 2015). Beyond the nexus, the flattening of HCN channel density produced a flattening in resonant frequency at ∼16–17 Hz. Blocking I_h eliminated the resonance gradient (× symbols).

DISCUSSION

In vitro whole cell somatic voltage recordings were used to develop computer models of SPI neurons at two levels of complexity: 1) a detailed morphological reconstruction of a SPI neuron with over 700 compartments representing the full apical and basal dendritic tree, soma, and abbreviated axon; and 2) a reduced six-compartment model neuron with representative apical and basal dendrites, a soma, and an axon. Detailed and simple model neurons captured key intrinsic electrophysiological properties observed in vitro: sag potentials due to I_h (Fig. 5), nonadapting firing during trains (Fig. 6), linear F–I relationships (Fig. 7), and F–I -dependent resonance (Fig. 8).

Simulations Suggest Need for Additional Depolarizing Influences

We based all ion channel distribution on the experimental literature (Kole et al. 2006; Harnett et al. 2013, 2015; Migliore and Shepherd 2002). By limiting ourselves to documented channels, we are likely to have omitted channels that are present in SPI cells but have not yet been documented. Further difficulties arise in dendrites where channel identities and densities are difficult to assess experimentally. Channels may have been missed experimentally for several reasons: 1) influential channels may be present some short distance out in the dendrites, allowing them to have an influence on somatic trajectories yet not be readily identifiable via somatic voltage clamp due to lack of space clamp; 2) some channels do not have clean blockers, making them difficult to identify pharmacologically; 3) different channel isomers may be present in the soma or proximal dendrites, which have activation properties, inactivation properties, and time constants different from the canonical version of the channel which may have been measured in other species, other ages, other brain regions, and other pyramidal cell subtypes; and 4) some channel effects may be due to different phosphorylation states of identified channels, making them more difficult to identify in a slice where these states cannot be readily manipulated.

Further evidence for the hypothesized missing channels comes from the simulations. Voltage trajectories were not precisely fit, as seen in interspike interval voltage (Fig. 3B), depolarized subthreshold trajectories (Fig. 5) and spike shape (not shown). In each of these cases, there appeared to be difficulty achieving an adequate degree of depolarization. We therefore predict that the models are missing one or more additional depolarizing influences. Specific depolarizing currents that we suspect may play a role in balancing out the hyperpolarizing influences of K_v channels would include I_T, T-type low-threshold activated Ca²⁺ channel: I_Nap, persistent Na⁺ current; and I_CAN, nonspecific cation channel. We also did not explicitly explore backpropagating APs, which will depend on densities of depolarizing dendritic channels.

Choice of Optimization Algorithms and Fitness Functions

There are a large variety of fitting and optimization tools available to the modeler, and each of these tools has many variants (Bahl et al. 2012; Jolivet et al. 2004, 2008; Van Geit et al. 2007). Selecting a good fitness tool is not easy, and it is in some cases desirable to use an optimization to find the better (never alas best) optimization algorithm or to set the specific parameters (learning rate, subpopulation selection criteria, etc.). We have done this type of optimization-optimization previously in discovering the learning parameters for a biomimetic learning model (reinforcement learning) using a genetic algorithm (Dura-Bernal et al. 2016). We note that these strategies have the potential for infinite regress: who shall optimize for choice of the optimization-optimization algorithms themselves?

In the present instance, we devised a two-step optimization procedure. We started with PRAXIS to determine initial passive parameters (e.g., capacitance, axial resistivity) by adaptive coordinate descent. This first step produced a relatively stable resting membrane potential from which firing properties could be molded. Strong nonlinearities, at whose heart lies the phenomenon of the spike threshold, militates against using any such continuous progression through parameter space to converge dynamics onto the other fitness functions, those for spiking and interspike trajectories. These nonlinearities instead suggested the use of algorithms in the genetic algorithm family, such as the evolutionary multiobjective optimization (EMO) used here, to move discontinuously in parameter space. We used EMO in this second stage to search broadly in the large parameter space of multiple ion channels. Our approach was able to optimize models of different degrees of complexity, simple and detailed, equally well.

Next, we must consider our selection of fitness functions (Van Geit et al. 2008, 2016). The models in the archives reflected competitive pressures between different fitness functions (Fig. 3) for selecting specific parameter values. For example, F–I and ISI voltage error were inversely correlated because high ḡ_Kdr was required for good F–I fit (to reduce hyperexcitability) but produced overhyperpolarization in between spikes, reducing ISI voltage fit. These tradeoffs demonstrate the multifactorial dynamic landscape that our neuronal models occupy and the difficulty of finding a best model. One approach to finding the best is to combine the different fitness scores, possibly with different weightings, to produce a single scalar value (Rumbell et al. 2016). Our approach was to select many different best models based on exhibiting desired dynamical features singly or in combination. Because our aim is make the models useful for incorporation into network models, we focused on F–I response as a surrogate for this cell type's likely responsivity to ongoing background activation. Responsiveness to irregular background activity, rather than current clamp, might provide a better indicator for this (Mainen and Sejnowski 1995).

In general, one chooses fitness functions that complement one another. Because of the complementarity, the fitness functions pushed channel densities in different directions, as shown in Figs. 2, B and C, and 3. Focusing on spike times, we also provided some fitness function redundancy by using both overall spiking rate (F–I), along with spike timing [instantaneous firing rate (IFR)]. The degree of redundancy of these two measures was demonstrated in the final archive (Fig. 2, A and C). We included subthreshold fit, determined initially by PRAXIS, as an EMO fitness function as well so as not to lose fitness for this criterion while optimizing for the others.

Depending on the type of measure being fit, there are multiple different methods for designing the fitness function. In the case of subthreshold voltage trajectory with current clamp, for example, the fitness function could be a simple least-mean-squared-error fit to voltage. For looking at spiking, the function ignored voltage, utilizing spike times. For interspike voltage trajectories, the fitness function was made more complicated by the need to fit the pattern of depolarization and hyperpolarization even in cases where the interspike interval was not precisely fit. Spike form was one of the more difficult fitness functions, one for which we tried a number of possibilities, finally utilizing a pattern matching algorithm making use of target voltage forms.

The Public Archive: Opportunities and Caveats

In contrast to the classical approach of developing an individual model that exhibits excellence across a desired set of fitness functions, using a database or ensemble of models allows exploring how different parameters contribute to diverse dynamics and allows determining tradeoffs between different fitness functions (Günay et al. 2008, 2009; Prinz et al. 2003). Databases also afford simulating and comparing a set of models under novel conditions that were not initially used in the optimization. Recent research has demonstrated that a subset of models will fail when tested with input conditions or activation functions that differ from those for which they were optimized (Holmes et al. 2006; Almog and Korngreen 2016).

There are several ways to populate model databases, ranging from multidimensional grid search to EMO algorithms. Grid search samples all parameter space equally, while EMO hones in on areas of particular parameter space and can get caught in local minima. A recent study used an exhaustive multidimensional grid search to sample parameters of detailed compartmental models of hippocampal interneurons, and offered predictions on the distribution of HCN channels in dendrites (Sekulíc et al. 2014, 2015). It is also possible to extend previously existing databases with new dynamical features. One such study on leech heart interneuron models added nonlinear dynamic features to a preexisting database and then determined factors that contribute to neuronal multistability (Marin et al. 2013; Doloc-Mihu and Calabrese 2011). Previous work used EMO to populate a database of cortical layer 5b pyramidal neurons, which displayed multiple realistic dynamics in the dendrites (backpropagating APs, calcium spikes, etc.) (Hay et al. 2011). Our approach was to also use EMO to create an archive and then hone in on models of interest for detailed exploration of their dynamics.

We have made our two model archives, each with ∼10,000 models, available in their entirety for public use as building blocks to be incorporated into neocortical models. Many users will elect to keep things consistent within a network by picking only a single model, whether a detailed model or a simplified one, and replicating that model multiple times to produce the SPI population for their network. In this case, we would suggest using one of the two exemplar models demonstrated in Figs. 6 and 7, which would be expected to provide the best approximation of excitability. Other users might instead elect to work with models that show better subthreshold or interspike fitness, perhaps to explore issues of activity resonance, whether in the single cell or in the network (see Fig. 8). In some network settings, it may turn out that models with more accurate resonant properties would produce more accurate patterns of population activity than would models with more accurate excitability under current clamp. This would be expected in settings where irregular ongoing background activity produces an irregular membrane potential near threshold. In this case, spikes would occur at peaks determined by some combination of the background activity and intrinsic resonance and would not be related to the timing seen with constant current injection (Mainen and Sejnowski 1995). Alternatively, it may be found that models with balanced fits across fitness functions are better for replicating network physiology. This determination will be made empirically by in silico experimentation with implications for physiological experiments that aim to produce single cell data, typically from an in vitro preparation, which is relevant to a cell's physiological behavior in vivo.

The principle of degeneracy, shown here again, states that diverse parameter sets can produce similar dynamical behaviors (Golowasch et al. 2002; Prinz et al. 2004; Neymotin et al. 2016a). Consideration of this principle suggests an alternative approach to neuronal network design that would embrace diversity by including many different models with different parameterizations in a network. A set of differently parameterized models could be chosen that all illustrate strong fitness in one area, be that firing rate or subthreshold properties. A still more diverse population could be selected that would represent fitness across different dynamical aspects. A further use of multiple models would be to confirm model robustness by utilizing multiple different models and confirming similar behavior, just as one utilizes multiple random seeds when assessing robustness in a simulation whose activity is in part determined by random wiring or randomly generated drive.

These diverse models can also be compared with measured physiological population diversity in SPI cells (Suter et al. 2013, Table 1). Substantial variability is seen in several of the measures used for our fitness assessment, including sag of 20.0 ± 3.6% (mV ± SD), input resistance of 35.7 ± 7.6 (MΩ), and F–I slope of 115 ± 29 (Hz/nA). This variability is seen despite common recording conditions: same species, same strain, same temperature, same age (Tripathy et al. 2015). The degree of heterogeneity could also be used as an additional criterion for selection of models for the archives. Ensemble methods could thereby offer further predictive power over the traditional one-model-fits-all strategy. Technically, maintenance and fitting of heterogeneity would also be useful since lack of diversity during EMO can prevent further improvements across multiple fitness functions. It would also be interesting to conduct further studies to determine whether some of the variability in particular measures could be explained by the tradeoff across measures that we note above. The model archive will suggest underlying parameter associations that could explain dynamic variability, e.g., an obvious prediction is that variability in density of somatic I_h will largely predict the variability in sag measured from the soma. Changes in dynamics as well as change in degree of variability are observed across maturation and could also be correlated with model variability overall and on a measure-by-measure basis.

Input Resonance

I_h played a prominent role in several dynamical features in both detailed and simple models, producing the characteristic sag with hyperpolarization and contributing to interspike voltage trajectory. I_h also provided band-pass filtering of artificial inputs producing peak resonant frequencies (4–6 Hz) similar to those observed in vitro (Fig. 8). This represents a dynamical property that was not explicitly fit and that emerged from a combination of the fitting of subthreshold responses and interspike voltage trajectories and the intrinsic dynamics of the I_h current itself.

Our results predict that the presence of increasing I_h density along the apical dendrite would produce a corresponding gradient of resonant frequencies, increasing with distance from the soma. This differential resonance would then provide differential responsiveness to particular patterns or ongoing frequencies of synaptic input at different cortical layers. Such a dynamical gradient of resonant frequencies would provide a novel signal processing function to these dendrites, which would then be tuned to respond to this frequency whether delivered to the layer by remote excitatory projections, interlaminar excitatory projections, intralaminar excitatory projections, or local inhibitory projections. Activating a particular section of dendrite at its characteristic stimulation frequency would augment voltage and calcium locally, potentially leading to local plasticity events, including plasticity involving I_h itself (Neymotin et al. 2013a, 2014, 2016). Additionally, this local depolarization would increase the chances of that cell generating a spike. Activating two or more layers at their different stimulation frequencies would be expected to further increase this output probability. In this way the SPI pyramidal neurons would have the ability to parse input frequencies in a layer-dependent manner. This mechanism is similar to one described previously by (Laudanski et al. 2014), although we were looking at far lower stimulation frequencies.

Different cortical layers utilize different frequencies for receiving and processing incoming information (Schroeder and Lakatos 2009; Lakatos et al. 2008, 2013, 2016). The general pattern that has emerged across several brain areas involves beta and gamma superficially (layer 2/3; supragranular in sensory areas) with lower frequencies, particularly alpha, deep (L5; infragranular) (Lundqvist et al. 2006; Silva et al. 1991; Ainsworth et al. 2011). Passing through these laminae, we would then a priori predict that apical dendrites would be tuned to respond optimally to the high gamma frequencies distally and lower alpha frequencies more proximally, matching resonance to the layer traversed. Although we found this pattern of lower to higher frequency proximal to distal, the frequencies that our model predict, alpha to low-beta ranges, do not match the spread of frequencies, up to gamma, expected from this physiological conjecture. We would expect that, as greater fidelity to dendritic physiology comes with improved knowledge of dendritic channel densities and types, these predictions will match. Experimentally, correlations between laminar population oscillation and apical dendrite resonance frequencies could be tested using laminar electrode arrays to span cortical layers and compare local field potentials, reflecting the former, with current source density, reflecting the latter (Mo et al. 2011; Neymotin et al. 2013b; Lakatos et al. 2014).

GRANTS

This research was supported by National Institutes of Health (NIH) Grants U01-EB-017695 (to W. W. Lytton and G. M. G. Shepherd); R01-EB-02290301 and R01-MH-086638 (to W. W. Lytton); T32-AG-020418 and T32-NS-041234 (to B. Suter); and NS-061963 (to G. M. G. Shepherd). The NIH had no role in study design; in the collection, analysis, and interpretation of data; in the writing of the report; and in the decision to submit the article for publication.

DISCLOSURES

No conflicts of interest, financial or otherwise, are declared by the author(s).

AUTHOR CONTRIBUTIONS

S.A.N., B.A.S., S.D.-B., G.M.G.S., M.M., and W.W.L. conception and design of research; S.A.N., B.A.S., S.D.-B., G.M.G.S., M.M., and W.W.L. performed experiments; S.A.N., B.A.S., S.D.-B., G.M.G.S., M.M., and W.W.L. analyzed data; S.A.N., B.A.S., S.D.-B., G.M.G.S., M.M., and W.W.L. interpreted results of experiments; S.A.N., B.A.S., S.D.-B., G.M.G.S., M.M., and W.W.L. prepared figures; S.A.N., B.A.S., S.D.-B., G.M.G.S., M.M., and W.W.L. drafted manuscript; S.A.N., B.A.S., S.D.-B., G.M.G.S., M.M., and W.W.L. edited and revised manuscript; S.A.N., B.A.S., S.D.-B., G.M.G.S., M.M., and W.W.L. approved final version of manuscript.