Effects of ion channel noise on neural circuits: an application to the respiratory pattern generator to investigate breathing variability

A major source of noise in neuronal circuits is the “flickering” of ion currents passing through the neurons' membranes (channel noise), which cannot be suppressed experimentally. Computational simulations are therefore the best way to investigate the effects of this physiological noise by manipulating its level at will. We investigate the role of noise in the respiratory pattern generator and show that endogenous, breath-to-breath variability is tightly linked to the respiratory pattern.

Abstract

Neural activity generally displays irregular firing patterns even in circuits with apparently regular outputs, such as motor pattern generators, in which the output frequency fluctuates randomly around a mean value. This “circuit noise” is inherited from the random firing of single neurons, which emerges from stochastic ion channel gating (channel noise), spontaneous neurotransmitter release, and its diffusion and binding to synaptic receptors. Here we demonstrate how to expand conductance-based network models that are originally deterministic to include realistic, physiological noise, focusing on stochastic ion channel gating. We illustrate this procedure with a well-established conductance-based model of the respiratory pattern generator, which allows us to investigate how channel noise affects neural dynamics at the circuit level and, in particular, to understand the relationship between the respiratory pattern and its breath-to-breath variability. We show that as the channel number increases, the duration of inspiration and expiration varies, and so does the coefficient of variation of the breath-to-breath interval, which attains a minimum when the mean duration of expiration slightly exceeds that of inspiration. For small channel numbers, the variability of the expiratory phase dominates over that of the inspiratory phase, and vice versa for large channel numbers. Among the four different cell types in the respiratory pattern generator, pacemaker cells exhibit the highest sensitivity to channel noise. The model shows that suppressing input from the pons leads to longer inspiratory phases, a reduction in breathing frequency, and larger breath-to-breath variability, whereas enhanced input from the raphe nucleus increases breathing frequency without changing its pattern.

NEW & NOTEWORTHY A major source of noise in neuronal circuits is the “flickering” of ion currents passing through the neurons' membranes (channel noise), which cannot be suppressed experimentally. Computational simulations are therefore the best way to investigate the effects of this physiological noise by manipulating its level at will. We investigate the role of noise in the respiratory pattern generator and show that endogenous, breath-to-breath variability is tightly linked to the respiratory pattern.

neuronal action potentials both in vivo and in vitro are not fully predictable and may occur spontaneously in the absence of stimulation. The mechanisms underlying the unpredictability of neural firing are known and, generally, are referred to as channel noise and synaptic noise (Hille 2001; Johnston and Wu 1995). At the microscopic level, ion channels in the neuron's membrane vibrate randomly at physiological temperature, thereby changing the size of their pores, which in turn causes fluctuations in ion currents (channel noise). The statistical nature of ion-channel gating is well described as a binomial random process, so that the mean current for a given channel type increases with the total number of open channels, N_open, in the neuron's membrane (or more precisely, in a membrane patch of given size), whereas the standard deviation of the current fluctuations grows as $\sqrt{N_{\mathrm{open}}}$. Because the number of open channels scales with the total number of channels, N, this implies that as the number of channels (or the channel density) increases, the current fluctuations relative to the mean decrease as 1/ $\sqrt{N}$. Thus, in the limit of an infinite number of channels, the ion currents, and hence the action potentials, become deterministic and predictable.

The mathematical modeling of physiological noise is well established in terms of Markov models of either the whole channel or its constitutive subunits, i.e., its conductance gates (Goldwyn et al. 2011; Goldwyn and Shea-Brown 2011; Hille 2001; Johnston and Wu 1995; Schmandt and Galán 2012; Schneidman et al. 1998). Other mathematical descriptions of channel noise based on fractal analysis have been proposed as well, motivated by the self-similarity of current fluctuations over a wide range of timescales, which is apparent in voltage-clamp conditions (Groff et al. 2010; Rowat 2007). In our study, however, only fast timescales are relevant, as the channels are not voltage-clamped and the membrane potential fluctuates on a millisecond timescale. We therefore consider the Markovian description here.

Whole-channel Markovian models are typically based on the analysis of single-channel recordings (Hille 2001; Johnston and Wu 1995; Keener and Sneyd 2004), but they are not necessarily unique: the same recordings may be explained by a different channel model—see chapter 18 in Hille (2001). In contrast, subunit models are based on the analysis of whole cell patch-clamp recordings (Johnston and Wu 1995), which characterize the activation and inactivation of ion currents by applying the classical protocols of Hodgkin and Huxley (1952) and their assumption on channel gates being independent, which yields a unique subunit model. Whole-channel models and subunit models describe currents with the same mean and variance for N >> 1.

Channel noise has been extensively studied in recent years (Goldwyn et al. 2011; Groff et al. 2010; Rowat 2007; Schmandt and Galán 2012), showing that it may alter the firing threshold (Clay and DeFelice 1983), spike timing (van Rossum et al. 2003), and its reliability (Schneidman et al. 1998). Markov chain models are computationally expensive to simulate, which limits their applicability to investigate the role of physiological noise beyond the single-cell level. Recently, the stochastic-shielding approximation of Markov chains for whole-channel models (Schmandt and Galán 2012) has enabled the study of information transfer in minimalist circuit motifs (Puzerey and Galán 2014). But still, the effect of realistic channel noise on circuit-level activity has not been investigated, mostly because if its computational cost. Here we demonstrate how a deterministic conductance-based model of the respiratory pattern generator can be efficiently expanded to incorporate the effect of physiological noise in an efficient manner.

The breathing pattern can be divided into three phases: inspiration, postinspiration, and expiration (Richter 1982). Experimental data demonstrate that this rhythmic pattern of respiratory activity depends on the pre-Bötzinger complex (pre-BötC) within the ventral respiratory column and is controlled by inputs from the Bötzinger complex, pons, and other nuclei (Richter 1996). In addition, four types of neurons have been classified on the basis of their firing patterns and their phases of activity related to the breathing cycle, including preinspiratory (Pre-I) neurons, early-inspiratory (Early-I) neurons, postinspiratory (Post-I) neurons, and augmenting-expiratory (Aug-E) neurons (Fig. 1). Based on these findings, a biophysically detailed model of the respiratory network consisting of interacting brain stem compartments has been proposed (Rybak et al. 2007; Smith et al. 2007). The model shows that the rhythmic behavior of the network is determined by the intrinsic bursting activity of Pre-I neurons, a pacemaker population, and the external excitatory inputs from the retrotrapezoid nucleus, the raphe nucleus, and the pons. We use a simplified version of this model that preserves the relevant physiology, which has been used previously to study the generation and transformation of respiratory patterns (Rubin et al. 2009). We chose this model not only for its realism but also because we hypothesized that the addition of channel noise to this simplified model would allow us to investigate endogenous mechanisms for breathing variability.

Fig. 1.

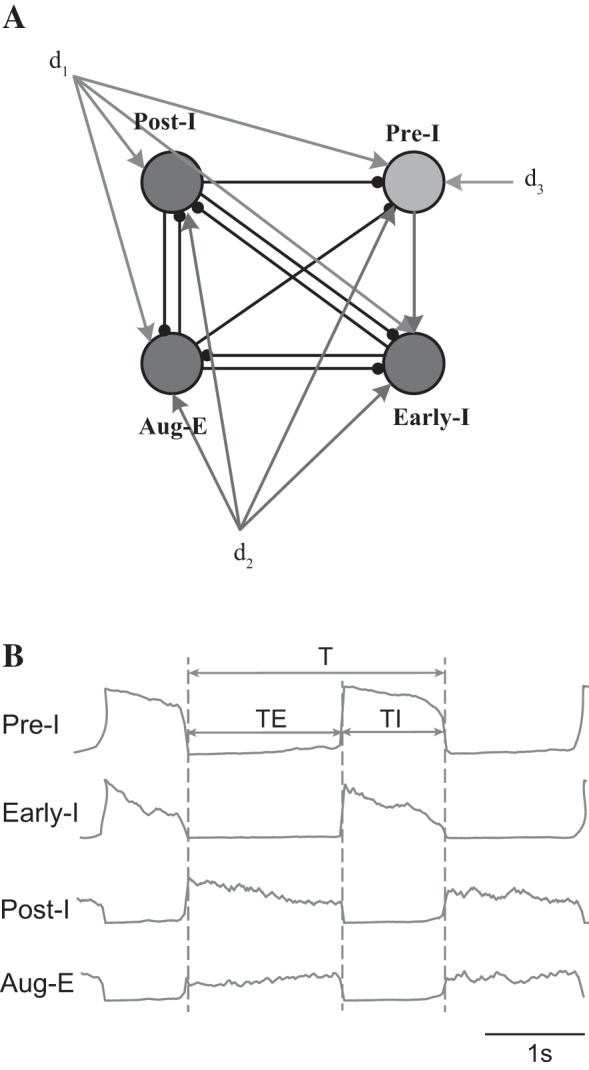
A: schematic of the respiratory network. Pre-I, preinspiration neuron; Early-I, early-inspiration neuron; Post-I, postinspiration neuron; Aug-E, augmenting expiratory neuron. d₁, d₂, and d₃ are external drives from the pons, retrotrapezoid nucleus, and raphe, respectively. B: typical traces and respiratory intervals for Pre-I, Early-I, Post-I, and Aug-E neurons. T, respiratory duration; TI, inspiratory duration; TE, expiratory duration.

Synaptic noise is not included in this study because the synaptic conductances in the model by Rubin et al. (2009) do not depend explicitly on time, which precludes the addition of stochastic fluctuations. We note, however, that the effect of the distribution and strength of synaptic connections on the variability of the respiratory pattern generator has been recently investigated with experiments and computational simulations by Fietkiewicz et al. (2016), showing that synaptic heterogeneity can account for the monotonic relationship between the mean and interquartile values of the interburst intervals in the respiratory pattern generator. Here we show that channel noise has differential effects on the respiratory pattern depending on the total number of channels. The model also demonstrates the effect of specific inputs to the network on breathing variability.

METHODS

Network model.

The stochastic model of the respiratory network presented here is an extension of the deterministic model by Rubin et al. (2009), which in turn is based on previous biophysical models of the respiratory network in the brain stem (Rybak et al. 2007; Smith et al. 2007). It contains four neurons (labeled with subindex i ∈ {1,2,3,4}), including an excitatory Pre-I neuron and three inhibitory neurons: early inspiratory neuron (Early-I), postinspiratory neuron (Post-I), and augmenting expiratory neuron (Aug-E), as well as three excitatory drives (d_k, k ∈ {1,2,3,4}) from the pons, retrotrapezoid nucleus, and raphe nuclei, respectively. The connectivity structure of the network is shown in Fig. 1. Each neuron represents a distinct, homogeneous neuronal population and is described by a conductance-based model of the Hodgkin-Huxley type (Hodgkin and Huxley 1952). The time-dependent variable V_i represents the average voltage of the ith population, and the output f(V_i) represents the integrated population activity at the corresponding average voltage (Ermentrout 1994). Specifically, the membrane potential of excitatory Pre-I neuron V₁ obeys the following differential equation:

$$C\frac{\text{d}{V}_1}{\text{d}t}=-I_{\text{NaP}}-I_{\text{K}}-I_{{\text{L}}_1}-I_{\text{Syn}{\text{E}}_{\mathrm{1}}}-I_{\text{Syn}{\text{I}}_{\mathrm{1}}}$$ (1)

For the three inhibitory neurons (Early-I, Post-I, and Aug-E), the corresponding membrane potential V_i (i = 2,3,4) is given by

$$C\frac{\text{d}{V}_i}{\mathrm{d}t}=-I_{\mathrm{A}{\mathrm{D}}_i}-I_{{\mathrm{L}}_i}-I_{\mathrm{S}\mathrm{y}\mathrm{n}{\mathrm{E}}_i}-I_{\mathrm{S}\mathrm{y}\mathrm{n}{\mathrm{I}}_i}$$ (2)

C is the neuronal capacitance; I_NaP represents the persistent sodium (NaP) current; I_K represents the potassium current; I_ADi(i = 2,3,4) represents the adaptive potassium (AD) current; I_Li(i = 1,2,3,4) is the leak current; I_SynEi and I_SynIi (i = 1,2,3,4) are the excitatory and inhibitory synaptic currents, respectively. These currents are given by

$$\begin{array}{l}{I}_{NaP}=g_{NaP}{m}_{\mathrm{N}a\mathrm{P}}{h}_{NaP}(V_1-E_{Na})\\ I_K=g_K{m}_K^4(V_1-E_K)\\ I_{A{D}_i}=g_{A{D}_i}{m}_{A{D}_i}(V_i-E_K)\\ I_{L_i}=g_{L_i}(V_i-E_L)\\ I_{Syn{E}_i}=g_{SynE}(V_i-E_{SynE}){\displaystyle \sum _{k=1}^3{c}_{ki}{d}_k}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\text{for}\hspace{0.17em}\text{i}\ne 2\\ I_{Syn{E}_2}=g_{SynE}(V_2-E_{SynE})\left[a_{12}{f}_1(V_1)+{\displaystyle \sum _{k=1}^3{c}_{k2}{d}_k}\right]\\ I_{Syn{I}_i}=g_{SynI}(V_i-E_{SynI}){\displaystyle \sum _{\begin{array}{l}j=2\\ j\ne i\end{array}}^4{b}_{ji}{f}_j(V_j)}\end{array}$$ (3)

where g_NaP, g_K, g_ADi, g_Li, g_SynE, g_SynI are the maximal conductances of the corresponding currents; E_Na, E_K, E_L, E_SynE, E_SynI are the corresponding reversal potentials; d₁, d₂, and d₃ are external drives (Fig. 1); a_ji defines the weight of the excitatory synaptic input from neuron j to neuron i; b_ji defines the weight of the inhibitory synaptic input from neuron j to neuron i; and c_ki defines the weight of the excitatory synaptic input from drive k to neuron i. For the persistent sodium channels and the adaptive potassium channels, whose gating is stochastic in our model, the maximal conductance is given by the product of their respective single-channel conductances, γ_NaP and γ_AD, with the total number of each channel type, N_NaP and N_ADi (i = 2,3,4). We thus have g_NaP = γ_NaPN_NaP and g_ADi = γ_ADN_ADi. Here we consider N_NaP = N_ADi = N (i = 2,3,4). The matrices of the synaptic weights are

$$a=\left[\begin{array}{cccc}0& 0.5& 0& 0\\ 0& 0& 0& 0\\ 0& 0& 0& 0\\ 0& 0& 0& 0\end{array}\right],\hspace{0.17em}b=\left[\begin{array}{cccc}0& 0& 0& 0\\ 0& 0& 0.25& 0.35\\ 0.3& 0.05& 0& 0.35\\ 0.2& 0.35& 0.1& 0\end{array}\right],\hspace{0.17em}c=\left[\begin{array}{cccc}0.115& 0.3& 0.63& 0.33\\ 0.07& 0.3& 0& 0.4\\ 0.025& 0& 0& 0\end{array}\right]$$

The nonlinear function f_i(V_i) defines the output activity of the neuronal population represented by each neuron

$$f_i(V_i)=1/\{1+\exp [-(V_i-V_{1/2})/k_{V_i}]\}$$ (4)

where V_1/2 is the half-activity voltage and k_Vi defines the slope for the output function for each neuron. The channel gates h_NaP and m_ADi (i = 2,3,4) are slow variables involved in persistent sodium and adaptive potassium currents, respectively. Their dynamics are given by the following stochastic differential equations:

$$\begin{array}{l}d{h}_{NaP}=dt\left(\frac{1}{{\tau }_{hNaP}(V_1)}(h_{\infty NaP}(V_1)-h_{NaP})\right)+\sqrt{dt}{\xi }_{NaP}(t)\\ d{m}_{A{D}_i}=dt\left(\frac{1}{{\tau }_{A{D}_i}}(k_{A{D}_i}{f}_i(V_i)-m_{A{D}_i})\right)+\sqrt{dt}{\xi }_{A{D}_i}(t)\end{array}$$ (5)

ξ_NaP(t) is channel noise in persistent sodium channels and ξ_ADi(t) (i = 2,3,4) is channel noise in adaptive potassium channels. The computation of channel noise is explained below. Other voltage-dependent gates (m, h) and time constants (τ) for Pre-I neurons are defined as follows

$$\begin{array}{l}{m}_{NaP}=1/\{1+\exp [-(V_1+40)/6]\}\\ h_{\infty NaP}=1/\{1+\exp [-(V_1+48)/6]\}\\ {\tau }_{hNaP}={\tau }_{hNaP\text{max}}/\cosh \hspace{0.17em}[(V_1+48)/12]\\ m_{\text{K}}=1/\{1+\exp [-(V_1+29)/4]\}\end{array}$$ (6)

The parameters of the model are reported in Table 1.

Table 1.

Model parameters

Membrane capacitance (C)	20 pF
Maximal potassium channel conductance (gK)	5 nS
Leakage conductance (gL)	2.8 nS
Excitatory synaptic conductance (gSynE)	10 nS
Inhibitory synaptic conductance (gSynI)	60 nS
Single persistent sodium channel conductance (γNaP)	0.025 nS
Single adaptive potassium channel conductance (γAD)	0.05 nS
Sodium reversal potential (ENa)	50 mV
Potassium reversal potential (EK)	−85 mV
Leakage reversal potential (EL)	−60 mV
Excitatory synaptic reversal potential (ESynE)	0 mV
Inhibitory synaptic reversal potential (ESynI)	−75 mV
Half-activity voltage (V1/2)	−30 mV
Slope for the output function (kV1)	8 mV
Slope for the output function (kV2, kV3, kV4)	4 mV
Time constant of persistent sodium current (τhNaPmax)	6,000 ms
Time constant of adaptive potassium current (τAD2, τAD4)	2,000 ms
Time constant of adaptive potassium current (τAD3)	1,000 ms
Adaptation parameters (kAD2, kAD4)	0.9
Adaptation parameters (kAD3)	1.3
External drives (d1, d2, d3)	0.3 pA

Channel noise.

We now show how to introduce stochasticity in all channel gates that depend explicitly on time. For each channel gate, the stochastic dynamics is described by a two-state Markov chain:

$$\text{Closed}\underset{\beta (V)}{\overset{\alpha (V)}{\rightleftharpoons }}\text{Open}$$ (7)

where α(V) and β(V) are the voltage-dependent transition probabilities. The probability p of a gate to be in the open state satisfies the differential equation

$$\frac{dp}{dt}=\alpha (V)(1-p)-\beta (V)p$$ (8)

or, equivalently,

$$\frac{dp}{dt}=\frac{1}{{\tau }_p(V)}[p_{\infty }(V)-p]$$ (9)

where $p_{\infty }(V)=\frac{\alpha (V)}{\alpha (V)+\beta (V)}$ and ${\tau }_p(V)=\frac{1}{\alpha (V)+\beta (V)}$ .

For each channel type, the expected number of open gates, N_open, out of a total of N is

$$N_{\text{open}}=Np$$ (10)

From Eq. 9, the expected number of gates that open over a time step dt is

$$d{N}_{open}=\text{d}t\left(N\frac{p_{\infty }(V)}{{\tau }_p(V)}-\frac{N_{open}}{{\tau }_p(V)}\right)$$ (11)

If the number of gates is finite, the fluctuations in the number of open gates are not negligible and follow a binomial distribution with standard deviation

$${\sigma }_{N_{open}}=\sqrt{Np(1-p)}=\sqrt{N_{open}\left(1-\frac{N_{open}}{N}\right)}$$ (12)

In the diffusion approximation, that is, for N_open >> 1, the binomial distribution approaches a Gaussian distribution and we may add to Eq. 11 an additional, stochastic term (diffusion) to account for the fluctuations, becoming an Ornstein-Uhlenbeck process (Gardiner 2004). In our simulations we verified that N_open >> 1 at all times and therefore are confident that the Gaussian approximation was valid. The diffusion term consists of Gaussian white noise with standard deviation (Goldwyn et al. 2011)

$${\sigma }_{noise}^2=\frac{2}{{\tau }_p(V)}{\sigma }_{N_{open}}^2$$ (13)

Thus the stochastic dynamics of each gate can be simulated with the following stochastic differential equation:

$$\text{d}{N}_{\text{open}}=\text{d}t\left(N\frac{p_{\infty }(V)}{{\tau }_p(V)}-\frac{N_{\text{open}}}{{\tau }_p(V)}\right)+\sqrt{\text{d}t}\eta (t)\sqrt{\frac{2}{{\tau }_p(V)}{N}_{\text{open}}\left(1-\frac{N_{\text{open}}}{N}\right)}$$ (14)

in which η(t) is Gaussian white noise with unitary variance. Equivalently, the stochastic differential equation for the probability of opening a gate is given by

$$\text{d}p=\text{d}t\left(\frac{p_{\infty }(V)}{{\tau }_p(V)}-\frac{p}{{\tau }_p(V)}\right)+\sqrt{\text{d}t}\eta (t)\frac{1}{\sqrt{N}}\sqrt{\frac{2}{{\tau }_p(V)}p(1-p)}$$ (15)

Thus, in Eq. 5, channel noise for the persistent sodium channels of the Pre-I neuron has the form

$${\xi }_{\text{NaP}}(t)=\frac{{\eta }_1(t)}{\sqrt{N_{\text{NaP}}}}\sqrt{\frac{2}{{\tau }_{h\text{NaP}}(V_1)}{h}_{\text{Nap}}(1-h_{\text{NaP}})}$$ (16)

and for the potassium channels of Early-I, Post-I, and Aug-E neurons, channel noise is given by

$${\xi }_{\text{A}{\text{D}}_i}(t)=\frac{{\eta }_i(t)}{\sqrt{N_{\text{A}{\text{D}}_i}}}\sqrt{\frac{2}{{\tau }_{\text{A}{\text{D}}_i}(V)}{m}_{\text{A}{\text{D}}_i}(1-m_{\text{A}{\text{D}}_i})}$$ (17)

where η_i(t) are four (i = 1,2,3,4) uncorrelated realizations of Gaussian white noise.

In the model by Rubin et al. (2009) each neuron represents a population of identical neurons of the same type. This simplification assumes that those neurons have similar channel numbers and conductances, synaptic connections among themselves and with neurons of other types, as well as external drives. Stricter assumptions such as all-to-all connectivity, which is often used in simplified mean-field models, are not required. Usually, population models of the mean-field type are based on simpler, firing rate dynamics for each neuron in the population, ignoring the ion channel dynamics (Deco et al. 2008; Nicola and Campbell 2013). This precludes the investigation of physiological channel noise in those models. In contrast, the simplified network model by Rubin et al. (2009) and other similar models of the central respiratory pattern generator (Molkov et al. 2014; Rubin et al. 2011; Rybak et al. 1997) explicitly include a detailed description of the ion channel gating. When expanding population models to incorporate channel noise, current fluctuations in different neurons of the same type will have the same statistical properties, as they have the same number of channels. Thus any given neuron in each population will be equally noisy and representative of the group. This enables the study of channel noise also in simplified network models in which a single neuron represents a homogeneous population.

All model simulations were performed in MATLAB R2015a. Differential equations for the membrane potential and slow variables were integrated with the Euler method, with dt = 0.1 ms. The simulation time was 4,200 s, and the first 200 s were removed to exclude any transient effects due to the initial conditions. The displayed results were averaged over 24 trials.

Measures of variability and Poincaré plots.

We used three different measures of variability for the inspiratory phase (TI), the expiratory phase (TE), and the total breathing cycle (T) that yield qualitatively the same results. To determine the duration of these intervals, we applied a hard threshold (at 0.15) to the output function for the Pre-I neuron and considered the sign of its first derivative to determine whether inspiration was being initiated or terminated. For each respiratory cycle, TI was determined as the time elapsed between the threshold crossing with positive derivative and the next threshold crossing with negative derivative (Fig. 1B). TE was determined as the time elapsed between the threshold crossing with negative derivative and the next threshold crossing with positive derivative (Fig. 1B). T was defined as the sum of TI and TE.

The first measure of variability is the coefficient of variation, defined as the standard deviation divided by the mean. This measure is agnostic to the order in the sequence of respiratory cycles and will yield identical results if the cycles are randomly permuted. The second measure is the irregularity score from Telgkamp et al. (2002), which in addition is sensitive to the recent history of the respiratory pattern. The irregularity score for the nth respiratory cycle, T_n, is calculated relative to the previous cycle, T_n−1, as S_n = 100 × |T_n − T_n−1|/T_n−1. In our analyses, we use the average of S_n across all cycles. The irregularity scores for TI or TE are computed similarly, using TI_n−1 and TI_n or TE_n−1 and TE_n, respectively. A low irregularity score represents a regular rhythm. The higher the irregularity score, the less regular the rhythm.

The third measure of variability is based on a three-dimensional (3D) Poincaré plot, in which the coordinates correspond to three successive values of the respiratory cycle T_n, T_n+1, T_n+2. For each cycle n there is a point in the Poincaré plot, and the whole series of respiratory cycles defines a cloud of points. The standard deviation of its radius relative to its center of mass gives a measure of variability, in fact, a 3D coefficient of variation, which is also sensitive to the sequence of respiratory cycles. The same procedure is applied to TI and TE.

RESULTS

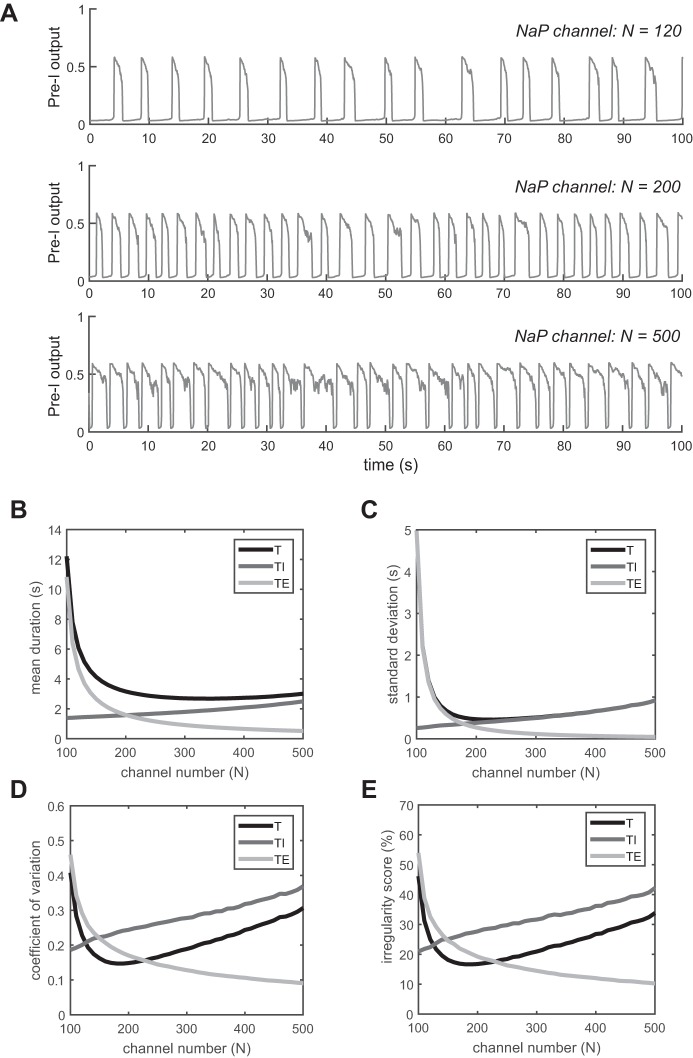
We first investigate the effect of channel noise in isolated Pre-I neurons, which are the pacemakers of the respiratory rhythm. The Pre-I neuron can intrinsically generate rhythmic activity through a persistent sodium current, I_NaP. In Fig. 2A, the traces for the output activity of the Pre-I population are shown as a function of the number of persistent sodium (NaP) channels. As the number increases, the respiratory period decreases, during which the duration of inspiration increases and the duration of expiration decreases quickly (Fig. 2, A and B). The respiratory period is T = 6.08 s (TE = 4.65 s and TI = 1.43 s) for N = 120. For N = 500, the respiratory period decreases further to T = 3.01 s (TE = 0.51 s and TI = 2.5 s). The variability of the breath-to-breath interval also depends on the number of persistent sodium channels as shown in Fig. 2, C and D. As the number of channels increases, the coefficient of variation of respiration first decreases and then increases. A minimum level of variability is attained around N = 180. For N ≤ 130, the mean conductance for persistent sodium is quite small, leading to a significantly shorter duration of inspiration relative to expiration (bradypnea). In this regime, the cumulative effect of fluctuations in the persistent sodium current lead to higher variability in its activation and therefore in the duration of the expiratory phase. For N > 200, the conductance of persistent sodium is quite large, leading to longer and more frequent inspiratory bursts (apneusis). In this regime, the cumulative effect of fluctuations in the persistent sodium current lead to more variability in its inactivation, thereby causing more variability in the duration of inspiration. In the range of 140 ≤ N ≤ 170, a normal respiratory pattern with inspiration-to-expiration ratio in the range 1:1.5 to 1:2 is observed. For N = 200 the ratio is 1.

Fig. 2.

Pattern variability in a stochastic Pre-I neuron. A: output traces of Pre-I neuron with 3 different numbers of NaP channels: 120, 200, and 500. B: mean duration of T, TI, and TE vs. channel number. C: standard deviation of T, TI, and TE vs. channel number. D: coefficient of variation of T, TI, and TE vs. channel number. E: irregularity score of T, TI, and TE vs. channel number.

The coefficient of variation is insensitive to the order of the respiratory cycles. To consider the potential effect that a previous breath has on the current one, we also computed the average irregularity score (see methods; Fig. 2E). The irregularity score yields the same qualitative dependence on the number of channels as the coefficient of variation.

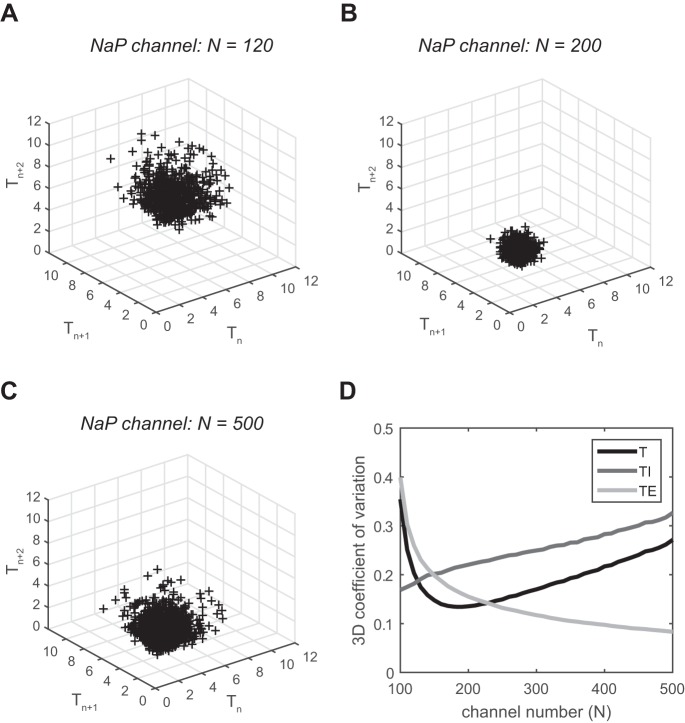
We also used Poincaré plots (see methods) to investigate how the recent history of the respiratory pattern contributes to its variability (Fig. 3, A–C). The size of the cloud of points in the plot relative to its center of mass provides another measure of variability, a 3D coefficient of variation, that is sensitive to the order of respiratory cycles. Figure 3A shows a fairly widespread cloud of points (T_n,T_n+1,T_n+2) far from the origin, which means that the respiratory pattern is slow and highly variable for N = 120. Figure 3B displays a tight cloud of points (T_n,T_n+1,T_n+2) closer to the origin, which means that the respiratory pattern is fast and highly regular for N = 200. Figure 3C shows a widespread cloud of points (T_n,T_n+1,T_n+2) close to the origin, which means that the respiratory pattern is fast and highly variable for N = 500. Figure 3D shows the 3D coefficient of variation of the Poincaré plots for T, TI, and TE as a function of the channel number. The results are qualitatively very similar to both the coefficient of variation in Fig. 2D and the irregularity score in Fig. 2E.

Fig. 3.

Poincaré plots of respiratory variability in a stochastic Pre-I neuron. A–C: plots for 3 different numbers of NaP channels: 120, 200, and 500. D: 3-dimensional (3D) coefficient of variation of T, TI, and TE vs. channel number.

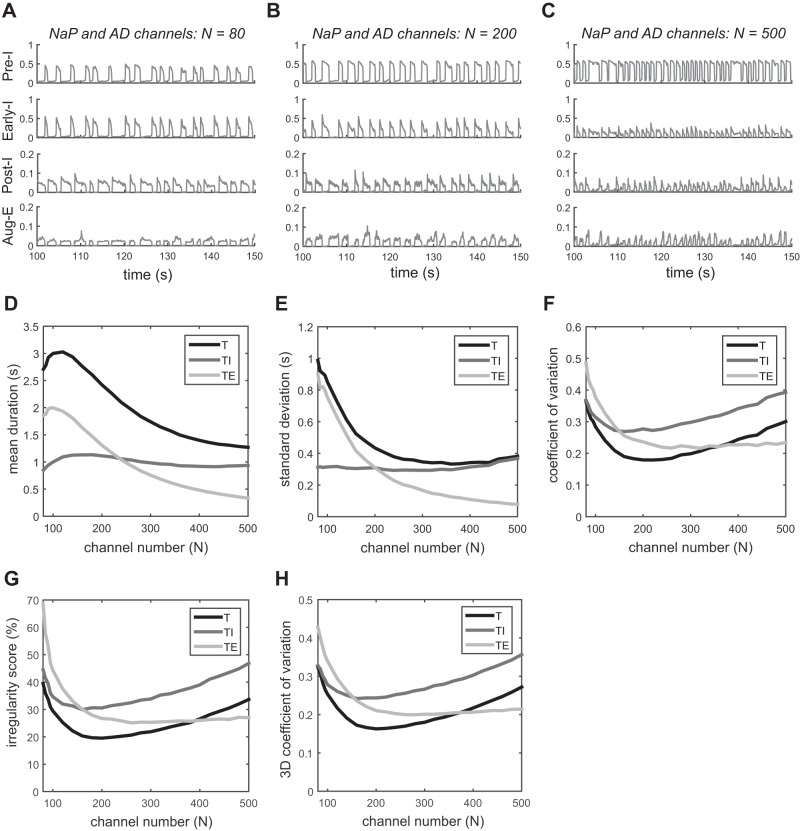
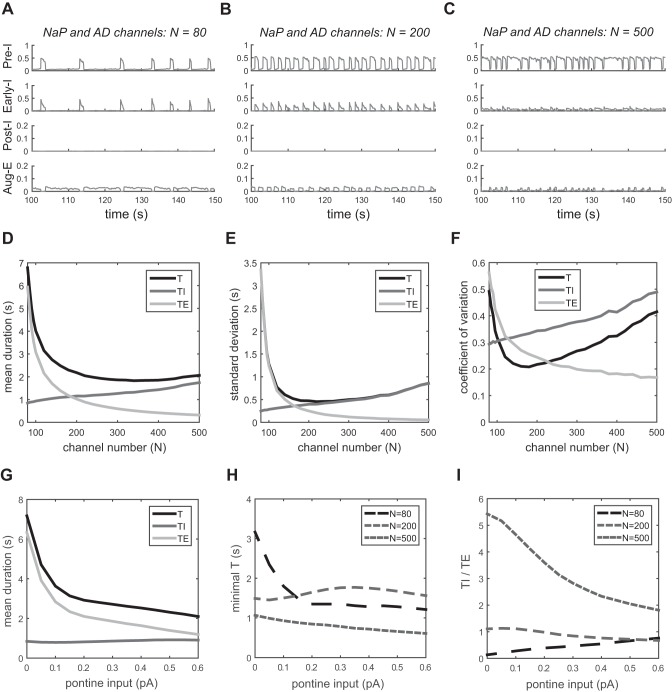
We next investigated the role of channel noise in the four neuronal populations of the respiratory network, with the three tonic, external inputs. The output of each neuron is shown in Fig. 4, A–C, for different channel numbers (of both persistent sodium and adaptive potassium channels). For N = 80, there is a short-inspiratory and long-expiratory pattern, and the duration of expiration varies largely in each respiration cycle. As the channel number increases to N = 200, the respiratory pattern becomes quite regular, with slightly longer expiration than inspiration. For a large channel number, N = 500, an apneustic-looking pattern is apparent with long-inspiratory and short-expiratory durations. In this regime, the inspiratory phase becomes more irregular. We show the duration and variability of the respiratory phases in Fig. 4, D–H. A nonmonotonic, concave relation of the coefficient of variation of breathing with the channel number is observed (Fig. 4F). The minimum appears around N = 200, where the mean duration of expiration is somewhat longer than that of inspiration (Fig. 4D). For small channel numbers, the variability of the expiratory phase dominates over the variability of the inspiratory phase, and vice versa for large channel numbers. Moreover, when more channels are included, the output of three inhibitory neurons (Early-I, Post-I, and Aug-E) decreases because of the increase in their adaptive potassium currents, which are repolarizing. The irregularity score (Fig. 4G) and the 3D coefficient of variation (Fig. 4H) both yield the same qualitative results as the coefficient of variation (Fig. 4F).

Fig. 4.

Variability in the stochastic respiratory pattern generator. Noise is added to persistent sodium (NaP) channels in the Pre-I neuron and to adaptive potassium (AD) channels in Early-I, Post-I, and Aug-E neurons. The number of channels is the same for each channel type. A–C: output traces for different channel numbers: 80, 200, and 500. D: mean duration of T, TI, and TE vs. channel number. E: standard deviation of T, TI, and TE. F: coefficient of variation of T, TI, and TE. G: irregularity score of T, TI, and TE. H: 3-dimensional (3D) coefficient of variation of T, TI, and TE.

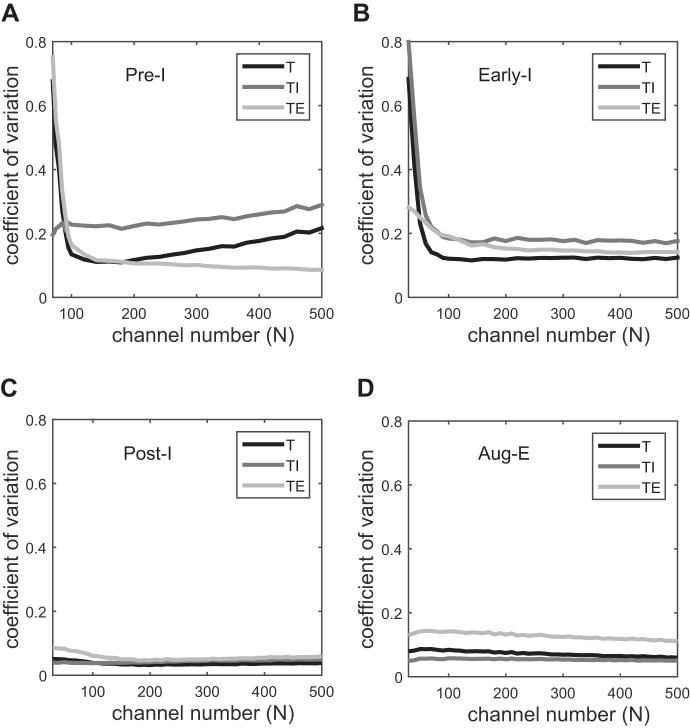
We next investigated the sensitivity of respiratory variability to channel noise in different neurons of the respiratory network. Channel noise was added to one neuron at a time (Fig. 5). By comparison with Fig. 4, we observed that Pre-I and Early-I neurons, but especially the former, are more sensitive to channel noise and thereby determine the whole network's variability (Fig. 5, A and B). The Pre-I neuron shows an intrinsic oscillatory behavior and functions as a pacemaker. It also provides excitatory input to the Early-I neuron. However, for small channel numbers (N < 100), the variability of the expiratory phase dominates when noise is added to the Pre-I neuron, whereas variability of the inspiratory phase dominates when noise is added to the Early-I neuron. Noise in the adaptive potassium current of the Early-I neuron affects the variability of inspiration by determining the end of inspiration. For the other two neurons (Post-I and Aug-E), channel noise has little impact on respiratory rhythm; the maximal value of the coefficient of variation was below 0.18 (Fig. 5, C and D). These observations indicate that Pre-I neurons are the main generators of respiratory rhythm variability. The effect of stochastic, adaptive potassium channels is investigated here for the whole network dynamics only because the isolated Early-I, Post-I, and Aug-E neurons cannot generate the respiratory pattern by themselves.

Fig. 5.

Sensitivity of respiratory variability to channel noise in different neurons. A: persistent sodium channel noise in Pre-I neuron. B–D: adaptive potassium channel noise in Early-I (B), Post-I (C), and Aug-E (D) neurons.

Finally, we considered the effect of changes in external inputs on the variability of respiration. The pons provides an important input to the network that regulates the transition from inspiration to expiration. In Fig. 6, we blocked the pontine input (d₁ = 0) and investigated the change in respiratory pattern as a function of the number of channels (Fig. 6, A–C). We observed that the activity of the Post-I neuron is completely depressed and the respiratory pattern is transformed from a three-phase rhythm into a two-phase rhythm (without the postinspiratory phase). This behavior is inherited from the deterministic respiratory network models (Rubin et al. 2009; Rybak et al. 2007; Smith et al. 2007). Additionally, the outputs of Early-I and Aug-E neurons are decreased. The mean duration of inspiration and expiration and the coefficient of variation of the breath-to-breath interval are shown in Fig. 6, D–F. Removing the pontine input leads to a severely apneustic pattern with a much longer inspiratory phase for N > 200. For N = 500, the TI-to-TE ratio (TI/TE) = 2.8 with d₁ = 0.3 pA, while TI/TE = 5.4 without pontine input. Removing pontine input also results in a longer respiratory period, especially for N < 140 (compare curves of T between Fig. 4D and Fig. 6D, before and after block of the pontine input), indicating a severe reduction in breathing frequency (bradypnea). Moreover, the variability of inspiration and expiration is largely increased because the depression of Post-I activity disinhibits the Pre-I and Early-I neurons, which can activate easily to switch between inspiration and expiration.

Fig. 6.

Respiratory variability with changes in pontine input. A–F: no input, d₁ = 0. A–C: output traces of 4 neurons with different channel numbers: 80, 200, and 500. D: mean duration of T, TI, and TE vs. channel number. E: standard deviation of T, TI, and TE vs. channel number. F: coefficient of variation of T, TI, and TE vs. channel number. G: mean duration of T, TI, and TE vs. pontine input (channel number N = 80). H: minimal respiratory duration of T vs. pontine input for channel numbers 80, 200, and 500. I: TI/TE vs. pontine input for channel numbers 80, 200, and 500.

We also investigated the sensitivity of respiratory pattern to the pontine drive, as shown in Fig. 6, G–I. The mean TI is barely affected over a wide range of pontine inputs, but the mean TE decreases quickly with increasing input (Fig. 6G; N = 80). The minimal T is more sensitive to changes in pontine input for small channel numbers (Fig. 6H). TI/TE changes more for large channel numbers (Fig. 6I).

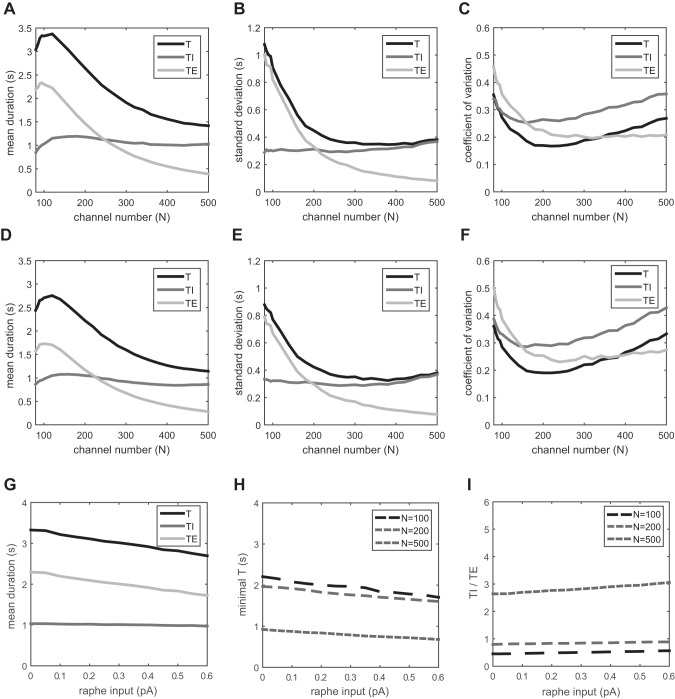
We also considered the effect of changing the excitatory input from the raphe nuclei to the Pre-I neuron. This was motivated by recent experimental work using optogenetics that demonstrated that activation of the raphe nuclei increases the frequency of the respiratory rhythm (Depuy et al. 2011). We therefore investigated what happens after blocking (d₃ = 0) and enhancing (d₃ = 0.6 pA) the input from the raphe nuclei relative to the baseline value of d₃ = 0.3 pA investigated above. Simulation results are shown in Fig. 7 for d₃ = 0 (Fig. 7, A–C) and d₃ = 0.6 pA (Fig. 7, D–F). There are no qualitative changes in respiratory pattern (compare Fig. 7, A and D), but the rhythm is slower for d₃ = 0 and faster for d₃ = 0.6 pA. In the former the maximal respiratory period is about T = 3.4 s, while in the latter it decreases to T = 2.8 s. These changes are consistent with increased depolarization of the Pre-I neuron, which terminates expiration more quickly. The mean TI is unaffected over a wide range of raphe inputs, and the mean TE decreases with increasing input (Fig. 7G; N = 100). The shortest T also decreases slowly, and the rate of decay is similar for different channel numbers (Fig. 7H). The TI/TE ratio barely changes with increasing raphe input (Fig. 7I). In terms of variability, larger raphe inputs lead to a slight increase in respiratory variability, especially in the expiratory phase (Fig. 7, C and F, compared with Fig. 4F).

Fig. 7.

Respiratory variability with changes in raphe input. A–C: no input, d₃ = 0. D–F: d₃ = double increase, 0.6 pA. A and D: mean duration of T, TI, and TE vs. channel number. B and E: standard deviation of T, TI, and TE vs. channel number. C and F: coefficient of variation of T, TI, and TE vs. channel number. G: mean duration of T, TI, and TE vs. raphe input (channel number N = 100). H: minimal respiratory duration of T vs. raphe input for channel numbers 100, 200, and 500. I: TI/TE vs. raphe input for channel numbers 100, 200, and 500.

In summary, blocking the pontine input leads to a large increase in variability in inspiration and expiration because the depression of Post-I activity disinhibits the Pre-I and Early-I neurons. Noise in Pre-I neurons determines the variability of expiration by initiating inspiration by escape, while noise in Early-I neuron determines the variability of inspiration because inspiration is ended when they repolarize, thereby releasing the Post-I neurons. In other words, the key role of Pre-I is to determine TE (by controlling when expiration ends) and the key role of Early-I is to determine TI (by controlling when inspiration ends), as observed in deterministic models (Rubin et al. 2009; Shpiro et al. 2007). Similarly, increasing the raphe input leads to more respiratory variability especially in the expiratory phase, which is mainly determined by noise in the Pre-I neuron.

DISCUSSION

Summary.

We have demonstrated how to expand conductance-based models of neuronal firing to investigate the role of physiological channel noise at the circuit level. We illustrate this for a well-established model of the respiratory pattern generator. Channel noise in this network introduces variability in the respiratory rhythm, which changes with the total number of channels. For small channel numbers (N < 150), the duration and variability of the expiratory phase exceed the duration and variability of the inspiratory phase. In contrast, for large channel numbers (N > 250), the duration and variability of the inspiratory period exceed the duration and variability of the expiratory phase. For an intermediate number of channels, the duration and variability of expiration and inspiration are comparable and the coefficient of variation of the breath-to-breath interval is minimal.

We also found that Pre-I neurons, as pacemakers of the network, exhibit the highest sensitivity to channel noise and dominate the variability of the whole respiratory network. The model further predicts that blocking the pontine input depresses the activity of the Post-I neuron, which leads to a longer inspiration period (apnea), a severe reduction in breathing frequency (bradypnea), and increased respiratory variability. In contrast, the input from the raphe does not affect the respiratory pattern but its frequency and variability.

From deterministic to stochastic network models.

In our model, channel noise is introduced in channels whose conductance depends explicitly on time, because only those support current fluctuations: the persistent sodium channels for the Pre-I neuron and the adaptive potassium channels for the three inhibitory neurons. These are also the channels that determine the main firing features of those neurons (Rubin et al. 2009; Rybak et al. 2007; Smith et al. 2007). In particular, the generation of rhythmic activity in the pre-BötC in vitro is due to persistent sodium currents, which activate even without external input (Koizumi and Smith 2008; Rybak et al. 2003, 2004; Smith et al. 2000). However, other channels that are not included in the original model by Rubin and colleagues may also contribute to the stochastic single-cell and network dynamics.

In the stochastic model, the noise level is determined by the total number of each ion channel type in the neurons' membranes. Because of the binomial statistics of channel noise, current fluctuations relative to their mean decay as the inverse of the square root of the number of channels, 1/ $\sqrt{N}$. In a real neuron, with a large but finite number of channels, the effect of channel noise is generally not negligible but affects the firing patterns of single neurons, and hence the overall network activity.

The channel numbers that we consider in our study are not to be interpreted as absolute values but rather as densities, that is, as the number of channels per membrane patch of a given size. In any conductance-based model there is an explicit or implicit membrane patch size. Unfortunately, the model by Rubin and colleagues does not provide us with this size, so we cannot directly translate our channel numbers into channel densities. The actual channel numbers in respiratory neurons are unknown. In our simulations we calculated the implicit channel number in their model by dividing the total conductance of each channel type, which is provided in their model, by the single-channel conductance. In this way we obtain an estimate for the implicit number of channels in the deterministic model by Rubin et al., which is ∼200. We thus investigated what happens as we decrease or increase this number and observed significant changes in the range from 100 to 500 channels, which is what we report.

In addition to channel noise, network activity in vivo and in vitro is affected by synaptic noise. We have not considered the latter in our study because in the network model we have used the synaptic conductances do not depend explicitly on time and therefore cannot fluctuate stochastically. In future studies with a more detailed model of synaptic interactions, it is expected that the stochasticity of the inhibitory synapses will have a larger effect on the variability of the inspiratory phase, because it is during inspiration that inhibitory currents have the largest driving force in the Pre-I neurons (Lal et al. 2011; Rybak et al. 2007; Smith et al. 2007). In contrast, stochasticity in the excitatory synapses should have a larger effect on the variability of expiration, when the driving force for excitation is largest in the Pre-I neurons (Lal et al. 2011; Onimaru et al. 1997; Rybak et al. 2007). The role of inhibitory currents in the variability of the respiratory pattern has been investigated experimentally by Mayer et al. (2006). They showed that GABAergic inhibition in immature rats is modulated by adenosine receptors, which are targeted with nonspecific blockers in premature infants of low weight to decrease respiratory irregularity and apneic episodes.

Physiological interpretation of respiratory variability.

Variability is inherent to respiration and correlates to physiological conditions. Previous studies of respiratory rhythm variability mainly focus on the pre-BötC, an important component in the generation of the respiratory rhythm. It has been shown that respiratory variability can be affected by chemical stimulation (Chen et al. 2005) and vagotomy (Dhingra et al. 2011). Perturbations of the respiratory rhythm and its variability can be caused by coughing (Poliacek et al. 2011), gasping (Rybak et al. 2008), and apnea (Longobardo et al. 2002). Other authors have also studied the relationship between the respiratory rate and its variability (Fietkiewicz et al. 2016) as well as the contribution of stochastically bursting neurons to the network rhythm (Carroll and Ramirez 2013). Experimental work has also demonstrated the role of inhibitory currents on the frequency and regularity of respiration in immature rats (Mayer et al. 2006). Respiratory variability has been investigated previously in terms of the diversity in relaxation times of adaptation currents. Nesse et al. (2008) studied breathing variability in the pre-BötC as a noise-driven oscillator. They concluded that the separation in relaxation timescales of adaptation currents contributes to the wide range of respiratory frequencies and the peaked coefficient of variation for inputs of intermediate strength. In their model the current noise is state independent. In contrast, our model includes the natural modulation of channel noise amplitude by the membrane potential and the number of open subunits, but the timescale of the adaptive currents is fixed.

Endogenous mechanisms for respiratory variability due to channel noise have not been investigated before. In this study, we have focused for the first time on the role of channel noise on respiratory network dynamics. We found that there is an optimal channel number of approximately N = 200 that minimizes breath-to-breath variability. At this minimum, the durations of inspiration and expiration are comparable, with expiration being slightly (∼10%) longer. The breathing frequency and TI/TE in this regime are consistent with a fast respiratory pattern, or tachypnea (Chen et al. 2013; Marlot and Duron 1976, 1981).

There are several physiological mechanisms that may control the availability of ion channels in vivo, and hence the level of channel noise. The first is the developmental stage of the network. For instance, Hirst et al. (2015) have shown developmental changes in sodium and potassium channel expression in the enteric system. Similarly, an immature respiratory network that has not yet expressed all of its channels will display high variability in the expiratory phase, and also longer expiratory periods, consistent with empirical observations (Hilaire and Duron 1999; Marlot and Duron 1981; Mortola 1984). Phosphorylation of ion channels by neuromodulators or their second messengers may also reduce the number of available ion channels (Bucher and Marder 2013; Lechner and Boehm 2004; Levitan 1994; Nadim and Bucher 2014). Similarly, the endocytosis and exocytosis of ion channels in response to biological stimuli, for instance, by pH changes in the extracellular milieu, will also affect the availability of functional ion channels (Dautry-Varsat et al. 1983; Jentsch et al. 2004). It is also possible that pharmacological interventions that block ion channels contribute to the overall level of channel noise (Camerino et al. 2007; Judge et al. 2007). In our model, the Pre-I neuron is the circuit element with highest sensitivity to noise, specifically through the conductance of persistent sodium channels, suggesting that these channels are the main contributors to intrinsic respiratory variability.

The respiratory pattern, its frequency, and variability change with the channel number, which increases during development. Respiration at birth is slow in infants and characterized by short inspirations and long expirations (Hathorn 1979; Hilaire and Duron 1999). In vivo studies with animals have reported that inspiration lengthens with age, while expiration shortens (Farber 1988; Marlot and Duron 1976, 1981; Mortola 1984). Furthermore, one of the main characteristics of the neonatal respiratory activity is its irregularity. Unpredictable spontaneous changes in respiration occur frequently in newborn animals and infants, when their ion channels may not be fully expressed. Respiration in infants always presents an exacerbated respiratory variability (Hilaire and Duron 1999). Most of the respiratory variability in neonates involves TE changes, whereas TI changes little (Fisher et al. 1982; Mortola 1984). This is consistent with our results that variability in TE dominates at low channel densities. Our results also predict that an overexpression of channels would lead to apneusis. There are conditions such as Rett syndrome in which such breathing patterns are observed (Stettner et al. 2008). However, there is no experimental evidence thus far relating apneusis to channel densities.

Respiratory variability and external drives.

Breathing variability may also originate from peripheral afferents acting on the rhythm generator. We investigated the effect of blocking the pontine drive, which provides excitatory inputs to the four neurons of the respiratory pattern generator. Pontine drive can dramatically control the pattern of respiration, including inspiratory duration and inspiratory/expiratory phase transition (Morschel and Dutschmann 2009). This pontine-based control is believed to come from the pontine Kölliker-Fuse nucleus and parabrachial complex. The pontine respiratory nuclei facilitate the mechanism for terminating the inspiratory phase and influence other phases in the respiratory cycle. After pontine lesions, increased breath-by-breath variability and prolonged inspiration were observed in cats (Oku and Dick 1992). Meanwhile, blockade of postsynaptic NMDA receptors in the Kölliker-Fuse nucleus suppressed the excitatory drive from the pons to the medulla and caused apneusis (Fung et al. 1994; Ling et al. 1994; Morschel and Dutschmann 2009). Chemical or electrical stimulation of these nuclei can evoke phase resetting and inspiratory off switch in animals with intact vagus nerves (Dutschmann and Herbert 2006; Okazaki et al. 2002). In our simulations, we found that blocking the pontine input increases the variability and duration of inspiration. These changes can be interpreted by the interaction of four neurons within the network. According to bifurcation analysis of the deterministic network model (Rubin et al. 2009), blocking the pontine input can completely depress the activity of the Post-I neuron, thereby decreasing the inhibition from the Post-I neuron to the other three neurons. In this case, ion channel noise is more likely to facilitate Pre-I depolarization, which leads to a longer and more irregular inspiratory phase, consistent with the experimental findings in animals after pontine lesions (Fung et al. 1994; Ling et al. 1994; Oku and Dick 1992).

Experimental studies have shown that activation of raphe nuclei through pharmacological, electrical (Cao et al. 2006a,b; Ptak et al. 2009; Yu et al. 2011), or optogenetic stimulation (Depuy et al. 2011) facilitates respiratory activity, which is also observed in our simulations. Although those studies do not report variability measures, our stochastic model shows that variability is only slightly enhanced by an increase in raphe inputs.

GRANTS

This work was supported by National Natural Science Foundation of China Grant No. 61302002 and the China Scholarship Council (H. Yu); National Heart, Lung, and Blood Institute Grants HL-087377 and 5P01 HL-101871-06 (T. E. Dick) and T32 HL-007913 (R. R. Dhingra); and a Biomedical Researcher Award of The Hartwell Foundation (R. F. Galán).

DISCLOSURES

No conflicts of interest, financial or otherwise, are declared by the author(s).

AUTHOR CONTRIBUTIONS

H.Y. and R.F.G. performed experiments; H.Y. and R.F.G. analyzed data; H.Y., R.R.D., T.E.D., and R.F.G. interpreted results of experiments; H.Y. and R.F.G. prepared figures; H.Y. and R.F.G. drafted manuscript; H.Y., R.R.D., T.E.D., and R.F.G. edited and revised manuscript; H.Y., R.R.D., T.E.D., and R.F.G. approved final version of manuscript.