Abstract
Fiber-like structures are prevalent in biological tissues, yet quantitative approaches to assess their three-dimensional (3D) organization are lacking. We develop 3D directional variance, as a quantitative biomarker of truly 3D fibrillar organization by extending the directional statistics formalism developed for describing circular data distributions (i.e. when 0° and 360° are equivalent) to axial ones (i.e. when 0° and 180° are equivalent). Significant advantages of this analysis include its time efficiency, sensitivity and ability to provide quantitative readouts of organization over different size scales of a given data set. We establish a broad range of applications for this method by characterizing collagen fibers, neuronal axons and fibroblasts in the context of cancer diagnostics, traumatic brain injury and cell-matrix interactions in developing engineered tissues. This method opens possibilities for unraveling in a sensitive, and quantitative manner the organization of essential fiber-like structures in tissues and ultimately its impact on tissue function.
Keywords: Three-dimensional organization, Collagen fiber, Neuronal axon, Cancer, Traumatic brain injury, Multi-photon microscopy
1. Introduction
Advances in high resolution optical imaging have enabled assessments of the structure of essential tissue components with micron scale resolution and are expected to contribute significantly towards our understanding of structure-function relationships that ultimately define cell-matrix interactions [1–4]. Disruption of cell-matrix interactions is associated with a wide range of diseases such as cancer, fibrosis, and neurodegenerative diseases [5–7]. Modified interactions have major effects upon key functional cellular features including gene regulation, cytoskeletal structure, differentiation, and cell growth control [8–10], as well as upon the matrix biophysical and biochemical properties, including collagen fiber organization and mechanical properties [11]. Thus, improved characterization of these structure-function connections may have important implications for our understanding of tissue growth, development, wound healing and disease progression.
Confocal and multi-photon microscopy, especially second harmonic generation (SHG) and two-photon excited fluorescence (TPEF) [12,13], provide the necessary axial resolution to capture fine structures within cells and the ECM in a 3D context. However, even as high-resolution 3D images of fiber-like tissue structures become more readily accessible, quantitative analysis algorithms for their orientation and organization have largely remained limited to analysis of 2D images [14–21], with only a few notable exceptions [22–25]. Schriefl et al. used polarized microscopy to determine the fiber orientation relying on the birefringence of collagen fibers, by sequentially rotating the sample slide in the azimuthal and the elevation plane to find the two Euler angles to depict an orientation in 3D space. This method eliminates the need for 3D imaging, which can be time consuming; however, it is limited to thin specimens (less than 10 μm), it requires picrosirius staining for enhancement of birefringence, and it doesn’t work well for wavy fibers [22]. Lau et al. acquired 3D SHG image stacks and used Fourier transform based approaches to quantify 3D orientation of collagen fibers at discrete regions of interest (ROIs). The overall orientation of collagen fibers within each ROI is determined by the filter bank method. The filter bank consists of various 3D orientation filters constructed in the Fourier space, and the filter orientation that corresponds to the maximum likelihood to the Fourier transform of each ROI is designated as the fiber orientation. However, the ROI size is a tradeoff between determination accuracy and computational time [23]. Further approaches, including inertia moments [24] and diffusion tensor imaging (DTI) in combination with two-photon microscopy [25], may be restricted by the characteristics of fibers (e.g., shape, cross section or thickness) or tissues (e.g., heterogeneity). Generally, these methods have been often limited by their computational expense or their inability to provide organization readouts at the microenvironment scale. Recently, we developed a 3D weighted vector summation algorithm, which provides voxel-wise orientation information with high accuracy that is not limited by the waviness or thickness of the fibers, and offers a number of computational time and sensitivity advantages over previous methods [26].
Here, we develop a metric, 3D directional variance, as a quantitative biomarker of truly 3D organization of fiber-like structures, based on this voxel-wise orientation algorithm. Analogous to variance in linear data which measures how far a set of numbers is spread out, directional variance extends this measure to a set of orientations — in this case, in a 3D context. A lower directional variance value reveals more highly aligned fibers, while a higher one corresponds to more random fiber alignment. In this study, we develop the formalism for extracting the 3D directional variance of fiber-like structures within 3D image stacks, and then apply this metric to the organization characterization of several such structures, including collagen fibers, neuronal axons, and fibroblasts, present within 3D multi-photon image data sets of different tissue systems. By using these tissue systems, we illustrate the capability of this approach to characterize 3D fiber-like structure organization in heterogeneous samples (cartilage) or as a detailed function of distance from a certain point of interest (traumatic brain injury model). In addition, we show that the choice of window over which 3D organization is assessed may be critical in some cases for identifying changes (human peritoneal metastasis model) and not in others (mouse breast cancer model) depending on the size and the tissue-level organization of the fibers. Finally, this approach is well-suited to assess alignment of multiple types of fiber-like structures within the same specimen, as exemplified by the lung engineered tissue model. Together these applications reveal a broad potential of this newly-developed metric for biomedical uses.
2. Materials and methods
2.1. 3D directional variance formalism to quantify fibrillar organization
The development of 3D directional variance relies on concepts from directional statistics [27]. Directional variance for circular data (for which orientations of 0° and 360° are equivalent), V3D, is defined as [27]:
| (1) |
where , and , , . The superscript c refers to the circular data, and n is the total number of voxels that contribute to the determination of the directional variance. θ and φ are the azimuthal and polar angles used to depict an orientation in 3D space, respectively (Fig. 1a). The azimuthal angle θ is determined by projecting fibers to a fixed 2D plane, i.e., the xy plane (Fig. 1a). However, according to the definition of the polar angle, φ, there is no fixed 2D plane onto which fibers could be projected for the determination of all possible φ orientations. To address this problem, we consider additional angles β and γ (Fig. 1a), which are azimuthal angles, like θ, and related to φ by [26]:
| (2) |
The determination of β and γ can be achieved using the same approach as that for θ. After projecting fibers to a fixed 2D plane, the orientation is determined from the weighted vector summation algorithm we described recently [18,26]. Briefly, to acquire the θ orientation of the center voxel of a n×n×n voxel cube window, we first average the cube along the z direction to project the cube window to a square window (n×n pixels), and then calculate the orientation of the center pixel of the square, based on the basic premise shown in Figs. 1b and c. First, we define the vectors passing through the center pixel (marked in purple) of the window size of choice (11×11 pixels in this case). Then these vectors are weighted by their length and intensity fluctuations along their direction [26], as shown in Fig. 1b. The orientation of the center pixel is defined as the summation of all these weighted vectors and shown in Fig. 1c, which corresponds well to the direction of fiber alignment. The determination of angles β and γ is achieved by averaging the cube along the other two directions, followed by the identical weighted vector summation algorithm.
Fig. 1. 3D directional variance quantifies the fiber organization.
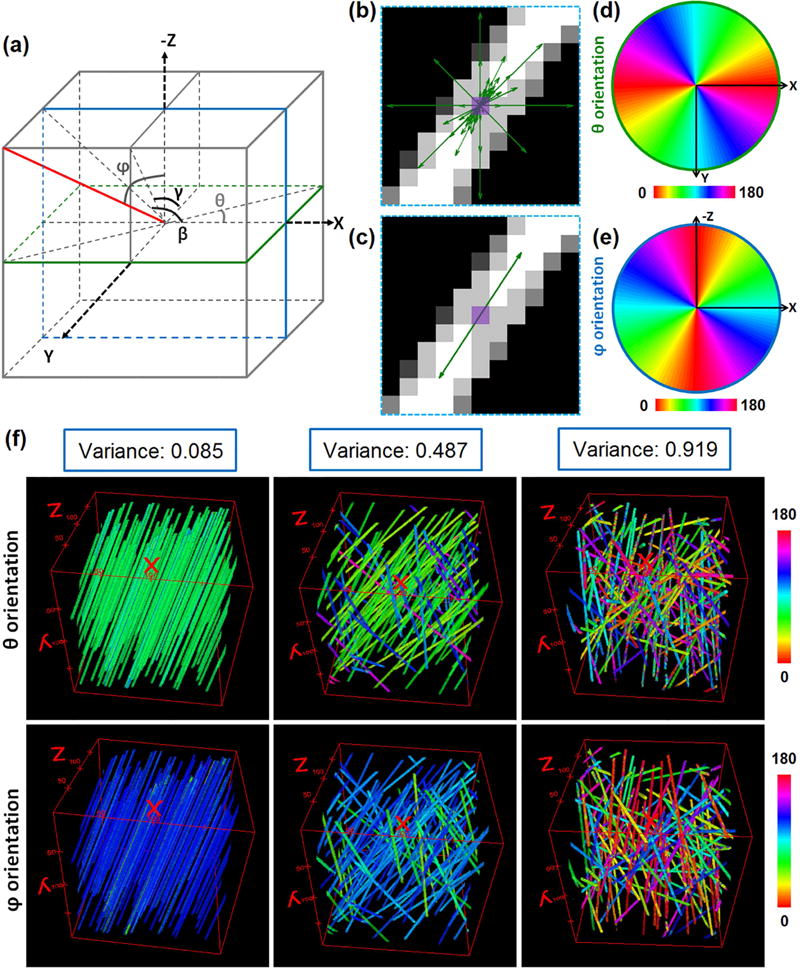
(a) An azimuthal angle θ in the transverse plane and a polar angle φ are used to define an orientation (red solid line) in 3D space. Angles β and γ, acquired by projecting the fiber to zx or yz plane, respectively, are defined and used in the determination of 3D directional variance. To find the θ, β, and γ angles a n×n×n voxel window is projected onto the xy, zx, and yz planes respectively. The weighted vector summation algorithm is then used to acquire the values of the corresponding angles as illustrated in (b) and (c). (b) Weighted vectors through the center pixel of the n×n projection are acquired by considering both the vector length and intensity fluctuations along the direction of all possible vectors crossing the pixel. (c) The orientation of the center pixel (marked in purple) is calculated by summation of all the weighted vectors. (d) θ distribution map of the plane marked in green shown in (a). Within this plane, all the voxels are corresponding to the same φ of 90°. (e) φ distribution map of the plane marked in blue shown in (a). All the voxels are corresponding to the same θ of 0° within this plane. (f) Simulated fiber stacks used to test the 3D directional variance algorithm. The θ (top) and φ (bottom) orientation maps of these stacks are represented by different colors (see color bar). Stacks with high (left), intermediate (middle) and low (right) levels of fiber alignment are shown along with the corresponding directional variance values on top of orientation maps.
Once we acquire the values of θ and φ for each voxel of a 3D stack containing fiber-like structures, whose orientations are equivalent for 0° and 180°, we need to modify the definition of 3D directional variance. A general approach to transforming axial (fiber like) data to circular data is to multiply angular values by 2. This strategy is sufficient for transforming the azimuthal angle θ, but not for the polar angle φ. Again, we use azimuthal angles β and γ to represent the polar angle φ, and define to derive the modified components as:
| (3) |
| (4) |
| (5) |
Where SI = (−1) · (φ − 90)/|φ − 90| when φ ≠ 90°, and SI = 1 when φ = 90°. The superscript a refers to the axial data. Using these modified components, we acquire the modified , and finally the V3D that is suitable to quantify the organization of 3D fiber-like structures. The custom code for the assessment of the 3D directional variance is written in MATLAB.
Orientation maps of two typical planes, as marked by green and blue (Fig. 1a), are plotted in Figs. 1d and e respectively, which serve as a reference for assessing the orientation values. Throughout this study, optical sections are all along the xy plane, and 3D image stacks are then reconstructed based on these sections at different z depths. Note that a φ of 90° corresponds to fibers that are parallel to the optical sections.
In this study, the 3D directional variance is assessed typically based on two types of analysis windows, a localized and a full image stack window. The size of the localized window is dependent on characteristics of the fibers, such as their diameter, waviness and tissue level organization. Every voxel within an image stack is assigned a directional variance value assessed based on this localized window. When applying the full image stack window, we characterize the 3D variance of all the fibers within the stack with a single value. The latter calculation is faster, but in some cases more detailed information may be needed to characterize important functional changes that may be present at smaller scales.
2.2. Generation of simulated fiber stacks
To validate the 3D directional variance algorithm, 3 simulated fiber stacks with a size of 200×200×200 voxels are generated with different levels of fiber alignment using MATLAB. There are ~105 fibers in each stack. The first stack has completely parallel fibers with a θ orientation of 70°, and a φ orientation of 120°. An intermediate fiber organization is generated in the second stack, where half of the fibers have the θ angle ranging randomly between 40° and 70°, and the φ angle ranging randomly between 100° and 120°, whereas the other half of the fibers have the θ angle ranging between 100° and 165°, and the φ angle ranging between 40° and 80°. The third stack has randomly defined θ and φ angles ranging between 0° and 180°.
2.3. Testing the robustness of the 3D directional variance analysis with respect to changes in fiber density
We generate fiber stacks with the same organization level (with a 3D directional variance of ~0.57), but with five different levels of fiber density, and assess the error in determining the fiber orientation angle and the percent error for assessing the 3D directional variance. We examine stacks with fiber densities of approximately 3.6, 4.3, 5.1, 5.6 and 6%, with the 6% stack having a density that is 67% higher than that of the 3.6% one, which is a significantly higher variation range than what we typically observe in the samples we examine (Supplementary Table 1). For each fiber density, we generate 10 fiber stacks. The percent error for the 3D directional variance estimates is calculated by: (|anticipated variance - calculated variance|) / anticipated variance. We determine the mean and standard deviation for the error in our estimations of the orientation angle and the percent error of the extracted 3D directional variance at different fiber density levels.
2.4. Multi-photon microscopy
SHG and TPEF images are obtained using a Leica TCS SP2 confocal microscope equipped with a tunable (710–920 nm) titanium-sapphire laser (Mai Tai; Spectra Physics; Mountain View, CA). Three non-descanned photomultiplier tube (PMT) detectors detect light in the 460 ± 20 nm, 525 ± 25 nm or 400 ± 10 nm regions. Objectives used in this study include a water-immersion 63× objective (NA 1.2; 220 μm working distance) for articular cartilage and mammary glands, a water-immersion 25× objective (NA 0.95; 2.4 mm working distance) for pancreatic cancer and collagen hydrogels, and a dry 20× objective (NA 0.70; 590 μm working distance) for the brain-like cortical tissue. Reconstruction of 3D images is performed by ImageJ (W. Rasband, National Institute of Health, USA), and image analysis is performed by the 3D directional variance algorithm in MATLAB.
2.5. Collagen hydrogel-based tissue preparation
Normal Human Lung Fibroblasts (NHLF) are obtained from Lonza (Lonza, Walkersville, MD) and cultivated using FGM-2 BulletKit (Lonza, Walkersville, MD), containing basal media, serum, hFGF-β, insulin and GA-1000. Fibroblasts between passages 4–6 are used for all experiments. To study fibroblast alignment in attached collagen hydrogels, 6 well Flexcell Tissue Train culture plates (Flexcell, Burlington, NC) are employed. Pulmonary fibroblasts are detached from tissue culture flasks using 0.05% Trypsin-EDTA (ThermoFisher Scientific, Cambridge, MA) and trypsin neutralizing solution (Lonza, Walkersville, MD) is added following cellular detachment. Cells are then centrifuged and counted prior to collagen hydrogel preparation. To prepare 1 ml of cell laden collagen hydrogels, high concentration rat tail type-I collagen (Corning, NY) (final concentration: 1 mg/ml) is mixed with cold DMEM (final concentration: 0.5×), 1 M NaOH, 100 μl of pulmonary fibroblast cell suspension (10 million cells/ml) and cold sterile water. Tissue Train culture plates are removed from their sterile wrappers and placed on a Flexcell baseplate containing Trough Loaders. Application of pressure using a vacuum pump connected to reservoir results in deflection of the rubber membrane into a trough format. Within the trough, 200 μl of cell laden acid neutralized collagen is added and incubated inside a tissue culture incubator (37 °C) to form the hydrogel construct. Following polymerization, cell laden collagen hydrogels are afloat FGM-2 media, but remain attached to anchor stems on either side of the wells in the Tissue Train culture plate. To study dynamic changes in cellular and collagen alignment, cell laden collagen constructs are sacrificed at 4, 10, 18 and 30 hours post seeding and fixed using 4% paraformaldehyde for 1 hour at room temperature. Fixed constructs are stored in 1× PBS at 4 °C for further analysis.
All hydrogel constructs are brought to room temperature (RT) on the day of immunostaining. Briefly, all constructs are washed three times for 20 min in PBST (1× PBS + 0.1% Tween-20). Blocking is performed for 1–2 hours at room temperature (RT) using PBST containing Normal Goat Serum (NGS; Vector Laboratories, Burlingame, CA), Bovine Serum Albumin (BSA) and 0.1% TritionX-100. Following blocking, all constructs are incubated in 1:1000 rabbit monoclonal anti-vimentin antibody (Abcam, Cambridge, MA) in PBST containing NGS and BSA for 24–48 hours. Secondary DyLight 488 conjugated goat anti-rabbit IgG antibody (Vector Laboratories, Burlingame, CA) is added at 1:500 dilution to constructs to visualize vimentin binding.
Simultaneous TPEF images of fibroblasts and SHG images of collagen fibers are both acquired for 3D directional variance analysis. TPEF images are acquired with an excitation wavelength of 760 nm and recorded by the 525 nm detector, and SHG images are excited using 800 nm and recorded by the 400 nm detector. There are three samples corresponding to each time point, and six 3D image stacks of either cell or collagen per group (2 per sample) are collected for analysis.
2.6. Articular cartilage preparation
Knee joints from 18 week old Balb/C mice are harvested by severing the femur and tibia at mid bone length. The samples are equilibrated in a 30% sucrose solution for 3 days at 4 °C before being embedded in optimal cutting temperature (OCT) compound. Embedded joints are cryosectioned sagittally in a Leica CM 1950 cryostat at 40 μm thickness using Cryofilm type IIC (10) (University of Connecticut Medical Center, Rowe Laboratory). A total of 3 mice (6 knees) are harvested as samples. These samples are rehydrated for 15 min in PBS before imaging. Twelve simultaneous TPEF and SHG 3D image stacks (2 per sample) are collected for analysis. Using 800 nm as the excitation wavelength, endogenous TPEF fluorescence images are obtained with the 525 nm detector, and SHG images are detected using the 400 nm detector. All animal procedures were approved by the Tufts University Institutional Animal Care and Use Committee (IACUC).
2.7. Mammary glands preparation
Normal mammary tissues are collected from the fourth mammary gland of two non-parous 12 week old FVB/N female mice, while mammary tumors are obtained from two mice of the human in mouse model [28]. These tumors are composed of cancer cells of human origin that have stromalized with mouse ECM and cancer associated fibroblasts as well as immune cells, which are transplanted into the glands of NOD/SCID mice. These fresh tissues are embedded in OCT compound and snap frozen in a methanol bath. They are immersed in phosphate buffered saline (PBS) to remove the OCT compound before use. All animal procedures were approved by the Tufts University IACUC.
With 800 nm as the excitation wavelength, we acquire TPEF images of endogenous fluorescence using the 525 nm detector, and SHG images using the 400 nm detector. A total of 6 simultaneous TPEF and SHG 3D image stacks per group (3 stacks per tissue sample) are collected for analysis.
2.8. Parietal peritoneum and primary pancreatic neoplastic tissue preparation
Freshly excised biopsies from healthy parietal peritoneum and primary pancreatic neoplastic tissue are acquired during abdominal surgery from 3 different patients that have a suspected or confirmed diagnosis of pancreatic malignancy and undergo open operative resection or biopsy of the malignancy as part of their treatment plan. These tissues are imaged within 3 hours after excision. Samples are excited with 900 nm to acquire depth-resolved TPEF and SHG 3D images. TPEF signal is detected using the 525 nm detector, whereas SHG signal is detected using the 460 nm detector. Although there is some crosstalk of fluorescence in the 460 nm channel, the SHG signal dominates in this region. Twelve simultaneous TPEF and SHG 3D images per group are acquired. Biopsy acquisition and imaging are conducted according to approved institutional review board protocols from Lahey Clinic and Tufts University.
2.9. Engineered brain-like cortical tissue preparation
Salt leached silk scaffolds are prepared and used for 3D neuronal culture as previously established [29]. Briefly, silk scaffolds are made by combining 30 ml of 6% silk solution with 60 g of 500–600 μm NaCl particles for a period of 48 hours at room temperature to allow the crosslinking of silk solution. Then, the salt is leached out for 48 hours by placing the crosslinked silk in distilled water, which leaves behind a porous silk scaffold. The scaffold is then punched using disposable biopsy punches (6 mm diameter). The designed constructs are autoclaved and coated for 1 hour at 37 °C with 0.1 mg/ml poly-D-lysine (Sigma) solution to prepare for cell seeding. Primary rat neurons dissociated from embryonic day 18 (E18) cortices are seeded at a concentration of 1 million cells/scaffold and allowed to adhere to the pores of the scaffold overnight at 37 °C. Next, collagen type I (Corning) gel is prepared as 3 mg/ml solution on ice and added at 100 μl volume per scaffold, with the constructs placed in a 96-well plate. After 30 min of gelation at 37 °C, the constructs containing primary neurons and collagen gel ECM are flooded with Neurobasal media (supplemented by 2% B27, 1% GlutaMAX and 1% penicillin streptomycin) and cultured at 37 °C for two weeks.
Controlled cortical impact (CCI) of the cell seeded constructs is performed at the two week time point by modifications to a custom built set up at Massachusetts General Hospital [30]. The injury is done using a 3 mm flat tip pneumatic piston that hits each construct at a velocity of 6 m/sec. The impact lasts for a duration of 100 ms, during which the piston penetrates a depth of 0.5 mm into the construct. The injured samples (n = 5) are fixed 10 min post-injury and an equal number of uninjured samples are fixed as well to serve as controls.
The uninjured and injured samples fixed with 4% paraformaldehyde (Fischer Scientific) for 30 min at room temperature, are subsequently washed for 30 min with PBS three times. Immunostaining of the fixed samples is done using a previously described protocol [29]. Primary antibody against β-III tubulin (rabbit, Sigma), a neuron-specific marker is diluted by 1:500 in a blocking solution (4% goat serum, 0.2% triton-X100, 0.05% bovine serum albumin). The samples are incubated overnight at 4 °C in the primary antibody solution, followed by 30 min washes with PBS for three times. Next, the secondary antibody Alexa 488 goat-anti-rabbit (Invitrogen) is added to the samples at a dilution of 1:250 in blocking solution. The samples are left to incubate for 2 hours at room temperature and washed three times with PBS. A total of 20 TPEF 3D image stacks of neuron axons per group (4 stacks per sample) are acquired at an excitation wavelength of 760 nm and the 525 nm detector.
2.10. Statistical analysis
For samples with multiple groups (articular cartilage and collagen hydrogels), a one-way ANOVA with post-hoc Tukey HSD test is used to assess significant differences using JMP 12. Otherwise a two-tailed t-test is used. Results are considered significant at p < 0.05.
3. Results
3.1. Validation of 3D directional variance model
To test the 3D directional variance algorithm, we prepare 3 simulated fiber stacks with varying levels of alignment (see Section 2.2). The weighted vector summation algorithm is used to acquire the voxel-wise orientation of these fibers [26], and the false-colored orientation maps for θ (top) and φ (bottom) are shown in Fig. 1f. 3D directional variance is then acquired based on the entire image stack, considering the contributions from all the fibers, and shown on top of the orientation maps (Fig. 1f). As expected, the 3D directional variance is ~0 for the 3D image with strictly parallel fibers (left), while it is close to 1 for the one with randomly distributed fibers (right). The stack with intermediate randomness has a moderate directional variance value (middle). Note that the 3D directional variance value for the perfectly aligned fiber stack (left) is not exactly 0, which is due to the error in orientation determination produced by the weighted vector summation algorithm. These results illustrate the capability of this approach to provide a simple but highly quantitative metric of 3D organization of fiber-like structures.
In order to test the robustness of the 3D directional variance analysis with respect to changes in fiber density, we generate fiber stacks with the same organization level, but with five different levels of fiber density (see Section 2.3). The θ (top) and φ (bottom) orientation maps of representative 3D fiber stacks for the low, medium and high densities are shown in Fig. 2a, with the corresponding fiber densities, anticipated and calculated 3D directional variance values shown on top of these orientation maps. The expected directional variance is acquired from the defined orientations when generating these fiber stacks, while the calculated one is obtained using the orientations achieved by our orientation algorithm. It is interesting to note that with fiber densities varying from 3.6% to 6.0%, i.e., a variation of 66.7% in fiber density (Fig. 2b), there is a small (~1°) but significant increase in the error of orientation (blue line, Fig. 2c); however, the 3D directional variance percent error doesn’t increase significantly and remains consistently below 0.06 (gray line, Fig. 2c).
Fig. 2. Testing the robustness of the 3D directional variance analysis relative to fiber density changes.
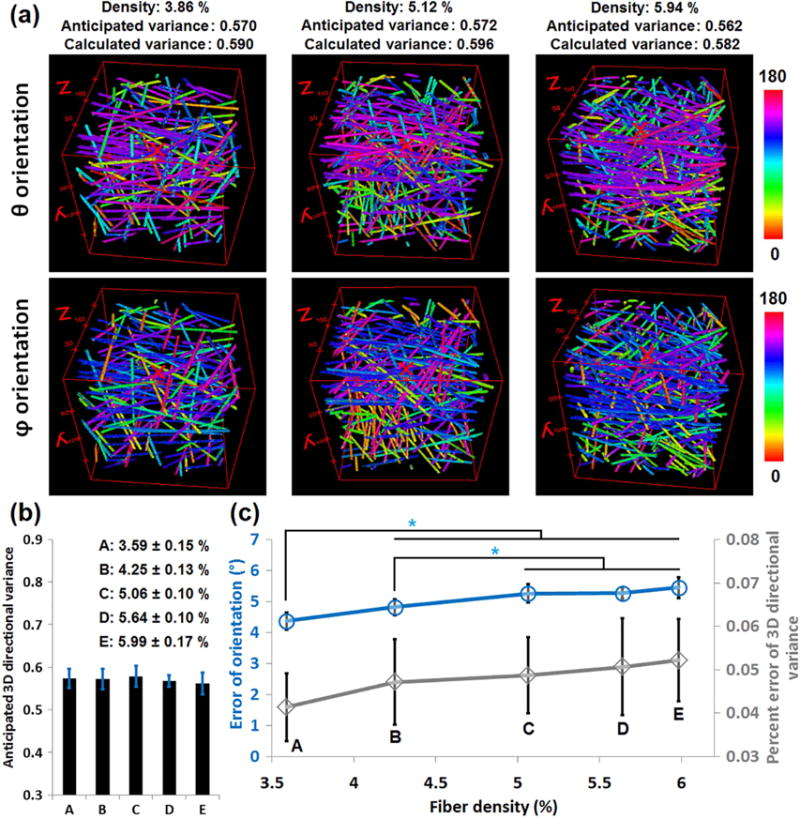
(a) The θ (top) and φ (bottom) orientation maps of representative 3D fiber stacks for the low, medium and high densities we tested. The fiber density, and the anticipated and calculated 3D directional variance values are shown on top of these maps. (b) The mean and standard deviation of the anticipated directional variance corresponding to each of the 5 fiber density levels (A–E, with the mean density and standard deviation indicated in the legend for each group). As can be seen from the histograms, these five groups have a consistent variance level at ~ 0.57. (c) The mean and standard deviation for the error in our determination of the orientation angle (blue) and the percent error of the extracted 3D directional variance (gray) at different fiber density levels. The error of orientation increases significantly with an increase in fiber density. However, no significant increase is observed in the percent error of the 3D directional variance estimates as the fiber density changes from 3.6% to 6.0% (~66.7% change in fiber density). *, p < 0.05.
3.2. 3D directional variance determines both cell and collagen alignment in tissue engineering
The 3D directional variance metric is developed to quantify any fiber-like structures. Here, we monitored simultaneously the alignment of human primary lung fibroblasts and their surrounding collagen fibers in simple engineered tissue models. We tracked such changes dynamically at 4, 10, 18 and 30 hours following the seeding of cells within the collagen-based hydrogels. Representative 2D cellular TPEF or collagen SHG images are shown in Figs. 3a and b, with the cell and collagen images corresponding to the same field. Note that the SHG collagen signal is much weaker in this case than that acquired from actual tissues (see Figs. 4–6 that follow) and the fibers are not as well defined. 3D orientations are calculated (Supplementary Fig. 1), and the θ distribution histograms of both cells (green) and collagen fibers (purple) reveal very similar alignment levels, which gradually increase as a function of time (Fig. 3c). The relationship between the dispersion of the θ and φ distributions (represented by the full width at half maximum-FWHM) and the 3D directional variance is shown in Figs. 3d (fibroblasts) and e (collagen fibers), which indicate that generally a higher dispersion in θ or φ distribution leads to a higher 3D directional variance value (Fig. 3d,e). A representative 3D image stack corresponding to the 30 hour time point with overlaid TPEF and SHG signals is shown along with a representative frame in Fig. 3f. As indicated by the arrows, the SHG signal is enhanced surrounding the cell locations (Fig. 3f, bottom), possibly as a result of fibroblast mediated collagen contraction [31]. Consistent with the changes reported for the θ distributions of the cell and collagen fibers (Fig. 3c), as well as the dispersion of the θ and φ distributions, the 3D directional variance of both components based on the entire image stacks gradually decreases as a function of time (Fig. 3g,h). The 3D directional variance metric is sensitive enough to identify significant alignment changes even between the 4 and 10 hour time points. Compared with the two dispersion metrics in θ and φ, the 3D directional variance metric is a single quantity that depends on the contributions from both θ and φ orientations, and takes into account the fact that 0° and 180° are equivalent for fiber-like data, therefore yielding a simpler and potentially more sensitive readout. Indeed, when we compare the dispersion in the θ or φ distributions separately, we find that some statistically significant differences in the 3D variance (for example, in collagen fiber alignment at 18 and 30 hours) are not present in either one of the collagen fiber orientation dispersions (Supplementary Fig. 2).
Fig. 3. 3D directional variance assesses the cell alignment and collagen fiber organization in a simple 3D hydrogel.
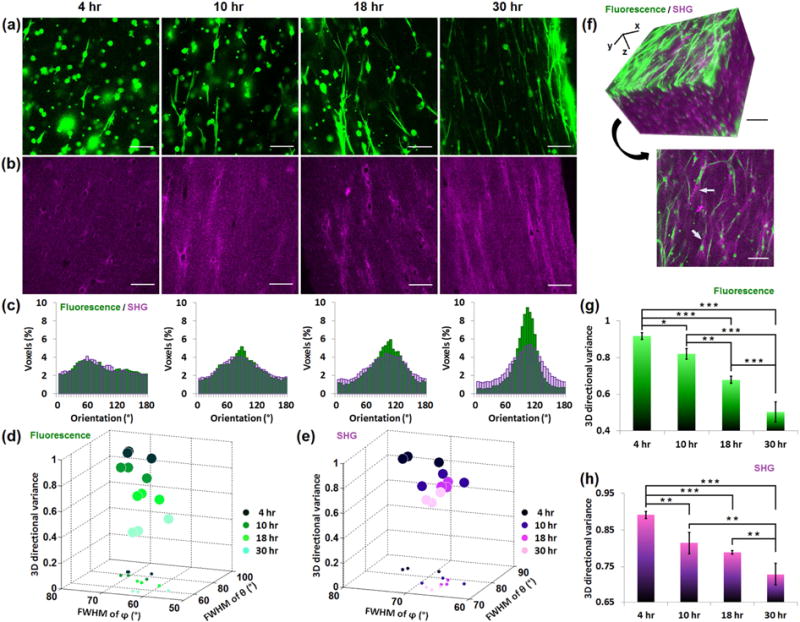
Primary human fibroblasts are seeded in collagen hydrogels, and dynamic changes during fibroblast-mediated collagen contraction are assessed at 4, 10, 18 and 30 hours post-cell seeding. (a) Representative TPEF images of fibroblasts immunostained with anti-vimentin, DyLight 488 conjugated antibody. (b) SHG images corresponding to the same field as the TPEF images. (c) θ distribution histograms of both the TPEF (green) and SHG (purple) representative images. The plot of 3D directional variance of fibroblasts (d) and collagen fibers (e) as a function of full width at half maximum (FWHM) of the corresponding θ and φ distributions. In each plot, different colors correspond to different time points post-cell seeding. The projections of these 3D scatter points are also plotted on the xy plane. (f) 3D reconstruction of TPEF and SHG signals from 68 images recorded 5 μm apart (top), along with a representative 2D image (bottom). Mean and standard deviation of 3D directional variance calculated separately from the entire 3D image (600.0×600.0×340.0 μm) of fibroblasts (g) or collagen fibers (h). ***, p < 0.001; **, p <0.01; *, p < 0.05. Scale bar, 100 μm.
Fig. 4. 3D directional variance identifies layered collagen organization in articular cartilage.
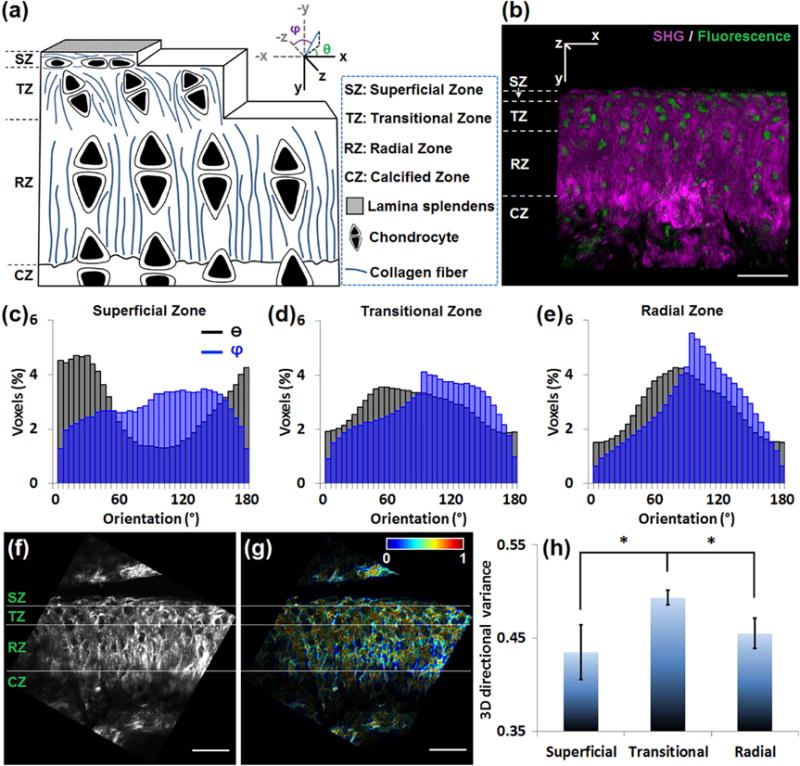
(a) Schematic of mouse articular cartilage showing the alignment of chondrocytes and collagen fibers in different histological zones. The picture does not reflect the actual sizes and spacing of the collagen fibers and the cells. In the coordinate system, the θ and φ angles of a fiber (blue line) are indicated. (b) 3D reconstruction of cartilage from 47 images recorded 1 μm apart. Simultaneous SHG (purple) and TPEF (green) images reveal the distinct localization of the collagen fibers and chondrocytes, respectively. (c–e) The θ (black) and φ (blue) distribution histograms of the (c) superficial, (d) transitional and (e) radial zone, reveal that the collagen fibers in the superficial zone are parallel to the surface (θ peaked near 0° or 180°), while those in the radial zone are perpendicular to the surface (θ peaked near 90°). (f) A representative SHG image of cartilage. (g) The corresponding voxel-wise 3D directional variance map, acquired based on a window size of 4.2×4.2×5.0 μm. (h) Mean and standard deviation of the 3D directional variance of the 3 different zones. *, p < 0.05. Scale bar, 50 μm.
Fig. 6. The 3D directional variance of collagen fibers is higher in healthy parietal peritoneum than in primary pancreatic neoplastic tissue.
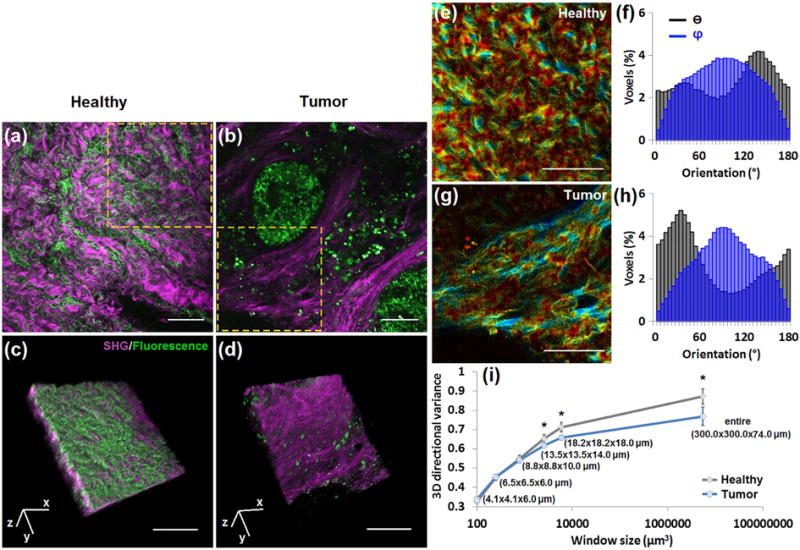
Representative large-field images of (a) healthy parietal peritoneum and (b) primary pancreatic neoplastic tissue, with overlays of SHG (purple) and TPEF (green) signals. (c, d) 3D reconstructions of 37 SHG-TPEF images recorded 2 μm apart, corresponding to marked regions in (a) and (b), respectively. (e, g) Voxel-wise 3D variance maps of SHG signals of the marked areas in (a, b) acquired by a window of 13.5×13.5×14.0 μm, with corresponding θ (black) and φ (blue) distribution histograms of all the fibers within this area (f, h). (i) Mean and standard deviation of 3D directional variance as a function of window size. Significant differences between healthy and tumor groups are detected for window sizes equal to or larger than 13.5×13.5×14.0 μm. The last assessment window, 300.0×300.0×74.0 μm, corresponds to the entire 3D image. *, p < 0.05. Scale bar, 100 μm.
3.3. 3D directional variance quantifies collagen fiber organization differences in distinct articular cartilage zones
Accurate assessment of the organization of fiber-like structures may be limited when using 2D-based analysis approaches, especially when their orientation can be parallel, perpendicular or anything in-between relative to the optical section plane. Articular cartilage is an example of biological tissue that includes collagen fibers of such distinct orientations depending on the location within the tissue. As shown in the schematic diagram (Fig. 4a) and a representative 3D image (Fig. 4b) of mouse articular cartilage, this tissue is divided into four zones: superficial, transitional, radial and calcified [32,33]. The chondrocytes and collagen fibers are oriented parallel to the articular surface in the superficial zone, while perpendicularly to this surface in the radial zone. In the transitional zone, the chondrocytes are oriented at an angle to the surface, surrounded by territorial matrix composed of sheets of collagen fibers [32,33]. Thus, compared to the highly aligned superficial and radial zones, we expect the transitional zone to have less regularly organized fibers. To quantify fiber orientation within articular cartilage image stacks acquired from cryosections of the knee joints of 18 week old Balb/c mice, we first rotate every 3D image such that the articular surface is horizontally aligned (Supplementary Fig. 3). The cryosections are parallel to the xy plane indicated by the coordinate system labeled in Figs. 4a and b, along with the corresponding θ and φ angles. We then calculate the voxel-wise orientation of collagen fibers (Supplementary Fig. 3), and acquire orientation distribution histograms in different zones (Fig. 4c–e). While θ is peaked at 0° or 180° in the superficial zone, it is peaked at approximately 90° in the radial zone, consistent with what is shown in the schematic diagram (Fig. 4a). In the radial zone, φ is peaked close to 90° (Fig. 4e), revealing that collagen sheets align parallel to the optical sections (the plane of paper in this case, as shown in Fig. 4b), consistent with what is observed by SEM [33].
We use a localized analysis window of 4.2×4.2×5.0 μm to acquire the directional variance. The segmentation of the different zones is made according to the cell alignment as assessed by the corresponding TPEF images after they have been rotated (Fig. 4f and Supplementary Fig. 3). Fig. 4g shows the voxel-wise 3D directional variance map, where every voxel is false-colored according to its assigned variance value, which ranges between 0 and 1. Redder hues are observed in the transitional zone compared to the superficial and radial zones, providing a qualitative means of visualizing 3D variance differences (Fig. 4g). Quantitative 3D variance assessments are shown in Fig. 4h, which demonstrate that the mean 3D directional variance is significantly higher in the transitional zone, consistent with a less regular collagen organization, which has also been observed by magnetic resonance imaging and polarized light microscopy [34]. However, compared to these imaging modalities our assessments are quantitative and based on images of higher resolution, which are likely to be more sensitive to subtle changes in collagen organization.
3.4. The 3D directional variance of collagen fibers decreases within cancerous breast tissue when compared to normal
Collagen fiber organization has been shown to affect the micro- and macro-mechanical properties of tissue [35], which in turn play a significant role in a number of mechanosensitive cellular signaling pathways, and ultimately in defining cell function. Such structure-function changes are thought to be critical for tumor initiation and progression [4, 36–40]. Here, we consider 3D directional variance as a quantitative metric of collagen fiber organization in normal and cancerous mouse mammary gland tissues. Representative TPEF and SHG images are shown in Figs. 5a and b. The TPEF signal emanates from cells, blood vessels and lipid droplets, while the SHG signal originates from the collagen fibers.
Fig. 5. The 3D directional variance of collagen fibers is higher in normal than in cancer breast tissue.
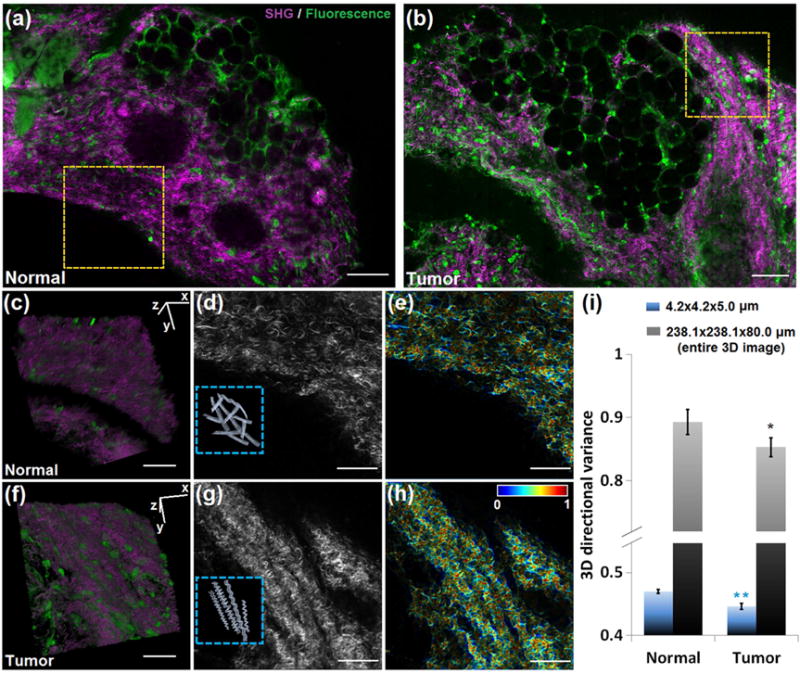
Representative large-field images of (a) normal mammary gland and (b) mammary tumor, with simultaneous SHG (purple) and TPEF (green) signals. 3D reconstruction of 80 SHG-TPEF images from (c) normal and (f) tumor groups recorded 1 μm apart, corresponding to the regions marked by the dashed yellow box in (a) and (b), respectively. The SHG 2D images of these two areas are shown in (d) and (g), with the schematic illustrations of groups of collagen fibers shown in the insets. The corresponding voxel-wise 3D directional variance maps are shown in (e) and (h), acquired with a localized window of 4.2×4.2×5.0 μm. (i) Mean and standard deviation of 3D directional variance in each group. Besides the localized window, the directional variance is also acquired with a 238.1×238.1×80.0 μm window, which corresponds to the entire 3D image. Significance is tested for each window size. **, p <0.001; *, p < 0.05. Scale bar in (a) and (b), 100 μm. Scale bar in other panels, 50 μm.
3D images are acquired and reconstructed (Fig. 5c,f), and the SHG-only 3D images are used for the calculation of 3D directional variance. Our findings show that groups of collagen fibers are “crosshatched” in the normal tissues, while they form highly regular helical structures in the tumor specimens (as indicated by the schematic illustrations shown in the Fig. 5d,g insets), consistent with observations from breast cancers [41,42]. The θ (black) and φ (blue) distribution histograms of these two representative frames are shown in Supplementary Fig. 4. The θ distribution of the normal tissue appears bimodal, which is evidence of the “cross-hatched” organization, while that of the mammary tumor shows a peak around 140°, consistent with a visually preferred orientation for the majority of fibers. Figs. 5e and h show the voxel-wise 3D directional variance maps of these representative frames acquired with a localized window of 4.2×4.2×5.0 μm. The mean 3D variance assessed using this window is shown in Fig. 5i, illustrating the significantly lower directional variance of the malignant mammary glands. A similar trend is observed between normal and tumor breast tissues when 3D variance is assessed using using a window size of 238.1×238.1×80.0 μm corresponding to the entire image stacks (Fig. 5i).
Differences in the 3D variance values calculated based on the two approaches reveal organizational disparities at the two distinct length scales assessed. The presence of more highly aligned fibers within tumors is consistent with previous studies which assessed collagen organization in breast tissues [43].
3.5. A decrease in 3D directional variance may reveal the presence of peritoneal metastases
The peritoneal cavity is a common target for metastatic lesions of gastrointestinal cancers, such as pancreatic cancer [44]. Detecting such metastatic lesions with high sensitivity is critical for proper patient staging and subsequent treatment decisions [45]. We thus compared the 3D directional variance of collagen fibers within freshly excised biopsies from healthy parietal peritoneum (Fig. 6a) and primary pancreatic neoplastic tissues (Fig. 6b), which served as surrogates of pancreatic peritoneal metastases [46] (prior knowledge of metastasis prohibits surgical intervention and consequently access to peritoneal metastatic lesions). Cellular clusters and blood vessels are often visible within the TPEF images, surrounded by collagen fibers providing the contrast in the SHG images. 3D images are reconstructed (Fig. 6c,d) and the SHG ones are used for assessment of 3D directional variance.
Voxel-wise directional variance maps are acquired and shown for a window size of 13.5×13.5×14.0 μm (Fig. 6e,g, and Supplementary Videos 1 and 2). Bluer hues are observed within the directional variance map of the neoplastic tissue (Fig. 6g) compared to the healthy peritoneum (Fig. 6e), representing a lower level of directional variance (according to the color bar). The θ (black) and φ (blue) distribution histograms of all the fibers within the representative frames are shown in Figs. 6f and h. There is one single peak of θ at ~35° (notice that 0° is equal to 180°) in the tumor tissue (Fig. 6h), in comparison to a wider, possibly bimodal distribution in healthy peritoneum (Fig. 6f) which is similar to that of the normal mammary tissue (Supplementary Fig. 4a). When we assess the directional variance as a function of window size (Fig. 6i), we find that with a window size equal to or greater than 13.5×13.5×14.0 μm, significantly lower directional variance is observed for the pancreatic neoplastic tissue than the normal parietal peritoneum. Notice that the minimum window size for 3D variance assessment required to observe significant differences between normal peritoneum and pancreatic cancers is larger than that used in the mammary gland case, indicating that the sensitivity of the local 3D directional variance metric depends on characteristics of the fibers, such as their diameter, waviness and tissue level organization, which are different from tissue to tissue [47]. The significant difference assessed by the entire window (300.0×300.0×74.0 μm) is consistent with the θ (black) and φ (blue) distribution histograms, as well as the visually apparent presence of more highly aligned fibers in the neoplastic tissue. It is interesting to note that both normal breast and parietal peritoneum tissues have very similar overall 3D variance values.
3.6. 3D directional variance quantifies changes in axonal organization within engineered brain-like cortical tissue in response to injury
Another important fiber-like structure within human tissues is the neuronal axon. Recently, we engineered functional 3D brain-like cortical tissues [29,48], and we sought to assess the potential use of 3D directional variance as a quantitative metric of axonal organization alterations in response to injury within these cortical tissues. A cortical unit module consists of neuron-rich grey matter-like regions and axon-only white matter-like regions (Fig. 7a). Controlled cortical impact (CCI) is applied to the module to cause injury [30,49] (Fig. 7b), and the axons are stained and imaged using TPEF. A representative 3D reconstruction with the injury pointed by the arrow is included in Fig. 7c. The analysis window with a size of 11.0×11.0×11.0 μm is used to acquire voxel-wise directional variance, which is then plotted as a function of distance away from the injury region (Fig. 7d). The data for the uninjured tissues are calculated using the same location profiles as the injured tissues for direct comparisons (Fig. 7d). The directional variance is highest right near the injury region, and gradually decreases with distance away from the injury. However, throughout the length scales assessed by the TPEF images, the directional variance of the injured samples is consistently significantly higher than that of the uninjured ones (Fig. 7d).
Fig. 7. 3D directional variance identifies changes in the organization of axons caused by injury in the engineered brain-like cortical tissue.
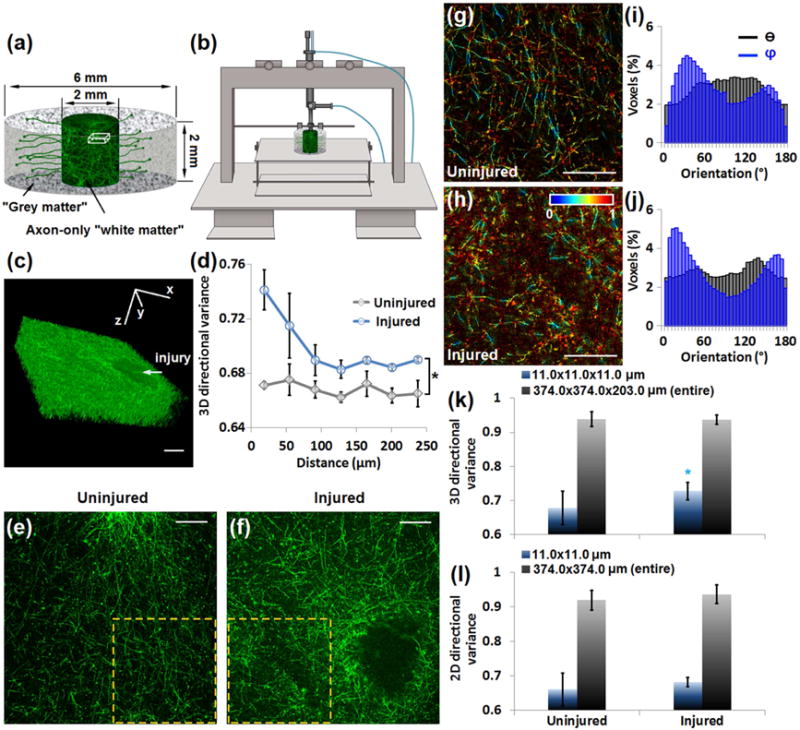
(a) Schematic of the brain unit module consisting of neuron-rich grey matter regions and axon-only white matter regions, with relevant sizes labeled. (b) The controlled cortical impact (CCI) injury model uses a driven piston to penetrate the cortical tissue at a known distance and velocity. (c) 3D reconstruction of axons of an injured sample from 203 images recorded 1 μm apart, corresponding to a cube within the white matter region, as marked in (a). The injury caused by CCI is pointed by the arrow. (d) 3D directional variance as a function of distance away from the injury, acquired by a window of 11.0×11.0×11.0 μm. (e, f) Representative large-field axon images of (e) uninjured and (f) injured samples. (g, h) Representative voxel-wise 3D variance maps of the marked areas in (e, f), with corresponding θ (black) and φ (blue) distribution histograms of all the fibers within this area (i, j). (k) Mean and standard deviation of 3D directional variance acquired from the localized window (11.0×11.0×11.0 μm) or entire 3D images (374.0×374.0×203.0 μm) in each group. (l) Mean and standard deviation of 2D directional variance from the localized window (11.0×11.0 μm) or the entire 2D images (374.0×374.0 μm). *, p < 0.05. Scale bar, 100 μm.
Representative images of axons (Fig. 7e,f) are shown along with the voxel-wise 3D directional variance maps within the marked regions (Fig. 7g,h). Generally redder hues are seen from the injured map, suggesting a higher level of directional variance (Fig. 7h). The orientation histograms of all the fibers within the representative images reveal fairly broad θ (black) distributions, with the φ (blue) distributions exhibiting some sharper features, especially for the injured tissues (Fig. 7i,j). A significantly higher directional variance is detected for the injured group via the localized window analysis (Fig. 7k), consistent with the location-dependent changes we report in Fig. 7d. However, these significant differences are masked when the 3D directional variance of the axons within the entire image stacks is considered (Fig. 7k). In addition, significant differences in axonal organization are not detected for a localized window analysis approach based on analysis of the individual 2D images using a previously reported approach [16]. These results demonstrate the enhanced sensitivity of the 3D-based analysis approach that may be highly important for some applications. In these tissues, it appears that the differences between the injured and uninjured sites are more prevalent along the φ rather than the θ orientation (Fig. 7i,j), and this could explain the improved ability of the 3D directional variance to identify significant changes in response to injury. The accurate characterization of axonal organization in 3D could be of great interest and importance not just in the case of brain injury, but also stroke, tumors and neurodegenerative diseases [50,51].
4. Discussion
We present a method to assess the levels of true three-dimensional alignment of fiber-like structures in a manner that is entirely automated, rapid, quantitative and flexible in terms of the scale at which information is provided. For example, on a desktop computer with a 3.4 GHz processor and 8 GB of RAM, the computational time for assessing the 3D directional variance of the mammary tissue stacks is 112 sec using the localized window (4.2×4.2×5.0 μm), and only 5 sec using the entire stack window (238.1×238.1×80.0 μm). Including the time of 102 sec needed for the calculation of the voxel-wise orientation of the collagen fibers, the complete assessment of fibrillar orientation and organization can be done within two to four min. A previous comparison study between our orientation determination method and the SHG-Fourier transform based approach by Lau et al. [23] revealed that the computational time of our orientation algorithm is over 30% more efficient than the time needed to implement the Fourier-based algorithm (1 min vs. 1.5 min) in resolving the same fiber stack with exactly the same configuration of computer [26].
In addition to speed, our approach yields a single, sensitive, quantitative metric of fiber alignment. This can be contrasted with the metrics provided by the other 3D approaches mentioned in Introduction. In Fourier-based analysis [23], each of the discrete ROIs (typically with a size of 5×5×5 μm) is qualitatively designated as anisotropic if a unique orientation of the overall fibers within this ROI can be determined by the filter bank method, isotropic if there is no unique orientation, or dark if the SHG intensity is below threshold. The other approaches characterize tissues directly based on the orientation information, such as orientation distribution by polarized microscopy [22], main orientations (the three most frequent orientations) by the inertia moments approach [24], or mean orientation by DTI in combination with two-photon microscopy [25]. However, orientation is in reference to a coordinate system; therefore, it matters how the samples are placed for imaging and artifacts may be introduced as a result. In contrast, the directional variance metric is independent of a coordinate system. Furthermore, the sensitivity advantage of using a single metric of 3D alignment, instead of, for example, two metrics of dispersion of the azimuthal and polar angles, are highlighted in our characterization of the collagen fiber alignment changes with the lung engineered tissue models (Fig. 3 and Supplementary Figs. 1, 2). The potential sensitivity enhancement related to using 3D directional variance over the corresponding 2D analysis metric is evident in our analysis of the axonal organization within the traumatic brain injury (TBI) tissue model (Figs. 7k and l), which demonstrates that significant differences are observed in the localized axon organization between the injured and uninjured engineered brain tissues, only when the 3D based variance is assessed.
The TBI tissue model is also a good example of an application in which it is important to be able to easily characterize organization at the microenvironment scale over small, localized windows that extend only a few microns in each direction. Clearly, such measurements are critical when location dependent variations are present within a sample, with the articular cartilage (Fig. 4) presenting another level of tissue heterogeneity that depends on localized measurements for its sensitive characterization. Assessment of collagen fiber organization at tumor margins would be another potential important application for this capability. The optimal window size over which the 3D directional variance is calculated to provide the most sensitive metric of alignment differences or changes depends on the size of the fibers, their tissue level organization, and the heterogeneity of the sample, as suggested by the results we achieve with the broad range of specimens we examine in this study. However, localized window-based calculations are significantly more computationally intensive, and for many applications, they may not be needed. For example, differences between normal and cancerous tissues can be reliably assessed from fast, full image stack-based assessments (Figs. 5 and 6). Similarly, such larger scale calculations are sensitive enough to reveal significant differences in the time-dependent alignment of both cellular and collagen fiber components of relatively homogeneous engineered lung stromal tissues (Fig. 3).
It is interesting to note that in both the breast cancer and the peritoneal metastases applications, the presence of more highly aligned collagen fibers is a feature associated with cancers. Several previous studies have demonstrated the diagnostic potential of SHG imaging for a number of cancers, as a result of its sensitivity to changes in collagen fiber organization [37,41–43,52]. Provenzano et al. identified distinct stages of growth and invasion in a breast cancer mouse model, based on the collagen fiber angle relative to the tumor boundaries extracted from 2D SHG images, with radially aligned collagen fibers indicative of the invasive and metastatic growth potential of a tumor [41,42]. Ambekar et al. utilized 2D Fourier transform-SHG (FT-SHG) to quantify the organization of collagen fibers in human breast tissues. Similar to their 3D approach [23], they divided each 2D image to a set of ROIs, and each of these ROIs was designated as anisotropic (if a unique orientation corresponding to the overall fibers within this ROI could be determined) or isotropic (no unique orientation). By defining the ratio of anisotropic over isotropic ROIs, they found an increased regularity in fiber orientation in malignant tissue [43]. Nadiarnykh et al. used SHG to visualize morphological changes of collagen fibers in malignant human ovarian biopsies, and further showed how several SHG signatures (such as the forward to backward SHG ratio) were correlated with sub-resolution structural changes, which collectively revealed that the diseased tissues were more highly organized than the corresponding normal ones [37]. These results together indicate that a highly aligned feature of collagen fibers might be a characteristic of several cancers, consistent with our findings. However, changes in collagen organization are likely cancer dependent. For example, Birk et al. examined human colon biopsies with SHG imaging, and the anisotropy parameter generated by the SHG intensity at orthogonal polarizations indicated that the normal tissue consists of more aligned collagen fibers than high-grade dysplasia tissues [52]. Although SHG provides the ability of 3D imaging, these previously published studies focused on collagen orientation or organization readouts based on analysis of 2D images; in contrast, the 3D directional variance provides a true three-dimensional assessment of collagen fiber organization in cancers at a scale ranging from ~4 μm (with a localized window) to ~300 μm (with a full-stack window). The outer limit for these calculations is based on the capabilities of the microscope and not the analysis technique.
The sensitivity of this metric is ultimately limited by the performance of the 3D orientation algorithm, whose accuracy is dependent on the fiber thickness and density, as previously reported [26]. Generally, the determination error of orientation increases with an increase in fiber thickness or density. Specifically, error estimates based on simulated fiber stacks, indicate that an orientation assessment window of two to three times the fiber diameter leads to optimized orientation results for straight fibers [26]. For wavy fibers, the window size to achieve the most accurate orientation readouts is more complicated to determine than for the straight ones, depending on both the fiber thickness and the curvature of the wavy structure [26]. Typically, to resolve fibers with the same thickness, the optimal window size for resolving wavy fibers is larger than that for straight ones (for example, 19×19×19 voxels vs. 13×13×13 voxels in that case), but the orientation determination accuracy decreases only slightly in the wavy cases (~ 1.2° increase in orientation error in that case) [26]. Note that the window used to calculate the orientation angle at each voxel is not the same as the window over which 3D variance is estimated. However, in both cases the presence of thicker and/or wavy fibers is associated with the need to use a larger assessment window to either characterize the fiber orientation more accurately or identify organization differences between tissue types. For example, the window size we used to estimate 3D orientation for the normal peritoneum and pancreatic tumor tissues was 6.5×6.5×6.0 μm, while that for the 3D variance calculations had to be larger than 13.5×13.5×14.0 μm to be sensitive to differences in organization (Fig. 6). The size of the windows over which 3D directional variance differences are detected in this case indicates that this metric is not as sensitive to individual fiber characteristics (e.g. straight vs. wavy) and more sensitive to microscopic, but tissue level collagen fiber organization. We also note that the 3D variance metric is even less susceptible to variations in some of the fiber/tissue characteristics than that of the 3D orientation algorithm. As shown in Fig. 2, the 3D directional variance percent error didn’t increase significantly and remained consistently below 0.06 for simulated fiber stacks with the same 3D directional variance value of ~ 0.57, but varying fiber densities from 3.6% to 6.0%, i.e., a variation of 66.7% in fiber density. The density differences between the control and experimental groups in this study are within this range (Supplementary Table 1), further supporting that the significant differences in 3D directional variance obtained in each application arises from the tissue level fiber organization itself.
5. Conclusions
In summary, the methodology reported here opens many possibilities for assessing with high sensitivity important 3D tissue organizational features of fiber-like structures through the use of 3D directional variance. The range of applications presented illustrate the versatile potential use of this metric in improving our ability to detect and quantify key tissue structural aspects in the context of tissue engineering, brain function, and diseases such as cancer. The ability of this approach to provide in an automated fashion metrics of alignment at both localized regions, that extend only a few microns, and larger tissue volumes, that occupy hundreds of microns in each direction, enhances its versatility and ease of use. The computationally efficient implementation of this metric also makes it well suited for applications that involve large data sets or can benefit from immediate feedback. The latter may be particularly relevant for in vivo diagnostic applications of two-photon microscopy [53,54].
Supplementary Material
Acknowledgments
This study was supported by the American Cancer Society (RSG-09-174-01-CCE to I.G.), the National Institutes of Health (NIH/NIBIB P41EB002520 to D.L.K., NIH R01NS092847 to D.L.K., NIH/NIBIB R00EB017723 to K.P.Q., NIH/NCI CA170851 to C.K. and NIH F31AR067638-01A1 to C.K.H.M.), Tufts University (Tufts Collaborates awards to T.S., L.Z. and I.G.), Raymond & Beverly Sackler Convergence Lab, the Breast Cancer Research Foundation and the Alexander S. Onassis Foundation. We acknowledge valuable help and support from Dr. Michael Whalen from the Massachusetts General Hospital in establishing the in vitro brain TBI model.
Footnotes
Publisher's Disclaimer: This is a PDF file of an unedited manuscript that has been accepted for publication. As a service to our customers we are providing this early version of the manuscript. The manuscript will undergo copyediting, typesetting, and review of the resulting proof before it is published in its final citable form. Please note that during the production process errors may be discovered which could affect the content, and all legal disclaimers that apply to the journal pertain.
Author contributions
Z.L., K.P.Q. and I.G. conceived and developed the method. D.P., D.S., A.K.S., C.K.H.M. and L.M.A. prepared tissue samples. Z.L., D.P., D.S. and A.K.S. acquired the data. Z.L., C.A. and I.G. performed the analysis. C.K., L.Z., T.S., D.L.K. and I.G. designed and planned the project. Z.L. and I.G. wrote the manuscript, which was reviewed and edited by all co-authors.
References
- 1.Condeelis J, Segall JE. Intravital imaging of cell movement in tumours. Nat Rev Cancer. 2003;3:921–930. doi: 10.1038/nrc1231. [DOI] [PubMed] [Google Scholar]
- 2.Roy P, Rajfur Z, Pomorski P, Jacobson K. Microscope-based techniques to study cell adhesion and migration. Nat Cell Biol. 2002;4:91–96. doi: 10.1038/ncb0402-e91. [DOI] [PubMed] [Google Scholar]
- 3.Ingber DE. Mechanical control of tissue morphogenesis during embryological development. Int J Dev Biol. 2006;50:255–266. doi: 10.1387/ijdb.052044di. [DOI] [PubMed] [Google Scholar]
- 4.Levental KR, Yu H, Kass L, Lakins JN, Egeblad M, Erler JT, et al. Matrix crosslinking forces tumor progression by enhancing integrin signaling. Cell. 2009;139:891–906. doi: 10.1016/j.cell.2009.10.027. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 5.Geiger B, Bershadsky A, Pankov R, Yamada KM. Transmembrane crosstalk between the extracellular matrix and the cytoskeleton. Nat Rev Mol Cell Biol. 2001;2:793–805. doi: 10.1038/35099066. [DOI] [PubMed] [Google Scholar]
- 6.Egeblad M, Werb Z. New functions for the matrix metalloproteinases in cancer progression. Nat Rev Cancer. 2002;2:161–174. doi: 10.1038/nrc745. [DOI] [PubMed] [Google Scholar]
- 7.Abbott NJ, Rönnbäck L, Hansson E. Astrocyte-endothelial interactions at the blood-brain barrier. Nat Rev Neurosci. 2006;7:41–53. doi: 10.1038/nrn1824. [DOI] [PubMed] [Google Scholar]
- 8.Discher DE, Mooney DJ, Zandstra PW. Growth factors, matrices, and forces combine and control stem cells. Science. 2009;324:1673–1677. doi: 10.1126/science.1171643. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 9.Frisch SM, Francis H. Disruption of epithelial cell-matrix interactions induces apoptosis. J Cell Biol. 1994;124:619–626. doi: 10.1083/jcb.124.4.619. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 10.Zamir E, Katz M, Posen Y, Erez N, Yamada KM, Katz BZ, et al. Dynamics and segregation of cell-matrix adhesions in cultured fibroblasts. Nat Cell Biol. 2000;2:191–196. doi: 10.1038/35008607. [DOI] [PubMed] [Google Scholar]
- 11.Butcher DT, Alliston T, Weaver VM. A tense situation: forcing tumour progression. Nat Rev Cancer. 2009;9:108–122. doi: 10.1038/nrc2544. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 12.Zipfel WR, Williams RM, Webb WW. Nonlinear magic: multiphoton microscopy in the biosciences. Nat Biotechnol. 2003;21:1368–1376. doi: 10.1038/nbt899. [DOI] [PubMed] [Google Scholar]
- 13.Campagnola PJ, Loew LM. Second-harmonic imaging microscopy for visualizing biomolecular arrays in cells, tissues and organisms. Nat Biotechnol. 2003;21:1356–1360. doi: 10.1038/nbt894. [DOI] [PubMed] [Google Scholar]
- 14.Zemel A, Rehfeldt F, Brown AEX, Discher DE, Safran SA. Optimal matrix rigidity for stress-fibre polarization in stem cells. Nat Phys. 2010;6:468–473. doi: 10.1038/nphys1613. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 15.Brown E, McKee T, diTomaso E, Pluen A, Seed B, Boucher Y, et al. Dynamic imaging of collagen and its modulation in tumors in vivo using second-harmonic generation. Nat Med. 2003;9:796–800. doi: 10.1038/nm879. [DOI] [PubMed] [Google Scholar]
- 16.Barnes C, Speroni L, Quinn KP, Montevil M, Saetzler K, Bode-Animashaun G, et al. From single cells to tissues: interactions between the matrix and human breast cells in real time. PLoS ONE. 2014;9:e93325. doi: 10.1371/journal.pone.0093325. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 17.Quinn KP, Golberg A, Broelsch GF, Khan S, Villiger M, Bouma B, et al. An automated image processing method to quantify collagen fibre organization within cutaneous scar tissue. Exp Dermatol. 2015;24:78–80. doi: 10.1111/exd.12553. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 18.Quinn KP, Georgakoudi I. Rapid quantification of pixel-wise fiber orientation data in micrographs. J Biomed Opt. 2013;18:046003. doi: 10.1117/1.JBO.18.4.046003. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 19.Bayan C, Levitt JM, Miller E, Kaplan D, Georgakoudi I. Fully automated, quantitative, noninvasive assessment of collagen fiber content and organization in thick collagen gels. J Appl Phys. 2009;105:102042. doi: 10.1063/1.3116626. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 20.Robertson C, Ikemura K, Krasieva TB, George SC. Multiscale analysis of collagen microstructure with generalized image correlation spectroscopy and the detection of tissue prestress. Biomaterials. 2013;34:6127–6132. doi: 10.1016/j.biomaterials.2013.04.019. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 21.Hanley CJ, Noble F, Ward M, Bullock M, Drifka C, Mellone M, et al. A subset of myofibroblastic cancer-associated fibroblasts regulate collagen fiber elongation, which is prognostic in multiple cancers. Oncotarget. 2016;7:6159–6174. doi: 10.18632/oncotarget.6740. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 22.Schriefl AJ, Zeindlinger G, Pierce DM, Regitnig P, Holzapfel GA. Determination of the layer-specific distributed collagen fiber orientations in human thoracic and abdominal aortas and common iliac arteries. J R Soc Interface. 2012;9:1275–1286. doi: 10.1098/rsif.2011.0727. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 23.Lau TY, Ambekar R, Toussaint KC., Jr Quantification of collagen fiber organization using three-dimensional Fourier transform-second-harmonic generation imaging. Opt Express. 2012;20:21821–21832. doi: 10.1364/OE.20.021821. [DOI] [PubMed] [Google Scholar]
- 24.Altendorf H, Decenciere E, Jeulin D, De sa Peixoto P, Deniset-Besseau A, Angelini E, et al. Imaging and 3D morphological analysis of collagen fibrils. J Microsc. 2012;247:161–175. doi: 10.1111/j.1365-2818.2012.03629.x. [DOI] [PubMed] [Google Scholar]
- 25.Napadow VJ, Chen Q, Mai V, So PT, Gilbert RJ. Quantitative analysis of three-dimensional-resolved fiber architecture in heterogeneous skeletal muscle tissue using NMR and optical imaging methods. Biophys J. 2001;80:2968–2975. doi: 10.1016/S0006-3495(01)76262-5. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 26.Liu Z, Quinn KP, Speroni L, Arendt L, Kuperwasser C, Sonnenschein C, et al. Rapid three-dimensional quantification of voxel-wise collagen fiber orientation. Biomed Opt Express. 2015;6:2294–2310. doi: 10.1364/BOE.6.002294. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 27.Mardia KV, Jupp PE. Directional Statistics, John Wiley and Sons, New York. :2000. [Google Scholar]
- 28.Proia TA, Keller PJ, Gupta PB, Klebba I, Jones AD, Sedic M, et al. Genetic predisposition directs breast cancer phenotype by dictating progenitor cell fate. Cell Stem Cell. 2011;8:149–163. doi: 10.1016/j.stem.2010.12.007. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 29.Chwalek K, Tang-Schomer MD, Omenetto FG, Kaplan DL. In vitro bioengineered model of cortical brain tissue. Nat Protoc. 2015;10:1362–1373. doi: 10.1038/nprot.2015.091. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 30.Dapul HR, Park J, Zhang J, Lee C, DanEshmand A, Lok J, et al. Concussive injury before or after controlled cortical impact exacerbates histopathology and functional outcome in a mixed traumatic brain injury model in mice. J Neurotrauma. 2013;30:382–391. doi: 10.1089/neu.2012.2536. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 31.Tingstrom A, Heldin CH, Rubin K. Regulation of fibroblast-mediated collagen gel contraction by platelet-derived growth factor, interleukin-1α and transforming growth factor-β1. J Cell Sci. 1992;102:315–322. doi: 10.1242/jcs.102.2.315. [DOI] [PubMed] [Google Scholar]
- 32.Dėdinaitė A. Biomimetic lubrication. Soft Matter. 2012;8:273–284. [Google Scholar]
- 33.Hughes LC, Archer CW, ap Gwynn I. The ultrastructure of mouse articular cartilage: collagen orientation and implications for tissue functionality. A polarised light and scanning electron microscope study and review. Eur Cell Mater. 2005;9:68–84. doi: 10.22203/ecm.v009a09. [DOI] [PubMed] [Google Scholar]
- 34.Nieminen MT, Rieppo J, Toyras J, Hakumaki JM, Silvennoinen J, Hyttinen MM, et al. T2 relaxation reveals spatial collagen architecture in articular cartilage: a comparative quantitative MRI and polarized light microscopic study. Magn Reson Med. 2001;46:487–493. doi: 10.1002/mrm.1218. [DOI] [PubMed] [Google Scholar]
- 35.Holbrook KA, Byers PH. Structural abnormalities in the dermal collagen and elastic matrix from the skin of patients with inherited connective tissue disorders. J Invest Dermatol. 1982;79:7s–16s. doi: 10.1111/1523-1747.ep12544609. [DOI] [PubMed] [Google Scholar]
- 36.Perentes JY, McKee TD, Ley CD, Mathiew H, Dawson M, Padera TP, et al. In vivo imaging of extracellular matrix remodeling by tumor-associated fibroblasts. Nat Methods. 2009;6:143–145. doi: 10.1038/nmeth.1295. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 37.Nadiarnykh O, LaComb RB, Brewer MA, Campagnola PJ. Alterations of the extracellular matrix in ovarian cancer studied by Second Harmonic Generation imaging microscopy. BMC Cancer. 2010;10:94. doi: 10.1186/1471-2407-10-94. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 38.Ingber DE. Can cancer be reversed by engineering the tumor microenvironment? Semin Cancer Biol. 2008;18:356–364. doi: 10.1016/j.semcancer.2008.03.016. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 39.Cox TR, Bird D, Baker AM, Barker HE, Ho MW, Lang G, et al. LOX-mediated collagen crosslinking is responsible for fibrosis-enhanced metastasis. Cancer Res. 2013;73:1721–1732. doi: 10.1158/0008-5472.CAN-12-2233. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 40.Paszek MJ, Weaver VM. The tension mounts: mechanics meets morphogenesis and malignancy. J Mammary Gland Biol Neoplasia. 2004;9:325–342. doi: 10.1007/s10911-004-1404-x. [DOI] [PubMed] [Google Scholar]
- 41.Provenzano PP, Eliceiri KW, Campbell JM, Inman DR, White JG, Keely PJ. Collagen reorganization at the tumor-stromal interface facilitates local invasion. BMC Med. 2006;4:38. doi: 10.1186/1741-7015-4-38. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 42.Provenzano PP, Inman DR, Eliceiri KW, Knittel JG, Yan L, Rueden CT, et al. Collagen density promotes mammary tumor initiation and progression. BMC Med. 2008;6:11. doi: 10.1186/1741-7015-6-11. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 43.Ambekar R, Lau TY, Walsh M, Bhargava R, Toussaint KC. Quantifying collagen structure in breast biopsies using second-harmonic generation imaging. Biomed Opt Express. 2012;3:2021–2035. doi: 10.1364/BOE.3.002021. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 44.Schnelldorfer T, Ware AL, Sarr MG, Smyrk TC, Zhang L, Qin R, et al. Long-term survival after pancreatoduodenectomy for pancreatic adenocarcinoma: is cure possible? Ann Surg. 2008;247:456–462. doi: 10.1097/SLA.0b013e3181613142. [DOI] [PubMed] [Google Scholar]
- 45.Li D, Xie K, Wolff R, Abbruzzese JL. Pancreatic cancer. Lancet. 2004;363:1049–1057. doi: 10.1016/S0140-6736(04)15841-8. [DOI] [PubMed] [Google Scholar]
- 46.Whatcott CJ, Diep CH, Jiang P, Watanabe A, Lobello J, Sima C, et al. Desmoplasia in primary tumors and metastatic lesions of pancreatic cancer. Clin Cancer Res. 2015;21:3561–3568. doi: 10.1158/1078-0432.CCR-14-1051. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 47.Li M, Mondrinos MJ, Gandhi MR, Ko FK, Weiss AS, Lelkes PI. Electrospun protein fibers as matrices for tissue engineering. Biomaterials. 2005;26:5999–6008. doi: 10.1016/j.biomaterials.2005.03.030. [DOI] [PubMed] [Google Scholar]
- 48.Tang-Schomer MD, White JD, Tien LW, Schmitt LI, Valentin TM, Graziano DJ, et al. Bioengineered functional brain-like cortical tissue. Proc Natl Acad Sci USA. 2014;111:13811–13816. doi: 10.1073/pnas.1324214111. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 49.Xiong Y, Mahmood A, Chopp M. Animal models of traumatic brain injury. Nat Rev Neurosci. 2013;14:128–142. doi: 10.1038/nrn3407. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 50.Choi S, Kim Y, Hebisch M, Sliwinski C, Lee S, D’Avanzo C, et al. A three-dimensional human neural cell culture model of Alzheimer’s disease. Nature. 2014;515:274–278. doi: 10.1038/nature13800. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 51.Hirokawa N, Niwa S, Tanaka Y. Molecular motors in neurons: transport mechanisms and roles in brain function, development, and disease. Neuron. 2010;68:610–638. doi: 10.1016/j.neuron.2010.09.039. [DOI] [PubMed] [Google Scholar]
- 52.Birk JW, Tadros M, Moezardalan K, Nadyarnykh O, Forouhar F, Anderson J, et al. Second harmonic generation imaging distinguishes both high-grade dysplasia and cancer from normal colonic mucosa. Dig Dis Sci. 2014;59:1529–1534. doi: 10.1007/s10620-014-3121-7. [DOI] [PubMed] [Google Scholar]
- 53.Balu M, Kelly KM, Zachary CB, Harris RM, Krasieva TB, König K, et al. Distinguishing between benign and malignant melanocytic nevi by in vivo multiphoton microscopy. Cancer Res. 2014;74:2688–2697. doi: 10.1158/0008-5472.CAN-13-2582. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 54.Balu M, Zachary CB, Harris RM, Krasieva TB, König K, Tromberg BJ, et al. In vivo multiphoton microscopy of basal cell carcinoma. JAMA Dermatol. 2015;151:1068–1074. doi: 10.1001/jamadermatol.2015.0453. [DOI] [PMC free article] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.


