Electronic spin state of iron in lower mantle perovskite

Abstract

The electronic spin state of iron in lower mantle perovskite is one of the fundamental parameters that governs the physics and chemistry of the most voluminous and massive shell in the Earth. We present experimental evidence for spin-pairing transition in aluminum-bearing silicate perovskite (Mg,Fe)(Si,Al)O₃ under the lower mantle pressures. Our results demonstrate that as pressure increases, iron in perovskite transforms gradually from the initial high-spin state toward the final low-spin state. At 100 GPa, both aluminum-free and aluminum-bearing samples exhibit a mixed spin state. The residual magnetic moment in the aluminum-bearing perovskite is significantly higher than that in its aluminum-free counterpart. The observed spin evolution with pressure can be explained by the presence of multiple iron species and the occurrence of partial spin-paring transitions in the perovskite. Pressure-induced spin-pairing transitions in the perovskite would have important bearing on the magnetic, thermoelastic, and transport properties of the lower mantle, and on the distribution of iron in the Earth's interior.

The lower mantle constitutes more than half of the Earth's interior by volume (1), and it is believed to consist predominantly (80–100%) of (Mg,Fe)(Si,Al)O₃ perovskite (hereafter called perovskite), with up to 20% (Mg,Fe)O ferropericlase (2). The electronic spin state of iron has direct influence on the physical properties and chemical behavior of its host phase. Hence, knowledge on the spin state of iron is important for the interpretation of seismic observations, geochemical modeling, and geodynamic simulation of the Earth's deep interior (3, 4). Crystal field theory (4, 5) and band theory (6) predicted that a high-spin to low-spin transition would occur as a result of compression. To date, no experimental data exist on the spin sate of iron in Al-bearing perovskite. To detect possible spinpairing transition of iron in perovskite under the lower mantle conditions, we measured the x-ray emission spectra of an Albearing perovskite sample to 100 GPa. For comparison, a parallel measurement was also carried out on an Al-free perovskite sample.

Experimental Methods

Both the Al-bearing and the Al-free perovskite samples were synthesized at the Geophysical Laboratory, Carnegie Institution of Washington. The method and condition of synthesis are similar to those described by Fei et al. (7). The final run products were crushed at 77 K, to avoid back transformation and amorphization of the metastable perovskite structure at ambient conditions. The composition of the perovskite samples, determined with the electron microprobe at the Geophysical Laboratory, are (Mg_0.87Fe_0.09)(Si_0.94Al_0.10)O₃ and (Mg_0.92Fe_0.09)Si_1.00O₃, respectively, with iron nominally assigned to Fe²⁺ at the 8- to 12-coordinated pseudododecahedral site (A site). These are widely accepted model compositions for perovskite in the Earth's lower mantle (2). The ferric iron content, according to Mössbauer spectra collected with an Austin Science drive at the Geophysical Laboratory, is 53(±4)% in the Al-bearing sample and 25(±2)% in the Al-free sample. The ferric iron content of the Al-bearing sample is consistent with the natural and synthetic samples examined by McCammon et al. (8, 9). The ferric iron content of the Al-free sample agrees with the synthetic sample by Fei et al. (7) when a three-doublet model is used to fit the Mössbauer spectra. Combining Mössbauer data with crystal chemistry considerations, we infer that Fe²⁺ in both Al-bearing and Al-free samples adopts the A site. The site occupancy of Fe³⁺ is uncertain: it could adopt the A site through a coupled substitution involving Al³⁺, enter the octahedral site (B site) with oxygen vacancy, or distribute equally between the two sites through a coupled substitution without Al³⁺ (7, 10). The x-ray diffraction spectra, acquired on a Rigaku microbeam diffractometer at the Geophysical Laboratory, can be fitted by the orthorhombic perovskite structure plus a small amount of stishovite. The cell parameters are 4.784(6), 4.911(4), and 6.850(5) Å for the Al-free sample and 4.786(1), 4.946(1), and 6.926(2) Å for the Al-bearing sample. Raman spectra of both samples showed the characteristic modes of the orthorhombic perovskite, with noticeable peak broadening in the Al-bearing sample compared with the Al-free one.

Each sample was loaded into a symmetrical Mao–Bell type diamond anvil cell, using beveled diamonds and x-ray-transparent beryllium gaskets. X-ray emission spectroscopy measurements were preformed on the undulator beam line at the Sector 13, Consortium for Advanced Radiation Sources, of the Advanced Photon Source at Argonne National Laboratory. The details of the experiments are similar to those described by Badro et al. (11). With the focused beam (7 × 7 μm) entering through one of the two diamond anvils parallel to the load axis, the pressure gradient across the probed area was estimated at ±5 GPa at 100 GPa. The undulator gap was set for the maximum sample signal, with the first harmonic energy at 12 keV. The accumulation time for each spectrum increased from 3 hr at low pressures to >6 hr at 100 GPa.

Results and Discussion

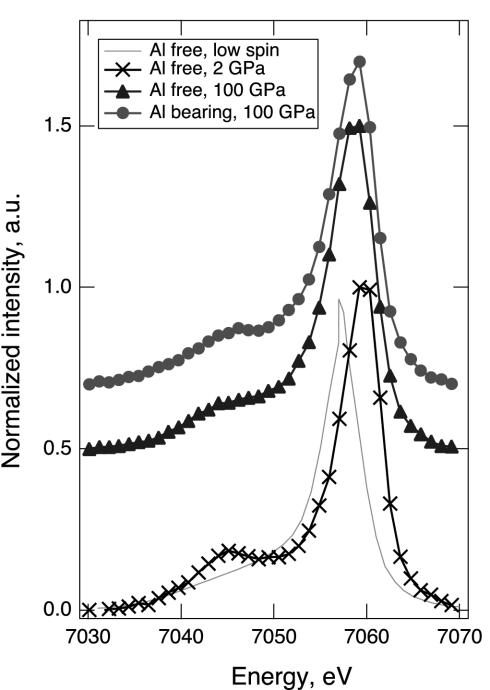
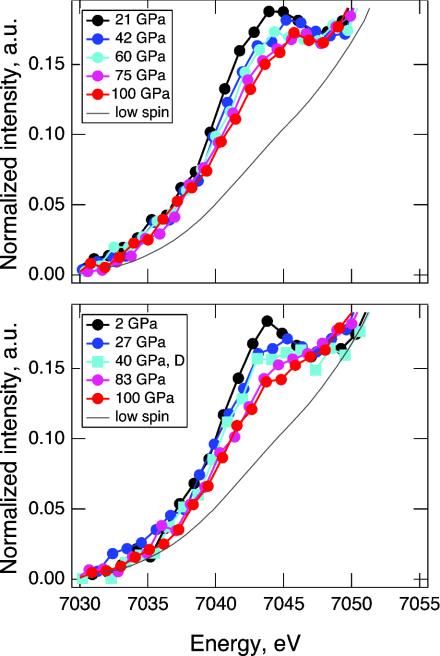
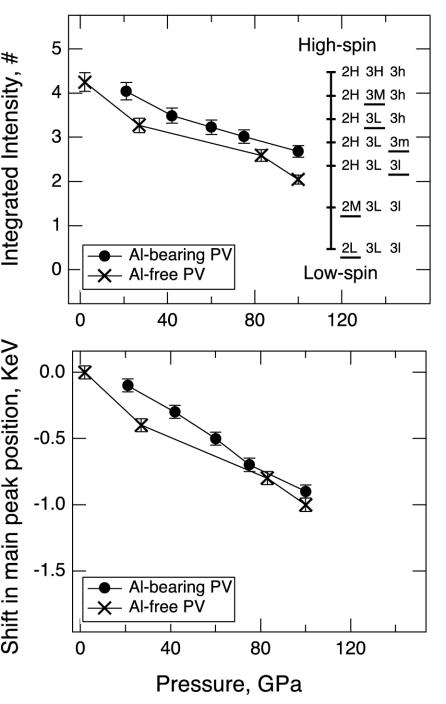
Shown in Fig. 1 are the iron Kβ x-ray emission spectra of perovskite samples at 100 GPa, and the high-spin emission of Al-free perovskite sample at 2 GPa. The spectrum of the low-spin iron in an Al-free perovskite (Mg_0.9Fe_0.1)SiO₃ at 145 GPa is included for comparison. Fig. 2 shows the evolution of x-ray emission spectra in the satellite region during compression and decompression. Previous studies have established that the x-ray emission spectra of iron-bearing phases are sensitive to the local magnetic moment (11–15). The spin state of iron can be determined from the intensity of the satellite peak Kβ′ at 7,045 eV relative to the main emission line Kβ_1,3, and from the peak position of Kβ_1,3. In Fig. 3, we plotted the normalized integrated intensity of the satellite peak and shift of the main peak position as a function of pressure. The relative intensity of the satellite peak indicates that at 2 GPa iron in the Al-free sample is in the high-spin state. As pressure increases, the satellite peak intensity decreases continuously in both sets of spectra, indicating a gradual increase of the lower spin components. At 100 GPa, both samples exhibit a spin state that is different from the initial high-spin state or the expected final low-spin state. The shift of the main peak position toward lower energy also indicates continuous loss of magnetic moment in both samples with increasing pressure.

Fig. 1.

X-ray emission spectra of two perovskite samples at 100 GPa (•, Al-bearing; ▴, Al-free) compared with the reference low-spin spectrum of an Al-free perovskite (15). a.u., arbitrary units. The high-spin emission of our Al-free perovskite sample at 2 GPa is also shown (×).

Fig. 2.

Evolution of x-ray emission spectra with pressure. All spectra are shifted so that the main emission line is at 7,058 eV. A low-spin spectrum of Al-free perovskite is shown for reference (15). (Upper) Evolution of x-ray emission spectra of the Al-bearing perovskite sample in the satellite region from 7,030 to 7,050 eV, during compression. (Lower) Evolution of x-ray emission spectra of the Al-free perovskite sample in the satellite region from 7,030 to 7,050 eV, during compression (circles) and decompression (squares, 40 GPa). The spectrum at 40 GPa is measured during decompression, and shows the reversibility of the observed intensity changes.

Fig. 3.

Pressure dependence of satellite peak intensity and main peak position. (Upper) Integrated intensities of the satellite peak as a function of pressure. •, Al-bearing perovskite; ×, Al-free perovskite. Error bars represent counting errors in the x-ray emission spectroscopy measurements. The bars on the vertical line are the expected intensities for the Al-bearing perovskite, based on the apparent numbers of unpaired electrons (#). The apparent numbers of unpaired electrons are calculated from the number of unpaired electrons in each iron species, weighed by its atomic fraction (assuming that Fe³⁺ is equally distributed between the A and B sites). For example, when Fe²⁺, Fe³⁺(A site), and Fe³⁺(B site) are in the high-spin state (2H3H3h), the expected intensity in terms of the apparent number of unpaired spin is 0.47·4 + 0.265·5 + 0.265·5 = 4.53. When Fe²⁺ is in the high-spin state, Fe³⁺(A site) is in the intermediate-spin state, and Fe³⁺(B site) is in the low-spin state (2H3M3l), the expected intensity is 0.47·4 + 0.265·3 + 0.265·1 = 2.94. Note that the order in which partial spin transitions occur under compression is unknown. Only one possible scenario is shown here (the underscore denotes the iron species that has just undergone a partial-pairing transition). (Lower) Shift of the main peak position as a function of pressure. The shifts are measured with respect to the main peak position at 2 GPa in the Al-free perovskite. •, Al-bearing perovskite; ×, Al-free perovskite. Error bars represent uncertainties in the fitted peak position.

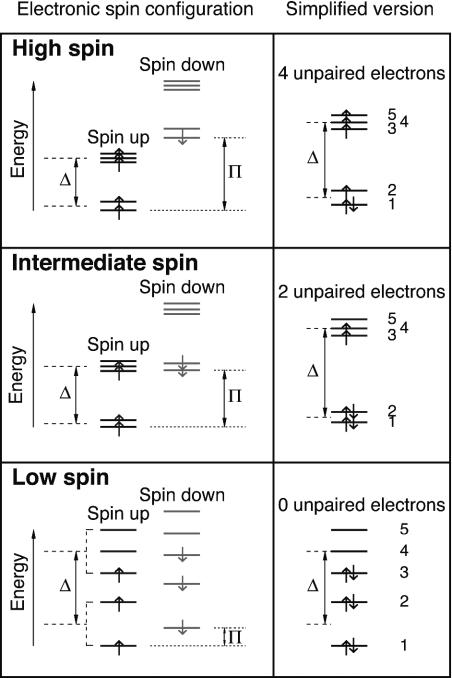
The observed gradual decrease of the satellite peak intensity with pressure is distinct from the previously known examples of spin-pairing transitions in elemental iron (16) and simple sulfide FeS (14), where the satellite peak intensity drops abruptly at a certain pressure. The pressure-induced gradual loss of magnetic moment can be explained by the presence of multiple iron species and the occurrence of partial spin-pairing transition in the perovskite. In our perovskite samples, iron has two valence states. Whereas Fe²⁺ probably adopts the A site (7, 10, 17), the site occupancy of Fe³⁺ is uncertain (7, 18). Depending on the site occupancy of Fe³⁺, there may be two or three iron species (as distinguished by their valence state and crystallographic site) in each perovskite sample. Lower mantle perovskite has a noncubic structure. As a result, each iron species undergoes two partial spin-pairing transitions under compression (Fig. 4). The total number of pressure-induced partial transitions for two or three iron species mounts to four or six, corresponding to five or seven spin states, respectively. At a given pressure, iron in perovskite may possess a mixed spin state, possibly including high-spin, intermediate-spin, and low-spin iron. The occurrence of a series of mixed-spin states would manifest as a gradual loss of magnetic moment with increasing pressure. In Fig. 3, we show the apparent numbers of unpaired electrons for all of the possible mixed-spin states in the Al-bearing perovskite. Normalizing the integrated intensity to the apparent number of unpaired electrons, it can be deduced that at 100 GPa, half of the Fe²⁺ in the Al-free sample has transformed to the intermediate-spin state (Fig. 4). The higher residual spin in the Al-bearing perovskite suggests higher transition pressure for one or both species of Fe³⁺, perhaps because of its higher spin-pairing energy (4). However, a recent synchrotron Mössbauer study suggests that Fe³⁺ in Al-free perovskite may undergo a continuous transition to reach the low-spin state by 70 GPa (19). Further understanding of pressure-induced spin evolution of iron in lower mantle perovskite awaits additional experimental and theoretical studies.

Fig. 4.

Schematic diagrams of electronic spin configuration of Fe²⁺ in the A site of perovskite based on crystal field theory (4). On the right are the simplified pictures that are commonly found in the literature. The 3d subshell of iron contains five orbitals, each capable of accommodating two electrons with opposite spins. The energy difference between the opposite spins on each orbital (dotted lines) is called spin-pairing energy (π). According to the crystal field theory, in a cubic environment, the 3d orbitals split into the t_2g and e_g levels (dashed lines). The energy difference between the two levels is called crystal field splitting energy (Δ). In a noncubic environment, additional splitting occurs between the t_2g levels and between the e_g levels, resulting in five different energy levels. At ambient condition, the 1st spin-down level is higher than the 5th spin-up level. Only one electron is forced to pair. Fe²⁺ has the largest number of unpaired electrons (high-spin state). Upon compression, crystal field splitting energy increases with increasing density (decreasing ligand bond lengths) and possibly increasing degree of distortion. Given fixed spin-pairing energy (5), certain lower spin-down levels will cross higher spin-up levels. When the 2nd spin-down level crosses the 5th spin-up level, the electron at the 5th orbital will switch spin and move to the 2nd orbital (intermediate-spin state, intermediate number of unpaired electrons). When the 3rd spin-down level crosses the 4th spin-up level, the electron at the 4th orbital will switch spin and move to the 3rd orbital (low-spin state, smallest number of unpaired electrons). In other words, each iron species goes through two pressure-induced partial spin-pairing transitions: Upon the first partial spin-pairing transition the number of unpaired 3d electrons drops to two, forming the intermediate-spin state. After the second partial transition, the number becomes zero, reaching the final low-spin state. Similar diagrams can be drawn for Fe³⁺ in either the A or the B site.

In our experiments, the transitions may have been broadened because of the low iron content and variable degree of distortion in the A site. At low iron content, an electronic spin-pairing transition is likely to occur without structural phase transformation. With variable degree of distortion, a purely electronic spin-pairing transition of iron in the A site would spread over a finite pressure range. In contrast, the spin-pairing transition in iron or FeS coincides with the structural phase transformation, leading to an abrupt loss of magnetic moment at a certain pressure. Additional broadening factors include the presence of pressure gradients and nonhydrostatic stresses in the sample (20) and possible amorphization of the sample due to nonhydrostatic stress or sample–x-ray beam interaction (21).

Our measurements were taken at room temperature. At the temperature of the Earth's lower mantle, the spin-pairing transitions of iron in perovskite would occur at higher pressure because of the thermal expansion effect and the larger entropy in the higher spin state. Given the equation-of-state of the higher and lower spin phases and the volume dependence of spinpairing energy and crystal-field splitting energy, the effect of temperature on transition pressure can be solved iteratively based on equation ΔG = ΔU – TΔS + PΔV, where ΔU is a function of spin-pairing energy and crystal-field splitting energy. In a cubic environment, ΔU = π – Δ for each electron that flips spin, where π is the spin-pairing energy, and Δ is the crystal-field splitting energy (Fig. 4). We estimated the effect of temperature on transition pressure in perovskite by using the approximate relations Δ ∼ R^–5 (R is the Fe–O bond length) in a cubic environment (4). Assuming that spin-pairing energy does not depend on pressure or temperature (5) and that the volume difference between the adjacent spin states is negligible, the increase in transition pressure due to thermal expansion is ≈ K_TαΔT (K_T is the isothermal bulk modulus and α is the volume thermal expansion coefficient). The increase in transition pressure because of larger entropy in the higher spin state is approximately ΔTΔS/–(d(nΔ)/dP)_P,300K = ΔTΔS/(5nΔ/3K_T)_P,300K. Taking π from Burns (4) and the thermoelastic parameters of perovskite from Mao et al. (22), we found that the partial transition pressure of 80 GPa at room temperature would increase by about 30 GPa at 2,000 K (10 GPa increase due to the thermal expansion effect, and 20 GPa increase due to the entropy effect). The estimated thermal expansion effects rely on the assumption Δ ∼ R^–5. It should be improved by more accurate calculations. The entropy effects do not depend on any assumption and should be quite reliable.

The observed spin transition has important ramifications for the magnetic, thermoelastic, and transport properties of the deep mantle (4). A transition toward the low-spin state decreases the number of unpaired electrons in the 3d subshell of iron and leads to a decrease in the magnetic susceptibility of its host phase; hence the observed spin-pairing transition of iron in perovskite would have appreciable effects on the magnetic properties of the lower mantle. The low-spin iron is expected to have a smaller ionic radius than its high-spin counterpart (23). A change in the magnetic state and ionic radius of iron would affect the thermoelastic properties of the host phases (5). More importantly, it would significantly modify the chemical bonding character of Fe²⁺ and Fe³⁺ ions (4, 6). The low-spin iron in the deep mantle would behave like different elements from the high-spin iron at the shallow depths. There may be phase separation between Fe-rich and Mg-rich phases. The melting temperature of the Fe-rich end member is probably higher than the Mg-rich end members. These factors could lead to enrichment of iron in the deep mantle as a result of partitioning between the deep and shallow mantle. Furthermore, it has been proposed that the high-spin Fe²⁺ ions in the lower mantle perovskite may hinder the blackbody radiation in near-infrared regions. The presence of low-spin Fe²⁺ ions in perovskite would confine the crystal field transitions to the visible region, hence allowing more efficient radiative heat transfer at near-infrared wavelengths in the deep mantle (4). Possible chemical stratification and change in heat transfer may affect the pattern of mantle convection and the fate of subducting slabs (e.g., refs. 24 and 25). Because the loss of magnetic moment in perovskite occurs gradually with increasing depth, its effects on the physical and chemical properties of the lower mantle would be relatively smooth. Detection and appreciation of such effects may be challenging but are necessary for our understanding of the Earth's deep interior.