An experimentally determined protein folding energy landscape

Abstract

Energy landscapes have been used to conceptually describe and model protein folding but have been difficult to measure experimentally, in large part because of the myriad of partly folded protein conformations that cannot be isolated and thermodynamically characterized. Here we experimentally determine a detailed energy landscape for protein folding. We generated a series of overlapping constructs containing subsets of the seven ankyrin repeats of the Drosophila Notch receptor, a protein domain whose linear arrangement of modular structural units can be fragmented without disrupting structure. To a good approximation, stabilities of each construct can be described as a sum of energy terms associated with each repeat. The magnitude of each energy term indicates that each repeat is intrinsically unstable but is strongly stabilized by interactions with its nearest neighbors. These linear energy terms define an equilibrium free energy landscape, which shows an early free energy barrier and suggests preferred low-energy routes for folding.

Protein folding is a complex process by which a relatively well defined rigid 3D structure is adopted from a very large ensemble of expanded, less structured conformations. In this process, which is often quite fast, a large number of configurational degrees of freedom must be fixed. Thus, in contrast to simple chemical reactions, for which structural rearrangements are limited to a few atoms or groups, dissection of protein folding reactions is challenging because the progress of the “reaction” cannot be represented with a simple structural coordinate (1). The application of energy landscape theory to the protein folding problem provides a step toward depicting the complexity of the protein folding process (2–4) by showing the interplay between structural coordinates and representing the degree of conformational heterogeneity (and thus entropy) associated with various stages of folding.

Although the application of energy landscape ideas to the protein folding problem has provided a conceptual advance (5) and has been used to analyze computer models of folding in quantitative detail (4, 6), experimentally determining energy landscapes for single-domain proteins (i.e., surfaces that depict energy as a function of the degree of folding of various parts of the protein) has remained a formidable challenge. A major barrier to obtaining such a picture is the high degree of cooperativity of folding of single-domain proteins: partly folded conformations are not populated; thus, their relative energies cannot be determined. Native-state hydrogen exchange (7–11) provides a means to access the stabilities of some of these partly folded conformations, but identifying the conformations that provide protection from exchange is not always straightforward.

Repeat proteins allow stability measurements of portions of a protein domain and, thus, the generation of an experimentally determined energy landscape. Repeat proteins such as the Notch ankyrin domain (Fig. 1) contain multiple units of secondary structure that are tandemly repeated in a roughly linear array (14). Ankyrin repeats, for example, contain two short (9- to 10-residue) α-helices connected to each other by a short turn, and to neighboring repeats by an extended segment that terminates with a tight turn flanked by a short interrepeat hydrogen-bonded β-sheet segment (15). Each repeat shows a high degree of structural similarity despite a relatively low degree of sequence identity (17% average pairwise identity for the Drosophila Notch ankyrin domain, the subject of this study) (16). Although repeat proteins are constructed from a collection of repetitive units, they contain rigid tertiary structures involving extensive packing between repeats, and often show very high degrees of cooperative unfolding (17–20). Thus, repeat proteins can be regarded as single, elongated domains. However, unlike the tertiary interactions of globular proteins, those of repeat proteins are all local; thus, repeat proteins are likely to be tolerant to significant chain truncation and extension (21–24).

Fig. 1.

The structure of the Drosophila Notch ankyrin domain. Shown is a ribbon representation of chain A (Protein Data Bank ID code 1OT8), with each of the seven sequence repeats colored differently. This figure was prepared by using molscript (12) and raster3d (13).

Here we determine a protein energy landscape by measuring stabilities of folded fragments of a repeat protein, the Notch ankyrin domain, taking advantage of the ability of such fragments to remain folded despite significant deletions (18, 21, 25). By quantifying the thermodynamics of unfolding of various fragments, we obtain a direct, rigorous measure of the stabilities of local regions of the polypeptide, experimentally mapping stability to different parts of the full-length protein structure. In addition to being determined from direct experimental measurements, the resulting energy landscape has the advantage that neighboring points in the landscape are structurally similar, in contrast with landscapes involving global structural parameters such as radius of gyration or number of native contacts.

Methods

Cloning, Expression, and Purification. The full-length construct Nank1–7* contains seven tandem ankyrin repeat sequences of the Drosophila melanogaster Notch receptor with the two internal cysteine residues replaced by serine residues (18) and an N-terminal His₆ tag (26). Shorter constructs are terminal truncations of entire repeats, as defined in ref. 18. Histidine tags are N-terminal for Nank1–6*, Nank1–5*, Nank1–4*, Nank2–6*, and Nank2–5* and C-terminal for Nank4–7*, Nank3–7*, and Nank2–7*. The numbers in each construct name are used to specify repeat boundaries; for example, Nank2–5* contains repeats 2, 3, 4, and 5 but is missing repeat 1 from the N terminus and repeats 6 and 7 from the C terminus. DNA fragments encoding deletion constructs were subcloned as PCR fragments into the T7 expression vector pET15b (Novagen), were expressed in Escherichia coli strain BL21(DE3), and were purified as described in refs. 18 and 26. Nank3–7*, which failed to express to high levels from pET15b, was expressed as a C-terminal fusion with maltose-binding protein (MBP). Nank3–7* was cleaved from MBP with tobacco etch virus (TEV) protease and was purified as described in refs. 18 and 26.

Equilibrium Denaturations. CD measurements were made with an Aviv Associates model 62DS CD spectropolarimeter (Lakewood, New Jersey) monitoring α-helical structure at 222 nm. Fluorescence was collected on the same instrument with excitation at 280 nm; perpendicular emission was monitored with a 320-nm cutoff filter. Data were collected and analyzed as described in refs. 19 and 25. Thermodynamic parameters were estimated by fitting a linear free energy model () (27, 28), transformed to express a population-weighted spectroscopic signal (29), to urea unfolding curves with nonlinear least-squares. Errors, shown in Table 1, indicate SDs on mean unfolding free energies and m values from n independent unfolding curves, where n is the value given in parentheses. For Nank1–4* and Nank4–7*, unfolding free energies were estimated by using global fitting to analyze conformational transitions in a mixed cosolvent system containing both urea and trimethylamine N-oxide (26). Protein concentrations ranged from 2 to 9 μM. Conformational transitions were measured in 25 mM Tris·HCl (pH 8.0) at 15°C.

Table 1. Thermodynamic parameters for folding of deletion constructs of the Notch ankyrin domain.

	Circular dichroism		Fluorescence
Construct	, kcal·mol-1	m value, kcal·mol-1·M-1	, kcal·mol-1	m value, kcal·mol-1·M-1
Nank1-7*	-6.65 ± 0.04 (5)†	-2.85 ± 0.02	-6.78 ± 0.6 (5)	-2.91 ± 0.03
Nank1-6*	-2.85 ± 0.03 (4)	-1.76 ± 0.01	-3.01 ± 0.03 (4)	-1.85 ± 0.02
Nank1-5*	-2.69 ± 0.04 (5)	-1.73 ± 0.03	-2.84 ± 0.16 (3)	-1.67 ± 0.08
Nank1-4*	+0.37	-0.85	ND	ND
Nank4-7*	+0.089	-2.12	ND	ND
Nank3-7*	-1.81 ± 0.09 (3)	-1.58 ± 0.06	-1.70 ± 0.23 (3)	-1.67 ± 0.08
Nank2-7*	-4.96 ± 0.04 (8)	-2.36 ± 0.02	-5.05 ± 0.04 (5)	-2.44 ± 0.03
Nank2-6*	-1.96 ± 0.002 (3)	-1.58 ± 0.02	-2.03 ± 0.02 (3)	-1.67 ± 0.02
Nank2-5*	-1.73 ± 0.03 (6)	-1.39 ± 0.02	-1.54 ± 0.03 (3)	-1.34 ± 0.01

Numbers in parentheses denote number (n) of independent folding curves. ND, not determined.

^† for Nank1-7* differs from that reported in ref. 25, which was determined in the presence of 150 mM NaCl.

Ising Model for Folding. To explore unfolding transitions that would result from nearest-neighbor coupling of each repeat, we used a 1D Ising model. Ignoring conformations containing two separate stretches of structured repeats (which are τ ≈ 1.5 × 10⁷ times less likely to form than conformations with the same number of structured repeats in a single contiguous stretch), the following zipper partition function (30) can be written:

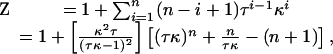where κ is an intrinsic equilibrium constant for folding of a single repeat, τ is an equilibrium constant for interactions between two folded repeats, i is the number of contiguous folded repeats, and n is the total number of repeats in the protein. By assigning a linear denaturant dependence (27, 28) to the intrarepeat folding free energy that is one-seventh of the m value for the Notch ankyrin domain, the fraction of molecules with i of n = 7 folded repeats can be calculated as f_i = κ ⁱτ ^i–1/Z as a function of urea concentration.

Results and Discussion

To determine the distribution of stability across a folded protein, we generated constructs of the Notch ankyrin domain in which multiple repeats are deleted from either (or both) end(s). The Notch ankyrin domain, which unfolds in a cooperative, two-state reaction (18, 19), retains much of its structure in solution despite deletion of several repeat units, as judged by far-UV CD spectroscopy, which monitors α-helical secondary structure (see Fig. 6, which is published as supporting information on the PNAS web site). Sigmoidal urea-induced unfolding transitions, monitored by far-UV CD, are obtained for constructs missing one (Nank1–6* and Nank2–7*) or two (Nank1–5* and Nank3–7*) of the seven sequence repeats from either the N terminus or the C terminus. Likewise, cooperative unfolding transitions are obtained when repeats are deleted from both termini, including a construct in which three repeats are deleted (Nank2–5*, wherein 114 of 256 residues have been removed). Constructs in which three repeats are deleted from one or the other terminus (Nank1–4* and Nank4–7*) display only partial unfolding transitions (Fig. 2A), although by adding the stabilizing osmolyte trimethylamine N-oxide we have been able to generate full unfolding transitions and extract reliable thermodynamic parameters for unfolding (Table 1) (26).

Fig. 2.

Deletions of the Notch ankyrin domain. (A) Structural transitions of Notch ankyrin deletion constructs monitored by CD. ×, Nank1–7*; ▴, Nank2–7*; ▵, Nank1–6*; □, Nank1–5*; ▪, Nank2–6*; ⊠, Nank3–7*; •, Nank1–4*; ○, Nank2–5*; ⊚, Nank4–7*. Solid lines are the result of fitting a two-state denaturation model to the data. (B) Relationship between repeat number and free energy of folding. The equation for the linear regression line is ΔG° = 7.53 – 1.96n_rep, with a correlation coefficient of 0.925.

For all of the constructs with full urea-induced unfolding transitions, unfolding curves are adequately fitted by a two-state unfolding model, assuming a linear dependence of unfolding free energy on urea concentration (27, 28). These constructs yield similar unfolding free energies (ΔG°_H2O) and m values (related to the steepness of the transition) when the transition is monitored by tryptophan fluorescence and by far-UV CD (Table 1 and Fig. 7, which is published as supporting information on the PNAS web site). This similarity suggests that unfolding remains cooperative even when significant portions (as many as 114 residues) of the ankyrin repeat domain are deleted. High cooperativity is supported by a significant linear correlation (r = 0.897) between the number of repeats and the m value, which is related to the size of the cooperative unit in unfolding (Fig. 8, which is published as supporting information on the PNAS web site).¶

In general, stability decreases with the number of repeats deleted in a roughly linear way (r = 0.925 in a linear regression of ΔG°_H2O vs. number of repeats) (Fig. 2B), although for constructs of a given repeat length, there is considerable variation in unfolding free energy, indicating that different repeats contribute differently to stability. ΔG°_H2O values for constructs containing six repeats differ by 2.2 kcal·mol^–1, and values for constructs that contain four repeats range over 2.1 kcal·mol^–1. The slope of the regression line (–1.96 kcal·mol^–1 per repeat) indicates that, on average, each repeat contributes about –2 kcal·mol^–1 to stability. The intercept of the regression line is significantly greater than zero, suggesting a large difference between the free energy of folding a single, isolated repeat (initiation) and the free-energy increment of adding repeats to an already-folded structure (propagation). The sign and magnitude of the intercept (+7.46 kcal·mol^–1) indicates that, in general, single ankyrin repeats of the Drosophila Notch receptor should be intrinsically unstable (+5.5 kcal·mol^–1; the value from the least-squares line in Fig. 2B evaluated at n = 1 repeat).

A Linear, Heterogeneous Model for Stability. To capture the variation in stability with repeat identity seen in Fig. 2B, a linear model was developed to account for the contribution of each repeat to stability (Fig. 3A). In this model, seven coefficients (ΔG°_i) are used to represent the stability contribution of each repeat, as defined experimentally by our deletion series. As such, each construct can be represented by a linear equation in which the sum of the coefficients for each of the repeats present (ΔG°_i through ΔG°_j) is equal to the experimentally determined folding free energy (ΔG°_i–j).

Fig. 3.

A linear heterogeneous model for the stability of the Notch ankyrin domain. (A) Linear model ascribing a free energy contribution of each repeat (ΔG₁° through ΔG₇°), as defined by end deletion. (B) Observed vs. predicted folding free energies of Notch deletion constructs. Predicted values were estimated from a jackknife procedure in which coefficients were iteratively calculated from subsets of the data in which different constructs were omitted. Coefficients were then used to calculate the folding free energies of each omitted construct. The correlation coefficient is 0.9556. Inset shows observed vs. predicted folding free energies of Notch ankyrin deletion constructs from a simple multiple-linear regression on all constructs. The correlation coefficient is 0.9975. (C) Coefficients for the energetic contribution of each ankyrin repeat calculated from the linear heterogeneous model. The coefficient for ankyrin repeat 4 reflects only the intrinsic stability of the repeat, whereas the other coefficients capture both the intrinsic and interfacial stabilities (see Results and Discussion).

Each of the coefficients in the set of linear equations shown in Fig. 3A includes the intrinsic contribution of each corresponding repeat to folding free energy. In addition, most of the free energy coefficients contain a contribution from an interface between the corresponding repeat and its nearest neighbor. Because our deletion series is centered on repeat 4, a given coefficient includes the contribution of the interface toward the center of the domain. For example, the coefficient associated with the third repeat (ΔG°₃) includes the contribution of the interface between repeats 3 and 4 to folding free energy. However, as there are seven repeat sequences but only six potential nearest-neighbor interfaces, ΔG°₄ lacks an interfacial contribution. In our deletion series (Fig. 3A), ΔG°₄ is associated with this structural interpretation because the interfaces involving repeat 4 (3/4 and 4/5) are accounted for in coefficients associated with repeats 3 and 5. The free energy of constructs lacking the fourth repeat could not be quantified because these constructs were completely unstructured, hence, the deletion series could not be centered on any repeat other than the fourth. The unique value of ΔG°₄ (which is simply a reflection of how the deletion series was constructed rather than a unique property of the fourth repeat) allows us to separate the energetics of intrinsic repeat formation from the energetics of interfacial interaction.

Multiple regression analysis (nonlin, Robelko Software, Carbondale, IL) was used to obtain numerical values for the seven coefficients depicted in Fig. 3A. Although folding free energies predicted from the seven-parameter equation with the optimized coefficients are highly correlated with experimental folding free energies (r = 0.997) (Fig. 3B Inset), some of this correlation results from the small number of degrees of freedom in the system of equations. To obtain an unbiased estimate of the degree to which this model captures the stability of the Notch ankyrin deletion series, jackknife analysis was used to iteratively generate blind predictions of folding free energies. The correlation between these blindly predicted and experimental folding free energies remains quite high (r = 0.956) (Fig. 3B), demonstrating that the linear heterogeneous model is indeed able to capture the stability of the deletion series. This correlation is significantly better than for the analogous jackknife analysis with the simple two-parameter linear model (r = 0.807) (data not shown), presumably because the substantial differences in the contribution of different repeats are taken into account in the heterogeneous model.

With the exception of ΔG°₄, each coefficient is negative (–2.2 kcal·mol^–1 on average), indicating that each repeat contributes favorably to stability (Fig. 3C). Because the coefficient associated with repeat 4 lacks an interfacial contribution, the difference between ΔG°₄ (+6.9 kcal·mol^–1, an intrinsic stability) and the other coefficients (containing both intrinsic and interfacial terms) should be related to the average stabilization afforded by each interface (–9.1 kcal·mol^–1). This picture suggests that individual repeats are very unstable, and that stability in tandemly repeated ankyrin clusters is provided by highly favorable interactions at interfaces between repeats. Single-repeat instability is likely to result from a significant loss in chain entropy on structure formation, combined with exposure of the unpaired nonpolar interface regions to solvent. This distribution of stability between individual repeats and their interfaces is qualitatively similar to the picture provided by the two-parameter linear regression (Fig. 2B), in which adding terminal repeats (and associated interfaces) decrease folding free energy by ≈2 kcal·mol^–1 per repeat, but the folding free energy of isolated repeats is large and positive (≈5.5 kcal·mol^–1).

High Cooperativity from Nearest-Neighbor Interactions. Stabilization of intrinsically unstable individual repeats through favorable interface interactions qualitatively explains how folding of the Notch ankyrin domain can be a highly cooperative two-state process, yet stability can be captured by using a linear model, which assumes that nonneighboring repeats are independent of one another. To determine whether the difference between measured intrinsic and interfacial free energy values (+6.9 and –9.1 kcal·mol^–1, respectively) is quantitatively large enough to produce an all-or-none folding transition, we used a simple 1D Ising model to represent the populations of all of the possible fully and partly folded conformations for a repeat protein with the same length (seven repeats) and stability parameters as the Notch ankyrin domain. In this model, we treat single repeats as monomer units that undergo individual conformational transitions. Stabilities of single repeats and interfacial interactions between repeats were represented with the equilibrium constants κ = exp(–6.9/RT) and τ = exp(9.1/RT), respectively. With the 1D Ising model, the fully folded and fully unfolded conformations comprise the dominant conformations at all urea concentrations (Fig. 4A). Partly folded conformations are predicted to be populated a maximum of ≈15%, which occurs in the unfolding transition region, with nearly all of the partly folded conformations (≈13%) containing six of seven folded repeats (Fig. 4B). Thus, this modeling demonstrates that nearest-neighbor interactions of the magnitude measured here for the Notch ankyrin domain, coupled with strongly unfavorable intrinsic stabilities, are sufficient to produce a highly cooperative folding transition.

Fig. 4.

A 1D Ising model captures equilibrium two-state unfolding of the Notch ankyrin domain. (A) The fully folded (solid line), partly folded (dashed line), and fully denatured (dotted line) conformations account for most (>85%) of the polypeptide chains. (B) Although partly folded conformations (defined as chains that are neither fully folded nor fully unfolded) are populated to ≈15% in the transition, the majority (13% of the total conformations) is made up of conformations that contain six of seven folded repeats (solid line with circles), with partly folded conformations containing fewer than six folded repeats populated to ≈2% (dashed line with X's).

The Energy Landscape of the Notch Ankyrin Domain. With the linear heterogeneous model and the experimentally determined free energy coefficients, we can estimate the free energies of folding of all contiguous partly folded conformations that contain a folded fourth repeat. These energies can be represented as a surface or free energy landscape, in which different partly folded conformations are arranged by the number of folded repeats on one axis, and the localization of folded structure (toward the N terminus or C terminus) on the other axis (Fig. 5A, gray-shaded surface). The vertical displacement and color of each partly folded conformation, each of which is depicted as a horizontal square, represents the folding free energy relative to the fully unfolded ensemble (at zero free energy).

Fig. 5.

Equilibrium energy landscape for the Notch ankyrin domain. Free energies were calculated from the linear heterogeneous model with experimentally determined coefficients. Free energies of each partly folded conformation are represented by the height along the vertical axis and by color. The denatured ensemble is presented as a flat tier (aqua) at a free energy of 0. Shown are the views from the native side (A) and the opposite side (B) showing the denatured ensemble and the early barrier. The diagonal surfaces connecting neighboring conformations are meant to aid the eye but do not represent the energetics of partial folding of single repeats. Diagonal surfaces connecting partly folded conformations that contain a folded fourth repeat are represented with gray shading; those connecting conformations lacking a folded fourth repeat are unshaded. This figure was prepared with mathematica (Wolfram Research, Champaign, IL).

One of the assumptions that is made in drawing this surface is that the unstructured regions of partly folded conformations do not interact in an energetically significant way with the structured regions. If this assumption is incorrect, energies determined from all-or-none unfolding reactions of deletion constructs (which are used to determine energy values at different points on the landscape) will differ from values for partly folded conformations of the full-length protein. Although testing this assumption for every partly folded conformation is not possible, there are a few comparisons we can make that test this assumption. Specifically, for destabilized constructs in which the folding of one or two terminal repeats is disrupted under native conditions (18, 19), urea-induced unfolding transitions match those of deletion constructs that include only the structured region (19, 25). Results from these constructs provide a few specific examples where the unstructured and structured regions do not appear to interact thermodynamically.

The requirement that the fourth repeat must be folded to predict folding free energy centers the landscape on this repeat and, when fewer than four repeats are folded (less than half of the molecule), this requirement limits the conformations that we can represent in the landscape. This requirement can be relaxed if we make the assumption that each interface contributes the same amount to folding free energy (–9.1 kcal·mol^–1). This expansion of the landscape has the advantage that it depicts a narrowing as folding progresses, similar to a funnel. As with theoretical energy landscapes that are depicted as “folding funnels” (2–4), this progressive narrowing represents a decreased conformational multiplicity and, thus, a decreased entropy as folding progresses.

Our experimentally determined energy landscape differs from most depictions of folding funnels in that a substantial early energy barrier separates the denatured ensemble from the rest of our landscape (Fig. 5B). Atop this barrier, i.e., at the tiers containing one and two folded repeats, there are significant differences in stability between different conformations. In particular, the two single-repeat structures composed of folded repeats 2 and 5 have low energies, especially compared with structures with single-repeat structures involving repeats 1 and 6,∥ suggesting that these low-energy points may initiate preferred routes for folding. The heterogeneity with which different repeats contribute to stability continues to influence the energy landscape at all levels of structure formation (Fig. 5A), carving low-energy channels that connect the denatured ensemble with the native state. For the repeat-4-centered landscape (Fig. 5A, gray-shaded surface), the low-energy channel that connects the denatured state ensemble to the native conformation involves the sequence 4 → 45 → 345 → 2345 → 12345 → 123456 → native. For the expanded landscape, pathways of low energy can be identified from each single-repeat minimum. For the repeat-2 and repeat-5 minima, the two low-energy channels converge to a four-repeat conformation in which folding spans the two entry points, i.e., 2345. Thus, these two folding channels would produce early structure in the central portion of the ankyrin domain. For the other single-repeat energy minimum (repeat 7 at the single-repeat tier), subsequent folded conformations (which involve folding of the sixth repeat) are relatively high in energy. Thus, this C-terminal side of the landscape lacks a low-energy channel and seems less likely to contribute significantly to folding if the rate-limiting steps involve formation of structure past the single repeat level.

Although the low-energy routes on the surface defined by the equilibrium studies here look like attractive paths for folding, these routes need not correspond to major channels for flux during kinetic refolding, partly because our equilibrium landscape lacks information about the barriers connecting the partly folded conformations. However, kinetic refolding studies that probe the degree to which different regions of the Notch ankyrin domain influence the folding rate can be used to establish this connection. Two predictions of the landscape, that the rate-limiting steps in folding should involve only the central repeats and that these steps should be early in folding, are borne out in studies of the folding kinetics of the deletion constructs depicted in Fig. 2. Although destabilizing, deletion of repeats 6 and 7 have no effect on refolding kinetics (unpublished data) as predicted by the energy landscape. The same is true for constructs that delete repeat 1. In contrast, constructs that delete repeat 2 significantly slow refolding, as do single-residue substitutions in the internal repeats, especially repeats 4 and 5 (C. M. Bradley and D.B., unpublished data). Thus, the low-energy channels in the equilibrium energy landscape, which initiate at repeats 2 and 5 and converge at the 2345 substructure, appear to be followed kinetically.