Alternatives for logistic regression in cross-sectional studies: an empirical comparison of models that directly estimate the prevalence ratio

Abstract

Background

Cross-sectional studies with binary outcomes analyzed by logistic regression are frequent in the epidemiological literature. However, the odds ratio can importantly overestimate the prevalence ratio, the measure of choice in these studies. Also, controlling for confounding is not equivalent for the two measures. In this paper we explore alternatives for modeling data of such studies with techniques that directly estimate the prevalence ratio.

Methods

We compared Cox regression with constant time at risk, Poisson regression and log-binomial regression against the standard Mantel-Haenszel estimators. Models with robust variance estimators in Cox and Poisson regressions and variance corrected by the scale parameter in Poisson regression were also evaluated.

Results

Three outcomes, from a cross-sectional study carried out in Pelotas, Brazil, with different levels of prevalence were explored: weight-for-age deficit (4%), asthma (31%) and mother in a paid job (52%). Unadjusted Cox/Poisson regression and Poisson regression with scale parameter adjusted by deviance performed worst in terms of interval estimates. Poisson regression with scale parameter adjusted by χ² showed variable performance depending on the outcome prevalence. Cox/Poisson regression with robust variance, and log-binomial regression performed equally well when the model was correctly specified.

Conclusions

Cox or Poisson regression with robust variance and log-binomial regression provide correct estimates and are a better alternative for the analysis of cross-sectional studies with binary outcomes than logistic regression, since the prevalence ratio is more interpretable and easier to communicate to non-specialists than the odds ratio. However, precautions are needed to avoid estimation problems in specific situations.

Background

Epidemiologic studies found in the literature are frequently cross-sectional, as this is a simple, fast and inexpensive design alternative. Often the outcomes are binary, and logistic regression is used for the analysis. This results in the odds ratio being frequently reported in situations where incidence or prevalence ratios are estimable, despite the fact that it is "biologically interpretable only insofar as it estimates the incidence-proportion or incidence-density ratio" [1].

From a survey done by the authors in the International Journal of Epidemiology and in the Revista de Saúde Pública (São Paulo, Brazil) published in 1998, 221 original articles were found. Among these, 110 (50%) were based on cross-sectional studies, and 45 (20%) on longitudinal studies. Logistic regression was used for the analysis of 37 (34%) and 10 (22%) of these studies, respectively. We have, therefore, that an important proportion of such studies end up reporting odds ratios, the effect measure yielded by logistic regression, rather than prevalence or incidence ratios.

The use of odds ratios is absolutely correct. There is nothing intrinsically wrong with them. But, when working with frequent outcomes, what is common in cross-sectional studies, the odds ratio can strongly overestimate the prevalence ratio. Here resides the most common mistake associated with odds ratios in our experience: the authors "forget" what their measure of association is and make interpretations such as "the exposed group has a risk of illness four times greater than the non-exposed group". The relative risk interpretation given to the odds ratio can be misleading, in theoretical and practical terms, especially if used for definition of policy priorities in conjunction with other true relative risks [1-4].

Additionally, logistic regression is often used for the sake of control of confounding and adjustment of interactions. But confounding and interaction are dependent on the measure of effect, so that controlling for confounding for the odds ratio is not the same thing as doing so for the prevalence ratio [5,6]. Therefore, interpreting the odds ratio as if it were a prevalence ratio is inadequate not only in terms of the possible overestimation, but also because confounding may not be appropriately controlled.

Several alternatives have been discussed in the literature for the analysis of binary outcomes in cross-sectional (or longitudinal) studies using the prevalence ratio rather than the odds ratio. The simplest way is to transform the odds ratios obtained by logistic regression into prevalence ratios [7-9]. Another possibility is to use a statistical model that estimates directly the prevalence ratio and its confidence interval. Alternatives explored in the epidemiological literature are Cox regression with equal times of follow-up assigned to all individuals [10], log-binomial regression (a generalized linear model with a logarithmic link function and binomial distribution for the residual) [7,11-13], Poisson regression [13] and complementary log-log model, where the link function is log(- log(1 - π)) and the distribution is binomial [13,14].

The authors that contributed to the discussion have not reached a conclusion on which would be the best approach, and only three publications make some comparison among available alternatives [4,13,15]. Possible fixes for the problems related to confidence intervals in some of the techniques proposed were dealt with to some extent by one of the papers [13], where the conclusion is that "there are no valid reasons for the systematic choice of odds ratio and of the logistic regression model to estimate prevalence rate ratios unless the type of study imperatively requires their use."

We have applied, in the context of a cross-sectional study, log-binomial regression, Cox regression, and Poisson regression. Corrections for the standard errors were included for Cox and Poisson regressions. Also, to increase the applicability of the results, a confounder was always included in the scenarios studied, which involved outcomes of varying prevalences. The point and interval estimates obtained with each approach were compared to the standard Mantel-Haenszel-like prevalence ratios and confidence interval estimators.

Methods

Using Cox regression to analyze a binary outcome in a cross-sectional study was suggested by Lee & Chia [10], and assessed by others [4,15]. Usually, Cox regression is used to analyze time-to-event data, that is, the response is the time an individual takes to present the outcome of interest. Individuals that never get ill are assigned the total length of time of the follow-up, and are treated as censored, meaning that it is not known when they will get ill, but at least until the time of the end of the follow-up they are well. Individuals lost to follow-up are treated in a similar way. Cox regression estimates the hazard rate function that expresses how the hazard rate depends upon a set of covariates. The model formulation is

h(t) = h₀(t) exp(β₁z₁ + ... + β_kz_k )(1)

where h₀(t) is the base hazard function of time, z_i are covariates and β_i, the coefficients for the k covariates. The Cox model treats h₀(t) as a nuisance function and actually does not estimate it [16].

When a constant risk period is assigned to everyone in the cohort, the hazard rate ratio estimated by Cox regression equals the cumulative incidence ratio in longitudinal studies, or the prevalence ratio in cross-sectional studies [17,18]. Although this model can produce correct point estimates, the underlying distribution of the response is Poisson. As prevalence data in a cross-sectional study follow a binomial distribution, the variance of the coefficients tends to be overestimated, resulting in wider confidence intervals compared to those based on the binomial distribution. This is easily explained by comparing the binomial variance, p(1-p), with a maximum of 0,25 when p = 0,5 with Poisson variance, λ, that grows steadily with the intensity of the process. That is, the variance estimated by the Poisson model will be very close to the binomial variance when the outcome is rare, but will be increasingly greater as the outcome becomes more frequent. In such a situation we have underdispersion, the opposite to the more commonly observed overdispersion, where the data is more dispersed than the model predicts.

It is possible to improve the situation using the robust variance estimates proposed by Lin & Wei [19], similar to other robust sandwich estimators proposed for parametric models, such as Huber's sandwich estimator [20]. In this paper, Cox regression with equal follow-up times was assessed, with standard and robust variance estimates.

Poisson regression is commonly used in epidemiology to analyze longitudinal studies where the outcome is a count of episodes of an illness occurring over time (e.g. episodes of diarrhea). The model formulation is

where n is the count of events for a given individual, t the time it was followed-up, and X_i the covariates. The model parameters (β_i) are log relative risks. In this context, Poisson regression is equivalent to Cox regression [21], and the parameters estimated are the same.

As described for Cox regression, the prevalence ratio is directly estimated by the model, and the confidence intervals are wider than those provided by a binomial model. A simple remedy is to multiply the estimated Poisson variance by some estimate of underdispersion (or overdispersion). These estimates can be based on the deviance or the chi-square of the model, dividing these quantities by the residual degrees of freedom [22,23]. In practice, this ratio is used as a scale parameter, replacing the original Poisson value of 1. A robust variance estimate is also available for the Poisson model, based on the Huber sandwich estimate [20] (which again yields results that are equal to Cox regression with robust variance). This alternative is known to underestimate the true variability with moderately sized samples, while adjusting the scale parameter tends to overestimate it. Other alternatives would be jackknife and bootstrap variance estimates [23]. We decided not to use the latter alternatives as they are not directly available in standard statistical software. Thus, Poisson regression was used in this paper with unadjusted variances, with scale parameter adjustment for both deviance and chi-square statistics, and with robust variance estimates.

The last model assessed was the log-binomial model [15] – a generalized linear model where the link function is the logarithm of the proportion under study and the distribution of the error is binomial [4,7,11,12,15]. The measure of effect in this model is also the relative risk.

For k covariates the model is written as

log(π) = β₀ +β₁X₁ + ... + β_kX_k (3)

where π is the probability of success (e. g., the proportion of sick persons in a group), and X_i the covariates. The relative risk estimate of a given covariate is e^β.

Since log(π) must be in the interval -∞ to 0, restrictions in the estimation process have to be used to avoid predicting probabilities out of the [0,1] interval. When estimates are on the boundaries of the valid parameter space, the estimates of the Newton-Raphson method will not converge to the maximum likelihood estimates [24]. Convergence problems in the estimation process are most likely to happen when the model contains a continuous covariate or multiple politomic covariates, or the outcome prevalence is high [12,24]. When the estimates are not on the boundary of the parameter space, convergence problems may still happen, and better starting values for the estimation process than the default used by the software will help. Most log-binomial models fitted in this paper used the default Stata estimation options, without convergence problems. In one case, when the model failed to converge, the "search" option, which makes the procedure search for a better starting value, was used [25].

The results obtained from the various models were compared to the pooled Mantel-Haenszel-like prevalence ratios (MHPR) and corresponding confidence intervals, used here as the reference results. Mantel-Haenszel estimates are easy to obtain in simple situations such as the ones dealt with in this work (one exposure and one confounder). However, for more complex situations, their estimation is more complicated and the use of statistical models is more efficient.

All the analyses were performed with Stata 7.0 [25], and the actual command lines used are listed below. Each outcome-exposure-confounder combination was represented by one row in the dataset and its frequency given by the variable freq.

*** M-H relative risk

cs ill exposed [fweight = freq], by(confounder)

*** Poisson regression unadjusted

poisson ill exposed confounder [fweight = freq], irr

*** Poisson regression adjusted by chi-squared

glm ill exposed confounder [fweight = freq], family(poisson) scale(x2) eform

*** Poisson regression adjusted by deviance

glm ill exposed confounder [fweight = freq], family(poisson) scale(dev) eform irls

*** Poisson regression with robust variance

poisson ill exposed confounder [fweight = freq], irr r

*** Log-binomial regression

glm ill exposed confounder [fweight = freq], family(binomial) link(log) eform

*** Odds ratio from logistic regression

logistic ill exposed confounder [fweight = freq]

For the comparison of the above techniques, real data from a population-based survey were used. A birth cohort was initiated in 1993, including all births happening in Pelotas, Southern Brazil [26]. These children were seen at birth, and their mothers interviewed. At 1 and 3 months of age, a sub-sample of 655 were sought for follow-up information. At 6 and 12 months, a larger sub-sample (including the 655 seen at 1 and 3 months) was sought, that comprised all children born with low birthweight and 20% of the remaining children. At these points, 1363 children were sought. The data used in this work came from another visit done between November 1997 and April 1998, when the children were 4–5 years-old. The children sought were the same as those in the 12-month revisit, and 1273 (93%) were actually interviewed. From the 90 children lost to follow-up, 61 (68%) had moved to other towns, 18 (20%) could not be found, 6 (7%) had died, and 5 (6%) refused to participate. The children were submitted to a nutritional assessment (weight and height) and their mothers answered a standardized pre-coded questionnaire including information on socioeconomic, demographic, reproductive, and health characteristics.

Three outcomes with different prevalences were used in the analyses, each in conjunction with a risk factor and a confounding factor, in a way to form 3 distinct situations. The three sets of variables used respectively as outcome, risk factor and confounder were: situation 1 – underweight (weight for age Z-score < -2), previous hospitalization and birth weight; situation 2 – asthma (asthma or bronchitis reported by the person responsible for the child in study), whether mother smoked and social class; situation 3 – status of maternal employment (whether or not in a paid job), father living with the family and social class. All variables were made dichotomous in order to simplify the comparisons and understanding of the models.

In order to widen the scenarios available, each set of variables was manipulated to increase the level of confounding. This was achieved by arbitrary changes in the prevalences of the risk and confounding factors, re-weighting the relevant strata in the data in a way to keep the sample size constant. The original and manipulated data are fully presented in the results section.

Confounding was measured by the proportional change from the crude prevalence ratio to the adjusted (Mantel-Haenszel) prevalence ratio using the expression 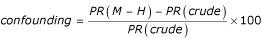, so that whenever the adjusted prevalence ratio was smaller than the crude, confounding was negative.

Results

Underweight was the least common outcome studied, with a prevalence of 4.1%. Asthma (prevalence = 31.2%), was intermediate and mother in a paid job was the commonest (prevalence = 51.4%). In the modified situation 1, underweight prevalence was increased in the low birth weight group from 7.8% to 10.4%, changing confounding from -14 to -18%. The overall prevalence of underweight changed to 4.9% (Tables 1 and 2). In situation 2, the prevalence of asthma was reduced from 22.7% to 12.7% in the upper class and increased from 38.1% to 52.1% in the lower class. Confounding changed from -8% to -17%. Overall asthma prevalence changed from 31.2% to 34.3% (Tables 3 and 4). In situation 3, confounding was increased by changing both the prevalences of the exposure and the outcome, achieving an increase from 4% to 25%. This was the only situation where the test for heterogeneity of prevalence ratios across strata was significant, indicating an interaction (Tables 5 and 6).

Table 1.

Absolute frequencies, outcome prevalences, exposure prevalences, crude and pooled prevalence ratio (PR) estimates, and relative confounding for the analysis of the original data using underweight (weight for age Z-score < -2) as the outcome, previous hospitalization as the risk factor and low birth weight as confounder (situation 1 original).

First stratum: Normal birth weight
	Underweight		Normal	All
	N	Prev.	N	N	Exp. prev. = 19.2%
Ever in hospital	8	4.7%	163	171	PR = 2.40
Never	14	1.9%	704	718	M-H weight = 2.69
All	22	2.5%	867	889
Second stratum: Low birth weight
	Underweight		Normal	All
	N	Prev.	N	N	Exp. prev. = 31.1%
Ever in hospital	16	13.4%	103	119	PR = 2.54
Never	14	5.3%	250	264	M-H weight = 4.35
All	30	7.8%	353	383
Combined strata: Normal and low birth weight
	Underweight		Normal	All	Exp. prev. = 22.8%
	N	Prev.	N	N	PR (crude) = 2.90
Ever in hospital	24	8.3%	266	290	PR (M-H) = 2.48
Never	28	2.9%	954	982	Confounding = -14.4%
All	52	4.1%	1220	1272	P-value(het)*= 0.9

* P-value for testing heterogeneity of the prevalence ratios across strata.

Table 2.

Absolute frequencies, outcome prevalences, exposure prevalences, crude and pooled prevalence ratio (PR) estimates, and relative confounding for the analysis of the modified data using underweight (weight for age Z-score < - 2) as the outcome, previous hospitalization as the risk factor and low birth weight as confounder (situation 1 modified).

First stratum: Normal birth weight
	Underweight		Normal	All
	N	Prev.	N	N	Exp. prev. = 19.2%
Ever in hospital	8	4.7%	163	171	PR = 2.40
Never	14	1.9%	704	718	M-H weight = 2.69
All	22	2.5%	867	889
Second stratum: Low birth weight
	Underweight		Normal	All
	N	Prev.	N	N	Exp. prev. = 31.1%
Ever in hospital	22	18.5%	97	119	PR = 2.71
Never	18	6.8%	246	264	M-H weight = 5.59
All	40	10.4%	343	383
Combined strata: Normal and low birth weight
	Underweight		Normal	All	Exp. prev. = 22.8%
	N	Prev.	N	N	PR (crude) = 3.17
Ever in hospital	30	10.3%	260	290	PR (M-H) = 2.61
Never	32	3.3%	950	982	Confounding = -17.8%
All	62	4.9%	1210	1272	P-value(het)*= 0.8

* P-value for testing heterogeneity of the prevalence ratios across strata.

Table 3.

Absolute frequencies, outcome prevalences, exposure prevalences, crude and pooled prevalence ratio (PR) estimates, and relative confounding for the analysis of the original data using asthma as the outcome, maternal smoking as the risk factor and social class as confounder (situation 2 original).

First stratum: High social class
	Asthma		No	All
	N	Prev.	N	N	Exp. prev. = 26.6%
Mother smokes	37	25.7%	107	144	PR = 1.19
No	86	21.6%	312	398	M-H weight = 22.85
All	123	22.7%	419	542
Second stratum: Low social class
	Asthma		No	All
	N	Prev.	N	N	Exp. prev. = 43.3%
Mother smokes	122	42.8%	163	285	PR = 1.24
No	129	34.6%	244	373	M-H weight = 55.87
All	251	38.1%	407	658
Combined strata: High and low social class
	Asthma		No	All	Exp. prev. = 35.8%
	N	Prev.	N	N	PR (crude) = 1.33
Mother smokes	159	37.1%	270	429	PR (M-H) = 1.22
No	215	27.9%	556	771	Confounding = -7.9%
All	374	31.2%	826	1200	P-value(het)*= 0.8

* P-value for testing heterogeneity of the prevalence ratios across strata.

Table 4.

Absolute frequencies, outcome prevalences, exposure prevalences, crude and pooled prevalence ratio (PR) estimates, and relative confounding for the analysis of the modified data using asthma as the outcome, maternal smoking as the risk factor and social class as confounder (situation 2 modified).

First stratum: High social class
	Asthma		No	All
	N	Prev.	N	N	Exp. prev. = 26.6%
Mother smokes	21	14.6%	123	144	PR = 1.21
No	48	12.1%	350	398	M-H weight = 12.75
All	69	12.7%	473	542
Second stratum: Low social class
	Asthma		No	All
	N	Prev.	N	N	Exp. prev. = 43.3%
Mother smokes	194	68.1%	91	285	PR = 1.70
No	149	39.9%	224	373	M-H weight = 64.54
All	343	52.1%	315	658
Combined strata: High and low social class
	Asthma		No	All	Exp. prev. = 35.8%
	N	Prev.	N	N	PR (crude) = 1.96
Mother smokes	215	50.1%	214	429	PR (M-H) = 1.62
No	197	25.6%	574	771	Confounding = -17.3%
All	412	34.3%	788	1200	P-value(het)*= 0.2

* P-value for testing heterogeneity of the prevalence ratios across strata.

Table 5.

Absolute frequencies, outcome prevalences, exposure prevalences, crude and pooled prevalence ratio (PR) estimates, and relative confounding for the analysis of the original data using mother in a paid job as the outcome, father living with the family as the risk factor and social class as confounder (situation 3 original).

First stratum: High social class
	Mother employed		No	All
	N	Prev.	N	N	Prev. exp. = 15.3%
Father Present	66	79.5%	17	83	PR = 1.46
No	250	54.5%	209	459	M-H weight = 38.28
All	316	58.3%	226	542
Second stratum: Low social class
	Mother employed		No	All
	N	Prev.	N	N	Prev. exp. = 24.0%
Father present	112	70.9%	46	158	PR = 1.88
No	189	37.8%	311	500	M-H weight = 45.38
All	301	45.7%	357	658
Combined strata: High and low social class
	Mother employed		No	All	Prev. exp. = 20.1%
	N	Prev.	N	N	PR (crude) = 1.61
Father present	178	73.9%	63	241	PR (M-H) = 1.69
No	439	45.8%	520	959	Confounding = 4.4%
All	617	51.4%	583	1200	P-value(het) *= 0.01

* P-value for testing heterogeneity of the prevalence ratios across strata.

Table 6.

Absolute frequencies, outcome prevalences, exposure prevalences, crude and pooled prevalence ratio (PR) estimates, and relative confounding for the analysis of the modified data using mother in a paid job as the outcome, father living with the family as the risk factor and social class as confounder (situation 3 modified).

First stratum: High social class
	Mother employed		No	All
	N	Prev.	N	N	Prev. exp. = 15.0%
Father Present	73	90.1%	8	81	PR = 1.80
No	230	50.0%	230	460	M-H weight = 34.44
All	303	56.0%	238	541
Second stratum: Low social class
	Mother employed		No	All
	N	Prev.	N	N	Prev. exp.= 80.0%
Father Present	295	56.0%	232	527	PR = 1.39
No	53	40.2%	79	132	M-H weight = 42.38
All	348	52.8%	311	659
Combined strata: High and low social class
	Mother employed		No	All	Prev. exp.= 50.7%
	N	Prev.	N	N	PR (crude) = 1.27
Father Present	368	60.5%	240	608	PR (M-H) = 1.58
No	283	47.8%	309	592	Confounding = 24.6%
All	651	54.3%	549	1200	P-value(het) *= 0.01

* P-value for testing heterogeneity of the prevalence ratios across strata.

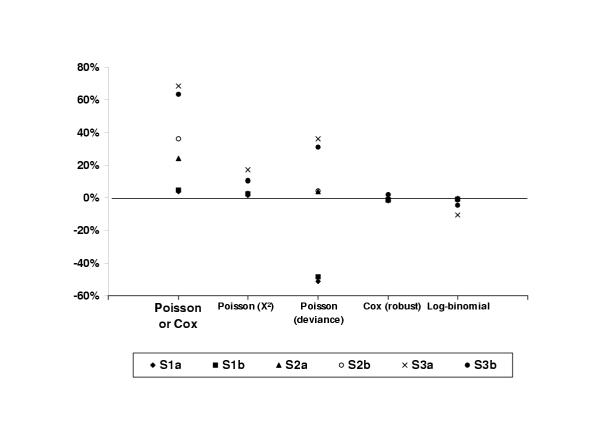
Comparing the results of the different models in situation 1 (Table 7), we see that the point estimates obtained with Cox, Poisson and log-binomial models are very close to the Mantel-Haenszel prevalence ratio (MHPR) for the original and modified data. In terms of the confidence intervals, the differences between Cox, Poisson and log-binomial models and the reference were less than 5%, except for Poisson scaled by deviance, where the CIs were approximately 50% narrower.

Table 7.

Comparison of prevalence ratios and respective confidence interval estimates (obtained by unadjusted Poisson/Cox regression, Poisson regression with scale factor adjusted by χ² and deviance, Poisson/Cox regression with robust variances, log-binomial regression and logistic regression) and odds ratio with confidence interval estimate (obtained by logistic regression) with the Mantel-Haenszel prevalence ratio in the analysis of the original and modified data using underweight (weight for age Z-score < -2) as the outcome, previous hospitalization as the risk factor and low birth weight as confounder (situation1).

Original data	Point estimate		95% Confidence interval
	value	% diff.	lower	upper	width	% diff.
PR Mantel-Haenszel	2.48	--	1.46	4.23	2.78	--
PR Poisson/Cox (unadj)	2.48	-0.2%	1.43	4.31	2.88	3.6%
PR Poisson (χ2)	2.48	-0.2%	1.44	4.26	2.82	1.5%
PR Poisson (deviance)	2.48	-0.2%	1.89	3.25	1.36	-51.1%
PR Poisson/Cox (robust)	2.48	-0.2%	1.46	4.22	2.76	-0.6%
PR log-binomial	2.48	-0.1%	1.46	4.22	2.77	-0.4%
OR logistic regression	2.64	6.3%	1.49	4.68	3.18	14.6%
Modified data	Point estimate		95% Confidence interval
	value	% diff.	lower	upper	width	% diff.
PR Mantel-Haenszel	2.61	--	1.61	4.23	2.61	--
PR Poisson/Cox (unadj)	2.60	-0.4%	1.57	4.30	2.73	4.6%
PR Poisson (χ2)	2.60	-0.4%	1.59	4.26	2.67	2.4%
PR Poisson (deviance)	2.60	-0.4%	2.01	3.36	1.35	-48.3%
PR Poisson/Cox (robust)	2.60	-0.4%	1.61	4.19	2.58	-1.2%
PR log-binomial	2.61	-0.1%	1.61	4.21	2.60	-0.7%
OR logistic regression	2.85	9.3%	1.68	4.84	3.15	20.7%

Situation 2 (Table 8) was similar to situation 1 in terms of point estimates. Confidence intervals were strongly overestimated by unadjusted Cox/Poisson models. In the modified data, the 95%CI was overestimated by 11% by Poisson regression with scale parameter adjusted by χ².

Table 8.

Comparison of prevalence ratios and respective confidence interval estimates (obtained by unadjusted Poisson/Cox regression, Poisson regression with scale factor adjusted by χ² and deviance, Poisson/Cox regression with robust variances, log-binomial regression and logistic regression) and odds ratio with confidence interval estimate (obtained by logistic regression) with the Mantel-Haenszel prevalence ratio in the analysis of the original and modified data using asthma as the outcome, maternal smoking as the risk factor and social class as confounder (situation 2).

Original data	Point estimate		95% Confidence interval
	value	% diff.	lower	upper	width	% diff.
PR Mantel-Haenszel	1.22	--	1.03	1.45	0.41	--
PR Poisson/Cox (unadj)	1.22	0.0%	0.99	1.51	0.51	23.9%
PR Poisson (χ2)	1.22	0.0%	1.03	1.45	0.42	2.7%
PR Poisson (deviance)	1.22	0.0%	1.03	1.46	0.43	3.9%
PR Poisson/Cox (robust)	1.22	0.0%	1.03	1.45	0.41	-0.2%
PR log-binomial	1.23	0.1%	1.04	1.45	0.41	-0.4%
OR logistic regression	1.36	11.0%	1.05	1.76	0.71	70.9%
Modified data	Point estimate		95% Confidence interval
	value	% diff.	lower	upper	width	% diff.
PR Mantel-Haenszel	1.62	--	1.41	1.87	0.47	--
PR Poisson/Cox (unadj)	1.62	-0.4%	1.33	1.96	0.63	36.0%
PR Poisson (χ2)	1.62	-0.4%	1.38	1.90	0.52	10.9%
PR Poisson (deviance)	1.62	-0.4%	1.39	1.88	0.49	4.3%
PR Poisson/Cox (robust)	1.62	-0.4%	1.40	1.86	0.46	-2.0%
PR log-binomial	1.65	1.7%	1.44	1.90	0.46	-1.5%
OR logistic regression	2.49	53.5%	1.90	3.27	1.37	193.1%

In situation 3 (Table 9), the outcome prevalence was highest, and there was a significant interaction between risk factor and confounder. Ignoring the interaction (i. e. using a misspecified model), the log-binomial model performed slightly worse than the Cox and Poisson models in relation to the point estimates. The latter presented a maximum difference of 2% compared to the MHPR, while the log-binomial estimates were up to 8.7% greater. In terms of interval estimates, only the Cox/Poisson models with robust variance presented differences less than 5% for both the original and modified data. An interaction term was included in the robust Poisson and log-binomial regressions. In the original situation, identical results (up to the third decimal place) were obtained from both models, matching the stratum-specific relative risks and confidence intervals. However, in the modified situation, the log-binomial model did not converge, while the robust Poisson model again reproduced the stratum-specific estimates. A common reason for non-convergence is inappropriate starting values for model parameters. Stata's option "search", which specifies that the command "glm" should search for good starting values, solved the problem and, with this option, the results obtained from the log-binomial model were again virtually identical to Poisson regression.

Table 9.

Comparison of prevalence ratios and respective confidence interval estimates (obtained by unadjusted Poisson/Cox regression, Poisson regression with scale factor adjusted by χ² and deviance, Poisson/Cox regression with robust variances, log-binomial regression and logistic regression) and odds ratio with confidence interval estimate (obtained by logistic regression) with the Mantel-Haenszel prevalence ratio in the analysis of the original and modified data using mother in a paid job as the outcome, father living with the family as the risk factor and social class as confounder (situation3).

Original data	Point estimate		95% Confidence interval
	value	% diff.	lower	upper	width	% diff.
PR Mantel-Haenszel	1.69	--	1.52	1.87	0.35	--
PR Poisson/Cox (unadj)	1.68	-0.3%	1.41	2.00	0.59	68.6%
PR Poisson (χ2)	1.68	-0.3%	1.49	1.90	0.41	17.2%
PR Poisson (deviance)	1.68	-0.3%	1.46	1.94	0.48	35.9%
PR Poisson/Cox (robust)	1.68	-0.3%	1.52	1.86	0.35	-1.5%
PR log-binomial	1.62	-4.0%	1.47	1.78	0.32	-10.4%
OR logistic regression	3.75	122.6%	2.72	5.17	2.45	597.6%
Modified data	Point estimate		95% Confidence interval
	value	% diff.	lower	upper	width	% diff.
PR Mantel-Haenszel	1.58	--	1.39	1.79	0.40	--
PR Poisson/Cox (unadj)	1.61	2.0%	1.31	1.97	0.66	63.2%
PR Poisson (χ2)	1.61	2.0%	1.40	1.85	0.45	10.3%
PR Poisson (deviance)	1.61	2.0%	1.37	1.89	0.53	31.0%
PR Poisson/Cox (robust)	1.61	2.0%	1.42	1.83	0.41	2.1%
PR log-binomial	1.71	8.7%	1.53	1.92	0.39	-4.7%
OR logistic regression	2.97	88.1%	2.14	4.11	1.96	385.9%

A graphical summary of the results concerning the interval estimates is shown in Figure 1. It is clear from the figure that robust Poisson/Cox regression and log-binomial regression are the best performers, consistently producing the confidence intervals with amplitude closest to the reference. In third place, but with some confidence intervals nearly 20% wider than the reference, ranked Poisson regression with the scale parameter adjusted by χ².

Figure 1.

Comparison of the relative differences between the 95% confidence intervals obtained by unadjusted Poisson/Cox regression, Poisson regression with scale factor adjusted by χ² and deviance, Poisson/Cox regression with robust variances and log-binomial regression and the Cornfield 95% confidence interval for each of the six situations studied. S1a (outcome prevalence / confounding): 4.1% / 14%; S1B: 4.9% / 18%; S2a: 31.2% / 8%; S2b: 34% / 17%; S3a: 51% / 4%; S3b: 54% / 25%.

Discussion

The literature on the different alternatives to analyze cross-sectional or longitudinal data using prevalence (or cumulative incidence) ratios instead of odd ratios has not yet proposed a strategy that produces both point and interval acceptable estimates. To our knowledge this is the first paper to focus on different strategies and compare them to a suitable reference in terms of the prevalence ratios and confidence intervals obtained.

We have shown that there are several alternatives available that will provide very good results in terms of point estimates: Cox, Poisson and log-binomial regression. The case of interval estimates is more complicated, as some models will overestimate or underestimate them, in different situations. Even so, we are still left with three viable alternatives: log-binomial regression, Cox/Poisson regression with robust variance, and Poisson regression with scale parameter adjusted by χ².

One limitation of this work is not having dealt with continuous covariates. The main reason was the reference used. The Mantel-Haenszel techniques work for categorical variables only. Furthermore, most epidemiological analyses involve only categorical variables. The main problem with this omission is that continuous variables are a potential cause for model misbehavior, that is, the log-binomial model not converging, and the Poisson model producing estimates of individual probabilities greater than 1. This situation happens when the estimates are on the boundary of the parameter space, and is illustrated with the artificial data presented by Deddens in a paper where a simple strategy, the COPY method, was proposed to achieve convergence when fitting log-binomial models in such a case [27].

The log-binomial regression, used without any correction to the standard errors, presented results that were equivalent to those yielded by robust Poisson/Cox regression in situations 1 and 2. In situation 3, where an interaction was ignored, the model tended to present confidence intervals that were too narrow (up to 10.4%) compared to the reference, and slightly different point estimates. This situation was included in this exercise to present a scenario with a misspecified model, situation that is bound to happen in reported analyses, as failing to look for or correctly identifying interactions is not infrequent. When the correct model (including the interaction) was fitted, the results were again equivalent to those yielded by the reference and robust Poisson/Cox regression in the original data. In the modified data the model failed to converge, what was solved by using better starting values for the estimation procedure. In situations where the estimates are on the boundary of the parameter space the model will not converge, unless a strategy such as the COPY method is used [27].

Cox regression has been suggested as an alternative to logistic regression but the problems with the variance estimates were not dealt with [4,10,15]. As expected, we showed that confidence intervals can be strongly overestimated (up to 69% in our examples using real data). The use of robust variance estimates [19], as we proposed, improved variance estimation considerably, limiting the difference relative to the reference confidence interval to less than 3% in the studied examples. Poisson regression, as mentioned before, works similarly, and has the advantage over Cox regression of using a command syntax similar to linear and logistic regressions in Stata.

The use of Poisson regression offers still other alternatives by means of changing the scale parameter to correct the standard errors when over or underdispersion is observed [22]. In the set of situations we presented, correction by the Pearson χ² was superior to correction by the deviance, and, although not as good as robust estimates, represented a considerable improvement in relation to the uncorrected standard errors. The maximum observed difference relative to the reference confidence intervals was17%. Poisson regression, however, can also present problems when the estimates are on the boundaries of the parameter space, as mentioned above. It is strongly advisable that the individual probabilities are calculated (Stata's "predict" command will do that) and examined.

We have used the robust Poisson model in the analysis of several epidemiological studies, three of which have been already published [28-30]. In all cases we have used the same modeling strategy with logistic regression and robust Poisson regression. In these real situations the final sets of selected variables were the same, and the differences in model parameters within the expected between odds ratios and prevalence ratios. Until more experience is gathered, this may be a useful strategy to help identify anomalous results with robust Poisson regression, along with assessing the predicted individual probabilities.

The rapid and continuous evolution of statistical software means that most packages will perform at least one of the analyses that performed best in this exercise. Stata 7.0, used here, and widely employed in epidemiology research groups, can perform them all. It was not possible for us to assess other packages in terms of what they can do, and how to do it, as software like SPSS, SAS, S-Plus, among others, were not available to us.

Conclusions

We have shown that the use of Cox or Poisson regression without any adjustment for the analysis of cross-sectional data, as suggested sometimes in the literature, may lead to large errors in interval estimates. On the other hand, taken the precautions discussed in the paper, the log-binomial model and the Cox or Poisson models with adjusted variances provide correct point and interval estimates. It is, therefore, not only possible, but actually easy to use other models than logistic regression to analyze cross-sectional (or longitudinal) data with binary outcomes, the advantage being the prevalence (or cumulative incidence) ratio as the measure of association, more interpretable and easier to communicate, especially to non-epidemiologists. It is for the analyst to choose among these methods, based on software availability and the analyst's training.

Competing interests

None declared.

Author's contributions

AB proposed the idea, carried out part of the literature review and modeling, and drafted the manuscript. VH carried out most of the literature review, analyses, and prepared the tables and figures.

Pre-publication history

The pre-publication history for this paper can be accessed here:

http://www.biomedcentral.com/1471-2288/3/21/prepub