MRI‐based computational hemodynamics in patients with aortic coarctation using the lattice Boltzmann methods: Clinical validation study

Abstract

Purpose

To introduce a scheme based on a recent technique in computational hemodynamics, known as the lattice Boltzmann methods (LBM), to noninvasively measure pressure gradients in patients with a coarctation of the aorta (CoA). To provide evidence on the accuracy of the proposed scheme, the computed pressure drop values are compared against those obtained using the reference standard method of catheterization.

Materials and Methods

Pre‐ and posttreatment LBM‐based pressure gradients for 12 patients with CoA were simulated for the time point of peak systole using the open source library OpenLB. Four‐dimensional (4D) flow‐sensitive phase‐contrast MRI at 1.5 Tesla was used to acquire flow and to setup the simulation. The vascular geometry was reconstructed using 3D whole‐heart MRI. Patients underwent pre‐ and postinterventional pressure catheterization as a reference standard.

Results

There is a significant linear correlation between the pretreatment catheter pressure drops and those computed based on the LBM simulation, $r=.85$, $P<.001$. The bias was ‐0.58 ± 4.1 mmHg and was not significant ( $P=0.64)$ with a 95% confidence interval (CI) of ‐3.22 to 2.06. For the posttreatment results, the bias was larger and at ‐2.54 ± 3.53 mmHg with a 95% CI of ‐0.17 to ‐4.91 mmHg.

Conclusion

The results indicate a reasonable agreement between the simulation results and the catheter measurements. LBM‐based computational hemodynamics can be considered as an alternative to more traditional computational fluid dynamics schemes for noninvasive pressure calculations and can assist in diagnosis and therapy planning.

Level of Evidence: 3

J. Magn. Reson. Imaging 2017;45:139–146.

Coarctation (or narrowing) of the aorta (CoA) is a congenital heart disease and accounts for 3–11% of all birth heart defects.1 The narrowing usually occurs distal to the carotids and its severity degree is variable. CoA causes upper‐body hypertension and lower‐body hypotension.2 Clinical guidelines recommend treatment by surgery, stent placement, or by balloon angioplasty.3

To evaluate the severity of the coarctation either preoperatively or postoperatively, the hemodynamic analysis is usually performed through measuring the pressure gradient across the coarctation site by means of an invasive and expensive cardiac catheterization.4 However, with developments in combining noninvasive MRI with modeling schemes, numerical simulations of hemodynamics could assist in diagnosis.5, 6 Recently, three‐dimensional spatial encoding combined with three‐directional phase‐contrast MRI (4D flow [PC] MRI) has drawn increased attention.7 Four‐dimensional (4D) flow MRI offers the ability to measure and to visualize the temporal evolution of complex blood flow patterns within an acquired 3D volume. These 4D flow MRI along with anatomical images can be used to extract hemodynamic and wall boundary conditions respectively, when performing patient‐specific computational fluid dynamics (CFD) simulations. In this regard, several authors used similar techniques to simulate patient‐specific hemodynamics.8 We further add that based on imaging techniques such as Doppler ultra sound and flow MRI, pressure computation schemes have been suggested.9, 10, 11 However, pressure gradients obtained from Doppler ultra sound suffer from overestimation and those based on flow MRI tend to underestimate pressure drop values.

In conventional computational studies, CFD schemes are based on Navier‐Stokes equations and are performed on body‐fitted volume meshes. In this work, however, our hemodynamics computation is based on an approach known as the lattice Boltzmann methods (LBM).12 The LBM is a relatively new development in CFD and even newer in the field of blood flow simulation.13, 14, 15, 16 They are easy and straightforward to implement, benefit from an automated and efficient mesh preprocessing, and due to their local operations, are an ideal candidate for a highly scalable parallelization.17 These promising features motivated us to use LBM as the method of choice for the purposes of this work.

Previously, Henn et al investigated a patient‐specific blood flow simulation using the lattice Boltzmann methods for one coarctation case and showed how realistic pressure values can be obtained when sufficient spatial and temporal resolutions are used.18 In this work, the aim was to demonstrate the fidelity of LBM for treatment planning through considering a versatile coarctation patient cohort and preliminary validation against catheter measurements.

Materials and Methods

Patient Data

The data include 12 patients (5 males, 7 females), all with clinical indication for catheterization, with the age ranging from 14 to 62 years, and mean and standard deviation of 26 ± 15 years. Patients were first scanned for 3D whole‐heart (WH) and 4D flow MRI. Then catheterization and pressure measurements were performed. The averaged time lapse between MRI acquisition and the catheterization procedure was 4 days (range between 1 day and 4 weeks). Table 1 provides the heart rates and pressure measurements of these 12 cases during the MRI acquisition and catheterization. Except for cases 6, 7, and 11 (Fig. 1) with native coarctation, the remaining cases were due to recoarctation. All CoAs were treated by an implantation of a bare Cheatham platinum (CP) stent premounted on a BIB (balloon in balloon) catheter (NuMED, Nicholville, NY), except case 9, which was treated by balloon angioplasty and case 4, which was not treated as the catheterization‐based pressure drop (<20 mmHg) together with an analysis of the anatomy (stenosis degree) and other parameters (e.g., hypertension) did not assign this patient to the treatment group according to the clinical guidelines. The study was approved by the institutional Research Ethics Committee, following the ethical guidelines of the 1975 declaration of Helsinki. Written informed consent was obtained from the participants and their guardians, where applicable.

Table 1.

Heart Rates and Pressure Measurements for CoA Cases^a

	MRI			Cath
Case	HR	Psys	Pdia	HR	Psys	Pdia
1	65	140	60	66	113	65
2	88	136	58	77	129	74
3	65	146	66	66	95	54
4	96	128	62	84	120	82
5	75	128	62	76	122	74
6	62	140	75	65	126	65
7	65	158	83	61	149	73
8	68	140	55	54	111	53
9	80	128	62	74	111	69
10	85	153	72	70	114	70
11	75	118	63	81	110	66
12	74	196	88	78	144	73

^aHeart rates (HR) and pressure measurements (in mmHg) during MRI and catheterization (Cath). Psys is the systolic pressure, and Pdia is the pressure at diastole. For the MRI acquisitions, cuff pressures are reported.

Figure 1.

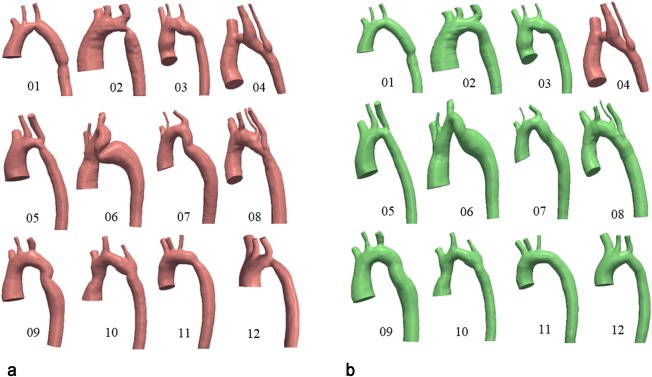
a: Pretreatment coarctation geometries. b: Posttreatment geometries. Case 4 was not treated. Treatment was performed through a stenting procedure to expand the narrowed region in the aortic arch.

MRI

MRI was done with a whole‐body 1.5 Tesla MR scanner Achieva R 3.2.2.0 using a five‐element cardiac phased‐array coil (Philips Medical System, Best, Netherlands). Anatomy of the aorta was acquired by a navigator‐triggered 3D WH MRI sequence in end diastole. The sequence parameters were: field of view (FOV) 212 × 212 × 121 mm, matrix size 320 × 320, 76 slices, acquired voxel 0.66 × 0.66 × 3.2 mm, reconstructed voxel 0.66 × 0.66 × 1.6 mm, repetition time (TR) 4.0 ms, echo time (TE) 2.0 ms, flip angle (FA) 90 °, and number of signal averages 3. The scan time was ∼8 min.

The 4D flow MRI of thorax was performed using an anisotropic 4D segmented k‐space phase contrast gradient echo sequence with retrospective electrocardiographic gating but without navigator gating of respiratory motion to minimize acquisition time. The sequence parameters were: FOV 180 × 216 × 75 mm, matrix size 100 × 128, 30 slices, acquired voxel 2.5 × 2.5 × 2.5 mm, reconstructed voxel 1.7 × 1.7 × 2.5 mm, TR 3.5 ms, TE 2.2 ms, FA 5 °, 25 reconstructed cardiac phases, velocity encoding 4.0 m/s, and number of signal averages 1. Scan time varied between 9 and 14 min, depending on the size of the patient's chest. The high velocity encoding in all three directions was used to avoid phase wraps in the presence of stenosis forming complex 3D flow.

Segmentation, Flow Analysis, and Posttreatment Geometry Reconstruction

Segmentation of the aorta was performed on the 3D WH images using level set methods similar to Goubergrits et al.19 Figure 1a depicts the 12 preoperative geometries used in this work.

The 4D flow MRI was analyzed using the MEVISFlow software (Fraunhofer MEVIS, Bremen, Germany). After the routine preprocessing of the PC MRI data including phase‐offset error correction and antialiasing, the extracted anatomy was fused with the flow data. For this purpose, first a PC MR angiography (PC MRA) image was computed and then coregistered with the anatomy image. As both anatomy and flow measurements were acquired in the same session using gated imaging sequences, only small perturbations occurred between the two which could be accounted for using rigid registration techniques.20 Based on this fusion, the necessary flow information required for CFD modeling could be extracted. More specifically, flow rate curves in the ascending aorta just above the sinotubular junction and in the descending aorta are computed. Figure 2 demonstrates this processing pipeline.

Figure 2.

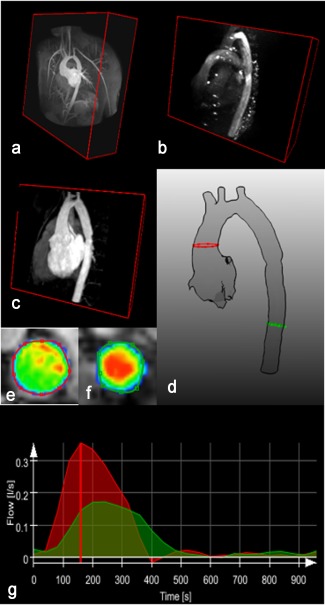
Extraction of flow rate curves at the inlet (red contour) and outlet (green contour) of the aorta geometry for simulation setup. a: The 3D WH MRI (anatomy). b: PC MR angiography (PC MRA). c: Anatomy after alignment with PC MRA through registration. d: The segmented geometry. e,f: Represent the magnitude of the velocity. g: Red: inlet flowrate curve. Green: outlet flowrate curve. The flow is distributed into the branches by subtracting the inlet and outlet flow rate at the time point of peak systole (red vertical line).

The posttreatment corresponding geometries can be seen in Figure 1b. Posttreatment MRI anatomy data were not available for this patient cohort; therefore, the treated geometry was reconstructed using projection image data acquired during catheterization similar to Goubergrits et al.8 These images provide an accurate (0.1 mm resolution) measurement of the posttreatment diameters.

Hemodynamic Computation with the Lattice Boltzmann Methods

The proposed hemodynamic modeling scheme in this work is based on the lattice Boltzmann methods. Rather than relying on the classical Navier‐Stokes equations as in conventional CFD solvers, LBM is a special finite‐difference discretization of the simplified Boltzmann equation from kinetic theory, which describes transport phenomena in a mesoscopic scale. Quantities of interest, such as velocity $u\left(x,t\right)$ and pressure $p\left(x,t\right)$, where $x$ is a point in space and $t$ represents time, are computed indirectly through simulating the dynamics of particle distributions. Fundamental to an LBM is a uniform lattice which defines the possible paths that fictitious particles are allowed to take. Central to the scheme are the streaming and collision operations. For instance, in a three‐dimensional implementation, a typical scenario is shown in Figure 3 where particles can stream in 19 different paths (the so‐called D3Q19 LBM scheme). Collision can be viewed as relaxation toward local equilibrium which should satisfy conservation of mass, momentum, and energy.

Figure 3.

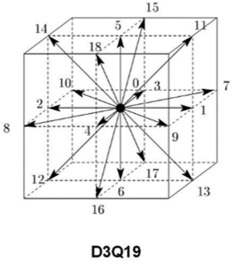
Lattice configuration D3Q19 in three dimensions with 19 discrete velocity directions.

In one time step, particles can move along the lattice only in the given lattice directions. The distribution functions $f_i\left(x,t\right)$ are defined at each grid point $x$ and time $t$ and represent the likelihood of particles moving along the certain directions $i.$ The LBM iteration with Bhatnagar‐Gross‐Krook (BGK) collision operator is

$$f_i\left(x+e_i\delta x, t+\delta t\right)-f_i\left(x, t\right)=-\frac{1}{\tau }\left(f_i\left(x,t\right)-f_i^{eq}\left(u,\rho \right)\right)$$ (1)

where $\left\{e_i\right\}$ are the set of discrete lattice direction vectors defining a local neighborhood of a grid point.21 $\delta x$ and $\delta t$ are the lattice spacing and time step. $\tau$ is a relaxation parameter and is $\tau =\nu /c_s^2+\frac{1}{2}$ with $\nu$ the kinematic viscosity and $c_s$ being the lattice speed of sound. $f_i^{eq}$ is the equilibrium distribution function and is a low Mach number approximation to the Maxwellian distribution defined as,

$$f_i^{eq}\left(u,\rho \right)= {\omega }_i\rho \left(1+3e_i.u+ \frac{9}{2}{\left(e_i.u\right)}^2-\frac{3}{2}{u}^2\right)$$ (2)

where ${\omega }_i$ are weight factors that can be found in literature.22 The hydrodynamic density $\rho$, and the macroscopic velocity $u$ are determined from the particle distribution functions using the laws of conservation of mass and momentum, $\rho =\sum _i{f}_i$ and $\rho u=\sum _i{f}_i{e}_i$, and the pressure is given by $p=\rho c_s^2$. The LBM reproduce the results of the Navier‐Stokes equations in the nearly incompressible limit and is second‐order accurate for the velocity and first‐order accurate for the pressure distributions in the body of the fluid.23

Simulation Setup

The computational domain, in our case the aorta, was divided into a uniform lattice. Additionally, it was further divided into blocks that were processed by separate processors for parallelization purposes. Figure 4 demonstrates a LB‐based discretization. A velocity boundary condition as given by Bouzidi et al with a Poiseuille flow profile based on the measured flow volume at the ascending aorta opening as shown in Figure 2 was used.24 A smooth startup phase was added to suppress undesired pressure fluctuations. Due to the limited resolution of the 4D flow MRI, the flow rates at the side branches are prone to noise and could not be extracted with enough accuracy. Therefore, the difference between flow rates in the ascending and descending aorta was distributed between side branches of the aortic arch according to their cross sectional area. The boundary condition at the descending aorta was set as a stress‐free condition, i.e., the pressure is fixed to zero. Moreover, a no‐slip (velocity zero) Bouzidi boundary condition was considered at the walls. The same boundary conditions are applied to the posttreatment geometries.

Figure 4.

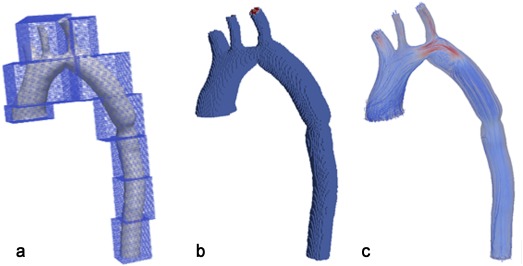
Lattice Boltzmann voxelization for a patient‐specific aorta geometry. a: Blocks are for parallelization and are distributed between processors. Each block normally contains between 1000 to 10,000 grid cells. b: The boundaries are fitted by taking the exact distances along the 19 paths from each voxel which is inside the computational domain and close to the wall. c: Streamline visualization of the simulated velocity.

As for the blood, it is assumed to be Newtonian with a density of $1000 kg/m^3$ and a kinematic viscosity of $0.004\times {10}^{-3} m^2/s$. In addition, a D3Q19 BGK‐LBM, supported by a Smagorinsky turbulence model with constant 0.12 was applied to account for the relatively coarse spatial resolution.25 The simulations are done using the open source lattice Boltzmann library OpenLB (www.openlb.net). A fixed spatial resolution of $0.001\times 0.001\times {0.001}_m$ was used in all the cases and the computation times were on average around 30 min for each case on Intel Core i7‐2600k CPU @ 3.4 GHz. Computations were done using 4 cores and no hyperthreading.

Simulation Outcome and Pressure Computation

At the end of the simulation, a velocity vector field was generated corresponding to the time point of peak systole. This velocity field was then used to compute the pressure field using the pressure Poisson equation (PPE) as described in Krittian et al and Meier et al.10, 11 As can be noticed, we did not use the pressure values computed directly from the LB simulation. Henn et al demonstrated that a very high spatial resolution is required to get pressure values compared with the reference measured values.18 In our work, however, as we are adhering to a fixed spatial resolution for efficiency purposes, we rely on the higher order of convergence of the velocity field in LBM and use this for pressure field computations using the PPE.

Statistical Analysis

The statistical analysis in this work was carried out using Excel data analysis toolbox and are expressed as mean ± standard deviation (SD). Effects were considered significant at $P$ < 0.05. Normality tests using normal probability plots was performed to ensure the normal distribution of the data. The Pearson's correlation coefficient was used to compute the linear relation between the measurement and computed results. The agreement between the values was investigated using Bland‐Altman plots.26 The difference between the methods was analyzed using a paired t‐test for comparing the means of the samples and the suitable sample size was determined using a power analysis with the following parameters: two‐tails α = .05, power = 1‐β = .8, effect size =  $\frac{means difference}{SD}$=1.08. In computing the effect size, a 5 mmHg difference in means between measurement techniques was assumed with a SD of pressure drops measured with catheter at 4.6 mmHg. Based on these values, the required sample size for this study was 9 patients.

Results

The mean flow rate at the inlet (ascending aorta) was 389 ± 111 mL/s which corresponds to a mean Reynolds number of 5299 ± 1675 for a mean diameter of 26.4 ± 5.18 mm. The mean flow rate at the outlet (descending aorta) was 192 ± 58 mL/s. A statistical analysis of pressure and heart rate data shown in Table 1 found no significant differences for heart rates during MRI acquisition and catheterization (71.9 ± 12.8 versus 68.5 ± 10.5 bpm; P = 0.112), diastolic pressure (66.7 ± 12.4 versus 62.1 ± 12.3 mmHg; P = 0.366), and mean aortic pressure (95.5 ± 12.9 versus 89.5 ± 10.9 mmHg; P = 0.129). The peak systolic pressure acquired during MRI was, however, significantly higher than the one measured by the catheterization (143.9 ± 19.8 versus 112.8 ± 14.6 mmHg; P = 0.001). A comparison of the pre‐ and posttreatment pressure drops between the catheter measurements and LBM‐based computations are provided in Table 2.

Table 2.

Pre‐ and Posttreatment Pressure Drops^a

Case	Cath Pre	Cath Post	LBM Pre	LBM Post
01	25	9	21	7
02	30	1	35	1
03	25	5	30	3
04	11	–	9	–
05	15	2	14	5
06	18	3	11	4
07	15	0	23	7
08	16	0	16	0
09	11	0	12	4
10	15	1	15	5
11	17	0	16	9
12	12	0	15	4

^aAscending‐descending aorta pressure drops (mmHg) computed for the cases in Figure 1 using catheter (Cath) and lattice Boltzmann methods (LBM), respectively.

Considering the pretreatment results, the mean pressure drop measured by catheter was 17.5 ± 6 mmHg and computed based on the LBM was 18 ± 7.8 mmHg. Figure 5a demonstrates the agreement between pressure gradients using a Bland‐Altman plot. There is a significant relationship between the pretreatment catheter pressure drops and those computed based on the LBM simulation, $r\left(10\right)=.85$, $P < 0.001$. The bias in Figure 5a is ‐0.58 ± 4.1 mmHg with a 95% confidence interval (CI) of ‐3.22 to 2.06 mmHg based on a t‐distribution with 11 degrees of freedom. The lower and upper limits of agreement are ‐8.7 (95% CI: ‐13.45–‐3.94) and 7.5 (95% CI: 2.75–12.25) mmHg correspondingly. The paired t‐test indicated no significant difference between the pretreatment catheter and LBM pressure drop values $(P=0.64$).

Figure 5.

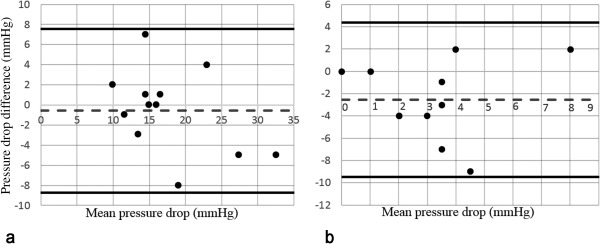
Bland‐Altman plots demonstrating the agreement between pressure gradients measured by catheter and LBM. a: pretreatment. b: posttreatment. Reference lines are mean and ± 1.96 × SD.

Regarding the posttreatment results, the mean pressure drop measured by catheter was 1.9 ± 2.84 mmHg and computed based on the LBM was 4.45 ± 2.62 mmHg. As can be noticed, treatment resulted in a reduced pressure drop computed by means of LBM for all the cases. The agreement between pressure gradients is demonstrated in Figure 5b. The bias is ‐2.54 ± 3.53 mmHg with a 95% CI of ‐0.17 to ‐4.91 mmHg based on a t‐distribution with 10 degrees of freedom. Based on the paired t‐test, $P=0.04$, indicating a difference between the sample means and, therefore, rejecting the null hypothesis. The lower and upper limits of agreement are ‐9.46 (95% CI: ‐13.34–‐5.58) and 4.37 (95% CI: 0.49–8.25) mmHg, respectively.

Discussion

In this study, MRI flow and anatomy data was used in a CFD scheme based on the lattice Boltzmann methods to estimate pressure gradient values in patients with a coarctation of the aorta. LBM has been used in a wide range of geometries in medical applications and a few studies have also reported on the agreement between LBM and Finite‐element‐based CFD.27, 28

Given the results in the previous section, we observed that the bias between the pretreatment catheter and LBM pressure gradient values was small. On the other hand, we noticed that the bias was much larger in the posttreatment results, but with a comparable standard deviation to pretreatment findings. For the posttreatment LBM values, case 7 and 11 produced the highest differences comparing to the catheter measurements. It is not immediately clear to the authors why these cases have resulted in higher pressure drops compared with their catheter counterparts and more investigation is required. If we, however, remove these two outliers, the bias will reduce to ‐1.33 ± 2.5 mmHg.

When comparing the modelling results with the clinical reference values, we should also take into account the sources of uncertainty and discrepancies in measurement and simulation during the whole processing pipeline. In our study, these can, among others, be generally related to (1) catheter measurements, (2) MRI postprocessing, and (3) simulation setup.

For this work, catheter measurements and the MRI acquisitions were performed sequentially and some days apart in sedated and awake patients, respectively. Comparing the heart rate and the mean pressure, there was no statistically significant difference between MRI and catheterization, however, the peak systolic pressure in MRI was significantly higher. We note that the difference in systemic pressure does not automatically mean a difference in the flow rate and subsequently in the pressure drop. Nonetheless, further investigation needs to be performed to analyze the impact of MRI‐based boundary setup on the discrepancies between simulation results and catheter measurements. Moreover, in clinical routines, systolic pressure drops are reported as peak‐to‐peak gradients, even though this nonphysiological difference might result in inaccuracies.29 Here, we simulated the pressure gradient along the vessel centerline and only at the time point of peak systole. Riesenkampff et al used a dynamic pressure calibration technique based on the catheter data to compare peak‐to‐peak pressure gradients based on catheterization and 4D flow MRI.30 A similar approach can be performed using a time‐harmonic simulation to gain more insight on the discrepancies between the methods. This is the subject of future research. We, moreover, note that the locations in the ascending and descending aorta chosen for the pressure drop calculation, corresponded only roughly to those measured by catheter.

In case of MRI data postprocessing, there is a level of uncertainty when constructing the 3D posttreatment geometry based on 2D angiography data, which ultimately contributes to the differences between the postinterventional simulation and catheterization pressure gradients. Moreover, uncertainties manifest themselves when extracting flow rates for a vessel cross‐section based on the 4D flow MRI data, which in turn affects the accuracy of the simulation outcome.31

Considering the LBM simulation, its relatively easy setup makes it an attractive alternative to traditional solvers. However, modeling blood flow in larger vessels with LBM involves a challenging set of constraints. Among these, accurate open and wall boundary conditions suited to the application area and the geometry under investigation is still an active topic of research.32, 33, 34 For this work, we adhered to a somewhat classic way of imposing boundary conditions, that is, velocity Poiseuille at the inlet, pressure zero at the outlet, and a second order no‐slip at the wall boundaries. The aim was to keep the computational effort as low as possible to examine the suitability of LBM for clinical applications. In this regard, more investigations should be done to study the effect of MRI‐based inflow on an LBM simulation, similar to Goubergrits et al.19 Additionally, for the posttreatment cases there was no flow information available and, therefore, the same boundary conditions used in pretreatment geometries, were applied. In future studies, MRI measurements after intervention should also be included.

Considering the limitations in this study, we note that the patient data for this work was obtained from one clinical site. A multicenter study should be carried on to examine the impact of different MR scanners and protocols on the robustness and accuracy of the results. Moreover, we only had access to 12 CoA patients with the required imaging data. The statistical analysis can certainly benefit from a larger patient cohort. Furthermore, one disease model was considered here. The merits of the LBM for pressure computation should be further investigated through its application to a diverse range of medical problems.

In conclusion, despite the aforementioned uncertainties, we demonstrated the accuracy of the lattice Boltzmann methods for pressure drop calculations in coarctation patients. Our findings are comparable to those obtained by Goubergrits et al using a traditional CFD approach.8 Both pre‐ and posttreatment results indicated a reasonable agreement with catheter measurements. In case of CoA, stenting is a recommended therapy to reduce the pressure gradients across the narrowed vessel segment.35 However, as we mentioned earlier, this procedure is associated with several complications. Recently Neugebauer et al, developed a virtual stenting tool that enables an interactive placement of stents into the narrowed aortic region.36 Combining this with an LBM‐based flow simulation, provides a means for a computer‐aided treatment planning and predicting possible hemodynamic alterations. Our first validation study in this work, provides evidence on the applicability of such tools in clinical settings.