Abstract
A perfect ultra-narrow band infrared metamaterial absorber based on the all-metal-grating structure is proposed. The absorber presents a perfect absorption efficiency of over 98% with an ultra-narrow bandwidth of 0.66 nm at normal incidence. This high efficient absorption is contributed to the surface plasmon resonance. Moreover, the surface plasmon resonance-induced strong surface electric field enhancement is favorable for application in biosensing system. When operated as a plasmonic refractive index sensor, the ultra-narrow band absorber has a wavelength sensitivity 2400 nm/RIU and an ultra-high figure of merit 3640, which are much better than those of most reported similar plasmonic sensors. Besides, we also comprehensively investigate the influences of structural parameters on the sensing properties. Due to the simplicity of its geometry structure and its easiness to be fabricated, the proposed high figure of merit and sensitivity sensor indicates a competitive candidate for applications in sensing or detecting fields.
Keywords: Metamaterials, Optical sensing and sensors, Surface plasmons, Absorption
Background
Recently, the plasmonic metamaterial absorbers based on the surface plasmon resonance (SPR) have attracted increasing attention due to their potential extensive applications in energy harvesting [1–3], hot-electron collection [4–7], thermal emitters [8–11], and biosensors [12–17]. Up to date, various plasmonic metamaterial absorbers have been proposed in different wavebands, which are mainly divided into two main categories: broadband absorbers and narrowband absorbers. As we all know, broadband absorbers are usually applied in solar energy harvesting and thermal emission, while narrowband absorbers are generally used in detectors and sensors.
It is generally known that the sensing performance are usually evaluated by wavelength sensitivity (S) and figure of merit (FOM), which are defined as S = Δλ/Δn and FOM = S/FWHM, respectively. Δλ is the variation of the resonance wavelength induced by the refractive index change Δn. The FWHM is the full width at half maximum of the absorption spectrum. For a plasmon sensor, the key parameter of high FOM means high sensitivity and high wavelength resolution. So far, numerous plasmonic refractive index sensors based on the various nanostructures have been reported, among them, the plasmonic refractive index sensors based on the narrowband absorbers have obtained significant progresses. However, the further applications of the previously published plasmonic sensors are still limited by their relatively complex geometries and low FOM value [18–35]. Zhengqi Liu et al. numerically investigated a sensor based on multispectral ultra-narrowband absorber. This sensor has a wavelength sensitivity exceeding 1000 nm/RIU and FOM of only 5 [25]. Liu et al. demonstrated theoretically a plasmonic sensor based on the plasmonic structure with network-type metasurface on the two-layer dielectric films, which have the FOM of 68.57 [26]. Using Au bowtie nanoantenna arrays with metal-insulator-metal configuration, Lin simulated numerically a sensor with the FOM of 254 [27]. With the efforts made by Luo, the relatively higher FOM of 1054 has been obtained via a metal-metal-dielectric-metal (MMDM) structure [28]. Lu proposed a metal nanobar array with nanoslits backed metal plate structure in theory, which has FOM reaching 25 [29]. Thus, it is desired to propose a simple plasmonic sensor with ultra-high FOM.
In this paper, we demonstrate a simple perfect infrared plasmonic metamaterial absorber based on the all-metal-grating structure [36–39]. Its absorption efficiency is over 98% at normal incidence. Operated as a plasmonic refractive index sensor, the structure has a high wavelength sensitivity 2400 nm/RIU and an ultra-narrow FWHM 0.66 nm. The FOM can reach to 3640, which is far higher than that of the similar published sensors [18–35]. Furthermore, we also investigate the sensing properties of the structure by scanning the structural parameters, such as the length and depth of two nanogrooves. In general, the proposed sensor is not only simple in geometry structure but also exhibits better sensing performance, which means great potential applications in biosensing and detecting areas.
Methods
Figure 1 illustrates the schematic of the designed all-metal-grating structure. The dimensional parameters are as follows: the periodic length of one unit cell along x-axis p, gold substrate thickness t 1, the shallow nanogroove width w, and height t 2, the deep nanogroove width l, and height t 3. The metal material is gold. In the near-infrared, the relative permittivity of gold can be well described by the Drude model ε m = ε ∞ − w p 2/[ω(ω + iγ)], where w p is the plasma frequency and its value is w p = 2π × 2175 THz. γ is the damping constant related to the electrons and its value is γ = 2π × 6.5 THz.
Fig. 1.
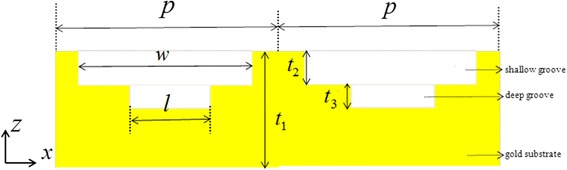
Schematic of the proposed metamaterial structure of a unit cell
The numerical simulation for the optical performance of the proposed structure is executed by using two-dimension finite-difference time-domain (FDTD) method. We set periodic boundary conditions in the x direction, and the incident plane wave is normal to the surface of the proposed structure with the electric field polarized along the x direction.
Results and Discussion
The transmission light is completely suppressed by the thicker gold substrate (T = 0), so the absorption can be defined as A = 1 − R (reflection). In Fig. 2a, the green and red lines, respectively, present the absorption and reflection spectra. The green line demonstrates that at the resonance wavelength 2403.15 nm, the peak absorption could exceed 98%. The FWHM of the proposed structure is only 0.66 nm, which is far narrower than that of the published narrowband absorbers [18–35]. The structure parameters are listed in the figure caption.
Fig. 2.
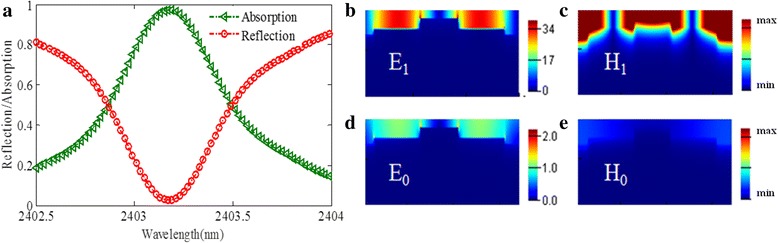
a Absorption and reflection spectra of the proposed sensor. Distributions of b the electric field E 1 and c the magnetic field H 1 at the resonant wavelength. Distributions of d the electric field E 0 and e the magnetic field H 0 at the nonresonant wavelength. Parameters: p = 1200 nm, w = 622 nm, l = 420 nm, t 1 = 328 nm, t 2 = 28 nm, and t 3 = 18 nm
To clearly explain the physical mechanism of ultra-narrow band light absorption of the all-metal-grating structure, we examine the distribution patterns of the electric field E1 and magnetic field H1 at the resonant wavelength 2403.15 nm, which are depicted in Fig. 2b, c, respectively. Besides, we also calculate and present the snapshots of the electric field distribution E0 and the magnetic field distribution H0 at the nonresonant wavelength 2423.31 nm for comparison. Note that enhanced field intensity on the surface of the proposed structure can be observed, which is due to the excitation of surface plasmon resonances (SPR). The electric field intensity at the resonant frequency is 40 times larger than that of the incident waves, which is a key point in biosensing applications.
As shown in Fig. 2b, c, the field distributions above the metal grating structure exhibits a slow attenuation, and only a small proportion of electromagnetic field penetrates into the metal grating, which implies a very small resistive rate. So the total damping rate under critical coupling condition is ultra-small, resulting in ultra-narrow band of the perfect absorber. To prove this, the absorption spectra are compared and analyzed among the structures, which are made of gold with different damping rates γ. As shown in Fig. 3, obviously, a decreased and broadened absorbance is observed as the damping rate of gold increases with the same geometrical parameters.
Fig. 3.
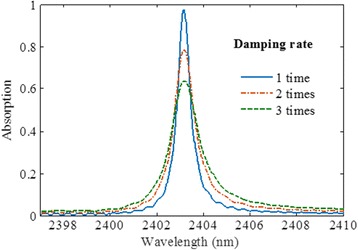
Simulated absorption spectra for damping constant of one, two, and three times that of gold
Properties and Performance
The proposed perfect absorber can be used as a sensor to detect the variation of refractive index of the surrounding dielectric environment, owing to its ultra-narrow bandwidth and ultra-low reflectivity dip. As is well known, the sensing properties are very closely related with the structure. In the following, we simulate numerically about the sensing properties, which include the resonance wavelength, the reflectivity dip, FWHM, and FOM by scanning the structural parameters such as the shallow nanogroove width w, height t 2, the deep nanogroove width l, and height t 3. In simulation, we assume that all variables other than the one under consideration are kept constant, and are listed in corroding the figure caption. In practical applications, it is necessary to detect the relative intensity change dI/dn at a fixed wavelength due to the refractive index change [18]. The corresponding figure of merit can be defined as FOM* = max |(dI/dn)/I| [20].
Figure 4a, b shows the reflection properties as functions of the shallow nanogroove height t 2. As t 2 changes from 8 to 48 nm, the resonance peak will blueshift. At the same time, the FWHM will become wider. When the shallow nanogroove height t 2 is interval of 30–40 nm, there is a minimum reflectivity dip. Based on the definition of FOM, the FOM will decrease as shown in Fig. 4c owing to the wider FWHM. The FOM* as function of t 2 is shown in Fig. 4c. The maximum value of FOM* can reach 1.83 × 106 with the t 2 of around 38 nm, which gives us a guide in designing of high-quality plasmonic refractive index sensor.
Fig. 4.
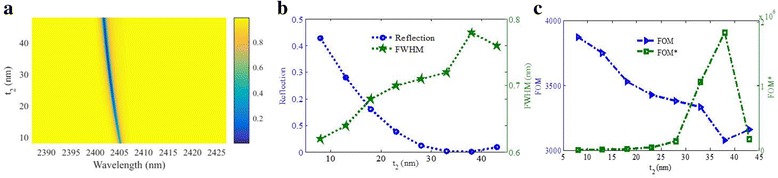
a Reflection spectra as a function of t 2. b Reflectivity of the resonance dip and its FWHM as functions of t 2. c FOM and FOM* as functions of t 2. Other parameters: p = 1200 nm, w = 622 nm, l = 420 nm, t 3 = 18 nm, and t 1 = 300 nm + t 2
The variational trend of the sensing properties with the increasing of t 3 is similar to that of t 2 except that the resonance wavelength exhibits redshift. And it is easy to observe that the FWHM is more influenced by t 3. The FOM decreases obviously and has a maximum value of 6315.8, which is much higher than that of the previously reported plasmonic refractive index sensor [18–35]. However, when the maximum FOM is obtained, the value of the reflectivity dip approaches 0.3, which is too high to be easily detected. Thus, we need to find a compromise method to obtain a higher FOM and lower reflectivity dip simultaneously.
Figure 6 presents the effects of the shallow nanogroove width w on the sensing performance. As shown in Fig. 6a, the resonance wavelength keeps nearly unchanged with changing of w. Figure 6b shows that when the w is 620 nm, the minimum values of the reflectivity dip and the FWHM can be simultaneously obtained, which is favorable to obtain the high-quality sensors. At the same time, the maximum FOM can reach to 3640 when the w is 620 nm.
Fig. 6.
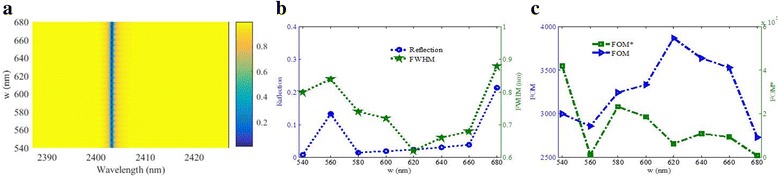
a Reflection spectra as a function of w. b Reflectivity of the resonance dip and its FWHM as functions of w. c FOM and FOM* as functions of w. Other parameters: p = 1200 nm, l = 420 nm, t 1 = 328 nm, t 2 = 28 nm, and t 3 = 18 nm
As shown in Fig. 7a, as the deep nanogroove width l increases from 340 to 500 nm; the resonance wavelength exhibits no-shift just as in Fig. 6a. According to Fig. 7b, the reflectivity dip will decrease, while the FWHM will increase as the increasing of l. The FWHM changes slightly and the reflectivity dip sustains an ultra-low value under 0.06, which are important to practical application due to its robustness. The maximum FOM exceeding 3871 can be obtained when l is 360 nm.
Fig. 7.
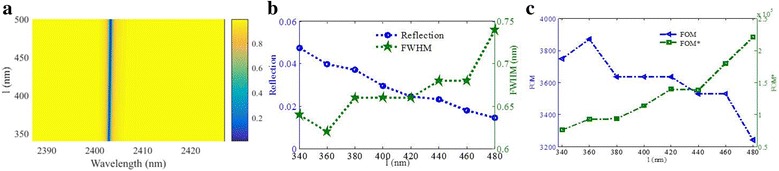
a Reflection spectra as a function of l. b Reflectivity of the resonance dip and its FWHM as functions of l. c FOM and FOM* as functions of l. Other parameters: p = 1200 nm, w = 622 nm, l = 420 nm, t 1 = 328 nm, t 2 = 28 nm, and t 3 = 18 nm
The resonance wavelength can be explained by the equivalent LC circuit model of the metamaterial structure [40–45]. The resonance wavelength can be given by . The gap capacitance C can be represented as C = ε 0 S/d, where ε 0 is the dielectric permittivity of the surrounding environment and S is the effective area of the capacitance. d is the effective width of the nanogrooves. The inductance of the gold substrate is expressed as L, which is inversely proportional to the volume of metallic bars. In the LC circuit model, we can qualitatively predict the effect of the structural parameters on the resonance wavelength.
As increasing of t 2, the effective area of the capacitance C will increase. However, the effective inductance L will decrease linearly with increasing of t 2, owing to the increase in volume of metallic bars, which will cause decreasing of resonance wavelength. In the designed structure, the shallow nanogroove w is much wider, which will result in the extremely slight effect of t 2 on the capacitance C. In other words, the increasing volume of metallic bars that induced variation of L perhaps have more influences on the position of the resonance frequency than that of the decreasing of effective area that induced the changing of C. Thus, the resonance wavelength will blueshift slightly with increasing t 2, which matches the simulated result in Fig. 4a quite well.
With the increasing of t 3, the C will be enhanced, which will increase the resonance wavelength of the SPR mode. At the same time, a larger t 3 will lead to a smaller volume of metallic bars, which will result in the increase of L. Considering the influences of the two parameters, the resonance wavelength will redshift slightly with increasing t 3. The qualitatively predicted results of the LC model and the simulated results (shown in Fig. 5a) are coincident.
Fig. 5.
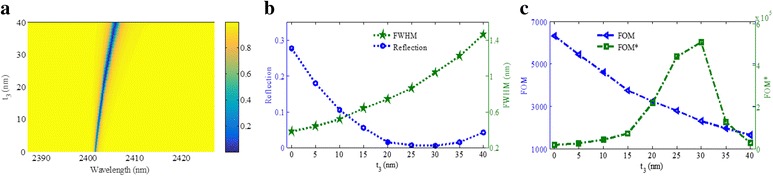
a Reflection spectra as a function of t 3. b Reflectivity of the resonance dip and its FWHM as functions of t 3. c FOM and FOM* as functions of t 3. Other parameters: p = 1200 nm, w = 622 nm, l = 420 nm, t 1 = 328 nm, and t 2 = 28 nm
The volume of the metal will decrease as in the increasing of w, which will cause larger L. Thus, the resonance wavelength will redshift. However, C will decrease linearly with the increasing of w, which will induce the blueshift of the resonance wavelength. The effects of the two parameters on the resonance wavelength can be counteracted. Thus, the position of the resonance keeps nearly unchanged, which is consistent with the simulation results shown in Fig. 6a. Similarly, as in the increasing of l, the resonance wavelength will change little shown in Fig. 7b. In practical application, this robustness is beneficial to structure design.
Based on the discussion above, in the following, we give a detailed analysis of the metamaterial structure as a refractive index sensor with various structure parameters. The structure parameters are shown in the caption of Fig. 8. We investigate the sensing properties of the absorber with various refractive index of the environment. According to Fig. 8a, the resonant wavelength will redshift as the surrounding refractive index varies from 1.000 to 1.010. At the same time, the reflectivity dip can sustain an ultra-low value. As shown in Fig. 8b, the proposed plasmonic refractive index sensor has a high linearity over a wide range of wavelength. For example, as the refractive index ranges from 1.00 (vacuum) to 1.06 with intervals of 0.02, the resonant wavelength is obtained at 2403.15, 2451.18, 2499.19, and 2547.18 nm, respectively. The slope of the fitting line represents the sensitivity (S) reaching 2400 nm/RIU. Meanwhile, the FWHM can be narrower than 0.66 nm. By the definition of FOM, the FOM of the proposed plasmonic sensor can reach up to 3640, which is much larger than that of the previously published similar sensors [18–35].
Fig. 8.
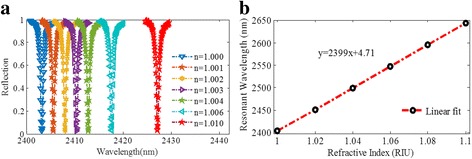
a Reflection spectra of the sensor with various refractive indexes of the environment. b Resonant wavelength shifts against the surrounding refractive index. Parameters: P = 1200 nm, w = 622 nm, l = 420 nm, t 1 = 328 nm, t 2 = 28 nm, and t 3 = 28 nm
Conclusions
In conclusion, we propose and demonstrate a perfect near-infrared plasmonic metamaterial absorber with a simple all-metal-grating structure by using a two-dimensional FDTD method. The structure shows that an ultra-narrow absorption bandwidth of 0.66 nm and the absorption efficiency over 98% are obtained. The high absorption with ultra-narrow bandwidth is mainly ascribed to the excitation of surface plasmon resonances and the ultra-small total damping rate under critical coupling condition. And the structure can obtain the giant surface electric field enhancement. Owing to its ultra-narrow bandwidth and ultra-low reflectivity dip, the absorber can be used as a sensor. We numerically investigate the effects of dimensional parameters on the properties of the sensor in detail. As a plasmonic refractive index sensor, the structure can present excellent performance with S of 2400 nm/RIU and FOM of 3640 in a wider spectral range. For its above-mentioned merits, especially the ultra-high S and ultra-high FOM, the plasmonic refractive index sensor with simple structure could provide a promising approach for gas detection, biosensors, and medical diagnostics.
Acknowledgements
This work was supported by the Ministry of Science and technology of China (Grant No. 2016YFA0301300), National Natural Science Foundation of China (Grants No. 61275201, No. 61372037, and No. 61671090), and Beijing Excellent Ph.D. Thesis Guidance Foundation (Grant No. 20131001301).
Authors’ contributions
RL, DW, and YL designed the study and analyzed the data. LY, ZY, and HY supervised the writing of the manuscript. All the authors have read and approved the final manuscript.
Competing Interests
The authors declare that they have no competing interests.
Abbreviations
- FDTD
Finite-difference time-domain
- FOM
Figure of merit
- FWHM
Full width at half maximum
- S
Sensitivity
- SPR
Surface plasmon resonance
Contributor Information
Ruifang Li, Email: liruifang@bupt.edu.cn.
Dong Wu, Email: dongwd@hotmail.com.
Yumin Liu, Email: microliuyumin@hotmail.com.
Li Yu, Email: bupt.yuli@gmail.com.
Zhongyuan Yu, Email: yuzhongyuan30@hotmail.com.
Han Ye, Email: dabombyh@aliyun.com.
References
- 1.Wang H, Sivan VP, Mitchell A, et al. Highly efficient selective metamaterial absorber for high-temperature solar thermal energy harvesting. Sol Energy Mater Sol Cells. 2014;137:235–242. doi: 10.1016/j.solmat.2015.02.019. [DOI] [Google Scholar]
- 2.Guo CF, Sun T, Cao F, et al. Metallic nanostructures for light trapping in energy-harvesting devices. Light Sci Appl. 2014;3(7):e161. [Google Scholar]
- 3.Bakir M, Karaaslan M, Dincer F. Perfect metamaterial absorber-based energy harvesting and sensor applications in the industrial, scientific, and medical band. Opt Eng. 2015;54(9):097102. doi: 10.1117/1.OE.54.9.097102. [DOI] [Google Scholar]
- 4.Auguié B, Barnes WL. Collective resonances in gold nanoparticle arrays. Phys Rev Lett. 2008;101(14):28–28. doi: 10.1103/PhysRevLett.101.143902. [DOI] [PubMed] [Google Scholar]
- 5.Clavero C. Plasmon-induced hot-electron generation at nanoparticle/metal-oxide interfaces for photovoltaic and photocatalytic devices. Nat Photonics. 2014;8(2):95–103. doi: 10.1038/nphoton.2013.238. [DOI] [Google Scholar]
- 6.Tang J, Xiao Z, Xu K, et al. Polarization-controlled metamaterial absorber with extremely bandwidth and wide incidence angle. Plasmonics. 2016;11(5):1–7. doi: 10.1007/s11468-016-0189-2. [DOI] [Google Scholar]
- 7.Chu Y, Schonbrun E, Yang T, et al. Experimental observation of narrow surface plasmon resonances in gold nanoparticle arrays. Appl Phys Lett. 2008;93(18):181108–181108-3. doi: 10.1063/1.3012365. [DOI] [Google Scholar]
- 8.Wang LP. Measurement of coherent thermal emission due to magnetic polaritons in subwavelength microstructures. J Heat Transfer. 2013;135(9):463–474. [Google Scholar]
- 9.Argyropoulos C, Le KQ, Mattiucci N, Aguanno GD, Alu A. Broadband absorbers and selective emitters based on plasmonic Brewster metasurfaces. Phys Rev B. 2013;87:205112. doi: 10.1103/PhysRevB.87.205112. [DOI] [Google Scholar]
- 10.Li Z, Butun S, Aydin K. Ultranarrow band absorbers based on surface lattice resonances in nanostructured metal surfaces. ACS Nano. 2014;8(8):8242–8. doi: 10.1021/nn502617t. [DOI] [PubMed] [Google Scholar]
- 11.Zoysa MD, Asano T, Mochizuki K, et al. Conversion of broadband to narrowband thermal emission through energy recycling. Nat Photonics. 2012;6(8):535–539. doi: 10.1038/nphoton.2012.146. [DOI] [Google Scholar]
- 12.Lu X, Wan R, Liu F, et al. High-sensitivity plasmonic sensor based on perfect absorber with metallic nanoring structures. J Mod Opt. 2016;9275:177–183. doi: 10.1080/09500340.2015.1066459. [DOI] [Google Scholar]
- 13.Wei W, Nong J, Zhang G et al (2014) An infrared biosensor based on graphene, plasmonic for integrated nanofluidic analysis. Proc SPIE. 9278
- 14.Guo Q, Zhu H, Liu F, et al. Silicon-on-glass graphene-functionalized leaky cavity mode nanophotonic biosensor. Acs Photonics. 2014;1(3):221–227. doi: 10.1021/ph400073w. [DOI] [Google Scholar]
- 15.Sabah C, Dincer F, Karaaslan M, et al. Biosensor applications of chiral metamaterials for marrowbone temperature sensing. J Electromagn Waves Appl. 2015;29(17):2393–2403. doi: 10.1080/09205071.2015.1084894. [DOI] [Google Scholar]
- 16.Yin S, Zhu J, Xu W, et al. High-performance terahertz wave absorbers made of silicon-based metamaterials. Appl Phys Lett. 2015;107(7):26. doi: 10.1063/1.4929151. [DOI] [Google Scholar]
- 17.Jia K, Zhang D, Ma J. Sensitivity of guided mode resonance filter-based biosensor in visible and near infrared ranges. Sensors Actuators B Chem. 2011;156(1):194–197. doi: 10.1016/j.snb.2011.04.013. [DOI] [Google Scholar]
- 18.Liu N, Mesch M, Weiss T, et al. Infrared perfect absorber and its application as plasmonic sensor. Nano Lett. 2010;10(7):2342–8. doi: 10.1021/nl9041033. [DOI] [PubMed] [Google Scholar]
- 19.Lu S, Li G, Lv Z, et al. Facile and ultrasensitive fluorescence sensor platform for tumor invasive biomaker β-glucuronidase detection and inhibitor evaluation with carbon quantum dots based on inner-filter effect. Biosens Bioelectron. 2016;85:358–362. doi: 10.1016/j.bios.2016.05.021. [DOI] [PubMed] [Google Scholar]
- 20.Wu T, Liu Y, Yu Z, et al. The sensing characteristics of plasmonic waveguide with a ring resonator. Optics Express. 2014;22(7):7669–77. doi: 10.1364/OE.22.007669. [DOI] [PubMed] [Google Scholar]
- 21.Wu J, Zhou C, Yu J, et al. TE polarization selective absorber based on metal-dielectric grating structure for infrared frequencies. Opt Commun. 2014;329(20):38–43. doi: 10.1016/j.optcom.2014.05.012. [DOI] [Google Scholar]
- 22.Sabah C, Dincer F, Karaaslan M, et al. Perfect metamaterial absorber with polarization and incident angle independencies based on ring and cross-wire resonators for shielding and a sensor application. Opt Commun. 2014;322(322):137–142. doi: 10.1016/j.optcom.2014.02.036. [DOI] [Google Scholar]
- 23.Lu X, Wan R, Liu F, et al. High-sensitivity plasmonic sensor based on perfect absorber with metallic nanoring structures. J Mod Opt. 2016;9275(2):177–183. doi: 10.1080/09500340.2015.1066459. [DOI] [Google Scholar]
- 24.Baqir MA, Ghasemi M, Choudhury PK, et al. Design and analysis of nanostructured subwavelength metamaterial absorber operating in the UV and visible spectral range. J Electromagn Waves Appl. 2015;29(18):2408–2419. doi: 10.1080/09205071.2015.1073124. [DOI] [Google Scholar]
- 25.Liu Z-q, Shao H-b, Liu G-q. λ3/20000 plasmonic nanocavities with multispectral ultra-narrowband absorption for high-quality sensing. Appl Phys Lett. 2014;104(8):081116–081116-4. doi: 10.1063/1.4867028. [DOI] [Google Scholar]
- 26.Liu G, Yu M, Liu Z, et al. Multi-Band High Refractive Index Susceptibility of Plasmonic Structures with Network-Type Metasurface. Plasmonics. 2016;11(2):677–682. doi: 10.1007/s11468-015-0101-5. [DOI] [Google Scholar]
- 27.Lin L, Zheng Y (2015) Optimizing plasmonic nanoantennas via coordinated multiple coupling. Sci Rep 5:14788 [DOI] [PMC free article] [PubMed]
- 28.Luo S, Zhao J, Zuo D, et al. Perfect narrow band absorber for sensing applications. Opt Express. 2016;24(9):9288. doi: 10.1364/OE.24.009288. [DOI] [PubMed] [Google Scholar]
- 29.Lu X, Zhang L, Zhang T. Nanoslit-microcavity-based narrow band absorber for sensing applications. Opt Express. 2015;23(16):20715–20. doi: 10.1364/OE.23.020715. [DOI] [PubMed] [Google Scholar]
- 30.Fang J, Igor L, Wei Y, et al. Plasmonic metamaterial sensor with ultra-high sensitivity in the visible spectral range. Adv Opt Mater. 2015;3(1):750–755. doi: 10.1002/adom.201400577. [DOI] [Google Scholar]
- 31.Verellen N, Dorpe PV, Huang C, et al. Plasmon line shaping using nanocrosses for high sensitivity localized surface plasmon resonance sensing. Nano Lett. 2011;11(2):391–7. doi: 10.1021/nl102991v. [DOI] [PubMed] [Google Scholar]
- 32.Liu Z, Liu G, Huang S, et al. Multispectral spatial and frequency selective sensing with ultra-compact cross-shaped antenna plasmonic crystals. Sensors Actuators B Chem. 2015;215:480–488. doi: 10.1016/j.snb.2015.04.009. [DOI] [Google Scholar]
- 33.Xiang X, Jiang S, Hu Y, et al. Structured metal film as a perfect absorber. Adv Mater. 2013;25(29):3993–3993. doi: 10.1002/adma.201370189. [DOI] [PubMed] [Google Scholar]
- 34.Le PJ, Quémerais P, Barbara A, et al. Why metallic surfaces with grooves a few nanometers deep and wide may strongly absorb visible light. Phys Rev Lett. 2008;100(6):1431–1432. doi: 10.1103/PhysRevLett.100.066408. [DOI] [PubMed] [Google Scholar]
- 35.Pardo F, Bouchon P, Haïdar R, et al. Light funneling mechanism explained by magnetoelectric interference. Phys Rev Lett. 2011;107(9):1132–1132. doi: 10.1103/PhysRevLett.107.093902. [DOI] [PubMed] [Google Scholar]
- 36.Liao YL, Zhao Y. A wide-angle TE-polarization absorber based on a bilayer grating. Opt Quantum Electron. 2015;47(8):2533–2539. doi: 10.1007/s11082-015-0135-0. [DOI] [Google Scholar]
- 37.Liao YL, Zhao Y. Ultrabroadband absorber using a deep metallic grating with narrow slits. Opt Commun. 2014;334:328–331. doi: 10.1016/j.optcom.2014.08.023. [DOI] [Google Scholar]
- 38.Liao Y, Zhao Y (2015) Near-perfect absorption with a metallic grating and dielectric substrate. J Nanophotonics 9(1):093087
- 39.Yang C, Shen W, Zhang Y, et al. Multi-narrowband absorber based on subwavelength grating structure. Opt Commun. 2014;331(22):310–315. doi: 10.1016/j.optcom.2014.06.036. [DOI] [Google Scholar]
- 40.Wang LP, Zhang ZM. Phonon-mediated magnetic polaritons in the infrared region. Opt Express. 2011;19(Suppl 2(6)):A126–A135. doi: 10.1364/OE.19.00A126. [DOI] [PubMed] [Google Scholar]
- 41.Wang H, Wang LP. Perfect selective metamaterial solar absorbers. Opt Express. 2013;21(22):A1078–A1093. doi: 10.1364/OE.21.0A1078. [DOI] [PubMed] [Google Scholar]
- 42.Zhou F, Wang C, Dong B, et al. Scalable nanofabrication of U-shaped nanowire resonators with tunable optical magnetism. Opt Express. 2016;24(6):6367–6380. doi: 10.1364/OE.24.006367. [DOI] [PubMed] [Google Scholar]
- 43.Sakurai A, Zhao B, Zhang ZM. Resonant frequency and bandwidth of metamaterial emitters and absorbers predicted by an RLC circuit model. J Quant Spectrosc Radiative Transfer. 2014;149:33–40. doi: 10.1016/j.jqsrt.2014.07.024. [DOI] [Google Scholar]
- 44.Feng R, Qiu J, Liu LH, Ding WQ, Chen LX. Parallel LC circuit model for multi-band absorption and preliminary design of radiative cooling. Opt Express. 2014;22(25):A1713–A1724. doi: 10.1364/OE.22.0A1713. [DOI] [PubMed] [Google Scholar]
- 45.Elaasser MA. Design optimization of nanostrip metamaterial perfect absorbers. J Nanophotonics. 2014;8(1):4085–4088. [Google Scholar]


