Measuring Genetic Knowledge: A Brief Survey Instrument for Adolescents and Adults

Abstract

Basic knowledge of genetics is essential for understanding genetic testing and counseling. The lack of a written, English language, validated, published measure has limited our ability to evaluate genetic knowledge of patients and families. Here, we begin the psychometric analysis of a true/false genetic knowledge measure. The 18-item measure was completed by parents of children with congenital heart defects (CHD) (n=465) and adolescents and young adults with CHD (ages 15-25, n=196) with a mean total correct score of 12.6 (SD=3.5, range 0-18). Utilizing exploratory factor analysis, we determined that one to three correlated factors, or abilities, were captured by our measure. Through confirmatory factor analysis, we determined that the two factor model was the best fit. Although it was necessary to remove two items, the remaining items exhibited adequate psychometric properties in a multidimensional item response theory analysis. Scores for each factor were computed, and a sum-score conversion table was derived. We conclude that this genetic knowledge measure discriminates best at low knowledge levels and is therefore well suited to determine a minimum adequate amount of genetic knowledge. However, further reliability testing and validation in diverse research and clinical settings is needed.

Introduction

Familiarity with general genetic concepts has been accepted as necessary for modern life due to the ubiquity of genetic testing throughout an individuals’ lifetime: prenatal carrier testing, fetal screening/diagnosis, newborn screening, direct to consumer genetic testing for a wide array of “indications,” disease specific genetic testing for both Mendelian and common diseases, pharmacogenomics testing, and most recently, whole exome/genome sequencing.

Knowledge is generally not sufficient for individuals to initiate health behavior changes, but it is a necessary component (1). Therefore, it is surprising that there is significant variability in the literature as to whether genetic knowledge is related to genetic test utilization and interest in genetic testing. Some studies have found a direct association (2-4), while others have detected an indirect relationship (5) or no relationship (6). This inconsistency may be due, in part, to the lack of a standard, validated method for assessing genetic knowledge.

While there are a number of published measures of genetic knowledge, they were generally developed and employed for a single study (7-12). As a result, content validity, as evaluated by the investigators of that particular study, was the only type of validation performed. While content validity is a necessary starting block in measure development, it is not adequate validation of a measure. A few studies report minimal analysis of the construct validity, such as factor analysis and internal consistency (13, 14), although neither study reports enough data to evaluate these analyses.

The most widely utilized written measure was published by Jallinoja and Aro in 1999 (15). This measure was updated to at least correct the number of genes in the human genome and utilized by other research groups (16, 17). However, there are a number of concerns with this measure, including outdated scientific facts, confusing language which is due, in part, to the original measure having been written in Finnish, and the absence of items on genetic testing. No studies have been performed to assess the reliability of this measure.

There are two published measures of genetic knowledge that have been more thoroughly validated: the Rapid Estimate of Adult Literacy in Genetics (REAL-G) (18), a measure of genetic literacy, which has been evaluated for concurrent and predictive validity, and the Genetic Knowledge Index (GKI) (19), a written measure, which has been subject to principle component analysis, internal consistency measurement, and correlation with educational attainment. Although sufficient data is presented on these measures, they both present issues that make them incompatible with current research methods and difficult to deploy in the clinical setting. First, the oral nature of the REAL-G measure severely limits its application in a field where most research is completed via telephone, online, or mailed surveys of the public or specific patient populations. The specific items on the GKI limit its application as it focuses on the outdated “genetic markers,” and one of its five items asks about “racial differences in academic ability,” which may make practitioners uncomfortable utilizing this measure.

There is thus a demonstrated lack of a written validated measure of genetic knowledge that would be useful for research and clinical applications. Since the measure of Jallinoja and Aro (15) has been the most widely used (16, 17, 20), we updated it thoroughly and started the psychometric evaluation process. We utilized exploratory and confirmatory factor analysis to determine the number of factors, or abilities, that underlie genetic knowledge, and then through the item response theory analysis, we determined scores that are more representative of one’s true capability on each of those factors. Through these investigations, we are taking the first steps to building a more informative genetic knowledge measure.

Methods

Adapted Genetic Knowledge Measure

We previously updated a 16-item true/false genetic knowledge measure (15) for readability and current understanding of genetics, while omitting redundant items and adding items to reflect current genetic concepts (21) (Table 1). This measure was scored by awarding one point for each item answered correctly while zero points were awarded for incorrect and unsure responses. A total correct score was calculated for all participants who responded to at least 14 of the 18 items. If the participant responded to 14-17 items, the points awarded for the items with responses were averaged and the average score was used for up to 4 items which lacked a response in the calculation of the total correct score (22).

Table 1.

Items of the genetic knowledge scale with the percent correct for each participant group, the factor loadings for one, two, and three factor models, the factor it was assigned to, the discrimination, and the difficulty.

#	Item (True/False)	% Correct			Factor Loadings						Final Factor	Discrimi nation	Difficu lty
		Parent-1	Parent-2	AYA-2	1	2		3
		n=285	n=180	n=196	Factor 1	Factor 1	Factor 2	Factor 1	Factor 2	Factor 3
1	Some diseases are caused by genes, environment, and lifestyle. (T)	97	95	92	0.78	0.72	0.12	0.57	0.35	0.05	1/Applied	2.06	−2.23
2	A gene is a disease. (F)	92	91	86	0.72	0.9	−0.15	0.81	−0.06	0.16	1/Applied	2.16	−1.64
3	You can see a gene with the naked eye. (F)	91	88	82	0.71	0.68	0.08	0.59	0.07	0.25	1/Applied	1.85	−1.58
4	Healthy parents can have a child with an inherited disease. (T)	96	97	88	0.71	0.8	−0.06	0.69	0.1	0.1	1/Applied	1.96	−2.08
5	A person with an altered (mutated) gene may be completely healthy. (T)	77	71	69	0.58	0.54	0.08	0.45	0.16	0.13	1/Applied	1.17	−1.07
6	All serious diseases are inherited. (F)	89	92	82	0.75	0.83	−0.03	0.69	0.13	0.12	1/Applied	2.3	−1.47
7	Genes are instruction for making proteins, which help the body grow and work properly. (T)	49	39	53	0.48	−0.08	0.74	−0.18	0.51	0.4	2/Basic	1.34	0.1
8	The child of a person with an inherited disease will always have the same disease. (F)	84	80	73	0.59	0.62	0.01	0.52	0.13	0.09	1/Applied	1.34	−1.32
9	A gene is a piece of DNA. (T)	81	82	82	0.49	0.27	0.31	0.1	0.61	−0.09	2/Basic	1.22	−1.55
10	Altered (mutated) genes can cause disease. (T)	79	61	67	0.75	0.41	0.46	0.29	0.34	0.39	-	-	-
11	Genes are inside of cells. (T)	64	50	53	0.58	−0.01	0.79	−0.13	0.56	0.45	2/Basic	2.1	−0.32
12	A chromosome contains many genes. (T)	64	59	64	0.49	0.08	0.55	0.12	0.73	0.08	2/Basic	1.5	−0.48
13	Genes determine traits such as height, eye color, and facial appearance. (T)	97	92	89	0.49	0.08	0.55	0.12	0.73	0.08	1/Applied	2.08	−1.97
14	A person has thousands of genes. (T)	69	57	66	0.49	0.18	0.41	0.05	0.47	0.13	2/Basic	1.04	−0.72
15	Identical twins have different sets of genes. (F)	48	44	31	0.47	0.41	0.1	0.33	0.16	0.1	1/Applied	0.91	0.4
16	Humans have 20 pairs of chromosomes. (F)	28	16	36	0.45	0.07	0.49	0.01	0.01	0.71	2/Basic	1.01	1.17
17	Parents pass both copies of each chromosome to their child. (F)	37	20	29	0.48	0.14	0.46	0.08	−0.12	0.87	2/Basic	-	-
18	A genetic test can tell you if you have a higher chance to develop a specific disease. (T)	85	80	64	0.7	0.51	0.27	0.4	0.26	0.26	1/Applied	1.7	−1.08

Participants

Participants, including adolescents and young adults (AYA) with congenital heart defects (CHD) and parents of individuals with CHD, a convenience sample for this study, were recruited from a tertiary children’s hospital’s cardiology clinic under two separate institutional review board (IRB)–approved studies. This resulted in three groups of participants: study 1 parents (parents-1), study 2 parents (parents- 2) and study 2 AYA (AYA-2). The adapted genetic knowledge measure and a demographics measure were administered as part of both of these larger studies.

Study 1

Parents of living children with CHD affecting the left ventricular outflow tract, who also had a valid address, were sent a packet of English language surveys to measure their genetic knowledge and attitudes and understanding of prior informed consent for participation in a genetic research study (previous consent was on average 3.1 ± 1.4 years prior). In short, at least one parent responded from 50% of eligible families, resulting in 285 parent participants; detailed descriptions of the eligibility, recruitment, and consent process have been previously published (23).

Study 2

This study utilized the Health Beliefs model as a theoretical framework to investigate the effect of genetic knowledge, in addition to other risk and knowledge variables, on three specific health behaviors: information seeking, contraception use, and communication with partner and health care provider. English speaking AYA, ages 15 to 25 years, with congenital heart defects (CHD) that were not the result of a genetic syndrome, who spoke English, and were cognitively able to participate were recruited during their clinic visit along with their parents. The study surveys were available on paper and electronically. AYA, who were required to complete the surveys in clinic, received a movie ticket upon completion, while the parents were not given an incentive. The data provided by the 196 AYA and 180 parents who participated in this study during 2012 were analyzed in this study.

Data Analysis

Demographic characteristics, the percent of participants answering each knowledge item correctly, and the total correct score were calculated for each participant group (parents-1, AYA-2, parents-2). Additionally, differences among the participant groups were determined by t-tests, ANOVAs with Tukey HSD post-hoc analyses, and Mann-Whitney tests, as appropriate. All raw-data (estimates of missing data were removed) were combined for the remaining analyses and all analyses were completed in SPSS, unless otherwise stated.

Exploratory Factor Analysis (EFA)

Exploratory factor analysis (EFA) was undertaken to identify the number of latent abilities that likely determine performance on the genetic knowledge measure. This is done by determining groups of items that perform similarly (i.e. if one answers #1 correctly you are likely to also answer #2 correctly). Comprehensive Exploratory Factor Analysis (CEFA) program with VARIMAX rotation (24) was utilized for this analysis to determine the number of factors while ensuring that each item is related primarily to a single factor. The extent to which each item “loaded onto” a factor was also calculated; factor loadings were scaled from −1.0 to 1.0.

Confirmatory Factor Analysis (CFA)

CFA was employed to determine how well each model implied by the EFA accounted for the variability in the data. All reasonable models of the factor structure (eigenvalues >1.2) from the EFA were tested using confirmatory factor analysis or structural equation modeling when accounting for local dependence utilizing the latent variable modeling program Mplus (25). Fit indices, including root mean square error of approximation (RMSEA), comparative fit index (CFI), Tucker-Lewis Index (TLI), and weighted root mean square residual (WRMSR) were reported for all models. As models were derived from the EFA, and therefore represented a post hoc analysis, a simple cross-validation was performed to ensure the selected model’s good fit was not due to chance characteristics and that the same model would likely fit additional data obtained in the future. This cross validation was performed by first dividing the data into two groups based on an even-odd split of the subjects and then the selected model fit to each group independently and the fit indices, as listed above, were reported.

Internal Consistency

Cronbach’s alpha was calculated for each factor.

Calibration and Scoring using Item Response Theory (IRT)

IRT analysis is a type of categorical confirmatory factor analysis that takes into account all response patterns present in the data. It was conducted to calculate meaningful scores for each identified factor and assist in identifying items with poor qualities (e.g., inability to discriminate between people with high or low levels of the measured factors). While item qualities can be inferred by CFA parameter estimates (26), the scores are unique to IRT parameter estimation. Therefore, the IRT analysis will result in scores that are better representations of the abilities that underlie each factor. IRT scores are on the standard normal metric, such that an ability score of zero indicates the mean ability, much like a z-score (27). As this is a true/false measure with two underlying traits or factors (identified by the EFA and CFA), the multidimensional two-parameter logistic model (M2PLM) in the flexMIRT (28) software was used to calibrate and score this measure for those participants who responded to all of the knowledge items. Marginal maximum likelihood with an expectation-maximization algorithm (MML-EM) (29) was utilized for the calibration step. In this two-step method, the discrimination and difficulty of each item are estimated using maximum likelihood while the underlying ability score is integrated out. The scoring step occurs after the item parameter estimates from the calibration step are added back. MML-EM continues iterating between these two steps until a convergence criterion is reached. The scoring method used was expected a posteriori, which calculates the mean of each test-taker’s scoring likelihood. Lastly, a conversion table was calculated so that sum scores could easily be translated into the two IRT scores.

Results

Demographic Characteristics

All three groups were primarily white and both parent groups were approximately two-thirds female while the AYA group was almost evenly split between males and females (Table 2). The study 2 parents were significantly older than the study 1 parents (47 vs. 39.5 years, p<0.001), although the distribution of education levels was not different between the parent groups. The mean age of the AYA was 19 years and the percent with some college or more was not calculated as this would reflect the age of the participant more than his/her eventual education attainment.

Table 2.

Demographic characteristics of each participant group.

	Parent-1	Parent-2	AYA-2
n	287	180	196
Age (mean)	39.5*	47*	19
Male (%)	36	34	54
White (%)	94	94	85
Some college + (%) ~	74	71	NA

^*Study 2 parents were significantly older than Study 1 parents (p<0.001)

^~No significant differences in the distribution of education between the two parental groups

Genetic Knowledge Measure Data

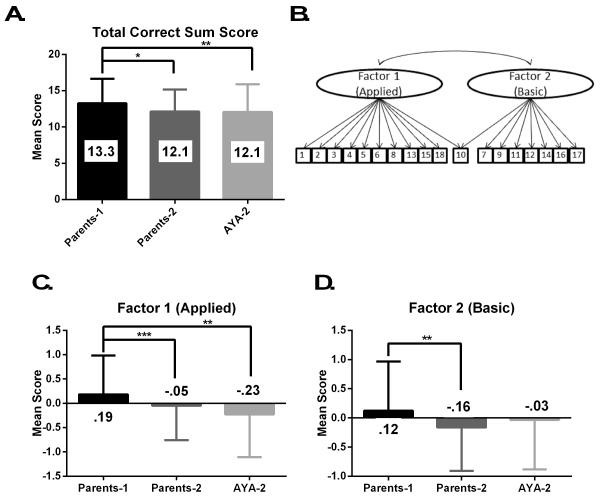
Seven items, item # 1, 2, 3, 4, 6, 9, and 13, were answered correctly by at least 80% of each participant group. On the other hand, items 7, 15, 16, and 17 were answered correctly by less than half of participants. The remaining items (# 5, 8, 10, 11, 12, 14, and 18) were answered correctly by 50-79% of participants. The mean total correct score for all of the participants was 12.6, and the mean scores for each participant group are reported in Fig. 1. The participants’ genetic knowledge scores were significantly different when evaluated by participant group (p<.001), and post-hoc analysis revealed that study 1 parents had significantly higher scores than both groups of study 2 participants (parents, p=.002; AYA, p=.001).

Figure 1.

The mean correct item sum score for each participant group (A; Parents-1 n=285, Parents-2 n=177, AYA-2 n=194). The best fit factor structure; two correlated factors (B). The factors scores for each participant group (C, D; Parents-1 n=265, Parents-2 n=164, AYA-2 n=179).

* p=.002

** p=.001

*** p<.001

Exploratory Factor Analysis

One, two, or three correlated factors were supported by EFA, and loadings for each of these models are reported in Table 1. Although the loadings in the one factor model were quite high, the introduction of a second factor increased these loadings, indicating two factors better described the data. When a third factor was added, only two items loaded onto this additional factor, indicating local dependence (LD). LD is a specific type of multicollinearity that results when the responses to a pair or set of items appear to depend on some extraneous factor and not the variable(s) of interest. The third factor clarified that item 9 belonged to the second factor, although which factor item 10 belonged to remained unclear.

Confirmatory Factor Analysis (CFA) and Structural Equation Modeling (SEM)

Based on the results of the exploratory factor analysis, the following models were tested: one-factor with and without LD, two-factors with and without the LD (Figure 1). The fit statistics, as seen in Table 3, indicated that the two-factor model accounting for local dependence was the only model that approached acceptable fit criteria (0.05<RMSEA<0.08, CFI>0.95, TLI>0.95, WRMSR<1.00). As this was a post hoc analysis of a model derived from the EFA, a cross-validation was necessary. Therefore, we used an even-odd data split and repeated the SEM analysis of the two-factor model with LD modeled on each of these data sets. The fit statistics of the calibration (2-SEM, c) and validation (2-SEM, v) data sets represent good fit (Table 3).

Table 3.

Fit measures for each of the confirmatory factor analysis models (1 factor (1-CFA), 2 factors (2-CFA)), structural equation modeling models (1 factor (1-SEM), 2 factors (2-SEM), the cross validation of the two factor SEM model (calibration (2-SEM, c) and validation (2-SEM, v)), the 2 factor SEM model for the 16-item measure used for IRT analysis (16 item, 2-SEM) and the cross validation of the two factor SEM model for 16-item measure (calibration (16-item, 2-SEM, c) and validation (16-item, 2-SEM, v)).

	Fit Measures
Model	RMSEA	CFI	TLI	WRMSR
1-CFA	0.06	0.89	0.88	1.4
1-SEM	0.05	0.92	0.91	1.27
2-CFA	0.04	0.94	0.93	1.14
2-SEM	0.04	0.96	0.95	1.03
2-SEM, c	0.03	0.97	0.96	0.89
2-SEM, v	0.03	0.96	0.96	0.89
16-item, 2-SEM	0.03	0.97	0.96	0.97
16-item, 2-SEM, c	0.03	0.96	0.96	0.88
16-item, 2-SEM, v	0.03	0.95	0.94	0.9
Acceptable	.05-.08	>.95	>0.95	<1.00

Internal Consistency of Applied and Basic Factors

Factor 1, onto which items 1, 2, 3, 4, 5, 6, 8, 13, 15, and 18 loaded, we named the “applied” factor due to the nature of these items. Cronbach’s alpha for the applied factor was 0.73 (n=632). Likewise, Factor 2, including items 7, 9, 11, 12, 14, 16, and 17, was named the “basic” factor. The Cronbach’s alpha for the basic factor was 0.66 (n=630).

Scoring and Calibration using Item Response Theory (IRT)

To facilitate interpretation of the IRT scores, item 10 was removed as it loaded equally onto both factors and item 17 was chosen for removal due to the local dependence between 16 and 17 (alternatively, item 16 could have been removed). When the structural equation model was re-run with this new 16 item measure, acceptable fit statistics were achieved (Table 3). The SEM for this measure also cross-validated well (Table 3). As this new model was acceptable, the discrimination and difficulty of each item were computed (Table 1). The items on this measure had acceptable discrimination estimates (>0.70) as the vast majority were above 1.0. On the other hand, difficulty scores tended to be negative, indicating that the measure is not very difficult for most test-takers. The measure was scored to obtain latent trait estimates for each participant who responded to all 16 items, and the negative skew of the score distributions for both factors again indicated the relative easy nature of this measure (Figure 2). For ease of use in future studies when IRT software is not available or IRT analysis is not feasible, a conversion table was calculated to convert sum scores into latent trait scores (Table 4). After determining a participant’s sum score, IRT score estimates for both factors may be inferred by finding the appropriate rows in both the Basic and Applied columns.

Table 4.

Sum score to IRT scores conversion table.

	Applied Factor		Basic Factor
Sum Score	IRT Score	SD	IRT Score	SD
0	−2.86	0.49	−2.33	0.67
1	−2.58	0.46	−2.04	0.66
2	−2.33	0.43	−1.82	0.66
3	−2.10	0.41	−1.64	0.66
4	−1.88	0.41	−1.48	0.66
5	−1.66	0.41	−1.34	0.66
6	−1.44	0.43	−1.21	0.66
7	−1.21	0.46	−1.09	0.66
8	−0.95	0.50	−0.95	0.65
9	−0.68	0.55	−0.79	0.64
10	−0.42	0.59	−0.58	0.63
11	−0.17	0.62	−0.33	0.61
12	0.07	0.65	−0.03	0.60
13	0.32	0.67	0.30	0.61
14	0.61	0.70	0.66	0.63
15	0.93	0.73	1.04	0.66
16	1.27	0.76	1.45	0.70

Group Differences in Knowledge

There were significant differences in mean factor 1 scores when the three participant groups were compared (p<.001). Post-hoc analysis revealed that this difference was driven by the high scores of the study 1 parents, whose mean score was significantly higher than the study 2 AYA (p<.001) and parents (p=.01). The study 2 AYA and parents were not significantly different from each other. Factor 2 also showed significant differences between the three groups (p=.002) and post-hoc analysis revealed only one significant relationship; the study 1 parents had a significantly higher mean score than the study 2 parents (p=.001).

Discussion

Here, we present the first steps in validation of our adapted genetic knowledge measure, which is applicable to both adolescents and adults. As this measure was administered to individuals starting at age 15, this measure can be used for older teenage and young adult patients and parents in the pediatric setting. Although we did not sample older adults, we would anticipate this this measure would also be applicable to this age range.

As we were unable to identify a previous factor analysis of the original or updated version of the Jallinoja and Aro genetic knowledge measure, we undertook this analysis and identified two underlying latent factors. We were surprised that the factor analysis resulted in two factors that are surprisingly similar to the “association of genes and diseases” and “association of genes, chromosomes, cells and the body” that the original measure was designed to capture (15) as no prior analysis had tested this. For ease of use, we have renamed these factors, applied and basic. The basic factor includes items that are facts about genetics, such as the number of genes and chromosomes, the size relationship between genes, chromosomes, and cells, and the function of genes in the body. The applied factor includes items pertaining to the relationship of genes and genetic testing with health and disease. While most items fell into the anticipated category, we were surprised that the item regarding whether a gene can be seen with the naked eye was determined to be in the applied category. As Jallinoja and Aro didn’t state which specific items were designed to measure which construct, we were unable to compare the placement of specific items.

This differentiation between basic and applied genetic knowledge is also similar to the difference between factual and conceptual knowledge in the revised Bloom’s Taxonomy of Educational Objectives, as summarized by Krathwohl (30). According to this taxonomy, based on cognitive psychology and educational terminology, the basic genetic knowledge factor closely resembles ‘remembering factual knowledge’ which is the most basic cognitive process (remembering) paired with the most basic knowledge dimension (factual knowledge). On the other hand, ‘understanding (i.e., classifying and inferring) conceptual knowledge (i.e., principles and generalizations) as would be required for our applied genetic knowledge factor is a step up in complexity of both the knowledge dimension and the cognitive process. While all of our participants likely engage in both of these types of tasks, in addition to the others included in the taxonomy, it is likely that the parents are more skilled at the more complex tasks, whereas the adolescents and young adults are more frequently required to ‘remember factual knowledge’.

When the scores of the AYA and the parents of study 2 are compared, while not statistically significant, we do see that the parents have higher average applied (factor 1) knowledge and the AYA have higher basic knowledge (factor 2), as would be predicted by Bloom’s Taxonomy. Additionally, AYAs may have higher basic knowledge as a result of their proximity to high school, and possibly college, science classes which likely included increased and more accurate genetic content as compared to the parents’. Additionally, parents’ higher applied knowledge may be related to their additional opportunities to develop and utilize applied genetic knowledge through such life events as pregnancy, child birth, and/or a cancer diagnosis when discussion of genetic concepts and genetic testing is common. Perhaps this explains why the item regarding whether genes can be seen with the naked eye item was placed on the applied factor, as through these life experiences it could be determined that genes could not be seen, whereas the specific number of genes humans possess may never be directly applicable.

The statistically significant differences in the mean total correct sum score and both factor scores were largely driven by the high scores of the study 1 parents. It is important to remember that this parent group is highly selected. These parents had previously consented to participate in a genetic etiology research study and then chose to participate in a subsequent study by completing and returning a mailed study. Therefore, their high scores could be the result of the genetic education they received as part of the consent process and/or that those parents already possessing higher genetic knowledge were more likely to participate in both of these studies.

Interestingly, while the total correct sum score of the parents and AYA of study 2 are very similar, the IRT factor scores show differences between these two groups. Thus, using the IRT scoring to pull out the different latent ability scores may be important as approaches to effective teaching may need to be adapted not only for specific age groups but potentially for each individual. This differentiation between basic and applied genetic knowledge may allow for more consistent research results which has been an issue amongst studies identifying predictors of genetic test utilization (31).

Lastly, the IRT scoring provides a better estimate of basic and applied genetic knowledge than sum scores as it accounts for the discrimination and difficulty of each item. Ideally, each application of this genetic knowledge measure would be scored using the IRT software. Unfortunately, this is not realistic as IRT software is expensive and specialized. Therefore, our conversion table provides a reliable estimate of the basic and applied knowledge score. Since these two traits are correlated, one can estimate both traits from the total sum score. This easy to use conversion table (Table 4) will allow wide application of this genetic knowledge measure.

There are a few limitations of this study due to its design. As this is a true/false measure, the statistical analysis was unable to account for accurate guessing. As study 1 utilized a mailed survey design, some of these individuals may have utilized resource material to determine the correct answer to the questions although they were advised not to do so. Lastly, all subjects were recruited from the cardiology clinic at a single tertiary children’s hospital, and our study participants were largely Caucasian and well educated. Therefore, the results of this study may not be applicable to the general population or to patients/families with Mendelian diseases.

The results of the analyses presented here indicate that this measure is most informative for individuals with below average genetic knowledge. As the difficulty of the measure is low, this measure gives better scoring estimates for individuals at the low end of the scale. Accordingly, it would be necessary to add more difficult items and re-analyze the measure to ensure better scoring estimates for the high scorers should this be desired. The current measure, therefore, is best applied to determine if individuals meet a specific threshold of genetic knowledge. Additional studies will be necessary to determine the minimum necessary genetic knowledge for a number of specific situations, including consenting to a genetic research study, decision-making following genetic counseling, and making treatment decisions based on genetic test results. After determination of the minimum genetic knowledge of patients, this measure could be used to tailor genetic counseling for those patients. This approach has the potential to improve use of providers' time and increase patient satisfaction with genetic counseling that was tailored to the patient/subject’s identified knowledge level as compared to counseling based either on the provider’s assumption of the patient/subject’s knowledge or providing the same information to all patients/subjects.

Separation of the basic and applied segments of genetic knowledge and use of IRT scoring are just the first steps on the road to a better genetic knowledge measure. While we have defined the underlying factor structure and enabled more informed scoring, in future studies we plan to continue assessing the psychometric properties of this measure by examining test-retest reliability and concurrent validity in a different sample of subjects. Additionally, it will be necessary to examine this knowledge measure as part of models that also account for other areas of knowledge such as health literacy and specific disease knowledge. Although knowledge is generally not sufficient to drive health behavior change (reviewed in (1)), it will also be necessary to examine these knowledge variables within models that also take such construct as risk perception, self-efficacy, cues to action, readiness to change and so on into account to determine the role that genetic knowledge plays in scenarios that more closely approximate the real world. The first step to develop and test those models is the availability of measures of the specific constructs, such as genetic knowledge.

While additional research is necessary, it is interesting to contemplate the effect that differing levels of basic and applied genetic knowledge may have on the decision making process of individuals considering clinical genetic testing or participation in a genetic research study. Perhaps basic knowledge is a better predictor of intended use/participation while applied knowledge may better predict actually usage/participation. Concomitantly, we should also consider as healthcare providers how we could tailor our genetic education to individuals across the spectrum of basic and applied knowledge so that the information they receive is as useful as possible. Through these and other future investigations, the validation and utilization of this genetic knowledge measure has the potential to increase the effectiveness of genetic health communication and also increase the consistency of genetic knowledge research.