The Current State and Future of Factor Analysis in Personality Disorder Research

Abstract

The major debates in the personality disorder (PD) field center on the structure of personality pathology. Factor analysis is designed to elucidate the underlying structure of observed phenomena. Therefore, factor analysis has already played a major role in the debates about the structure of PD, and will continue to be an often-used and indispensable tool moving forward. However, misconceptions about the utility and interpretation of factor analyses abound. The purpose of this article is to provide a conceptual primer on available factor analytic techniques, how they have been applied in PD research, and highlight novel ways of using factor analysis moving forward. The techniques reviewed include exploratory and confirmatory factor analysis, exploratory structural equation modeling, multilevel structural equation modeling, and person-specific (i.e., p-technique) factor analysis. Additionally, the notion that exploratory and confirmatory factor analytic approaches lie on a spectrum is introduced. Examples from the published literature are used to illustrate key points.

Personality disorders (PDs), as psychiatric diagnoses, were recently the source of heated debate (see e.g., Gunderson, 2013; Krueger, 2013; Widiger, 2013). The proposed revision to the classification of PDs in the Diagnostic and Statistical Manual of Mental Disorders – Fifth Edition (DSM-5; American Psychiatric Association, 2013) was the immediate catalyst. Even though many considerations drove the diversity of opinions in the deliberations (Zachar, Krueger, & Kendler, 2016), this was ultimately a field-wide debate about the structure of PD. No topic is more elemental, because structure should dictate how PD is assessed, diagnosed, and studied. Factor analysis is, at its core, a statistical technique designed to inform how the underlying structure of phenomena are understood. Leading up to the DSM-5 proposal, factor analysis played a central role in suggesting that the structure of PDs was not one of 10 discrete categories, but rather might be better understood using a different structural framework. Moving forward, factor analysis will continue to figure prominently in scientific debates about the structure of PD.

The foundations of factor analyses are now over a century old (Spearman, 1904), and yet they remain a relevant and ever-developing set of techniques. Despite the central role they have played in the field, they are often misinterpreted and misapplied. Further, although factor analytic methods are well-worn techniques, they have the potential to continue to generate important insights in the hotly debated topic of PD structure. The goal of this paper is to provide a conceptual review on basic and advanced applications of factor analysis that have been used in and are relevant to the study of PD (and psychopathology more generally as well). There are now several reviews of factor analytic studies in the PD literature (e.g., O'Connor, 2005; Sheets & Craighead, 2007; Wright & Zimmermann, 2015). Therefore this paper is not meant to serve as another exhaustive review of the empirical results, but rather a non-technical primer on the breadth and applicability of factor analytic techniques available to clinical researchers, including a showcase of underused techniques suitable for intensive longitudinal data (i.e., ambulatory assessment, ecological momentary assessment, etc.). The level of this discourse is conceptual, emphasizing model selection and interpretation. Although certain highly technical aspects will be covered (e.g., rotation algorithms, variance decompositions), they will be presented in a nontechnical manner and translated in to applied clinical questions and theoretical issues. Exemplar analyses in the published literature will be summarized to illustrate the covered techniques.

Foundations of Factor Analysis

The aim of all factor analytic techniques is to explain patterns of covariation among observed or manifest (i.e., directly measured) variables using unobserved or latent constructs. That is to say, given that responses to some stimuli (e.g., responses to clinical interview questions or inventories) show patterns of covariation, it is reasonable to hypothesize that that there is an explanation for this patterning (e.g., a personality trait). In fact, this was exactly the logic that prompted Spearman (1904) to develop factor analysis. He had observed that those individual's who performed well on one mental test tended to perform well on others, which gave rise to his general theory of intelligence and the need for a quantitative method to test it. Factor analysis was thus born. As it applies to the domain of PD, the conceptual parallel is perhaps the observation that PD diagnoses are highly co-morbid (i.e., co-vary), which led to the application of factor analytic techniques to diagnoses, criterion counts, and individual symptoms in an effort to determine the underlying structure of PD.

Since its early beginnings, factor analysis has grown in sophistication and complexity, and now encompasses a family of related techniques that vary in several important ways (e.g., how exploratory versus confirmatory they are, the estimation technique, ability to handle nested data, etc.). Regardless of the specific instantiation of the method, all share the same fundamental goal. Factor analysis can also be understood to fall within a broader organization of latent variable models, which includes Structural Equation Modeling, Item Response Theory/Latent Trait Models, Latent Class/Profile Analysis, and perhaps most generally Factor Mixture Modeling (Hallquist & Wright, 2014). The scope of this review will focus on factor analysis per se, as other contributions in this special issue will provide more detailed coverage of some or all of these alternative latent variable models. This review will start where factor analysis started, with exploratory factor analysis (EFA), and will then cover confirmatory factor analysis (CFA; Joreskog, 1969), and exploratory structural equation modeling (ESEM; Asparouhov & Muthén, 2009), which are all suitable for multivariate cross-sectional data as is commonly generated from diagnostic interviews and patient- and informant-report inventories. The coverage will then shift to multilevel structural equation modeling (MSEM; Muthen, 1991, 1994) and P-technique factor analysis (Cattell, 1943), techniques that can leverage intensive longitudinal data, which is increasingly being collected in ambulatory assessment studies (Carpenter, Wycoff, & Trull, 2016), to address questions about between- and within-person personality structures.

Exploratory Factor Analysis

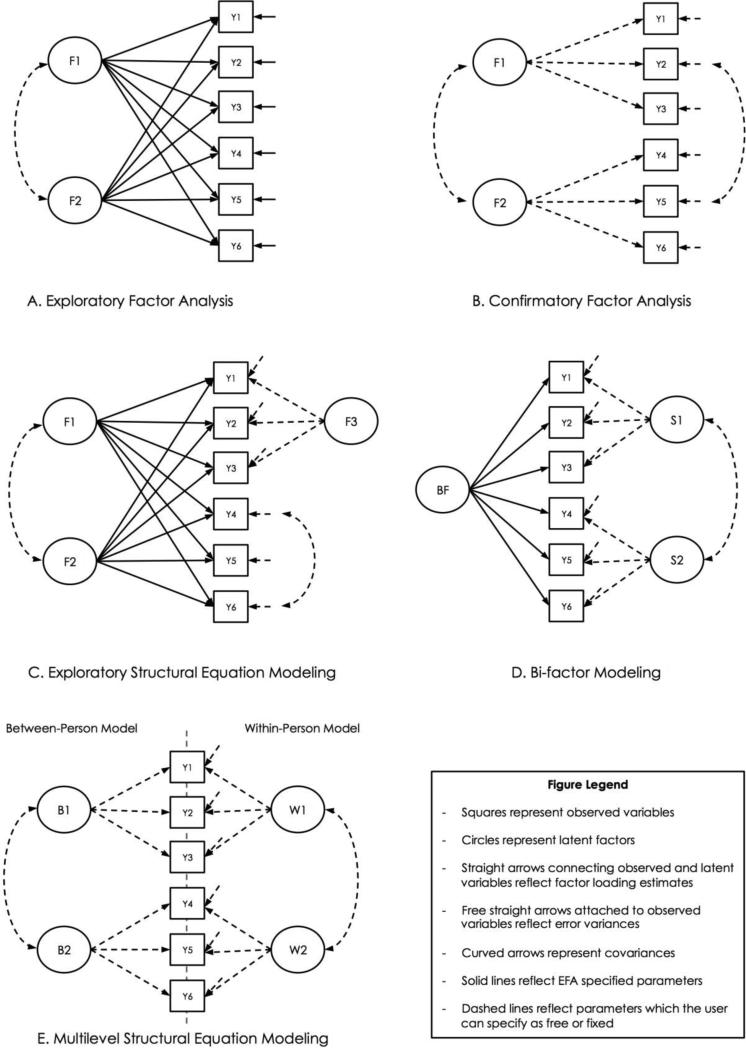
Initially, factor analytic approaches were limited to EFA, which are termed exploratory because the investigator does not specify the patterning of items loading on factors, and instead all associations between latent and observed variables are freely estimated (the reader is referred to Mulaik [2010] for detailed discussions of EFA). In Figure 1, Panel A provides a graphical representation of EFA. In this diagram square boxes represent observed variables, circles represent latent variables or factors, straight arrows connecting circles and squares represent factor loadings (i.e., the regression of the observed variable on the latent variable), arrows only pointing towards squares represent observed variable uniqueness (i.e., variability not accounted for by the latent factors, which includes both unique variance and error variance), and curved arrows represent covariances/correlations. Additionally, solid lines are used to represent model specified parameters, whereas dashed lines represent parameters that can be specified by the investigator. In this example there are six observed variables and two correlated factors (i.e., an oblique model), and each of the observed variables loads on each of the two factors.

Figure 1.

Conceptual diagram of different factor analytic techniques.

In EFA the investigator does not assign observed variables to factors, rather the relationship between each is estimated and the pattern of loadings is evaluated or “interpreted” after the analysis is run. Because of this, EFA has sometimes been called an atheoretical analytic approach, which is unfortunate as many aspects of EFA are, in fact, theoretically driven. For one, EFA rests on the assumption that the underlying structure of unobservable natural phenomena can be uncovered by studying patterns of covariation in measurable behaviors (in this case PD features). Second, it is frequently the case that the investigator has some hypothesis about how many factors are needed to account for the observed variables. Accordingly, usually there is a theory about which observed variables serve as significant markers for the same factors. More generally, the key modeling decisions in EFA (e.g., selecting items to include, number of factors to retain, etc.) should ideally be made based on substantive theory. For instance, factors must be interpreted and labeled, and the emergence of a factor that is uninterpretable may prompt one to select fewer factors, drop items, or collect more data. Admittedly, EFA is often a very interactive technique, in the sense that several models are often run under different conditions and compared before settling on a final solution. Readers who may initially experience some discomfort with this aspect of EFA are encouraged to give serious thought to how many decisions and modifications are actually made behind the scenes in other analytic frameworks (Hint: a lot).

The three major questions an investigator should consider when conducting an EFA are: 1. Which observed variables should be included in order to arrive at a valid structure (this is true of all factor analytic techniques and statistical modeling in general)? A major concern here is that if too few indicators for a specific construct are included, a corresponding factor is unlikely to emerge and will not be well determined if it does. In PD research a prime example of how this plays out can be found in factor analyses of DSM PD symptom counts/dimensions, which only rarely find an oddity/peculiarity factor, given that schizotypal PD is the only prototypical marker of this domain. On the flip side of that coin, an over representation of content from a particular construct will almost guarantee a separate factor, even if the construct is subordinate to another domain (i.e., a bloated specific; see Oltmanns & Widiger, 2016 for a relevant example). 2. How many factors should be retained? Contemporary best practices for selecting the number of factors to retain involve the use of quantitative criteria like Horn's (1965) parallel analysis, Velicer's (1976) minimum average partial test, Ruscio and Roche's (2012) comparison data technique, and model fit criteria (e.g., chi-square, RMSEA) when available based on the estimator (e.g., Maximum Likelihood) to inform the number to retain. However, regardless of which methods are used, these are fallible tools that should be weighed in the decision but not followed blindly. The investigator is still required to make careful choices based on all pertinent information, especially theory. 3. How should these factors be rotated? Despite the many options available for factor rotation (e.g., Varimax, Geomin; see Sass & Schmitt, 2010 for a review), the most important distinction is between orthogonal or oblique factors. In an orthogonal rotation, the factors are forced to be unrelated to each other, whereas in an oblique rotation factors are allowed to correlate. Oblique rotations methods are generally preferable because they do not preclude an orthogonal solution from emerging, but allow for substantial factor correlations when indicated. This is a key consideration in PD research, given that there are theoretical and empirical rationales for why factors might be expected to correlate substantially (e.g., Bender et al., 2011). However, factor rotation will potentially have nonnegligible effects on factor interpretation, and therefore it should be given explicit consideration.

Many studies have now used EFA to investigate the latent structure of DSM PDs. These studies have varied considerably in terms of the basic unit of analysis (e.g., individual PD criteria or dimensional PD scores), assessment method (e.g., self- or clinician report), sample type (e.g., community or clinical sample), and statistical procedures (e.g., factor retention rule used). More detailed reviews of these studies are available (Wright & Zimmerman, 2015), but several issues bear mention: First, studies using PD diagnoses as observed variables (i.e., either categorical diagnoses, or criteria counts) have generally not supported the DSM's three “cluster” solution in the form of three (correlated) latent dimensions (e.g., Fossati et al., 2006; Fossati et al., 2000; Wright, Scott, et al., 2015). Rather, a latent structure that better accounts for diagnosis-level PD covariation requires more than three factors, which are likely to resemble major domains of general personality (i.e., the five-factor model; O'Connor, 2005). However, the limitation of focusing solely on covariation between PD diagnoses or scales is that it assumes that PDs are unidimensional, homogenous constructs.

Thus, using individual PD criteria are likely to be more informative for future EFAs of PD. A number of studies have also explored the latent structure of DSM PD criteria using EFA or principal components analysis¹ (e.g., Blackburn, Logan, Renwick, & Donnelly, 2005; Blais & Malone, 2013; Durrett & Westen, 2005; Howard, Huband, Duggan, & Mannion, 2008; Huprich et al., 2010; Thomas, Turkheimer, & Oltmanns, 2003; Trull, Vergés, Wood, Jahng, & Sher, 2012). In a recent review of these studies (Wright & Zimmermann, 2015), it was found that the number of retained factors varied considerably, ranging from five to eleven, with a median of nine. This might be in part due to differences in the sets of indicators, or this might also be influenced by differences in factor retention decision rules, which are inconsistently applied across studies. In any case, the findings of these studies might appear to run counter to the emerging consensus in PD research that suggests five latent dimensions might be needed to comprehensively capture the covariation of DSM PD criteria (Widiger & Trull, 2007). Yet, a more parsimonious set of factors might still be valid at a higher level of abstraction in a hierarchically organized structure (see below).

Shifting focus to the DSM-5 alternative model of PD, EFA figured prominently in the development of the Criterion B trait model (Krueger et al., 2012). The process began by the committee members developing an in initial list of 37 features thought to cover the PD domain. Scales for these features were developed and administered to large samples of individual who had previously sought mental health treatment or were representative of the population. Through a series of factor analyses, the 37 features were winnowed down to 25, which were found to load on to five factors. This process also culminated in the development of the Personality Inventory for the DSM-5 (PID-5; Krueger et al., 2012). These five factors were easily interpretable as maladaptive variants of the Big-5/five-factor model identified in factor analysis in basic personality research (see Wright, in press for a review). This structure has now been well replicated in diverse samples, different reporters, and across cultures (Krueger & Markon, 2014).

That the DSM-5 PD model corresponds to the consensual models from basic personality science should not be a surprise given the clear mapping of content across diverse dimensional models (Widiger & Simonsen, 2005), and it lends validity to its scientific foundation. However, debates about the precise number of factors or dimensions underlying PD may not be the most fruitful framing of the structural question. Rather, understanding that the structure may vary across levels of conceptual abstraction may offer higher scientific yield. Therefore, instead of trying to find a single optimal solution, an alternative approach to is to consider a hierarchical structure that ranges from a large number of specific indicators up to moderate numbers of intermediate factors, and finally on to relatively fewer subordinate factors. Each level of abstraction may be best suited for different empirical and clinical questions (e.g., broadest domains may serve as the best prognostic markers, intermediate domains may serve best as diagnostic constructs, and narrow behavioral markers might serve best to formulate specific interventions), although this remains an open empirical question. Hierarchies of this type can be estimated in EFA using Goldberg's (2006) irreverently named “bass-ackwards” technique. In this approach solutions with increasing number of factors are estimated and factor scores are saved after each. These factor scores can then be correlated across solutions to examine the “unfolding” of the hierarchy. The seminal example of this approach can be found in Markon, Krueger, and Watson (2005), where a large number of normative and pathological personality trait scales were factored together. The resulting hierarchy generated interpretable two, three, four, and five factor structures.

More recently, Wright, Thomas, and colleagues (2012) used this technique on the PID-5 scales, finding that at the two-factor level a general domain of PD split in to factors interpreted as Internalizing and Externalizing, at the three-factor level Internalizing split in to Detachment and Negative Affect, at the four-factor level Externalizing split in to Antagonism and Disinhibition, and finally at the five-factor level a Psychoticism factor emerged. Similar results have been found when examining the PID-5 with other adaptive and pathological trait inventories (Wright & Simms, 2014) and in other maladaptive personality trait inventories (Kushner et al., 2011). Although investigators have tended to stop at the intermediate level of factoring, continuing the hierarchical analyses to the fine-grained level is desirable and a needed aim for future work. Thus, although EFA is the oldest of the factor analytic techniques, it remains highly relevant and is generating interesting new results that are shaping the dialogue on the structure of personality pathology. In the following section an additional example is presented in which EFA is directly compared with CFA by virtue of using the same estimator (i.e., maximum likelihood).

Confirmatory Factor Analysis

As the name indicates, unlike EFA, CFA is intended to serve primarily as a hypothesis testing analytic approach (the reader is referred to Brown [2015] for detailed discussion of CFA techniques). CFA shares the major conceptual underpinning of EFA, in that the goal is to represent patterns of covariation among a set of observed items with a smaller set of unobserved factors. The confirmatory aspects are that (a) the user may specify any of the model parameters, and (b) the fit (or, more specifically, the lack of fit) of the specified model to the observed data is tested. Figure 1, Panel B, illustrates a hypothetical typical two-factor CFA. In this model the observed variables Y1-Y3 serve as indicators of latent factor F1 only, and Y4-Y6 serve as indicators of F2 only. Please note that the CFA in Panel B differs from the EFA in Panel A in that each factor loading was user specified, and not all items load on each factor. Much like the EFA model the factors are allowed to correlate, making it an oblique model. However, there is no rotation to choose, in CFA factors are either correlated (oblique) or uncorrelated (orthogonal). This is because in CFA the investigator has the ability to impose true simple structure (i.e., indicators load one factor not at all on other factors), which rotation algorithms are designed to approximate. Further, each observed variable has a residual variance, reflecting unique variability unaccounted for by the factor plus measurement error. Finally, notice the curved arrow between Y2 and Y5. This reflects a residual covariance, indicating that there is shared variance in items Y2 and Y5 unaccounted for by the modeled factors.

When testing this model, the statistical package would first optimize the values of the parameters in an effort to match the data set using some form of estimator (e.g., maximum likelihood, weighted least squares, etc.), then it would compare the fit of the model implied covariance matrix to the observed covariance matrix and generate goodness-of-fit indices based on the degree of match. Please note that each model implies a certain pattern of covariation based on its parameterization. For instance, in the case where there are no free error covariances, the factors must account for all of the covariation among the observed variables. Any unaccounted for residual covariation in the actual data will contribute to worse fit.

CFA does allow for deviation from the assumption of conditional independence. Factor models are usually specified such that there is no covariance among the indicator residuals, the assumption being that the observed variables are independent from each other once the factors are accounted for (i.e., conditional on the factors). Although reasonable given the goal of factor analysis, relaxing this assumption has legitimate uses. For instance, it can be used to account for method variance between specific item sets (e.g., scales from the same instrument). However, unprincipled use of residual covariances is discouraged, as it can capitalize on chance in any given data set, especially when sample size is large, and result in non-replicable model complexity.

Despite the benefits of CFA, it has been used less frequently in structural studies of PD, especially for item level investigations. Several studies have used CFA to test whether the DSM's three-cluster system for organizing PDs. That is, given that the DSM organizes PDs in to three clusters based on putatively shared features, CFA can be used to test whether the patterns of diagnostic (or dimensional symptom count) covariation support a three factor solution. This is a good example of matching a hypothetical assertion based on clinical observation to a statistical model that can be tested in clinical data. However, as suggested by the EFA results reviewed above, in the majority of studies testing this question the estimated CFA models showed unacceptable fit to the data (Bastiaansen, Rossi, Schotte, & Fruyt, 2011; Chabrol, Rousseau, Callahan, & Hyler, 2007; Yang, Bagby, Costa, Ryder, & Herbst, 2002), or produced improper solutions (Trull et al., 2013).

Bastiaansen and colleagues (2011) extended this general question by comparing the relative fit of the DSM's 3-cluster model with a model based on the five-factor model, including factors for Negative Affectivity (termed high neuroticism in Bastiaansen et al.), Detachment (low extraversion), Antagonism (low agreeableness), and Constraint (high conscientiousness), in a large sample of patients. They found that the five-factor model based structure achieved considerably better fit than the DSM's model using the Akaike information criterion and the expected cross validation index. However, they also found that the five-factor model structure achieved good fit by some indices (e.g., comparative fit index; goodness of fit index), but comparably poor on others (e.g., the root mean square residual). They then proceeded to make modifications to the model by trimming non-significant loadings (e.g., removing the loading of paranoid PD on the Constraint factor), and using Lagrange multiplier tests (i.e., modification indices) to free paths that would be significant but were not included in the initial model (e.g., histrionic PD was allowed to load on the Negative Affectivity factor). With minor modifications the final model achieved good fit, and replicated across patients and community samples.

Two aspects of the post-hoc modifications adopted in this study are noteworthy. First, this approach highlights that CFA studies are rarely exclusively confirmatory, just as EFAs are not exclusively exploratory (more on this below). CFAs can be used as direct tests of a theoretical structure, if theory is sufficiently clear to specify every factor loading. Yet in practice an investigator will frequently find that a theoretical model achieves reasonable fit, but there is room for substantial improvement in fit. Moreover, in those situations there will often be modifications that can be theoretically justified and will result in significant improvements in fit. This leads to the second point, that Bastiaansen and colleagues (2011) took care to consider whether suggested modifications were theoretically justified. When in this situation, it is the responsibility of the investigator to make the call on whether adding a parameter is theoretically defensible. In many cases adding a parameter might be reasonable, but researchers should be careful not to merely over-fit the model to one particular dataset. In particular, freeing residual variances should be approached with caution. Bastiaansen et al.'s cross-validation in a separate sample following post-hoc modifications is therefore exemplary factor analytic work.

Relatively fewer studies have attempted to fit CFA models to symptom/criterion level data across several disorders. However, two studies tested the latent structure of DSM-IV PD criteria using CFA (Durrett & Westen, 2005; Huprich et al. 2010). They found only modest support for a model with ten correlated factors for the ten specific PDs, with fit indices below or around the lower bound of acceptability.

More commonly, CFA has been used to study the structure of a single disorder, notably borderline PD (BPD). There are now at least eight studies that have subjected interview based BPD symptom criteria to CFA (Clifton & Pilkonis, 2007; Conway, Hammen, & Brennan, 2012; Feske et al., 2007; Fossati et al., 1999; Hawkins et al., 2014; Johansen et al., 2004; Sanislow et al., 2002; Sharp et al., 2015). In six of these studies (Clifton & Pilkonis, 2007; Conway et al., 2012; Feske et al., 2007; Fossati et al., 1999; Hawkins et al., 2014; Sharp et al., 2015) results showed that a single latent factor provided good fit to the data. The remaining two studies (Johansen et al., 2004; Sanislow et al., 2002) settled on good-fitting 3-factor models. However, the factor correlations in these two studies ranged from .90-1.00, suggesting that the factors are hardly distinguishable and a single factor model would provide a more parsimonious summary of the data. On the one hand, these studies could be used to argue that BPD reflects a conceptually and statistically coherent diagnostic unit. On the other hand, though, these results are ambiguous because they do not test the structure of BPD in the context of other diagnostic features. That is, it is unclear whether the BPD criteria hang together because of something specific to these 9 criteria, or because, perhaps the factor represents severity of impairment and any 9 criteria would form a well-fitting unitary factor. A more stringent test would examine whether a BPD factor would retain its structure in the presence of the criteria from other disorders.

To complete this section, the findings from Sharp and colleagues (2015) are summarized to highlight how several factor analytic techniques can be used in conjunction to test theoretical propositions. The motivation behind this study was to address the noted ambiguity in the structure of BPD using a large sample of psychiatric patients assessed for a range of PDs (antisocial, avoidant, borderline, narcissistic, obsessive-compulsive, and schizotypal). Specifically, clinical theory (Kernberg, 1984) argues that the criteria codified in DSM BPD do not mark a unitary categorical disorder, but rather are indicators of impairments in personality organization (i.e., a dimension of personality functioning). In other words, BPD symptoms are markers of a particular degree of severity of personality dysfunction, and individuals can vary in the stylistic manifestation within that level. Thus, the challenge was to develop statistical models that would adjudicate between the DSM's perspective of BPD as a discrete disorder and Kernberg's (1984) perspective that BPD symptoms are makers of general PD severity.

Three models were selected for comparison. First, the DSM's discrete diagnosis model was represented with a CFA model that included a factor for each diagnosis (i.e., six factors), on which all symptoms from that diagnosis freely loaded, and no symptom cross-loadings were permitted. Second, because a strict item-level CFA represents an implausible model, an EFA with oblique Geomin rotation was chosen as a more reasonable alternative. However, because the EFA did not constrain the BPD items to all load exclusively on one factor, it represented a test of their coherence in the presence of criteria of diverse content. Finally, a bi-factor EFA model was estimated, using recently developed bi-factor rotation techniques (Jennrich & Bentler, 2011; 2012). In a CFA framework a bi-factor model simultaneously estimates a general factor on which all indicators load and specific (or group) factors on which only a subset of indicators load (see Figure 1, Panel D). As noted, EFA rotation techniques are now available that approximate these structures but allow all items to load on all factors. Thus, the general factor represents what all indicators share, and specific factors represent what only a subset of indicators shares, net of the general factor. Of particular interest for this study was whether the BPD symptoms would load most strongly on the general factor or form a specific factor.

Results showed that the DSM's model provided the worst fit to the data, fit was significantly improved moving to the EFA, but ultimately the bi-factor model provided the best fit to the data (due to the estimation of an additional factor). More interesting than each model's absolute fit were the pattern of BPD symptom loadings across models. Although all BPD items loaded strongly on a single factor in the CFA, this factor was correlated strongly with all other factors (range of rs = .47-.61). In the EFA model the BPD criteria no longer loaded strongly on a single factor, with 6 loading most strongly on one factor (3 of which had marked cross-loadings, i.e., > .30), and the 3 remaining items had their highest loading on other factors. In the presence of indicators of diverse content the BPD structure begins to disassemble. Finally, in the bi-factor model, the BPD items all loaded most strongly on the general factor, with uniformly large loadings (range = .53-.74), with little in the way of loading on the specific factors. Thus, through a combination of CFA and EFA models, Sharp and colleagues (2015) pitted the DSM model against Kernberg's theoretical model and the results strongly favored Kernberg's model. This should not be too surprising, given that Kernberg's model and patients diagnosed by resident psychiatrists working on his inpatient service were used as the prototypes during initial validation of the diagnosis (Spitzer, Williams, & Endicot, 1979). Additionally, although not yet published, emerging results replicate Sharp et al.'s (2015) findings in a different patient sample (Williams, Scalco, & Simms, 2016).

Exploratory Structural Equation Modeling

As noted throughout, EFA is rarely exclusively exploratory, and CFA is rarely exclusively confirmatory. Rather, as commonly implemented, each technique involves exploratory and confirmatory aspects. A recently developed technique, ESEM (Asparouhov & Muthén, 2009), blends the core features of EFA (i.e., exploratory factors, range of rotations) and CFA (i.e., the ability to specify parameters, user specified factors, multiple group analysis) allowing for near total flexibility in modeling. Numerous advantages are gained by this innovation. These include the ability to estimate method factors in EFA analyses of multiple scales from different measures, correlated residuals, and adding parameter equalities across two scientifically interesting groups (e.g., genders, patient vs. non-patients). Figure 1, Panel C, provides a hypothetical example of an ESEM model. In this diagram, in addition to two obliquely rotated EFA factors (F1 and F2), there is a third, investigator specified factor (F3) that is orthogonal to the other two. F3 could perhaps represent shared method variance for observed variables Y1-Y3, or that they are markers for more than one construct. Finally, the residuals for Y4 and Y6 are allowed to correlate. In the modeling of complex personality data that has large item sets, ESEM benefits from the efficiencies of the EFA framework, while allowing the investigator the control over specific modeling features that are afforded with CFA.

Similar to CFA, ESEM relies on estimation methods that ultimately result in in an implied covariance matrix that can be compared to an observed matrix in various ways to generate goodness-of-fit indices. The fact that the EFA portion of the structure can model a large number of potentially conceptually negligible but statistically significant cross-loadings generally results in considerable improvement in fit over a strict (and implausible) simple structure imposed by many CFAs. However, it is worth emphasizing that factor analytic techniques are largely separable from the estimation approach. While certain estimation methods (e.g., principle factor analysis) are reserved for EFA, estimators like maximum likelihood and weighted least squares can be applied to EFA, CFA, or ESEM. This underappreciated fact often results models erroneously labeled as ESEMs, when in reality only a maximum likelihood EFA has been conducted. Although this produces fit criteria, no additional user specified parameters have been included. EFA is a very useful technique, and the objection with labeling a maximum likelihood EFA an ESEM is that it creates the perception that there are user specified parameters without the user having specified any beyond a standard EFA. Alternatively, a maximum likelihood EFA can be considered a very basic form or a special case of an ESEM, and the same an be said for CFA. Therefore, with the advent of ESEM factor analytic models can now be understood as falling along an exploratory to confirmatory spectrum, both conceptually and quantitatively. From this perspective users should give thought to the degree to which they can specify, or have hypotheses about, the underlying structure of their observed variables, and they can then select the appropriate model accordingly: fully exploratory (EFA), fully confirmatory (CFA), or some hybrid of the two (ESEM).

Given that well validated personality inventories often fit poorly in CFA models (Hopwood & Donnellan, 2010), personality researchers generally have been early adopters of ESEM. There are now several published examples using PD scales. For instance, Gore and Widiger (2013) estimated the joint factor structure of four personality inventories, including the PID-5, to examine whether the normal range and pathological scales combined to indicate the same five factors. An initial maximum likelihood EFA resulted in poor fit to the data, so an ESEM was estimated allowing the residuals of indicators from the same personality inventory to correlate across factors. This ultimately resulted in an excellently fitting model, and a theoretically expected five-factor structure. In this case an ESEM allowed Gore and Widiger (2013) to account for the dependency among scales from the same inventory within an otherwise exploratory analytic framework. Other examples include Wright and Simms (2014, 2015), who dealt with the same issue in a similar but distinct fashion by estimating method factors for each inventory used in an otherwise exploratory model. For example, Wright and Simms (2015) tested whether the joint structure of clinical syndromes, DSM PD dimensions, and the PID-5 would conform to a recognizable five-factor structure (Negative Affectivity, Detachment, Antagonism, Disinhibition, and Psychoticism). In addition to estimating correlated substantive exploratory factors on which all items loaded, orthogonal measure specific factors were included for the clinical syndrome interview, the PD interview, and the PID-5, on which all indicators from each measure loaded. This served to isolate shared method variance while retaining substantive variance in each indicator.

The advent of ESEM offers investigators considerably more flexibility. Researcher encouraged to think of models not as either exploratory or confirmatory, but as falling somewhere along a continuum between those two poles. Thought should be given to whether any parameters can be specified and tested, even if parts of the model will be determined via exploratory techniques. A note of caution is warranted, however, because not all data sets will be suitable for ESEM. Like all SEM techniques, the models are ideally estimated in reasonably large sample sizes, and investigators should be mindful of the assumptions and requirements of their chosen estimators (e.g., maximum likelihood assumes normally distributed continuous variables, etc.).

Factor Analysis for Intensive Longitudinal Data

The field has now demonstrated more than a passing interest in ambulatory assessment, and there are an increasing number of studies that are generating intensive longitudinal data in the service of studying the real-time dynamic processes of PD (e.g., Ebner-Priemer et al., 2007; Miskiewicz et al., 2015; Russell et al., 2007; Sadikaj et al., 2013; Trull et al., 2008; Wright, Hopwood, & Simms, 2015). Ambulatory assessment studies of PD are following individuals closely for days to months at a time sampling multiple dimensions (e.g., affect, interpersonal behavior, cognitions) intensively and repeatedly over minutes, hours, and days. The data generated by these studies have a complex structure, with repeated samplings nested within individuals. That is, observations within each person are, to some degree, dependent on each other, and therefore are not appropriate for standard between-person factor analyses. At the same time, these complex data bring with them the opportunity to answer questions about the dynamic within-person structure of PD, as well as individual differences in those structures. Up to this point the focus has been on “traditional” clinical data, of the type that emerges from clinical interviews and self-report inventories. Factor analysis applied to this type of data model the between-person structure of PD, or individual differences in the endorsement patterns of PD features. However, this may or may not tell us about the dynamic structure of these features within each individual as they play out over time, and individuals may differ in their idiographic symptom structure in ways that are important (Molenaar, 2004; Beltz, Wright, Sprague, & Molenaar, 2016). The next two sections cover factor analytic methods appropriate for intensive longitudinal data.

Multilevel Structural Equation Modeling

One promising approach to simultaneously studying between- and within-person structure in PD is multilevel structural equation modeling (MSEM; Muthén, 1991, 1994). Readers are likely familiar with multilevel regression (i.e., multilevel modeling; hierarchical linear modeling; mixed effects models), which extends the general linear model to accommodate nested data by including both fixed and random effects and adjusted standard errors. In a similar fashion, MSEM extends covariance and mean structural models to accommodate nested data. As EFA and CFA represent special cases of the broader latent variable modeling framework (i.e., SEM), multilevel factor analysis (MFA) is also available. Not all statistical packages include MSEM, although MPlus and recent versions of LISREL and Stata do. MSEM works by partitioning the total variance in the observed variables into the latent between-person variance (commonly referred between-cluster or -group variance), and the observed within-person (also within-cluster or -group) variance (Muthén, 1991). In the case of ambulatory assessment data, the between-person variance reflects average variance in the indicators over time, whereas the within-person variance reflects the net fluctuations around an individuals average once that variance is removed.

The partitioned variance can then be used to calculate both between- and within-person covariance matrices. Although the within-person covariance matrix is straightforwardly calculated and understood, calculation of the between-person covariance matrix is more complex (i.e., it is weighted for differences in cluster size) and is conceptually akin to the covariance among random intercepts (see Muthén, 1994 and Heck, 1999 for technical details, and Reise et al., 2005 and Preacher et al., 2010 for accessible summaries). With the variance thus partitioned, MSEM offers the opportunity to separately estimate and compare between- and within-person structures by fitting standard latent variable models, like CFA. A multilevel CFA allows different factor structures to emerge at each level of the data, if indicated. Again, as it relates to intensive longitudinal data, the between-person structure reflects the pattern of covariation in average item endorsements over the course of the study, or, conceptually, the trait structure of these behaviors. In contrast, the within-person structure reflects the tendency for individual behaviors to covary at the momentary level, or, conceptually, the dynamic structure of these behaviors as they fluctuate together over time.

To date there has been only one MFA study in the PD arena. Recently Wright, Beltz, Gates, Molenaar, and Simms (2015) used multilevel CFA to test whether the within-person dynamic structure of daily maladaptive behaviors, and the between-person structure that emerges from daily assessments conformed to the well-replicated Internalizing and Externalizing structure of psychopathology, and which has also shown relevance as a higher order structure of PD (Widiger & Simonsen, 2005; Wright & Simms, 2014; Wright, Thomas, et al., 2012). This question was tested in a sample of individuals (N=101) diagnosed with PD who reported nightly on daily maladaptive behaviors over the course of 100 consecutive days. Results suggested that similar structures emerged at the individual (i.e., between) and daily (i.e., within) levels, although the within-person structure was more differentiated, likely due to the dramatically increased power to detect differences between factors. As such, the between-person structure bore strong resemblance to the predicted two-factor Internalizing-Externalizing structure, and the within-person structure resulted in a four-factor Negative Affectivity-Detachment-Disinhibition-Antagonism model, which reflects a lower level in the same conceptual hierarchy. Additionally, the between-person factors exhibited unique associations with Internalizing and Externalizing factors estimated from diagnostic interviews.

In practice, when estimating MSEM one must be mindful of the between-person sample size, which will place limits on the complexity of the between-person portion of the model that can be estimated. Many ambulatory assessment studies have large total numbers of observations (e.g., in the thousands), but many fewer individual participants, especially when clinical samples are included. The smaller between-person sample size may prove problematic for estimating a parallel model both within- and between-person. Because MSEM uses the pooled within-person covariance matrix, the within-person portion of the model is generally immune to these considerations.

Person-Specific (P-Technique) Factor Analysis

In clinical practice, the aim of the work is to uncover the individual patient's structure, being then able to understand the particular patterning and contingencies of behavior that give rise to the maladaptive functioning of the presenting problem. This task is generally accomplished with a combination of clinical interviews, close observation, and narrative summaries over several consultations, as might be the case in the early part of a course of psychotherapy. The expectation is, that by understanding the patterning of various behaviors key processes will be revealed, that if altered might cause a disruption of the psychopathology. Readers may recognize that this process is an informal approximation of what factor analysis is intended to do: uncover the pattern of covariation of observable behavior. With appropriate data, this process can be formalized with quantitatively rigorous approaches in the form of p-technique factor analysis (Cattell, 1943, 1946; Cattell & Luborsky, 1951).

P-technique factor analysis is the application of factor analysis to the multivariate time-series of an individual's data sampled repeatedly over time. As such, it can be either exploratory or confirmatory, and both EFA and CFA have been used in this way. MSEM provides a much-needed window into the patterns of dynamic covariation of behavioral targets. However, it generally maintains the focus on the average or pooled within-person structure, ignoring the possibility of truly person-specific or idiographic structures. P-technique instead focuses in on the individual, explicitly allowing for potentially highly diverse factor structures across individuals (Molenaar, 2004).

As Cattell and Luborsky (1951) argued, noting the complexity of the clinical task associated with truly understanding an individual's personality, “p-technique... is a system of factor analysis capable of revealing the unique trait structure in a single individual, and it is this method, therefore, that promises to be of particular value to the clinical diagnostician” (p. 4). The key point is that clinicians, and by extension patients, may not have access to the patterns and processes of their own behavior, which are oftentimes too complex to track directly unaided with appropriate tools. With the advent of widely available ambulatory assessment techniques for data capture and cheap but powerful computing power, it is now possible to intensively sample many target variables (e.g., behavior, psychophysiology, contextual variables) and submit them to objective statistical models that can reveal the patterns that are otherwise elusive or require considerable clinical contact and observation. Just as with cross-sectional interview data, factor analytic techniques (i.e., p-technique) allow an investigator to make sense of multivariate data by establishing its underlying structure.

For those unfamiliar with this approach, interpreting a p-technique factor analysis may not be immediately intuitive. The factors naturally do not represent trait differences, but rather represent dynamic state differences within an individual over time. Even a well-recognized factor (i.e., that corresponds in structure to an individual difference factor), for instance indicated only by negative affect items sampled repeatedly over time, would represent an individual's distribution of negative affect states over time, not their level of negative affectivity relative to others. That the factors represent states over time opens up interesting research questions. For instance, a general negative affect factor may not be all that remarkable, but differences in this structure across individuals may be. For instance, assuming sufficient negative affect items, one could use the number of emerging factors, or the strength of factor loadings, to represent the degree of emotional differentiation. Alternatively, by including items of diverse content (e.g., affective, perceptual, behavioral) one can begin to target more complex constructs.

As an example of this, Wright and colleagues (2016) demonstrated how p-technique models could be used to study between- and within-person heterogeneity among individuals diagnosed with BPD. Specifically, they modeled interpersonal situational structures, defined by perceptions of self, other, and linking affect, consistent with a variety of theories of personality pathology, including attachment (Mikulincer & Shaver, 2007), object-relations (Kernberg, 1984), and interpersonal theory (Hopwood, Pincus, & Wright, in press). P-technique was applied to data collected over 21-days using an event contingent protocol, such that after each interaction of > 10min participants rated their perception of the other's behavior, their own behavior, positive and negative affect. Individual participant factor models varied considerably in the number of resulting factors, and in the pattern of loadings. For instance, one individual's model was defined by a single factor, on which negative affects and perceptions of others’ dominance loaded strongly, whereas positive affect, self and other affiliation loaded negatively. This might be suggestive of processes associated with “splitting” or a “black and white” perceptual style. That is, interpersonal situations vary along a single dimension of positivity versus negativity. In contrast, another participant had a clearly discernable four-factor structure, with distinct factors labeled negative affectivity, positive affectivity, agreeableness, and engaged other. For this participant, variation in these states correlated with incidences of self-harm.

This example is intended to illustrate the ability of p-technique models to derive theoretically consistent idiographic structures of the type that are difficult to ascertain using other techniques, and hopefully generate enthusiasm for the method. Although p-technique has not yet been widely used in PD research, in addition to the study described above, it is currently being implemented to test individual fit to diverse theoretical models of BPD (e.g., Ellison et al., 2016), and is also being used in other areas of psychopathology (e.g., Fisher & Boswell, 2016).

P-technique does not require any specialized software; in fact, any statistical package that can perform factor analyses, whether exploratory or confirmatory, will do. The major consideration is collecting enough observations within a single individual to ensure a reliable estimation of their person-specific structure. Naturally, the minimum suitable number of observation will vary depending on the complexity of the model (i.e., number of indicators and factors). However, good recovery of parameter estimates has been observed for relatively non-complex models with only 50 observations (Molenaar & Nesselroade, 2009). Investigators are advised to plan to collect substantially more observations, though, as this will result in more stable estimates, smaller standard errors, and will be better insulated against missed observations.

Conclusion & Future Directions

Currently, the major points of contention in the PD field are largely debates about the underlying structure of personality pathology. Because factor analysis is ultimately a method designed to determine the latent structure of observable phenomena, it therefore has played, and will continue to play, a central roll in contemporary PD research. This review sought to provide researchers with a conceptual overview of the various ways in which factor analytic techniques should be and have been applied in PD research. As part of this review, underused techniques that allow for the study of structure in intensive longitudinal data were introduced. To summarize, several overarching observations are made, as well as suggestions for future applications of factor analysis in PD research.

First, factor analyses have traditionally been construed as either exploratory or confirmatory, but reviewing the way these models are actually applied suggests that there is no bright boundary between methods. Further, with the addition of ESEM, it is now clear that fully confirmatory and exploratory models are really endpoints along an exploratory-confirmatory spectrum. Ambiguity can be unnerving, but flexibility should be embraced. Researchers are encouraged to approach future factor analyses with a thoughtful consideration of whether they intend it to be fully exploratory, fully confirmatory, or whether there are aspects of both involved in the study.

Second, although the intermediate to higher order levels of the PD hierarchy appear reasonably well delineated, much work remains to be done at the level of specific scales and overall mapping of content. For instance, it has been observed that the DSM-5 alternative model lacks specificity in the areas of interpersonally warm problems (e.g., Widiger, 2010; Wright, Pincus, et al., 2012). Principled expansion of this scientifically supported model via factor analytic techniques would be advisable.

Third, more work is necessary to integrate PD with extant empirical models of personality and psychopathology. Only a handful of studies have thus far studied structural models of psychopathology including all or the majority of PDs. However, when included, PDs begin to reshape the structure from Internalizing and Externalizing to more nuanced structures that include interpersonal dysfunction. Now that the DSM has dispensed with the arbitrary distinction of Axis I and Axis II, it will be important to demonstrate the role of PD constructs in the structure of mental disorders writ large. By a similar token, with estimates placing the rate of DSM defined PD at 10% of the population (Lenzenweger et al., 2007), there is increased impetus for integrating the structure of PD with normative personality. Currently the broad-brush stokes have been laid down, and it is clear that maladaptive variants of the big-5 go a long way toward accounting for the structure of those features identified as central to personality pathology (e.g., Krueger et al., 2012). Nevertheless, more fine-grained integration of facet level structure is necessary.

Finally, with the rapid increase of studies using intensive longitudinal designs, novel opportunities and challenges have been generated for the use of appropriate factor analytic techniques. For instance, there is the particular need for basic psychometric and scale development work to ensure that the items being administered at the momentary and daily level adhere to theoretically prescribed structures. MFA is ideally suited to address this issue. Additionally, MFA offers the ability to control for measurement error in intensive longitudinal investigations, allowing for more reliable estimates of constructs. However, these aspects will need to be balanced with the challenges of administering larger items sets, which can be difficult in intensive repeated designs. P-technique and related approaches bring the individual into sharp focus, placing the person at the center of personality pathology. Many theoretical models of PD focus on within-person structures and processes, and the majority of our methods are best suited for between-person questions. At the same time, N=1 analyses raise the timeless question of how best to bridge the nomothetic and idiographic (Beltz et al., 2016)? Investigators who are stimulated by these opportunities and challenges have a wide-open field ahead of them.