Canalization, Developmental Stability, and Morphological Integration in Primate Limbs

Abstract

Canalization and developmental stability refer to the tendency of developmental processes to follow particular trajectories, despite external or internal perturbation. Canalization is the tendency for development of a specific genotype to follow the same trajectory under different conditions (different environments or different genetic backgrounds), while developmental stability is the tendency for the development of a specific genotype to follow the same trajectory under the same conditions. Morphological integration refers to the tendency for structures to show correlated variation because they develop in response to shared developmental processes or function in concert with other structures. All three phenomena are emergent properties of developmental systems that can affect the interaction of development and evolution. In this paper, we review the topics of canalization, developmental stability, and morphological integration and their relevance to primate and human evolution. We then test three developmentally motivated hypotheses about the patterning of variability components in the mammalian limb. We find that environmental variances and fluctuating asymmetries (FA) increase distally along the limb in adult macaques but not in fetal mice. We infer that the greater variability of more distal segments in macaques is due to postnatal mechanical effects. We also find that heritability and FA are significantly correlated when different limb measurements are compared in fetal mice. This supports the idea that the mechanisms underlying canalization and developmental stability are related. Finally, we report that the covariation structure of fore- and hindlimb skeletal elements shows evidence for morphological integration between serially homologous structures between the limbs. This is evidence for the existence of developmental modules that link structures between the limbs. Such modules would produce covariation that would need to be overcome by selection for divergence in hind- and forelimb morphology.

INTRODUCTION

Canalization, developmental stability, and morphological integration are three related components of phenotypic variability. By variability, we mean the tendency or propensity to vary and not variation itself (Wagner and Altenberg, 1996). These three components of variability describe how the tendency to vary is structured. Canalization refers to “the suppression of phenotypic variation” among individuals (Wagner et al., 1997). Developmental stability refers to the suppression of phenotypic variation within individuals, and morphological integration refers to how variability is structured by the under-lying developmental and genetic connections between traits. We follow Smith (1996) and Lieberman et al. (2000b) in distinguishing between the processes that produce integration and observed patterns of covariation. In this paper, the definition of morphological integration is process-based, in that it refers to the underlying processes that produce the pattern of phenotypic correlations among traits and not to the patterns of correlations themselves. As all three aspects of variability can have important effects on the rate and direction of evolutionary change, the study of these emergent properties of developmental systems is relevant to all aspects of evolutionary change. Here, we summarize what is known about canalization, developmental stability, and morphological integration. We then relate these concepts to the evolution of primate limb morphology, and test developmentally motivated hypotheses about the patterning of variability components in the mammalian limb. Finally, we discuss future avenues of research that apply current approaches in developmental genetics to the study of variability in evolutionary and biomedical contexts.

THE SIGNIFICANCE OF VARIABILITY COMPONENTS

Patterns of variability are important because they tell us something about how developmental systems structure the production of phenotypic variation. This, in turn, is crucial to understanding how development interplays with natural selection to produce evolutionary change. Developmental systems structure the production of variation in two ways. One is by modulating the amount of phenotypic variation, and the other involves the biasing of the distribution of the variants that are produced. Processes that minimize variation contribute to canalization and developmental stability, while those that bias the direction of variation contribute to morphological integration. Both are probably related to the evolution of organismal complexity. For organisms to develop as functionally integrated systems, structures have to develop in highly predictable ways. For example, cusps in the upper and lower dentition of most mammals, including primates, develop highly concordant morphologies, producing specific shearing patterns. This requires a tightly coordinated developmental system that produces concordant directions of variation in functionally or developmentally related structures, and minimizes variation orthogonal to these concordant directions. Presumably it is selection for this kind of predictability in developmental systems that has favored the evolution of both morphological integration and mechanisms that reduce variability in development (Hall, 1999).

Canalization, developmental stability, and morphological integration affect both the magnitude of phenotypic variances and bias the production of variation. This, in turn, affects both the rate and direction of evolutionary change. Since any property of development that biases the production of phenotypic variation can be viewed as a developmental constraint (Alberch, 1982; Maynard Smith et al., 1985), these three aspects of variability are closely related to this concept. Interestingly, the rate of evolution is both decreased and increased by canalization and developmental stability (Gibson and Wagner, 2000; Kawecki, 2000). Mechanisms that reduce the phenotypic effects of mutations will decrease the rate at which selection can act on them. This can result in the buildup of hidden genetic variation, which is exposed when buffering mechanisms are impaired (Rutherford and Lindquist, 1998; Wagner et al., 1999; Yahara, 1999). Buffering mechanisms could be impaired by environmental stress or by mutations, and thus create situations where a hidden reserve of genetic variation is exposed to selection, creating a period of rapid evolution. The extent to which the mechanisms underlying canalization and developmental stability modulate evolutionary rates in this way is an open empirical question.

Morphological integration also affects the rate of evolution. The evolution of an integrated trait is hampered or enhanced, depending on whether the fitness effects on the correlated traits are negative or positive. When a trait is selected in a direction that negatively impacts the fitness of other traits, evolution is slowed. When the reverse is true, integration facilitates the evolution of a complex of traits (Lande, 1979). In the view of Wagner and Altenberg (1996), modularity increases evolvability by decreasing pleiotropic effects (most of which are disadvantageous) among traits that are not functionally related.

Variability components also affect the direction of evolutionary change. Bias in the types of mutations that are likely to be buffered could bias the nature of the genetic variation that can accumulate as the result of canalization and developmental stability. More obviously, integration patterns can bias the direction of evolutionary change by structuring the variation exposed to selection. Of course, selection can also shape integration patterns. Covariance structures evolve and are partly shaped by the pattern of stabilizing selection (Cheverud, 1984, Lande, 1980). The degree to which integration produces constraints or bias on the direction of evolutionary change is therefore an empirical question that can be addressed through studies of the evolution of morphological integration patterns.

The study of variability holds particular interest for biological anthropologists interested in developmental approaches to understanding evolutionary change. This is because patterns of variation are often the main source of data that can be applied to problems in primate and human evolution. Like Chiu and Hamrick (2002), we advocate an approach to morphological evolution in primates that integrates the study of patterns of phenotypic variation with parallel studies of the developmental-genetic determinants of variation in experimental models such as mice. Within the context of an increasing understanding of the developmental biology of model organisms, patterns of phenotypic variation can be used as a conceptual tool to dissect out aspects of the developmental architecture, underlying important morphological transformations in primate and human evolution. The work by Lieberman (2000) and Lieberman et al. (2000a, b) on the role of the cranial base in human evolution, or by Hamrick (2001) on digital ray patterning and segmentation, provide great examples of this. Understanding how developmental systems structure the tendency to vary, therefore, is of even greater importance to research in biological anthropology than for other areas in which the subjects of study can be experimentally manipulated.

Canalization, developmental stability, and morphological integration also have important and underappreciated biomedical implications. Variability is particularly relevant to the study of congenital anomalies and syndromes characterized by a suite of such malformations. Understanding the mechanisms of variability in concert with a thorough understanding of normal developmental pathways will aid in predicting the phenotypic outcome of genetic and molecular aberrations.

Although little research has been conducted on the biomedical relevance of variability, two interesting approaches to this issue have been proposed. The first of these, amplified developmental instability, relates canalization and developmental stability with the manifestation of symptoms (Shapiro, 1971, 1983, 1992), while the concept of developmental field defects associates the role of morphological integration with the presence of malformations (Lammer and Opitz, 1986).

An association between developmental stability and various kinds of congenital malformations such as cleft lip with or without cleft palate, Down syndrome, or scoliosis is fairly well-established. The extensive literature on this topic was recently reviewed by Thornhill and Møller (1997). Shapiro (1975, 1983, 2001) described Down syndrome as a consequence of amplified developmental instability. He argued that the symptoms that occur in conjunction with trisomy 21 are found in the general population, and as such, the characters that are affected are less stable than unaffected elements. Therefore, the symptoms of Down syndrome reflect an amplification of instability. Naugler and Ludman (1996b) made a similar argument, proposing that the association between developmental instability and various types of malformations is sufficiently strong that measures of developmental stability can serve as risk markers. Naugler and Ludman (1996a) provided an example of odds ratios for developmental delay, calculated on the basis of fluctuating asymmetry (FA) in human children. Fluctuating asymmetry refers to the normally distributed deviations from perfect symmetry that are usually attributed to developmental instability. The application of FA to the prediction of malformations seems unlikely, however. Although FA can be used to measure developmental instability in populations, morphological asymmetry is actually a poor predictor of an individual’s developmental stability (Palmer and Strobeck, 2002). The reason for this is that an individual’s developmental instability is a variance of potential outcomes, which asymmetry measures with one degree of freedom. Certainly, this ambitious proposal demands further research before infants are subjected to multivariate anthropometric measurements in the family physician’s clinic.

Lammer and Opitz (1986) investigated the role of developmental integration in the manifestation of syndromes. They defined developmental field defects as groups of symptoms that are caused by the disruption of single underlying developmental process. Using DiGeorge syndrome as an example, they show how a disruption of the migration of neural crest cells could be responsible for the many symptoms involved with this syndrome. Neural crest cells play a critical role in the development of the facial skeleton, providing much of the mesenchyme of the head, as well as the development of the branchial arches. DiGeorge syndrome is associated with a duplication of chromosome region 22q11 (Goldmuntz and Emanuel, 1997), and generally presents with an aplastic or hypoplastic thymus, aplastic or hypoplastic parathyroid glands, craniofacial anomalies, and heart defects, all of which could be affected by disturbances to patterns of neural crest migration (Lammer and Opitz, 1986; Sulik et al., 1986).

Several investigators have noted the high degree of phenotypic variation between monozygotic twins diagnosed with a variety of syndromes (Berry et al., 1980; Goodship et al., 1995). Similarly, it is well-known that many syndromes exhibit such a large range of variation in the presence and severity of symptoms that it is often difficult to diagnose individuals. Some individuals will show all of the classic symptoms associated with a syndrome, and others will appear phenotypically normal. Berends et al. (2001) discussed this issue, using cat eye syndrome as an example. Cat eye syndrome is associated with an aberration of chromosome region 22q11, and is characterized by three main anomalies: anal atresia, preauricular tags/pits, and coloboma of the iris (Berends et al., 2001; Luleci et al., 1989; Schinzel et al., 1981). However, only 41% of individuals diagnosed with this syndrome demonstrate these hallmark symptoms (Berends et al., 2001).

Canalization and developmental stability can help explain these discrepancies among individuals diagnosed with the same syndrome, as well as the phenotypic discordancy among monozygotic twins. When developmental stability is decreased, one can argue that there is the potential for an increase in phenodeviants, but it is not necessary that everything that can change will change. Therefore, as argued by Shapiro (1983), one would expect an increased frequency of developmental malformations in affected individuals. Individuals with exactly the same genotype and similar environmental exposures, such as monozygotic twins, can thus express very different phenotypes. Morphological integration is also a useful tool in deciphering the various symptomatic consequences of syndromes. Integration can be used to help determine the pathways that will most likely be disrupted, and therefore the traits that will presumably show increased variability.

COMPONENTS OF VARIABILITY: A REVIEW

Canalization

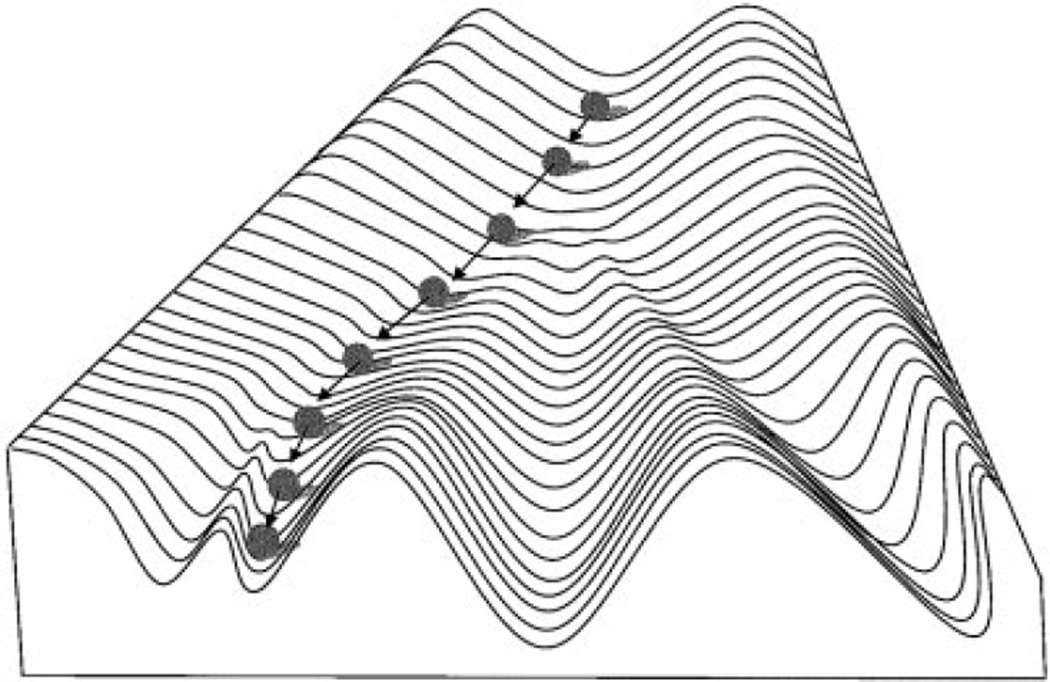
The term “canalization” was first used by Waddington (1942, 1957) to describe the buffering of developmental processes against influences such as environmental perturbations or mutations. The concept of canalization, however, was independently arrived at by Schmalhausen (1949; published in 1938 in Russian), who used the term autonomization (in the English translation) for the same idea. The argument by Waddington (1942, 1957) for the existence of canalization was as follows: 1) Components of organisms, such as cells or organs, are discrete types and do not present a gradation of possible forms. In other words, developmental pathways find their way to discrete endpoints. 2) Developmental processes often recover from major insults, to arrive at the same endpoint and produce a normal adult. This implies that developmental processes follow predefined pathways, and that developmental mechanisms exist to compensate for the effects of perturbations during development. The visual metaphor by Waddington (1942, 1957) for this property of development, which he referred to as the epigenetic landscape, is a ball rolling down a grooved slope (Fig. 1).

Fig. 1.

Epigenetic landscape of Waddington (1957). Topography of landscape represents genetic predetermination to follow particular developmental pathways. Ball rolling down landscape represents a particular developmental process playing out within an individual. Such pathways are represented by valleys that lead to discrete developmental endpoints. Steepness of sides of valleys represents degree of buffering against perturbations affecting developmental process. Modified from Waddington (1957).

While Waddington (1942, 1957) was explicitly concerned with developmental mechanisms, Schmalhausen (1949) arrived at the same idea from a different perspective. Concerned with the role of stabilizing selection in evolution, Schmalhausen (1949) argued that natural selection favors mechanisms that allow organisms to resist the effects of environmental insults, and at the same time respond adaptively to environmental changes. Schmalhausen (1949) wrote, “the process of slow and stabilizing selection is always and continuously causing the development of regulating mechanisms which protect the slowly changing norm against disturbances by external influences.” The conceptual core of the work of Schmalhausen (1949) is the norm of reaction and its relation to stabilizing selection. The norm of reaction refers to the relationship between the distribution of phenotypes for a particular genotype and a determining environmental factor. First proposed by Woltereck (see Stearns, 1989), the modern concept of the norm of reaction and its evolutionary significance were first fully articulated by Schmalhausen (1949). In his view, the ability to resist random environmental influences goes hand in hand with the ability to respond adaptively to the environment. Unlike Waddington (1942, 1957), he thus saw canalization and phenotypic plasticity as complementary and not opposing processes.

Genetic assimilation and the evidence for canalization

Closely related to the concept of canalization is genetic assimilation, or the idea that environmentally induced phenotypic changes, once they become sufficiently frequent in a population to be subject to stabilizing selection, can become sufficiently canalized that they develop in the absence of the original environmental cue. Although the basic idea can be traced back to Baldwin and Morgan in the late 19th century (Hall, 2001), the concept in its modern form is usually attributed to Waddington (1942) and Schmalhausen (1949). Waddington (1942) attempted to provide experimental evidence for genetic assimilation by showing that selecting for environmentally induced traits in Drosophila, such as changes in wing vein morphology, or the ether-induced bithorax phenotype, eventually resulted in the expression of the trait without the environmental stimulus (Waddington, 1953, 1956; Waddington and Robertson, 1966). These experiments are reviewed elsewhere (Hall, 1999; Hallgrímsson, 2002; Scharloo, 1991). Waddington (1953, 1956) argued that these experiments showed that under selection for the environmentally induced phenotype, modifier loci that stabilize the expression of that phenotype are favored. In his view, these experiments provided the strongest evidence for canalization as a general property of development.

The emphasis by Waddington (1953, 1956) on the link between canalization and genetic assimilation, however, had unfortunate consequences. While it attracted the attention of evolutionary biologists who were intrigued by the demonstration that an apparently Lamarkian outcome could result from natural selection-based theory, it also conflated the argument over the validity of canalization as a process with interpretation of the genetic assimilation experiments (Scharloo, 1991). As Scharloo (1991) convincingly argued, the canalization concept is not necessary to explain Waddington’s results (1953, 1956). As originally proposed by Bateman (1959), the early genetic assimilation experiments can be explained using a threshold model in which selection for the environmentally induced phenotype produces a shift in the underlying distribution of the developmental basis for the trait. The environmentally induced phenotype in such cases must be a phenocopy, which means that it mimics a phenotype that has a genetic basis. Although recent work has begun to reveal the developmental-genetic basis for the bithorax phenotype obtained in the experiment by Waddington (1956), it is still not possible to establish with certainty that his results were due to genetic assimilation (Gibson and van Helden, 1997).

There is, however, compelling empirical evidence for canalization. This can be summarized as follows:

1. Mutant phenotypes tend to be more variable. It is commonly recognized but rarely quantified that mutant phenotypes are more variable than wildtype (Wilkins, 2002). The argument here is that mutants with significant phenotypes represent developmental configurations that have not undergone selection for canalization, and are thus more sensitive to environmental perturbations. Both Waddington (1957) and Schmalhausen (1949) provided anecdotal evidence for this, and Scharloo (1991) reviewed the experimental evidence for this observation. Recent phenotypic analyses of transgenic and induced mutant mouse models dramatically increased the range of altered developmental configurations available for study. In the few studies where variability of phenotypic expression was quantified, an increase was generally reported. Mansour et al. (1993), for example, showed an increase in phenotypic variance for inner-ear morphology in mice, with a targeted insertion in the int-2 (Fgf-3) proto-oncogene. Similarly,Tanaka et al. (1997) showed that the incidence of skeletal abnormalities is increased in mice heterozygous for a null mutation in the Cpb gene. Recently,Taddei et al. (2001) reported on the increased phenotypic variability in a mouse model for DiGeorge syndrome.

2. Variability is increased in stressful environments. Canalizing selection should reduce variability within the most frequently encountered environmental contexts. Hence, unusual environments can reveal genetic variation that remains hidden in the more highly canalized phenotype that is expressed under more usual circumstances. This hypothesis is supported by several studies (Burla and Taylor, 1982; Hoffman and Parsons, 1991). Environmental changes that deviate from the norm are usually but not always stressful, as they represent conditions to which a species has not adapted. Recent studies confirm that stressful environments increase variability (Blows and Sokolowski, 1995; de Moed et al., 1997). Recently, Rutherford and Lindquist (1998) suggested that the heat-shock protein Hsp90 provides one explanation for a relationship between environmental stress and phenotypic variability. They interfered with the function of the Drosophila heat-shock protein Hsp90 through mutation or an administered drug, and produced increases in the incidence of phenotypic abnormalities. Hsp90 is a molecular chaperone that stabilizes a variety of signalling proteins. Rutherford and Lindquist (1998) suggested that under conditions of environmental stress, such as temperature extremes, available Hsp90 levels could fall, as it is used up by stress-damaged proteins. This, in turn, results in increased morphological variability.

3. Selection produces less phenotypic change closer to the mean of a phenotypic distribution. This is the most direct evidence for canalization, as it implies that gene effects are reduced as one approaches the mean of a phenotypic distribution. Much of this evidence comes from early experiments by Waddington (1957), Rendel (1967), and others, and is critically reviewed by Scharloo (1991).

4. The tendency to vary (variability) can have a genetic basis. The concept of canalization requires that stabilizing selection can alter the tendency of a developmental system to vary. In other words, stabilizing selection must be able to affect the responsiveness of a developmental system to genetic and environmental changes. There is abundant evidence to support this claim. One is the frequent observation that the phenotypic effect of a mutation depends on the genetic background. Such effects, due to epistatic interactions between genes, are thought to be the rule rather than the exception. For a recent review of the evidence for the influence of the genetic background on the phenotypic effects of mutations, see Nadeau (2001). A more direct source of evidence is the discovery of genes that specifically affect variability. The only example of this so far is the heat-shock protein Hsp90 discussed above (Rutherford and Lindquist, 1998), but this study suggests the possibility that other molecular chaperones may have similar dampening effects on the expression of genetic variation and responses to environmental effects (McLaren, 1999; Rutherford, 2000).

The evolution of canalization

Much progress in understanding canalization has been made in recent years through the development of quantitative genetics models, which show how canalization could be produced by natural selection. In the first of these studies,Wagner et al. (1997) defined canalization as a reduction in the phenotypic effect of a mutation or environmental change. Based on this definition,Wagner et al. (1997) constructed a quantitative genetic model for how canalization could be produced by selection acting on the determinants of variability. Their model predicts that stabilizing selection will have different effects on the canalization of environmental vs. genetic changes. While stabilizing selection should always favor variants that reduce environmental variability, a reduction in the effect of mutations is only predicted under fairly specific conditions. Most importantly, traits must exhibit a high genetic variance in order for stabilizing selection to produce an increase in canalization. This is because genetic canalization in the model of Wagner et al. (1997) occurs through epistatic interactions, or the influence of one gene on the phenotypic effects of another. In the absence of allelic variation at both loci involved, epistasis cannot be selected for. This results in the counterintuitive expectation that the traits most closely related to fitness, and hence with the lowest genetic variance, will be subjected to the weakest canalizing selection. This expectation needs to be tested with empirical data. Another counterintuitive aspect of the model of Wagner et al. (1997) is that strong stabilizing selection can prevent the evolution of canalization by eliminating genetic variation for a trait.

Subsequent quantitative genetic models support the idea that canalization can evolve through stabilizing selection in the presence of genetic variation and epistasis (Eshel and Matessi, 1998). In a related finding, Wagner (1996a) showed that nonlinearity in the epigenetic interactions of transcriptional regulators produces variation in genetic canalization. Finally, Kawecki (2000) widened the natural selection conditions under which canalization can evolve by presenting a model in which canalization is produced by fluctuating selection.

The evolution of redundancy in gene networks has also been suggested as a mechanism by which canalization can evolve (Wilkins, 1997, 2002). Gene duplication has been an important mechanism underlying evolutionary change on a macroevolutionary scale. On shorter time scales, gene duplication events produce sets of genes with varying degrees of overlapping function. Wilkins (1997) argued that duplication is an important mechanism underlying canalization and developmental stability, and Wagner (1999, 2000) developed a population genetic model in which selection favors individuals with genetic redundancy because they produce lower numbers of offspring with deleterious mutations. Selection for genetic redundancy and selection on epistatic interactions among genes are not mutually exclusive mechanisms by which canalization can evolve. It is possible, however, that these mechanisms operate on different time scales, with genetic redundancy being more important for longer time scales.

Canalization studies in biological anthropology

Canalization has not been extensively studied in humans and other primates. A few studies have addressed the relationship between phenotypic extremeness and fluctuating asymmetry (FA) in humans (Livshits and Smouse, 1993; Reddy, 1999). Reddy (1999) argued that the frequent failure to demonstrate such a relationship implies that developmental stability and canalization are decoupled. This is a weak argument, however. Asymmetry is a poor estimator of the developmental stability of an individual, which is really a distribution of possible outcomes (Palmer and Strobeck, 2002). Similarly, an individual’s phenotypic value is drawn from a range of possible outcomes, the variance of which is determined by the degree of canalization of the trait. A relationship between individual asymmetry and phenotypic value requires the compounding of two initially weak correlations, and is thus unlikely to be observed. The opposite conclusion was reached by Livshits et al. (1998) in a study that demonstrated a very high positive correlation between FA variances and coefficients of variation for osteometric traits in the human hand. As the authors recognized, however, this is a problematic relationship to interpret, since the genetic variances are unknown in this sample.

Tague (2002) compared the phenotypic variances of rudimentary digits with neighboring digits in three primate species. He argued that the loss of function and consequent relaxation of stabilizing se- lection should produce increased variability in the vestigial digits. He found a contradictory pattern, however, which he interpreted in light of current knowledge about limb development.

Given the nature of the evidence, canalization is very difficult to study in hominid evolution. Nonetheless, Tardieu (1999) presented a convincing, albeit anecdotal, argument for genetic assimilation in the evolution of hominid knee morphology.

DEVELOPMENTAL STABILITY AND DEVELOPMENTAL NOISE

Developmental noise is a surprisingly elusive concept, especially in light of the number of papers published on it. Waddington (1957) thought that developmental noise was different from the variation that canalization minimizes. In his epigenetic landscape metaphor, Waddington (1957, p. 40) described developmental noise as “the imperfection of the sphericalness of the ball which rolls down the valley.” The distinction is between internal and external effects. While canalization buffers developmental processes from external perturbations, developmental noise refers to imprecision in the processes themselves. We see the same perspective in early work on developmental noise, where developmental noise is thought of as “thermal” noise at some unspecified molecular level (Reeve and Robertson, 1953).

Recently, we have begun to understand the nature of molecular level noise in biological processes. The regulation of gene transcription and translation is now known to exhibit complex stochastic cyclical behavior that contributes to phenotypic variation in gene expression among cells (McAdams and Arkin, 1997, 1999). Following on these results,Ozbudak et al. (2002) provided the first molecular level analysis of the origins of developmental noise. They introduced a gene coding for green fluorescent protein into the bacterium Bacillus subtilis. They constructed a series of strains of this bacterium that varied in the efficiency of gene transcription or gene translation. For each of these strains, they measured the among-cell (or individual) variation in the expression of green fluorescent protein. They found that gene translational efficiency, as altered through point mutations in the ribosome binding site, had a greater impact on the variance of gene expression. This experiment suggests that the gene translation process may be an important source of phenotypically significant developmental noise. Since developmental processes depend on the regulation of gene expression, variation in the efficiency of gene translation is one plausible molecular-level source of developmental noise-induced variation at the morphological level. More importantly, this study shows that it is possible to generate genetic variation for a potential source of developmental noise: variation that could be heritable and could be acted on by natural selection.

In addition to variation in the timing of gene transcription cycles and the efficiency of translation, Klingenberg (2002) suggests other molecular-level sources of developmental noise, such as the stability of RNA transcripts and their protein products, and the effects of haploinsufficiency on the variability of gene expression.

Developmental stability refers to the absence of developmental noise. How is this measured at the morphological level? The most common method relies on the analysis of the minor differences between the sides in symmetrical organisms. The argument is that the sides of symmetrical organisms develop in roughly the same environment and from the same developmental-genetic programs. The differences between them, therefore, are mostly due to stochastic variation in the developmental system. Van Valen (1962) distinguished three different types of deviations from symmetry. Directional asymmetry refers to asymmetry distributions that are biased towards one side. Antisymmetry refers to cases where there is a negative correlation between the sides. Finally, fluctuating asymmetry (FA) refers to asymmetry distributions that are normally distributed around a mean of 0. This last type of asymmetry, he argued, measures developmental noise because it meets the expectations of a random probability distribution. Obviously, FA does not only measure the effects of developmental noise at the molecular level. In fact, FA reflects the molecular-level noise discussed above with microenvironmental effects at various levels, both internal and external to the organism.

Nonetheless, FA correlates with a variety of interesting factors such as heterozygosity, fitness, selection intensity, stress, and congenital malformations. The large literature on these various correlations is reviewed elsewhere (Hallgrímsson, 1998; Møller and Swaddle, 1997; Thornhill and Møller, 1997). These correlations lie behind the intense interest in developmental stability, and indicate that it does measure some fundamental and important property of developmental systems. They must, however, be interpreted cautiously because of the difficult methodological problems inherent in the measurement and analyses of FA data (Palmer, 1994; Palmer and Strobeck, 2002).

Developmental stability studies in biological anthropology

In contrast to canalization, a fair amount of work has been done by biological anthropologists on developmental stability. Some of these studies have been attempts to understand the causes of FA from patterns at the morphological level (Corruccini and Potter, 1981; Hallgrímsson, 1993, 1999; Jantz and Webb, 1980; Reddy, 1999; Saunders and Mayhall, 1982). Others have addressed the relationship between FA and heterozygosity (Comuzzie and Crawford, 1990; Corruccini and Potter, 1981; Hutchison and Cheverud, 1995; Kobyliansky and Livshits, 1989; Livshits and Kobyliansky, 1991) with conflicting results. Several studies address the relationship between stress of various kinds and developmental stability in humans and other primates (Kieser, 1992; Kieser and Groeneveld, 1994; Kieser et al., 1986a, 1997; Kohn and Bennet, 1986), while others have applied this relationship to interpret stress in bioarcheological contexts (Albert and Greene, 1999; Doyle and Johnston, 1979; Noss et al., 1983; Perzigian, 1977).

The heritability of developmental stability has been studied in external measurements in humans (Livshits and Kobyliansky, 1989) and in dermatoglyphic traits (Pechenkina et al., 2000). These studies report low but significant heritabilities for multivariate FA (0.2–0.35). The latter study reports a weak maternal effect for FA as well.

The hypothesis that morphological asymmetry signals mate quality and is thus important for sexual selection is one of the more controversial applications of fluctuating asymmetry. The argument is that low asymmetry in an individual signals a developmental system of good genetic quality. This is supposedly particularly true for epigamic traits such as elongate tail feathers in birds. Such traits are often costly to produce and carry around. The idea that asymmetry of epigamic traits is important for mate selection, first proposed by Møller (1990), was recently severely criticized on the basis of selective reporting of results (Palmer, 1999). Several studies addressed the relationship between FA and sexual selection in humans and other primates (Manning and Chamberlain, 1993; Møller et al., 1995; Singh, 1995; Thornhill et al., 1995). These results are implausible, given that they rely on the compounded effects of several weak correlations. Individual asymmetry is a poor predictor of developmental stability. Each asymmetry value for a single character in an individual estimates a variance of potential outcomes with one degree of freedom. Secondly, the asymmetry of particular characters is not highly correlated with the magnitude of asymmetry of other characters in the same individual. This is partly because each the asymmetry of each character is a poor estimator of developmental stability, but also because developmental stability probably varies among developmentally distinct structures within individuals. Finally, one must question the ability of individuals to “eyeball” the magnitude of asymmetry in potential mates when precise and repeated measurements are necessary to verify them by researchers. Thus, an individual’s assessment of the asymmetry of a few epigamic features in a potential mate and that potential mate’s genetic quality is separated by several weak correlations.

The analysis of fluctuating asymmetry data

The analysis of FA data is complicated by the fact that asymmetry variances are usually very small and difficult to separate from measurement error. The authoritative work on the analysis of FA data was done by Palmer and Strobeck (Palmer, 1994; Palmer and Strobeck, 1986, 1992, 2002). They developed a mixed-model ANOVA method which partitioned measurement error from the asymmetry variance. Klingenberg and MacIntyre (1998) extended the method of Palmer and Strobeck (2002) to principal components analysis of Procrustes data. A Euclidean distance matrix based method for the analysis of FA was also recently developed by Richtsmeier et al. (2002).

MORPHOLOGICAL INTEGRATION

Morphological integration refers to the study of covariation in organismal structure. Patterns of covariation are used to infer the underlying developmental or functional connections between traits. This field of study was initiated by Olson and Miller (1951), who advocated the use of correlation coefficients to quantify the degree to which structures are related, and later expanded their work to develop a theoretical foundation for dissecting out covariation patterns among morphological structures and understand their evolutionary importance (Olson and Miller, 1958).

Although the importance of Olson and Miller (1951, 1958) was recognized by Van Valen (1965), the study of morphological integration was largely dormant until Cheverud (1982) published a study on morphological integration in Macaca mulatta. His insight was to place his studies in a quantitative genetic theoretical context built upon the work of Lande (1979, 1980) on the evolution of genetic covariance structures. In a series of landmark studies, Cheverud (1982, 1984, 1995) showed that covariance structures tend to be patterned according to functional and developmental relationships among structures, and that these relationships affect how characters evolve. Cheverud (1988) also showed that genetic and phenotypic correlations tend to be highly correlated, implying that the phenotypic covariance structure can be used as a proxy for the genetic covariance structure, greatly facilitating the study of integration patterns.

Cheverud (1996) distinguished three levels of morphological integration. Functional and developmental integration operate at the individual level, and refer to the effects of a common function on morphological structure or connections among the developmental processes that produce them. At the population level, genetic integration occurs as the result of either pleiotropy among genes or linkage disequilibrium. Finally, at the evolutionary level, there is the coordinated evolution of structures. Cheverud (1996, p. 45) argued that “patterns of developmental and functional integration cause genetic integration which, in turn, results in evolutionary integration.”

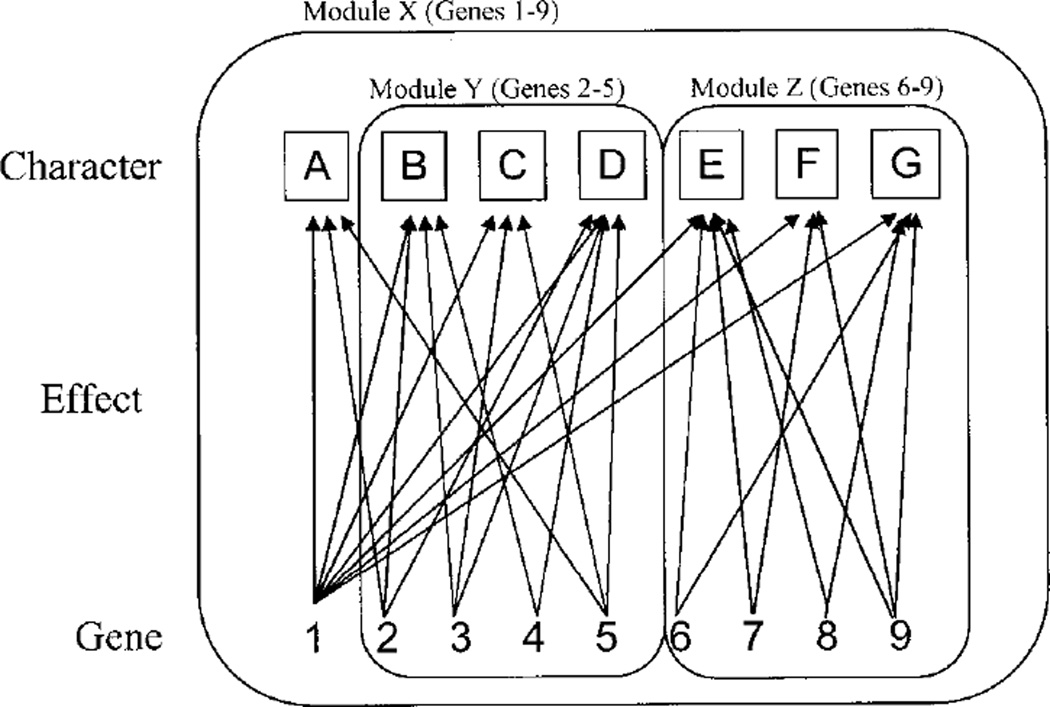
The idea that organisms are composed of semi-independent parts has a long history in both evolutionary and developmental biology (Atchley and Hall, 1991; Hall, 1995; Wagner, 1995). Recently, work by Wagner (1995, 1996b) on the quantitative genetic basis for modularity resulted in the emergence of the concept of modularity as a key integrative concept for understanding morphological integration. Wagner (1996b) defined a module as a complex of characters for which pleiotropic connections between the genes that affect it are stronger than those with other characters or character complexes. Figure 2 illustrates this concept. The modularity concept has guided much of the subsequent work on morphological integration (Magwene, 2001; Marroig and Cheverud, 2001).

Fig. 2.

Schematic illustration of modularity concept, showing three hierarchically arranged modules. Gene 1 affects all characters and thus comprises a higher-order module. Effects on body size would be an example of this. Effects of other genes and their pleiotropic interactions are confined to subsets of characters, each of which comprises a module. This figure is based on Wagner (1996b).

The basic idea behind modularity (that dissociability and “packaging” of developmental processes is necessary for evolution to occur) is a good one. Pleiotropy among functionally unrelated characters should be selected against. It is disadvantageous, for example, for changes in limb length to be correlated with some aspect of insulin regulation. However, the structuralist connection drawn between modularity and morphological characters, as initially articulated by Wagner (1996b), is probably overly simplistic. Atchley and Hall (Atchley, 1993; Atchley and Hall, 1991) provided an alternative view of the units or modularity of development that is more process-based. In their view, developmental units can be thought of as intersecting hierarchies of processes. They constructed an evolutionary developmental model for the mouse mandible in which the mandible is divided into component parts, based on embryologic origin. The size and shape of each of these components are determined by five developmental units which represent the developmental processes underlying variation in each component. In the case of the mandible, these developmental units are factors such as rate of cell division, rate of cell death, and time of initiation of condensation.

These different views of the organization of development and its relation to integration might be reconciled by expanding the concept of the module to incorporate developmental processes and by allowing the existence of intersecting hierarchies of modularity (Gass and Bolker, 2002). By this, we mean that a character can belong to multiple modules as defined on the basis of underlying developmental processes. This view of modularity, recently articulated by Wolf et al. (2001) and Gass and Bolker (2002), is consistent with the emerging view of developmental processes in which the same molecular level interactions are reused in different developmental contexts. This idea was articulated by True and Carroll (2002) as generalized “genetic toolkits” that are coopted and then tweaked to perform new functions to generate evolutionary novelty. An example of this would be the process of epithelial fusion, which is used in a variety of developmental contexts as well as in the healing of wounds (Jacinto et al., 2001). Variation in common processes of this kind will cause effects that cross multiple developmental processes and multiple anatomical structures. Another example would be interactions between specific gene products that recur in different developmental contexts. FGF-10 and FGFr-2, for example, show a similar regulatory interaction in the development of diverse organs (Ohuchi et al., 2000). There are probably many examples of these recurring interactions, and networks of this kind were proposed as a type of development al module. See von Dassow and Munro (1999), Winther (2001), and various papers in Wagner (2001) for recent perspectives on modularity and the difficulties inherent in the concept.

Morphological integration studies in biological anthropology

A great deal of work has been done on morphological integration in primates. Seminal work in the area dealt with intergration in the primate skull, and has led to further studies on the evolution of covariance patterns in the primate skull (Ackermann and Cheverud, 2001; Marroig and Cheverud, 2001). Lieberman et al. (2000a,b) used morphological integration to help understand the role of changes in the basicranium in the cranial evolution of hominids and other primates. These studies show that variation in the cranial base has cascading effects throughout the skull, and suggest that evolutionary changes in the cranial base played important roles in key evolutionary transitions in primates.

THE INTERACTION OF VARIABILITY COMPONENTS

Canalization, developmental stability, and morphological integration are represented here as components of morphological variability, or the tendency for organisms to vary. These components are epigenetic phenomena. By epigenetic, we mean the level at which genes and gene products interact during the translation from genetic to phenotypic variation. All three “components” are emergent properties of the architecture of development that affect the way in which genetic variation is translated into phenotypic variation. Canalization, developmental stability, and integration can be viewed as related descriptors of epigenetic systems. All three components of variability interact in complex and interesting ways that complicate any question dealing with phenotypic variation.

Canalization and developmental stability

The potential intersections of canalization and developmental stability are fairly obvious, as both deal with the minimization of phenotypic variation. However, many authors draw a clear distinction between developmental stability and canalization. Clarke (1998, p. 562), for example, argued that “canalization enhances phenotypic constancy regardless of the underlying genotype or environment whereas developmental stability enhances constancy for a given genotype and environment.” In this view, canalization refers to variation among individuals, and developmental stability refers to variation within individuals. This view is consistent with that of Waddington (1975), in that developmental stability refers to the reduction of variation that is not of environmental origin. Implicit in this distinction is that the mechanisms that minimize variation among individuals and within individuals are not the same.

Upon closer inspection, the distinction between external and internal sources of variability and the assumption that they are minimized by different mechanisms is problematic. Composed of imperfect materials and constructed with imperfect mechanisms, organisms are subject to noise-like effects at many levels. There is thus a continuum of noise-like effects from stochastic behavior at the molecular level to broader aspects of environmental variability. One could argue, therefore, that the distinction made by Waddington (1975) and Clarke (1998) between developmental noise and environmental canalization represents an arbitrary distinction imposed upon a continuous range of phenomena. Further, the molecular substrate of development is not independent of its environment. Factors in the cellular, tissue-level, and external environments of organisms, such as temperature, nutrient availability, characteristics of the extracellular matrix, or osmolarity, can influence processes such as the efficiency of gene transcription, translation, or the half-life of RNA transcripts. If such processes contribute to variation within individuals, they can also contribute to variation among individuals.

This is the perspective taken in much of the recent literature, in which the distinction between canalization and developmental stability is blurred. Palmer and Strobeck (1986) defined developmental noise as “the minor environmentally induced departures from some ideal developmental program.” Similarly, in their discussion of environmental canalization,Wagner et al. (1997) clearly equate environmental canalization with reduction in developmental noise, and a recent model by Gavrilets and Hastings (1994) for how selection operates on developmental noise equated microenvironmental effects with developmental noise.

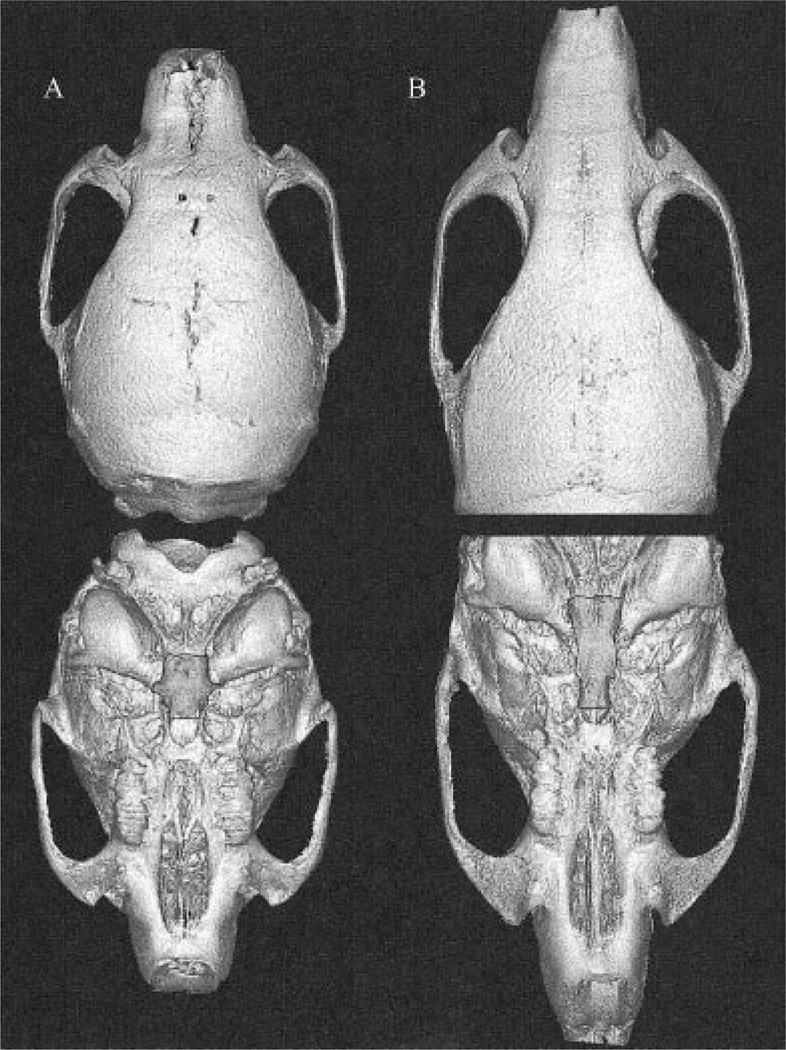
The question of to what extent the mechanisms that promote canalization and developmental stability are shared can be addressed in several ways. Scharloo (1962, 1964) found that asymmetry is increased in association with bimodal phenotypic distributions as the result of directional selection for wing vein length in Drosophila. In this experiment, the bimodal among-individual distribution created by directional selection was mirrored by bimodality within individuals, in which some individuals had a short vein on one side and a long one on the other. Although the asymmetry produced in this way was probably antisymmetry, this finding does support a link between canalization and developmental stability Debat et al. (2000) reported the opposite, finding a lack of correspondence between FA and phenotypic variance for mouse cranial morphology. This study was weakened, however, by the fact that the genetic variance was uncontrolled. Willmore et al. (2002) tested the effect of the Br mutation on canalization and developmental stability in mice. Brachyrrhine (Br) heterozygotes develop midfacial clefting associated with deficient midfacial growth and calcification (Lozanoff, 1993; Lozanoff et al., 1994; Ma and Lozanoff, 1993, 1996; Singh et al., 1998). The primary skeletal element affected is the sphenoid. Figure 3 presents reconstructions from micro-CT scans that compare a Br heterozygote to a wild-type littermate. The area shown highlighted is directly affected by the mutation. Using analysis of three-dimensional (3D) landmark data, Willmore et al. (unpublished findings) showed that the midfacial region, which is most directly affected by the mutation, exhibited both reduced developmental stability and canalization. These results will be presented in detail elsewhere.

Fig. 3.

3D reconstructions of brachyrrhine heterozygote (A) and C3H wild-type littermate (B). Highlighted region is most directly affected by brachyrrhine (Br) mutation.

Other tests are possible. At the phenomenological level, one can examine the relationship between FA variances and the environmental variance, given a suitable experimental design. Such a test is addressed by hypothesis 2 in this paper, below. Another approach is to examine the effect of a specific mutation on FA and the phenotypic variance in cases where the genetic background is the same between groups. A more direct test would be to perturb a molecular-level process predicted to have systemic effects on both developmental stability and canalization. Surprisingly, the effect of knocking out Hsp90 on FA has not been investigated in Drosophila. In mice, this hypothesis is difficult to test, as heat-shock protein knockouts are not viable. More direct still would be to perturb the efficiency of translation of a regulatory protein such as a growth factor involved in limb development, measure the variance of its phenotypic expression during development, and then measure the variability of the phenotypic outcome at the morphological level. In the next few years, such studies should dramatically improve our understanding of the developmental-genetic bases for canalization and developmental stability, and how they are related.

Morphological integration and variability

While the relationship between canalization and developmental stability is obvious, the connection between morphological integration and the other two components of variability is less so. Morphological integration is potentially related to canalization and developmental stability in three ways. Firstly, Cheverud (1982, 1995, 1996) has shown that there is a high level of correspondence between genetic, environmental, and phenotypic correlations. As Waddington (1957) pointed out, responses to environmental effects also have a genetic basis. The correspondence of genetic and environmental covariance structures means that the architecture of development shapes variation and variability in similar ways.

Secondly, there is reason to believe that more highly integrated traits also show higher degrees of phenotypic stability, or that integration and phenotypic stability are directly related. Poorly correlated traits in shrew mandibles show higher responses to environmental stress (Badyaev and Foresman, 2000). Again, the common link is how genetic and environmental effects are filtered through a developmental architecture that responds to both kinds of perturbations in similar ways. A case of a direct environmentally mediated link was provided by Corruccini and Beecher (1984), who found increased variation and decreased integration in facial structures in baboons fed soft diets. In this case, both changes were due to a reduction in the influence of the mechanical stresses produced during mastication on both variation and integration.

Thirdly, if the developmental architecture is modular and this organization structures both the genetic and environmental correlations among structures, then modules are developmentally based units of both variation and variability. This idea is implicit in the homology concept of Wagner (1989), in which he argues that “a part of the body is (epi-)genetically individualized if it exhibits its own norm of reaction.”

A recent study by Klingenberg et al. (2001) provided an example of modularity in developmental reactions to perturbations. Using geometric morphometrics, he used the covariation of asymmetry for Procrustes deviations to identify developmental modules in bumblebee wings. The logic behind this analysis is that structures that share common developmental pathways should show correlated responses to developmental perturbations.

Epigenetics and variability

Waddington (1975, p. 218) defined epigenetics as “the branch of biology which studies the causal interactions between genes and their products which bring the phenotype into being.” Canalization and developmental stability, which deal with how developmental systems suppress variation of genetic or environmental origin, are clearly epigenetic phenomena. Morphological integration, which deals with developmentally based connections between traits, is also an epigenetic concept, although integration caused by linkage disequilibrium is trivially so. The study of variability deals with phenomena that emerge from the complexity of developmental architectures, and thus fits clearly within the scope of epigenetics as envisioned by Waddington (9175).

As Hall (2002) points out, without epigenetics, we’d all be geneticists. In other words, the study of development would hold no interest, as it would add nothing to what could be inferred directly from genes. Obviously, this is not true, but the comment does illustrate the fact that the concept is so broad that it is rarely useful in discussions of evolutionary developmental biology. It is interesting that in a recent volume devoted entirely to the evolution of epigenetic systems, the word “epigenetic” occurs only once (Wilkins, 2002), and in the context of the epigenetic landscape metaphor of Waddington (1975). The concept may even be detrimental, in that it can lead to the misplaced view that epigenetic and genetic factors can be opposed, or that epigenetic phenomena are not also genetic (Hall, 1998).

In cell, developmental, and cancer biology, the term epigenetic has acquired a narrower definition, refering to the mechanisms by which cell fates (including tumor cells) are determined. This definition is also derived from the original conception of the term by Waddington (1975), but is perhaps more useful in that it pertains to a specific class of developmental processes.

COMPONENTS OF VARIABILITY IN THE MAMMALIAN LIMB

The vertebrate limb is a highly successful model system for the study of mechanisms of pattern formation and morphogenesis (Tickle, 2000). Recent advances in understanding the developmental-genetic basis for limb development provide a firm basis for generating hypotheses about morphological integration and variability in the vertebrate limb. Below, we use what is currently known about the developmental biology of the limb to inform hypotheses about the patterning of variability components in the limb. These hypotheses are tested in two samples. One is composed of random-bred CD1 fetal mice, and the other of adult rhesus macaques from the Cayo Santiago collection at the Caribbean Primate Research Center. The mouse sample is used here to lay the groundwork for the study of the effects of genetic perturbations on variability components, using transgenic mouse models. Table 1 provides a guide to the genes discussed in the text below.

TABLE 1.

Limb development genes discussed in text. This list is not intended to be exhaustive, but rather to serve as a guide to genes and proteins discussed in text.

Gene or gene family	Putative function of product
Bone morphogenetic protein-5 (Bmp-5)	A growth factor that belongs to the transforming growth factor β (TGF-β) superfamily and bone morphogenetic protein family. This gene is involved in anteroposterior and proximodistal patterning during early limb development, and regulating cartilage growth in later development (Bailon-Plaza et al., 1999)
Engrailed 1 (En-1)	A transcription factor expressed in the ventral ectoderm which helps establish the dorso-ventral patterning of the limb.
Fibroblast growth factors	One of the major families of protein signaling molecules. FGF proteins play major roles in many different developmental contexts.
Fgf-4	Involved in the regulation loop between FGF-8 and FGF-10.
Fgf-8	Expressed in the limb ectoderm in the region of the apical ectodermal ridge (AER). FGF-8 is a signaling protein that promotes limb outgrowth through mitosis in the region underlying the AER.
Fgf-10	A signaling protein which is expressed in the lateral plate mesoderm in the region where limb outgrowth takes place. This protein induces initial outgrowth of the limb.
Fibroblast growth factor receptor 2 (Fgfr-2)	Mediates the regulation loop between FGF-8 and FGF-10.
Growth differentiation factor-5 (Gdf-5)	A growth factor that belongs to the transforming growth factor β (TGF-β) superfamily. This gene is involved in anteroposterior and proximodistal patterning during early limb development, and joint formation later on (Strom and Kingsley, 1996).
Homeobox (Hox) genes	This family of genes is defined by a common “homeodomain” sequence code for transcription factors that play fundamental roles in specifying regional identity along the craniocaudal axis of the body. In the limb, various members of this family are involved in specifyious members of this family are involved in specifying regional identity along both the proximodistal and anteroposterior axes.
Pituitary homeobox 1 (Ptx-1)	A transcription factor that is a member of the Ptx homeobox gene family. Ptx1 is expressed in the lateral mesoderm in the hind limb region and is thought to act upstream of Tbx 4 in specifying hindlimb identity.
Radical Fringe (Rfng)	A signaling molecule that is expressed in the dorsal ectoderm of the limb bud and is involved in establishing the dorso-ventral patterning of the limb.
Sonic hedgehog (Shh)	A signaling molecule expressed in the posterior mesenchyme of the limb bud that may be anterposterior patterning of the limb. It may act as a diffusible morphogen.
T-box genes	A family of transcription factors that share a unique DNA-binding domain (T- box). Members of this family are crucial for pattern formation in many different developmental contexts.
Tbx-4	A transcription factor that specifies hindlimb identity.
Tbx-5	A transcription factor that specifies forelimb identity. It appears to initiate mesenchyme migration into the forelimb region (Ahn et al., 2002).
Wnt (Wingless Interactive) 7a	A signaling protein expressed in the dorsal ectoderm of the limb bud which helps establish the dorso-ventral patterning of the limb.

The developmental basis for the patterning of variability components in the vertebrate limb

The broad outlines of limb development are quite similar in the forelimb and hindlimb. These shared developmental mechanisms between the limbs reflect serial homology, in the sense that they share a common evolutionary origin. This occurred either through the replication of a forelimb (pectoral fin) developmental pattern more caudally along the body axis (Tabin and Lauffer, 1993), or through the differentiation of a single longitudinal lateral fin fold into the two paired limbs (Tanaka et al., 2002). In either case, the developmental mechanisms that produce the fore- and hindlimb can be traced to a single evolutionary and developmental origin: a classic case of serial homology.

The vertebrate fore- and hindlimbs develop as lateral outgrowths from the body wall. Although forelimb development precedes that of the hind limb, both limbs are initially very similar. The limb buds consist initially of a mass of mesenchymal cells derived from the lateral plate mesoderm, covered by an ectodermal shell (Fig. 4). The mesenchymal core gives rise to the connective tissue of the limb, including the skeletal elements, while somite-derived mesenchyme migrates into the limb to form the limb musculature (Chevallier et al., 1977, 1978).

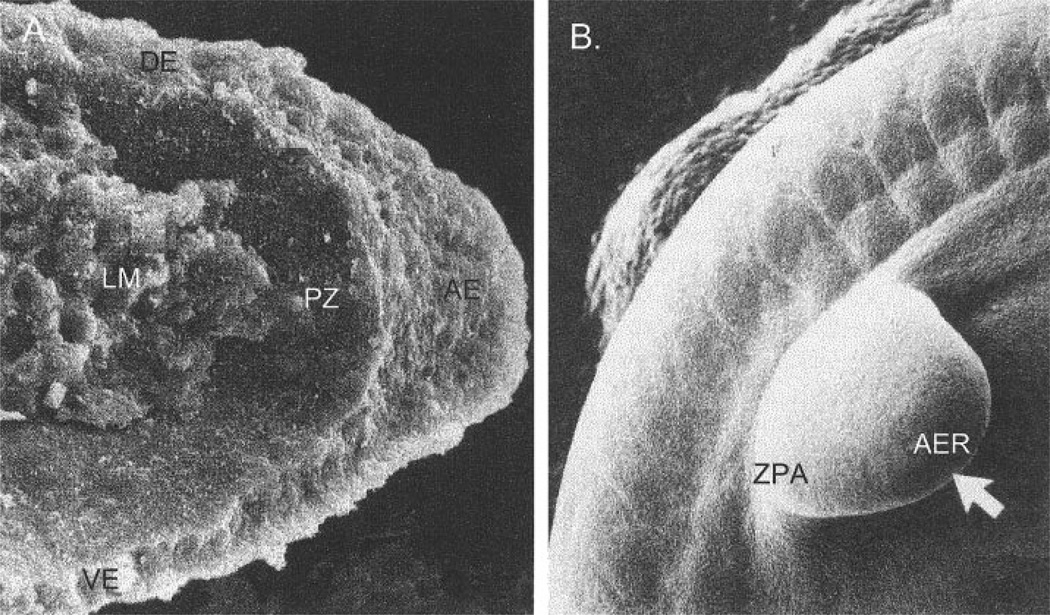
Fig. 4.

Scanning electromicrographs of human forelimb buds on gestational day 29. A: Transverse section through a limb bud. From Kelley (1985). B: External view at a similar stage of development. AER, apical ectodermal ridge; LM, limb mesenchyme; PZ, progress zone; DE, dorsal ectoderm; VE, ventral ectoderm; ZPA, zone of polarizing activity. From Larsen (2001).

The molecular mechanisms that initiate and maintain outgrowth of the limb bud and that determine the patterning of the limb are remarkably conserved across vertebrates (Tickle, 2000). Initiation of limb outgrowth involves the expression of FGF-10 in the lateral plate mesoderm in the region that will produce a limb. FGF-8 is then activated in the overlying ectoderm, and the outgrowth of the limb involves a regulation loop between these two fibroblast growth factors, mediated by FGF receptor-2 (Xu et al., 1998). The region in which FGF-8 is activated becomes a ridge-like structure at the end of the limb-bud known as the apical ectodermal ridge (AER) (Fig. 4). The AER is required for outgrowth of the limb, as it maintains a region of dividing mesenchymal cells immediately beneath it. This region, known as the progress zone, is critical for the proximo-distal patterning of the limb. As cells are displaced by dividing cells in the progress zone, they lay down the elements of the limb in a proximodistal sequence. Cells that leave the progress zone early become proximal elements, whereas those that leave late become the distal elements.

Dorso-ventral patterning follows the establishment of the apical ectodermal ridge. This involves expression of the gene engrailed-1 (En-1) in the ventral ectoderm of the limb, while Wnt-7a and radical fringe are expressed on the dorsal side (Capdevila and Izpisua Belmonte, 2001). Antero-posterior patterning of the limb is directed from a region of mesenchyme on the posterior margin of the limb, referred to as the zone of polarizing activity (ZPA). The ZPA appears to orchestrate a complicated network of gene interactions involving sonic hedgehog, Gdf-5, Bmp-5, Hoxb8, Hoxa13, and Hoxd13. Only broad outlines of this system are currently known, but it interacts with the AER to establish the antero-posterior patterning that is appropriate for the position along the proximo-distal axis. For thorough reviews of these issues, see Capdevila and Izpisua Belmonte (2001) for limb development, and Olsen et al. (2000) for limb skeletal development.

The patterning of the limb proceeds along a proximo-distal gradient, i.e., the more distal elements are laid out later than the more proximal ones, even though they are relatively larger during much of the fetal growth period than postnatally. To the extent that later events during limb growth are affected by the events that precede them, one can predict that variation will accumulate distally along the limb. This prediction is tested in hypothesis 1, below.

Genes that specify regional identity within the developing limb tend to be similar for corresponding elements in the fore- and hindlimb. The homeobox genes Hoxa9 and Hoxd9 have similar but not identical functions in the pectoral and pelvic regions (Fromental-Ramain et al., 1996). Similarly, Hoxa11 and Hoxd11 are involved in specifying the zeugopod, while Hoxa13 and Hoxd13 are involved in specifying the autopod in both limbs (Davis and Capecchi, 1996). Interestingly, Hox genes may also affect the growth of the regions that they specify (Goff and Tabin, 1997). As Chiu and Hamrick (2002) point out, this provides one possible genetic basis for covariation between homologous elements between the limbs.

So how do differences in fore- and hindlimb morphology arise? Recent work has begun to unravel the developmental mechanisms that produce these differences. It was recently shown that the T-box genes 4 and 5 specify limb identity (Rodriguez-Esteban et al., 1999). Tbx-5 is expressed in the lateral plate mesoderm, in the region where the forelimb will develop, while Tbx-4 is expressed in the region of the developing hindlimb. Tbx-5 appears to be involved in initiating lateral plate mesoderm migration into the forelimb region (Ahn et al., 2002). Recent work showed that Ptx-1 acts upstream of Tbx-4 in specifying the hindlimb (Logan et al., 1998; Logan and Tabin, 1999), and an important role for members of the Wnt gene family appears to be emerging as well (Martin, 2001). These findings provide a molecular basis for earlier experiments which suggested that limb identity is specified very early in limb development, through signals residing in the mesoderm (Capdevila and Izpisua Belmonte, 2001). The black box that remains to be opened, however, is the set of developmental mechanisms that determine how the activity of the gene networks common to both limbs can be modulated or interpreted differently, to produce the differences in morphology between the forelimb and hind limb. The recent development of a SAGE (serial analysis of gene expression) library of gene expression profiles for the forelimb and hindlimb is an important step towards solving this mystery, as it will inform hypothesis-generation about specific developmental mechanisms (Logan 2002; Margulies et al., 2001).

Broadly similar in pattern, the fore- and hind-limbs differ significantly in anatomical detail in all extant vertebrates, and many lineages, such as birds, bats, or whales, have evolved radical divergences in fore- and hindlimb morphology. Given their common origin and the extensive overlap in developmental mechanisms, one must ask to what extent the developmental pathways that are shared between the two sets of limbs constrain evolutionary divergences in hind- and forelimb morphology. A first step towards addressing this question is to determine whether the intersection of shared and unique developmental mechanisms is reflected in the pattern of morphological integration between and across fore- and hindlimb structures. This question is addressed by hypothesis 3, below.

Hypothesized patterns of variability in the mammalian limb

Based on this simple picture of limb development, we test two developmentally motivated hypotheses about the patterning of variability components in the mammalian limb. These are:

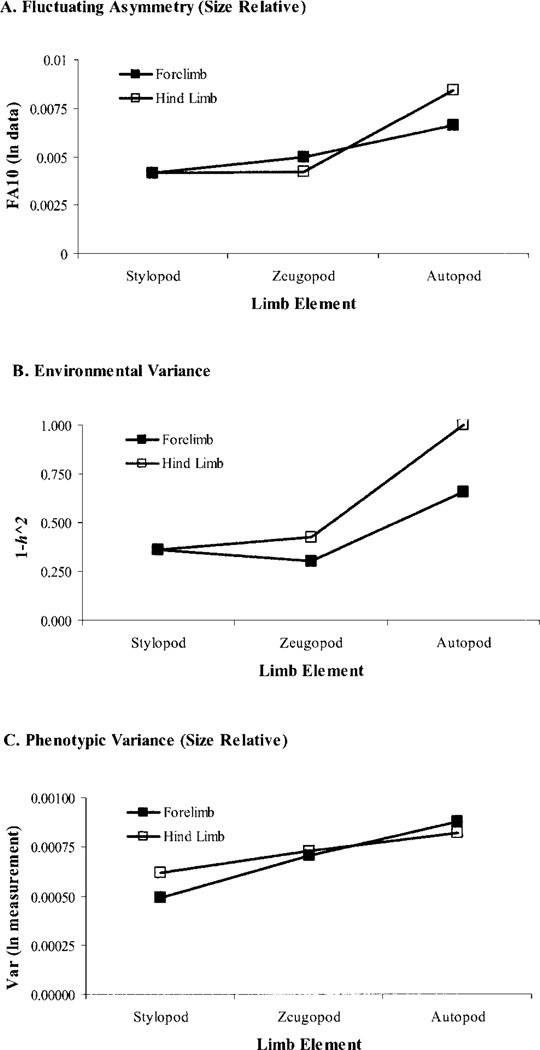
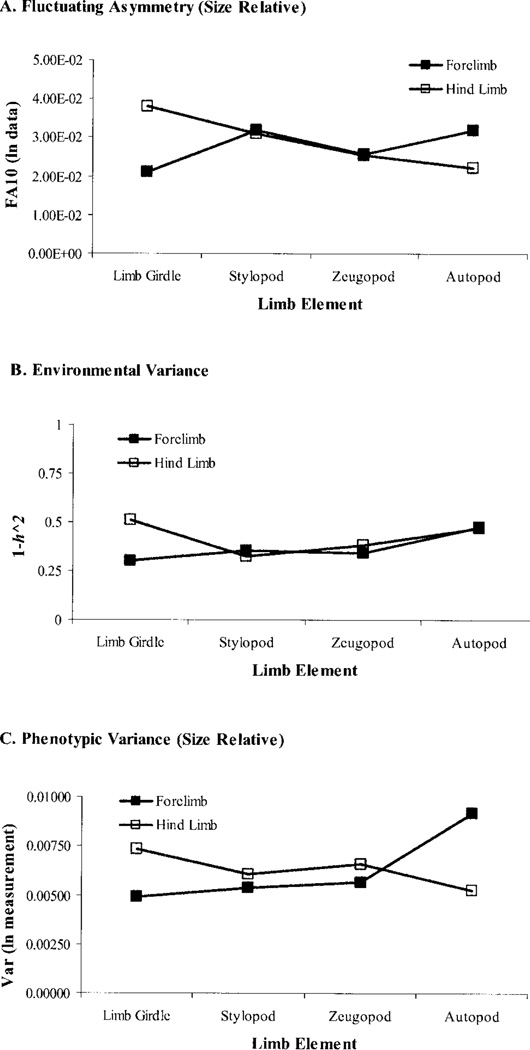
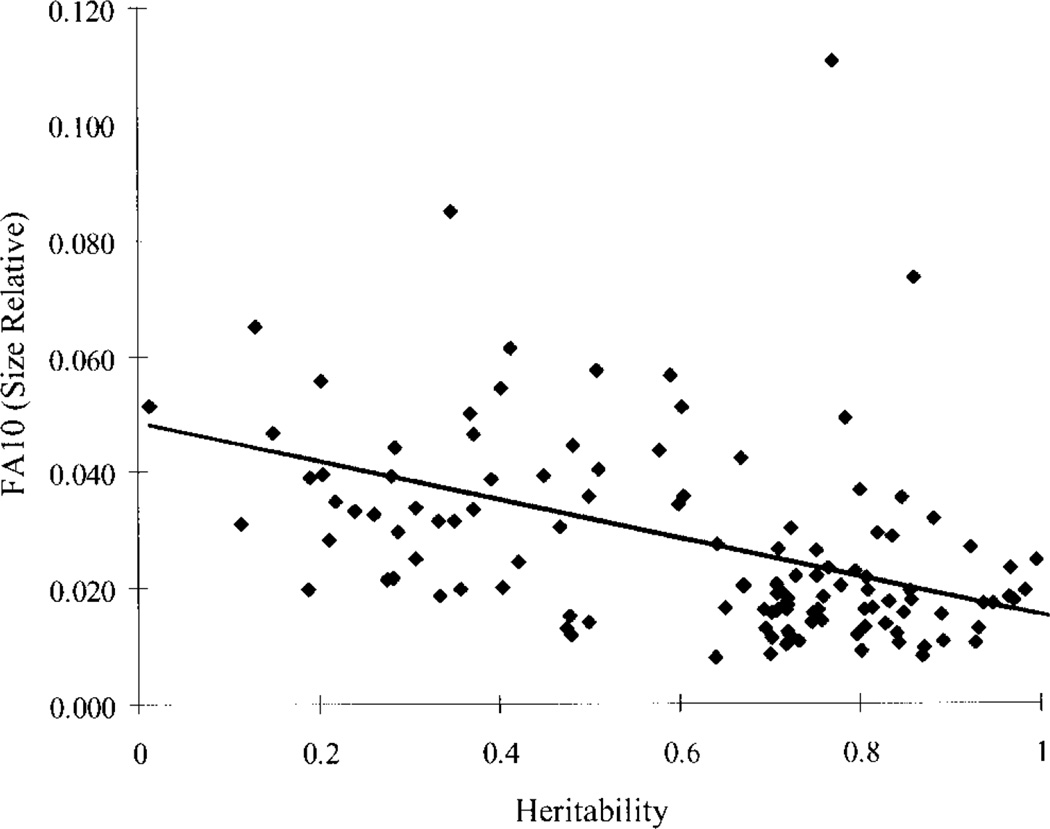
1. Environmental and FA variances show a proximo-distal gradient along the limb. The formation of limb elements proceeds in a proximo-distal sequence as mesenchymal cells leave the progress zone. If perturbations that affect the activity of the progress zone are cumulative in effect, there should be an increase in both the FA and environmental variances (i.e., a decrease in developmental stability and canalization) along the proximo-distal axis of the limb.

2. Environmental and FA variances are related in across characters in the limb. If the mechanisms that reduce variation within and among individuals are not the same or closely related, then FA and environmental phenotypic variances will not be correlated across traits. Failing this, to reject this hypothesis would provide strong incremental evidence for a relationship between the mechanisms underlying canalization and developmental stability.

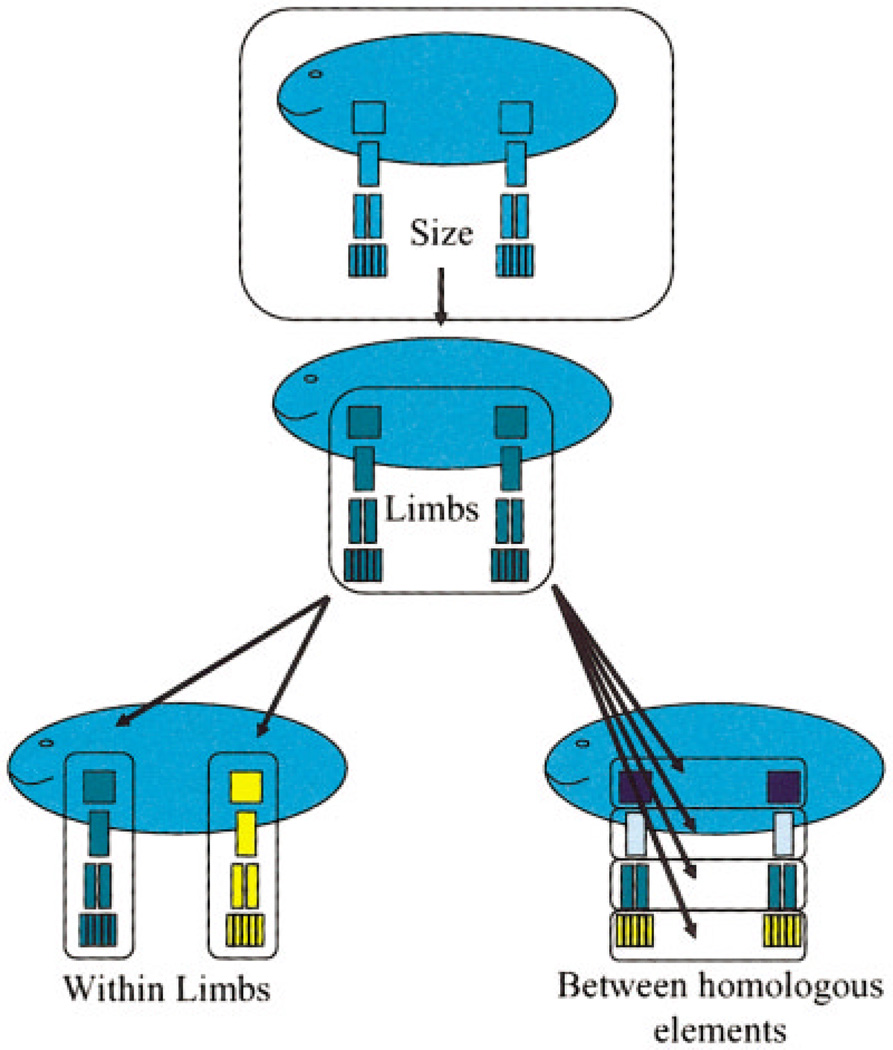
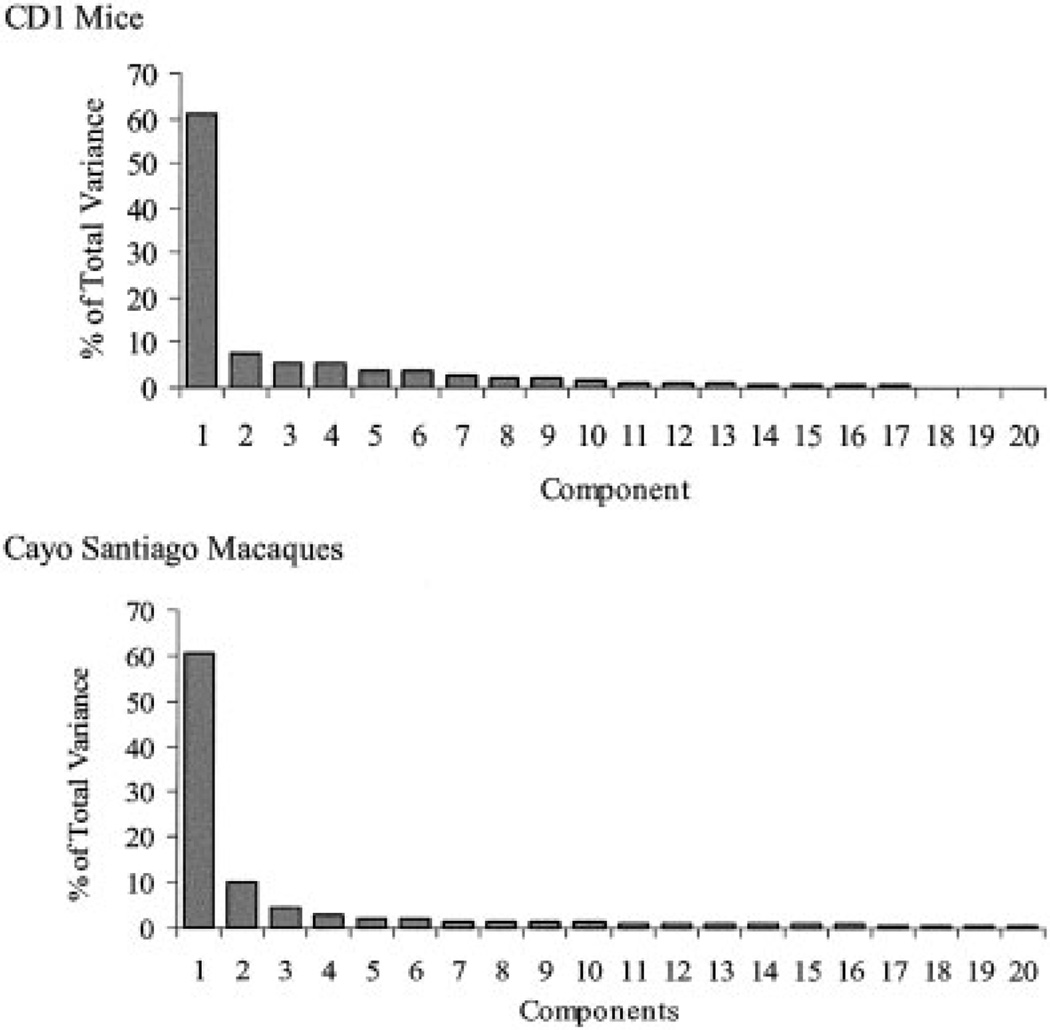
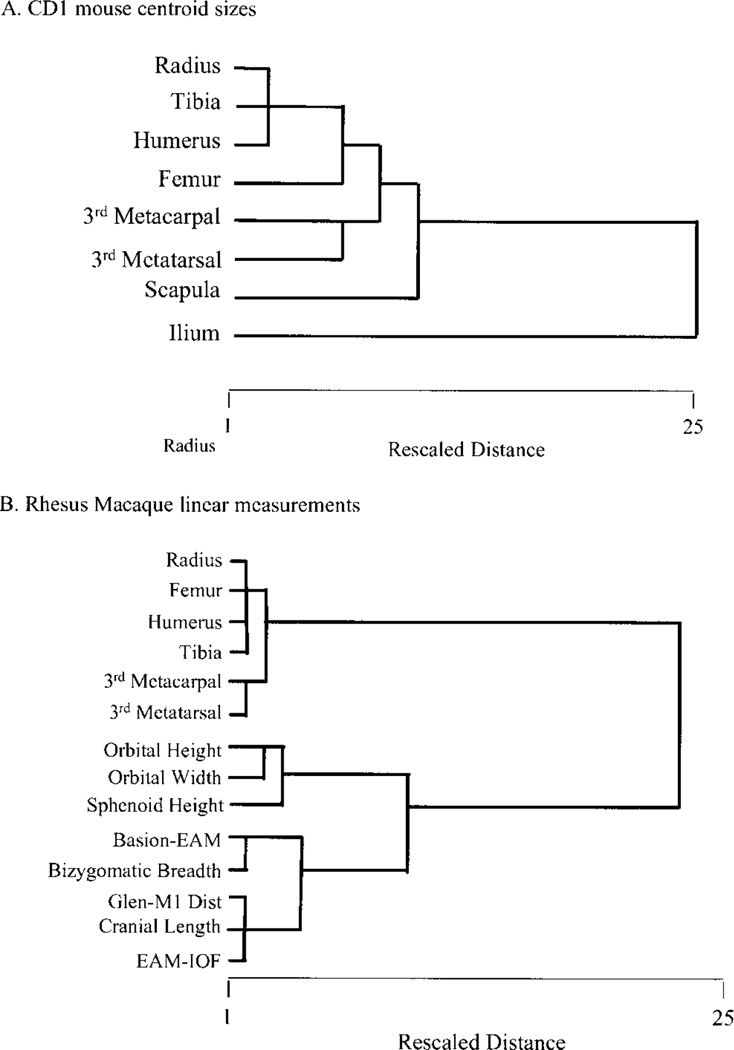
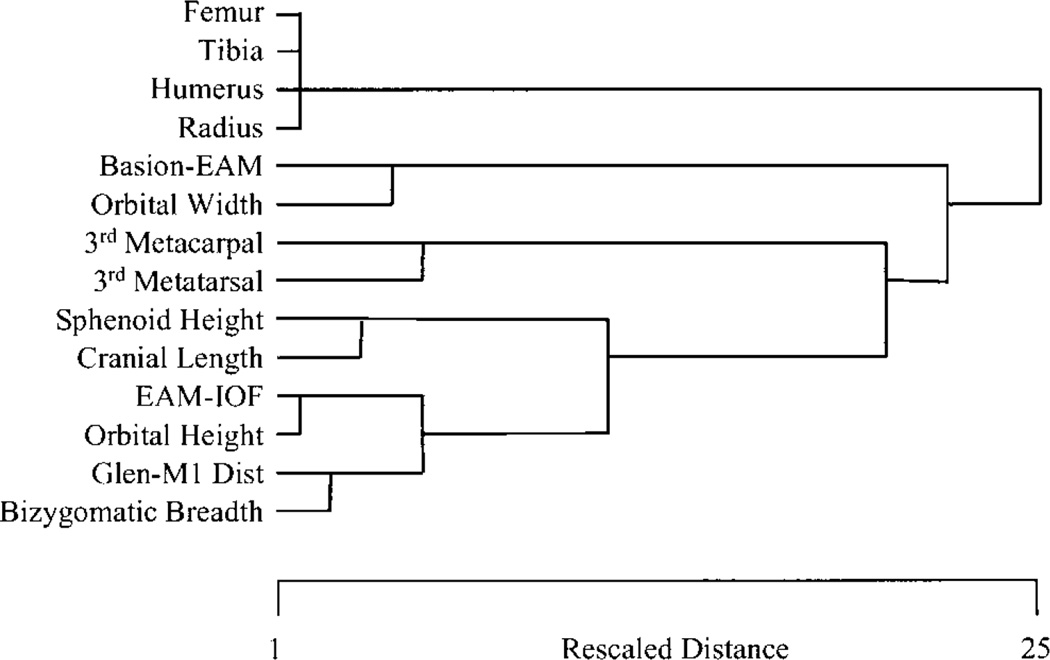
3. Limb element integration patterns are characterized by intersecting and hierarchically arranged “modules” which link structures within limbs and homologous structures across the fore- and hind-limb. Limb development proceeds from a set of mechanisms that are shared between the limbs but modulated in some way by different mechanisms in each limb. Morphological integration patterns of limb structures should reflect the balance of shared and limb-specific mechanisms in limb development. Figure 5 depicts this hypothesis. In this scheme, “size module” refers to the correlation introduced by overall size. The “limb module” refers to overall covariation between limbs, such as the tendency for an individual with longer forelimbs to have longer hindlimbs. This module reflects the effects of developmental mechanisms that affect the size of both limbs in nonspecific ways. The “within-limb module” refers to integration among elements within limbs. This module would reflect the effects of developmental mechanisms that are specific to each limb. The “homologous limb element” module refers to integration between homologous elements between the limbs, such as the radius and tibia. This module would reflect the effects of mechanisms that are either doing similar things at similar times in both limbs, or affecting the same region of both limbs.

Fig. 5.

Schematic depiction of hypothesized modules affecting patterning of morphological integration in vertebrate limb.

METHODS AND MATERIALS

The composition of the samples

CD1 mice

In all, 124 fetuses were obtained at ages 16, 17.5, 19, and 20.5 days by 2-hr random mating of randombred CD1 mice from Charles River. These mice are appropriate, because inbreeding may increase developmental stability (Ben-David et al., 1989; Kieser et al., 1986b; Markow and Martin, 1993). The adult mice were kept on a reverse light cycle (10 PM on, 10 AM off) and fed ad libitum. Fetuses were collected at precise gestational ages ( ±1 hr), using 2-hr mating. The fetuses were not sexed, as previous analysis of FA of limb skeletal structures in 10 different mammalian species did not reveal differences between sexes (Hallgrímsson, 1998).

Specimens were cleared and stained according to the method of Hanken and Wassersug (1981). In this method, specimens are cleared with trypsin and double-stained with alcian blue and alizarin red, to reveal both cartilage and bone (or osteoid). The specimens are stored in 100% glycerin, with a small amount of thymol added as a preservative.

Rhesus macaques

The macaque sample consists of adult semifree-ranging Macaca mulatta from Cayo Santiago (Caribbean Primate Research Center) (N = 194). Although the colony is provisioned, the monkeys supplement their commercial monkey diet considerably by foraging on the abundant tropical vegetation on the island (Rawlins and Kessler, 1986). Adults were defined as older than 5 years.

Data collection and analysis

CD1 mice

Bilateral morphometric measurements were obtained from images of the cleared and stained limb whole mounts, using a Polaroid digital camera (DMC-1) and an Olympus stereoscope (SZH 10). The images were captured in 24-bit color at 1,600 × 1,200 pixels. For image capture, specimens were placed in a 3.5″ petri dish containing 25 ml of glycerin. Early analysis of measurement error revealed that parallax was a significant source of error for distance measurements. To solve this problem, the limbs were placed under a glass coverslip with 20-g weights placed on either end. This compresses the limb, so that skeletal elements lie in the same plane and their long axes are perpendicular to the camera. To orient the metatarsals of all specimens and the metacarpals of the 20-day group so that their long axes were perfectly perpendicular to the camera, it was necessary to detach them so that they could be positioned separately.

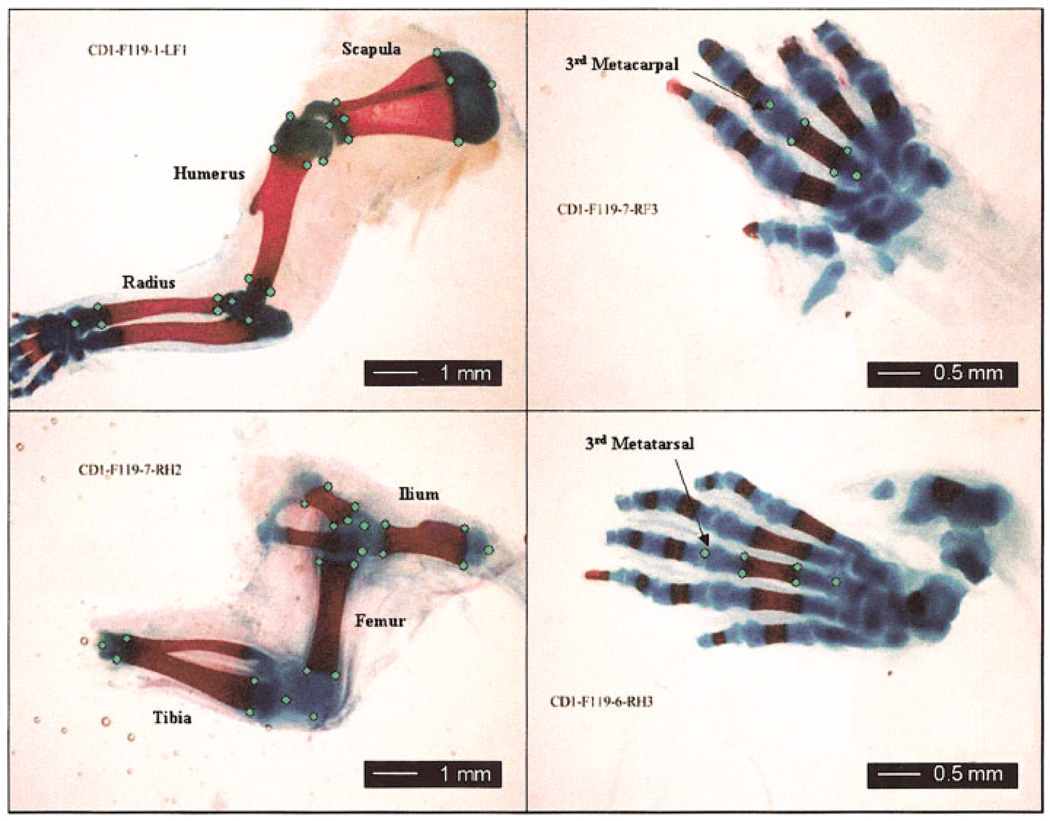
2D landmarks were collected for the scapula, humerus, radius, third metacarpal, ilium, femur, tibia, and third metatarsal. These landmarks were selected so that their configuration within each skeletal element captured variation in the aspects of shape that change with the maturation of the element. Thus, points were chosen so as to describe the region of the limb element composed of osteoid vs. cartilage, as well as to capture the skeletal elements’ overall size and shape. Figure 6 shows the 2D landmarks collected for all skeletal elements. For each skeletal element, the set of all possible Euclidean distances between landmarks was obtained. We opted to analyze the set of interlandmark distances rather than the Procrustes deviation because of concern that the Procrustes superimposition was arbitrarily distributing variances across landmarks. See Lele and Richstmeier (2001) for a thorough discussion. The centroid size of the landmark configuration was also used as a measure of size for each element.

Fig. 6.

Landmarks collected for fore- and hindlimb elements for CD1 sample. Specimen shown is a neonate (20.5-day sample). Mouse fetuses were cleared and stained with alcian blue for cartilage, and alizarin red for bone/osteoid.

2D landmarks were recorded as x,y coordinates from digital images, using SigmaScan Pro on a 21” monitor with a screen size of 1,600 × 1,200 pixels, on which the entire image could be displayed at full resolution. This screen size was chosen to minimize the potential effect of pixelation error. Each skeletal element was digitized separately.

To quantify measurement error, each individual was imaged and landmarked three times. Each trial was performed on a separate day by the same investigator (B.H.), and all steps, including alignment of the specimen for imaging, were repeated for each trial. Error resulting from variation in the effects of flattening the limb under a coverslip was thus included in our estimate of measurement error.

Rhesus macaques

The macaque data consist of bilateral linear measurements of limb skeletal elements, as well as a set of linear cranial measurements. Measurements were taken with an osteometric board or 6- and 12-inch digital calipers. These measurements are described in Table 2. Each individual was measured twice by the same observer (B.H.) on different days, to allow assessment of measurement error.

TABLE 2.

Descriptions and abbreviations of measurements used in this study

Cranial measurements

Glen-M1: Lateral edge of articular eminence (glenoid tubercle) of the mandibular fossa to the mesial margin of M1.

Bas-EAM: Maximum distance from basion to anterior margin of the external auditory meatus.

EAM-IOF: Anterior margin of external auditory meatus to lateral margin of the infraorbital foramen. If multiple infraorbital foramina were present, we measured the most lateral foramen.

Orb-Ht: Maximum distance from superior margin of the infraorbital foramen to the supraorbital rim.

Orb-Wd: Maximum orbital width (or length).

Sphn-ht: Maximum height of greater wing of the sphenoid.

Cranial-lgth: Maximum length of skull as measured from alveolare to most posterior point on the occiput.

BiZyg-D: Maximum bizygomatic diameter of skull.

Postcranial measurements

Hum-length: Maximum length of humerus.

Rad-length: Maximum length of radius.

Mcarp3: Maximum length of third metacarpal.

Fem-length: Bicondylar length of femur (maximum femoral length with both condyles in contact with lower caliper arm or stationary edge of osteometric board).

Tib-length: Maximum length of tibia.

Mtars3: Maximum length of third metatarsal.

Data analysis

Fluctuating asymmetry

Analyses of FA followed the methods outlined by the two-way mixed model ANOVA of Palmer and Strobeck (1986, 2002). Data were analyzed for robustness and statistically significant outliers in both measurement error and asymmetry, using visual inspection of scatterplots and Grubb’s test for outliers. Outliers for both measurement error and asymmetry that were significant within age groups at P < 0.01 were eliminated from further analysis. Since FA variances were later adjusted for measurement error (see below), outliers for measurement error due to entry errors or gross measurement error could artificially reduce the FA variances by inflating the ME variance. Similarly, outliers for asymmetry (usually due to specimen damage) can artificially inflate the FA variances (Palmer and Strobeck, 2002). The significance of FA over measurement error was determined using a two-way mixed model ANOVA (sides fixed, individuals random), where the significance test for FA is F = MS_sj/MS_m, where MS_sj is the sides/individuals interaction mean square, MS_m is the measurement error mean square among trials, and M is the number of replicate measurements. The measure of FA employed is FA10 in the classification by Palmer and Strobeck (2002). This is calculated as $0.798\sqrt{2({\text{MS}}_{\text{sj}}-{\text{MS}}_{\mathrm{m}})/\mathrm{M}}$. Asymmetry distributions were tested for directional asymmetry, using the same two-way mixed model ANOVA and for departure from normality using the Kolmogorov-Smirnov test (Palmer and Strobeck, 2002). Since FA is size-dependent in both samples used in this study, all data were natural log-transformed. Simple or linear size dependence for measures of variance can be removed by log transformation (Lewontin, 1966; Van Valen, 1978; Wright, 1952). Once this is done, FA10 is a proportional or size-scaled measure of FA. FA10 was compared between groups, using F-tests and the degrees of freedom estimate provided by Palmer and Strobeck (2002).

Calculation of variance components

Heritabilities were estimated differently in the two samples due to the nature of the data. For the Cayo Santiago macaques, the identity of the mother is known, but that of the father is not. Siblings in this sample, therefore, can be either half- or full-sibs. Heritability estimates were obtained using mother offspring-pairs and siblings, using the equation provided by Cheverud (1982). Cotterman’s k-coefficients were calculated according to Roff (1997). This method is somewhat problematic for this sample, as we do not know how frequently the half-sibs are actually full-sibs. Dominance and maternal effects are thus not available for this sample. For CD1 mice, maternal values are not available, as the data set is based on fetal limbs. In this case, the ratio of within-litter vs. among-individual variance provides a crude estimate of heritability. Since these estimates confound within-litter environmental effects with genetic effects, these heritability estimates can only be used to compare traits within this particular sample, and should not be compared directly to values obtained from other samples.

Morphological integration

For analysis of integration, sex- and age-related variations were removed from the sample, following Cheverud (1982). Within age (mice) and sex (macaques) classes, all distributions were standardized to a mean of 0 and a variance of 1. This procedure adjusts for differences in mean and variance between subsamples. Matrices of phenotypic correlations were constructed for all sets of interland-mark distances and centroid sizes in the mouse sample and the linear measurements in the macaque sample. Genetic correlation matrices were constructed for the macaque sample but not for the CD1 mouse sample. The genetic correlations obtained from the latter sample would be difficult to interpret, due to the confounding of within-litter and other environmental effects. Work by Cheverud (1988, 1995) showed that the patterns obtained from phenotypic and genetic correlations tend to be very similar. Genetic correlations were obtained for the macaque sample, using the equation provided for use in the same sample by Cheverud (1982).

The matrices of phenotypic and genetic correlations were analyzed in two ways. Since we are testing a priori hypotheses about patterns of integration, we needed a means of testing for the significance of correlations among the sets of structures identified by our hypotheses. Simply obtaining the significance of those correlations is misleading, since the matrices as a whole tend to be tightly integrated as the result of size, and most of the correlations are significant. We therefore used the following randomization test. The matrix from which a set of correlations was drawn, such as the matrix of all limb measurements, was randomized. At each iteration, the set of correlations linking the structures specified by the hypotheses was obtained from the reordered matrix and stored, and the average z-transformed value was calculated. The routine then calculated the probability of obtaining the observed mean correlation (after z-transform) by dividing the number of times a value was obtained that equaled or exceeded the observed value, and dividing by the total number of iterations. For all tests, 1,000 iterations were used.

Following Cheverud (1982), the matrices were also subjected to principal components analysis. The first seven principal components were used to calculate the Euclidean distances between traits in a seven-dimensional space. These distances were subjected to hierarchical cluster analysis, to assess the relationships among traits.

Matrices were compared using the matrix correlation, and the significance of these correlations were obtained using Mantel’s test.

RESULTS

The patterning of FA along the limb

CD1 mice

As the fetal age groups used in this study differ in FA, the patterning of FA along the limb was analyzed separately for each age group. The results of the FA and age analysis are presented elsewhere (Hallgrímsson et al., unpublished findings). For the Euclidean distance data, 265 out of 529 distances within age groups showed significant FA above measurement error. The remaining distances were discarded from further analysis of asymmetry. Plots of mean FA of Euclidean distances per skeletal element as well as FA of centroid size revealed no significant patterning along the limb. This was confirmed both with pairwise F-tests and linear regression. Thus in the mouse sample, no tendency for FA to increase along the limb was detected.

Rhesus macaques

Figure 7 presents the patterning of size-relative FA along the limb in the Cayo Santiago macaque sample. There is a clear tendency for FA to increase along the limb. This was confirmed with pairwise F-tests, the results of which are provided in Table 3.

Fig. 7.

Variability along limb in Macaca mulatta. A: Size-relative ($0.798\sqrt{2({\text{MS}}_{\text{sj}}-{\text{MS}}_{\mathrm{m}})/\mathrm{M}}$ on In transformed data) against limb segment for the forelimb and hindlimb. Significance values for comparisons between segments are provided in Table 2. B: Environmental variance (1 – h²) against limb segment. C: Overall phenotypic variance. In C, the overall variance is the mean of male and female variances (Table 4).

TABLE 3.

FA comparisons for limb segments in Macaca mulatta

	Humerus	Radius	Third metacarpal	Element	df
Humerus		1.203	1.605	Humerus	195
Radius	P = 0.096		1.335	Radius	211
Third metacarpal	P < 0.001	P < 0.05		Third metacarpal	206
	Femur	Tibia	Third metatarsal	Element	df
Femur		1.002	2.014	Femur	215
Tibia	P = 0.495		2.011	Tibia	213
Third metatarsal	P < 0.001	P < 0.001		Third metatarsal	211

Separate matrices are provided for forelimb and hindlimb. Within each matrix, F-ratios are above diagonal, and P-values are provided below. Significant P values are in bold. Degrees of freedom for F-tests were calculated as df_FA10 = (MS_m − MS_m)²/{(MS_sj)²/[(S − 1)(J − 1)] + (MS_m)²/[SJ(M − 1)]} (Palmer, 1994), where S is number of sides, J is number of individuals (genotypes), and M is number of replicate measurements.

The patterning of variances along the limb

CD1 mice

The patterning of the environmental variance along the limb was calculated from the heritability estimates for each trait. Table 4 lists the mean heritabilities for the Euclidean distances obtained from each limb element. These values are inflated by within-litter and maternal effects, which cannot be assessed given the available data. We assume here that these effects affect all traits in similar ways, and so heritability can be compared across traits within this sample. Figure 8 presents the patterning of FA, environmental variance, and overall phenotypic variance along the limb for the CD1 mouse sample. As these graphs show, there is no clear pattern of change along the limb. Pairwise comparisons of mean variances (Mann-Whitney U test) show no significant differences between elements.

TABLE 4.

Means of variability components for interlandmark Euclidean distances in CD1 mice¹

Limb	Element	No. of distances	Mean σ of In (measurement)	Heritability	FA10
Forelimb	Scapula	21	0.0049	0.696	0.021
	Humerus	19	0.0054	0.647	0.032
	Radius	14	0.0057	0.657	0.026
	Mcarp	12	0.0092	0.524	0.032
Hindlimb	Ilium	10	0.0073	0.488	0.038
	Femur	21	0.0061	0.672	0.031
	Tibia	15	0.0066	0.617	0.026
	Mtars	13	0.0053	0.527	0.022

¹Heritabilities were calculated from full-sib covariances and are thus overestimates of true values for this sample. Variances are calculated on In-transformed data and then averaged across fetal age groups. Variances on In-transformed data are size-relative. FA10 is calculated as described elsewhere in this paper, and is size-scaled as it represents a variance of In-transformed distribution (Palmer and Strobeck, 2002).

Fig. 8.

Variability along limb in CD1 mice. A: Size-relative FA ($0.798\sqrt{2({\text{MS}}_{\text{sj}}-{\text{MS}}_{\mathrm{m}})/\mathrm{M}}$ on In transformed data) against limb segment for forelimb and hindlimb. Significance values for comparisons between segments are provided in Table 2. B: Environmental variance (1 – h²) against limb segment. C: Overall phenotypic variance.

Although there is no significant change in variability components along the fetal mouse limb, heritability of the interlandmark distances in the sample is significantly related to fluctuating asymmetry (Fig. 9). Traits with lower heritabilities show higher FA, and heritability explains 23% of the variance for FA in this sample of traits. This provides evidence that the degree of genetic determinancy for a trait is related to its developmental instability (hypothesis 2).

Fig. 9.

Heritability plotted against size-relative FA for 262 within-element interlandmark distances in CD1 mice. FA10 values are averaged across age groups for each trait. Heritability is calculated on z-transformed sample, adjusted for differences in mean and variance between age groups. Pearson’s correlation coefficient (r = 0.48) is significant at P < 0.001. Graph shows a general relationship between FA and magnitude of environmental variance in CD1 mouse limb sample.

Rhesus macaques

Table 5 lists the heritabilities of limb element lengths for the Cayo Santiago sample. Figure 7 shows the environmental and phenotypic variances plotted against limb segment. Clearly, there is an increase in both the overall variance and the environmental variance (and a decrease in heritability) along the limb. The heritabilities of the third metacarpal and third metatarsal are significantly lower than those of the proximal two segments (P < 0.001, Fisher’s z-transformation).

TABLE 5.

Heritability and size-relative variances for Macaca mulatta¹

		σ of In (measurement)
Element	Heritability	Female	Male
Humerus	0.640	0.00042	0.00056
Radius	0.700	0.00056	0.00085
Third metacarpal	0.344	0.00085	0.00091
Femur	0.639	0.00052	0.00072
Tibia	0.573	0.00054	0.00091
Third metatarsal	0.002	0.00099	0.00065
Glen-M1	0.280	0.00141	0.00122
BaseEAM	0.009	0.00061	0.00075
EAM-IOF	0.276	0.00058	0.00072
Orb ht	0.402	0.00109	0.00072
Orb wd	0.379	0.00035	0.00041
Shnt	0.068	0.00087	0.00136
Bizwd	0.127	0.00345	0.00366
Cranial Wd	0.108	0.00247	0.00239

¹Bold values are significant at p < 0.01.

Morphological integration among limb structures

Morphological integration was assessed through analyses based on correlation matrices for values standardized within age and sex for all traits. Phenotypic and genetic correlation matrices were obtained for the Cayo Santiago macaques, while only phenotypic variances were analyzed for the mouse sample. Within-litter, dominance, and maternal effects will inflate the genetic correlations obtained in the mouse sample and thus inflate the similarity between genetic and phenotypic correlation matrices for this sample (Flaconer and Mackay, 1996; Roff, 1997). The Cayo analysis, which is based on individual mother offspring pairs as well as a mixture of half-sibs and full sibs, is much less likely to be biased in this way.

As shown by the distributions of the percentage of variance explained by principal components (Fig. 10), both data sets are highly integrated due to the underlying effects of overall size. Four a priori hypotheses specifying integration patterns were tested, using the randomization method explained above, to determine whether sets of correlations are significantly different from the expected correlations, given the integrating effects of overall size. These hypothesis correspond to the four hypothetical modules shown in Figure 5. Table 6 presents the results of tests for integration of interlandmark distances within limb elements in fetal mice. As expected, most limb elements show significant integration above the level expected due to size. Table 7 presents the results of tests for integration within and across limbs in fetal mice. Table 7 shows that there is no significant tendency for forelimb and hindlimb structures to be integrated within each limb above the level expected, given the overall integrating effects of size. Across homologous elements, however, there is some evidence for integration. The correlations between homologous elements all tend to be higher than the overall mean except for that between the scapula and ilium, which is much lower than the overall mean. When this pair is excluded from the list of homologous elements, integration between homologous elements is significant. In Table 8, tests of integration hypotheses are provided for the macaque data, based on both phenotypic and genetic correlations. Again, there is no evidence for integration within limbs, but there is some support for the existence of significant integration between homologous elements across the limbs. While the average correlations within limbs are not significantly greater than those expected due to size, the average correlations between homologous limb elements are significant for both the genetic and phenotypic correlation matrices.

Fig. 10.

Percentage of total variance explained by principal components for mouse Euclidean distance matrix data and rhesus macaque linear measurement data. Corresponding histogram for CD1 mouse centroid size data is very similar.

TABLE 6.

Morphological integration within limb-elements in CD 1 mouse foetuses

Element	r	Fisher’s z	95% confidence interval (of z value)	p-value
Scapula	0.843	1.231	0.094	p < 0.001
Humerus	0.818	1.150	0.064	p < 0.001
Radius	0.753	0.981	0.073	p < 0.001
Mcarp	0.378	0.398	0.368	ns
Ilium	0.610	0.709	0.105	ns
Femur	0.734	0.936	0.072	p < 0.001
Tibia	0.665	0.802	0.088	p < 0.050
Mtars	0.641	0.760	0.163	ns

TABLE 7.

Tests of integration hypotheses for limb-element centroid sizes in CD1 mouse foetuses

Element set	r	Fisher’s z	95% confidence interval (of z value)	p-value
Forelimb	0.759	0.993	0.144	ns
Hindlimb	0.621	0.726	0.144	ns
Scap-ilium	0.173	0.175	0.651	ns
Hum-fem	0.850	1.257	0.634	ns
Rad-tib	0.946	1.796	0.621	p < 0.05
Mtars-Mcarp	0.817	1.147	0.648	ns
Nonhomologous elements	0.682	0.833	0.160	ns
Homologous elements	0.798	1.094	0.307	ns
Homologous elements excluding ilium	0.885	1.400	0.362	p < 0.05
Overall average for all limb elements	0.706	0.879	NA	na

TABLE 8.

Tests of integration hypothesis for adult macaques, using genetic and phenotypic correlation matrices

Element set	r	Fisher’s z	95% confidence interval (of z value)	p-value
Genetic correlations
Forelimb	0.416	0.443	0.157	ns
Hindlimb	0.225	0.229	0.162	ns
Humerus-femur	0.600	0.693	0.272	p < 0.001
Radius-tibia	0.533	0.595	0.272	p < 0.05
Mcarp-Mtars	0.158	0.159	0.268	ns
Nonhomologous elements	0.332	0.345	0.110	ns
Homologous elements	0.448	0.482	0.154	p < 0.01
Overall average for all limb elements	0.320	0.331	NA	na
Phenotypic correlations
Forelimb	0.668	0.808	0.136	ns
Hindlimb	0.694	0.855	0.138	ns
Humerus-femur	0.821	1.159	0.492	ns
Radius-tibia	0.906	1.503	0.513	p < 0.05
Mcarp-Mtars	0.815	1.143	0.474	ns
Nonhomologous elements	0.756	0.986	0.129	ns
Homologous elements	0.867	1.320	0.251	p < 0.01
Overall average for all limb elements	0.746	0.964	NA	NA

Overall, the phenotypic and genetic correlation matrices reveal a fairly consistent pattern, although the genetic correlations are lower. Comparison of the two matrices using Mantel’s test revealed that the matrix correlation of 0.644 is significant at P < 0.001. Comparison of only the limb element correlations using Mantel’s test revealed a somewhat higher correlation (0.756, P = 0.032).

In addition to tests of a priori hypotheses for patterns of integration, principal components and hierarchical cluster analyses were also used to look for groupings of traits in both data sets. Figure 11 shows dendrograms obtained using hierarchical cluster analysis (Ward’s method) on the phenotypic correlation matrices for limb element centroid sizes in mice and linear measurements in macaques. This method involves sequentially clustering at each step the pair of variables that produces the smallest possible increase in the squared distance of each node to the centroid of the cluster. While inconclusive, these dendrograms are more consistent with integration between limbs than within limbs. The dendrogram obtained from the genetic correlation matrix for the macaque data (Fig. 12) does not distinguish between the among-limb and across-limb integration patterns.

Fig. 11.

Dendrograms derived from hierarchical cluster analysis, using Ward’s method for CD1 mouse centroid size correlation matrix (A) and the rhesus macaque phenotypic correlation matrix (B).

Fig. 12.

Dendrograms derived from hierarchical cluster analysis, using Ward’s method for rhesus macaque genetic correlation matrix.

DISCUSSION

This study addresses three developmentally motivated questions about the patterning of variability in two mammalian species. The first is the extent to which variability components change along the proximo-distal axis of the limb. The second addresses the relationship between developmental stability and canalization in the limb, and the third addresses the degree to which the pattern of phenotypic limb integration reflects the interplay of developmental factors that affect each limb individually and both limbs jointly.

We found that while both FA and nongenetic variability increase distally along the limb in macaques, no such pattern is evident in fetal limb structures in mice. Both species share the developmental basis for the prediction that variability will increase distally along the limb. For this reason, the most parsimonious interpretation of these results is that the increase in variability in more distal segments of the limb in macaques is a postnatal phenomenon, and does not reflect the effects of the mechanisms of limb bud pattern formation and growth on the patterning of variability in the limb. Instead, the patterning of variability in the adult macaque would reflect the differential effects of the mechanical environment on skeletal growth in different elements of the limb. A study of the patterning of FA and canalization in a postnatal ontogenetic mouse sample, coupled with data from adult samples in other mammalian species, would determine whether or not this explanation is correct. A mechanical explanation for the patterning of variability seen in macaques would predict that a similar pattern would be seen in adult mice, but not in neonates obtained from the same population.

Although FA and the environmental variance did not show significant patterning along the proximodistal axis in the mouse sample, an analysis of the relationship between heritability and asymmetry variances showed that traits with lower degrees of genetic determinancy also showed higher FA (after correction for measurement error). This result is interesting, because it points to a relationship between the determinants of environmental canalization and developmental stability. While such relationships may well be particular to developmental contexts and populations, we interpret this as supporting evidence for the hypothesis that the mechanisms that buffer against environmental effects among individuals and those that buffer against such effects within individuals are either the same or show extensive overlap. In other words, the mechanisms behind canalization and developmental stability are closely related. This conclusion is at odds with claims made in other studies which examined the relationship between phenotypic variance and FA in suites of traits (Debat et al., 2000; Reddy, 1999). Neither of these studies, however, examined the relationship between heritability and FA.

Our analyses of morphological integration in the limbs of fetal mice and adult macaques are consistent with the hypothesis that limb integration reflects the interplay of factors acting within limbs and across homologous limb elements. Although the patterns found are not strongly conclusive, they provide more evidence for the existence of significant integration across homologous limb elements than for integration within the forelimb or hindlimb. This suggests that in both mice and macaques, there are developmental processes that affect structures in both limbs in similar ways. Evolutionary divergence in hind and forelimb morphology, therefore, must break down or overcome the tendency for fore- and hindlimb structures to covary. A prediction of this hypothesis is that species that do show significant divergence in hind- and forelimb morphology, such as humans or bats, will show relatively stronger patterns of within-limb and weaker among-limb covariation patterns. A comparative study of interlimb covariation in different vertebrate species is necessary to address this question.

Leamy (1977) reported a somewhat different pattern of integration in a large sample of adult mice. He showed, using cluster analysis, that the humeral and radioulnar length grouped, as did femoral and tibial lengths in the genetic but not in the environmental correlation matrices. One possible explanation for this difference is that the within-limb integration pattern reported by Leamy (1977) develops postnatally, due to shared mechanical environments within each limb. This would not explain, however, why we do not find a strong within-limb pattern of integration in our adult macaque sample. There are differences between the studies that could explain the difference in conclusions. Leamy (1977) measured two element lengths from each limb, while we have a much larger set of measurements for the mouse sample and an additional element in the macaque sample (metacarpal/metatarsal). The studies also differ in that a priori hypotheses about integration patterns are tested here, while Leamy (1977) simply reported the results of cluster analyses.

In an analysis of the correlation pattern of limb elements in hens, Van Valen (1965) also reported a stronger within- than among-limb pattern of covariation. This result is not inconsistent with ours. Hens obviously exhibit a dramatic degree of hindand forelimb divergence in size, morphology, and function. The evolution of the dramatic difference in fore- and hindlimb morphology in birds may well have involved breaking down the pattern of interlimb integration. It would be interesting to see if a similar reduction in the degree of among-limb covariation is seen in other species with highly divergent limb morphology, such as bats or whales.

The work presented here on the patterning of variability in the limbs of two mammalian species is intended as a background against which to examine the developmental-genetic determinants of variation in variability components (FA, canalization, and morphological integration), using known mutant mouse models. Ongoing work in our laboratory is examining the effects of knockout or loss-of-function mutations that perturb limb development in different ways on components of variability. Thus we are currently examining the relative effects of genes that directly affect growth rates, limb pattern formation, and bone structure and metabolism on FA and canalization in the limb skeleton. Similarly, we are comparing the effects of mutations in genes that are involved in limb-specific mechanisms to those that play similar roles in both limbs on the pattern of morphological integration in the limb. Knowledge of the patterning of these variability components in natural populations is a necessary background to understanding the results of these studies.

If there is, as the present results suggest, a developmentally based constraint on the evolutionary divergence of hind- and forelimb morphology, this would have important implications for the evolution of limb morphology in primates, including humans. Such a constraint would predict that selection for a change in size and shape in a specific limb element would produce a corresponding change in the serially homolgous element in the other limb. If the change in the serially homologous element negatively impacts fitness, selection should favor breaking down the tendency for interlimb covariation between the homologous elements. How difficult a developmental step this is would determine the extent to which interlimb integration produces a developmental constraint on divergence in fore- and hindlimb morphology. Morphological and functional divergence among the limbs is a central component of locomotor adaptation in many primate species. Hominoid hands and feet, and limb proportions in a variety of species, provide examples of this. Whether or not covariation among homologous elements in the forelimb and hindlimb poses an evolutionary constraint at the level of divergence seen in primates is an empirical question that could be addressed through a comparative study of limb structure integration patterns in primates.

Future directions

An important issue facing evolutionary developmental biology is to understand the developmental mechanisms that regulate variability in natural populations, as well as their significance in both evolutionary and biomedical contexts. Gene knock-outs and lack-of-function mutations offer a crude next step towards approaching this question. While the magnitude of the perturbations is much larger than those encountered in natural populations, this approach does have the advantage that more severe perturbations to development should produce more easily detectible effects on variability. The next and more difficult step will be to relate the results of such experiments to variability in natural systems and in species such as primates, for which experimental manipulation is not feasible or desirable. Naturally occurring variation at loci identified in transgenic mouse models could be related to components of variability in primate species. Studies of variation at single or a small number of loci, however, are unlikely to yield significant results. While there may be some genes that affect variability directly, such as heat-shock proteins (Rutherford, 2000), the genetic determinants of variability are likely to be much more diffuse. A model for the genetic basis for FA (Klingenberg, 2000; Klingenberg and Nijhout, 1999) assumes that nonlinear dynamics are inherent in the regulation of phenotypic expression. They show that in such a system, almost any mutation that influences trait expression can generate variation in FA. In the model by Wagner et al. (1997) for the quantitative genetics of canalization, any mutation with pleiotropic effects can affect canalization. Pleiotropy, of course, is also the principal genetic basis for morphological integration.

Variability is thus likely to be an emergent property of the genetic architectures of developmental systems, rather than being determined by specific genes. We will therefore need to look to more complex approaches in order to understand the causes and evolutionary significance of variability. The model by Jernvall and Jung (2000) for the genetic basis for tooth-shape evolution in mammals points to a potential future direction. The construction of realistic models for how gene networks can produce phenotypic variation in specific developmental contexts will provide a basis for generating predictions that relate naturally occurring genetic variation to variability in those same systems. Studies of this kind will play a major role in the ongoing integration of studies of variation and variability at the phenotypic level with advances in developmental biology.

GLOSSARY

Autopod

The most distal segment of the limb (hand and foot in humans).

Antisymmetry

Deviations from symmetry (across planes of organismal symmetry) that, when obtained for a population, show a tendency towards bimodality (or a negative correlation between the two sides).

Canalization

The buffering of developmental processes against influences such as environmental perturbations or mutations. The population genetic definition of Wagner et al. (1997) is the reduction of the phenotypic effect of a mutation or environmental change.

Environmental canalization

The reduction of the phenotypic effect of an environmental change.

Genetic canalization

The reduction of the phenotypic effect of a mutation.

Developmental instability

The tendency for development of a specific genotype to follow the same trajectory under the same conditions. Developmental instability produces a phenotypic variance component that is not explained by the broad-sense genetic or among-individual environmental variance.

Developmental stability

The absence or minimization of developmental instability.

Directional asymmetry

Deviations from symmetry (across planes of organismal symmetry) that, when obtained for a population, deviate significantly from a mean of 0. The difference between the size of the right and left ventricle of the heart is an example of directional asymmetry.

Epigenetics

“… the sum of the genetic and non-genetic factors acting upon cells to control gene expression selectively to produce increasing phenotypic complexity during development and evolution” (Hall, 2002, p. 11).

Fluctuating asymmetry (FA)

Deviations from symmetry (across planes of organismal symmetry) that, when obtained for a population, are random in direction and normally distributed in magnitude about a mean of 0.

Genetic assimilation

Genetic assimulation occurs when a phenotype that is initially induced by an environmental stimulus comes to be expressed in the absence of that stimulus.

Morphological integration

The tendency for characters to covary as the result of common underlying developmental factors.

Morphogenesis

The changes in shape and structure that take place once the fate of a cell or group of cells has been determined.

Norm of reaction

The relationship between the distribution of phenotypes for a particular genotype and a determining environmental factor.

Pattern formation

The specification of cell fates within a uniform mass of cells that leads to the development of differentiated structures.

Phenocopy

An environmentally induced phenotype that is very similar to one that is genetically based.

Phenodeviant

An individual that is at the extreme of a phenotypic distribution for some character.

Somite

Blocks of cells of mesodermal origin that form alongside the neural tube. Each pair of somites corresponds to a single body segment. The somites give rise to the skeletal muscles of the trunk and limbs, the axial skeleton, and the dermis of the skin.

Stylopod

The most proximal segment of the limb, excluding the limb girdle (arm and thigh in humans).

Variation

Observed phenotypic differences. Variation can be defined at multiple levels, including within individuals (among structures or between sides), among individuals, or among means or other aggregate properties of groups of individuals such as populations, species, or higher taxonomic groups.

Variability

The tendency or propensity to vary (Wagner et al., 1997).

Zeugopod

The middle segment of the limb (forearm and leg in humans).