Driving Structure-Based Drug Discovery through Cosolvent Molecular Dynamics

Abstract

Identifying binding hotspots on protein surfaces is of prime interest in structure-based drug discovery, either to assess the tractability of pursuing a protein target or to drive improved potency of lead compounds. Computational approaches to detect such regions have traditionally relied on energy minimization of probe molecules onto static protein conformations in the absence of the natural water environment. Advances in high performance computing now allow us to assess hotspots using molecular dynamics (MD) simulations. MD simulations integrate protein flexibility and the complicated role of water, thereby providing a more realistic assessment of the complex kinetics and thermodynamics at play. In this review, we describe the evolution of various cosolvent-based MD techniques and highlight a myriad of potential applications for such technologies in computational drug development.

Graphical Abstract

Introduction

Identifying binding sites and hotspots on protein surfaces has been of long-standing interest to the scientific community. With the explosion of protein targets, we need to focus time, resources, and efforts on those where high-affinity ligands are attainable. Experimental approaches have been developed to partly fulfill this need. The seminal work of Dagmar Ringe’s Multiple Solvent Crystal Structures (MSCS) has provided the experimental benchmarks that are used to create a variety of hotspot-mapping techniques.¹ In brief, MSCS involves solving crystal structures of proteins in the presence of various organic cosolvents. Overlapping locations of different cosolvents were found to be highly correlated with regions of biological significance. MSCS studies played a pivotal role in the development of several, recent computational analogs. Here, we follow the natural progression of events from the first experimental studies to the current state of the art in mapping methods that rely on cosolvent Molecular Dynamics (MD) simulations. Though the initial motivation for cosolvent MD was identifying binding hotspots, we also discuss the diverse nature of problems that can be addressed with these methods.

Multiple Solvent Crystal Structures

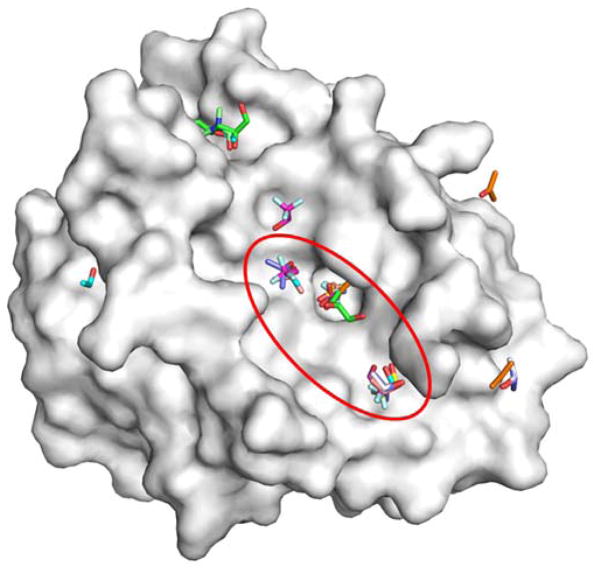
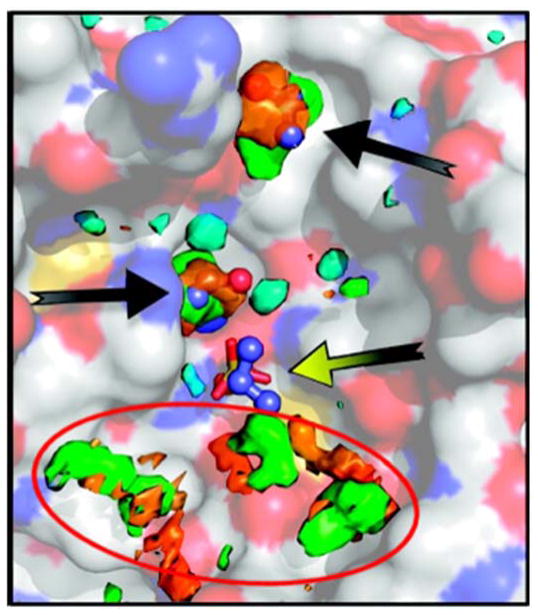
Some of the first studies of protein crystal structures with cosolvents were motivated by the difference in catalytic activities in the presence of organic solvents. Subsequently, the crystal structure of subtilisin was solved in the presence of water and acetonitrile to determine if the difference in activities resulted from geometric changes in the active site.² Similar studies were performed with γ-chymotrypsin in hexane.³ While there was no difference in the active site of the protein in both cases, these studies formed the basis for MSCS for locating binding sites on protein surfaces.¹ Initial validation studies for MSCS were performed on elastase using acetonitrile as the cosolvent.¹ Acetonitrile was found to map the active site and crystal-packing interfaces. Subsequent studies with elastase extended the range of solvents to include acetone, dimethylformamide, 5-hexene-1,2-diol, isopropanol, ethanol, and trifluoroethanol.⁴ Interestingly, when the range of solvents was extended, many different cosolvent molecules were found to populate the active site (Figure 1) and bind along the crystal-packing regions. From these results, it was proposed that potential binding sites can be identified by regions that bind a diverse set of cosolvent molecules. Several subsequent studies have come to a similar conclusion using MSCS.^5–7

Figure 1.

An overlay of the all the MSCS crystal structures of elastase is shown (PDB structures: 2FOE, 2FOD, 2FOG, 2FOH, 2FOF, 2FOA, 2FOB, 2FO9, and 2FOC).^1,4 Many different cosolvent molecules occupy the same hotspots within the active site (red circle). The overlay provides “clusters” of probes on the protein surface (white). Probes outside the active site tend to bind along crystal-packing interfaces.

One of the limitations of MSCS is that most protein crystals are destabilized by the organic cosolvents. This results in a loss of resolution at best and no useful spectra at worst. In fact, the MSCS method was developed using cross-linked proteins to stabilize the crystals, but this is not possible in all systems. For the many proteins are simply intractable to MCSC, simulation methods allow us to examine cosolvents on a wide variety of targets.

Computational approaches for mapping rigid protein structures

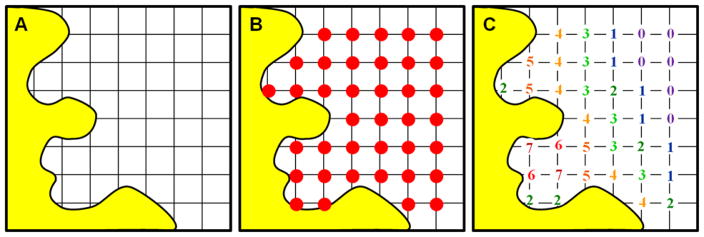
Truth be told, the idea of mapping protein surfaces was introduced roughly a decade before the MSCS method was developed. In 1985, Goodford revolutionized the field with the introduction of GRID.⁸ Figure 2 shows how the method placed a protein target inside a mathematical grid, and “probes” were used to calculate which functional groups would best complement the different surfaces of the binding site. The probes included water, a methyl group, an amine nitrogen, a carboxy oxygen, and a hydroxyl. The grid points with the most favorable energetics identified regions of attraction between each unique probe and the protein. The grids could be displayed in contours, much like crystallographic electron density. The spatial arrangement of each favorable region was then used to design lead molecules to complement the binding site. The use of grids and probes underlie many computational approaches developed after GRID. The most popular alternative is to energy minimize small, organic molecules on the protein surface in vacuum. For many years, all these methods focused on using static protein conformations from X-ray and NMR experiments.⁹ A few of the most important ones are described in further detail below.

Figure 2.

The original GRID program used a regularly spaced grid (A) to place probe atoms (red circles, B) throughout the binding site and across the protein surface (yellow). (C) At each position, the interaction energy is calculated for the probe, summing over all atoms in the protein binding site. The energies are based on van der Waals contacts, Coulombic charges, and a hydrogen-bonding term. Across the surface, different sub-pockets can provide a good combination of favorable contacts (red/orange numbers). Far from the protein surface, there is only weak interaction (purple/blue numbers), and some points can be too close and clash with the protein atoms. Different probes create different maps; clearly, the favorable regions for a hydrophobic probe are not the same as a hydrophilic one.

Multiple Copy Simultaneous Search

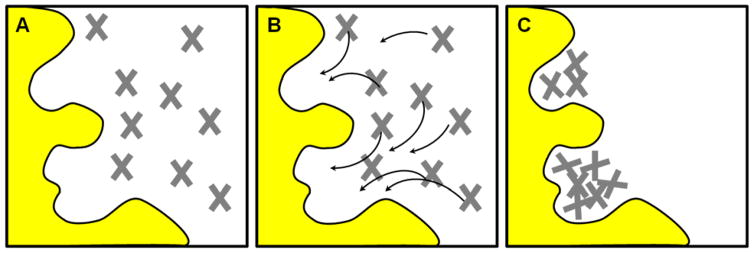
Multiple Copy Simultaneous Search (MCSS) was developed by Nobel Laureate Martin Karplus. In an MCSS calculation, small organic molecules (probes like acetate, methanol, methylammonium, methane, and water) are energy minimized onto the protein surface (Figure 3).^10,11 Several copies of the probes are dispersed in the site of interest (ranging from 1,000 – 5,000). The probes are minimized independently of each other.¹² Convergence is achieved during the minimization procedure typically after 3,000 – 6,000 steps. The probes are then further sampled on a grid limited to the vicinity of its final minimized location. This is achieved by fixing the center of mass of the probe at each grid point and exploring the rotational degrees of freedom. These results are then visualized as density maps. In the first application of MCSS for Structure-Based Drug Discovery (SBDD), the sialic acid binding site of influenza hemagglutinin was examined.¹⁰ The probe molecules were found to satisfactorily map the sialic acid binding site. In a follow up study on HIV-1 protease (HIVp), the technique was extended to include N-methylacetamide as an additional probe. Using the MCSS approach, favorable locations for N-methylacetamide in the active site were used successfully to reconstruct the binding orientation of MVT-101, a peptide known to bind HIVp.¹³

Figure 3.

The MCSS method is based on energy minimization of probe molecules in the target binding site. Different probes map different interactions with the pocket, just like the GRID method, but the underlying mathematic implementation is different. (A) The binding site is initially flooded with thousands of probe molecules in random locations. (B) Each probe is treated independently, and its energy is based only on its interaction with the protein atoms. The arrows show the pathways toward the closest, local energy minima. The probes are systematically stepped “downhill” toward locations with more favorable energy. (C) No interactions between the probes are included in the calculations, so they can overlap one another at the end of the minimization. These clusters of probes map the favorable interaction sites on the protein surface. Further refinement of the probe locations and orientations uses a grid-based approach.

The fact that the probes do not interact with one another results in the loss of any possible cooperativity in their binding. This limitation was first addressed by Joseph-McCarthy et al. when they compared MCSS minima to MSCS for formate bound to Ribonuclease A (RNase A).¹⁴ The experimental method showed two formate bound near one another, but MCSS reproduced only one formate binding site. To accurately reproduce occupancy at the second binding site, the first formate had to be present (the same way one might include a cofactor within a protein in any SBDD calculation).

Dynamic pharmacophore models and the Multiple Protein Structure method

Our Multiple Protein Structure (MPS) method is an experimentally verified computational mapping approach for obtaining receptor-based pharmacophore models.^15–25 Our method was originally called the dynamic pharmacophore method because the static protein conformations were obtained from snapshots of traditional MD simulations of proteins in water. Later, we changed the name to MPS to reflect that the static conformations can come from any source: crystallography, NMR ensembles, or MD snapshots. The approach is similar to MCSS. A binding site is initially flooded with benzene, ethane, and methanol probe molecules. These probes are then minimized independent of each other using a Monte Carlo method called Multi-Unit Search for Interacting Conformers as implemented in the BOSS program.^16,26 The minimized probe molecules are clustered²³ to identify favorable interaction sites on the protein surface (much like the two sites for probes in Figure 3C). These clusters are then converted into pharmacophore elements. Benzene clusters are converted into aromatic pharmacophore elements, but overlapping benzene and ethane clusters are converted to more generic hydrophobic pharmacophore elements. Donor, acceptor, and doneptor pharmacophore elements are obtained from methanol clusters. The size of the pharmacophore elements is based on the root mean square deviation (RMSD) of the elements in the cluster. Using the MPS method, the first receptor-based pharmacophore model was derived for HIV-1 integrase.¹⁶ Subsequently, several optimization studies were undertaken to obtain robust pharmacophore models using structures from X-ray,^16,19,20 NMR,²⁰ and MD simulations.^17,18,21,22 A common theme throughout our method development was the positive impact on MPS performance when using larger ensembles to capture more protein flexibility. Additionally, MPS pharmacophore models were shown to exhibit species specificity for human vs Pneumocystis carinii variants of dihydrofolate reductase (DHFR).¹⁹ Several MPS pharmacophore models were experimentally validated by the identification of inhibitors from MPS pharmacophore screening. Small molecules that target MDM2 were identified using MPS pharmacophore models.²¹ More recently, pharmacophore models created from an allosteric site on HIVp were experimentally verified to be active against drug-resistant strains of HIVp.^24,25

FTMap

FTMap developed by Vajda and co-workers is a mapping technique that samples billions of probe molecules on a densely space grid.²⁷ This mapping is performed using sixteen different probe molecules which include ethanol, isopropanol, isobutanol, acetone, acetaldehyde, dimethyl ether, cyclohexane, ethane, acetonitrile, urea, methylamine, phenol, benzaldehyde, benzene, acetamide, and N,N-dimethylformamide. Sampling of several copies of many different probe molecules is achieved by an energy function that is evaluated using a fast-Fourier transform approach. The adoption of this approach in FTMap provided significant acceleration over their earlier probe mapping technique CS-Map.²⁸ FTMap’s energy function incorporates cavity terms to reward hydrophobic enclosure and a statistical, knowledge-based, pair-wise potential to account for solvation effects. In an early application of FTMap, the binding sites of the proteins elastase and renin were shown to be mapped by probe molecules. The FTMap technique was also applied to the proteins DJ-1 and glucocerebrosidase.²⁹ The binding sites identified by FTMap were shown to be in agreement with subsequent MSCS solved for these proteins.²⁹ Favorable results were also found upon application to H5N1 neuraminidase,³⁰ Ras GTPase,³¹ and Hen Egg-White Lysozyme (HEWL).³² In fact, the H5N1 neuraminidase study applied CS-Map across an ensemble of protein structures from MD simulations, much like MPS.

MD simulations of proteins in mixed-solvent environments

MD simulations are based on the same computational framework as the energy minimizations shown in Figure 3, except that all molecules interact with one another and cannot occupy the same space. Newton’s equations of motion are used to integrate the system through time and sample the behavior of a protein in water. The reader has likely done this same exercise in Physics 101: a ball at point x has velocity v and acceleration a; where will it be after Δt time? Each atom is a point in space, and all atoms have a velocity vector in an MD simulation. The velocities are based on the temperature of the simulation (hotter systems have faster moving atoms). A “downhill” energy surface creates a force that pulls on the molecules, and “uphill” surfaces push molecules away, both of which provide acceleration. MD simulations solve these equations of motion for thousands of atoms over millions of femtosecond time steps. This provides physically reasonable conformational sampling for the interaction of the protein and its solvent environment.

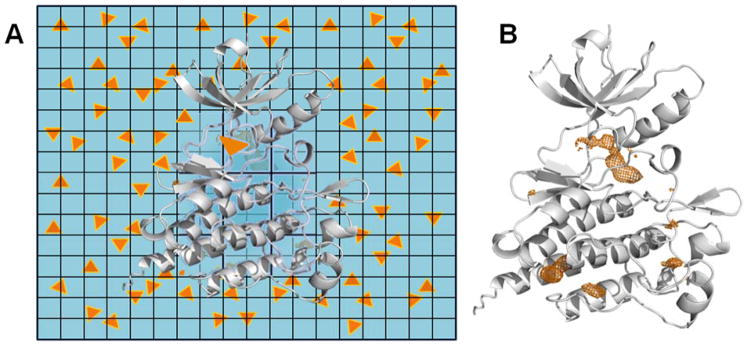
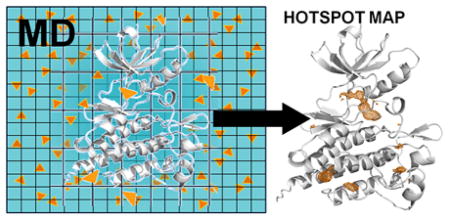
MD-based approaches for mapping protein surfaces involve simulating proteins in a solution of water and cosolvent molecules. The conformational sampling incorporates protein flexibility and allows the protein to adapt to the presence of the probes. Furthermore, the probes have to compete with water to occupy sites on the protein surface. It is important to know which subsites prefer organic molecules and which prefer water. Such techniques have the potential to present a cost effective and widely applicable alternative to MSCS. Several approaches that use MD-based methods are summarized in Table 1 and are described in further detail below. All of these methods use grids to count the presence of probe molecules on the surface of proteins. These occupancy maps identify binding sites by the grid points that most frequently contain the cosolvents (a high density of probes, see Figure 4).

Table 1.

Cosolvent MD techniques that have been used to identify hotspots and binding sites on protein surfaces (protein abbreviations defined in the text).

Developer (Method)	Highlights, Needed Improvements, Published Cosolvents & Proteins
Barril (MDmix) 33–36	Highlights: This was the first method of this type, and it laid the foundation for using occupancy grids and calculating free energies from cosolvent populations. MDmix focuses on water-miscible cosolvents. Needed Improvements: MDmix produces many “extra” hotspots that may be misleading in prospective applications. Cosolvents: Isopropanol, ethanol, acetonitrile, methanol, acetamide Proteins: Thermolysin, p53, elastase, MDM2, LFA-1/ICAM-1, PTP1B, p38 MAPK, AR, HEWL, Hsp90, HIVp
MacKerell (SILCS) 37–48	Highlights: This method has the most extensive development with significant progress in translating occupancy grids into pharmacophore models and scoring schemes. Needed Improvements: It uses high concentrations of cosolvent with artificial repulsion terms to prevent aggregation. This may unnaturally perturb any cooperative behavior between the cosolvent and create artifacts in the maps. SILCS also produces many extra hotspots that may be misleading in prospective applications. Cosolvents: Benzene, propane, water (as a hydrogen-bonding probe), acetonitrile, methanol, formamide, acetaldehyde, methylammonium, acetate, imidazole Proteins: BCL-6, trypsin, α-thrombin, HIVp, FKBP, FXa, NadD, RNase A, IL-2, p38 MAPK, DHFR, FGFr1 kinase, adenosine deaminase, ERα, AmpC β-lactamase, T4-L99A, AR, PPARγ, mGluR5, β2AR
Carlson (MixMD) 49–53	Highlights: Very careful development has lead to clean maps with a significantly reduced number of extra hotspots. MixMD focuses on very low concentrations of miscible solvents to avoid artificial repulsion terms. Needed Improvements: At this point, MixMD is qualitative in its identification of hotspots, and a quantitative scoring scheme is needed. Cosolvents: Acetonitrile, isopropanol, pyrimidine, imidazole, N-methylacetamide, acetate, methylammonium Proteins: HEWL, elastase, p53, RNase A, thermolysin, HIVp, ABL kinase, AR, CHK1 kinase, glucokinase, PDK1 kinase, PTP1B, farnesyl pyrophosphate synthase
Yang and Wang 54–58	Highlights: The authors have used more rigorous free energy calculations to estimate binding affinities. Other applications have focused on qualitatively identifying differences in PPI that might help provide specificity for designed ligands. Needed Improvements: More development is needed. Cosolvents: Isopropanol, phenol, trimethylamine N-oxide Proteins: Thermolysin, Bcl-xL, Mcl-1, IL-1R1
GlaxoSmithKline and Bahar 59	Highlights: The method is specifically developed for assessing druggability of individual binding sites. They use their grids in a slightly different way, and they have very interesting rules for combining hotspots into druggability estimates. Needed Improvements: More development is needed. Cosolvents: Isopropanol, isopropylamine, acetic acid, acetamide Proteins: MDM2, PTP1B, LFA-1, kinesin Eg5, p38 MAPK
Caflisch 60,61	Highlights: This method estimates kinetic on/off rates and binding affinities of the cosolvents based on the MD, but only a few applications are published. Cosolvents: Dimethylsulfoxide, methanol, ethanol Proteins: FKBP, BAZ2B, CREBBP
Tan and Abell 62–64	Highlights: This method proposes low concentrations of hyrdrophobic cosolvents to reduce aggregation, but only a few applications are published. Cosolvents: Benzene, chlorobenzene Proteins: Polo-box domain of polo-like kinase 1, MDM2, MDMX, IL-2, Mcl-1, Bcl-xL, Aurora-A, RAD51, ERα, ERβ
Fersht 65	Highlights: The application focuses on cryptic binding sites, and more work is needed. Cosolvent: Isopropanol Protein: p53-Y220C
Gorfe (pMD) 66,67	Highlights: This method is also developed to map proteins embedded in membranes, but more applications are needed. Cosolvent: Isopropanol Protein: K-ras

Figure 4.

Cosolvent MD simulations are conceptually very simple. (A) The schematic shows how a traditional MD simulation is modified. A protein (white ribbon) is placed in a box of explicit water molecules (blue background) with a modest number of small, organic molecules (orange triangles) in the solvent. Over the course of the simulation, the waters and cosolvents sample the local environments around the protein and out in the bulk. The cosolvents displace water on the protein surface and identify regions where drug-like, organic molecules may favorably bind. A grid is used to count the number of times a cosolvent probe occupies every position in the simulation box. The more frequently a grid point is occupied, the more favorable the interaction. (B) The occupancy grid counted from an entire MD simulation can be viewed in isodensity contours (orange mesh surfaces) that show the grid points of the most favorable interactions with the cosolvents.

The differences between the methods in Table 1 lie in detailed choices for MD setup and execution. Those details are familiar to scientists with computational backgrounds. For experimentalists, how the details change the predictions is what matters most. The figures emphasize the bottom-line outcomes that can be used by SBDD teams.

Barril’s MDmix

The first cosolvent-based simulations for mapping protein surfaces were reported by Barril and co-workers.³³ In this approach, simulations of isopropanol and water at concentrations of 20% were run for at least 16ns. The approach was evaluated by its ability to reproduce the locations of isopropanol molecules located in MSCS structures of thermolysin,⁶ p53 core domain (p53),⁶⁸ and elastase.⁴ The maps of the protein surfaces were broken down into separate occupancy grids for isopropanol’s hydroxyl oxygen and methyl carbons. While it is reported that the densities from the isopropanol maps matched the location of isopropanol molecules from MSCS, there are several additional sites that are mapped on the protein surface that are not discussed, despite their likelihood of complicating prospective applications of the method (Figure 5). Also, the reasons for not comparing the density of the entire isopropanol probe with the location of isopropanol found in MSCS structures were not discussed.

Figure 5.

MDmix maps compared to experimentally determined isopropanol binding sites on the surface of elastase. Isosurfaces of the maps are color-coded as follows: orange, 16 times the expected density of OH group in isopropanol; green, 16 times the expected density of Me group in isopropanol; cyan, 4 times the expected water density. The ball-and-stick molecules are isopropanol from experimental MSCS. The maps coincide with two of the isopropanol sites (black arrows), but the site with the yellow arrow was not identified at this contour level. More concerning are the highly occupied green/orange hotspots (red circle) that do not match the known sites and could be misleading in a prospective study. It should be noted that many cosolvent MD methods produce these “spurious” sites, and this is not a weakness that is specific to MDmix alone. This figure is a modified version of Figure 1c from reference 33. The color saturation of the protein surface of elastase was reduced to better emphasize the maps and the isopropanol binding sites, and the red circle was added.

They calculated free energies with equation (1) where N_i and N_o are the bin counts at grid point i and the expected bin count in the absence of any bias from the protein, respectively. This is a measure of the free energy change for moving an atom from the bulk solvent to grid point i. In their case, this atom could be the oxygen atom or the methyl groups of the cosolvent isopropanol.

$$\mathrm{\Delta }{G}_i=-\mathit{RTln}\left(\raisebox{1ex}{$N_i$}\!\left/ \!\raisebox{-1ex}{$N_{\mathrm{o}}$}\right.\right)$$ (1)

When the “atomic” free energies were computed, they note that in some cases, the ΔG_bind per non-hydrogen atom exceeded the empirical limit of free energy of −1.5 kcal/mol·atom that was observed by Kuntz et al.⁶⁹ Subsequent work from our group set the limit as −1.75 kcal/mol·atom,⁷⁰ and it is unclear if Barril’s values reported exceeded this limit as well. The authors propose that this behavior for isopropanol is a result of partial phase separation cause by apolar patches on the protein surface. However, our work has indicated the phase separation was caused by bad parameters for isopropanol, not by the protein environment.⁵¹ We note that the authors no longer use the alcohol parameters from their first paper, which we suspect caused the difficulties with phase separation that they found.³⁵

Because of the unusual behavior in those simulations, the expected bin counts were rescaled so that the free energy values conformed to the limit of −1.5 kcal/mol·atom. The maximal affinity of the probe molecules were then estimated using the principle that atoms in a drug-sized molecule are not only involved in establishing affinity, but also form a framework for allowing molecules to optimize such interactions. The authors noted that probe molecules are under no such constraint and proposed their free energies on a per atom basis could be much higher. As such, their maps were used to establish an upper limit for the volume of drug-like molecules. In validating this concept, a comparison is made between the maximal limits established by their approach and examples of drug molecules with the most favorable free energies. Comparisons between predicted and observed free energies were made for the protein targets MDM2, LFA-1/ICAM-1 complex, Protein Tyrosine Phosphatase 1B (PTP1B), p38 mitogen-activated protein kinase (p38 MAPK), Androgen Receptor (AR).

In a follow up study, prompted by our finding that full protein flexibility was needed for properly mapping hotspots with cosolvent MD simulations,⁴⁹ they examined the relationship between protein flexibility and its effect on binding free energy.³⁵ They derived a logarithmic relationship between flexibility and its effect on ΔG_bind. They concluded that if the restrained protein has a preformed binding site, ΔG_bind would become more favorable as the entropic cost of restraining the protein had already been paid. However, if this was not the case, then clashes with the protein binding site would make ΔG_bind less favorable.

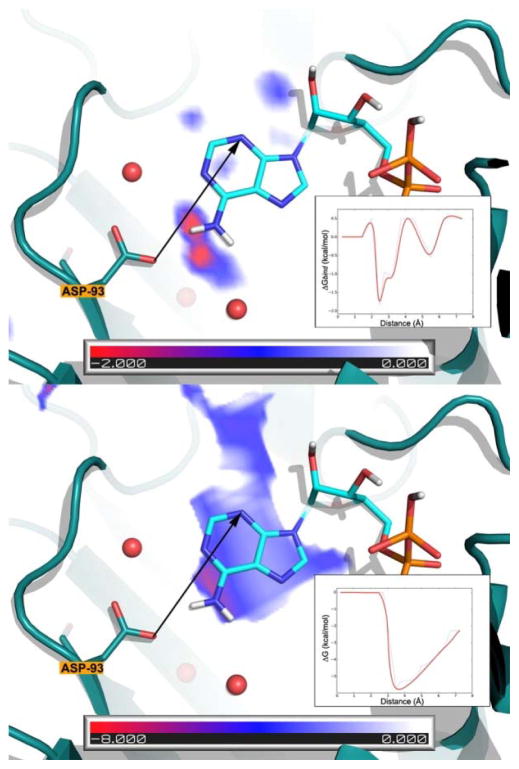
More recently, they have moved to a setup where two cosolvent simulations are performed separately with 20% ethanol in water and 20% acetamide in water.³⁶ An updated simulation protocol consists of 3 runs of 20ns while holding the heavy atoms in the protein with a weak restraint. The method was validated on Heat Shock Protein 90 N-terminal domain (Hsp90) and HIVp. Pharmacophore models created from ligands bound in crystal structures of these proteins were compared with the binding free energy maps calculated by equation (1). They observed that some key features in the HIVp pharmacophore model were not mapped and proposed to extend the technique by using other probes in the future. Furthermore, they state that using atoms within the probe molecule to define pharmacophore elements is limited by the assumption that these atoms behave independently of the probe molecules as a whole. It is notable that the authors compared their MDmix maps with those created by GRID and showed a marked improvement with MDmix (Figure 6). The role of explicit water creates much more detail in the maps and indicates regions were bridging water molecules may play an important role in binding. The authors specifically note, “GRID lacks selectivity because polar probes acquire negative values almost everywhere on the binding site. […] By contrast, the ensemble of conformations obtained with MDmix reflects both the excluded volume and the electrostatic screening effects created by water molecules...”

Figure 6.

Interaction potential of an –NH2 probe in the active site of Hsp90 derived from MDmix (acetamide’s N atom; top) and GRID (N2 probe; bottom). ADP is superimposed on the maps for reference only. The inset shows a smoothened 2D profile of the interaction potentials along the drawn vector. The role of explicit water creates much more detail in the MDmix maps and indicates regions were bridging water molecules may play an important role in binding. This is Figure 3 in reference 36.

MacKerell’s SILCS

By far, SILCS (Site-Identification by Ligand Competitive Saturation) is the technique that has made the most progress, expanding use of cosolvent simulations from only identifying binding sites to improvements such as pharmacophore modeling, free energy perturbation, and developing methods for sampling occluded pockets in proteins. The first study used a 1M benzene and propane solution on the BTB domain of BCL-6.³⁷ Benzene probes were used to identify aromatic interactions, propane molecules were used to identify aliphatic interactions, and water molecules were used to report upon the hydrogen-bond donating and accepting properties. Unique to the SILCS methodology is the use of artificial repulsive terms centered on dummy atoms in the center of benzene and the central carbon of propane. The repulsive term was necessary to avoid aggregation of the hydrophobic cosolvents. SILCS results were analyzed using simulation data generated from 10 runs of 5ns. Notably, a weak restraint was placed on the Cα atoms during the simulations to establish a stable frame of reference. Snapshots from the simulations are combined and visualized as density, described as “FragMaps”. Results from SILCS simulations of BCL-6 were verified by their ability to predict biologically relevant binding sites on the protein.

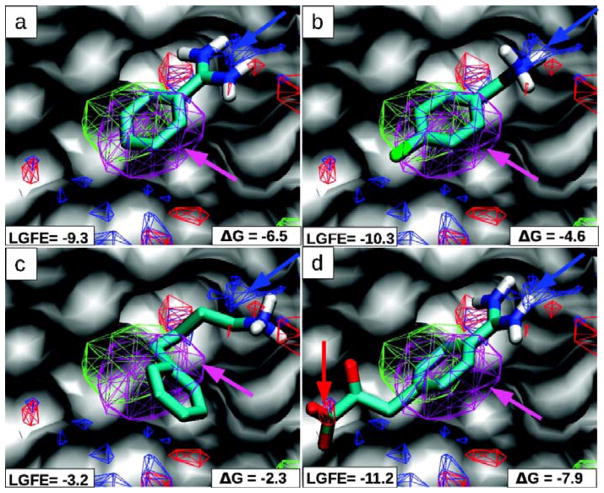
In a second study, a much wider set of systems were used: trypsin, α-thrombin, HIVp, FK506-binding protein 12 (FKBP), Factor Xa (FXa), NadD, and RNase A. The length of SILCS simulations was increased to 20ns, and the authors converted their FragMaps to Grid Free Energies (GFE).³⁸ These GFE were computed in a manner similar to the Barril approach, wherein equation (1) is used to report upon the free energy at each grid point. Using these GFEs, crystal ligand poses were found to score higher than decoy sets. Ligands were scored by assigning each atom in the ligand to one of aromatic, aliphatic, hydrogen-bond donor, and hydrogen-bond acceptor types. These atom types correspond to different probes used in SILCS simulations. After bringing the crystal ligands into the GFE frame of reference, the atom type of the ligand and its position within the grid were used to obtain the free energy value from the corresponding GFE grid. These values were then summed to arrive at the Ligand Grid Free Energy (LGFE) score for a given pose of the ligand (Figure 7).

Figure 7.

The S1-pocket of trypsin is shown with MacKerell’s FragMaps of benzene (purple), propane (green), hydrogen-bond donor (blue) and acceptor (red). Crystallographic poses of four inhibitors are overlaid (A–D) with the maps; polar hydrogens are shown. The benzene/propane FragMaps overlap the central aromatic rings of all the inhibitors (purple arrows). A critical recognition element is the hydrogen bonding between trypsin’s Asp189 and positively charged groups in the inhibitors; it is captured in the hydrogen-bond donor FragMap (blue arrows). The last inhibitor in (D) places an acid group in an appropriate position in the hydrogen-bond acceptor FragMap. The units of the LGFE and experimental binding affinities are in kcal/mol. This is Figure 2 from reference 38.

In a follow up to that study, the authors assessed the use of free energy perturbation to expand the range of fragments that can be predicted to bind to proteins.⁴⁰ Using benzene as an example, they first demonstrate that relative hydration energies for moving to mono-substituted benzene were correctly captured with an R² of 0.95. These benzene analogues were chosen based on experimental binding affinities that existed for ligands in α-thrombin and p38 MAPK. Then, a comparison was made between single-step free energy perturbations of benzene to its analogues with changes in experimental binding free energy that involved a similar transition. It is exciting that promising results were obtained for α-thrombin, but the same could not be said for p38 MAPK. This highlights the inherent limitations of extrapolating results from fragments to those found in drug-like ligand molecules.

SILCS simulations were also used to present an optimum solution for balancing target flexibility and possible denaturation in cosolvent-based simulations.³⁹ Using various levels of positional restraints on Interleukin-2 (IL-2), the authors found that allowing for full protein flexibility resulted in denaturation of the protein in certain runs. The authors in this SILCS study present two strategies to overcome unfolding problems, removing trajectories that denature or restraining the backbone of the protein while performing cosolvent simulations. It could be argued that the first option seems more appealing since restraining the protein will limit the breathing motions, thereby hampering the identification of cryptic pockets on the protein surface. In the case of IL-2, this did not seem to be an issue, and these cryptic pockets were found even when using a restrained potential on the protein. It is interesting that the authors’ simulation with acetonitrile at 50% concentration did not map the binding site in IL-2. In our application of MixMD, we have not seen target denaturation like MacKerell’s team, but their studies clearly demonstrate that target denaturation should be considered a possibility when running cosolvent simulations and adequate inspection of the protein’s behavior should be performed to detect them. In order to reduce these concerns, we moved from our initial simulations of 50% cosolvent to a 5% setup in MixMD.⁵²

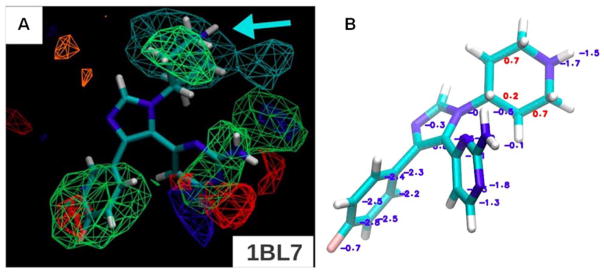
In the SILCS Tier-II update,⁴¹ more cosolvents were introduced. Probes were added to the initial benzene/propane protocol that included methanol, formamide, acetaldehyde, methylammonium, and acetate. All the aforementioned cosolvents were simulated in a single box of protein and water using a concentration 0.2 M for each probe. The simulations were performed for 20ns using weak restraints on the Cα to prevent the unfolding of the protein in the high concentration of probes, and repulsion terms between the probes were used to prevent aggregation. The densities of the cosolvents were combined in the following manner for analysis, generic nonpolar (benzene and propane carbons), neutral donor (methanol and formamide polar hydrogens), neutral acceptor (methanol, formamide, and acetaldehyde oxygens), positive donor (methylammonium polar hydrogens), and negative acceptor (acetate oxygens). Using these combined atom grids, GFE values were computed. These were then contoured at various values for each grid type and compared by visual inspection of the overlap with example of ligands from crystal structures. The technique was validated using FXa, p38 MAPK, RNase A, and HIVp. In addition to a visual inspection, the authors developed a suite of scoring functions based around the LGFE scoring scheme that they used earlier. A Monte Carlo-based sampling of the ligands within the GFE grids gave the best correlation between the scores generated and the experimental binding affinity of the ligands, see Figure 8. This approach worked for FXa, p38 MAPK, and RNase A, but the values were anti-correlated for HIVp. The authors note that this deviation of HIVp behavior emphasized how measures of affinity obtained from GFE come from cosolvents and do not reflect the configurational entropy and strain in real ligands.

Figure 8.

A) For p38 MAPK, the minimized crystal conformation is shown for the 1BL7 complex from the PDB, but the protein is not shown to emphasize the fit of the ligand in the maps. All FragMaps are drawn with a −1.2 kcal/mol cutoff. The FragMaps are colored green for nonpolar, blue for hydrogen-bond donor, red for hydrogen-bond acceptor, orange for negative acceptor, and cyan for positive donor. (B) Boltzmann-averaged GFE are shown for the atoms of the ligand in 1BL7. Favorable GFE values are displayed in blue and unfavorable in red. This figure is a composite of Figure 2d and Figure 7b from reference 41.

SILCS simulations have also been converted to pharmacophore models.^42,44 In their initial study, the pharmacophore models were derived from benzene, propane, and water locations from SILCS ternary simulations. The authors found that generating pharmacophore models from SILCS simulations using a GFE cutoff of −1.2 kcal/mol for aromatic|aliphatic FragMaps and −0.5 kcal/mol for water-based, hydrogen-bond donors|acceptors to be an ideal starting point. Grid points that were below the earlier mentioned GFE cutoffs were then clustered using a distance cutoff of 1 Å, 2.8 Å, and 2.6 Å for the water, aromatic, and aliphatic SILCS maps, respectively. These clusters are converted to “FragMap features” which are modeled as spheres whose center is the center of cluster. The radius of the FragMap feature is defined as the radius that encloses all the grid points that belong to this cluster. FragMap features were not allowed to have a radius greater than 2.5 Å for hydrophobic and 1.5 Å for hydrogen-bond features. The sum of the GFE within each cluster is then reported as the Feature Grid Free Energy (FGFE) of the FragMap feature. In a subsequent step, the FragMap features are converted to pharmacophore elements. The most important considerations in generating pharmacophore elements was the use of overlapping FragMaps features for defining aromatic|aliphatic features and donor|acceptor pharmacophore elements. Overlapping clusters of aromatic and aliphatic FragMap features are considered aromatic|aliphatic pharmacophore elements. Given that these simulations are conducted in a ternary system, it might be hard to establish overlapping features and this may be an area where simulations using a single cosolvent have an advantage. Using an automated approach, water locations of high density were converted to donor, acceptor, or donor|acceptor pharmacophore elements. These pharmacophore elements are then combined in different combinations and ranked using the cumulative FGFE of the elements in the pharmacophore model. That measure is called the Hypothesis Grid Free Energy (HGFE). The pharmacophore models using this approach were obtained from SILCS simulations of HIVp, FXa, and DHFR. Pharmacophore models with the lowest HGFE values using 3 to 6 pharmacophores were selected for screening. These pharmacophore models were then screened against ligands and decoys from the DUD dataset.⁷¹ A hit was reported when all pharmacophore elements in the model matched features in the ligands using MOE.⁷² Furthermore, a comparison is made between results from pharmacophore screening to the docking programs Dock⁷³ and AutoDock.⁷⁴ The authors note that the best performing SILCS pharmacophore model outperformed results from Dock and AutoDock. A comparison is also made with a receptor-based pharmacophore model technique based on hydration data⁷⁵, and the authors note the superior performance of their approach.

In a more elaborate study, the authors used SILCS Tier-II to obtain pharmacophore models.⁴⁴ The primary advantage served by this approach was the use of cosolvents that allowed them to better probe hydrogen-bond donating and accepting capabilities. This meant they could move away from using water to obtain such information. As the number of cosolvents expanded, the authors were able to add more pharmacophore element types to their repertoire. The additions included positive-donor and negative-acceptor pharmacophore elements. Also, excluded volumes were placed wherever grid points were not occupied by water or other cosolvents. In screening the pharmacophore models, all pharmacophore elements were used. However, certain pharmacophore elements were required for a match, which the authors describe as “key features.” In testing their pharmacophore models, these key features were selected after sorting all the pharmacophore elements based on the FGFE value. The authors note that using 3 or 4 key features resulted in the best enrichment. When 5 or more key features were used, degradation in performance was observed. The effects of HGFE on model performance was also tested, wherein it was found that models that performed well for the most part had a low HGFE. The performance of the pharmacophore models using this approach was tested against the systems that were used in their earlier approach for pharmacophore models (HIVp, FXa, and DHFR). Additional systems were also used to test SILCS pharmacophore models, including p38 MAPK, Fibroblast Growth Factor Receptor 1 (FGFr1) kinase, adenosine deaminase, ligand binding domain of the Estrogen Receptor α (ERα), and AmpC β-lactamase. The data sets for evaluating the performance of pharmacophore models were obtained from the DUD dataset⁷¹. Screening results for SILCS pharmacophore models were also compared with results from Dock,⁷³ AutoDock,⁷⁴ AutoDock Vina,⁷⁶ Full Protein Pharmacophore, and Hydration Site Restricted Pharmacophore.⁷⁵ In comparing across all the methods, the authors note that SILCS pharmacophore models outperformed other methods except the case of AmpC β-lactamase. For most of the proteins, an area under the curve of 0.7 was observed for ROC plots when SILCS pharmacophore models were screened. However, FGFr1 kinase and p38 MAPK yielded values that were lower than 0.6. Interestingly, similar results were seen for these proteins with the other methods, suggesting that they were challenging targets for virtual screening in general, not a limitation specific to SILCS.

Further advancements in the application of SILCS were made by implementing a type of Grand Canonical Monte Carlo (GCMC) approach coupled with MD simulations.⁴³ In this method, the excess chemical potential of water and solutes is varied to arrive at the target concentrations during the simulation process. The method in brief involves the simulated system being coupled to a reservoir of water and cosolvents. The water/cosolvent molecules from the reservoir are inserted/deleted from the reservoir into the system being simulated or translated and rotated if they are already present in the system. These moves are accepted or rejected based on Metropolis criteria, which depends on the change in energy upon the occurrence of the move, the target density, and excess chemical potential. Following several such moves (100,000 moves when used for simulating the protein), an MD simulation is performed. Finally, the excess chemical potential is changed. This change in excess chemical potential is based on a function of the deviation of the current concentration from the target concentration of the species under consideration. The whole process described above is repeated several times till the excess chemical potential converges. This approach was validated by reproducing the hydration free energies of the cosolvent molecules used in SILCS-Tier II simulations. Following this validation, the authors investigated the use of the method to map the occluded binding site of T4 lysozyme L99A mutant (T4-L99A). Following the GCMC-MD procedure, the occluded binding site of T4-L99A was successfully mapped by SILCS simulations. Moreover, the LGFE values correlated with a R² of 0.72 to the experimental binding affinities for the different molecules that are known to bind within this occluded pocket.

The GCMC-MD approach was further applied to several systems with occluded ligand-binding pockets.⁴⁶ These systems included AR, peroxisome proliferator activated-γ (PPARγ), metabotropic glutamate receptor 5 (mGluR5), and β2-adreneric receptor (β2AR). The occluded binding sites in all the protein targets were successfully mapped during SILCS simulations. Furthermore, a SILCS pharmacophore model obtained from β2AR was screened against a compound collection of 1.8 million from the Chembridge and Maybridge libraries. Following an elaborate procedure of docking with AutoDock Vina⁷⁶ into the active and in-active conformations of β2AR, molecules were identified that preferentially bound the active conformation, see Figure 9. The hits were clustered. Of the 16 molecules that were handpicked and tested, seven were found to be active. At this point, it is unclear if the molecules target the binding site of β2AR, but this exciting result nevertheless points to the utility of cosolvent simulations in prospective SBDD.

Figure 9.

FragMaps of the active and inactive states of β2AR are overlaid with ligands BI-167107 (right, PDB: 3P0G) and carazolol (center, PDB: 2RH1), respectively. Differential maps (right) highlight differences between the two maps; the red, dashed circle marks a large nonpolar region that overlaps well with the agonist B1-167107. The FragMaps are colored green for nonpolar, blue for hydrogen-bond donor, red for hydrogen-bond acceptor, orange for negative acceptor, and cyan for positive donor. Hydrogen-bonding FragMaps are set to a cutoff of −0.5 kcal/mol, while the nonpolar and charged FragMaps are set to a cutoff of −1.2 kcal/mol. This is Figure 4A of reference 46; for clarity, the protein surface has been lightened and the amino acid labels are changed to black font.

Additional prospective applications of the GCMC-MD approach were undertaken with a homology model of mGluR5.^47,48 Specific derivatives of two different scaffolds of interest to the project were screened to identify those with favorable LGFE values eventually leading to satisfactorily active molecules. The IC₅₀ values for the tested compounds for these two different scaffolds were converted to binding free energies and compared with LGFE values. The resulting correlation with LGFE values was R² ~ 0.35⁴⁷ and R² ~ 0. 26.⁴⁸ While promising, the low correlations underscore the need for further development in this area.

Carlson’s MixMD

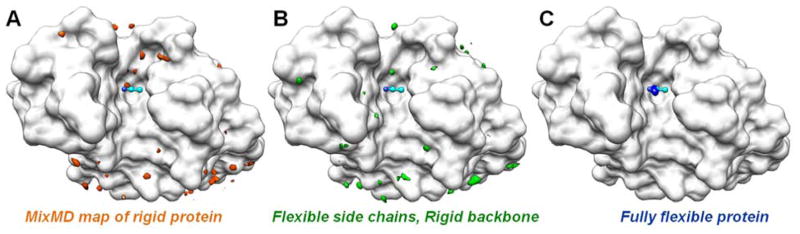
Our approach for performing cosolvent simulations is called mixed-solvent MD (MixMD). MixMD involves binary solvent simulations of proteins with water and water-miscible, organic probe solvents. An emphasis on using water-miscible organics as cosolvent distinguishes our approach from other techniques that rely on artificial repulsive terms between cosolvents. A first step in validating MixMD was evaluating its ability to reproduce the cosolvent binding location obtained from MSCS experiments. Using the acetonitrile binding site in HEWL as a test case, MixMD was shown to recapture the binding location of acetonitrile.⁴⁹ Our first MixMD simulations used a 50% concentration of acetonitrile and were run five times for 10 ns duration. The last 2ns of these simulations were used for obtaining the preferential location of acetonitrile binding on the protein surface. This work also noted the importance of protein flexibility on the accuracy of mapping the acetonitrile binding site. Using a series of MixMD simulations wherein the protein was subjected to varying levels of restraint, the acetonitrile binding site was mapped accurately and without spurious minima only when full protein flexibility was allowed, see Figure 10. When the protein was held rigid, we found that the acetonitrile binding site was mapped as strongly as many (incorrect) local minima across the whole protein surface. When the protein is flexible, those spurious minima “smear” out and become less densely occupied. With flexible proteins, the true hotspots are still strongly mapped.

Figure 10.

Our MixMD results from restrained vs unrestrained protein simulations of acetonitrile and HEWL (white surface).⁴⁹ The single hotspot for acetonitrile that was experimentally identified by MSCS is shown in cyan ball-and-stick in the center of each figure. (A) High occupancy regions of the map from the fully restrained simulation are shown in orange, (B) the backbone-restrained density in green, and (C) the occupancy map from fully flexible MixMD is in blue. Many incorrect local minima in green and orange can be seen, but the correct position alone dominates the blue map from the simulation of the fully flexible protein.

In a follow up to our first MixMD study, we focused on extending the approach to protic solvents.⁵⁰ Isopropanol was used as the cosolvent, and several proteins were used as test cases: elastase, HEWL, p53, RNase, and thermolysin. MixMD results were shown to be in excellent agreement with the isopropanol binding sites found in MSCS of these proteins. During the course of optimizing the technique, the number of runs and the simulation length were also investigated. The importance of multiple, short simulations was highlighted, and using 10 runs of 20ns was found to be optimal.

More recently, the importance of probe parameters⁵¹ was established by comparing cosolvent simulations using our approach and parameters for isopropanol to that of the original Barril approach³³. These cosolvent simulations were performed on thermolysin using 50% isopropanol. To our surprise, the cosolvents separated into two phases when using Barril’s parameters (see Figure 11). Our simulations based on OPLS parameters for alcohols⁷⁷ remained evenly mixed.⁵¹ This result made us step back and evaluate water-cosolvent mixtures alone without proteins. We used radial distribution functions to monitor miscibility. We recommend that all cosolvent simulations include radial distribution functions of the solvents to show proper behavior of the environment. This is just as important as monitoring protein’s RMSD to show no unfolding. We investigated the use of several different organic probes for MixMD simulations. Upon testing eleven different solvents, six were found to have even mixing with TIP3P water. These cosolvents were acetonitrile, isopropanol, acetone, N-methylacetamide, imidazole, and pyrimidine.

Figure 11.

Snapshots of MixMD simulations of thermolysin in 50% w/w isopropanol and water. (A) When using Barril’s original isopropanol parameters,³³ the solvent separated into two phases after a few nanoseconds of simulation time. This behavior is unrealistic because isopropanol and water are completely miscible. (B) The same simulation using OPLS parameters⁷⁷ for the isopropanol molecules resulted in both solvents remaining well-distributed for the entire simulation time. This is Figure 1 of reference 51.

Using HIVp as a test case, we have successfully mapped the catalytic site and potential allosteric sites.⁵² In that work, we compared the use of 50% concentration to a low concentration of 5%. Experimentally, proteins unfold at high concentrations of cosolvents. Though this might not be a problem in the short time scales of MD, comparing back to experiments may not be feasible. Therefore, lower concentrations of cosolvents could facilitate the comparison of results from cosolvent simulations with real experimental data. Most surprisingly, we found this reduction in the concentration of the cosolvent resulted in a significantly improved signal-to-noise ratio, meaning the occupancy of real hotspots and spurious minima had greater differences with less cosolvent.

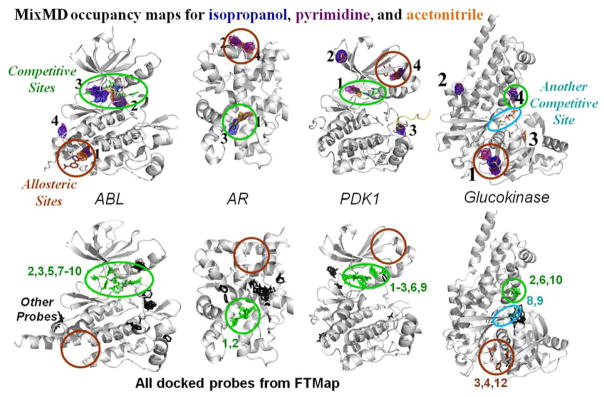
In a more recent study, we have established a rigorous protocol for the identification and ranking of binding sites on the protein surface.⁵³ Our approach requires binding sites to be mapped by more than one type of probe at a high signal-to-noise ratio. Using cosolvent simulations of 5% acetonitrile, isopropanol, and pyrimidine, we have successfully detected both competitive and allosteric sites within the top four ranked sites across several allosteric systems which included ABL kinase, AR, CHK1 kinase, glucokinase, PDK1 kinase, PTP1B, and farnesyl pyrophosphate synthase. Interestingly, lower-ranked sites consistently mapped multimerization interfaces, other biologically relevant sites, or crystal-packing interfaces. Also, we compared our results to FTMap as a benchmark, see Figure 12. FTMap identified all competitive binding sites, but it did not identify the allosteric sites in four of the seven systems used in our study: ABL kinase, AR, PDK1 kinase, and PTP1B. There were also many spurious hotspots identified outside the known sites. However, there was a case where FTMap identified all subsites of the competitive site in glucokinase, whereas MixMD only mapped part of the competitive site occupied by the cofactor (Figure 12).

Figure 12.

Maps⁵³ from MixMD are compared to the hotspots provided by the FTMap server. Competitive sites are circled in green and the allosteric sites are marked with brown. Both competitive and allosteric sites are mapped by the top-four sites in MixMD. In FTMap, hotspots are determined from clusters of probe molecules and ranked according to their average energy (cluster numbers are shown). Each cluster above is colored on the basis of whether it overlaps with known ligands. Green indicates a cluster that overlaps with competitive ligands, and brown clusters overlap allosteric ligands. Black clusters do not overlap either binding site, and their rank numbers are not shown. Cyan clusters in glucokinase overlap correct positions for sugar binding that were not mapped by MixMD. Please note that numbering in FTMap starts at 0, and we have shifted the numbers to start at 1.

Yang and Wang’s method

In their first use of cosolvent simulations, Yang and Wang compared the cosolvent locations in MSCS structures of thermolysin.⁵⁴ This important study was the first to compare free energies obtained from equation (1) with more rigorous statistical mechanics-based approaches such as the double-decoupling method.^78,79 For this study, the MSCS structures of thermolysin with three different probes (isopropanol, phenol, and acetone) were used.⁵ Their primary focus was on two isopropanol sites identified on thermolysin named site 1 and site 2 that appeared at high (≥10%) and low (5%) concentrations of isopropanol, respectively. Site 2 was also mapped by phenol and acetone whereas site 1 was not. The double decoupling method^78,79 was initially used to compute the free energies of site 1 and site 2. In applying this technique, they note that site 2 (−4.87 kcal/mol) had a more favorable free energy for binding isopropanol compared to site 1 (−3.25 kcal/mol); this observation was consistent with the identification of site 2 at a lower concentration of isopropanol. For site 1, they note the free energy changes for the different cosolvents ranged from −3.35 to −4.32 kcal/mol. These results from the double decoupling method were compared with the values obtained from performing and computing the free energies of isopropanol using the Barril approach. The binding free energy for isopropanol in site 1 and site 2 were found to be −3.91 and −5.01 kcal/mol. The authors note that the values computed using the cosolvent occupancies was higher compared to the more rigorous double decoupling method, but both methods give free energies of binding within 1 kcal/mol for both sites, which is the limit of the best free energy calculations. We consider the agreement in the methods much more interesting than differences within error of the best techniques available.

In a subsequent study of protein-protein interfaces (PPI), the authors compared simulations of different conformations of Bcl-xL and Mcl-1 in mixures of water and isopropanol.⁵⁵ Starting from conformations obtained from one apo and three holo Bcl-xL crystal structures, 32ns simulations in water were shown to exhibit hydrophobic collapse which prevented Bcl-xL from adopting conformations that allowed it to bind to its partners. However, in the presence of 20% isopropanol, conformations that resembled those used to bind with other partners were retained. Furthermore, the authors note that the hotspots identified on the protein surface changed based on the starting conformation used for cosolvent simulations of Bcl-xL. They suggest that such information in principle allows one to target different conformations separately. In continuation of their earlier work, cosolvent simulations using isopropanol (20%), phenol (10%), and 2M trimethylamine N-oxide were performed on Bcl-xL and Mcl-1.⁵⁶ In that study, the authors note that there were similarities and differences in the location of hotspots within both the proteins, Figure 13. Using this information, it was suggested that the differences (green arrows) in the location of hotspots within the active site between the two proteins could be exploited to obtain potent and selective drug-like molecules.

Figure 13.

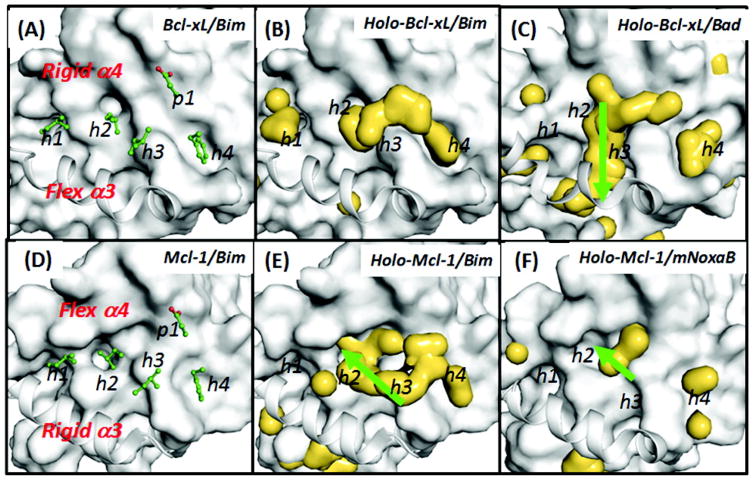
Hydrophobic hotspots are shown as yellow enveloped surfaces in holo-Bcl-xL/peptide and holo-Mcl-1/peptide. Analyses are based on 16 ns cosolvent simulations of the (B) holo-Bcl-xL/Bim and (C) holo-Bcl-xL/Bad and those of the (E) holo-Mcl-1/Bim and (F) holo-Mcl-1/mNoxaB from the crystal structures. Probe molecules include 20% isopropanol and 10% phenol v/v. The reference structures used in the surface representation are the crystal structures of Bcl-xL/peptide and Mcl-1/peptide. Key Bim residues are shown in green stick models in A and B. Important hydrophobic binding sites are labelled as h1–h4 and a single polar site as p1. Green arrows highlight important differences in the hotspot maps. This is Figure 4 of reference 56.

More recently, hotspots on the protein surface of the ectodomain of interleukin-1 receptor type 1 (IL-1R1) were investigated using cosolvent simulations of 10% phenol.⁵⁷ The authors’ primary motivation for using phenol cosolvent simulations came from the frequent observation of these groups in fragment screening libraries for targeting protein-protein interactions. Cosolvent simulations were used to investigate three druggable sites identified using Sitemap,^80,81 which were named P1, P2, and P3. As P1 and P3 could already be identified from crystal structures, they focused their attention on assessing the druggability of the P2 site using cosolvent simulations. While Sitemap identified four conformations in which the P2 site was deemed as druggable, cosolvent simulations identified only two conformations of the protein in which the P2 site exhibited high affinity for phenol cosolvent. These studies highlight the importance of including protein flexibility in assessing druggability of proteins. Based on this analysis, further efforts were focused on one of the two conformations that adopted a novel conformation. Using in silico screening methodology, fragments that bound to the P2 site were identified and further simulations of these fragments revealed that when bound to the P2 site, these fragments restricted the conformations accessible to IL-1R1.

The effect of cosolvent simulations on protein conformations was further investigated using the protein Bcl-xL.⁵⁸ In this study, the authors compared different cosolvent simulation setups. A comparison of pure water MD simulations, cosolvent simulations, accelerated MD simulations, and a combination of cosolvent simulations with accelerated MD were performed. The authors used apo conformations of Bcl-xL as a starting point for all the simulations Interestingly, the combination of cosolvent simulations with accelerated MD resulted in the generation of ideal protein conformations that were found to be the most useful in docking.

GlaxoSmithKline and Bahar

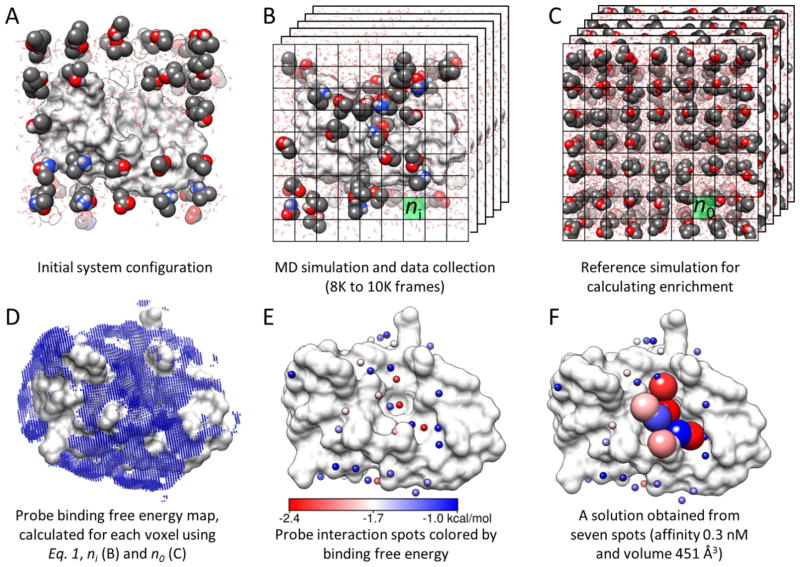
Bahar and colleagues at GlaxoSmithKline (GSK) used cosolvent simulations to address the druggability of protein binding sites.⁵⁹ In this approach, two cosolvent simulations were conducted, one in the presence of isopropanol and another using a mixture of acetamide, acetic acid, and isopropylamine. The ratio of probes to water was set at one probe molecule for every 20 water molecules. This corresponds to ~2.3M probe concentration in the cosolvent simulations. Several simulations of varying time length of 32 and 40ns were performed. Free energies were calculated using equation (1). However, it is important to note that the free energies were calculated based on the maximally occupied grid point in the volume of an entire probe (Figure 14). This is a very important distinction from other approaches where these measures are reported on a per-atom basis. These free energies calculated for volumes of the size of a probe were termed “interaction spots”. Reasonable constraints were placed on the definition of these interaction spots. They were required to not overlap with other interaction spots. Only those interaction spots with energy lower than −1 kcal/mol were considered, and the energy of an interaction spot was determined to be that of the central grid point (all other grid points within the radius of the probe were eliminated). In cosolvent simulations using mixtures, the radius of the interaction site was the sum of the radii of all the probes used in the simulation. An interaction spot was given a charge based on the fraction of time it is occupied by a charged probe. The interaction spots were then clustered using a 6.2Å distance to identify druggable sites under the constraint that the clusters can have a charge of no more than 2e⁻. Finally, maximum achievable free energies of binding were obtained from the free energies of the interaction spots within the clusters (Figure 14).

Figure 14.

Overview of methodology used by GSK and Bahar; this is Figure 1 in reference 59. (A) The druggability simulation box is prepared by immersing the target protein in a box of water and probe molecules. (B) After the superposition of frames onto the X-ray structure using Cα atom positions, a grid representation is used to measure the probe density (n_i). (C) A protein-free system is simulated to calculate the expected probe density (n_o) used in equation 1. (D) The binding free energy for each voxel is calculated using equation 1. Note that only the outer layer (weaker) interactions are visible in the map. (E) Interaction spots (small spheres) are identified by removing the voxels that overlap with the lower energy voxels. The energy scale in this panel holds for panels D and F as well. (F) Proximal spots are merged to predict maximal affinity. Interaction spots that are in a druggable site are shown as larger spheres color-coded by the corresponding interaction energies with the target.

These cosolvent simulations were applied to a test set of five proteins: MDM2, PTP1B, LFA-1, kinesin Eg5, and p38 MAPK. The authors found that the maximal free energies of binding computed using their approach are in perfect agreement with the affinities of the best known ligands for the binding sites on these proteins. Interestingly in MDM2, the occluded binding site was open for access only in cosolvent simulations. Similar results were obtained for LFA-1 and Eg5 where rearrangement of side chains resulted in access to the allosteric site. The authors attribute the opening of partially occluded sites to the use of an annealing procedure during the equilibration protocol wherein the system was heated to 600K under a restraint placed on the heavy atoms to prevent unfolding. Furthermore, in comparing the water and cosolvent simulations, it was noted that the probe molecules prevented hydrophobic collapse of binding sites during the equilibration (a phenomenon also observed by Yang and Wang in their simulations of Bcl-xL⁵⁴). In Eg5, the pocket opening happened more frequently when a mixture of polar and charged cosolvents were used instead of isopropanol. In p38 MAPK, the druggability of the allosteric site was better captured by a mixture of probes instead of the use of isopropanol alone. These results certainly highlight the advantages of using probe mixtures over the single-cosolvent simulations used in our approach. The authors note that many drug molecules are either charged or zwitterionic in nature, so mixtures of probes that include charged cosolvents are likely required for many druggable proteins.

Caflisch approach

What sets this work apart from the aforementioned is the fact that the cosolvent MD was used to estimate on/off rates and binding affinities based on kinetics. Caflisch and co-workers performed simulations of FKBP with dimethylsulfoxide (DMSO).⁶⁰ Ten simulations lasting for 70ns each using 50 molecules of DMSO (~440mM) were performed. DMSO primarily mapped the active site of FKBP in these simulations. Interestingly, the binding and unbinding events of DMSO in these simulations were used to obtain the dissociation constant of DMSO for the active site (~300mM). These values were in agreement with results from experiments. The authors also note that using DMSO concentrations higher or lower by a factor of two did not change the obtained results.

In a follow up study, cosolvent simulations were performed for two bromodomains: zinc finger domain 2B (BAZ2B) and the CREB binding protein (CREBBP).⁶¹ These simulations were conducted separately using the cosolvents DMSO, methanol, and ethanol. Two 0.5μs simulations for each cosolvent were performed using 50 cosolvent molecules (~440mM). Cosolvent simulations were able to successfully map the acetyl-lysine binding site of CREBBP. Furthermore, the location of DMSO in these simulations was in perfect agreement with the position of DMSO found in a crystal structure of CREBBP.⁸² Similar mapping of the acetyl-lysine binding site by different cosolvents was also noted for BAZ2B. The authors note that there were several binding and unbinding events of the cosolvents observed in the simulation. An analysis of the kinetics of cosolvent binding revealed that unbinding events for DMSO and ethanol were slower than methanol possibly due to their larger size and hydrophobicity. Interestingly, an analysis of the water molecules within the acetyl-lysine binding revealed that while some were retained during the entire simulation, others were transiently replaced by cosolvents. Based on this information, the authors proposed that water molecules that do not exchange with cosolvent should be included in the protein binding site during high-throughput docking studies. Furthermore, they suggested that hydroxyl substituents could be designed into ligands when water molecules are replaced by cosolvents.

Additional variations on the methods described above

Tan and Abell

Tan et al. used cosolvent simulations with a low concentration of benzene (0.2M) to reduce aggregation issues.⁶² In an application of this method to the polo-box domain of polo-like kinase 1, they note that a tyrosine residue lining the secondary binding site of this protein adopts a closed conformation during water simulations. However, when cosolvent simulations were performed with benzene, this residue flipped to open a cryptic pocket. Furthermore, a ligand was successfully designed to take advantage of this cryptic binding site. These studies highlight the potential of cosolvent simulations to open cryptic pockets on the protein surface that can then be targeted through SBDD.

More recently, the authors were motivated by the abundance of halogens in drug-like molecules to focus on the use of chlorobenzene as a cosolvent.⁶³ They note that chlorobenzene aggregates when used at a concentration of 0.2M and thus decreased the concentration of the probe molecules to 0.15M. This decrease in chlorobenzene concentration necessitated an increase the simulation length from 5ns to 10ns to achieve adequate sampling. Protein targets with halogenated ligands were selected to test the approach. This set of test cases included MDM2, Mcl-1, IL-2, and Bcl-xL. In starting their cosolvent simulations, they chose conformations of the protein where these halogen binding sites were absent. For the most part, simulations were able to identify cryptic binding sites on the protein surface. The authors note that the only site not mapped by cosolvent simulations was in Bcl-xL, but opening that site required major rearrangement of helices.

In a follow up study, their approach was used to detect hydrophobic binding sites at PPI. Using Aurora-A, RAD51, and MDM2 as a test set with benzene as a cosolvent they were able to identify hydrophobic binding sites at the PPI.⁶⁴ Interestingly, cryptic pockets that opened in cosolvent simulations of MDM2 and RAD51 were absent when run using regular water MD simulations. The ability of benzene cosolvent simulations to detect binding sites of hydrocarbon staples of stapled peptides was also investigated. Benzene cosolvent simulations were applied to a dataset of crystal structures with known locations of hydrocarbon staples, which added MDMX, Mcl-1, ERα and ERβ to the study. The resulted indicated agreement between benzene cosolvent simulations and locations of hydrocarbon staples in stapled peptides from crystal structures.

Fersht’s application

Fersht and co-workers used isopropanol-based, cosolvent simulations to study a cancer causing mutant of the p53 protein.⁶⁵ This mutant protein, p53-Y220C, has a mutation of the wild type’s tyrosine to a cysteine that results in a pocket being opened. The authors investigated the use of cosolvent simulations to identify druggable binding sites on the protein surface. Interestingly, the site with the highest isopropanol density was located at the dimer interface. Two other sites were also found, one within the cavity created by the mutation and another which the authors could not account for. The authors note that during their experimental fragment screen, they were only able to identify hits that targeted the mutation-induced cavity on p53-Y220C and could not find hits for the other two sites. The setup and execution of the isopropanol simulations was similar to the Barril approach but using a concentration of 20%. In the initial equilibration period, the protein was simulated at 600K while placing a restraint on the heavy atoms of the protein to allow for the distribution of probes. This was followed by an equilibration of 1ns followed by 19ns of production simulation under constant pressure at 300K. Binding free energies for the isopropanol molecules were also estimated using the Barril approach.

Gorfe’s pMD

Gorfe and co-workers have investigated the location of hotspots on the protein surface of K-ras using pMD, an approach that uses isopropanol as a probe in cosolvent simulations.⁶⁶ In their approach a simulated annealing procedure was used similar to the one reported by Bahar and GSK collaborators. Here, the system was initially equilibrated by heating to 650K followed by cooling to 310K, all while significantly restraining the protein’s heavy atoms. In their opinion, this procedure prevented kinetic trapping of the probe molecules inside the protein. Following further equilibration wherein the restraints on the protein were gradually removed, the system was simulated for three runs for varying lengths of time ranging from 30 to 100 ns. Further analysis was then performed by combining the three runs. The results were visualized by converting each grid point to free energy values using equation (1). The maps were then subsequently contoured at −0.5 kcal/mol for visualization. In an approach similar to the one adopted by Bahar and co-workers, maximal free energies were calculated for binding sites. The grid point with the most favorable free energy was identified, and all other points within a 5Å radius were discarded. After exhaustively processing the grid points in this manner, the retained points were clustered using a 6Å clustering distance. “Druggable sites” were defined as clusters with four or more interaction points and “subsites” were defined as clusters with two or three interaction points. Five druggable sites and three subsites were identified on K-ras. These sites were then found to capture known allosteric sites on K-ras. An additional comparison was made between pockets identified using the curvature analysis MDpocket⁸³ and pMD simulation maps. The authors note that some of the sites were not identified by MDpocket as they did not conform to the definition of a pocket. Thereby, the authors point to the advantage of using cosolvent maps to identify binding sites as opposed to those obtained from techniques that rely on protein curvature.⁸³ A comparison was also made between water simulations and pMD using MDpocket, wherein they found that pockets formed during pMD simulations were larger in size.

More recently, the authors extended the pMD technique to work on protein targets embedded in membranes.⁶⁷ Noting that cosolvent simulation with membranes represent a unique problem since they can exert a disrupting influence on the integrity of the membrane, they altered non-bonded interactions between cosolvents and lipid bilayers. The pMD-membrane approach was used to identify allosteric ligand binding sites on mutant K-Ras protein in the presence of lipid bilayer.

Future Directions

With the ever-increasing accessibility of computing power, cosolvent MD simulations are a practical mechanism to better incorporate the role of protein flexibility and competition with water into SBDD. Their use for identifying hotspots on protein surfaces has been highlighted by several research groups. However, the domain of applicability for cosolvent simulations extends beyond hotspot mapping. Here, we comment on current and potential future applications of cosolvent simulations in SBDD.

Converting cosolvent simulations into pharmacophore models

The location of cosolvent molecules during cosolvent simulations are not only indicative of hotspots, but point to the interactions required to achieve optimal potency. The latest developments in cosolvent MD have focused on converting the information derived from simulations into pharmacophore models. Currently, protocols for extracting pharmacophore models exist for the Barril approach³⁶ and the MacKerell approach.^42,44 Most development in this direction has been very similar to our MPS method.^{15–20,22,23} Creating pharmacophore models by wedding our ideas of MPS and MixMD would be a natural progression of our method development.

Using cosolvent simulations to assist in scoring and ranking ligands

What cosolvent MD needs most is an accurate method for translating occupancy grids into a quantitative measure of binding. MacKerell and co-workers in their development of SILCS simulations^{37–46,84,85} have moved beyond the concept of simple pharmacophores. By presenting the binding preference of cosolvents on a grid and summing up the occupancies at grid points which overlap with known crystal structure ligands, they provide a more quantitative picture of the agreement between cosolvent simulations and known active ligands for proteins.³⁸ This description allows one to move beyond a typical binary, hit/no-hit outcome from screening pharmacophore models. These developments have the potential to add immense value to current computational techniques by providing means of ranking active and inactive molecules. As the preference for cosolvent probes in MD simulations is a complex interplay between competition with water and favorable interaction energies with the protein, accounting for it through scoring and ranking would provide an extra dimension to current docking approaches that typically lack a means of dealing with solvation effects or treat it in a rudimentary fashion.

Identifying allosteric sites and cryptic pockets using cosolvent simulations

Cosolvent simulations have demonstrated that it is possible to map cryptic allosteric pockets that open upon side-chain movement are achievable. However, it is yet to be determined if such simulations are enough to allow large-scale backbone motions that are accurate. Methods that accelerate conformation sampling such as accelerated MD⁸⁶ and metadynamics⁸⁷ are attractive alternatives to these problems and need to be investigated in conjunction with cosolvent simulations. A recent study using the Yang and Wang approach suggests this to be a promising area of research.⁵⁸ Using cosolvent simulations with accelerated MD, they were able to identify suitable conformations (starting from an apo conformation of Bcl-xL) that performed better at docking known ligands. Identifying cryptic allosteric pockets is an area on immense interest as one could then drive selectivity between proteins where the orthosteric sites are similar. Further studies in this direction, might unravel important applications of cosolvent simulations.

Assessing druggability of PPIs

Targeting protein-protein interactions using small molecules is challenging as these interactions are typically spread over a larger shallow surface area.⁸⁸ Understanding whether sites that disproportionately contribute to binding exist and targeting them will be key in assessing the druggability and success rate of disrupting PPIs. In an application of MixMD to farnesyl pyrophosphate synthase, we have observed strong mapping of the protein-protein interaction interface.⁵³ These results prompt the need to assess the utility of cosolvent simulations in prioritizing which protein-protein interactions to target with small molecules.

Expanding the range of probe molecules used with cosolvent simulations

The identity of cosolvents used in MD simulations can have a significant impact on the outcome and interpretation of results. The choice of “probe” solvents in most implementations of cosolvent MD has primarily tried to provide a representative set of frequently occurring fragments in drug-like molecules. Using only water-miscible cosolvents has been a defining principle in our development of MixMD and in Barril’s development of his approach, but others have used repulsive terms to include less soluble fragments in their cosolvent MD. With a wide variety of organic solvent possible, it remains to be seen if cosolvent simulations with different sets of probes can be used to tailor the technology to various SBDD applications like fragment-based design. Identifying the optimal set of cosolvents for pursing each application will be one of the big challenges for the future.

Cosolvent simulations with multiple probe molecules

The use of single cosolvent simulations is needed if one defines druggable binding sites through independent mapping by multiple cosolvents, like MSCS and FTMap. However, several of the methods discussed above use a mixture of cosolvents, not a single cosolvent. Currently, no guidelines exist for choosing one approach over the other, and it may depend on the application. It is possible that the optimal combinations of cosolvents may be system dependent, and it requires investigation. There is great potential for synergistic effects that arise from two different cosolvents binding near each other, and this may yield further insights that could be exploited in SBDD.

Exploring conformational dependence of cosolvent simulations

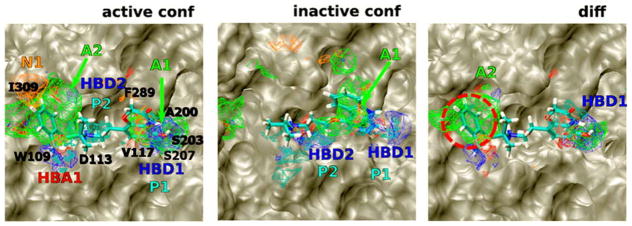
The effect of starting conformation on the outcome of cosolvent simulations has not been explored in depth. The only notable exception in this area was work done by Yang and Wang who found that hotspots identified on the protein surface differed based on the starting conformation used for cosolvent simulations.⁵⁵ In principle, one could target different protein conformations. More recently, they found that conformations extracted from cosolvent simulations (in tandem with accelerated MD) resulted in improved docking of ligands for Bcl-xL.⁵⁸ In our application of MixMD, we have similar observations using active vs inactive conformations of ABL kinase.⁵³ MixMD simulations starting from two ABL kinase conformations resulted in hotspot mapping consistent with the biological function of the two different conformations. The inactive conformation, which is not expected to bind peptide substrates, showed no hotspot mapping in this region with MixMD. However, the active conformation of ABL kinase that processes peptide substrates, did yield hotspots in this region. Similar results across other systems would strengthen the argument for the use of cosolvent simulations to evaluate the importance of different conformations in the context of biological function.

Summary

The successful application of cosolvent simulations to a wide variety of protein targets by various groups has presented a very encouraging picture for this nascent field. Improvements in MD simulation codes, coupled with significant advances in computing power, have finally brought MD methods to the point of practical use in SBDD. Cosolvent simulations are a way of using MD for more than just conformational sampling of a protein system. However, there remain several pressing questions on the optimal use and best practices for the various approaches. Future developments will provide these answers and continue the significant strides to integrate cosolvent MD with mainstream computational approaches for SBDD. The progress thus far suggests that cosolvent MD is poised to become the next significant advance in computational techniques to drive drug discovery forward.

Abbreviations

AR

androgen receptor

β2AR

β2-adreneric receptor

BAZ2B

zinc finger domain 2B

CREBBP

CREB binding protein

DHFR

dihydrofolate reductase

DMSO

dimethylsulfoxide

ERα

estrogen receptor α

ERβ

estrogen receptor β

FGFE

feature grid free energy

FGFr1

fibroblast growth factor receptor 1

FKBP

FK506-binding protein 12

FXa

Factor Xa

GCMC

grand canonical Monte Carlo

GFE

grid free energies

GSK

GlaxoSmithKline

HEWL

hen egg-white lysozyme

HGFE

hypothesis grid free energy

HIVp

HIV-1 protease

Hsp90

heat shock protein 90 N-terminal domain

IL-1R1

interleukin-1 receptor type 1

IL-2

Interleukin-2

LGFE

ligand grid free energy

MCSS

multiple copy simultaneous search

MD

molecular dynamics

mGluR5

metabotropic glutamate receptor 5

MixMD

mixed-solvent molecular dynamics

MPS

multiple protein structure

MSCS

multiple solvent crystal structures

p38 MAPK

p38 mitogen-activated protein kinase

p53

p53 core domain

PPARγ

peroxisome proliferator activated-γ

PPI

protein-protein interface

PTP1B

protein tyrosine phosphatase 1B

SBDD

structure-based drug discovery

SILCS

site-identification by ligand competitive saturation

T4-L99A

L99A mutant of T4 lysozyme

RMSD

root mean square deviation

RNase A

ribonuclease A

Biographies

Heather A. Carlson is a Professor of Medicinal Chemistry, Biophysics, and Chemistry at the University of Michigan, Ann Arbor. She received her B.S. (1991) from North Central College and her M.S. (1992) and Ph.D. (1997) at Yale University. Her postdoctoral studies at UCSD (1997–2000) focused on computational biology. She has received several honors: Fellow of the American Association for the Advancement of Science (2011), Novartis Chemistry Lectureship (Novartis Pharma AG, 2009), the Corwin Hansch Award (Cheminformatics and QSAR Society, 2008), an NSF CAREER Award (2006), and a Beckman Young Investigator Award (2002). She researches computer modeling of protein-ligand interactions, from the basic biophysics of molecular recognition to applied inhibitor design. She is particularly interested in protein flexibility, allosteric control, binding-site druggability, and structural databases (www.BindingMOAD.org).

Phani Ghanakota is currently a postdoctoral associate at Schrödinger, working in collaboration with Janssen Pharmaceuticals. He received his B. Pharmacy from Kakatiya University (2006). He received his M.S. in Drug Discovery (2008) from The School of Pharmacy, University of London where he worked on the total synthesis of sibiromycin, an anti-cancer natural product. He obtained his Ph.D. in Medicinal Chemistry from The University of Michigan, Ann Arbor (2015) under the guidance of Heather A. Carlson. His graduate work focused on mixed-solvent simulations, where he developed methods for hotspot mapping, allosteric-site detection, and thermodynamic decomposition of binding events. His research interests include cosolvent MD, druggability analysis, protein-protein inhibitors, and drug design.