Quantifying the Metabolic Contribution to Photoreceptor Death in Retinitis Pigmentosa via a Mathematical Model

Abstract

Retinitis Pigmentosa (RP) is a family of inherited retinal degenerative diseases that leads to blindness. In many cases the disease-causing allele encodes for a gene exclusively expressed in the night active rod photoreceptors. However, because rod death always leads to cone death affected individuals eventually lose their sight. Many theories have been proposed to explain the secondary loss of cones in RP; however, most fail to fully explain the different pathological transition stages seen in humans. Incorporating experimental data of rod and cone death kinetics from two mouse models of RP, we use a mathematical model to investigate the interplay and role of energy consumption and uptake of the photoreceptors as well as nutrient availability supplied through the retinal pigment epithelium (RPE) throughout the progression of RP. Our data driven mathematical model predicts that the system requires a total reduction of approximately 27% to 31% in nutrients available to result in the complete demise of all cones. Simulations utilizing retinal degeneration 1 (rd1) mouse cell count data in which cone death was delayed by altering cell metabolism in cones show that preventing a 1-2% decrease in nutrients available can permanently halt cone death even when 90% have already died. Our results also indicate that the ratio of energy consumption to uptake of cones, D_c, is mainly disrupted during the death wave of the rods with negligible changes thereafter and that the subsequent nutrient decrease is mainly responsible for the demise of the cones. The change in this ratio D_c highlights the compensation that the cones must undergo during rod death to meet the high metabolic demands of the entire photoreceptor population. Global sensitivity analysis confirms the results and suggests areas of focus for halting RP, even at later stages of the disease, through feasible therapeutic interventions.

Introduction

Retinitis Pigmentosa (RP) is a heterogeneous group of inherited disorders that often result in blindness and affect approximately 1 in 4000 individuals (nearly 1.5 million) worldwide [1–3]. To date, more than 45 genes have been identified that, when mutated, cause RP. These genes account for about 60% of all cases of RP with 20% to 30% identified as autosomal recessive, 15% to 20% autosomal dominant, and 6% to 10% X-linked. Mutations that cause RP are mostly found in genes that encode for proteins involved in the phototransduction cascade, the visual cycle, or the photoreceptor structure [2, 4–7]. A small subset of these mutations are in genes exclusively expressed in the night active rods [4]. However, because rod death always leads to cone death, these mutations ultimately result in complete blindness. Mutations in rod specific genes are usually diagnosed only at the beginning of cone death, when individuals start experiencing serious vision problems, since initially rod death causes only night blindness. While the clinical manifestations of the various sub-types of RP are well-documented [2, 8-10], the onset and speed at which the disease progresses is more difficult to predict as it varies from individual to individual even if they carry the exact same mutation [6,8-9]. The biggest challenge in RP, however, is deciphering why the healthy cones degenerate when the mutation is in a gene that is exclusively expressed in rods [11-15]. Such knowledge could help develop a mutation independent therapy that would apply to many individuals. This is because even though the number of rod specific genes that cause RP is rather small, these genes account for a disproportionately large share of RP cases.

There are several data driven hypotheses explaining cone loss in RP. The first proposes that the death of rods leads to higher oxidative stress in the retina, which is assumed to eventually kill cones [16]. Consistent with that, antioxidants promote cone survival and vision in the retinal degeneration 1 (rd1) mouse model of RP [17]. A second theory that gathered a lot of popularity comes from the idea that rods produce some kind of signal/protein that is essential for keeping cones alive. Consequently, the disappearance of rods would deprive the cones of this signal/protein and trigger their degeneration [3,18-20]. This theory is supported by various experiments on mice and rats and led to the discovery of the Rod-derived Cone Viability Factor (RdCVF). Other known growth and neuroprotective factors such as PEDF, bFGF, and CNTF that are normally produced in the eye or upon injury, have also been tested by intravitreal injections (with various degrees of successes) for their ability to delay cone death [20-22]. Finally, a third theory proposes that the massive loss of rods, which outnumber cones at a ratio >20:1, leads to a disruption of the interactions between the photoreceptors and retinal-pigment epithelium (RPE) preventing cones from receiving enough nutrients and glucose needed to function properly [23-24]. Consequently, cones die of starvation over time due to inadequate nutrient supply by the RPE. This theory of cone starvation was based on investigations on the insulin/mammalian target of rapamycin (mTOR) pathway, a pathway that balances nutrient demand with supply and was found to be altered during the periods of cone degeneration.

All three hypotheses presented here are supported by experimental evidence making it difficult to understand how much each hypothesis may contribute to cone death in RP. Joint experimental and mathematical efforts can help decipher the cause of cone death through data-guided in silico testing of various hypotheses and scenarios. Mathematical models have been used successfully in the past to identify the critical contributions of different mechanisms in various retinal systems [25-27]. Using computer simulation and in silico experimentation we investigate the contribution of various processes during the death kinetics of rods and cones. This current work builds on our previous two mathematical models that described the stable solutions for the co-existence of rods and cones in a healthy retina and the possible stable solutions that occur during the progression of RP, respectively [28-29]. The latter model provided a theoretical and qualitative description of the progression of RP but was not applied to any dataset nor did it reveal how much each process in the photoreceptor death kinetics contributed to the demise of the cones. It predicted that there are multiple possible failures within the system that can lead to blindness with all failures involving some amount of nutrient deprivation. Although the model could not distinguish between the individual factors that may affect nutrient availability it did confirm that the focus would likely be on nutrients.

In order to test the hypotheses mentioned above we consider four datasets from 2 different mouse models of RP with mutations in rod specific genes. One model we consider is the Rhodopsin knock-out (Rho-KO) mouse and the other the retinal degeneration 1 (rd1) mouse with a mutation in the Phosphodiesterase-6-beta gene. The 4 datasets from these two models were as follows: rd1 and Rho-KO transcript data for rod and cone specific genes serve as a proxy for rod and cone cell death; rd1 rod and cone cell counts and cone cell counts from the same rd1 strain with delayed cone death caused by changes in cone metabolism. The rd1 cone cell count dataset consisting of delayed cone death was generated by directly and constitutively activating mTOR in cones of rd1 mice. This was achieved by conditional deletion of the negative regulator of mTOR regulator, namely Hamartin (also referred to as tuberous sclerosis complex 1: TSC1), using the Cre-lox system [30]. As a consequence of constitutively activated mTOR nutrient uptake, retention and utilization was improved, which promoted the survival of starved cones in rd1 [30]. Applying this delayed cone death data to our mathematical model allows us to test more in depth the role of nutrients in RP. Incorporating the four datasets into our model we investigate the interplay and role of energy consumption and uptake and quantify their changes over time. Simulation shows a 10% and 16% change in the ratio of energy consumption to uptake of cones during the rod death wave in the rd1 mouse and Rho-KO mouse retina, respectively. We mathematically analyze the progression of RP from the beginning stages of the disease to complete blindness. Utilizing actual data of the rod and cone death kinetics from these two different mouse models of RP allows us to better understand the key interactions between the rods and cones and identify the processes that would need to be altered, according to the stability of the mathematical solutions, to halt cone death in RP [28-29]. Global sensitivity analysis permits us to investigate the influence of each process (defined by our parameters and variables) on the demise of the cones. Our results show that the largest contributor to the degeneration of all cones is a drop in nutrient availability of 27-31% over the course of the disease. Interestingly, our results also show that a total increase of 1-2% in nutrient availability would result in a permanent halt of the disease even when 90% of cones have died. This work suggests that cone death can be halted at any point during the disease progression by stopping the decline in nutrient availability. Given that only a small percentage of cones are sufficient to maintain some visual function [31] our results suggest that intervention at later stages of RP can still be beneficial.

Materials and Methods

Population and Model

We utilize a continuous time mathematical model that considers populations of rods, cones, and RPE cells [29]. The populations of rods and cones are approximated by a continuous range of values because both cell types contain outer segments (OS) with nearly 1000 discs that are constantly shed and resynthesized. Thus even though no new rods or cones are born in a mature retina, the process of shedding and renewal of photoreceptor OS discs lends itself to the interpretation of birth and death of rod and cone OS [32-34]. We view our units as “cells” and therefore the OS discs are fractions of the cell. Experiments have shown that in a rod-free retina the absence of cone OS corresponds to blindness even though living cone cell bodies remain [35-36]. We take the same perspective in our mathematical model. In order to focus on the mechanisms behind the various manifestations of RP, our model includes two different classes of rod cells, denoted R_n and R_s (corresponding to the number of normal functioning rods and sick rods, respectively), one type of cone, denoted by C (for the total number of cones and where green, red, and blue cones are grouped together since there is no evidence that cones respond differently in RP according to their type), and a nutrient pool from which the rods and cones draw their energy, denoted T (representative of the total number of RPE-supplied neuroprotective factors, growth factors and nutrients). The classification of rods into two classes according to their phenotypes — one in which the rod mutation has begun to compromise the cells' functionality (referred to as “sick” rods) and one in which the mutation has not affected functionality (“normal” rods) — is essential to track the progression of RP mathematically [25,29,37]. While very little experimental data has quantified this distinction, we use the statistical technique of Latin Hypercube sampling together with known parameter values in our system of equations to estimate the values of R_n and R_s (see the Results section for more detail on the estimation of R_n and R_s). The numerous genes and processes in the retina affected by the mutations associated with RP [2, 6, 10] as well as the great variability of the disease [38] make it difficult to mathematically quantify the degree of the disease in any other tangible way. The RPE is considered the facilitator of energy consumption and uptake as it permits the passage of glucose, oxygen, growth factors, metabolites, ions, and water to the photoreceptors. For mathematical simplicity, we refer to all these collectively as nutrients (e.g., PEDF, CNTF, bFGF, Gas6, PDGF, ATP, glucose, retinal, and omega-3 fatty acids) that travel to and from photoreceptors and are provided or secreted by the RPE [21-22, 39–44]. From experimental studies we know that the events leading to cone degeneration in RP are similar and independent of the mutant rod gene; thus, we do not focus on the rod specific mutation or how such a mutation affects rod function. This allows the model not to be tied to a specific mutation and thereby we can focus the investigation on how and why the cone population changes over the course of RP. The model considers a homogeneous mixture of photoreceptors instead of their known distribution and thus moves away from the hypothesis that the release of a toxic factor by dying rods kills neighboring cones. Experimental studies in mouse models have shown that cone death often commenced after the end of the major phase of rod death (occurring many months after rod degeneration) challenging the hypothesis of the liberation of a toxic factor [23-24]. Finally, the model incorporates the role of the RdCVF as a direct connection from rods to cones [3,20,45]. RdCVF is produced by both types of rods, R_n and R_s, and its presence and release by the rods does not hinder or benefit the functionality or viability of rods [46-47]. Our previous mathematical work showed that RdCVF allows for co-existence of these two species, rods and cones, without any disease or external threat [28]. Physiologically this means that RdCVF is needed when both rods and cones are present in order to maintain both populations of photoreceptors. Our current model suggests that while exogenous RdCVF helps in prolonging the survival of cones in the absence of rods [30], RdVCF is more crucial when rods are present. Recent work has shown that RdCVF helps increase the uptake of glucose by the cones [48].

Our mathematical model is then

$$\begin{array}{c}{\mathrm{R}}_{\mathrm{n}}^{\prime }={\mathrm{R}}_{\mathrm{n}}({\mathrm{a}}_{\mathrm{n}}\mathrm{T}-{\mathrm{\mu }}_{\mathrm{n}}-\mathrm{m})\\ {\mathrm{R}}_{\mathrm{s}}^{\prime }={\mathrm{R}}_{\mathrm{s}}({\mathrm{a}}_{\mathrm{s}}\mathrm{T}-{\mathrm{\mu }}_{\mathrm{s}})+\mathrm{m}{\mathrm{R}}_{\mathrm{n}}\\ {\mathrm{C}}^{\prime }=\mathrm{C}({\mathrm{a}}_{\mathrm{c}}\mathrm{T}-{\mathrm{\mu }}_{\mathrm{c}}+{\mathrm{d}}_{\mathrm{n}}{\mathrm{R}}_{\mathrm{n}}+{\mathrm{d}}_{\mathrm{s}}{\mathrm{R}}_{\mathrm{s}})\\ {\mathrm{T}}^{\prime }=\mathrm{T}(\mathrm{\Gamma }-\mathrm{k}\mathrm{T}-{\mathrm{\beta }}_{\mathrm{n}}{\mathrm{R}}_{\mathrm{n}}-{\mathrm{\beta }}_{\mathrm{s}}{\mathrm{R}}_{\mathrm{s}}-\mathrm{\gamma }\mathrm{C}),\end{array}$$ (1)

where all parameters are nonnegative; see Table 1 for definitions of the parameters. Taking T as the nutrient pool for both rods and cones allows our work to stay consistent with all experiments in the literature where no distinction between a rod-nutrient and a cone-nutrient pool is made [16, 46]. Our model assumes that both the rods and the cones take more nutrients from the pool than they contribute (as recycled products) and that they convert these nutrients into new OS discs at some ratio. It does not isolate or distinguish between any of the items contributing to the energy uptake by the photoreceptors (nutrients, oxygen, etc.). To the best of our knowledge, no experimental work has been done to date that discusses the amount of nutrients released by the RPE in the absence of photoreceptors; this current work supposes that the release of nutrients will approach a particular level of saturation (governed by parameters Γ and k) in the absence of photoreceptors, instead of growing without bound [28]. The structure of this mathematical model incorporates the presence of the RdCVF protein and its mechanism by which it helps cone survivability and functionality yet does not negatively influence the rod population through the parameters d_s and d_n [3,6,46,49]. Experimental evidence suggests that the RdCVF directly affects the cones and thus we model this as a direct rod-cone interaction, the necessity of which was already established [28]. The literature does not suggest that sick rods stop or decrease their production of RdCVF and thus our model includes this possible contribution of RdCVF by the sick rods via d_s [46].

Table 1.

Key physiological abbreviations.

Retina	RP	Retinitis pigmentosa
	RPE	retinal pigment epithelium
	OS	Outer segment
Mutant mouse models	rd1	retinal degeneration 1
	Rho-KO	Rhodopsin knock-out
Genes involved in nutrient sensing, uptake and aspects of cellular function and growth	RdCVF	Rod-derived Cone Viability Factor
	mTOR	mammalian target of rapamycin
	mTORC1	mTOR complex 1
	PEDF	Pigment epithelium-derived factor
	PDGF	Platelet-derived growth factor
	CNTF	Ciliary neurotrophic factor
	bFGF	Basic fibroblast growth factor
	Gas6	Growth arrest-specific 6
	TSC1	tuberous sclerosis complex 1

We define the following key quantities:

$$\begin{array}{cccc}{\mathrm{D}}_{\mathrm{c}}={\mathrm{\mu }}_{\mathrm{c}}/{\mathrm{a}}_{\mathrm{c}},& {\mathrm{D}}_{\mathrm{s}}={\mathrm{\mu }}_{\mathrm{s}}/{\mathrm{a}}_{\mathrm{s}},& {\mathrm{D}}_{\mathrm{n}}=({\mathrm{\mu }}_{\mathrm{n}}+\mathrm{m})/{\mathrm{a}}_{\mathrm{n}},& {\mathrm{D}}_{\mathrm{T}}=\mathrm{\Gamma }/\mathrm{k}.\end{array}$$ (2)

We interpret the first two quantities, D_c and D_s, as the ratio of energy consumption to energy uptake for the cones and sick rods, respectively, while the third quantity contains these processes for normal functioning rods in addition to the rate at which the normally functioning rods become sick, denoted by m. The last quantity represents the carrying capacity of nutrients in the absence of photoreceptors.

Tracing the Various Stages of RP Mathematically

Using data values from the literature together with mathematical techniques of parameter estimation via ordinary least squares and the inverse problem, estimates on all variables and parameter values for the mathematical model were found in [29]. The steady-state solutions describing the levels of the photoreceptor OS and the supply of nutrients from the RPE in the retina were also found. Three such solutions showed the progression of rod-cone dystrophy in RP by mathematically describing the possible parameters that could be involved in the progression to blindness in the disease. In other words, bifurcation analysis was utilized to mathematically identify the conditions and parameters involved in the progression of RP in humans through three key stages (defined by three steady-state solutions): (i) all photoreceptors present (consistent with day and night vision), (ii) only cones present (consistent with loss of night and peripheral vision), and (iii) no photoreceptors alive (consistent with complete blindness). Mathematically we observed all photoreceptors present in certain parameter ranges. Continuously changing the parameter values outside of these ranges resulted in a steady-state solution with no rods and only cones alive. Further changes in parameters led to the stable steady-state solution consistent with total blindness. The parameters that were varied and the conditions that allowed the progression from one stage to another were tracked [29].

The four key quantities, identified in (2), allowed RP to progress: (i) D_T, the availability of nutrients via the RPE; (ii) D_c, the ratio of energy consumption to energy uptake of cones; (iii) D_s, the ratio of energy consumption to energy uptake of sick rods; (iv) D_n, the ratio of “leaving” the R_n class to energy uptake where “leaving” is the energy consumption of normal functioning rods plus the rate at which their functionality is compromised. From a mathematical point of view, the changes in the difference of various pairs of these key quantities, e.g., (D_T -D_c), resulted in only one steady-state solution being stable for any given set of parameter values. Our model gave six possible stable steady-state solutions, three consisting of the stages in the rod-cone dystrophy in RP (described above) and three others consisting of the stages in reverse RP (consisting of both rods and cones, only rods, and neither photoreceptor). Moreover, in each of the set of three solutions the bifurcation sequence that takes us from one stage to the next contained many different paths to blindness that were consistent with and experimentally observed in the progression in RP (where a path is quantified by changes in the values of any parameters) [29]. We now utilize experimental datasets together with our model to identify specific paths in parameter space that correspond to the RP progression to blindness.

Datasets

Transcript data for the rd1 and RhoKO mouse models

Rod and cone transcript data for the rd1 mouse model (Figure 2, Panel A) were published previously [50]. The data is presented as an open circle (blue for rods and red for cones) in Figure 2. Cone transcript data for the RhoKO model (Figure 2, Panel B) were published previously in [23] while rod transcript data for the RhoKO model were generated by using the same RNA extracts as for cones; however, the qRT-PCR was performed for the Neural Retina-specific Leucine zipper protein (NRL) transcript. The following primers and PCR conditions were used: Forward: TTCTGGTTCTGACAGTGACTACG; reverse: AACACCTCTCTCTGCTCAGTCC; PCR: 95° for 2 s, 55° for 10 s, 72° for 10 s for 40 cycles.

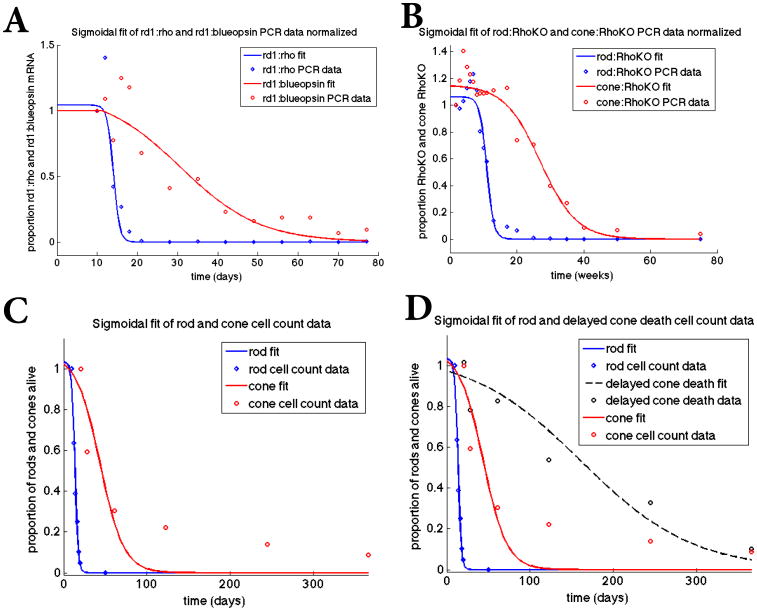
Figure 2.

Sigmoidal fit of mathematical model to datasets. Top panels: Fit of sigmoidal curves to the rd1 transcript data (Panel A) from P10 to P77 and the Rho-KO transcript data (Panel B) from P12 to 75 weeks, where the transcript data is used as a proxy for the number of rods and cones alive. The data points in all panels were obtained by normalizing the data by its first data point thus making all the data points as a proportion of this first data point value (before degeneration began). We use a sigmoidal function of the form p/(1 + exp(q*(t-r))) together with a nonlinear least squares method to find p, q, and r via MATLAB's nlinfit. In Panel A, [p,q,r]=[1.04, 1.29, 14.0] for the rods and [p,q,r]= [1.14, 0.101, 30.6] for the cones. In Panel B, [p,q,r]= [1.06, 0.938, 10.9] for the rods and [p,q,r]= [1.15, 0.185, 27.1] for the cones. Panel C: Fit of sigmoidal curves to actual cell count data from rd1 mice for rods from P10-P20 and cones from P21 to P365. For the rods, [p,q,r]= [1.03, 0.545, 13.4] and for the cones, [p,q,r]= [1.07, 0.0703, 43.6]. Panel D: Fit of sigmoidal curves to cone data from rd1 mice data (red curve same as in Panel C) and rd1 mice in which cone death was delayed by improving nutrient uptake and utilization (black line) through the mTOR pathways. The experimental data was taken over 365 days and represents actual cone quantification.

Cell count data for the rd1 mouse model

Rod cell count data for the rd1 mouse model (Figure 2, Panel C) was published previously in [50]. Cone cell count data for the rd1 mouse model (Figure 2, Panel C) including data of delayed cone death (Figure 2, Panel D) was also published previously [30].

Results

Sigmoidal fit to datasets

In each of the curve-fitting results illustrated in Figure 2, a Hill-type (sigmoidal) function was utilized with time being the independent variable (either in days or weeks depending on the experiment and thus the dataset) and the proportion of photoreceptor OS being the dependent variable. Specifically, we chose a sigmoidal function of the form p/(1 + exp(q*(t-r))) in which a nonlinear least squares method is used to identify p, q, and r by minimizing the error between the sigmoidal curve and the data points. For the variable t, the data points are the corresponding time points and we normalize by dividing every point by the 1^st data point in the respective set. We then apply the function nlinfit from MATLAB to implement this curve fitting method. In Figure 2 we show the fit of the sigmoidal curves to each of the four datasets. Due to the nature of the datasets in which (i) the data value values were only available beginning at some initial time whereas the mathematical curve is defined for all time in the four panels and (ii) the data values in Panels A and B were a proxy for the number of photoreceptors alive, the fit was noticeably not a perfect fit during the initial period. Even though the final result gives the best fit, the initial imperfect fit over the first set of time points translates to the sigmoidal curve predicting that cone degeneration beginning before the rod degeneration for an extremely small number of cones cells. After this initial period, rod degeneration is correctly predicted to occur much faster than that of cones. Similarly, Panels C and D of Figure 2 are not expected to have a perfect fit of theoretical curve and data. Indeed, even though the sigmoidal curve accurately fits the number of rods alive at a given time, it suggests that the cones go to zero faster than what is experimentally observed. In spite of predicting a faster cone death of the cell count datasets, these sigmoidal curves accurately demonstrate many aspects of the death kinetics of rods and cones observed in the various experiments after the initial time period [50, 23] (Figure 3). For example, the simulated wave death speeds and duration for the cone and rod death waves coincide with experimental observations. In particular, we see in Figure 3 Panels A, B, and C that the death wave for the cones is relatively fast (days in the simulations corresponding to the rd1 mouse as opposed to weeks in the simulation for the RhoKO model) if the death wave for the rods is fast. It can also be observed in these panels that cone degeneration takes off (illustrated by the steepest positive slope when the curve is rising) when about 90% of the rod cell population is gone, an observation that was also confirmed experimentally across multiple mouse models of RP [23].

Figure 3.

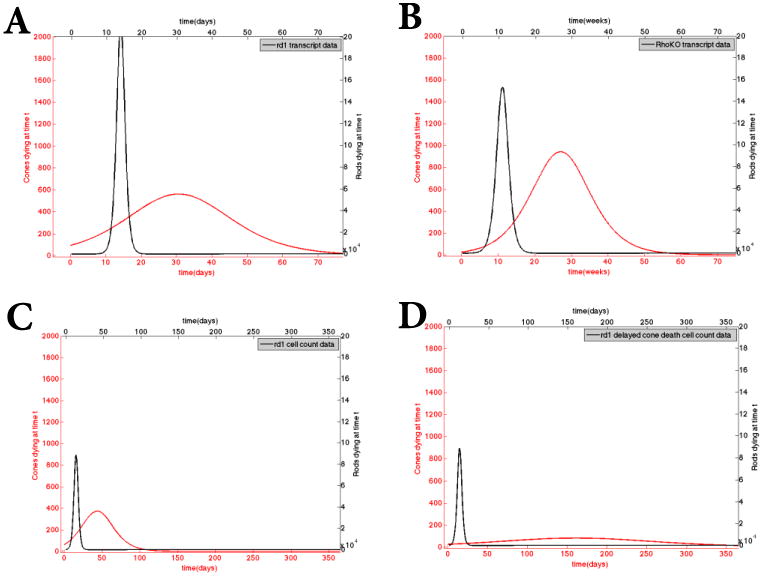
Calculated death kinetics using the sigmoidal fits of the datasets. These curves are obtained by taking the first derivative of the sigmoidal curves obtained in Figure 2. Top panels: Rod (in black) and cone (in red) death kinetics based on the transcript data from the rd1 (Panel A) and the Rho-KO (Panel B) model. Panel C: Rod (in black) and cone (in red) death kinetics based on rd1 cell count data. Panel D: rod curve (in black) is the same as in Panel C but the cone curve corresponds to delayed cone death kinetics due to improved nutrient uptake. In all cases, the largest proportion of the rod death precedes that of cone death. The plotted cone death kinetics from the sigmoidal fit appear to begin sooner than that of the rods but this is simply an artifact of the sigmoidal fit of the curve through the data.

Calculating key quantities during progression of RP

We gain an understanding of exactly how certain parameters change during the course of RP by using the sigmoidal curve fit as input for the variables of our model. Parameter values for humans and mice suggest that any approach to equilibrium is on a much faster time scale than the evolution of the equilibrium over the course of the disease. Thus, the set of four ordinary differential equations in (1), rather than being numerically solved, were solved analytically at equilibrium for factors involved in the four key quantities of D_T, D_n, D_s, and D_c, given in (2):

$$\begin{array}{c}{\mathrm{a}}_{\mathrm{n}}=({\mathrm{\mu }}_{\mathrm{n}}+\mathrm{m})/\mathrm{T}\\ {\mathrm{a}}_{\mathrm{s}}=({\mathrm{R}}_{\mathrm{s}}{\mathrm{\mu }}_{\mathrm{s}}-\mathrm{m}{\mathrm{R}}_{\mathrm{n}})/({\mathrm{R}}_{\mathrm{s}}\mathrm{T})\\ {\mathrm{a}}_{\mathrm{c}}=({\mathrm{\mu }}_{\mathrm{c}}-{\mathrm{d}}_{\mathrm{n}}{\mathrm{R}}_{\mathrm{n}}-{\mathrm{d}}_{\mathrm{s}}{\mathrm{R}}_{\mathrm{s}})/\mathrm{T}\\ \mathrm{k}=(\mathrm{\Gamma }-{\mathrm{\beta }}_{\mathrm{n}}{\mathrm{R}}_{\mathrm{n}}-{\mathrm{\beta }}_{\mathrm{s}}{\mathrm{R}}_{\mathrm{s}}-\mathrm{\gamma }\mathrm{C})/\mathrm{T}.\end{array}$$ (3)

On the right-hand-side of the equations in (3), the variable C is the cone population of the sigmoidal curve (Figure 2), while the sum R_n + R_s is the rod population of the sigmoidal curve (Figure 2). The value of R_n versus R_s at any point in time is determined by the transition rate m, from R_n to R_s and the proportion of rods that are initially considered to be sick. Each of the 14 inputs on the right-hand-side of (3) have a range of reasonable possible values obtained from the literature or previous application of inverse problem methodology [29]. We use Latin Hypercube Sampling (LHS) together with inverse problem methodology to select the actual value for these 14 inputs. Because both of the sigmoidal curves were scaled so as to have an initial value of 1, the initial values C(0) and R(0) were also estimated using LHS (e.g., the number of cones in a mouse retina is approximately between 160,000 and 200,000 and thus C(0) should be between these values). We allowed the 14 inputs to vary within their reasonable ranges and then sampled 20,000 points from the 14-dimensional hypercube [51]. Each of these 20,000 realistic-valued sample points were then input into the mathematical model and the input parameters and initial conditions were determined from the best maximum likelihood estimator (MLE) compared to the data of a healthy retina. Once all the other parameters on the right-hand-side of (3) are estimated they are assumed not to change, together with T, during the progression of RP.

Observation of the death kinetics of rods from the datasets gives a reasonable range of values for m, the transition rate from R_n to R_s, as well as a range of proportion of rods that are initially considered R_n and R_s. Thus the best estimates for R_s(0) and m were also obtained from LHS application giving additional information that lets us know the rate at which rods' functionality is compromised and how many initial sick rods there are. More specifically, we use the values of the healthy rods, R_n(0) (obtained from the LHS applied to the healthy model [29]), to estimate a range for the sick rods, R_s, and then allowed the LHS algorithm to identify the values of R_s(0) and m that give the best fit to the sigmoidal curves in Figure 3 for each respective dataset. Thus, while R_s(0) is defined as a phenotype “sick rod” whose functionality is somewhat compromised, we obtain additional information to clarify these associated quantities, R_n versus R_s, based on the results of the LHS and subsequent MLE curve fit [52].

We tracked these quantities and investigated the specific role of D_T, D_c, D_s, and D_n (calculated from equation (3)) during the first and second death waves. We plot the change of D_T and D_c over time in Figures 4-7 (each corresponds to a different dataset), assuming that the parameters in the system change at a slow enough rate that we are always at or near equilibria. Our previous work revealed that these key quantities (in equation (2)) are critical in progressing from one stage to the next in RP but could not specify exactly how they changed. The interval marked on the graphs between the second and third key points (labeled as a diamond and a square, respectively) in time corresponds to the time of rod degeneration while the interval after the third key point (labeled as a square) to the end of the curve corresponds to cone degeneration. We observed that the carrying capacity D_T, decreases most during the cone death wave (see Panel A in each of Figures 4-8). This larger decrease of nutrients available to support the retinal cells during the cone death wave, quantified by the change in D_T, supports the hypothesis of cone starvation due to inadequate nutrient supply by the RPE caused by a significant disruption in the interactions between the photoreceptors and RPE, thereby triggering a massive loss of cones. Furthermore our simulation results indicate that alterations in energy consumption and uptake of cones is mainly affected during the rod death wave, as quantified by the reduction in D_c. Our results show a strong correlation between the rod death wave kinetics and the decrease in the ratio of energy consumption to uptake of cones, D_c (Panels B and D in each of Figures 4-8). During the death of the rods the quantity D_c decreases by 7-16%. After the rods have all died, the change in D_c is less than 0.01%. The observed changes in D_c support the hypothesis of cone overcompensation that occurs during rod degeneration in an effort for photoreceptors (and the visual system) to meet their metabolic demands and deal with oxidative stress that increases as rods die [24]. Thus we focus our analysis on D_T and D_c and study the parameters that contribute to their overall change. At every step we confirm that our model is in line with the experimental observations and known physiological theories.

Figure 4.

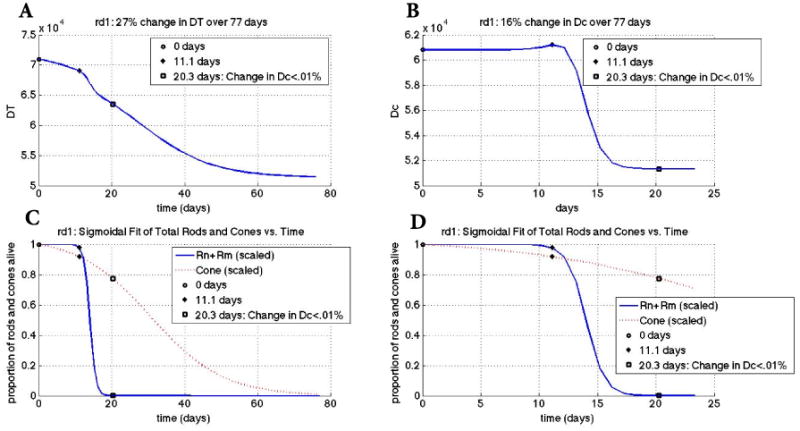
Changes in key quantities D_T and D_c for rd1 mouse transcript data. Key points in time are marked on every graph (see legend). Panel A: change in D_T vs. time. Panel B: change in D_c vs. time. The graph of D_c shows a 16% overall change whereas the change in D_T shows a 27% overall change. Panel C: scaled rod (solid curve) and cone (dotted curve) populations vs. time. Populations were scaled to make the first value 1 by dividing every point for the value of the first point. The key points of 11.1 days and 20.3 days correspond to the beginning of rod degeneration and when the change in D_c is less than 0.01%, respectively. Panel D: zoomed plots in Panel C on the horizontal axis. The input parameters and variables to (3) were determined from the best maximum likelihood estimator of 20,000 realistic-valued sample points using Latin Hypercube Sampling. Non-time dependent parameter values are [μ_n, μ_s, μ_c, Γ, a_n, a_s, a_c, β_n, β_s, k, d_n, d_s, γ] = [0.0995, 0.0971, 0.121, 4.69, 4.78e-6, 5.49e-6, 4.925e-6, 2.32e-8, 2.44e-8, 5.88e-5, 3.28e-9, 3.79e-9, 6.76e-6].

Figure 7.

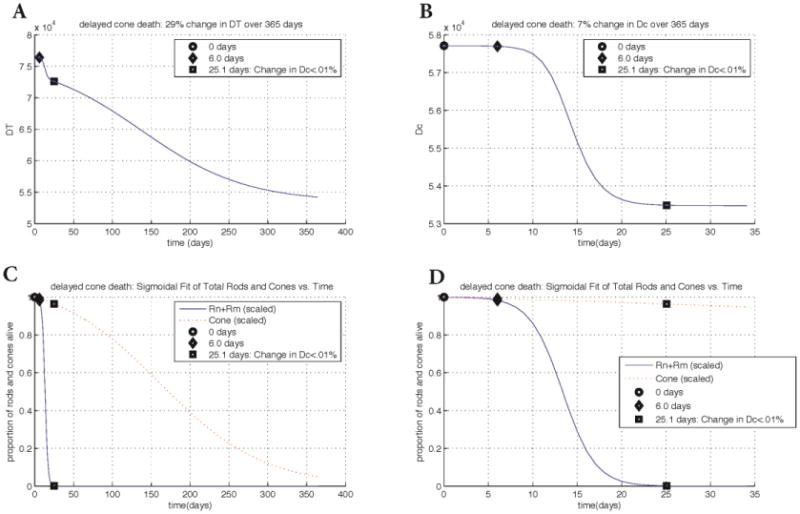
Changes in key quantities D_T and D_c for the rd1 cell count data with delayed cone death. Key points in time are marked on every graph. Panel A: change in D_T vs. time. The key points of 6.0 days and 25.1 days correspond with the beginning of rod degeneration and when the change in D_c is less than 0.01%, respectively. Panel B: change in D_c vs. time. The graph of D_c shows a 7% overall change whereas the change in D_T shows a 29% overall change. Panels C and D: scaled rod and cone populations vs. time. Populations at every point were divided by the population at time 0. Plots in Panel D are zoomed in with respect to the horizontal axis. With strategies to delay cone death, the duration of the cone death wave more than doubles, taking 365 days instead of approximately 120 days. However, the overall change in nutrients by the end of the wave is only 1% less than in the cell count data without cone death delay. The input parameters and variables to (3) were determined from the best maximum likelihood estimator of 20,000 realistic-valued sample points using Latin Hypercube Sampling. Non-time dependent parameter values are the same as in Figure 6.

Figure 8.

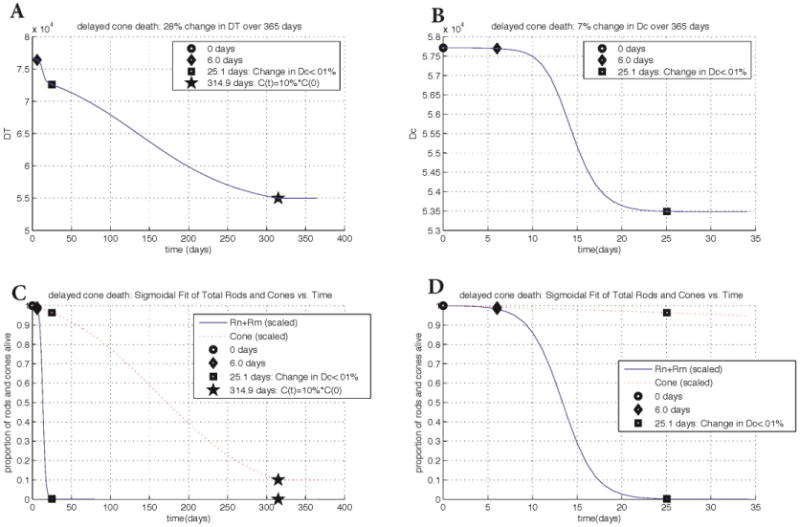
Changes in key quantities D_T and D_c for rd1 cell count data with delayed cone death if their degeneration is stopped when they reach 10% of their initial value. Key points in time are marked on every graph. Panel A: change in D_T vs. time. The cones are forced to remain at 10% of their original value to determine the nutrient levels that could sustain this. Panel B: change in D_c vs. time. Forcing the cones to remain at 10% of their original value has no effect on D_c or the overall rod population. The graph of D_c shows a 7% change whereas the change in D_T shows a 28% overall change (approximately 1-2% less than if cones are allowed to die). Panels C and D: scaled rod and cone populations vs. time. Populations at every point were divided by the population at time 0. Plots in Panel D are zoomed in with respect to the horizontal axis. The input parameters and variables to (3) were determined from the best maximum likelihood estimator of 20,000 realistic-valued sample points using Latin Hypercube Sampling. Non-time dependent parameter values are the same as in Figure 6.

The accurate fit of our mathematical model to the datasets demonstrates that the model captures the death wave kinetics for rods and cones. Moreover, it quantifies the amount of change needed in nutrient availability, energy consumption and energy uptake of the photoreceptors throughout the respective death wave kinetics. Simulations in conjunction with all four datasets show that a decrease in nutrient availability is necessary in order to have cone degeneration. Simulations show that energy consumption and uptake only have an effect at the initial phase of the cone death wave (see the change in D_T and D_c compared to the cone death kinetics in Figure 4-8). Our work shows that an approximate 30% decrease in nutrient availability results in the eventual death of all the cones and this number is consistent across the two different mutations (i.e., Rho-KO and rd1).

Our simulations indicate that the first steep drop in the nutrient availability, D_T, is correlated with the death wave of the rods and the second steep drop with the initial phase of the cone death. The complete time interval involved in the death of the rods coincides with the time interval of the largest drop in D_c. Once the cone death wave has begun, the required decrease in nutrients for continual demise of the cones is more significant at the initial phase of this secondary death wave even though nutrients continue to decrease throughout this entire death wave (Figures 4-8). The decrease in D_T over time corresponds with a decrease in the available nutrients supplied by the RPE over time, preventing the photoreceptors from receiving and uptaking the necessary nutrients, and further leading to metabolic imbalances. The decrease in D_c during rod death gives insight into the amount of overcompensation that cones must undergo to deal with the oxidative stress during the rod death wave. An approximately 7-16% change in energy consumption to energy uptake ratio in cones, D_c, is seen during the rod death wave. The change of D_c during the rod degeneration also illustrates the role of rods in RP as the drivers in the disease. Thus their demise affects the consumption and uptake of energy and the corresponding processes in cones. The model focuses on the key relationship between the photoreceptors that could decipher important factors that lead to the death of the healthy cones in RP and therefore does not describe the specific delivery pathways of nutrients into the cell nor distinguishes between various nutrients (such as glucose, oxygen, etc.). However, the results suggest that halting the decrease in nutrient availability will allow the cones to continue to survive.

Mathematical model results for the rd1 transcript data

Our mathematical model reveals a 27% change (decrease) in D_T over 77 days; minimal change happens over the first 11.1 days and then there is a significant drop (approximately exponential, demonstrated by the steepness of the slope) from 11.1-20.3 days. The decrease is initially linear and then becomes approximately exponential after this and a little steeper during rod death than cone death. Figure 4 shows the change of the key quantities in our mathematical model for the rd1 mouse data, which are summarized here. The time 11.1 days coincides with the time when the secondary death wave of photoreceptors takes off as signified by its faster rate of cone death. It is just before the intersection between the rod death wave and cone death wave (Figure 4, Panel D). Also the 11.1 days marks the beginning of a faster rate of change in the decrease in the nutrients supplied by the RPE, D_T, as well as a faster rate of change in the ratio of energy consumption to energy uptake of the cones, D_c (Figure 4, Panels A and B). We infer from this result that while nutrient ability contributes significantly to the demise of the cones, the initial disruption in the cones' energy consumption and uptake magnifies the impact of the lack of nutrients pushing things beyond a critical value that allows the death of cones to take off. The overall change in D_T of 27% with a larger percent decrease during the cone death wave points to the role of disrupted interactions between the photoreceptor and RPE that interrupt the flow of nutrients and glucose needed for proper functioning of the photoreceptors during RP. The 16% change observed in Dc, from day 11.1 to day 20.3 with only a 0.01% change occurring after this time, quantifies the overcompensation that cones undergo to deal with the higher oxidative stress and metabolic demands during the rod death wave.

Mathematical model results for the RhoKO transcript data

Similar to the case of rd1 transcript data with our model we observe a 31% change (decrease) in D_T over 75 weeks with minimal change over the first 9.1 weeks and then a significant drop (approximately exponential, demonstrated by the steepness of the slope) occurring from 9.1-20.3 weeks. The decrease in D_T continues to be exponential beyond 20.3 weeks but at a slower rate. Figure 5 shows the change of the key quantities D_T and D_c utilizing the RhoKO transcript data. In D_c, a 10% change is observed over the first 20.3 weeks with less than a 0.01% change occurring after this time. The main decrease in Dc coincides with the rod death wave while the decrease of the cone population that occurs after the rod loss coincides with the decrease in nutrient availability.

Figure 5.

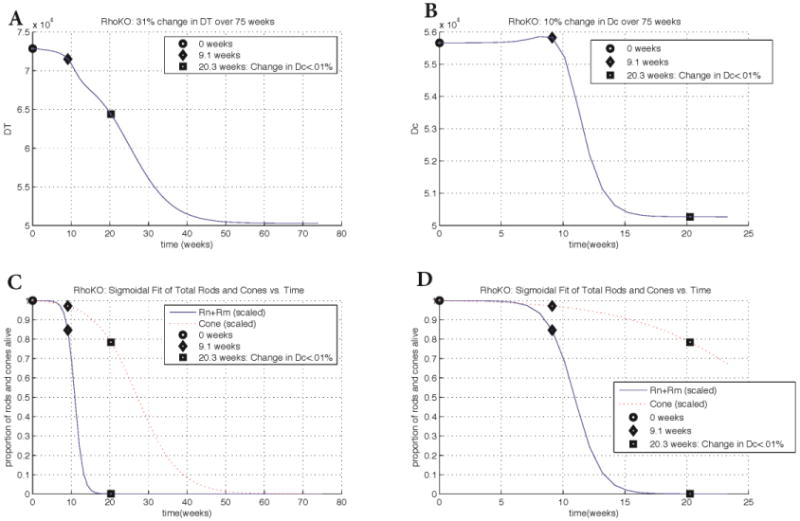
Changes in key quantities D_T and D_c for Rho-KO transcript data. Key points in time are marked on every graph. Panel A: change in D_T vs. time. The key points of 9.1 weeks and 20.3 weeks correspond to the beginning of rod degeneration and when the change in D_c is less than 0.01%, respectively. Panel B: change in D_c vs. time. The graph of D_c shows a 10% overall change whereas the change in D_T shows a 31% overall change. Panels C and D: scaled rod (solid curve) and cone (dotted curve) populations vs. time. Populations at every point were divided by the population at time 0, i.e., the first value. Plots in Panel D are zoomed in with respect to the horizontal axis. The input parameters and variables to (3) were determined from the best maximum likelihood estimator of 20,000 realistic-valued sample points using Latin Hypercube Sampling. Non-time dependent parameter values are [μ_n, μ_s, μ_c, Γ, a_n, a_s, a_c, β_n, β_s, k, d_n, d_s, γ]=[0.103, 0.0994, 0.119, 4.93, 4.909e-6, 5.24e-6, 5.12e-6, 2.50e-8, 2.29e-8, 6.37e-5, 1.91e-9, 3.69e-9, 7.54e-6].

Mathematical model results for the rd1 cell count data

We observe an approximate 30% change (decrease) in the key quantity D_T over the first 120 days, with minimal relative change occurring over the remainder of the experiment. The change in the ratio of energy consumption to uptake of cones, D_c, is 3.1% less than in the simulation with the transcript rd1 mouse data. This difference in simulation results is likely due to the fact that we are incorporating cell count data instead of transcript data. The time interval is also different and takes approximately 120 days from beginning to end in contrast to 77 days. The mathematical model accurately captures the death kinetics of the photoreceptors. Figure 6 shows the change of the key quantities D_T and D_c for the cell count data. For D_T, there was a significant drop from 6-25.1 days. In Dc we observed a 7% overall change mainly accounted for the time interval between 6 to 25.1 days when the rod death wave took place. The ratio, D_c, changed only by 0.01% after 25.1 days. The decrease in D_c is due to the cones compensating for additional available nutrients as the rods die. As before, the death of the cones coincides with a decrease in available nutrients.

Figure 6.

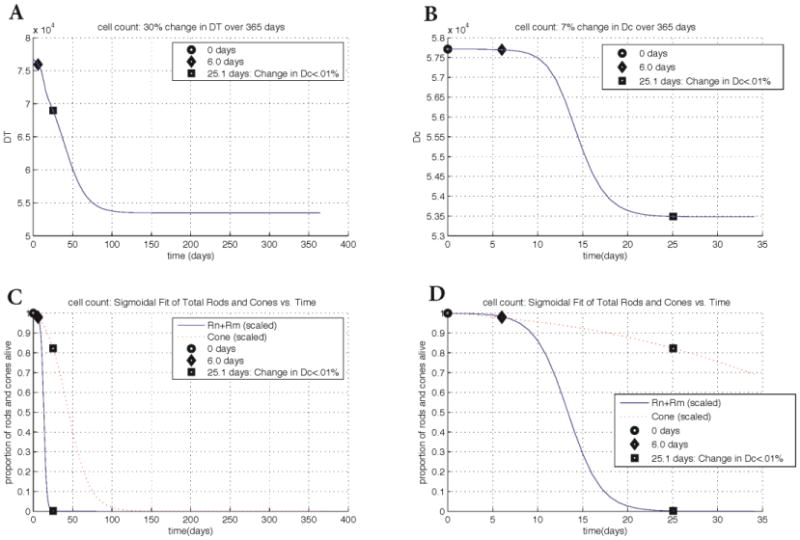
Changes in key quantities D_T and D_c for cell count data in rd1. Key points in time are marked on every graph. Panel A: change in D_T vs. time. The key points of 6.0 days and 25.1 days correspond to the beginning of rod degeneration and when the change in D_c is less than 0.01%, respectively. Panel B: change in D_c vs. time. The graph of D_c shows a 7% overall change whereas the change in D_T shows a 30% overall change. Panels C and D: scaled rod (solid curve) and cone (dotted curve) populations vs. time. Populations at every point were divided by the population at time 0. Plots in Panel D are zoomed in with respect to the horizontal axis. While the experimental data was taken for 365 days, the cone death wave takes approximately 120 days from beginning to end. The input parameters and variables to (3) were determined from the best maximum likelihood estimator of 20,000 realistic-valued sample points using Latin Hypercube Sampling. Non-time dependent parameter values are [μ_n, μ_s, μ_c, Γ, a_n, a_s, a_c, β_n, β_s, k, d_n, d_s, γ]= [0.101, 0.0990, 0.112, 4.73, 4.78e-6, 4.90e-6, 4.91e-6, 2.38e-8, 2.58e-8, 5.93e-5, 1.41e-9, 4.05e-9, 6.72e-6].

Mathematical model results for the rd1 cell count data with delayed cone death

To further validate our model we include a data set in which cone death was delayed by altering cell metabolism in cones directly. In the rd1 delayed cone death simulation a 29% change (decrease) in D_T is observed over the 365 days of the experiment. The drop in D_T during the rod death wave is very quick and exponential but slower during the cone death wave. There is a significant drop (demonstrated by the steepness of the slope) from 6-25.1 days, and a slightly less exponential decrease from 25.1 days through 365 days. With the experimental delayed cone death strategy, the duration of the cone death wave more than doubles, taking 365 days. However, the overall change in D_T, the nutrients provided by the RPE, is only 1% less than the rd1 cell count without cone delay simulation. These results highlight the fact that, even with strategies that delay cone death (those that alter the metabolic pathway of the cones and thus allow them to uptake more nutrients), D_T is still essential for survival. Figure 7 shows the change of the key quantities for the delayed cone death data, which are summarized here. For D_c, a 7% change is observed through day 25.1, with no change occurring after this time. As with the other three datasets, we interpret this decrease in the ratio of energy consumption to energy uptake in cones as a response to the disruptions in oxidative stress and metabolic demands brought about by rod degeneration. In addition, the simulations reveal that the death of the cones coincides with a decrease in nutrients supplied by the RPE. In the delayed cone death simulations, the change in D_T is nearly the same as the rd1 cell count without delay simulation, suggesting that the same drop in nutrient availability is responsible for the cone death in both cases except that in the former the death is prolonged. Figure 8 considers the delayed cone death data when the cones are forced to remain at 10% of their original value. The overall change in D_T of 28% compared to that in Figure 7 suggests that it is the last 1-2% change in the nutrient supply levels that ultimately lead to the demise of the cones. Given that vision can be maintained even when most of the photoreceptors are gone, this result suggests that strategies should be pursued for maintaining the flow of nutrients from the RPE above a critical level.

Uncertainty and Sensitivity Analysis

In order to shed light on the key parameters that drive the nutrient supply below a critical level we perform an uncertainty and global sensitivity analysis of the overall change in D_T on the parameters and initial conditions for each dataset. This mathematical approach allows us to investigate the influence of the parameters and initial conditions in our model that play a role in the change in D_T over time. The results are consistent for all four data sets and we thus present only the delayed cone death data in rd1 (Figure 9). D_T is most sensitive to changes in Γ, which quantifies the nutrient supply, as well as γ and C(0), which together remove available nutrients for the cones and affect how many cones remain. The parameters Γ and γ and initial condition C(0) are most responsible for affecting the overall change in D_T. This is quantified by using partial rank correlation coefficients (PRCC); bar graphs over 0.5 can be considered as influential while those under 0.5 not influential; see Figures 9 and 10 [51]. The corresponding p-values of the significant quantities Γ, γ, and C(0) were small (p<01; data not shown).

Figure 9.

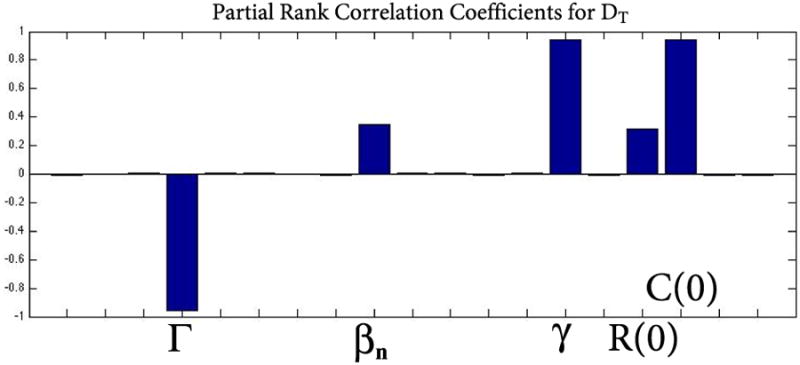
Uncertainty and global sensitivity analysis of the overall change in D_T on the parameters for rd1 cell count data with delayed cone death. D_T is most sensitive to two parameters and the initial number of cones: Γ, γ, and C(0). The parameter Γ quantifies the nutrient supply while γ and C(0) together quantify the removal of available nutrients. The three are most responsible for affecting the overall change in D_T. Using partial rank correlation coefficients (PRCC), bar graphs over 0.5 in absolute value are considered to be influential while those under 0.5 are not. The corresponding p-values of Γ, γ, and C(0) were small (p<01) but are not shown here. β_n and R(0)= R_n(0) + R_s(0) are the only other quantities that have a large PRCC but fall below the accepted threshold of 0.5 and thus are not considered to be influential.

Figure 10.

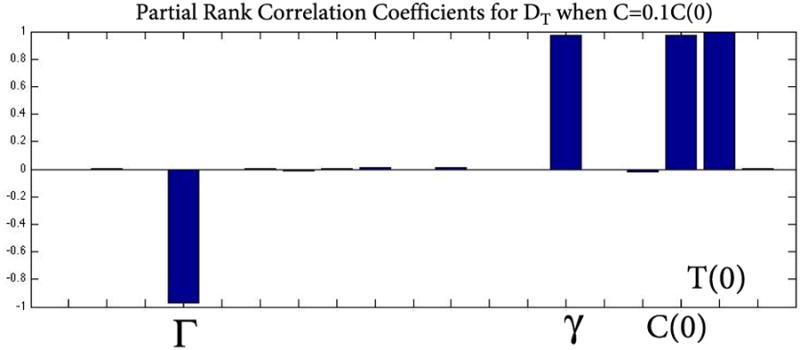
Uncertainty and global sensitivity analysis of the overall change in D_T on the parameters for rd1 cell count data with delayed cone death when the cones have reached 10% of their original value. D_T is most sensitive to changes in Γ, γ, C(0), and T(0). T(0) quantifies the role of the RPE, Γ quantifies the nutrient supply, while γ and C(0) together quantify removal of available nutrients. The RPE plays a significant role when the cones have reached 10% of their original value. Using partial rank correlation coefficients (PRCC), bar graphs over 0.5 in absolute value can be considered as most influential while those under 0.5 are not. The corresponding p-values of these significant quantities were small (p<.01) but are not shown here.

Since keeping cones at a level of 10% is still sufficient to save sight, we also investigated the sensitivity of the overall change in D_T for the case when the cones are forced to remain at 10% of their original value. Figure 10 shows the sensitivity of the overall change in D_T to changes and perturbations in the parameters and initial conditions of our model for this case. Our results show that D_T is most sensitive to Γ, γ, C(0), and T(0). The latter quantity represents the RPE and its influence highlights the importance of having the RPE present and available to deliver the nutrients at this critical time when only 10% of the photoreceptors remain alive. To help mitigate the enormous metabolic demands and continue to function properly these few cones depend significantly on RPE and the sensitivity analysis confirms this. The parameter β_n, which quantifies the removal of available nutrients by the rods, and R_n (0) + R_s(0), had a PRCC value less than 0.5. Therefore these quantities were not influential to the overall change in D_T.

Discussion

Our mathematical model allows us to examine the fundamental mechanisms between rods and cones that are linked to the degeneration of healthy cones when rods are the carriers of the mutant gene. Using the mathematical equations in (1), we are able to capture the death kinetics of both the rods and cones in RP across two mouse models. This allows us to estimate the evolution of certain parameters in the math model from four different datasets and quantify the change in nutrient availability, energy consumption and energy uptake of the photoreceptors in each case throughout the respective death wave kinetics. Our analysis indicates that across both mouse models deficiencies in the nutrient availability, possibly due to metabolic imbalances, are at the core of the secondary cone death in RP. In all simulations we observe that even though nutrient availability decreases at a faster rate during the rod death wave, its overall decrease is significantly larger during the cone death wave. Interestingly, energy consumption (quantified by OS shedding and metabolism) and energy uptake (quantified by OS renewal and metabolism) by the cones seem to be crucial before the onset of the cone death but not during the major cone death wave. Across all four datasets most of the change in D_c occurs during rod degeneration with a change of less than 0.01% afterwards. Once cone death has accelerated, nutrient availability appears to be the most important factor that contributes to cone death. The changes in the ratio of energy consumption to energy uptake are minimal compared with the change in nutrient availability. This means that the cones are able to balance consumption with uptake (in terms of protein synthesis, fatty acid synthesis, etc.) and it is the lack of available nutrients that seems to have the largest effect on survival.

All the model parameters have been estimated with various datasets using inverse problem methodology [52]. Qualitatively our model predicts the same changes in nutrients, energy consumption and uptake for all four datasets. It describes how, when, and by how much these key components will change during the course of RP. Across mouse models, we observed that an approximate 30% decrease in nutrient availability results in the eventual death of all the cones. While the model does not distinguish between uptake and retention of nutrients, a key observation is the model's prediction that cone death could, in principle, be halted at any time by keeping the nutrient availability above a certain amount. For example, if the nutrient availability only decreases by around 14%, the model predicts that only half of the cones will die (Figure 8). Because having only 5% of the cones remaining in a retina can permit daylight vision, the model suggests that increasing the nutrient availability, uptake, or retention may have a significant impact on the life of the cones. It is interesting to note that the death of the first 25% of cones is caused by the initial 10% decrease in nutrient availability, yet the next 18-20% decrease in nutrient availability results in complete cone loss. Any intervention in nutrient availability to keep the levels above those seen in Figures 4-7 (before complete cone degeneration) is predicted to prevent further degeneration. While the model does not predict that there is a point past which saving cones is impossible, it does suggest that sooner interventions may have a greater impact.

Simulations show that nutrients supplied by the RPE, quantified by D_T, decay the most during the cone death wave. This larger decrease of nutrient availability during the cone death wave supports the hypothesis of cone starvation due to inadequate nutrient supply by the RPE because of a significant disruption of the interactions between the photoreceptor and RPE that was triggered by the massive loss of rods. Our results indicate that the disruptions in energy consumption and uptake of the cones, quantified by the decrease in D_c and that occurred during the rod death wave, play a key role in triggering the cone death wave. While D_T decreases at a faster rate during the rod death wave, its overall decay during this time is small. The significant and further decrease of the D_T after the cone death onset facilitates the demise of the cones. The observed changes in D_c support the hypothesis that cones overcompensate during rod degeneration in an effort for photoreceptors (and the visual system) to meet their metabolic demands and deal with oxidative stress that increases as rods die. Comparing the overall change in D_T with that of D_c during the cone death wave we can infer that the hypothesis of cone starvation plays a more significant role in explaining cone death. The decrease of D_c in all datasets highlights how the cone population must compensate during rod death to meet the high metabolic demands on the entire photoreceptor population. After the rod death wave, it is mainly the nutrients supplied by the RPE that drives the cone death wave.

The model does not distinguish between different interpretations of nutrient availability. Thus, it could be that many different methods of increasing nutrient availability, uptake, or retention will prolong cone survival. The data from the delayed cone death model considered here demonstrates how one approach can delay cone death. The approach constitutively activates the mTOR pathway, specifically the mTOR complex 1 (mTORC1), in cones. The mTORC1 is a key regulator of cell metabolism in charge of balancing demand with supply at the cellular level. By forcefully increasing its activity under nutrient poor conditions the cell rather than decreasing consumption increases expenditure and synthesizes more proteins that specifically improve nutrient uptake and retention. As predicted by the model on an intermediate time scale this approach appeared to be beneficial for cones in delaying their death. However, the decline in D_T is not stopped but rather is slowed, thus ultimately leading to the death of all cones. Why activation of mTORC1 is not sufficient to stop D_T from declining remains to be determined. In summary, the mathematical model suggests that by increasing nutrient availability to the cones the secondary loss of cones in RP can be halted. Thus increasing nutrient availability by activating mTORC1 is not the only viable approach worth pursuing and alternative and supplementary methods should be considered.

Figure 1.

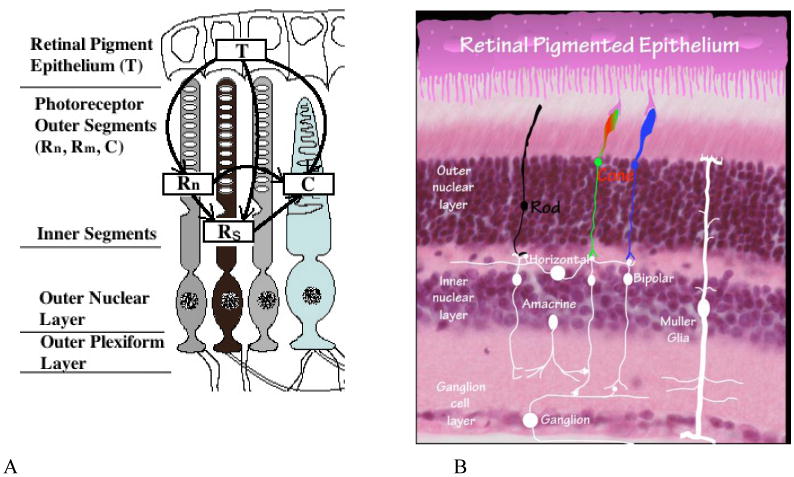
Anatomy of the retina. Panel A. Flow-diagram of photoreceptor interactions affecting RP. Here we assume two distinct classes of rod cells depending on whether or not they have had their functionality compromised in any way as a result of the genetic mutation and distinguish them as normal and sick rods, R_n and R_s respectively. See [29]. Panel B. Histology image of retina. This picture shows the histology of the retina to compare with the interactions in Panel A.

Table 2.

Summary of parameters for system (1).

Variable	Description	Units
Γ,	Total inflow rate into the trophic factors	1/t
k	Limiting capacity of trophic factors	1/Tt
bn	Constant per cell rate at which Rn withdraws T	1/Rnt
bs	Constant per cell rate at which Rs withdraws T	1/Rst
g	Constant per cell rate at which C withdraws T	1/Ct
dn	Constant per cell rate at which Rn helps C via RdCVF	1/Ct
ds	Constant per cell rate at which Rs C via RdCVF	1/Ct
mn	Per cell energy consumption rate of Rn	1/t
ms	Per cell energy consumption rate of Rs	1/t
mc	Per cell energy consumption rate of C	1/t
m	Per cell rate of normal rods Rn becoming sick Rs	1/t
an	Per cell energy uptake rate bnq1 of Rn	1/Tt
as	Per cell energy uptake rate bsq2 of Rs	1/Tt
ac	Per cell energy uptake rate gq3 of C	1/Tt

Highlights.

• Math model of RP presented together with datasets.

• Results suggest nutrient availability is key to halting degeneration.

• Global sensitivity confirms important role of nutrients.

• Cone death theoretically able to be halted.