Protein-Ligand Electrostatic Binding Free Energies From Explicit and Implicit Solvation

Abstract

Accurate yet efficient computational models of solvent environment are central for most calculations that rely on atomistic modeling, such as prediction of protein-ligand binding affinities. In this study, we evaluate the accuracy of a recently developed generalized Born implicit solvent model, GBNSR6 (Aguilar et al. J. Chem. Theory Comput. 2010, 6, 3613–3639), in estimating the electrostatic solvation free energies (ΔG_pol) and binding free energies (ΔΔG_pol) for small protein-ligand complexes. We also compare estimates based on three different explicit solvent models (TIP3P, TIP4PEw and OPC). The two main findings are as follows.

First, the deviation (RMSD=7.04 kcal/mol) of GBNSR6 binding affinities from commonly used TIP3P reference values is comparable to the deviations between explicit models themselves, e.g. TIP4PEw vs. TIP3P (RMSD=5.30 kcal/mol). A simple uniform adjustment of the atomic radii by a single scaling factor reduces the RMS deviation of GBNSR6 from TIP3P to within the above “error margin” – differences between ΔΔG_pol estimated by different common explicit solvent models. The simple radii scaling virtually eliminates the systematic deviation (ΔΔG_pol) between GBNSR6 and two out of the three explicit water models, and significantly reduces the deviation from the third explicit model.

Second, the differences between electrostatic binding energy estimates from different explicit models is disturbingly large; for example, the deviation between TIP4PEw and TIP3P estimates of ΔΔG_pol values can be up to ~50% in relative error, or ~9 kcal/mol in absolute error, which is significantly larger than “chemical accuracy” goal of ~1 kcal/mol. The absolute ΔG_pol calculated with different explicit models could differ by tens of kcal/mol. These discrepancies point to unacceptably high sensitivity of binding affinity estimates to the choice of common explicit water models. The absence of a clear “gold standard” among these models strengthens the case for the use of accurate implicit solvation models for binding energetics, which may be orders of magnitude faster.

Graphical Abstract

1 Introduction

An accurate yet efficient determination of the electrostatics in protein-ligand interactions is of profound importance in molecular design and drug discovery.^1–6 The computational prediction of binding free energies is however complex and challeng-ing,^7,8 and its outcomes can depend strongly on the molecular modeling technique used.⁹ In particular, accuracy of solvation and binding free energies calculations depends critically on the quality of the underlying solvent model.^10–12

Extensive studies have been performed to evaluate the accuracy of solvent models in predicting solvation free energies for small molecular systems;^10–13 in many cases the desirable “chemical accuracy” of 1 kcal/mol was reported ,^{10,11,14–16} at least on average. Yet, the high accuracy in predicting individual solvation free energies does not necessarily translate into high accuracy in atomistic binding free energy calculations.^17–19 High accuracy and robustness of the force fields and solvent models in these calculations has proven difficult to achieve.^20–25 Errors in even some of the highly accurate calculated binding energies can represent a significant percentage of the target binding free energies, sometimes as large as ~50% in relative error or ~7 kcal/mol in absolute error,²⁶ in particular when the number of interactions in a protein-ligand complex increases.¹⁹ Even for small and relatively rigid host-guest systems, predicting binding affinities within typical chemical accuracy of ~1 kcal/mol remains elusive.^22,23,27 Perhaps not surprisingly, binding free energies can be sensitive to the method parameters: the relatively small binding affinities are the difference between large free energy terms corresponding to the bound and unbound states.¹⁷ The interactions between proteins and ligands are short ranged and strong, which leads to the strong dependence of energy functions on the details of molecular conformation.²² Effects of systematic error cancellation can also be consequential in binding free energy calculations.^17,18 Since long-range electrostatic interactions play a dominant role in biomolecular simulations, a careful treatment of electrostatic interactions is essential,^28–34 and merits especial attention: this is the focus of the current work.

Implicit solvent models are currently routinely employed for evaluation of electrostatic interactions in many scenarios of biomolecular modeling.^{35,36,36–52} By replacing discrete water models with a continuum medium using the average dielectric properties of water, implicit solvents provide significant decrease in the computational cost of simulations. Within the implicit solvent framework, the Generalized Born (GB) model^43,53–75 provides a relatively simple, efficient and robust estimate to calculate the long-range electrostatic interactions in molecular simulations.^43,76 Methods based on the implicit solvent framework, such as MMPB(GB)/SA,^77,78 are extensively used in estimates of solvation free energies and protein-ligand binding interactions.^{31,37,41,62,79}

Recently, a new flavor of GB model, the so-called GBNSR6,⁸⁰ was reported; unlike most of its predecessors, the model relies on the “R6”^81–84 effective Born radius, which is calculated as a single r/|r|⁶ integral over the Lee-Richard molecular surface.⁸⁰ A good agreement of the electrostatic component of the solvation free energies (ΔG_pol) by the R6 flavor compared to the more fundamental Poisson-Boltzman (PB) model for small proteins and DNA was previously reported.⁸⁴ It was also shown that GBNSR6 and the TIP3P explicit model are in close agreement for different conformations of alanine polypeptide.⁸⁰ In a recent study, it was shown that GBNSR6 (with an appropriate non-polar contribution added) reproduces experimentally measured solvation free energies of small molecules with near “chemical” accuracy,¹³ on average.

Given the high promise of GBNSR6 method in predicting solvation free energies of some molecular systems, here we evaluate the accuracy of the model in predicting protein-ligand binding energies, crucial for rational drug design. To address this question, in this study we evaluate the binding free energies from GBNSR6 for a set of 15 small protein-ligand complexes, using explicit solvent free energies as reference.

While using explicit solvent as accuracy reference for an implicit solvent model is natural, the question arises which of the great many⁸⁵ available explicit water models should be used. The question is non-trivial, as none of the current models can be considered as uncontested “gold standard”.^86–88 Explicit water models are built to reproduce bulk properties, but being imperfect,^86–88 improved performance in pure water properties does not necessarily translate into better performance in solvated systems. For example, TIP4PEw is more accurate than TIP3P in predicting water bulk properties,⁸⁸ but less accurate in predicting hydration energies of small molecules;¹¹ TIP5P is superior to both in reproducing details of water structure,⁸⁹ but trails behind TIP4PEw in accuracy of predicted small molecule hydration energies.¹¹ Besides, the transferability of the observed accuracy of these explicit models in predicting solvation free energies of small molecules (RMS errors slightly over 1 kcal/mol) to macromolecular systems is not guaranteed,¹⁹ nor is it certain whether the same level of accuracy is achievable in binding free energy calculations, which is of main interest to us here. The question would be moot, however, if commonly used water models showed consistent performance in these calculations, say within 1 kcal/mol of each other. Whether or not common (and some new) explicit water models are equivalent in this respect is the second main question we address in this work. For this purpose we compare ΔG_pol and ΔΔG_pol computed with two highly popular, fixed-charge, rigid explicit water models for which free energy calculation protocols are well-established and their computational expense is reasonable: TIP3P⁹⁰ and TIP4PEw.⁹¹ We also make a comparison with a recently developed 4-point rigid explicit water model, OPC,⁹² which is arguably the first model of this class that predicts hydration free energies of small molecules with RMSD accuracy of less than 1 kcal/mol.⁹²

The remainder of the paper is organized as follows. In Section 2 we present the specifics of the protein-ligand complexes used for the comparative studies. The details of implicit solvent calculations and explicit solvent calculations using Thermodynamics Integration are provided in Section 2. The comparative studies are presented in Section 3. A summary of our findings is discussed in Section 4.

2 METHODS

2.1 Preparation of Complexes

A set of 15 protein-ligand complexes was selected (Table 1). One feature of the selected complexes is their small size (~1635–1995 atoms), essential to ensure convergence of the (lengthy) free energy perturbation (FEP) estimates. As a result of the limitation on the structure size, the diversity of the set is limited in terms of biological function of the complexes. However, the set is diverse with respect to values of electrostatic binding free energies: it covers a wide range of those (see Section 3), which is sufficient for our purpose. Another feature of the collected set is that ligands are neutral and proteins are either neutral or are forced to be neutral. The neutralization is performed to avoid various uncertainties and complications⁹³ due to the use of Ewald summation and periodic boundary conditions in explicit solvent simulations. For each component that needed to be neutralized, the neutralization was performed as follows. First, its isoelectric point pI was computed. Then, protonation state and charge states of each titratable group was set according to its computed pK value at pH = pI, which forced over-all neutrality of the structure. The calculations of pK, pI, the titration curves, and the protonation state adjustments were performed using H++ server⁹⁴ with the default settings; the server employs a continuum electrostatic approach to pK prediction. In principle, the explicit solvent box could alternatively be neutralized by adding counterions, however we did not follow this approach due to notably slow convergence of counterion distributions in MD simulations⁹⁵ (tens of nanoseconds for monovalent ions), which would make our TI-based estimates of ΔG_pol prohibitively expensive here.

Table 1.

Specifics of protein and ligand components for the set of 15 small complexes studied here

PDB ID	Protein name	Number of atoms in protein	Ligand name	Number of atoms in ligand
1b11	FELINE IMMUNODEFICIENCY VIRUS PROTEASE	1824	TL- 3–093	66
1bkf	FK506 BINDING PROTEIN FKBP MUTANT R42K/H87V	1659	FK506	128
1f40	FKBP12	1662	GPI-1046	54
1fb7	HIV-1 PROTEASE MUTANT	1566	SAQUINAVIR	99
1fkb	HUMAN IMMUNOPHILIN FKBP-12	1662	RAPAMYCIN	144
1fkf	IMMUNOPHILIN FKBP	1662	FK506	126
1fkg	FKBP	1662	SB3	68
1fkh	FKBP	1662	SBX	74
1fkj	FKBP12	1662	FK506	128
1fkl	FKBP12	1661	RAPAYMYCIN	146
1pbk	FKBP25	1851	RAP	144
1zp8	HIV PROTEASE	1566	INHIBITOR AB-2	88
2fke	FK-506-BINDING PROTEIN	1662	8-DEETHYL-8-[BUT-3- ENYL]-ASCOMYCIN	126
3kfp	HIV PROTEASE	1569	INHIBITOR TL-3	66
2hah	FIV/HIV chimeric protease	1800	broad-based inhibitor, TL 3	66

For setting up the structures we used H++⁹⁴ server that creates topology and coordinates files in Amber⁹⁶ format. The ff99bsc0 parameters and the GAFF force field, both part of Amber12,⁹⁷ were used for preparing the topology and coordinate files which includes partial charges. We performed 500 steps of minimization on the neutral complexes (without restraint) in vacuum to relax the structure. The minimization was performed in SANDER molecular dynamics module of Amber with a 12 cutoff distance. After minimization, the complex structures were broken down to the protein and ligand components to be used for the binding free energy calculations. The Amber format topology and coordinate files as well as the corresponding ΔG_pol values are available in the Supporting Information.

2.2 Implicit Solvent Details

GBNSR6

GBNSR6 is an implementation of the Generalized Born (GB) model in which the effective Born radii are computed numerically, via the so-called “R6” integration,^13,80 over the Lee-Richards molecular surface.⁹⁸ The polar component of the solvation energy, ΔG_pol, is calculated by the ALPB model,⁹⁹ which introduces physically correct dependence on dielectric constants into the original GB model of Still et al.,⁵⁴ while maintaining the efficiency of the original:

$$\mathrm{\Delta }{G}_{\mathit{\text{el}}}\approx -\frac{1}{2}(\frac{1}{{\epsilon }_{\mathit{\text{in}}}}-\frac{1}{{\epsilon }_{\mathit{\text{out}}}})\frac{1}{1+\beta \alpha }\sum _{\mathit{\text{ij}}}{q}_i{q}_j(\frac{1}{f^{\mathit{\text{GB}}}}+\frac{\alpha \beta }{A}),$$ (1)

where ε_in and ε_out are the dielectric constants of the solute and the solvent respectively, β = ε_in/ε_out, α = 0.571412, and A is the electrostatic size of the molecule, which is essentially the overall size of the structure, that can be computed analytically. Here, q_i is the partial charge of atom i. The most widely used functional form⁷⁶ of $f^{\mathit{\text{GB}}}={[r_{\mathit{\text{ij}}}^2+R_i{R}_j\mathit{\text{exp}}(-r_{\mathit{\text{ij}}}^2/R_i{R}_j)]}^{1/2}$ is employed, where R_i is the effective Born radius of atom i, and r_ij is the distance between atoms i and j. We set ε_in = 1 and ε_out = 80 in Eq. (1). Note that to mitigate uncertainties related to conformational sampling,^23,100 and to facilitate direct comparison between implicit with explicit solvent model predictions, we eliminated structural fluctuations by keeping all of the structures fixed by strong coordinate restraints in all of the explicit solvent simulations performed in this study (see Section 2.3). As a result, there was no dielectric response from the protein. This scenario is consistent with a value of unity for the solute dielectric constant (ε_in = 1) in the corresponding implicit solvent modeling^62,101 (Eq. (1)). The assignment of solute dielectric constant can, however, be different for a direct comparison to experiment.

The effective Born radii R_i are calculated via:

$$R_i^{-3}=(-\frac{1}{4\pi }{\oint }_{\partial V}\frac{\mathbf{r}-{\mathbf{r}}_{\mathbf{i}}}{{|\mathbf{r}-{\mathbf{r}}_{\mathbf{i}}|}^6}.d\mathbf{S})$$ (2)

where ∂V represents the molecular surface of the molecule, dS is the infinitesimal surface element vector, r_i is the position of atom i, and r represents the position of the infinitesimal surface element. In contrast to most GB practical models, GBNSR6 model is essentially parameter-free in the same sense as the numerical PB framework is. Thus, accuracy of GBNSR6 relative to the PB standard is unaffected by the choice of input atomic radii. Here we use the simple, standard Bondi¹⁰² radii set to determine the surface of the molecule. The solvent probe radius is equal to 1.4 Å. We use the same constant offset B = 0.028 Å⁻¹ to the inverse radii as in Mongan et al.⁸⁴

The GBNSR6 model exploits the Cartesian grid developed previously for PBSA module of Amber,¹⁰³ to build a numerical discretization of the Lee–Richards molecular surface.⁹⁸ The spacing between two neighboring grid points is uniformly set to h=0.3 Å, for the molecular surface resolution. The arc resolution (arcres), defined as the arc length between two neighboring solvent probe sites as the probe rolls over the atoms,¹⁰³ is set to 0.1 Å. This implementation of GBNSR6 is currently available as a part of Amber Tools suit of programs in Amber15.¹⁰⁴

PB model

The Adaptive Poisson-Boltzmann Solver (APBS) software package¹⁰⁵ was used for evaluating the polar part of solvation energies. The solute dielectric constant was set to 1 and the solvent dielectric constant was 80, which are consistent with the values chosen for GBNSR6. The grid spacing was set to 0.3 Å. To set the dimensions of the grids, we keep a distance equal to the size of the structure between the protein boundary and the grid boundary for the largest structure. Accordingly, the grid dimension size was set to 449 in x, y and z directions for all of the structures. The solvent probe radius is 1.4 Å. We use APBS default values for the remaining parameters, and assume no monovalent salt present, as in both the GB and the explicit solvent calculations.

2.3 Explicit Solvent Calculations

Electrostatic components ΔG_pol of explicit solvation free energies are computed by using the Thermodynamic Integration (TI) method of the SANDER module in Amber12.⁹⁷ Here we only compute the free energy transformations where the charges on protein-ligand complexes are removed: state 0 represents all solute atomic charges “on”, and state 1 represents all solute atomic charges “off”. We have used 5 values of lambda for TI calculations, λ = 0.04691, 0.23076, 0.50000, 0.76923, 0.95308. The TI values were obtained from Gaussian integration over the λ values. TI calculations were performed in water (TIP3P, TIP4PEw, or OPC explicit model) and in vacuum. Then the corresponding free energy values were subtracted to cancel out the intrasolute charge interactions as well as the restraint energies.¹⁰⁶ In all the simulations, the bonds to hydrogen atoms were constrained with the SHAKE algorithm using a geometrical tolerance of 0.000001 Å. The nonbonded interaction cutoff was 9 Å for simulations in water and 99 Å (effectively infinite) for simulations in vacuum. A time step of 2 fs is used (reduced to 1.8 fs if numerical instability was encountered). The following process is performed for each value of lambda: first, we run 1000 steps of minimization using steepest decent method. Then, we run 30 ps of NVT ensemble by gradually increasing the temperature from 0 K to 300 K. Then we run 1 ns of NPT ensemble at 300 K, for density equilibration. For the production we run 2 ns of NVT ensemble at 300 K. We run 200 ps MD simulation in vacuum. Protein-ligand complexes have many degrees of freedom that makes exploring all potentially relevant conformations computationally intractable.^23,100 Thus, 200 kcal/mol/Ų harmonic Cartesian coordinate restraints were imposed to all atoms, except during the minimization step for which 500 kcal/mol/Ų harmonic Cartesian coordinate restraints were applied to all atoms.

Robustness of the Protocol and Error Estimate

The standard deviation of computed ΔG_pol values is smaller than ± 0.7 kcal/mol for complexes and protein components, and smaller than 0.14 kcal/mol for ligands components. The standard deviations are calculated by assuming a correlation time of 1 ps, which is a conservative assumption considering that it is usually smaller than 0.8 ps.¹⁰⁷ The analysis is performed on the last 1.5 ns of 2 ns long simulation to ensure convergence. To test sensitivity to initial conditions we repeated the calculations for two complexes using different random seeds for the random number generator, and obtained differences less than the average standard deviation of computed ΔG_pol values given above. To further test that the TI results have reached convergence, we extended the simulation time from 2 ns to 5 ns for two randomly selected complexes and noticed the resulting TI values differ by less than the standard deviation above.

2.4 The Electrostatic Component of Binding Free Energies, ΔΔG_pol

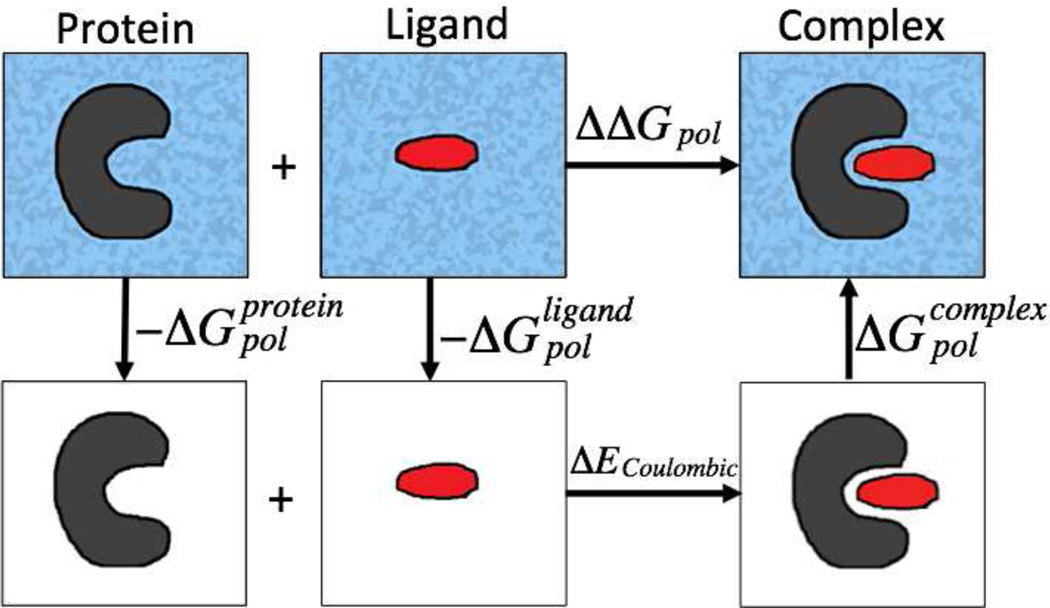
The electrostatic component of the binding free energies can be calculated using the thermodynamics cycle shown in Figure 1. The first step is to transfer the individual protein and ligand from the solvent into vaccum, with the energy costs of $-\mathrm{\Delta }{G}_{\mathit{\text{pol}}}^{\mathit{\text{protein}}}$ and $-\mathrm{\Delta }{G}_{\mathit{\text{pol}}}^{\mathit{\text{ligand}}}$, respectively. The second step is to combine the protein and the ligand into a complex in vaccum. The energy cost would be the difference in Coulombic energies in vaccum ($\mathrm{\Delta }{E}_{\mathit{\text{Coulombic}}}=E_{\mathit{\text{Coulombic}}}^{\mathit{\text{complex}}}-E_{\mathit{\text{Coulombic}}}^{\mathit{\text{protein}}}-E_{\mathit{\text{Coulombic}}}^{\mathit{\text{ligand}}}$). Calculation of ΔE_Coulombic is the same for all models. The final step is to solvate the complex into the solvent, where the corresponding energy cost would be $\mathrm{\Delta }{G}_{\mathit{\text{pol}}}^{\mathit{\text{complex}}}$. Using this cycle, the electrostatic component of binding free energies (ΔΔG_pol) can be computed as

$$\mathrm{\Delta }\mathrm{\Delta }{G}_{\mathit{\text{pol}}}=\mathrm{\Delta }{G}_{\mathit{\text{pol}}}^{\mathit{\text{complex}}}-\mathrm{\Delta }{G}_{\mathit{\text{pol}}}^{\mathit{\text{protein}}}-\mathrm{\Delta }{G}_{\mathit{\text{pol}}}^{\mathit{\text{ligand}}}+\mathrm{\Delta }{E}_{\mathit{\text{Coulombic}}}$$ (3)

Figure 1.

Illustration of the thermodynamic cycle for the decomposition of the electrostatic component of the binding free energies. The surrounding dielectric medium is shaded for water and is white for vaccum.

The standard deviation of computed ΔΔG_pol values from TI is smaller than ± 0.58 kcal/mol.

2.5 Computational Expense

A general performance comparison of the different methods used here to compute the electrostatic solvation free energies of the protein-ligand complexes is given in Table 2. The computations of GBNSR6 and PB are performed on a commodity PC with Intel(R) Core(TM) i7–3770 CPU 3.40GHz processor and 16 GB of RAM memory. All of the explicit solvent free energy TI calculations were performed on Virginia Tech’s HokieSpeed supercomputing cluster (http://www.arc.vt.edu) on a single node that has 12 processors. Expectedly, GB-NSR6 is significantly faster than the PB and explicit models studied here. Our studies show that the computational time required for grid-based calculation of the molecular surface needed by GB-NSR6 is similar to that of MSMS-based calculations; a detailed and exhaustive performance analysis of GBNSR6 based on MSMS molecular surface¹⁰⁸ is presented in Ref.¹³

Table 2.

Average computational time for calculating ΔG_pol per complex

Method	Computational time
explicit solvent TI	≈ 12 hours
PB	≈ 15 minutes
GBNSR6	≈ 6 seconds

3 Results and Discussion

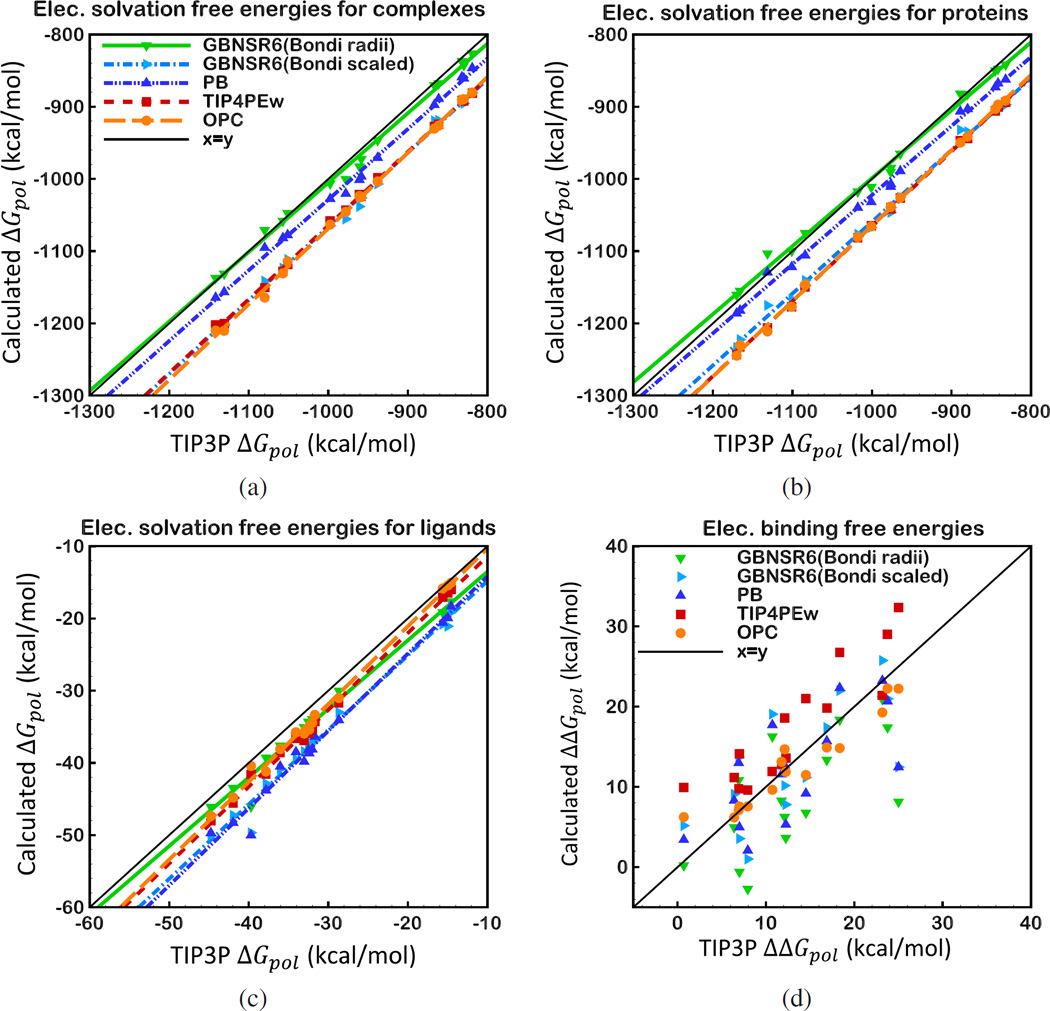
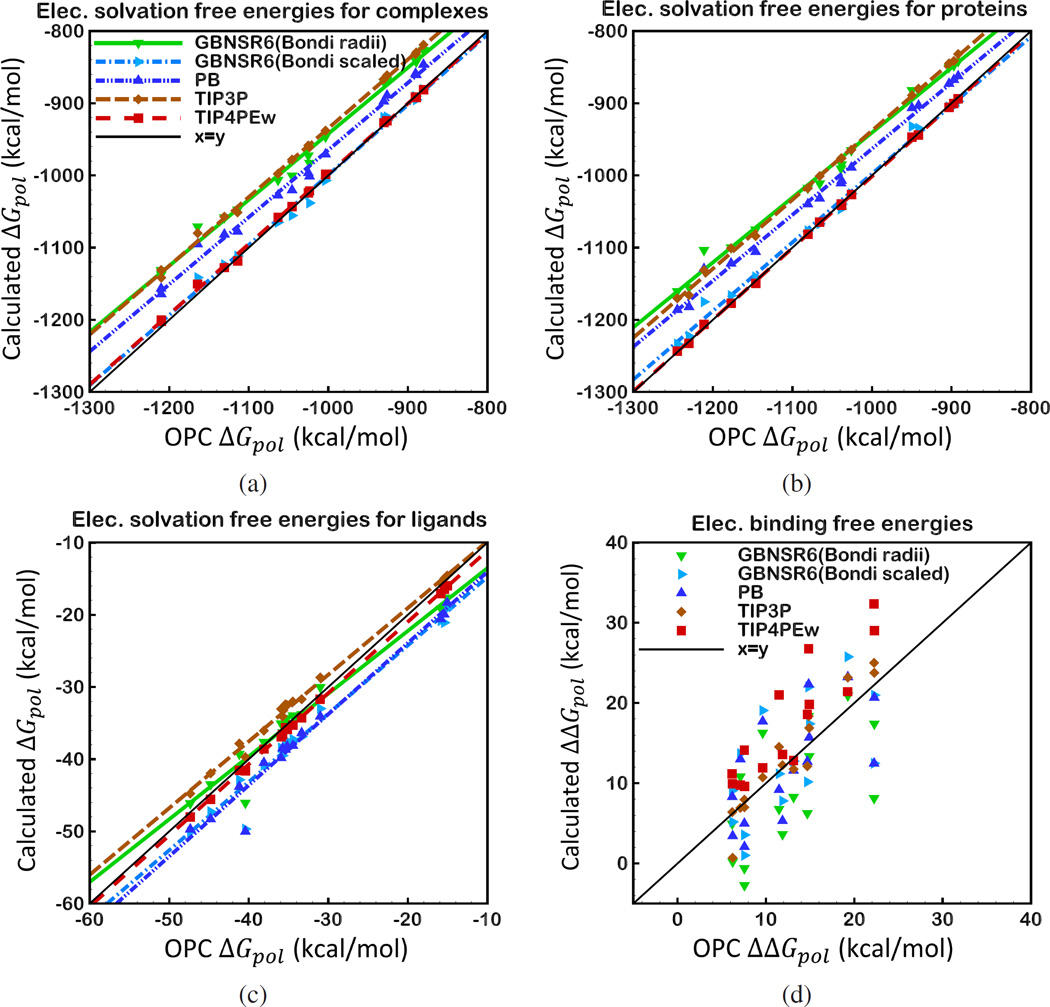
At the moment, comparison with explicit solvent predictions is a natural way to evaluate accuracy of implicit solvent models such as the GB. Among the most commonly used explicit water models, TIP3P is known to give better accuracy in hydration free energy calculations than many other water models tested previously;¹¹ TIP3P has been commonly used for benchmarking implicit solvent models. However, recent developments in building explicit water models yielded a model (OPC water model⁹²) that shows better agreement with experiment in hydration free energy calculations of small molecules. To be consistent with earlier works, we first compare deviation of the implicit models relative to TIP3P as reference, although we do not imply that TIP3P is any better or worse than the other explicit models studied here. We also benchmark computed electrostatic solvation free energy ΔG_pol and electrostatic binding free energy ΔΔG_pol values against free energy estimates performed in OPC water. Below, we give a brief summary of the agreement of GBNSR6 compared with the explicit solvent and also the numerical PB model. The correlation of ΔG_pol and ΔΔG_pol values relative to TIP3P and OPC are presented in Figure 2 and Figure 4, respectively. The statistics of ΔG_pol and ΔΔG_pol values relative to TIP3P are given in Table 3 and Table 4, and relative to OPC are given in Table 6 and Table 7, respectively.

Figure 2.

Correlation between ΔG_pol and ΔΔG_pol computed by GBNSR6, PB, TIP4PEw and OPC solvent models relative to TIP3P for 15 small protein-ligand complexes specified in Table 1, a) ΔG_pol of protein-ligand complexes b) ΔG_pol of protein components, c) ΔG_pol of ligand components, d) Electrostatic binding free energies, ΔΔG_pol

Figure 4.

Correlation between ΔG_pol and ΔΔG_pol computed by GBNSR6, PB, TIP4PEw and TIP3P solvent models relative to OPC for 15 small protein-ligand complexes specified in Table 1, a) ΔG_pol of protein-ligand complexes b) ΔG_pol of protein components, c) ΔG_pol of ligand components, d) Electrostatic binding free energies, ΔΔG_pol

Table 3.

Deviation of (ΔG_pol) values (kcal/mol) from those computed with TIP3P explicit solvent model. Atomic radii sets used in implicit solvent estimates are given in parenthesis.

RMSD	TIP4PEw	OPC	PB(Bondi)	GBNSR6(Bondi)	GBNSR6(Bondi scaled)
$\mathrm{\Delta }{G}_{\mathit{\text{pol}}}^{\mathit{\text{complexes}}}$	63.9	67.3	30.2	10.8	65.8
$\mathrm{\Delta }{G}_{\mathit{\text{pol}}}^{\mathit{\text{proteins}}}$	65.6	64.8	24.3	10.5	59.8
$\mathrm{\Delta }{G}_{\mathit{\text{pol}}}^{\mathit{\text{ligands}}}$	2.9	2.2	5.9	2.8	5.6

Table 4.

Deviation of (ΔΔG_pol) values (kcal/mol) from those computed with TIP3P explicit solvent model. Atomic radii sets used in implicit solvent estimates are given in parenthesis.

	TIP4PEw	OPC	PB(Bondi)	GBNSR6(Bondi)	GBNSR6(Bondi scaled)
RMSD	5.30	2.47	5.14	7.04	5.31
avg	4.29	−0.57	−0.99	−4.37	−0.36
corr. coef. (r2)	0.81	0.91	0.52	0.47	0.50
RMS of worst 20%	8.36	4.41	9.2	12.56	9.57

Table 6.

Deviation of (ΔG_pol) values (kcal/mol) from those computed with OPC explicit solvent model. Atomic radii sets used in implicit solvent estimates are given in parenthesis.

RMSD	TIP3P	TIP4PEw	PB(Bondi)	GBNSR6(Bondi)	GBNSR6(Bondi scaled)
$\mathrm{\Delta }{G}_{\mathit{\text{pol}}}^{\mathit{\text{complexes}}}$	67.3	5.62	39.38	62.14	8.92
$\mathrm{\Delta }{G}_{\mathit{\text{pol}}}^{\mathit{\text{proteins}}}$	64.8	2.49	44.00	66.82	11.99
$\mathrm{\Delta }{G}_{\mathit{\text{pol}}}^{\mathit{\text{ligands}}}$	2.2	0.83	4.08	2.26	3.98

Table 7.

Deviation of (ΔΔG_pol) values (kcal/mol) from those computed with OPC explicit solvent model. Atomic radii sets used in implicit solvent estimates are given in parenthesis.

	TIP3P	TIP4PEw	PB(Bondi)	GBNSR6(Bondi)	GBNSR6(Bondi scaled)
RMSD	2.47	5.92	5.00	6.80	5.38
avg	−0.57	4.86	−0.42	−3.80	0.20
corr. coef. (r2)	0.91	0.80	0.44	0.37	0.41
RMS of worst 20%	4.41	10.56	8.5	11.20	8.86

3.1 Implicit models

ΔG_pol Deviations from TIP3P

The computed values of ΔG_pol for the protein-ligand complexes and their components obtained from GBNSR6 are compared with the corresponding TIP3P (TI) values. Figure 2(a) and (b) show that among different implicit and explicit models, $\mathrm{\Delta }{G}_{\mathit{\text{pol}}}^{\mathit{\text{complex}}}$ and $\mathrm{\Delta }{G}_{\mathit{\text{pol}}}^{\mathit{\text{protein}}}$ values from GBNSR6 agree best with TIP3P ΔG_pol values, with RMSD value of 10.76 and 10.53 kcal/mol, respectively (Table 3). Deviation of $\mathrm{\Delta }{G}_{\mathit{\text{pol}}}^{\mathit{\text{ligand}}}$ values computed using GBNSR6 from TIP3P is comparable to that of OPC from TIP3P (Figure 2(c)). The next model to best reproduce TIP3P’s $\mathrm{\Delta }{G}_{\mathit{\text{pol}}}^{\mathit{\text{complex}}}$ and $\mathrm{\Delta }{G}_{\mathit{\text{pol}}}^{\mathit{\text{protein}}}$ values is the PB model, although it shows the lowest agreement with TIP3P for $\mathrm{\Delta }{G}_{\mathit{\text{pol}}}^{\mathit{\text{ligand}}}$, among all the solvent models studied here. At the same time, the better agreement of GBNSR6 with TIP3P values holds for the ligands as well.

ΔΔG_pol Deviations from TIP3P

The RMSD error of PB’s ΔΔG_pol relative to TIP3P is 5.14 kcal/mol, which is slightly lower than the deviation of TIP4PEw from TIP3P (RMSD = 5.30 kcal/mol) (Table 4). The RMSD error of GBNSR6 based on Bondi radii relative to TIP3P (7.04 kcal/mol) is higher than that of the PB (5.14 kcal/mol). However, the difference between the RMSD errors of GBNSR6 and PB is within the differences in ΔΔG_pol between the explicit water model calculations; e. g. the deviation of TIP4PEw or OPC from TIP3P. As can be seen in Table 4, the average error in ΔΔG_pol values of GBNSR6 is relatively large (−4.37 kcal/mol) which indicates a systematic error¹⁹ relative to TIP3P. The systematic deviation reflects the uncertainties associated with the “best” definition of the dielectric boundary needed by the GB and PB models.¹⁰⁹ To confirm the boundary definition origin of the systematic component of the deviation between GBNSR6 and TIP3P electrostatic binding energies, we show that the average error can be virtually eliminated (−0.36 kcal/mol) by a uniform scaling (multiplication) of the Bondi radii^101,109 with a single coefficient of 0.968 (Table 4 and Figure 2). The resulting RMSD error of GBNSR6 based on scaled Bondi radii relative to TIP3P is reduced to 5.31 kcal/mol, and becomes comparable to the RMS deviations of TIP4PEw and PB models relative to TIP3P (5.3 kcal/mol). We stress that uniform radii scaling by a single multiplicative factor^101,109 is not tantamount to full reoptimization^110,111 of the radii intended for best fit against a specific explicit solvent reference. The same scaling of Bondi radii by 0.968 also virtually eliminates the systematic deviation between ΔΔG_pol from GBNSR6 and a very different explicit solvent model (OPC) (as we shall see later), and nearly halves the deviation between GBNSR6 and TIP4PEw (from −8.66 kcal/mol to −4.65 kcal/mol).

3.2 Explicit models

ΔG_pol Deviations from TIP3P

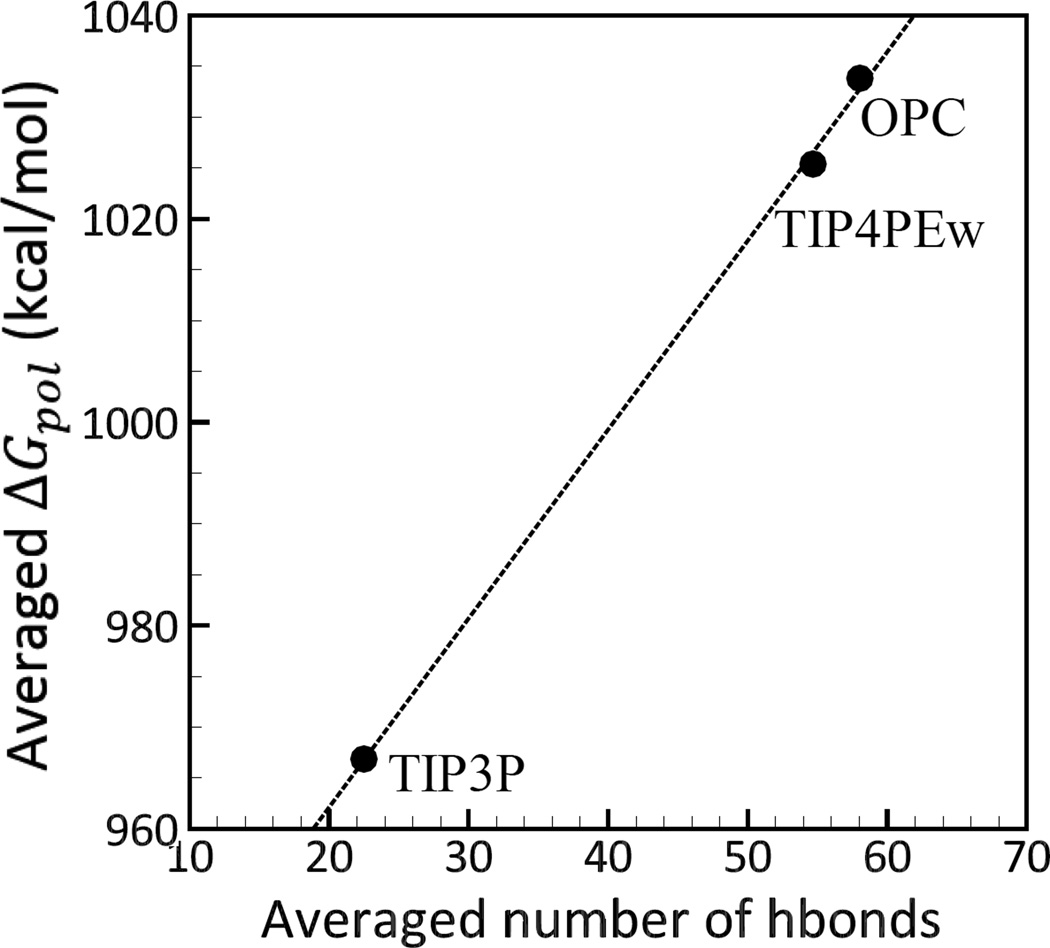
The absolute ΔG_pol values calculated using explicit water models differ significantly between themselves, Figure 2 and Table 3. Surprisingly, TIP4PEw and OPC show the lowest agreement with TIP3P in $\mathrm{\Delta }{G}_{\mathit{\text{pol}}}^{\mathit{\text{complex}}}$ and $\mathrm{\Delta }{G}_{\mathit{\text{pol}}}^{\mathit{\text{protein}}}$ values compared to implicit models. As seen from Figure 2, ΔG_pol values from TIP4PEw and OPC deviate systematically from the TIP3P values, with over-all average errors of −43.96 and −44.45 kcal/mol, and RMSD errors of 52.89 and 53.96 kcal/mol, respectively. Significant discrepancies between the values from OPC and TIP4PEw relative to TIP3P is likely due to stronger electrostatic interactions in OPC and TIP4PEw compared to TIP3P. For instance, while the dipole moment for TIP3P and TIP4PEw are close to each other (2.35D vs 2.32D, respectively) (Table 5), TIP4PEw’s square quadrupole is significantly larger than that of TIP3P (2.16DÅ vs 1.72DÅ) (Table 5). OPC’s dipole and square quadrupole moments are both larger (and closer to Quantum Mechanical predictions, Table 5) than those of TIP3P and TIP4PEw (Table 5). As a result of the differences in the strength of electrostatic interactions,³⁰ the numbers of hydrogen bonds formed by the three explicit water models differ (Figure 3). Specifically, the average number of hydrogen bonds formed between the solute and the solvent for our molecular systems in TIP4PEw is higher than that in TIP3P, and it is the highest for OPC (Figure 3). Solvation free energies increase almost linearly with the average number of hydrogen bonds, Figure 3. As a result, OPC yields the largest ΔG_pol values, followed by TIP4PEw and TIP3P. We did not find a correlation between the value of the static dielectric constant and electrostatic solvation free energies for the explicit solvent models studied here.

Table 5.

Three lowest order multipole moments of the water molecule; the values found in explicit water models are compared to experiment (EXP) where available, and liquid phase quantum calculations (QM). Moments are computed relative to oxygen center: dipole (µ), linear (Q₀) and square (Q_T) quadrupole, linear (Ω₀) and square (Ω_T) octupole.

Model	µ [D]	Q0 [DÅ]	QT [DÅ]	Ω0 [DÅ2]	ΩT [DÅ2]
EXP112	2.5–3	NA	NA	NA	NA
QM113	2.55	0.20	2.81	−1.52	2.05
TIP3P90	2.35	0.23	1.72	−1.21	1.68
TIP4PEw91	2.32	0.21	2.16	−1.53	2.11
OPC92	2.48	0.20	2.3	−1.484	2.068

Figure 3.

Correlation between the electrostatic sol-vation free energies ΔG_pol and the number of hydrogen bonds formed between the complexes and the explicit solvent models (TIP3P, TIP4PEw and OPC). The ΔG_pol values shown for each model are averages over complexes, and the number of hydrogen bonds represents averages over MD trajectory and over complexes. The hydrogen bond is considered to be formed if the distance between the acceptor (A) and the donor (D) atoms is smaller than 3Å, and angle D-H-A is greater than 135°.¹¹⁴ Connecting lines are shown to guide the eye.

ΔΔG_pol Deviations from TIP3P

The RMSD error in ΔΔG_pol calculated with OPC and TIP4PEw water models relative to the TIP3P reference are 2.47 and 5.3 kcal/mol, respectively. The RMSD of “worst” (largest deviation) 20% of TIP4PEw’s ΔΔG_pol values relative to TIP3P is as large as 8.36 kcal/mol. The deviations of ΔΔG_pol from explicit models appear much smaller than the deviations in ΔG_pol; however, ΔΔG_pol values are relatively much smaller (tens of kcal/mol) than ΔG_pol (thousands of kcal/mol), see Figure 2 and Figure 4, which results in large relative errors in ΔΔG_pol. For instance, deviation of TIP4PEw from TIP3P can be up to 50% in relative error of ΔΔG_pol values. Note that, expectedly, the correlation between ΔΔG_pol estimated by solvent models of the same class (e.g. TIP4PEw vs TIP3P) is considerably better than that between very different solvent models such as the GB and TIP3P (Table 4). At the same time, the average deviations between ΔΔG_pol computed by explicit models (e.g., TIP4PEw vs TIP3P) is still large, essentially comparable to the deviations between implicit and explicit models. The high correlation between the explicit solvent estimates suggests that the deviations between them may be systematic. This observation is further strengthened by the fact that the systematic error between the implicit and explicit solvent ΔΔG_pol can be virtually eliminated by a one-parameter adjustment of the dielectric boundary used in the implicit estimates, as discussed earlier.

Another interesting observation is that the ability of one explicit model to emulate estimates of ΔG_pol by another model can be independent of its ability to emulate ΔΔG_pol; for instance, among all implicit and explicit models studied here, OPC shows closest agreement with TIP3P in ΔΔG_pol while its ΔG_pol is furthest from TIP3P.

3.3 ΔG_pol and ΔΔG_pol Deviations from OPC

Here we investigate deviation of computed electrostatic solvation free energy ΔG_pol and electrostatic binding free energy ΔΔG_pol values from the values estimated with a recently developed explicit water model, OPC. The GBNSR6’s ΔG_pol values based on Bondi radii are systematically shifted from the OPC reference values (Figure 4 (a), (b) and (c)). Yet, deviation of GBNSR6’s ΔΔG_pol values from OPC is comparable to that of TIP4PEw from OPC. The same simple uniform scaling (multiplication) of all the radii in the Bondi set by 0.968 introduced earlier also virtually eliminates the systematic deviation between GBNSR6 and OPC in ΔG_pol and ΔΔG_pol values simultaneously (Figure 4 and Table 6). Interestingly, the radii rescaling, which amounts to the dielectric boundary adjustment, makes the deviation of GBNSR6’s ΔΔG_pol from OPC even smaller than that of TIP4PEw from OPC (average error 0.2 kcal/mol vs 4.86 kcal/mol).

Optimizing atomic radii, including uniform scaling, was used earlier^{101,109–111,115–117} to better reproduce solvation free energies from explicit solvent models. Here the scaling is used mainly to show that the apparent systematic deviation between the GB and explicit solvent is a consequence of a (radii-specific) definition of the dielectric boundary, which can be removed by a uniform “shift” of the latter. Still, achieving a good agreement with 3 different explicit water models simultaneously by a single-parameter uniform scaling of the Bondi radii, one of the smallest and simplest radii sets available in literature, seems noteworthy. Obviously, transferability of the scaled Bondi radii set optimized for the limited set protein-ligand complexes is not guaranteed, which motivates future studies.

To further illustrate the sensitivity of electrostatic binding free energies to the choice of explicit water model, we have also compared the TIP4PEw to the OPC-based estimates, (Figure 4, Table 6 and Table 7). In this comparison, TIP4PEw and OPC water models are more similar to each other than to TIP3P: both are 4-point models parametrized for use in long-range electrostatics interactions, and the polarization correction is included in calculations of heat of vaporization in the parametrization pro-cedure.^88,91,92 It is evident from Figure 4 (a), (b) and (c) that ΔG_pol values estimated with TIP4PEw and OPC are highly correlated, and the RMSD error of ΔG_pol calculations using TIP4PEw relative to OPC is relatively small. Yet, ΔΔG_pol values from TIP4PEw substantially deviate from that of OPC (RMSD= 5.92 kcal/mol). Despite the much smaller absolute ΔΔG_pol values compared to ΔG_pol values, the RMS deviation of TIP4PEw from OPC in ΔΔG_pol values is even larger than that in ΔG_pol (5.92 kcal/mol for ΔΔG_pol vs 5.62 kcal/mol for $\mathrm{\Delta }{G}_{\mathit{\text{pol}}}^{\mathit{\text{complex}}}$). The deviation of TIP4PEw from OPC is even larger than the one between TIP4PEw and TIP3P – water models that are parametrized quite differently (Table 3). Surprisingly, the RMSD error of TIP4PEw relative to OPC is similar to the RMSD error of implicit models (GBNSR6 based on scaled Bondi radii and PB) relative to TIP3P.

4 Conclusion

An accurate representation of the solvent is crucial for realistic and physically rigorous calculations of solvation and protein-ligand binding free energies. In this work, we have evaluated the accuracy of a recently developed generalized Born model, GB-NSR6, in predicting the electrostatic binding free energies ΔΔG_pol and electrostatic solvation free energies ΔG_pol of small protein-ligand complexes and their components. The estimates from GBNSR6 (and also the standard numerical PB) were compared to the estimates based on three explicit solvent models: RMS deviations of GBNSR6 and the PB from the explicit models were found to be comparable. It was shown that RMS deviation from TIP3P of GBNSR6 (Bondi radii) is comparable to the “error margin” of the explicit models themselves – the differences between the ΔΔG_pol values obtained from the explicit models (e.g. TIP4PEw vs TIP3P). Expectedly, the r² correlation between either of the implicit models and the explicit solvent is lower than between different explicit solvent models. GBNSR6’s ΔΔG_pol is closer to estimates based on OPC – a new 4-point rigid water model shown to give higher accuracy in estimation of solvation free energies of small molecules compared to TIP3P.⁹² A simple uniform scaling of Bondi radii set was shown to bring GBNSR6 RMS deviation essentially within the “error margin” of the three explicit models. The same simple scaling of Bondi radii was shown to virtually eliminate the systematic deviation of GBNSR6 from two out of the three explicit models and reduce the deviation from the third one by about fifty percent. Although the scaled Bondi radii set presented here is not guaranteed to be transferable to protein-ligand systems other than the ones studied here, the fact that a single-parameter uniform scaling of radii significantly improves the agreement of implicit solvent GBNSR6 with all three explicit models simultaneously is noteworthy.

A perhaps unexpected finding is that computed binding and solvation free energies using explicit water models can deviate significantly from each other. Also counterintuitively, lowest RMS deviation from TIP3P’s ΔG_pol is achieved by GBNSR6, rather than by the solvent models of the same class such as TIP4PEw and OPC, with RMS errors being up to tens of kcal/mol smaller. The results show that RMS deviations of ΔΔG_pol values obtained from different explicit models can be larger than that of ΔG_pol, although ΔΔG_pol is often orders of magnitude smaller than ΔG_pol in absolute values. The discrepancies between results from explicit models indicate the high sensitivity of electrostatic solvation and protein-ligand binding free energy calculations to the choice of explicit water models. Other studies have previously reported that Poisson-Boltzamn based approaches that are accurate in calculating ΔG_pol may not be equally successful at predicting ΔΔG_pol.¹⁷ The high sensitivity of ΔΔG_pol values to the choice of explicit water models observed in this work suggests that the sensitivity is not necessarily inherent to implicit solvent models.

In the absence of a “gold standard” explicit solvent model, the large discrepancy in free energy estimates from explicit water models is of paramount concern as it is unclear which of these models is most accurate in these calculations. Some of the water models most commonly used for solvation free energy calculations (e. g. TIP3P) can misrepresent key bulk properties by as much as 250 percent off the experimental values, suggesting the presence of serious physical flaws in these models. At the same time, these explicit models are often treated as accuracy “gold standard” for implicit solvents such as the GB, justified by the idea that implicit solvent models are designed to mimic the effects of explicit models as their higher level predecessors in the hierarchy of approximations leading to these models. In fact, the approach of fitting GB models to explicit solvent models seems reasonable because going directly from GB models to experimental observations with multiple levels of approximation can lead to over-fitting of the GB model parameters. Yet, given the significantly improved accuracy of most recently developed GB models, the strategy is called into question by the large discrepancies between free energy estimates obtained from commonly used explicit models. Efforts to develop more accurate explicit models,^92,118,119 or identifying the best among the existing ones, will ultimately help improve accuracy of implicit solvent models as well. In the meantime, adjusting implicit solvent theory to provide best match with several explicit models simultaneously might be the best practical strategy.

A direct comparison with experiment is needed for a decisive accuracy evaluation of explicit models in protein-ligand interactions. However, these comparisons are not straightforward. Protein-ligand complexes are very flexible and have many degrees of freedom introducing large uncertainties in calculations of entropy that make a direct comparison with experiment often difficult. An appealing alternative is to compare the computed binding enthalpies with experimental enthalpies for small host-guest systems.^100,120 Many fewer degrees of freedom and relative rigidity of host-guest systems compared to protein-ligand systems make these calculations computationally more straightforward and robust, albeit being still time consuming.^23,100