Calmodulin Gates Aquaporin 0 Permeability through a Positively Charged Cytoplasmic Loop

Abstract

Aquaporin 0 (AQP0), the major intrinsic protein of the eye lens, plays a vital role in maintaining lens clarity by facilitating the transport of water across lens fiber cell membranes. AQP0 reduces its osmotic water permeability constant (P_f) in response to increases in the external calcium concentration, an effect that is mediated by an interaction with the calcium-binding messenger protein, calmodulin (CaM), and phosphorylation of the CaM-binding site abolishes calcium sensitivity. Despite recent structural characterization of the AQP0-CaM complex, the mechanism by which CaM modulates AQP0 remains poorly understood. By combining atomistic molecular dynamics simulations and oocyte permeability assays, we conclude that serine phosphorylation of AQP0 does not inhibit CaM binding to the whole AQP0 protein. Instead, AQP0 phosphorylation alters calcium sensitivity by modifying the AQP0-CaM interaction interface, particularly at an arginine-rich loop that connects the fourth and fifth transmembrane helices. This previously unexplored loop, which sits outside of the canonical CaM-binding site on the AQP0 cytosolic face, mechanically couples CaM to the pore-gating residues of the second constriction site. We show that this allosteric loop is vital for CaM regulation of the channels, facilitating cooperativity between adjacent subunits and regulating factors such as serine phosphorylation. Similar allosteric interactions may also mediate CaM modulation of the properties of other CaM-regulated proteins.

Introduction

Aquaporins (AQPs),³ a ubiquitous family of tetrameric transmembrane proteins, facilitate the transport of water across biological membranes (1). Each aquaporin monomer consists of a six-helix bundle with its own water-selective pore (2). The AQP transmembrane permeation pathway has three regions that modulate the transport of water molecules across the membrane. At the extracellular interface sits a 3 Å-wide hydrophilic selectivity filter (also known as the first constriction site (CSI)) that excludes larger molecules from the outside while easily accommodating water (2). In the central region, a pair of Asn-Pro-Ala (NPA) motifs excludes protons from the channel while ordering water molecules into a single file (2, 3). These two regions are highly conserved among the 13 members of the AQP family. The differences between the AQP isoforms are restricted to the intracellular and C-terminal regions (4). These regions are responsible for the observed differences in osmotic water permeability (P_f) between AQPs as well as the allosteric regulation of the channels by cytosolic modification. In particular, AQP0 and AQP6 bind calmodulin (CaM) at their C termini in a Ca²⁺-dependent manner (5–7).

AQP0 is unique in that it is expressed almost exclusively in the eye lens, where it plays an essential role in water transport and possibly cell-cell adhesion (8, 9). AQP0 water permeability is modulated by CaM, which interacts with its C-terminal helical domain (10, 11). The reported structure of the AQP0-CaM interaction is noncanonical, in that CaM interacts simultaneously with two C-terminal helices of AQP0 in antiparallel fashion (4, 6). This gives rise to a 2:1 CaM:AQP0 tetramer stoichiometry. Because increases in intracellular calcium lead to an ∼2-fold reduction in water permeability, it has been hypothesized that CaM physically “plugs” 2 of the 4 AQP0 monomers. However, we have shown in previous work that CaM does not occlude the pore permeation pathway (4). Instead, AQP0 possesses a modifiable second constriction site (CSII) near its cytoplasmic opening, whose dynamics and configuration are influenced by the presence of bound CaM. Molecular dynamics (MD) simulations of CaM-bound AQP0 revealed a reduction of the root mean square fluctuations of the CSII gating residues, specifically Tyr-149, reducing the size of the pore opening to the cytosol (4). In this study we investigate the poorly understood molecular mechanism of the CaM-induced modulation of the AQP0 channel.

The interaction between AQP0 and CaM is of considerable interest because the structure of the complex between CaM and the holo protein is known, albeit at relatively low resolution (4). Most CaM-protein structures include only the CaM-binding peptide portion of the protein and thus may leave out critical interactions with the remainder of the protein, interactions with which may well be critical for the modulation of protein function by CaM. The structure of Reichow et al. (4) strongly suggests that the electrostatic interface between predominantly negatively charged CaM and predominantly positively charged AQP0 may well play such a role. In this work we experimentally and theoretically explored the role of the electrostatic interactions between CaM and AQP0 in modulating the water permeability of AQP0. We found that the electrostatic interface between the two proteins interacts with the more conventional CaM binding site to adjust the position of tyrosine 149 (Tyr-149) at constriction site II and thus modulate the P_f of AQP0. In particular, we demonstrate a role for the previously overlooked amino acids in the arginine-rich loop adjacent to Tyr-149, namely, their coupling to the CaM molecule and their allosteric effects on the water permeability of AQP0.

Many natural modifications of AQP0 occur at a C-terminal helical domain, which is often referred to as the AQP0 CaM binding domain (AQP0^CBD) (8, 12, 13). These modifications include mutations that are known to cause cataracts in humans, such as R233K, as well as serine phosphorylation at Ser-229, Ser-231, and Ser-235 (8, 12, 13). Additionally, the phosphorylation state of the AQP0^CBD is highly dependent on its distance from the lens periphery and is involved in the translocation of AQP0 into lens fiber cell membranes (14–16). Hypotonic swelling experiments in Xenopus laevis oocytes have shown that AQP0^CBD modifications reduce the sensitivity of AQP0 P_f to calcium (17). However, the effects of these modifications on the AQP0-CaM interaction remain unknown. NMR and mass spectroscopy experiments have revealed that phosphorylation of the AQP0^CBD peptide fragment reduces its binding affinity for CaM (11, 18). Adding phosphates to AQP0 would, in principle, reduce its ability to associate with the negatively charged CaM. However, some AQP0^CBD mutations retain partial calcium sensitivity (17), suggesting that CaM is still able to bind the phosphorylated AQP0 tetramer.

In this paper we employ water permeability assays and molecular simulations to reveal the functional details of CaM-modulation of AQP0 water permeability. We use Brownian dynamics (BD) simulations to study the effects of charge mutation on the formation of the AQP0-CaM complex and atomistic MD simulations to elucidate the effects of these mutations on the structure and function of AQP0. We then expressed the wild type and mutated forms of AQP0 in oocytes and assessed their permeability to validate insights from the MD simulations with experimental measurements and to guide further analysis and observations of our MD trajectories. Our data revealed that an arginine-rich cytosolic loop (Fig. 1) of AQP0 allows CaM to allosterically control the dynamics of the CSII, whereas the AQP0^CBD functions primarily as the CaM-binding site and as a modulatory feature of AQP0.

FIGURE 1.

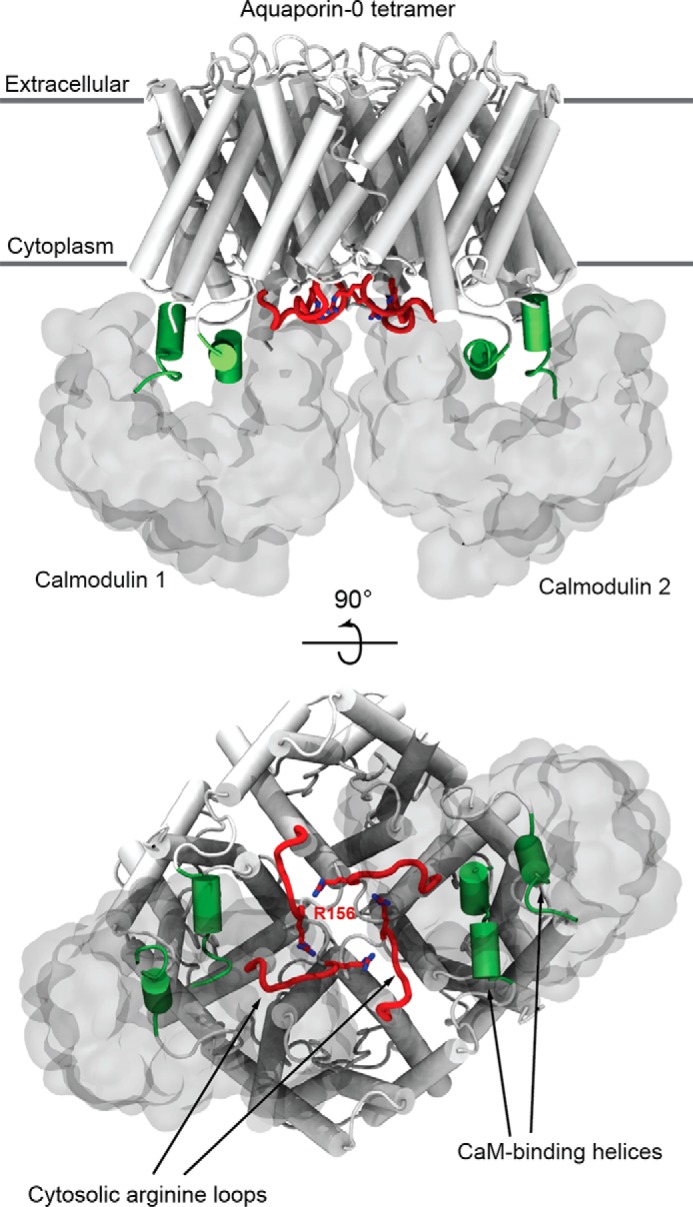
An arginine-rich loop of AQP0 gated the channels from the cytosolic face. Shown is the atomistic model of the AQP0-CaM complex (PDB code 3J41), highlighting the important structural features of AQP0 for CaM-sensing (4). CaM (shown in a white molecular surface representation) binds AQP0 (shown in white secondary structure representation) at its CaM binding domain (helical regions are shown in green) in antiparallel fashion. CaM reduces the water permeability of AQP0 by interacting with the Arg-156 residue (shown in red licorice representation) of the cytosolic arginine loop (shown in red) located at the center of the AQP0 tetramer.

Results

Electrostatic Interactions between AQP0 and CaM Occur Outside of the AQP0 CaM Binding Domain

We performed BD simulations of the association of AQP0 with CaM using the atomistic model reported by Reichow et al. (4) as the initial configuration by separating the CaM proteins from AQP0. BD simulations are often used to study the effects of charge mutation on protein association (19–23). BD docking of a globular protein, such as CaM, to a membrane protein is not unprecedented, but it is challenging due to the potential burial of interprotein contacts in the membrane environment, which may be inaccessible when the membrane-embedded protein is modeled as a rigid body (24, 25). Thus, we chose to remove the membrane environment surrounding the AQP0 structure. Our BD trajectories were able to reproduce the correct AQP0-CaM binding orientation but only when MD-equilibrated input configurations of AQP0 and CaM, taken from the simulated AQP0-CaM complex reported in Reichow et al. (4), were used (Fig. 2 and supplemental Movie 1). The atomic structure of the AQP0-CaM complex (Reichow et al. (Ref. 4) (PDB code 3J41) was produced using the petunia glutamate decarboxylase calmodulin complex (PDB code 1NWD) as the template for the interaction between CaM and the AQP0^CBD. Consequently, interactions outside of the CaM binding domain were not explicitly included in the interpretation of the experimental electron microscopy maps used to solve the structure (4, 26). These results suggest that regions of AQP0, other than the AQP0^CBD, form contacts with CaM (which we will elaborate on below) that are important both for stabilizing the complex and modulating the CSII.

FIGURE 2.

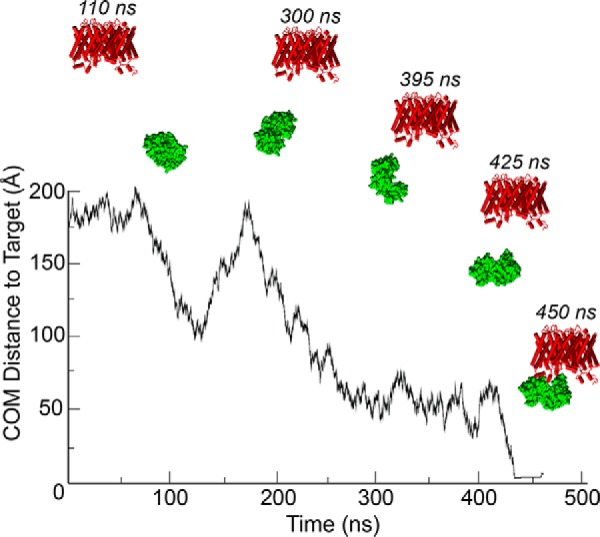
Brownian dynamics docking of CaM to AQP0. A representative Brownian dynamics trajectory shows CaM docking to WT AQP0. The center of mass distance between the mobile CaM protein (shown in green molecular surface representation) and its docked position on AQP0 (shown in red secondary structure representation) shows CaM diffusing to its bound configuration at ∼450 ns. The initial configurations used for BD simulations were taken from an equilibrated MD simulation of CaM-bound AQP0 (4).

To study the effects of serine phosphorylation on the association of the AQP0-CaM complex, we performed additional BD simulations of the association of CaM and AQP0, introducing negative charges to the C-terminal serine residues Ser-229 and Ser-235. We deleted the Ser-229 and Ser-235 hydroxyl hydrogens to leave a negatively charged side chain, thereby mimicking experimental pseudo-phosphorylation without adding additional steric bulk that could interfere with the formation of the complex. Using nonspecific contacts to define the association of the complex (see “Experimental Procedures”), we compared the BD complex formation in a total of 500,000 trajectories for Ser-229, Ser-235, and Ser-229/Ser-235 variants versus WT. The binding fractions for each AQP0 variant are reported in Table 1. It is evident that serine phosphorylation of the AQP0^CBD does not alter the frequency of AQP0-CaM complex formation significantly in our BD simulations. We also ran BD simulations of arginine-to-alanine mutations (R152A, R153A, and R156A) of AQP0 (Table 1). These mutations reduce CaM binding only marginally but more than mutations of the AQP0^CBD. The compound mutants AQP0-R153A/S229P and AQP0-R153A/S229P/S235P produced the largest effect, around an order of magnitude reduction of the binding fraction. It is important to contrast the results of our BD simulations of CaM binding to the AQP0 holo protein and the experimental NMR measurements of CaM binding to the AQP0 C-terminal peptide fragment. Experiments have shown that Ser-235 phosphorylation of the AQP0 C-terminal peptide reduces its binding affinity to CaM by more than an order of magnitude (10, 11). Our BD simulations, which take advantage of the full structure of the AQP0-CaM complex, suggest that serine phosphorylation does not inhibit CaM binding to the whole protein.

TABLE 1.

CaM binding fractions from Brownian dynamics simulations

AQP0 variant	Binding fraction
	%
WT	2.846 ± 0.019
S229P	2.143 ± 0.027
S235P	2.475 ± 0.025
S229P/S235P	1.246 ± 0.021
R152A	1.734 ± 0.021
R153A	2.009 ± 0.025
R156A	1.039 ± 0.013
R153A/S229P	0.413 ± 0.009
R153A/S229P/S235P	0.143 ± 0.004

AQP0 Phosphorylation Changes CaM Contacts with the Arginine-rich Cytosolic Loop of AQP0

To study the effects of AQP0^CBD serine phosphorylation on the AQP0-CaM interaction, we performed atomistic MD simulations of the AQP0-CaM complex structure (PDB code 3J41) by converting the standard Ser-229 and/or Ser-235 side chain to a monoanionic phosphoserine (henceforth denoted as S229P and/or S235P). This model was chosen to mimic experimental pseudo-phosphorylation, which utilizes a serine-to-aspartate mutation. The CaM-AQP0 interaction potential energies computed from our MD simulations were not significantly altered by serine phosphorylation (Table 2). A small weakening of the attractive electrostatic interactions was expected due to the excess of exposed acidic residues on CaM and was consistent with our BD results (Table 1).

TABLE 2.

The MD interaction potential energies of a single CaM monomer (with bound calcium ions) interacting with four variants of the AQP0 tetramer

The energies are given as an average value with S.D. in kcal/mol. The values are averaged over the two CaM monomers over the course of an ∼500-ns equilibrated MD trajectory.

AQP0 variant	Interaction energy (electrostatic only)	Interaction energy (electrostatic + VdW)
	kcal/mol	kcal/mol
WT	−1014.77 ± 26.59	−1072.19 ± 29.63
S229P	−968.98 ± 31.76	−1031.84 ± 34.32
S235P	−961.95 ± 32.18	−1009.03 ± 34.93
S229/235P	−876.79 ± 31.82	−942.54 ± 33.54

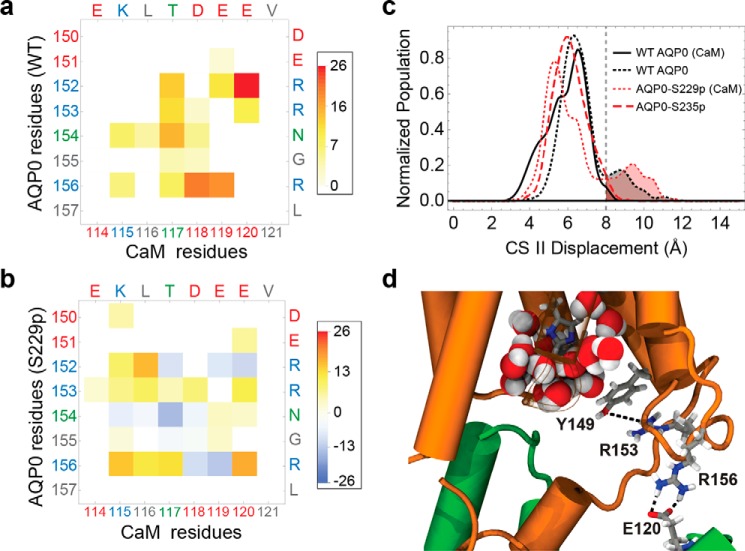
To assess the effect of serine phosphorylation on the pore opening, we monitored the distance between the CSII residues Phe-75 and Tyr-149 of each subunit (Fig. 3c). Previous studies suggest that the corresponding distance distribution accurately describes the conformational landscape of the CSII between an open and closed state (4, 27). In particular, for distances of >8 Å, Tyr-149 rotates away from the pore toward the cytosol, allowing pore waters previously constrained by the aromatic side chain to access the bulk. The distance distribution for all four of the pores (Fig. 3c) shows CSII open-state populations for both CaM-free WT AQP0 and CaM-bound AQP0-S229P (4) but not in CaM-bound WT AQP0. Thus, serine phosphorylation in the CBD modifies the CSII configuration and leads to a similar open-state probability in CaM-bound AQP0 as in CaM-free AQP0. We hypothesize that this change in the CSII configuration of AQP0-S229P locks the channel in a high P_f state (17). To gain insight into the underlying molecular mechanism, we performed a detailed analysis of the atomic-level interactions between CaM and AQP0 by mapping the atomistic MD configurations onto a chemical group graph representation (28).

FIGURE 3.

Phosphorylation of AQP0 modified the permeability of the channels by modulating the CaM interaction. a, matrix representation of the interprotein contacts formed between WT AQP0 residues and CaM residues at the cytosolic arginine loop. The color scale indicates the average number of atomic-level contacts over a MD trajectory (see “Experimental Procedures”). Residues are color-labeled on the axis by type (red, negative; blue, positive; green, polar; gray, nonpolar). b, matrix plot of contact differences between CaM-bound AQP0-S229P and CaM-bound WT AQP0 (subtraction of the CaM-bound WT AQP0 from the CaM-bound AQP0 S229P matrix). Darker red and darker blue indicate, respectively, contact formation and contact elimination upon Ser-229 phosphorylation. In the color scale, positive values correspond to a net increase in the average number of contacts, and negative values correspond to a net decrease in the number of contacts upon Ser-229 phosphorylation. c, CSII distance distributions for different AQP0 variants, indicating the size of the pore opening to the cytosolic vestibule. The different AQP0 variants consist of WT and phosphorylated AQP0 with and without CaM. d, configuration snapshot from an MD simulation of CaM-bound AQP0-S229P showing Arg-153 interacting with the Tyr-149 hydroxyl group, which displaces Tyr-149 away from the water pore. This is caused by the AQP0 Arg-156 interaction with CaM shifting from Asp-118 to Glu-120. An increase in the density of the AQP0 pore lumen waters (shown in filled sphere representation colored by atom type) can be seen near the cytoplasmic opening in response to the Tyr-149 displacement.

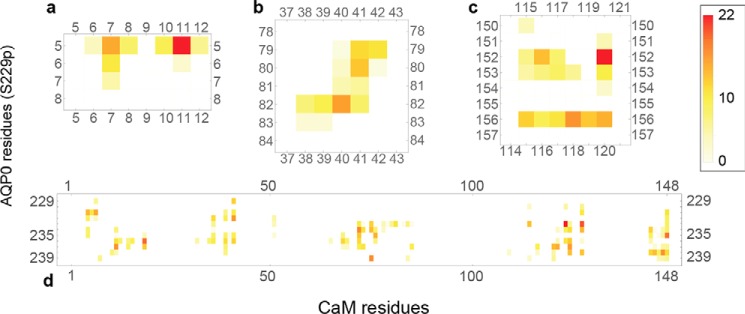
In the AQP0-S229P system, CaM formed significant interactions with four distinct regions of AQP0 (Fig. 4). First, the CaM N-terminal lobe interacted with the N terminus of AQP0 (Fig. 4a). The conformational flexibility of the CaM monomers allowed their N termini to contact the N-terminal residues of AQP0 while preserving the bound conformation (Fig. 5). When Ser-229 was phosphorylated, the N-terminal CaM lobes interacted with the cytosolic loop around residues 78–84 (Fig. 4b). These interactions occurred between polar side chains of the AQP0 loop and acidic side chains of the CaM N-terminal lobe. As expected, the most extensive interaction region was between CaM and its canonical binding site AQP0^CBD (Fig. 4d).

FIGURE 4.

Matrix representation of the interprotein contacts formed between residues of AQP0-S229P (on the vertical axis) and CaM (on the horizontal axis). The color scales indicate the number of atomic-level contacts averaged over a MD simulation trajectory (see “Experimental Procedures”). White indicates that the two residues do not interact, whereas a darker red indicates a strong interaction. Four plots show each of the four regions of AQP0 that make contact with CaM: the N terminus (a), the 78–84 loop (b), the arginine-rich cytosolic loop (c), and the C-terminal AQP0^CBD helix (d).

FIGURE 5.

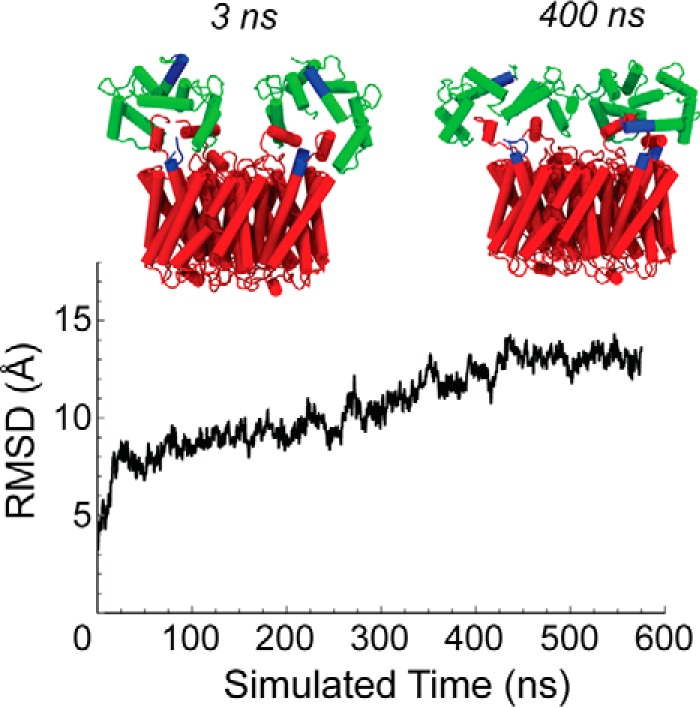
Root mean square displacement of bound-CaM reveals structural rearrangements that produce interactions between the N-terminal residues of AQP0 and CaM. The Cα root mean square deviation (RMSD) of the two CaM monomers from the original configuration over the course of a WT AQP0-CaM MD simulation trajectory; for the root mean square deviation calculation, the AQP0 tetramer configurations were aligned with the initial configuration. The configuration changes of CaM along the simulation trajectory allow the displacement of the N-terminal domains (shown in blue), which are initially far from AQP0 (snapshot at 3 ns), but are able to form contacts with AQP0 N-terminal residues (also highlighted in blue) in the stationary portion of the trajectory (snapshot at 400 ns).

The interactions outside the AQP0^CBD pertinent to the modulation of CSII occurred between the C-terminal lobe of CaM and the cytosolic loops that connect the fourth and fifth transmembrane helices (residues 150–156; Fig. 4a). The CaM C-terminal lobes (residues 115–120) formed electrostatic interactions with three arginine residues (Arg-152, Arg-153, and Arg-156) (Fig. 3a). We showed previously that these arginine residues play an important role in the formation of the AQP0-CaM complex in BD simulations (Table 1). In Fig. 3b, the WT AQP0/CaM contact matrix was subtracted from the AQP0-S229P/CaM matrix. Vanishing contacts as a result of the phosphorylation appeared in the difference matrix as negative-valued features. These changes were concentrated in the arginine loop region and corresponded to a shift in the interaction of AQP0 Arg-156 with CaM Asp-118 to CaM Glu-120. The increased CSII distance (Fig. 3c) resulted from this contact shift, which caused Arg-153 to interact with Tyr-149, displacing Tyr-149 away from the pore opening to allow pore waters to access the bulk (Fig. 3d). This mechanism is entirely consistent with the experimentally observed locked-high P_f of AQP0-S229P, opening the pore in the presence of bound-CaM (17).

The behavior of AQP0-S235P is quite different from AQP0-Ser-229. Ser-235 phosphorylation locks the channel in a P_f low irrespective of calcium concentration (17), suggesting that AQP0 is able to reduce its permeability in the absence of bound CaM. The CSII distance distribution from our CaM-free AQP0-S235P is consistent with CaM-bound WT AQP0, where the distribution shifts toward smaller distance (Fig. 3c). We observed that Ser-235 phosphorylation in CaM-free AQP0 induced additional contacts between the AQP0^CBD and the arginine loop, specifically with Glu-151 (Fig. 6, a and b). A salt bridge between Arg-233 and Glu-151 reduced the fluctuations in the side chain of the proximal Tyr-149 in a similar way as CaM-bound WT AQP0, lowering the P_f. This suggests that AQP0 phosphorylation not only regulates channel permeability by modifying the CaM-interaction but also through intraprotein interactions with the AQP0 arginine loop.

FIGURE 6.

Ser-235 phosphorylation of CaM-free AQP0 reveal additional contacts formed between the AQP0CBD and the arginine-rich cytosolic loop. a and b, matrix representation of the intraprotein contacts formed between AQP0^CBD (on the vertical axis) and the arginine-rich cytosolic loop (on the horizontal axis) in CaM-free simulation systems. The color scale indicates the number of atomic-level contacts averaged over a MD simulation trajectory (see “Experimental Procedures”). White indicates that the two residues do not interact, whereas a darker red indicates a strong interaction. Residues are color-labeled on the axis according to residue type (red, acidic; blue, basic; green, polar; gray, nonpolar). The AQP0^CBD in CaM-free WT AQP0 interacts primarily with Arg-152 of the cytosolic loop (a), whereas CaM-free AQP0-S235P (b), which displays a smaller CSII opening (Fig. 3c), develops an additional strong interaction between Arg-233 and Glu-151, a residue that we have identified as being part of the CaM gating mechanism (Fig. 3). c, a snapshot from an MD simulation of CaM-free AQP0-S235P showing the salt-bridge interaction between Arg-233 and Glu-151. This interaction decreased the distance between Tyr-149 and Phe-75 of CSII, breaking the single file of water molecules in the pore lumen (shown in filled sphere representation).

Mutations of the AQP0 Arginine Loop to Alanine Interfered with Calcium Sensitivity

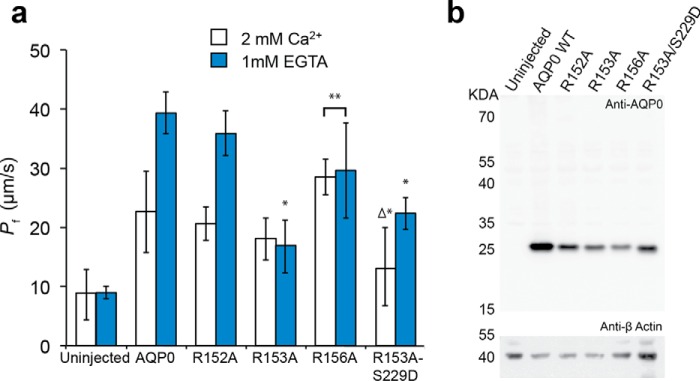
Our MD simulations suggested that CaM modulates AQP0 through the arginine-rich cytosolic loops proximal to the gating Tyr-149 residues. Prior research on the CaM-Ca²⁺ modulation of AQP0 has focused on the C-terminal AQP0^CBD helix due to its known interaction with CaM, its similarity to other CaM binding domains, and the accessibility of solution state NMR and mass spectroscopy experiments on the soluble peptide fragment (4, 18). However, oocyte-swelling assays allowed us to experimentally measure the permeability of the entire AQP0 tetramer. We expressed various arginine mutants of AQP0 into X. laevis oocytes, measuring the water permeabilities (Fig. 7a) by monitoring cell swelling in response to hypotonic stress at differing external calcium concentrations. A Western blot assay shows that the AQP0 mutants are all expressed (Fig. 7b).

FIGURE 7.

Arginine-to-alanine mutations of AQP0 interfered with calcium sensitivity. a, water permeability rates (P_f in μm·s⁻¹) obtained from oocytes expressing WT and various arginine loop mutants of AQP0 (R152A, R153A, R156A, and the double mutant R153A/S229D). Calcium buffer conditions of 2 mm Ca²⁺ (white) and 0 mm Ca²⁺ with 1 mm EGTA (blue) were used to probe the calcium sensitivity of AQP0 P_f for each mutant and WT AQP0. R152A displays WT behavior, whereas the R153A and R156A mutants lock the pore in a low and elevated P_f state, respectively. The compound mutant R153A/S229D has an unusual, zero permeability state (i.e. not different from uninjected) at 2 mm Ca²⁺. n = 3 for R152A. *, significantly different from wild type (p < 0.006). **, identical (p = 1.00). Δ, identical to uninjected (p = 1.00). b, Western blot analysis confirmed AQP0 protein expression resulting from RNA injected of WT AQP0 as well as all the mutants tested, R152A, R153A, R156A, and R153A/S229D, at the expected molecular mass of 26 kDa but not in uninjected oocytes (top panel). Protein loading in all lanes was confirmed by stripping the blot and re-probing for β-actin (bottom panel).

Previous experimental results have shown that oocytes expressing WT AQP0 exhibit a 2-fold increase in the water permeability rates when calcium is removed from the buffer (4, 6, 17). We observed that the Ca²⁺ response of R152A is precisely that of wild type; the water permeability at 2 mm Ca²⁺ is ∼21 μm/s and doubles to ∼36 μm/s in 0 mm Ca²⁺ (Fig. 7a). In contrast, Ca²⁺ sensitivity is eliminated for both R153A and R156A. R153A locks the P_f low, whereas the P_f of R156A is locked high (Fig. 7a).

We show in previous studies that the Tyr-149 residue of the CSII acts as a dynamic gate for the control of channel water permeability by the action of bound CaM (4). The different effects caused by these Arg-to-Ala mutations give clues to the specific actions of each of the three arginines. The locked low permeability of R153A is consistent with our observation that the Arg-153 side chain sits near Tyr-149 where it can open the CSII. MD simulations do not show substantial contacts formed between Arg-153 and CaM like those formed between CaM and Arg-152 and Arg-156 (Fig. 3). But Arg-153 interacted directly with the hydroxyl group of Tyr-149 in our CaM-bound AQP0-S229P trajectory (Fig. 3d). This accounts for the experimental result that the double mutant AQP0-R153A/S229D is no longer locked in a high P_f state like AQP0-S229D because Arg-153 is no longer present to exert its influence on Tyr-149. Thus AQP0-R153A/S229D exhibited a low P_f in 2 mm Ca²⁺, similar to AQP0-R153A (Fig. 7a). But the double mutant added a surprising twist; at 2 mm Ca²⁺, its P_f displayed a novel zero-permeability state (Fig. 7a). We confirmed this result by injecting oocytes with 10 and 20 ng of cRNA (Fig. 8).

FIGURE 8.

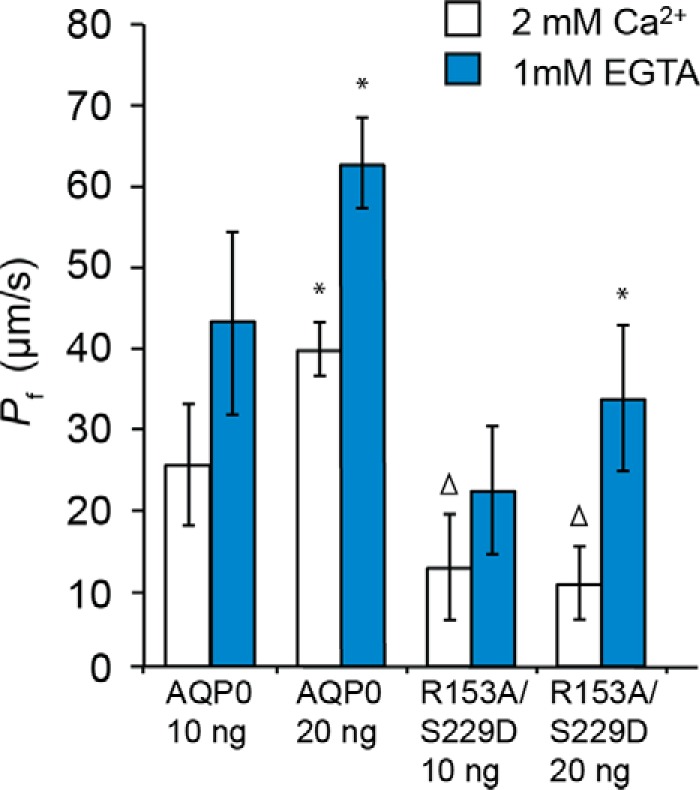
Water permeability of the R153A/S229D double mutant in 2 mm Ca²⁺ did not depend on amount of cRNA injected. AQP0 P_f (minus uninjected oocyte P_f) doubled with a doubling of the amount of cRNA in both 2 mm Ca²⁺ and 1 mm EGTA. R153A/S229D double mutant P_f (minus uninjected oocyte P_f) in 1 mm EGTA doubled, but the P_f in 2 mm Ca²⁺ did not change. *, identical to 2 times 10 ng of cRNA P_f (minus uninjected oocyte P_f) (p = 1.00). Δ, identical to uninjected (p = 1.00). Uninjected oocyte P_f = 7.4 μm/s.

Because R156A is locked in a high P_f state, we hypothesize that the interaction between Arg-156 and CaM is critical for decreasing pore permeability. MD simulations revealed that residues Arg-152 and Arg-156 form strong salt bridge interactions with CaM (Fig. 3, a and b). However, R152A had no effect on the P_f of AQP0 (Fig. 7a), suggesting that Arg-152 contributes to the electrostatic interaction with CaM but does not facilitate CaM-Ca²⁺ modulation. Because Arg-152 and Arg-153 are closer in amino acid sequence to the gating Tyr-149, it is surprising that the interaction between CaM and Arg-156, however indirectly mediated, appeared to be essential to lower the permeability of AQP0-S229D (Fig. 3, c and d).

A Chain of Interactions Couples the Pore-gating Tyr-149 of AQP0 to Calmodulin through Arg-156 and Asp-151

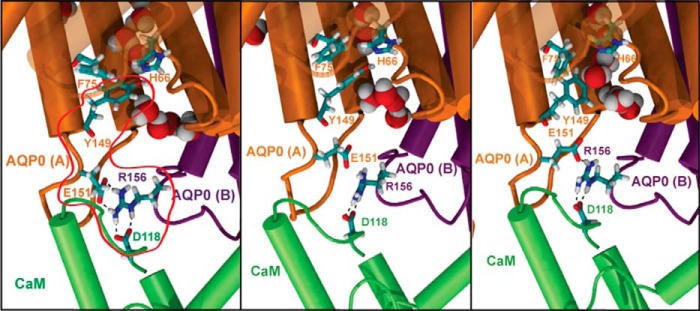
Our experimental and simulation results indicate that Arg-156 mechanically couples CaM to the AQP0 CSII. However, it remains unclear how Arg-156 is able to control the CSII dynamically when CaM forms significant interactions with residues closer to the gating Tyr-149, such as Arg-152, and it is also puzzling that the AQP0-R152A mutant displays water permeabilities similar to WT AQP0 (Fig. 7a). To resolve this conundrum, we identified potential interaction networks by determining the shortest paths between Arg-156 and Tyr-149 in our chemical group graph representation. Interestingly, we find that the shortest path between Arg-156 and Tyr-149 of a single subunit is the trace of the backbone. Because CaM also contacts Arg-152, it is unlikely that Arg-156 directly couples CaM to Tyr-149 through the backbone. When looking at intersubunit contacts, we find that Arg-156 forms a salt bridge with the Glu-151 side chain of an adjacent AQP0 subunit (Fig. 9). The Arg-156 interaction with Glu-151, which is a single amino acid residue upstream of Tyr-149, is dependent on the CaM Asp-118 side chain to properly orient Arg-156 (Fig. 9). The breaking of the single file of water molecules in the lumen of the water pore coincides with the formation of this salt bridge (Fig. 9). We hypothesize that the conformation of the gating Tyr-149 residue is restricted by the formation of salt bridge interactions between Glu-151 and Arg-156 of an adjacent subunit, which are facilitated by CaM Asp-118.

FIGURE 9.

A chain of electrostatic interactions mechanically coupled CaM to the pore-gating residues of AQP0. Snapshots from an MD simulation of CaM-bound WT AQP0 are shown. An interaction chain from Asp-118 of CaM to Arg-156 of AQP0 to Glu-151 of an adjacent AQP0 subunit (highlighted by the red enclosure in the first panel) connects CaM to the gating Tyr-149 residue of the CSII. Movement of the Tyr-149 side chain in the third panel follows the breaking of the salt bridge between Arg-156 and Glu-151 in the second panel, resulting in the reformation of the single file of water molecules through cytosolic portion of the lumen.

Discussion

CaM reduces the water permeability of AQP0 in response to increases in the intracellular calcium concentration (6). However, little is known of the molecular mechanisms by which CaM regulates AQP0 P_f or for that matter how it modulates the functions of other membrane proteins. We employed molecular simulations and biophysical permeability assays to elucidate the molecular mechanism by which CaM modulates AQP0 water permeability as well as how modifications (such as phosphorylation) are able to allosterically change calcium sensitivity. Our data suggest critical and hitherto unexpected features of the AQP0-CaM complex that may also be important in CaM interactions with other regulated proteins. First, electrostatic interactions between CaM and the cytoplasmic face of AQP0 play a critical role. Second, a series of side chain interactions couples CaM to the CSII of AQP0 through a cytosolic arginine-rich loop located near the center of the tetramer.

AQP0^CBD phosphorylation interferes with the calcium sensitivity of AQP0, locking the P_f either high or low (17). It has been hypothesized that phosphorylation reduces calcium sensitivity by inhibiting or reducing CaM binding to AQP0. Phosphorylation has been shown to inhibit CaM binding to the AQP0^CBD peptide fragment (18), which lends credence to this hypothesis. However, our BD simulations, which utilize the full-length structures of AQP0 and CaM, suggest that the interfacial arginine residues Arg-153 and Arg-156 at the interface play a dominant role in the formation of AQP0-CaM complex, whereas phosphorylation alone produced little effect on the formation of the complex (Table 1). The AQP0 charge mutants R152A and R153A/S229D maintain calcium sensitivity in oocyte permeability assays (Fig. 7a) even though they can reduce the positive charge of the tetramer by as much as eight elementary charges. This means that CaM binding occurs in both AQP0-R152A and AQP0-R153A/S229D and implies that phosphorylation of AQP0 disrupts calcium sensitivity by altering the AQP0-CaM interaction interface and not by inhibiting CaM binding. CaM is negatively charged and has been experimentally shown to bind to neutral and positively charged peptides but there appear to be no examples of charge mutations inhibiting CaM binding to a full-length protein.

Our MD simulations predict that phosphorylation of the AQP0^CBD changes the interactions that CaM makes with the arginine residues of the 150–156 cytosolic loop of AQP0. Particularly AQP0-S229P, which is locked in a high permeability state, disrupts the interaction between Asp-118 of CaM with Arg-156 of AQP0, shifting it toward Glu-120. This shift causes the Arg-153 residue to interact with the gating Tyr-149 residues via its hydroxyl group, opening the CSII of one of the four pores. Experimental oocyte swelling assays confirm that AQP0-R156A is locked in the high P_f state (Fig. 7a). This suggests that the electrostatic interactions between the Arg-156 side chain and CaM are critical for closing the CSII in response to calcium, and AQP0-S229P has a locked-high P_f because it is able to disrupt this interaction (Fig. 3). Using a shortest-path algorithm to analyze our MD trajectories of CaM-bound AQP0, we found that Arg-156 simultaneously forms a salt bridge with Asp-151 of an adjacent AQP0 subunit and Asp-118 of CaM. We hypothesize that, through this interaction network, CaM mechanically couples to the backbone atoms of AQP0 Asp-151, restricting the conformational dynamics of the nearby Tyr-149 side chain to block the channel waters from accessing the cytosolic opening.

Conversely, R153A exhibits a locked-low P_f, suggesting that the basic side chain is critical for maintaining high water permeability states at low calcium concentrations. MD simulations of WT AQP0 (CaM) show that CaM rarely forms salt bridges with Arg-153 (Figs. 3 and 4). Instead, the guanidine group of Arg-153 sits near the pore opening, where it can interact with the hydroxyl oxygen of the Tyr-149 side chain. MD simulations show that S229P causes Arg-156 to shift its salt bridge from Asp-118 to Glu-120 of CaM, in turn causing Arg-153 to interact with the hydroxyl group of Tyr-149. This is remarkably consistent with our experimental result that AQP0-R153A/S229D is water-impermeable at normal calcium concentrations. The alanine side chain of this mutant can no longer interact with the Tyr-149 hydroxyl group to move it out of the pore opening, which is likely why AQP0-S229D exhibits locked-high permeability even in the presence of unmodified Arg-153. Additionally, Arg-153 and Glu-151 play a role in the reduced P_f of AQP0-S235D at 0 mm Ca²⁺. MD simulations of CaM-free AQP0-S235P revealed additional contacts formed between the AQP0^CBD and the cytosolic loop residues Glu-151 and Arg-153. These contact changes coincide with an increase in the CSII opening (Figs. 3c and 6). This suggests that AQP0^CBD modifications can alter P_f in a CaM-independent manner, similar to CaM-bound AQP0, in which the AQP0^CBD interacts with the cytosolic loop, decreasing the size of the CSII opening (Figs. 6c and 9).

Calmodulin is able to bind and modulate the functions of a diverse set of proteins in remarkably different ways. Our study has shown that the 150–156 arginine-rich loop region of AQP0 couples CaM to the pore opening, modulating the channel permeability. The arginine-rich loop region is not only conserved among fish and mammalian AQP0s, but similar loops can be found in other AQPs (29–34). Our results emphasize the importance of characterizing regulatory proteins like CaM with the complete target protein and not just a peptide derived from the target protein. As we have shown, whole protein-CaM studies can lead to some unexpected surprises. Future studies will likely expand the roles of these charged loops and electrostatic interactions in the cytosolic modulation of AQP water permeability by CaM and perhaps discover similar interactions between CaM and other types of proteins.

Experimental Procedures

BD Simulations

We used BD simulations to assess the effects of specific electrostatic features of AQP0 on the formation of the AQP0-CaM complex. The BD method simulates the diffusive dynamics of proteins modeled as atomically detailed rigid bodies in a continuum solvent. Protein translational and rotational displacements are generated using the Ermak-McCammon algorithm (35). The SDA 7 software package (36, 37) was used to carry out the BD simulations. The SDA protein-protein potential energy function contains four terms (36): interactions of the charges on one protein with the electrostatic potential of the other protein, an electrostatic desolvation penalty due to the charges on one protein entering the low dielectric cavity of the other protein, an attractive nonpolar desolvation contribution due to the burial of solvent-accessible surface atoms on one protein in the cavity of the other protein, and short-ranged repulsion modeled using an exclusion volume that prevents overlap of the proteins.

The electrostatic potentials were computed by finite-difference solution of the Poisson-Boltzmann equation, taking into account the inhomogeneous dielectric medium and the surrounding electrolyte solution using the APBS 1.4 program package (38). We utilized a manual multigrid calculation with a single Debye-Hückel boundary condition for each solute on a 200 × 200 × 200 grid of 1 Å spacing. Atomic charge and radii parameters were assigned to CaM and AQP0 using the CHARMM36 force field (39). The dielectric boundary was defined by the Van der Waals surface of the protein. Harmonic dielectric boundary smoothing and charge anti-aliasing were implemented using the method developed by Novotny et al. (40). The solute and protein dielectric constants were set to 78 and 2, respectively, at 298.15 K for all electrostatic potential grid calculations. An ionic strength of 50 mm NaCl, which was represented by charges of +1 and −1 with radii of 1.1 and 1.7 Å, respectively, was used for the electrostatic potential calculations. The solvent radius was set to 1.4 Å.

To increase computational efficiency, the number of charged protein sites involved in electrostatic interactions during the BD simulations was reduced using the effective charge formalism (41). The protein charges are fit on effective charge sites (nitrogen and oxygen atoms of acidic and basic side chains and terminal residues) so that, in a shell around the protein surface, the precomputed electrostatic potential in an inhomogeneous dielectric is recreated with a homogeneous dielectric solvent (41). The exclusion probe radius and skin thickness were set to 4 Å and 3 Å, respectively. For consistency, we used the same ionic strengths and solvent dielectric constant as the computed electrostatic potential. At each BD time step, electrostatic forces and torques acting on one protein are computed by placing its effective charges over the other protein's electrostatic potential grid (37).

The electrostatic desolvation energy grids (200 × 200 × 200 with a 1 Å spacing) were computed using Equation 2 in Gabdoulline and Wade (42) with the scaling factor α set to 1.67. A single ionic radius of 1.5 Å at 50 mm concentration was used. The nonpolar desolvation energy grids (200 × 200 × 200 with a 1 Å spacing) were computed using Equation 3 in Martinez et al. (36) with the distance parameters a and b set to 3.10 Å and 4.35 Å, respectively, and the normalization constants c and β set to 0.5 and −0.0065 kcal/(mole·Å²), respectively. The exclusion grids were calculated as described in Gabdoulline and Wade (43) using a probe radius of 1.77 Å.

In our BD simulations of the formation of AQP0-CaM complexes, the trajectory of CaM relative to AQP0 is computed by holding AQP0 fixed at the center of a sphere of radius 250 Å, while CaM was allowed to diffuse from a random starting position on the surface of the sphere. A single trajectory can either result in a binding event (defined below) or an escape event in which the center of mass to center of mass distance between the two proteins reaches a predefined 350 Å. The integration time step was linearly decreased from 20 ps to 1 ps over a protein surface-to-surface distance of 90 Å to 60 Å. This allows for the simulation to capture the finer details of the protein dynamics at close proximity while maintaining an efficient time step at large separation distances. The diffusion coefficients for CaM, which appear in the Ermak-McCammon algorithm, were calculated using the Hydropro 10 software package (44). The rotational and translational diffusion coefficients were calculated to be 5.424 × 10⁻² Ų ps⁻¹ and 2.453 × 10⁻⁶ rad² ps⁻¹, respectively.

A total of 500,000 BD trajectories were generated at 298.15 K for each charge variant (see Table 1). A successful binding trajectory was determined using standard SDA protocols. Specifically, a list of 14 donor-acceptor atom pairs between CaM and AQP0 in the complex structure with a maximum distance of 4.5 Å between each pair was generated using SDA 7. A binding trajectory occurs when any 3 of these atom pairs achieves a 5 Å separation simultaneously. The error estimates in the binding fraction were obtained by using the Bootstrap_multiCPU tool in SDA 7 (36, 37). Serine pseudo-phosphorylation was modeled by removing the hydroxyl hydrogen of the side chain and adding a single negative charge to the hydroxyl oxygen. In silico arginine to alanine mutations were made by truncating atoms of the side chain beyond the β-carbon followed by the creation of new structure and parameter files using the psfgen tool in VMD, version 1.9.1 (45).

Atomistic MD Simulations

To better understand the effects of phosphorylation on the structure and function of AQP0, we performed atomistic MD simulations of AQP0 and the AQP0-CaM complex embedded in a lipid bilayer in excess water. The model of Reichow et al. (4) (PDB code 3J41) with Ser-229 and/or Ser-235 modified to a monoanionic phosphoserine was used as the initial configuration (39). Each system was composed of an AQP0 tetramer (residues 5–239) complexed with 2 CaM monomers bound to 8 Ca²⁺ ions, embedded in a membrane of 410 POPC lipid molecules and 56,701 waters. Sodium counterions were added to neutralize the system. The CaM-free systems were constructed from the complex structure model through the deletion of the CaM monomers.

All MD simulations were performed using the NAMD 2.9 software package (46). The CHARMM36 force field was used for proteins (47–49) and lipids (50), and the TIP3P model was used for water (39). The system was subjected to 1500 steps of conjugate gradient energy minimization beore MD simulation. The simulations were carried out for ∼600 ns each at a constant temperature of 300 K and a constant pressure of 1 atm using Langevin dynamics for temperature control and a Nosé-Hoover-Langevin piston for pressure control (51, 52). In addition, we extended the trajectories of the CaM-free and CaM-bound WT AQP0 from Reichow et al. (4) by ∼450 ns. A multiple time step algorithm was used to integrate the equations of motion with timesteps of 4 fs for the electrostatic interactions and 2 fs for the bonded and short-ranged nonbonded interactions (53). The smooth particle mesh Ewald algorithm (54) was used to treat the electrostatic interactions, and the real-space part of the Ewald sum and the Lennard-Jones interactions were smoothly switched off between 10 Å and 12 Å. The SHAKE algorithm was used to constrain all bonds lengths involving hydrogen atoms (55). The VMD 1.9.1 software package was used for visualization and analysis (45). The statistical uncertainties in the interaction energies were computed using the block transformation method for correlated data (56).

Graph Representation and Contact Analysis

To analyze the interactions formed between AQP0 and CaM as well as the intraprotein interactions of AQP0, we utilized the chemical group graph representation developed by Benson and Daggett (28). In this scheme, each amino acid residue is parsed into small molecular moieties constituting the graph nodes. The node types include nonpolar, dipolar, negatively charged, and positively charged moieties. Graph edges are defined by a contact function, χ(u_i,v_j), which equals 1 when atom i of node u is within 4.5 Å of atom j of node v, and 0 otherwise. If atoms i and j are both carbon, a cutoff distance of 5.4 Å is used instead of 4.5 Å. The edge weight (w) between nodes u and v gives a quantification of the strength of the contact.

$$w\left(u,v\right)={\displaystyle \sum _{i=1}^n{\displaystyle \sum _{j=1}^m\chi \left(u_i,v_j\right)}}$$ (Eq. 1)

We took the time average of this quantity over a number of MD timesteps (T).

$$\langle w\left(u,v\right)\rangle =\frac{1}{T}{\displaystyle \sum _{t=1}^T{\displaystyle \sum _{i=1}^n{\displaystyle \sum _{\text{j}=1}^m{\chi }_t\left(u_{i,t},v_{j,t}\right)}}}$$ (Eq. 2)

We then summed 〈w(u,v)〉 for all independent nodes of each residue pair to get a contact score that weighs the contact by both strength and frequency. A rectangular matrix was constructed using residue contact scores for each pair of residues between AQP0 and CaM. The CBD contact matrices were produced using the same scheme to generate the intraprotein residue contact scores between the AQP0^CBD region and the remainder of the AQP0 tetramer. All contact matrix plot images were rendered using the Mathematica software package, version 10.1 (57).

Path Analysis

We utilized a modified Floyd-Warshall algorithm to compute a shortest path between all AQP0 nodes for individual MD configurations of the AQP0-CaM complex (58). Shortest paths connecting the Tyr-149 hydroxyl and Arg-156 guanidine nodes for each configuration were computed by ignoring edge weights. The resulting interaction networks were subsequently characterized and visualized using VMD 1.9.1 (45).

Xenopus Oocyte Permeability Assays

Forms of AQP0 containing mutations R152A, R153A, R156A, or R153A/S229D were cloned into a transcription vector (pXbG) containing BglII cloning site flanked by 5′- and 3′-untranslated regions (UTRs) of the X. laevis β-globin gene driven by the T3 transcription promoter. Oocytes from X. laevis were obtained from Ecocyte (Austin, TX) and injected typically with 10 ng of RNA encoding wild type, R152A, R153A, R156A, or R153A/S229D AQP0 generated using the mMessage mMachine T3 kit (Ambion/Life Technologies) as described previously (6) (when different amounts of RNA were injected, they are noted in the text or figure legends). The oocytes were incubated in 100% ND96 (100% ND96: 96 mm NaCl 96, 2 mm KCl, 5 mm HEPES, 1.8 mm CaCl₂, 1 mm MgCl₂, pH 7.5) with the desired test Ca²⁺ concentration for 5 min before the swelling assay. Swelling assays were performed at room temperature (20–21 °C) by transferring oocytes from a 200 mosmol to a 70 mosmol (30% (v/v) ND96) solution adjusted to the desired calcium concentration. Water permeability, P_f, was calculated from optical measurements of the increase in cross-sectional area of the oocyte with time in response to diluted ND96 using the formula,

$$P_f=\left[\frac{d\left(V/V_0\right)}{dt}\right]\left[\frac{V_0}{S_0}\right]/\left[{\Delta }_{\text{osm}}\hspace{0.17em}{V}_w\right]$$ (Eq. 3)

where V is the volume as a function of time, V₀ is the initial volume, S is the geometric surface area, Δosm is the osmotic gradient, and V_w is the molar volume of water. Each data point is the average of at least six measurements (at least two different batches of oocytes, three oocytes from each batch unless otherwise noted). Error bars are shown as ± S.D.

Oocyte Permeability Statistical Analysis

Two-way analysis of variance performed on the data sets of Figs. 7 and 8 using the statistical package R (R-project) showed that the differences between means were highly significant (p < 10⁻¹⁵) (59). We performed pairwise t tests on all of the data in each data set using the R function “pairwise.t.test.” We show p values for appropriate conditions in the legends of Figs. 7 and 8.

Oocyte Membrane Isolation and Western Blot Assays

Total membrane protein was isolated using the ProteoExtract^R native membrane protein extraction kit (Calbiochem) according to the manufacturer's directions. Two oocytes worth of membrane protein in each lane was separated on a 4–12% SDS NuPAGE gel (Invitrogen) and transferred onto a nitrocellulose membrane. The blot was blocked in 5% milk in Tris-buffered saline with 0.1% Tween (TBS-T), then incubated with anti-AQP0 (H-44, Santa Cruz Biotechnology) antibody diluted at 1:500 in blocking solution (1% BSA, 2 mm EDTA in TBS-T). The blot was then washed and incubated with goat anti-rabbit HRP conjugated antibody (Pierce) for 1 h at room temperature and visualized by ECL Prime Blotting Detection reagent (Amersham Biosciences). Blots were then stripped and re-probed with an anti-β actin (ab8227 Abcam) antibody diluted at 1:500 in blocking solution followed by secondary antibody labeling and development as above.

Author Contributions

J. B. F. performed the simulations. J. B. F. and J. A. F. analyzed the simulations. K. L. N.-K. conducted the Oocyte swelling experiments. I. V. conducted the Western blot experiments. The study was conceived and designed by J. E. H. and D. J. T. All authors discussed the results, contributed to the paper, and approved its final version.

Note Added in Proof

In the version of this paper that was published as a Paper in Press on September 22, 2016, the supplemental data was not incorporated into the main text of the article. Supplemental Figs. 1–4 and a table have been incorporated into the article and do not affect the results or conclusions of this work.