Skip to main content
PMC home page
NIHPA Author Manuscripts logoLink to NIHPA Author Manuscripts
. Author manuscript; available in PMC: 2017 Jan 6.
Published in final edited form as: Hear Res. 2011 Jan 25;277(1-2):143–151. doi: 10.1016/j.heares.2011.01.008

Observer weighting of interaural cues in positive and negative envelope slopes of amplitude-modulated waveforms

I-Hui Hsieh 1, Agavni Petrosyan 2, Óscar F Gonçalves 3, Gregory Hickok 4, Kourosh Saberi 5
PMCID: PMC5217712  NIHMSID: NIHMS276617  PMID: 21272630

Abstract

The auditory system can encode interaural delays in highpass-filtered complex sounds by phase locking to their slowly modulating envelopes. Spectrotemporal analysis of interaurally time delayed highpass waveforms reveals the presence of a concomitant interaural level cue. The current study systematically investigated the contribution of time and concomitant level cues carried by positive and negative envelope slopes of a modified sinusoidally amplitude-modulated (SAM) high-frequency carrier. The waveforms were generated from concatenation of individual modulation cycles whose envelope peaks were extended by the desired interaural delay, allowing independent control of delays in the positive and negative modulation slopes. In experiment 1, thresholds were measured using a 2-interval forced-choice adaptive task for interaural delays in either the positive or negative modulation slopes. In a control condition, thresholds were measured for a standard SAM tone. In experiment 2, decision weights were estimated using a multiple-observation correlational method in a single-interval forced-choice task for interaural delays carried simultaneously by the positive, and independently, negative slopes of the modulation envelope. In experiment 3, decision weights were measured for groups of 3 modulation cycles at the start, middle, and end of the waveform to determine the influence of onset dominance or recency effects. Results were consistent across experiments: Thresholds were equal for the positive and negative modulation slopes. Decision weights were positive and equal for the time cue in the positive and negative envelope slopes. Weights were also larger for modulations cycles near the waveform onset. Weights estimated for the concomitant interaural level cue were positive for the positive envelope slope and negative for the negative slope, consistent with exclusive use of time cues.

1. Introduction

The duplex theory of binaural localization states that humans use interaural time differences (ITD) at low frequencies (below 1.5 kHz) and interaural level differences (ILD) at high frequencies to localize sounds in azimuth (Rayleigh, 1907). In the early to mid 1970s the viability of this theory was challenged by studies that demonstrated use of ITDs in envelopes of high-frequency amplitude-modulated (AM) sinusoidal carriers (Henning, 1974; McFadden and Pasanen, 1975; Nuetzel and Hafter, 1976). Neurophysiological studies, in addition, reported that auditory afferents can encode ITDs in high-frequency AM sounds by phase-locking to their slowly modulating amplitude envelopes (Crow et al., 1980). The binaural system’s ability to encode interaural cues in AM sounds has since become one of the most widely studied areas of the spatial hearing, with sinusoidal amplitude modulation (SAM) in particular being the stimulus of choice (Nuetzel and Hafter, 1976; Dreyer and Delgutte, 2006; Hsieh et al., 2010).

The current study was motivated by two questions. The first is theoretical and based on the idea that the binaural system can extract ITDs from temporal envelopes of high-frequency sounds. The envelopes of interaurally time delayed high-frequency AM waveforms, however, also contain concomitant interaural level cues. Panel A of Figure 1 shows a dichotic SAM waveform with the right (red) channel leading the left (blue) by τ μs. A secondary ILD cue (λ) exists that is consistent with the ITD cue in the rising (positive) slopes of the modulation envelope, and opposite to the ITD cue in the falling (negative) slopes.1 Panel B shows the output of a model of the auditory periphery consisting of a GammaTone filterbank (Holdsworth et al., 1988) and an inner hair-cell model (Meddis et al., 1990, Slaney, 1998) in response to a SAM waveform, and panel C shows this output delayed by 250 μs. The resulting cross-channel level difference is shown in panels D and E (see caption for details). If one assumes that the rising envelope slopes induce a larger neural spike count than negative slopes, as has been demonstrated in neurophysiological studies of ramped and damped envelopes (Pressnitzer et al., 2000; Neuert et al., 2001; Lu et al., 2001), the lateralization of high-frequency modulated waveforms may be partially (or entirely) influenced by level difference cues in positive slopes of the modulation envelope, a proposition consistent with the original tenets of the duplex theory. The current study investigates this idea by measuring thresholds and the distribution of decision weights for interaural cues in the positive and negative envelope slopes of modified SAM sounds. The algebraic sign of the weights for the decaying slopes of the modulation envelope will reveal whether time or level cues dominate lateralization decisions at high frequencies, whereas the magnitude of decision weights for rise and decay slopes will reveal the relative influence of the positive and negative envelope modulation slopes.2

Figure 1.

Figure 1

Open in a new tab

Panel A shows a schematic of a dichotic sinusoidally amplitude modulated (SAM) waveform with one channel (blue) delayed by τ relative to the other (red). Note the presence of a concomitant interaural level difference cue λ favoring the blue waveform in the negative slope of the modulation envelope. Panel B shows the output of a computational model of the auditory periphery consisting of a GammaTone filterbank with 50 filters whose resonant frequencies were logarithmically spaced from 2.5 to 6 kHz, followed by an inner hair-cell model. The stimulus was a SAM waveform with a 4-kHz carrier modulated at 150 Hz. Activity is shown during the sustained part of the waveform after the 10-ms rise time. The striations result from ringing of the filters. Panel C shows the same waveform delayed by 250 μs. Panel D shows the predicted interaural level difference in dB (from panels B and C). Panel E shows level differences integrated across frequency channels (from D) and normalized to a maximum value of 1.

The second question that motivated this study is whether interaural delays in high-frequency SAM sounds are uniformly weighted throughout the entire duration of the waveform. Given the central role that this important class of stimuli has played in binaural research, an evaluation of the relative perceptual weights given to information carried at different temporal loci throughout its ongoing duration is an important issue that can only be empirically addressed. This issue is especially relevant because of studies that have demonstrated both onset dominance (Hafter and Dye, 1983; Saberi, 1996; Stecker and Brown, 2010, Brown and Stecker, 2010) and recency effects (Stecker and Hafter, 2002, 2009; Zurek, 1980) in localization of complex sounds. Onset dominance is strong for stimuli which have temporal regularity (e.g., click trains, frozen noise pulses; Saberi and Perrott, 1995; Freyman et al., 1997; Zurek and Saberi, 2003; Freyman et al., 2010) and is weaker for stochastic and nonstationary waveforms (e.g., running noise, speech; Tobias and Schubert, 1959; Brungart et al., 2005; Freyman et al., 2010). Recency effects or upweighting in localization, observed for some but not all complex binaural stimuli, suggest that later-arriving information near the offset of a waveform may carry more weight than that at the waveform’s ongoing segment (Stecker and Hafter, 2002, 2009). Here we test whether interaural delays in a SAM waveform are equally or asymmetrically weighted throughout its duration by measuring decision weights associated with individual modulation cycles at different temporal positions.

In the current set of experiments we measured psychophysical thresholds and decision weights for interaural cues in high-frequency AM tones. In experiment 1, ITD thresholds were measured using a 2-interval forced-choice adaptive task for a dichotic AM tone with an ITD in either the positive, or separately, the negative modulation slopes. To this end, we developed a technique for generating dichotic AM sounds with independent control over interaural delays in the positive and negative modulation slopes by concatenating individual modulation cycles of a SAM waveform whose envelope peaks were extended by the desired interaural delay (Fig. 2). In a control condition, thresholds were also measured for a standard SAM tone. In experiment 2, decision weights were estimated in a single-interval forced-choice lateralization design for ongoing cycles of a SAM waveform which simultaneously carried ITDs in the positive, and independently, negative slopes of the modulation envelope. Decision weights were measured using a multiple-observation correlational analysis technique (Richards and Zhu, 1994) in which the interaural information in positive and negative slopes was independently perturbed. The goal was to determine the relative contribution of ITD and concomitant ILD cues to lateralization judgments. In experiment 3, decision weights were measured for groups of 3 modulation cycles at the start, middle, and end of the AM tone, with the remaining cycles having a zero ITD (diotic), to determine whether interaural delays are uniformly weighted throughout the duration of the stimulus, or asymmetrically weighted by onset dominance or recency effects (Stecker and Hafter, 2002, 2009; Saberi, 1996).

Figure 2.

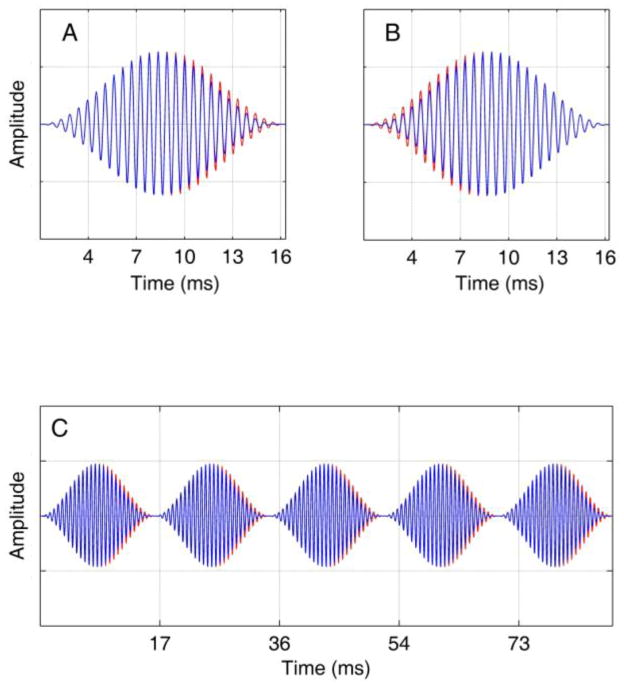
Figure 2

Open in a new tab

Stimuli used in experiment 1 contained an interaural delay either in the negative (A) or positive (B) modulation slope, and were generated from concatenation of individual modulation cycles whose envelope peaks were extended by the desired interaural delay (C). The blue waveforms are plotted on top of the red waveforms, with the blue representing the stimulus delivered to one ear, and the red the stimulus to the other ear. The stimulus shown in panel C is a 4-kHz carrier modulated at 150 Hz with a 250-μs interaural delay applied to the negative slope.

2. Experiment 1: Interaural delay thresholds measured for positive and negative modulation slopes

2.1. Methods

2.1.1. Stimuli and Apparatus

Stimuli were generated using Matlab software (Mathworks) on a Dell PC (Optiplex GX620) and presented at a rate of 44.1 kHz through 16-bit digital-to-analog converters (Creative Sound Blaster Audigy 2ZS) and Sennheiser headphones (HD 380 Pro) in a double-walled steel acoustically isolated chamber (Industrial Acoustics Company). The AM waveforms were fully modulated (100%), had a carrier frequency of 4 kHz, and a nominal modulation rate of 150 Hz. This rate was selected because prior studies have shown that, for lateralization of high-frequency carriers, modulation rates near this value produce the lowest ITD thresholds (Henning, 1974; Nuetzel and Hafter, 1981; Saberi, 1998). Each SAM waveform was generated from:

x(t)=sin(2πfc(t+ITD)+φc)(1+cos(2πfm(t+ITD)+φm)) [1]

where fc and fm are the carrier and modulation frequencies respectively, and φc and φm are their respective phases. To generate dichotic waveforms, the ITD was set to zero in one channel and to the desired delay in the other channel. The carrier phase was zero and the modulation phase was φm=+π such that the modulator began at its zero crossing (minima) resulting in each cycle being centered on the cosine phase (maxima). This was done to create equivalent conditions to those used to generate the modified AM waveforms which were generated from concatenation of individual cycles centered on the modulator’s cosine phase. Equation 1 can be expanded to:

x(t)=sin(2πfc(t+ITD)+φc)+0.5sin(2π(fc+fm)(t+ITD)+φc+φm)+0.5sin(2π(fc−fm)(t+ITD)+φc−φm) [2]

which shows that the spectrum of the SAM waveform is composed of a carrier component and two sidebands at fc±fm with a modulator phase (φm) term that is opposite in sign for the two sidebands.

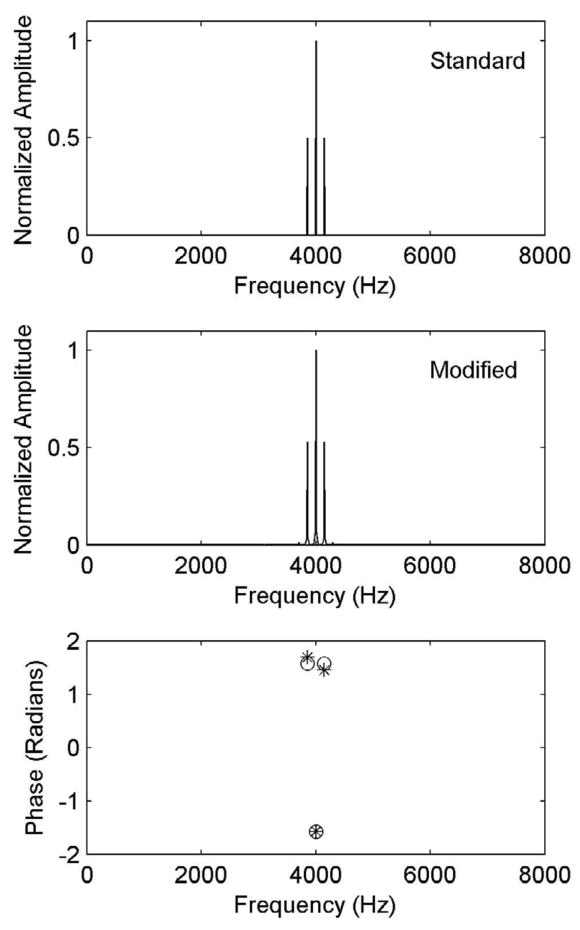
In addition to the standard SAM waveform, we generated two other types of stimuli for which the interaural delay was carried either by the rising (positive) slope of each cycle of the modulation envelope, or by the falling (negative) slope, with the other slope having a zero ITD. A sample dichotic waveform is shown in Fig. 2. The waveforms were generated from concatenation of individual modulation cycles whose envelope peaks were extended by the desired interaural delay prior to multiplication by the carrier, allowing independent control of delays in the positive and negative modulation slopes. For example, if the desired ITD was 250 μs, the envelope peak remained at its maximum value of +1 for 250 μs prior to decaying as expected based on a standard SAM envelope. Panels A and B show the ITD contained in the negative and positive slopes of a single modulation cycle, respectively, and panel C shows the modified AM waveform concatenated from individual cycles at the envelope minima (with the ITD carried only in the negative slope). The amplitude spectra of a standard SAM waveform and a modified waveform with the positive envelope-slope extended by 250 μs are shown in the top and middle panels of Fig. 3 respectively. We selected this ITD value for comparing spectra of the modified and standard SAM waveforms because, as will be shown, ITD thresholds were nearly always smaller than this upper limit. The effect of envelope extension on the amplitude spectrum, even in the extreme case (250 μs) is relatively small. The main difference between the two spectra is the presence of very low-level harmonics in the modified SAM spectrum, symmetrically above and below the carrier. The first harmonic below the main sidebands at 3700 Hz is −40 dB down relative to the carrier amplitude, with a rapid drop in levels of lower components. Our measurements show that below 1300 Hz, where carrier interaural phase may be of concern, the largest component frequency is approximately −90 dB down, and since the overall level at which stimuli were presented to subjects was 70 dB, these low-frequency components are inaudible and will have no effect on performance. The interaural phase of components at higher frequencies, near the waveform carrier, also do not affect lateralization as the binaural system is insensitive to interaural phase of individual components at high frequencies. The main difference between the two spectra is the presence of very low-level harmonics in the modified SAM spectrum, symmetrically above and below the carrier. The first harmonic below the main sideband is at 3700 Hz and is −40 dB down relative to the carrier amplitude, with a further rapid drop in levels of lower-frequency components. Our measurements show that below 1300 Hz, where carrier interaural phase may be of concern, the largest component frequency is approximately −90 dB down, and because the overall level at which the waveform was presented to subjects was 70 dB SPL, these low-frequency components are inaudible and will have no effect on performance. The interaural phase of low-level components near the waveform carrier, also do not affect lateralization as the binaural system is insensitive to interaural phase of individual components at these high frequencies. These components are, by definition, caused by and contribute to the difference in the shape of the envelope between the standard and modified SAM waveforms. The phase spectra of the standard and modified waveforms are shown in the bottom panel of Fig. 3.3

Figure 3.

Figure 3

Open in a new tab

Amplitude and phase spectra of a standard SAM tone (top panel) and modified (middle panel) waveform with the latter’s envelope extended by 250 μs in the negative modulation slope. The phase spectra (bottom panel) at the carrier and sideband frequencies are shown by circles (standard SAM) and asterisks (modified waveform).

All stimuli were 300 ms in duration with 20 ms linear rise-decay envelopes. Delays between left and right channels were checked for accuracy with a dual-channel digital storage oscilloscope (Tektronix, Model TDS210). Stimulus levels were calibrated to 70 dB SPL using a 6-cc coupler, 0.5-inch microphone (Bruel & Kjaer Model 4189), and a Precision Sound Analyzer (Bruel & Kjaer, Model 2260).

2.1.2. Procedure

Three normal-hearing adults served as subjects. All subjects were highly practiced in psychoacoustic experiments and were additionally practiced on the various conditions of the experiment for two hours prior to data collection. At the beginning of every run, a diotic sample of the signal for that run was presented over the headphones and repeated at a rate of twice per second. Subjects were instructed to center the image as best as they could by adjusting the positioning of the headphones. This was done to ensure proper placement of headphones resulting in symmetrically perceived lateral positions given either a left-leading or right-leading interaural delay of the same magnitude (Domnitz, 1973; Hafter and Dye, 1983; Saberi, 1996).4

The experiment was run in a block design in which the waveform type was held constant within a run (i.e., a waveform with a delay in the positive slope, in the negative slope, or a standard SAM waveform). Each subject completed 6 runs per condition in a random-block design in which one of the 3 conditions was randomly selected until a full set of 18 runs was completed. Each run consisted of 50 trials in a 2-interval forced-choice (2IFC) 2-down 1-up adaptive design which tracks the 71% correct-response threshold (Levitt, 1971). Our prior work has shown that 50 trials are usually sufficient for obtaining approximately 8 to 10 reversals in a 2-down 1-up adaptive procedure.

On the first interval of each trial, the dichotic waveform led at one randomly selected ear by a specific ITD and, in the second interval, it led at the other ear by the same ITD. The interstimulus interval was 300 ms. The subject’s task was to identify the order of presentation of the AM tones, i.e., left-leading then right, or, right-leading then left. Perceptually, this is equivalent to determining if the two intracranial auditory images in the two intervals of the trial were heard left then right, or right then left. The subject pressed a left or a right key to respond (left key response meant that they perceived the sound orders as right to left). No response feedback was provided to allow use of all available cues in determining perceived lateral position. Because there were two possible cues, ITDs and ILDs, that in some conditions were in conflict, providing feedback would have encouraged subjects to select one cue over the other. For example, in the case where the ITD was imposed on the negative envelope slope, feedback indicating that a subject was correct in responding to the side of the head which carried the leading waveform (i.e., correct response based on an ITD) would have meant that the subject should avoid using the ILD cue in order to get a correct response (or respond in a manner opposite to that based on the ILD cue).

The initial value of the total interaural delay on each run was 1500 μs, i.e., 750 μs in each interval. Two successive correct responses led to a reduction of the total interaural delay by 0.15 log units (Saberi, 1995), and an incorrect response led to an increase in ITD by the same factor. Threshold on each run was estimated as the geometric average of the ITD values at track reversal points. The first 3 or 4 reversals from each run were discarded and threshold was estimated as the average of the ITD values at the remaining even-number of reversal. Usually, four to six reversals went into the calculation of each threshold. All procedures were approved by the University of California, Irvine’s Institutional Review Board.

2.2. Results

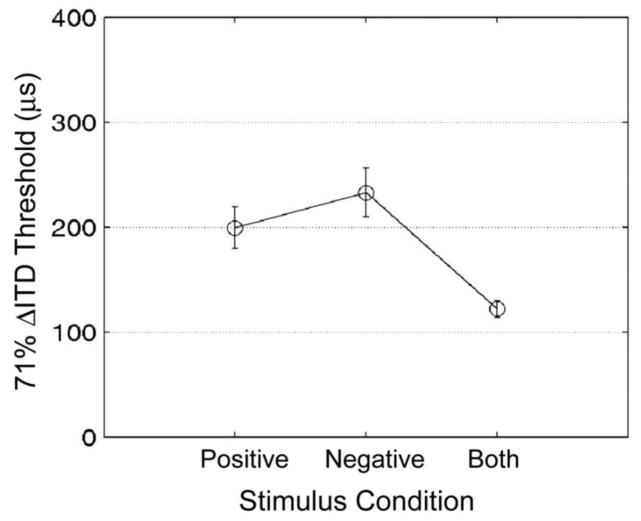
Figure 4 shows results averaged across the three observers. The abscissa shows the three stimulus conditions, with the ITD carried by: 1) positive envelope slopes, 2) negative slopes, and 3) a standard SAM waveform. The ordinate represents ITD threshold. Error bars show +/− 1 standard deviation. An analysis of variance (ANOVA) showed a significant effect of stimulus condition on ITD thresholds (F(2,34)=12.06, p<0.001). When the ITD was carried only in the positive slopes, performance was nearly the same as for the negative slope. The slightly higher threshold for the negative slopes was not statistically significant (t(17)=1.12). This suggests that ITDs carried by the decaying modulation slopes are as effective in influencing lateralization as ITDs carried in the rising slopes, and implies that the ILD cue in the negative slope has little or no effect. Thresholds for the standard SAM waveform, which contains ITDs in both the positive and negative modulation slopes, were significantly lower than those for the waveforms with information in the positive (t(17)=4.73, p<0.001) or negative (t(17)=5.28, p<0.001) slopes. A detection-theory analysis of optimum summation of independent sources of information predicts ITDSAM=(ITD+slope−2+ITD−slope−2)−1 and a threshold equal to 148 μs for the standard SAM waveform, which is close to but slightly larger than the empirically obtained value (122 μs). That the measured ITD threshold was smaller than predicted implies a common source of internal noise.

Figure 4.

Figure 4

Open in a new tab

Results from experiment 1 averaged across three observers. The abscissa represents the stimulus condition, with the ITD carried by: 1) the positive envelope slopes, 2) negative slopes, and 3) both slopes (standard SAM waveform). The ordinate represents interaural delay threshold. Error bars show +/− 1 standard deviation.

3. Experiment 2: Decision weights estimated for positive and negative modulation slopes

In experiment 2, decision weights were estimated for interaural cues carried in modulation slopes of an interaurally time delayed AM tone in a single-interval forced-choice design to determine the relative contribution of ITD and ILD cues. There were two main differences between the designs of experiments 1 and 2. First, the ITD cue in experiment 2 was imposed simultaneously and independently on both the positive and negative envelope slopes (see top panels of Fig. 6 for example) whereas in experiment 1 it was imposed on either the positive or negative slope, but not both. Second, instead of threshold measurements, we estimated decision weights for the contribution of ITD/ILD cues in the positive/negative slopes. The method used in this experiment allows estimation of decision weights by correlating the vector containing trial-by-trial values of each interaural cue (ITD or ILD) with the subject’s response vector. A negative decision weight associated with the negative slope, when correlating the ITD cue with the response vector, would imply a substantial contribution of the concomitant ILD cue to lateralization judgments. This is predicted from the top panel of Fig. 1 which shows that the two potential cues in the negative slope, τ and λ, favor opposite ears. If the binaural system only uses ITDs in this stimulus, then the decision weight calculated from correlating the response vector with τ will be positive. However, if the system uses ILDs and not ITDs, then the weight calculated from correlating the response vector with τ will be negative because λ favors the channel opposite to that favored by τ. Equal weights for positive and negative slopes would imply not only that ILD cues are not used, but that the asymmetry of neuronal responses to rise and decay envelope slopes observed in neurophysiological studies does not specifically extend to binaural cues in lateralization of amplitude-modulated waveforms.

Figure 6.

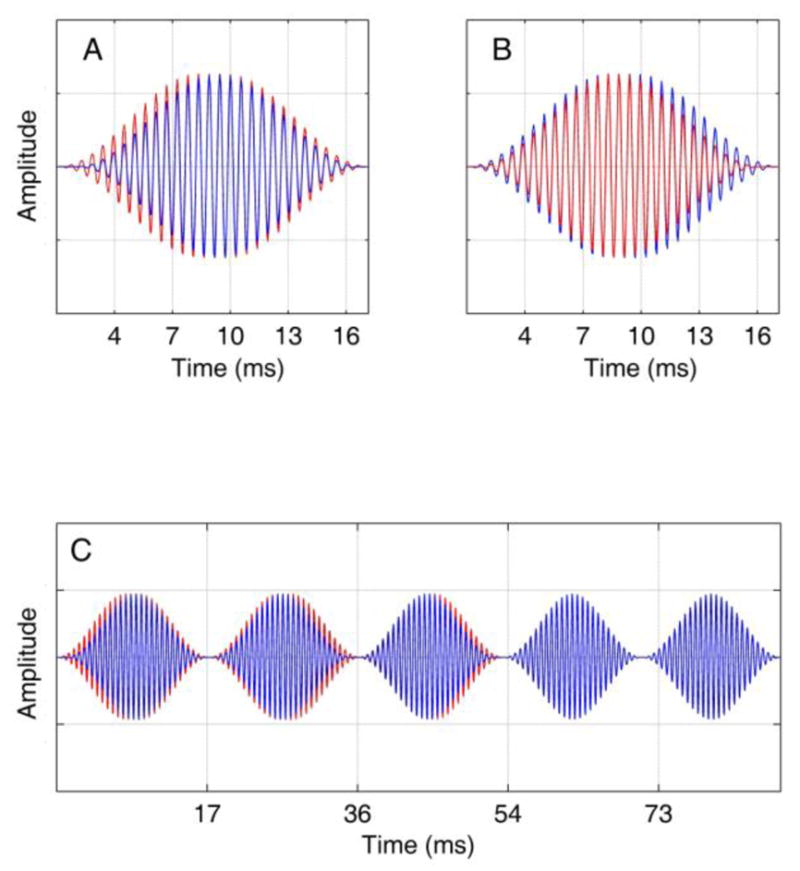
Figure 6

Open in a new tab

Panels A and B represent the types of modulation cycles used in experiments 2 and 3 in which interaural delays were selected on each trial from a normal distribution separately for the positive and negative slopes. Panel A shows a sample modulation cycle with ITDs of +450 and −200 μs in the positive and negative slopes respectively, and panel B shows ITDs of −210 and +435 μs. The delays shown in this figure are larger than those used in the experiment to facilitate visual inspection. Panel C shows the first five cycles of a representative waveform used in experiment 3, with the first 3 cycles dichotic and the next two diotic (zero ITD).

3.1. Methods

3.1.1. Stimuli

All stimuli and apparatus were the same as described for experiment 1 except for the following. On a given trial, the ITD cue was selected independently for the positive and negative modulation slopes5 from a Gaussian distribution with a mean of μ = 100 μs (or μ=−100 μs) and a standard deviation of σ = 60 μs, where negative and positive ITDs, by convention, represent waveforms leading to the left and right channels, respectively. Note that within a trial, first, a distribution mean was selected (either +100 or −100 μs), and then all ITDs for both the positive and negative slopes were selected from that same distribution. These distribution parameters were chosen based on pilot work which showed that subjects could identify, without feedback, which of the two distributions (i.e., μ=100 μs or μ=−100 μs) the ITDs were selected from with an accuracy of approximately 75%, a performance level that allows reliable estimation of decision weights (Berg, 1989; Saberi, 1996). Although the ITD cue was different for the positive and negative slopes on a given trial, it was fixed across all positive slopes (i.e., across all cycles) on a given trial, and fixed across all negative slopes. Thus, for example, a waveform may have contained an ITD of 143 μs in positive slopes of all its modulation cycles, and an ITD of 72 μs in all negative slopes.

3.1.2. Procedure

On each trial, one of two normal distributions NR~(μ=100 μs, σ=60 μs) or NL~(μ=−100, σ=60) was selected randomly. Once a distribution was selected, the ITDs for the positive and negative slopes were picked independently from that distribution. In a single-interval forced-choice design, the subject’s task was to determine which of two distributions the ITDs were sampled from. This was equivalent to determining if the sound was located to the left or right of the center of the interaural axis (corresponding to 0° azimuth). Note that, for a given distribution of ITDs (e.g., μ=+100 μs and σ=60), the ITDs in the positive and negative slopes may have had different signs (e.g., +100 and −72 μs). Subjects were instructed that if they heard split images on different sides of the midline, they should make a decision based on the more dominant image. However, no split images were perceived based on post-experiment interviews. As in experiment 1, a diotic version of the waveform was presented at the beginning of every run to allow subjects to adjust the headphones to perceptually center the image. Subjects were the same as those who participated in experiment 1. Each subject completed 20 runs of 100 trials each. No feedback was provided.

Decision weights for each subject were estimated by calculating the Pearson product-moment correlation between the response vector (2000 trials) for that subject and the ITD vector for the positive (2000 values), and separately, the negative envelope slope, and normalizing the results such that the magnitude of weights summed to unity (see Richards and Zhu, 1994, for details). The model is based on the assumption that a decision weight, w+, is given to ITDs in the positive slopes and another weight, w−, given to ITDs in the negative slopes. The weights may be thought of as representing an internal process, either one that the observer may control, for example, by directed attention, or one that may be out of the observer’s control, for example, differences in neural firing rates associated with cues in the positive or negative slopes. Let ITD+ and ITD− represent the interaural delays in the positive and negative slopes, respectively. It is assumed that a decision statistic, D, is formed from the weighted sum of ITD+ and ITD-, corrupted by normally distributed additive internal noise ε∼normal(0,σε2). The decision variable is then compared with criterion C to arrive at a decision:

D=NRiffw+(ITD+)+w−(ITD−)+ε>C;NLotherwise [3]

Decision weights are derived from point-biserial correlation of the observer’s binary response vector with vectors containing trial-by-trial ITD values. Within a trial, all ITD+ were equal for all modulation cycles, and all ITD− were equal, but ITD+ and ITD− were selected independently from the distribution chosen on that trial (NL or NR).

Note that weights were calculated based on ITD values, that is, a “correct” response was that which was consistent with ITDs. If the observer was instead relying on the ILD cue in making decisions, then a large ILD cue in the negative slope would result in the subject consistently picking the “wrong” side relative to the ITD cue, and hence the estimated weights for the ITD cue would be negative. Furthermore, if the observer’s response vector was correlated with the ILD cue in the negative slope (bottom panel), but the observer was responding based on ITDs, then the estimated weight would be negative since ITDs and ILDs are themselves negatively correlated with each other.

3.2. Results

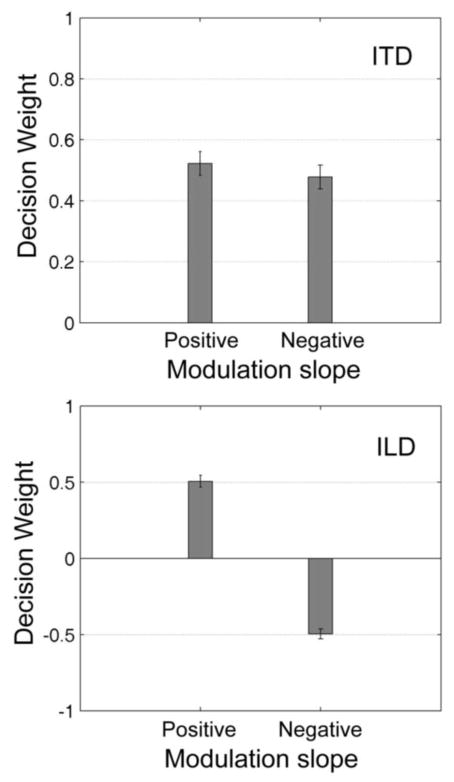
Results averaged across the three observers are shown in Fig. 5. The top panel shows estimated decision weights associated with ITDs in the positive and negative modulation slopes. Weights for the positive and negative slopes are nearly the same (t(2)= 0.56), suggesting that ITDs carried by these slopes are equally effective in influencing lateralization judgments. The bottom panel shows decision weights associated with ILDs in the positive and negative modulation slopes. The ILD cue in the negative slope is itself negatively correlated with the ITD cue, and as this latter weight was positive, the weight associated with the ILD in the negative modulation slope is negative. This suggests that the concomitant ILD cue, which is in conflict with the ITD cue, has little or no influence on lateralization, supporting the findings from experiment 1.

Figure 5.

Figure 5

Open in a new tab

Results from experiment 2 averaged across three observers. Top panel plots estimated decision weights associated with ITDs in the positive and negative modulation slopes (τ in Panel A of Fig. 1). Bottom panel shows decision weights associated with ILDs in the positive and negative modulation slopes (λ in Fig. 1). Error bars show +/− 1 standard deviation.

4. Experiment 3: Decision weights for positive and negative slopes in onset, ongoing, and offset modulation cycles

Experiment 3 investigated the effectiveness of ITD cues in early, middle, and late segments of a modified SAM waveform. A number of studies have demonstrated differential weighting of binaural cues in click trains, with a large number of studies showing that the onset click in a series has a dominant effect (Zurek, 1980; Divenyi, 1992; Saberi, 1996; Stecker and Hafter, 2002, 2009, Stecker and Brown, 2010). Other studies have shown recency effects in that late arriving spatial information carries more weight than information in the ongoing middle clicks (Stecker and Hafter, 2002, 2009). Here, we used the correlational method described earlier to measure decision weights for the early, middle, and late modulation cycles of a modified SAM waveform. Weights were estimated for the first 3 modulation periods, the middle 3 periods, and the last 3 periods of the waveform, as well as, independently, for the positive and negative slopes of each interaurally delayed cycle.

4.1. Methods

4.1.1. Stimuli and Procedure

The stimuli and apparatus were the same as for experiment 1, except for the following changes. The AM rate was set to 100 Hz to allow 30 full modulation periods in the 300 ms waveform duration. No rise-decay ramps were used at the onset or offset of waveforms. The first three, the middle three, and the last three cycles were dichotic, while the remaining cycles were diotic (ITD=0). As in experiment 2, on a given trial we first selected one of two normal distributions NR~(+μ, σ) or NL~(−μ, σ), and then picked ITDs independently for the positive and negative slopes of each of the 9 dichotic cycles, resulting in 18 independent ITDs per stimulus per trial. The value of σ was fixed at 100 μs. The mean of each distribution of ITDs, however, was determined individually for each subject to obtain approximately 75% accuracy in identifying the distribution from which ITDs were selected. The distributions for the three subjects had means of 80, 100, and 90 μs.6 The first five modulation cycles of a sample waveform are shown in the lower panel of Fig. 6, with the first 3 cycles dichotic and the last 2 diotic. Note that each positive and negative slope carried independently selected ITDs. The delays shown in this figure are larger than those used in the experiment to facilitate visual inspection (see caption). A similar procedure to that for experiment 2 was used to estimate decision weights, except that weights were calculated independently for each of 18 conditions (2 slopes × 3 cycles per group × 3 groups of cycles).7 All other procedures were the same as for experiment 2. The same three subjects participated in this experiment. Each subject completed 20 runs of 100 trials each.

4.2. Results

A 3×3×2 repeated measures ANOVA was conducted on the decision weights. The 3 factors were: 1) modulation cycle number within a 3-cycle group, 2) the temporal position of the groups (start, middle, and end), and 3) the sign of the modulation slope (positive or negative). Results of this analysis showed a significant effect of group position (F(2,4)=13.78, p<0.05), but no significant effect of cycle number within a group (F(2,4)=2.30), and consistent with results of experiments 1 and 2, no significant effect of modulation slope (F(1,2)=0.002). Of the interaction terms, the position-by-slope (F(2,4)=19.21, p<0.01), position by cycle number (F(4,8)=20.57, p<0.001), and the 3-way interaction term (F(4,8)=25.72, p<0.001) were significant. Because there was no significant effect of cycle position within a group of 3 cycles, we averaged the decision weights within each group of 3 cycles for subsequent analysis. However, to allow direct comparison with the results of experiments 1 and 2, the estimated weights for positive and negative slopes were not averaged, even though this difference was not statistically significant. Figure 7 shows estimated decision weights averaged across the three subjects for the first 3 modulation cycles, middle 3 cycles, and the last 3 cycles, and for both for the positive and negative modulation slopes. Error bars show +/−1 standard deviation. Note that the sum of the weights across conditions equals to one. The significant interaction effect between modulation slope and temporal position is clearly evident in this figure. Collapsing across modulation slopes, posthoc t-test comparisons showed a significant difference between weights at the beginning of the waveform and the middle (t(5)=2.76, p<0.05), and between the beginning and end (t(5)=2.67, p<0.05), but no significant difference between the middle and end of the waveform (t(5)=0.349) suggesting a significant onset dominance and an absence of recency effects.

Figure 7.

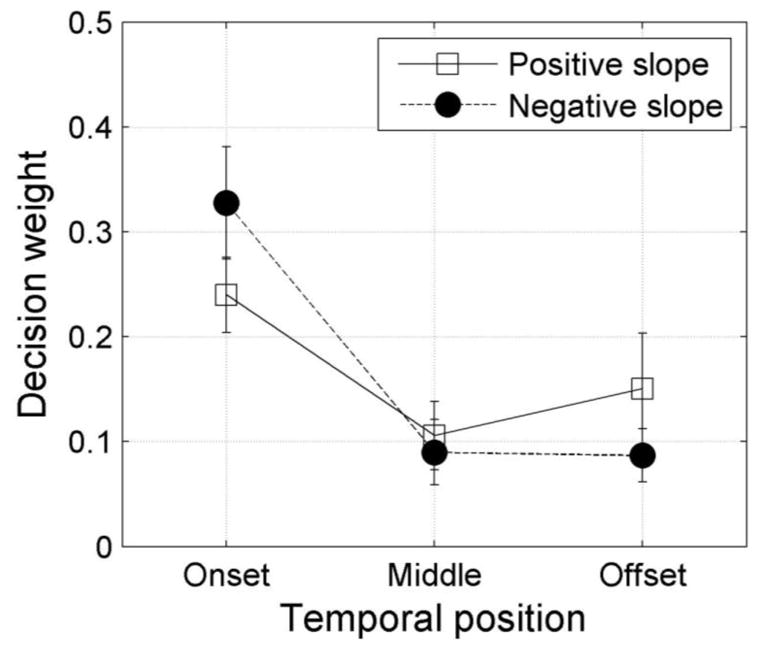
Figure 7

Open in a new tab

Results from experiment 3 averaged across three observers. Decision weights are shown for ITDs in the first 3 modulation cycles (onset), the 3 modulation cycles in the center of the waveform, and the final 3 modulation cycles (offset). The parameter is modulation slope (positive or negative). The stimulus had a modulation rate of 100 Hz and a duration of 300 ms, resulting in 30 full cycles, 21 of which were diotic. Error bars show +/−1 standard deviation. Note that the sum of the weights across conditions is equal to one.

5. Discussion

The motivation for the current study was, first, to determine the relative influence of ITDs and ILDs carried in the positive and negative envelope slopes of interaurally delayed high-frequency AM tones, and second, to determine if interaural cues are differentially weighted throughout the waveform’s duration as has been reported for other complex sounds (Zurek, 1980; Stecker and Hafter, 2002, 2009). Findings from the first two experiments showed that ITD thresholds measured separately for positive and negative modulation slopes were nearly identical, and that decision weights given to simultaneous ITDs in positive and negative slopes are equal and positively weighted. These results were somewhat unexpected given neurophysiological findings that rising envelope slopes often induce a larger neural spike count than negative slopes (Pressnitzer et al., 2000; Neuert et al., 2001; Lu et al., 2001). That the sign of the decision weights for the negative slopes was positive suggests that the influence of concomitant ILD cues, which are in conflict with ITDs in the negative modulation slopes, is negligible. Findings from the first two experiments clearly support reformulations of the duplex theory (Henning, 1974; McFadden and Pasanen, 1975; Nuetzel and Hafter, 1976; Saberi and Hafter, 1995; Saberi, 1998) and discount potential influences of ILD cues in lateralization of interaurally delayed high-frequency SAM tones.

It may be argued that the ability to lateralize a very brief interaurally delayed transient (click) whose left/right-channel waveforms do not overlap in time, and hence carry no ILD, demonstrates a priori that ITDs can be exclusively used to lateralize high-frequency waveforms. However, several studies (e.g., Yost et al., 1971; Yost, 1976) have shown that when one carefully eliminates all low-frequency cues, lateralization of interaurally delayed highpass transients becomes extremely difficult. In addition, the response to temporally non-overlapping transients in the left/right channels, after passing through the headphone transfer function and the middle/inner ear and auditory nerve transfer functions, is substantially extended in time (De Boer and de Jongh, 1978; Recio et al., 1998; Lin and Guinan, 2004; Temchin et al., 2005), generating overlapping representations and thus a potential ILD cue in the internal representation of the signal’s envelope.

Findings from experiment 3 showed that ITD information near the onset of the SAM waveform carries more weight than that in the middle or offset of the waveform. Previous reports using highpass pulse trains have shown that onset dominance peaks at interpulse intervals of 1 to 2 ms, and is nearly non-existent at 10 ms (Hafter and Dye, 1983; Saberi, 1996; Stecker and Hafter, 2002). That we observed larger weights for the beginning of the SAM waveform was somewhat surprising given that the modulation period used in experiment 3 was 10 ms. Furthermore, the weights given individually to the first 3 cycles at the onset were not significantly different from each other. This and other documented differences across studies caution against assuming that onset dominance is a static neural inhibitory phenomenon related to echo suppression. Rather, it should be considered as a complex context-dependent process that is affected by the nature of the stimulus (Saberi, 1995; Freyman et al., 1997, 2010), the nature of the environment (Ashmead and Wall, 1999; Keen and Freyman, 2009), and higher-level processes (Clifton 1987), with a time-constant that appears to depend significantly on the type of stimulus used. Onset dominance, for example, has been shown to last for 30 to 50 ms for complex sounds such as speech and music (Wallach et al., 1949) or noise (Zurek, 1980) and may last for over 100 ms when using two-pulse trains (see Fig. 7 of Saberi and Hafter, 1997). Several studies in addition have shown either an absence or significant reduction of onset dominance for some cue types (e.g., ILDs, Stecker and Brown, 2010), or for individual subjects (Champoux et al., 2009), in infants (Clifton et al., 1981), after extensive experience (Saberi and Perrott, 1990, Saberi and Antonio, 2003), or from top-down influences (e.g., the Clifton effect; Clifton, 1987; Grantham, 1996; Clifton et al., 2002; Keen and Freyman, 2009).

Experiment 3 also showed an absence of recency effects (or upweighting), which refers to an increase in the weight given by listeners to late-arriving information in a sequence of events. Recency effects have been reported for lateralization of noise bursts (Zurek, 1980) and for free-field localization of high-frequency click trains (Stecker and Hafter, 2002). Zurek (1980) has suggested that recency effects may reflect recovery of binaural processing from temporary effects of onset dominance. Stecker and Hafter (2009) tested this hypothesis and found that it cannot satisfactorily account for recency effects. They suggested that the reason why some studies show recency effects and others do not (Hafter and Dye, 1983; Saberi, 1996) may potentially be traced to stimulus- or task-dependant differences across studies; these include use of different stimulus cues (ILD, ITD, or spectral-shape cues) and memory demands on subjects (Stecker and Hafter, 2009). As Stecker and Hafter point out, no single explanation appears to be able to fully account for the different findings on recency effects across all studies.

In summary, we found that interaural delays carried by the rising (positive) and decaying (negative) slopes of high-frequency modified SAM waveforms are equally weighted in influencing lateralization judgments, and that the concomitant ILD cue in the negative slope is negatively correlated with the observer’s response vector. This suggests that lateralization of interaurally delayed SAM waveforms is either not influenced by the presence of concomitant ILD cues in the negative slope or dominated by envelope ITDs, consistent with reformulations of the duplex theory (Neutzel and Hafter, 1976; Hafter, 1984). Furthermore, we found that ITDs in the first few modulation cycles of a waveform are more heavily weighted than ITDs in the remaining cycles, with no recency effects at the offset. This asymmetric weighting may be related to findings from neurophysiological studies that have shown phasic neural response patterns to SAM sounds in a large proportion of neurons (Rees and Moller, 1983). Even cells which display a sustained binaural response to SAM sounds show an initial adaptation period (Yin and Chan, 1990). Such neural response patterns may either underlie decision weights favoring onsets of SAM waveforms, or may themselves originate from lower-level processes that cause onset dominance. In either case, these patterns have previously only been considered in categorization of neurons as phasic or sustained and not for their potential role in temporal weighting of envelope information. A careful consideration of this potential link in future studies of modulation coding would be merited.

Acknowledgments

We thank Virginia M. Richards and Bruce G. Berg for helpful discussions. We also thank Brian C. J. Moore and an anonymous reviewer for their insightful comments on an earlier draft of the manuscript. Work supported by grants from the National Science Council, Taiwan NSC 98-2410-H-008-081-MY3 and NIH R01DC009659.

Footnotes

1

For a modulation frequency of 150 Hz the instantaneous ILD associated with an ITD of 750 μs, which is approximately the largest naturally occurring ITD (Fedderson et al., 1957), is 4.4 dB at the point where the envelope amplitude is 50% down from its peak (1.7 dB for an ITD of 250 μs).

2

It is a priori unknown whether the binaural system can integrate short-term interaural cues across segments of individual modulation cycles, particularly when these cues are in conflict with each other (McFadden and Pasanen, 1975; Bernstein and Trahiotis, 1996; Sek et al., 2010). The current experiments were partly designed to address this issue.

3

The phase spectrum behaves erratically when frequency-component levels are near the system noise floor, and hence phase angles were derived from the Fourier spectra at the carrier and sideband frequencies, which are well defined in the amplitude spectrum (eq. 2). Note that given φm =π the sideband are in-phase relative to each other and equivalently π out of phase with the carrier (−π=π in polar coordinate)

4

The image-centering procedure was employed because the levels of high-frequency stimuli in the ear canal are easily affected by minor asymmetries in positioning of headphones, resulting in a potential ILD offset. In addition, experiments 2 and 3 required that subjects identify the side of the interaural axis to which they heard the image in a single-interval design, and we wanted to ensure that a diotic referent would be perceived at the center of the interaural axis.

5

See panels A and B from Fig. 6.

6

A similar procedure was used to obtain distribution parameters independently for each subject in experiment 2. However, in that experiment all subjects performed at about 75% correct when the ITDs were sampled from a normal distribution with μ=100 μs and σ = 60 μs. These parameters were estimated from 300 to 400 trials per subject.

7
In experiment 3, all ITDi+ and ITDi− values were selected independently across modulation cycles and slopes, hence:
D=NRiff∑Alliwi+(ITDi+)+wi−(ITDi−)+εi>C;NLotherwise [4]
where, wi+ and wi− are the decision weights given to the positive and negative slopes of each modulation cycle i, ITDi+ and ITDi− represent the interaural delays of the ith modulation cycle in the positive and negative slopes respectively, and the decision statistic, D, is formed from the weighted sum of ITDi+ and ITDi− corrupted by additive internal noise εi∼normal(0,σε2).

Publisher's Disclaimer: This is a PDF file of an unedited manuscript that has been accepted for publication. As a service to our customers we are providing this early version of the manuscript. The manuscript will undergo copyediting, typesetting, and review of the resulting proof before it is published in its final citable form. Please note that during the production process errors may be discovered which could affect the content, and all legal disclaimers that apply to the journal pertain.

Contributor Information

I-Hui Hsieh, Institute of Cognitive Neuroscience, National Central University, Jhongli City, Taiwan.

Agavni Petrosyan, Neuropsychophysiology Lab - CIpsi, School of Psychology, University of Minho, Braga, Portugal.

Óscar F. Gonçalves, Neuropsychophysiology Lab - CIpsi, School of Psychology, University of Minho, Braga, Portugal

Gregory Hickok, Department of Cognitive Sciences, University of California, Irvine, CA, 92697-5100 USA.

Kourosh Saberi, Department of Cognitive Sciences, University of California, Irvine, CA, 92697-5100 USA.

References

  1. Ashmead DH, Wall RS. Auditory perception of walls via spectral variations in the ambient sound field. J Rehab Res Dev. 1999;36:313–322. [PubMed] [Google Scholar]
  2. Berg BG. Analysis of weights in multiple observation tasks. J Acoust Soc Am. 1989;86:1743–1746. doi: 10.1121/1.399962. [DOI] [PubMed] [Google Scholar]
  3. Brown AD, Stecker GC. Temporal weighting of interaural time and level differences in high-rate click trains. J Acoust Soc Am. 2010;128:332–341. doi: 10.1121/1.3436540. [DOI] [PMC free article] [PubMed] [Google Scholar]
  4. Brungart DS, Simpson BD, Freyman RL. Precedence-based speech segregation in a virtual auditory environment. J Acoust Soc Am. 2005;118:3241–3251. doi: 10.1121/1.2082557. [DOI] [PubMed] [Google Scholar]
  5. Champoux F, Houde MS, Gagne JP, Kelly JB. Uniform degradation of auditory acuity in subjects with normal hearing leads to unequal precedence effects. Ear Hear. 2009;30:377–379. doi: 10.1097/AUD.0b013e31819c3e84. [DOI] [PubMed] [Google Scholar]
  6. Clifton RK, Morrongiello BA, Kulig JW, Dowd JM. Newborns’ Orientation toward Sound: Possible Implications for Cortical Development. Child Develop. 1981;52:833–838. [PubMed] [Google Scholar]
  7. Clifton R. Breakdown of echo suppression in the precedence effect. J Acoust Soc Am. 1987;82:1834–1835. doi: 10.1121/1.395802. [DOI] [PubMed] [Google Scholar]
  8. Clifton RK, Freyman RL, Meo J. What the precedence effect tells us about room acoustics. Percept Psychophys. 2002;64:180–188. doi: 10.3758/bf03195784. [DOI] [PubMed] [Google Scholar]
  9. Crow G, Langford TL, Moushegian G. Coding of interaural time differences by some high-frequency neurons of the inferior colliculus: responses to noise bands and two-tone complexes. Hearing Res. 1980;3:147–153. [Google Scholar]
  10. De Boer E, de Jongh HR. On cochlear encoding: potentialities and limitations of the reverse-correlation technique. J Acoust Soc Am. 1978;63:115–135. doi: 10.1121/1.381704. [DOI] [PubMed] [Google Scholar]
  11. Divenyi PL. Binaural suppression of nonechoes. J Acoust Soc Am. 1992;91:1078–1084. doi: 10.1121/1.402634. [DOI] [PubMed] [Google Scholar]
  12. Domnitz RH. A headphone monitoring system for binaural experiments below 1 kHz. J Acoust Soc Am. 1973;58:510–511. doi: 10.1121/1.380665. [DOI] [PubMed] [Google Scholar]
  13. Dreyer A, Delgutte B. Phase locking of auditory-nerve fibers to the envelopes of high-frequency sounds: Implications for sound localization. J Neurophysiol. 2006;96:2327–2341. doi: 10.1152/jn.00326.2006. [DOI] [PMC free article] [PubMed] [Google Scholar]
  14. Feddersen WE, Sandel TT, Teas DC, Jefftess LA. Localization of high-frequency tones. J Acoust Soc Am. 1957;29:988–991. [Google Scholar]
  15. Freyman RL, Zurek PM, Balakrishnan U, Chiang YC. Onset dominance in lateralization. J Acoust Soc Am. 1997;101:1649–1656. doi: 10.1121/1.418149. [DOI] [PubMed] [Google Scholar]
  16. Freyman RL, Balakrishnan U, Zurek PM. Lateralization of noise-burst trains based on onset and ongoing interaural delays. J Acoust Soc Am. 2010;128:320–331. doi: 10.1121/1.3436560. [DOI] [PMC free article] [PubMed] [Google Scholar]
  17. Grantham DW. Left-right asymmetry in the buildup of echo suppression in normal-hearing adults. J Acoust Soc Am. 1996;99:1118–1123. doi: 10.1121/1.414596. [DOI] [PubMed] [Google Scholar]
  18. Hafter ER. Spatial hearing and the duplex theory: how viable is the model? In: Edelman GM, Gall WE, Cowan WM, editors. Dynamic Aspect of Neocortical Function. Wiley; New York: 1984. pp. 425–448. [Google Scholar]
  19. Hafter ER, Dye RH. Detection of interaural differences of time in trains of high-frequency clicks as a function of interclick interval and number. J Acoust Soc Am. 1983;73:644–651. doi: 10.1121/1.388956. [DOI] [PubMed] [Google Scholar]
  20. Henning GB. Detectability of interaural delay in high-frequency complex waveforms. J Acoust Soc Am. 1974;55:84–90. doi: 10.1121/1.1928135. [DOI] [PubMed] [Google Scholar]
  21. Holdsworth J, Nimmo-Smith I, Patterson R, Rice P. Annex C of the SVOS final report (Part A: The auditory filter bank), Medical Research Council, APU (Applied Psychology Unit) Report 2341. Cambridge; UK: 1988. Implementing a Gammatone filter bank. [Google Scholar]
  22. Hsieh I, Petrosyan A, Goncalves O, Hickok G, Saberi K. Cross-modulation interference with lateralization of mixed-modulated waveforms. J Speech Lang Hearing Res. 2010 doi: 10.1044/1092-4388(2010/09-0206). (in press) [DOI] [PubMed] [Google Scholar]
  23. Keen R, Freyman RL. Release and re-buildup of listeners’ models of auditory space. J Acoust Soc Am. 2009;125:3243–3252. doi: 10.1121/1.3097472. [DOI] [PMC free article] [PubMed] [Google Scholar]
  24. Levitt HL. Transformed up-down methods in psychophysics. J Acoust Soc Am. 1971;49:467–477. [PubMed] [Google Scholar]
  25. Lin T, Guinan JJ., Jr Time-frequency analysis of auditory-nerve-fiber and basilar-membrane click responses reveal glide irregularities and non-characteristic-frequency skirts. J Acoust Soc Am. 2004;116:405–416. doi: 10.1121/1.1753294. [DOI] [PubMed] [Google Scholar]
  26. Lu T, Liang L, Wang XQ. Neural representations of temporally asymmetric stimuli in the auditory cortex of awake primates. J Neurophys. 2001;85:2364–2380. doi: 10.1152/jn.2001.85.6.2364. [DOI] [PubMed] [Google Scholar]
  27. McFadden D, Pasanen EG. Binaural beats at high frequencies. Science. 1975;190:394–396. doi: 10.1126/science.1179219. [DOI] [PubMed] [Google Scholar]
  28. Meddis R, Hewitt MJ, Shackleton TM. Implementation details of a computation model of the inner hair-cell/auditory-nerve synapse. J Acoust Soc Am. 1990;87:1813–1816. [Google Scholar]
  29. Neuert V, Pressnitzer D, Patterson RD, Winter IM. The responses of single units in the inferior colliculus of the guinea pig to damped and ramped sinusoids. Hearing Res. 2001;159:36–52. doi: 10.1016/s0378-5955(01)00318-5. [DOI] [PubMed] [Google Scholar]
  30. Nuetzel JM, Hafter ER. Lateralization of complex waveforms: Effects of fine structure, amplitude and duration. J Acoust Soc Am. 1976;60:1339–1346. doi: 10.1121/1.381227. [DOI] [PubMed] [Google Scholar]
  31. Nuetzel JM, Hafter ER. Lateralization of complex waveforms: Spectral effects. J Acoust Soc Am. 1981;69:1112–1118. doi: 10.1121/1.381227. [DOI] [PubMed] [Google Scholar]
  32. Pressnitzer D, Winter IM, Patterson RD. The responses of single units in the ventral cochlear nucleus of the guinea pig to damped and ramped sinusoids. Hearing Res. 2000;149:155–166. doi: 10.1016/s0378-5955(00)00175-1. [DOI] [PubMed] [Google Scholar]
  33. Rayleigh Lord, Strutt JW. On our perception of sound direction. Philosoph Mag (Ser 6) 1907;13:214–232. [Google Scholar]
  34. Recio A, Rich NC, Narayan SS, Ruggero MA. Basilar-membrane responses to clicks at the base of the chinchilla cochlea. J Acoust Soc Am. 1998;103:1972–1989. doi: 10.1121/1.421377. [DOI] [PMC free article] [PubMed] [Google Scholar]
  35. Rees A, Møller AR. Responses of neurons in the inferior colliculus of the rat to AM and FM tones. Hearing Res. 1983;10:301–330. doi: 10.1016/0378-5955(83)90095-3. [DOI] [PubMed] [Google Scholar]
  36. Richards VM, Zhu S. Relative estimates of combination weights, decision criteria, and internal noise based on correlation coefficients. J Acoust Soc Am. 1994;95:423–434. doi: 10.1121/1.408336. [DOI] [PubMed] [Google Scholar]
  37. Saberi K. Some considerations on the use of adaptive methods for measuring interaural-delay thresholds. J Acoust Soc Am. 1995;98:1803–1806. doi: 10.1121/1.413379. [DOI] [PubMed] [Google Scholar]
  38. Saberi K. Observer weighting of interaural delays in filtered impulses. Percept Psychophys. 1996;58:1037–1046. doi: 10.3758/bf03206831. [DOI] [PubMed] [Google Scholar]
  39. Saberi K. Modeling interaural delay sensitivity to frequency modulation at high frequencies. J Acoust Soc Am. 1998;103:2551–2564. doi: 10.1121/1.422776. [DOI] [PubMed] [Google Scholar]
  40. Saberi K, Perrott DR. Minimum audible movement angles as a function of sound-source trajectory. J Acoust Soc Am. 1990;88:2639–2644. doi: 10.1121/1.399984. [DOI] [PubMed] [Google Scholar]
  41. Saberi K, Hafter ER. A common neural code for frequency and amplitude-modulated sounds. Nature. 1995;374:537–539. doi: 10.1038/374537a0. [DOI] [PubMed] [Google Scholar]
  42. Saberi K, Perrott DR. Lateralization of click-trains with opposing onset and ongoing interaural delays. Acustica. 1995;81:272–275. [Google Scholar]
  43. Saberi K, Hafter ER. Experiments on auditory motion discrimination. In: Gilkey RH, Anderson TR, editors. Binaural and Spatial Hearing in Real and Virtual Environments. Erlbaum; New Jersey: 1997. pp. 315–327. [Google Scholar]
  44. Saberi K, Antonio JV. Precedence-effect thresholds for a population of untrained listeners as a function of stimulus intensity and interclick interval. J Acoust Soc Am. 2003;114:420–429. doi: 10.1121/1.1578079. [DOI] [PubMed] [Google Scholar]
  45. Sek A, Glasberg BR, Moore BCJ. The origin of binaural interaction in the modulation domain. J Acoust Soc Am. 2010;127:2451–2460. doi: 10.1121/1.3327798. [DOI] [PubMed] [Google Scholar]
  46. Slaney M. Technical Report #1998-010. Interval Research Corporation; Palo Alto, California: 1998. Auditory toolbox: A Matlab toolbox for auditory modeling work. [Google Scholar]
  47. Stecker GC, Hafter ER. Temporal weighting in sound localization. J Acoust Soc Am. 2002;112:1046–1057. doi: 10.1121/1.1497366. [DOI] [PMC free article] [PubMed] [Google Scholar]
  48. Stecker GC, Hafter ER. A recency effect in sound localization? J Acoust Soc Am. 2009;125:3914–3924. doi: 10.1121/1.3124776. [DOI] [PMC free article] [PubMed] [Google Scholar]
  49. Stecker GC, Brown AD. Temporal weighting of binaural cues revealed by detection of dynamic interaural differences in high-rate Gabor click trains. J Acoust Soc Am. 2010;127:3092–3103. doi: 10.1121/1.3377088. [DOI] [PMC free article] [PubMed] [Google Scholar]
  50. Temchin AN, Recio-Spinoso A, van Dijk P, Ruggero MA. Wiener kernels of chinchilla auditory-nerve fibers: verification using responses to tones, clicks, and noise and comparison with basilar-membrane vibrations. J Neurophys. 2005;93:3635–3648. doi: 10.1152/jn.00885.2004. [DOI] [PMC free article] [PubMed] [Google Scholar]
  51. Tobias JV, Schubert ED. Effective onset duration of auditory stimuli. J Acoust Soc Am. 1959;31:1595–1605. [Google Scholar]
  52. Wallach H, Newman EB, Rosenzweig MR. The precedence effect in sound localization. J Acoust Soc Am. 1949;62:315–336. [PubMed] [Google Scholar]
  53. Yin TCT, Chan JCK. Interaural time sensitivity in medial superior olive of cat. J Neurophys. 1990;64:465–488. doi: 10.1152/jn.1990.64.2.465. [DOI] [PubMed] [Google Scholar]
  54. Yost WA, Wightman FL, Green DM. Lateralization of filtered clicks. J Acoust Soc Am. 1971;50:1526–1531. doi: 10.1121/1.1912806. [DOI] [PubMed] [Google Scholar]
  55. Yost WA. Lateralization of repeated filtered transients. J Acoust Soc Am. 1976;60:178–181. doi: 10.1121/1.381061. [DOI] [PubMed] [Google Scholar]
  56. Zurek PM. The precedence effect and its possible role in the avoidance of inter-aural ambiguities. J Acoust Soc Am. 1980;67:952–964. doi: 10.1121/1.383974. [DOI] [PubMed] [Google Scholar]
  57. Zurek P, Saberi K. Lateralization of two-transient stimuli. Percept Psychophys. 2003;65:95–106. doi: 10.3758/bf03194786. [DOI] [PubMed] [Google Scholar]

RESOURCES