Abstract
Spectral computed tomography (CT) produces an energy-discriminative attenuation map of an object, extending a conventional image volume with a spectral dimension. In spectral CT, an image can be sparsely represented in each of multiple energy channels, and are highly correlated among energy channels. According to this characteristics, we propose a tensor-based dictionary learning method for spectral CT reconstruction. In our method, tensor patches are extracted from an image tensor, which is reconstructed using the filtered backprojection (FBP), to form a training dataset. With the Candecomp/Parafac decomposition, a tensor-based dictionary is trained, in which each atom is a rank-one tensor. Then, the trained dictionary is used to sparsely represent image tensor patches during an iterative reconstruction process, and the alternating minimization scheme is adapted for optimization. The effectiveness of our proposed method is validated with both numerically simulated and real preclinical mouse datasets. The results demonstrate that the proposed tensor-based method generally produces superior image quality, and leads to more accurate material decomposition than the currently popular popular methods.
Index Terms: Dictionary learning, tensor decomposition, spectral CT, iterative reconstruction, material decomposition
I. Introduction
Recently, spectral CT (multi-energy CT) has attracted an increasing attention. This imaging mode discriminates photon energies in the data acquisition process, and provides multiple projection datasets of an object in different energy bins, which can be achieved using different techniques such as a photon counting detector (PCD) [1], a sandwich (multi-layer) detector [2], a kV switching [3], [4], a multiple x-ray source [5], etc. The multichannel datasets can be utilized to generate material basis images for material decomposition [6], [7]. Such a material decomposition capability has great potential for functional and molecular imaging aided by contrast agents or probes [8]. In a photon counting detector, the number of photons can be counted in each energy channel or above a given threshold. As a result, different photon energies can be distinguished to generate multiple projection datasets simultaneously. Because the electronic noise is eliminated, PCD provides a higher signal-to-noise ratio (SNR) than the conventional CT detector [9]. However, multichannel projections obtained from a PCD usually contain very strong Poisson noise for two main reasons. First, a single energy channel only contains a fraction of the total photons. Second, most PCDs can only tolerate a limited counting rate [1]. Thus, the data noise could significantly reduce the SNR of the decomposed material image, which would compromise the clinical value of spectral CT [10]. Therefore, the development of dedicated spectral CT algorithms for low-dose reconstruction is of great importance to improve material decomposition for clinical applications.
Over recent years, the sparsity-exploiting methods (e.g., total variation (TV) [11]–[14], tight frame (TF) [15], wavelet [16], and dictionary learning [17]) have been applied to low-dose CT reconstruction with various degrees of success. A simple and direct way to apply sparsity exploiting methods to spectral CT is to use conventional low-dose CT methods in each energy channel independently. In 2012, Xu et al. [18] considered multichannel data as a group of conventional CT datasets, and iteratively reconstructed each channel image independently with TV regularization. In the same year, Xu et al. [17] proposed a dictionary learning based method for conventional low-dose CT reconstruction and demonstrated a performance superior to the TV based method. Then, the dictionary learning method was applied to spectral CT reconstruction [19]–[21]. In 2013, Zhao et al. [22] developed a tight-frame based iterative reconstruction method for spectral breast CT. All the aforementioned spectral CT reconstruction methods only use the sparsity in the spatial domain. On the other hand, since the projection datasets in different channels are collected from the same object, the resultant images are highly correlated. The utilization of both the sparsity and correlation in images can significantly improve the spectral CT reconstruction performance. The low rank prior information is one of the major constraints to encourage the synergy among channels, and the nuclear norm of an image matrix or image gradient matrix can be included in the objective function to address this consideration. In 2011, Gao et al. [23] proposed a general framework for spectral CT reconstruction, named as PRISM (prior rank, intensity, and sparsity model) algorithm. PRISM is based on the robust principle component analysis (RPCA) [24], which employs both low rank and spatial sparsity. Chu et al. [25], [26] combined TV and low rank regularizations and demonstrated better spectral CT results than that from the sparsity-only reconstruction. Also, Rigie and Rivière developed a vectorial total variation (VTV) based spectral CT reconstruction method, which incorporates the nuclear norm to encourage the rank-sparsity of a multichannel gradient vector field [27]. In 2015, Kim et al. [28] used a spectral patch-based low rank penalty to solve the noisy and few view problem for kVp switching-based spectral CT.
As a mathematical tool to describe a multidimensional array [29], a tensor provides another way to handle correlation among energy channels for spectral CT. For example, Semerci et al. treated x-ray attenuation coefficients in different energy channels as a tensor and used a tensor nuclear norm regularization for spectral CT reconstruction [30]. In 2014, the PRISM method was extended from a vector formulation to a tensor counterpart [31], [32]. There are two widely used tensor decompositions [29]: Tucker decomposition and Candecomp/Parafac decomposition (abbreviated CP decomposition or CPD). These two decompositions can be viewed as generalizations of singular value decomposition (SVD) [33]. With a tensor decomposition method, the conventional dictionary learning (denoted as vectorized dictionary learning, abbreviated as VDL) can be extended into tensor-based dictionary learning (TDL) [34]–[36], which ought to be more powerful in capturing structures and more sparsely representing a multidimensional array. In 2015, we proposed an adaptive tensor-based spatio-temporal dictionary learning method for 4D CT reconstruction [37]. The preliminary experiments including a sheep lung perfusion study and a dynamic mouse cardiac study demonstrated that our proposed algorithm had a better performance than the VDL based method in the case of few-view reconstruction. Very recently, we reported a tensor-based spectral CT reconstruction method via spatio-spectral dictionary learning [38].
In this paper, we propose a spectral CT reconstruction method based on the following consideration. Generally speaking, an animal or patient spectral CT image consists of no more than three basis materials (this number can increase when multiple contrast agents are injected), and a small image patch usually contains only one or two basis materials, which mean low rank in the spectral dimension [28]. Therefore, a spectral image patch can be represented sparsely with a well-trained spatio-spectral dictionary. Because TDL accommodates sparsity in both spatial and spectral dimensions, the sparsity and correlation properties can be fully integrated into a tensor-based image reconstruction framework. Consequently, the noise and artifacts in reconstructed images can be effectively suppressed to depict fine tissue features well, which leads to more accurate material decomposition results. Along this direction, the current paper reports a major improvement and extension of our previous conference paper [38].
The rest of this paper is organized as follows. Section II reviews tensor decomposition. Section III summarizes tensor-based dictionary learning. Section IV develops the tensor dictionary learning based spectral CT reconstruction method. Section V describes numerically simulated and real preclinical experiments and key results. Finally, Section VI discusses related issues and concludes the paper.
II. Preliminaries on Tensor
A. Basic Notations of Tensor
Tensor is a multidimensional array. An nth-order tensor is denoted as 𝒳 ∈ ℝI1×I2×…×In, whose (i1, i2, ⋯, in) element is xi1i2⋯in, 1 ≤ ik ≤ Ik, k = 1, 2, ⋯, n. Specifically, for n = 1 and n = 2, tensors are vectors and matrices respectively. Without loss of generality, we consider a 3rd-order tensor 𝒳 ∈ ℝI1×I2×I3 in the rest of this paper.
A 3rd-order is called a rank-one tensor if it can be written as the outer product of three vectors,
| (1) |
where the symbol “∘” denotes the vector outer product, and a ∈ ℝI1, b ∈ ℝI2 and c ∈ ℝI3. The (i1, i2, i3) element of the tensor is the product of the corresponding vector elements
| (2) |
A tensor can be transformed into a matrix using an unfolding operator, which is an element reordering process. The mode-k (k = 1, 2, 3) unfolding of 𝒳 is denoted by X(k),
| (3) |
i.e. X(1) ∈ ℝI1×I2I3, X(2) ∈ ℝI2×I1I3, X(3) ∈ ℝI3×I1I2. A tensor can be multiplied by a matrix or vector. The k-mode (k = 1, 2, 3) matrix product of a 3rd-order tensor by a matrix U ∈ ℝJ×Ik is denoted by 𝒳 𝗑k U ∈ ℝI1×⋯×Ik−1×J×Ik+1×⋯×In, n = 3, which is still a 3rd-order tensor, whose elements are
| (4) |
For example, if k = 2, then . The k-mode (k = 1, 2, ⋯, n) product of a nth-order tensor by a vector v ∈ ℝIk is denoted by 𝒳 𝗑̄k v ∈ ℝI1×⋯×Ik−1×Ik+1×⋯×In which is a matrix, and its elements are
| (5) |
Here we propose a new tensor operation, which is denoted as
| (6) |
where k = 1, 2, ⋯, n, w ∈ ℝIk, and 𝒴 has the same size as that of 𝒳. ℋk (𝒳, w) is defined as follows:
| (7) |
ℋk (𝒳, w) is a tensor weighting operator, which weights the tensor 𝒳 by the weighting vector w in the kth mode. Likewise, we define the inverse operator of ℋk (𝒳, w), which is denoted as and computed as
| (8) |
Thus, we have
| (9) |
B. Tensor Decomposition
The Tucker and CP methods are important for tensor decompositions. The Tucker decomposition transforms a tensor 𝒳 ∈ ℝI1×I2×I3 into a core tensor 𝒢 ∈ ℝJ1×J2×J3 multiplied by a matrix in each mode:
| (10) |
where A1 ∈ ℝI1×J1, A2 ∈ ℝI2×J2 and A3 ∈ ℝI3×J3 are decomposed matrices in three modes respectively, gj1j2j3 is the (j1, j2, j3) element of the core tensor, a1j1, a2j2 and a3j3 are the corresponding normalized columns in the matrices A1, A2 and A3 respectively. The Tucker decomposition becomes CPD if the core tensor is diagonal. That is, a tensor can be decomposed into the sum of several rank-one tensors via the
| (11) |
where a1r ∈ ℝI1, a2r ∈ ℝI2 and a3r ∈ ℝI3 are normalized vectors, and λr is the weight. The tensor decomposition can be implemented using an alternating least squares (ALS) method [29].
III. Tensor-Based Dictionary Learning
Given a set of 3rd-order training tensors 𝒳(t) ∈ ℝN1×N2×N3, t = 1, 2, ⋯, T, the tensor-based dictionary learning can be formulated as the following optimization problem:
| (12) |
where 𝒟 = {𝒟(k)} ∈ ℝN1×N2×N3×K is a tensor dictionary, K is the number of atoms, αt is the coefficient vector, ‖·‖F is the Frobenius norm, ‖·‖0 means the ℓ0-norm (namely, the number of nonzero elements), and L represents the sparsity level. 𝒟(k) ∈ ℝN1×N2×N3 is the kth atom, which is a rank-one tensor. The atom can be rewritten as , where , i = 1, 2, 3, are normalized vectors.
In the conventional dictionary learning approach, extracted image patches are first transformed into vectors to form a training dataset, and then the K-SVD method is used to learn a vector-based dictionary [39]. Likewise, the K-CPD was developed to learn a tensor-based dictionary [34]. The objective function Eq. (12) can be optimized in an alternating way. The first step is to fix 𝒟 and update αt in the objective function Eq. (13), which can be solved using the multilinear orthogonal matching pursuit (MOMP) algorithm [34], and the MOMP method is presented as Algorithm 1.
| (13) |
The next step is to update the tensor dictionary by fixing the sparse coefficient matrix. Similarly, atoms are updated
Algorithm 1.
MOMP
|
Input: Sparsity level L and tolerance of representation error ε; Tensor signal 𝒳, tensor dictionary 𝒟 = {𝒟(k)}, k = 1, ⋯, K. | ||
| Output: Representation vector α. | ||
| 1: | Initialize the error and the counter: ℰ0 = 𝒳, c = 0; | |
| 2: | while c < L & ‖ℰc‖F ≥ ε do | |
| 3: | Project the error to each atom: ; |
|
| 4: | Update the accessorial dictionary by adding the atom corresponding to the maximal pk: , i = 1, ⋯, c + 1; |
|
| 5: | Update the sparse coefficient: ; |
|
| 6: | Update the error: ℰc+1 = 𝒳 − 𝒟asr 𝗑̄4 αc; | |
| 7: | Update the counter: c = c + 1; | |
| 8: | end while | |
| 9: | return α = αc | |
alternatingly. To update the kth atom 𝒟(k), we need to fix other atoms. Then, we find 𝒳(t), whose sparse representation coefficients on 𝒟(k) are nonzero, and group those 3rd-order tensors into a 4th-order tensor 𝒳nz. The sparse representation coefficient matrix of 𝒳nz is denoted as Λnz,k, whose elements in the kth row are written as αnz,k. Thus, the approximation error without the atom 𝒟(k) is
| (14) |
and 𝒟(k) can be obtained by solving the following objective function
| (15) |
where the superscript “⊤” denotes the transpose operator. Clearly, the above formulation gives a general optimization problem of CPD:
| (16) |
Therefore, the updated kth atom and the corresponding coefficients vector are
| (17) |
| (18) |
The tensor-based dictionary learning using K-CPD algorithm is summarized as Algorithm 2.
IV. Tensor-based Dictionary Learning for Spectral CT Reconstruction
A. Method
Similar to the conventional dictionary learning based CT reconstruction [17], the tensor dictionary based spectral CT reconstruction can be formulated as
| (19) |
Algorithm 2.
Tensor-based Dictionary Learning Using K-CPD
|
Input:
LD, K and other parameters; Training set of tensors 𝒳(t), t = 1, ⋯, T. | ||
| Output: Tensor dictionary 𝒟 ={𝒟(k)}, k = 1, ⋯, K. | ||
| 1: | Initialize dictionary and setting c = 1; | |
| 2: | Obtain the sparse representation matrix αc−1 of {𝒳(t)} using MOMP. |
|
| 3: | for k = 1 : K do | |
| 4: | Find 𝒳(t), whose sparse representation coefficients on 𝒟(k) are nonzero, and grouping them as a 4th-order tensor 𝒳nz; |
|
| 5: | Calculate the error tensor using Eq. (14); | |
| 6: | Decompose the error tensor using Eq. (16); | |
| 7: | Update the kth atom and the corresponding coefficients using Eqs. (17) and (18); |
|
| 8: | end for | |
| 9: | c = c + 1; | |
| 10: | Repeat steps 2–9 until the convergence criteria are met (e.g. c > LD); |
|
| 11: | return 𝒟 | |
where 𝒳 ∈ ℝI1×I2×S and 𝒴 ∈ ℝJ1×J2×S are the 3rd-order CT image tensor and projection tensor respectively, I1 and I2 are the image width and height respectively, J1 and J2 are the numbers of detector bins and projection views respectively, S is the total number of channels, X(3) and Y(3) are respectively the mode-3 unfoldings of 𝒳 and 𝒴, xs and ys are respectively the sth columns of and (the vectorized sth image and projection respectively), A is the system matrix which is determined using the ray driven method [40], 𝒟 = {𝒟(k)} ∈ ℝN×N×S×K is the learned tensor dictionary, K is the number of atoms, the operator ℰr extracts the rth spatio-spectral image patch (a 3rd-order tensor) from 𝒳 of N×N×S, and αr ∈ ℝK is the sparse representation vector of the rth extracted tensor patch. The parameter λ is used to balance the data fidelity and the sparse representation terms, and υr determines the trade-off between the representation precision and the sparsity level.
Because the attenuation coefficients depend on photon energies, they vary significantly among energy channels. Generally speaking, the norm of xs decreases with respect to the increment of the energy level. As a result, to minimize the error of dictionary sparse coding in the objective function Eq. (19), lower index channels corresponding to lower energy levels naturally have larger weights than higher index channels. It may induce overfitting in low energy channels and smoothness in high energy channels since the image norms are remarkably different among channels. To address this issue, we introduce a weighting vector w ∈ ℝS to modify each channel for comparable norms across energy channels:
| (20) |
The weighting vector can be computed from the obtained projection data in advance. Thus, the normalized projection data is
| (21) |
To prevent the aforementioned problem of TDL, instead of reconstructing the image tensor 𝒳 directly, the normalized image tensor is reconstructed from 𝒴̂. Furthermore, to represent signals sparsely we prefer that each atom has a zero mean in each channel. Hence, the channel means of patches were removed before dictionary learning and signal representation. Similar to VDL [17], the mean removal process is equivalent to introducing S channel-mean atoms: (k = 1, 2, ⋯, S), where , e0 is an all-one-value vector, the kth element of ek is one, and others are set to zero. Hence, the new TDL-based reconstruction method can be rewritten as
| (22) |
where x̂s and ŷs are respectively the sth energy channel vectorized 𝒳̂ and 𝒴̂, mr is the channel-mean vector for the rth patch, and 𝒟̂ is the tensor dictionary trained with the normalized image tensor in advance via the tensor-based dictionary learning. For a given spectral CT dataset, its FBP reconstruction results can be used for training of a global dictionary. Although the FBP images contain noise, it has been found in our studies that the tensor dictionary training is robust against noise. The tensor dictionary can be learned using the K-CPD algorithm, which is an extension of K-SVD in terms of the embedded low-rank constraint, and each atom (rank-one enforced by K-CPD) serves as a motif to preserve structural signature and suppress image noise. Consequently, K-CPD based dictionary learning is more robust than K-SVD and it outperforms the K-SVD based counterpart as described below. Multiple studies in other areas have also demonstrated that the tensor dictionary gives superior performance [35], [37]. At the beginning, an image in each energy channel is reconstructed from the normalized projection {ŷs} using the conventional FBP method. Then, overlapped small image tensors of size N × N × S pixels are extracted from the image tensor, where N=8 in this paper and S is the number of energy channels. Similar to conventional DL, here the mean value in each energy channel of the extracted small image tensor is removed. After that removal, the tensors with small variance are removed, and the rest of the patches are grouped into a training set. Finally, 𝒟̂ is learned using Eq. (12).
We apply an alternating minimization scheme to solve for 𝒳̂, mr and αr. Thus, Eq. (22) can be rewritten into the following three sub-problems:
| (23) |
| (24) |
| (25) |
where 𝒳̂n+1, and are the results from the (n + 1)th iteration. Eqs. (23)–(25) can be alternatingly solved. In this work, Eq. (23) is solved using the separable surrogate method [41]:
| (26) |
where the symbols [·]i1i2 and [·]i1i2s indicate the (i1, i2)th element of a matrix and the (i1, i2, s)th element of a tensor. The operator puts a tensor patch in ℝN×N×S into the original image tensor space ℝI1×I2×S. Hence, means that the difference between the rth extracted tensor patch and its sparse representation is put into the original image tensor space. In Eq. (26), the parameter λ balances between the fidelity and regularization terms. Since A varies for different scanning configurations, it is not easy to find the most suitable parameter λ. To deal with this problem, we rewrite λ into the following form
| (27) |
where η is a scale parameter, and the numerator and denominator of Eq. (27) are respectively the sums of the second order derivatives of the fidelity and regularization terms in Eq. (23). In Eq. (24), because atoms of 𝒟̂ have zero-means in individual energy channels, each element in mr is the mean of ℰr (𝒳̂n+1) in the corresponding channel. The update of αr according to Eq. (25) is basically equivalent to solving a constrained problem, for example, using a multilinear orthogonal matching pursuit (MOMP) algorithm. The sparse representation is controlled by the sparsity level L and the precision level ε, which replace the intermediate variable υr in Eq. (25). The sparse coding process will stop when either ‖αr‖0 ≥ L or . In this work, a simple stopping criterion is applied. The reconstruction process stops after a fixed number of iterations at which point the change in the image domain becomes rather small. Finally, the reconstructed image tensor is denormalized as
| (28) |
The overall flowchart of the proposed approach is summarized as Algorithm 3.
In the objective function Eq. (22), the sparsity term is defined in terms of the ℓ0-norm, which leads to a nonconvex problem. This issue can be addressed by relaxing the ℓ0-norm to the ℓ1-norm to reach a global minimizer [39]. While in the numerical implementation, we prefer a sparser regularizer, many experiments indicate that solving the ℓ0-norm problem with MOMP can usually give satisfactory results. Also, the proposed reconstruction process involves solving two
Algorithm 3.
Tensor-DL for Spectral CT Reconstruction
| Input: η, ε, L, K and other parameters; Initialization of 𝒳̂. | ||
| Output: Image tensor 𝒳. | ||
| Part I: Dictionary training | ||
| 1: | Normalize the projection datasets using Eq. (21); | |
| 2: | Reconstruct images from the normalized projection using FBP; |
|
| 3: | Extract tensor patches to form a training set; | |
| 4: | Train a tensor dictionary using the K-CPD. | |
| Part II: Image reconstruction | ||
| 5: | while the stopping criteria are not satisfied do | |
| 6: | Update 𝒳̂n+1 using Eq. (26); | |
| 7: | Update ; | |
| 8: | Update using MOMP; | |
| 9: | end while | |
| 10: | Denormalize the image tensor using Eq. (28). | |
| 11: | return 𝒳 | |
sub-problems. Although the solution to each sub-problem is approximate during iteration, the final result should converge after a sufficiently large number of iterations based on our empirical observation.
B. Numerical Implementation Details
The dictionary is typically over-complete to improve the sparsity of representation. Hence, the number of atoms in a dictionary should be much larger than that of pixels in an atom, i.e., K ≫ N × N × S. In the image processing field, K is usually four times the number of pixels in an atom for VDL [39]. However, due to high correlation among different channel images in the spectral CT, we found that it is not necessary to set K = 4 × N × N × S. We can achieve satisfactory results if we choose K > N × N × S. Therefore, K was uniformly set to 1024 in our experiments. The sparsity level LD in the dictionary training can be set empirically between 5 and 10, and it was uniformly set to 5 in this paper. The ordered subset (OS) technique [42] was applied in our implementation to speed up the reconstruction, and the projections were divided into 20 subsets for all datasets. The tensor dictionary representation was performed after updating all subsets. The MATLAB Tensor toolbox [43] developed by Sandia National Laboratories was used to perform CPD and other tensor related operations. The size of each channel image was 512×512. The reconstruction process stopped after 50 iterations. The parameters η, ε and L were empirically set for different datasets.
V. Experiments
In this study, numerical tests were first performed to quantitatively evaluate the performance of the proposed method relative to competing methods. The image quality was evaluated in terms of the root mean square error (RMSE) as well as two widely used image quality assessment metrics: the feature similarity (FSIM) [44] and the structural similarity (SSIM) [45]. Furthermore, post-reconstruction material decomposition was carried out. Then, a real preclinical dataset was employed to demonstrate the merits of the proposed method.
A. Numerical Simulation
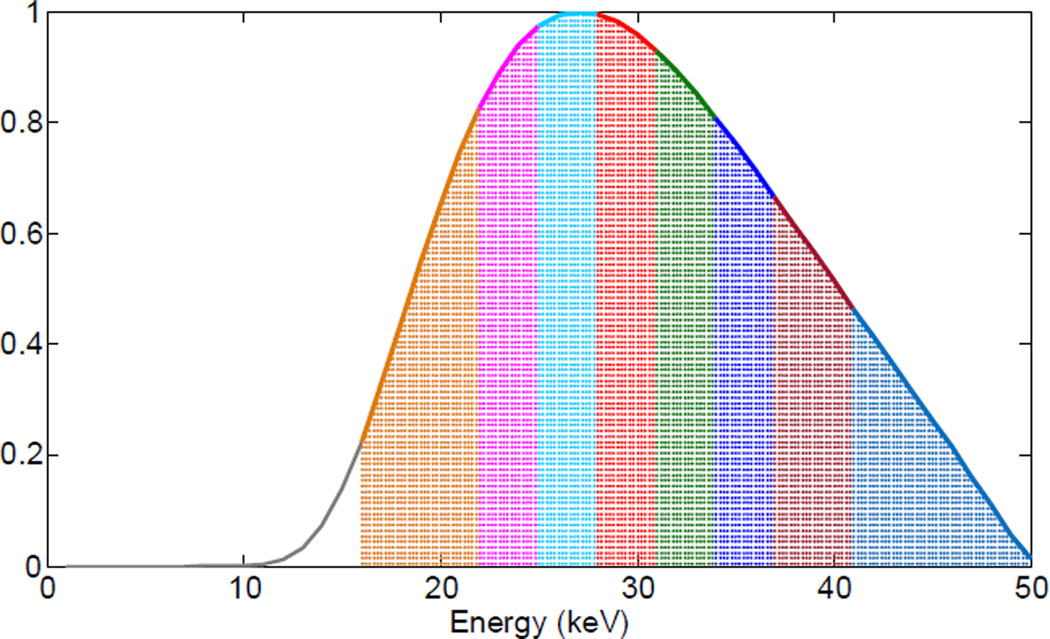
In the numerical tests, an equidistant fan-beam geometry was assumed. There were 512 detector bins of a 0.1 mm width per bin. 640 projections were uniformly collected over a full scan range. The distance from the source to the system origin was 132 mm, and the distance from the source to the detector was 180 mm. A 50 kVp x-ray spectrum was assumed, which was generated from the SpectrumGUI software [46]. The spectrum was divided into eight energy channels: [16, 22) keV, [22, 25) keV, [25, 28) keV, [28, 31) keV, [31, 34) keV, [34, 37) keV, [37, 41) keV, [41, 50) keV. The energy channels are shown in Fig. 1. In the simulation, a realistic mouse thorax phantom was used [47], and 1.2% (by weight) iodine contrast agent was introduced into the blood circulation (see Fig. 2). For each x-ray path 5000 photons were assumed emitted from the x-ray source. To generate multichannel projections, the emitted photons were distributed to each energy channel (in a step of 1 keV) according to the x-ray spectrum. We computed the expected number of photons in each energy channel along every x-ray path. To simulate data noise, random numbers were generated according to the Poisson distribution in which the variances were the aforementioned expected photon numbers. Then, the noise-free and noisy projections were obtained after a logarithmic operation [48]. The reconstructed CT images formed a 3rd-order tensor (512×512×8) with each pixel covered an area of 0.075×0.075 mm2. In this simulation, the default parameters were η=3.2, ε=0.0018, L=6 and K=1024 for TDL reconstruction.
Fig. 1.
Spectrum and eight energy channels used in the numerical simulations.
Fig. 2.
Mouse thorax phantom (left) and the iodine contrast agent distribution (right).
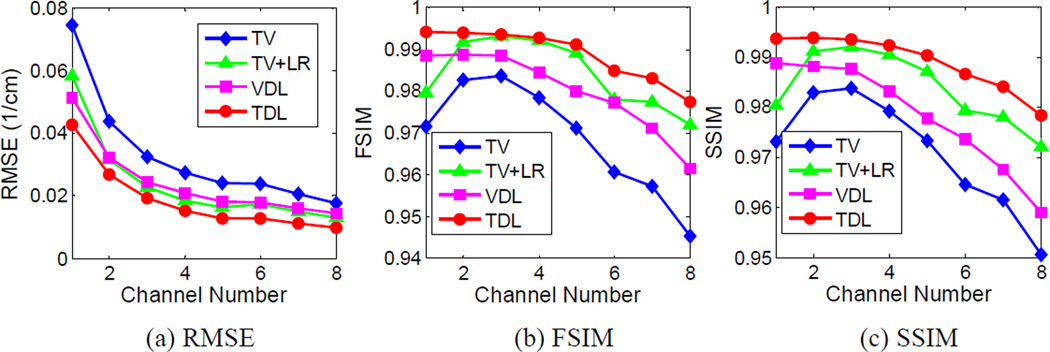
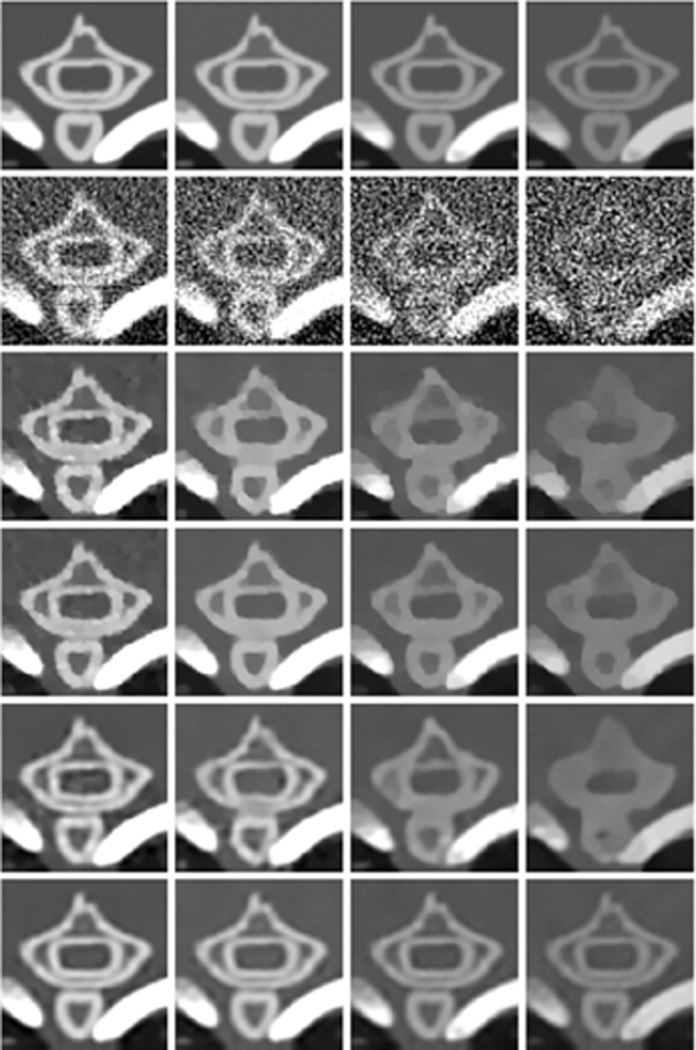
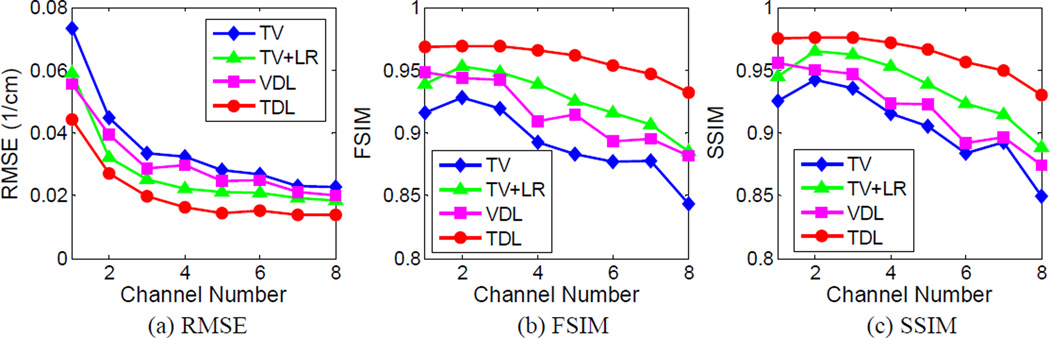
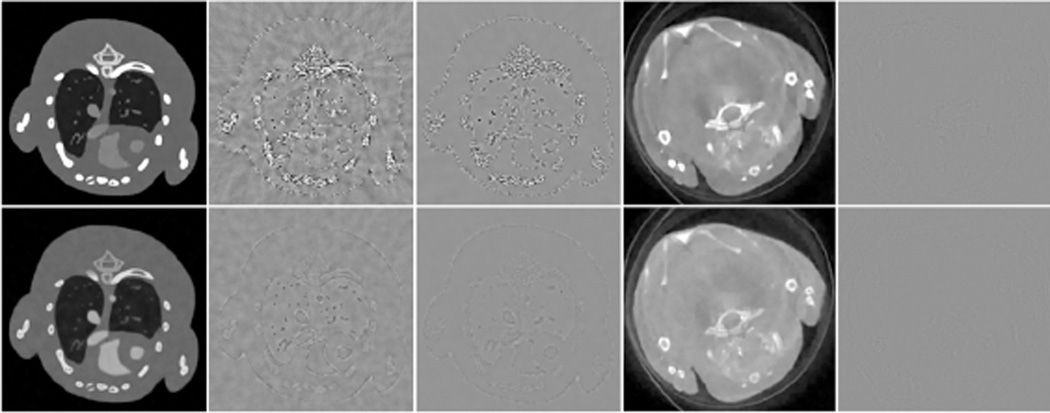
Fig. 3 shows the reconstructed four representative channels of the mouse phantom. These images were reconstructed using the conventional FBP, TV, TV combined with low rank (TV+LR), conventional vector-based dictionary learning (VDL) and the proposed tensor-based dictionary learning (TDL). To compare image quality, many combinations of the parameters were tested for the proposed and competing methods, and the best results in terms of RMSE were selected for further comparison. Otherwise, it would be too time-consuming to tune regularization parameters individually for all energy channels. A common TV regularization parameter was used for all the channels. In the case of VDL, an empirical strategy was employed for parameter selection with a single tolerance parameter for all channels [21], [49]. Here, the image reconstructed from the noise-free projection using the FBP method was used as the reference. Fig. 3 illustrates that TDL can obtain very clear images, and the resultant difference images are weaker than those obtained from other competing methods. Fig. 4 shows the quantitative evaluation indexes of the reconstructed image quality. Because the image quality metrics of the FBP images are far worse than those of the iteratively reconstructed images, they are not listed in Fig. 4. It can be observed from Fig. 4(a) that the TDL based reconstruction has the smallest RMSE in all the eight channels, followed by the TV+LR approach which has slightly smaller RMSE than VDL. The TV minimization method has the largest RMSE in all channels. The results were also evaluated in terms of FSIM and SSIM, which measure the similarity between two images and have been widely reported to be consistent with human visual perception [44], [45]. Recently, they were used to evaluate CT image quality [17] [37]. To compute FSIM and SSIM, the FBP images reconstructed from noise-free projections were used as the references. In addition, the dynamic range of each channel image was scaled to [0 255] in advance, and the default parameter setting in the source codes was used [50], [51]. The closer to 1.0 FSIM and SSIM are, the better the image quality is. In Fig. 4(b), TDL has the greatest FISM index in all channels, followed by the TV+LR and VDL. In Fig. 4(c), the TDL has a remarkably larger SSIM value than the other three competing methods in all channels. Fig. 4 illustrates that TDL has the best overall image quality in terms of quantitative evaluation.
Fig. 3.
Numerical simulation results with the mouse thorax phantom. (a) From left to right columns, the images correspond to four representative channels 1, 4, 6 and 8 respectively. The first row images were reconstructed from noise-free projections using the FBP. From the second to bottom rows, the images were reconstructed from a noisy dataset using FBP, TV, TV+LR, VDL and TDL respectively. From the left to right columns, the display windows are [0 3], [0 1.2], [0 0.8] and [0 0.8] cm−1 respectively. (b) Difference images of the results in (a) with respect to the noise-free FBP images in the first row of (a). The rows and columns correspond to that of (a), and the display window is [−0.5 0.5] cm−1
Fig. 4.
Quality assessment for the reconstructed mouse thorax phantom images.
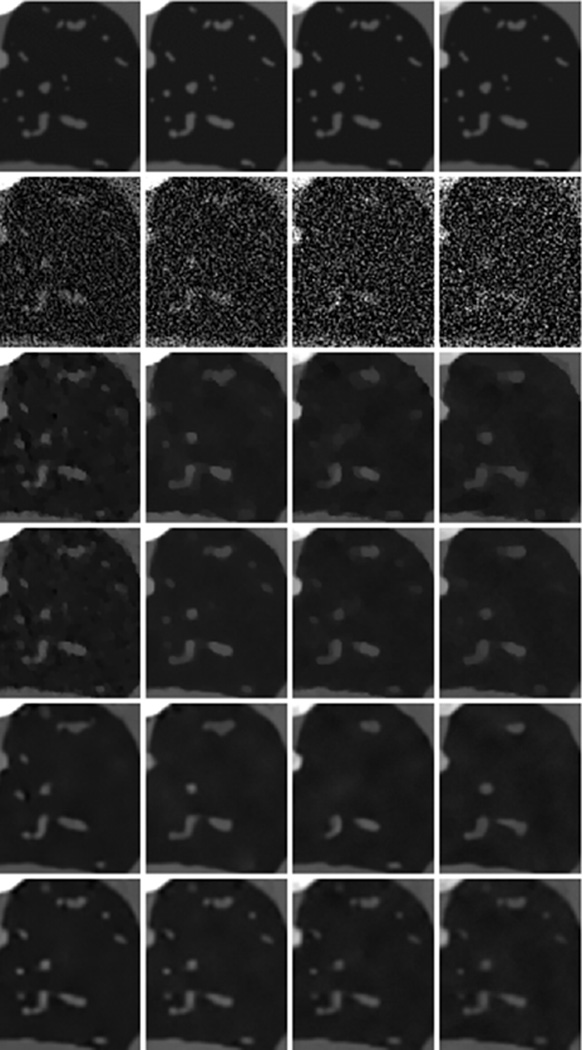
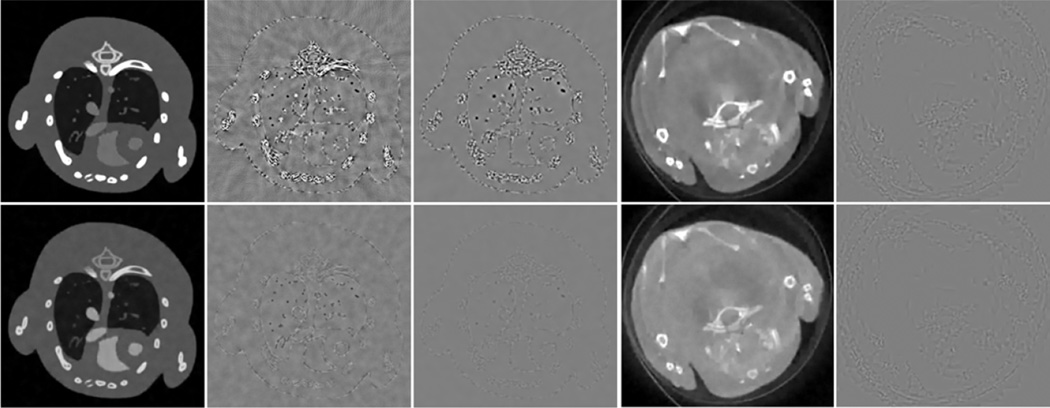
Two regions of interest (ROIs), which have abundant detailed features, are indicated by the squares in Fig. 3. The magnified ROIs are in Figs. 5 and 6, respectively. Fig. 5 shows a bone ROI, where thoracic vertebra bones are separated by low-density tissues. From the second row, it is seen that noise was severe in the conventional FBP reconstruction, especially in the last channel where the signal-to-noise ratio (SNR) was so low that the thoracic vertebra bones structure could hardly be distinguished from noise. As a result, in the last few channels, the thoracic vertebra bones merged together, and the anatomical structure was lost in the TV and VDL images. By employing correlation between channels, the TV+LR approach preserved more bone structures than the TV and VDL based methods. However, the finer soft tissue features between bones were lost. On the other hand, the proposed TDL improved the image quality and suppressed noise much better. As a result, the vertebra bones and their surrounding soft tissue details were faithfully reconstructed. Fig. 7 gives the image quality assessment indexes of the bone ROI in Fig. 5. It is clearly seen that TDL yielded the best image quality in all channels according to the three indexes. Fig. 6 shows a lung ROI indicated in Fig. 3. Although the lung ROI contains abundant details, most of them cannot be distinguished due to the severe noise in the second row, especially for the small size features. In the first column in Fig. 6, the TV and TV+LR results are contaminated by noise to some extent, while the VDL and TDL results show better image visibility. In the last three columns in Fig. 6, the TV and VDL methods reconstructed only a few of the larger features, while the TV+LR approach preserved more details. However, some shapes of these reconstructed features were not sufficiently accurate. In comparison, the TDL algorithm accurately reconstructed most of the detail features in all channels. Fig. 8 presents the image quality indexes of the lung ROI in Fig. 6. Evidently, the TDL method achieves the best image quality in all channels.
Fig. 5.
Magnified bone ROI indicated in Fig. 3. The row and column have the same meaning as those in Fig. 3.
Fig. 6.
Same as Fig. 5 but for the lung ROI.
Fig. 7.
Image quality assessment over the bone ROI shown in Fig. 5.
Fig. 8.
Image quality assessment over the lung ROI shown in Fig. 6.
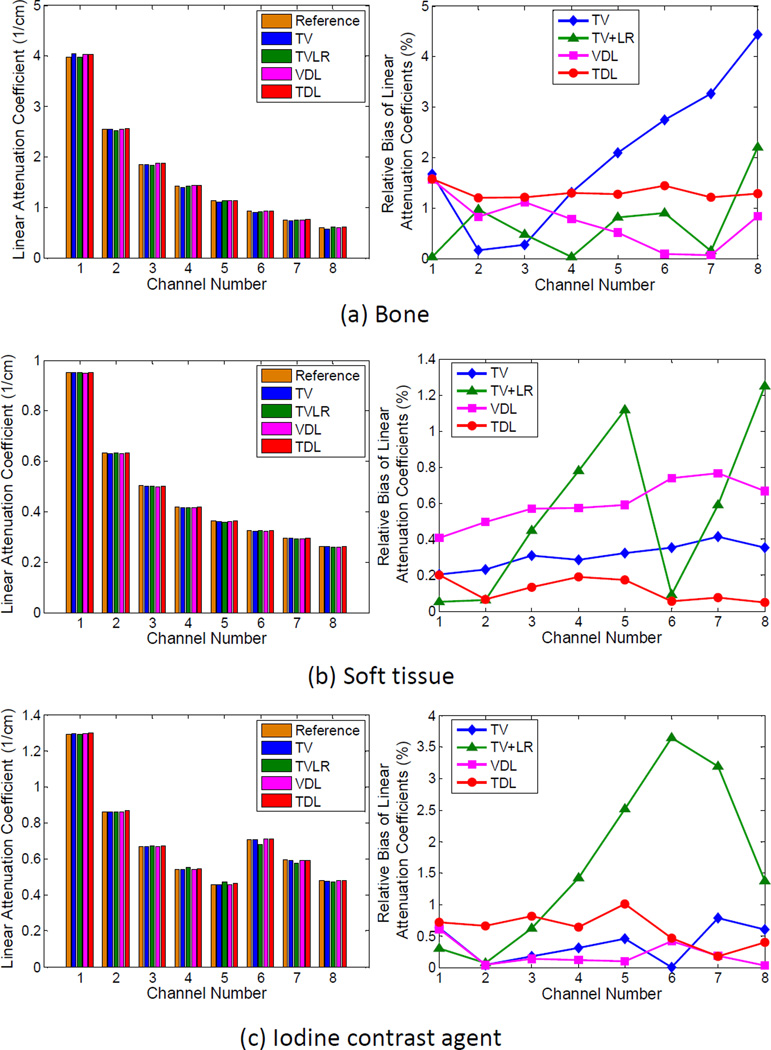
Fig. 9 shows the mean values and relative biases of bone, soft tissue and iodine enhanced regions in each channel for the selected iterative reconstruction methods. The relative bias, which indicates the absolute bias divided by the corresponding mean value of the reference in an energy channel, was used for comparison. The mean values of tissues in FBP images reconstructed from noise-free projection data served as the reference. Because the bone regions consist of small structures which tend to be smoothed by the TV regularization, the TV method has the greatest relative bias for bone (up to 4.4% in channel 8), followed by TV+LR (2.2% in channel 8). The mean values of bone in VDL and TDL images are the most accurate. Their relative biases are below 1.6% in all channels. In terms of soft tissue, TV+LR has the greatest relative bias with 1.3% in channel 8, and the soft tissue relative biases of other methods are below 0.8%. Particularly, TDL reaches <0.2% relative biases in all channels. Fig. 9(c) shows that the mean values of TV+LR are 2.5% higher in channel 5, 3.6% and 3.2% lower in channels 6 and 7 respectively than that of the reference. This reflects the spectral flattening effect associated with TV+LR near the K-edge of iodine. The other methods have a relative bias of <1.0% for iodine, where VDL is generally the most accurate for iodine (relative bias of <0.7% in all the channels). In summary, TV results in large bias due to the fine structural tissue; and low rank regularization encourages images to have the signal flattened across different channels. Overall, two dictionary based methods are very accurate, with VDL especially preferred due to its consistent and excellent performance with respect to material types and energy channels.
Fig. 9.
Mean values of the three types of tissues in each channel (left) and the corresponding relative biases.
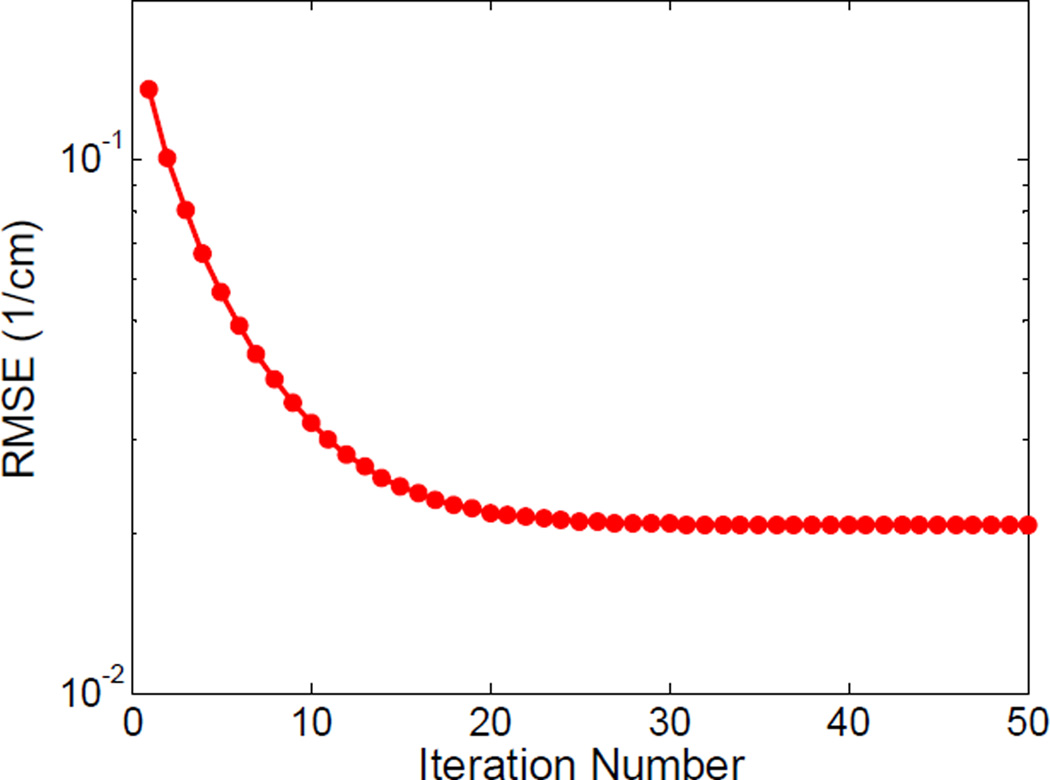
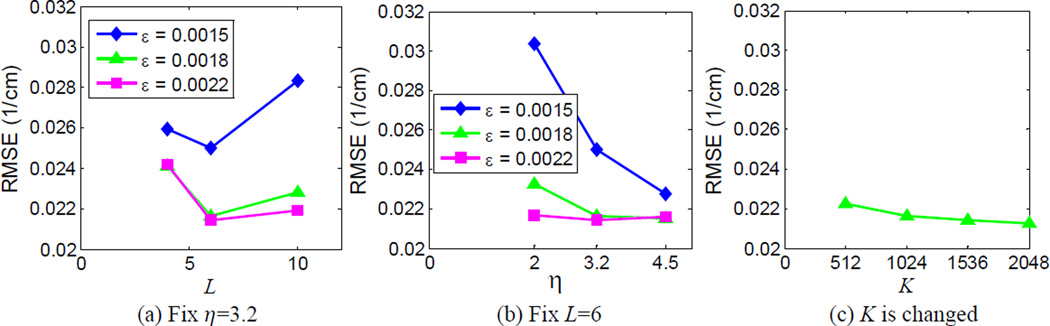
Fig. 10 plots the convergence curve of TDL based spectral image reconstruction. It is observed that the error decreased monotonously and remained stable after about 25 iterations. The RMSE of the whole spectral image tensor is as low as 0.0217 cm−1. To investigate the influence of the parameters on the reconstruction performance, we compared the results of TDL with different parameter settings. Fig. 11 shows the RMSE of TDL with respect to different parameter settings. In each subfigure, one or two parameters was/were changed while other parameters were fixed. Fig. 12 shows, one representative channel (channel 6) images and the corresponding difference images related to the reference image and the optimal parameter setting image (TDL in Fig. 3). It is observed from Figs. 11 and 12 that ε is the key parameter for controlling the reconstructed image quality: a smaller ε can induce noise/fake structures, while a larger one can compromise structural details in the lung region. The larger η is, the smoother the image is. In terms of L, a smaller value can induce more blurred edges. Relatively speaking, the reconstruction quality is not sensitive to the number of atoms K in the dictionary, and a larger K can slightly reduce RMSE.
Fig. 10.
Convergence curve for the TDL reconstruction.
Fig. 11.
RMSE of the TDL with respect to different parameter settings. (a) The RMSE plots for η = 3.2, (b) those for L = 6, and (c) the RMSE plot with respect to K.
Fig. 12.
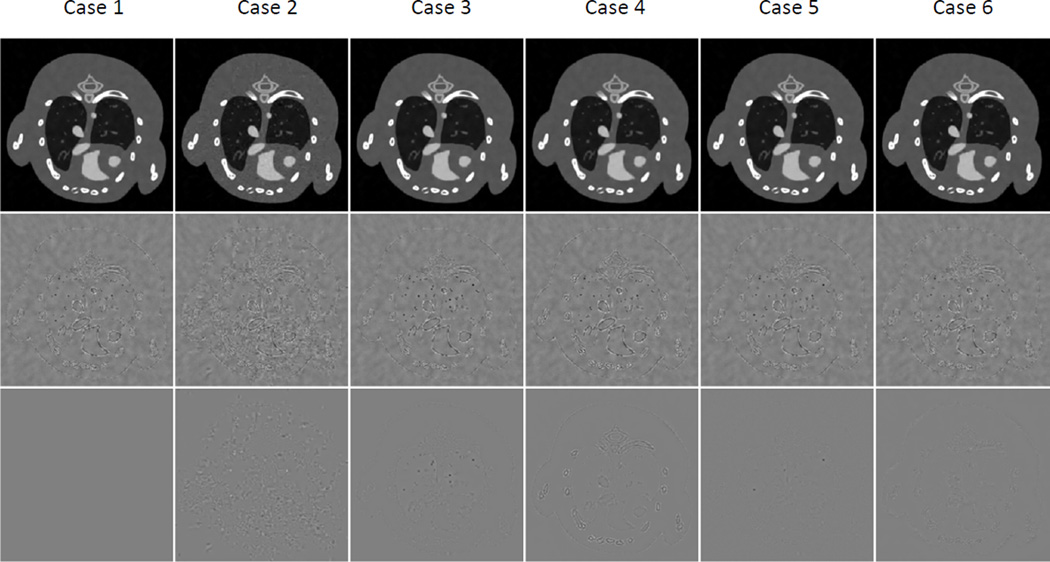
Reconstructed mouse thorax phantom images using the TDL approach with respect to different parameter settings. From the left to right columns, the images correspond to cases 1 – 6. Case 1: default parameters η=3.2, ε=0.0018, L=6; Case 2: η=3.2, ε=0.0015, L=6; Case 3: η=3.2, ε=0.0022, L=6; Case 4: η=3.2, ε=0.0018, L=4; Case 5: η=4.5, ε=0.0018, L=6; Case 6: η=3.2, ε=0.0018, η=6, K=2048. The top row lists the reconstructed images in channel 6 in a display window [0 0.8] cm−1, and the next two rows are the corresponding difference images relative to the reference images and the TDL with the default parameter setting, respectively. The display window is [−0.2 0.2] cm−1.
To validate the proposed tensor-based dictionary learning method for material decomposition, the reconstructed spectral images were decomposed into three basis materials (bone, soft tissue and iodine contrast agent) using the post-reconstruction material decomposition algorithm [7]. Fig. 13 represents the proportions of three basis materials and the corresponding color images. It is seen from the third column that many pixels from the competing methods are wrongly classified as containing iodine, and the TDL provides the most accurate iodine components. To quantitatively evaluate the decomposition results, the RMSE values of each decomposed basis material are summarized in Table I. The FBP has the greatest RMSE in all the materials, and generally the error decreases gradually from TV, TV+LR to VDL. This suggests that the high quality of TDL reconstruction leads to excellent material decomposition results.
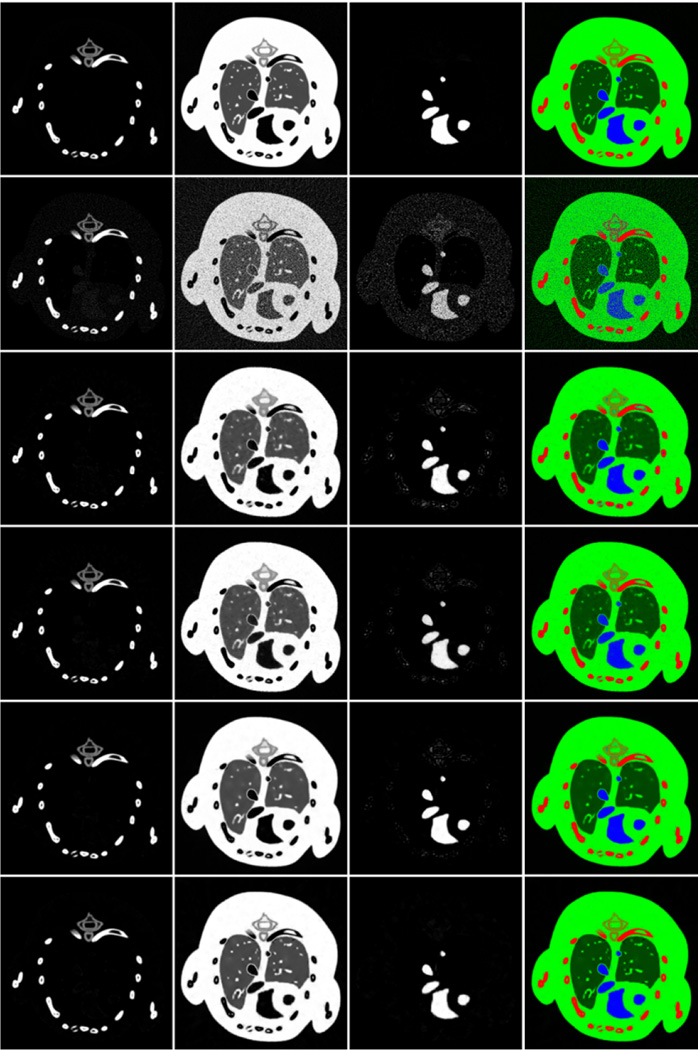
Fig. 13.
Material decomposition results from the phantom study. From the left to right, the first three columns are the decomposed bone, soft tissue and iodine contrast agent components, respectively. The fourth column is the color representation of the decomposed images where red, green and blue components correspond to the three basis materials respectively.
TABLE I.
RMSE of Each Decomposed Basis Materials in the Numerical Simulation Study (cm−1)
| Tissues | FBP | TV | TV+LR | VDL | TDL |
|---|---|---|---|---|---|
| Bone | 3.86 × 10−2 | 1.51 × 10−2 | 1.34 × 10−2 | 9.65 × 10−3 | 9.63 × 10−3 |
| Soft tissue | 1.82 × 10−1 | 4.03 × 10−2 | 3.78 × 10−2 | 3.12 × 10−2 | 2.77 × 10−2 |
| Iodine | 1.24 × 10−1 | 3.31 × 10−2 | 2.83 × 10−2 | 1.89 × 10−2 | 1.44 × 10−2 |
All the compared methods were implemented in MATLAB on an Intel(R) Core(TM) i7-4790 CPU, 3.60 GHz and 16 GB RAM PC platform. As a pilot study, we ran our un-optimized codes with a single core from the CPU. For the tensor dictionary training, it took 26.5 seconds per iteration, and the maximum number of iterations was 100. In each reconstruction iteration, the computational cost to update the fidelity term (forward and backward projections) was 5.10 minutes, and the costs to perform the regularization with TV, TV+LR, VDL and TDL were 2.18 minutes, 2.21 minutes, 52.8 seconds and 9.1 seconds respectively. The TV regularization requires remarkably longer time than the TDL regularization because it was implemented with an inner loop for sparse representation. For the TDL method, the computational cost mainly consists of dictionary training and forward/backward projection, and the time-consuming task can be done using hardware accelerating techniques such as GPU [15].
B. Preclinical Mouse Study
The proposed TDL based reconstruction method was also evaluated using preclinical projections from a mouse injected with 0.2 ml of 15 nm Aurovist II gold nanoparticles (GNP) (Nanoparticles; Yaphank, NY). GNP was injected into the mouse’s tail vein, and the mouse was alive for about three hours between the injection and euthanasia. Then, the mouse was scanned on a MARS (medipix all resolution system) micro-CT with a Medipix MXR CdTe layer detector [52]. The x-ray source (SB-120-400, Source-Ray Inc., New York) used a minimum focal spot of 75 µm. The distances from the source to the system origin and to the detector were 158 and 255 mm respectively. Over a full scan range, 371 projections were uniformly collected. Thirteen energy channels were used to collect projections with the source being operated at 120 kVp and 175 mA. The channels of real datasets were different from that for the aforementioned numerical simulation. Here each energy channel received x-ray photons, whose energies were above a given energy threshold, which increased with the increment of the energy channel index. Hence, the first channel had the lowest energy threshold, and almost all the photons were included, while the last channel took the fewest photons. The detector chip was moved horizontally with overlapped pixels to cover a wider FOV of 34.89 mm in diameter that the detector aperture and to correct production defects in the detector sensor layer. To reduce noise in the sinogram, neighboring detector bins were merged to form a new sinogram of size 512×371. We applied the wavelet-Fourier filtering method [53] to reduce ring artifacts. Because of detector defects, only part of the projections were usable. Thus, we reconstructed two representative slices in the vicinity of the thorax. The reconstructed CT images were 3rd-order tensors of 512×512×13 covering an area of 18.41×18.41 mm2. The parameters were η=1.5, ε=0.001, L=8 and K=1024 for TDL based reconstruction.
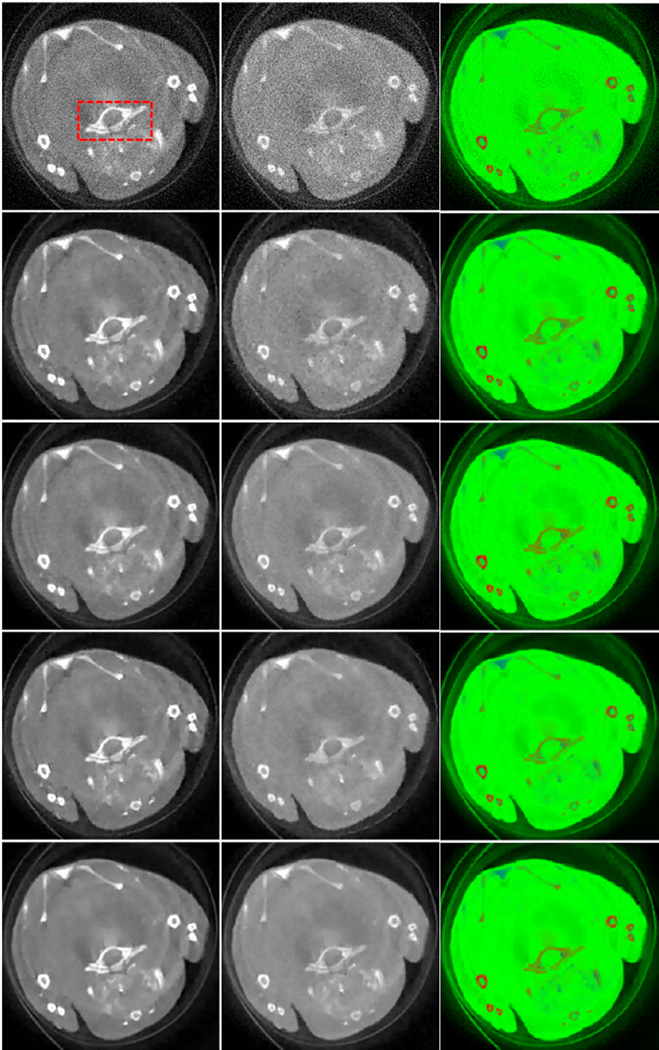
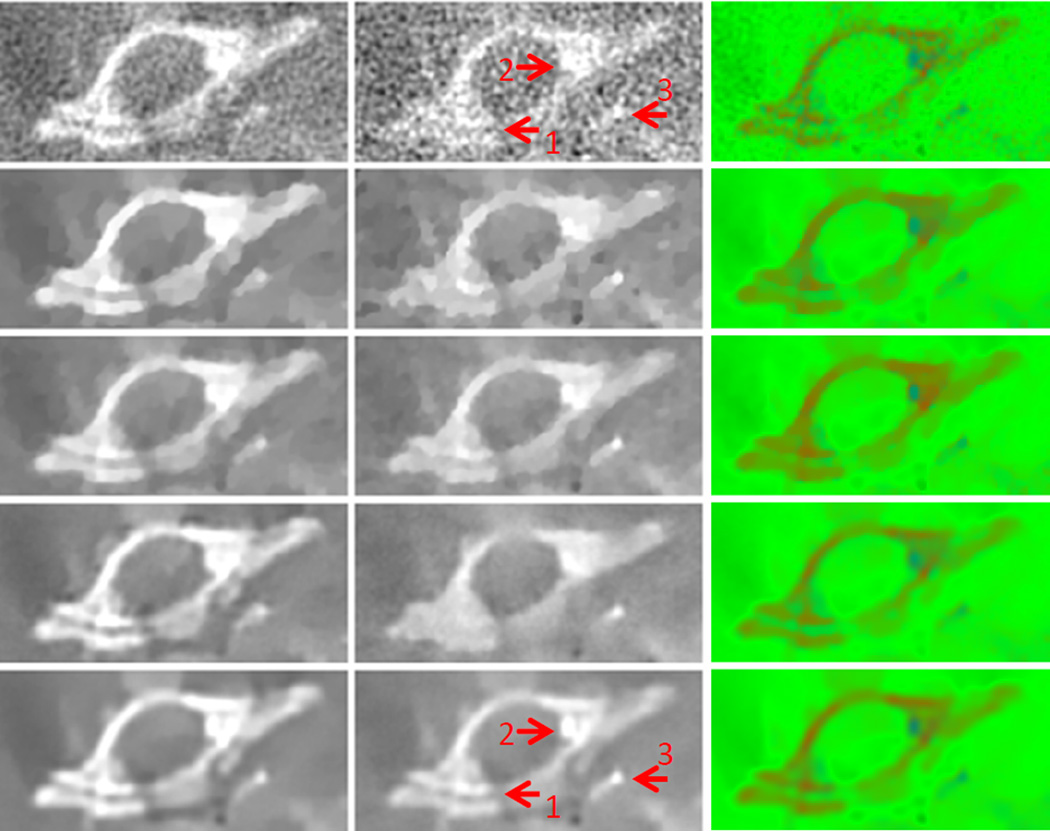
Fig. 14 shows the reconstructed images in two representative channels (channels 1 and 13) and material decomposition results. Fig. 15 shows a magnified region of interest (ROI) containing the thoracic vertebra. Fig. 16 shows another ROI on a different slice in the vicinity of the thorax. Because the first channel used nearly all the detected photons, it was assumed as the conventional gray-scale CT image. In contrast, the SNR of the thirteenth channel images is the worst. It is observed from the middle column in Fig. 15 that the images reconstructed using the FBP method contain severe noise. Detailed features of the thoracic vertebra, such as the soft tissue gap between bones, were strongly contaminated, as indicated by the arrow 1. In addition, the structures indicated by the arrows 2 and 3, can hardly be distinguished. Although the images reconstructed by TV, TV+LR and VDL contain less noise, the tissue structures were blurred to some extent, and the blocky effects caused by the TV minimization were noticeable. By comparison, the finer tissue features were well preserved by the proposed TDL technique. In the middle column of Fig. 16, only TDL and TV+LR can preserve the structures of the rib and sternum, as indicated by the arrows 1 and 2. The improved image quality can benefit the material decomposition. In the right columns of Figs. 14 – 16, soft tissue, bone and GNP were decomposed and colored in green, red and blue, respectively. As far as GNP regions are concerned, the color in the first slice was very light because there was no major vasculature, and the concentration of GNP was low; in the second slice, the vasculature containing high concentration GNP, colored in blue, can be clearly observed. It is encouraging that TDL gives more accurate decomposition results for each material without blocky artifacts. For example, while a few pixels at the boundary of vasculature were incorrectly decomposed as bone (colored in red) using the competing method, the decomposition result obtained from TDL was correct, as shown in Fig. 16.
Fig. 14.
Representative results of the first real mouse dataset. The left column lists the first channel images, and the middle for the last channel images (channel 13), both of which are in the display window [0 0.8] cm−1. The right column is the color representation of the material decomposition results, where the red, green and blue components correspond to the three basis materials: bone, soft tissue and GNP respectively. From top to bottom, the images were reconstructed using the FBP, TV, TV+LR, VDL and TDL respectively.
Fig. 15.
Magnified bone ROI indicated in Fig. 14. The row and column have the same meaning as those in Fig. 14. The display windows are [0 0.8] cm−1 for the left column and [0.1 0.7] cm−1 for the middle column.
Fig. 16.
Same as Fig. 14 but for another slice. The display window is [0 1.0]
VI. Discussions and Conclusion
The proposed TDL method requires a normalization of raw projection datasets before reconstruction. Otherwise, the image quality will be compromised in some cases. Fig. 17 shows the reconstructed images using the TDL method with the same parameter settings but without the normalization. It can be seen from the results of the simulated data that the first channel contains a few artifacts in the vicinity of some edges, and the last channel has slightly smoother edges. In comparison, the reconstructed results of the real data are of very good quality, and the differences are small for the ones obtained from the proposed TDL (as shown in Fig. 14). This is due to the normalization weighting vector w: the ratio between the maximum and minimum of w in the simulated dataset is 3.6, compared with 1.2 in the real preclinical dataset, which means that the image value differences among channels in the simulated mouse are substantially greater than those of the preclinical datasets. Fig. 17 demonstrates that the normalization is necessary for the proposed TDL method if the ratio of the maximum and minimum of w is large.
Fig. 17.
Images reconstructed using the proposed TDL method without data normalization. The first column images are the numerical simulation results of channels 1 and 8 in the display windows [0 3] and [0 0.8] cm−1 respectively. The second and third columns present the corresponding difference images with respect to the reference image and the standard TDL results in the display window [−0.2 0.2] cm−1. The fourth column images are the mouse results in channels 1 and 13 in the display windows [0 0.8] cm−1. The fifth column images are the corresponding difference images with respect to the standard TDL results in the display window [−0.2 0.2] cm−1.
Because TDL considers data redundancy in true spatiospectral space, its performance will be compromised to some extent if fewer channels are available. To evaluate this aspect, the aforementioned numerical experiments were repeated for only 4 channels. Particularly, channels 1, 4, 6 and 8 in the numerical simulation were selected to form a new dataset, and channels 1, 3, 8 and 13 in the mouse measurement were chosen for re-testing. It is seen from Fig. 18 that the image quality was reduced a little bit, but the proposed method remained superior to the competitive methods.
Fig. 18.
Same as Fig. 17 but reconstructed from four-channels datasets using the standard TDL method.
The main reconstruction parameters of the TDL based method are η, ε, L and K. Among these parameters, K is not sensitive and can be set as a constant, and it is proper to set L between 6 and 8 for various datasets. η balances the data fidelity and signal sparsity. Generally speaking, it can be selected from a relatively wide range. In contrast, ε is the most crucial parameter that needs to be tuned carefully. ε indicates the representation error of a tensor patch, and a proper ε enables all channels to reach the best image quality collectively. The parameters for numerical simulation and preclinical studies were not the same, because of different imaging configurations in terms of the x-ray spectrum, exposure, energy channels, etc. In practice, imaging conditions could be typically fixed for a given CT scanner and specific types of applications. This makes it feasible to empirically optimize parameters or adaptively determine them in advance or on fly [54].
The TDL method achieves better image quality than that of its competitors because it effectively uses two characteristics of spectral CT imaging: sparsity and correlation in the true physical space. A tensor atom represents a signal as a whole, where represents spatial structures, and represents physical association across different energy channels. Thus, a tensor atom shares the same spatial structures in each channel, and the lost signal (compromised by severe noise) in a certain channel can be restored from the remaining channels. Therefore, a tensor-based spatio-spectral dictionary is desirable for analyzing spectral datasets and preserving structural details than a vectorized dictionary.
Although encouraging results were obtained by the proposed TDL based method, there is still room for improvement. One way for improvement is to combine it with statistical reconstruction [41], which could help eliminate streaks along the direction of photon starvation. While CPD was employed in this paper, the Tucker decomposition based dictionary learning could be also a good choice for spectral CT. In the near future, we will compare these two tensor-based dictionary learning methods for spectral CT reconstruction.
In conclusion, we have developed a tensor-based dictionary learning approach for spectral CT image reconstruction and evaluated it relative to several competing methods. The proposed approach can preserve detailed features and allow superior material decomposition to the competitors. Further work is underway to improve and characterize this approach for preclinical and clinical applications.
Acknowledgments
This work was supported in part by the National Natural Science Foundation of China (NSFC) under Grant Nos. 61172163, 90920003, 61401349 and 61302136, in part by NIH/NIBIB U01 grant EB017140 and R21 grant EB019074, in part by Natural Science Basic Research Plan in Shaanxi Province of China (Program No. 2014JQ8317), in part by China Postdoctoral Science Foundation (Program No. 2012M521775).
The authors would like to thank the MARS team in New Zealand for providing the mouse dataset, and thank Mr. Ibrahim Mkusa at UMass Lowell for his proof-reading. The authors are especially grateful to the anonymous reviewers for their valuable comments.
Contributor Information
Yanbo Zhang, Department of Electrical and Computer Engineering, University of Massachusetts Lowell, Lowell, MA 01854, USA.
Xuanqin Mou, Institute of Image Processing and Pattern Recognition, Xian Jiaotong University, Xian, Shaanxi 710049, China.
Ge Wang, Biomedical Imaging Center/Cluster, CBIS, Rensselaer Polytechnic Institute, Troy, NY 12180, USA.
Hengyong Yu, Department of Electrical and Computer Engineering, University of Massachusetts Lowell, Lowell, MA 01854, USA.
References
- 1.Taguchi K, Iwanczyk JS. Vision 20/20: Single photon counting x-ray detectors in medical imaging. Medical Physics. 2013;40(10):100901. doi: 10.1118/1.4820371. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 2.Kim DW, Kim HK, Youn H, Yun S, Han JC, Kim J, Kam S, Tanguay J, Cunningham IA. Signal and noise analysis of flat-panel sandwich detectors for single-shot dual-energy x-ray imaging. Proc. of SPIE. 2015:94 124A–94 124A–13. [Google Scholar]
- 3.Zou Y, Silver MD. Analysis of fast kV-switching in dual energy CT using a pre-reconstruction decomposition technique. Proc. of SPIE. 2008;6913:691 313–691 313–12. [Google Scholar]
- 4.Szczykutowicz TP, Chen G-H. Dual energy CT using slow kVp switching acquisition and prior image constrained compressed sensing. Physics in Medicine and Biology. 2010;55(21):6411–6429. doi: 10.1088/0031-9155/55/21/005. [DOI] [PubMed] [Google Scholar]
- 5.Faby S, Kuchenbecker S, Sawall S, Simons D, Schlemmer H-P, Lell M, Kachelrieß M. Performance of today’s dual energy CT and future multi energy CT in virtual non-contrast imaging and in iodine quantification: A simulation study. Medical Physics. 2015;42(7):4349–4366. doi: 10.1118/1.4922654. [DOI] [PubMed] [Google Scholar]
- 6.Taguchi K, Zhang M, Frey EC, Xu J, Segars WP, Tsui BMW. Image-domain material decomposition using photon-counting CT. Proc. of SPIE. 2007;6510:651 008–651 008–12. [Google Scholar]
- 7.Granton PV, Pollmann SI, Ford NL, Drangova M, Holdsworth DW. Implementation of dual- and triple-energy cone-beam micro-CT for postreconstruction material decomposition. Medical Physics. 2008;35(11):5030–5042. doi: 10.1118/1.2987668. [DOI] [PubMed] [Google Scholar]
- 8.Anderson NG, Butler AP. Clinical applications of spectral molecular imaging: potential and challenges. Contrast Media & Molecular Imaging. 2014;9(1):3–12. doi: 10.1002/cmmi.1550. [DOI] [PubMed] [Google Scholar]
- 9.Shikhaliev PM. Projection x-ray imaging with photon energy weighting: experimental evaluation with a prototype detector. Physics in Medicine and Biology. 2009;54(16):4971–4992. doi: 10.1088/0031-9155/54/16/009. [DOI] [PubMed] [Google Scholar]
- 10.Dong X, Niu T, Zhu L. Combined iterative reconstruction and image-domain decomposition for dual energy CT using total-variation regularization. Medical Physics. 2014;41(5):051909. doi: 10.1118/1.4870375. [DOI] [PubMed] [Google Scholar]
- 11.Yu G, Li L, Gu J, Zhang L. Total variation based iterative image reconstruction. Computer Vision for Biomedical Image Applications Proceedings, Lecture Notes in Computer Scince. 2005;3765:526–534. [Google Scholar]
- 12.Sidky EY, Kao CM, Pan XH. Accurate image reconstruction from few-views and limited-angle data in divergent-beam CT. Journal of X-Ray Science and Technology. 2006;14(2):119–139. [Google Scholar]
- 13.Yu HY, Wang G. Compressed sensing based interior tomography. Physics in Medicine and Biology. 2009;54(9):2791–2805. doi: 10.1088/0031-9155/54/9/014. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 14.Yu H, Wang G. A soft-threshold filtering approach for reconstruction from a limited number of projections. Physics in Medicine and Biology. 2010;55:3905–3916. doi: 10.1088/0031-9155/55/13/022. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 15.Jia X, Dong B, Lou Y, Jiang S. GPU-based iterative cone-beam CT reconstruction using tight frame regularization. Physics in Medicine and Biology. 2011;56:3787–3807. doi: 10.1088/0031-9155/56/13/004. [DOI] [PubMed] [Google Scholar]
- 16.Borsdorf A, Raupach R, Flohr T, Hornegger J. Wavelet based noise reduction in CT-images using correlation analysis. Medical Imaging, IEEE Transactions on. 2008;27(12):1685–1703. doi: 10.1109/TMI.2008.923983. [DOI] [PubMed] [Google Scholar]
- 17.Xu Q, Yu HY, Mou XQ, Zhang L, Hsieh J, Wang G. Low-dose x-ray CT reconstruction via dictionary learning. Medical Imaging, IEEE Transactions on. 2012;31(9):1682–1697. doi: 10.1109/TMI.2012.2195669. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 18.Xu Q, Yu H, Bennett J, He P, Zainon R, Doesburg R, Opie A, Walsh M, Shen H, A B, Butler P, Mou X, Wang G. Image reconstruction for hybrid true-color micro-CT. IEEE Transactions on Biomedical Engineering. 2012;59(6):1711–1719. doi: 10.1109/TBME.2012.2192119. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 19.Xu Q, Yu H, Mou X, Wang G. IEEE International Symposium on Biomedical Imaging (ISBI) IEEE; 2014. Dictionary learning based image reconstruction for spectral CT. [Google Scholar]
- 20.Zhao B, Ding H, Lu Y, Wang G, Zhao J, Molloi S. Dual-dictionary learning-based iterative image reconstruction for spectral computed tomography application. Physics in Medicine and Biology. 2012;57(24):8217–8229. doi: 10.1088/0031-9155/57/24/8217. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 21.Zhang Y, Yu H, Mou X, Wang G. Dictionary learning and low rank based multi-energy CT reconstruction; The Third International Conference on Image Formation in X-Ray Computed Tomography; 2014. pp. 79–82. [Google Scholar]
- 22.Zhao B, Gao H, Ding H, Molloi S. Tight-frame based iterative image reconstruction for spectral breast CT. Medical Physics. 2013;40(3):031905. doi: 10.1118/1.4790468. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 23.Gao H, Yu H, Osher S, Wang G. Multi-energy CT based on a prior rank, intensity and sparsity model (PRISM) Inverse Problems. 2011;27(11):115012. doi: 10.1088/0266-5611/27/11/115012. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 24.Candès EJ, Li X, Ma Y, Wright J. Robust principal component analysis. Journal of the ACM (JACM) 2011;58(3):11. [Google Scholar]
- 25.Chu J, Cong W, Li L, Wang G. Combination of current-integrating/photon-counting detector modules for spectral CT. Physics in Medicine and Biology. 2013;58(19):7009–7024. doi: 10.1088/0031-9155/58/19/7009. [DOI] [PubMed] [Google Scholar]
- 26.Chu J, Li L, Chen Z, Wang G, Gao H. Multi-energy CT reconstruction based on low rank and sparsity with the split-bregman method (MLRSS); IEEE Nuclear Science Symposium and Medical Imaging Conference (NSS/MIC); 2012. pp. 2411–2414. [Google Scholar]
- 27.David SR, Patrick JLR. Joint reconstruction of multi-channel, spectral CT data via constrained total nuclear variation minimization. Physics in Medicine and Biology. 2015;60(5):1741. doi: 10.1088/0031-9155/60/5/1741. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 28.Kyungsang K, Jong Chul Y, Worstell W, Jinsong O, Rakvongthai Y, El Fakhri G, Quanzheng L. Sparse-view spectral CT reconstruction using spectral patch-based low-rank penalty. Medical Imaging, IEEE Transactions on. 2015;34(3):748–760. doi: 10.1109/TMI.2014.2380993. [DOI] [PubMed] [Google Scholar]
- 29.Kolda TG, Bader BW. Tensor decompositions and applications. SIAM Review. 2009;51(3):455–500. [Google Scholar]
- 30.Semerci O, Hao N, Kilmer ME, Miller EL. Tensor-based formulation and nuclear norm regularization for multi-energy computed tomography. Image Processing, IEEE Transactions on. 2014;23(4):1678–1693. doi: 10.1109/TIP.2014.2305840. [DOI] [PubMed] [Google Scholar]
- 31.Li L, Chen Z, Wang G, Chu J, Gao H. A tensor PRISM algorithm for multi-energy CT reconstruction and comparative studies. Journal of X-Ray Science and Technology. 2014;22(2):147–163. doi: 10.3233/XST-140416. [DOI] [PubMed] [Google Scholar]
- 32.Li L, Chen Z, Cong W, Wang G. Spectral CT modeling and reconstruction with hybrid detectors in dynamic-threshold-based counting and integrating modes. Medical Imaging, IEEE Transactions on. 2015;34(3):716–728. doi: 10.1109/TMI.2014.2359241. [DOI] [PubMed] [Google Scholar]
- 33.De Lathauwer L, De Moor B, Vandewalle J. A multilinear singular value decomposition. SIAM Journal on Matrix Analysis and Applications. 2000;21(4):1253–1278. [Google Scholar]
- 34.Duan G, Wang H, Liu Z, Deng J, Chen Y-W. K-CPD: Learning of overcomplete dictionaries for tensor sparse coding; International Conference on Pattern Recognition (ICPR 2012); 2012. pp. 493–496. [Google Scholar]
- 35.Peng Y, Meng D, Xu Z, Gao C, Yang Y, Zhang B. Decomposable nonlocal tensor dictionary learning for multispectral image denoising; Computer Vision and Pattern Recognition (CVPR), 2014 IEEE Conference on; 2014. pp. 4321–4328. [Google Scholar]
- 36.Zubair S, Wenwu W. Tensor dictionary learning with sparse tucker decomposition; 2013 18th International Conference on Digital Signal Processing (DSP); 2013. pp. 1–6. [Google Scholar]
- 37.Tan S, Zhang Y, Wang G, Mou X, Cao G, Wu Z, Yu H. Tensor-based dictionary learning for dynamic tomographic reconstruction. Physics in Medicine and Biology. 2015;60(7):2803–2818. doi: 10.1088/0031-9155/60/7/2803. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 38.Zhang Y, Mou X, Xu Q, Yu H, Wang G. Tensor-based dictionary learning for spectral CT reconstruction; The 13th International Meeting on Fully Three-dimensional Image Reconstruction in Radiology and Nuclear Medicine; 2015. pp. 507–510. [Google Scholar]
- 39.Aharon M, Elad M, Bruckstein A. K-SVD: An algorithm for designing overcomplete dictionaries for sparse representation. IEEE Transactions on Signal Processing. 2006;54(11):4311–4322. [Google Scholar]
- 40.Zhuang W, Gopal SS, Hebert TJ. Numerical evaluation of methods for computing tomographic projections. Nuclear Science, IEEE Transactions on. 1994;41(4):1660–1665. [Google Scholar]
- 41.Elbakri I, Fessler J. Statistical image reconstruction for polyenergetic x-ray computed tomography. IEEE Transactions on Medical Imaging. 2002;21(2):89–99. doi: 10.1109/42.993128. [DOI] [PubMed] [Google Scholar]
- 42.Wang G, Jiang M. Ordered-subset simultaneous algebraic reconstruction techniques (OS-SART) Journal of X-Ray Science and Technology. 2004;12(3):169–177. [Google Scholar]
- 43. [Online]. Available: http://www.sandia.gov/%7Etgkolda/TensorToolbox/
- 44.Zhang L, Zhang L, Mou X, Zhang D. FSIM: a feature similarity index for image quality assessment. Image Processing, IEEE Transactions on. 2011;20(8):2378–2386. doi: 10.1109/TIP.2011.2109730. [DOI] [PubMed] [Google Scholar]
- 45.Wang Z, Bovik A, Sheikh H, Simoncelli E. Image quality assessment: From error visibility to structural similarity. Image Processing, IEEE Transactions on. 2004;13(4):600–612. doi: 10.1109/tip.2003.819861. [DOI] [PubMed] [Google Scholar]
- 46. http://spectrumgui.sourceforge.net/ [Google Scholar]
- 47.Segars WP, Tsui BM, Frey EC, Johnson GA, Berr SS. Development of a 4-D digital mouse phantom for molecular imaging research. Molecular Imaging and Biology. 2004;6(3):149–159. doi: 10.1016/j.mibio.2004.03.002. [DOI] [PubMed] [Google Scholar]
- 48.Yu H, Ye Y, Zhao S, Wang G. Local ROI reconstruction via generalized FBP and BPF algorithms along more flexible curves. International journal of biomedical imaging. 2006;2006:14989. doi: 10.1155/IJBI/2006/14989. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 49.Zhang Y. Thesis. Xi’an Jiaotong University; 2015. Mar, Key techniques for artifacts and noise reduction in x-ray computed tomography. [Google Scholar]
- 50. [Online]. Available: https://ece.uwaterloo.ca/%7Ez70wang/research/ssim/ [Google Scholar]
- 51. http://sse.tongji.edu.cn/linzhang/IQA/FSIM/FSIM.htm. [Google Scholar]
- 52.Butler A, Anderson N, Tipples R, Cook N, Watts R, Meyer J, Bell A, Melzer T, Butler P. Bio-medical x-ray imaging with spectroscopic pixel detectors. Nuclear Instruments and Methods in Physics Research Section A. Accelerators, Spectrometers, Detectors and Associated Equipment. 2008;591(1):141–146. [Google Scholar]
- 53.MŘnch B, Trtik P, Marone F, Stampanoni M. Stripe and ring artifact removal with combined wavelet-Fourier filtering. Optics Express. 2009;17(10):8567–8591. doi: 10.1364/oe.17.008567. [DOI] [PubMed] [Google Scholar]
- 54.Mou X, Wu J, Bai T, Xu Q, Yu H, Wang G. Dictionary learning based low-dose x-ray CT reconstruction using a balancing principle. Proc. of SPIE. 2014;9212:921 207–921 207–15. [Google Scholar]