Abstract
Although a number of studies have reported that cells cultured on a stretchable substrate align away from or perpendicular to the stretch direction, how cells sense and respond to compression in a three-dimensional (3D) matrix remains an open question. We analyzed the reorientation of human prostatic normal tissue fibroblasts (NAFs) and cancer-associated fibroblasts (CAFs) in response to 3D compression using a Fast Fourier Transform (FFT) method. Results show that NAFs align to specific angles upon compression while CAFs exhibit a random distribution. In addition, NAFs with enhanced contractile force induced by transforming growth factor β (TGF-β) behave in a similar way as CAFs. Furthermore, a theoretical model based on the minimum energy principle has been developed to provide insights into these observations. The model prediction is in agreement with the observed cell orientation patterns in several different experimental conditions, disclosing the important role of stress fibers and inherent cell contractility in cell reorientation.
Keywords: Cell Reorientation, NAFs, CAFs, Stress Fiber, Energy Minimization
1 Introduction
Most cells and organs, from the simplest to the most complex, are mechanosensitive (1). This property enables a cell to sense and respond to mechanical stimuli in its immediate surroundings, leading to biological signaling cascades that allow the cell to adapt to its local microenvironment through changes in cell morphology, proliferation, contractility, motility, orientation, and viability (1–10).
Numerous reports have demonstrated that cells cultured on an elastic substrate subjected to a uniaxial cyclic stretch tend to reorient themselves away from or perpendicular to the stretch direction (2, 6, 8, 10–14), which is often referred to as stretch-avoidance or strain-avoidance (15). Concurrent with cell reorientation, the remodeling of stress fibers (SFs) in response to a stretch stimulus has also been observed. Ventral SFs, as the most commonly observed SF type, are long and extend most of the length of cells (16). The two ends of ventral SFs are anchored to the extracellular matrix (ECM) via focal adhesions (FAs), forming both outside-in and inside-out mechanotransduction pathways (17). Numerous studies have suggested that SFs play a critical role in cell reorientation and morphogenesis under mechanical stimuli (3, 6, 7, 10, 11, 18, 19). Furthermore, it has been shown that inhibition of SF formation leads to cell alignment with the stretch direction, indicating SFs are critical for cell stretch-avoidance or strain-avoidance (20).
The mechanism of the observed cell reorientation in response to a uniaxial stretch has been discussed. For example, one theoretical model proposed that actin filaments orient to the direction in which the deformation of the stretched substrate is a minimum so that the energy of SFs is least disturbed (4). This hypothesis was confirmed with experiments conducted on both fibroblasts and endothelial cells. Another study suggested that the reorientation was driven by a dissipative process in which the passively stored cell elastic energy relaxed to a minimum through aligning cell bodies away from the stretch direction (10). A statistical thermodynamics analysis considering passive mechanical responses and active subcellular dynamic remodeling predicted that cells would orient in the direction in which SF formation is energetically most favorable (21). Other studies suggested that SFs would align in the direction in which the total energy reaches a minimum (7, 14) and explained realignment of SF-FA assembly in response to substrate stretching (22) on the basis of Maxwell’s global criterion for stability. In addition to these analyses based on an energetic argument, it has also been predicted that stretch-induced SF disassembly is an important factor in determining the rate of cell alignment (18). In short, it is believed that cell reorientation under stress is driven by the tendency of cell energy minimization, and that SFs play a critical role in mediating this process.
Despite these significant findings, some important issues of cell behavior under stress still need to be addressed. First, most studies of cell reorientation in response to a mechanical stimulus, whether experimental or theoretical, are conducted with cells on a flexible two-dimensional (2D) substrate, which is different from the 3D microenvironment in vivo. To date, only a few investigations have been carried out to probe cellular responses to mechanical forces in a 3D environment, and the resulting cell behaviors differ from those observed in 2D studies. For example, two studies reported that fibroblasts aligned themselves along the stretch direction in 3D, which is contradictory to the stretch-avoidance displayed in 2D (23–25). This apparently inconsistent behavior has been hypothesized as a result of cells in 3D interacting with the matrix, sensing the applied force, and reorienting in a different manner (26). However, this speculation does not adequately address the mechanisms by which cells behave differently in 2D and 3D environments. Another report demonstrated that cells, as well as F-actin, exhibited stretch-avoidance at the surfaces of a collagen matrix but showed no preferable orientation in the core of the gel under stretching (27). The authors hypothesized that the different cell behaviors observed at the surface and inside the gel are due to contact guidance from the collagen fibrils interfering with cell orientation in the bulk of the matrix; however, in another work (23), it was shown by scanning electron microscopy (SEM) for cell-seeded and cell-free collagen fibrils that contact guidance only plays a marginal role. As such, cell response to mechanical stimuli in 3D environments is different from and more complex than those observed on 2D substrates, and the underlying mechanism is still not clear.
Importantly, while the role of cell contractility in cell orientation has been recognized in previous stretching studies in 2D through inhibition of cell contractility (8, 11, 13, 14, 20), studies with 3D conditions are still lacking. Moreover, besides the tensile forces that have been examined in most previous studies, compression is another common type of mechanical stimulus in vivo. For example, articular cartilage and cardiac fibroblasts experience both tensile and compressive forces (28). Uncontrolled tumor growth in a limited space can induce a continuous mechanical compressive stress in the tumor and the surrounding cells and tissue (29). Reports have shown that compression alters gene expression (30–33), cell morphology (32, 34), differentiation (35), alignment (26, 32, 36), and proliferation/apoptosis (33). Interestingly, it has been shown that fibroblasts and smooth muscle cells realign themselves perpendicular to the direction of compression due to the contact guidance of collagen fibrils (35). However, again, this possibility might be discounted by SEM images of collagen fibrils in other reports (23, 26). As such, the mechanism underlying cell alignment in response to compression is still largely unknown.
In view of the fact that it is currently not clear how and why cells of different contractility realign in response to 3D compression, we investigated the response of human prostatic normal tissue fibroblasts (NAFs) and cancer-associated fibroblasts (CAFs) to static compression in a 3D collagen I matrix. We experimentally demonstrate that inherent cell contractility affects cell realignment in response to compression and construct a theoretical model based on the minimum energy principle to provide insights into the different behaviors of NAFs and CAFs under compression.
2 Material and methods
2.1 Cell culture
The human prostatic NAFs and CAFs used in this study were isolated as previously described (37). Cells were maintained in Roswell Park Memorial Institute (RPMI) 1640 medium with 10% fetal bovine serum (FBS) and penicillin–streptomycin as previously described (38, 39).
2.2 Preparation and loading of 3D collagen I gel and cell mixture for compression assays
NAFs and CAFs were labeled with CellTracker™ Green dye (Life technology, Carlsbad, CA) 24 h prior to being embedded in 3D collagen I gels (rat-tail type I collagen, BD Biosciences, Bedford, MA). Then, the collagen I was mixed in PBS to a final concentration of 2 mg/ml, and the pH was neutralized with 1 N NaOH on ice, per manufacturer’s instructions. NAFs and CAFs were dissociated and re-suspended in RPMI culture media (250,000 cells/ml) on ice. Cells were then mixed with collagen I solution to a final suspension of ~75,000 cells/ml for each 2 mg/ml collagen I gel mixtures. Next, 700 μl of the cell-gel mixture was loaded into a 4-well Nunc™ Lab-Tek™ II Chamber Slide™ (Cole Parmer, Vernon Hills, IL) and incubated for 30 min at 37°C to allow the collagen I gel with embedded cells to solidify. Subsequently, culture media was loaded into the cell chambers, and the cells were incubated at 37°C overnight and then used for compression assays and imaging.
2.3 The cell-compression fixture
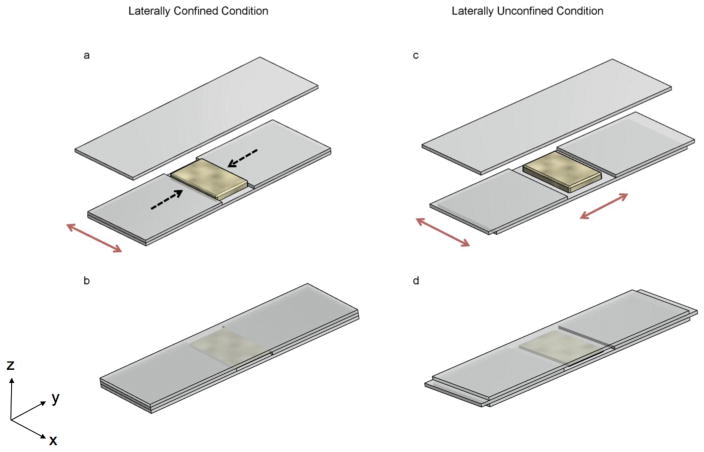
The cell-compression fixture is composed of three layers of glass slides (25 mm in width, 75 mm in length and 1.0 mm in height, VWR International, LLC, Suwanee, GA). The middle layer consists of two shorter glass slides (32.5 mm in length) that were stacked on top of the bottom glass slide with a ~10 mm gap between them (see Fig. 1a). For the laterally confined case, the gap was made the same as the width of the cell-gel mixture. In this case, when subjected to vertical compression by another glass slide from the top (Fig. 1b), the cell-gel mixture was restricted in the lateral direction denoted by the black dotted arrows in Fig. 1a, but could expand freely in the direction denoted by the red arrows. In the laterally unconfined scenario (see Fig. 1c), the gap between the two middle layer glass slides was wider than the cell-gel mixture, allowing the mixture to expand freely in both directions under vertical compression (see Fig. 1d). During the compression assay, the cell-gel mixture was carefully transferred from the Nunc™ Lab-Tek™ II Chamber Slide™ to the fixture, and another glass slide was placed on top as shown in Fig. 1b, d. The cell-gel mixture (1.4~1.5 mm thick) was compressed to 1 mm thick; thus, ~30% compressive strain was applied to the gel along the vertical direction. The assembly was secured using binder clips and submerged in a petri dish filled with media, and the cell-gel mixture was subjected to compression overnight (~18 h).
Fig. 1.
Schematic of the cell-compression assay. In the laterally confined condition (a, b), the middle layer of glass slides formed a gap the same as the width of the cell-gel mixture so that the expansion of the gel in this direction was restricted. In the laterally unconfined condition (c, d), the middle layer of glass slides formed a gap wider than the cell-gel mixture so that the gel can expand in both directions. The cell-gel mixture was compressed vertically by pressing another glass slide from the top (b, d). The black dashed arrows denote the laterally confined direction, while the red ones indicate the free (unconfined) directions.
2.4 Determining cell orientation using fluorescence microscopy
Images of the cells in the 3D compression fixture were collected using a Quorum WaveFX-X1 spinning disk confocal system, which contained a Nikon Eclipse Ti microscope (Melville, NY), an EM-CCD camera (Hamamatsu, Hamamatsu City, Japan), and a 10X ADL objective (NA 0.25), with MetaMorph software. The Quorum confocal system has a Yokogawa CSU-X1 spinning disk (Yokogawa Electric Corporation, Newnan, GA) with Borealis upgrade/modifications (Guelph, Canada) and the CellTracker™ Green dye was excited using a 491 nm laser line. The emission filter used was 525/50 from Semrock (Rochester, NY).
2.5 Determining cell orientation using Fast Fourier Transform
Fast Fourier Transform (FFT) was used as previously reported (40) to statistically characterize the cell orientation for each compression result. The FFT was performed on a fluorescence confocal microscopy image of the cells using ImageJ software (NIH, http://rsb.info.nih.gov/ij) with the Oval Profile plug-in (authored by William O’Connnell). A 512 pixel diameter circle was overlapped with the FFT output image (2048×2048 pixels) in the center, and a radial summation of gray value intensities over the circle was conducted with a resolution of single radial degree. We further normalized the radial intensity through dividing it by the total intensity. Note that in order to generate more statistically significant data, nine representative fluorescence micrsocopy images from different locations within the cell-gel mixture were merged into a single montage. These stitched images were then analyzed using the FFT method described above.
2.6 Collagen gel contractility assay
NAFs and CAFs were suspended in full growth medium at a density of 600,000 cells/ml. Rat tail collagen I was diluted to 3 mg/ml in PBS, and the pH was neutralized with 1N NaOH. Cell suspension and the collagen I gel solution were mixed at a 1:2 ratio to get a final mixture with 200,000 cells/ml of cells and 2 mg/ml of collagen I gel. 600 μl of the above mixture was loaded into each well of a 12-well-plate and incubated at 37°C for 1 h to allow the gel to polymerize. Gels were then covered with 1 ml of medium and detached from plates using a pipette tip by gently circling around the inside wall of each well. Gels were incubated at 37°C for the indicated time to allow for contraction. The gels were imaged, and the gel area was measured from scanned gel images using imageJ. Cell contractility was assessed by calculating the percentage of the final gel area to the initial gel area after different time periods.
2.7 Western blot
Cell lysates from NAFs and CAFs were prepared using RIPA buffer (50 mM Tris-HCl, pH 7.4, 150 mM NaCl, 1% NP-40, 0.25% sodium deoxycholate and 1 mM EDTA), supplemented with a protease inhibitor cocktail (Sigma-Aldrich, San Louis, MO). Equal amount of cell lysates (30 μg) were run in polyacrylamide gels and transferred to nitrocellulose membranes, which were then blotted for α-smooth muscle actin (αSMA, clone 1A4) and anti-tubulin (clone DM1A) (Sigma-Aldrich). Infra-red dye conjugated secondary antibodies (IRDye 680 and 800, LI-COR Biosciences, Lincoln, NE) were used to detect bands in the Odyssey infrared imaging system (LI-COR Biosciences). Western blot band intensities were determined using Image Studio Lite version 4 (LI-COR Biosciences). αSMA band intensity was normalized to tubulin, which was a loading control.
2.8 Transforming growth factor β (TGF-β) stimulation assay
The NAF-gel mixture was prepared following the same protocol as described in section 2.2 and 2.3, with 10 μl TGF-β (1 μg/ml) added to the media before being subjected to compression overnight (~18 h).
2.9 Assumptions in the theoretical model based on the minimum energy principle
In the theoretical modeling, we first deal with the laterally confined case and then extend the model to the laterally unconfined scenario. For the laterally confined case, we consider a single cell embedded in a collagen I gel subjecting to compression in the z-direction. The gel is confined in the y-direction but can expand freely in the x-direction. We construct the model based on the energy minimization principle, i.e., cells tend to realign themselves to achieve minimum energy. The model also considers the important role of SFs in the reorientation and morphogenesis of cells. We assume that the cell is composed of bundles of SFs that are parallel to the axis of the cell. From an energy consideration, this bundle can be regarded as equivalent to a single SF with corresponding stiffness of the whole bundle. Since the SF is composed of assembled actin filaments, we assume that the SF is a spring system that consists of a number of identical short actin filament springs connected in series.
For simplicity and based on the fact that the model is a thermodynamic analysis, we treat the collagen gel as a linearly elastic material (41, 42) with linear stress-strain relationship. The boundary conditions imposed led to no normal force in the x-direction at equilibrium; however, forces in the y- and z- directions always exist and will be transmitted to the cell. It is important to note that before reaching equilibrium, the expansion of the gel in the x-direction will also stretch the cell.
The energy analysis on the cell was conducted following the minimum energy principle requiring that the equilibrium orientation of the cell should be energetically preferred. The favored orientation for cells exhibiting lower contractility is the free, unconfined x-direction in the case of laterally confined compression. This is because in the x-direction, the tension of the cell caused by the expansion of the gel can be gradually relaxed by aggregated actin filaments, which is consistent with the fact that when exposed to external mechanical stress, actin polymerizes to form SFs (43). The rearrangement and redistribution of actin filaments serve to reduce the overall stress (44). Therefore, at the equilibrium length, we assume that the axial tension is eventually eliminated by the assembled actin filaments if the polarity of the cell body is aligned in the unconfined x-direction. By adjusting its orientation and assembling actin filaments, the total energy of the cell could be minimized.
Because living cells, even in the absence of external mechanical loads, possess pre-stressed SFs due to inherent cell contractility (22), we take this pre-stressed condition into account in our model. Previous studies have shown that the contractile force direction is parallel to the polarity of an elongated cell (45). Recognizing that fibroblasts are highly elongated cells, it is reasonable to assume that the contractile force only exists in the polarized direction while contractile forces in other directions can be neglected. Importantly, it has been shown that SF shortening is prevented in normal live and healthy cells (16); and therefore, the stress in the vertically compressed and laterally confined directions cannot be released by shortening SFs. Built on the above understanding, our model predicts that cells both with or without significant inherent contractility will realign in an equilibrium orientation where the total cell energy is minimized.
3 Results
3.1 Cell reorientation under 3D compression
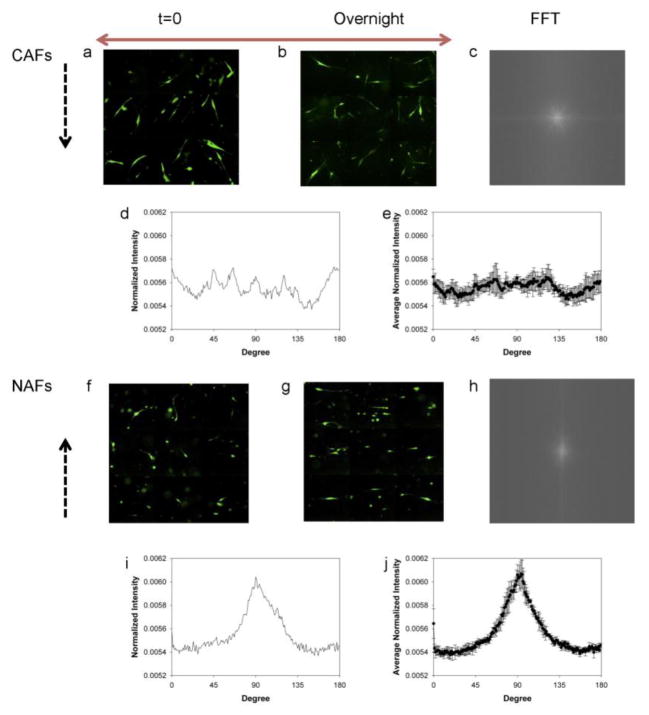
The fluorescence images of NAFs and CAFs were taken at both the beginning and the end of the 3D compression assay. We found that CAFs exhibited a random distribution after overnight compression in the laterally confined condition (see Fig. 2a, b), i.e., no favorable orientation of CAFs was observed. In contrast, NAFs initially exhibiting a random distribution (Fig. 2f) were aligned to the free direction (denoted by a red arrow) and away from the laterally confined direction (indicated by black dotted arrows) after compression, as shown in Fig. 2g.
Fig. 2.
Different alignments in the horizontal plane for CAFs and NAFs exposed to laterally confined compression. Montages of fluorescence images show CAFs and NAFs immediately after compression (a, f). Montages of fluorescence images show CAFs and NAFs after overnight compression (b, g). FFT output images of CAFs and NAFs after overnight compression (c, h). Normalized radial summation of pixel intensities over a circle projection of FFT images of CAFs and NAFs after overnight compression (d, i). The average normalized pixel intensity of CAFs and NAFs from four independent experiments (e, j). The black dashed and red arrows indicate the laterally confined and free directions, respectively.
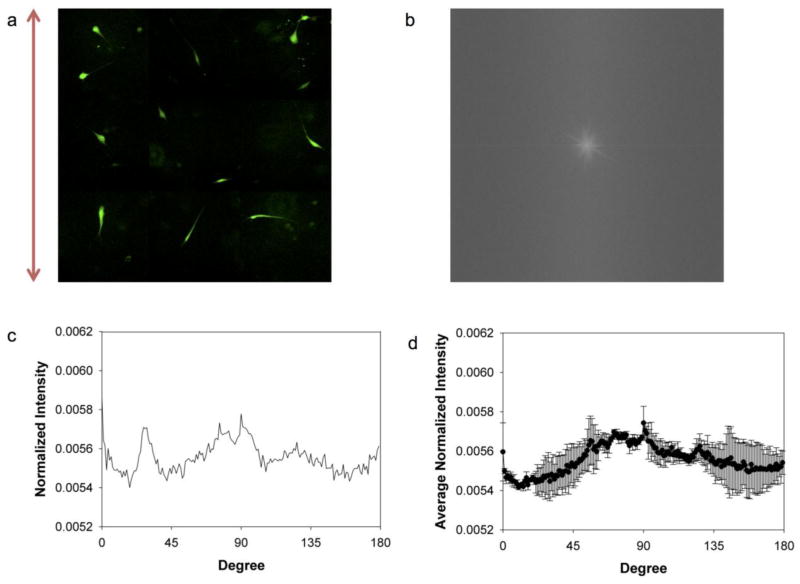
To quantify the cell orientation, FFT was performed on the fluorescence images. The image of CAFs at the end of compression (Fig. 2b) generates a round-shaped FFT output image with rather evenly distributed pixel intensities (Fig. 2c) in which no particular angle is favored. In contrast, the image of compressed NAFs (Fig. 2g) produces a spindle-shaped FFT image, as shown in Fig. 2h, meaning the pixel intensities are higher along one specific direction.
The FFT frequency distribution with respect to the angle was generated by carrying out a radial summation of the pixel intensities over the aforementioned circle for every degree between 0° and 179°. The FFT image is symmetrical; and therefore draws no distinction for the other semi-circle (46). Fig. 2d and 2i show the normalized summed pixel intensities versus angles, which provides a quantitative description of cell alignment. The shape and location of the peaks of the FFT plots exhibit the extent and direction to which the cells align. Fig. 2i clearly shows a prominent peak at 90°, indicating that NAFs aligned along the free direction after being compressed overnight. It is worth noting that the FFT output images yield frequencies orthogonal to those in the original images (46). On the other hand, Fig. 2d shows that CAFs do not exhibit a preferred direction in which the pixel intensity is noticeably higher (note that the fluctuations are due to the limited number of samples and the distributed peaks are not preferred directions, which appear at different angles in different tests). The same trends were observed for multiple trials and the average of the normalized intensities from four independent experimental results are plotted in Fig. 2e and 2j. For NAFs, the averaged distribution is very similar to that from each test while for CAFs, the fluctuation peaks are canceled out significantly, leading to an even flatter average distribution. The error bars in Fig. 2e are significantly larger than those in Fig. 2j, further underscoring the random orientation of CAFs from experiment to experiment.
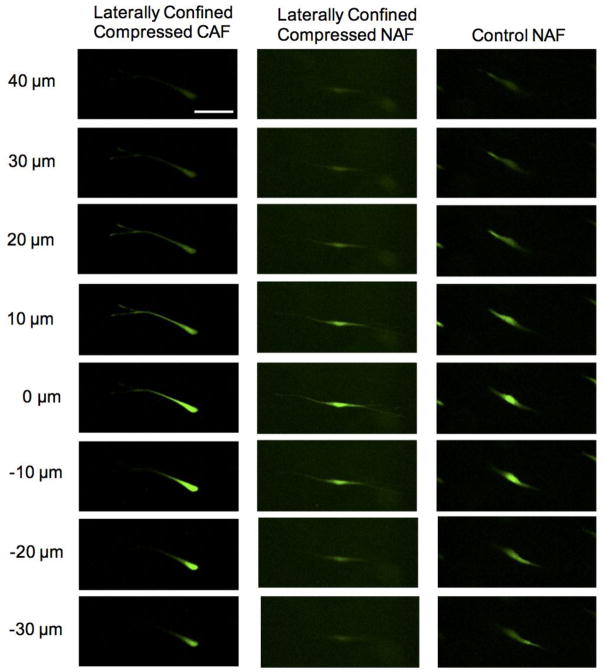
Importantly, not only did NAFs realign themselves in the horizontal plane to the free direction, they also steered away from the compressed direction. A set of z-stack fluorescence images in Fig. 3a and a supplementary animation (Online Resource 1) clearly demonstrate that laterally confined compressed CAF cells distributed in different focal planes in a range of 70 μm. In contrast, laterally confined compressed NAFs, in Fig. 3b and Online Resource 2, located in almost the same focal plane under compression. The whole cell body gradually came into sight and went out of sight at the same time. Without any compression, NAF cells showed no favored direction and were situated in different focal planes with protrusions spanning 70 μm in the z-direction, as shown in Fig. 3c and a supplementary animation (Online Resource 3).
Fig. 3.
Different alignments in the vertical direction for CAFs and NAFs exposed to laterally confined compression. A CAF distributes in different focal planes under laterally confined compression (a). A NAF realigns perpendicular to the compressed direction under laterally confined compression and locates in the same focal plane (b). A NAF in the control group locates in different focal planes (c), the scale bar is 100 μm
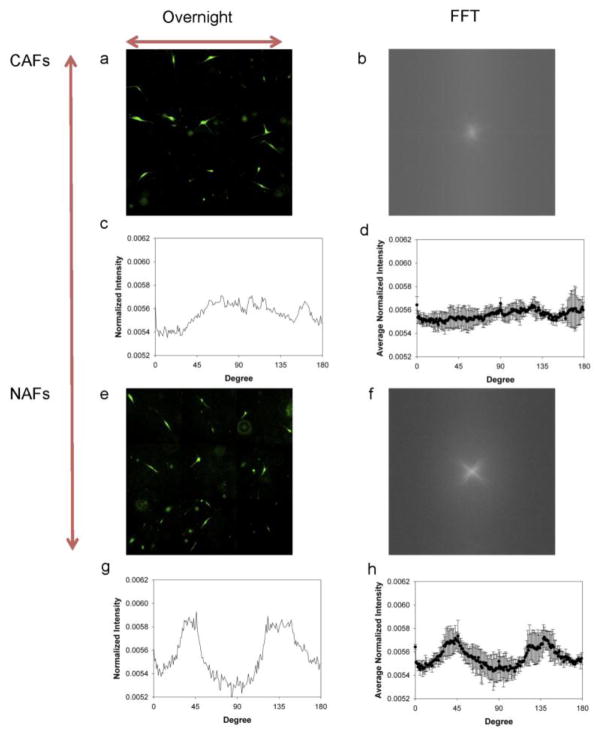
For the laterally unconfined case, the fluorescence images (Fig 4a, e), FFT output images (Fig. 4b, f) and radial summation plots (Fig. 4c, g) all show that similar to the laterally confined case, CAFs show a random distribution after being compressed overnight; however, the NAFs, instead of aligning to one direction, are reoriented into two directions with angles around 45° and 135° relative to the x-direction. Again, the trend was observed for multiple experiments (Fig. 4d, h).
Fig. 4.
Different alignments in the horizontal plane for CAFs and NAFs exposed to laterally unconfined compression. Montages of fluorescence images of CAFs and NAFs after being compressed overnight (a, e). FFT output images of CAFs and NAFs (b, f). Normalized radial summation of pixel intensities over a circle projection of FFT images of CAFs and NAFs (c, g). The average normalized pixel intensity of CAFs and NAFs from three independent experiments (d, h). The red arrows show the free directions
3.2 Model formulation
Laterally confined condition
The total energy E of a cell consists of the homeostatic elastic potential E0 due to cell contraction (4), the elastic potential converted from the external mechanical load Ee, the chemical potentials of assembled and disassembled actin filaments Ea and Ef, and the energy exchanged with the surrounding microenvironment Es (47).
| (1) |
We consider the cell energy under two situations, i.e., with and without external mechanical load. Assuming that the cell axis forms angles of θx, θy, θz with the coordinate axes x, y and z (Fig. 5a) and without losing any generality, we can set 0 ≤ cosθx ≤ 1, 0 ≤ cosθy ≤ 1, 0 ≤ cosθz ≤ 1.
Fig. 5.
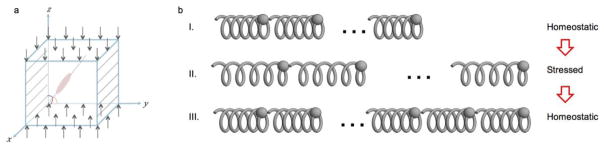
A single cell embedded in a cubic collagen gel (a). The cell represented by a pink oval forms angles of θx, θy, θz with coordinate axes x, y and z (denoted by red, green and purple curves). The gel-cell mixture is subjected to confinement in the y-direction and compression in the z-direction (denoted by black skew lines and black arrows, respectively). Actin filaments represented by individual springs connected in series to form a SF spring system (b). SF at homeostatic state (I) is elongated due to gel expansion. The tension caused by elongation of actin filaments (II) is relaxed with additional actin filaments assembled in the SF (III), then the homeostatic state is recovered.
Considering the SF as a spring system that is composed of a series of identical actin filament springs, then ksf = ka/Na, where ksf is the spring constant of the SF, ka is the spring constant of each actin filament, and Na is the number of assembled actin filaments. With these assumptions, we can rewrite the total energy of the cell given by Eq. 1 as (see Appendix):
| (2) |
Here, e0 = kala2ε02/2, which is the elastic potential of each actin filament due to cell contraction; la is the length of each actin filament; ε0 is the pre-stretch strain; εxc is the strain along the long axis of the cell body caused by the gel displacement in the x-direction, σyc and σzc are the stress components along the long axis of the cell body caused by the forces applied to the cell from the gel in the y- and z- directions, which are equal to σycosθy and σzcosθz, respectively; l = Nala, which is the length of the cell; μa and μf are the chemical potentials of assembled and disassembled actin filaments, and Nf is the number of disassembled actin filaments.
Since we assume that the SF is a spring system along the long axis of the polarized cell body, only strains along this direction change the elastic potential and contribute to Ee. Here εxc is the strain along this axis of the cell body caused by the gel displacement in the x-direction, which is released by gradually assembled actin filaments before reaching equilibrium. This component results in stretching of the cell. Note that σyc and σzc cause compression to the cell, which is opposite to the direction of εxc. As such, the total strain along the long axis of the cell body is εxc − σycosθyNa/ka − σzcosθzNa/ka. Since the pre-stretch energy has already been considered in the first term, the displacements in the second term are from the external mechanical load alone.
Now we consider εxc. The strain that results from the elongation of individual actin filaments due to gel expansion is eventually released by the assembly of additional actin filaments, and SF return back to the homeostatic state prior to the application of mechanical force, as shown in Fig. 5b I, II, and III. This concept is consistent with previous observations that cells actively respond to perturbations from the ECM by re-establishing the homeostatic level of force and maintaining fiber strain under normal condition (19, 48). Therefore, SF elongation caused by gel expansion εx is achieved by more assembled actin filaments and εxc satisfy the equation as follows.
| (3) |
where N0 is the number of the assembled actin filaments prior to external stimulus. Therefore, the strain along the axis of the cell body caused by the displacement in the x-direction is:
| (4) |
Substituting Eq. 4 and l = Nala into Eq. 2 yields
| (5) |
When E reaches a minimum, dE/dNa = 0. For sufficiently small homeostatic strain ε0, ε0 can be neglected. Under this condition, solving for dE/dNa = 0 yields cosθy = cosθz = 0 and cosθx=1, i.e., θx = 0°, θy = θz = 90° (see Appendix for more details). This means cells are aligned to the x-direction and perpendicular to the y- and z-direction to achieve a minimum energy state, as observed in our experimental results. In this way, the homeostatic level of force is re-established. In the Discussion section, we will demonstrate that this is the reason for NAFs to show an overall alignment along the unrestricted direction under compression.
On the other hand, for cells with large inherent stress, ε0 cannot be neglected in Eq. 5. In this case, dE/dNa = 0 gives
| (6) |
Along with cos2θx +cos2θy + cos2θz = 1, there are three unknowns, θx, θy and θz and only two equations. Therefore, no specific combination of angles θx, θy, θz can be obtained. This is why CAFs, with large inherent stress, do not show any preferred alignment direction.
Laterally unconfined condition
Now we extend the model to the laterally unconfined condition. In this case, the gel is free to expand along both the x- and y- directions. Thus, these two directions are equivalent to each other. For cells with low inherent ε0, the minimum energy principle leads to cos θz = 0, and . Therefore, θx = θy = 45°, and θz = 90° (see Appendix for details). In this case, cells are aligned diagonally with the x- and y- directions and away from the z-direction, which is again consistent with our experimental observation.
On the other hand, for cells with large inherent ε0, Eq. 6 becomes
| (7) |
Again, no specific combination of angles θx, θy and θz can be obtained in this case.
4 Discussion
To date, most investigations on the effects of mechanical stimuli on cell reorientation have been done by cyclically stretching cells laying on 2D deformable substrates (2, 6, 8, 10, 11). In these studies, cells reorient themselves away from (i.e., perpendicular to) the stretch direction where the membrane deformation is the least and thus is most energetically favorable. However, this “stretch-avoidance” or “strain-avoidance” phenomenon does not occur when cells are embedded in a 3D matrix. Reported results have shown that fibroblasts in a 3D matrix align themselves along the axis of tensile force in response to stretching (23–25) and away from the axis of compressive force in response to compression (36). Even though various hypotheses have been proposed to account for the difference between the 2D and 3D cases (26, 49), it is still not clear why cells do not show “stretch-avoidance” or “strain-avoidance” in 3D.
In our studies, the seemingly different response for cells in 3D matrices is in fact consistent with their behavior in 2D, i.e., both follow minimum energy principle with cells realigning themselves to achieve minimum energy. Cells in a 3D matrix encounter complex tensile and compressive forces from three different directions simultaneously; thus, “stretch-avoidance” or “strain-avoidance” in 2D models, which is equivalent to energy minimization is not directly applicable in a 3D environment. The present study found that cells such as NAFs in 3D prefer to align in the free/stretching direction (note that in our experiment, the free direction is passively stretched) and avoid the compressive direction. This is because cells can reorient the axis of cell bodies to the free/stretching direction and release tension through remodeling SFs via actin filament assembly. However, the compressive stress cannot be released by shortening SFs since SF shortening is prevented in normal living cells (16). Therefore, cells such as NAFs possess lower energy when they align with the free/stretching direction. This could explain why cells embedded in a 3D matrix subjected to stretching or compression would realign themselves to the stretching direction. Moreover, with more cell-matrix interaction involved in 3D, inherent cell contractility could play an important and complex role. This leads to the observation that cells with a high inherent contractility exhibit random distribution even though they have achieved minimum energy states through reorientation. Overall, our study suggests that even though the mechancially triggered cell reorientation in 3D can show more complex patterns, their behavior is still governed by the minimum energy principle.
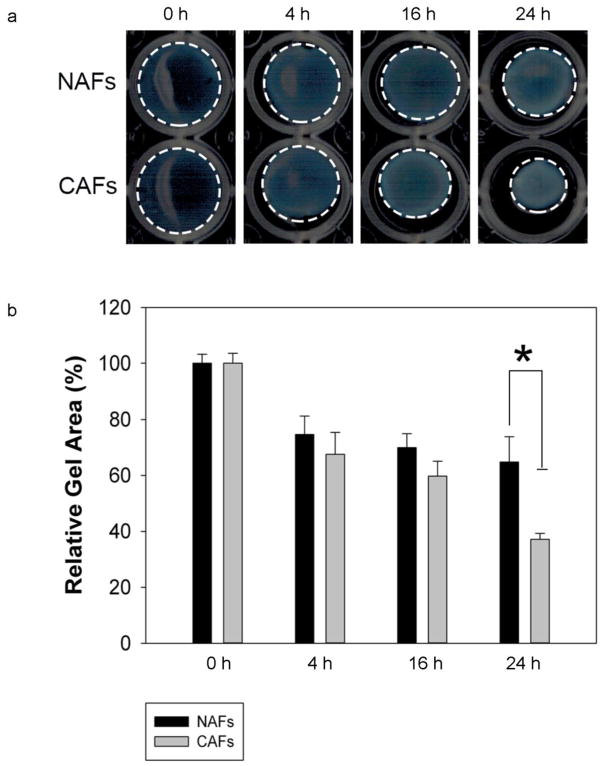
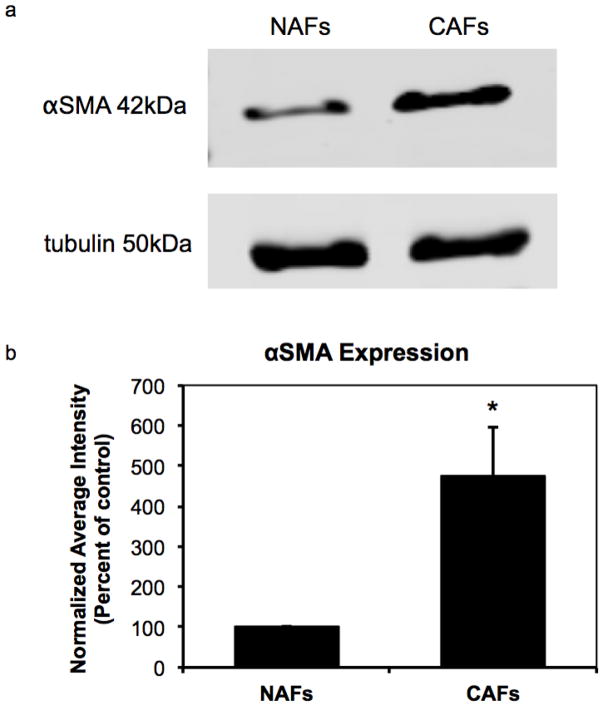
To verify that the NAFs and CAFs in our studies are of very different contractility, we conducted a cell contractility assay by embedding NAFs and CAFs in collagen I gels and measured the reduction of the gels’ diameter after 0 h, 4 h, 16 h, and 24 h’s incubation (see Fig. 6a and 6b). The collagen gel containing CAFs exhibits significantly more contraction than its counterpart, indicating that CAFs have a much higher inherent stress than NAFs. In addition, we studied α-smooth muscle actin (αSMA) expression in NAFs to CAFs, as an established CAF marker (50–52). Elevated expression of the αSMA isoform has been shown to confer a high contractile activity (53). As shown in Fig. 7a and 7b, CAFs used in this study express 5 times higher levels of αSMA than NAFs, indicating higher cell contractility.
Fig. 6.
CAFs exhibited much higher contractility than NAFs. CAFs and NAFs were embedded in type I collagen gels, which were subsequently incubated for 24 h at 37°C to allow for contraction. Images of contracted gels with NAFs and CAFs were taken after 0 h, 4 h, 16 h, and 24 h. The gel circumferences are outlined with dashed white lines (a). At the end of the contraction assay, the area of the gels was measured and expressed as a percentage of the original gel area before contraction. Error bars represent s.e.m. from N=3 independent experiments. A significant difference in relative gel area appeared 24 h after beginning the incubation, *P<0.005 (b)
Fig. 7.
Western blot analysis shows higher αSMA expression in CAFs than in NAFs (a). αSMA band intensity was normalized by tubulin loading control. Normalized average intensity plot indicates a significant difference in αSMA expression between NAFs and CAFs, *P<0.005, N=4 (b)
To further confirm that cell contractility is the determining factor leading to the different orientation patterns between NAFs and CAFs, we stimulated NAFs with TGF-β and subjected them to compression. Cells treated with TGF-β has been previously shown to have increased cell contractility (54–56). Our results show that TGF-β treated NAFs do not realign towards the free direction in the lateral confined condition (see Fig. 8a, b and c), but present a random distribution, which further confirms the important role of cell contractility in cell reorientation.
Fig. 8.
NAFs with increased cellular contractility induced by TGF-β exposed to laterally confined compression. Montages of fluorescence images of NAFs after being compressed overnight (a). FFT output images of NAFs (b). Normalized radial summation of pixel intensities over a circle projection of FFT images of NAFs (c). The average normalized pixel intensity of NAFs from three independent experiments (d). The red arrows show the free direction
While the developed model in this work includes biomechanical contributions, such as cell contractility, SF assembly, and chemical potentials, it does not include the dynamic contribution of biochemical signaling. For example, the small GTPases RhoA, Rac1 and Cdc42 are reported to be central regulators of actin dynamics (57), and the MAPK family including JNK, ERK and p38 (48) have been found to be activated in cells cultured on a substrate under cyclic stretch. Although it is known that cells are able to coordinate mechanical responses and biological signaling when subjected to mechanical stimuli, this process involves a large number of proteins and signaling activities, many of which are still not fully understood. As such, the theoretical model here, built upon a thermodynamic consideration of the minimum energy principle, still needs further verification. However, the fact that the model successfully predicted the cell reorientation under different conditions suggests that it considers the essential factors directly determining the equilibrium states achieved through cellular response to the external stimuli. We would like to point out that in our model, we focus on the effects of SFs, which is consistent with the understanding that they are the main contractile cytoskeletal machinery that play a key role in regulating cell orientation (11, 14, 18, 21, 22, 43, 44, 48, 57–60).
It is worth noting that we employed a linear elasticity assumption in our model; however, in the real compression scenario, both the collagen gel and SFs exhibit viscoelastic properties (22). We believe that even with this simplification, our model still provides a meaningful explanation of the experimental observations because the model was developed on the basis of equilibrium states rather than dynamic adaptation. Viscous effects are eliminated at equilibrium. For example, if we consider the collagen gel as a viscoelastic material, using the Kelvin model (61) the relationship between stress and strain is given by
| (8) |
where η is the viscosity describing the viscous behavior of the material. In our study, time t is large enough so that the equation goes back to a linear relationship . As such, the assumption of linear elasticity is reasonable in this thermodynamics-based model. It is worth noting that according to Roeder et al (42), the 30% strain we applied lies in the linear elastic region of collagen gel at a concentration of 2 mg/ml.
Another assumption employed in the model is that SFs are oriented parallel to the long axis of the elongated cell body. In reality, SF distributions within individual cells can vary. For example, endothelial cells can have a large variety of the SF orientations. However, for highly elongated cells such as fibroblasts and smooth muscle cells, SFs tend to be oriented in parallel (18). For example, SFs in REF-52 fibroblasts exhibited perfect alignment with the polarity of the cell body (10). Additional evidence includes the reported fluorescence images of SFs in MC3T3-E1 osteoblast cells, which show highly aligned SFs on the long axis of the cell body (62). Therefore, we believe that it is reasonable to assume that SFs are distributed along the polarized direction of the fibroblasts.
One more factor that has not been discussed is the effect of the shear force near the wall. The fluorescence images were obtained at locations away from the boundaries throughout the sample to ensure that the shear forces caused by any boundary effects were marginal. It has been reported that shear strain is negligible compared to normal strains in the central region of a 3D gel matrix (23). This finding supports our normal-force based model.
We would like to re-emphasize the important role of boundary conditions in this study. The cell reorientation is a result of combined z-direction compression and stretch along the x-direction for the laterally confined case and along both the x- and y-diections for the laterally unconfined case. In our work, the gel was made into square. As such, in the laterally-unconfined case, the gel only expands freely along the two lateral axes, i.e., the x- and y-directions in the model. This boundary condition has been taken into account in the model by simply setting a square gel in a Cartesian coordinate system with the two axes of the gel parallel to the x- and y-directions, and only allowing the gel to expand freely in these two directions. In fact, we also observed that if there is no boundary constrain, i.e., in a circular gel, NAFs only respond to the compression by realigning perpendicular to the z-direction but without a preferred orientation in the x-y plane.
It should also be noted that, static and cyclic loading are both biologically relavent. For example, CAFs experience continuous compressive stress in the normal direction with a growing tumor (63). In addition, in contrast to the fact that cyclic loading is a necessity for cell reorientation on a 2D substrate (2, 6, 8, 10–14), it is not required to induce cell reorientation in 3D. For example, cells as well as SFs show realignment parallel to the direction of tensile strain in both static and cyclic strain cases in 3D (25).
5 Conclusion
We experimentally studied the reorientation of human prostatic NAFs and CAFs that were embedded in 3D collagen I matrices and subjected to compression. NAFs realign themselves to specific directions while CAFs show a random distribution. A theoretical model indicates that the minimum energy principle can be used to account for the behavior of both NAFs and CAFs and the significant difference in the phenotype is due to their inherent cell contractility. The importance of cell contractility in cell reorientation is further confirmed by the observation that TGF-β treated NAFs with enhanced contractile force behave in a similar manner as CAFs. This new understanding of the contribution of the cell mechanical properties to their reorientation upon external mechanical stimuli in 3D has not been reported in the literature. Taken together, the experimental and theoretical studies presented here provide new insights into the mechanisms governing the behavior of cells in a mechanically stressed 3D environment.
Supplementary Material
Highlights.
NAFs and CAFs show very different reorientation upon compression in 3D.
NAFs treated with TGF-β and of high contractility behave like CAFs.
The difference between NAFs and CAFs is due to different cell contractility.
A theoretical model based on minimum energy principle is established.
The model results correctly predict the behavior of NAFs and CAFs.
Acknowledgments
The authors thank Dr. Simon W. Hayward and his lab for providing the NAF and CAF cells and the National Institute of Health (Grant#CA155572) for the financial support.
Appendix: A Mathematic Model on Cell Reorientation in Response to Compression in 3D
Here we describe a theoretical model based on the minimum energy principle in order to address the mechanism underlying cell reorientation in response to compression in 3D.
1 Laterally confined condition
1.1 Stress and strain analysis for the collagen gel
To model the cell reorientation, we first consider a small collagen gel cube surrounding a cell. According to the 3D Hooke’s Law, at equilibrium, the strains ε along the x-, y-, and z-directions are as follows:
| (A1) |
| (A2) |
| (A3) |
Here νg is the Poisson’s ratio, Eg is the Young’s modulus, and σi is stress. We assume that the collagen gel is linear elastic. The gel is compressed along the z-direction and laterally the gel is confined in the y-direction but can expand freely in the x-direction. As such, we have σx = 0, εy = 0, and εz = ΔZ/lg. Here ΔZ is the displacement caused by compression in the z-direction and lg is the length of each side of the cube. The stresses in the x-, y-, and z- directions are therefore,
| (A4) |
Meanwhile, the strains in the x-, y-, and z- directions can be re-written as
| (A5) |
1.2 Energy analysis for the cell
The total energy E of a cell can be written as:
| (A6) |
where E0 is the homeostatic elastic potential due to cell contraction, Ee is the elastic potential converted from the external mechanical load, Ea and Ef are the chemical potentials of assembled and disassembled actin filaments, respectively, and Es is the energy exchanged with the surrounding microenvironment.
Without an external mechanical load
Under the normal, undisturbed condition, the total energy is
| (A7) |
This can be expanded to
| (A8) |
where l is the length of the cell, ε0 is the pre-stretched strain, μa and μf are the chemical potentials of assembled and disassembled actin filaments, and Nf is the number of disassembled actin filaments.
As mentioned before, we further assume that the cell is composed of a single equivalent SF that is parallel to the axis of the cell body and extend the length of the cell. Also, the SF consists of a number of actin filaments of length la. Each actin filament can be regarded as a spring with a spring constant of ka; and therefore, the SF is a spring system that is composed of a series of identical actin filament springs. The spring constant of the SF is ksf = ka/Na. Hence,
| (A9) |
| (A10) |
Taking the derivative of E yields
| (A11) |
In cells, actins exist in two forms: actin filaments and free monomeric actins that can polymerize into actin filaments. The pool of actin monomers is typically steady in a cell, and hence the total amount of actins is conserved (64), which leads to the following relation: Na + Nf = const. Therefore, dNa = −dNf, and Eq. A11 can be rearranged as:
| (A12) |
At equilibrium, the cell energy achieves a minimum, and dE/dNa = 0.
Therefore,
| (A13) |
where es = dEs/dNa; and e0 = kala2ε02/2, which is the elastic potential of each actin filament due to cell contraction.
With an external mechanical load
Under this condition, the total energy of the cell given by Eq. A6 can be expanded as
| (A14) |
where εxc is the strain along the long axis of the cell body caused by the gel displacement in the x-direction, σyc and σzc are the stress components along the long axis of the cell body caused by the forces applied to the cell from the gel in the y- and z-directions, which are σycosθy and σzcosθz, respectively. The different signs of terms of εxcl, σycl/ksf, σzcl/ksf reflect the opposite directions.
The strain that results from the elongation of individual actin filaments due to external stimuli is eventually released by the assembly of additional actin filaments. Based on this assumption, εxc can be solved from Nala(1+εxc) = N0la(1+εxcosθx), therefore,
| (A15) |
where N0 is the number of the assembled actin filaments prior to compression.
Substituting this into the total energy equation yields
| (A16) |
For convenience, we define . Then Eq. A16 can be simplified as
| (A17) |
When E reaches a minimum, the derivative of E with respect to Na is zero:
| (A18) |
In Eq. A13, we have already shown that e0 + μa − μf + es = 0. As such,
| (A19) |
For sufficiently small homeostatic strain ε0, we neglect ε0 in Eq. A19, which leads to . The term 2NaF′(Na) + F(Na) can be further expanded as
| (A20) |
Since cos2θx + cos2θy + cos2θz = 1, 0 ≤ cosθx ≤ 1, 0 ≤ cosθy ≤ 1, 0 ≤ cosθz ≤ 1 and all the rest parameters are positive, Eq. A20 is always smaller than zero. Then to satisfy Eq. A19, F(Na) has to be zero.
| (A21) |
According to the assumption that the strain along the long axis of the cell body caused by the displacement in the x-direction is released by the additional assembly of actin filaments, the first term [N0(1 + εxcosθx) − Na]/Na in Eq. A21 is zero at equilibrium.
Therefore,
| (A22) |
Under this condition, θx = 0°, θy = θz = 90°. This means that cells are aligned along the x-direction and perpendicular to the y- and z- directions to achieve a minimum energy state. In this way, the homeostatic level of cell elastic force is re-established.
On the other hand, for cells with large inherent stress, ε0 cannot be neglected in Eq. A19, so F(Na)[2NaF′(Na) + F(Na)] − ε02 = 0. This can be expanded as:
| (A23) |
Along with cos2θx + cos2θy + cos2θz = 1, there are three unknowns, θx, θy, and θz and only two equations. Therefore, no specific combination of angles θx, θy, θz can be obtained and many combinations of θx, θy, θz can satisfy these two equations. This renders a random cell orientation distribution.
2 Laterally unconfined condition
Next, we extended the model to the laterally unconfined condition. In this case, cells are free to extend in both x- and y- directions.
Based on Eq. A1–A3, the strains of the gel in the x- and y- directions are equal:
| (A24) |
Then, for cells with low inherent ε0, Eq. A21 becomes
| (A25) |
which leads to,
| (A26) |
Hence, θx = θy = 45°, and θz =90°, indicating that cells are aligned diagonally with the x- and y- directions and perpendicular to the z-direction.
For cells with large inherent ε0, Eq. A23 becomes
| (A27) |
Again, no specific combination of angles θx, θy and θz can be obtained and cells can align in many directions but still meet the minimum energy principle.
Footnotes
Conflict of interest statements
The authors declare that they have no conflict of interest.
Author contributions
L. Yang designed the experiments, developed the mathematical model and processed images and data. L. Yang, L. J. Carrington, B. Erdogan and M. Ao conducted the experiments. L. Yang, L. J. Carrington, B. Erdogan, B. M. Brewer, D. J. Webb and D. Li contributed to data analysis and discussions. D. Webb and D. Li supervised the project. L. Yang and D. Li prepared the manuscript.
Publisher's Disclaimer: This is a PDF file of an unedited manuscript that has been accepted for publication. As a service to our customers we are providing this early version of the manuscript. The manuscript will undergo copyediting, typesetting, and review of the resulting proof before it is published in its final citable form. Please note that during the production process errors may be discovered which could affect the content, and all legal disclaimers that apply to the journal pertain.
References
- 1.Jaalouk DE, Lammerding J. Mechanotransduction gone awry. Nat Rev Mol Cell Biol. 2009;10:63–73. doi: 10.1038/nrm2597. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 2.Iba T, Sumpio BE. Morphological response of human endothelial cells subjected to cyclic strain in vitro. Microvasc Res. 1991;42:245–254. doi: 10.1016/0026-2862(91)90059-k. [DOI] [PubMed] [Google Scholar]
- 3.Petroll WM, Cavanagh HD, Barry P, Andrews P, Jester JV. Quantitative analysis of stress fiber orientation during corneal wound contraction. J Cell Sci. 1993;104(Pt 2):353–63. doi: 10.1242/jcs.104.2.353. [DOI] [PubMed] [Google Scholar]
- 4.Wang JH. Substrate deformation determines actin cytoskeleton reorganization: A mathematical modeling and experimental study. J Theor Biol. 2000;202:33–41. doi: 10.1006/jtbi.1999.1035. [DOI] [PubMed] [Google Scholar]
- 5.Li G, Fu N, Yang X, Li M, Ba K, Wei X, Fu Y, Yao Y, Cai X, Lin Y. Mechanical compressive force inhibits adipogenesis of adipose stem cells. Cell Prolif. 2013;46:586–594. doi: 10.1111/cpr.12053. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 6.Neidlinger-Wilke C, Grood ES, Wang JH-C, Brand Ra, Claes L. Cell alignment is induced by cyclic changes in cell length: studies of cells grown in cyclically stretched substrates. J Orthop Res. 2001;19:286–93. doi: 10.1016/S0736-0266(00)00029-2. [DOI] [PubMed] [Google Scholar]
- 7.Lazopoulos Ka, Pirentis a. Substrate stretching and reorganization of stress fibers as a finite elasticity problem. Int J Solids Struct. 2007;44:8285–8296. [Google Scholar]
- 8.Krishnan R, Canovic EP, Iordan AL, Rajendran K, Manomohan G, Pirentis AP, Smith ML, Butler JP, Fredberg JJ, Stamenovic D. Fluidization, resolidification, and reorientation of the endothelial cell in response to slow tidal stretches. Am J Physiol Cell Physiol. 2012;303:C368–75. doi: 10.1152/ajpcell.00074.2012. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 9.Burridge K, Wittchen ES. The tension mounts: stress fibers as force-generating mechanotransducers. J Cell Biol. 2013;200:9–19. doi: 10.1083/jcb.201210090. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 10.Livne A, Bouchbinder E, Geiger B. Cell reorientation under cyclic stretching. Nat Commun. 2014;5:3938. doi: 10.1038/ncomms4938. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 11.Wang JH, Goldschmidt-Clermont P, Yin FC. Contractility affects stress fiber remodeling and reorientation of endothelial cells subjected to cyclic mechanical stretching. Ann Biomed Eng. 2000;28:1165–71. doi: 10.1114/1.1317528. [DOI] [PubMed] [Google Scholar]
- 12.De R, Zemel A, Safran SA. Dynamics of cell orientation. Nat Phys. 2007;3:655–659. [Google Scholar]
- 13.De R, Safran SA. Dynamical theory of active cellular response to external stress. Phys Rev E Stat Nonlin Soft Matter Phys. 2008;78:31923. doi: 10.1103/PhysRevE.78.031923. [DOI] [PubMed] [Google Scholar]
- 14.Pirentis AP, Peruski E, Iordan AL, Stamenović D. A Model for Stress Fiber Realignment Caused by Cytoskeletal Fluidization During Cyclic Stretching. Cell Mol Bioeng. 2011;4:67–80. doi: 10.1007/s12195-010-0152-9. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 15.Li Y, Huang G, Zhang X, Wang L, Du Y, Lu TJ, Xu F. Engineering cell alignment in vitro. Biotechnol Adv. 32:347–65. doi: 10.1016/j.biotechadv.2013.11.007. [DOI] [PubMed] [Google Scholar]
- 16.Burridge K, Wittchen ES. The tension mounts: stress fibers as force-generating mechanotransducers. J Cell Biol. 2013;200:9–19. doi: 10.1083/jcb.201210090. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 17.García JR, García AJ. Cellular mechanotransduction: sensing rigidity. Nat Mater. 2014;13:539–40. doi: 10.1038/nmat3996. [DOI] [PubMed] [Google Scholar]
- 18.Kaunas R, Hsu HJ. A kinematic model of stretch-induced stress fiber turnover and reorientation. J Theor Biol. 2009;257:320–30. doi: 10.1016/j.jtbi.2008.11.024. [DOI] [PubMed] [Google Scholar]
- 19.Gavara N, Roca-Cusachs P, Sunyer R, Farré R, Navajas D. Mapping cell-matrix stresses during stretch reveals inelastic reorganization of the cytoskeleton. Biophys J. 2008;95:464–71. doi: 10.1529/biophysj.107.124180. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 20.Kaunas R, Nguyen P, Usami S, Chien S. Cooperative effects of Rho and mechanical stretch on stress fiber organization. Proc Natl Acad Sci U S A. 2005;102:15895–900. doi: 10.1073/pnas.0506041102. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 21.Qian J, Liu H, Lin Y, Chen W, Gao H. A mechanochemical model of cell reorientation on substrates under cyclic stretch. PLoS One. 2013;8:e65864. doi: 10.1371/journal.pone.0065864. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 22.Stamenović D, Lazopoulos KA, Pirentis A, Suki B. Mechanical Stability Determines Stress Fiber and Focal Adhesion Orientation. Cell Mol Bioeng. 2009;2:475–485. doi: 10.1007/s12195-009-0093-3. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 23.Eastwood M, V, Mudera C, McGrouther DA, Brown RA. Effect of precise mechanical loading on fibroblast populated collagen lattices: morphological changes. Cell Motil Cytoskeleton. 1998;40:13–21. doi: 10.1002/(SICI)1097-0169(1998)40:1<13::AID-CM2>3.0.CO;2-G. [DOI] [PubMed] [Google Scholar]
- 24.Henshaw DR, Attia E, Bhargava M, Hannafin JA. Canine ACL fibroblast integrin expression and cell alignment in response to cyclic tensile strain in three-dimensional collagen gels. J Orthop Res. 2006;24:481–90. doi: 10.1002/jor.20050. [DOI] [PubMed] [Google Scholar]
- 25.Riehl BD, Park JH, Kwon IK, Lim JY. Mechanical stretching for tissue engineering: two-dimensional and three-dimensional constructs. Tissue Eng Part B Rev. 2012;18:288–300. doi: 10.1089/ten.teb.2011.0465. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 26.Au-Yeung KL, Sze KY, Sham MH, Chan BP. Development of a micromanipulator-based loading device for mechanoregulation study of human mesenchymal stem cells in three-dimensional collagen constructs. Tissue Eng Part C Methods. 2010;16:93–107. doi: 10.1089/ten.TEC.2008.0707. [DOI] [PubMed] [Google Scholar]
- 27.Foolen J, V, Deshpande S, Kanters FMW, Baaijens FPT. The influence of matrix integrity on stress-fiber remodeling in 3D. Biomaterials. 2012;33:7508–18. doi: 10.1016/j.biomaterials.2012.06.103. [DOI] [PubMed] [Google Scholar]
- 28.Connelly JT, Vanderploeg EJ, Mouw JK, Wilson CG, Levenston ME. Tensile loading modulates bone marrow stromal cell differentiation and the development of engineered fibrocartilage constructs. Tissue Eng Part A. 2010;16:1913–23. doi: 10.1089/ten.tea.2009.0561. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 29.Tse JM, Cheng G, Tyrrell JA, Wilcox-Adelman SA, Boucher Y, Jain RK, Munn LL. Mechanical compression drives cancer cells toward invasive phenotype. Proc Natl Acad Sci U S A. 2012;109:911–6. doi: 10.1073/pnas.1118910109. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 30.He Y, Macarak EJ, Korostoff JM, Howard PS. Compression and tension: differential effects on matrix accumulation by periodontal ligament fibroblasts in vitro. Connect Tissue Res. 2004;45:28–39. doi: 10.1080/03008200490278124. [DOI] [PubMed] [Google Scholar]
- 31.El-Awady AR, Lapp CA, Gamal AY, Sharawy MM, Wenger KH, Cutler CW, Messer RLW. Human periodontal ligament fibroblast responses to compression in chronic periodontitis. J Clin Periodontol. 2013;40:661–71. doi: 10.1111/jcpe.12100. [DOI] [PubMed] [Google Scholar]
- 32.Kwok CB, Ho FC, Li CW, Ngan AHW, Chan D, Chan BP. Compression-induced alignment and elongation of human mesenchymal stem cell (hMSC) in 3D collagen constructs is collagen concentration dependent. J Biomed Mater Res A. 2013;101:1716–25. doi: 10.1002/jbm.a.34475. [DOI] [PubMed] [Google Scholar]
- 33.Jain RK, Martin JD, Stylianopoulos T. The role of mechanical forces in tumor growth and therapy. Annu Rev Biomed Eng. 2014;16:321–46. doi: 10.1146/annurev-bioeng-071813-105259. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 34.Shachar M, Benishti N, Cohen S. Effects of mechanical stimulation induced by compression and medium perfusion on cardiac tissue engineering. Biotechnol Prog. 28:1551–9. doi: 10.1002/btpr.1633. [DOI] [PubMed] [Google Scholar]
- 35.Altman GH, Horan RL, Martin I, Farhadi J, Stark PRH, Volloch V, Richmond JC, Vunjak-Novakovic G, Kaplan DL. Cell differentiation by mechanical stress. FASEB J. 2002;16:270–2. doi: 10.1096/fj.01-0656fje. [DOI] [PubMed] [Google Scholar]
- 36.Girton TS, V, Barocas H, Tranquillo RT. Confined compression of a tissue-equivalent: collagen fibril and cell alignment in response to anisotropic strain. J Biomech Eng. 2002;124:568–75. doi: 10.1115/1.1504099. [DOI] [PubMed] [Google Scholar]
- 37.Olumi AF, Grossfeld GD, Hayward SW, Carroll PR, Tlsty TD, Cunha GR. Carcinoma-associated Fibroblasts Direct Tumor Progression of Initiated Human Prostatic Epithelium. Cancer Res. 1999;59:5002–5011. doi: 10.1186/bcr138. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 38.Ao M, Franco OE, Park D, Raman D, Williams K, Hayward SW. Cross-talk between paracrine-acting cytokine and chemokine pathways promotes malignancy in benign human prostatic epithelium. Cancer Res. 2007;67:4244–53. doi: 10.1158/0008-5472.CAN-06-3946. [DOI] [PubMed] [Google Scholar]
- 39.Ao M, Brewer BM, Yang L, Franco Coronel OE, Hayward SW, Webb DJ, Li D. Stretching Fibroblasts Remodels Fibronectin and Alters Cancer Cell Migration. Sci Rep. 2015;5:8334. doi: 10.1038/srep08334. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 40.Ayres C, Bowlin GL, Henderson SC, Taylor L, Shultz J, Alexander J, Telemeco TA, Simpson DG. Modulation of anisotropy in electrospun tissue-engineering scaffolds: Analysis of fiber alignment by the fast Fourier transform. Biomaterials. 2006;27:5524–34. doi: 10.1016/j.biomaterials.2006.06.014. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 41.Achilli M, Mantovani D. Tailoring mechanical properties of collagen-based scaffolds for vascular tissue engineering: The effects of pH, temperature and ionic strength on gelation. Polymers (Basel) 2010;2:664–680. [Google Scholar]
- 42.Roeder BA, Kokini K, Sturgis JE, Robinson JP, Voytik-Harbin SL. Tensile Mechanical Properties of Three-Dimensional Type I Collagen Extracellular Matrices With Varied Microstructure. J Biomech Eng. 2002;124:214. doi: 10.1115/1.1449904. [DOI] [PubMed] [Google Scholar]
- 43.Walcott S, Sun SX. A mechanical model of actin stress fiber formation and substrate elasticity sensing in adherent cells. Proc Natl Acad Sci U S A. 2010;107:7757–62. doi: 10.1073/pnas.0912739107. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 44.Kang J, Steward RL, Kim Y, Schwartz RS, LeDuc PR, Puskar KM. Response of an actin filament network model under cyclic stretching through a coarse grained Monte Carlo approach. J Theor Biol. 2011;274:109–19. doi: 10.1016/j.jtbi.2011.01.011. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 45.Shao Y, Mann JM, Chen W, Fu J. Global architecture of the F-actin cytoskeleton regulates cell shape-dependent endothelial mechanotransduction. Integr Biol (Camb) 2014;6:300–11. doi: 10.1039/c3ib40223a. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 46.Alexander JK, Fuss B, Colello RJ. Electric field-induced astrocyte alignment directs neurite outgrowth. Neuron Glia Biol. 2006;2:93–103. doi: 10.1017/S1740925X0600010X. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 47.Çengel Y. Fundamentals of thermal-fluid sciences. Boston: McGraw-Hill Higher Education; 2012. [Google Scholar]
- 48.Hsu HJ, Lee CF, Locke A, Vanderzyl SQ, Kaunas R. Stretch-induced stress fiber remodeling and the activations of JNK and ERK depend on mechanical strain rate, but not FAK. PLoS One. 2010;5:e12470. doi: 10.1371/journal.pone.0012470. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 49.Eastwood M, Mudera VC, McGrouther Da, Brown Ra. Effect of precise mechanical loading on fibroblast populated collagen lattices: Morphological changes. Cell Motil Cytoskeleton. 1998;40:13–21. doi: 10.1002/(SICI)1097-0169(1998)40:1<13::AID-CM2>3.0.CO;2-G. [DOI] [PubMed] [Google Scholar]
- 50.Mao Y, Keller ET, Garfield DH, Shen K, Wang J. Stromal cells in tumor microenvironment and breast cancer. Cancer Metastasis Rev. 2013;32:303–15. doi: 10.1007/s10555-012-9415-3. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 51.Madar S, Brosh R, Buganim Y, Ezra O, Goldstein I, Solomon H, Kogan I, Goldfinger N, Klocker H, Rotter V. Modulated expression of WFDC1 during carcinogenesis and cellular senescence. Carcinogenesis. 2009;30:20–7. doi: 10.1093/carcin/bgn232. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 52.Gabbiani G. The myofibroblast in wound healing and fibrocontractive diseases. J Pathol. 2003;200:500–3. doi: 10.1002/path.1427. [DOI] [PubMed] [Google Scholar]
- 53.Hinz B. Masters and servants of the force: the role of matrix adhesions in myofibroblast force perception and transmission. Eur J Cell Biol. 2006;85:175–81. doi: 10.1016/j.ejcb.2005.09.004. [DOI] [PubMed] [Google Scholar]
- 54.Liu XD, Umino T, Ertl R, Veys T, Skold CM, Takigawa K, Romberger DJ, Spurzem JR, Zhu YK, Kohyama T, Wang H, Rennard SI. Persistence of TGF-beta1 induction of increased fibroblast contractility. Vitr Cell Dev Biol. 2001;37:193–201. doi: 10.1290/1071-2690(2001)037<0193:POTIOI>2.0.CO;2. [DOI] [PubMed] [Google Scholar]
- 55.Lijnen P, Petrov V, Rumilla K, Fagard R. Transforming growth factor-beta 1 promotes contraction of collagen gel by cardiac fibroblasts through their differentiation into myofibroblasts. Methods Find Exp Clin Pharmacol. 2003;25:79–86. doi: 10.1358/mf.2003.25.2.723680. [DOI] [PubMed] [Google Scholar]
- 56.Ura H, Obara T, Yokata K, Shibata Y, Okamura K, Namiki M. Effects of transforming growth factor-á released from gastric carcinoma cells on the conreaction of collagen-matrix gels containing fibroblasts. Cancer Res. 1991;51:3550–3554. [PubMed] [Google Scholar]
- 57.Tojkander S, Gateva G, Lappalainen P. Actin stress fibers--assembly, dynamics and biological roles. J Cell Sci. 2012;125:1855–64. doi: 10.1242/jcs.098087. [DOI] [PubMed] [Google Scholar]
- 58.Wang JH. Substrate deformation determines actin cytoskeleton reorganization: A mathematical modeling and experimental study. J Theor Biol. 2000;202:33–41. doi: 10.1006/jtbi.1999.1035. [DOI] [PubMed] [Google Scholar]
- 59.Kaunas R, Nguyen P, Usami S, Chien S. Cooperative effects of Rho and mechanical stretch on stress fiber organization. Proc Natl Acad Sci U S A. 2005;102:15895–900. doi: 10.1073/pnas.0506041102. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 60.Nagayama K, Kimura Y, Makino N, Matsumoto T. Strain waveform dependence of stress fiber reorientation in cyclically stretched osteoblastic cells: effects of viscoelastic compression of stress fibers. Am J Physiol Cell Physiol. 2012;302:C1469–78. doi: 10.1152/ajpcell.00155.2011. [DOI] [PubMed] [Google Scholar]
- 61.Basic Orthopaedic Biomechanics & Mechano-biology. Lippincott Williams & Wilkins; 2005. [Google Scholar]
- 62.Nagayama K, Kimura Y, Makino N, Matsumoto T. Strain waveform dependence of stress fiber reorientation in cyclically stretched osteoblastic cells: effects of viscoelastic compression of stress fibers. Am J Physiol Cell Physiol. 2012;302:C1469–78. doi: 10.1152/ajpcell.00155.2011. [DOI] [PubMed] [Google Scholar]
- 63.Tse JM, Cheng G, Tyrrell Ja, Wilcox-Adelman Sa, Boucher Y, Jain RK, Munn LL. From the Cover: Mechanical compression drives cancer cells toward invasive phenotype. Proc Natl Acad Sci. 2012;109:911–916. doi: 10.1073/pnas.1118910109. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 64.Tilney LG, Tilney MS. The actin filament content of hair cells of the bird cochlea is nearly constant even though the length, width, and number of stereocilia vary depending on the hair cell location. J Cell Biol. 1988;107:2563–74. doi: 10.1083/jcb.107.6.2563. [DOI] [PMC free article] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.