Coupling between one-dimensional networks reconciles conflicting dynamics in LIP and reveals its recurrent circuitry

Summary

Little is known about the internal circuitry of the primate lateral intraparietal area (LIP). During two versions of a delayed-saccade task, we found radically different network dynamics beneath similar population average firing patterns. When neurons are not influenced by stimuli outside their receptive fields (RFs), dynamics of the high-dimensional LIP network during slowly-varying activity lie predominantly in one multi-neuronal dimension, as described previously. However, when activity is suppressed by stimuli outside the RF, slow LIP dynamics markedly deviate from a single dimension. The conflicting results can be reconciled if two LIP local networks, each underlying an RF location and dominated by a single multineuronal activity pattern, are suppressively coupled to each other. These results demonstrate the low dimensionality of slow LIP local dynamics, and suggest that LIP local networks encoding the attentional and movement priority of competing visual locations actively suppress one another.

In Brief

Zhang et al. found that slow LIP network dynamics can appear inconsistent with confinement to a single multi-neuronal dimension, unlike previous observations. Their model reconciles the conflict and reveals the circuitry underlying surround suppression.

Introduction

It has become increasingly appreciated that neural functions need to be understood in terms of neuronal populations and the dynamics of the circuits to which they belong (Miller and Wilson, 2008; Shenoy et al., 2013). However, the field of systems neuroscience in nonhuman primates has traditionally been dominated by studies of the properties of single neurons. While we have a wealth of knowledge of single neuron behaviors in many areas of the primate brain, this knowledge remains largely phenomenological—we know what neurons do, but not how they do it. Especially on the circuit level, the mechanisms and connectivity underlying neuronal behaviors are often obscure.

Such is the case in LIP, where a large body of literature has revealed that the activity of single neurons encodes visual attention and saccadic eye movements, as well as decision making variables, abstract categories, and other cognitive variables (Bisley and Goldberg, 2010; Freedman and Assad, 2011; Gold and Shadlen, 2007; Kable and Glimcher, 2009). However, little is known about the circuitry inside or outside the LIP network that produces such activity, and therefore the role of LIP in many of these functions is controversial. A step in understanding this circuitry was taken by Ganguli et al. (2008), who analyzed LIP network dynamics during two different tasks: a delayed saccade task (Bisley and Goldberg, 2003, 2006) and a random-dot motion discrimination task (Roitman and Shadlen, 2002). They found that the dynamics of the high-dimensional LIP network are dominated by one multi-neuronal dimension on slow timescales, which could be explained by a simple circuit model. This one-dimensionality was key to explaining an unexpected correspondence between LIP single neuron responses and the timing of attentional shifts (examined in more detail below). More recently, Fitzgerald et al. (2013) found further evidence for one-dimensional dynamics in three experiments in which LIP encoded learned associations between visual stimuli.

Using a delayed saccade task similar to the task of Bisley and Goldberg (2003, 2006; hereafter BG), Falkner, Krishna et al. (2010; hereafter FK) reported “surround suppression” in LIP (see also Louie et al., 2011), i.e., stimuli outside the RF of a cell suppress the cell’s activity. In the FK study, the population-averaged activity over time is very similar to that in the BG study, as expected given the very similar tasks. However, we find that the pattern of activity across neurons changes over time in a very different way in the FK study. In particular, the network dynamics in the FK dataset markedly deviate from the one-dimensional dynamics observed in the BG dataset, calling into question the validity of the one-dimensional LIP model of Ganguli et al. We show that the two sets of conflicting results can be reconciled and well characterized by a more general low-dimensional model, in which each of two local LIP networks in isolation would have its own single dominant dimension, but suppressive coupling between them gives rise to two dominant multi-neuronal activity patterns. Analysis of the FK data directly confirms the two-dimensional dynamics predicted by the model. Our study thus represents a step forward in discovering circuit mechanisms and connectivity from single neuron recordings, and in understanding mechanisms underlying LIP functions.

Results

One-dimensional dynamics in LIP

We begin by describing the first of the two conflicting datasets (Bisley and Goldberg, 2003), along with the one-dimensional model (Ganguli et al., 2008) to which it gave rise.

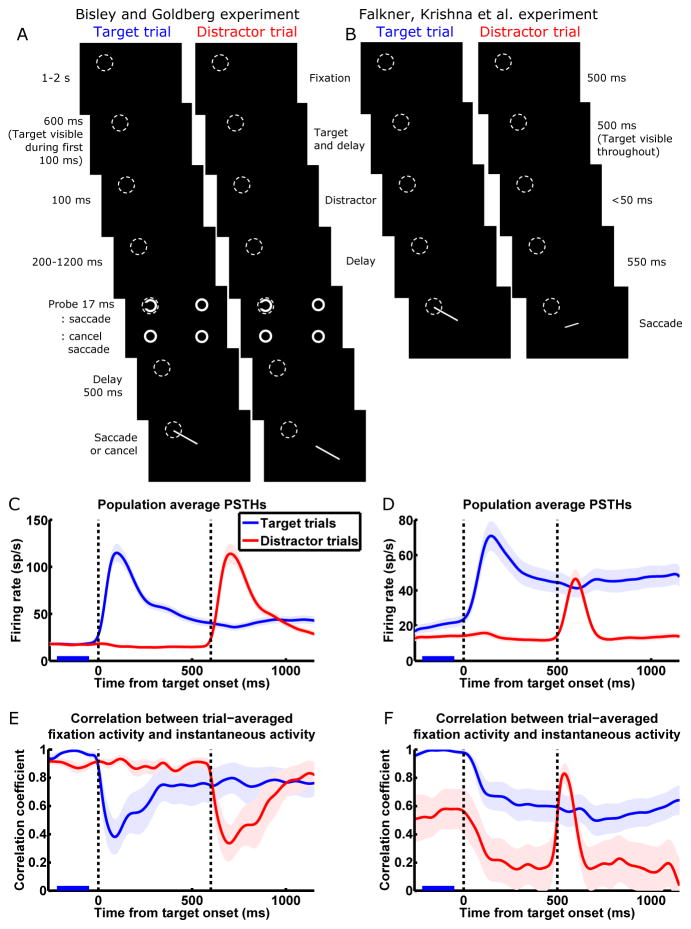
The delayed saccade task of BG is illustrated in Fig. 1A (details in Supplemental Information [SI] section 1). During this task, LIP neurons exhibit a large transient visual response to the onset of a saccade target or distractor in the RF, and sustained delay period activity (delay activity) when a saccade is planned to the RF (Fig. 1C). When a distractor is flashed away from the target location during the delay period, attention is transiently attracted away from the target location to the distractor location. At the same time, the average visual response level of LIP neurons whose RFs contain the distractor location (the distractor population) rises above the average delay activity level of neurons whose RFs contain the target location (the target population). As the visual activity of the distractor population decays back to baseline, the locus of attention shifts back to the target location. This shift in attention coincides with the shift in the peak of LIP activity from the distractor population to the target population: when the decaying visual activity of the distractor population drops to a level statistically indistinguishable from the sustained delay activity of the target population (the “crossing time”—when the decaying red trace crosses the blue trace in Fig. 1C), neither the target nor the distractor location has attentional advantage, whereas 100–250 ms before or after this crossing time, the distractor or target location, respectively, is the clear locus of attention.

Figure 1.

The conflicting population dynamics observed by Bisley and Goldberg (2003; BG; left column) and Falkner, Krishna et al. (2010; FK; right column).

(A and B) Task schematics. While the monkey fixates a central spot, a target appears. The monkey is required to hold fixation until the disappearance of the fixation spot, at which time it makes a saccade to the location of the target. During the delay between target onset and fixation spot disappearance, a task-irrelevant distractor stimulus is flashed. We call a given trial a target trial or distractor trial when the target or distractor, respectively, is in the RF (dashed circles) of the neuron being recorded. In the BG task, the target and distractor are in opposite visual quadrants and equidistant from the fixation spot; in the FK task, either the target or the distractor is in the RF, and the other stimulus is at the location that elicits maximum surround suppression for the recorded neuron. In the BG task, between 200 and 1200 ms after the distractor disappears, a probe (a Landolt ring) is flashed at either the target or the distractor location, along with three complete rings elsewhere; a left-facing or right-facing ring instructs the monkey to proceed with or cancel the planned saccade, respectively. In C and E, we only include trials in which the probe appeared at least 700 ms after distractor onset. For task details, see SI section 1.

(C and D) Population average peristimulus time histograms (PSTHs) in the BG (C; n = 41 cells) and FK (D; n = 27) studies. Blue/red traces denote trials in which the target/distractor appears in the RF of the neuron being recorded; every neuron was recorded during both target and distractor trials and contributes to both traces. The first and second vertical dashed lines denote the onset of the target and the distractor, respectively. Shading around traces indicates SEM. PSTHs have been smoothed by convolution with a Gaussian kernel (σ = 30 ms; firing rates and correlations appearing to change before stimuli onset in Fig. 1C–F are artifacts of this smoothing).

(E and F) Correlation analysis for the BG (E) and FK (F) datasets. We define a trial-averaged population fixation activity vector F⃗, each element of which is the activity of one cell on target trials, averaged over trials and over the period from 220 ms to 50 ms before target onset (marked by blue bars in C–F). At each millisecond time point over the course of the target trial (blue traces) or distractor trial (red traces), the correlation coefficient was computed between the trial-averaged population instantaneous activity vector at that point in time and F⃗. The BG correlation patterns (E; presented in similar format in Ganguli et al., 2008) exhibit one-dimensional dynamics on slow timescales (high correlations during stable fixation activity and delay activity), while the FK correlation patterns (F) markedly deviate from one dimension (on distractor trials, low correlations during stable activity, and transient increase in correlation during distractor visual response). Vertical dashed lines are as in C and D. Shading around traces indicates standard error estimated from 1000 bootstrap samples.

See Fig. S1A for correlations between distractor trials fixation activity and instantaneous activity of the FK data, and Fig. S2A–D for the FK data plotted separately for different reward conditions.

Further analyses of these results (Bisley and Goldberg, 2006) revealed that this correspondence between activity crossing and attentional switching also held at the level of single LIP neurons. The crossing time of a single neuron is defined as the time at which the neuron’s decaying response to a distractor, on trials in which a distractor is in its RF (distractor trials), crosses its own level of delay activity on trials in which a target is in its RF (target trials). These single-neuron crossing times are surprisingly invariant across neurons and closely aligned with the monkey’s attentional switching time, despite high variability across neurons in their peak visual responses, time constants of visual response decay, and delay period responses.

Ganguli et al. (2008) explained this observation with the proposal that the dynamics of a local network (LN) of LIP neurons are dominated on slow timescales by one multi-neuronal activity pattern (i.e., a pattern or vector of relative firing rates across the cells of the network). Throughout this paper, we use the term “local network” (or “LN”) to mean a network of LIP neurons that share the same RF (explained more fully in the section “Simple model of coupled local networks reconciles the results”). Briefly, the recurrent connectivity of an LN causes certain multi-neuronal activity patterns to persist longer in the absence of input; given steady input, these slowly decaying patterns also build up to be strongly amplified. If the network has only a single pattern that decays slowly, we refer to it as the network’s “slow mode,” where “mode” is a term borrowed from physics that describes a characteristic pattern of a system’s response. As the visual response to a distractor decays, it becomes dominated by this slow mode after all other patterns decay away. Because the slow mode is more strongly amplified than other patterns, it also dominates steady-state responses, such as delay activity and activity during the initial fixation before target onset (fixation activity). Thus, after the other patterns in the distractor response decay away, the decaying distractor activity and the ongoing delay activity are both dominated by the slow mode, meaning that the pattern of distractor activity across neurons is very nearly a scaled-up version of the delay activity pattern. At the crossing time, when the amplitudes of distractor and delay activity are the same, the distractor activity pattern is very nearly identical to the delay activity pattern. As a result, each individual neuron has roughly the same activity in its delay response as in its distractor response at the crossing time, so that all neurons have about the same single-neuron crossing time.

This one-dimensional model predicts that multi-neuronal activity patterns that change on slow timescales are all highly correlated with one another, because all are dominated by the same strongly amplified pattern. These include fixation and delay activity patterns and, to a lesser extent, slowly decaying visual activity patterns and slowly increasing activity patterns during decision-making tasks. On the other hand, during the initial transient visual response, many other activity patterns are activated, so the transient visual activity pattern is not highly correlated with the steady-state activity patterns. Ganguli et al. (2008) confirmed these predictions using the following analysis, which reveals network dynamics from the activity of a population of singly recorded neurons. At any millisecond time point t during a trial, we represent the trial-averaged activity of a population of N neurons as an N-dimensional vector, r⃗(t), in an N-dimensional multi-neuronal firing rate space; each of the N elements of r⃗(t) is the activity of one neuron at time t, averaged over trials. We also compute the N-dimensional fixation activity vector, F⃗, where each element is the activity of one neuron averaged over the fixation period before target onset and over target trials. Then, at each time point t over the course of the trial, a correlation coefficient is computed between F⃗ and r⃗(t). Fig. 1E shows that the correlation to fixation activity is indeed high for delay activity or distractor activity after the transient visual response decays away, indicating that fixation, delay, and post-transient distractor activity patterns all lie roughly in a single dimension, corresponding to the dominant activity pattern. The drop in correlation coefficient during the visual response indicates the transient deviation of activity from this one dimension caused by the transient activation of other non-dominant patterns.

Surround suppression and violations of one-dimensional dynamics

We continue by describing the second of the two conflicting datasets (Falkner, Krishna et al., 2010) and how it exhibits large deviations on both fast and slow timescales from the predictions of the one-dimensional model.

The task of FK (Fig. 1B) is very similar to that of BG. For both tasks, we analyze data in each trial during time windows ending shortly after distractor onset (i.e., before the onset of the probe in the BG task; see Fig. 1A), up to which point the two tasks are virtually identical aside from three differences. First, BG used a flashed target while FK presented a target that stayed visible during the delay. This does not result in qualitatively different delay activity levels (compare delay activity between Fig. 1C and D), consistent with LIP encoding the attentional and saccadic priority of the target location regardless of the visibility of that target. Second, BG randomly interleaved target trials and distractor trials, while FK presented target and distractor trials in blocks. Thus, in the FK experiment, on almost every trial the monkey had an expectation of where the target and distractor would be. This is reflected in higher anticipatory firing on target trials compared to distractor trials during the fixation period before target onset. The third difference is likely to be the key difference that led to different neural responses observed during the two tasks. In the BG task, the target and distractor are in opposite visual quadrants and equidistant from the fixation spot. In the FK task, in contrast, either the target or the distractor is in the RF of the cell being recorded in a given session, and the other stimulus is at the location eliciting maximum surround suppression of the recorded neuron. With this placement of stimuli, a saccade plan to the surround significantly suppressed the visual response to the distractor, while distractor appearance in the surround transiently and weakly, but significantly, suppressed delay activity during saccade planning (Fig. 1D; quantified in Falkner, Krishna et al., 2010). Surround suppression was not observed in the BG dataset (quantified in Bisley and Goldberg, 2006), in which the stimulus locations were not selected for suppression. Other than the surround suppression of response amplitudes, the FK dataset displays the same overall pattern of fixation, visual, and delay activity as the BG dataset (compare Fig. 1C and D).

However, beneath this apparent similarity in population average activity, the network dynamics are radically different; moreover, the FK dynamics clearly violate the predictions of the one-dimensional model. Fig. 1F shows the result of the correlation analysis on neural activity from the FK experiment. Most strikingly, on distractor trials (red trace), even though the appearance of the target in the surround only minimally affects the mean firing rate of the distractor population, target appearance causes a large, sustained drop in correlation, when the one-dimensional model would predict an unchanging and high level of correlation, as in Fig. 1E. This indicates that the activity pattern of the population has changed dramatically while its mean firing rate has remained about the same. Furthermore, the later appearance of the distractor in the RF causes a large, transient rise in correlation which subsequently returns to the steady low level present before distractor onset, when the one-dimensional model would predict the opposite change—a large and transient drop in correlation upon distractor onset, as in Fig. 1E. On target trials (blue traces), the difference is more subtle, with target onset evoking a small, sustained drop in correlation, similar to the sustained drop in the BG case, but without the initially larger transient decrease.

Note that in the BG dataset, the two trial types are randomly interleaved; thus, the monkey does not know the trial type during the initial fixation, and fixation activities are the same on the two trial types. In the FK dataset, however, fixation activities are different on the two trial types due to the block design. We chose to use the fixation activity on target trials as opposed to distractor trials to calculate correlations because it reveals salient patterns in the network dynamics. Using distractor trial fixation activity is another angle from which to examine the network dynamics that gives less informative results, i.e., correlations do not rise and drop saliently over time (Fig. S1A).

Thus, the results of BG and of FK seem incompatible. The robust one-dimensional dynamics observed by Ganguli et al. (2008) in the data of Bisley and Goldberg (2003, 2006) require that the local anatomical connectivity of LIP selectively amplify only one multi-neuronal activity pattern. How can this same anatomical connectivity realize dynamics that deviate so far from the one activity pattern that it so strongly amplifies?

Simple model of coupled local networks reconciles the results

We found the answer in a simple model of the interactions between two coupled LIP LNs. This model replicates the FK findings and yet reduces to the one-dimensional dynamics that characterize the BG findings when the two LNs are not coupled.

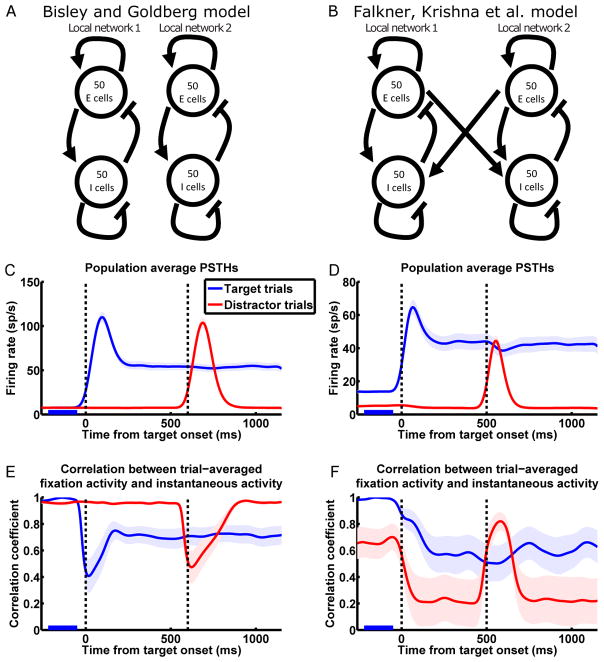
We model two LNs in LIP, each composed of excitatory (E) and inhibitory (I) neurons that share an RF, with randomly distributed neuronal time constants (Fig. 2A and B; see SI section 2.2 for details of the model). Connections between the neurons are sparse and their strengths are randomly distributed. Within each LN, excitatory connections are on average stronger than inhibitory connections. This dominance of excitation is consistent with evidence based on dendritic structure of increased connectivity between excitatory cells in LIP compared to primary sensory cortices (Elston and Rosa, 1997). Such connectivity within an LN, when it’s not connected to another LN, amplifies a single pattern, one of increased activity across most cells, more strongly than all other patterns.

Figure 2.

Model reproduces the response and network dynamics of Bisley and Goldberg (2003; left column) and Falkner, Krishna et al. (2010; right column).

(A and B) Schematics of the model network connectivity for the BG (A) and the FK (B) scenarios. In both cases we model two recurrently connected local LIP networks (together referred to as a global network) corresponding to two RF locations, with each LN consisting of E and I cells. Connectivity within each LN is such that each LN by itself amplifies a single multi-neuronal activity pattern much more strongly than other patterns (see Results for details). The FK model network (B) differs from the BG model network (A) in the addition of coupling between the LNs that mediates interaction between them.

(C and D) Model reproduces LIP activity patterns observed by BG (C; n = 41 cells; in all simulation results except where noted, each neuron was “recorded” from a different simulated global network) and FK (D; n = 27). Population average PSTHs with same conventions as Fig. 1C and D. PSTHs have been smoothed by convolution with a Gaussian kernel (σ = 30 ms; firing rates and correlations appearing to change before stimuli onset in Fig. 2C–F are artifacts of this smoothing).

(E and F) Model reproduces LIP network dynamics observed by BG (E) and FK (F). Correlation analysis with same conventions as Fig. 1E and F.

See Fig. S1B for correlations between distractor trials fixation activity and instantaneous activity of the FK simulation, and Fig. S2E–H for separate simulations of the different reward conditions of the FK experiment.

The LIP cortical surface contains rough topological maps of visual space (Blatt et al., 1990; Patel et al., 2010). Neurons sharing an RF, which are more likely to be located close to each other on the cortical surface, make up an LN in our model. We model the connections of I cells to be restricted to the LN to which they belong, as inhibitory interneurons generally only make short-range projections, whereas E cells can potentially make long-range projections to the other LN. Since no significant interaction between RFs was observed in the BG dataset (quantified in Bisley and Goldberg, 2006), we infer that, for these RFs, the corresponding LNs are not directly connected (Fig. 2A). In contrast, by maximizing surround suppression, FK selected for RFs that did interact. Since the interaction observed was predominantly suppressive, it’s likely that the excitatory connections from each LN are stronger to the I cells than to the E cells of the other LN. For simplicity, we model the across-network connections as being from the E cells of each LN to the other LN's I cells only, with sparse and random connectivity (Fig. 2B). Our results do not change if we include weaker across-network E-to-E connections (data not shown).

We use a standard linear firing rate model (SI section 2.2; Dayan and Abbott, 2005) to simulate the trial-averaged activity in the experiments. We do not explicitly simulate single trials, as we have no knowledge of the single-trial population dynamics during the tasks. The experiments involve a variety of sensory, motor, and cognitive processes that likely give rise to a variety of external inputs to LIP during a trial, which we model as the following four types. (1) Fixation input: spontaneous firing from the external input sources when there is no stimulus in or saccade plan to the RF, such as during the fixation period. (2) Visual input: bottom-up input to an LN when a visual stimulus is in the RF, which is strong upon stimulus onset and becomes weak as the stimulus is sustained. Visual input arrives from areas that could include V2, V3, V3A, V4, middle temporal area (MT), and inferotemporal cortex (Baizer et al., 1991; Blatt et al., 1990; Lewis and Van Essen, 2000). (3) Delay input: persistent top-down input to an LN when a saccade is being planned to the RF, arriving from frontal areas such as the frontal eye field (FEF) or dorsolateral prefrontal cortex (dlPFC; Blatt et al., 1990; Stanton et al., 1995; in SI section 3 we discuss other possible mechanisms underlying delay activity and their implications for our model). (4) Expectation input: top-down input to one LN during the fixation period before target onset, when the animal is in a block of trials during which the target always appears in the RF of that LN (as in the blocked experiment of FK). Expectation input likely also arrives from frontal areas such as FEF or dlPFC (Coe et al., 2002; Roesch and Olson, 2003). The total external input to the neurons at any time is the sum of one or more of these four types of input. For each of the four types of input, input to each cell is independently drawn from a uniform distribution, with ranges of the distributions chosen to fit experimentally observed neural responses. Thus, importantly, the inputs from different sources are uncorrelated. In addition, the external input contains weak, temporally correlated noise that is independent for different neurons, simply to produce small firing rate fluctuations similar to those seen in the experiments.

In the experiments, different neurons are recorded from different LIP locations and have different RF positions. As in Ganguli et al. (2008), we interpret this to mean that these neurons are situated in different LNs, which share the same set of connectivity, neuronal, and input statistics. To model this, we run the simulation multiple times, each time with a different random instantiation of network connectivity, neuronal time constants, and input patterns, and “record” from a single randomly chosen cell during each simulation. Each simulation includes target and distractor trials for the recorded cell. Fig. 2C and D show the population PSTHs from such simulations of the BG (Fig. 2C) and FK (Fig. 2D) experiments, which reproduce the experimentally observed firing patterns, including the observed absence or presence of surround interactions. More significantly, our model reproduces the apparently conflicting network dynamics of the two experiments as revealed from the correlation analysis: the BG model shows one-dimensional dynamics on slow timescales (Fig. 2E), and the FK model shows the same higher-dimensional dynamics as experimentally observed (Fig. 2F).

If we compute correlations of instantaneous activity to distractor trials fixation activity, rather than to target trials fixation activity, the model also qualitatively reproduces the experimental results (Fig. S1B). Furthermore, modeling higher reward levels as resulting in higher levels of delay input (Leon and Shadlen, 1999; Kennerly and Wallis, 2009), we reproduce the results found when the data of FK, which consists of trials with large or small reward, is analyzed separately by reward level (Fig. S2). Because the activity and correlation patterns are qualitatively similar across reward levels in the data (Fig. S2A–D), in all other simulations we simply modeled the average reward level.

In addition to the correlation analysis, another way to examine network dynamics is to calculate, for each instantaneous activity vector, the norms of its component parallel to F⃗ and its component orthogonal to F⃗. This reveals a similar picture for the FK data to the correlation analysis, which our model reproduces (Fig. S3).

Conceptual picture: coupling of local slow modes explain LIP dynamics

We fully analyze the behaviors of the model in the next sections, but first, in this section, we presage those results by presenting a simplified conceptual understanding.

Each LN has its own single dominant activity pattern (its slow mode), and therefore each on its own would follow one-dimensional dynamics. The circuitry that creates surround suppression causes these two patterns to suppress one another, and this mutual suppression in turn qualitatively explains the FK correlation patterns, as follows.

Suppose we are recording in one of the LNs, call it LN1, and let the other LN be LN2. F⃗, the fixation activity of LN1 on target trials, is dominated by its slow mode, being driven by both fixation input and expectation input. At other times, the correlation of LN1’s instantaneous activity with F⃗ is high or low according to whether or not that instantaneous activity is dominated by the slow mode. Now consider LN1 on distractor trials. During the initial fixation period, LN1 receives fixation input but not expectation input. Thus, its slow mode is activated less than on target trials; in addition, its slow mode is suppressed by the more activated slow mode of LN2, which is receiving both fixation and expectation inputs. As a result, the relative contribution of activity patterns other than the slow mode to LN1’s activity is larger than on target trials, resulting in reduced correlation between distractor trial fixation activity and F⃗. After the target appears in LN2’s RF, LN1’s slow mode continues to be driven only by fixation input; in addition, it is strongly suppressed by the slow mode of LN2, which is strongly driven by both visual stimulation and the subsequent top-down delay input. This greatly reduces the correlation. Finally, when the distractor appears, strong visual stimulation transiently drives up LN1’s slow mode as well as other patterns. In BG, this would lower the correlation—LN1 was dominated by the slow mode before distractor onset, and is now less so. In FK, LN1’s slow mode was strongly suppressed before distractor onset, and is now driven up to dominate LN1’s activity, resulting in the transient rise in correlation.

The conceptual picture just given is simplified in that it describes each LN as having only one dimension of activity that is strongly amplified. In reality, a second strongly amplified dimension is created in each LN by the coupling between the two LNs. When LN2 is the more strongly driven LN, it strongly drives the I cells of LN1. In addition to suppressing LN1's slow mode, this amplifies a pattern of differential firing between the E and I cells in LN1, making the slow mode an even less dominant part of LN1’s activity. This will become clear with the detailed analysis below.

Detailed analysis: two-dimensional dynamics result from the coupling of local slow modes

We now take a closer look at the mechanisms of the model. We modeled the BG scenario with two unconnected LNs, each having a slow mode. The model simply behaves like two copies of the one-dimensional model of Ganguli et al., reproducing one-dimensional dynamics and the absence of surround interaction.

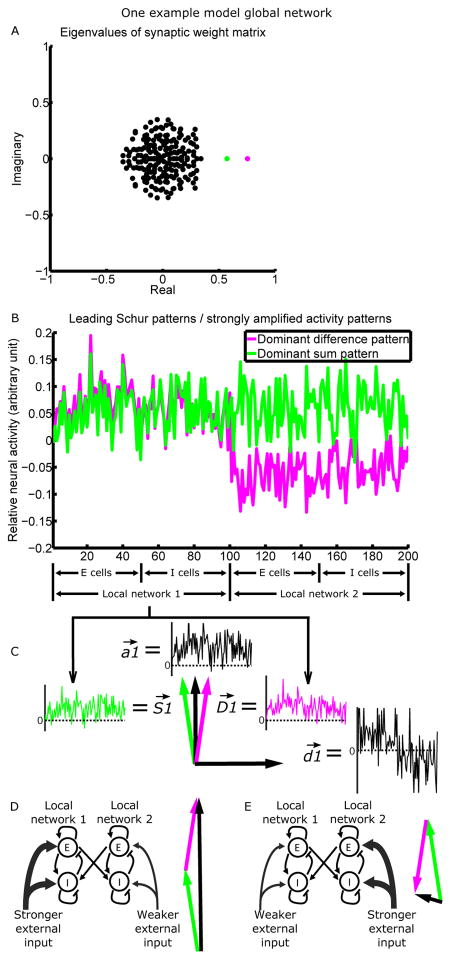
The only difference in network architecture in our model of the FK scenario is the presence of connections between the two LNs. Thus, the dominant activity patterns of the two LNs influence each other and are no longer independent. To understand the activity patterns of the global network consisting of the two coupled LNs, we examine the global connectivity matrix, which describes all of the global network’s connections, both within and between the LNs. This connectivity between neurons determines how strongly each neuron excites or inhibits other neurons. The connectivity can equivalently be described as connections between sets of activity patterns, determining how strongly activity in one pattern excites or inhibits activity in itself and in other patterns. For a network composed of separate excitatory and inhibitory neurons, it is often informative to analyze its connectivity as the connections between its Schur activity patterns (Murphy and Miller, 2009; Goldman, 2009; described in more detail in SI section 4). These are an ordered set of orthogonal activity patterns whose connections with each other are as simple as possible for a set of orthogonal patterns: each Schur pattern has a self-connection, and in addition there is a set of purely feedforward connections between the patterns. We choose to order the patterns by their self-connection strength. Then, activity in pattern 1 (the pattern with the strongest self-excitation) can only influence itself by its self-connection; activity in pattern 2 can excite or inhibit activity in pattern 1, in addition to influencing itself; pattern 3 can excite or inhibit pattern 1, pattern 2, and itself, etc. Thus, given similar external inputs to the patterns, the dominance of any pattern in the network's dynamics can be predicted by the strengths of its self-connection and the feedforward connections it receives. The activity of the network at any moment can be uniquely decomposed as a weighted sum of all Schur patterns. The dominant patterns will generally have weights with the largest absolute values (the weights can be positive or negative).

A set of numbers called eigenvalues can be calculated from the connectivity matrix; each eigenvalue is associated with a Schur pattern, and the real part of the eigenvalue corresponds to the strength of that pattern's self-connection. Plotting the eigenvalues of the global connectivity matrix from one representative simulation, we see that two eigenvalues have real parts more positive than the rest, indicating that there are two strongly self-excitatory activity patterns (Fig. 3A; SI section 5). Analysis of the feedforward connections between patterns (SI section 4 and Fig. S4) shows that: (1) these two patterns are nearly independent, with only a very weak feedforward connection from one to the other (Fig. S4G); (2) these two patterns receive approximately orthogonal sets of feedforward inputs from the less self-excitatory patterns (Fig. S4B, C, F); (3) the less self-excitatory patterns form much stronger feedforward connections to the two strongly self-excitatory patterns than to each other (Fig. S4G). Thus, given similar external input to all patterns, these two patterns will dominate the network’s activity.

Figure 3.

Recurrent connectivity strongly amplifies two activity patterns.

(A) The eigenvalue spectrum of the connectivity matrix (matrix plotted in Fig. S4D), for a model network composed of two interconnected LNs of 100 neurons each. Each eigenvalue is associated with a Schur vector, representing a pattern of relative activation across neurons (see Results for details). The more positive the real part of an eigenvalue, the more strongly the network amplifies the corresponding Schur activity pattern. Two patterns (magenta and green) are more strongly amplified than others and are plotted in B.

(B) Relative activation across neurons in the dominant difference pattern (differential activation of the two LNs; magenta) and the dominant sum pattern (equal activation of the two LNs; green), or equivalently, the two leading Schur vectors of the connectivity matrix. The difference/sum pattern is driven by the difference/sum of the mean inputs to the two LNs. Note the similarity of the two patterns across cells of the same LN.

(C) The LN1 portion of the sum ( $\overrightarrow{S1}$) and difference ( $\overrightarrow{D1}$) patterns can be represented as vectors in the two-dimensional space they define. We can take the axes of the 2D space to be $\overrightarrow{a1}$, a vector proportional to the average of $\overrightarrow{S1}$ and $\overrightarrow{D1}$, and $\overrightarrow{d1}$, a vector proportional to their difference.

(D and E) When LN1 receives stronger (D)/weaker (E) mean external input than LN2, $\overrightarrow{S1}$ is activated positively, and $\overrightarrow{D1}$ is activated positively (D)/negatively (E). Thus, the $\overrightarrow{a1}$ components of $\overrightarrow{S1}$ and $\overrightarrow{D1}$ add (D)/cancel (E), while the $\overrightarrow{d1}$ components of $\overrightarrow{S1}$ and $\overrightarrow{D1}$ cancel (D)/add (E). The actual activity vectors (black) thus point in very different directions in D and E.

See Fig. S4 for analysis of the feedforward connections between the Schur patterns, and Fig. S5A for comparisons of the directions of dominant activity patterns.

To understand the structure of these two potentially dominant activity patterns, in Fig. 3B we plot the relative activation of different neurons in these two Schur patterns. We have arbitrarily chosen the overall sign of each pattern in Fig. 3B such that both have mostly positive elements in LN1, and we have arbitrarily set the amplitude (i.e. the vector norm) of each pattern to 1. We note two key points about these two global patterns, which together show that they represent the coupled activation of the two local slow modes. (1) The two patterns represent two different forms of coupled activation of the two LNs: one is a “sum pattern,” representing roughly equal activation of the two LNs; the other is a “difference pattern,” representing differential activation of the two LNs, i.e., this pattern increases the activity of one LN and decreases the activity of the other. (2) The portions of the sum and difference patterns within a given LN are very similar to each other (e.g., in Fig. 3B, compare the two patterns restricted to neurons 1–100; for this comparison, the overall sign of activation within an LN is arbitrary; also see Fig. S5A), as well as to the slow mode of that LN if it were not connected with the other LN (Fig. S5A), which reflects the connectivity within that LN.

The sum and difference patterns, in addition to being strongly amplified by recurrent connectivity, also typically receive stronger external input than the other patterns. The intuition for this is the following. The external input is non-negative, since we assume it's carried by purely excitatory projection neurons. The purely excitatory input to an LN most strongly activate patterns that represent concerted activation of cells in the LN, and the sum and difference patterns are the only such patterns (Fig. S6). We now present the math behind this intuition.

For a given global network, consider the vector of external inputs I⃗, each of whose elements is the input to one neuron of the network. Let's decompose it as I⃗ = I⃗_mean + I⃗_res, where the LN1 elements of I⃗_mean all equal the mean input to LN1, which we call I₁, and similarly the LN2 elements all equal the mean input to LN2, I₂. I⃗_res contains the residuals which sum to zero over each LN. Similarly we can decompose a Schur pattern P⃗ of the given global network as P⃗ = P⃗_mean + P⃗_res, where the elements of P⃗_mean are P₁ and P₂, the LN means of P⃗. Given the orthonormality of the Schur patterns, the external input to P⃗ is I⃗· P⃗. Over each LN, the residuals sum to zero while the mean vectors are constant, so the dot product of any residual vector with any mean vector is 0. Thus I⃗ · P⃗= I⃗_mean · P⃗_mean + I⃗_res · P⃗_res. The first term I⃗_mean · P⃗_mean = N(I₁ P₁+I₂ P₂), where N is the number of neurons in an LN. The second term is a dot product of random vectors drawn independently for each global network and input type. By the central limit theorem, for large N, I⃗_res · P⃗_res across different random instantiations of networks and inputs approaches a Gaussian distribution with mean zero and standard deviation $\sqrt{N}\sqrt{2}{\sigma }_I{\sigma }_P$, where σ_I and σ_P are the standard deviations across the elements of I⃗_res and P⃗_res, respectively. Thus, the typical order of magnitude of I⃗_res · P⃗_res in any given global network will be $\sqrt{N}\sqrt{2}{\sigma }_I{\sigma }_P$. To compare the magnitude of N(I₁ P₁+I₂ P₂) and $\sqrt{N}\sqrt{2}{\sigma }_I{\sigma }_P$, we note that N is much greater than $\sqrt{N}$, and I₁ and I₂ are larger than or comparable to σ_I (since external inputs are positive). Similarly, for the sum and difference patterns, the absolute values of P₁ and P₂ are comparable to σ_P (Fig. S6). Thus, $N(I_{\mathit{1}}{P}_{\mathit{1}}+I_{\mathit{2}}{P}_{\mathit{2}})\gg \sqrt{N}\sqrt{2}{\sigma }_I{\sigma }_P$, so the inputs to these two patterns are approximately N(I₁ P₁+I₂ P₂). For the other patterns, P₁ and P₂ are close to zero, much smaller than σ_P (specifically, for our model with N = 100, P₁, $P_{\mathit{2}}<{\sigma }_P/\sqrt{N}$; Fig. S6) and much smaller than the means of the sum and difference patterns (Fig. S6). Thus, their mean-driven inputs are small, and their input is dominated by the relatively small input from the residual terms—intuitively, they represent random activations of cells, and are weakly driven by the random fluctuations of inputs about their mean. In our model, the range of the uniform distribution from which visual inputs for different cells are drawn is larger than that for delay inputs, which is larger than those for fixation and expectation inputs (SI section 2.2). A larger input variance (i.e. σ_I) means larger random fluctuations of inputs across cells, thus patterns other than the sum and difference patterns are activated more strongly by visual and delay inputs than by fixation and expectation inputs. This is consistent with the large variance of activity across cells during visual and delay responses (Fig. 1C–D), and the strong activation of weak patterns by the visual input (Ganguli et al., 2008).

When inputs are randomly redrawn for simulations of different global networks, the means of the inputs will be consistent across simulations. The large means of the sum and difference patterns within each LN will also be consistent across simulations (Fig. S6), because these are primarily determined by the statistically consistent strength of the overall excess of excitation in each LN’s connectivity. The means of the other patterns will be consistently small (Fig. S6), because they are determined by random factors in the connectivity. Thus, across different global networks, the same analysis will apply and the sum and difference patterns will consistently receive strong input, while the other patterns will receive weaker inputs that will vary from simulation to simulation.

We note that for a small proportion of random instantiations of connectivity matrices, a pair of complex patterns (which are complex conjugates in the eigenvector basis) take the place of the single real sum pattern described above. We show in SI section 6 and Fig. S5 that, in these cases, the complex pattern pair behaves effectively like the single real sum pattern.

We can use our understanding of the two dominant global activity patterns to understand the activity within a single LN, which we take to be LN1. We will call the LN1 portions of the sum and difference patterns $\overrightarrow{S1}$ and $\overrightarrow{D1}$, respectively, and take them to be normalized to unit vector length. Because these two patterns are not exactly equal to one another, they define a two-dimensional space of strongly amplified activity patterns in LN1. A convenient orthogonal pair of vectors to serve as a basis for this space is a vector $\overrightarrow{a1}$ proportional to the average of $\overrightarrow{S1}$ and $\overrightarrow{D1}$, and a vector $\overrightarrow{d1}$ proportional to their difference (again, both normalized to unit vector length; Fig. 3C). $\overrightarrow{a1}$ represents concerted firing of the cells in LN1, while $\overrightarrow{d1}$ represents differential firing of the E and I cells in LN1. $\overrightarrow{a1}$ is almost precisely the slow mode of LN1 if it were isolated, while $\overrightarrow{d1}$ is very nearly orthogonal to that slow mode (Fig. S5A). From the analysis above, the activation of $\overrightarrow{S1}$ and $\overrightarrow{D1}$ is largely determined by the mean inputs to the two LNs, as illustrated in Fig. 3D–E.

In Fig. S7 and SI section 7, we show that, because there are two strongly amplified activity patterns, single neurons in both the FK data and model no longer have a common “crossing time” as observed in BG by Ganguli et al. (2008). In SI section 7, we also discuss possible consequences of this for attentional switching.

Detailed analysis: two-dimensional dynamics explain correlation patterns

We are now in a position to understand the behavior of correlations between fixation and instantaneous activities in the FK model. Here we consider a population of neurons simultaneously recorded from a single LN, part of a single global network (Fig. 4). In SI section 8 we explain why the conclusions we reach remain valid for a population in which each neuron is recorded from a different global network (the case of our main simulations in Fig. 2 and likely of the experiments in Fig. 1).

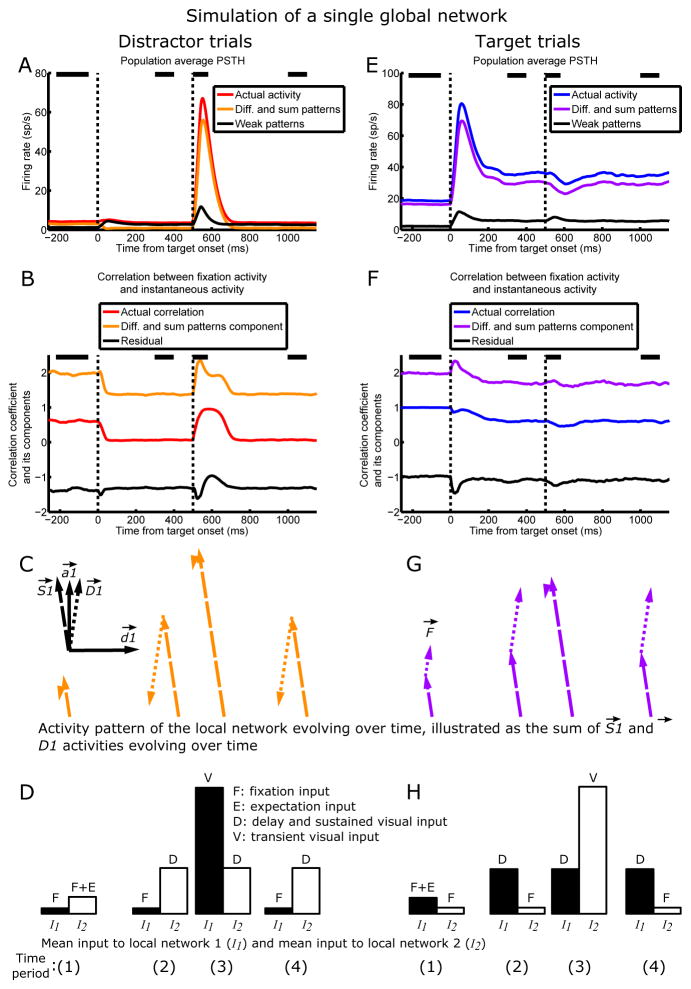
Figure 4.

Two multi-neuronal activity patterns explain LIP dynamics. One global network composed of LNs 1 and 2 is simulated, and the dynamics in LN1 on distractor trials (A–D) and target trials (E–H) are analyzed.

(A and E) $\overrightarrow{S1}$ and $\overrightarrow{D1}$ patterns dominate activity. Population average activity (red/blue), its component in the space of $\overrightarrow{S1}$ and $\overrightarrow{D1}$ patterns (orange/purple), and its component in the space of all other patterns (black) on distractor/target (A/E) trials (n = 100 cells). In A the orange and black traces add up to the red trace, and in E the purple and black traces add up to the blue trace.

(B and F) Actual correlation (red/blue), Corr_sum,diff (orange/purple, the component of correlation due to the $\overrightarrow{S1}$ and $\overrightarrow{D1}$ patterns alone), and Corr_residual (black, the residual component) on distractor/target (B/F) trials. The orange and black traces add up to the red trace, and the purple and black traces add up to the blue trace. Corr_sum,diff mirrors the salient ups and downs in the actual correlation, while Corr_residual largely does not change with time—thus, the changes in actual correlation over a trial are largely due to the $\overrightarrow{S1}$ and $\overrightarrow{D1}$ patterns. See Results for how the correlation was broken down into two components. Note that the actual correlation, but not Corr_sum,diff or Corr_residual, is restricted to lie within −1 and 1.

(C top-left inset) The two-dimensional space spanned by the two N-dimensional dominant activity patterns of LN1, $\overrightarrow{S1}$ (dashed vector) and $\overrightarrow{D1}$ (dotted vector), with $\overrightarrow{a1}$ and $\overrightarrow{d1}$ as axes.

(C and G) The evolution of $\overrightarrow{S1}$ (dashed vectors) and $\overrightarrow{D1}$ (dotted vectors) activity during distractor (C; orange vectors) and target (G; purple vectors) trials, as a result of the evolving inputs illustrated in D and H. For each trial type, activities in the $\overrightarrow{S1}$ and $\overrightarrow{D1}$ directions are each averaged over each of four time periods (spanned by black bars in A, B, E, and F), and are illustrated in their two-dimensional subspace, with the relative lengths of and the angle between $\overrightarrow{S1}$ and $\overrightarrow{D1}$ activities accurately rendered. In this 2D space, at a given time, the activity pattern across cells of LN1 is the vector sum of $\overrightarrow{S1}$ and $\overrightarrow{D1}$ activities at that time. Thus, F⃗, the vector of target trial fixation activities, is the vector sum of the $\overrightarrow{S1}$ and $\overrightarrow{D1}$ vectors at time (1) in G. The angle between F⃗ and the vector sum of $\overrightarrow{S1}$ and $\overrightarrow{D1}$ activities at a given time period generally determines the actual correlation at that time: the larger the angle, the lower the correlation, and vice versa (see Fig. S8 for the precise relationship between the vectors and correlation.). For example, the angle between the vector sum during the delay on distractor trials (vector sum of the $\overrightarrow{S1}$ and $\overrightarrow{D1}$ activities at time (2) in C) and F⃗ is large, so the correlation during that time period is low; the vector sum following distractor onset on distractor trials (vector sum of $\overrightarrow{S1}$ and $\overrightarrow{D1}$ activity at time (3) in C) points in similar directions as F⃗, so the correlation during that time period is high.

(D and H) The relative input to LNs 1 and 2 during the four time periods on distractor (D) and target (H) trials. Black and white bars denote the mean input to LN1 (I₁) and mean input to LN2 (I₂), respectively. As illustrated in Fig. 3D and E, during each time period, the sum of (difference between) the black and white bars largely determines the magnitude and direction of $\overrightarrow{S1}(\overrightarrow{D1})$ activity, which is plotted directly above the bars in C and G (see SI section 9 for explanations of why the inputs here do not perfectly predict the activations in C and G).

First, we see in simulations of a single global network that, indeed, the two dominant activity patterns, $\overrightarrow{S1}$ and $\overrightarrow{D1}$, largely explain the population-averaged activity of LN1 (Fig. 4A and E; the results and analysis are identical for LN2). Moreover, we can see the contributions of $\overrightarrow{S1}$ and $\overrightarrow{D1}$ activity to the correlation patterns by breaking up the correlations into two components, the component due to activity in the $\overrightarrow{S1}$ and $\overrightarrow{D1}$ patterns alone and the residual component, as follows. At any given time point, the correlation between instantaneous activity and fixation activity is $\frac{\widehat{r}·\widehat{F}}{\mid \widehat{r}\mid \mid \widehat{F}\mid }$, where r̂ is the vector of mean-subtracted instantaneous activities (each element of r̂ is the instantaneous activity of one neuron minus the population mean instantaneous activity), F̂ is the vector of mean-subtracted fixation activities (each element of F̂ is the fixation activity of one neuron minus the population mean fixation activity), and |•| denotes vector norm. We break r̂ into components r̂_sum, ₊, r̂_diff, and r̂_weak, the mean-subtracted instantaneous activity in the $\overrightarrow{S1}$ pattern, the $\overrightarrow{D1}$ pattern, and all other patterns, respectively, and do likewise for F̂ :

$$\begin{array}{l}\frac{\widehat{r}·\widehat{F}}{\mid \widehat{r}\mid \left|\widehat{F}\right|}=\frac{\left({\widehat{r}}_{\mathit{sum}}+{\widehat{r}}_{\mathit{diff}}+{\widehat{r}}_{\mathit{weak}}\right)·\left({\widehat{F}}_{\mathit{sum}}+{\widehat{F}}_{\mathit{diff}}+{\widehat{F}}_{\mathit{weak}}\right)}{\mid \widehat{r}\mid \left|\widehat{F}\right|}\\ =\frac{\left({\widehat{r}}_{\mathit{sum}}+{\widehat{r}}_{\mathit{diff}}\right)·\left({\widehat{F}}_{\mathit{sum}}+{\widehat{F}}_{\mathit{diff}}\right)}{\mid \widehat{r}\mid \left|\widehat{F}\right|}+\frac{\left({\widehat{r}}_{\mathit{sum}}+{\widehat{r}}_{\mathit{diff}}\right)·{\widehat{F}}_{\mathit{weak}}+{\widehat{r}}_{\mathit{weak}}·\left({\widehat{F}}_{\mathit{sum}}+{\widehat{F}}_{\mathit{diff}}\right)+{\widehat{r}}_{\mathit{weak}}·{\widehat{F}}_{\mathit{weak}}}{\mid \widehat{r}\mid \left|\widehat{F}\right|}\\ ={\mathit{Corr}}_{\mathit{sum},\mathit{diff}}+{\mathit{Corr}}_{\mathit{residual}}\end{array}$$

The two terms Corr_sum,diff and Corr_residual that sum to the actual correlation are plotted in Fig. 4B and F—we see that $\overrightarrow{S1}$ and $\overrightarrow{D1}$ activities largely explain the qualitative changes in correlations over time.

Thus, the actual activity pattern across cells of the LN, r⃗, can be approximated as the vector sum of $\overrightarrow{S1}$ and $\overrightarrow{D1}$ activities, which determines the correlation patterns. Fig. 4C and G and Fig. S8 illustrate $\overrightarrow{S1}$ and $\overrightarrow{D1}$ activities evolving over four time periods during a trial, as well as how their dynamics explain the correlation patterns. In SI section 10 we explain why correlations at the peaks of visual responses are higher in FK than in BG. In Fig. S9–10 and SI section 11 we show how the model dynamics change smoothly from the BG to the FK case for varying strengths of surround suppression.

Now we turn to examine how the dynamics of $\overrightarrow{S1}$ and $\overrightarrow{D1}$ activities are determined by their inputs. We have shown above that the external input to the sum or difference pattern is approximately N(I₁ P₁+I₂ P₂). We note that the absolute values of P₁ and P₂ for the sum and difference patterns are all about equal (Fig. 3B), which we can call m. That is, for the sum pattern, P₁ ≈ P₂ ≈ m, while for the difference pattern, P₁ ≈ m and P₂ ≈ -m. Thus, the inputs to the sum and difference patterns are approximately Nm(I₁+I₂) and Nm(I₁−I₂), respectively. When the network is in a steady state, these inputs are amplified by the connectivity: $\overrightarrow{S1}$ and $\overrightarrow{D1}$ activations are approximately given by $\frac{1}{\sqrt{2}}Nm(I_{\mathit{1}}+I_{\mathit{2}})/(\mathit{1}-{\lambda }_S)$ and $\frac{1}{\sqrt{2}}Nm(I_{\mathit{1}}-I_{\mathit{2}})/(\mathit{1}-{\lambda }_D)$ respectively, where λ_S and λ_D are the eigenvalues of the sum and difference patterns, respectively (for this approximation, we ignore the feedforward input from the other patterns, which is weak relative to the mean-driven input; the $\frac{1}{\sqrt{2}}$ factor arises because $\overrightarrow{S1}$ is only the LN1 half of the sum pattern, and similarly for $\overrightarrow{D1}$). As N, m, λ_S, and λ_D are all fixed properties of the network, $\overrightarrow{S1}$ and $\overrightarrow{D1}$ activities just depend on the dynamics of the mean inputs I₁ and I₂, being simply proportional to I₁+I₂ and I₁−I₂, respectively (Fig. 4C, D, G, H).

Direct evidence for two-dimensional dynamics in the Falkner, Krishna et al. dataset

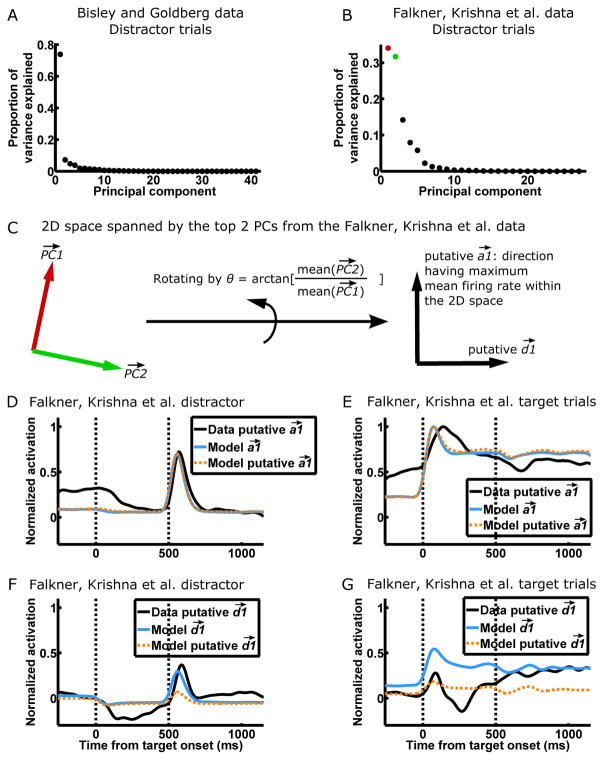
Since we propose that the BG data is dominantly one-dimensional and the FK data two-dimensional, we used principal component analysis (PCA) to directly examine the dimensionality of the two datasets. We focus on distractor trials because our correlation analysis revealed that they show the most salient dynamical differences between BG and FK. Furthermore, our model predicts that the activity on FK distractor trials has both large $\overrightarrow{a1}$ and $\overrightarrow{d1}$ activations, and thus is likely to reveal two dynamical dimensions, whereas the activity on FK target trials is more strongly one-dimensional, dominated by the single $\overrightarrow{a1}$ direction (Fig 4C and G). We excluded the transient visual responses to the distractor as they involve activation of weak patterns, and performed PCA on the remaining slowly varying activity patterns of distractor trials. The results indeed confirm the one-dimensionality of the BG data and two-dimensionality of the FK data (Fig. 5A–B).

Figure 5. Direct evidence for two-dimensional dynamics in the Falkner, Krishna et al. dataset.

(A and B) PCA, where the variables are neurons and the observations are the instantaneous activity vectors during distractor trials, for the BG (A) and FK (B) datasets. Activity vectors during the transient visual responses to the distractor (600–1100 ms after target onset for BG, 450–750 ms after target onset for FK) were not included for this analysis because they involve activation of weak patterns. The majority of the variance is explained by one PC in BG, while a comparable proportion is explained by two PCs in FK, consistent with one-dimensional dynamics in BG and two-dimensional dynamics in FK.

(C) We hypothesize that the 2D space spanned by the top 2 PCs (colored as in B) in the FK data is the 2D space of $\overrightarrow{S1}$ and $\overrightarrow{D1}$ (Fig. 3C and Fig. 4C, G). We further hypothesize that the direction having the maximum mean firing rate within the 2D space of the 2 PCs is the putative $\overrightarrow{a1}$ direction, since $\overrightarrow{a1}$ represents concerted firing of neurons in an LN. We can thus find the putative $\overrightarrow{a1}$ and $\overrightarrow{d1}$ of the FK data by rotating the two PCs by an angle of arctan[mean( $\overrightarrow{PC1}$)/mean( $\overrightarrow{PC2}$)], where mean(•) denotes mean over the elements of a vector.

(D–G) The activation of $\overrightarrow{a1}$ (D–E) and $\overrightarrow{d1}$ (F–G) on FK distractor trials (D and F) and target trials (E and G). In D–E, the data putative $\overrightarrow{a1}$ was derived as in C. To determine activation in the model, one cell was “recorded” from each of multiple simulated global networks to form the model population. To determine the model $\overrightarrow{a1}$, suppose the ith cell of the model population is the jth cell from LN1 of the ith global network. Then the ith element of the model $\overrightarrow{a1}$ is the jth element of the actual $\overrightarrow{a1}$ of the ith global network. The model putative $\overrightarrow{a1}$ was derived as in C but from the model population. The $\overrightarrow{d1}$ directions are determined similarly. Each set of activations (e.g. the four activation traces of data putative $\overrightarrow{a1}$ and $\overrightarrow{d1}$ on target and distractor trials comprise a set) is normalized by its peak $\overrightarrow{a1}$ activation on target trials—thus, DG share the same scale. Vertical dashed lines denote the onsets of the target and distractor.

Given the 2D space spanned by the top two principal components (PCs) identified from the FK data, we ask further, do activity patterns in this dominant 2D space actually behave as our model predicts? To answer this question, we first estimate the activity directions in the data that correspond to those in our model. We take the direction having the maximum mean firing rate within the 2D space of the two PCs as the putative $\overrightarrow{a1}$ direction, since $\overrightarrow{a1}$ is a direction representing concerted firing of neurons in an LN, and take the direction orthogonal to the putative $\overrightarrow{a1}$ as the putative $\overrightarrow{d1}$ (Fig. 5C). In Fig. 5D–G we plot the activities over time in the $\overrightarrow{a1}$ and $\overrightarrow{d1}$ directions in the data and model (in SI section 12 we discuss differences between data and model). The activities in the putative $\overrightarrow{a1}$ and $\overrightarrow{d1}$ directions in the data match those predicted by the model, providing direct evidence that our proposed two-dimensional dynamics underlie the FK data.

In SI section 13, we discuss the dynamics and dimensionality of E and I subpopulations.

Two-dimensional dynamics suggest a recurrent origin for LIP surround suppression

Surround suppression is observed in multiple cortical areas (reviewed in Rubin et al., 2015) and has been extensively studied as a model for understanding cortical computations and circuit mechanisms (e.g. in V1, Ozeki et al., 2009, Rubin et al., 2015, and see review by Nurminen and Angelucci, 2014). When considering surround suppression two LNs of a given cortical area, a key mechanistic question is the following: to what extent is it inherited from surround suppression in other areas, i.e. resulting from a withdrawal of input from those areas, and to what extent is it due to reciprocal, suppressive coupling between the two LNs?

Of areas that directly or indirectly project to LIP (Blatt et al., 1990; Clower et al., 2001), surround suppression has been observed in MT (Hunter and Born, 2011; Tsui and Pack, 2011), V4 (Desimone and Schein, 1987;; Sundberg et al., 2009), superior colliculus (Dorris et al., 2007), FEF (Schall and Hanes, 1993; Cavanaugh et al., 2012), and dlPFC (Suzuki and Gottlieb, 2013). Thus, it is possible that LIP surround suppression is inherited from one or more of these areas. However, according to our model, the observed pattern of correlation between fixation and instantaneous activity depends on activity patterns arising from the coupling of local LIP networks. We argue that the experimentally observed correlation pattern is a signature indicating that surround suppression of external input alone cannot account for LIP surround suppression.

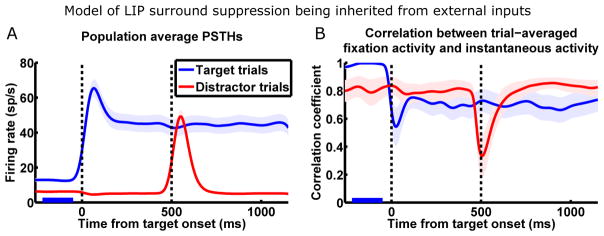
This can be demonstrated by simulating the scenario of the null hypothesis—LIP surround suppression being inherited from external inputs. In this version of the model, the two LNs are uncoupled. Whenever a stimulus appears or a saccade is planned, the LN with the corresponding RF is activated by visual or delay input; at the same time, the external input to the other LN is reduced, modeling surround suppression inherent in one or more input sources (see SI section 2.2 for model details). Fig. 6A shows the population average PSTHs from a simulation of the FK experiment using this model. On the surface, if we examine only the firing rates, this model of surround suppression reproduces the experimental data. However, if we examine the underlying network dynamics using the correlation analysis (Fig. 6B), we find that this model cannot reproduce the experimentally observed correlation pattern. Specifically, the dynamics of each LN here is dominated by its slow mode, as in the BG dataset (Fig. 1E and 2E).

Figure 6.

Model of inherited surround suppression cannot reproduce observed network dynamics. The model: two LIP LNs are uncoupled; whenever one LN receives visual or delay input, the external input to the other LN is reduced.

(A) Population average PSTHs (n = 27 cells; same conventions as Fig. 1D) shows that this model reproduces firing rates observed by FK (Fig. 1D) during surround interactions.

(B) This model fails to reproduce network dynamics observed by FK (Fig. 1F) during surround interactions. Correlation analysis with same conventions as Fig. 1F.

There are alternative mechanisms that conceivably could account for the FK correlations. We consider these in SI section 14 but conclude, for multiple reasons, that the most likely and parsimonious interpretation is that surround suppression in LIP arises primarily from direct suppressive coupling between LIP LNs.

Discussion

By demonstrating that recurrent interactions between LIP LNs are likely to drive LIP surround suppression, our study suggests the active involvement of LIP in attentional and saccadic selection. LIP is part of a fronto-parietal-collicular network that mediates attentional guidance and eye movements, and the attentional and saccadic priorities associated with different locations (a “priority map”) are encoded in the activity of neurons in this network with the corresponding RF locations (Bisley and Goldberg, 2010). It has long been theorized that different locations on this priority map mutually suppress each other to facilitate attentional and saccadic selection, to allow persistent focus by resisting distraction, and to allow the planning and execution of sequential saccades (Itti and Koch, 2001; Constantinidis and Wang, 2004; Xing and Andersen, 2000). However, the neural substrates and mechanisms of these processes are not clear. Our results suggest that LIP directly participates in these processes and shapes the priority map, instead of merely reflecting computations achieved in other areas.

Ganguli et al. (2008) showed that the slow dynamics of a local LIP network (i.e. neurons sharing the same RF) are 1D, but we can now see that this result is restricted to the case in which a single LN is activated without activation of other LNs to which it is coupled. Nonetheless, we can simply understand the more complex, 2D slow dynamics we have found in the FK data as resulting from coupling between networks that, in isolation, each have 1D slow dynamics. This lays a basis for understanding higher-dimensional local dynamics induced by interactions between larger numbers of simultaneously activated LNs. For example, during visual search, it takes longer to find a target when there are more distractors, and, correspondingly, LIP activity is lower when there are more distractors (Balan et al., 2008). This likely results from increased surround suppression by larger numbers of activated LNs, which would yield correlations corresponding to a higher-dimensional dominant activity space (e.g., number of dimensions equal to the number of mutually interacting networks). Our study thus provides a basis for analyzing activity dynamics when multiple stimuli evoke interaction of multiple local LIP networks, as occurs in natural visual environments.

Our results have implications for the mechanisms underlying certain types of perceptual decision making, where saccadic decisions are made based on noisy sensory evidence (Roitman and Shadlen, 2002; Gold and Shadlen, 2007). This type of decision making has been posited to involve two neuronal pools that integrate opposing sensory evidence, with each either accumulating evidence independently and racing toward a decision (Mazurek et al., 2003), or competing with the other by mutual inhibition (Wong and Wang, 2006; Usher and McClelland, 2001). Recent results show that these neuronal pools are not exclusively in LIP (Katz et al., 2016), but if they are distributed across multiple areas that include LIP, which of the two classes of models applies to each instance of decision making would depend on whether the two neuronal pools are recurrently coupled. When they are not coupled (like the neuronal pools studied by BG), the independent accumulator model would apply, and when they are coupled, the mechanisms described here would contribute to the competition that leads to decision making. In the future it would be interesting to study decision making separately for cases in which the two alternative choices engage LIP LNs that do or do not suppress one another (as BG and FK have done in studying attentional switching), examine the neural correlates on the population level, and compare them with behavior.

These LIP interactions would cause priority assignments to be in part determined in relative terms, as has been observed in certain forms of value-based decision making. In saccade tasks where different saccade targets are associated with different magnitudes of reward or reward probabilities, some LIP neurons encode the expected value of different saccades (Platt and Glimcher, 1999; Dorris and Glimcher, 2004). Importantly, the value representation in LIP is relative, such that the response to one saccade target depends on its value relative to those of other possible saccade targets; this relative value encoding is well described by the phenomenological model of divisive normalization (Louie et al., 2011; Carandini and Heeger, 2012). Surround suppression, computed within LIP in ways similar to those described here, provides a circuit mechanism for divisive normalization of value representations (Louie et al., 2014; LoFaro et al., 2014; Rubin et al., 2015).

Regardless of the cognitive context in which LIP function has been investigated, research has often focused on single neuron activity or the average activity of LIP populations. Our work adds to other recent work (e.g., Churchland et al., 2012; Cunningham and Yu, 2014) in suggesting that there is much information in the activity patterns across neurons, which change as a function of external stimuli and internal goals such as saccade plans. As we have seen, even when the mean activity of a population changes only subtly, the pattern of activity across neurons can change drastically (e.g., when a target appears in the suppressive surround of a local LIP population). Thus, beyond the information carried by single neurons or their average activity, downstream areas could potentially read out information from the activity pattern across LIP neurons—although, whether or how downstream areas do this remains to be tested. This is potentially important in the natural context, where LIP LNs must interact to process a multitude of changing visual stimuli and internal goals to guide visuomotor behavior.

Experimental Procedures

A full description of modeling procedures is found in SI section 2.

Highlights.

• Slow dynamics of LIP local population can appear one-dimensional or high-dimensional

• Model of coupling between local networks reconciles conflicting data

• Reveals LIP’s internal, recurrent circuitry underlying surround suppression

• Data show two-dimensional slow dynamics as predicted by model