Abstract
Mitochondria are semi-autonomous organelles that supply energy for cellular biochemistry through oxidative phosphorylation. Within a cell, hundreds of mobile mitochondria undergo fusion and fission events to form a dynamic network. These morphological and mobility dynamics are essential for maintaining mitochondrial functional homeostasis, and alterations both impact and reflect cellular stress states. Mitochondrial homeostasis is further dependent on production (biogenesis) and the removal of damaged mitochondria by selective autophagy (mitophagy). While mitochondrial function, dynamics, biogenesis and mitophagy are highly-integrated processes, it is not fully understood how systemic control in the cell is established to maintain homeostasis, or respond to bioenergetic demands. Here we used agent-based modeling (ABM) to integrate molecular and imaging knowledge sets, and simulate population dynamics of mitochondria and their response to environmental energy demand. Using high-dimensional parameter searches we integrated experimentally-measured rates of mitochondrial biogenesis and mitophagy, and using sensitivity analysis we identified parameter influences on population homeostasis. By studying the dynamics of cellular subpopulations with distinct mitochondrial masses, our approach uncovered system properties of mitochondrial populations: (1) mitochondrial fusion and fission activities rapidly establish mitochondrial sub-population homeostasis, and total cellular levels of mitochondria alter fusion and fission activities and subpopulation distributions; (2) restricting the directionality of mitochondrial mobility does not alter morphology subpopulation distributions, but increases network transmission dynamics; and (3) maintaining mitochondrial mass homeostasis and responding to bioenergetic stress requires the integration of mitochondrial dynamics with the cellular bioenergetic state. Finally, (4) our model suggests sources of, and stress conditions amplifying, cell-to-cell variability of mitochondrial morphology and energetic stress states. Overall, our modeling approach integrates biochemical and imaging knowledge, and presents a novel open-modeling approach to investigate how spatial and temporal mitochondrial dynamics contribute to functional homeostasis, and how subcellular organelle heterogeneity contributes to the emergence of cell heterogeneity.
Introduction
Mitochondria are essential sources of ATP, and their morphology is dynamic; mitochondria are highly mobile within a cell [1, 2] and undergo fusion and fission events, resulting in a continuum of morphologies among populations of mitochondria, from tubular to small puncta [3]. Furthermore, mitochondrial homeostasis is dependent on biogenesis through fission-dependent duplication [4] and mitochondrial quality control is carried out by autophagy-mediated degradation, i.e. mitophagy [5–8]. Systems biology studies on mitochondrial morphology have contributed insights into how dynamic mitochondrial behavior relates to homeostasis and functional maintenance. Frequency of fusion and fission cycles determines efficiency of mitophagy [9], and suggests that altered cycles in aging organisms may contribute to maintaining mitochondrial mass [10]. Simulations also suggest that spatial limitations, which decrease fusion and fission capacities during aging, can increase the heterogeneity of mitochondrial genotypes within a cell, and consequently increase heterogeneity among a population of cells [11]. Furthermore, mitochondrial mobility has been predicted to have a role in maintaining a healthy mitochondrial population [12]. Of note, these studies did not address how morphological states and mass homeostasis coordinate bioenergetic supply and demand. Indeed, fission, fusion, biogenesis and mitophagy activities both respond to, and shape, the cellular bioenergetic state [13–20]. Thus, in this study, we sought to analyze how reactions of individual mitochondria form a collective population response, to organize morphological states and maintain mass homeostasis, under basal conditions and in response to bioenergetic stress.
To that end, we employed agent-based modeling (ABM), a computational method to simulate spatial and temporal population activities [21–25], which has been applied in several areas of systems biology, including, apoptotic death receptor dynamics [26], autophagy dynamics [27], dosage screening of drug combinations [28] and lipid composition [29]. This discrete modeling approach involves the repetitive update of rules describing the behavior of autonomous agents, thus relying on computational power to simulate global behavior emerging from collective action of all agents. Using ABM, we simulated individual spatial and temporal behaviors of mitochondria, and bi-directional mitochondria-environment bioenergetic signaling. We analyzed the temporal behavior of mitochondrial subpopulations with variable masses, and report that the distribution of mitochondrial subpopulations is determined by fusion-fission activities and the total mitochondrial mass, but is minimally impacted by the directionality of mitochondrial movement. Further, the time required to establish sub-population homeostasis, and to effectively transmit information among the population, is determined by fusion/fission events and mitochondrial velocities. Our simulations also suggest that the ability of mitochondrial populations to re-establish homeostasis following damage requires environmental bioenergetic stress sensing. Overall, these findings demonstrate that ABM permits a precise investigation of the link between subcellular and cell decisions, and provides a framework for understanding the bidirectional relationship of organelle dynamics with cellular environmental signaling processes, and the emergence of cell heterogeneity.
Results
Agent based model of mitochondrial fusion-fission cycles
Mitochondrial fusion and fission processes were modeled using a discrete approach, since a continuous approximation was unreasonable due to the low copy number of mitochondria. To this end, we employed agent-based modeling (ABM), considering mitochondria as discrete agents which can move, fuse with each other, or undergo fission (Fig 1A and 1B). Without explicitly deriving phenomenological equations, time-course ABM simulations proceed by increasing time (t) with a discrete step (Δt = 1s), followed by iterative evaluation of a set of behavioral rules for all mitochondrial agents. Simulations were performed in the NetLogo modeling environment [30] as described in ‘Materials and Methods’. The cellular spatial domain and the set of behavioral rules governing mitochondrial movement, and fusion and fission processes were implemented as follows.
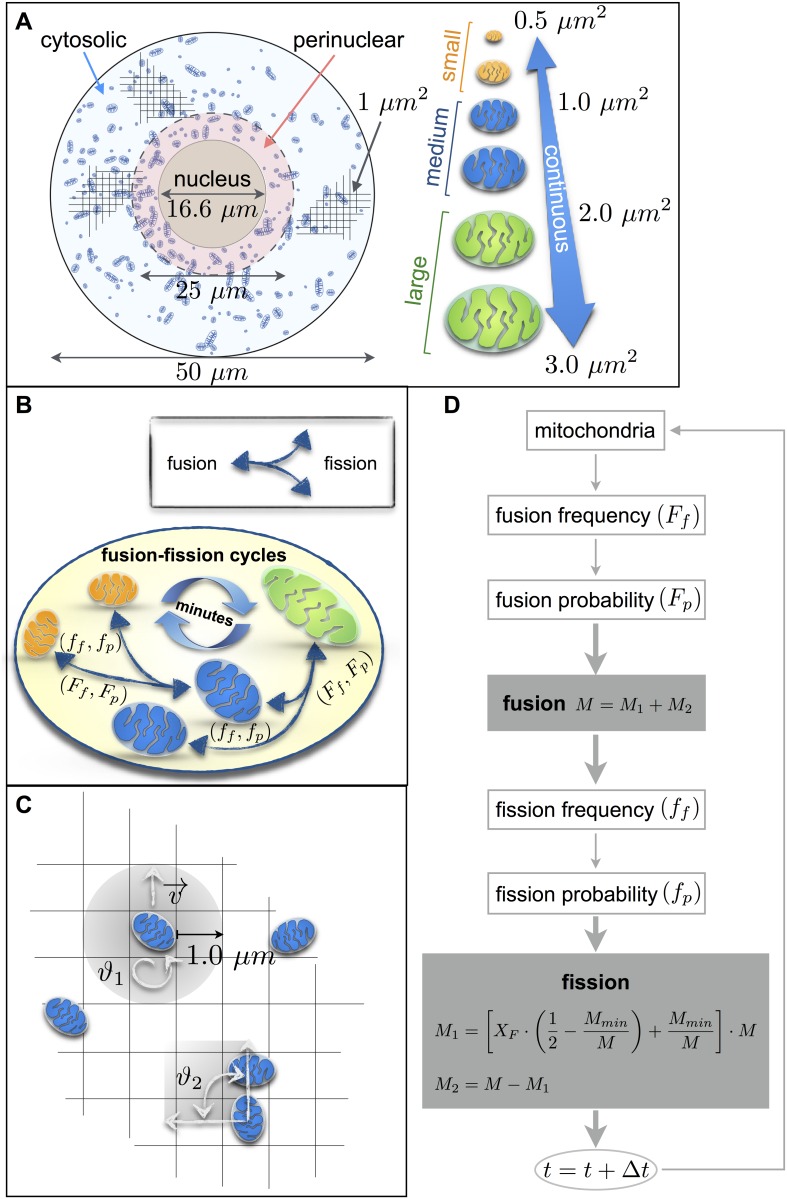
Fig 1. An agent-based model of mitochondrial dynamics determined by organelle mobility and fusion-fission cycles.
(A) Model representation. The model consists of a two-dimensional grid (elements of 1 μm × 1 μm) in which the cell is represented by a circle with a diameter of 50 μm, and a nucleus with a diameter of 16.6 μm. The dashed circle (diameter, 25 μm) divides the cell in two regions, perinuclear (red arrow) and cytosolic (blue arrow), with different mitochondrial mobility. The mitochondrial population consists of agents with masses ranging continuously from a minimum value Mmin of 0.5 μm2 to a maximum value Mmax of 3 μm2. The mitochondria population is in turn subdivided into three groups: small (mass smaller or equal 1 μm2, orange), medium (mass between 1 μm2 and 2 μm2, blue) and large (mass greater than 2 μm2, green). (B) Schematic describing mitochondrial dynamics, consisting of fusion (f) and fission (F) cycles occurring with temporal frequencies (ff, Ff) of minutes. Mitochondria of all masses are able to undergo fusion and fission events according to fusion and fission probabilities (fp, Fp). Time step used in all the simulation, Δt = 1sec. (C) Schematic describing mitochondrial movement and unfeasible actions. Each mitochondrion checks, with an internal control, the surrounding area with a radius of 1.0 μm in order to avoid unfeasible actions such as moving outside the cell or inside the nucleus and overlapping other mitochondria. If the area is free, the mitochondrion first move one step forward, with a velocity v, and than rotates by a random angle ϑ1 ϵ [0°, 360°]. If the mitochondrion encounters either another mitochondrion (and no fusion occur), the nucleus, or the cell border, the mitochondrion rotates by a random angle ϑ2 ϵ[0°, 90°]. (D) Basic flow chart of the model representing the fusion-fission cycle and main components of the model. Shaded boxes indicate the main processes of the model (fusion and fission) with the respective governing equations.
Spatial domain and agent’s properties
For simplicity, the cellular domain was modeled in two dimensions, represented as a circle with a diameter of 50 μm containing a central nucleus with a diameter of 16.6 μm [31] and a variable number of mitochondria (Fig 1A). Each mitochondrial agent has the following three properties: mass (M) with units μm2, velocity magnitude (v) with units μms-1, and directionality (ϑ), with units angular degrees. As morphologies of individual mitochondria are heterogeneous within a cell and among cell types [3], we introduced a continuous range of mitochondrial masses, from a minimum value (Mmin) of 0.5 μm2 [31] to a maximum value (Mmax) of 3 μm2 [32, 33] (Fig 1A).
Mitochondrial movement rule set
In order to prevent unfeasible actions such as overlaps, each mitochondrion first checks its surrounding area within a radius of 1.0 μm. If this area is free, the mitochondrion first moves with a velocity v following its current directionality ϑ. In each time iteration, the velocity v is randomly chosen within pre-set intervals depending on the intracellular position as explained below. After movement, the directionality is updated by choosing random angle ϑ1 between 0° and 360° (Fig 1C). If the surrounding area is occupied by another mitochondrion (without fusing with it), the nucleus, or the cell border, the mitochondrion does not move and its directionality is updated by choosing a random angle ϑ2 between 0° and 90° (Fig 1C).
Mitochondrial mobility can vary in relation to its position inside the cell [34], as the average velocity of mitochondria in the cytosolic region is faster (0.22–0.50 μms-1) than of mitochondria localized in the perinuclear region (0.10 μms-1) [33, 35–38]. Therefore, to simulate mitochondrial spatial dynamics, we subdivided the cell into two regions (Fig 1A). The first region corresponds to the perinuclear area (diameter ≤ 25 μm), where mitochondria were assigned low velocity magnitudes (vl) in the interval 0 ≤ vl ≤ 0.44 μms-1. The second region corresponds to the bulk cytosolic area, where mitochondria were assigned high velocity magnitudes (vh) in the interval 0 ≤ vh ≤ 1 μms-1. Finally, since small mitochondria move faster than large mitochondria [1, 39], we assumed that mitochondrial velocities are inversely proportional to the mass, i.e., v = v*/m, where v* assumes a value of vl or vh according to the intracellular position.
Mitochondrial fusion rule set
Mitochondrial fusion kinetics was parameterized in terms of a fusion probability (Fp), with higher Fp values relating to larger fusion rates. A given mitochondrion can fuse with another mitochondrion according to the following two rules. (I) Before moving, a random number is sampled between 0 and 100. If this number is below the value of Fp, the mitochondrion is allowed to fuse given that there is another mitochondrion within an area of twice its own radius. (II) To avoid formation of unrealistically large mitochondria, the fusion process only takes place if the sum of the mass of the two fused mitochondria is below a maximal mitochondrial mass (Mmax) (Fig 1D and S1 Fig).
Mitochondrial fission rule set
Mitochondrial fission kinetics were parameterized in terms of a fission probability (fp). A given mitochondrion can undergo fission according to the following two rules. (I) A random number is sampled between 0 and 100, and if this number is below the value of fp, the mitochondrion splits into two daughter mitochondria. (II) To avoid unrealistically small mitochondria, the fission process can only occur in mitochondria of a mass greater than two times the minimum mass (M > 2Mmin) (Fig 1D and S1 Fig). The mass of the parent mitochondrion is distributed randomly among the two daughters, satisfying mass conservation and bounds as follows:
| (1) |
| (2) |
Where M is the mass of the parent mitochondrion, M1 and M2 are the masses of the smallest and biggest daughter mitochondrion, respectively, and XF is a scaling coefficient estimated uniformly in the interval [0,1] (XF ~ U[0,1]) (S1 Fig).
Notably, mitochondrial fusion and fission cycles occur on the order of minutes [40–42], and thus, at larger time scales than mitochondrial movement. To capture these time scale differences, the rule sets for mitochondrial fission and fusion were only evaluated every 5 minutes [43, 44], while the rule set for mitochondrial movement was evaluated at all time iterations. The update frequency of fusion and fission rules is denoted here as fusion frequency Ff and fission frequency ff, respectively, both of them set to 1 event per 5 minutes for all simulations [45, 46] (Fig 1B and 1D, S1 Fig and S1 Code). Table 1 summarizes all model parameters and their respective value.
Table 1. Description of the parameters used in the model.
| Parameter | Description | Value | Biological evidence |
|---|---|---|---|
| DC | Cell diameter. | 50 μm | 2–100 μm human cell [31]. |
| DN | Nucleus diameter. | 16.6 μm | 2–10 μm human cell [31]. |
| Mmin | Minimum mitochondrial mass. | 0.5 μm2 | Mitochondrial morphologies vary within the cell [3, 47]. Length: 1–10 μm mammalian cell [31]. Area: 2–10 μm2 myelinated axon [33], 0.1–0.2 μm2 HeLa cell [48]. |
| Mmax | Maximum mitochondrial mass. | 3 μm2 | |
| vl | Mitochondrial velocity in the perinuclear region. | [0,0.44] μms-1 | 0.5 μms-1 along cytoskeleton, 0.22 μms-1 perinuclear region, BY-2 cell [35]. 0.24–0.69 μms-1 axon [37]. 0.6 μms-1 myelinated axon [33]. |
| vh | Mitochondrial velocity in the cytosolic region. | [0,1] μms-1 | |
| ϑ1 | Directionality. Rotational angle of mitochondria in free space. | [0°,360°] | Changes in the directionality vector allow full range of directional movements. |
| ϑ2 | Directionality. Rotational angle of mitochondria constrained by other agents. | [0°,90°] | Restricts movements in crowded conditions to avoid unfeasible actions. |
| Initial mitochondrial mass | Total mitochondrial mass at time point 0. | 300 μm2 | Mitochondrial volume percentage of HeLa cells: 10%-15% [48, 49] and 20.1%-44.6% [49]. |
| Fusion probability (Fp) | Probability of fusion. | [0,100] % | Fusion events can vary according to the cellular state [47]. In our model this probability varies (is enhanced) according to the level of cellular stress. |
| Fission probability (fp) | Probability of fission. | [0,100] % | Fission events can vary according to the cellular state [47]. In our model this probability varies (is reduced) according to the level of cellular stress. |
| Fusion frequency (Ff) | Frequency of fusion. | 5 min | Frequency of fusion/fission events per mitochondrion in COS7 and INS1 cells: ~1 event per 5–20 min [43, 46]. |
| Fission frequency (ff) | Frequency of fission. | 5 min | Frequency of fusion/fission events per mitochondrion in COS7 and INS1 cells: ~ 1 event per 5–20 min [43, 46]. |
| Biogenesis probability (Bp) | Probability of biogenesis. | [0,100] % | Biogenesis is upregulated by bioenergetic stress and nutrient deprivation [4]. In our model this probability varies (is enhanced) according to the level of cellular stress. |
| Biogenesis frequency (Bf) | Frequency of biogenesis. | 28.9 min | Biogenesis occurs according to cellular needs [4]. Value estimated by maximizing Eq 4, optimizing the repopulation of mitochondria in a cell, starting from mitochondrial mass equal 1 to 15% of the cell area (mass) within 2 days. |
| Damage probability (Dp) | Probability of damage. | [0,100] % | Damaging events can vary according to different external/internal cell factors [5–7, 47]. |
| Degradation frequency (Df) | Frequency of degradation of damaged mitochondria. | 5.7 min | Quality control mechanism to eliminate damaged mitochondria [5–7, 47]. Value estimated by maximizing Eq 5, optimizing the complete depletion of damaged mitochondria within one day starting from a damaged mitochondrial mass of 15% of the cell area. |
| Ratio low/high damage | Probability of having a low or high damage. | [0,100] % | Mitochondrial damage levels vary according to mitochondrial activity [47]. |
| Damage threshold (dT) | Threshold for a low damaged mitochondrion to become highly damaged. | 12.4 min | Value estimated by maximizing Eq 5, optimizing the complete depletion of damaged mitochondria within one day starting from a damaged mitochondrial mass of 15% of the cell area. |
| MR threshold (MRT) | Mitophagy receptor threshold for autophagosome formation. | 12 min | Autophagosome formation for clearance of damaged mitochondria [5–7, 47]. Value estimated by maximizing Eq 5, optimizing the complete depletion of damaged mitochondria within one day starting from a damaged mitochondrial mass of 15% of the cell area. |
| Δt | Time step increment. | 1 sec | Increment of the simulations time steps. |
| Number of cells | Number of cells considered in each simulation. | 100 | Number of cells considered to account for cell-to-cell variability. |
The effect of fusion and fission on mitochondrial morphology is intrinsically connected to the total mitochondrial mass
We first studied how the combined effect of variations in mass and fusion/fission kinetics affect the mitochondrial population. To this end, simulations were performed using three combinations of fusion-fission probabilities, i.e. dominant fission (Fp = 20%, fp = 80%), dominant fusion (Fp = 80%, fp = 20%), and balanced fusion-fission (Fp = fp = 50%). As mitochondrial masses range from approximately 10–40% of cellular volume [48] we simulated three total mitochondrial masses: 100 μm2 (5% of the total cell area), 200 μm2 (10% of the total cell area) and 300 μm2 (15% of the total cell area) (Fig 2A–2C and S1 Movie). Simulations were run for 2 hours and were initialized by randomly distributing the total mitochondrial mass among a population of mitochondria with masses between Mmin and Mmax.
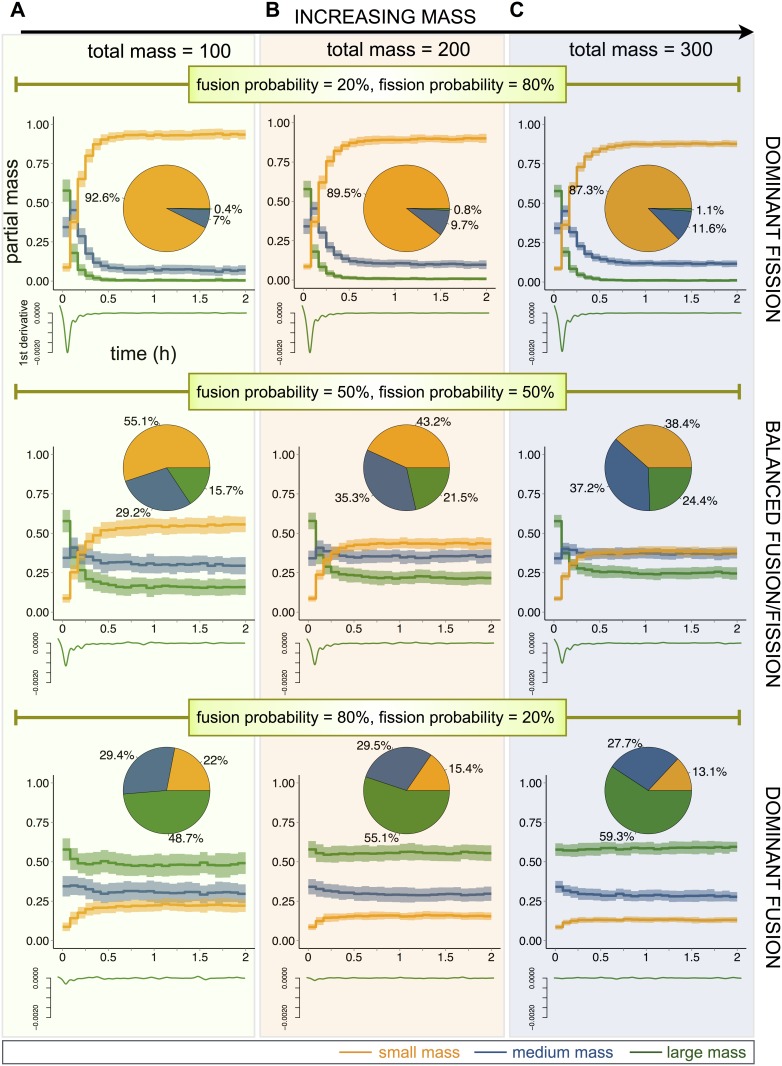
Fig 2. Impact of fusion and fission probabilities and mitochondrial mass on mitochondrial subpopulations.
(A) Time course response of mitochondrial subpopulations for low total mass (M = 100; 5% of the whole cell area). Three mitochondrial subpopulations are considered: small mass (orange line), medium mass (blue line) and large mass (green line). The partial mass reports the sum of the masses from all mitochondria in a given subpopulation divided by the total mitochondrial mass. Lines display the mean among 100 simulations, and shaded regions display the standard deviation. Small graphs underneath show the evolution of the first derivative of mitochondria with large mass (green line). Three different fusion/fission probability rates are used: 20%/80%, 50%/50% and 80%/20%. Pie charts report the partial mass (in terms of percentages) for the subpopulations at the final simulation time (2 hours). (B) Same as (A) but with a total mitochondrial mass of 200 (10% of the whole cell area). (C) Same as (A) but with a total mitochondrial mass of 300 (15% of the whole cell area).
To analyze simulations, we classified mitochondria into three subpopulations: small (M ≤ 1 μm2, color orange), medium (1 μm2 < M < 2 μm2, color blue) and large (M ≥ 2 μm2, color green) (Fig 1A). To evaluate the distribution of mitochondria among subpopulations, a partial mass was estimated for each subpopulation by adding the masses of all mitochondria in the subpopulation divided by the total mass. For each set of parameters, the average of 100 simulations is reported, where each simulation is interpreted as one stochastic cell. To indicate the transition to steady state, the first time-derivative was calculated for the large mass subpopulation (green trace). Pie charts report average subpopulations distributions at the final time point (2 hours).
As indicated by the first time-derivatives, mitochondrial subpopulation distributions stabilized within approximately 15 minutes (Fig 2A–2C). For all masses, under conditions of dominant fission, mitochondrial populations adopted a fragmented state (87% to 92% small subpopulation). In contrast, under conditions of dominant fusion, the large subpopulation was most abundant (49% to 69%). Notably, increasing the total mitochondrial mass further increased the abundance of large mitochondria.
These results suggest that mitochondrial morphology homeostasis depends on both, fusion and fission probabilities and the total mitochondrial mass. With low total masses (M = 100 μm2), the fusion process is limited by the probability that two mitochondria are in proximity with each other. We suggest then that for low masses, the cell has very little control over the morphology of its mitochondrial network. Alternatively, at masses equivalent to 15% of the cell area (M = 300 μm2), which corresponds to the mitochondrial content of a typical cell line (e.g. HeLa) [49], physical proximity is less limiting. Therefore, higher mitochondrial mass grants the cell better controllability over its mitochondrial network morphology.
Importantly, variations in the total mass of mitochondria affect both heterogeneity of the intracellular mitochondrial population and cell-to-cell variability. Namely, higher masses and balanced probabilities of fusion and fission allow for more heterogeneous populations with mitochondria of different sizes, as indicated by the distributions on the pie charts (Fig 2C, middle graph). On the other hand, higher masses lead to less cell-to-cell variability with respect to smaller ones, as can be observed from the spread of the partial mass in the time course plots (Fig 2A–2C).
Influence of mitochondrial directionality on subpopulation distributions
Mitochondrial movement is essential to meet energy demands and prevent cell death [50], and is coordinated by different components of the cytoskeleton such as microtubules [51], which mediate directed movement of organelles [52]. Therefore, we sought to investigate the effect of directed vs. free movement on the behavior of the mitochondrial subpopulations. To this end, we modified the range of variation of the directionality property of mitochondrial agents, assigning unrestricted rotation values (ϑ1 ϵ [0°, 360°]) (Fig 3A), and restricted rotation values (ϑ1 ϵ [0°, 10°]) (Fig 3B and S2 Movie). The total mass was set to 300, and fusion and fission probabilities to 50%.
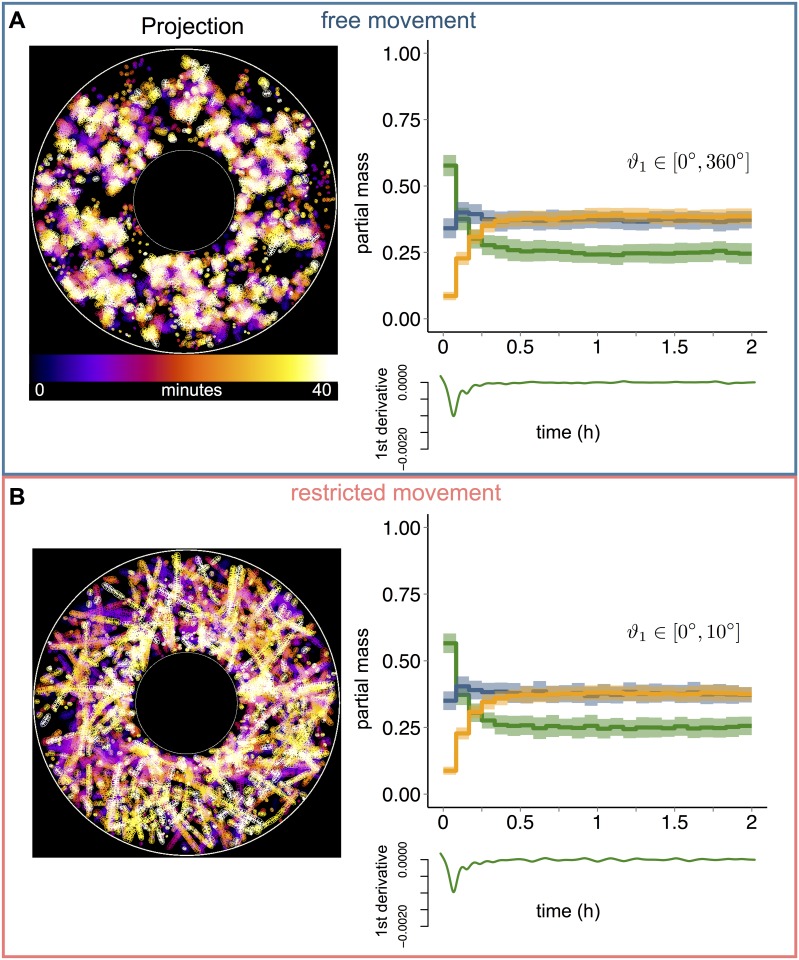
Fig 3. Impact of mitochondrial directionality on mitochondrial mass subpopulation distributions.
(A) Mitochondrial movements are indicated by projecting 25 images, one every 100 time steps, representing a total of ~40 minutes of a simulation. Time points are indicated according to color-code. Line graphs display mean values and standard deviation (shaded regions) of 100 simulations for mitochondrial population with free movement. The initial mass value was fixed to 300 and the angle ϑ1 ϵ [0°, 360°]. The plot represents the evolution of three mitochondrial subpopulations, small mass (orange line), medium mass (blue line) and large mass (green line), normalized to the total mass at time point 0. Small graphs underneath show the evolution of the first derivative of mitochondria with large mass (green line). The simulations were performed for a total time of 2 hours. (B) Same as (A) but with restricted movement, ϑ1 ϵ [0°, 10°].
Compared to unrestricted movement (Fig 3A), restricted directionalities (Fig 3B) resulted in mitochondrial trajectories that followed straight lines, effectively mimicking directed movements. However, the time course distribution of mitochondrial subpopulations was unchanged between restricted and unrestricted movements. These findings suggest that the impact of mitochondrial directionality on the state of the mitochondrial population is negligible.
Transmission dynamics of the mitochondrial network
We next investigated how fusion and fission dynamics, directionality and mobility impact the mitochondrial network transmissivity [41], defined here as the ability to transmit signals among the mitochondrial population by consecutive fusion-fission events. Mitochondrial network transmissivity has been previously measured by photoactivatable GFP within a subpopulation of mitochondria (~10%), finding that the complete mitochondrial population was fluorescent within 30–60 minutes [53, 54]. Here, to simulate transmission dynamics, we introduced the following rule set for inter-mitochondrial GFP heritability: (I) fusion of an unlabeled mitochondrion with a GFP-labeled mitochondrion, results in a parent GFP-labeled mitochondrion. (II) Fission of a GFP-labeled mitochondria results in two GFP-labeled daughter mitochondria. We simulated the effect of a localized photoactivation of 10% of the cellular mitochondria, and quantified GFP transmission through the cell for several values of mitochondrial mass and fusion/fission probabilities (Fig 4A).
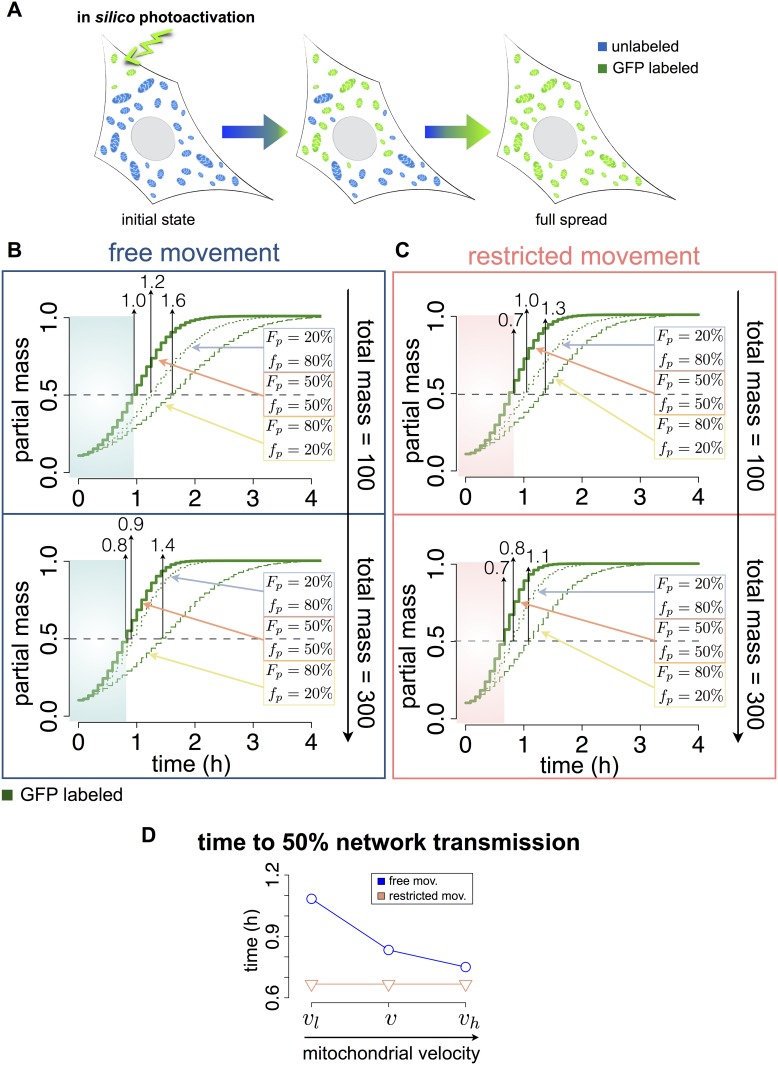
Fig 4. In silico photoactivation to quantify transmission dynamics in mitochondrial networks.
(A) Schematic representation of an in silico photoactivation. 10% of mitochondrial mass is assigned a GFP label, which transmit through the cell upon a fusion event: fusion of a mitochondrion with a GFP-labeled mitochondrion, results in a parent GFP-labeled mitochondrion, which upon fission results in two GFP-labeled daughter mitochondria. (B) Transmission dynamic of photoactivated GFP across the mitochondria population moving with free motion (ϑ1 ϵ [0°, 360°]), starting from 10% of labeled mitochondria (green). Simulations were performed with total mitochondrial masses of 100 and 300 and three different fusion/fission probability rates: Fp/fp = 20%/80% (dotted line), Fp/fp = 50%/50% (solid line) and Fp/fp = 80%/20% (dashed line). 100 simulations were performed each and plots represent the average values normalized to the total mass at time point 0. Blue regions indicate the time to 50% network transmission with fusion/fission probability rates of 50%/50%. (C) Same as (B) but with restricted movement, ϑ1 ϵ [0°, 10°]. Pink regions indicate the time to 50% network transmission with fusion/fission probability rates of 50%/50%. (D) Effect of the mitochondria mobility on transmission dynamics in the case of free movement (blue circles, line) and restricted movement (pink triangles, line). Detailed representation of the time needed to the GFP labeled mitochondrial population to exceed the unlabeled population for an initial total mitochondrial mass of 300 with a fixed fusion/fission probability rate of 50%/50% and three different velocities: vl ϵ [0, 0.44] μms-1, vh ϵ [0, 1] μms-1 and v, equal to vl in the perinuclear region and to vh outside.
Simulations were performed with total mitochondrial masses of 100 and 300, fusion/fission probability ratios of 20%/80%, 50%/50% and 80%/20%, and unrestricted (ϑ1 ϵ [0°, 360°]) (Fig 4B and S3 Movie) or restricted movement (ϑ1 ϵ [0°, 10°]) (Fig 4C). To quantify network transmissivity, we calculated the time to transmit the GFP signal to 50% of mitochondrial mass, denoted as 50% transmission time (shaded areas in Fig 4B and 4C).
Under conditions of free movement (Fig 4B), a balanced probability of fusion and fission (50%/50%) produced the fastest GFP transmission (smallest 50% transmission time), while a fusion/fission probability of 80%/20% showed the slowest transmission. Moreover, by increasing total mass, the 50% transmission time was slightly reduced (Fig 4B, blue regions). Similar tendencies were obtained under conditions of restricted movement, but the 50% transmission time was decreased relative to free movement (Fig 4C, pink regions).
We further examined the impact of mitochondrial mobility on network transmissivity by changing the velocity intervals of mitochondria (Fig 4D). Mitochondria were assumed to (I) adopt low velocities in all the cellular spatial domain (vl ∀ x), (II) adopt high velocities in all spatial domain (vh ∀ x) or (III) adopt low velocities in the perinuclear region and high velocities in the bulk cytosol (v = vl, or v = vh),as it was implemented in the previous sections. Simulations were performed using fusion and fission probabilities of 50%, a total mass of 300 μm2, and either free or restricted mitochondrial directionalities, and the 50% transmission time was calculated (Fig 4D). Notably, under conditions of restricted movement (pink line), decreasing or increasing velocities had no impact, and compared to free movement, GFP transmission was considerably faster. In contrast, under conditions of free movement, increasing velocities reduced the 50% transmission time (blue line). These findings suggest that restricted mitochondrial movements suppress sensitivities to alterations in spatial dynamics. Therefore, all subsequent simulations were performed under conditions of free mitochondrial movements. Overall, simulation results indicate that fusion and fission events and levels of mitochondrial mass together determine morphology distributions, while the transmission of signals across the mitochondrial population is determined by fusion and fission events and mitochondrial velocities.
Given these distributed contributions, we subsequently sought to quantify the impact of parameter perturbations. Sensitivity analysis is an indispensable procedure to test and tune in silico experiments, since it emphasizes the role and the biological relevance of the parameters involved [55]. As an essential tool able to evaluate and refine mathematical models [56], we applied a global sensitivity analysis using Latin-Hypercube Sampling (LHS) and Extended Fourier Amplitude Sampling Test (eFAST) [57].
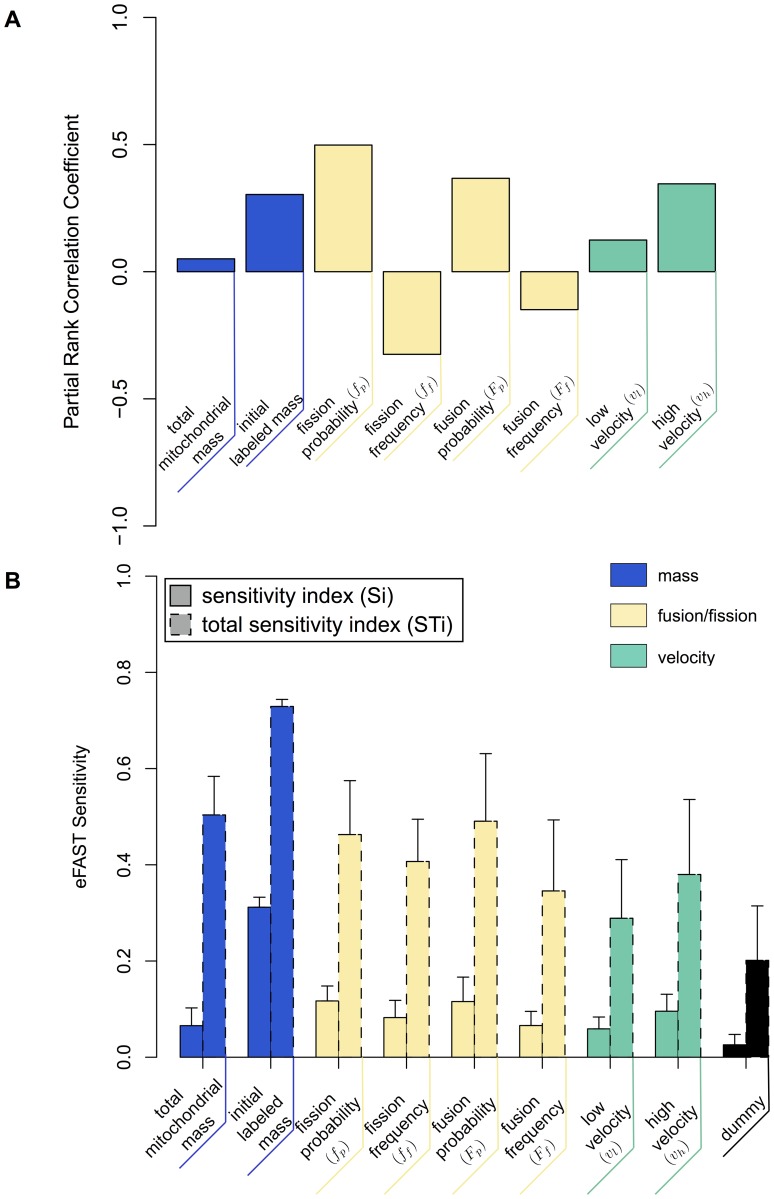
We concentrated on seven parameters, each constrained to the following respective ranges: fusion frequency (0–30), fusion probability (0–100), fission frequency (0–30), fission probability (0–100), mitochondrial mass (50–500 μm2) and mitochondrial velocities in bulk cytosol vh (0.01–1 μms-1) and in the perinuclear region vl (0.01–1 μms-1). Specifically, we sought to assess how parameter perturbations impact the mass of GFP-labeled mitochondria. Using the Latin-Hypercube sampling approach, parameters were simultaneously perturbed, to identify parameters that are highly influential on simulation behavior. Five hundred parameter value sets were generated from the parameter space and simulated (each for the duration of 6 hours). For each parameter, median response values (evolution over time of the GFP-labeled mitochondrial population) were plotted against corresponding parameter value used (S2 Fig), and partial rank correlation coefficients were calculated (Fig 5A).
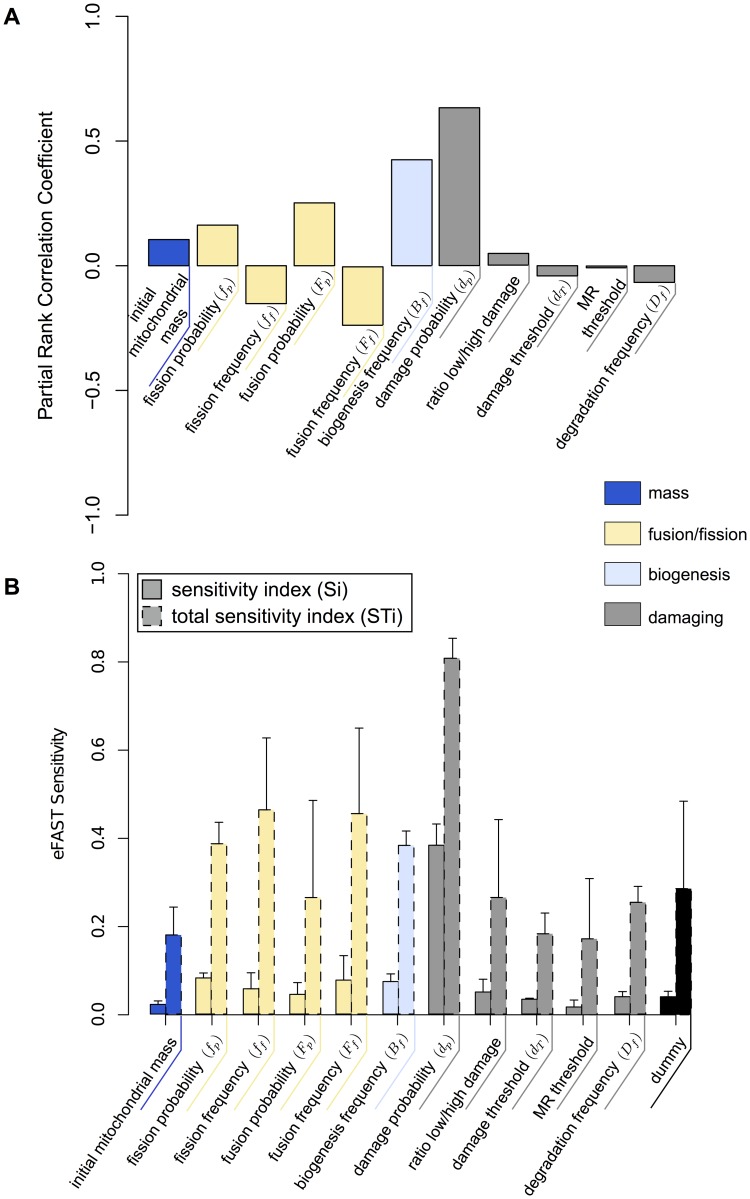
Fig 5. Sensitivity analysis of the transmission dynamics model.
(A) Effect of parameters perturbation on transmission dynamic. Bar graph represents Partial Rank Correlation Coefficient values for each parameter-output response pairing resulting from a Latin-hypercube sampling of 500 parameter value sets (parameter ranges are described in section “Transmission dynamics of mitochondrial network connectivity”). For each parameter set the model was performed over 6 hours. (B) Results of the eFast method used to partition variance in simulation results between parameters. Solid Bars: sensitivity index (Si)–the fraction of output variance explained by the value assigned to that parameter when parameter of interest; Dashed Bars: total sensitivity index (STi)–the variance caused by higher-order non-linear effects between that parameter and the other explored (includes value of Si). Error bars are standard error over four resample curves. Parameter values sets were generated using the sinusoidal sampling approach. 65 parameters were obtained from each of the 4 resampling curves, producing 2080 parameter value sets (260 per parameter).
The correlation coefficients (Fig 5A and S2 Fig) indicate that the total mitochondrial mass and low-perinuclear velocity (vl) have the least impact on the network transmission, and that fusion and fission-related parameters and high-cytoplasmic velocity (vh) have distributed control over transmission. Positive correlation coefficients indicate that increases in fission probability, fusion probability and velocity contribute to a faster transmission dynamics. In contrast, negative correlations for fusion and fission frequencies indicate that their decrease contributes to an increased transmission. Additionally, the positive correlation between fusion and fission probabilities with the population of GFP-labeled mitochondria, emerged mostly for lower ranges and stabilized for values greater than ~60% (S2C and S2E Fig).
We further utilized eFAST global sensitivity analysis to identify highly influential parameters. For nine parameters (eight plus the ‘dummy’ used as negative control), we generated parameter value sets using the sinusoidal curve sampling approach. Briefly, 65 parameter values from each curve were produced, and employed four resampling curves, producing 2080 parameter value sets, 260 per parameter. Simulation responses were analyzed using the Fourier frequency approach and median responses (evolution over time of the GFP-labeled mitochondrial population) calculated [57]. Plots were created detailing the first-order (Si) and total-order (STi) sensitivity indexes calculated for each parameter (Fig 5B). To quantify the impact of a parameter on the simulation, we used the “initial-labeled mass” as a positive control, and as a negative control “dummy”, a parameter which has an arbitrary value range but no actual impact on model behavior. Note, “dummy” parameters result in non-zero sensitivity indexes due to noise derived from the intrinsic stochasticity of the model [57, 58]. Compared to “initial-labeled mass”, eFAST analysis indicates an overall equilibrium of 7 out of 8 parameters, since variations in the Si and STi sensitivity indexes between parameters is low. This indicates the current state of the model is not over-parametrized.
Integrating mitochondrial dynamics with mitochondrial biogenesis
So far, our model captured essential spatial and temporal behavior of mitochondrial morphology and mobility dynamics at a time scale of seconds-to-hours assuming a constant total mitochondrial mass. However, mitochondrial populations are not a closed systems, and on a time scale of hours to days mitochondrial biogenesis occurs from growth and division of pre-existing mitochondria [34]. Furthermore, over time and in response to stress, mitochondria become dysfunctional and quality control of mitochondria occurs through the process of mitophagy [47]. We therefore subsequently incorporated biogenesis and mitophagy behavior.
We first established a rule set to describe mitochondrial biogenesis (Fig 6A). Sub-maximal mitochondria (M < 3 μm2) undergo a growth event based on a biogenesis probability (Bp), which can occur according to a biogenesis frequency (Bf) (Fig 6B). All mitochondria grow by increasing their actual mass M to a new value MB, according to the following relation:
| (3) |
Where XB ~ U[0, M·50%]. In this way, every mitochondrion can at most double its mass during one growth event. Additionally, in order to avoid unrestricted growth, the resulting mass of the biogenesis process MB can not exceed a preset maximum value Mmax.
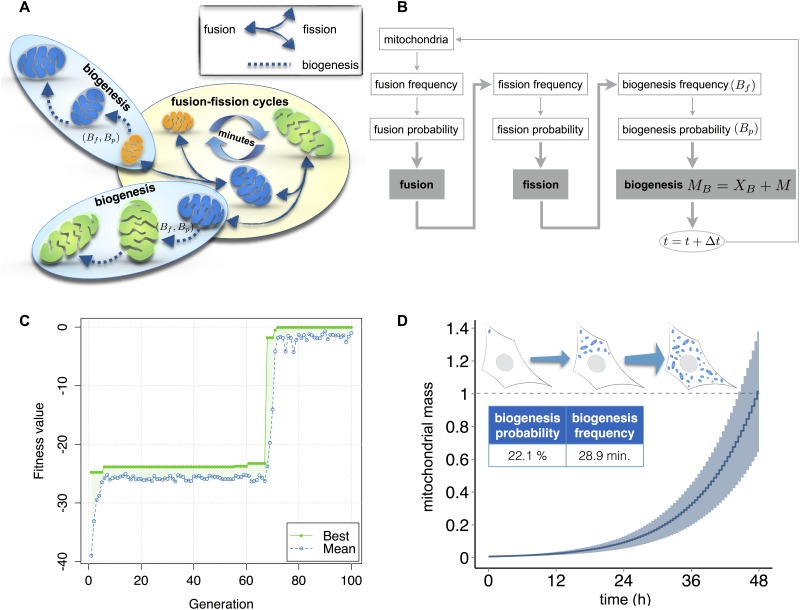
Fig 6. Integration of mitochondrial biogenesis through parameter fitting.
(A) Schematic representation of mitochondrial fusion, fission and biogenesis events. Biogenesis is represented by frequency (Bf) and probability (Bp) parameters, and can occur in all mitochondria with a mass less than Mmax = 3.0 μm2. (B) Basic flow chart of the model representing fusion, fission and biogenesis events. Shaded boxes indicate the main processes of the model (fusion, fission and biogenesis) with governing equation of the biogenesis process. Time step used in all the simulation, Δt = 1 sec. (C) Maximization of the fitness function OB within 100 iterations, reaching a value of -0.049, using a classic genetic algorithm (settings described in the Methods section). (D) Mean of 100 simulations of mitochondrial mass growth over 48 hours, beginning with a mitochondrial mass of 1 and using the parameter values obtained from the optimization (C), biogenesis probability = 22.1% and biogenesis frequency = 28.9 minutes.
Different lines of evidence give insight into mitochondrial biogenesis rates. Biogenesis can double the population of mitochondria during a typical cell division cycle of 48 hours [59], and following near depletion, mitochondrial repopulation occurs over days [60, 61]. Moreover, activated mitochondrial biogenesis increases mitochondrial markers by approximately 2–4 fold [62]. From these biological constraints, using a genetic algorithm [63], we optimized biogenesis frequency and biogenesis probability parameters. Starting with a total initial mass of one, fusion and fission probabilities of 50%, and fusion and fission frequencies of 5 minutes, we optimized biogenesis frequency and biogenesis probability, in order to reach a total mitochondrial mass equal to 300 μm2 within 48 hours. Therefore, we maximized the following objective function (OB):
| (4) |
Where TF represents the final simulation time, i.e., the time needed to reach a total mass of 300 μm2.
The genetic algorithm was able to achieve a final fitness function value of -0.049 within 100 iterations (Fig 6C), generating a biogenesis frequency of 28.9 minutes and a biogenesis probability of 22.1%. With these optimized values, the mass of mitochondria increases from 1 to 15% of the cell within two days (Fig 6D and S4 Movie). Note, with these parameters doubling of the mitochondrial population following cell division occurs in approximately 9 hours (S3 Fig), which is less than, and therefore compatible with, the HeLa cell division cycle [64].
Integrating mitochondrial dynamics with mitochondrial damage and mitophagy
We next implemented quality control of damaged mitochondria by mitophagy [6, 8, 65, 66], using the parameter-fitting approach developed for mitochondrial biogenesis (Fig 7A) and a rule-set describing mitochondrial damage and removal (Fig 7B and S4 Fig). As mitochondria utilize fission to segregate healthy from damaged mitochondria [47], we included a probability variable (dp) for the fission process whereby one mitochondrion fragments into one healthy and one damaged mitochondrion [43]. Furthermore, we specified two damage states: low and high, corresponding to pre-mitophagy and mitophagy induction states [8]. To simulate the mitochondrial capture and degradation, we introduced two autophagy agents: sequestering autophagosomes and degrading lysosomes (Fig 7C), which undergo a multi-step interaction with mitochondria to approximate mitophagy dynamics. Over time, low damage levels increase, until levels exceed a fixed-damage threshold (dT), and become high damaged. Highly-damaged mitochondria acquire a mitophagy receptor (MR) level, which is updated at every time step. To approximate the sequestration process, once a receptor threshold is reached, an autophagosome forms at the damaged mitochondrion (Fig 7A) and the receptor level is again set to zero. Subsequently, when the receptor level exceeds threshold a second time; the mitochondrion is considered irreversibly sequestered. Concurrently, a mobile, degradative lysosome is randomly generated within the cell, and the lysosome is attracted to sequestered mitochondrion and both are degraded upon contact. All the above rules are evaluated according to a degradation frequency (Df). The parameters receptor level and damage level are updated and increased at every time step.
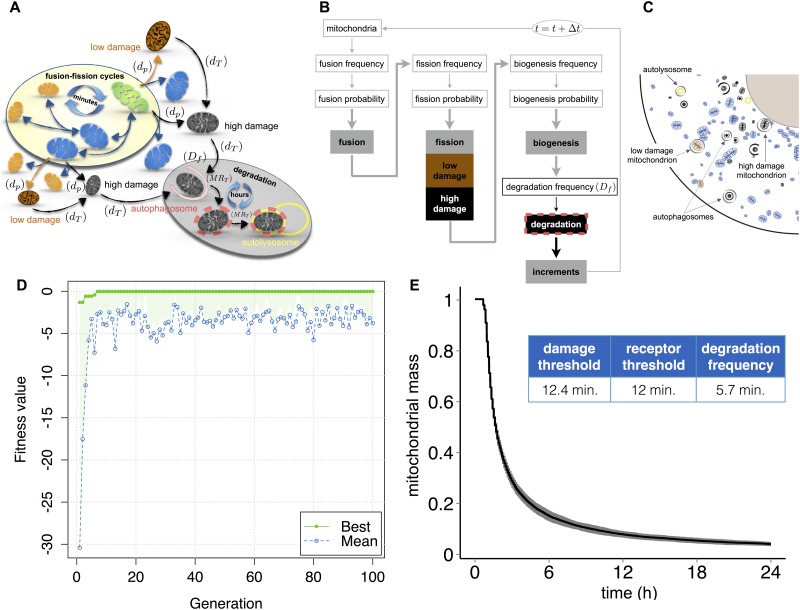
Fig 7. Integration of mitochondrial damage sensing and mitophagy through parameter fitting.
(A) Schematic representation of mitochondrial fusion and fission cycles, damage and mitochondrial degradation events. Degradation is represented by frequency (Df) parameter and damage (dT) and receptor (MRT) thresholds. (B) Basic flow chart of the model representing fusion, fission, biogenesis and degradation events. Shaded boxes indicate the main processes of the model (fusion, fission, biogenesis, low/high damage, degradation and increments). Time step used in all the simulation, Δt = 1 sec. (C) Spatial model representation. Highly-damaged mitochondria are represented in black and mitochondria with low damage in brown. The yellow circle indicates an autolysosome and the black circle and semicircle indicate stages of autophagosome formation. (D) Maximization of the fitness function OD within 100 iterations, reaching a value of -0.02, using a classic genetic algorithm. Algorithm (settings described in the Methods section). (E) Mean of 100 simulations of degradation of damaged mitochondria over 24 hours, beginning with 50% low damaged and 50% high damaged mitochondria and using the parameters obtained from the optimization (D), receptor threshold = 12 minutes, damage threshold = 12.4 minutes and degradation frequency = 5.7 minutes. The initial total mass consists of two equal parts of high-damaged and low-damaged mitochondria.
Upon full mitophagy activation, mitochondrial populations can be eliminated by mitophagy within 1–2 days [67, 68]. Based on these measurements we optimized three parameters, receptor threshold, damage threshold and degradation frequency, to deplete the population of mitochondria (total mass of 300 μm2). Simulations were initialized by setting 50% of the mitochondrial mass to a low damage state and 50% to a high damage state. The following objective function (OD) was maximized:
| (5) |
Where TF represents the final simulation time, i.e., the time needed to achieve degradation of the total mitochondrial population.
The genetic algorithm achieved a final fitness function value of -0.02 within 100 iterations (Fig 7D) generating a receptor threshold of 12 minutes, a damage threshold of 12.4 minutes and a degradation frequency of 5.7 minutes. The resulting model fit eliminates all damaged mitochondria within one day (Fig 7E and S5 Movie).
Energetic sensing, mitophagy and mitochondrial biogenesis must be considered as integrated processes
With the parameters obtained from the optimization of biogenesis and mitophagy, our model can simulate the mitochondrial repopulation within two days, and remove a population of damaged mitochondria within one day, respectively. However, when these processes are combined, in the absence of damage, biogenesis is dominant and uncontrolled growth occurs (Fig 8A). In contrast, if we introduce a fixed probability of damage, the total mass of healthy mitochondria eventually decays over time, in a manner proportional to the probability of damage, and the model fails to maintain mitochondrial homeostasis. This split between biogenesis and degradation dominant regions reveals instability in the system, suggesting biogenesis and degradation must be considered as integrated processes. We thus considered functions of the metabolic sensor AMP-activated protein kinase (AMPK). AMPK is activated in response to decreased ATP production, i.e. bioenergetic stress [69], and activates PGC-1alpha [70], the master regulator of mitochondrial biogenesis [71]. Moreover, AMPK regulates the removal of defective mitochondria [72].
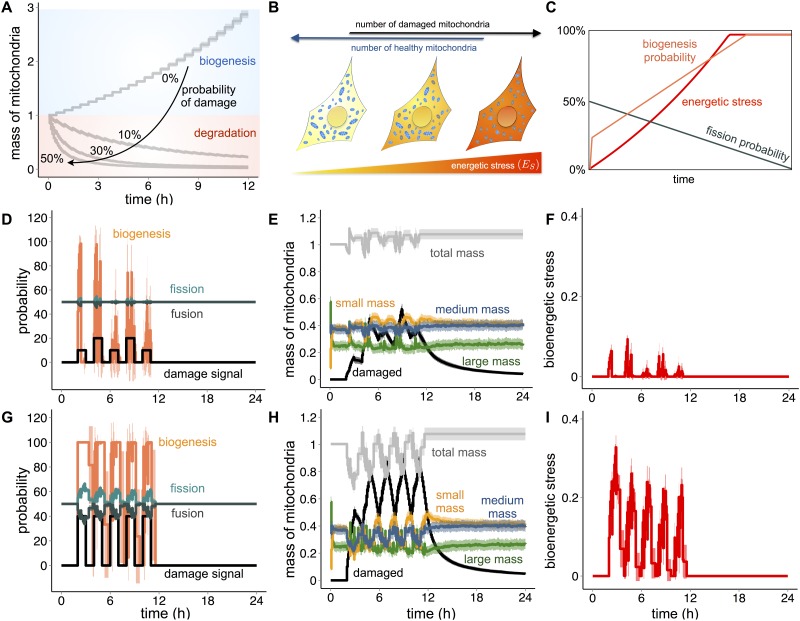
Fig 8. Interaction between mitochondrial health and cellular energetic state, based on the energetic stress.
(A) Evolution of mitochondrial mass (grey lines) over time subjected to four different damage signals (black line). Line graphs display mean value and standard deviation (shaded regions) of 100 simulations for an initial total mitochondrial mass of 300 normalized to the total mass at time point 0. Parameter values obtained from the optimization were used, in particular, fusion probability = fission probability = 50%, fusion frequency = fission frequency = 5 minutes, biogenesis probability = 22.1%, biogenesis frequency = 28.9 minutes, receptor threshold = 12 minutes, damage threshold = 12.4 minutes, degradation frequency = 5.7 minutes and damage probabilities: 0%, 10%, 30% and 50%. Simulations were performed for a total of 12 hours. Blue region indicates the area in which biogenesis is dominant while red region indicates the area in which degradation is dominant. (B) Schematic representation of the link between the number of healthy and damaged mitochondria with the energetic stress (ES) of the cell. (C) Schematic representation of the connection between energetic (red line) stress and fission (dark green line) and biogenesis (orange line) probabilities. (D) Line graphs display mean value and standard deviation (shaded regions) of 100 simulations of probabilities of fusion (dark green line), fission (light green line), biogenesis (orange line) and damage signal (black line). Initial values assigned to the model: fusion probability = fission probability = 50%, fusion frequency = fission frequency = 5 minutes, biogenesis probability = 22.1%, biogenesis frequency = 28.9 minutes, receptor threshold = 12 minutes, damage threshold = 12.4 minutes, degradation frequency = 5.7 minutes. All the simulations were performed for a total time of 24 hours. (E) Line graphs display mean value and standard deviation (shaded area) of 100 simulations for an initial mitochondrial mass of 300 of the total mitochondrial mass (grey line) and three mitochondria subpopulations: small mass (orange line), medium mass (blue line) and big mass (green line) subjected to five different damage signals (10% and 20%) every two hours for one hour. The plot represents the evolution of the total mass and of three mitochondrial subpopulations normalized to the total mass at time point 0. Initial values assigned to the model: fusion probability = fission probability = 50%, fusion frequency = fission frequency = 5 minutes, biogenesis probability = 22.1%, biogenesis frequency = 28.9 minutes, receptor threshold = 12 minutes, damage threshold = 12.4 minutes, degradation frequency = 5.7 minutes. All the simulations were performed for a total time of 24 hours. (F) Line graphs display mean value and standard deviation (shaded regions) of 100 simulations of bioenergetics stress (red line). Initial values assigned to the model: fusion probability = fission probability = 50%, fusion frequency = fission frequency = 5 minutes, biogenesis probability = 22.1%, biogenesis frequency = 28.9 minutes, receptor threshold = 12 minutes, damage threshold = 12.4 minutes, degradation frequency = 5.7 minutes. All the simulations were performed for a total time of 24 hours. (G) Same as (D) but with mitochondria subjected to five different damage signals (40%) every two hours for one hour. (H) Same as (E) but with mitochondria subjected to five different damage signals (40%) every two hours for one hour. (I) Same as (F) but with mitochondria subjected to five different damage signals (40%) every two hours for one hour.
To simulate the role of AMPK, we included in our model a dependency between mitochondrial health and cellular bioenergetic state, based on the variable environmental energetic stress (ES) (Fig 8B). We further included additional rules describing that (I) during bioenergetic stress mitochondrial fission is reduced, resulting in mitochondrial networks which can escape mitophagy [40, 73], and (II) complementation of mitochondrial content by fusion [47] permits low-damaged mitochondria to fuse with healthy ones, and recover from the damage (Fig 8C). As such, the probabilities of fusion, fission and biogenesis integrate with the level of bioenergetic stress: a loss of healthy mitochondria intensifies the energy demand level, which, in turn, increases proportionally the probabilities of fusion and biogenesis, and decreases the probability of fission.
Given an initial probability of fusion (PF0) and fission (Pf0) equal to 50% and a probability of biogenesis (PB0) equal to 0%, we define the energy stress at time point t, (ESt), as follows:
| (6) |
Where MT is the total mass of healthy mitochondria and MC is the critical mass (300 μm2).
Given a stress level , we defined accordingly the probabilities of fusion (PF), fission (Pf) and biogenesis (PB) as:
| (7) |
| (8) |
| (9) |
Where is the biogenesis probability previously obtained with the optimization, equal to 22.1%. E assumes values in [0,1], while PF, Pf and PB assume values in [0,100]. The equation governing the biogenesis probability is formulated in order to avoid unrestricted growth, since it links the biogenesis probability to the increase of energetic stress. The receptor threshold was set to 12 minutes, the damage threshold to 12.4 minutes and a degradation frequency to 5.7 minutes (values obtained from the optimization).
A system subjected to continuous damage levels resulted in a loss of healthy mitochondria proportional to the damage intensity. Although the probabilities of fusion, fission and biogenesis varied dynamically with the increased stress, the model was unable to maintain cellular homeostasis (S5 Fig).
However, under normal circumstances, a cell is not constantly subjected to loss of mitochondria; but rather, external factors can induce acute mitochondrial damage, which the cell then eliminates [74–76]. We therefore simulated repeating damage pulses, starting with an initial damage probability of zero, and then transiently (for 1-hour), inducing damage every two hours. Initial probabilities of fusion/fission were set to 50% and biogenesis to 0%. First, we alternated two different probabilities of damage, 10% and 20%, for a period of twelve hours, and subsequently set again the probability of damage to zero (Fig 8D and S6 Movie). During this “low-damage” simulation, the mass of damaged mitochondria transiently increased, proportionally to the damage probability, and, after the damage pulses, it was decreasing to zero during the damage-free intervals due to removal by mitophagy (Fig 8E). These dynamics were paralleled by stable variations in the average total healthy mass (Fig 8E), which, in turn, generated small variations in the stress level (Fig 8F). Since the probabilities of fusion, fission and biogenesis are responsive to the stress levels, variations in healthy mass ultimately lead to variations in these probabilities. Thus, under the simulated stress conditions, our model was able to respond to transient damage impulses and maintain the cell close to its initial state. Interestingly, variations were mainly visible in the small-mass mitochondria subpopulation, while the medium and large subpopulations remained nearly unchanged.
We next tested the scenario of increased mitochondrial damage, using with a transient probability of damage of 40%, for one hour every two hours (Fig 8G and S7 Movie). Under these “high-damage” conditions, damaged mitochondria accumulated while the mass of healthy mitochondria was subjected to wide variations (Fig 8H), and after twelve hours, the mass of damaged mitochondria was approximately the same as the healthy population. Following the first damage impulse, the dynamic probability rates of fusion and biogenesis were largely increased (Fig 8G), resulting in altered subpopulations. These simulations highlight that biogenesis and degradation are critical limitations to mitochondrial homeostasis, and suggest that experimental focus on the mechanisms which can increase their capacities [7, 77].
The bioenergetic stress response of the two damage scenarios (Fig 8F and 8I) indicate that dynamic adaptation of the probabilities of fusion, fission and biogenesis to the loss of healthy mitochondria is essential in maintain cellular homeostasis. Despite damage-provoked alterations to total mitochondrial mass and subpopulation distributions, the model rapidly regained homeostasis (Fig 8E and 8H). Additionally, since a stress increment is responsible in amplifying the probability of fusion, low damaged mitochondria were more subjected to the recovery process (S6B Fig) as highlighted in minor loss in the total healthy mitochondrial mass (S7A Fig) and in the lower level of stress (S7B Fig).
Finally, we assessed parameter influence on this integrated model using sensitivity analysis. We considered eleven parameters, each constrained to the following respective range: MR threshold (0–30), fission probability (0–100), initial mitochondrial mass (50–500), fusion frequency (0–30), fusion probability (0–100), damage probability (0–100), damage threshold (0–30), degradation frequency (0–30), ratio low/high damage (0–100), fission frequency (0–30) and biogenesis frequency (0–30). Specifically, we sought to assess how parameter perturbations impact the total mass of healthy mitochondria.
With the Latin-hypercube sampling approach, five hundred parameter value sets were generated from the parameter space, and a total of 500 simulations (each for the duration of 24 hours) were performed. Taking each parameter in turn, median response values (total mass of healthy mitochondria) were plotted against the parameter value that generated them (S8 Fig), and partial rank correlation coefficients were calculated (Fig 9A). The correlation coefficients, as expected, showed the biogenesis frequency and the damage probability to have significant influence on the simulation response (Fig 9A, S8F and S8G Fig). A high value in the damage probability produces a decrease in the total mass of healthy mitochondria while a high biogenesis frequency reduces the production of new mitochondria. Both of these factors that directly influence the augment in the energy demand of the cell. Moreover, positive correlation in the damage probability occurred mainly for high values of this parameter, greater than ~60%, while low values appeared to be almost irrelevant to the energetic stress (S8G Fig), indicating that the model is able to counter low level of damage. Similarly, the biogenesis frequency has a positive correlation only for high values (S8F Fig), demonstrating that the model is not able to contain energetic stress without an appropriate biogenesis frequency, thus underling the importance of this process in restoring mitochondrial homeostasis during nutrient deprivation. Additionally, similar to the case of transmission dynamic, fission, fusion and degradation frequencies appeared to be negative correlated with the energy demand (S8C, S8E and S8K Fig). While these parameters require small values to rapidly react to the changes, the correlation in these parameters is close to zero, indicating low influence in the energetic stress behavior of the cell.
Fig 9. Sensitivity analysis of the full model.
(A) Effect of parameters perturbation on the full model. Bar graph represents Partial Rank Correlation Coefficient values for each parameter-output response pairing resulting from a Latin-hypercube sampling of 500 parameter value sets (parameter ranges are described in section “Energetic sensing, mitophagy and mitochondrial biogenesis are integrated processes”). For each parameter set the model was performed over 24 hours. (B) Results of the eFast method used to partition variance in simulation results between parameters. Solid Bars: sensitivity index (Si)–the fraction of output variance explained by the value assigned to that parameter when parameter of interest; Dashed Bars: total sensitivity index (STi)–the variance caused by higher-order non-linear effects between that parameter and the other explored (includes value of Si). Error bars are standard error over four resample curves. Parameter values sets were generated using the sinusoidal sampling approach. 65 parameters were obtained from each of the 4 resampling curves, producing 3120 parameter value sets (260 per parameter).
We further determined parameter impact on model performance. From twelve parameters (eleven plus the ‘dummy’ used for statistical comparison), we took 65 parameter values from each curve, and employed four resampling curves, producing 3120 parameter value sets, 260 per parameter. Plots were created for the energy demand, detailing the first-order (Si) and total-order (STi) sensitivity indexes calculated for each parameter (Fig 9B). The result of the eFAST approach confirmed the precedent sensitivity analysis and indicates an overall general balance among most parameters, with the damage probability to be the most influencing parameter on the model behavior (Fig 9B). Additionally, both two sensitivity analysis methods indicate an overall equilibrium in parameter impact on system behavior, which we interpret to indicate that our final integrative model is not over-parametrized.
Discussion
The deregulation of mitochondrial dynamics is a contributing factor to many diseases [16, 78, 79]. Here we developed an agent-based model integrating mitochondrial function, dynamics, biogenesis and mitophagy, and investigated how mitochondrial populations establish and maintain homeostasis, and respond to bioenergetic demands. Our modeling approach offers insights into the systemic properties of mitochondrial population dynamics, and sources of cell-to-cell variability.
Under conditions of typical physiological mitochondrial content [49], we predict spatial proximity of mitochondria to be a major determinant for distribution of mitochondrial morphologies. Since mitochondria must interact in order to fuse, mitochondrial density contributes independently of a probability for fusion and fission. Importantly, variations in the total mass of mitochondria affect both heterogeneity of the intracellular mitochondria population and therefore resulted in cell-to-cell variability. We found that higher mitochondrial masses are more responsive to the probability of fusion, and in this case physical proximity does not represent a limiting factor. As a result, higher mitochondrial masses allow for more heterogeneous populations and lead to less cell-to-cell variability. Further, our simulations of network connectivity revealed that fusion and fission probabilities have a minor impact compared to velocities which determine the mobility of mitochondria. Importantly, when integrating isolated mitochondrial biogenesis and degradation processes, we did not obtain stable behavior in mitochondrial morphology dynamics and mass. Only by implementing crosstalk between cellular bioenergetic state and mitochondrial morphologies were we able to obtain a homeostatic-capable dynamic model.
Thus, our integrative approach suggests that model-based investigation of organelle dynamics requires incorporating functional and environmental considerations. Similarly, we previously found that in order to accurately simulate experimental data, modeling autophagy dynamics required the consideration of bi-directional signaling, in which recycled nutrients, provided through autophagy activation, establish a negative feedback on autophagy [27]. Here, our modeling approach highlights the limitations of mitochondrial mass homeostasis. Most obviously, during prolonged stress mitochondrial biogenesis is not sufficient to compensate in response to increasing mitochondrial stress, and mitophagy. These limitations directly relate to the role of mitochondria in cell death signaling, and future work will focus on integrating apoptotic stress and different modes of regulated mitophagy [7, 80].
An important advantage of our approach to multi-scale modeling is that parameters can be used to account for qualitatively- and quantitatively-measured behavior. Here we employed parameter sweeping [63, 81] to find parameter combinations which produced the best description of experimentally-established dynamics of mitochondrial growth and degradation, and two sensitivity analysis methods [57, 82] to analyze the influence of the parameters on transmission dynamic and energetic sensing. Parameter sweeping identified parameters that best predict experimental observations. For example, optimizing mitophagy, our model predicts recognition and sequestration dynamics (a receptor threshold of 12 minutes, and a damage threshold of 12.4 minutes) and a subsequent degradation event of 5.7 minutes. Thereby these values represent a precise description of cellular mechanisms to be experimentally tested, which has recently become possible due to advances in biosensors for measuring mitochondrial damage, mitophagy and biogenesis (reviewed in [8]). Further, by analyzing the distributions of the parameters obtained from the optimization, and their influence by the sensitivity analysis, we gain insight into parameter impact on model behavior, and relationships between parameters. The result of two different global sensitivity analysis methods on our model in the case of transmission dynamic confirmed our hypothesis that mitochondrial mobility is an essential component for transmission dynamics rather than the total mitochondrial mass. Similarly, in the context of energetic sensing, the model appeared to be mainly subjected to the damage probability and to the frequencies of fusion, fission and biogenesis, determinant components for maintaining homeostasis in the cell. Further, low correlation and an overall equilibrium between parameters suggest that our model performs robustly and is not over-parameterized. This modeling approach could be adopted as framework to transform experimental observation into quantitative statements, thereby driving follow-up target experiments. However, it is important to note that our model represents a generalized mammalian cell. As mitochondrial dynamics and morphologies, as well as cellular size and architecture, vary among cell types [3, 83, 84], our model can be adapted for cell-type specific simulations. For example, altering cellular dimensions in order to determine the impact of restricted mitochondrial movements in neuronal processes [33, 37], or restricting mitochondrial movement in order to analyze the highly-static and ordered mitochondrial arrangement in cardiomyocytes [85].
In summary, we propose that ABM is uniquely suited to model complex, multi-scale systems such as mitochondrial dynamics and morphology, and advances model-guided investigation of sources of subcellular heterogeneities towards the goal of understanding cellular behavior, and emergence of cell heterogeneity.
Materials and Methods
Modeling
ABM was implemented using the multi-agent programmable modeling environment NetLogo (v5.2.0) [30]. In NetLogo, mobile agents (turtles) interact in a 2-dimensional environment subdivided into micro-compartments (patches). Our model consists of five classes of agents, two static (cell and nucleus) and three dynamic (mitochondria, autophagososmes and autolysosomes), in particular:
cell (static agent): it contains all the other agents, represents the external boundary of the system beyond which mobile agents are not allowed to exceed,
nucleus (static agent): it represents the internal boundary of the system inside which mobile agents are not allowed to enter,
mitochondria (mobile agents): they are able to move inside the cell assuming variable velocity (vl and vh depending on their position in the cell), rotate in relation to an angle (ϑ1 and ϑ2 depending on their surrounding) and with the properties to undergo fusions (according to a fusion probability Fp and at a fusion frequency Ff), fission (according to a fission probability fp and at a fission frequency ff) and biogenesis (according to a biogenesis probability Bp and at a biogenesis frequency Bf). Also, they can undertake a damage state (according to a damage probability Dp),
autophagosomes (mobile agents): they are able to move inside the cell and they are involved in the mitochondrial degradation process representing sequestering autophagosomes,
autolysosomes (mobile agents): they are able to move inside the cell and they are involved in the mitochondrial degradation process representing degrading lysosomes,
a more detailed description of the model agents is available in the Result section.
In order to map the time and space of our model to real physical time and space we decided that a distance of 1 in our simulation space corresponds to a physical distance of 1 μm and each time step of our simulation corresponds to 1 seconds. Therfore, dt and ds are defined as follows:
Accordingly, in order to convert the real velocity to a NetLogo velocity vNL, we defined:
where v assumes the values vl or vh previously defined in the text.
As a conceptual characterization of the ABM approach adopted in this work we present here a detailed explanation of the model iterations describing the mitochondrial fusion and fission cycle (Fig 1B and 1C and S1 Fig). At time point dt = 0 the model is initialized and mitochondria are assigned a random position inside the cell with and a random size (ranging continuously from Mmin to Mmax) until a total initial mass value, decided from the user (e.g. 300 μm2), is reached. In the first time step (dt = 1) each mitochondrion first moves and rotates (as explained in the results section) then the fusion and fission cycle starts. The program loops over all mitochondria, starting from a randomly chosen mitochondrion j, if the time step matches the fusion frequency (Ff) (e.g. if it is equal to 5 minutes or a multiple of 5 minutes) then a random number is sampled uniformly between 0 and 100, if this number is less than the fusion probability (Fp) the program checks the distance to the closest mitochondrion, if (I) the distance is less or equal to the dimension of j, the program controls if (II) the mass of j plus the mass of the closest mitochondrion is less or equal to Mmax, if this conditions are satisfied the fusion process occurs (if either one of these two conditions are not satisfied the program switch to the next mitochondrion). The two mitochondria fuse to a resulting mitochondrion with a mass equal to the sum of the two masses. The model cycles over all the mitochondria repeating the procedures described above and then moves to the fission process. In the fission process the program loops again over all mitochondria. Starting from a randomly chosen mitochondrion j, if the time step matches the fission frequency (ff) (e.g. if it is equal to 5 minutes or a multiple of 5 minutes) then a random number is sampled uniformly between 0 and 100, if this number is less than the fission probability (fp), the program checks if the mass of j is greater or equal to 2Mmin. If this condition is satisfied the fission process occurs (if not the program switch to the next mitochondrion). The mitochondrion j splits then in two mitochondria of size M1 and M2 given by Eqs (1) and (2). The model cycles over all the mitochondria repeating the procedures described above. Following, the time is incremented of one unit (t = t + Δt) and all the process is repeated until reaching the final time point desired (chosen by the user).
The fusion and fission cycle was taken as example since it is both the simplest and the core of the program. The model increases then in complexity and new processes are integrated (S4 and S6 Figs) nevertheless, they work along the lines of this basic procedure.
Optimization
Optimization search was performed with the R package for genetic algorithm [63] using a classic Genetic Algorithm (settings: type = real-valued, popSize = 10, maxfitness = 0, pcrossover = 0.8, pmutation = 0.01). In order to optimize the two objective functions OB and OD (defined in the text) we performed each time 100 iteration. Moreover, in the optimization process, the objective function analyzed at each time step is an average of 10 model simulation runs. The parameters optimized (biogenesis probability, biogenesis frequency, damage threshold, receptor threshold and degradation frequency) were constrained in the range [1,60].
Sensitivity analysis
Sensitivity analysis was performed with the Simulation Parameter Analysis R Toolkit ApplicatioN: Spartan (v2.2.1) [57, 82, 86], specifically using the Latin-Hypercube Sampling and Analysis and the eFast Sampling and Analysis. In the section “Transmission dynamics of the mitochondrial network” the GFP-labeled mass of mitochondria was used as a response variable, while in the section “Energetic sensing, mitophagy and mitochondrial biogenesis must be considered as integrated processes” the total mass of healthy mitochondria was used as a response variable.
Additional analysis
Statistical analysis and plotting were executed with the open source environment for statistical computing R (v3.2.1) [87]. All the simulations were performed in R profiting of the link between R and NetLogo given by the R package RNetLogo (v1.0–1) [88, 89].
Supporting Information
Detailed description of the complete algorithm for the fusion/fission cycle represented in Fig 1D.
(TIF)
-
(A)Fusion frequency sorted by the value assigned to total mass.
-
(B)Fusion frequency sorted by the value assigned to initial labeled mass.
-
(C)Fusion frequency sorted by the value assigned to fission probability.
-
(D)Fusion frequency sorted by the value assigned to fission frequency.
-
(E)Fusion frequency sorted by the value assigned to fusion probability.
-
(F)Fusion frequency sorted by the value assigned to fusion frequency.
-
(G)Fusion frequency sorted by the value assigned to vl.
-
(H)Fusion frequency sorted by the value assigned to vh.
Red lines represent the lowess smoother lines.
(TIFF)
-
(A)Line graphs display mean value and standard deviation (shaded regions) of 100 simulations of total mitochondria mass for an initial mass of 150 fragmented mitochondria with (dark grey line) and without (light grey line) biogenesis integrated with cellular bioenergetics state. Initial parameters values: fusion probability = fission probability = 50%, fusion frequency = fission frequency = 5 minutes, biogenesis probability = 22.1%, biogenesis frequency = 28.9 minutes, receptor threshold = 12 minutes, damage threshold = 12.4 minutes, degradation frequency = 5.7 minutes). All simulations were performed for a total time of 12 hours.
-
(B)Line graphs display mean value and standard deviation (shaded regions) of 100 simulations of total mitochondria mass for an initial mass of 150 fragmented mitochondria and with biogenesis integrated with cellular bioenergetics state subjected to three different initial biogenesis frequency values: 28.9 (light blue line), 57.8 (blue line) and 86.7 (dark blue line) minutes. Initial parameters values: fusion probability = fission probability = 50%, fusion frequency = fission frequency = 5 minutes, receptor threshold = 12 minutes, damage threshold = 12.4 minutes, degradation frequency = 5.7 minutes). All simulations were performed for a total time of 12 hours.
- Line graphs display mean value and standard deviation (shaded regions) of 100 simulations for an initial total mitochondrial mass of 150 fragmented mitochondria of the total mitochondrial mass (grey line) and three mitochondrial subpopulations: small mass (orange line), medium mass (blue line) and large mass (green line) without biogenesis integrated with cellular bioenergetics state. Initial parameters values: fusion probability = fission probability = 50%, fusion frequency = fission frequency = 5 minutes, biogenesis probability = 22.1%, biogenesis frequency = 28.9 minutes, receptor threshold = 12 minutes, damage threshold = 12.4 minutes, degradation frequency = 5.7 minutes). All simulations were performed for a total time of 12 hours.
- Same as (C) but with biogenesis integrated with cellular bioenergetics state.
(TIFF)
Detailed description of the complete algorithm for the degradation cycle represented in Fig 7B.
(TIFF)
-
(A)Line graphs display mean value and standard deviation (shaded regions) of 100 simulations of probabilities of fusion (dark green line), fission (light green line), biogenesis (orange line) total mitochondrial mass (grey line), three mitochondria subpopulations: small mass (orange line), medium mass (blue line) and big mass (green line), and bioenergetics stress (red line) subjected to a constant damage signals of 5%. The plot represents the evolution of the total mass normalized to the total mass at time point 0. Initial values assigned to the model: fusion probability = fission probability = 50%, fusion frequency = fission frequency = 5 minutes, biogenesis probability = 22.1%, biogenesis frequency = 28.9 minutes, receptor threshold = 12 minutes, damage threshold = 12.4 minutes, degradation frequency = 5.7 minutes. All the simulations were performed for a total time of 24 hours.
-
(B)Same as (A) but with constant damage signals of 20%.
-
(C)Same as (A) but with constant damage signals of 40%.
-
(D)Same as (A) but with constant damage signals of 60%.
(TIFF)
Detailed description of the complete algorithm for the recovery cycle.
(TIFF)
-
(A)Line graphs display mean value and standard deviation (shaded area) of 100 simulations for an initial mitochondrial mass of 300 of the total mitochondrial mass with (dark grey) and without (light grey) the recovery process, subjected to five different damage signals (40%) every two hours for one hour with and without recovery process. The plot represents the evolution of the total mass and of three mitochondrial subpopulations normalized to the total mass at time point 0. Initial parameters values: fusion probability = fission probability = 50%, fusion frequency = fission frequency = 5 minutes, biogenesis probability = 22.1%, biogenesis frequency = 28.9 minutes, receptor threshold = 12 minutes, damage threshold = 12.4 minutes, degradation frequency = 5.7 minutes). Line graphs represent the mean value of 100 simulations. All the simulations were performed for a total time of 24 hours.
-
(B)Line graphs display mean value and standard deviation (shaded area) of 100 simulations for an initial mitochondrial mass of 300 of the bioenergetics stress with (dark red) and without (light red) the recovery process, subjected to five different damage signals (40%) every two hours for one hour with and without recovery process. The plot represents the evolution of the total mass and of three mitochondrial subpopulations normalized to the total mass at time point 0. Initial parameters values: fusion probability = fission probability = 50%, fusion frequency = fission frequency = 5 minutes, biogenesis probability = 22.1%, biogenesis frequency = 28.9 minutes, receptor threshold = 12 minutes, damage threshold = 12.4 minutes, degradation frequency = 5.7 minutes). Line graphs represent the mean value of 100 simulations. All the simulations were performed for a total time of 24 hours.
(TIFF)
-
(A)MR threshold sorted by the value assigned to total mass.
-
(B)MR threshold sorted by the value assigned to fission probability.
-
(C)MR threshold sorted by the value assigned to fission frequency.
-
(D)MR threshold sorted by the value assigned to fusion probability.
-
(E)MR threshold sorted by the value assigned to fusion frequency.
-
(F)MR threshold sorted by the value assigned to biogenesis frequency.
-
(G)MR threshold sorted by the value assigned to EN stress level.
-
(H)MR threshold sorted by the value assigned to ration L/H damage.
-
(I)MR threshold sorted by the value assigned to damage threshold.
-
(J)MR threshold sorted by the value assigned to MR threshold.
-
(K)MR threshold sorted by the value assigned to degradation frequency.
Red lines represent the lowess smoother lines.
(TIFF)
NetLogo File for the mitochondrial population full model including fusion/fission, biogenesis, damage and degradation cycles and energetic sensing. Load and use with NetLogo 5.2.0 or newer.
(NLOGO)
This movie shows the time-course of one model run describing mitochondrial directionality. Starting with an initial total mass of 300 mitochondria, the movie represents the evolution of the population with fusion/fission probabilities of 50%/50% and fusion/fission frequencies of 5 minutes (Fig 2C middle graph).
(AVI)
This movie shows the time-course of one model run describing mitochondrial directionality. Starting with an initial total mass of 300 mitochondria, the movie represents the evolution of the population with fusion/fission probabilities of 50%/50%, fusion/fission frequencies of 5 minutes and ϑ1 ϵ [0°, 10°] (Fig 3B).
(AVI)
This movie shows the time-course of one model run describing transmission dynamic in mitochondrial network. Starting with an initial total mass of 300 mitochondria with 10% of them GFP labeled (green), the movie represents the GFP transmission through the cell. Fusion/fission probabilities of 50%/50% and fusion/fission frequencies of 5 minutes (Fig 4B lower graph).
(AVI)
This movie shows the time-course of one model run describing mitochondrial biogenesis. Starting with an initial mitochondrial mass of 1, the movie represents the repopulation of the cell. Fusion/fission probabilities of 50%/50%, fusion/fission frequencies of 5 minutes, biogenesis probability of 22.1% and biogenesis frequency of 28.9 minutes (Fig 6D).
(AVI)
This movie shows the time-course of one model run describing mitochondrial damage sensing and mitophagy. Starting with an initial mitochondrial mass of 300 (50% high-damaged and 50% low-damaged), the movie represents mitochondrial degradation (Fig 7E). Receptor threshold of 12 minutes, damage threshold of 12.4 minutes and degradation frequency of 5.7 minutes.
(AVI)
This movie shows the time-course of one model run describing mitochondrial energetic sensing. Starting with an initial mitochondrial mass of 300 subjected to five different damage signals (10% and 20%) every two hours for one hour, the movie represents the evolution of the population (Fig 8E).
(AVI)
This movie shows the time-course of one model run describing mitochondrial energetic sensing. Starting with an initial mitochondrial mass of 300 subjected to five different damage signals (40%) every two hours for one hour, the movie represents the evolution of the population (Fig 8H).
(AVI)
Data Availability
All relevant data are within the paper and its Supporting Information files.
Funding Statement
This work was supported by the German Cancer Research Center (DKFZ), through SBCancer within the Helmholtz Alliance on Systems Biology funded by the Initiative and Networking Fund of the Helmholtz Association (NRB); and the e:Bio grant #0316191 (LysoSys) of the Federal Ministry of Education and Research (BMBF), Germany (AH-B). The funders had no role in study design, data collection and analysis, decision to publish, or preparation of the manuscript.
References
- 1.Chen H, Chan DC. Mitochondrial dynamics—fusion, fission, movement, and mitophagy—in neurodegenerative diseases. Hum Mol Genet. 2009;18(R2):R169–76. 10.1093/hmg/ddp326 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 2.MacAskill AF, Kittler JT. Control of mitochondrial transport and localization in neurons. Trends Cell Biol. 2010;20(2):102–12. 10.1016/j.tcb.2009.11.002 [DOI] [PubMed] [Google Scholar]
- 3.Collins TJ, Berridge MJ, Lipp P, Bootman MD. Mitochondria are morphologically and functionally heterogeneous within cells. EMBO J. 2002;21(7):1616–27. 10.1093/emboj/21.7.1616 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 4.Boland ML, Chourasia AH, Macleod KF. Mitochondrial dysfunction in cancer. Front Oncol. 2013;3:292 10.3389/fonc.2013.00292 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 5.Hamacher-Brady A, Brady NR, Logue SE, Sayen MR, Jinno M, Kirshenbaum LA, et al. Response to myocardial ischemia/reperfusion injury involves Bnip3 and autophagy. Cell Death Differ. 2007;14(1):146–57. 10.1038/sj.cdd.4401936 [DOI] [PubMed] [Google Scholar]
- 6.Hamacher-Brady A, Brady NR, Gottlieb RA, Gustafsson AB. Autophagy as a protective response to Bnip3-mediated apoptotic signaling in the heart. Autophagy. 2006;2(4):307–9. [DOI] [PubMed] [Google Scholar]
- 7.Zhu Y, Massen S, Terenzio M, Lang V, Chen-Lindner S, Eils R, et al. Modulation of serines 17 and 24 in the LC3-interacting region of Bnip3 determines pro-survival mitophagy versus apoptosis. J Biol Chem. 2013;288(2):1099–113. 10.1074/jbc.M112.399345 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 8.Hamacher-Brady A, Brady NR. Mitophagy programs: mechanisms and physiological implications of mitochondrial targeting by autophagy. Cell Mol Life Sci. 2016;73(4):775–95. 10.1007/s00018-015-2087-8 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 9.Mouli PK, Twig G, Shirihai OS. Frequency and selectivity of mitochondrial fusion are key to its quality maintenance function. Biophys J. 2009;96(9):3509–18. 10.1016/j.bpj.2008.12.3959 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 10.Figge MT, Reichert AS, Meyer-Hermann M, Osiewacz HD. Deceleration of fusion-fission cycles improves mitochondrial quality control during aging. PLoS Comput Biol. 2012;8(6):e1002576 10.1371/journal.pcbi.1002576 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 11.Tam ZY, Gruber J, Halliwell B, Gunawan R. Mathematical modeling of the role of mitochondrial fusion and fission in mitochondrial DNA maintenance. PLoS One. 2013;8(10):e76230 10.1371/journal.pone.0076230 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 12.Patel PK, Shirihai O, Huang KC. Optimal dynamics for quality control in spatially distributed mitochondrial networks. PLoS Comput Biol. 2013;9(7):e1003108 10.1371/journal.pcbi.1003108 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 13.Macdonald PJ, Stepanyants N, Mehrotra N, Mears JA, Qi X, Sesaki H, et al. A dimeric equilibrium intermediate nucleates Drp1 reassembly on mitochondrial membranes for fission. Mol Biol Cell. 2014;25(12):1905–15. 10.1091/mbc.E14-02-0728 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 14.Montessuit S, Somasekharan SP, Terrones O, Lucken-Ardjomande S, Herzig S, Schwarzenbacher R, et al. Membrane remodeling induced by the dynamin-related protein Drp1 stimulates Bax oligomerization. Cell. 2010;142(6):889–901. 10.1016/j.cell.2010.08.017 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 15.Renault TT, Floros KV, Elkholi R, Corrigan KA, Kushnareva Y, Wieder SY, et al. Mitochondrial shape governs BAX-induced membrane permeabilization and apoptosis. Mol Cell. 2015;57(1):69–82. 10.1016/j.molcel.2014.10.028 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 16.Serasinghe MN, Wieder SY, Renault TT, Elkholi R, Asciolla JJ, Yao JL, et al. Mitochondrial division is requisite to RAS-induced transformation and targeted by oncogenic MAPK pathway inhibitors. Mol Cell. 2015;57(3):521–36. 10.1016/j.molcel.2015.01.003 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 17.Blackstone C, Chang CR. Mitochondria unite to survive. Nat Cell Biol. 2011;13(5):521–2. 10.1038/ncb0511-521 [DOI] [PubMed] [Google Scholar]
- 18.Li L, Chen Y, Gibson SB. Starvation-induced autophagy is regulated by mitochondrial reactive oxygen species leading to AMPK activation. Cell Signal. 2013;25(1):50–65. 10.1016/j.cellsig.2012.09.020 [DOI] [PubMed] [Google Scholar]
- 19.Rambold AS, Kostelecky B, Elia N, Lippincott-Schwartz J. Tubular network formation protects mitochondria from autophagosomal degradation during nutrient starvation. Proc Natl Acad Sci U S A. 2011;108(25):10190–5. 10.1073/pnas.1107402108 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 20.Rambold AS, Kostelecky B, Lippincott-Schwartz J. Together we are stronger Fusion protects mitochondria from autophagosomal degradation. Autophagy. 2011;7(12):1568–9. 10.4161/auto.7.12.17992 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 21.Macal CM, North MJ. Agent-based modeling and simulation. Winter Simulation Conference. 2009.
- 22.Axelrod R, Tesfatsion L. Appendix AA guide for newcomers to agent-based modeling in the social sciences. Handbook of computational economics. 2006;2:1647–59. [Google Scholar]
- 23.de Marchi S, Page SE. Agent-Based Models. Annual Review of Political Science. 2014;17(1):1–20. [Google Scholar]
- 24.Helbing D, Balietti S. How to do agent-based simulations in the future: From modeling social mechanisms to emergent phenomena and interactive systems design. How to do agent-based simulations in the future: From modeling social mechanisms to emergent phenomena and interactive systems design. 2011. [Google Scholar]
- 25.Politopoulos I. Review and analysis of agent-based models in biology. University of Liverpool; 2007. [Google Scholar]
- 26.Schleich K, Warnken U, Fricker N, Oztürk S, Richter P, Kammerer K, et al. Stoichiometry of the CD95 death-inducing signaling complex: experimental and modeling evidence for a death effector domain chain model. Molecular cell. 2012;47(2):306–19. 10.1016/j.molcel.2012.05.006 [DOI] [PubMed] [Google Scholar]
- 27.Borlin CS, Lang V, Hamacher-Brady A, Brady NR. Agent-based modeling of autophagy reveals emergent regulatory behavior of spatio-temporal autophagy dynamics. Cell Commun Signal. 2014;12(1):56. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 28.Kühn C, Tyc KM, Klipp E. Dosage and dose schedule screening of drug combinations in agent-based models reveals hidden synergies. Frontiers in physiology. 2015;6. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 29.Frechin M, Stoeger T, Daetwyler S, Gehin C, Battich N, Damm E-M, et al. Cell-intrinsic adaptation of lipid composition to local crowding drives social behaviour. Nature. 2015. [DOI] [PubMed] [Google Scholar]
- 30.Wilensky U. NetLogo. NetLogo. 1999.
- 31.Milo R, Jorgensen P, Moran U, Weber G, Springer M. BioNumbers—the database of key numbers in molecular and cell biology. Nucleic Acids Res. 2010;38(Database issue):D750–3. 10.1093/nar/gkp889 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 32.Jiang H, Song C, Chen CC, Xu R, Raines KS, Fahimian BP, et al. Quantitative 3D imaging of whole, unstained cells by using X-ray diffraction microscopy. Proc Natl Acad Sci U S A. 2010;107(25):11234–9. 10.1073/pnas.1000156107 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 33.Kiryu-Seo S, Ohno N, Kidd GJ, Komuro H, Trapp BD. Demyelination increases axonal stationary mitochondrial size and the speed of axonal mitochondrial transport. J Neurosci. 2010;30(19):6658–66. 10.1523/JNEUROSCI.5265-09.2010 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 34.Westermann B. Mitochondrial fusion and fission in cell life and death. Nat Rev Mol Cell Biol. 2010;11(12):872–84. 10.1038/nrm3013 [DOI] [PubMed] [Google Scholar]
- 35.Watanabe W, Shimada T, Matsunaga S, Kurihara D, Fukui K, Shin-Ichi Arimura S, et al. Single-organelle tracking by two-photon conversion. Opt Express. 2007;15(5):2490–8. [DOI] [PubMed] [Google Scholar]
- 36.Harris JJ, Jolivet R, Attwell D. Synaptic energy use and supply. Neuron. 2012;75(5):762–77. 10.1016/j.neuron.2012.08.019 [DOI] [PubMed] [Google Scholar]
- 37.Morris RL, Hollenbeck PJ. The Regulation of Bidirectional Mitochondrial Transport Is Coordinated with Axonal Outgrowth. Journal of Cell Science. 1993;104:917–27. [DOI] [PubMed] [Google Scholar]
- 38.Patil H, Cho KI, Lee J, Yang Y, Orry A, Ferreira PA. Kinesin-1 and mitochondrial motility control by discrimination of structurally equivalent but distinct subdomains in Ran-GTP-binding domains of Ran-binding protein 2. Open Biol. 2013;3(3):120183 10.1098/rsob.120183 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 39.Narayanareddy BR, Vartiainen S, Hariri N, O'Dowd DK, Gross SP. A biophysical analysis of mitochondrial movement: differences between transport in neuronal cell bodies versus processes. Traffic. 2014;15(7):762–71. 10.1111/tra.12171 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 40.Liesa M, Shirihai OS. Mitochondrial dynamics in the regulation of nutrient utilization and energy expenditure. Cell Metab. 2013;17(4):491–506. 10.1016/j.cmet.2013.03.002 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 41.Wikstrom JD, Twig G, Shirihai OS. What can mitochondrial heterogeneity tell us about mitochondrial dynamics and autophagy? … journal of biochemistry & cell biology. 2009. [DOI] [PubMed] [Google Scholar]
- 42.Berman SB, Chen YB, Qi B, McCaffery JM, Rucker EB 3rd, Goebbels S, et al. Bcl-x L increases mitochondrial fission, fusion, and biomass in neurons. J Cell Biol. 2009;184(5):707–19. 10.1083/jcb.200809060 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 43.Twig G, Elorza A, Molina AJ, Mohamed H, Wikstrom JD, Walzer G, et al. Fission and selective fusion govern mitochondrial segregation and elimination by autophagy. EMBO J. 2008;27(2):433–46. 10.1038/sj.emboj.7601963 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 44.Berman SB, Pineda FJ, Hardwick JM. Mitochondrial fission and fusion dynamics: the long and short of it. Cell Death Differ. 2008;15(7):1147–52. 10.1038/cdd.2008.57 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 45.Nunnari J, Marshall WF, Straight A, Murray A, Sedat JW, Walter P. Mitochondrial transmission during mating in Saccharomyces cerevisiae is determined by mitochondrial fusion and fission and the intramitochondrial segregation of mitochondrial DNA. Molecular Biology of the Cell. 1997;8(7):1233–42. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 46.Twig G, Hyde B, Shirihai OS. Mitochondrial fusion, fission and autophagy as a quality control axis: the bioenergetic view. Biochim Biophys Acta. 2008;1777(9):1092–7. 10.1016/j.bbabio.2008.05.001 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 47.Youle RJ, van der Bliek AM. Mitochondrial fission, fusion, and stress. Science. 2012;337(6098):1062–5. 10.1126/science.1219855 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 48.Posakony JW, England JM, Attardi G. Mitochondrial growth and division during the cell cycle in HeLa cells. J Cell Biol. 1977;74(2):468–91. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 49.Campanella M, Seraphim A, Abeti R, Casswell E, Echave P, Duchen MR. IF1, the endogenous regulator of the F(1)F(o)-ATPsynthase, defines mitochondrial volume fraction in HeLa cells by regulating autophagy. Biochim Biophys Acta. 2009;1787(5):393–401. 10.1016/j.bbabio.2009.02.023 [DOI] [PubMed] [Google Scholar]
- 50.Wu M, Kalyanasundaram A, Zhu J. Structural and biomechanical basis of mitochondrial movement in eukaryotic cells. Int J Nanomedicine. 2013;8:4033–42. 10.2147/IJN.S52132 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 51.Anesti V, Scorrano L. The relationship between mitochondrial shape and function and the cytoskeleton. Biochim Biophys Acta. 2006;1757(5–6):692–9. 10.1016/j.bbabio.2006.04.013 [DOI] [PubMed] [Google Scholar]
- 52.Schnapp BJ, Vale RD, Sheetz MP, Reese TS. Microtubules and the Mechanism of Directed Organelle Movement. Ann Ny Acad Sci. 1986;466:909–18. [DOI] [PubMed] [Google Scholar]
- 53.Karbowski M, Arnoult D, Chen H, Chan DC, Smith CL, Youle RJ. Quantitation of mitochondrial dynamics by photolabeling of individual organelles shows that mitochondrial fusion is blocked during the Bax activation phase of apoptosis. J Cell Biol. 2004;164(4):493–9. 10.1083/jcb.200309082 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 54.Twig G, Graf SA, Wikstrom JD, Mohamed H, Haigh SE, Elorza A, et al. Tagging and tracking individual networks within a complex mitochondrial web with photoactivatable GFP. Am J Physiol Cell Physiol. 2006;291(1):C176–84. 10.1152/ajpcell.00348.2005 [DOI] [PubMed] [Google Scholar]
- 55.Saltelli A, Ratto M, Andres T, Campolongo F, Cariboni J. Global sensitivity analysis: the primer 2008. [Google Scholar]
- 56.Tam ZY, Gruber J, Halliwell B, Gunawan R. Context-Dependent Role of Mitochondrial Fusion-Fission in Clonal Expansion of mtDNA Mutations. PLoS Comput Biol. 2015;11(5):e1004183 10.1371/journal.pcbi.1004183 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 57.Alden K, Read M, Timmis J, Andrews PS, Veiga-Fernandes H, Coles M. Spartan: a comprehensive tool for understanding uncertainty in simulations of biological systems. PLoS Comput Biol. 2013;9(2):e1002916 10.1371/journal.pcbi.1002916 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 58.Marino S, Hogue IB, Ray CJ, Kirschner DE. A methodology for performing global uncertainty and sensitivity analysis in systems biology. J Theor Biol. 2008;254(1):178–96. 10.1016/j.jtbi.2008.04.011 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 59.Mishra P, Chan DC. Mitochondrial dynamics and inheritance during cell division, development and disease. Nat Rev Mol Cell Biol. 2014;15(10):634–46. 10.1038/nrm3877 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 60.Tait SW, Green DR. Mitochondria and cell death: outer membrane permeabilization and beyond. Nat Rev Mol Cell Biol. 2010;11(9):621–32. 10.1038/nrm2952 [DOI] [PubMed] [Google Scholar]
- 61.Tait SW, Parsons MJ, Llambi F, Bouchier-Hayes L, Connell S, Munoz-Pinedo C, et al. Resistance to caspase-independent cell death requires persistence of intact mitochondria. Dev Cell. 2010;18(5):802–13. 10.1016/j.devcel.2010.03.014 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 62.Wang X, Moraes CT. Increases in mitochondrial biogenesis impair carcinogenesis at multiple levels. Mol Oncol. 2011;5(5):399–409. 10.1016/j.molonc.2011.07.008 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 63.Scrucca L. GA: a package for genetic algorithms in R. Journal of Statistical Software. 2012;53(4). [Google Scholar]
- 64.Kumei Y, Nakajima T, Sato A, Kamata N, Enomoto S. Reduction of G1 Phase Duration and Enhancement of C-Myc Gene-Expression in Hela-Cells at Hypergravity. Journal of Cell Science. 1989;93:221–6. [DOI] [PubMed] [Google Scholar]
- 65.McLelland GL, Soubannier V, Chen CX, McBride HM, Fon EA. Parkin and PINK1 function in a vesicular trafficking pathway regulating mitochondrial quality control. EMBO J. 2014;33(4):282–95. 10.1002/embj.201385902 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 66.Ding WX, Ni HM, Li M, Liao Y, Chen X, Stolz DB, et al. Nix is critical to two distinct phases of mitophagy, reactive oxygen species-mediated autophagy induction and Parkin-ubiquitin-p62-mediated mitochondrial priming. J Biol Chem. 2010;285(36):27879–90. 10.1074/jbc.M110.119537 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 67.Ashrafi G, Schwarz TL. The pathways of mitophagy for quality control and clearance of mitochondria. Cell Death Differ. 2013;20(1):31–42. 10.1038/cdd.2012.81 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 68.Novak I. Mitophagy: a complex mechanism of mitochondrial removal. Antioxid Redox Signal. 2012;17(5):794–802. 10.1089/ars.2011.4407 [DOI] [PubMed] [Google Scholar]
- 69.Mihaylova MM, Shaw RJ. The AMPK signalling pathway coordinates cell growth, autophagy and metabolism. Nat Cell Biol. 2011;13(9):1016–23. 10.1038/ncb2329 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 70.Jager S, Handschin C, St-Pierre J, Spiegelman BM. AMP-activated protein kinase (AMPK) action in skeletal muscle via direct phosphorylation of PGC-1alpha. Proc Natl Acad Sci U S A. 2007;104(29):12017–22. 10.1073/pnas.0705070104 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 71.Scarpulla RC. Metabolic control of mitochondrial biogenesis through the PGC-1 family regulatory network. Biochim Biophys Acta. 2011;1813(7):1269–78. 10.1016/j.bbamcr.2010.09.019 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 72.Egan DF, Shackelford DB, Mihaylova MM, Gelino S, Kohnz RA, Mair W, et al. Phosphorylation of ULK1 (hATG1) by AMP-activated protein kinase connects energy sensing to mitophagy. Science. 2011;331(6016):456–61. 10.1126/science.1196371 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 73.Gomes LC, Di Benedetto G, Scorrano L. During autophagy mitochondria elongate, are spared from degradation and sustain cell viability. Nat Cell Biol. 2011;13(5):589–98. 10.1038/ncb2220 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 74.Federico A, Cardaioli E, Da Pozzo P, Formichi P, Gallus GN, Radi E. Mitochondria, oxidative stress and neurodegeneration. J Neurol Sci. 2012;322(1–2):254–62. 10.1016/j.jns.2012.05.030 [DOI] [PubMed] [Google Scholar]
- 75.Schmidt CW. Mito-Conundrum Unraveling Environmental Effects on Mitochondria. Environmental Health Perspectives. 2010;118(7):A292–A7. [Google Scholar]
- 76.Meyer JN, Leung MC, Rooney JP, Sendoel A, Hengartner MO, Kisby GE, et al. Mitochondria as a target of environmental toxicants. Toxicol Sci. 2013;134(1):1–17. 10.1093/toxsci/kft102 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 77.Bingol B, Tea JS, Phu L, Reichelt M, Bakalarski CE, Song Q, et al. The mitochondrial deubiquitinase USP30 opposes parkin-mediated mitophagy. Nature. 2014;510(7505):370–5. 10.1038/nature13418 [DOI] [PubMed] [Google Scholar]
- 78.Vafai SB, Mootha VK. Mitochondrial disorders as windows into an ancient organelle. Nature. 2012;491(7424):374–83. 10.1038/nature11707 [DOI] [PubMed] [Google Scholar]
- 79.Malpass K. Neurodegenerative disease: defective mitochondrial dynamics in the hot seat-a therapeutic target common to many neurological disorders? Nat Rev Neurol. 2013;9(8):417 10.1038/nrneurol.2013.138 [DOI] [PubMed] [Google Scholar]
- 80.Hollville E, Carroll RG, Cullen SP, Martin SJ. Bcl-2 family proteins participate in mitochondrial quality control by regulating Parkin/PINK1-dependent mitophagy. Mol Cell. 2014;55(3):451–66. 10.1016/j.molcel.2014.06.001 [DOI] [PubMed] [Google Scholar]
- 81.Stonedahl FJ. Genetic algorithms for the exploration of parameter spaces in agent-based models: Northwestern University; 2011. [Google Scholar]
- 82.Alden K, Timmis J, Coles M. Easing Parameter Sensitivity Analysis of Netlogo Simulations using SPARTAN. Easing Parameter Sensitivity Analysis of Netlogo Simulations using SPARTAN. [Google Scholar]
- 83.Birkedal R, Shiels HA, Vendelin M. Three-dimensional mitochondrial arrangement in ventricular myocytes: from chaos to order. Am J Physiol Cell Physiol. 2006;291(6):C1148–58. 10.1152/ajpcell.00236.2006 [DOI] [PubMed] [Google Scholar]
- 84.Cheng A, Wan R, Yang JL, Kamimura N, Son TG, Ouyang X, et al. Involvement of PGC-1alpha in the formation and maintenance of neuronal dendritic spines. Nat Commun. 2012;3:1250 10.1038/ncomms2238 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 85.Brady NR, Elmore SP, van Beek JJ, Krab K, Courtoy PJ, Hue L, et al. Coordinated behavior of mitochondria in both space and time: a reactive oxygen species-activated wave of mitochondrial depolarization. Biophys J. 2004;87(3):2022–34. 10.1529/biophysj.103.035097 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 86.Alden K, Read M, Andrews P, Timmis J. Package 'spartan'. Package 'spartan'. 2015.
- 87.Team RC. R: A language and environment for statistical computing. Vienna, Austria; 2014. URL http://www.R-project.org. 2015. [Google Scholar]
- 88.Thiele JC. R Marries NetLogo: Introduction to the RNetLogo Package. Journal of Statistical Software. 2014;58(2):1–41. [Google Scholar]
- 89.Thiele JC, Kurth W, Grimm V. RNetLogo: an R package for running and exploring individual-based models implemented in NetLogo. Methods in Ecology and Evolution. 2012;3(3):480–3. [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.
Supplementary Materials
Detailed description of the complete algorithm for the fusion/fission cycle represented in Fig 1D.
(TIF)
-
(A)Fusion frequency sorted by the value assigned to total mass.
-
(B)Fusion frequency sorted by the value assigned to initial labeled mass.
-
(C)Fusion frequency sorted by the value assigned to fission probability.
-
(D)Fusion frequency sorted by the value assigned to fission frequency.
-
(E)Fusion frequency sorted by the value assigned to fusion probability.
-
(F)Fusion frequency sorted by the value assigned to fusion frequency.
-
(G)Fusion frequency sorted by the value assigned to vl.
-
(H)Fusion frequency sorted by the value assigned to vh.
Red lines represent the lowess smoother lines.
(TIFF)
-
(A)Line graphs display mean value and standard deviation (shaded regions) of 100 simulations of total mitochondria mass for an initial mass of 150 fragmented mitochondria with (dark grey line) and without (light grey line) biogenesis integrated with cellular bioenergetics state. Initial parameters values: fusion probability = fission probability = 50%, fusion frequency = fission frequency = 5 minutes, biogenesis probability = 22.1%, biogenesis frequency = 28.9 minutes, receptor threshold = 12 minutes, damage threshold = 12.4 minutes, degradation frequency = 5.7 minutes). All simulations were performed for a total time of 12 hours.
-
(B)Line graphs display mean value and standard deviation (shaded regions) of 100 simulations of total mitochondria mass for an initial mass of 150 fragmented mitochondria and with biogenesis integrated with cellular bioenergetics state subjected to three different initial biogenesis frequency values: 28.9 (light blue line), 57.8 (blue line) and 86.7 (dark blue line) minutes. Initial parameters values: fusion probability = fission probability = 50%, fusion frequency = fission frequency = 5 minutes, receptor threshold = 12 minutes, damage threshold = 12.4 minutes, degradation frequency = 5.7 minutes). All simulations were performed for a total time of 12 hours.
- Line graphs display mean value and standard deviation (shaded regions) of 100 simulations for an initial total mitochondrial mass of 150 fragmented mitochondria of the total mitochondrial mass (grey line) and three mitochondrial subpopulations: small mass (orange line), medium mass (blue line) and large mass (green line) without biogenesis integrated with cellular bioenergetics state. Initial parameters values: fusion probability = fission probability = 50%, fusion frequency = fission frequency = 5 minutes, biogenesis probability = 22.1%, biogenesis frequency = 28.9 minutes, receptor threshold = 12 minutes, damage threshold = 12.4 minutes, degradation frequency = 5.7 minutes). All simulations were performed for a total time of 12 hours.
- Same as (C) but with biogenesis integrated with cellular bioenergetics state.
(TIFF)
Detailed description of the complete algorithm for the degradation cycle represented in Fig 7B.
(TIFF)
-
(A)Line graphs display mean value and standard deviation (shaded regions) of 100 simulations of probabilities of fusion (dark green line), fission (light green line), biogenesis (orange line) total mitochondrial mass (grey line), three mitochondria subpopulations: small mass (orange line), medium mass (blue line) and big mass (green line), and bioenergetics stress (red line) subjected to a constant damage signals of 5%. The plot represents the evolution of the total mass normalized to the total mass at time point 0. Initial values assigned to the model: fusion probability = fission probability = 50%, fusion frequency = fission frequency = 5 minutes, biogenesis probability = 22.1%, biogenesis frequency = 28.9 minutes, receptor threshold = 12 minutes, damage threshold = 12.4 minutes, degradation frequency = 5.7 minutes. All the simulations were performed for a total time of 24 hours.
-
(B)Same as (A) but with constant damage signals of 20%.
-
(C)Same as (A) but with constant damage signals of 40%.
-
(D)Same as (A) but with constant damage signals of 60%.
(TIFF)
Detailed description of the complete algorithm for the recovery cycle.
(TIFF)
-
(A)Line graphs display mean value and standard deviation (shaded area) of 100 simulations for an initial mitochondrial mass of 300 of the total mitochondrial mass with (dark grey) and without (light grey) the recovery process, subjected to five different damage signals (40%) every two hours for one hour with and without recovery process. The plot represents the evolution of the total mass and of three mitochondrial subpopulations normalized to the total mass at time point 0. Initial parameters values: fusion probability = fission probability = 50%, fusion frequency = fission frequency = 5 minutes, biogenesis probability = 22.1%, biogenesis frequency = 28.9 minutes, receptor threshold = 12 minutes, damage threshold = 12.4 minutes, degradation frequency = 5.7 minutes). Line graphs represent the mean value of 100 simulations. All the simulations were performed for a total time of 24 hours.
-
(B)Line graphs display mean value and standard deviation (shaded area) of 100 simulations for an initial mitochondrial mass of 300 of the bioenergetics stress with (dark red) and without (light red) the recovery process, subjected to five different damage signals (40%) every two hours for one hour with and without recovery process. The plot represents the evolution of the total mass and of three mitochondrial subpopulations normalized to the total mass at time point 0. Initial parameters values: fusion probability = fission probability = 50%, fusion frequency = fission frequency = 5 minutes, biogenesis probability = 22.1%, biogenesis frequency = 28.9 minutes, receptor threshold = 12 minutes, damage threshold = 12.4 minutes, degradation frequency = 5.7 minutes). Line graphs represent the mean value of 100 simulations. All the simulations were performed for a total time of 24 hours.
(TIFF)
-
(A)MR threshold sorted by the value assigned to total mass.
-
(B)MR threshold sorted by the value assigned to fission probability.
-
(C)MR threshold sorted by the value assigned to fission frequency.
-
(D)MR threshold sorted by the value assigned to fusion probability.
-
(E)MR threshold sorted by the value assigned to fusion frequency.
-
(F)MR threshold sorted by the value assigned to biogenesis frequency.
-
(G)MR threshold sorted by the value assigned to EN stress level.
-
(H)MR threshold sorted by the value assigned to ration L/H damage.
-
(I)MR threshold sorted by the value assigned to damage threshold.
-
(J)MR threshold sorted by the value assigned to MR threshold.
-
(K)MR threshold sorted by the value assigned to degradation frequency.
Red lines represent the lowess smoother lines.
(TIFF)
NetLogo File for the mitochondrial population full model including fusion/fission, biogenesis, damage and degradation cycles and energetic sensing. Load and use with NetLogo 5.2.0 or newer.
(NLOGO)
This movie shows the time-course of one model run describing mitochondrial directionality. Starting with an initial total mass of 300 mitochondria, the movie represents the evolution of the population with fusion/fission probabilities of 50%/50% and fusion/fission frequencies of 5 minutes (Fig 2C middle graph).
(AVI)
This movie shows the time-course of one model run describing mitochondrial directionality. Starting with an initial total mass of 300 mitochondria, the movie represents the evolution of the population with fusion/fission probabilities of 50%/50%, fusion/fission frequencies of 5 minutes and ϑ1 ϵ [0°, 10°] (Fig 3B).
(AVI)
This movie shows the time-course of one model run describing transmission dynamic in mitochondrial network. Starting with an initial total mass of 300 mitochondria with 10% of them GFP labeled (green), the movie represents the GFP transmission through the cell. Fusion/fission probabilities of 50%/50% and fusion/fission frequencies of 5 minutes (Fig 4B lower graph).
(AVI)
This movie shows the time-course of one model run describing mitochondrial biogenesis. Starting with an initial mitochondrial mass of 1, the movie represents the repopulation of the cell. Fusion/fission probabilities of 50%/50%, fusion/fission frequencies of 5 minutes, biogenesis probability of 22.1% and biogenesis frequency of 28.9 minutes (Fig 6D).
(AVI)
This movie shows the time-course of one model run describing mitochondrial damage sensing and mitophagy. Starting with an initial mitochondrial mass of 300 (50% high-damaged and 50% low-damaged), the movie represents mitochondrial degradation (Fig 7E). Receptor threshold of 12 minutes, damage threshold of 12.4 minutes and degradation frequency of 5.7 minutes.
(AVI)
This movie shows the time-course of one model run describing mitochondrial energetic sensing. Starting with an initial mitochondrial mass of 300 subjected to five different damage signals (10% and 20%) every two hours for one hour, the movie represents the evolution of the population (Fig 8E).
(AVI)
This movie shows the time-course of one model run describing mitochondrial energetic sensing. Starting with an initial mitochondrial mass of 300 subjected to five different damage signals (40%) every two hours for one hour, the movie represents the evolution of the population (Fig 8H).
(AVI)
Data Availability Statement
All relevant data are within the paper and its Supporting Information files.