Evolution of Human Immunodeficiency Virus Type 1 Coreceptor Usage during Antiretroviral Therapy: a Bayesian Approach

Abstract

There is substantial evidence for ongoing replication and evolution of human immunodeficiency virus type 1 (HIV-1), even in individuals receiving highly active antiretroviral therapy. Viral evolution in the presence of antiviral therapy needs to be considered when developing new therapeutic strategies. Phylogenetic analyses of HIV-1 sequences can be used for this purpose but may give rise to misleading results if rates of intrapatient evolution differ significantly. To improve analyses of HIV-1 evolution relevant to studies of pathogenesis and treatment, we developed a Bayesian hierarchical model that incorporates all available sequence data while simultaneously allowing the phylogenetic parameters of each patient to vary. We used this method to examine evolutionary changes in HIV-1 coreceptor usage in response to treatment. We examined patients whose viral populations exhibited a shift in coreceptor utilization in response to therapy. CXCR4 (X4) strains emerged in each patient but were suppressed following initiation of new antiretroviral regimens, so that CCR5-utilizing (R5) strains predominated. By phylogenetically reconstructing the evolutionary relationship of HIV-1 obtained longitudinally from each patient, it was possible to examine the origin of the reemergent R5 virus. Using our Bayesian hierarchical approach, we found that the reemergent R5 virus detectable after therapy was more closely related to the predecessor R5 virus than to the X4 strains. The Bayesian hierarchical approach, unlike more traditional methods, makes it possible to evaluate competing hypotheses across patients. This model is not limited to analyses of HIV-1 but can be used to elucidate evolutionary processes for other organisms as well.

A key characteristic of human immunodeficiency virus type 1 (HIV-1) is its great potential for genetic variation. Even in a single infected individual, the virus exists as a quasispecies of highly related but genetically distinct variants (11, 22). Successful viral mutants persist and may eventually emerge as the dominant quasispecies under selective pressure from antiretroviral therapy or the immune response. This heterogeneity poses a formidable obstacle to drug treatment and vaccine design. To understand the pathogenesis of HIV-1 and halt its spread, it is critical to study the mechanisms driving HIV-1 evolution.

Phylogenetic analyses have traditionally been used to reconstruct the evolutionary histories of contemporaneous sequences. To address questions of intrahost evolution, however, it becomes necessary to examine the evolutionary relatedness of sequences sampled at different times. In general, such analyses do not allow for the estimation of intrahost evolution across multiple patients simultaneously. Many studies either calculate rates of nucleotide substitution and infer trees for each set of sequences independently or, alternatively, construct a single multipatient tree governed by the same substitution process for all individuals.

In one such analysis of viral evolution following primary infection, changes in the V3 region of HIV-1 env were examined by independently constructing phylogenetic trees for each of eight patients (16). A similar study examined evolutionary changes in the C2-V5 portion of env by constructing a single multipatient phylogenetic tree (27). In these two studies, the impact of antiretroviral therapy on HIV-1 evolution was not addressed. Frost et al. (7) examined the divergence and diversity of HIV-1 envelope at two time points: before the initiation of highly active antiretroviral therapy (HAART) and 2 years into HAART. They found strong evidence of divergence and positive selection in two of six patients. Viral evolution under HAART has also been studied to examine viral reservoirs, latency, and drug resistance (8, 24, 38, 39). In this study, we examine envelope evolution under antiretroviral therapy across multiple patients simultaneously.

To investigate the forces shaping HIV-1 evolution, we extended the Bayesian hierarchical phylogenetic model of Suchard et al. (29) by incorporating gamma-distributed rate variation across sites. Within the analytical framework outlined in the Bayes theorem, all information or knowledge about a data set is taken into account; the initial probability assessment of the evolutionary parameters (the prior distribution) is used to update the probability estimates obtained after the data are analyzed (the posterior distribution). Further, Bayesian techniques are adept at handling averaging across discrete quantities that have uncertainty, such as multipatient phylogenetic analyses, where evolutionary parameters, like trees, may vary from patient to patient (20).

We used our Bayesian model to examine a recently recognized phenomenon with direct relevance to antiretroviral treatment: changes in HIV-1 coreceptor usage during antiretroviral therapy. HIV-1 strains transmitted in vivo generally use the coreceptor CCR5 (R5 viruses), but strains using CXCR4 (X4 viruses) later emerge in approximately 50% of infected individuals (2, 18, 26, 27). The appearance of X4 strains predicts an acceleration of HIV-1 disease progression (2, 18, 26, 27). The natural course of disease progression, however, can be altered by antiretroviral therapy (1, 23). It has been shown that potent antiretroviral therapy can preferentially suppress X4 strains of HIV-1 in patients, shifting the viral population back to R5 after treatment (25). It is not known whether the R5 isolates that predominated after therapy evolved from a predecessor R5 strain or from circulating X4 virus.

In the present study, we investigated HIV-1 sequence evolution, examining changes in coreceptor usage in patients who received antiretroviral therapy but did not achieve complete virologic suppression. We tested for common patterns in intrahost viral evolution by using a Bayesian hierarchical model that allows for interpatient variation while estimating phylogenetic tendencies across patients simultaneously. Using this model, we found that the R5 virus present after therapy was most closely related to predecessor R5 virus. It is unlikely that this virus arose through continued evolution of X4 strains. These analyses illustrate the applicability of our hierarchical Bayesian method for evolutionary studies of HIV-1 and other viruses.

MATERIALS AND METHODS

Study population.

We identified three patients whose viral populations displayed a shift in coreceptor utilization while they were on antiretroviral therapy (25). All patients were enrolled in the Bronx-Manhattan site of the Women's Interagency HIV Study, a multicenter study of the natural history of HIV-1 infection in women (25). Each woman provided informed consent at enrollment. The institutional review boards at each clinical site and the New York State Department of Health approved the investigation.

Virologic and immunologic characteristics of the patients are listed in Table 1. Patients 17 and 28 were described previously (17). Patients 9 and 17 were also described in a separate study, where they were referred to as subjects 5 and 8, respectively (25). Human genotypes for the CCR5 coreceptor were previously determined; all patients were homozygous for the wild-type coreceptor (5).

TABLE 1.

Clinical, virologic, and immunologic characteristics of patients

Patient no.	Sample dated	Plasma HIV-1 load (no. of copies/ml)	Lambda value (λ)a	CD4+ count, cells/mm3	Antiretroviral treatmentb
9	3/96	90,500	0.90	11	3TC, d4T, SQV
	6/96	2,300,000	0.36	37	d4T, IDV
	1/97	320,000	1.00	35	3TC, d4T, IDV
28	1/96	19,000	0.52	670	None
	4/96	34,000	0.28	NAc	None
	1/97	10,500	1.00	274	AZT
17	6/96	195,000	1.00	23	3TC, d4T, IDV
	7/96	200,000	0.90	11	3TC, d4T, IDV
	11/96	72,000	1.00	21	3TC, ddC, IDV

^aλ is a nonlinear variable representing the proportion of strains using CCR5: λ = 1 represents an isolate in which all strains prefer CCR5 whereas λ = 0 indicates that all prefer CXCR4 (16).

^bSQV, saquinavir, IDV, indinavir; 3TC, lamivudine; d4T, stavudine; AZT, zidovudine; DDC, dideoxycytosine.

^cNA, not available.

^dShown as month/year (1996 or 1997).

For each patient, viral sequences from three time points were examined. In most patients with detectable X4 virus, the X4 strains exist as a mixture along with R5 isolates. We therefore quantitated the proportion of virus that uses each coreceptor in each patient sample by using a mathematical model developed earlier (25). In this system, λ represents the proportion of viruses using CCR5: λ = 1 represents an isolate in which all strains prefer CCR5 whereas λ = 0 indicates that all isolates prefer CXCR4. We selected three time points as follows: at the first time point the patient quasispecies was dominated by R5 strains of HIV-1, defined as λ ≥ 0.5. At the second time point, the patient exhibited a higher proportion of X4 strains, as suggested by a decrease in λ from the previous time point. The last time point selected was either after initiation of antiretroviral therapy or following a change in treatment, when each patient exhibited a high proportion of R5 strains. No patient achieved complete virologic suppression, regardless of antiretroviral regimen.

Determination of coreceptor usage of biological clones.

Primary isolates of HIV-1 were obtained by coculture of the patients' peripheral blood mononuclear cells with healthy donor peripheral blood mononuclear cells; biological clones were then derived from primary isolates by short-term limiting dilution cloning (25). On average, there were 25 (range, 22 to 27) clones per patient time point. The coreceptor phenotype of each clone was determined by the HOS-CD4 assay (25). Determination of coreceptor utilization was based upon a functional, biologic assay rather than genotypic analysis of viral env sequences, because such a sequence-based approach might lead to inadvertent phenotype attraction during phylogenetic reconstruction. Phenotypic attraction may occur when the genotype of the organism that is under analysis codes for the same phenotype that is the basis for inclusion in the study. That is, if we use the sequence information to determine the phenotype and then use the same genotypic information to determine the phylogenetic relationship, we can get more clustering among phenotypes than would be otherwise expected by chance, thus biasing the true phylogenetic relationships among the sequences.

PCR amplification, cloning, and sequencing.

Reverse transcription-PCR was used to clone the V1-C5 portion of the HIV-1 env gene from each biological clone with use of primers HX6556F (5′-ATGGGATCAAAGCCTAAAGCCATGTG-3′) and HX7792R (5′-AGTGCTTCCTGCTGCTCCCAAGAACCCAAG-3′). Measures to ensure representative HIV-1 env clones were performed (14). High-fidelity rTth DNA polymerase was used to limit sequence variation due to misincorporation errors. Limiting dilution reaction conditions designed to minimize the likelihood of recombination between molecules during PCR amplification were used (6). Cloned env fragments were sequenced using an automated DNA sequencer (Applied Biosystems).

Phylogenetic analysis.

To account for the interhost variability and uncertainty in describing viral evolution among multiple hosts, we used a Bayesian hierarchical phylogenetic model (29). The general idea behind Bayesian analysis is to combine what is known about the data and parameters a priori (called the prior) to obtain updated (posterior) probability assessments of the hypotheses. In this way, what is known scientifically or what is believed by experts can be incorporated into the overall analysis. The main objective of the Bayesian approach is to estimate the posterior distribution of the unknown model parameters given the observed phylogenetic data, where the posterior distribution also includes prior knowledge about the parameters and the data. This is accomplished using Bayes theorem. Given a statistical model with parameters θ and data Y, Bayes theorem states that the posterior distribution of θ is proportional to the sampling density of the data given θ (commonly referred to as the model likelihood) multiplied by the prior distribution of θ:

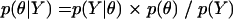where the prior distribution (the prior) on θ incorporates any knowledge that we may have about θ before observing the data and the denominator p(Y) is a normalizing factor that ensures that the posterior density integrates to 1. Bayes theorem thus specifies how beliefs about θ change from before to after an experiment is performed. Various competing models or hypotheses may be described by restricting one or more parameters in θ to specific ranges of values and then compared using Bayesian model selection (10, 19, 20, 31, 35).

Bayesian approaches are advantageous in phylogenetics because the primary analysis provides an estimate of the tree and measurements of uncertainty often faster than estimates that can be obtained by using maximum likelihood bootstrapping techniques (14, 15, 31). Bayesian analysis can also provide estimates of complex models where maximum likelihood methods would be intractable or too computationally burdensome. Finally, Bayesian model selection offers advantages over likelihood methods in that the competing evolutionary hypotheses need not be nested and the Bayesian approach does not rely on standard likelihood asymptotics (32, 35).

The Bayesian hierarchical phylogenetic model allows information from all patients to be used simultaneously to improve estimate precision in individual patients. The general idea behind hierarchical modeling is to think of the smallest (lowest-level) unit as being organized into a hierarchy of successively higher units. In this case the within-patient distributions are the smallest unit and the between-patient distributions are the top level. Effects at the lower level can be thought of as one of an exchangeable collection of effects that is drawn from a common distribution at the higher levels. When data are sparse, pooling information via a hierarchical model smoothes the parameter estimates of the evolutionary model, providing more precise estimates than analyses that treat each patient as an isolated entity. The hierarchical framework also permits the estimation and testing of patterns across patients while allowing the uncertainty in each individual's evolutionary parameters to vary. This is accomplished by constructing hierarchical priors on the parameters within a patient. The model thus combines the results from the individual patients to provide population-level summaries. The population-level model and the patient-level models are fit simultaneously, enabling the population-level model to feed back information, in the form of a prior, to help in the estimation of the individual patient parameters. In regression terms, the population-level parameters can be thought of as fixed effects and the patient-level parameters can be thought of as random effects that describe how individual patient parameters may vary from the population-parameter means.

To reconstruct an evolutionary tree at the patient level, we employed a continuous-time Markov chain model for nucleotide substitution that assumes that the substitution mechanism is independent across branches in the patient-specific tree and is a memory-less process. The probability of nucleotide X mutating to Z, where X, Z = {A, C, T, or G}, along a branch with length t equals exp (tΛ)_X,Z, where Λ is a 4 × 4 infinitesimal rate matrix similar to that of Tamura and Nei (33). Matrix Λ is constrained so that the branch lengths are expressed in terms of the expected number of nucleotide substitutions per site (37). Since branch lengths may not retain definition between trees, we modeled branch lengths t_is within patient i as Exponential(μ_i), where s = 1,…,5. The prior expected divergence, μ_i, is interpretable across trees, and thus we can share branch length information across patients. Site-to-site rate variation follows a discrete gamma distribution with 4 bins and shape parameter α_i (36). Let θ_i = (τ_i, t_is, α_i, κ_1i, κ_2i, μ_i, π_i) for patient i, where τ_i is the unknown tree relating all of the sequences from patient i, κ_1i is the transition/transversion rate ratio for transitions between the purines, κ_2i is the transition/transversion rate ratio for transitions between the pyrimidines, and π_i are the stationary nucleotide frequencies. We extend over i = 1,…,N multiple patients simultaneously by assuming the following hierarchical priors:

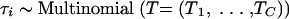where C is the number of possible trees to be examined and Σ = diag(σ²_α, σ²_k1, σ²_k2, σ²_μ). The priors state that the log of the rate variation parameter α_i, the average divergence μ_i, and the transition/transversion rate parameters κ_1i and κ_2i are multivariate-normally distributed across patients with estimable population-level mean vector M and variance-covariance matrix Σ. The nucleotide frequencies, π_i, came from a common distribution with an estimable mean Π and precision N_Π, where a Dirichlet is the natural parameterization for proportions. The trees, τ_j, drawn with estimable population-level probabilities T, where T = (T₁,…,T_C), are the population-level probabilities for each of the C = 3 (in this case) possible trees. For hyperpriors on the population-level parameters, we took T ∼ Dirichlet (N_Q × Q) where Q is the prior probabilities of the C different trees and N_Q is the weight given to the prior probabilities Q; here we take N_Q = 1. We took vague priors over (M, Σ, N_Π, Π). For example, M was a diffuse normal and Π was a flat Dirichlet. We incorporate half-Cauchy priors on σ²_α, σ²_k1, σ²_k2, and σ²_μ, as the half-Cauchy has been recently shown to have more desirable properties than the inverse gamma as an uninformative prior when the number of groups is small (9).

Each model was run for 300,000 iterations. After discarding the first 50,000 iterations as burn-in, we subsampled every 25th iteration to yield 10,000 posterior samples with decreased autocorrelation. The largest model ran in 3 h and 48 min on a 1-GHz Pentium III PC. The burn-in times and total Markov chain Monte Carlo (MCMC) chain lengths were significantly longer than what appeared to be required from examining model log-likelihood time-series plots (3). The Bayesian hierarchical phylogenetic model is available for download at http://www.biomath.ucla.edu/msuchard.

Nucleotide sequence accession number.

The sequences of the cloned env fragments have been deposited in GenBank under accession numbers AY322081 through AY322106.

RESULTS

We identified three patients with HIV-1 populations that exhibited a change in coreceptor usage during antiretroviral therapy. No patient achieved complete virologic suppression. After initiation of a new potent antiviral regimen, plasma strains of HIV-1 predominantly used CCR5 (Table 1). An average of 25 (range, 22 to 27) biologic clones of HIV-1 was obtained at each time point, with the coreceptor usage of each clone determined by a functional, phenotypic assay. For each patient time point, R5 and X4 clones were chosen at random and then sequenced. To ensure that our conclusions were not influenced by sampling bias, a second random set of samples from each patient time point was also sequenced. The V1-C5 portion of the env gene of each biological clone was analyzed by aligning serial HIV-1 sequences from each patient. Each alignment contained four sequences: an R5 viral clone obtained prior to the initiation of new therapy, called the predecessor R5 (R5-p); an emergent X4 clone; a second R5 clone obtained following suppression of X4 strains by antiretroviral therapy, called R5-r; and an outgroup. Two outgroup sequences, the X4 strain HXB2 and the R5 strain JR-CSF, were obtained from the Los Alamos HIV Database (http://www.hiv.lanl.gov/).

R5 strains that persist after antiretroviral therapy (R5-r) may have evolved either from earlier R5 strains (R5-p) or from circulating X4 virus. Three possible phylogenetic trees can be constructed from a data set containing four sequences: R5-p, R5-r, X4, and an outgroup sequence (Fig. 1). When R5-r is most closely related to X4 in a phylogenetic tree (Fig. 1, tree X), the hypothesis that R5-r evolved from X4 virus is favored. If R5-r and R5-p are neighbors (Fig. 1, tree R), there is evidence supporting evolution of reemergent R5 virus from earlier R5 strains. The final tree has R5-r and an outgroup as neighbors (Fig. 1, tree O) and is unlikely a priori. The Bayesian hierarchical model was fitted such that the prior probabilities of trees R and X were equal and were 10 times more likely than tree O. This is equivalent to setting the prior for each tree to Q = (Q_R, Q_X, Q_O) = (0.45, 0.45, 0.10).

FIG. 1.

Possible phylogenetic topologies relating three longitudinal sequences. The first sequence is taken at the initial time point, when R5 strains dominate the viral quasispecies (R5-p); the second sequence is taken at an intermediate time point when X4 strains are circulating (X4); and the third sequence is collected at the final time point, following initiation of potent new therapy and a concomitant suppression of X4 strains, resulting in a shift back to predominantly R5 strains (R5-r). The fourth sequence is an outgroup (O).

Using the published sequence of HIV-1 strain HXB2 as an outgroup (34), we found that the model favoring evolution from the predecessor R5 strains had greater than 99% support for two patients and 85% support in patient 9. Figure 2 shows the phylogenetic trees constructed for each patient. The individual-level estimates of the posterior probabilities for each possible tree (X, R, and O) are shown in Table 2. Estimates of the transition/transversion rate ratios κ_1i and κ_2i, expected divergences μ_i, gamma shape parameter α_i, and stationary distributions π_i are also given in Table 2. The table illustrates the variability between corresponding parameters. Expected divergences demonstrated considerable variability between patients, with patient 9 demonstrating the highest rate of evolution and patient 17 demonstrating the lowest. The posterior probabilities provided estimates of the likelihood that each tree is correct, given the data and the outgroup chosen.

FIG. 2.

Most probable phylogenetic tree for each patient, with use of HXB2 as the outgroup. Branch lengths are drawn to scale across patients and represent posterior mean estimates.

TABLE 2.

Hierarchical individual-level estimates for each patient, with HXB2 used as the outgroup^a

i	τi (tree)			κ1i	κ2i	αi	μi × 100	πi
	R	X	O					A	G	C	T
9	0.85	0.14	<0.01	3.1 (0.45)	2.4 (0.45)	0.40 (0.14)	5.5 (2.2)	0.39	0.21	0.16	0.24
28	>0.99	<0.01	<0.01	3.4 (0.49)	2.8 (0.55)	0.44 (0.19)	5.2 (2.1)	0.38	0.22	0.17	0.24
17	>0.99	<0.01	<0.01	3.2 (0.53)	1.7 (0.42)	0.58 (1.20)	4.7 (1.9)	0.38	0.21	0.16	0.24

^aFor each patient i, the estimates of τ_i are posterior probabilities of each possible tree (R, X, and O); estimates of κ_1i, κ_2i, α_i, and μ_i are posterior means with the standard deviations shown in parentheses; and estimates of π_i are posterior means.

Our Bayesian model also allows us to estimate overall probabilities for the competing hypotheses across patients. Bayes factors, defined as the ratio of the probability of one model over another, were used to assess significance. The Bayes factor was written as

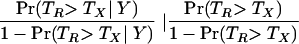where Τ_R and Τ_X are the population-level probabilities of trees R and X, respectively. As such, the Bayes factor can be thought of as a measure of the support for one model over another given the data. Table 3 lists the hierarchical population-level estimate of the overall probability for each possible tree. The Bayes factor in favor of tree R versus tree X was 14.7, roughly equivalent to a P value of ≤0.03 (12).

TABLE 3.

Hierarchical population-level estimate for the probability of each tree for all patients given the outgroup^a

Variable	Estimate with outgroup:
	HXB2	HXB2 without V3
TR	0.93 (0.25)	0.95 (0.21)
TX	0.06 (0.24)	0.04 (0.21)
TO	0.01 (0.08)	0.01 (0.08)
K1	1.15 (0.25)	1.16 (0.25)
K2	0.79 (0.33)	0.78 (0.32)
M	−3.01 (0.39)	−3.05 (0.40)
A	−0.87 (0.42)	−0.88 (0.48)
σκ1	0.33 (0.22)	0.33 (0.21)
σκ2	0.45 (0.27)	0.43 (0.26)
σμ	0.42 (0.26)	0.43 (0.27)
σα	0.44 (0.28)	0.50 (0.34)
Nπ	33.23 (17.14)	32.80 (17.35)
IIA	0.37 (0.05)	0.36 (0.05)
IIG	0.22 (0.04)	0.22 (0.05)
IIC	0.17 (0.04)	0.17 (0.04)
IIT	0.24 (0.05)	0.25 (0.05)
Bayes factor	14.65	20.69

^aThe estimates are posterior means with standard deviations shown in parentheses.

Although the samples chosen for analysis were selected on the basis of phenotype, we may have inadvertently enriched for a specific genotype as well. Phenotype attraction may occur if the sequences under analysis encode specific phenotypic traits that also serve as the basis for selecting samples for study. To exclude the possibility of phenotype attraction to the outgroup, we deleted the V3 loop portion of the HIV-1 sequences derived from the three study patients and outgroup HXB2, realigned the sequences, and repeated our analysis. The posterior probability of the predecessor tree (tree R) constructed by using the V3-deletion sequences was ≥0.95 in all patients. Table 4 lists the estimated probability for each model tree. The Bayes factor was 20.69 in favor of continued evolution of reemergent R5 virus from earlier R5 strains, P ≤ 0.03. Similar results were obtained when JR-CSF, an R5 virus, was used as the outgroup (data not shown).

TABLE 4.

Hierarchical individual-level estimates for each patient, with HXB2 without V3 used as the outgroup^a

i	τi (tree)			κ1i	κ2i	αi	μi × 100	πi
	R	X	O					A	G	C	T
9	0.95	0.04	<0.01	3.3 (0.50)	2.4 (0.47)	0.38 (0.14)	5.4 (2.2)	0.38	0.21	0.16	0.24
28	>0.99	<0.01	<0.01	3.5 (0.54)	2.6 (0.53)	0.40 (0.19)	5.1 (2.0)	0.37	0.22	0.17	0.24
17	>0.99	<0.01	<0.01	3.1 (0.53)	1.8 (0.44)	0.68 (0.76)	4.5 (1.9)	0.38	0.21	0.16	0.25

^aThe V3 loop was deleted from all sequences. For each patient i, the estimates of τ_i are posterior probabilities of each possible tree (R, X, and O); estimates of κ_1i, κ_2i, and μ_i are posterior means with the standard deviations shown in parentheses; and estimates of π_i are posterior means.

To compare the results obtained by using our hierarchical Bayesian model with those obtained by using more traditional phylogenetic methods, we reexamined the data using two additional methods: independent analysis of each set of patient sequences and concatenation. Independent analysis treated each patient's sequences as a separate data set. Thus, for each patient, individual evolutionary parameters were estimated and a separate tree was calculated. For all three patients, independent phylogenetic analyses supported the hypothesis that the reemergent R5 virus evolved from predecessor R5 strains. There was greater than 99% support for this model for patients 17 and 28 and 44% support for patient 9 (Table 5). In this framework it is not possible to “average” across trees. Although each patient data set independently supported tree R, we cannot make assertions of the overall probability of our hypothesis or draw conclusions. The parameter estimates from these independent analyses also had wider confidence intervals than the estimates given using our hierarchical model (Tables 4 and 5).

TABLE 5.

Analysis of the data with each patient treated independently and with sequence data for each time point concatenated so that a single evolutionary tree is created^a

Analysis type	τi (tree)			κ1i	κ2i	αi	μi × 100	πi
	R	X	O					A	G	C	T
Patient treated independently (i)
9	0.44	0.40	0.16	3.1 (0.51)	2.5 (0.51)	0.37 (0.16)	7.0 (4.2)	0.39	0.21	0.16	0.24
28	>0.99	<0.01	<0.01	3.5 (0.58)	3.1 (0.62)	0.49 (0.40)	6.2 (3.7)	0.38	0.22	0.17	0.24
17	>0.99	<0.01	<0.01	2.9 (0.58)	1.4 (0.39)	55.6 (415.5)	4.6 (2.8)	0.38	0.21	0.16	0.24
Sequence data concatenated
	>0.99	<0.01	<0.01	3.2 (0.32)	2.3 (0.30)	0.33 (0.08)	6.0 (3.4)	0.38	0.21	0.16	0.24

^aFor each patient i, τ_i is the estimated posterior probability for each possible tree. Estimates for κ_1i, κ_2i, α_i, and μ_i are posterior means with standard deviations in parentheses and estimates of π_i are posterior means.

We also reanalyzed the data by concatenating the sequences obtained from each patient. In this analysis, patient sequences for each time point were concatenated such that there were four total sequences, each three times as long as that in the independent analysis. That is, patient sequences were concatenated linearly by category, in this case R5-p, X4, R5-r, so that all patients could be analyzed simultaneously by one phylogenetic tree. Using this approach, we obtained greater than 99% support for the hypothesis that the reemergent R5 virus evolved from earlier R5 strains (Table 5). Although this approach allows us to calculate population-level estimates for each possible tree, concatenated analysis also forces each patient to have the same evolutionary parameters; individual parameters for each patient could not be determined.

We compared model fit using the deviance information criterion (DIC), which is analogous to the Akaike information criterion (28). The DIC utilizes a measure of model fit, D, and a measure of model complexity, pD. Minimizing D + pD yields the most parsimonious model with the best fit; thus, the model with the smallest value for DIC is the model with the best fit. D equals −2 times the mean posterior log likelihood, and pD equals D − D̂, where D̂ is −2 times the log likelihood at the posterior mean. For the trees, we took the mean branch lengths of the mode topology. We used this criterion to compare the hierarchical model to the concatenated model. For the hierarchical model, D was equal to 16,925 and pD was equal to 26, yielding 16,951 for the DIC estimate. The value for D for the concatenated model was equal to 16,970, and the value for pD was 10; thus, the DIC estimate was 16,980 for the concatenated model. From the DIC estimates, we found that the hierarchical model had a better fit than the concatenated model.

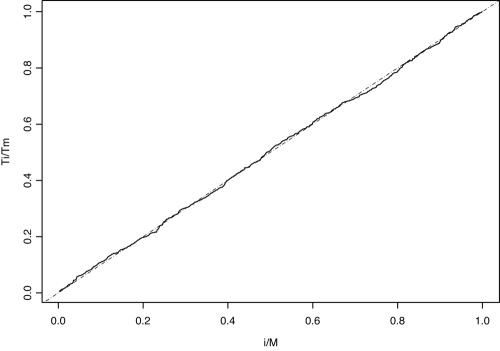
To assess the performance of our sampler's mixing in estimating the posterior probability of a particular tree, we used scaled regeneration quantile (SRQ) plots (21, 30). Regeneration times are defined as the time that it takes the Markov chain to return to a specific topology. Tours of the chain between these times do not have to be completely independent and identically distributed to assess the performance of our sampler (21). The slope between two scaled regeneration times in an SRQ plot is the ratio of the posterior probability estimate based on the entire chain to the estimate based on the chain between these tours. Substantial deviations from a slope of 1 indicate that the chain is not long enough. Figure 3 shows a representative SRQ plot from the MCMC chains. We superimposed a dashed line with slope equal to 1 and found that there is no large deviation. This suggests that our chains were mixing well and were sufficiently long enough to produce stable posterior estimates. We make our complete datasets available to interested readers at http://www.bol.ucla.edu/∼cr/Datasets.htm.

FIG. 3.

SRQ plot to assess model performance in estimating the posterior probability of tree X under the hierarchical model. The absence of a substantial deviation from a slope of 1 (dashed line) implies that the chain is long enough to produce stable estimates.

DISCUSSION

In this paper, we describe a novel Bayesian hierarchical model that we developed and then used to examine viral evolution in populations of HIV-1-infected individuals. Unlike more traditional methods, this model permits us to infer evolutionary relationships across multiple patients simultaneously while allowing the phylogenetic parameters of each patient to vary. We used this method to examine an issue of considerable importance to the design of new antiviral therapies: evolutionary changes in HIV-1 coreceptor usage in response to treatment.

We focused on patients whose viral populations in the blood displayed a shift in HIV-1 coreceptor utilization in response to therapy. In each case, although X4 strains emerged, the viral population later reverted to R5 following initiation of new therapeutic regimens. By phylogenetically reconstructing the evolutionary relationship of HIV-1 obtained longitudinally from each patient, it was possible to examine the origin of the reemergent R5 virus.

By using our hierarchical approach, we found evidence that the R5 virus reemerging after antiretroviral therapy evolved from predecessor R5 strains rather than from X4 virus. All analyses supported this model, regardless of the outgroup chosen. Our method also allowed us to detect evolutionary patterns that could have been missed by more traditional phylogenetic techniques. Analyzing each set of patient sequences independently allowed each individual to have his or her own evolutionary parameters but did not take into account what was known about the other patients. Because of not allowing pooling of information across patients, estimates of each patient's evolutionary parameters had a wider confidence interval than did estimates obtained from the hierarchical model. Furthermore, while the independent method allows probability calculations for each individual phylogenetic tree, population-level estimates of support for competing evolutionary models cannot be determined. Analysis of concatenated sequences, on the other hand, allows patients to be examined simultaneously but also forces all patients to have the same evolutionary parameters, an assumption that may not be justified.

The Bayesian hierarchical model represents an alternative to analyzing sequences obtained from each patient separately or concatenating all of the sequences together. The superiority of this model is illustrated in its ability to simultaneously estimate patient parameters while allowing for individual variation in the evolutionary parameters. The sharing of information across patients allows for narrower errors in parameter estimates compared with other methods. However, this comes at the cost of bias due to shrinkage effects. Finally, this method can calculate the overall probability of competing hypotheses across patients. This aspect of the model can become especially important in studies where there may be considerable variation in the support for each tree across patients.

Our analyses were based upon RNA sequences of biologically cloned HIV-1. Although culture of HIV-1 can result in selection of minor variants, it is unlikely that the brief series of in vitro passages performed here significantly affected the coreceptor utilization of these biological clones. Even following repeated passage of HXB2 and JR-CSF isolates in our laboratory; for example, no change has ever been observed in the coreceptor utilization of these viral stocks (data not shown). It is important that, although our phylogenetic reconstructions were performed using env sequences, the coreceptor phenotype for each viral isolate was determined independently. Sequence selection was initially based on biological phenotype, eliminating any bias that may have arisen from genotypically predicting coreceptor utilization and then using the same sequences to estimate evolutionary relationships. To ensure that our results were not based on a sampling artifact, we sequenced another random sample of clones at each time point and reran the analysis. Support for tree R was again supported with similar probability (data not shown).

Our results support the hypothesis of reemergence of predecessor strains following a major change in therapy. These results, however, were obtained from study of a limited number of patients. None of the individuals studied here achieved complete viral suppression even while receiving HAART (4, 13, 25). It is possible that the evolutionary pattern of the reemergent virus may be different in patients who have sustained viral suppression. Understanding viral evolution under the selective pressure of antiretroviral therapy is an important step in understanding viral dynamics, drug resistance, and the durability of clinical response to treatment. Additional studies of viral evolution in well-characterized patients are needed.

Finally, this paper illustrates the usefulness of our Bayesian hierarchical model. This model is not limited to phylogenetic analysis of HIV evolution. Rather, this model is generalizable to situations where it is necessary or desirable to pool sequence information across multiple patients to improve estimate precision of individual patient parameters while simultaneously estimating shared patterns across patients.