Abstract
Background and Aims Plants depend on photosynthesis for growth. In nature, factors such as temperature, humidity, CO2 partial pressure, and spectrum and intensity of irradiance often fluctuate. Whereas irradiance intensity is most influential and has been studied in detail, understanding of interactions with other factors is lacking.
Methods We tested how photosynthetic induction after dark–light transitions was affected by CO2 partial pressure (20, 40, 80 Pa), leaf temperatures (15·5, 22·8, 30·5 °C), leaf-to-air vapour pressure deficits (VPDleaf-air; 0·5, 0·8, 1·6, 2·3 kPa) and blue irradiance (0–20 %) in tomato leaves (Solanum lycopersicum).
Key Results Rates of photosynthetic induction strongly increased with CO2 partial pressure, due to increased apparent Rubisco activation rates and reduced diffusional limitations. High leaf temperature produced slightly higher induction rates, and increased intrinsic water use efficiency and diffusional limitation. High VPDleaf-air slowed down induction rates and apparent Rubisco activation and (at 2·3 kPa) induced damped stomatal oscillations. Blue irradiance had no effect. Slower apparent Rubisco activation in elevated VPDleaf-air may be explained by low leaf internal CO2 partial pressure at the beginning of induction.
Conclusions The environmental factors CO2 partial pressure, temperature and VPDleaf-air had significant impacts on rates of photosynthetic induction, as well as on underlying diffusional, carboxylation and electron transport processes. Furthermore, maximizing Rubisco activation rates would increase photosynthesis by at most 6–8 % in ambient CO2 partial pressure (across temperatures and humidities), while maximizing rates of stomatal opening would increase photosynthesis by at most 1–3 %.
Keywords: Dynamic photosynthesis, CO2 concentration, temperature, humidity, stomatal conductance, diffusional limitation, Rubisco, tomato, Solanum lycopersicum
INTRODUCTION
When a dark-adapted leaf is illuminated, photosynthesis (A) starts, and increases over a period of time to a stable steady-state rate. This process, photosynthetic induction, was discovered almost a century ago (Osterhout and Haas, 1918), and its underlying mechanisms have been studied extensively (Pearcy and Way, 2012; Kaiser et al., 2016). The main mechanisms that affect photosynthetic induction, and A in fluctuating irradiance, are activation of Calvin cycle enzymes and stomatal opening (Pearcy et al., 1996). Additionally, the history of irradiance intensity, plant functional type and environmental conditions modulate the amplitude and kinetics of photosynthetic induction. While previous studies (reviewed in Kaiser et al., 2015) have shown that environmental factors such as leaf external CO2 partial pressure (Ca), leaf temperature (Tleaf), leaf-to-air vapour pressure deficit (VPDleaf-air) and blue irradiance can modulate the responses of A to variable irradiance, no study has systematically compared the effects of all of these factors on the photosynthetic response to dark–light transitions.
Due to the wind-induced movement of leaves, canopies and clouds, irradiance incident on a leaf can fluctuate, often resulting in time-dependent changes in A and reductions in irradiance use efficiency compared to the theoretical situation of instantaneous changes in assimilation. Currently, there is renewed interest in the dynamic components of photosynthesis, as (1) faster activation of Rubisco could increase resource use efficiency and productivity (Carmo-Silva et al., 2015), (2) stomata that react faster to changes in irradiance could increase intrinsic water use efficiency (WUEi; Lawson and Blatt, 2014), (3) faster relaxation of non-photochemical quenching (NPQ) could increase photosynthetic quantum yield in limiting irradiance (Murchie and Niyogi, 2011) and (4) predictions of assimilation that account for dynamics could lead to more accurate forecasts of plant productivity (Kaiser et al., 2015). To address these questions, the behaviour of dynamic photosynthesis in C3 crops must be thoroughly understood. However, most effort has been directed towards understorey shrubs and trees, and only a few studies have investigated dynamic photosynthesis and its environmental modulation in C3 species with high photosynthetic capacity (Yamori et al., 2012; Carmo-Silva and Salvucci, 2013; Soleh et al., 2016). Such experiments are necessary to quantify limitations to dynamic photosynthesis and to assess how each limiting factor is affected by environmental conditions.
The enzymes that regenerate ribulose-1,5-bisphosphate (RuBP) are activated rapidly during photosynthetic induction (Sassenrath-Cole and Pearcy, 1992). Consequently, RuBP supply to Rubisco is considered to be non-limiting after the first minute of induction (Woodrow and Mott, 1989; Pearcy et al., 1996). Rubisco itself typically takes 7–10 min to fully activate in vivo (Pearcy et al., 1996), and the extent of its limitation during photosynthetic induction and the apparent time constant of its activation (τR) can be calculated from gas exchange data (Woodrow and Mott 1989). A low stomatal conductance (gs) can impose an additional diffusional limitation on induction. By estimating the assimilation rate that would occur if CO2 partial pressure in the chloroplast (Cc) were identical to Ca (i.e. leaf conductance being infinite), the diffusional limitation acting on transient and steady-state A can be quantified. This diffusional limitation normally includes a component in the mesophyll, which is quantified as mesophyll conductance (gm). Mesophyll conductance may vary with irradiance, Ca and temperature (Flexas et al., 2007, 2008; von Caemmerer and Evans, 2015). However, to our knowledge, no study has examined possible changes of gm during induction and their implications on diffusional limitation.
During photosynthetic induction, electron and proton transport processes undergo rapid changes, affecting the efficiency of electron transport through photosystem II (ΦPSII) and NPQ. As in the case of steady-state A, linear electron transport rate (ETR) correlates linearly with gross photosynthesis (Agr) during induction (Košvancová-Zitova et al., 2009; Yamori et al., 2012), and changes in the slope of this relationship can be used to infer changes in photorespiration. NPQ often overshoots at the start of induction (e.g. Johnson et al., 1994), which is probably due to the decrease of lumen pH that develops when ETR is limited by low photosynthetic metabolic activity. Hence, measuring ΦPSII and NPQ concurrent with gas exchange can provide detailed information on processes affecting photosynthetic induction.
Dynamic A and its modulation by environmental factors must be better understood in order to improve it. Tomato (Solanum lycopersicum), a C3 model species with intermediate leaf photosynthetic capacity and an important crop in open field and protected cultivation, was used in this study. During photosynthetic induction after a dark–light transition, it was shown how transient diffusional and biochemical limitations, stomatal and mesophyll conductance, apparent Rubisco activation, WUEi and electron transport processes are affected by Ca, Tleaf, VPDleaf-air and blue irradiance. The benefits and costs of faster Rubisco activation or stomatal opening on dynamic photosynthesis are discussed.
MATERIALS AND METHODS
Plant material
Tomato seeds (Solanum lycopersicum ‘Cappricia’; Rijk Zwaan, De Lier, the Netherlands) were germinated in Rockwool plugs (Grodan, Roermond, the Netherlands), which after 1 week were transferred to Rockwool cubes (10 cm × 10 cm × 7 cm; Grodan). Plants were grown in a climate chamber with 16/8-h photoperiod, 22/20 °C (day/night) temperature, 70 % relative humidity and 320 µmol m−2 s−1 photosynthetically active radiation (PAR), measured at table height. Irradiance was provided by a mixture of white, red and far-red LEDs with emission peaks at 440, 550, 660 and 735 nm. Rockwool cubes were standing in a layer (height: 1–2 cm) of nutrient solution (Yara Benelux B.V., Vlaardingen, the Netherlands), which was replenished every 1–2 d and contained 12·4 mm , 7·2 mm K+, 4·1 mm Ca2+, 3·3 mm , 1·8 mm Mg2+, 1·2 mm , 1·1 mm , 30 μm , 25 μm Fe3+, 10 μm Mn2+, 5 μm Zn2+, 0·75 μm Cu2+ and 0·5 μm (EC 2·1 dS m−1, pH 5·5). When plants were between 5 and 6 weeks old, leaves 4 and 5, counting from the bottom, were used for measurements. At this stage, growth of these leaves was almost complete (data not shown).
Gas exchange and chlorophyll fluorescence measurements
All measurements were performed using the LI-6400 photosynthesis system (Li-Cor Biosciences, Lincoln, NB, USA) equipped with the leaf chamber fluorometer (Li-Cor Part No. 6400-40, area 2 cm2).
Photosynthetic induction.
To assess the response of gas exchange to a step increase in irradiance, leaves were first dark-adapted at the treatment levels described below until gs was constant (60–120 min). Then, irradiance was increased to 1000 µmol m−2 s−1 in a stepwise change and gas exchange values were logged every second for 60 min. Although such a dark–light transition does not resemble a natural situation, we chose these extreme irradiance levels in an attempt to maximize the effect of the treatment levels (see below) on photosynthetic induction. An irradiance of 1000 µmol m−2 s−1 was ∼5 % below saturation, which was a compromise between using a fully saturating irradiance (determined in pilot experiments, see Supplementary Data File S1) and the desire to avoid photoinhibition of photosynthesis. The flow rate of air was 500 µmol s−1. Other than when adjusted as part of a treatment, the standard conditions in the cuvette were: 39·7–40·3 Pa Ca (range of lowest to highest value), 0·7–1·0 kPa VPDleaf-air, 22·3–23·3 °C Tleaf and 90:10 % red/blue irradiance mixture provided by LEDs. The values of all cuvette conditions reported here are averages over whole induction curves. Peak intensities of red and blue LEDs were at wavelengths of 635 and 465 nm, respectively. Treatments were applied individually and included: 20, 40 and 80 Pa Ca, 15·5, 22·8 and 30·5 °C Tleaf, 0·5, 0·8, 1·6 and 2·3 kPa VPDleaf-air (0·4, 0·9, 1·7 and 2·5 VPDair) and 0, 1, 5, 10 and 20 % blue irradiance in a red irradiance background. For each treatment, five biological replicates were used (n = 5). All measurements were performed in a lab except the 15·5 and 30·5 °C Tleaf treatments, which were performed in climate chambers. Despite efforts to keep VPDleaf-air similar between Tleaf treatments, it was, on average, 0·97 kPa at 15·5 °C, 0·80 kPa at 22·8 °C and 0·84 at 30·5 °C (Supplementary Data File S2). Transient An, gs and Ci were averaged over five data points using a moving average filter to reduce measurement noise. Assimilation was corrected for CO2 leaks using dried leaves (Long and Bernacchi, 2003).
To analyse the effect of Ca and Tleaf on photosynthetic electron transport processes, another set of induction curves was performed on different leaves, with the same cuvette conditions as described above. ETR was estimated from measurements of ΦPSII, which was calculated from measurements of Fs (fluorescence yield under continuous actinic irradiance) and Fm′ (maximum fluorescence yield during a saturating irradiance pulse). The measurements of Fm′ were also used to calculate NPQ according to the Stern–Volmer quenching model (i.e. as 1 − Fm/Fm′) and using Fm from dark-adapted leaves. Measurements of Fm′ were made once a minute during the first 10 min of induction, and once every 2 min thereafter. To ensure the accurate measurement of Fm′, the multi-phase flash (MPF) protocol of the Li-Cor fluorometer was used (Loriaux et al., 2013). Using MPFs instead of single saturating pulses prevents underestimation of maximum chlorophyll fluorescence yield in light-adapted leaves of high photosynthetic capacity. Fm′ estimated by the MPF was ∼4 % larger than measured Fm′ (Supplementary Data File S3). Settings of the MPF were determined in preliminary measurements. These were 8500 and 1–2 µmol m−2 s−1 flash and measuring beam intensity, respectively; 60 % decrease of flash intensity during the 2nd phase of the MPF; and 0·3, 0·7 and 0·4 s duration of the three flash phases. These settings yielded high correlations (R2 ≈ 0·99) between flash intensity and Fm′ during flash phase 2 after the first or second minute of induction (data not shown). Preliminary data indicated limited effects of VPDleaf-air on ΦPSII or NPQ (data not shown); therefore, those measurements were not repeated here.
A/Ci curves.
To estimate the parameters VCmax, ETRmax, TPU and Γ*, A/Ci curves were first performed in photorespiratory and then in non-photorespiratory conditions (21 and 2 kPa oxygen, respectively; Supplementary Data File S4). Leaves were first adapted to 50 Pa CO2 and 21 kPa O2 for ∼30 min, then CO2 partial pressure was reduced in a stepwise manner until 5 Pa, each step taking ∼4 min. Then, CO2 was again raised to 50 Pa for ∼15 min, after which it was increased to 150 Pa in several steps, each step taking ∼5 min. Then, O2 partial pressure was reduced to 2 kPa, and the procedure was repeated. Altogether, A was logged at 11 CO2 partial pressures per O2 partial pressure, and each complete A/Ci curve took ∼2·5 h. Data were logged every 5 s, and averages of 10 values at each Ca step, after steady-state A had visibly been reached, were used. Other cuvette conditions were: 1000 µmol m−2 s−1 PAR, 0·8 kPa VPDleaf-air and 23 °C Tleaf.
A/PAR curves.
To estimate parameters Rd and s (lumped parameter used to scale the product of irradiance and ΦPSII onto ETR), irradiance-limited curves were performed in 2 % oxygen [File S4]. The intercept of the linear A/(PAR × ΦPSII × 0·25) relationship was Rd, while the slope was s (Yin et al., 2009). Leaves were adapted to 200 µmol m−2 s−1, until A and gs were stable. Then, leaves were exposed to a range of PAR values between 0 and 200 µmol m−2 s−1. Assimilation was determined as described for the A/Ci curves. ΦPSII was determined as described above. Other cuvette conditions were: 40 Pa Ca, 0·8 kPa VPDleaf-air and 22 °C Tleaf.
Calculations
All calculations described here were performed on single replicates, and then used for further (statistical) analysis. Photosynthetic induction was calculated after Chazdon and Pearcy (1986): transient A (µmol m−2 s−1) was expressed as a percentage of the final rate (Af), corrected for the initial, dark-adapted rate (Ai)
| (1) |
The relative rate of increase of gs (mol m−2 s−1) during induction was calculated similarly. For the calculation of several parameters, gas exchange data were corrected for transient changes in Ci or Cc (using gm as in Table 1 in Supplementary Data File S5) during induction. For diffusional limitation (LD; %), A was multiplied by the percentage by which A would increase if CO2 partial pressure in the chloroplast (Cc, Pa) during induction was equal to leaf external partial pressure, Ca (). For biochemical limitation (LB; %) and the apparent rate constant of Rubisco activation (τR; min), A was multiplied by the percentage by which A would increase if transient Ci was similar to final, steady-state Ci ), following Woodrow and Mott (1989). However, unlike Woodrow and Mott (1989), for calculations of and no linear relationship between Ci and the CO2 compensation point , Pa) was assumed. Instead, information from complete A/Ci curves was used to correct A using the steady-state, curvilinear response of A to Ci. In the case of , A was corrected for the minimum of either Rubisco activity-limited A (Ac), RuBP-limited A (Aj) or triose phosphate utilization-limited A (At) at Ca (in the numerator) and at Cc (in the denominator):
| (2) |
Ac, Aj and At were calculated after the FvCB model (Farquhar et al., 1980) modified to account for TPU limitation (Sharkey 1985). In eqns (3)–(5), the calculations for A at Ca are shown. For calculating A at Cc, Ci or Cif, Ca was replaced by any of these variables (not shown here):
| (3) |
| (4) |
| (5) |
where VCmax (µmol m−2 s−1) is maximum velocity of Rubisco for carboxylation, Rd is day respiration (µmol m−2 s−1), O (kPa) is the chloroplast O2 partial pressure, Kc (Pa) and Ko (kPa) are the Michaelis-Menten constants of Rubisco for CO2 and for O2, respectively, ETRmax (µmol m−2 s−1) is the maximum rate of electron transport in the absence of regulation and TPU (µmol m−2 s−1) is the triose phosphate utilization rate. Parameters VCmax, ETRmax and TPU were estimated using the Excel routine of Sharkey et al. (2007). The first five points of A/Ci curves at 21 kPa O2 partial pressure were used to estimate VCmax (initial slope), the next four points to estimate ETRmax and the uppermost two points to estimate TPU (n=3). Rd and Γ* were determined after Yin et al. (2009). Additionally, Rd was corrected for respiration under the gasket of the gas exchange cuvette (Pons and Welschen, 2002). Parameters Kc and Ko were taken from Sharkey et al. (2007). All parameters were temperature-adjusted (Bernacchi et al., 2001); their values are given in Table 1. We acknowledge that the use of a steady-state model to correct A during transients may be inaccurate (e.g. VCmax and Jmax change during induction; Soleh et al., 2016), and that further work should be dedicated to refining this method. LD was determined by analogy to stomatal limitation as in Urban et al. (2007):
| (6) |
Table 1.
Parameters used in the calculations of diffusional limitation, biochemical limitation and the apparent time constant of Rubisco (eqns 3–5)
| Parameter | Unit | Temperature (°C) |
||
|---|---|---|---|---|
| 15·5 | 22·8 | 30·5 | ||
| ETRmax | µmol m−2 s−1 | 94·33 | 148·16 | 232·97 |
| Kc | Pa | 9·29 | 21·36 | 49·25 |
| Ko | kPa | 12·04 | 15·37 | 19·63 |
| Rd | µmol m−2 s−1 | 0·77 | 1·23 | 2·00 |
| TPU | µmol m−2 s−1 | 5·98 | 10·32 | 17·84 |
| VCmax | µmol m−2 s−1 | 43·35 | 84·86 | 166·44 |
| Γ* | Pa | 3·62 | 5·34 | 7·88 |
Parameters ETRmax, TPU and VCmax were determined from A/Ci curves after Sharkey et al. (2007), Kc and Ko were taken from Sharkey et al. (2007), Rd and Γ* were determined from A/PAR and A/Ci curves after Yin et al. (2009). All parameters were temperature-adjusted after Bernacchi et al. (2001).
LB was calculated by using , i.e. final steady-state Ci (Cif) in the numerator and Ci in the denominator of eqn (2) instead of Ca and Cc, respectively. LB was calculated after Urban et al. (2007):
| (7) |
was calculated after Woodrow and Mott (1989):
| (8) |
For the Ca and VPDleaf-air treatments, data from minutes 2–5 during induction were used for Δtime [it has been determined by Woodrow and Mott (1989) that during this phase Rubisco activation is the main limiting factor], while in the case of varying Tleaf, data were taken from minutes 5–8 during induction, to account for a possible slower activation of RuBP regeneration in the beginning of induction due to low Tleaf. WUEi (μmol mmol−1) was calculated as:
| (9) |
ΦPSII and NPQ were calculated after Genty et al. (1989) and Bilger and Björkman (1991), respectively. The coefficient of photochemical quenching (qP) and PSII maximum efficiency (Fv′/Fm′) was calculated after Oxborough and Baker (1997). ETR was calculated after Yin et al. (2009):
| (10) |
where s is a unitless lumped calibration factor used to scale ΦPSII to ETR (Yin et al., 2009). The maximum change in A (in percent) that would occur if either Rubisco instantly became fully activated or gs immediately reached its final steady-state level (gsf, Table 2) directly after the onset of illumination was calculated as the average of LB and LD between minutes 2 and 60 during induction, respectively. LB and LD data from the first minute after the onset of illumination were left out, as the activation of RuBP regeneration is known to be the main limiting factor of photosynthetic induction during that phase (Pearcy et al., 1996). The changes in WUEi (in percent) were calculated as:
| (11) |
and
| (12) |
after which their averages during minutes 2–60 were determined. WUEi_instantRubisco and WUEi_instantgs are the changes in WUEi that would occur if Rubisco became immediately fully activated, or gs increased immediately to its final value. WUEif is final, steady-state WUEi.
Table 2.
Dynamic and steady-state parameters of photosynthetic induction in tomato leaves, as affected by Ca, Tleaf, VPDleaf-air and blue light
| Treatment | Dynamic parameters |
Mean at start and end of induction |
||||||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| IS60 | tA50 | tA90 | tgs50 | tgs90 | Ai | Af | gsi | gsf | ||||||||||
| 20 Pa | 25·7 ± 3·0 | 3·2 ± 0·6b | 18·5 ± 4·0b* | 19·8 ± 1·2 | 46·7 ± 1·4b | −1·1 ± 0·6 | 11·7 ± 1·3a | 0·22 ± 0·04 | 0·65 ± 0·05c | |||||||||
| 40 Pa | 21·6 ± 2·7 | 2·6 ± 0·2a | 10·8 ± 1·4ab* | 18·7 ± 3·1 | 38·2 ± 5·6a | −1·6 ± 0·3 | 22·2 ± 1·4b | 0·27 ± 0·06 | 0·56 ± 0·07b | |||||||||
| 80 Pa | 21·9 ± 4·4 | 2·2 ± 0·3a | 6·2 ± 0·3a* | 18·2 ± 2·2 | 39·9 ± 4·7a | −1·3 ± 0·6 | 27·1 ± 2·3c | 0·25 ± 0·06 | 0·46 ± 0·07a | |||||||||
| 15·5 °C | 15·8 ± 4·5a* | 2·7 ± 0·3b | 12·6 ± 1·4 | 24·4 ± 4·8 | 42·5 ± 1·4 | −1·1 ± 0·3b | 15·6 ± 2·2a | † | 0·17 ± 0·16a | 0·34 ± 0·14a | ||||||||
| 22·8 °C | 21·6 ± 2·7b* | 2·6 ± 0·2b | 10·8 ± 1·4 | 18·7 ± 3·1 | 38·2 ± 5·6 | −1·6 ± 0·3ab | 22·2 ± 1·4b | † | 0·27 ± 0·06b | 0·56 ± 0·07b | ||||||||
| 30·5 °C | 37·8 ± 7·8c* | 1·6 ± 0·4a | 13·4 ± 1·6 | 17·2 ± 1·9 | 34·5 ± 2·2 | −2·3 ± 0·5a | 21·3 ± 3·8b | † | 0·21 ± 0·03ab | 0·36 ± 0·10a | ||||||||
| 0·5 kPa | 22·3 ± 1·1 | 2·4 ± 0·8 | 10·7 ± 1·9A | 20·7 ± 0·8b | 45·3 ± 15·6c | −1·3 ± 0·1 | 21·5 ± 0·9 | 0·30 ± 0·01b | 0·57 ± 0·02b | |||||||||
| 0·8 kPa | 21·6 ± 3·9 | 2·6 ± 0·3 | 10·8 ± 2·6A | 18·7 ± 5·3b | 38·2 ± 13·8bc | −1·6 ± 0·8 | 22·2 ± 1·8 | 0·27 ± 0·04b | 0·56 ± 0·14b | |||||||||
| 1·6 kPa | 24·3 ± 2·7 | 2·8 ± 0·2 | 13·5 ± 1·4B | 11·7 ± 3·1a | 20·2 ± 5·6a | −1·5 ± 0·3 | 20·0 ± 1·4 | 0·11 ± 0·06a | 0·34 ± 0·07a | |||||||||
| 2·3 kPa | 25·5 ± 1·8 | 3·1 ± 0·1 | 11·5 ± 5·2Ab | 8·7 ± 4·5a | 31·2 ± 7·2ab | −1·7 ± 0·5 | 19·4 ± 0·7 | 0·09 ± 0·05a | 0·26 ± 0·05a | |||||||||
| 0 % blue irradiance | 24·6 ± 4·4 | 2·5 ± 0·4 | 13·8 ± 2·1 | 17·5 ± 3·1 | 33·2 ± 6·7 | −1·7 ± 0·4 | 20·5 ± 1·3 | 0·19 ± 0·07 | 0·42 ± 0·07 | |||||||||
| 1 % blue irradiance | 23·0 ± 4·3 | 2·7 ± 0·3 | 13·0 ± 1·4 | 15·3 ± 3·8 | 30·8 ± 9·2 | −1·9 ± 0·5 | 20·9 ± 2·1 | 0·16 ± 0·04 | 0·46 ± 0·08 | |||||||||
| 5 % blue irradiance | 21·5 ± 6·4 | 2·7 ± 0·3 | 14·7 ± 3·0 | 16·8 ± 1·8 | 35·2 ± 5·5 | −2·2 ± 0·4 | 20·9 ± 1·7 | 0·17 ± 0·08 | 0·45 ± 0·09 | |||||||||
| 10 % blue irradiance | 21·6 ± 2·7 | 2·6 ± 0·2 | 10·8 ± 1·4 | 18·7 ± 3·1 | 38·2 ± 5·6 | −1·6 ± 0·3 | 22·2 ± 1·4 | 0·27 ± 0·06 | 0·56 ± 0·07 | |||||||||
| 20 % blue irradiance | 18·6 ± 5·3 | 2·7 ± 0·4 | 12·4 ± 1·2 | 18·2 ± 1·3 | 37·6 ± 2·8 | −1·4 ± 0·6 | 22·0 ± 2·5 | 0·22 ± 0·07 | 0·51 ± 0·09 | |||||||||
Dynamic parameters include IS60 (induction 60 s after illumination, %), tA50, tA90, tgs50 and tgs90 [time (min) to reach 50 and 90 % of photosynthetic induction and time to reach 50 and 90 % of full stomatal opening]. Steady-state parameters were calculated by averaging single values over 2 min (either in dark-adapted leaves or at the end of induction) and include Ai, Af, gsi and gsf (A and gs in darkness and in 1000 µmol m−2 s−1, respectively; units: A expressed in µmol m−2 s−1 and gs in mol m−2 s−1). Means followed by different letters differ significantly, according to a LSD test conducted at the P = 0·05 level (n = 5); absence of letters denotes absence of significant effects.
One-way ANOVA performed on log-transformed data.
Data compared using non-parametric Kruskal–Wallis test.
Statistical analysis
Most data are expressed as mean ± standard error (SE). Parameters shown in Table 2 and in Fig. 4 were tested for normality (Shapiro-Wilk test; Genstat 16th edn, VSN International, Hempstead, UK) and homogeneity of variances (Fligner–Killeen test; R, R Core Team). On datasets where those requirements were fulfilled, one-way analysis of variance (ANOVA; Genstat) was performed, followed by Fisher’s protected LSD (Genstat) to determine significant differences between treatments. When datasets did not meet the requirement of normality or homogeneity of variances, they were log-transformed. On datasets where homogeneity of variances could be assumed, but the requirement of normality was not fulfilled, a non-parametric Kruskal–Wallis (Genstat) test was conducted.
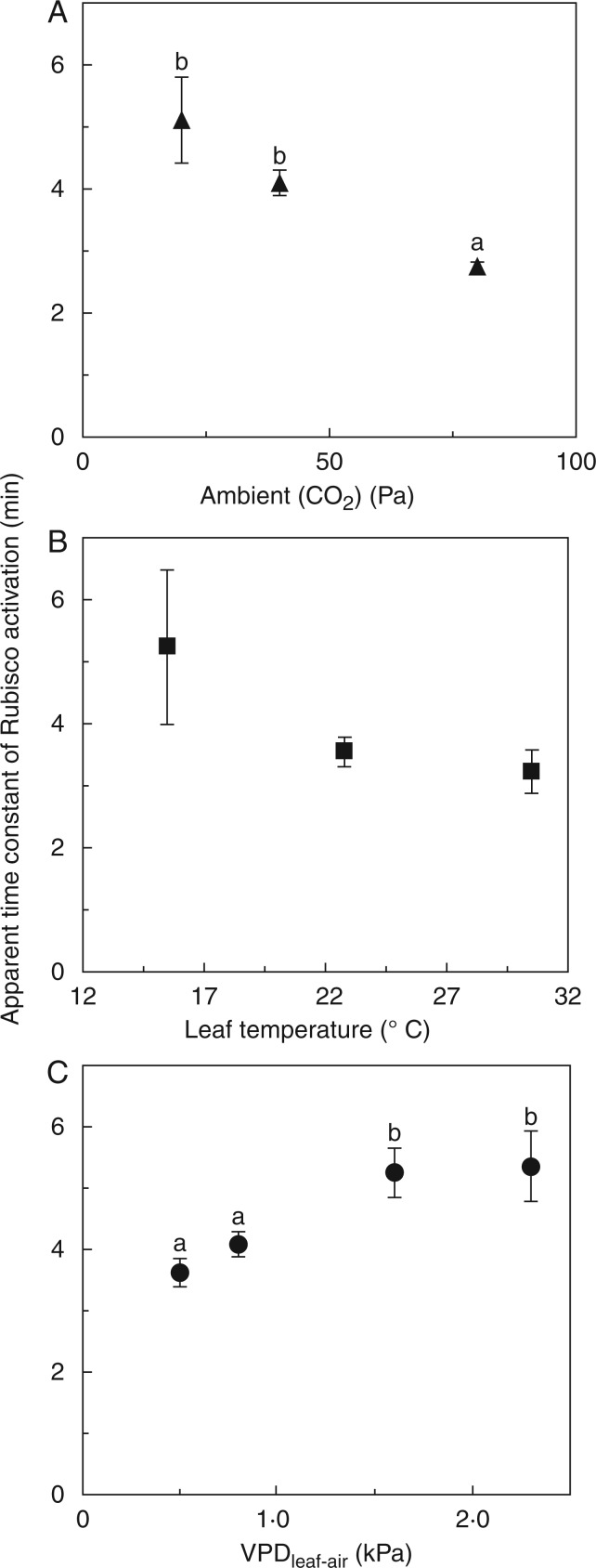
Fig. 4.
Apparent time constants of Rubisco activation (τR) during photosynthetic induction, as affected by Ca (A), VPDleaf-air (B) and leaf temperature (C). Small letters denote significant differences between treatments, error bars denote ± SE (n = 5).
RESULTS
Induction of photosynthetic CO2 fixation
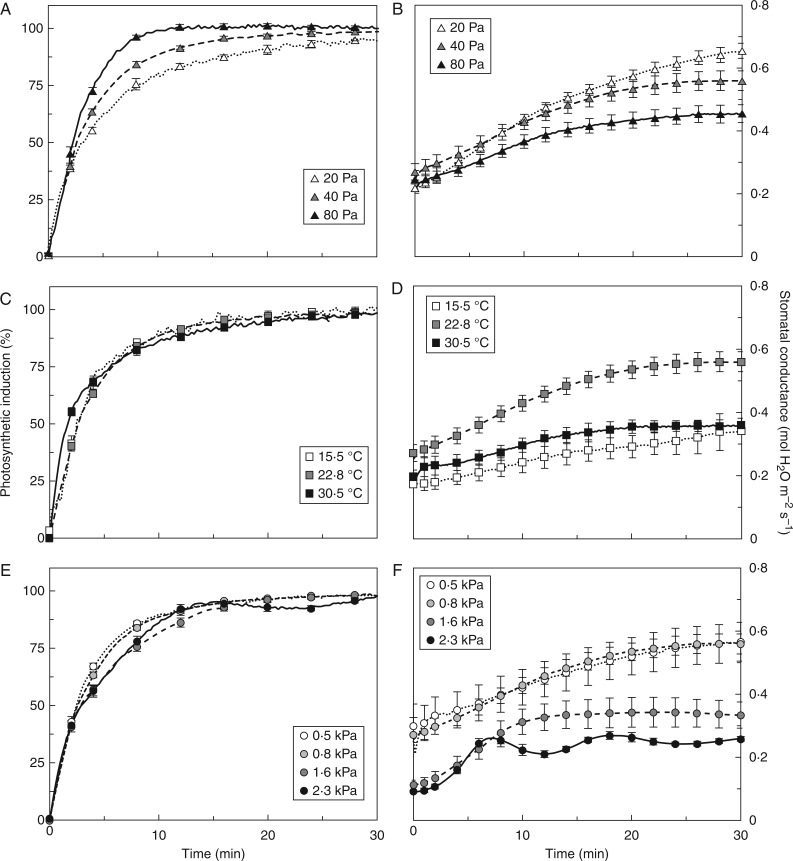
Rates of photosynthetic induction increased with Ca (Fig. 1A), affecting the time to reach 50 and 90 % of full induction (tA50 and tA90, respectively), but not induction 60 s after illumination (IS60; Table 2). High Tleaf (30·5 °C) increased induction slightly in the first 5 min (Fig. 1C), affecting IS60 and tA50 but not tA90 (Table 2). Elevated VPDleaf-air slowed down induction after ∼5 min (Fig. 1E), increasing tA90 in 1·6 kPa (Table 2). High VPDleaf-air (2·3 kPa) induced oscillations of induction rates (Fig. 1E), without affecting the various induction parameters. However, it is difficult to determine those parameters in an oscillating time series. Varying blue irradiance (0–20 %) did not affect any parameter in Table 2, nor did it have noticeable effects on other parameters discussed here (data not shown).
Fig. 1.
Photosynthetic induction (A, C, E) and stomatal conductance (B, D, F) in dark-adapted tomato leaves, as affected by Ca (A, B), Tleaf (C, D) and VPDleaf-air (E, F). Irradiance was raised from 0 to 1000 µmol m−2 s−1 at time = 0 and kept steady for 60 min. In A, C and E, the first 30 min of induction are shown. Mean ± SE (n = 5).
Stomatal conductance
Stomata opened faster in low Ca (Fig. 1B) and reached higher final conductance (gsf, Table 2). However, because gs levelled off earlier in intermediate and high Ca, the time to reach 90 % of full stomatal conductance (tgs90) was significantly longer in low Ca (Table 2). Low (15·5 °C) and high Tleaf decreased gs in darkness (gsi, Table 2) and decreased the extent of stomatal opening during induction (Fig. 1D), leading to lower steady-state gsf compared to intermediate Tleaf (22·8 °C). Elevated VPDleaf-air affected stomata by (1) decreasing gsi and gsf, (2) increasing relative opening rates in the first 15 min of induction, (3) inducing damped stomatal oscillations at the highest VPDleaf-air (2·3 kPa) and (4) causing stomata to reach steady-state gs more quickly (or quasi steady-state in the case of an oscillating gs; Fig. 1F, Table 2). Despite decreasing gsi by 40–55 % compared to low VPDleaf-air, high VPDleaf-air did not affect final A (Af; Table 2), suggesting that in the steady state, diffusional limitation of A was no longer sensitive to VPDleaf-air. Time courses of Cc during photosynthetic induction are shown in Supplementary Data File S6.
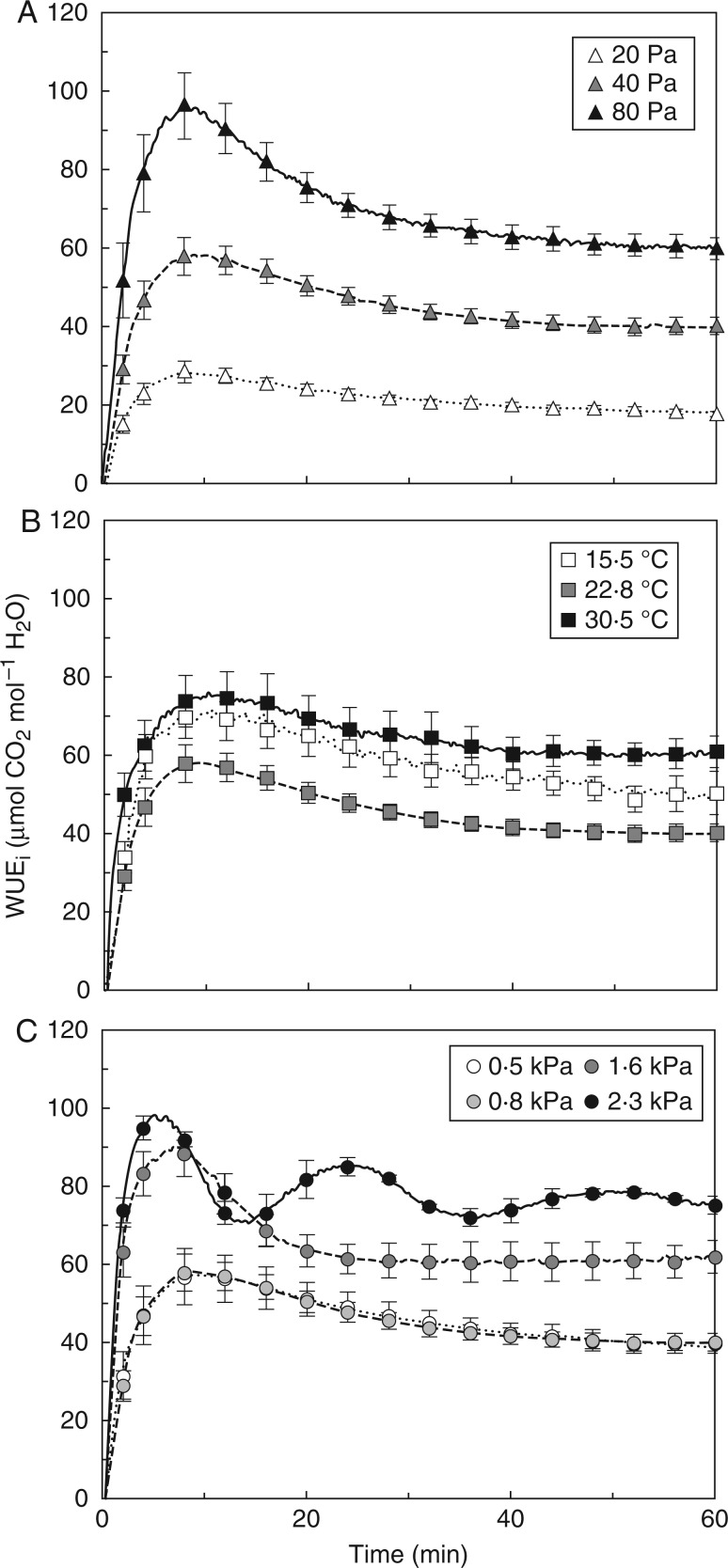
Intrinsic water use efficiency (WUEi)
WUEi, a result of dynamic changes in A and gs, was strongly affected by Ca: both its steady-state level and its rate of change in the first 30 min of induction were increased in high compared to low Ca (Fig. 2A). At low and high Tleaf, gs increased more slowly, with similar increases in A, in the beginning of induction, so both resulted in a higher WUEi than for an intermediate Tleaf (Fig. 2B). A similar reasoning applies to VPDleaf-air: because elevated VPDleaf-air reduced gs more strongly than A during and after induction, WUEi was highest in 2·3 kPa, followed by 1·6 kPa (Fig 2C). The 0·5- and 0·8-kPa treatments showed lowest WUEi and were no different from each other (Fig. 2C).
Fig. 2.
Intrinsic water use efficiency (WUEi) during photosynthetic induction, as affected by Ca (A), Tleaf (B) and VPDleaf-air (C). Mean ± SE (n = 5).
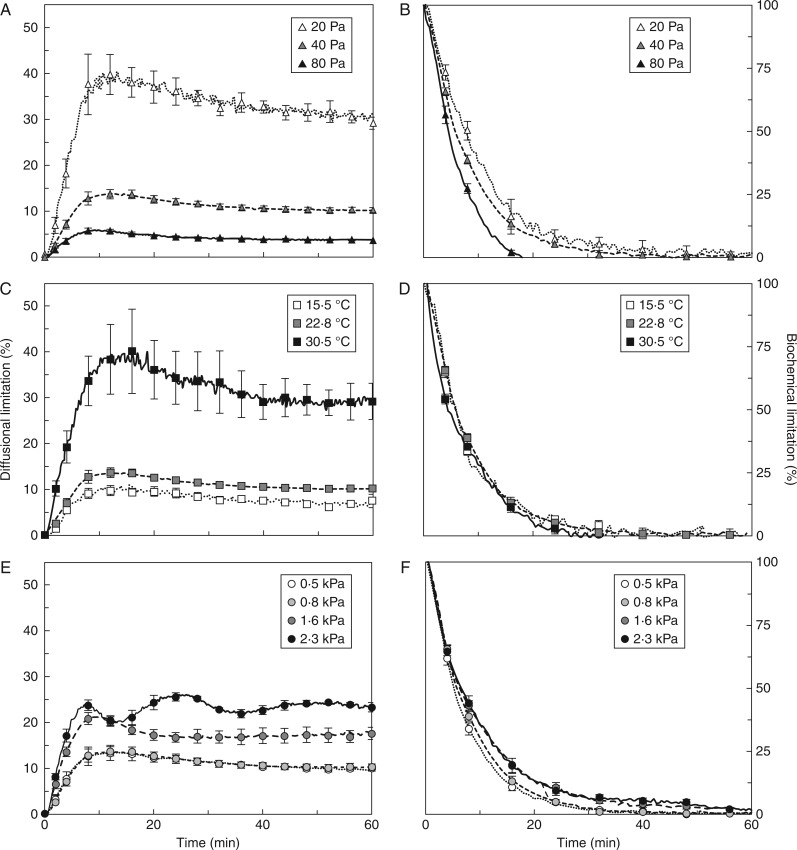
Diffusional and biochemical limitations during photosynthetic induction
Diffusional limitation quantifies the reduction in A due to Cc being lower than Ca. This is a complex parameter that depends on the combined effects of Ca, A and total leaf diffusive conductance on Cc, as well as the extent to which Cc imposes a limitation on A. Biochemical limitation quantifies the extent to which biochemical processes that activate during induction limit A during induction, but not in the steady state. Note that the sum of these limitations is not 100 %, as they are calculated not with respect to the total limitation for A, but to reference gaseous diffusion and biochemical states. In all treatments except at high VPD (2·3 kPa), transient diffusional limitation increased to its maximum within the first 15 min due to the activation of Rubisco, and then slowly relaxed to its steady-state level as stomata opened. Biochemical limitation was at its maximum in the very beginning of induction, and relaxed rapidly within the first 10–15 min. The extent, as well as the rates, of buildup and relaxation of diffusional and biochemical limitation scaled negatively with Ca (Fig. 3A, B). Diffusional limitation was higher in low compared to intermediate Ca, while there was no difference in biochemical limitation between these treatments. High Ca decreased the diffusional limitation and produced a faster relaxation of biochemical limitation than both low and intermediate Ca (Fig. 3A, B). When biochemical limitation had relaxed entirely at high Ca (∼10 min), ∼10 % of biochemical limitation remained at intermediate and low Ca, taking another 10 min to relax (Fig. 3B). High Tleaf induced strong diffusional limitation (Fig. 3C), while maintaining slightly positive effects on the rates of relaxation of biochemical limitation (Fig. 3D). The effects of high VPDleaf-air (1·6 and 2·3 kPa) on gs translated into very different kinetics of diffusional limitations during induction than moderate VPDleaf-air. The 1·6-kPa treatment led to a faster decrease in diffusional limitation than 0·5 or 0·8 kPa, while 2·3 kPa produced an oscillating diffusional limitation (Fig. 3E). Biochemical limitation was affected less strongly, although it tended to relax more slowly in elevated VPDleaf-air (Fig. 3F).
Fig. 3.
Diffusional limitation (A, C, E) and biochemical limitation (B, D, F) during photosynthetic induction, as affected by Ca (A, B), Tleaf (C, D) and VPDleaf-air (E, F). In B, D and F, the first 30 min of induction are shown. Mean ± SE (n = 5).
Apparent time constants of Rubisco activation
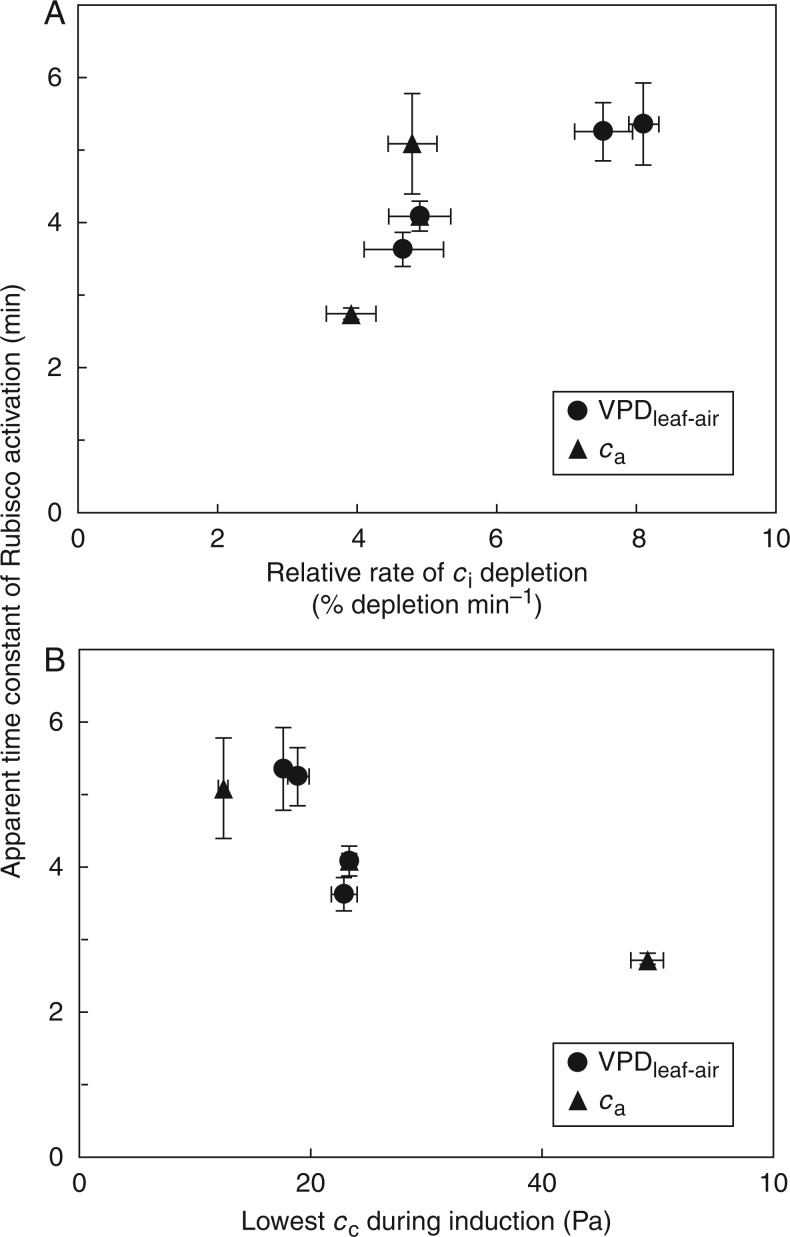
The apparent time constant for Rubisco activation (τR), defined as the time to reach 63 % of final Rubisco activation, decreased with increasing Ca (Fig. 4A), reflecting faster activation of Rubisco with larger abundance of CO2. Compared to τR in low Ca, τR at intermediate and high Ca was 20 and 56 % lower, respectively. Leaf temperature did not have a statistically significant effect on τR, although there was a trend towards higher τR in low Tleaf (Fig. 4B). Elevated VPDleaf-air significantly increased τR, by 45 and 48 % in the 1·6- and 2·3-kPa treatments (compared with 0·5 kPa; Fig. 4C).
Slower apparent Rubisco activation in elevated VPDleaf-air (compared to low VPDleaf-air) was probably related to lower values of Ci, due to the lower gs at high VPDleaf-air. The decrease in Ci at the start of induction was stronger in elevated compared to low VPDleaf-air. τR tended to increase with the relative rates of decrease in Ci, and data from the Ca treatments showed a similar trend (Fig. 5A), indicating that if Ci depleted too rapidly, apparent Rubisco activation was slowed down. Also, in an attempt to estimate the lowest CO2 partial pressure reached in the chloroplast, Cc was calculated at the time of induction when Ci reached its lowest point. Plotting τR against this Cc, a tendency towards lower τR at higher Cc emerged (Fig. 5B), indicating that a very low Cc during induction slows down the activation of Rubisco. Different leaf temperatures could affect the rate of Rubisco activation in addition to their effect on Ci, so they were not taken into account in Fig. 5, which shows only the effect of Ci and Cc on τR.
Fig. 5.
Relationships between τR in the VPDleaf-air and Ca treatments and (A) the rate of Ci depletion (), normalized by Ci in darkness (initial Ci) during the first 5 min of induction and (B) the lowest value of Cc during induction, using the lowest value of Ci during induction and corresponding values of An and gm, then calculating . Mean ± SE (n = 5).
Mesophyll conductance
Mesophyll conductance increased markedly during induction in all treatments, and the fastest changes were observed in the first 10 min of induction. Rates of increase and steady-state levels of gm were higher at low than at high Ca. At different leaf temperatures, gm increased with Tleaf. Details of dynamic gm changes and their determination can be found in File S5.
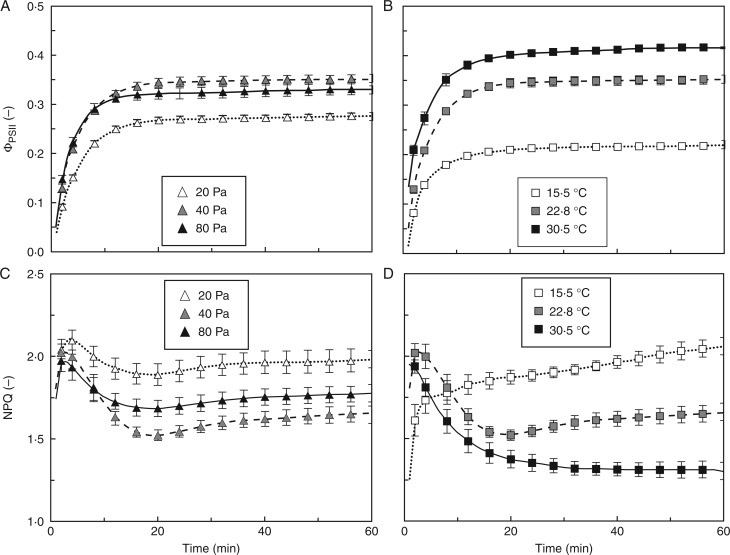
ΦPSII and NPQ during photosynthetic induction
The maximum, dark-adapted quantum efficiency of electron transport through photosystem II (Fv/Fm) ranged between 0·79 and 0·82 across Ca and Tleaf treatments. During induction, ΦPSII increased to its steady-state level within 20 min. Between minutes 2 and 14, the relative rates of increase of ΦPSII were significantly higher in high compared to low Ca. Furthermore, steady-state levels of ΦPSII were highest in intermediate Ca (0·35), followed by the high (0·33) and low Ca treatments (0·28; Fig. 6A). During induction, NPQ initially increased towards a peak of ∼2 after 5 min. This peak was followed by a decline, which was most pronounced at intermediate Ca (Fig. 6C). The lowest value of NPQ (1·5) was found at intermediate Ca and occurred after ∼15 min in all Ca treatments, after which NPQ increased slowly. This last phase was similar at all CO2 partial pressures, but values of NPQ were highest in low Ca (NPQ of 2), followed by high Ca (1·8) and the lowest value of NPQ (1·7) was found at intermediate Ca (Fig. 6C). Between minutes 2 and 5, high leaf temperature increased the relative rate of change of ΦPSII compared to low Tleaf. Furthermore, steady-state ΦPSII values scaled positively with Tleaf, reaching 0·42 at high, 0·35 at intermediate and 0·22 at low Tleaf (Fig. 6B). At intermediate and high Tleaf and varying Ca, the time courses of NPQ during induction were similar, rising rapidly to a maximum within 1–4 min, after which there was a decline to a minimum at ∼20 min (Fig 6C, D), followed by a rise to the steady-state value, except for the 30·5 °C treatment in which there was a continuous decline (Fig. 6D). At low Tleaf the response was different: an initial rapid increase in NPQ was less pronounced and was followed by a slow increase that did not reach a stable value during the experiment. Final NPQ values were therefore highest at low Tleaf (∼2), followed by intermediate (NPQ of 1·7) and high Tleaf (1·3). While changes in qP paralleled ΦPSII and were of the same magnitude, changes in Fv′/Fm′ were rather small (Supplementary Data File S7). As a result, ΦPSII correlated linearly and positively with qP, while Fv′/Fm′ correlated strongly and negatively with NPQ (data not shown).
Fig. 6.
Changes in ΦPSII (A, B) and NPQ (C, D) during photosynthetic induction, as affected by Ca (A, C) and Tleaf (B, D). Mean ± SE (n = 5).
Electron transport and gross photosynthesis rates
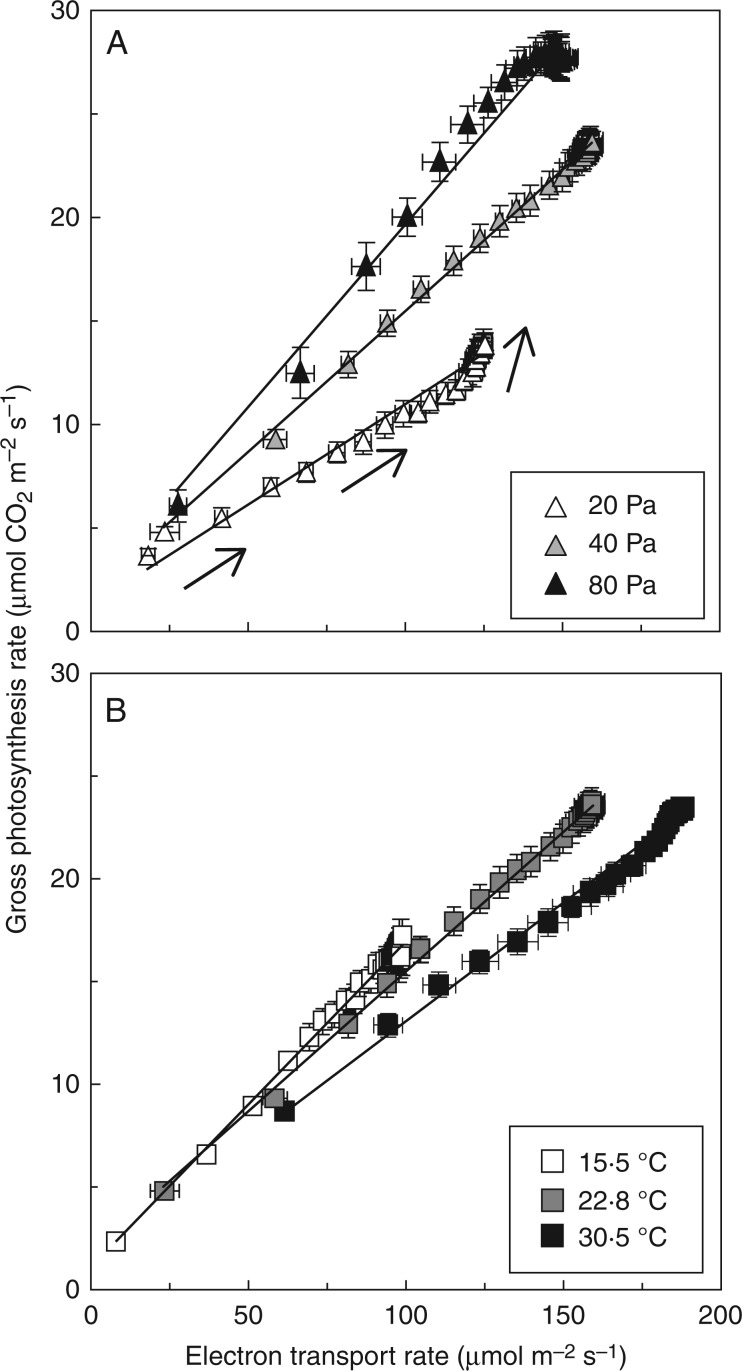
Regressions of gross photosynthesis (Agr = An+Rd) vs. ETR were predominantly linear (Fig. 7), but the slopes of this relationship increased with Ca and decreased slightly with Tleaf. Additionally, at low Ca and at high Tleaf, increases in Agr became progressively independent of increases in ETR at high values of ETR and Agr.
Fig. 7.
Relationship between electron transport rate and gross photosynthesis rate (An + Rd) during photosynthetic induction, as affected by Ca (A) and Tleaf (B). Arrows indicate the direction of change over time. Mean ± SE (n = 5).
DISCUSSION
The environmental factors CO2 partial pressure, temperature and VPDleaf-air had significant impacts on rates of photosynthetic induction, and on underlying diffusional, carboxylation and electron transport processes. For the first time, their effects have been compared using the same experimental set-up, and explored in a highly detailed manner. The results indicate the maximum gains that improvements in dynamic photosynthesis would have in various environments and atmospheres.
CO2 partial pressure: effects via diffusional and biochemical limitations
By lowering diffusional and biochemical limitations, increased Ca sped up photosynthetic induction considerably. This was reflected in gas exchange (Fig. 1A) and chlorophyll fluorescence data (Fig. 6A, C; discussed below). Despite decreasing gs and gm, increased Ca actually lowered diffusional limitation. There are two reasons for this: firstly, due to the curvilinearity of the A/Cc response, a difference between A at Ca and A at Cc (which is the basis of the calculation of diffusional limitation) is larger at low Ca (e.g. 20 Pa) than at high Ca (e.g. 80 Pa). Secondly, the gradient for diffusion between Ca and Cc was steeper (File S6) with increases in Ca, thus decreasing diffusional limitation. A decrease in biochemical limitation was achieved by faster activation of Rubisco (Fig. 4A), but not by faster activation of RuBP regeneration, as visible from the similarity of the initial slopes (Fig. 1A) and the parameter IS60 (Table 2). The positive effect of increased Ca on apparent Rubisco activation has been noted before (Mott and Woodrow, 1993; Woodrow et al., 1996), and is hypothesized to be due to faster carbamylation of Rubisco.
Because A increased faster and reached a higher value, and gs increased to a smaller extent, WUEi was strongly enhanced during and after photosynthetic induction (Fig. 2A) in high Ca. In absolute terms, elevated Ca is positive for WUEi in fluctuating irradiance. After sudden drops in irradiance, WUEi decreases quickly as A decreases more quickly than gs (Lawson and Blatt, 2014). Since gs is depressed in elevated Ca, the drops in WUEi after decreases in irradiance are likely to be smaller compared to current atmospheric Ca. Stomatal opening, and the concomitant increase in Ci, decreased the rate of photorespiration in low Ca, as seen from the change in the slope of Agr/ETR (Fig. 7A): when reaching higher values of Agr, this was achieved almost without increases in ETR (i.e. there was a deviation from the previous linear relationship of Agr/ETR), meaning that the rate of oxygenation decreased relative to the rate of carboxylation.
Effects of Ca on the rate of photosynthetic induction have been explored experimentally before (Chazdon and Pearcy, 1986; Naumburg and Ellsworth, 2000; Naumburg et al., 2001; Leakey et al., 2002; Tomimatsu and Tang, 2012; Tomimatsu et al., 2014; Soleh et al., 2016), and have been reviewed twice recently (Kaiser et al., 2015; Tomimatsu and Tang, 2016). Kaiser et al. (2015) found that across studies, tA90 decreased near-linearly with increases in Ca, while tA50 was unaffected. In the current study, tA50 was significantly increased in low Ca, while tA90 was three times lower in high (6·2 min) compared to low Ca (18·5 min; Table 2). Altogether, the stronger response to Ca observed in the current study (compared to the general response summarized by Kaiser et al., 2015) may be due to the use of C3 plants with high photosynthetic rate compared to most species summarized by Kaiser et al. (2015).
Leaf temperature: effects on the rate of RuBP regeneration and on stomatal opening
Effects of different leaf temperatures on the rate of photosynthetic induction were small compared to those of Ca and VPDleaf-air (Fig. 1C), but they strongly affected the levels and kinetics of ΦPSII and NPQ (Fig. 6B, D; discussed below). While apparent Rubisco activation rates were not significantly increased by elevated Tleaf (Fig. 4B), IS60 was significantly larger and tA50 significantly smaller (Table 2), suggesting a faster activation of the enzymes controlling the rate of RuBP regeneration (Sassenrath-Cole and Pearcy, 1992). This had slight effects on the initial relaxation of biochemical limitation (Fig. 3D). Stomatal opening was depressed at both low and high Tleaf (by 41–44 % compared to intermediate Tleaf): the difference between initial and final gs was only 0·17 (low Tleaf) and 0·16 (high Tleaf), compared to 0·29 mol m−2 s−1 at intermediate Tleaf (Table 2). At the same time, the difference between initial and final A was virtually the same at intermediate and high Tleaf, while it was 30 % lower at low Tleaf (Table 2). Thus, while at low Tleaf (weak gs and A increase) and intermediate Tleaf (strong gs and A increase) diffusional limitation was low and comparable, at high Tleaf (combination of weak gs increase and strong A increase) there was large diffusional limitation (Fig. 3C). The value of VPDleaf-air was only 0·04 kPa larger at high compared to intermediate Tleaf (File S2), and was therefore not responsible for the increase in diffusional limitation at high Tleaf.
The effect of Tleaf on the rate of photosynthetic induction has been explored several times in a spectrum of species and growth conditions (Küppers and Schneider, 1993; Pepin and Livingston, 1997; Leakey et al., 2003; Yamori et al., 2012; Carmo-Silva and Salvucci, 2013). Across these studies, increasing Tleaf decreased tA50 and tA90 up to an optimum of ∼30 °C (i.e. smallest tA50 and tA90, meaning highest rate of induction), above which these indices increased again (Kaiser et al., 2015). Further, it was noted that effects of Tleaf on induction rates were not uniform between studies (Kaiser et al., 2015). The data in the current study add to the scatter: tA50 was lower at high Tleaf, but tA90 was unaffected by treatment levels (Table 2). Apparently, there is large interspecific variation in the temperature response of photosynthetic induction.
VPDleaf-air: lower gs affects apparent Rubisco activation kinetics, diffusional limitation and WUEi
Increases in VPDleaf-air (i.e. dryer air) strongly decreased gs before, during and after photosynthetic induction (Fig. 1F). Very high VPDleaf-air even induced stomatal oscillations (feeding back on A), a phenomenon whose mechanisms are still under debate (Buckley, 2005; Kaiser, 2009; Kaiser and Paoletti, 2014). By decreasing Cc (File S6), elevated VPDleaf-air slowed down the rate of photosynthetic induction (Fig. 1E). This had strong effects on diffusional and, surprisingly, biochemical limitations (Fig. 3E, F), by decreasing the rate of apparent Rubisco activation (Fig 4B). A VPDleaf-air effect on apparent Rubisco activation rates has, to our knowledge, not been found before. Slower apparent Rubisco activation is probably caused by lower Ci or Cc during induction, as indicated by the relationships of τR with the relative rate of Ci decrease and the lowest partial pressure of Cc reached during induction (Fig. 5). Further support for this hypothesis comes from a study on water stress: short-term leaf desiccation, which led to stomatal closure, decreased both Cc and initial (i.e. extracted) Rubisco activity (Flexas et al., 2006). While the rate of Rubisco activation after a dark–light transition and initial Rubisco activity are not the same, they are both likely to be affected by the rate or the total extent of carbamylation, respectively. Furthermore, apparent Rubisco activation rates after increases in irradiance correlated positively with Ci (see above).
While higher VPDleaf-air undoubtedly had a negative impact on A after illumination was raised, it had positive effects on WUEi (Fig. 2C). The global climate is predicted to be dryer (at least in mid-latitude and subtropical regions), warmer and enriched in CO2 (IPCC, 2013). It can thus be hypothesized that WUEi in such a climate will increase in fluctuating irradiance, as increases in all of these factors improved WUEi (Fig. 2).
In contrast to Ca and Tleaf, published data describing the effects of VPDleaf-air on rates of photosynthetic induction are scarce. Nevertheless, Tinoco-Ojanguren and Pearcy (1993a, b) reported that high VPD decreased steady-state gs, slowed down photosynthetic induction and increased stomatal limitations in a pioneer rainforest tree (Piper auritum) and a shade-tolerant shrub (Piper aequale), similar to the present findings on tomato. Thus, stomatal dynamics of widely varying species seem to be similarly affected by elevated VPDleaf-air.
Lack of effects of blue irradiance: possible reasons
Surprisingly, varying blue irradiance (0–20 %) had no effects on stomatal opening or photosynthetic induction (Table 2). Blue irradiance generally promotes rapid stomatal opening when combined with red irradiance, and could be a cue for overall radiation load (Shimazaki et al., 2007). In the current experiment, 1000 µmol m−2 s−1 may have provided such a strong stimulus for stomatal opening that the rate of opening could not have been accelerated by increasing the percentage of blue irradiance. Assmann and Grantz (1990a, b), however, superimposed blue irradiance on 900 µmol m−2 s−1 red irradiance in sugarcane and soybean and found an additional opening response (data on photosynthesis were not shown in these studies). The reported effects of blue irradiance on photosynthetic induction are ambiguous: Košvancová-Zitová et al. (2009) reported faster induction in beech (Fagus sylvatica L.) with increasing blue irradiance (25–75 % blue irradiance in 800 µmol m−2 s−1), while data reported in Zhang et al. (2011) for the orchid Cypripedium flavum showed the opposite (0–100 % blue irradiance in 250 µmol m−2 s−1). The effects of blue irradiance on induction are therefore variable with no clear correlations between the effects of blue irradiance and other environmental responses or preferences.
Changes in chlorophyll fluorescence parameters during photosynthetic induction
Changes in ΦPSII during induction were primarily explained by changes in photochemical quenching (qP) rather than Fv′/Fm′. Overall, this suggests that changes in NPQ, acting via decreases in Fv′/Fm′, did not contribute substantially to the changes in ΦPSII (Baker et al., 2007); the total span of changes of Fv′/Fm′ was 0·55–0·65, while that for qP was 0·05–0·7 (File S7). Changes in qP occurred in the first 12 min of induction, making its time course similar to that of ΦPSII, but distinct from that of NPQ (Fig. 6). Steady-state ΦPSII was slightly higher in ambient compared to high Ca (Fig. 6A), while NPQ was slightly higher in high compared to ambient Ca (Fig. 6C). This may be explained by triose phosphate utilization limitation slowing down ETR in high Ca.
All Ca and Tleaf treatments (except low Tleaf) produced initial overshoots in NPQ (Fig. 6). It is hypothesized that the overshoot was caused by low metabolic activity that resulted in a low rate of electron transport, which caused a decrease in lumen pH, thereby activating NPQ. Upon the subsequent activation of Calvin cycle enzymes and increase in linear electron transport, the lumen pH increased and energy-dependent quenching (qE) decreased, lowering NPQ. The slow build-up of zeaxanthin during induction would then have produced a slower increase in energy-dependent quenching (qE) by enhancing the effect of pH on NPQ. This was visible between minutes 20 and 60 in all treatments except high Tleaf (Bilger and Björkman, 1991). Leaves that contained fully activated Rubisco in low irradiance did not exhibit an NPQ overshoot when transferred to high irradiance (Carmo-Silva and Salvucci, 2013). Also, in leaves containing less Rubisco activase, NPQ kept increasing throughout induction, indicating that Rubisco activation, and by implication photochemical quenching, increased more slowly (Yamori et al., 2012). Both examples demonstrate how the rate of change of metabolism sets the demand for the products of electron transport during photosynthetic induction, thereby affecting the transient excess irradiance condition and the parallel induction of NPQ.
Mesophyll conductance
The change in gm during photosynthetic induction has, to our knowledge, never been assessed. This has been attempted here using the often-used variable J method (Harley et al., 1992) (File S5). However, because possible changes in alternative electron transport, stoichiometry of ATP and NADPH production, leaf absorbance (due to chloroplast movement), Rd, and the overall validity of gm especially in the early phases of induction cannot be accounted for, we refrain from speculations on the correctness of gm during photosynthetic induction, but note this as a topic that deserves more dedicated experimentation. Two more things are noteworthy: firstly, the steady-state values of gm (Table in File S5) compare very well to published data (Bernacchi et al., 2002; Flexas et al., 2008; von Caemmerer and Evans, 2015). Secondly, the fact that at the beginning of photosynthetic induction none of the slopes of Agr/ETR (Fig. 7) deviated strongly from linearity implies that neither changes in gs nor changes in gm limited induction, as in such a case Cc would have dropped momentarily (oxygenation would have increased relative to carboxylation). This suggests that potentially low gm was not a (strongly) limiting factor during photosynthetic induction.
Methodological considerations
Diffusional and biochemical limitation were calculated for the first time assuming a curvilinear A/Ci relationship instead of the linear relationship previously used in such analyses (e.g. Woodrow and Mott, 1989; Jackson et al., 1991; Allen and Pearcy, 2000). This strongly affected the estimation of diffusional limitation at 40 and 80 Pa (Supplementary Data File S8). Most studies using this correction were performed with atmospheric or below-atmospheric Ca, where assuming a linear A/Ci relationship may be reasonable. However, some authors used a linear relationship at Ca of ≥ 70 Pa (Košvancová-Zitová et al., 2009; Tomimatsu and Tang, 2012). Their measures of stomatal limitation in high Ca are probably substantial overestimations.
In light-adapted leaves, the conventionally measured Fm′ (obtained using single saturating pulses) underestimated ‘true’ Fm′ (obtained using multiple saturating pulses), by approx. 4 %. It is shown here for the first time that this underestimation develops within 10 min during induction (File S3). Steady-state measurements on tobacco, pea and maize leaves (grown at 300 µmol m−2 s−1) showed comparably large underestimations of Fm′, translating into underestimations of ΦPSII (Loriaux et al., 2013). Here, steady-state ΦPSII would have been underestimated by 8–15 % if single rather than multi-phase pulses were used.
Improving crop photosynthesis in fluctuating irradiance: why and how?
Improving crop productivity via photosynthetic efficiency is considered a crucial pathway for future global food security (Zhu et al., 2010). Faster regulation of Rubisco activity may increase A in naturally fluctuating irradiance (Carmo-Silva et al., 2015). Also, a more dynamically regulated gs, which can, for example, be reached by smaller stomata, could help save water by increasing dynamic WUEi (Drake et al., 2013; Lawson and Blatt, 2014). Two scenarios were therefore explored using the present data on induction rates and stomatal opening in various atmospheres: changes in average A and WUEi during photosynthetic induction in the case of (1) instantaneous Rubisco activation and (2) instantaneous gs increase.
The analysis (Table 3) revealed that average A could increase by 6–8 % in ambient Ca (across VPDleaf-air and Tleaf treatments), if Rubisco activated instantaneously. In elevated Ca, a form of Rubisco that activates instantaneously would be less advantageous (2·5 instead of 5·6 % increase in A), because Rubisco already activates faster in high Ca. The faster increase in A due to faster Rubisco activation would also positively impact WUEi, by up to 12–19 % in ambient Ca. Rubisco activation can be sped up by manipulating the isoform composition of Rubisco activase (Zhang et al., 2002), although always-active Rubisco activase reduced growth in the Arabidopsis thaliana mutant rwt43 compared to its wild type (Carmo-Silva and Salvucci, 2013). The elucidation of how the activation state of Rubisco affects the balance of intermediates in the Calvin cycle should therefore be central to future research on improving dynamic photosynthesis.
Table 3.
Change ( %) in net photosynthesis rate or intrinsic water use efficiency (WUEi) if either Rubisco activated directly after illumination or stomatal conductance directly increased to its final, steady-state value
| Treatment | Net photosynthesis rate |
WUEi |
||
|---|---|---|---|---|
| Rubisco kinetics | Stomatal opening | Rubisco kinetics | Stomatal opening | |
| 20 Pa | 7·5±1·5 | 3·6±0·8 | 24·7±1·7 | −32·1±2·0 |
| 40 Pa | 5·6±0·4 | 1·1±0·1 | 12·2±0·9 | −20·6±1·4 |
| 80 Pa | 2·5±0·6 | 0·6±0·1 | 5·8±0·8 | −19·8±2·2 |
| 15·5 °C | 5·2±0·7 | 1·4±0·3 | 11·7±1·8 | −24·7±6·3 |
| 22·8 °C | 5·6±0·4 | 1·1±0·1 | 12·2±0·9 | −20·6±1·4 |
| 30·5 °C | 4·1±0·9 | 3·3±1·2 | 11·5±1·3 | −13·9±2·6 |
| 0·5 kPa | 4·9±0·4 | 1·4±0·4 | 11·5±1·3 | −23·3±3·6 |
| 0·8 kPa | 5·6±0·4 | 1·1±0·1 | 12·2±0·9 | −20·6±1·4 |
| 1·6 kPa | 7·6±0·6 | 0·6±0·2 | 18·5±2·2 | −15·6±2·5 |
| 2·3 kPa | 8·0±0·8 | 0·7±0·1 | 17·3±2·1 | −13·7±2·1 |
Values are means over minutes 2–60 during photosynthetic induction ± SE (n = 5).
Instantaneous stomatal opening would improve average photosynthesis rates by up to 1–3 % in ambient Ca and across air humidities and leaf temperatures. Thus, increasing the kinetics of Rubisco activation seems to be a more useful strategy than increasing gs, especially as higher gs would strongly decrease WUEi (by 21–25 % in ambient Ca). Stomata that react faster to decreases in irradiance, on the other hand, would be very beneficial for dynamic WUEi (Lawson and Blatt 2014); whether or not quickly reacting stomata enhance WUEi is therefore dependent on the situation.
A transition from completely inactivated photosynthesis in darkness to near-saturating irradiance does not represent natural conditions; the modulation of dynamic photosynthesis by environmental factors and the benefits of faster Rubisco activation or stomatal opening may be smaller when photosynthesis is somewhat induced. Therefore, these numbers can only be used to provide a first guess for the benefits of ‘immediate’ Rubisco activation or stomatal opening.
CONCLUSIONS
Increased CO2 partial pressure led to faster photosynthetic induction, by decreasing diffusional limitation and by speeding up the relaxation of biochemical limitation. Increased leaf temperature led to slightly faster induction rates, due to faster relaxation of biochemical limitation. Elevated leaf-to-air vapour pressure deficit mainly lowered the relaxation rates of biochemical limitation, by slowing down apparent Rubisco activation via decreased availability of CO2. Increasing the rates of Rubisco activation would be more beneficial for dynamic photosynthesis than increasing initial stomatal conductance or the rate of stomatal opening.
SUPPLEMENTARY DATA
Supplementary data are available online at www.aob.oxfordjournals.org and consist of the following. File S1: preliminary irradiance response curves. File S2: traces of VPDleaf-air during photosynthetic induction as affected by Tleaf. File S3: measured Fm′ underestimates true Fm′ in light-adapted but not in dark-adapted leaves. File S4: A/Ci and A/PAR curves. File S5: changes in gm during photosynthetic induction. File S6: changes of chloroplast CO2 partial pressure (Cc) during photosynthetic induction. File S7: qP and Fv′/Fm′ during photosynthetic induction. File S8: implications of using curvilinear instead of linear A/Cc relationships when determining diffusional limitation.
ACKNOWLEDGEMENTS
We thank Shizue Matsubara, Tracy Lawson, Tsu-Wei Chen and Alejandro Morales for useful discussions. This work was supported by the BioSolar Cells open innovation consortium, supported by the Dutch Ministry of Economic Affairs, and by Powerhouse.
LITERATURE CITED
- Allen MT, Pearcy RW. 2000. Stomatal versus biochemical limitations to dynamic photosynthetic performance in four tropical rainforest shrub species. Oecologia 122: 479–486. [DOI] [PubMed] [Google Scholar]
- Assmann SM, Grantz DA. 1990a. Stomatal response to humidity in sugarcane and soybean: effect of vapour pressure difference on the kinetics of the blue light response. Plant, Cell & Environment 13: 163–169. [Google Scholar]
- Assmann SM, Grantz DA. 1990b. The magnitude of the stomatal response to blue light: modulation by atmospheric humidity. Plant Physiology 93: 701–709. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Baker NR, Harbinson J, Kramer DM. 2007. Determining the limitations and regulation of photosynthetic energy transduction in leaves. Plant, Cell & Environment 30: 1107–1125. [DOI] [PubMed] [Google Scholar]
- Bernacchi CJ, Portis AR, Nakano H, von Caemmerer S, Long SP. 2002. Temperature response of mesophyll conductance. Implications for the determination of Rubisco enzyme kinetics and for limitations to photosynthesis in vivo. Plant Physiology 130: 1992–1998. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Bernacchi CJ, Singsaas EL, Pimentel C, Portis AR, Long SP. 2001. Improved temperature response functions for models of Rubisco-limited photosynthesis. Plant, Cell & Environment 24: 253–259. [Google Scholar]
- Bilger W, Björkman O. 1991. Temperature dependence of violaxanthin de-epoxidation and non-photochemical fluorescence quenching in intact leaves of Gossypium hirsutum L. and Malva parviflora L. Planta 184: 226–234. [DOI] [PubMed] [Google Scholar]
- Buckley TN. 2005. The control of stomata by water balance. New Phytologist 168: 275–292. [DOI] [PubMed] [Google Scholar]
- von Caemmerer S, Evans JR. 2015. Temperature responses of mesophyll conductance differ greatly between species. Plant, Cell & Environment 38: 629–637. [DOI] [PubMed] [Google Scholar]
- Carmo-Silva AE, Salvucci ME. 2013. The regulatory properties of Rubisco activase differ among species and affect photosynthetic induction during light transitions. Plant Physiology 161: 1645–1655. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Carmo-Silva AE, Scales JC, Madgwick PJ, Parry MAJ. 2015. Optimizing Rubisco and its regulation for greater resource use efficiency. Plant, Cell & Environment 38: 1817–1832. [DOI] [PubMed] [Google Scholar]
- Chazdon RL, Pearcy RW. 1986. Photosynthetic responses to light variation in rainforest species I. Induction under constant and fluctuating light conditions. Oecologia 69: 517–523. [DOI] [PubMed] [Google Scholar]
- Drake PL, Froend RH, Franks PJ. 2013. Smaller, faster stomata: scaling of stomatal size, rate of response, and stomatal conductance. Journal of Experimental Botany 64: 495–505. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Farquhar GD, von Caemmerer S, Berry JA. 1980. A biochemical model of photosynthetic CO2 assimilation in leaves of C3 species. Planta 149: 78–90. [DOI] [PubMed] [Google Scholar]
- Flexas J, Diaz-Espejo A, Galmés J, Kaldenhoff R, Medrano H, Ribas-Carbo M. 2007. Rapid variations of mesophyll conductance in response to changes in CO2 concentration around leaves. Plant, Cell & Environment 30: 1284–1298. [DOI] [PubMed] [Google Scholar]
- Flexas J, Ribas-Carbó M, Bota J, et al. 2006. Decreased Rubisco activity during water stress is not induced by decreased relative water content but related to conditions of low stomatal conductance and chloroplast CO2 concentration. The New Phytologist 172: 73–82. [DOI] [PubMed] [Google Scholar]
- Flexas J, Ribas-Carbó M, Diaz-Espejo A, Galmés J, Medrano H. 2008. Mesophyll conductance to CO2: current knowledge and future prospects. Plant, Cell & Environment 31: 602–621. [DOI] [PubMed] [Google Scholar]
- Genty B, Briantais JM, Baker NR. 1989. The relationship between the quantum yield of photosynthetic electron transport and quenching of chlorophyll fluorescence. Biochimica et Biophysica Acta 990: 87–92. [Google Scholar]
- Harley PC, Loreto F, Di Marco G, Sharkey TD. 1992. Theoretical considerations when estimating the mesophyll conductance to CO2 flux by analysis of the response of photosynthesis to CO2. Plant Physiology 98: 1429–1436. [DOI] [PMC free article] [PubMed] [Google Scholar]
- IPCC. 2013. Fifth assessment report climate change 2013: summary for policymakers. Cambridge: Cambridge University Press. [Google Scholar]
- Jackson RB, Woodrow IE, Mott KA. 1991. Nonsteady-state photosynthesis following an increase in photon flux density (PFD): effects of magnitude and duration of initial PFD. Plant Physiology 95: 498–503. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Johnson GN, Young AJ, Horton P. 1994. Activation of non-photochemical quenching in thylakoids and leaves. Planta 194: 550–556. [Google Scholar]
- Kaiser H. 2009. The relation between stomatal aperture and gas exchange under consideration of pore geometry and diffusional resistance in the mesophyll. Plant, Cell & Environment 32: 1091–1098. [DOI] [PubMed] [Google Scholar]
- Kaiser E, Morales A, Harbinson J, Heuvelink E, Prinzenberg AE, Marcelis LFM. 2016. Metabolic and diffusional limitations of photosynthesis in fluctuating irradiance in Arabidopsis thaliana. Scientific Reports doi:10.1038/sr. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Kaiser E, Morales A, Harbinson J, Kromdijk J, Heuvelink E, Marcelis LFM. 2015. Dynamic photosynthesis in different environmental conditions. Journal of Experimental Botany 66: 2415–2426. [DOI] [PubMed] [Google Scholar]
- Kaiser H, Paoletti E. 2014. Dynamic stomatal changes In: Tausz M, Grulke N, eds. Plant ecophysiology. Trees in a changing environment. Dordrecht: Springer Netherlands, 61–82. [Google Scholar]
- Košvancová M, Urban O, Šprtová M, et al. 2009. Photosynthetic induction in broadleaved Fagus sylvatica and coniferous Picea abies cultivated under ambient and elevated CO2 concentrations. Plant Science 177: 123–130. [Google Scholar]
- Košvancová-Zitová M, Urban O, Navrátil M, Špunda V, Robson TM, Marek M V. 2009. Blue radiation stimulates photosynthetic induction in Fagus sylvatica L. Photosynthetica 47: 388–398. [Google Scholar]
- Küppers M, Schneider H. 1993. Leaf gas exchange of beech (Fagus sylvatica L.) seedlings in lightflecks: effects of fleck length and leaf temperature in leaves grown in deep and partial shade. Trees 7: 160–168. [Google Scholar]
- Lawson T, Blatt MR. 2014. Stomatal size, speed, and responsiveness impact on photosynthesis and water use efficiency. Plant Physiology 164: 1556–1570. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Leakey ADB, Press MC, Scholes JD. 2003. High-temperature inhibition of photosynthesis is greater under sunflecks than uniform irradiance in a tropical rain forest tree seedling. Plant, Cell & Environment 26: 1681–1690. [Google Scholar]
- Leakey ADB, Press MC, Scholes JD, Watling JR. 2002. Relative enhancement of photosynthesis and growth at elevated CO2 is greater under sunflecks than uniform irradiance in a tropical rain forest tree seedling. Plant, Cell and Environment 25: 1701–1714. [Google Scholar]
- Long SP, Bernacchi CJ. 2003. Gas exchange measurements, what can they tell us about the underlying limitations to photosynthesis? Procedures and sources of error. Journal of Experimental Botany 54: 2393–2401. [DOI] [PubMed] [Google Scholar]
- Loriaux SD, Avenson TJ, Welles JM, et al. 2013. Closing in on maximum yield of chlorophyll fluorescence using a single multiphase flash of sub-saturating intensity. Plant, Cell & Environment 36: 1755–1570. [DOI] [PubMed] [Google Scholar]
- Mott KA, Woodrow IE. 1993. Effects of O2 and CO2 on nonsteady-state photosynthesis. Further evidence for ribulose-1,5-bisphosphate carboxylase/oxygenase limitation. Plant Physiology 102: 859–866. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Murchie EH, Niyogi KK. 2011. Manipulation of photoprotection to improve plant photosynthesis. Plant Physiology 155: 86–92. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Naumburg E, Ellsworth DS. 2000. Photosynthetic sunfleck utilization potential of understory saplings growing under elevated CO2 in FACE. Oecologia 122: 163–174. [DOI] [PubMed] [Google Scholar]
- Naumburg E, Ellsworth DS, Katul GG. 2001. Modeling dynamic understory photosynthesis of contrasting species in ambient and elevated carbon dioxide. Oecologia 126: 487–499. [DOI] [PubMed] [Google Scholar]
- Osterhout WJ V, Haas ARC. 1918. Dynamical aspects of photosynthesis. Proceedings of the National Academy of Sciences, USA 4: 85–91. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Oxborough K, Baker NR. 1997. Resolving chlorophyll a fluorescence images of photosynthetic efficiency into photochemical and non-photochemical components – calculation of qP and Fv′/Fm′ without measuring Fo′. Photosynthesis Research 54: 135–142. [Google Scholar]
- Pearcy RW, Krall JP, Sassenrath-Cole GF. 1996. Photosynthesis in fluctuating light environments. In: Baker NR, ed. Photosynthesis and the Environment. Dordrecht: Kluwer, 321–346. [Google Scholar]
- Pearcy RW, Way DA. 2012. Two decades of sunfleck research: looking back to move forward. Tree Physiology 32: 1059–1061. [DOI] [PubMed] [Google Scholar]
- Pepin S, Livingston NJ. 1997. Rates of stomatal opening in conifer seedlings in relation to air temperature and daily carbon gain. Plant, Cell & Environment 20: 1462–1472. [Google Scholar]
- Pons TL, Welschen RAM. 2002. Overestimation of respiration rates in commercially available clamp-on leaf chambers. Complications with measurement of net photosynthesis. Plant, Cell & Environment 25: 1367–1372. [Google Scholar]
- Sassenrath-Cole GF, Pearcy RW. 1992. The role of ribulose-1,5-bisphosphate regeneration in the induction requirement of photosynthetic CO2 exchange under transient light conditions. Plant Physiology 99: 227–234. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Sharkey TD. 1985. O2-insensitive photosynthesis in C3 plants. Its occurrence and a possible explanation. Plant Physiology 78: 71–75. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Sharkey TD, Bernacchi CJ, Farquhar GD, Singsaas EL. 2007. Fitting photosynthetic carbon dioxide response curves for C3 leaves. Plant, Cell and Environment 30: 1035–1040. [DOI] [PubMed] [Google Scholar]
- Shimazaki K, Doi M, Assmann SM, Kinoshita T. 2007. Light regulation of stomatal movement. Annual Review of Plant Biology 58: 219–247. [DOI] [PubMed] [Google Scholar]
- Soleh MA, Tanaka Y, Nomoto Y, et al. 2016. Factors underlying genotypic differences in the induction of photosynthesis in soybean [Glycine max (L.) Merr.]. Plant, Cell & Environment 39: 685–693. [DOI] [PubMed] [Google Scholar]
- Tinoco-Ojanguren C, Pearcy RW. 1993. Stomatal dynamics and its importance to carbon gain in two rainforest Piper species. II. Stomatal versus biochemical limitations during photosynthetic induction. Oecologia 94: 395–402. [DOI] [PubMed] [Google Scholar]
- Tomimatsu H, Iio A, Adachi M, Saw L-G, Fletcher C, Tang Y. 2014. High CO2 concentration increases relative leaf carbon gain under dynamic light in Dipterocarpus sublamellatus seedlings in a tropical rain forest, Malaysia. Tree Physiology 34: 944–954. [DOI] [PubMed] [Google Scholar]
- Tomimatsu H, Tang Y. 2012. Elevated CO2 differentially affects photosynthetic induction response in two Populus species with different stomatal behavior. Oecologia 169: 869–878. [DOI] [PubMed] [Google Scholar]
- Tomimatsu H, Tang Y. 2016. Effects of high CO2 levels on dynamic photosynthesis: carbon gain, mechanisms, and environmental interactions. Journal of Plant Research 129: 365–377. [DOI] [PubMed] [Google Scholar]
- Urban O, Košvancová M, Marek M V, Lichtenthaler HK. 2007. Induction of photosynthesis and importance of limitations during the induction phase in sun and shade leaves of five ecologically contrasting tree species from the temperate zone. Tree Physiology 27: 1207–1215. [DOI] [PubMed] [Google Scholar]
- Woodrow IE, Kelly ME, Mott KA. 1996. Limitation of the rate of ribulosebisphosphate carboxylase activation by carbamylation and ribulosebisphosphate carboxylase activase activity: development and tests of a mechanistic model. Australian Journal of Plant Physiology 23: 141–149. [Google Scholar]
- Woodrow IE, Mott KA. 1989. Rate limitation of non-steady-state photosynthesis by ribulose-1,5-bisphosphate carboxylase in spinach. Australian Journal of Plant Physiology 16: 487–500. [Google Scholar]
- Yamori W, Masumoto C, Fukayama H, Makino A. 2012. Rubisco activase is a key regulator of non-steady-state photosynthesis at any leaf temperature and, to a lesser extent, of steady-state photosynthesis at high temperature. The Plant Journal 71: 871–880. [DOI] [PubMed] [Google Scholar]
- Yin X, Struik PC, Romero P, et al. 2009. Using combined measurements of gas exchange and chlorophyll fluorescence to estimate parameters of a biochemical C3 photosynthesis model: a critical appraisal and a new integrated approach applied to leaves in a wheat (Triticum aestivum) canopy. Plant, Cell & Environment 32: 448–464. [DOI] [PubMed] [Google Scholar]
- Zhang SB, Guan ZJ, Chang W, Hu H, Yin Q, Cao KF. 2011. Slow photosynthetic induction and low photosynthesis in Paphiopedilum armeniacum are related to its lack of guard cell chloroplast and peculiar stomatal anatomy. Physiologia Plantarum 142: 118–127. [DOI] [PubMed] [Google Scholar]
- Zhang N, Kallis RP, Ewy RG, Portis AR. 2002. Light modulation of Rubisco in Arabidopsis requires a capacity for redox regulation of the larger Rubisco activase isoform. Proceedings of the National Academy of Sciences, USA 99: 3330–3334. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Zhu XG, Long SP, Ort DR. 2010. Improving photosynthetic efficiency for greater yield. Annual Review of Plant Biology 61: 235–261. [DOI] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.