Joint MR-PET reconstruction using a multi-channel image regularizer

Abstract

While current state of the art MR-PET scanners enable simultaneous MR and PET measurements, the acquired data sets are still usually reconstructed separately. We propose a new multi-modality reconstruction framework using second order Total Generalized Variation (TGV) as a dedicated multi-channel regularization functional that jointly reconstructs images from both modalities. In this way, information about the underlying anatomy is shared during the image reconstruction process while unique differences are preserved. Results from numerical simulations and in-vivo experiments using a range of accelerated MR acquisitions and different MR image contrasts demonstrate improved PET image quality, resolution, and quantitative accuracy.

I. Introduction

Hybrid multi-modality imaging methods exploit the specific strengths of each individual modality to complement deficits in the other by delivering joint information that is more than the sum of its parts. For example, in the case of MR-PET, the strengths of excellent soft tissue contrast and high spatial resolution associated with MR are combined with the functional information provided by imaging the distribution of a radioactively labeled molecule in PET [1]. Current state-of-the-art MR-PET scanners even allow for simultaneous acquisition of PET and MR data. Typically, however, images are then reconstructed separately, and, with the exception of the use of the MR-estimated attenuation correction map, results are only combined at the visualization stage. PET images are reconstructed using the Expectation Maximization (EM) [2] algorithm or one of its variants like Ordered Subset Expectation Maximization (OSEM) [3]. MR images are reconstructed using an inverse Fourier transform, a non-uniform variant in the case of non-Cartesian imaging [4] or a more generalized algorithm for inverse problem solution in cases like parallel imaging (PI) [5], [6], [7] or compressed sensing (CS) [8], [9]. When distinct reconstruction algorithms are used, of course, the feature of simultaneous data acquisition is not exploited during the image reconstruction step.

Methods that use anatomical information obtained from MR during PET image reconstruction have been proposed in the literature. It was shown that these so-called anatomical-prior based methods allow enhancement of PET resolution and improved quantification [10], [11], [12], [13], [14], [15]. However, these methods were not developed in the context of integrated MR-PET systems. PET and MR scans are performed sequentially on separate scanners and, after co-registration, the MR images are treated as anatomical ground truth and are used for improved retrospective PET image reconstruction. Initial concepts and ideas for truly simultaneous MR and PET reconstruction were first described independently by Ehrhardt et al. [16] and some of the authors of the present paper [17], [18]. The work [16] is based on 2D simulations of geometrical phantoms, and the authors report improvements for both MR and PET reconstructions when using joint reconstruction.

We propose a novel joint reconstruction framework that treats MR and PET data on an equal footing, and complements the joint data acquisition of current integrated multimodality MR-PET systems. Our approach exploits anatomical correlations between MR and PET images by using second order Total Generalized Variation (TGV) as a dedicated multi-channel regularization functional [19], [20], [21], [22], [23] that couples the two modalities during the image reconstruction step. The coupling is carried out on the level of first and second order derivatives by using nuclear and Frobenius matrix and tensor norms, respectively. This allows a mutual benefit for the reconstruction of each channel that arises from joint structures and is robust against changes of signal intensity and contrast, in particular being independent of global intensity shifts and sign flips of image gradients between the two channels. Similar approaches have also been considered for Total Variation regularization in [24], [25], [26] and [27] for color images and CT reconstruction, respectively, and a Frobenius norm coupling for TGV has been considered in [28] for multi-contrast MRI. We refer to the Discussion section for more details concerning related work. In the context of joint MR-PET reconstruction, it is important that the exchange of information between modalities with fundamentally different contrast mechanisms does not compromise quantitative signal values. This is especially critical for PET since it is an inherently quantitative imaging modality. Additionally, since PET and MR sometimes show complementary information and specific structures might only be visible in one of the two modalities, such individual structures must be allowed by the coupling. Ideally they should neither be dampened nor transferred to the other modality where they are supposed to be invisible.

We report on experiments comparing the proposed method to separate reference reconstruction approaches for the two modalities and to anatomical-prior-based PET reconstruction. We describe the results of numerical simulations, and, to the best of our knowledge, this is the first time that a joint MR-PET reconstruction approach is demonstrated in-vivo.

II. Theory

A. Joint regularization

The proposed multi-modality reconstruction framework is based on a convex variational method, employing a vectorial second order Total Generalized Variation (TGV) functional as joint regularization.

The TGV functional has been introduced as regularization for single channel images in [19], with the aim of overcoming defects of existing derivative based regularization approaches such as Total Variation (TV) [29] or second order Total Variation [30]: The TV functional measures an ℓ¹-type norm of the derivative of the image, thereby allowing jump discontinuities which in practice correspond to sharp edges in the reconstruction. A defect of TV regularization, however, is the introduction of artificial edges (the staircasing effect). While this can be overcome by penalizing an ℓ¹-type norm of the second order derivative instead, as done with second order TV regularization, such an approach requires sufficient regularity of the first order derivative. This prevents the reconstruction of jump discontinuities and in practice leads to a blurring of edges. These defects can be overcome by TGV regularization which, in the second order case, uses an auxiliary variable to optimally balance between first and second order derivatives of the image. As as consequence, TGV does not suffer from the defects of TV while still allowing the recovery of sharp edges. This effect can best be understood when considering the minimum representation of second order TGV [20], which is for a single channel image u defined as

$${\mathrm{TGV}}_{\alpha }^2\left(u\right)=\underset{w}{\min }{\alpha }_1{\Vert \mid \nabla u-w\mid \Vert }_1+{\alpha }_0{\Vert {\mid \mathcal{E}w\mid }_{\text{frob}}\Vert }_1.$$

The balancing is achieved by subtraction of the vector field w, which in turn is penalized via a symmetrized gradient $\mathcal{E}w=\frac{1}{2}(\mathit{Jw}+{\left(\mathit{Jw}\right)}^T)$, with Jw being the Jacobian matrix. As w is chosen to minimize the sum of the two penalties, it can be expected to be zero in regions where the image is already constant, i.e., where ∇u = 0, and to be equal to ∇u in regions where the image is almost linear, yielding a penalization of the Hessian matrix $\mathit{Hu}=\mathcal{E}\nabla u$. The point-wise norms |·| and |·|_frob are the standard Euclidean vector norm and the Frobenius matrix norm, i.e., the root of the sum of the squares of all entries, respectively. It has been shown for instance in [31] that in practice TGV regularization indeed allows for a significantly improved reconstruction quality for undersampled MRI compared to classical methods as well as TV regularization. This motivates the usage of TGV as image prior for our setting.

The extension to multi-modality imaging works as follows: Instead of performing a TGV regularized reconstruction for each modality separately, one can regard the two images as a single multi-channel image and extend the TGV functional for vector valued data. Doing so, the terms ∇u – w and $\mathcal{E}w$ in the above minimum representations are now matrix and tensor fields, respectively, and the point-wise norms need to be adapted accordingly. Comparing to the single-channel case, Frobenius norms seem to be natural extensions and indeed, multi-channel TGV regularization using point-wise Frobenius norms has, for instance, already been applied in [21], [22], [23] for color image processing. In the context of MR-PET reconstruction, the columns of ∇u – w correspond to the edge information in the gradients of the MR and PET images and hence, a Frobenius norm coupling promotes joint sparsity of the edge sets. If the assumption of structural similarity of the two components holds, this can already be expected to give an improvement upon separate reconstruction, which corresponds to summing the Euclidean norm of each column of ∇u – w and adapting the point-wise tensor norm accordingly.

To further exploit structural similarities in MR-PET, we propose to choose the nuclear norm, i.e., the ℓ¹ norm on the singular values of ∇u – w, as point-wise matrix norm (and again the point-wise Frobenius tensor norm for $\mathcal{E}w$). This is motivated by the goal of aligning image edges independent of quantitative signal values. Indeed, one can interpret this choice as enforcing sparsity on the singular values, which promotes linear dependence of the gradients of the two image channels and, consequently, aligned edges. Alternatively, the nuclear norm can also be interpreted as convex relaxation of a penalization of the rank. As such, it is independent of sign flips in the gradients but not entirely independent of signal magnitudes. Nevertheless, besides obvious computational advantages, the relaxation might in fact also be beneficial when it comes to unwanted feature transfer. Indeed, when penalizing the rank, non-zero PET gradients for example can be introduced in points with non-zero MR gradients at no cost, while our approach still puts a cost on the magnitude of the PET gradient.

A particularity of the nuclear-norm based coupling of MR and PET images is also the fact that one aims at promoting linear dependence of the gradients of a complex and a real valued function. To this aim, the nuclear norm is computed in a complex vector space setting, regarding both components as complex signals. The above considerations then naturally transfer to this situation, in particular sparsity of the singular values corresponds to linear dependence of the gradients in a complex vector space. Now as the PET image is constraint to be real, the linear dependence means that both the real and imaginary part of the MR gradient must be a real multiple of the PET gradient. This seems natural as an alignment of the edges sets of the MR magnitude image and the PET image induces such a situation.

In summary, we expect a nuclear-norm based coupling of the gradients to benefit from structural similarities between PET and MR images, largely independent of the signal intensity. A motivating, artificial example for this type of coupling is also provided in Figure 1. As can be seen there, even though MR and PET contrasts are quite different at first glance, the difference in the direction of image gradients (modulo π to visualize linear dependence) is only marginal, and hence one can expect a reconstruction method that promotes a linear dependence of the gradients to be beneficial.

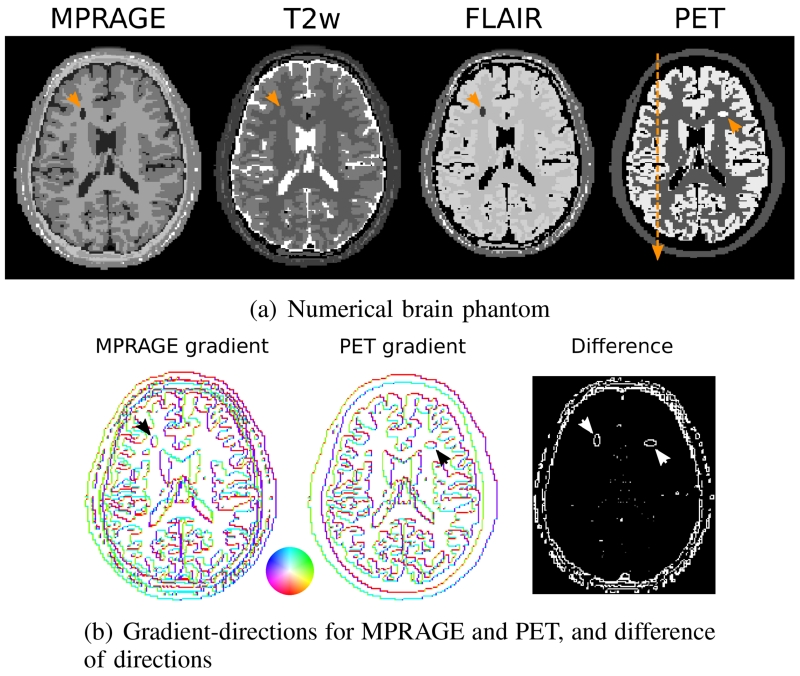
Fig. 1.

a) Ground truth MPRAGE, T2w, FLAIR and PET numerical brain simulation. The additional separated structures in MR and PET are indicated by arrows, as well as the position of the cross-sectional plot that was used during evaluation of the PET signal values. b) 2D visualization of the direction of the image gradient for a single slice of MPRAGE and PET, and difference of the directions (modulo π). The color-circle indicates the angle of the gradient vector in polar coordinates. The phantom is designed so that the majority of edges overlap exactly. Notable exceptions are the two individual lesions (again indicated by arrows) and some additional fine structures, especially around the skull, which only show up as distinct features in MR.

B. Variational model

Motivated by the considerations above, we formulate joint MR-PET reconstruction with nuclear-norm based TGV regularization as the following convex minimization problem:

$$\begin{array}{cc}\hfill \underset{\left(u,v\right)\in C}{\min }{\mathrm{TGV}}_{\alpha }^2& \left(\left(u,v\right)\right)+\lambda {\Vert \mathit{Mu}-u_0\Vert }_2^2\hfill \\ \hfill & +\mu \int \left(\mathit{Pv}+c_0-v_0\log \left(\mathit{Pv}+c_0\right)\right).\hfill \end{array}$$ (1)

In Equation (1), u and v are 3D MR and PET images, u₀ and v₀ are MR and PET raw data and c₀ is an additive correction for random events and scattering in PET. M is the MR sampling operator consisting of an undersampled Fourier transform and coil sensitivity modulation. P models the PET forward operator and comprises a convolution with a Gaussian filter (FHWM=4.5cm) in image space for resolution modeling [32], followed by a Radon transform along the lines of response connecting two measurement crystals and a subsequent, pointwise attenuation correction. We refer to Section III for more details about the forward models. The set C defines the set of admissible reconstructions by constraining the PET channel to the positive reals. The scalars λ and μ are parameters weighting individual MR and PET data fidelity terms. The functional is comprised of three distinct terms: Data fidelity to the acquired MR raw data using a squared ℓ²-norm (suitable for Gaussian noise in the complex multi-coil MR data), PET data consistency using the Kullback-Leibler divergence (suitable for Poisson noise) and the proposed multi-channel regularizer TGV, which is for y = (u, v) defined as

$${\mathrm{TGV}}_{\alpha }^2\left(y\right)=\underset{w}{\min }{\alpha }_1{\Vert {\mid \nabla y-w\mid }_{\text{nuc}}\Vert }_1+{\alpha }_0{\Vert {\mid \mathcal{E}w\mid }_{\text{frob}}\Vert }_1.$$ (2)

Here, ∇ and $\mathcal{E}$ denote a gradient and symmetrized gradient, operating on the vector field y and on the matrix field w, respectively, |∇y – w|_nuc is the point-wise nuclear norm of the matrix field (∇y – w) and ${\mid \mathcal{E}w\mid }_{\text{frob}}$ is the point-wise Frobenius tensor norm of the tensor field $\mathcal{E}w$.

We remark that, as discussed above, simpler alternatives to using the point-wise nuclear norm of ∇y – w, whose evaluation requires a point-wise singular value decomposition, would be to either use the matrix Frobenius norm for ∇y – w or to use decoupled norms for both ∇y – w and $\mathcal{E}w$. While the former also promotes joint edge sets of the channels, the latter is equivalent to an independent reconstruction of each channel and we present numerical experiments that compare these alternatives.

C. Numerical solution

Accounting for non-differentiability of the objective functional as well as the large problem size due to volumetric image data, we employ the first-order primal-dual algorithm of [33] (see also [31], [23]) to approximate a globally optimal solution of Equation (1). To this aim, we reformulate the minimization problem to a saddle-point problem in a way that the proximal mapping of all involved functions, given as

$${\text{prox}}_{f,\gamma }\left(z\right)=\arg \underset{\xi }{\min }f\left(\xi \right)+\frac{{\Vert \xi -z\Vert }_2^2}{2\gamma },$$

can be calculated explicitly and fast. In an abstract setting, this can be done as follows: Denote by $u\mapsto D_{\text{MR}}^{\lambda }(\mathit{Mu}-u_0)$ and $v\mapsto D_{\text{PT}}^{\mu }(\mathit{Pv}+c_0)$ the data fidelity functions for the MR and PET component, respectively, define (u, v, w) ↦ R(∇(u, v) – w, $\mathcal{E}w$) with R accordingly such that

$${\mathrm{TGV}}_{\alpha }^2\left(\left(u,v\right)\right)=\underset{w}{\min }R\left(\nabla \left(u,v\right)-w,\mathcal{E}w\right),$$

and denote by (u, v) ↦ I_C((u, v)) the convex indicator functional corresponding to the constraint set C, being 0 if (u, v) ∈ C and ∞ else. Using the notion of convex conjugates, i.e.,

$$f^{\ast }\left(z\right)=\underset{\xi }{\sup }\left(z,\xi \right)-f\left(\xi \right),$$

the optimization problem (1) can be reformulated as

$$\begin{array}{cc}\hfill \underset{\left(u,v\right)}{\min }\underset{w}{\min }& R\left(\nabla \left(u,v\right)-w,\mathcal{E}w\right)+{\mathcal{I}}_C\left(\left(u,v\right)\right)\hfill \\ \hfill & +D_{\text{MR}}^{\lambda }\left(\mathit{Mu}-u_0\right)+D_{\text{PT}}^{\mu }\left(\mathit{Pv}+c_0\right)\hfill \\ \hfill \iff \underset{x=\left(u,v,w\right)}{\min }\underset{\left(p,q,r,s\right)}{\max }& \left(\mathit{Kx}\left(p,q,r,s\right)\right)-R^{\ast }\left(p,q\right)+H\left(x\right)\hfill \\ \hfill & -{\left(D_{\text{MR}}^{\lambda }\right)}^{\ast }\left(r\right)-{\left(D_{\text{PT}}^{\mu }\right)}^{\ast }\left(s\right)-\left(r,u_0\right)+\left(s,c_0\right)\hfill \\ \hfill \iff \underset{x=\left(u,v,w\right)}{\min }\underset{z=\left(p,q,r,s\right)}{\max }& \left(\mathit{Kx},z\right)-F^{\ast }\left(z\right)+H\left(x\right),\hfill \end{array}$$

where F* in the last line summarizes all conjugate functionals of the line above, H (u, v, w) = I_C (u, v) and

$$K\left(u,v,w\right)=\left(\begin{array}{c}\hfill \nabla \left(u,v\right)-w\hfill \\ \hfill \mathcal{E}w\hfill \\ \hfill \mathit{Mu}\hfill \\ \hfill \mathit{Pv}\hfill \end{array}\right).$$

The iteration steps of algorithm [33] employed to the saddle-point problem are now given as

$$\{\begin{array}{c}{z}_{+}\leftarrow {\text{prox}}_{F^{\ast },\sigma }\left(z+\sigma K\overline{x}\right)\hfill \\ x_{+}\leftarrow {\text{prox}}_{H,\tau }\left(x-\tau K^{\ast }{z}_{+}\right)\hfill \\ \overline{x}\leftarrow 2x_{+}-x\hfill \\ \left(x,z\right)\leftarrow \left(x_{+},z_{+}\right).\hfill \end{array}\phantom{\}}$$ (3)

As the proximal mapping of F* decouples to component-wise proximal mappings of a simple form and the proximal mapping of H is a simple projection, all iterates can be calculated explicitly and fast. Furthermore, convergence of (u, v) in the primal iterates to a globally optimal solution of Equation (1) can be guaranteed for appropriate, constant stepsizes σ and τ. We refer to the Appendix for details about the numerical scheme and an implementation-friendly description.

III. Methods

A. Numerical simulations

The proposed approach was first tested in simulations. The goal of this set of experiments was quantitative evaluation of the performance of the method in comparison to a known ground truth. To show feasibility of the proposed coupling independent of the particular MR contrast, three different contrasts were tested. A numerical brain phantom, based on the design presented in [34], was used. Tissue parameter values (T1, T2, proton density, PET activity) were chosen according to [34] as well. In addition to existing structural differences in the PET and MR images that result from the phantom simulation, an individual, very distinct object, simulating the contrast of a Glioblastoma Multiforme (GBM) [35] lesion, was added to each modality. These spatially separated structures serve as a particularly challenging test scenario for the joint reconstruction approach and simulate situations in which a particular lesion might be strongly visible in one of the two modalities but not in the other. Numerical values of MR and PET parameters for cerebrospinal fluid (CSF), gray matter (GM), white matter (WM) and the individual lesions are given in Table I. MR images for three widely used sequences in brain protocols (MPRAGE: TR=2569ms, Echo spacing 6.6ms, TI=900ms, FA=9, T2 weighted spin echo: TR=4140ms TE=90ms and FLAIR: TR=10000ms, TE=90ms, TI=1781ms) were then forward simulated according to their respective signal equations ([36], [37]). Figure 1 shows the central slices of the ground truth MR and PET images that were the basis for the numerical simulations. Additionally, the direction of the 2D gradient of MPRAGE, PET and the difference of the gradient directions (modulo π) is shown. The phantom is designed so that the majority of edges overlap exactly. Notable exceptions are the two individual lesions and some additional fine structures, especially around the skull, which only show up as distinct features in MR.

TABLE I.

Tissue parameters for the numerical brain phantom simulation

	T1 (ms)	T2 (ms)	PD (a.u.)	PET activity (Bq/cm3)
CSF	2569	329	1	0
GM	833	83	0.86	22900
WM	500	70	0.77	8450
MR GBM lesion	1970	101	0.77	-
PET GBM lesion	-	-	-	25799

The simulated matrix size was 190 × 190 × 208 with an isotropic spatial resolution of 1mm³. Coil sensitivities were obtained from measurements of a water bottle using a conventional 12-element head coil array on a clinical 3T MR-PET System (Siemens Biograph mMR). Complex Gaussian noise was added to the simulated multi-channel k-space data such that the ratio of the standard deviation of the noise to the signal intensity of the DC-peak in k-space (averaged over slices and coils) was 200. An accelerated acquisition using an undersampling factor R=4 with 24 reference lines at the center of k-space to estimate coil sensitivities was simulated. PET sinogram data were forward projected according to the crystal geometry of a whole body 3T MR-PET system (Siemens Biograph mMR) [38]. The sinograms were corrupted using the Poisson noise model. Two situations were simulated: A 10min Fluorodeoxyglucose (FDG) PET head scan with a total number of 5.04 · 10⁸ counts and a shorter 5min scan (total number of counts of 2.52 · 10⁸). These numbers are based on the 10 minutes in-vivo measurement described below, where the total number of original list-mode prompts was 5.04 · 10⁸. In contrast to the in-vivo modeling, the simplified PET model for these simulations does not include additive scatter and random correction (hence c₀ = 0) or attenuation maps, as those would again depend on the simulated data and their inclusion in the forward modeling does not change the ill-posedness of the inversion significantly (as opposed to resolution modeling, which is included also in the simulations).

The results were evaluated by calculating global and local region of interest based root mean square differences from the MR and PET ground truths, and by comparing the mean quantitative signal values of the PET reconstructions for selected tissues.

B. Image reconstruction for numerical simulations

As the first step in the image reconstruction process, coil sensitivity maps were estimated from the MR data using the approach described in [31]. In addition to the proposed method, MR images were reconstructed iteratively using the conjugate gradient CG SENSE [39] algorithm with a tolerance of 10⁻⁶ and PET images were reconstructed using an in-house implementation [40] of EM with resolution modeling [32] using the system geometry of our PET-MR system [38]. While it is known that the resolution of PET scanner varies over the field of view, i.e., the further away from the center of the FOV, the worse the resolution, for the data used in this work the filter was used with uniform parameters since the brain data is assumed to be reasonably close to the center of the FOV. A known issue of the Biograph mMR are measurement gaps resulting from to the large distance between adjacent crystal blocks. Those gaps were filled using the interpolation approach presented in [41] leading to a closed ring and hence to complete sinograms. No OSEM-type acceleration with subsets was used in any PET reconstruction (i.e., the number of subsets was 1). TGV-regularized reconstructions were performed with the approach described in the theory section. For the numerical phantom experiments we also tested joint TGV regularization with the nuclear norm coupling as in Equation (2) replaced by a Frobenius norm. Since the proposed 3D TGV regularizer, along with the corresponding numerics, is a novel method in itself even without the coupling of MR and PET, we also performed experiments in which MR and PET image reconstructions were performed separately, but with TGV regularization. This corresponds to replacing the nuclear and Frobenius norm of Equation (2) by a separate penalization of the two channels. The goal of this comparison was to separate the effects of the shared information between PET and MR from the effects of the regularizer itself. Reconstructions were also performed using EM iterations and a well known MR-anatomical-prior guided PET reconstruction proposed by Bowsher et al. [11], for which the separate TGV regularized MR reconstruction was used as the anatomical prior.

Concerning parameter choice for TGV, EM and the Bowsher-prior, an exhaustive parameter search was performed based on RMSE to the ground truth for joint PET reconstruction with MPRAGE MR contrast. In the case of Bowsher, we used the parameters presented in [14] as the starting point of the search. For EM and Bowsher, 1000 iterations were performed and the RMSE to the ground truth was calculated in each iteration step. For the primal dual method we used a fixed number of 1000 iterations. This large number of iterations was chosen to ensure convergence of the reconstruction. In practice, we saw only minor differences in the images after 500 iterations (see the Appendix for a more detailed explanation).

The following parameter values were identified:

10min PET dataset:

• EM method: 387 iterations.

• Bowsher prior: 3 × 3 × 3 neighborhood using the 16 closest neighbors, prior strength β = 100, 795 iterations.

• Separate TGV MR and PET reconstruction: λ = 1, μ = 90.

• Frobenius norm coupled TGV MR and PET reconstruction: λ = 1, μ = 50.

• Nuclear norm coupled TGV MR and PET reconstruction: λ = 1, μ = 90.

5min PET dataset:

• EM method: 243 iterations.

• Bowsher prior: 3 × 3 × 3 neighborhood using the 16 closest neighbors, prior strength β = 100, 624 iterations.

• Separate TGV MR and PET reconstruction: λ = 1, μ = 60.

• Frobenius norm coupled TGV MR and PET reconstruction: λ = 1, μ = 30.

• Nuclear norm coupled TGV MR and PET reconstruction: λ = 1, μ = 60.

Regarding Frobenius norm coupling and separate TGV reconstruction, we remark that the corresponding norms were also scaled a-priori to yield approximately the same cost as the nuclear norm on random data.

In order to test the generalization potential of the individual methods, the parameters obtained for the MPRAGE MR contrast were then kept fixed for the reconstructions with the other two MR contrasts (T2 weighted and FLAIR). In addition to a single-case evaluation, also 30 different realizations with different noise corruption were generated for MPRAGE MR and 5min PET. Reconstructions were performed with all methods and maps of the difference of the pixel based mean over the 30 different reconstructions to the ground truth (bias) as well as the pixel-by-pixel standard deviations (estimate of noise) were generated.

C. In-vivo measurements

The proposed method was then tested with in-vivo data that were acquired on a clinical 3T MR-PET System (Siemens Biograph mMR) with the same 12-element head coil array that was used in the simulations. The study was approved by the NYU institutional review board (IRB), and written informed consent was obtained from all subjects prior to examination. 10 mCi 18F-FDG were injected. A standard Dixon sequence was obtained for PET attenuation correction prior to the start of a 10min PET acquisition and accelerated MR acquisitions were acquired simultaneously with PET. In the first protocol, approximate uptake time was 150min and a 3D MPRAGE sequence with the following parameters was acquired: TR=2300ms, Echo spacing 7.1ms, TI=900ms, FA=9°, 190 × 190 × 208 matrix, voxel size=1.15 × 1.15 × 1.2mm³ and BW=240Hz/pixel. Regular Cartesian sampling with an acceleration factor of 2 was used. The number of original prompts in the PET raw data after resorting to sinograms from listmode, but before axial compression or gap filling was 1.42 · 10⁸. The number of randoms and the scatter fraction, as estimated by the vendors implementation, was 2.94 · 10⁷ and 28%, respectively. The second scan was started after an approximate uptake time of 75min. The same 3D MPRAGE sequence was used with following sequence parameters: TR=2200ms, Echo spacing 6.6ms, TI=1100ms, FA=12°, 256 × 256 × 192 matrix, voxel size=0.86 × 0.86 × 1mm³ and BW=260Hz/pixel. An acceleration factor of 4 was used. The number of original prompts in the PET raw data was 5.04 · 10⁸. The number of randoms and the scatter fraction, as estimated by the vendors implementation, was 1.75 · 10⁸ and 29%, respectively. This level of acceleration and PET counts was also used in the phantom simulations. In both protocols the central 24 lines of k-space were fully sampled as a reference region to estimate coil sensitivities.

D. Image reconstruction for in-vivo measurements

Coil sensitivity maps were estimated in the same way as for the numerical simulations [31]. PET attenuation correction maps were obtained using an offline version of the reconstruction pipeline of the vendor together with estimates for scatter and random coincidences, and were included in the PET forward model as in Equation (1). Reference reconstructions were again obtained with CG SENSE and EM, also including corrections for attenuation, scatter and random events in the iterations. Since MR and PET were acquired with different resolution, the smaller of the two voxel sizes was used for all reconstructions. For the first protocol, reference reconstructions are compared to joint TGV regularized reconstructions using Frobenius and nuclear norm coupling as well the anatomical-prior-based reconstruction method of Bowsher [11], where the TGV regularized reconstruction of the MR image was used as anatomical prior. For the second protocol, the reference reconstruction is compared to the joint TGV regularized reconstruction using nuclear norm coupling. Due to the lack of a ground truth for parameter optimization in the in-vivo case, we used the results from the numerical simulation as a starting point and then chose the parameters of the different reconstructions based on visual inspection of the results. The parameter choices for the in-vivo measurements are given as follows:

First protocol:

• EM: 250 iterations.

• Bowsher prior: 3 × 3 × 3 neighborhood using the 16 closest neighbors, prior strength β = 0.5, 500 iterations.

• Frobenius norm coupled TGV MR and PET reconstruction: λ = 10, μ = 120.

• Nuclear norm coupled TGV MR and PET reconstruction: λ = 10, μ = 130.

Second protocol:

• EM: 250 iterations.

• Nuclear norm coupled TGV MR and PET reconstruction: λ = 10, μ = 300.

IV. Results

A. Numerical simulations

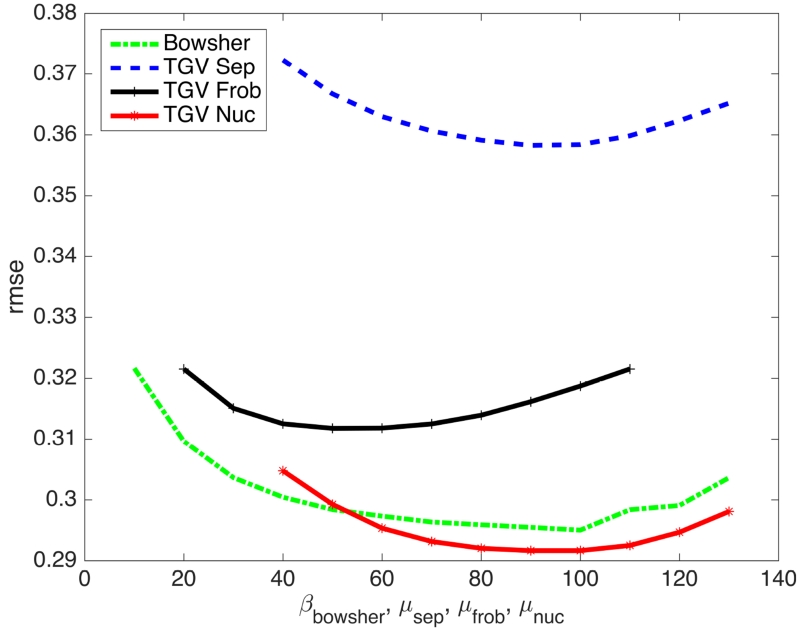
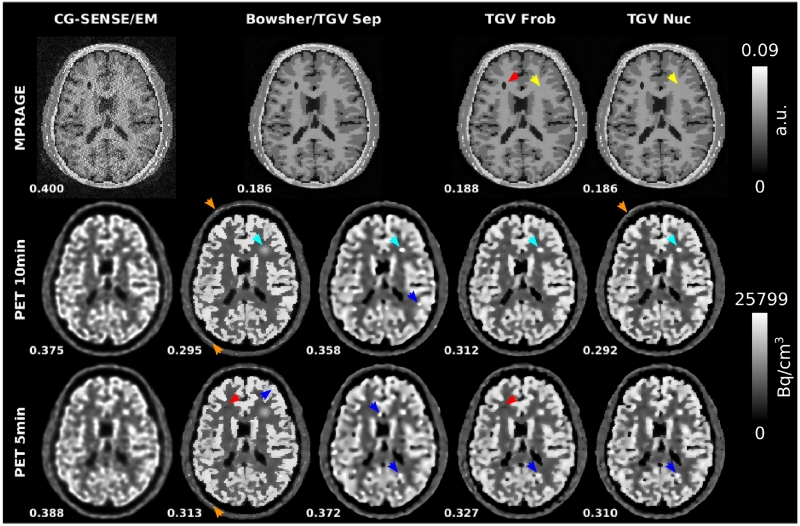
The proposed MR-PET TGV reconstruction is shown with Frobenius and nuclear norm coupling, as well as separate penalization of the two modalities. CG SENSE parallel imaging MR [39], PET EM [2] and MR-anatomical-prior PET reconstructions [11] using the separate TGV MR reconstruction as the prior, are shown as well. Figure 2 shows PET RMSE values of the results of the parameter optimization process for prior strength of the Bowsher prior (β) and PET data fidelity (μ) for separate, Frobenius norm and nuclear norm TGV. Figure 3 shows numerical phantom MPRAGE contrast results. Results with the other two MR contrasts are shown in Figs. 4 and 5. Sharpness and visibility of fine image features is improved for the PET images with the multi-channel TGV reconstruction and the Bowsher prior. The experiments also demonstrate that the improvements are consistent over a range of MR contrasts. It can also be noticed that some structures have an inverted MR and PET contrast. For example, while FDG uptake is higher in gray matter and signal intensities are higher than in white matter for T2w and FLAIR, the contrast is inverted in an MPRAGE scan. Since information exchange is only performed on the level of the gradient and symmetrized gradient fields, the proposed multi-channel regularizer is unaffected by this. RMSEs with respect to the ground truth images are also displayed next to the corresponding reconstructions and confirm the visual impressions of the reconstructions. The two joint TGV reconstructions result in substantially lower errors than separate TGV, which in turn outperforms EM for all three MR contrasts and both PET scan durations. The RMSE of the Bowsher prior is close to the nuclear norm reconstruction for MPRAGE contrast, which was used in the parameter search. For the other two contrasts (T2 weighted and FLAIR) Bowsher is outperformed by both Frobenius and nuclear norm coupling in terms of RMSE, while itself outperforming the separate TGV regularized PET reconstruction and EM. Overall the nuclear norm resulted in the lowest RMSEs for all experiments. In addition to global RMSE evaluation over the whole FOV presented in the figures, Table II gives region-of-interest specific RMSE values for gray matter in the head of the caudate nucleus (bilaterally), the left insula, and the PET-only GBM lesion.

Fig. 2.

10min PET RMSE values of the results of the parameter optimization process for prior strength of the Bowsher prior (β) and PET data fidelity (μ) for separate, Frobenius norm and nuclear norm TGV.

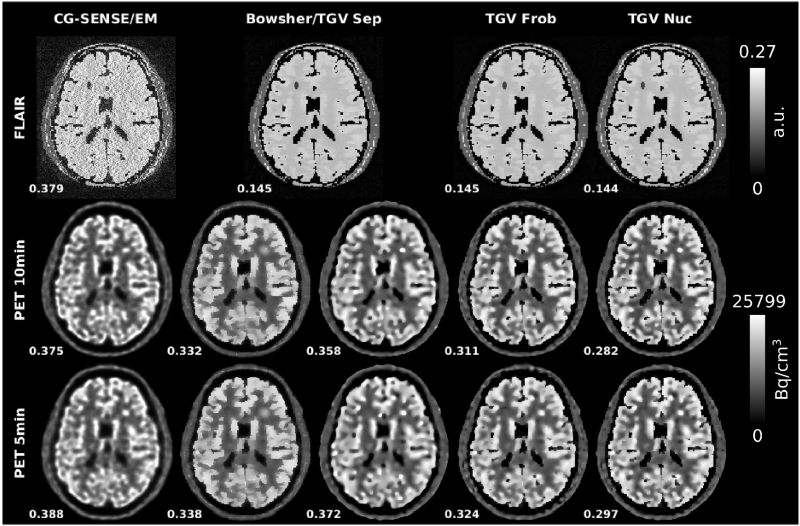
Fig. 3.

Reconstruction results from the numerical simulations of R=4 MPRAGE-MR acquisitions and two PET scan durations (10min and 5min). RMSEs to respective ground truths are displayed next to the reconstructed images. CG SENSE MR and PET EM reference reconstructions are shown together with separate, Frobenius and nuclear norm TGV and a Bowsherprior PET reconstruction using the separate TGV MR reconstruction as the MR prior. 10min PET data was used for the joint MR reconstructions shown here. RMSE values for MPRAGE jointly reconstructed with 5min PET are identical to those reconstructed jointly with 10min PET: 0.188 for Frobenius norm and 0.186 for nuclear norm. The strongest difference between the Bowsher prior and all TGV reconstructions can be observed in the area of the PET only lesion (cyan arrows, only added for 10min PET). For all Bowsher reconstructions, the unique PET lesion is heavily smoothed out and the signal intensity is decreased. In contrast, lesion sharpness and visibility is almost identical for the TGV reconstructions with and without MR coupling. Subtle sharp edges appear in the Bowsher and Frobenius norm 5min PET reconstruction in the area of the MR-only lesion (red arrows). Comparable artifacts appear in regions where no individual MR-lesions are present (some examples highlighted by blue arrows). In the skull region the nuclear norm shows no transfer of MR-specific features while small MR-only features start to appear in the Bowsher reconstruction (orange arrows). No transfer of edges or contrast of PET-only features occurs to MR (yellow arrows).

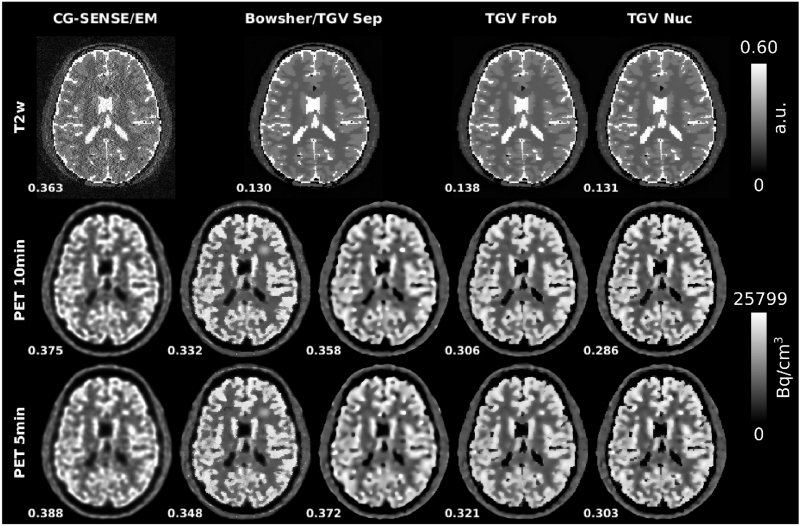
Fig. 4.

Reconstruction results from the numerical simulations of R=4 T2w-MR acquisitions with 10min and 5min PET.

Fig. 5.

Reconstruction results from the numerical simulations of R=4 FLAIRMR acquisitions with 10min and 5min PET.

TABLE II.

Region-of-interest specific PET RMSE values for gray matter in the head of the caudate nucleus (bilaterally), the left insula and the unique PET GBM lesion (a.u). For each combination of PET duration and MR contrast, the reconstruction result closest to the ground truth is depicted bold faced.

	10min PET dataset			5min PET dataset
	Caudate	Insula	GBM lesion	Caudate	Insula	GBM lesion
EM	0.243	0.250	0.203	0.248	0.269	0.196
TGV Sep	0.206	0.257	0.139	0.207	0.255	0.193
Joint MPRAGE
Bowsher	0.090	0.192	0.369	0.111	0.203	0.374
TGV Frob	0.124	0.217	0.138	0.139	0.220	0.191
TGV Nuc	0.126	0.202	0.147	0.148	0.206	0.190
Joint T2
Bowsher	0.187	0.238	0.366	0.195	0.239	0.373
TGV Frob	0.133	0.212	0.135	0.146	0.214	0.199
TGV Nuc	0.133	0.191	0.136	0.148	0.198	0.190
Joint FLAIR
Bowsher	0.144	0.212	0.355	0.152	0.215	0.367
TGV Frob	0.145	0.214	0.141	0.155	0.217	0.185
TGV Nuc	0.145	0.194	0.145	0.157	0.201	0.188

Assessment of MR- and PET-specific features provides additional insight in the behavior of the different methods and coupling norms. It can be seen that an edge appears subtly in the joint TGV and Bowsher prior PET reconstruction in the area of the MR-only lesion (highlighted by red arrows in Fig. 3). This transfer is slightly stronger for the Bowsher prior and the Frobenius-norm coupled TGV than for the nuclear-norm coupled TGV, in particular for the 5 minutes measurements. It can also be observed that comparable artifacts appear in regions where no individual MR-lesions are present (blue arrows). This effect is strongest in the separate PET TGV reconstruction but also visible in the other methods with the exception of EM. The strongest difference between the Bowsher prior and all TGV reconstructions can be observed in the area of the PET only lesion (cyan arrows, only added for 10min PET). For all Bowsher reconstructions, the unique PET lesion is heavily smoothed out and the signal intensity is decreased. In contrast, lesion sharpness and visibility is almost identical for the TGV reconstructions with and without MR coupling. This can also be observed in the corresponding GBM lesion RMSE values in Table II, which show pronounced deviations for the Bowsher prior. In the skull region the nuclear norm shows no transfer of MR-specific features (orange arrows). In contrast, the Bowsher reconstruction includes several small structures that are found in the MR-, but not the PET ground truth. Finally, no transfer of edges or contrast of PET-only features is visible in MR at all (yellow arrows in Fig. 3) in the two simultaneous MR-PET reconstructions with coupling (TGV Frob and TGV Nuc). A more detailed explanation of this behavior is presented in the discussion.

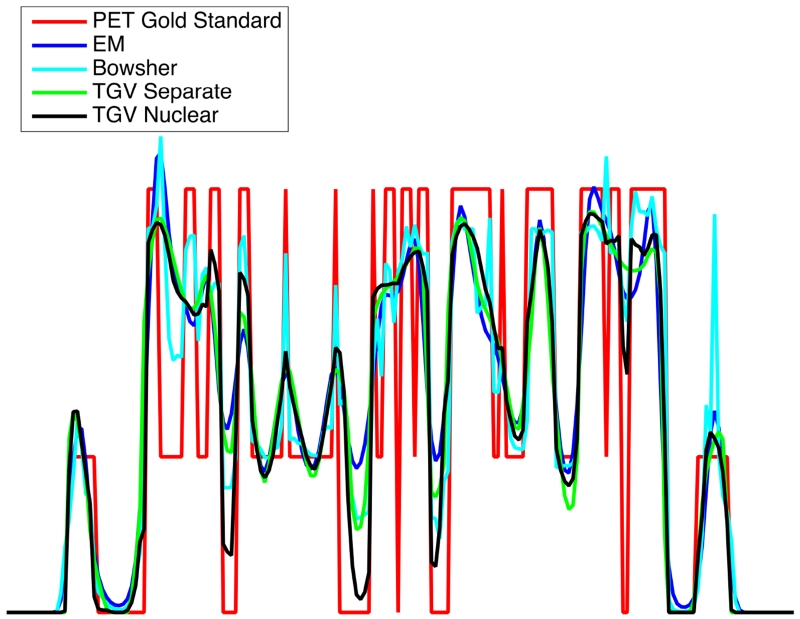
For EM, Bowsher, separate TGV and nuclear norm TGV, cross-sectional plots are drawn along a cortical section of the PET slice shown in Fig. 3 to visualize separation of gray and white matter as well as fidelity of the quantitative PET signal in comparison to the underlying ground truth (Fig. 6). They demonstrate that the fidelity of the quantitative PET signal to the ground truth is higher for nuclear norm coupling with MR than for EM and the PET reconstruction using separate TGV. The Bowsher reconstruction shows a distinctive artificial outlier in the signal from the cortex (far right peak in the plot) that corresponds to transfer of MR-specific features (highlighted by orange arrows in Figure 3).

Fig. 6.

Cross sectional plots across the left insula for PET EM, Bowsher, separate TGV and nuclear norm TGV reconstruction results from the R=4 MPRAGE numerical simulation and 5min PET, as shown in Figure 3.

The principal improvement observed in MR images is a reduction of parallel imaging noise amplification due to TGV in comparison to CG SENSE, which also results in pronounced reductions in RMSE for all investigated contrasts. The differences between coupled and separate TGV are minor. We provide a more detailed explanation of this behavior and the relation to the reported improvements for the MR-side of the reconstruction in [16] in the discussion section. We also found only minor differences between the MR reconstruction quality of the joint reconstructions with 10min and 5min PET scans. In particular, the RMSE values for the MR images coupled with the 5 minute PET scan were identical to those coupled with the 10min scans.

Overall quantitative PET signal values were evaluated in CSF, gray matter, white matter, caudate, left insula and the PET-only GBM lesion. The results are given in Table III and they confirm the findings from the cross sectional plots. For each combination of PET duration and MR contrast, the result closest to the ground truth is depicted bold faced. EM in general underestimates uptake in gray matter and overestimates uptake in white matter and CSF. While the PET reconstruction with the separate TGV constraint already reduces these deviations, the differences are further reduced substantially when a coupling norm to MR is used. The Bowsher prior performs best for the reconstructions with MPRAGE contrast, which was used for parameter optimization, while for the other cases, nuclear-norm based TGV performs best. With the exception of the 5min data PET-only GBM lesion, joint reconstruction resulted in the value closest to the ground truth for each experiment. The caudate has a simple structure and the results of the joint reconstruction are already very close to the ground truth. Due to the more complex interfaces between gray matter, white matter and CSF in the insula, partial voluming effects and therefore signal deviations of all methods are stronger there. The strongest deviations can be observed for the PET-only GBM lesion with the Bowsher prior.

TABLE III.

Quantitative analysis of the numerical brain simulations: PET signal activity levels (Bq/cm³) ± standard deviation. For each combination of PET duration and MR contrast, the reconstruction result closest to the ground truth is depicted bold faced.

(a) 10min PET dataset
	CSF	GM	WM	Caudate	Insula	GBM lesion
Ground truth	0±0	22990±0	8450±0	22990±0	22990±0	25799±0
EM	6358±5048	18812±4977	10648±3366	20620±5057	18704±3817	22288±3776
TGV Sep	5838±5932	18993±4096	10719±3383	20718±4159	18605±3932	26472±2285
Joint MPRAGE
Bowsher	4489±4585	20292±3590	9804±2721	21959±1809	19794±3031	16307±629
TGV Frob	4746±5313	19709±3295	10375±2887	21422±2374	19239±3294	24602±2089
TGV Nuc	4089±4881	20056±3119	10228±2773	21553±2509	19506±3066	25932±2920
Joint T2
Bowsher	5244±4869	19748±4360	10107±2984	21234±3922	19096±3858	16370±532
TGV Frob	4215±5301	19643±3143	10624±2941	21210±2503	19250±3144	24476±2008
TGV Nuc	3469±4591	20066±3018	10420±2901	21397±2606	19646±2860	25980±2616
Joint FLAIR
Bowsher	5215±5159	19101±3139	10817±2994	20358±2012	18981±2789	16678±928
TGV Frob	3702±5369	19711±3294	10719±3120	21206±2822	19322±3265	24762±2284
TGV Nuc	2910±4481	20081±3114	10605±3129	21324±2889	19678±2984	25907±2838

(b) 5min PET dataset
	CSF	GM	WM	Caudate	Insula	GBM lesion
Ground truth	0±0	22990±0	8450±0	22990±0	22990±0	25799±0
EM	6819±5078	18483±4861	10817±3461	19713±4681	18175±3898	23291±4090
TGV Sep	6214±5958	18743±4142	10850±3522	20114±3794	18403±3637	23550±4061
Joint MPRAGE
Bowsher	4872±4845	20026±3708	9950±2969	21654±2189	19461±3068	16154±693
TGV Frob	5169±5488	19409±3337	10553±3022	20901±2419	18937±3043	21693±2233
TGV Nuc	4488±5088	19780±3258	10388±2987	21006±2756	19275±2942	23052±3721
Joint T2
Bowsher	5628±5047	19464±4421	10266±3185	20823±3934	18864±3636	16189±591
TGV Frob	4630±5494	19334±3163	10817±3050	20767±2518	18980±2855	21314±2135
TGV Nuc	3836±4844	19803±3139	10575±3086	20939±2727	19384±2770	23066±3715
Joint FLAIR
Bowsher	5429±5236	19015±3204	10827±3032	20244±2183	18841±2679	16360±1020
TGV Frob	4034±5590	19431±3323	10897±3215	20751±2779	19005±3010	21996±2393
TGV Nuc	3188±4706	19854±3215	10746±3286	20847±2900	19360±2867	23169±3678

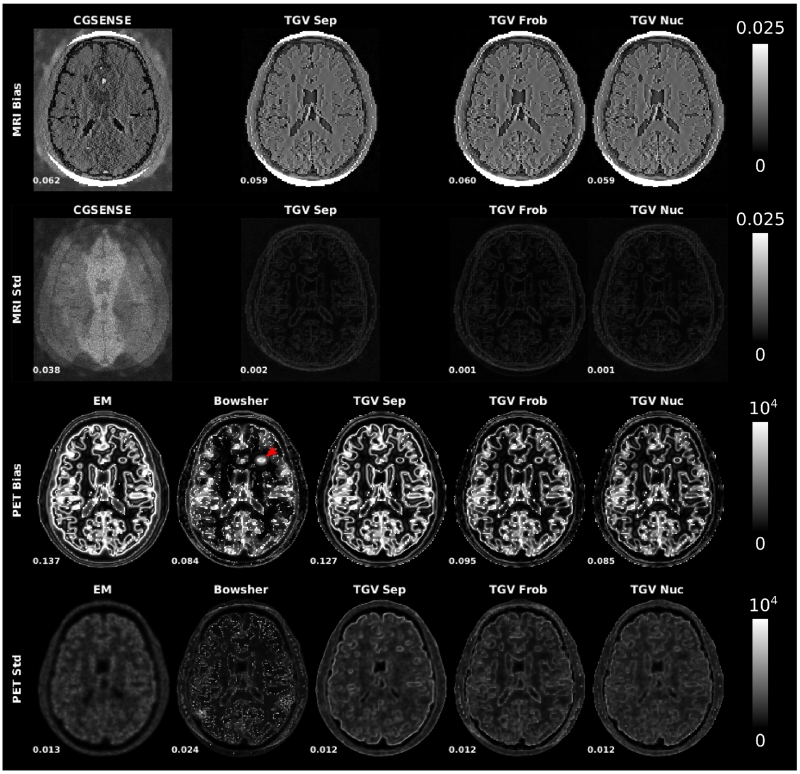
Bias and noise maps from the multiple replica experiment are shown in Figure 7 for MPRAGE and 5min PET datasets. The signal energy (squared sum of the map intensity values, normalized by the squared sum of the signal of the corresponding ground truth) is displayed next to each map. Standard deviation maps for MRI CG SENSE reconstructions show characteristic g-factor based noise amplification generated by the parallel imaging reconstruction. This effect is reduced substantially with all TGV reconstructions. The bias of EM-PET and separate TGV indicates loss of sharp edges, an effect that is reduced in all methods that use MR-information during the reconstruction (Bowsher, TGV Frob and TGV Nuc). The Bowsher reconstruction shows a pronounced spot of high bias in the area of the unique PET lesion (indicated by red arrow). PET standard deviation maps are comparable between EM and all TGV methods. In contrast, Bowsher reconstructions lead to a number of high intensity single pixel deviations that are visible in both standard deviation and bias maps.

Fig. 7.

Bias and noise maps from the multiple replica experiment. R=4 MPRAGE and 5min PET datasets. The signal energy (squared sum of the map intensity value, normalized by the squared sum of the signal of the corresponding ground truth) is displayed next to each map. The Bowsher reconstruction shows a pronounced spot of high bias in the area of the unique PET lesion (indicated by red arrow).

B. In-vivo measurements

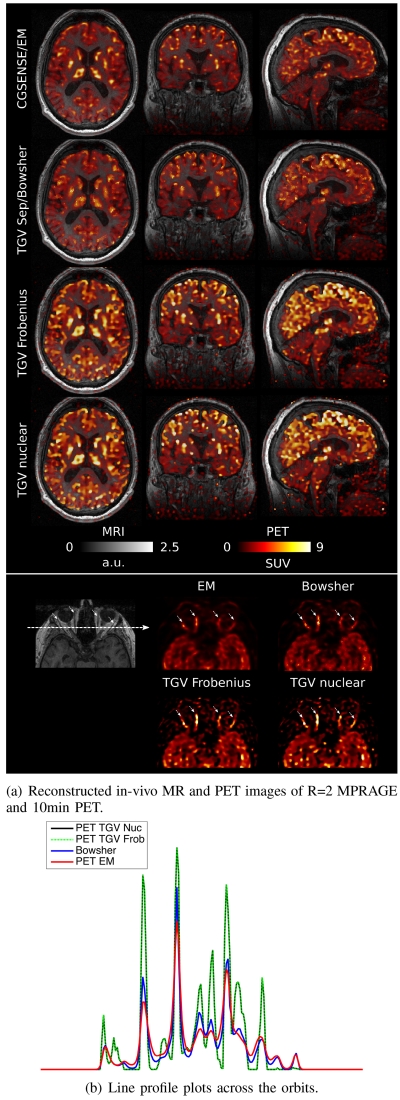
A comparison of CG-SENSE/EM, Bowsher using separate TGV MR as the image prior and multi-channel joint MR-PET TGV reconstruction with Frobenius and nuclear norm coupling for the first patient data set (R=2) is shown in Figure 8. PET reconstruction results were corrected for patient weight, injected dose and injection time, and are displayed as standardized uptake values. A general overview of the respective image qualities is given in the two top rows, which show overlays of MR and PET in a single transversal plane and in coronal and sagittal reformats. As in the phantom case, FDG uptake is higher in gray matter, which has lower signal intensity in an MPRAGE MR contrast. It can also be observed that features like the high signal intensity of subcutaneous fat in the MR image are not falsely imposed on the PET in the joint TGV reconstructions. The bottom row shows a zoom to a region in the transversal plane depicting ocular muscles and orbital fat. This region is interesting for evaluation of the joint reconstruction approach because the ocular muscles (highlighted by four small arrows) have a high glucose metabolism and therefore show a strong FDG uptake. The surrounding orbital fat can be assumed to have very little FDG uptake and therefore a strong contrast and sharp edge can be expected in PET. On the other hand, the MPRAGE sequence shows an inverted contrast, with hyper-intense fat signal. A line profile plot was generated across the orbits and is shown in Figure 8.b). The orbital muscles show up as four distinct peaks (again highlighted by arrows), which show sharper separation from the surrounding fat region in the Joint TGV reconstructions. In line with the findings in the phantom experiments, the peak signal values are higher for Joint TGV, while fat signal is higher for EM and, to a lesser extent, Bowsher. Visual differences between Nuclear norm and Frobenius norm joint TGV are hardly noticeable for this data set.

Fig. 8.

a) Overlays of MR and PET in a single transversal plane and coronal and sagittal reformats for the R=2 MPRAGE and 10min PET scan, comparing reference CG SENSE MR and a PET EM reconstruction (first row), Bowsher using separate TGV MR as the image prior (second row) and multi-channel joint MR-PET TGV reconstruction with Frobenius (third row) and nuclear (fourth row) norm coupling. A zoomed view of a region in the transversal plane depicting ocular muscles and orbital fat is shown in the third row. Sharpness and visibility of fine image features is clearly improved for the PET images with a multi-channel TGV regularizer. b) A line profile plot along the dashed arrow in the MR image of the orbital region. The orbital muscles show up as four distinct peaks (again highlighted by arrows), which show sharper separation from the surrounding fat region in the Joint TGV reconstructions.

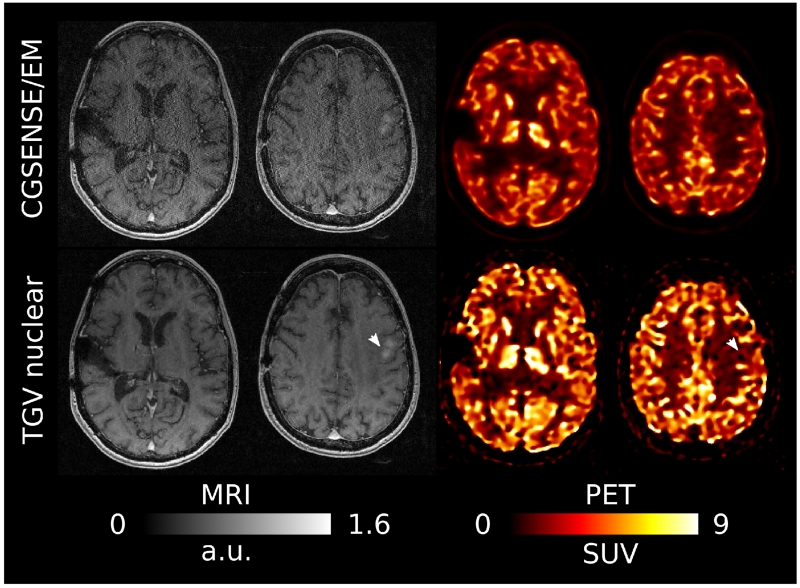
Two transversal slices of EM/CG-SENSE and TGV with nuclear norm coupling from the second patient data set are shown in Figure 9. Since the MR acquisition was performed with higher acceleration here (R=4), it is not possible to obtain artifact-free images with a conventional reconstruction. Therefore the difference in MR image quality is more obvious than in the R=2 case (Figure 8). An interesting feature of this particular dataset is that the MR scan shows a distinct hyper intense lesion in the cranial slice (highlighted by arrow), which is invisible in PET. The joint PET reconstruction is completely unaffected by this.

Fig. 9.

Two transversal slices for the R=4 MPRAGE and 10min PET scan. The MR scan shows a distinct hyper intense lesion in the cranial slice (highlighted by arrow), which is completely invisible in PET.

V. Discussion

In comparison to EM, our results demonstrate improved sharpness and visibility of fine structures for PET when using the proposed TGV method. The phantom experiments also show that the joint reconstructions outperform separate TGV reconstructions in terms of image sharpness, RMSE and quantitative PET signal values. Overall, the nuclear norm yielded the best results and therefore was selected for both in-vivo experiments. The quantitative evaluations of the PET signal values in the phantom experiments demonstrate that the jointly reconstructed signal values show smaller deviations from the true values than the EM reconstructions. The reason for this is the reduced signal spillover to spatially adjacent structures. This is evident in the signal from CSF, which was simulated to have zero FDG uptake. The signal spillover to CSF was reduced substantially in the joint MR-PET-TGV reconstruction in comparison to regular EM. In contrast, EM results showed systematic under-estimation in high-uptake regions like gray matter. These were also reduced with the proposed joint reconstruction approach. It should be noted that the main contribution to the standard deviations of the PET activity in Table III is not noise, but systematic errors from signal spill over at the tissue boundaries. When removing the border-voxels from the evaluation, CSF activity (ground truth 0 Bq/cm³) drops from 6358 ± 5048 Bq/cm³ to 3236±2674 Bq/cm³ for EM (10min dataset) and 4089±4881 Bq/cm³ to 1391±1956 Bq/cm³ for nuclear norm TGV (10min dataset, joint reconstruction with MPRAGE). GM activity (ground truth 22990 Bq/cm³) changes from 18812 ± 4977 Bq/cm³ to 21663 ± 3718 Bq/cm³ for EM (10min dataset) and 20056 ± 3119 Bq/cm³ to 21628 ± 1966 Bq/cm³ for nuclear norm TGV (10min dataset, joint reconstruction with MPRAGE). The in-vivo experiments demonstrate that the standardized uptake values obtained with our approach are in line with findings in the literature [42].

When comparing the TGV PET reconstructions to an anatomical prior method [11], two interesting observations can be made: The proposed TGV method is substantially more robust with respect to preserving unique features. The anatomical prior led to severe degradation of the unique PET lesion, and, consequently, substantial deviations of the signal values. In addition, the overall performance (global RMSE values, signal values and RMSE values of structures where corresponding features in MR are present) of the anatomical prior was comparable to the joint TGV reconstructions for the MPRAGE contrast, which was used to optimize the parameters for the individual methods. However, while TGV results were entirely robust with respect to variations in MR contrast (overall RMSE values for nuclear norm coupling were actually lower for joint reconstructions with T2 weighted and FLAIR contrasts than for MPRAGE), the performance of the anatomical prior dropped substantially.

Having a ground truth available, our numerical phantom experiments allow systematic assessment of reconstruction artifacts as well as the behavior of the individual coupling norms in areas where joint and individual features are present. Most notably, some additional lump-like structures are visible in particular in the separately regularized PET reconstructions (blue arrows in Fig. 3). This effect can be understood when considering the properties of a variational regularizer like TGV in the context of PET reconstruction. The regularization functional penalizes structures with high incoherence, like noise. However, our PET reconstruction operator includes resolution modeling with a Gaussian filter in each iteration. This increases intervoxel covariance [43] and allows the noise to form structures that fit to the image model promoted by the regularizer. As a result, with decreasing quality of the original PET signal, noise structures are clustered together as larger lumps and, depending on the trade-off between data fidelity and regularization, might be preserved in the regularized reconstruction. For the joint reconstruction, when MR-unique features are present at the same location as a noise cluster, lumps with a structure similar to the MR feature might appear (red arrows in Fig. 3). In phantom experiments, this effect was slightly stronger with Frobenius norm coupling and the Bowsher prior, but also appeared with the nuclear norm coupling. It is worth noticing, however, that the latter effect of the joint reconstruction is much weaker than the unstructured lumps that appear in the separate reconstruction and also seems to be a consequence of the particularly challenging, sharply separated small structure that we added in our simulations. Indeed, as marked by the orange arrow in Fig. 3, other MR-unique features of the phantom are not transferred to the PET signal at all and, as highlighted in Fig. 9, this behavior did not occur with MR-only features in real data. Unlike the PET operator, the MR forward mapping does not include resolution modeling and, consistent with the explanation above, the separately regularized MR reconstruction does not suffer from the generation of lump-like structures. For the joint reconstruction, no transfer of PET-only features to the MR component has been observed (yellow arrows in Fig. 3).

While our findings in terms of the improvement of the PET component of the reconstruction are in line with the numerical simulation study by Ehrhardt et al. [16], the authors of that study report much stronger improvements for MR. Our TGV results show clear improvements over CG SENSE for both phantom and in-vivo experiments. The difference between the coupling norms in the phantom study was less obvious. One difference of our approach compared to [16] is that our MR reconstruction also incorporates parallel imaging, which already increases reconstruction quality. Therefore our method does not completely rely on the regularizer to remove aliasing artifacts. For consistency of phantom and in-vivo experiments, our phantom study was based on moderately accelerated protocols that are currently used in clinical practice in our institution. In this setting the proposed separate 3D MR TGV reconstruction already resulted in almost ground truth image quality. We plan to investigate the use of joint reconstruction in MR acquisitions that are severely accelerated such that even a state of the art nonlinear PI-CS reconstruction breaks down (see below for more details). In addition, our MR acquisition followed a parallel imaging protocol, with regular Cartesian undersampling. In order to unleash their full potential, nonlinear L¹-based MR image reconstruction methods usually require incoherent aliasing artifacts generated by pseudo random [8] or non-Cartesian [9], [31] sampling patterns. However, these acquisition methods are in general only available in research settings and the vast majority of clinical scans is performed with regular Cartesian sampling and conventional PI. Therefore we chose to perform all our experiments according to protocols that are available on all MR-PET systems, even though they are an especially challenging scenario for our proposed method.

A. Relations to comparable work

The main principle of using the redundancies from multiple image series during the image reconstruction step is already well known. Joint reconstruction of multiple MR contrasts of a single acquisition protocol was recently described by several groups (e.g. [28], [44], [45], [46], [47], with [28] being the closest match to our proposed approach). Other examples for MR applications are Non-Proton MR [48], hyper polarized imaging [49] and diffusion imaging [50].

To the best of our knowledge, Ehrhardt et al. [51], [16] is the only other work that investigates joint image reconstruction in the context of MR-PET. The authors propose to exploit structural similarity between PET and MR images by either using a joint Total Variation with a Frobenius norm coupling of the image gradients, or by a parallel level set approach. The latter is motivated geometrically by the intention of aligning image gradients. Results in [16] show an improvement compared to non-regularized reconstruction for both settings, with superior results being obtained with the level set approach. In practice, [16] uses smoothed versions of the objective functionals and a quasi-Newton type method for the numerical solution.

While also being motivated by the idea of aligning image gradients, our method differs from [16] in various aspects. Most importantly, we use the second order TGV functional with nuclear norm based gradient coupling as image prior. From the numerical viewpoint, this results in an optimization problem comparable with the one arising from joint TV regularization. Conceptually, however, the nuclear norm coupling is in fact more closely related to the idea of aligning image gradients since, as mentioned in the theory section, the nuclear norm enforces sparsity of the singular values of the Jacobian, and hence, aligned edges. An important difference to the parallel level set method of [16], however, is the fact that our approach is convex and hence, independently of the initialization, always approximates globally optimal solutions.

Nuclear norm based regularization has already been proposed in [26] for TV regularization of color images and, in the context of medical imaging, in the work on reconstruction of tissue density maps from spectral CT data by Rigie et al. [27]. There, the authors also use a nuclear norm multi-channel vector valued total variation functional to exploit the correlations between the individual energy level channels of a spectral CT system. They also find that the nuclear norm is robust regarding unwanted transfer of individual features to other channels. An interesting parallel of their application is that individual energy channels of a spectral CT system often have significantly different noise levels. The main difference from MR-PET is that the channels are still subject to the same imaging physics. As a consequence the same types of mathematical operations are performed in the evaluation of the system matrices. This is a very different situation than for MR-PET, where the contrast mechanisms of our individual channels are fundamentally different, as well as the noise statistics and the imaging resolution.

B. Extensions and future work

This work describes the combination of a single MR-contrast with PET. However, in a typical MR-PET scan, multiple MR image contrasts are acquired during the PET acquisition. Therefore the MR component is usually the time limiting factor in an MR-PET scan, as it is not possible to obtain a full range of MR contrasts in the time that is required to obtain a single FDG-PET bed position. This basically renders the PET component of the system idle for a significant fraction of the total examination time. As a consequence further acceleration of the MR acquisition is of particular interest in the context of MR-PET.

Our current work is targeted at the integration of multiple contrasts in the proposed joint reconstruction framework. It is expected that this will further improve the redundancies in the multi-channel data and therefore lead to further improvements. A very interesting new MR data acquisition scheme in this context is MR fingerprinting [52]. In this approach the traditional procedure of multiple sequential MR sequences, each encoding a different contrast, is replaced by a single continuous data acquisition. For each voxel, the biophysical MR contrast parameters (T1 and T2 relaxation and spin density) are then estimated by fitting the temporal signal behavior to simulated properties of the spin system using the Bloch equations. When combined with concepts like fingerprint compression [53] to reduce the computational workload and demands on memory, this approach provides interesting synergies with a joint MR-PET reconstruction because it yields a time series of several image volumes, each with a slightly different image contrast and extremely high undersampling. This has the potential to reduce the MR data acquisition process to a single ≈10 minutes continuous measurement from which the desired contrasts can then be synthesized retrospectively [54].

At the moment our proof of concepts implementation in Matlab and C++ takes about 30s per iteration on a computing workstation configured to be similar to the image reconstruction workstation of our 3T PET-MR system (Two 8-core Intel Xeon 2.4Ghz processors with hyper-threading, 64GB of memory, Ubuntu 14.04 and Matlab R2015b). The total reconstruction times for 1000 iterations of the proposed primal-dual method are roughly 8 hours for the 3D volumes that were processed in the experiments in this work, independent of the used coupling norm. More than 95% of the computational burden is taken up by the evaluation of our in-house-implementation of the PET operator. In comparison, even the reconstruction times of our EM experiments were around 3 hours. We therefore expect a pronounced reduction of computation time when replacing the PET operator with implementations that are more optimized for computational efficiency, as used by the scanner vendors. This is obviously a prerequisite for clinical translation of the approach.

One advantage of the proposed framework is its flexibility. Because the only input is the raw data from both modalities, with proper adjustment of the forward operators, additional modules like motion correction or kinetic modeling can be incorporated. While the examples shown in this manuscript were taken from neurological applications, the potential for increased acceleration of MR acquisitions should have even greater impact in body applications. Whole body MR-PET places significantly higher time constraints on the MR acquisition of multiple bed positions. With 5-10min time slots available for each bed position, it is extremely challenging to acquire the needed range of MR contrasts simultaneously. Furthermore, we expect that the combination of joint image reconstruction with highly accelerated dynamic acquisitions and motion correction [55] will be particularly valuable for cardiac applications. Finally, the clinical impact of the observed improvements using the proposed approach remain to be evaluated in larger clinical studies.

Appendix: Numerical Implementation

This section details the numerical implementation for the solution of the convex optimization problem associated with TGV regularized joint MR-PET reconstruction. We denote by U = ℂ^N the space of vectorized 3D PET or MR image sets at the joint resolution, by C = ℂ^N × [0, ∞]^N the set of admissible reconstructions, by u₀ and v₀ the given PET and MR data, respectively, and by c₀ a given additive correction term for scattering and random events in PET. In a discrete setting, we we aim at solving

$$\begin{array}{cc}\hfill \underset{\left(u,v\right)\in C}{\min }& {\mathrm{TGV}}_{\alpha }^2\left(\left(u,v\right)\right)+\frac{\lambda }{2}{\Vert \mathit{Mu}-u_0\Vert }_2^2\hfill \\ \hfill & +\mu \sum _i{(\mathit{Pv}+c_0)}_i-{\left(v_0\right)}_i\log \left({(\mathit{Pv}+c_0)}_i\right),\hfill \end{array}$$ (4)

with ∥ · ∥₂ being a discrete ℓ² norm and Σ discretizing the integral appearing in the Kullback-Leibler divergence. The discrete vector-${\text{TGV}}_{\alpha }^2$ functional is defined according to Equation (2) with the ℓ¹, nuclear and Frobenius norms defined in a standard way. The discrete gradient ∇ : U² → U^2×3 and symmetrized gradient $\mathcal{E}:U^{2\times 3}\to U^{2\times 6}$ are defined as

$${(\nabla a)}^{c,1}={\delta }_{1+}{a}^c,{(\nabla a)}^{c,2}={\delta }_{2+}{a}^c,{(\nabla a)}^{c,3}={\delta }_{3+}{a}^c,$$

for a = (a¹, a²) ∈ U², and

$$\begin{array}{cc}\hfill {\left(\mathcal{E}w\right)}^{c,1}& ={\delta }_{1-}{w}^{c,1},{\left(\mathcal{E}w\right)}^{c,2}={\delta }_{2-}{w}^{c,2},{\left(\mathcal{E}w\right)}^{c,3}={\delta }_{3-}{w}^{c,3}\hfill \\ \hfill {\left(\mathcal{E}w\right)}^{c,4}& =\frac{{\delta }_{2-}{w}^{c,1}+{\delta }_{1-}{w}^{c,2}}{2},{\left(\mathcal{E}w\right)}^{c,5}=\frac{{\delta }_{3-}{w}^{c,1}+{\delta }_{1-}{w}^{c,3}}{2},\hfill \\ \hfill {\left(\mathcal{E}w\right)}^{c,6}& =\frac{{\delta }_{3-}{w}^{c,2}+{\delta }_{2-}{w}^{c,3}}{2},\hfill \end{array}$$

for $w=\left(\begin{array}{ccc}\hfill w^{1,1}\hfill & \hfill w^{1,2}\hfill & \hfill w^{1,3}\hfill \\ \hfill w^{2,1}\hfill & \hfill w^{2,2}\hfill & \hfill w^{2,3}\hfill \end{array}\right)\in U^{2\times 3}$, c = 1, 2, with

$${\delta }_{1+},{\delta }_{2+},{\delta }_{3+}:U\to U\text{and}{\delta }_{1-},{\delta }_{2-},{\delta }_{3-}:U\to U$$

being standard forward and backward finite difference operators with respect to the 1st, 2nd and 3rd coordinate, respectively, using symmetric boundary extension.

For the derivation of the primal-dual solution scheme as outlined in Section II we define the functionals

$$\begin{array}{cc}\hfill D_{\text{MR}}^{\lambda }\left(a\right)& ≔\frac{\lambda }{2}{\Vert a\Vert }_2^2,R\left(a,b\right)≔{\alpha }_1{\Vert {\mid a\mid }_{\text{nuc}}\Vert }_1+{\alpha }_0{\Vert {\mid b\mid }_{\text{frob}}\Vert }_1,\hfill \\ \hfill D_{\text{PT}}^{\mu }\left(a\right)=& \{\begin{array}{cc}\mu \sum _i{a}_i-{\left(v_0\right)}_i\log \left(a_i\right)\hfill & \text{if}{a}_i\in [0,\infty )\text{for all i},\hfill \\ \infty \hfill & \text{otherwise},\hfill \end{array}\phantom{\}}\hfill \end{array}$$

where we set (v₀)_i log(0) = −∞ if (v₀)_i > 0 and 0 log(0) = 0. Now by convex duality [56], we can rewrite

$$\begin{array}{cc}\hfill D_{\text{MR}}^{\lambda }\left(\mathit{Mu}-u_0\right)& =\underset{r}{\sup }\left(\mathit{Mu},r\right)-{\left(D_{\text{MR}}^{\lambda }\right)}^{\ast }\left(r\right)-\left(u_0,r\right),\hfill \\ \hfill D_{\text{PT}}^{\mu }\left(\mathit{Pv}+c_0\right)& =\underset{s}{\sup }\left(\mathit{Pv},s\right)-{\left(D_{\text{PT}}^{\mu }\right)}^{\ast }\left(s\right)+\left(c_0,s\right),\hfill \end{array}$$

with ${\left(D_{\text{MR}}^{\lambda }\right)}^{\ast }\left(r\right)=\frac{1}{2\lambda }{\mid \mid r\mid \mid }_2^2$ and

$${\left(D_{\text{PT}}^{\mu }\right)}^{\ast }\left(s\right)=\mu \sum _{\begin{array}{c}\hfill i\hfill \\ \hfill {\left(v_0\right)}_i\ne 0\hfill \end{array}}{\left(v_0\right)}_i\left(\log (-\frac{{\left(v_0\right)}_i\mu }{s_i-\mu })-1\right),$$

if s_i < μ for all i such that (v₀)_i ≠ 0 and s_i ≤ μ for all i such that (v₀)_i = 0, and ${\left(D_{\text{PT}}^{\mu }\right)}^{\ast }\left(s\right)=\infty$ otherwise, and

$$\begin{array}{cc}\hfill R\left(\nabla \left(u,v\right)-w,\mathcal{E}w\right)=\underset{p,q}{\sup }& \left(\nabla \left(u,v\right)-w,p\right)+\left(\mathcal{E}w,p\right)\hfill \\ \hfill & -{\mathcal{I}}_{A_1}\left(p\right)-{\mathcal{I}}_{A_2}\left(q\right),\hfill \end{array}$$

with A₁ := {p | ∥|p|_spec∥_∞ ≤ α₁} and A₀ := {q | ∥|q|_frob∥_∞ ≤ α₀}, where | · |_spec and | · |_frob denote the point-wise spectral and Frobenius norm, respectively, and ∥ · ∥_∞ the supremum norm over all points in space. The functional I_S again denotes the convex indicator function of a set S. Following the lines of Section II, the minimization problem (4) can then be rewritten as

$$\begin{array}{cc}\hfill \underset{\left(u,v\right)\in C}{\min }\underset{w}{\min }& R\left(\nabla \left(u,v\right)-w,\mathcal{E}w\right)+D_{\text{MR}}^{\lambda }\left(\mathit{Mu}-u_0\right)\hfill \\ \hfill & +D_{\text{PT}}^{\mu }\left(\mathit{Pv}+c_0\right)\hfill \\ \hfill \iff \underset{u,v,w}{\min }\underset{p,q,r,s}{\max }& \left(\mathit{Mu},r\right)+\left(\mathit{Pv},s\right)+\left(\nabla \left(u,v\right)-w,p\right)\hfill \\ \hfill & +\left(\mathcal{E}w,q\right)-\left(u_0,r\right)+\left(c_0,s\right)-\frac{1}{2\lambda }{\Vert r\Vert }_2^2\hfill \\ \hfill & -{\left(D_{\text{PT}}^{\mu }\right)}^{\ast }\left(s\right)-{\mathcal{I}}_{A_1}\left(p\right)-{\mathcal{I}}_{A_2}\left(q\right)+{\mathcal{I}}_C\left(\left(u,v\right)\right)\hfill \\ \hfill \iff \underset{u,v,w}{\min }\underset{p,q,r,s}{\max }& \left(K\left(u,v,w\right),\left(p,q,r,s\right)\right)-F^{\ast }\left(p,q,r,s\right)\hfill \\ \hfill & +{\mathcal{I}}_C\left(\left(u,v\right)\right),\hfill \end{array}$$ (5)

with

$$K\left(u,v,w\right)=\left(\begin{array}{c}\hfill \nabla \left(u,v\right)-w\hfill \\ \hfill \mathcal{E}w\hfill \\ \hfill \mathit{Mu}\hfill \\ \hfill \mathit{Pv}\hfill \end{array}\right)$$

and

$$\begin{array}{cc}\hfill F^{\ast }\left(p,q,r,s\right)=& \left(u_0,r\right)-\left(c_0,s\right)+\frac{1}{2\lambda }{\Vert r\Vert }_2^2+{\left(D_{\text{PT}}^{\mu }\right)}^{\ast }\left(s\right)\hfill \\ \hfill & +{\mathcal{I}}_{A_1}\left(p\right)+{\mathcal{I}}_{A_2}\left(q\right).\hfill \end{array}$$

Application of the iterations steps (3) together with an adaptive stepsize choice as in [22] to the saddle-point problem in the last line of Equation (5) then yields the iterative scheme given in Algorithm 1.

There, proj_α1(p) and proj_α0(q) denote the projections to the sets A₁ and A₀, respectively. The former requires a point-wise computation and projection of the singular values, for which we use a fast custom implementation tailored to large arrays of 3 by 2 matrices. The latter requires the computation of the point-wise Frobenius tensor norm followed by a point-wise division and can hence also be computed explicitly and fast. Further, ${\text{prox}}_{{\left(D_{\text{MR}}^{\lambda }\right)}^{\ast },\sigma }$, and ${\text{prox}}_{{\left(D_{\text{PT}}^{\mu }\right)}^{\ast },\sigma }$, are the proximal mappings of the convex conjugates of the data fidelity maps, and are given as

$${\text{prox}}_{{\left(D_{\text{MR}}^{\lambda }\right)}^{\ast },\sigma }\left(r\right)=\frac{r}{1+\frac{\sigma }{\lambda }}$$

and

$${\text{prox}}_{{\left(D_{\text{PT}}^{\lambda }\right)}^{\ast },\sigma }\left(s\right)=s-\frac{s-\mu +\sqrt{{(s-\mu )}^2+4\sigma \mu v_0}}{2},$$

where all operations are understood point-wise. The operator proj_C is the proximal mapping of the indicator function that restricts the reconstruction to C and corresponds to a projection of the PET channel to the non-negative reals. The operators div and div₂ denote discrete divergence operators

Algorithm 1.

TGV regularized MR-PET reconstruction

1:	function TGV-MR-PET(u0, v0, c0, λ, μ)
2:	M ← rescale_operator(M, ζM)
3:	P ← rescale_operator(P, ζP)
4:	u0 ← rescale_data(M*u0) · u0
5:	(v0, c) ← rescale_data(P*(v0 – c0)) · (v0, c0)
6:	u ← M*u0, v ← P*(v0 – c0), (ū, v̄) ← (u, v)
7:	w → 0, w̄ ← 0, p ← 0, q ← 0, r ← 0, s ← 0
8:	choose η > 0, σ > 0, τ = σ/η2
9:	repeat
10:	p ← projα1 (p + σ(∇(ū, v̄) – w̄))
11:	q ← projα0 (q + $\sigma \mathcal{E}\overline{w}$)
12:	r ← prox(${\left(D_{\text{MR}}^{\lambda }\right)}^{\ast }$),σ(r + σMū – σu0)
13:	s ← prox(${\left(D_{\text{PT}}^{\mu }\right)}^{\ast }$),σ(s + σPv̄ + σc0)
14:	(u+, v+) ← (u, v) – τ(−div p + (M*r, P*s))
15:	(u+, v+) ← projc((u+, v+))
16:	w+ ← w – τ(−p − div2 q)
17:	(ū, v̄, w̄) ← 2(u+, v+, w+) – (u, v, w)
18:	${\sigma }_{+}\leftarrow \eta \mathcal{S}\left(\sigma \tau ,\frac{\mid \mid (u_{+},v_{+},w_{+})-(u,v,w)\mid \mid }{\mid \mid K\left(\right(u_{+},v_{+},w_{+})-(u,v,w\left)\right)\mid \mid }\right)$
19:	τ+ ← σ+/η2
20:	(u, v, w) ← (u+, v+, w+)
21:	until Stopping criterion fulfiled
22:	return (u+, v+)
23:	end function

and are defined as the negative adjoints of ∇ and $\mathcal{E}$, respectively. The parameter η defines a fixed ratio of the dual and primal stepsizes and σ and τ the mapping S realizes an adaptive stepsize choice that ensures convergence of the algorithm (see [22]). For θ ∈ (0, 1), it is defined as

$$\mathcal{S}\left(\sigma \tau ,\mathfrak{n}\right)=\{\begin{array}{cc}\mathfrak{n}\hfill & \text{if}\sqrt{\theta \sigma \tau }\ge \mathfrak{n},\hfill \\ \sqrt{\theta \sigma \tau }\hfill & \text{if}\sqrt{\sigma \tau }\ge \mathfrak{n}>\sqrt{\theta \sigma \tau },\hfill \\ \sqrt{\sigma \tau }\hfill & \text{otherwise}.\hfill \end{array}\phantom{\}}$$ (6)

Empirically we have observed that this reduces the stepsize only during the first 10 iterates and hence, to save computational cost, S is evaluated only during the first 50 iterations and after that every 50th iteration. Alternatively, as K needs to be evaluated once on each iterate anyway, it would also be possible to re-formulate the algorithm in such a way that the stepsize criterion does not require additional evaluations (at the cost of using slightly more memory).

Initialization

Regarding the initialization of the algorithm, we stress that prior to starting our method, the operators M and P are re-scaled to have operator norm approximately 1. This is done once for a particular setup by estimating their norm via power iteration [57]. Furthermore, the normalized operators are rescaled (as in lines 2 and 3 of the algorithm), which in practice accelerates convergence. Also the given data u₀, v₀ and c₀ is rescaled to be approximately at the same scale. This is done by the function rescale_data, which is designed to robustly scale the range to approximately [0,100] and in detail returns a scalar given as 100 divided by the mean of all entries of the input that are above 80% of the maximal entry.

Parameter choice

A list of the chosen values for all parameters (except for the regularization parameters which are discussed in Section III) is provided in Table IV. We stress that those are all parameter entering the method (mostly algorithmic parameters) and the procedure is rather robust against their choice. In particular, the values σ and θ are only shown for the sake of completeness and should only be chosen reasonably, i.e., σ should be not too small and θ close to one. Also the rescaling of the MR and PET operator as well as the ratio between the primal and dual stepsize are algorithmic parameters and have been chosen empirically to accelerate convergence. The choice of the TGV weights can be seen as default value that has already been used in diverse applications and has not been tuned.

TABLE IV.

List of fixed parameters

Parameter	Value	Meaning
(ζM, ζP)	(3,10)	Rescaling of MR and PET operator
η	10	Ratio between primal and dual stepsize
σ	10/$\sqrt{12}$	Initialization of primal stepsize
θ	0.95	Stepsize reduction factor
(α0,α1)	($\sqrt{2}$, 1)	TGV weights

Stopping criterion

To ensure a proper implementation and convergence of our method we have evaluated an approximation of the primal-dual gap (similar to [22]), which is zero only for optimal solutions to the saddle-point problem in the last line of Equation (5). For an iterate (u, v, w, p, q, r, s), the normalized primal-dual gap is defined as

$$\begin{array}{cc}\hfill \mathcal{G}(u,v,w& ,p,q,r,s)≔N^{-1}[F\left(K\left(u,v,w\right)\right)+H\left(u,v,w\right)\phantom{]}\hfill \\ \hfill & \phantom{[}-\left(-H^{\ast }\left(-K^{\ast }\left(p,q,r,s\right)\right)-F^{\ast }\left(p,q,r,s\right)\right)].\hfill \end{array}$$

The definition of $\mathcal{G}$ contains indicator functions of set constraints. Some of those, such as the positivity constraint on the PET variable, are satisfied at each iteration and hence can be skipped. Others are fulfilled only in the limit of the iterates, and we replace such indicator functions by a penalization of the deviation from these constraints. In concrete, this yields the following modified primal-dual gap:

$$\begin{array}{cc}\hfill & \tilde{\mathcal{G}}\left(u,v,w,p,q,r,s\right)≔N^{-1}[R\left(\nabla \left(u,v\right)-w,\mathcal{E}w\right)\phantom{]}\hfill \\ \hfill & +D_{\text{MR}}^{\lambda }\left(\mathit{Mu}-u_0\right)+D_{\text{PT}}^{\mu }\left(\mathit{Pv}+c_0\right)+\sum _i\mid {(p+{\text{div}}_{2}q)}_i\mid \hfill \\ \hfill & +\sum _i\max \{{\left(\text{div}p\right)}_{2,i}-{\left(P^{\ast }r\right)}_i,0\}-\left(c_0,s\right)+{\left(D_{\text{PT}}^{\mu }\right)}^{\ast }\left(s\right)\hfill \\ \hfill & \phantom{[}+\sum _i\mid {\left(\text{div}p\right)}_{1,i}-{\left(M^{\ast }r\right)}_i\mid +\left(u_0,r\right)+\frac{1}{2\lambda }{\Vert r\Vert }_2^2].\hfill \end{array}$$

As the evaluation of this quantity comprises significant computational cost, and as it comprises a rather conservative estimate of optimality in practice, we did not employ the modified primal-dual gap as stopping criterion, but rather used a fixed number of 1000 iterations for the proposed experiments. Empirically, we have observed that this is sufficient to ensure proper convergence of the algorithm and reduces modified primal-dual gap by three orders of magnitude.