The fractal heart — embracing mathematics in the cardiology clinic

Abstract

For clinicians grappling with quantifying the complex spatial and temporal patterns of cardiac structure and function (such as myocardial trabeculae, coronary microvascular anatomy, tissue perfusion, myocyte histology, electrical conduction, heart rate, and blood-pressure variability), fractal analysis is a powerful, but still underused, mathematical tool. In this Perspectives article, we explain some fundamental principles of fractal geometry and place it in a familiar medical setting. We summarize studies in the cardiovascular sciences in which fractal methods have successfully been used to investigate disease mechanisms, and suggest potential future clinical roles in cardiac imaging and time series measurements. We believe that clinical researchers can deploy innovative fractal solutions to common cardiac problems that might ultimately translate into advancements for patient care.

Introduction

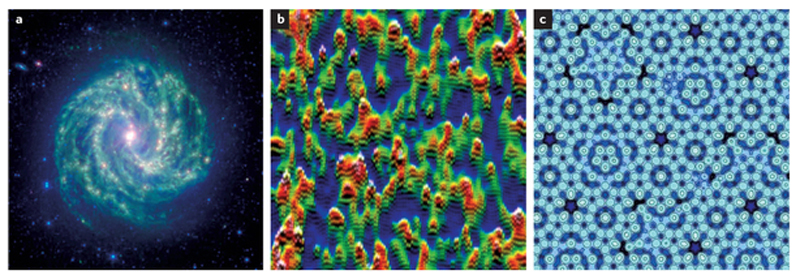
Fractal patterns are everywhere: in mathematics¹, industry², the stock market³, climate science⁴, galaxies⁵, trees⁶, and even in the films we watch and games we play^{7, 8} (Fig. 1). Fractal theory has a major role in biology, including in the human heart. As in the entertainment industry, the role of fractals in biology has gone beyond helping us to formulate theoretical abstractions, and has reached a practical level that expands the boundaries of the field. Indeed, one of the first lessons learned from studying the fractal nature of the cardiovascular system was that it strives to preserve not stability, but adaptive variability — a discovery that redefined canonical notions of cardiac homeostasis^{9, 10}. Today in cardiology, we face a new frontier in translating lessons learned from fractal theory to care at the bedside^{11, 12}. In this Perspectives article, we update the field with relevant results from the studies in the cardiovascular sciences that have successfully used fractal analyses to investigate disease mechanisms, and we outline their potential future clinical role in measuring the complex biological processes of the human heart.

Figure 1.

Examples of natural fractal phenomena. a | This photograph by NASAs Spitzer Space Telescope shows the spectacular fractal complexity of barred spiral galaxy Messier 83 (colloquially, the Southern Pinwheel), constellation Hydra at 15 million light years away. Image reprinted courtesy of NASA/JPL-Caltech. b | Multifractal patterns have been spotted in the quantum realm — at the atomic-scale resolution of a scanning tunnelling microscope, the sudden transition at which a material changes from a metal to an insulator, the waves associated with individual electrons gain a distinct multifractal pattern⁷⁴. Permission obtained from Ali Yazdani, Physics Department, Princeton University, USA. c | The quasifractal complexity of the 'conceptually impossible' fivefold symmetrical arrangement seen in the atomic model of an aluminium–palladium–manganese quasicrystal surface. Its surface structure can be modelled by a mathematical Penrose tiling that is self-similar at different scales. Image reprinted from Thiel, P. A. et al. A distinctive feature of the surface structure of quasicrystals: intrinsic and extrinsic heterogeneity. Isr. J. Chem. 51, 1326–1339 (2011), with permission from John Wiley and Sons.

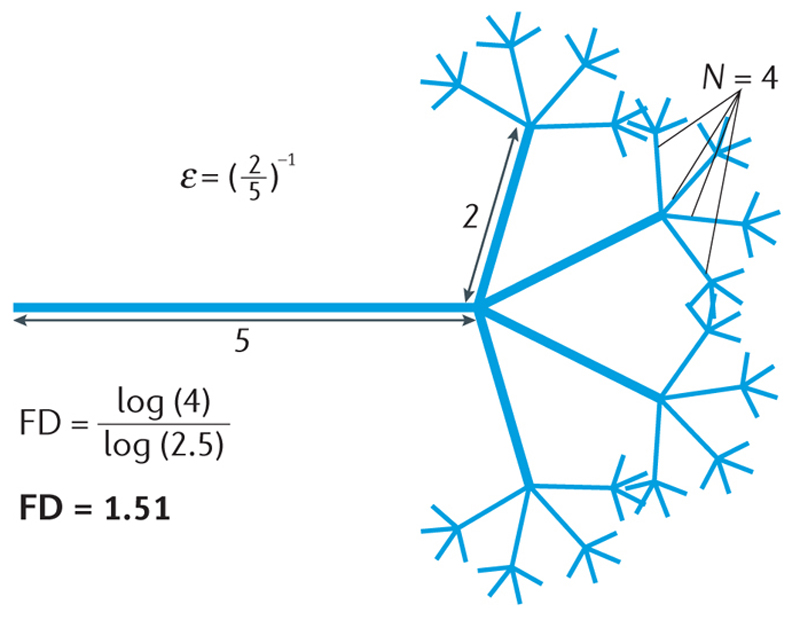
The link between fractal theory and practical applications to cardiovascular medicine is the fractal dimension (FD), a unitless number that measures nontrivial, self-similar scaling. A phenomenon is self-similar if the whole resembles its scaled parts, and its self-similarity is 'nontrivial' if, in essence, the design detail and repetitive arrangement creates a pattern too 'rough' or 'irregular' to be defined by Euclidean geometry. For example, a simple line is self-similar, but only trivially so. By contrast, a branching line that sprouts four branches each two-fifths the size of, but otherwise identical to, the parent is nontrivially self-similar. Moreover, this branching line is infinitely self-similar if every branch forever sprouts new branches using that same four to two-fifths scaling rule¹³ (Fig. 2).

Figure 2.

Theoretical fractal dimension (FD). The concept of nontrivial and infinite self-similarity can be appreciated in this hypothetical branching fractal set with theoretical FD of 1.51. Although the diagram illustrates three levels of branching, the theoretical pattern persists infinitely. ε⁻¹, scale; N, number of measuring segments.

In fractal parlance, the FD measures a phenomenon's 'complexity', which is the logarithmic ratio of the change in detail to the change in scale. The changes in detail and scale are related by the fundamental fractal relation N ∝ ε^FD, from which the FD is found by taking the log of each side and solving for the exponent: FD = log N/log ε (Ref. 13). The change in detail in our hypothetical pattern is the number of sprouts per branch (N = 4), and the change in scale is the factor relating sprout size to parent size (ε = (2/5)⁻¹ = 5/2). Its FD, then, is log 4/log (5/2) = 1.51. This number describes a phenomenon existing between the bounds of the familiar notion of dimension: a simple line, for instance, has an FD of 1, and a plane has an FD of 2 (Fig. 3), but the length of the branching line described above falls between these. This example illustrates a general rule that separates the FD from traditional notions of dimension: whereas the familiar dimension must adopt only integer values, fractal dimensions can be integer or fractional^{1, 13}.

Figure 3.

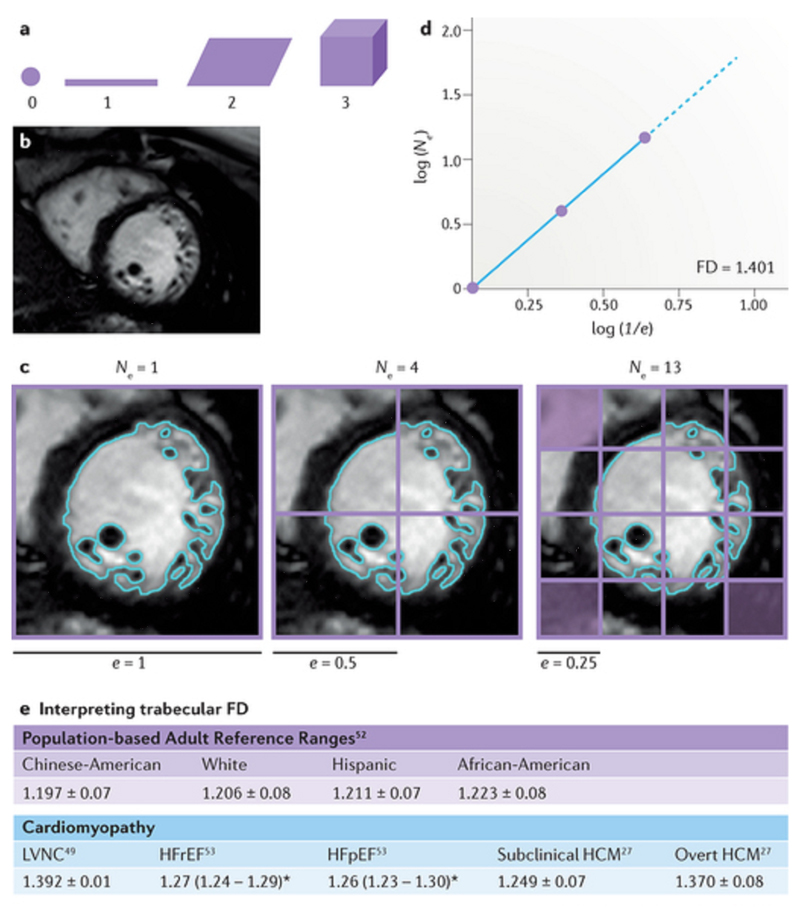
Traditional geometry and spatial fractals. a | The regular Euclidean dimension, meaning the familiar geometrical descriptors, assigns an integer to each point or set of points in space: 0 to a point, 1 to a straight line, 2 to a plane surface, and 3 to a volume or 3D figure. Complex macroanatomical or microanatomical structures cannot be analysed by regular Euclidean geometry, but can be described quantitatively by fractal geometry as a fractal dimension (FD) falling inclusively between these integer topological dimensions. b | The FD for the trabeculae in a 2D digitized image such as this cardiovascular magnetic resonance cine left ventricular short-axis slice will lie inclusively between 1 and 2, and for a 3D image, between 2 and 3. c | The box-counting method works by applying a grid of boxes of side length (e) over the image of the fractal (>60 grids are needed for this contour, but only three are shown) and counting the number (N_e) of the smallest number of boxes of side length (e) required to cover the surface or outline of the object completely. d | The empirical box-counting FD (1.401 in this example) is estimated from the slope of a regression line when log(N_e) is plotted against log(1/e); therefore, FD = log (N_e)/log(1/e). e | Summary of the clinically relevant ranges of FD in health and disease derived from cardiovascular magnetic resonance research studies in the literature to date. All data reported as mean ± SD or mean and interquartile ranges (denoted by *). HCM, hypertrophic cardiomyopathy; HFpEF, heart failure with preserved ejection fraction; HFrEF, heart failure with reduced ejection fraction; LVNC, left ventricular noncompaction.

The FD can be calculated for other types of patterns. One type is the classic example of a theoretical contour, analogous to the classic example of a coastline¹³ or — relevant to cardiology — the edge of an infarction scar. If the pattern of a contour scales as a fractal, the boundary appears equally invaginated regardless of the magnification with which it is examined or, in other words, it never resolves into a smooth curve lacking detail. Measuring the changes in detail and scale for a contour can be understood through the mental exercise of measuring it by laying sticks of a fixed length, end to end, along the contour and counting the sticks, then reiterating the process using shorter and shorter sticks. The number of sticks at any size is the detail (N) and the length of the measuring stick relative to its previous length is the scale (ε⁻¹) in the fundamental fractal relation. If the pattern scales as a fractal, the number of sticks required increases as shorter and shorter sticks are used. For an infarction, decreasing the size of the measuring stick is analogous to zooming in with a microscope or increasing the resolution of a digital image.

The essential principles inherent in the fundamental fractal relation can be applied to virtually any pattern type or number set. In cardiology, this means, in addition to the branching patterns and contours discussed above, textures, 2D and 3D spaces, and time series data. In practice, fractal analysis is usually done with automated, user-friendly software that rapidly analyses patterns obtained from a variety of digital signal recording methods, bioinformatics tools, and imaging modalities.

The empirical FDs thus determined differ from theoretical FDs in particular ways. One is the limit of scaling, which manifests in two important ways: in the phenomenon itself and in the methods of determining the FD. The limits of natural spatial phenomena relevant to cardiology rest in the body not allowing infinite self-similarity over progressively smaller distances, because organs are composed of cells, solutions, and embedding matrices, all of which are in turn made up of components that at some point reach a finite size. Just as spatial fractal behaviour can be seen in anatomical structures, temporal fractals can be seen in physiological signals such as blood pressure or heart rate, characterized by fluctuations that show equivalence across a range of timescales (cf. space-scales)¹⁴. Again, these parameters are limited at short timescales because heart rate is observable only once per heart beat.

The second factor — scaling limits attributable to methodology — rests in the resolution of the method used to obtain and then analyse temporal and spatial signals. In cardiology, examples include low-resolution versus high-resolution echocardiography for temporal signals and the resolution available in magnetic resonance versus X-ray versus light microscopy for spatial signals. Further methodologically imposed limits exist in the process of obtaining a pattern: for digital images of cardiovascular fractals, for instance, pixel and image size limits of the software and particular computer hardware used superimpose limits on the original signal-gathering methods.

Another way in which empirical FDs differ from theoretical FDs is that phenomena in nature generally do not reproduce the identical pattern, but statistically similar patterns. As an example, the branching coronary tree (Fig. 4a) differs from our hypothetical branching model (Fig. 2) by sprouting not in a strictly repeated pattern relative to parent branches, but in an essentially similar repeating pattern. This general feature of natural scaling is not an error of imprecision; rather, in biology it supports adaptive variability¹⁵ and is likely to be determined by different recursive generative processes that operate across space-scales within systems (for example, the 'rules' responsible for generating capillaries are not identical to those generating large arteries, probably because physical influences of viscosity and inertia differ). Consequently, the fractal complexity of spatial structures in cardiology would be expected to differ based on physiology^{16, 17, 18}. It has been argued that such natural patterns are more accurately called 'random', 'statistical', or 'quasi' fractals rather than simply 'fractals', and that the term 'scale-invariant' should be used to distinguish patterns that are not strictly self-similar. In most of the published literature and in this Perspectives article, however, the term 'fractal' is used to describe biological phenomena irrespective of practical limits, just as the terms 'cyclical' and 'constant' are used for behaviours that are not so in a mathematical sense. Readers should, therefore, consider the idiom as well as the method by which fractal scaling is measured when reading that a biological phenomenon has a fractal dimension or fractal architecture^{13, 19}. The important point is that fractal patterns in the heart, although they might not scale indefinitely in space or time, are nevertheless perfectly amenable to fractal analysis²⁰, so the FD can still be used to describe them (Fig. 3b–e).

Figure 4.

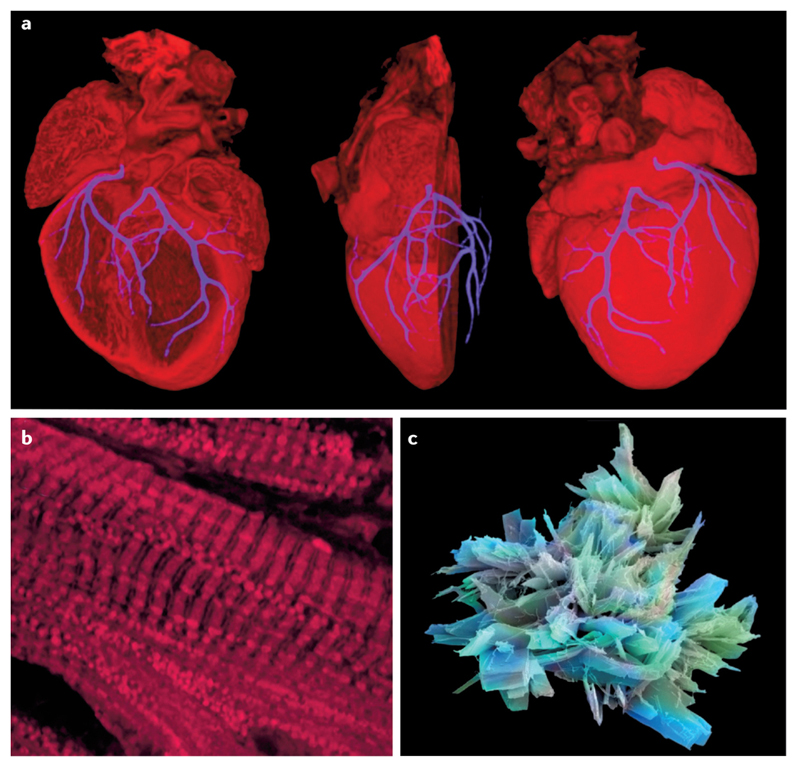
Cardiology is replete with examples of fractal structures. a | The coronary arterial tree is an example of a space-filling fractal network. The fractal branching of the coronary vasculature of a mouse heart at embryonic day 18.5 is shown here as a 3D composite image derived by high-resolution episcopic microscopy. Image reprinted courtesy of NIMR, MRC/Wellcome Images [B0007341]. b | Fractal patterning is seen in this confocal micrograph of cardiac muscle stained for mitochondria. Image reprinted courtesy of NIMR, MRC/Wellcome Images [B0006854]. c | Aspirin, the most iconic cardiovascular drug has a beautiful crystalline structure of fractal complexity. Image reprinted courtesy of Annie Cavanagh/Wellcome Images [B0006216].

Biological systems and organogenesis

In general, biological systems do not have one overarching FD. From genome to proteome to morphology to function, developmentally and over time, the heart exhibits features in both the spatial and temporal domains that are amenable to fractal analysis. Features for which FDs have been found in the heart include temporal recordings of signals, such as electrocardiograms¹⁴, pulse²¹, pressure and flow^{22, 23}, as well as arrangements of spatial components such as DNA sequences²⁴, proteins²⁵, extracellular matrix constituents²⁶, trabeculae²⁷, and, as already alluded to, coronaries and infarction scar boundaries^{28, 29, 30}. Spatial fractal patterns in the heart are extracted by imaging instruments and bioinformatics tools at various levels of its organization (genome, proteome, organellar, cellular, tissue, whole-organ), and they can describe the complexity of signalling pathways, metabolic networks, and macroscopic structures²⁸.

Despite the diverse range of phenomena within the cardiovascular system amenable to fractal analysis, some motifs can be expected to repeat over broad scales. Cells, tissues, and organs perform specific tasks in a coordinated manner. At the cellular and subcellular levels, diffusion has a major role in the transport of food, waste, gas, and heat. At this end of the scale, cell size is constrained by the surface-to-volume ratio needed for efficient diffusion³¹, as dictated by the fundamental laws of thermodynamics³².

For multicellular organisms, the smallest theoretical unit is not really 'one cell', but the combined 'service volume–transport system complex'. This theoretical unit supports transportation, distribution, and exchange over a wide range in volume and mass as it fills the 3D space of organs and organisms¹⁸, covering nine orders of magnitude from the cell to a gram of tissue³³ and, for mammals, a further eight orders of magnitude (for example, from the 1.5 g of a white-toothed pigmy shrew to the 130 tonnes of a blue whale³⁴).

The allometric scaling required for organogenesis is a familiar and pervasive topic in biology, and typically follows simple quarter-power laws (such as three-quarter power scaling for metabolism, or one-quarter power for growth rates, size, or heart rates). Indeed, the whole of metazoan organogenesis is underlain by fractal principles, whether by confluence, intussusception, clefting, or sprouting³⁵, resulting in hierarchical, branching patterns of cellular clusters and transportation networks that repeat a fundamental design detail over many orders of magnitude. Several human organs are founded on such a fractal anatomy. Some examples are coronary vessels and Purkinje fibres in the heart, neurons, bronchial trees, and the biliary and urinary tubing systems in liver and kidneys, respectively³⁰. From material science, moreover, we have learned that fractal 3D solids can be created using only three things: growth, competition or selective pressure (for a resource needed for energy-efficient growth), and a degree of randomness³⁶. All these factors also apply to biological tissues, in which controlled intercellular communication is layered on top of diffusion to determine the destination architecture.

Fractal applications in cardiology

'Omic' complexity

Many of the FDs that have been determined for the heart have far-reaching practical implications. One practical matter that fractal analysis is helping to resolve is today's data deluge of genomic, transcriptomic, proteomic, and metabolomic information³⁷ (Fig. 5). At the cellular level, the cardiac myocyte, like all cells, is a complex series of highly interconnected 'omic' systems whose structure and functional behaviour are fractal, variable, and adaptive¹⁵. With regard to the genome, for instance, two topics that fractal analysis is helping to clarify are the inherited heart muscle disease hypertrophic cardiomyopathy (HCM) and our understanding of so-called 'junk DNA'. HCM is the most common monogenic heart disease, predominantly caused by autosomal dominant mutations in sarcomere protein genes^{38, 39}, in 20% of patients involving mutations in the β-myosin heavy chain (myosin 7) gene (MYH7) — an intron-containing gene⁴⁰. Unexpected MYH7 intron retention in mature mRNA transcripts has been linked to heart failure⁴¹, suggesting that the introns might be especially important in HCM. 1D DNA walks that provide a graphical representation of the human MYH7 DNA sequence²⁴ have shown statistical scale-invariance in the arrangement of introns, in the form of long-range correlations consistent with a fractal pattern²⁴. Coding DNA and intron-free genes do not have this property²⁴. Given that these introns can be pathogenic, coupled with the assumption that their fractal complexity and algebraic distribution⁴² potentially underlies a biologically relevant organizational role, adds support to a growing body of evidence⁴³ suggesting that their designation as 'junk DNA' might be a misnomer. This fractal landscape does not stop with the genome, but persists into the human proteome: the distribution of pentapeptide redundancies in human proteins has been studied by fractal analysis, and the proteomic FD has been used to qualitatively distinguish and catalogue short linear peptide motifs critically involved in cell biology²⁵.

Figure 5.

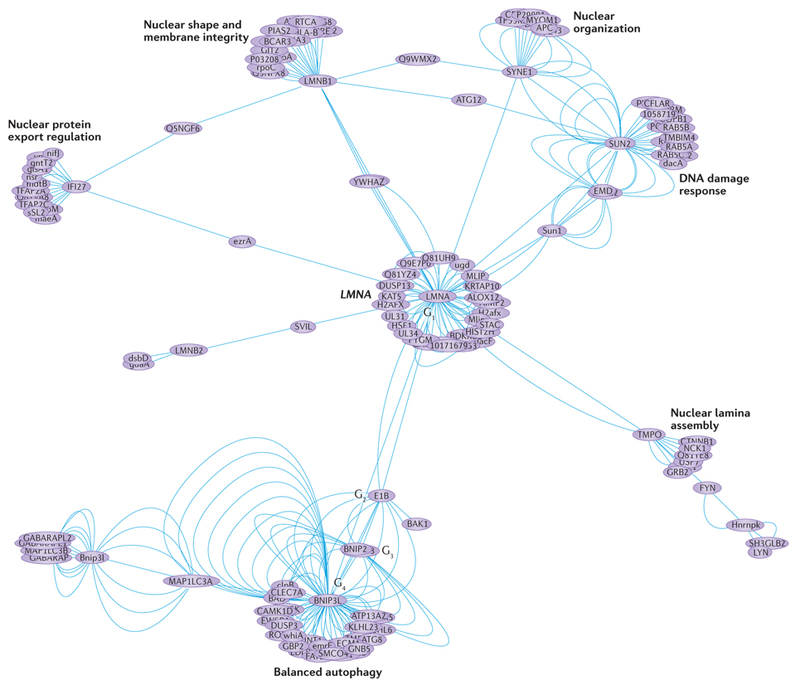
Omic-level complexity in the human heart. Mutations in the lamin gene (LMNA) cause dilated cardiomyopathy. The edge-weighted spring embedded human LMNA protein–protein interactome can be regarded as an example of a 'Sierpinski' weighted fractal network. It is constructed from a single node (LMNA) as the initial network (G₁), emanating from which are further network generations (G₂–G₄). This interactome was constructed from 287 binary interactions and excludes spoke-expanded complexes. Topological and functional clusters (modules) are visible and it is now possible to use multifractal analysis (a modified sandbox algorithm⁷⁵) to quantify the probability distribution of the clustering coefficient in such weighted real-world networks. Interactions sourced using IntAct⁷⁶ and The Molecular INTeraction database [MINT] and manually curated; network created using IntAct View v.4.2.3.2 and Cytoscape v.3.0.2. For example dataset, see Supplementary information S1 (spreadsheet).

Cellular and tissue complexity

Fractal analysis has also provided insights into the cardiovascular system at the cellular and tissue levels. Fractal concepts have been used to study the morphology of microtubules and the actin cytoskeleton⁴⁴ in cardiac myocytes (Fig. 4b), to grade the severity of acute rejection in haematoxylin and eosin-stained biopsy samples from patients who have undergone heart transplantation⁴⁵, and to compare collagen deposition and organization in the hearts of normotensive and hypertensive mice²⁶. The last study suggested that FD results can be used to quantitate differences between two types of myocardial extracellular matrix fibrosis:reparative fibrosis, in which voids from myocyte loss fill in with characteristically disordered and space-filling collagen; and reactive fibrosis, in which there is little myocyte loss but increased collagen deposition occurs in a characteristically ordered, less space-filling pattern. The investigators suggest that what the FD quantitates is potentially related to stiffening of the myocardium and might be relevant to models of scarring in general, and specifically to pharmaceutical strategies targeting transcription factors implicated in human cardiac fibrosis.

In cardiac electrophysiology, a need exists to combine in vivo imaging techniques with computational modelling to reconstruct accurately the 3D geometry of the complex human Purkinje network. These technologies could support the design of personalized strategies for single-ventricle or biventricular pacing, radiofrequency ablation, and cardiac defibrillation. Manual generation of Purkinje networks is complicated, low-quality, and time-consuming, so electrophysiologists and bioengineers have partnered to develop fractal tree algorithms for a more realistic simulation of the human cardiac excitation sequence⁴⁶.

Clinical, high-resolution myocardial tissue perfusion imaging technologies across modalities, including cardiovascular magnetic resonance (CMR)²², stand to gain from fractal insights into the roles of myocardial local mechanics, metabolism, and regional flows in causing regional myocardial blood flow heterogeneity. Animal-based fractal analysis research of the myocardium using microspheres has shown that, in the absence of coronary disease, regional myocardial blood flow heterogeneity was caused by local, metabolically-driven differences in vasomotor regulation and not by local differences in vascular anatomy²³. This revelation — that physiologically there are normally some low-flow regions in the heart that are not at all ischaemic — might be highly clinically relevant. If this phenomenon is occurring on the macroscopic scale, appreciating it could potentially avoid some false-positive diagnoses of regional ischaemia and unnecessary referrals for invasive coronary angiography.

Macroscopic structure and function

Fractal analysis has been applied to transthoracic echocardiography images, and recent work indicates that the FD might have a role in clinical echocardiography. One study, for example, used texton-based feature extraction to detect areas of myocardial infarction automatically⁴⁷. 'Texton' refers to fundamental microstructures in natural images or subtleties of image texture related to preattentive human visual perception⁴⁸. The algorithm used in the study examined minute pixel variations in single echocardiographic views of the heart. It used a total of eight features, including one based on fractal analysis that measured surface roughness as an FD⁴⁷. The results from the 160 individuals (50% with infarction) are especially promising given that the method is automated, foregoing the need for the operator manually to define the part of the image to assess.

We have successfully applied box-counting fractal analysis (Fig. 3b–d) to CMR images to quantify left ventricular myocardial trabeculae⁴⁹. We initially used the FracLac for ImageJ plug-in, then translated to MATLAB, and finally to dedicated commercially and publicly available Fractal Analysis plug-ins (implemented in cvi⁴² and OsiriX⁵⁰, respectively). Using this method, the endocardial complexity of the normal human left ventricle can be measured (that is, a measure of the extent to which endocardial contours fill the 2D image space). The FD of the human left ventricle changes in a characteristic pattern from base to apex⁴⁹, recapitulating the fractal observations along the length of the left ventricle in the developing mouse heart, where a 'compaction' process accompanies the development of the coronary arteries⁵¹. The FD of trabeculae varies considerably in the adult population (Fig. 3e), differing by ethnicity, left ventricular mass, the presence of hypertension, and increased body mass index⁵².

In another study, CMR fractal analysis revealed how heart failure with either reduced or preserved ejection fraction⁵³ shared a common trabecular phenotype, and how the method could have a role in refining the diagnosis of left ventricular noncompaction⁴⁹. CMR trabecular fractal analysis could be used to detect the subtle abnormalities in HCM before the development of left ventricular hypertrophy²⁷. An increased trabecular FD seems to be a feature of the subclinical HCM phenotype, and might be useful as part of a scoring system for the prediction of genetic carriage in relatives of affected probands during family screening. Further work is needed to understand the role of such imaging approaches in family screening when genotyping finds no pathogenic mutation in the proband⁵⁴. Fractal analysis could be particularly useful in HCM, because studies in mouse models suggest that HCM might be a form of 'cardiac neotonization' (Ref. 55), with preservation of embryological crypts and alterations in trabeculae. These alterations would be expected to manifest as increased FD.

Heart physiology analysis

Embedded in the signal of the healthy human heart rate and blood pressure power spectrum is a characteristic frequency regime over time with three power components: a high-frequency component reflecting respiratory fluctuations, a low-frequency component, and a very low-frequency component. Fractal measures have been used to provide a quantitative description of irregularities within these complex signals and to study their autonomous modulation at multiple levels¹⁴. Generally, a loss of heart-rate variability predicts higher mortality⁵⁶. Results have aided the diagnosis, characterization, and classification of cardiac pathologies, informed about patients' risks of adverse events (malignant and nonmalignant arrhythmias, sudden cardiac death) and, when applied to intrapartum fetal heart-rate variability monitoring, yielded better acidosis detection compared with traditional methods⁵⁷, thus potentially reducing morbidity, mortality, and long-term sequelae associated with fetal hypoxia.

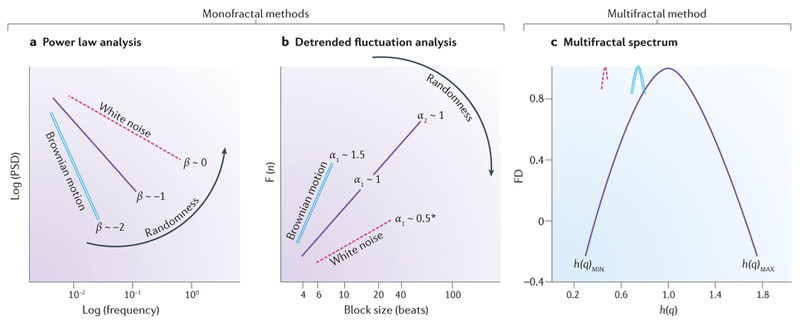
Temporal fractal analysis of physiological signals aims to identify the presence of one or more of the following features: self-similarity, power law scaling relationship, and scale invariance⁵⁸. Signals in physiology can be regarded as analogous to either of two types of discretely sampled fractal processes: stationary fractional Gaussian-type (of constant variance over time) or nonstationary fractional Brownian-type (more common for physiological signals, where variance increases with time)⁵⁸. Dichotomizing a signal by this model a priori can guide the choice of fractal method for a given time series analysis. The three main fractal methods (two monofractal, and one multifractal) that have been used to study physiological cardiac signals are respectively: a power law analysis using the Fourier method that evaluates the inter heart-beat intervals to generate a power spectrum density (PSD) summarizing the frequency harmonics embedded within the cardiac rhythm (that is, it characterizes power law scaling in the frequency domain); a detrended fluctuation analysis (DFA), which measures the degree of correlation among timescales embedded within the heart-beat intervals (that is, it characterizes power law scaling in the time domain); and a multifractal analysis which assumes that different subparts of the heterogeneous heart-rate signal are characterized by local regularities, each with different FD (it also characterizes power law scaling in the time domain). Although these methods differ in their operational domain (frequency versus time), their fractal measures do relate to each other and to the overarching FD in a simple manner (conversion equations linking PSD and DFA outputs to the FD are provided in the legend to Fig. 6).

Figure 6.

Monofractal and multifractal analyses applied to heart-rate variability. a | In power law analysis, the fractal index β (negative slope) is derived from a log–log plot of the power spectrum density (PSD) analysis (calculated from Fourier analysis of heart-rate intervals) versus frequency. β is related to fractal dimension (FD) by the following equation: FD = (5 − β)/2 (Ref. 58). b | In detrended fluctuation analysis (DFA), the short-term and long-term exponents, α₁ and α₂, are derived from a plot of the amplitude of detrended fluctuations (F(n)), calculated from heart-rate intervals versus the block size n (in beats), on a logarithmic scale. The short-term exponent, α₁, is a measure of the degree to which the beat intervals are correlated on a scale of 4–16 beats, whereas the long-term exponent, α₂, is a measure of the degree to which the beat intervals are correlated on a scale of 16–64 beats. α is related to FD by the following equation: FD = 3 −α (Ref. 58). Fractal indexes from systems with paradigmatic properties are represented by a solid line for the ideal fractal signal which has a β, α₁, or α₂ of 1. Increase in the slopes implies allostasis and rigidity with the maximum being Brownian motion at ~1.5 for α₁ or ~−2 for β (double line). Decrease in the slopes implies more randomness, that is, approaching white noise (dashed line). *Some cardiovascular time series exhibiting antipersistent behaviour can occasionally have α₁ <0.5 (Ref. 68,77). c | The plot of FD versus the generalized (DFA-derived) Hurst coefficient (h(q))⁷⁸ is referred to as the multifractal spectrum⁷⁹ (single solid line). The width of the spectrum in this example is consistent with multifractal behaviour which contrasts with the narrower spectrum (with more constant h(q)) that is observed with monofractal signals (double line) or white noise (dashed line) to the left. h(q)_MIN and h(q)_MAX indicate the multifractal spectrum width.

For the PSD/Fourier method, the slope of the line relating log frequency to log PSD is the single fractal scaling exponent, β (Fig. 6a). For the DFA method, the average amount of fluctuation over bins of different sizes is measured (similar to the box-counting method, but this time in the temporal domain). DFA, therefore, measures the root mean square deviation between the signal and its trend in each bin and then plots this as a function of bin size. DFA generates a short-term exponent (α₁) and a long-term exponent (α₂)²¹ (Fig. 6b). The DFA for a healthy (young) heart forms almost straight-line segments with two slopes, α₁ and α₂ — a hallmark of ideal fractal behaviour. Patients with type 2 diabetes mellitus, for example, show increased α slopes which are suggested as indicators of autonomic dysfunction⁵⁹. Fractal indices of heart-rate variability have demonstrable prognostic capacity when applied clinically: α₁ predicts sudden cardiac death in the elderly⁶⁰ and echocardiographic deterioration in dilated cardiomyopathy⁶¹, whereas α₂ predicted sudden cardiac death and survival functions in patients with heart failure and implantable cardioverter–defibrillators in SCD-HeFT⁶². Although survival in patients with heart failure can be improved by implantable defibrillators, <25% of patients who receive a device actually experience sudden cardiac death or appropriate shock therapy⁶³. If sudden cardiac death prediction models for heart failure were to incorporate fractal indices of heart-rate variability, patient selection for implantable defibrillators might be refined, helping to exclude those unlikely to benefit from device implantation. Multifractal analysis, which produces a range of exponents (Fig. 6c), has been used to distinguish between healthy and diseased heart signals in heart failure and coronary artery disease^{64, 65}, and to measure the effect of percutaneous coronary intervention and open-heart surgery on the behaviour of the human heartbeat⁶⁶.

Practical challenges

Clinicians seeking to use fractal algorithms to interrogate human biology should bear in mind this statement published in The Lancet: “Since fractal analysis is essentially mathematical, as with all mathematical models, there must be a close link with the biological event, if the model is to be useful” (Ref. 67). For spatial or temporal fractal analyses to be deployed securely in clinical hands, their mathematical bases need to be understood; they must be applied using rigorous, repeatable, and validated methods; and their outputs must be interpreted within an ever-changing clinical context.

If a spatial fractal analysis is to be undertaken in patients, many aspects of image acquisition and postprocessing (such as segmentation algorithm to create a binary outline, mask size, limits of the bounding box, range of grids) need to be carefully specified because they can affect the computed FD. For example, in the case of boundary-line fractal analysis of myocardial trabeculae by CMR, initial studies have shown that the most valid trabecular contours were obtained using an automated level-set segmentation algorithm that avoided user-dependent image-intensity histogram adjustment and incorporated a correction for intensity inhomogeneities across the cine slice. Using a standardized image acquisition/postprocessing protocol, the box-counting FD was shown to be robust to field strength change (from 1.5 to 3.0 Tesla) and to limited cine slice-thickness variations (from 7 to 8 mm)⁵⁴.

For fractal analysis of time series in patients, similar challenges exist. For heart-rate variability analysis, some fractal techniques still require the preprocessing or editing of premature beats in the recordings⁶⁸, and particular methods remain sensitive to artefacts and alterations in recording conditions (such as duration, body temperature, body position, free-breathing versus controlled-breathing and physical activities⁶⁹, and effect of drug therapy and dosage alteration⁶⁶). These factors can all substantially affect short-term metrics, making comparisons between studies challenging. Clinicians should also bear in mind that fractal measures of heart-rate variability provide only an indirect (qualitative) assessment of cardiac autonomic activity, because no direct measurement of either cardiac parasympathetic or sympathetic nerve activity is currently possible⁷⁰.

Future directions

The fractal nature of the human heart should be harnessed for its descriptive, diagnostic, prognostic, and therapeutic insights⁷¹, which requires the development of innovative bedside products based on fractal mathematics. For both spatial and temporal fractal analyses, it is not unreasonable to expect these metrics to be of greatest prognostic utility when combined with other more familiar clinical or imaging cardiac biomarkers (such as blood pressure and serum cholesterol level), so researchers in future studies should aim to investigate prospectively the role of such novel compound risk-scoring systems in clinical practice. Large-scale studies are needed to explore the superiority of fractal analysis methods compared with standard methods in diagnostics and risk stratifications.

For the best-studied application of fractal analysis in heart-rate variability, the global boom of wearable fitness technologies means that longitudinal, valid, and potentially reliable RR-interval data⁷² are now suddenly available for billions of people around the world. This development calls for the establishment of an open-source, Internet-based, high-availability, high-throughput, fractal analysis pipeline in which participants can deposit their heart-rate data in exchange for meaningful personalized health statistics, while also providing vital cardiac insights⁷³.

Many cardiac research groups are already working on new and repurposed fractal tools for use in the clinic, but a major barrier to their routine bedside delivery remains the need to demonstrate meaningful improvements in patient care when used in randomized, controlled trials — an arduous, expensive, and time-consuming process. Thankfully, a number of successful and fascinating research applications of fractal analyses have been presented here, underscoring the versatility, sensitivity, and multiple potential applications in the cardiovascular domain.

We suggest that clinical delivery of any fractal tool across the cardiovascular domain will require three important elements: close collaboration among researchers from different disciplines; shared access to good-quality, multicentre 'big data' (Ref. 73) (imaging, functional phenotyping, and multi-omics); and fractal toolkits of open-source software, discussion sites, online tutorials, publications, and openly accessible training datasets.

Conclusions

The cardiovascular system exhibits fractal complexity at every level and systematic analysis has the potential to identify pathological patterns of cardiac 'decomplexification' (such as the loss of heart-rate variability in heart failure) or 'hypercomplexification' (such as the excessive trabeculation in left ventricular noncompaction). Creative experimentation with fractals has yielded encouraging results — cardiologists moonlighting as mathematicians are steadily working out the fractal sums to expand our understanding of cardiac development, structure, and function.