Perspective: Revisiting the Field Dependence of TROSY Sensitivity

Abstract

The discovery of the TROSY effect (Pervushin et al. 1997) for reducing transverse relaxation and line sharpening through selecting pathways in which dipole-dipole and CSA Hamiltonians partially cancel each other had a tremendous impact on solution NMR studies of macromolecules. Together with the methyl TROSY (Tugarinov and Kay 2004) it enabled structural and functional studies of significantly larger systems. The optimal field strengths for TROSY have been estimated to be on spectrometers operating around 900 MHz (21.14 T) for the ¹H_N TROSY (Pervushin et al. 1997) while the aromatic ¹³C (¹³C_aro) TROSY is posited to be optimal at around 600 MHz (14.09 T) (Pervushin 2000; Pervushin et al. 1998b). The initial rational was based on the consideration of where the quadratic B₀ field dependences of the TROSY relaxation rates reach a minimum. For sensitivity consideration, however, it is interesting to estimate which field strengths yield the tallest peaks. Recent studies of ¹⁵N-detected TROSYs suggested that maximal peak heights are expected at 1.15 GHz (27.01 T) although the slowest relaxation rates or longest transverse relaxation times T₂ are indeed expected around 900 MHz (21.14 T) (Takeuchi et al. 2016; Takeuchi et al. 2015). This was based on the fact that the heights of Lorentzian lines are proportional to B_o^3/2 * T₂ (B_o). Thus, multiplying the parabolic T₂(B_o) dependence with the increasing function of B_o^3/2 shifts the maxima of peak-height field dependence from the T₂ maximum at 900 MHz to higher fields. Moreover, besides shifting the peak height maximum for ¹⁵N TROSY, this analysis yields estimates for optimal peak heights for ¹H_N detected TROSY to 1.5 GHz, and to 900 MHz for ¹³C-detected ¹³C_aroTROSY as is detailed below. To our knowledge, this aspect of field dependence of TROSY sensitivity has not been in the attention of the NMR community but may affect perspectives of NMR at ultra-high fields.

Though nuclear magnetic resonance (NMR) has intrinsically low sensitivity compared to other spectroscopic techniques, its slowly relaxing coherences are rich in structural and dynamics information. Therefore, solution NMR has been a widely used approach for structural and dynamics analyses of macromolecules at atomic resolution, especially since NMR can analyze samples at near-physiological conditions. However, with a shift of focus to higher molecular weight (MW) systems, the application of solution NMR has become more challenging, primarily because of the shortening of the transverse relaxation time (T₂) and the associated line broadening of the resonances. In addition to the broader lines, larger systems have a proportionally larger number of resonances within a given spectral width, which hampers unambiguous resonance assignment. Furthermore, as the heights of Lorentzian lines are directly proportional to T₂ (Fig. 1A), the sensitivity of solution NMR spectroscopy without the TROSY effect decreases with higher MW.

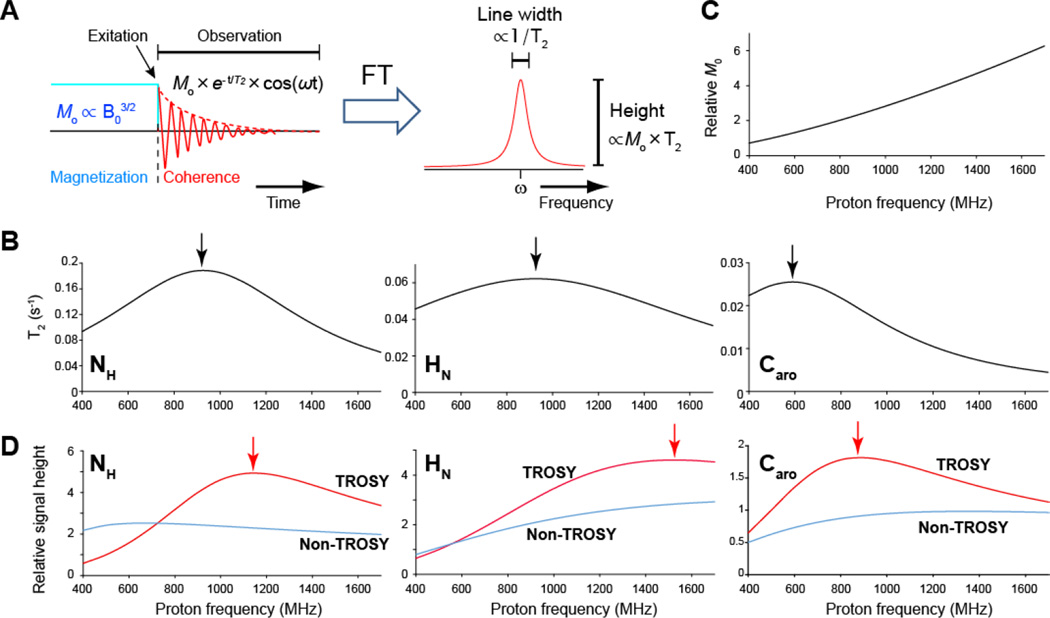
Figure 1. Resolution and sensitivity of TROSY resonances.

(A) Relation of T₂ and initial magnetization (M₀) in time domain to resolution (line width) and sensitivity (signal height), respectively, in frequency domain. (B) T₂ of the ¹⁵N_H, ¹H_N, and ¹³C_aro TROSY resonances for the protein with rotational correlation time of 20 ns. For the ¹⁵N_H and ¹H_N TROSY resonances, α-helical part of ²H¹⁵N labeled protein is assumed. For the ¹³C_aro TROSY resonances, non-deuterated altenately¹³C-¹²C labeled protein that is labeled with 3-¹³C labeled pyruvate was assumed. Detail of the calculation of T₂ are shown below. (C) Field dependence of M₀ relative to that at 500 MHz. (D) 1D Signal height of TROSY (red) and conventional decoupled non-TROSY (cyan) resonances relative to the signal height of TROSY resonances at 500 MHz. The signal height for the non-TROSY resonances are doubled.

Several innovative strategies have been introduced to cope with the short transverse relaxation times of larger systems. These include perdeuteration for reducing dipole-dipole (DD) broadening (Farmer and Venters 1996; Kushlan and LeMaster 1993; LeMaster 1989; Venters et al. 1995), and the use of slowly relaxing methyl resonances for detection (Goto et al. 1999; Lemaster 1990; Markus et al. 1994; Rosen et al. 1996). Subsequently, the introduction of transverse relaxation-optimized spectroscopy (TROSY) has revolutionized solution NMR and enabled studies of significantly larger systems (Loria et al. 1999; Meissner and Sorensen 1999; Pervushin 2000; Pervushin et al. 1998a; Pervushin et al. 1997; Pervushin et al. 1998b; Pervushin et al. 1998c; Pervushin et al. 1998d; Salzmann et al. 1998; Weigelt 1998). The TROSY method offsets a major part of the transverse relaxation by the cross-correlated DD-chemical shift anisotropy (CSA) interference to elongate T₂ (Pervushin et al. 1997). While the principle and anticipation for the cross-correlated relaxation resulting in different line widths of heteronuclear doublet components have also been described in earlier literatures (Farrar and Quintero-Arcaya 1985; Griffey and Redfield 1987) it has only later been recognized as a major tool for improving resolution, and thus sensitivity as well, of protein spectra (Pervushin et al. 1997). This TROSY effect is most efficient in the isolated two-spin systems that have CSA large enough to interfere with DD. In addition, the angle between DD and principal CSA component should be close to parallel, to have an optimal TROSY effect. The “methyl TROSY” effect for methyl groups in deuterated proteins had also a dramatic effect on NMR studies of large proteins. However, it is not derived from the interference of DD-CSA relaxations but from interference between auto- and cross-correlated ¹H-¹H dipolar relaxations (Tugarinov et al. 2003) and is not be discussed in this perspective.

In the past, the TROSY effect for ¹⁵N_H or ¹³C_aro has primarily been used in ¹H-detected multidimensional experiments. However, the long T₂ of TROSY ¹⁵N_H and ¹³C_aro resonances have made these nuclei attractive for direct detection (Takeuchi et al. 2016; Takeuchi et al. 2015). Due to their low gyromagnetic ratio (γ), these spins do not experience much dipolar broadening from ¹H nuclei in remote positions even at non-deuterated conditions. Therefore, we have recently shown that the TROSY effect can be utilized for ¹⁵N_H-detection even if proteins are not deuterated (Takeuchi et al. 2016; Takeuchi et al. 2015). This has important advantages as it opens avenues for studies of systems that cannot be deuterated because they can only be expressed in cells that do not grow at high concentrations of ²H₂O, such as insect or mammalian cells. Furthermore, this largely eliminates the problem of incomplete amide back exchange encountered when working with large perdeuterated proteins that cannot be refolded. In addition, the T₂ ratio of TROSY vs decoupled non-TROSY coherences is insensitive to the molecular weight of the system for any nuclei (Takeuchi et al. 2016; Takeuchi et al. 2015). Thus, the TROSY strategy significantly pushed the upper limit for systems that solution state NMR can address.

It has been widely postulated that 900 MHz is the optimal frequency for the both ¹⁵N_H and ¹H_N TROSY, because the optimal DD-CSA interference give rise to the longest transverse relaxation times T₂ of TROSY components at the magnetic field strength of 21.14 T (900 MHz). As shown in Fig. 1B, the T₂ value has a quadratic dependence on the field strength, in the shape of parabolic T₂ dependence with a vertex at 900 MHz as noted in previous publications (Pervushin 2000; Pervushin et al. 1997). Therefore, the aforementioned assumption is entirely true for minimal line width, which is inversely proportional to T₂. However, we posit that this has to be revisited with respect to sensitivity. For sensitivity, the peak height is what matters and the peak height is not only directly proportional to T₂ but also depends on the strength of the magnetic field by B₀^3/2.

Therefore, the sensitivity is proportional to the product of T₂(B₀) and B₀^3/2. The product of the T₂ field dependence with the increasing B₀^3/2 function (Fig. 1C) shifts the maximum of the peak height significantly to higher field (Fig. 1D, red). We have discussed this previously and have shown that the ¹⁵N_H-deteced TROSY resonance is estimated to be most sensitive at 1.1-1.2 GHz, while the narrowest line widths can be obtained at 900 MHz (Takeuchi et al. 2016; Takeuchi et al. 2015). The difference between the optimal field strength for slowest transverse relaxation and for sensitivity varies depending on parabolic T₂ dependence that reflects the relative contribution of the DD and CSA of each nucleus and the angle between the respective tensors (Fig. 1D, red). The maximum sensitivity of the ¹H_N TROSY shifts to around 1.5 GHz, which is at significantly higher field than the maximum for ¹⁵N_H TROSY. This is due to a smaller contribution of CSA relative to DD to ¹H relaxation, which makes the tangent of the parabolic T₂ dependence less steep for ¹H_N than for ¹⁵N_H and sensitivity is more affected by the B₀ strength. Therefore, it is clear that 900 MHz is only optimal for obtaining longest T₂, and higher field strength near and above a 1 GHz is required to gain the benefit of maximal sensitivity. Relative to 900 MHz, the predicted sensitivity gain of the TROSY components at the optimal field strength of 1.2 GHz is 1.3-fold for ¹⁵N_H and 1.6-fold at 1.5 GHz for ¹H_N. Compared to 1.2 GHz, the ¹H_N TROSY sensitivity is expected to increase at 1.5 GHz by a factor of 1.1. On the other hand ¹⁵N_H TROSY sensitivity is expected to decrease from 1.2 GHz to 1.5 GHz by a factor of 0.82, based on the assumptions described in the Supplement.

This reasoning can also be extended to the ¹³C_aro TROSY. The ¹³C_aro TROSY effect is reported to be optimal at 600 MHz when considering T₂ (Pervushin et al. 1998b). However, the maximum signal height of the ¹³C_aro TROSY should actually be achieved at around a 1 GHz. The sensitivity gain for the ¹³C_aro TROSY at this optimal field strength for sensitivity, as compared to 600MHz is 1.4-fold (Fig. 1D, red).

In all cases, optimal sensitivity of the TROSY resonances is achieved at higher field compared to that for optimal relaxation rates and these are at or above 1 GHz (23.5 T) magnetic field strength. It should also be noted that even though the TROSY selection schemes only recover half of the coherence pathways as compared to the conventional non-TROSY detection, TROSY is the most sensitive detection method at and near the optimal field strength (Fig. 1D, cyan for non-TROSY detection scheme).

Although this perspective is focused on the sensitivity in detecting 1D TROSY resonances for the sake of simplicity, the advantage of higher-field magnets also holds for multidimensional TROSY experiments. For the aromatic ¹³C TROSY there is essentially no TROSY effect in the ¹H dimension, thus the prediction shown in Fig. 1 will also be valid in 2D or 3D experiments. For the ¹⁵N_H detected and ¹H_N detected TROSYs of the amide groups the peak heights would depend on the product of the field dependent T₂ curves of ¹H and ¹⁵N, multiplied with a single B_o^3/2 curve. This will place the optimum field for 2D amide TROSYs in between 1.1 and 1.5 GHz. A more detailed analysis is beyond the scope of this manuscript, however, the T₂(B₀) of indirectly frequency labeled nuclei and the coherence loss in the pulse scheme also affect the resultant sensitivity. Theoretical estimates clearly show the advantage of higher-field magnets, above 1 GHz, however, in practice, this gain in sensitivity for ¹H-detected TROSY can be partly offset by adverse salt effects in high-Q probes at higher field strengths, an effect that is less significant for low γ nuclei (Takeuchi et al. 2016).

Although, the calculations shown in Figure 1 do not take dynamics into account, it is worth simulating the contribution of additional relaxation due to exchange broadening (R_ex) for the field dependence of the peak heights. This will be especially true when the chemical exchange is fast on the NMR time scale, where R_ex is proportional to the field strength. As expected, the advantage of higher field magnets will be less in magnitude while the field dependencies are largely unchanged (Figure S1). Since the intrinsic relaxation becomes larger for higher molecular weight systems, the contribution of R_ex to the signal height will be smaller. The variation of ¹H_N T₁ with field might also influence the sensitivity; however, ¹H_N can have rather short T₁ values even at high protein molecular weight, due to a strong coupling between the ¹H magnetization of water and the macromolecule (Riek et al. 2002). In addition, there are many experimental options to address this point, such as using relaxation agents that reduce the ¹H longitudinal relaxation (Takeuchi et al. 2010) and water management in pulse sequences (Schanda et al. 2005). Likewise, structure dependence of CSA would also affect the optimal B_o values. Nevertheless, our calculation is consistent with previously published experimental data (Takeuchi et al. 2015). The ratio of signal heights of TROSY vs. regular HSQC at two different field strengths closely match the calculation presented here.

This perspective warrants rethinking the maximum field strength limit, the design and development of higher field magnets over 1 GHz and the associated development in probe technology that will allow taking advantage of the increased sensitivity.