¹⁵N and ¹³C-SOFAST-HMQC editing enhances 3D-NOESY sensitivity in highly deuterated, selectively [¹H,¹³C]-labeled proteins

Abstract

The ongoing NMR method development effort strives for high quality multidimensional data with reduced collection time. Here, we apply ‘SOFAST-HMQC’ to frequency editing in 3D HMQC-NOESY-HMQC and demonstrate the sensitivity benefits using highly deuterated and ¹⁵N, methyl labeled samples in H₂O. The experiments benefit from a combination of selective T₁ relaxation (or L-optimized effect), from Ernst angle optimization and, in certain types of experiments, from using the mixing time for both NOE buildup and magnetization recovery. This effect enhances sensitivity by up to 2.4× at fast pulsing versus reference HMQC sequences of same overall length and water suppression characteristics. Representative experiments designed to address interesting protein NMR challenges are detailed. Editing capabilities are exploited with heteronuclear ¹⁵N,¹³C-edited, or with diagonal-free ¹³C aromatic/methyl-resolved 3D-SOFAST-HMQC-NOESY-HMQC. The latter experiment is used here to elucidate the methyl-aromatic NOE network in the hydrophobic core of the 19kDa FliT-FliJ flagellar protein complex. Incorporation of fast pulsing to reference experiments such as 3D-NOESY-HMQC boosts digital resolution, simplifies the process of NOE assignment and helps to automate protein structure determination.

INTRODUCTION

Multidimensional NMR is a proven tool for studying protein structure and dynamics in the native state. (Gelis et al. 2007; Sprangers and Kay 2007) NMR-based structural biology efforts rely on nuclear Overhauser effect spectroscopy (NOESY) for structure elucidation and modeling to gain insights about the system function. Three dimensional ¹⁵N,¹³C-edited HMQC-NOESY-HMQC (Kay et al. 1990; Vuister et al. 1993; Zwahlen et al. 1998) experiments are used routinely in the study of intermediate size proteins (~50 kDa) produced with labeled ²H, ¹⁵N and [¹H,¹³C] on methyl groups. (Tugarinov et al. 2003) The methyl resonance assignment is conducted using a combination of methyl to backbone correlation and 3,4D-NOESY-HMQCs experiments. The simple HMQC editing scheme is ideally suited to leverage the methyl-TROSY effect in methyl labeled samples.

Fast pulsing techniques for rapid NMR data collection known as SOFAST-HMQC (Schanda et al. 2005) have garnered interest by making 2D ¹³C and ¹⁵N correlation spectroscopy possible within a few seconds in proteins and nucleic acids. (Amero et al. 2009; Sathyamoorthy et al. 2014) The SOFAST experiment has been applied to kinetic (Theillet et al. 2013), diffusion (Augustyniak et al. 2011), structural heterogeneity studies (Schanda et al. 2006a; Solyom et al. 2013), and 3D triple resonance experiments (Schanda et al. 2006b).

In this manuscript, we describe a series of heteronuclear NOESY experiments that combine 2D SOFAST-HMQC and NOESY with the goal of maximizing sensitivity and data quality. The experiments are intended for use with deuterated with U-¹⁵N and selectively [¹H,¹³C]-methyl and(or) aromatic labeled proteins. In such samples, the amide, methyl and aromatic moieties appear at distinct regions of the spectrum and are poised for selective excitation/observation. The experiments are based on the ¹⁵N and ¹³C-resolved versions of the 3D-HMQC-NOESY-HMQC, also known as the methyl NOESY, and 3D NOESY-HMQC.

We describe in detail several variations on the 3D SOFAST HMQC-NOESY-HMQC and 3D SOFAST NOESY-HMQC experiments, compare their sensitivity to that of the reference HMQC sequences and show that significant sensitivity and resolution improvements can be obtained. In order to support our findings, we conduct direct measurements of the selective T₁ recovery (L-optimized effect) (Pervushin et al. 2002) in our MBP ¹⁵N methyl labeled sample, illustrate the theory basis for the experiment, compare the sensitivity and NOE buildup results of SOFAST and traditional NOESY. In addition, we characterize the contribution of the Ernst angle, its correct positioning in the sequence and its role in enhancing the NOE signal during fast pulsing. Depending on the experiment in question, distinct mechanisms are responsible for sensitivity enhancement, a significant effect is due to the additional recovery allowed during mixing time. At fast pulsing regime (0.2 s interscan delay) and ~0.3 s mixing that results into a doubling of the recovery time for the same overall acquisition time. As proof of principle, we demonstrate acquisition of four fully sampled methyl-amide 3D NOESYs in under one day on maltose binding protein (MBP, 42.5 kDa). Further applications and benefits of the experiments will be discussed.

MATERIALS AND METHODS

Production of methyl-aromatic labeled protein samples

A 1 mM U-[¹³C,¹⁵N] FliT^Δα4-FliJ^51–101 and 1 mM U-[²H,¹⁵N] and Ala-¹³CH₃, Met-¹³CH₃, Ile-δ1-¹³CH₃, Leu,Val-¹³CH₃/¹³CH₃, Thr-¹³CH₃ and Phe, Tyr-[¹H,¹³C,¹⁵N] FliT^Δα4-FliJ⁵¹-101 samples were produced following a previously published protocol. (Saio et al. 2014) The sample conditions were: 20 mM sodium phosphate buffer (pH 7.0), 10 mM BME and 100 mM KCl. The labeling is referred throughout to in short form as ‘double labeled’ and ‘¹⁵N-methyl/aromatic’ labeled, respectively. The protein is referred to as ‘FliT-FliJ’ in short form in the manuscript. A 1 mM U-[²H,¹⁵N] and Ileδ1-[¹³CH³], Leu-[¹³CH₃/¹²CD³], Val-[¹³CH₃/¹²CD₃] (‘¹⁵N-methyl’ in short form) maltose binding protein (MBP) sample was produced as previously described. (Gardner et al. 1998) Conditions were 20 mM sodium phosphate buffer (pH 7.0), 5 mM BME and 100 mM KCl.

NMR spectroscopy

Pulse sequence development and data collection were conducted on a Bruker Avance III 850 MHz and Bruker Avance 700 MHz spectrometers each equipped with a proton-optimized triple resonance TCI CryoProbe. Topspin 3.2 and 2.1 (Bruker BioSpin) were used for data collection on the 850 and 700 MHz spectrometers, respectively. NMRPipe (Delaglio et al. 1995) was used for spectra processing followed by analysis with NMRFAM-SPARKY. (Lee et al. 2015) Backbone, methyl and aromatic assignments for FliT-FliJ were obtained using established protocols. (Rossi et al. 2015) MBP assignments were obtained from the literature. All samples for testing were run at 32 °C. Unless specified otherwise, the NOESY mixing period was set to the standard 300 ms value in all the ¹⁵N-methyl/aromatic labeled samples throughout testing.

Structure calculation and NOE analysis

Structure calculations were conducted with CYANA 3.97 automated NOESY assignment protocol (Guntert and Buchner 2015) using backbone dihedral angles (TALOS-N (Shen and Bax 2015)) and 3D-NOESY peaklists. Two datasets were prepared for CYANA that included ¹⁵N and ¹³C resolved-NOESY or their SOFAST implementations, plus, in common for the two datasets, the new SF aromatic to methyl NOESY peak list. Peak tolerances in F₁ dimension (¹H NOE) were set from ±0.02 ppm to ±0.01 ppm when using either the traditional or the SOFAST dataset, respectively. The ¹³C and ¹⁵N tolerances (F₂ dimension) and ¹H observed (F₃ dimension) remained set to ±0.1 ppm and ±0.01 ppm, respectively. NOE analysis was conducted with PdbStat v5.1. (Tejero et al. 2013)

RESULTS

Proton T₁ relaxation measurements

Proton T₁ relaxation enhancement was measured in order to evaluate the magnitude of the effect and feasibility of an L-optimized NOESY experiments in intermediate size proteins in ¹H₂O. The measurements were conducted by inversion recovery at 32° C using a deuterated ¹⁵N, [¹H,¹³C]-Ile, [50%-¹H,¹³C]-Leu and Val methyl labeled MBP (42.5 kDa) sample as detailed in Supp. Table S1. The resulting series of 1D spectra acquired with variable delay (τ) were integrated and fitted with the function:

$$I(\tau )=\mathrm{I}(0)[1-2e^{-R_z\tau }]$$

Inversion recovery experiments with both hard and selective ¹H pulses (Supp. Fig. S1) were run in order to extract and separate the T₁ relaxation enhancement contributions from each ¹H-type within the molecule and from water. The results are listed in Supp. Table S1.

The results (Supp. Table S1) show that the amides experience a ~25% decrease in T₁ by keeping the water at equilibrium and an additional ~25% L-optimized effect by pulsing only on the amides and maintaining the sidechain magnetization at equilibrium. The effect is also present but lower in magnitude for the methyl groups where the overall drop in T₁ due to both intra and intermolecular (solvent) effects is only about 30%. With relaxation T₁ of 0.79 and 0.40 s (Supp. Table S1), the recovered magnetization [= I(0)(1 − e^−d₁/T₁)] during interscan delay d1 of 0.2 sec is 0.22 × I(0) and 0.39 × I(0), respectively. The signal can be increased by 1.76× (= 0.39/0.22). The recovered magnetization during interscan delay d1 of 1.0 sec is 0.72 × I(0) and 0.92 × I(0), respectively. The signal can be increased by 1.28× (= 0.92/0.72). Based on these results, the use of selective pulses and HMQC-based editing in NOESY should be beneficial in achieving higher sensitivity and reduce data collection time in selectively protonated samples.

¹⁵N and ¹³C-edited 3D SOFAST-HMQC-NOESY-HMQC

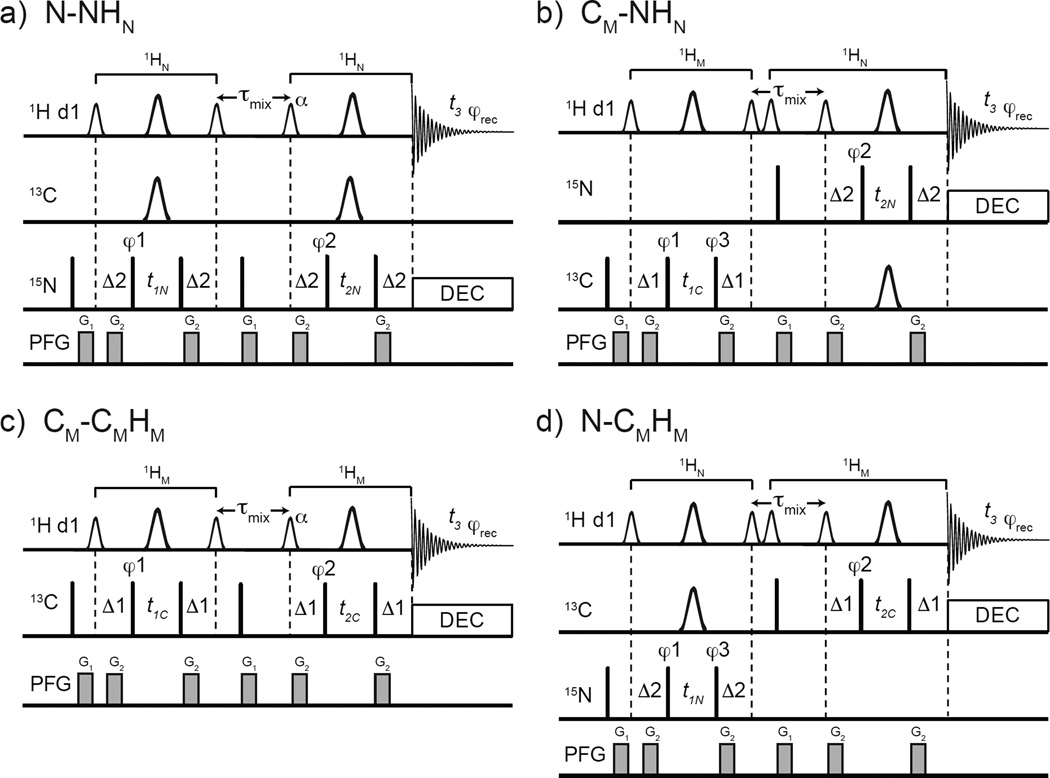
The four basic variants of the 3D SOFAST HMQC-NOESY-HMQC are depicted in Fig. 1. The experiments can be subdivided into X-XH or X-YH-based experiments where the X and Y are either ¹⁵N, ¹³C_M or ¹³C_Aro. The X-XH-type sequences give 3D N-NH_N or 3D C_M-C_MH_M correlations Fig. 1a and 1c, respectively; the X-YH experiments give diagonal-free 3D C_M-NH_N and 3D N-C_MH_M correlations Fig. 1b and 1d, respectively. The selective pulse profiles used in this work are shown in Supp. Fig. S1. The Ernst angle optimization for these sequences is shown in Supp. Fig. S2. All the sequences presented here are listed in Supp. Table S2. All the pulse programs and parameter sets can be found in Appendix S2–S11.

Fig. 1.

Pulse sequences for 3D SOFAST HMQC-NOESY-HMQC with the following frequency labeling combinations: a) N(F₁)-N(F₂)H_N(F₃), b) C_M(F₁)-N(F₂)H_N(F₃), c) C_M(F₁)-C_M(F₂)H_M(F₃), and d) N(F₁)-C_M(F₂)H_M(F₃). The smaller and larger ¹H shaped pulses are 1.69 ms long 90° PC9_4_90 (Smith 2001) and 1.15 ms long 180° REBURP (Geen and Freeman 1991), respectively. The flip angle α (110° to 90°, depending on the value of d1 and the experiment type) of the shaped pulse after τ_mix should be optimized (see text). Depending on the sequence, the offsets of the ¹H shaped pulses are −3,230 Hz (at 0.9 ppm) for methyl type pulses and 3,230 Hz (at 8.5 ppm) for amides. The narrow bars represent 90° hard pulses. The shaped pulse on ¹³C channel represents a 500 µs long 180° smoothed CHIRP. (Hwang et al. 1997) The spectral centers of ¹⁵N, ¹³C, and ¹H dimensions are at 118.0, 16.5, and 4.7 ppm, respectively. The delays are: d1 = 0.2 sec, Δ1 = 1/(2×¹J_CH3) = 4.0 ms, Δ2 = 1/(2×¹J_NH) = 5.2 ms τ_mix = 0.3 sec. The phase cycling for X-XH-type are φ1 = (x, −x), φ2 = (x, −x, −x, x), φ_rec = (x, −x, −x, x) and for X-YH-type are φ1 = (x, −x), φ2 = (x, −x, −x, x), φ3 = 4(x), 4(−x), φ_rec = (x, −x, −x, x, −x, x, x, −x). Bruker decoupling scheme bi_garp_2pl is used. The quadrature detections in t1 and t2 dimensions are acquired via States-TPPI of φ1 and φ2, respectively. The durations and strengths of the gradients are G1 = (1 ms, 15 G/cm), G2 = (1 ms, 5 G/cm).

In X-YH-type sequences such as in the example N-C_MH_M (Fig. 1d), a pair of shaped pulse are used immediately before the NOE mixing time in order to avoid artifacts. If only the amide flip-up shaped 90° pulse is used prior to mixing, strong artifacts are observed at the edge of the F₂ dimension. Because all pulses before NOE mixing time are acting only on amide moieties, the methyl ¹H signal (I_z) is not perturbed. Since that methyl (I_z) signal is observed during the second HMQC after the NOE mixing time it will appear as axial peaks in F₂ dimension. Using States-TPPI, the axial peaks are moved to the two edges of the F₂ dimension. These artifact peaks are very strong compared with pure NOE cross peaks and significantly degrade the quality of the spectrum at the edges. Different combinations of phase cycling up to 32 steps could not remove them while using a shaped pulse before mixing. Instead, two soft pulses are used, one set to at the correct ¹J_NH spacing to flip-up aromatic ¹H I_y to I_z, immediately following that another other one to flip-up only methyl I_z to I_y. Then the PFG during NOE mixing time dephases the methyl I_y. Therefore, the methyl ¹H signal before the second HMQC is suppressed and a clean spectrum is obtained.

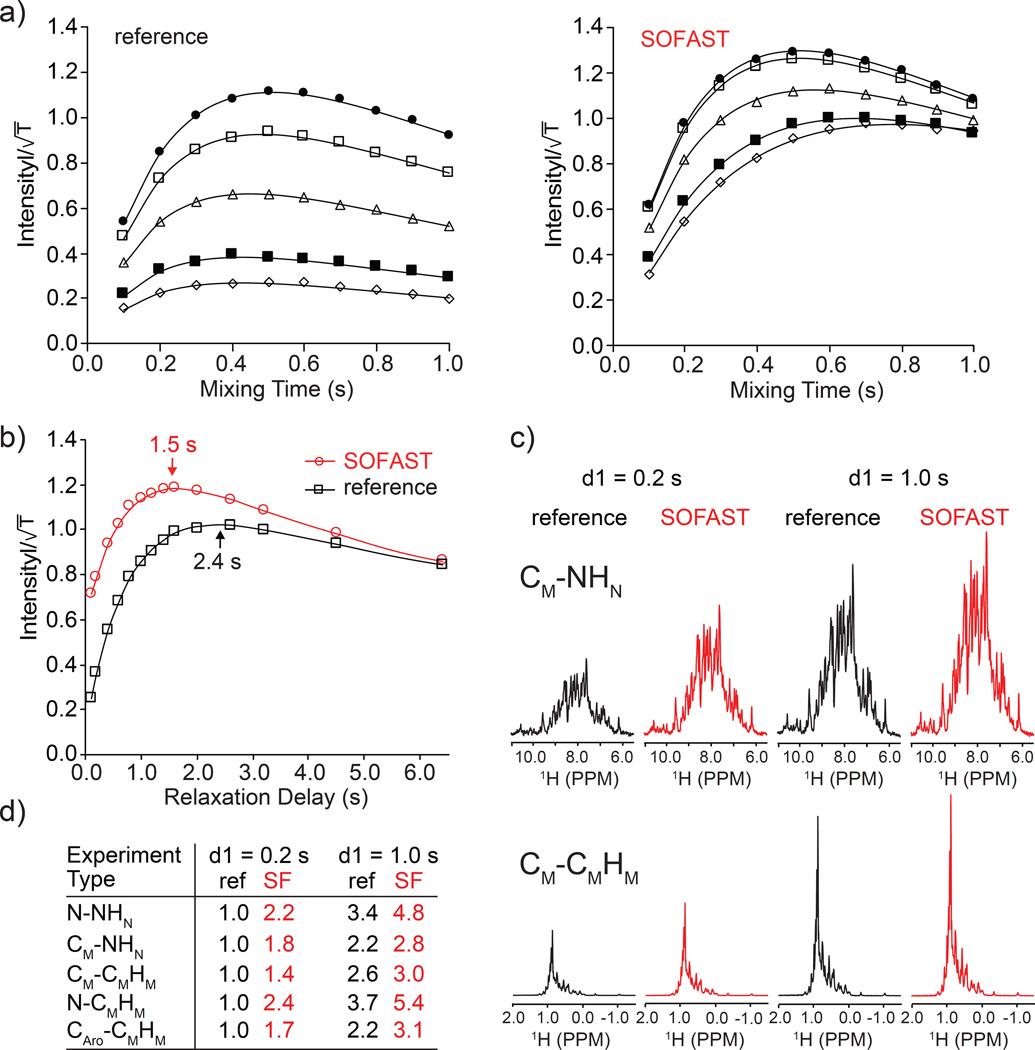
In order to evaluate the performance of the sequences, we conducted NOE buildup experiments (Fig. 2a and Supp. Fig. S3). Integrated NOE intensities as a function of mixing time and interscan delay (d1) were collected for both SOFAST 3D and a reference WG-based 3D NOESY sequences (Kay et al. 1990) (Supp. Fig. S3a). A diagonal-free 3D ¹⁵N-HMQC-NOESY-¹³C-HMQC type-experiment that correlates N-C_MH_M and produces ‘pure’ NOE spectrum was used (Fig. 1d.). The integrated intensity from 1D experiments as a function of mixing time (τ) was fitted with an expression for two spins cross-correlation in the slow-motion limit (Jeener et al. 1979):

$$I(\mathrm{\tau })=\frac{M_0}{2}{e}^{-R\tau }(1-e^{-{\sigma }_{{(H_N,H_M)}^{\tau }}})$$

where M₀ is the initial magnetization, σ_(HN,HM) is to the intra-molecular cross-relaxation term between amides and methyls (MBP sample) that depends on the correlation time (τ_c) and R is the longitudinal relaxation rate at the slow-limit (Supp. Fig. S3b).

Fig. 2.

Comparisons of NOE buildup and sensitivity for MBP U-¹⁵N, [¹H,¹³C]-methyl labeled sample. NOE buildup curves (a): $\text{Intensity}/\sqrt{T}$ vs. mixing time where T is total experiment time were plotted at five different d1 values: 0.1 (open diamonds), 0.2 (filled squares), 0.5 (open triangles), 1.0 (open squares) and 2.0 s (filled circles). Sensitivity curves (b): $\text{Intensity}/\sqrt{T}$ vs. recycle delay (d1). The first 1D spectra of diagonal-free 3D HMQC-NOESY-HMQC (N-C_MH_M) experiments used here for reference and for SOFAST are shown in Fig. 1c and Supp. Fig. S3a, respectively. The series of 1D experiments that give pure NOE intensity were acquired with 32 scans. The first 1D spectra used for intensity comparisons are shown for C_M-NH_N and C_M-C_MH_M (c). Tabulated intensity comparison for 3D HMQC-NOESY-HMQC sequences (d). Recycle delays 0.2 and 1.0 sec were used in (c) and (d) for reference and SOFAST versions.

The sensitivity, or intensity scaled over the square root of total experiment time, as a function of d1 with fixed τ = 0.3 s are compared in Fig. 2b. The reference sequence (Supp. Fig. S3a) is optimized with W5 H₂O suppression (Liu et al. 1998) and flip-back pulse to remove the influence of water exchange (Stoesz et al. 1978) effects in the comparison. The results of indicate a significant benefit in sensitivity of the SOFAST-based experiment. Even at d1 = 1.0 s there is a clear advantage in using the SOFAST based sequence. Fig. 2c shows examples of excellent sensitivity gains (C_M-NH_N) and more modest ones for the C_M-C_MH_M NOESY. The sensitivities of the reference and SOFAST experiments become equal at impractically long d1 values (Fig. 2b) but the main advantage of the experiments are realized at 0.2 – 0.5 s recycle delay. The sensitivity at 0.2 s and 1.0 s are compared in Fig. 2c for the C_M-NH_N and C_M-C_MH_M 3D SOFAST HMQC-NOESY-HMQC experiments as higher and lower-level enhancement, respectively. The complete set of experiment comparison for X-XH and X-YH variants is tabulated in Fig. 2d. The results appear to follow the general trend of the measured T₁ relaxation enhancement, the methyl-methyl NOESY type experiment shows the least benefit from the SOFAST effect (Supp. Table S1).

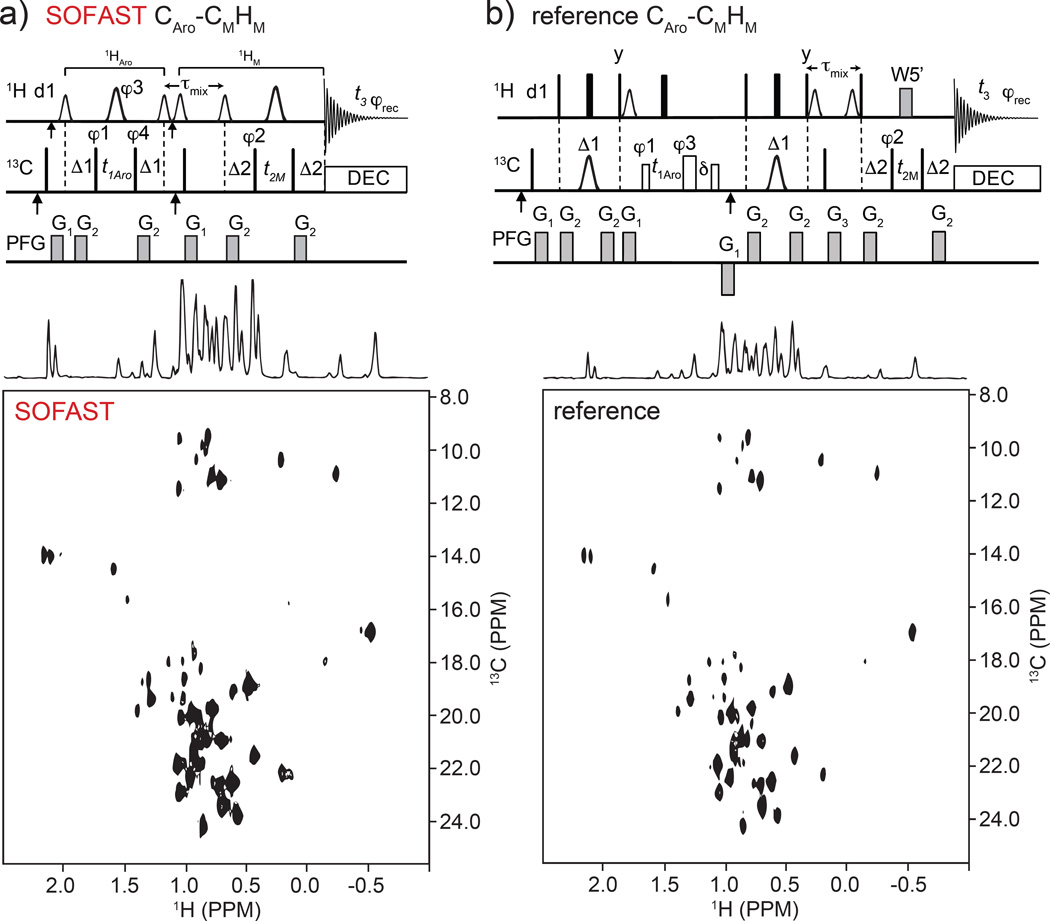
Diagonal-free ¹³C-aromatic to methyl 3D SOFAST-HMQC-NOESY-HMQC

The high degree of ¹³C chemical shift separation between aromatic and methyl moieties, generally > 115ppm, makes it advantageous to restrict the acquisition window around each group in order to identify specific aromatic to methyl NOEs. For that purpose, we developed the ¹³C-aromatic/methyl-edited 3D-SFHMQC-NOESY-HMQC. The NOE crosspeaks are acquired with high ¹³C digital resolution and without autocorrelation and folded peaks. (Stanek et al. 2013) The pulse sequence details are given in Fig. 3a and results of the Ernst angle optimization are shown in Supp. Fig. S4. The pulse program and parameter set are displayed in Supp. Appendix S2–S11. As for all other X-YH sequences the effect of the α pulse is minimal (<5% enhancement) the reasons for that are addressed later. A schematic view of the magnetization pathway and representative ¹³C(F₁)-¹H(F₃) projection of 3D spectrum for the 18.8 kDa complex between flagellar proteins FliT and FliJ are presented in (Supp. Fig. S5). The two HMQC periods before and after NOE mixing are spaced appropriately according to the aromatic and methyl proton-carbon J-couplings (¹J_CH). Previously, we had developed a reference 3D HSQC-NOESY-HMQC (unpublished work) using hard pulses and WATERGATE water suppression and compared the performance of that to the SOFAST sequence (Fig. 3a,b bottom panels). Even at d1 = 1.0 s and above the SOFAST outperforms the reference sequence by a very significant margin (last entry in Fig. 2d). This is partly due to the enhanced recovery in the SOFAST-based sequence (see ‘Fast pulsing in NOESY’ section below) and to the more complex nature of the HSQC-based reference sequence which carries a significant S/N penalty. We were not able to achieve adequate aromatic filtering with a simpler HMQC sequence with hard ¹H pulses before the mixing and that alone makes the new SOFAST based sequence preferable.

Fig. 3.

Pulse sequences in top panels are for diagonal-free Aro-Methyl 3D SOFAST HMQC-NOESY-HMQC (a) and reference 3D HSQC-NOESY-HMQC sequence (b). Frequency labeling is C_Aro(F₁)-C_M(F₂)H_M(F₃). Top a): the smaller and larger ¹H shaped pulses are 1.69 ms long 90° PC9_4_90 and 1.15 ms long 180° REBURP, respectively. The first and second vertical arrows on ¹H and ¹³C channels indicate the ¹H(¹³C) carrier frequency setting to 8.5 ppm (122 ppm) and 4.7 ppm (17.5 ppm), respectively. The offsets of ¹H shaped pulses before and after τ_mix are 0 (at 4.7 ppm) and −3,230 Hz (at 0.9 ppm), respectively. The narrow bars represent 90° hard pulses. The spectral centers of ¹³C(F₁), ¹³C(F₂), ¹H(F₃) dimensions are at 122.0, 16.5, and 4.7 ppm, respectively. The delays are: d1 = 200 ms, Δ1 = 3.1 ms, Δ2 = 4.0 ms, τ_mix = 300 ms. The phase cycling are: φ1 = (x, −x), φ2 = (x, −x, −x, x), φ3 = 4(x), 4(y), φ4 = 8(x), 8(−x), φ_rec = (x, −x, −x, x, −x, x, x, −x, −x, x, x, −x, x, −x, −x, x). Bruker decoupling scheme bi_garp_2pl is used. The quadrature detections in t₁ and t₂ dimensions are acquired via States-TPPI of φ1 and φ2, respectively. The durations and strengths of the gradients are G1 = (1 ms, 15 G/cm), G2 = (1 ms, 5 G/cm). Top (b): reference WATERGATE (W5’) 3D HSQC-NOESY-HMQC pulse sequence used for the S/N comparison. The filled narrow and wide bars represent 90° and 180° hard pulses, respectively. The open narrow (41.6 µs) and wide (37.2 µs) bars on ¹³C channel represent 90° and 180° soft pulses, respectively, that have null excitation at an offset of 109 ppm. ¹³C shaped pulses are 423 µs IBURP2.1000 180° pulses (Geen and Freeman 1991). The first and second vertical arrows indicate the 13C carrier frequency setting to 122.0 ppm and 17.5 ppm (centers of aromatic and methyl ¹³C chemical shifts), respectively. The distances between 3-9-19 W5’ pulses are 148 µs. The delays are: d1=1.0 sec, Δ1 = 3.1 ms, Δ2 = 4.0 ms, δ = t₁(0) + 2*pw (initial t₁ value and ¹H 180° pulse width), τ_mix = 0.3 sec. The phase cycling is: φ1 = (x, −x, −x, x), φ2 = (x, −x), φ3 = 4(x), 4(y), φ_rec = (x, −x, −x, x, −x, x, x, −x). Bruker decoupling scheme bi_garp_2pl is used. The quadrature detections in t1 and t2 dimensions are acquired via States-TPPI of φ1 and φ2, respectively. The durations and strengths of the gradients are G1 = (1 ms, 10 G/cm), G2 = (1 ms, 5 G/cm), G3 = (2 ms, 10 G/cm). Bottom panels show comparison of pure NOE F2(C_M)-F3(H_M) planes run using the FliT-FliJ complex sample (see main text Materials and Methods) that contained both ¹H-¹³C methyl and aromatic labels. Mixing time was 0.3 s, d1 = 0.2 s, and 90 degrees variable angle pulse (α) for SOFAST version.

One additional sequence for diagonal-free 3D ¹³C_Aro/¹⁵N-edited SFHMQC-NOESY-HMQC is also available (see entry 7 in Supp. Table S2). In that pulse sequence the first SFHMQC editing is centered at the aromatic ¹³C frequency. Following the NOESY period the magnetization is ¹⁵N-edited during the second SFHMQC module. This experiment can simplify the aromatic residues assignment and can be used if the sample is labeled only on ¹⁵N and aromatic moieties.

¹³C-3D SOFAST-NOESY-HMQC

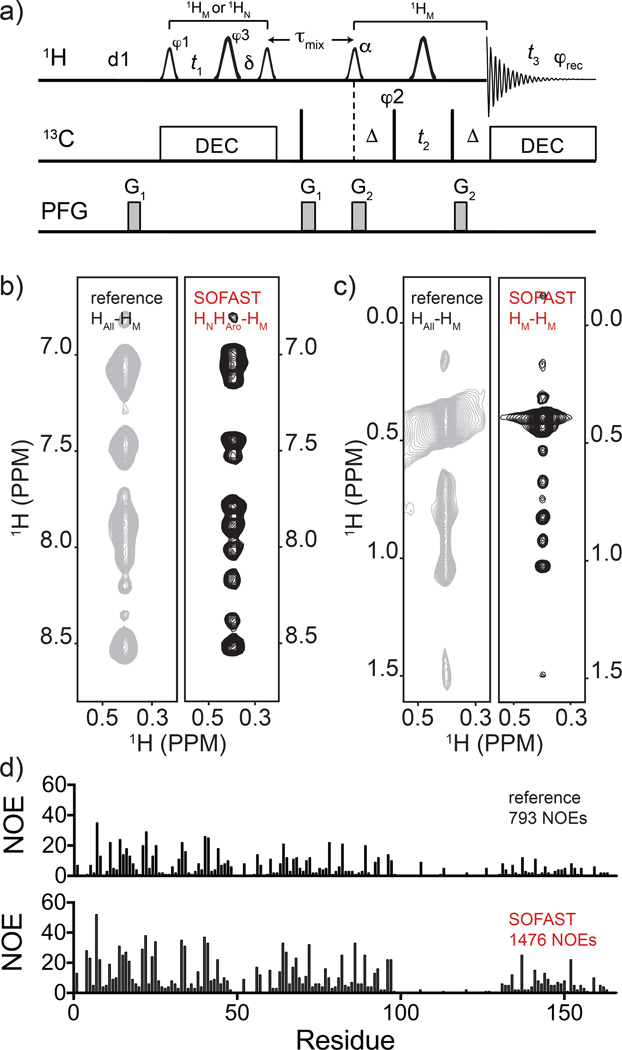
The pulse sequence diagram for ¹³C-edited 3D SOFAST NOESY-HMQC is shown in Fig. 4a. Briefly, the selective pulses are applied to both the initial NOESY module (plus t₁ evolution), and in the SFHMQC module. Employing selective ¹H pulses allows for acquisition of clean sub-spectra free from aliasing at the cost of longer NOESY and t₁ evolution portion of the sequence. compared to the hard pulse version. Analogously to the aromatic-methyl experiment, selecting specific spectral windows and editing schemes allows to acquire the diagonal-free portions of the ¹H(F₁)-¹H(F₃) spectrum. In the ¹³C-edited 3D SOFAST NOESY-HMQC the ¹H carrier frequency can be centered at either the amide/aromatic or the methyl position during the ¹H(F₁) frequency labeling (NOESY dimension) and two sub-spectra can be obtained, one that gives diagonal-free H_NH_Aro-C_MH_M-only NOEs and one that gives H_M-C_MH_M-only NOEs (see Supp. Table S2 entries 11 and 12, respectively). The pulse program and parameter set for the H_NH_Aro-C_MH_M and H_M-C_MH_M are displayed in Supp. Appendix S2–S11.

Fig. 4.

Panel a): pulse sequence of ¹³C-edited 3D SFNOESY-HMQC for frequency labeling H_M(F₁)-C_M(F₂)H_M(F₃) or H_N,Aro-C_MH_M (with addition of two ¹⁵N 180° hard pulses at the t₁ and δ midpoint). The smaller and larger ¹H shaped pulses are 1.69 ms long 90° PC9_4_90 and 1.15 ms long 180° REBURP, respectively. The flip angle (α) of the shaped pulse after τ_mix should be optimized as discussed in maintext. The first and second vertical arrows indicate the ¹H carrier frequency setting to 0.9 ppm for C_M(F₂)H_M(F₃) (8.5 ppm for H_N,Aro-C_MH_M) and 4.7 ppm, respectively. The offsets of ¹H shaped pulses before and after τ_mix are 0 Hz (at 4.7 ppm) and −3,230 Hz (at 0.9 ppm), respectively. Please note that two refocusing ¹⁵N 180° hard pulses at the midpoint of t₁ and δ should be added for H_N,Aro-C_MH_M. The spectral centers of ¹H(F₁), ¹³C(F₂), ¹H(F₃) dimensions are at 1.0, (8.5 for H_N,Aro-C_MH_M), 16.5, and 4.7 ppm, respectively. The delays are: d1 = 200 ms, δ = t₁(0) + 2×pwN (initial t₁ value and ¹⁵N 180° pulse width), Δ = 4.0 ms, τ_mix = 300 ms. The phase cycling are: φ1 = (x, −x), φ2 = (x, −x, −x, x), φ3 = 4(x), 4(y), φ_rec = (x, −x, −x, x, −x, x,×−x). Bruker decoupling scheme bi_garp_2pl is used. The quadrature detections in t₁ and t₂ dimensions are acquired via States-TPPI of φ1 and φ2, respectively. The durations and strengths of the gradients are G1 = (1 ms, 15 G/cm), G2 = (1 ms, 5 G/cm). Comparisons of ¹³C-resolved 3D NOESY-HMQC with ¹³C-resolved SFNOESY-HMQC counterpart are shown in b) and c) left and right strips, respectively. Experiments were run on ¹⁵N-methyl-aromatic labeled FliT-FliJ sample and processed in an identical manner. In the reference spectrum the full 11ppm indirect ¹H dimension is sampled (H_All) while in the SOFAST sequence the acquisition is split into two 3Ds, one centered on the indirect-detected amide/aromatic (H_NH_Aro) (b), and one on the methyl (H_M) ¹H chemical shift (c). Note that the same 3D-NOESY-HMQC strip marked as ‘reference’ is split into two halves for side-by-side comparison. In (d) the number of NOE per residue (and totals) resulting from CYANA automated NOESY assignment protocol for the FliT-FliJ protein are shown for the ‘reference’ (upper) and SOFAST datasets (lower).

The resulting spectra acquired in 10 h for each SOFAST-NOESY (d1 = 200 ms) have ~1.3× higher sensitivity and ~2× higher digital resolution compared to the ‘reference’ 3D spectrum acquired in 50 h (d1=1.0 s) (Fig. 4b,c). High digital resolution in the indirect dimension can be reached without sparse sampling (Mobli et al. 2006) in a comparatively short time. It is worth noting that the only way to obtain such diagonal free spectrum with traditional sequences would be to use an HMQC-NOESY-HMQC scheme with ¹H evolution in t₁. In our testing that experiment performed very poorly compared to the SFNOESY-HMQC since the additional carbon or nitrogen HMQC evolution make the sequence longer (the lengths of a SFNOESY and a SFHMQC when t₁ is zero are 4.4 ms and 9.6 ms, respectively).

Sub-dividing the ¹H chemical shift window enhances the data quality and resolution particularly with high field magnets where wide frequency ranges need to be sampled. This has a tangible impact on the structure determination process (see relevant technical details in Materials and Methods section). In the case of FliT-FliJ complex peak tolerances are reduced and automated CYANA (Guntert and Buchner 2015) NOE assignment protocol yields almost twice the number of distance restraints from the SOFAST NOESY dataset vs. the reference dataset in approximately 35% of the total acquisition time (Fig. 4d).

In addition to the experiment detailed above, similar pulse sequences were developed that utilize traditional hard proton pulses for the NOESY module in the 3D SFNOESY-HMQC sequence, in that case the ¹H dimension is called H_All (all protons in the t₁ dimension). Three separate experiments ¹⁵N-only ¹³C-only and simultaneous ¹⁵N,¹³C-edited versions are also available (entries 12, 13, and 14 in Supp. Table S1). The experiments retain the advantages of the fast pulsing and are more suitable to double-labeled protein samples albeit without L-optimized effect. Substituting selective pulses with hard pulses in the NOESY module gives some added sensitivity in return.

Other interesting variants designed for amide/methyl labeled samples utilize the cosine modulated PC9 pulse that excites all but water protons and maintains selective pulse usage in both NOESY and HMQC modules. The sequences have H_NH_M descriptor as the t₁ frequency labeling (entries 15 and 16 in Supp. Table S1). The sequences can be either ¹³C-edited with a carbon-only SFHMQC or simultaneously ¹⁵N,¹³C-edited using the new simultaneous ¹⁵N,¹³C SFHMQC (see more description below for the new simultaneous ¹⁵N,¹³C SFHMQC). The first sequence gives two 3D sub-spectra while the second gives four 3D sub-spectra similarly to the ¹⁵N,¹³C-edited 3D SOFAST-HMQC-NOESY-HMQC but with amide, and methyl ¹H incremented during t₁ instead of ¹⁵N and ¹³C. Lastly, if a simple PC9 pulse is utilized during NOESY, then H_NH_Aro-editing is achieved during t₁. Choosing ¹⁵N-editing gives H_NH_Aro-NH_N sequences (entry 14 in Supp. Table S2). The sequence is a useful complement to the triple resonance dataset to help confirm the accuracy of backbone assignment and in favorable cases can be acquired in just a few hours. The 3D NOESY-SFHMQC can also be adapted to run on the aromatic region (C_AroH_Aro-edited) and used to obtain a useful 3D H_M-C_AroH_Aro spectrum (entry 16 in Supp. Table S2).

¹⁵N,¹³C-edited 2D SOFAST-HMQC

A new simultaneously ¹⁵N, ¹³C-edited 2D SOFAST sequence was created for rapid titrations and for NOESY editing applications in ¹⁵N, methyl labeled samples (Fig. 5a, and see entry 1 in Supp. Table S2 and Supp. Appendix S2–S11 parameters). The 2D spectrum (Fig. 5b) is acquired in ~5 minutes on an ¹⁵N-methyl labeled maltose binding protein (MBP, 42 kDa) sample. This experiment slightly compromises ¹³C sensitivity due to complications in coordinating delays Δ1 and Δ2 and different evolution times t_1C and t_1N. In addition, most of the L-optimized effect is removed since both amides and methyls are pulsed. However, it retains the Ernst angle benefit during fast pulsing (Supp. Fig. S4) and the water suppression benefit from keeping the water magnetization at equilibrium. The experiment performs better at 0.2 s d1 than either ¹⁵N and ¹³C-edited 2D HMQC with water flip-back pulses as shown in Supp. Fig. S6.

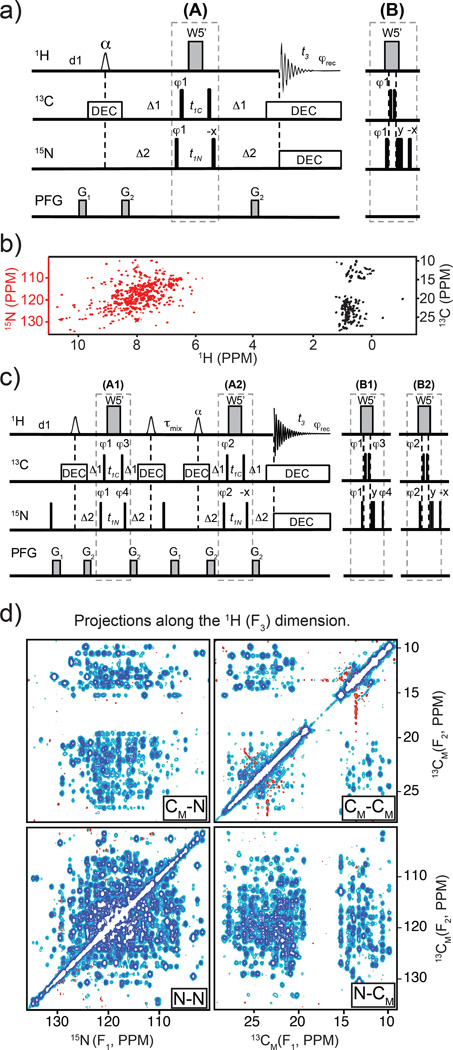
Fig. 5.

Panel a): pulse sequence diagram for simultaneous ¹⁵N,¹³C-edited 2D SFHMQC. When t1 equals to zero, the inset (B) replaces the part (A) to avoid simultaneous ¹³C and ¹⁵N hard pulses. The ¹H shaped pulse is a cosine-modulated PC9 pulse of 1.69 ms in length, its frequency offset is 0 Hz (at 4.7 ppm), the modulation frequency is 3,230 Hz (see detail in text). The narrow bars represent π/2 hard pulses. The distances between W5’ are 148 µs. The spectral centers of ¹⁵N(F₁), ¹³C(F₁), and ¹H(F₂) dimensions are at 118.0, 17.0, and 4.7 ppm, respectively. The delays are: d1 = 200 ms, Δ1 = 4.0 ms (methyl 1/(2¹J_CH), and Δ2 = 5.2 ms (amide 1/(2¹J_NH). The phase cycling is: φ1 = (x, −x), φ_rec = (x, −x). Bruker decoupling scheme bi_garp_2pl is used for both ¹³C and ¹⁵N, respectively. The quadrature detection in t₁ dimension is done via States-TPPI of φ1. G1 = (1.0 ms, 15 G/cm), G2 = (0.3 ms, 10 G/cm). Panel b): 2D simultaneous ¹⁵N,¹³C-edited SFHMQC spectrum of MBP. Panel c): pulse sequence diagram for simultaneous ¹³C,¹⁵N-edited 3D SFHMQC-NOESY-HMQC. When t1 equals to zero, the inset (B1) and (B2) replace the parts (A1) and (A2), respectively, to avoid simultaneous ¹³C and ¹⁵N hard pulses. The shaped pulses, delays, pulse field gradients (PFG) and decoupling schemes are the same as those in (a). The phase cycling are: φ1 = (x, −x), φ2 = (x, −x, −x, x), φ₃ = 4(x), 4(−x), φ₄ = 4(x), 4(−x), φ_rec = (x, −x, −x, x, −x, x, x, −x). The quadrature detections in t₁ and t₂ dimension are acquired via States-TPPI of φ1 and φ2, respectively. Two sets of two 3Ds are acquired with alternate φ4 phases (adding 0 or 180°). Addition and subtraction of the two sets result in cross-correlated ¹⁵N and ¹³C signals during t₁. Bruker AU program “split ipap 2” is used to split the two data sets. Panel d): 2D projections of simultaneously ¹⁵N,¹³C-resolved 3D SFHMQC-NOESY-HMQC run on ¹⁵N-methyl labeled MBP at 32 °C. The four 2D planes are labeled as shown in the 2D axis, for example: C_M-C_M signifies ¹³C_M(F₁)-¹³C_M(F₂)-¹H_M(F₃). The third dimension of each 3D is the observed proton dimension, either the amide (¹H_N) or methyl (¹H_M).

¹⁵N,¹³C-edited 3D SOFAST-HMQC-NOESY-HMQC

The 2D ¹⁵N, ¹³C-edited SOFAST-HMQC module is incorporated in the 3D-HMQC-NOESY-HMQC (Frenkiel et al. 1990; Zwahlen et al. 1998) experiment to give simultaneously ¹⁵N,¹³C-edited 3D SFHMQC-NOESY-HMQC (Fig. 5c, entry 8 in Supp. Table S2 and parameters in Supp. Appendix S2–S11) in ¹⁵N-selectively methyl labeled samples. The NOESY mixing period is sandwiched in between two SFHMQC pulse modules and a total of four 3D sub-spectra are obtained in a single experiment. In short notation, these sub-spectra are referred to as N-NH_N, C_M-NH_N, C_M-C_MH_M, and N-C_MH_M 3D-SFNOESYs, where the nucleus labels follow the acquisition order (t₁, t₂, and t₃-obs). The two mixed amide and methyl (C-N or N-C) planes are diagonal-free spectra. High quality data were obtained in only ~19h (full 3D projections are shown in Fig. 5d). The experiment was done in an effort to push the boundaries of the technique and maybe useful in sampling-limited situations as in the MBP testing sample, and only when amides and methyls are labeled. The presence of aromatics would not be optimal for carbon editing in that case.

The number of t₁ and t₂ increments depends upon the chemical shift window used for the ¹³C and ¹⁵N dimensions. In methyl/¹⁵N amide labeled samples using ~35ppm in ¹⁵N and ~22ppm in ¹³C dimensions, adequate digital resolution is obtained with the current limit, that is ~118 real t₂ points (i.e. 59 complex points or 59 increments), and more points can be acquired with a smaller ¹³C spectral width or larger ¹⁵N spectral width. In t₁ dimension, the number of data points should be doubled because two sets of data acquired simultaneously.

2D Sensitivity Comparisons

Sensitivity comparison between 2D SOFAST HMQC and the 2D HSQC, HMQC and TROSY-based sequences that are currently utilized for 3D or 4D NOESY editing was conducted at fast pulsing regime (0.2 s) (Supp. Fig. S6). Comparison for relevant experiments were also conducted at 1 s and with a ¹⁵N/¹³C-labeled protein (Supp. Fig. S7). SOFAST 2D ¹⁵N and ¹³C-HMQC experiments enhance sensitivity by 3.8× and 2.0×, respectively, compared with 2D regular HSQC experiments in H₂O. The same acquisition and processing parameters were used for these 2D experiments with a sample ¹⁵N/methyl labeled MBP. Typically, relaxation delay d1, acquisition times in t₂ and t₁ dimensions were 0.2 s, 50 ms and 24 ms, respectively. The positive projections of these 2D spectra were used to compare the signal to noise (S/N). Care was taken in reporting the sensitivity results on backbone amides and accounting for differences in phases sensitive t₁ acquisition mode of TROSY vs. HMQC (Echo-AntiEcho and States-TPPI, respectively).

In the case of a uniformly ¹⁵N/¹³C labeled sample, the change in signal strength on the amides is more pronounced (2× from 1.6 to 3.2, Supp. Fig. S7b) because of the addition of all sidechain ¹H’s enhance the T₁ relaxation (or L-optimized) effect. (Diercks et al. 2005) We anticipate the benefit of SOFAST on aliphatic groups in double labeled samples to be modest due to the fact that it is difficult to excite specific non-exchangeable side-chain moieties while leaving the rest at equilibrium.

Surprisingly, the time-shared ¹⁵N,¹³C 2D experiment that compromises the L-optimized effect produces good results at fast pulsing. This is in spite of the ¹³C evolution taking a moderate sensitivity penalty. However, the sequence benefits chiefly from the use of Ernst angle pulse (Supp. Fig. S4) to enhance the signal at fast pulse.

Fast pulsing in NOESY with SOFAST-HMQC

SOFAST-HMQC leverages the flip angle (α) to increase sensitivity by increasing steady-state polarization with short recycle delay (d1 < 0.5 s). The impact of the flip angle (α) was carefully evaluated when applied to the 3D NOESY experiment. Supp. Fig. S2 and S4 show the flip angle (α) 1D optimizations for the six 3D SFHMQC-NOESY-HMQC variants in this work. The same principles apply to the simpler 3D NOESY-HMQC sequence with some notable difference. For the moment, we will assume that the final residual magnetization to be recycled is compatible and can be transferred to become starting magnetization in the following scan. Under these conditions, the location of the variable flip angle pulse in the 3D SFHMQC-NOESY-HMQC experiment type (Fig. 1 or Fig. 3a) should be restricted to the first ¹H pulse after the NOE mixing period. In contrast, the flip angle of the first pulse in the HMQC before mixing should be kept equal to π/2. If the flip angle is α, the signal evolution (see Supp. Appendix S1) when t₁ equals zero is:

$$I_z\stackrel{\alpha I_x}{\to }-I_y\mathit{\text{sin}}\alpha +I_z\mathit{\text{cos}}\alpha \stackrel{\pi I_x+\pi 2I_z{S}_z}{\to }-I_y\mathit{\text{sin}}\alpha -I_z\mathit{\text{cos}}\alpha \stackrel{(\pi /2)I_x}{\to }-I_z\mathit{\text{sin}}\alpha +I_y\mathit{\text{cos}}\alpha$$

After the flip-up π/2 pulse, a PFG is applied during the NOE mixing time, that causes the second term I_ycosα to be dephased and only the first term −I_zsinα to survive. As a result, the maximum signal can only be achieved when α of the first frequency selective ¹H pulse of the first HMQC equals π/2. Experimentally, the flip angles of the first and last pulse in the first HMQC before NOE mixing time were changed independently, and the maximum signal was obtained when both flip angles were 90°. Conversely, the flip angle of the first pulse in the second HMQC after NOE mixing time may be tuned for higher sensitivity at faster pulsing regime. The magnetization progresses as in the above equation with the difference that the second HMQC lacks the last π/2, and the signal is −I_ysinα − I_zcosα before signal detection. The first term −I_ysinα will evolve during t₃ and the second term, −I_zcosα, will positively contribute to the next scan if the magnetization is of the compatible kind. Here α is more than or equal to 90° (α ≥ 90°), therefore the −cosα is more than or equal to 0 (−cosα ≥ 0).

Compatible proton magnetization that can be transferred to the next scan is only present in X-XH-type experiments such as the N-NH_N 3D SFHMQC-NOESY-SFHMQC. Experiments of the X-YH-type, for example the N-C_MH_M sequence have incompatible magnetization and marginal Ernst angle effect is observed.

The following section details the distinct operating mode for the two experiment types (Fig. 1a,b and Fig. 1c,d, respectively). The spin operator analysis for the HMQC experiment is detailed in Appendix S1. Overall, the input is kI_z, and the output from the first HMQC is ∓kI_z cos(Δω₁t₁) in which the ∓ sign depends on the phase setting of φ₁. During the mixing time τ, if we only consider the diagonal signal (not cross peak) the magnetization M(τ) is:

$$M(\tau )=M_0+[M(0)-M_0]e^{-\tau R_1}$$ (2)

in which, M₀ is equilibrium magnetization; M(0) is the initial magnetization, i.e. M(0) = ∓k cos(Δω₁t₁); R₁ is longitudinal relaxation rate ( = 1/T₁). Resulting in:

$$M(\tau )=M_0+[\mp k\text{ cos}(\mathrm{\Delta }{\omega }_1{t}_1)-M_0]e^{-\tau R_1}$$ (3)

After the second HMQC in 3D N-NH NOESY (or any X-XH), signal will be:

$$M(\tau )(-I_y\mathit{\text{sin}}\alpha -I_z\mathit{\text{cos}}\alpha )$$ (4)

The first term of I_ysinα will be detected by the receiver. For two scans of φ₁ = (+x, −x) and φ_rec = (+x, −x), the detected signal will be:

$$\text{scan }i:\hspace{1em}M(\tau )=M_0+[-k\text{ cos}(\mathrm{\Delta }{\omega }_1{t}_1)-M_0]e^{-\tau R_1}$$ (5)

$$\text{scan }i+1:\hspace{1em}M(\tau )=-\{M_0+[+k\text{ cos}(\mathrm{\Delta }{\omega }_1{t}_1)-M_0]e^{-\tau R_1}\}$$ (6)

and the total detected signal by adding Eq. (5) and (6) after two scans will be proportional to −k cos(Δω₁t₁) sinα. The second term of −M (τ)I_zcosα is residual z component and will not be detected by the receiver, so it will not be affected by the change in receiver phase. For two scans of φ₁ = (+x, −x) and φ_rec = (+x, −x), the residual z component are:

$$\text{scan }i:\hspace{1em}M(\tau )=M_0+[-k\text{ cos}(\mathrm{\Delta }{\omega }_1{t}_1)-M_0]e^{-\tau R_1}$$ (7)

$$\text{scan }i+1:\hspace{1em}M(\tau )=M_0+[+k\text{ cos}(\mathrm{\Delta }{\omega }_1{t}_1)-M_0]e^{-\tau R_1}$$ (8)

and the total residual z component by adding (7) and (8) with two scans will be proportional only to:

$$-M_0(1-e^{-\tau R_1})\mathit{\text{cos }}\alpha$$ (9)

In other words, the residual z component is created from thermal recovery during the mixing time τ and the signal in the first HMQC does not contribute to the residual z component. This residual z component will be positively added to the magnetization recovered during d1 in next scan and that will be:

$$M(d1+aq)=M_0+[M_0(1-e^{-\tau R_1})\text{ cos }\alpha -M_0]e^{-(d1+aq)R_1}=M_0(1-e^{-\tau R_1})\text{ cos }\alpha e^{-(d1+aq)R_1}+M_0[1-e^{-(d1+aq)R_1}]$$ (10)

We assume that in the very first scan of the experiment, the residual z component is supplied by the steady state scan. The signal in subsequent scan is increased because of the addition of:

$$-M_0(1-e^{-\tau R_1})\text{ cos }\alpha e^{-(d1+aq)R_1}$$ (11)

Please note that α ≥ 90°, and −cosα ≥ 0. At longer τ and shorter d1, the first term in Eq 10 (or Ernst-angle contribution to signal) is more significant (see Supp. Fig. S2).

The contribution that starts at about 20% boost in signal, will vanish at longer d1 and the optimal α will become 90°.

In the N-CH NOESY (or any X-YH), the second ¹H-¹³C HMQC does not affect the ¹H_N’s magnetization from thermal recovery during τ at all. Therefore the total recovery time for the ¹H_N’s magnetization is τ + aq + d1 instead of aq + d1 in a regular NOESY experiment using hard pulse. The recovered ¹H_N magnetization will be:

$$M_0[1-e^{-(\tau +d1+aq)R_1}]$$ (12)

When τ, aq and d1 are 0.3, 0.08 and 0.2 sec, the signal strength is increased by ~40% (see the effect of this term on the spectrum in Supp. Fig. S8).

The conclusions from the analysis are that the Ernst angle dependent term M₀(1 − e−τR1cosα contributes to the higher steady state magnetization in the X-XH type experiments while the term M₀[1 − e^{−(τ+d1+aq)R₁}] contributes to the enhancement in the X-YH type experiments with a negligibly small contribution from the α pulse (<5%).

In the simpler 3D NOESY-HMQC of X-YH-type, both ‘X’ and ‘Y’ types ¹H magnetization benefit from an overall τ + aq + d1 recovery period. Taking the H_N-C_MH_M 3D NOESY-HMQC as an example, starting from the flip-up H_N pulse and ending to the first selective pulse in the subsequent scan (Fig. 4a), the H_N magnetization is not operated upon and has time to recover to equilibrium. Analogously, starting from acquisition time and ending on the flip-down pulse after τ in the following scan, the H_M magnetization is left unperturbed and has aq + d1 + (t1) + τ to recover until it is pulsed again. Here, contrary to the 3D HMQC-NOESY-HMQC, there seem to be no significant issues with axial peaks artifacts so there is no need to apply a selective pulse to flip-up the proton magnetization of the HMQC step.

We believe that the above section accounts for most our experimental findings but we do not exclude that depending upon the specific experiment the effects may combine in a way that is not trivial to elucidate at this time.

DISCUSSION

Longitudinal relaxation optimization (L-opt) is achieved in proteins by selective excitation of a subgroup of spins leaving the surrounding population of intramolecular spins at equilibrium. (Pervushin et al. 2002) Such unperturbed spins syphon the magnetization from the excited spins allowing for faster recovery to equilibrium state. The observed effect is a decrease in proton T₁ and concomitant increase in sensitivity.

Practically, it is very straight forward to achieve significant L-opt effect on amides in small doubly labeled proteins. The amides ¹H’s are almost completely separate from the sidechain atoms (minus the overlapping aromatics). Conversely, even with relatively narrow ~4ppm PC9 pulses it is difficult to selectively pulse on specific types of ¹³C-bound protons (for example methyls) without perturbing a large number of surrounding spins and therefore the L-optimized effect is not very significant on the ¹³C-bound protons. In the case of ²H methyl labeled sample made with fresh ²H₂O to insure minimal spurious protonation (< 3%) it should be possible to selectively pulse ‘mostly’ methyls protons. We estimated, from integration of the 1D proton spectrum, that our protein may contain up to 5% spurious protonation due to the use of repeatedly recycled ²H₂O during sample preparation.

Based on the proton relaxation experiments (Supp. Table S1) and the 2D comparisons we concluded that SOFAST-HMQC may be advantageous for 3D NOESY acquisitions in deuterated selectively protonated samples in ¹H₂O buffer. The SOFAST experiment is HMQC rather than HSQC-based, it adopts ¹H shaped pulses for excitation and refocusing and uses an optimized flip angle value (Ernst angle) ‘α’ to further increase signal strength by carrying residual magnetization over to the next scan during fast pulsing. (Schanda et al. 2005) The HMQC pulse sequence has fewer RF pulses than HSQC and it alleviates the signal decay from pulse imperfection. The shaped pulses excite or refocus only amide ¹H_N or methyl ¹H_M (N=amide, M=methyl) and leave H₂O peak unperturbed.

In our 2D testing (Supp. Fig. S6) the SOFAST produced the highest sensitivity at 0.2 s d1. In migrating the 2D to 3D NOESYs, we painstakingly investigated the effects of water flip-back pulses in the reference WATERGATE 2D ¹⁵N and ¹³C-HMQC spectra in order to rule out that the enhancement was simply the result of not pulsing water. The enhancement figures for the basic amide, methyl and aromatic edited 3D SOFAST HMQC-NOESY-HMQC in Fig. 2d are obtained with the same number of transients, same d1 and identical acquisition parameters. Both reference and SOFAST use States-TPPI for phase sensitive acquisition. The data show that NOE buildup curves are skewed favorably toward the SOFAST experiments (Fig. 2). The maximum gains are achieved at lower d1 value and the enhancement persists even at the normal 1s d1 delay that is used in most regular NOESY experiments for practical purposes. In high field instruments with cryoprobes and samples with concentration >0.3 mM, SOFAST-NOESY experiments can be successfully run with as little as 0.2 – 0.5 s relaxation delay (d1). Under these conditions, the signal from reference experiment is significantly attenuated.

The SOFAST NOESY experiments benefit from a combination of the L-optimized effect and Ernst Angle (α) optimization (Supp. Fig. S2 and S4) indicating that the residual −I_zcosα magnetization is carried from the preceding scan to boost sensitivity in the current scan by increasing the steady state polarization during fast pulsing. In some experiment types, SOFAST NOESY also intrinsically uses the mixing time to enhance the recovery of the proton magnetization that is not used until the next transient.

There are three types of experiments and we identified two consistent mechanisms that explain the results: 1) In NOE experiments that are starting and ending on the same moiety/atom type (X-XH), such as N-NH_N, H_N-NH_N, C_M-C_MH_M, H_M-C_MH_M (and the corresponding NOESY-HMQC versions that are ¹H incremented in t₁), the residual magnetization is positively added to the magnetization recovered during d1 to increase the overall steady state polarization. Plus, the decreases in overall T₁ facilitates recovery. Optimizing the flip angle α increases the S/N by 10–15% (Supp. Fig. S2).

2) When the experiment starts on atom type ‘X’ and ends on atom type ‘Y’ (X-YH) for example as the case of N-C_MH_M 3D HMQC-NOESY-HMQC (or C_M-NH_N, C_Aro-C_MH_M), the residual magnetization of H_M in N-C_MH_M is not compatible and will not add to the magnetization of H_N in the next scan. The Ernst angle effect becomes marginal and optimizing the flip angle α only increases the S/N by <5% (Supp. Fig. S2). Instead, the thermal recovery of the H_N magnetization during the mixing time τ is not affected by the second HMQC because its ¹H shaped pulses are set at the H_M frequency. As a result, the relaxation recovery time for H_N will be τ + aq + d1 (aq is acquisition time) instead of aq + d1 in a regular experiment using hard 90° pulses. When mixing time (τ), aq and d1 are 0.3, 0.08 and 0.2 sec the signal is increased by 40%. Spoiling the recovery of the ‘X’ magnetization with a flip-up pulse removes that gain as shown in Supp. Fig. S8. The effect carries to the case of X-YH-type 3D NOESY-HMQC experiments such as H_N-C_MH_M, H_M-NH_N and H_M-C_AroH_Aro. Here, in the absence of artifacts, both the X and Y-type proton magnetization can have τ + aq + d1 relaxation periods since the ‘Y’ magnetization is operated upon only during the HMQC.

3) In time-shared NOE experiment such as H_NH_M-NC_MH_NH_M both residual −I_zcosα for H_N and H_M magnetizations are positively added to their respective spin magnetization recovered during d1 and contribute to higher steady state polarization. Optimizing the flip angle α increases the S/N by ~15–20% (Supp. Fig. S4). Here the L-optimized effect is marginal since we pulse all the protons except water but there is perhaps improvement from the better water suppression achieved with selective pulses as opposed to the hard/flip-back composite pulse in the traditional sequence.

Intermediate size deuterated samples that tend to have longer longitudinal relaxation and require longer mixing for NOESY (0.2 – 0.4 s) should benefit from the new experiments. Rapid collection at ultrahigh field in H₂O is a key advantage when dealing with time sensitive, degradation-prone proteins which often prove to be more biologically active and interesting.

Notoriously weak experiments such as the 3D ¹⁵N-resolved HMQC-NOESY-HMQC are possible even in intermediate size systems (see N-N, N-C, C-N 2D projections along H_N or H_M in Fig. 5d). These are, in fact, the most sensitive experiments of dual SOFAST-HMQC-type.

Diagonal-free editing schemes can be implemented in a very straightforward manner in both 3D NOESY-HMQC and 3D HMQC-NOESY-HMQC. Diagonal-free methyl to amide and amide to methyl versions of the experiment work extremely well and provide very important crosspeaks that are symmetric and helpful to cross validate the NOE assignment. The data acquisition can be split into smaller frequency windows to greatly enhance the resolution in the NOE dimension. The example of SOFAST aromatic-methyl NOESY pulse sequence (Fig. 3a) is simpler than the counterparts using HSQC schemes (Morshauser and Zuiderweg 1999; Stanek et al. 2013; Xia et al. 2001) (Fig. 3b) and scales well to larger methyl-aromatic labeled systems. We have successfully used the sequence to assign aromatic moieties in systems up to 35 kDa kinase domain (KD) at 10° C and at relatively low concentration (200 µM). This is a particularly powerful experiment in large systems when selective ¹H-¹³C aromatic ring labeling reagents are utilized. (Lichtenecker 2014) For smaller proteins, aromatic-methyl and methyl-methyl core connectivity are extracted in a very straightforward manner in fully protonated samples.

In the 3D SFNOESY-HMQC experiment, removing the first SFHMQC transfer shortens the sequence by ~5.2ms (the lengths of a SFNOESY and a SFHMQC when t₁. is zero are 4.4 ms and 9.6 ms, respectively; length of selective pulses depends on field strength) compared to the 3D SFHMQC-NOESY-HMQC with ¹H(F₁) incremented during t₁ and gives the more sensitive 3D SFNOESY-HMQC experiment. Diagonal-free data with high digital resolution can therefore be acquired more efficiently. The increase in resolution and reduced data collection time have a positive influence on the quality of model-based methyl and aromatic NOE assignment. During automated run protocol in CYANA (Guntert and Buchner 2015) more extensive NOE restraint network with twice the number of restraints was obtained when using the higher resolution SOFAST-based NOESY dataset.

Presently, the possible limitations of the technique emerge when attempting to study amide, aromatic or aliphatic resonances that are too close to the water ¹H resonance (between ~4 and 6 ppm) and are outside the selective excitation PC9 pulse bandwidth. Additionally, the methyl-based NOESY shows a very modest improvement at 1.0 s. We anticipate that for highly deuterated proteins with protons only at methyl positions in ²H₂O the gains in sensitivity will be limited to a small Ernst angle enhancement effect <10%. Therefore the sequences are intended for proteins in non-deuterated buffer.

CONCLUSION

A new approach to 3D NOESY spectroscopy based on fast pulsing SOFAST-HMQC technology is outlined. The experiments, intended for intermediate or large size deuterated and selectively methyl or aromatic labeled proteins in ¹H₂O. The experiments are easily to implement and, compared to traditional hard-pulse implementations, they offer shorter collection time, with enhanced sensitivity and resolution. In most cases, even with normal 1.0 s interscan delay SOFAST NOESY outperforms the traditional experiment. We have developed a series of 3D SFNOESY experiments that cover most acquisition scenarios and labeling schemes. The results demonstrate that the approach should positively impact the field of protein structure determination by liquid state NMR.