Volumetric Doppler angle correction for ultrahigh-resolution optical coherence Doppler tomography

Abstract

Ultrahigh-resolution optical coherence Doppler tomography (μODT) demonstrates great potential for quantitative blood flow imaging owing to its large field of view and capillary resolution. However, μODT only detects the axial flow velocity and requires Doppler angle correction to retrieve the absolute velocity. Although methods for Doppler angle tracking of single or few large vessels have been reported, a method that enables angle correction of the entire 3D microvascular networks remains a challenge. Here, we present a method based on eigenvalue analysis of 3D Hessian matrix to retrieve the orientation of each tubular vessel. As the algorithm is voxel based, it is suitable for effective tracking of Doppler angle matrix and restoring the absolute flow over the 3D vascular flow networks. We present results on simulation and flow phantom studies to show its efficacy for accurate 3D angle tracking and absolute flow correction. Then, we perform an in vivo validation study on mouse micro-circulatory cerebral blood flow (CBF) networks, which clearly demonstrates the capability of this method for tracking the Doppler angle matrix of the highly complex 3D CBF networks.

Ultrahigh-resolution optical coherence Doppler tomography (μODT) has been shown to enable determination of 3D cerebral blood flow velocity (CBFv) of mouse brain capillary networks over a large field of view (FOV).¹ Owing to its intrinsic Doppler effect induced by the red blood cell velocity (v_RBC), μODT detects the apparent v_RBC, i.e., the averaged axial component v_z of v_RBC by calculating the accumulative phase shift between two successive A-scans.² In other words, the Doppler angle θ_z, the angle between v_RBC and the beam incidence, ought to be decoupled to retrieve the absolute flow velocity v_RBC (i.e., v_RBC = v_z/cosθ_z).² As θ_z(x, y, z) is a 3D matrix and varies dramatically with flow locations, this remains a challenge for μODT to accurately image absolute flow velocities.

Approaches to decoupling θ_z and retrieving absolute Doppler velocity have been reported, including multiple-beam strategies that used different incident angles to retrieve full velocity profile of blood flow.^3–5 Alternatively, post-image processing methods were commonly applied to circumvent the need for complex hardware modifications. For example, θ_z was retrieved by connecting the center of vessels between two cross-sectional flow images.^6,7 Alternatively, continuous gradient tracking was proposed based on the gradient profile of extracted skeleton of individual vessels.⁸ Similarly, the method was extended to retrieve Doppler angles of multiple branches of middle cerebral artery (MCA).⁹ However, most of these methods are limited to only correct the Doppler angles of a few large vessels (e.g., MCA) and are unable to calculate θ_z(x, y, z) of individual micro flows within 3D cerebral blood flow (CBF) networks. Here, we propose a method for tracking Doppler angle matrix θ_z(x, y, z) based on 3D Hessian matrix. Although 2D Hessian filter has been shown to greatly enhance en-face microangiographic images,¹⁰ its unique properties to retrieve 3D orientation of tubular object (e.g., blood vessel) is so far neglected. Our method relies on the analysis of eigenvalues of 3D Hessian matrix at each pixel whose smallest eigenvector corresponds to the longitudinal direction of a tubular shape.¹¹

For proof of concept, we first applied the method to a simulated helix and evaluated the error of reconstructed angles against the theoretical angles. Then we tested the algorithm on flow phantom with 1% intralipid emulsion for continuous θ_z(x, y, z) tracking and flow rate correction. Finally, we validated the method in vivo on mouse cerebrovascular networks to demonstrate its utility for correcting 3D CBFv quantifications.

To retrieve an arbitrary Doppler angle θ_z(x, y, z) within the entire 3D volumetric μODT image, 3D Hessian matrix H_o,σ was applied to compute the 2nd-order derivative of a pixel of interest based on its local phase shift variation, i.e.,

$$H_{o,\sigma }=\left[\begin{array}{ccc}\frac{{\partial }^{2}I}{\partial x^2}& \frac{{\partial }^{2}I}{\partial x\partial y}& \frac{{\partial }^{2}I}{\partial x\partial z}\\ \frac{{\partial }^{2}I}{\partial x\partial y}& \frac{{\partial }^{2}I}{\partial y^2}& \frac{{\partial }^{2}I}{\partial y\partial z}\\ \frac{{\partial }^{2}I}{\partial x\partial z}& \frac{{\partial }^{2}I}{\partial y\partial z}& \frac{{\partial }^{2}I}{\partial z^2}\end{array}\right],$$ (1)

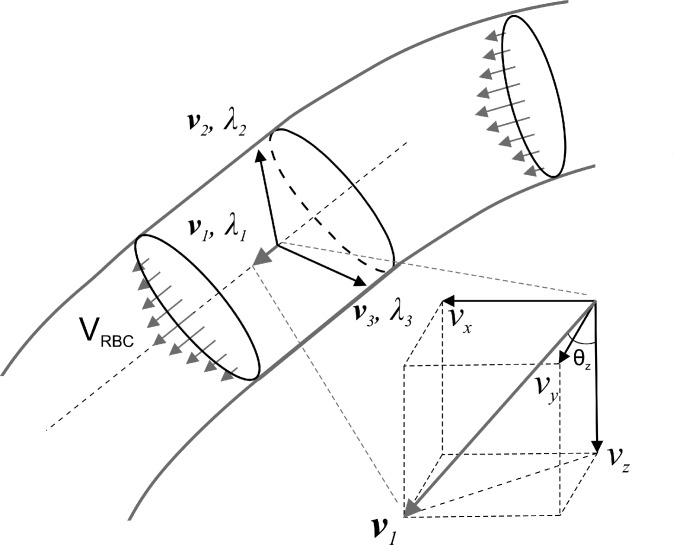
where I(x, y, z) is the raw (apparent) flow value. For a tubular object (e.g., blood flow), H_o,σ along the longitudinal (flow) direction shows less change than those along the radial directions, namely, whose λ₁ is smaller than the other two, i.e., |λ₁|≪|λ₂|, |λ₁|≪|λ₃|, and usually |λ₂| ≈ |λ₃|. Each eigenvalue corresponds to its own orthogonal eigenvector. For example, the eigenvector v₁ (v_x, v_y, v_z) corresponds to the lowest eigenvalue λ₁ as illustrated in Fig. 1, thus the longitudinal or the flow direction of individual pixel (x, y, z) within a tubular flow can be represented by the eigenvector v₁. With v₁ extracted from Eq. (1), the Doppler angle θ_z(x, y, z) can be readily computed assuming the direction of light is incident along the z-axis

$$\text{cos}\hspace{0.17em}{\theta }_z=\frac{\left|v_z\right|}{\sqrt{v_x^2+v_y^2+v_z^2}}.$$ (2)

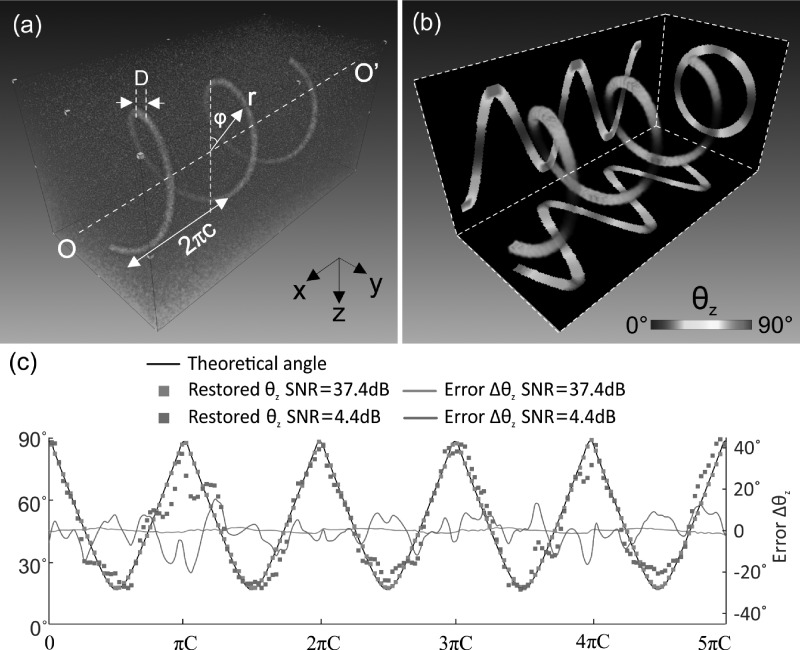
To validate this method, we first applied it to a simulated helix H(cφ, rsinφ, rcosφ; 0 ≤ φ ≤ 5π) whose longitudinal angle is defined as

$$\text{cos}\hspace{0.17em}{\theta }_{z,Theoretical}=\frac{\left|r\hspace{0.17em}\text{sin}\hspace{0.17em}\phi \right|}{\sqrt{r^2+c^2}},$$ (3)

where r and c denote the radius and the helical pitch, respectively. Fig. 2 shows the simulated helix (a) and the 3D color coded longitudinal angle θ_z(x, y, z: 0°–90°) derived from the 3D Hessian matrix method. The three planar images in Fig. 2(b) are the corresponding maximum intensity projection (MIP) images of the 3D angle map projected onto the x-z, y-z, and x-y planes. Quantitative comparison between the theoretical and the modeled θ_z presented in Fig. 2(c) demonstrates the efficacy of our method to restore the angle with an overall accuracy for x from 0 to 5πc to less than 1.18° ± 0.60° error for SNR = 37.4 dB and 5.73° ± 3.99° for SNR = 4.4 dB.

FIG. 1.

A sketch to illustrate Hessian matrix for 3D Doppler angle detection. v₁ is the vector with lowest eigenvalue λ₁ corresponding to the longitudinal direction of tubular vessel.

FIG. 2.

3D θ_z detection for a simulated helix. (a) Simulated helix curve H(cφ, rsinφ, rcosφ: r = 50pixels, c = 15pixels, D = 9pixels, 0 ≤ ϕ ≤ 5π, Δϕ = 0.01 rad/step) with salt and pepper noise (i.e., SNR ≈ 37.4dB), (b) 3D longitudinal angle calculated by Hessian method, (c) quantitative θ_z comparison between theoretical (black line) and restored angles (green, red dots for SNR = 37.4, 4.4 dB, respectively) and their errors (green, red lines for SNR = 37.4, 4.4 dB, respectively). Image size (cropped): 150 × 150 × 300 pixels.

In addition, a flow phantom experiment was performed to assess the utility of this method to retrieve the θ_z matrix for absolute flow correction. In this experiment, 1% intralipid emulsion (Intralipid^® 20%) in a ϕ280 μm translucent micro-tube was driven by a precision syringe pump (CMA400, Microdialysis) at a constant pump rate of v_p = 8.12 mm/s. The microtube was wound onto a cylinder (e.g., ϕ10 mm) to provide continuously varying θ_z from 70° to 90° to allow for Doppler angle tracking and flow correction. Phantom flow images were acquired by our newly developed 1.3 μm μODT setup,¹² in which a spectral-domain OCT engine consisting of a 2 × 2 broadband fiberoptic Michelson interferometer was illuminated with an ultra-broadband source (λ = 1310 nm, λ_FWHM = 220 nm) and the backscattered signal was detected by a custom high-resolution, fast line-scan InGaAs spectral imager (2048-pixels, 145k-lines/s; GL2048, Sensors Unlimited). A high axial resolution of 2.5 μm in biological tissue as defined by coherence length L_c = 2(ln2)/π λ₀²/Δλ was reached by spectral reshaping and dispersion compensation in the reference arm. The sample arm was connected to a fast servo mirror for transverse light scan and an f16 mm/NA0.25 NIR objective to yield a lateral resolution of 3.2 μm in biological tissue or tissue phantom. Graphics processing unit (GPU) programming was implemented to boost FFT and phase detection, which facilitated real-time rendering and display of 3D μODT images up to 473 fps B-scans. For flow phantom study, 3D μODT was acquired at 25 kHz A-scan rate. Both the Hessian matrix method and the continuous gradient tracking method⁹ were applied to the acquired phantom flow for Doppler angle and absolute flow correction.

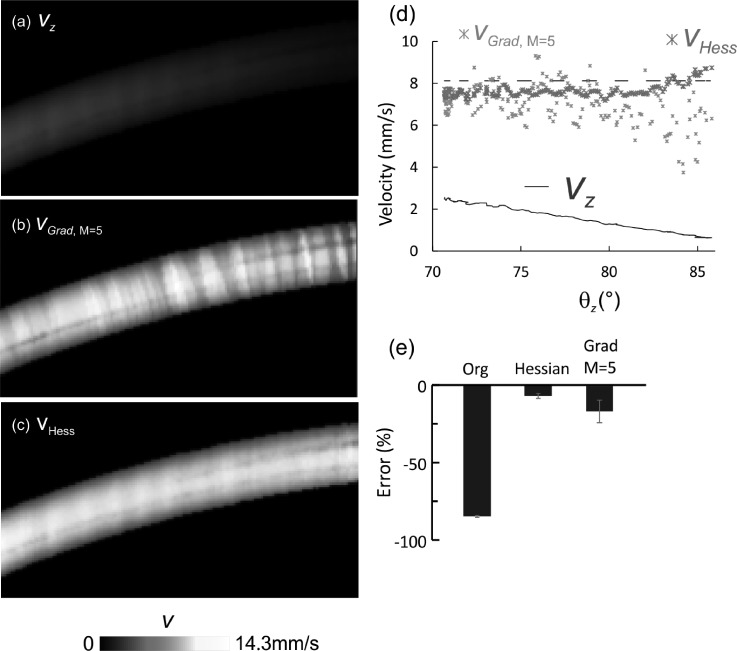
Fig. 3 compares the phantom flow images before and after Doppler angle correction. As expected, the apparent flow v_z acquired by 3D μODT exhibited obvious artifacts (a), i.e., v_z decreased with θ_z and diminished when θ_z → 90°. Angle correction by Hessian matrix (c) or continuous gradient (b) tracking method (averaging number M = 5) was effective for θ_z = 71°–81°, which raised the severely underestimated flow rates to v_Hess = 7.2–7.93 mm/s and to v_Grad,M=5 = 5.23–9.30 mm/s (M = 5), both of which are close to v_p = 8.12 mm/s. As a result, the corrected flow velocity profile appeared more uniform (b) and (c) with varying θ_z. Quantitative analysis (d) revealed that both methods are able to accurately trace the skeleton gradients or the θ_z matrix (e.g., with error less than 10% for θ_z = 71°–81°); however, correction of v_z, to v by v = v_z/cosθ_z was less accurate for θ_z > 82.6°. For instance, deviation of v_p by gradient tracking (v_Grad, M = 5) drastically increased from −7.7% at θ_z = 82.6° to >−47.6% when θ_z > 85.0°. By comparison, deviation by Hessian (v_Hess) was <2% at θ_z = 83.5°, then increased to 7.1% at θ_z = 86°.

FIG. 3.

3D θ_z correction for phantom flow with 1% intralipid in a ф280 μm micro tubing at a pump rate of 30 μl/min or v_p = 8.12 mm/s. (a) Side view of original flow image acquired by 3D μODT at 25 kHz A-line rate. (b) Flow image after θ_z correction with Gradient tracking method. (c) Flow image after θ_z correction with Hessian method. (d) Comparison of flow rates with θ_z among original flow velocity v_z (blue), after Hessian correction v_Hess (red), gradient tracking v_Grad (green) (M = 5), and pump rate v_p (dashed black). (d) Errors before and after Hessian or gradient tracking correction (80° ≤ θ_z ≤ 81°).

Despite that both gradient tracking and Hessian matrix methods can effectively correct the angle-induced errors of Doppler flow in a single vessel (Fig. 3), it is noteworthy that gradient tracking of multiple flows is cumbersome and impractical for the capillary CBF networks. Meanwhile, the Hessian method is voxel-based and therefore potentially suitable for tracking the complex microvascular networks. To further validate the present method, we applied the method to the flow images of C57BL/6 mice in vivo. In the experiment, mice were anesthetized by inhalation of 2% isoflurane and mounted onto a custom stereotaxic frame. A cranial window was surgically created on the mouse sensorimotor cortex with the dura remained intact, and the exposed cortex was filled with 1% agarose and sealed by a glass coverslip to minimize motion artifacts. To enhance the capillary sensitivity, 6 ml/kg intralipid was injected into the animal's circulation system through tail vein before μODT imaging.¹³ 3D μODT was acquired at 10 kHz A-scan rate to reconstruct the CBFv images over 2.4 × 2 × 1.4 mm³ (6k A-lines by 400 B-scans) on the mouse cortical brain.

Fig. 4 compares the 3D CBFv images before and after Doppler angle correction. Because of overwhelming vascular turnouts, pie-cut cross-sections are presented to illustrate the effects on flow quantitation. Without angle correction, the apparent CBFv image (a) showed severely underestimated flow rates, especially for most pial arterial and venous flows that were perpendicular to the direction of incident light beam (θ_z → 90°, cos θ_z → 0). 3D Doppler angle image (b) computed from the Hessian matrix (σ = 1,2,3,4,5) tracked the θ_z distributions of these flow compartments and thus allowed for angle correction to retrieve the absolute 3D CBFv image (c) based on matrix computation v_RBC = v_z/cosθ_z. After angle correction, pial venous flows were dramatically increased from under 1.08 ± 0.21 mm/s (a) to over 5 mm/s as highlighted by white arrows (c). Moreover, horizontally oriented capillary flows in deep cortical layers which were usually weak (a) can be readily restored by Doppler angle correction as highlighted by the yellow arrows (e.g., at ∼1.2 mm below cortical surface).

FIG. 4.

3D CBFv network image of mouse sensorimotor cortex (2.4 × 2.0 × 1.4 mm³) before and after θ_z correction. (a) Raw 3D μODT image (i.e., v_z) without θ_z correction, (b) 3D Doppler angle θ_z image, (c) 3D absolute v_RBC image after θ_z correction by 3D Hessian matrix. Yellow arrow: horizontally oriented capillary flow in deep cortex usually undetectable without angle correction; white arrows: correction of pial flows. 2D pie-cut images are MIP images of 200 μm-thick sub-volume.

In summary, we present an approach based on the 3D Hessian matrix that enables accurate tracking of Doppler angles of 3D microcirculatory CBFv networks. Unlike the previously reported skeleton gradient methods,^8,9 the method is voxel-based and retrieves θ_z matrix by utilizing eigenvalue analysis of 3D Hessian matrix. For proof of concept, we presented the simulation result that clearly demonstrated the efficacy of this method to trace θ_z of a Gaussian profiled helix with an overall error less than 1.18° ± 0.60°. Then we evaluated the algorithm on flow phantom (1% intralipid) with θ_z ramping from 70° to 85° and showed that it was able to accurately restore the absolute flow rate with error less than 7.1% even at a very flat angle of θ_z = 86°, while gradient tracking method showed escalating deviation (>47%). Finally, we performed in vivo validation study on mouse sensorimotor cortex and showed that unlike previous methods such as gradient tracking that only corrected individual vessels, 3D Hessian matrix approach is voxel-based and was thus able to correct the entire microcirculatory CBFv networks, which included the correction of severely underestimated pial flows (mostly horizontally oriented) and uncovering those horizontally oriented capillary flows in the deep cortical layers (e.g., >1.2 mm of depths). Additionally, the present method is reasonably robust for low and intermediate noises (e.g., SNR ≈ 4 dB in Fig. 2(c)) and therefore allows for detecting axial angle of complex capillary networks which usually suffer low SNR. Such a capability for quantitative imaging of the absolute CBFv networks is important to understand the cortical hemodynamics and the related disease progressions (e.g., ischemia). The limitation of this method occurs in the extreme cases when Gaussian kernel scale and targeted vessels are mismatched.¹⁰

To calculate the Hessian matrix of each voxel, the original image I(x, y, z) was convoluted with its second derivative of the Gaussian kernel with pre-define scale σ. When the kernel size is as small as a small capillary (∼ϕ6 μm), it is insensitive for detecting vessel orientation of a large branch (∼ϕ150 μm) and vice versa. Another drawback is over-correction of horizontal flows due to the inherent limitation of Doppler methodology for flow detection (i.e., v_z → 0 if θ_z → 90°). It is noteworthy that for an ODT system with a higher NA (e.g., NA > 0.2), θ_z is no longer a single angle but rather a span of angles. Therefore, more modeling work is needed to take this into account. Also, further work is needed to enhance the accuracy for multiple-scale vascular networks with vessels of diverse calibers.