Effect of Cilia Beat Frequency on Muco-ciliary Clearance

Abstract

Background:

The airway surface liquid (ASL), which is a fluid layer coating the interior epithelial surface of the bronchi and bronchiolesis, plays an important defensive role against foreign particles and chemicals entering lungs.

Objective:

Numerical investigation has been employed to solve two-layer model consisting of mucus layer as a viscoelastic fluid and periciliary liquid layer as a Newtonian fluid to study the effects of cilia beat frequency (CBF) at various amounts of mucus properties on muco-ciliary transport problem.

Methods:

Hybrid finite difference-lattice Boltzmann-method (FB-LBM) has been used to solve the momentum equations and to simulate cilia forces, and also the PCL-mucus interface more accurately, immersed boundary method (IBM) has been employed. The main contribution of the current study is to use an Oldroyd-B model as the constitutive equation of mucus.

Results:

Our results show that increasing CBF and decreasing mucus viscosity ratio have great effects on mucus flow, but the effect of viscosity ratio is more significant. The results also illustrate that the relation between cilia beat frequency and mean mucus velocity is almost linear and it has similar behavior at different values of viscosity ratio.

Conclusion:

Numerical investigation based on hybrid IB-FD-LBM has been used to study the effect of CBF at various mounts of mucus viscosity ratio on the muco-ciliary clearance. The results showed that the effect of viscosity ratio on the muco-ciliary transport process is more significant compared with CBF.

Introduction

The surface liquid layer of the airways of human respiratory system which protects the airways of the lung from inhaled dust, bacteria and other harmful substances by an extremely thin surface liquid (ASL), is normally from 5 to 10 µm deep [1]. This liquid consists of two sub-layers: the innermost watery periciliary liquid layer (PCL) and the outermost viscoelasitc mucus layer [2]. Mucus is a sticky, non-linear and viscoelastic secretion composed mainly of long chain glycoproteins and salts in a suspension of water [3]. Some polluted particles in inhaled air are entrapped in this mucus layer. Muco-ciliary clearance is primarily responsible for the removal of mucus and cellular debris from lung. The airways of the lung are lined with a dense mat of cilia, which beat back and forth in a coordinated wave and hence the mucus layer together with entrapped particles are propelled out of lungs [4]. These Cilia have two quite distinct stages of their beating cycle in which the effective stroke when the cilium is extended out of the cell surface and the recovery stroke when it moves back slowly to the start of its effective stroke. The effective stroke occupies a shorter period of the beat than the recovery stroke, so the work done during the effective stroke is several times the amount of work done performed during the recovery stroke [5].

Cilia force which imposes into ASL can be mainly categorized as volume force models in which cilia are represented by discrete cilia models (discrete bodies [3]) or represented as distributed forces [2]. The cilium motion also can be prescribed as the interaction between the cilium and the external fluid [5-7].

Morphological and functional disorders of cilia may be caused by inherited disorders such as Primary Ciliary Dyskinesia (PCD) and some acquired insults such as exposing to toxins and pollutants leading to inefficiency in mucu-ciliary transport [8]. PCD is a cilia-related disease in which cilia beat in abnormal patterns or beat slowly or become completely stationary resulting from some defects in the components of axonemes [9]. Due to the disorder in cilia motion, the velocity of mucus layer reduces and mucus would accumulate with airways leading to airway blockage, lung damage and infections [10]. PCD leads to abnormalities in cilia beat frequency (CBF), cilia beat pattern (CBP) and Nitric Oxide (NO) diseases as reported in the literature. Rossman et al. [11] reported two patterns of abnormal ciliary beats (CBP); an oscillating and a rotating type of motion. Their results show that this abnormal motion was present in up to 40 percent of cells and the remainder cases were totally immotile. Another abnormal CBP is reported in Rutland et al. [12] which is called “windscreen wiper” motion. Chilvers et al. [13] stated that abnormalities in cilia beat frequency (CBF) are the result of nasal rhinorrhea or blockage and moist-sounding cough which results from PCD. Their study [13] showed that determining ciliary beat pattern related to specific ultrastructural ciliary defects might help in the diagnosis of PCD. In addition, some investigations [14-16] stated that nasal NO is found in very small quantities in PCD patients.

Variation in CBF plays a vital role in the muco-ciliary transport process [2,5]. Although smoking has no effect ([17]) or has a less effect ([12]) on CBF, CBF increases by ethanol [17]. The characteristics of PCL layer such as temperature, PH, tonicity, viscosity, relative humidity and pressure influence CBF [8].

Jayathilake et al. [7] in a numerical investigation studied the effects of CBP, ciliary length, immotile cilia, beating amplitude and uncoordinated beating of cilia on the muco-ciliary transport process. Their results demonstrate that windscreen wiper motion and rigid planar motion greatly reduce or almost stop the mucus transport. Their results also showed that by decreasing beating amplitude and changing the ciliary length from its standard length mucus velocity decreases. The main shortcoming in this study is that they consider mucus as a Newtonian fluid while, as mentioned before mucus is a viscoelastic fluid and the elastic properties of it has a great effect on the muco-ciliary transport [18]. Many researchers study the effects of Non-Newtonian behavior of mucus on the muco-ciliary transport. Ross [19] probably is the first investigator to study the viscoelastic effect of mucus on the mucus flow. In this study, mucus was modelled as a nonlinear Maxwell fluid, and the resulting system of equations was solved analytically using Fourier series. In this study, PCL was not modelled. In addition, the mucus-PCL interface was modelled as an impermeable wavy wall. While Blake [20] stated that this kind of boundary would not be appropriate for the interface because the tips of the cilia might penetrate into the mucus layer during the effective stroke. King et al. [21] using a simple analytical model, studied the effect of mucus viscoelasticity on the muco-ciliary system. They concluded that mucus transport intensifies by reducing the shear modulus of elasticity. One of the shortcomings of this study is that they showed there was no net transport of PCL in the cilia sub-layer while the experiment of Matsui et al. [22] on human tracheobronchial epithelial culture revealed the transport of PCL is approximately equal and significant for mucus transport. Smith et al. [2] in an analytical investigation studied the transport of mucus and periciliary liquid in the airways by considering mucus as a linearly viscoelastic fluid. They considered ASL as a three- fluid layer separated by flat interfaces. The lower layer (PCL), was modelled by a Newtonian fluid, the middle layer (traction layer) representing the region in which the cilia penetrate the mucus was modelled by a Maxwell viscoelastic fluid with viscosity μ_M1 and relaxation time λ₁. The upper layer representing the mucus above the penetration region was modelled by a Maxwell fluid of viscosity μ_M2 (which is greater than μ_M2) and the same relaxation time λ₁. Moreover, the mat of cilia was modelled as an active porous medium. The propulsive effect of cilia was modelled by time-dependent force acting in a shear-thinned traction layer between the mucus and the PCL. They studied various parameters on the motion of mucus. Their results showed that the dependence of mucus transport on the choice of physical parameters was nonlinear. Their result demonstrated that mucus transport was significantly affected by cilia beat frequency (CBF). One shortcoming of this study is that they [2] considered mucus as a linear viscoelastic fluid. While Bird et al. [23] stated that such materials in which the non-Newtonian viscosity is dominant cannot be studied by linear viscoelastic models. Another shortcoming is that they [2] considered the mucus-PCL interface as totally flat.

As mentioned before, the process of muco-ciliary transport is critically affected by CBF and mucus properties. In this investigation by considering mucus as a viscoelastic fluid, 2D numerical model is developed to study the effects of CBF at various amounts of mucus properties. A schematic of the problem is shown in Figure 1. The main contribution of the present study is considering mucus as an Oldroyd-B fluid for the first time. This model is discussed in terms of convected components of the stress tensor and the metric coefficients of the convected coordinate system. Material constants appear in this constitutive equation, and also temperature history may be included if it is desired to account for non-isothermal effects [23].

Figure1.

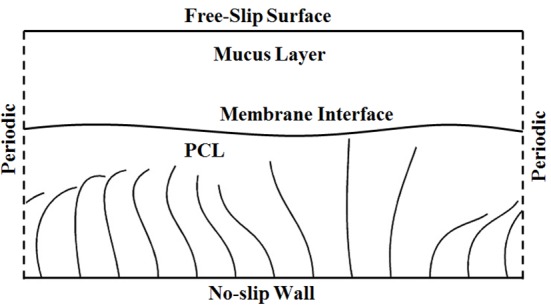
A schematic Geometry for Muco-ciliary Transport Problem

Material and Method

In this part, the governing equations of muco-ciliary problem and the numerical method for solving are defined. As Figure 1 shows, in this problem ASL is considered as two separate layers; the lower periciliary liquid layer consists of watery and nearly Newtonian liquid and the upper mucus layer is a viscoelastic fluid. Immersed boundary method is used to simulate precise effects of cilia and PCL-mucus interface on the fluid.

Governing Equations

The governing equations of incompressible fluid flow in a model shown in Figure 1 can be written as follows [5]

$\overrightarrow{\nabla }.\overrightarrow{u}=0$ (1a)

$\frac{\partial \overrightarrow{u}}{\partial t}+\overrightarrow{u}.\overrightarrow{\nabla }\overrightarrow{u}+\frac{1}{\rho }\overrightarrow{\nabla }p=\frac{1}{\rho }\overrightarrow{\nabla }.\sigma +f$ (1b)

$\overrightarrow{f}\left(\overrightarrow{x},t\right)={\int }_{\Gamma }\overrightarrow{F}\left(\mathrm{s,t}\right)\delta (\overrightarrow{x}-\overrightarrow{X}(\mathrm{s,t}\left)\right)\mathrm{ds}$ (1c)

$\frac{\partial \overrightarrow{X}}{\partial t}=\overrightarrow{U}\left(\overrightarrow{X}\right(\mathrm{s,t}\left),t\right)={\int }_{\Omega }\overrightarrow{u}\left(\overrightarrow{x},t\right)\delta (\overrightarrow{x}-\overrightarrow{X}(\mathrm{s,t}\left)\right)d\overrightarrow{x}$ (1d)

Where $\overrightarrow{x}$ is the Eulerian coordinates, $\overrightarrow{u}$ is the velocity vector, ρ is density, p is static pressure, t is time, σ is the stress tensor and f is the boundary force acting on the fluid field. Also $\overrightarrow{U}$ is the Lagrangian coordinate, is the velocity vector of Lagrangian nodes, s is the arc length of Lagrangian nodes and $\overrightarrow{F}$ is the boundary force density which contains cilia and membrane forces. In addition, $\delta (\overrightarrow{x}-\overrightarrow{X}(\mathrm{s,t}\left)\right)$ is a Dirac delta function. Eqs (1c) and (1d) describe the interaction between the immersed boundary and the fluid by distributing the boundary force at Lagrangian points to Eulerian points and interpolating the velocity at Eulerian points to Lagrangian points.

The cilia have a cyclic motion in PCL. There is no material interface between PCL and mucus layers so the cilia can penetrate the mucus-PCL interface. In addition, the effect of surface tension is added by the force generated due to an imaginary elastic membrane. In this study, the flow is assumed to be periodic in horizontal direction. The bottom boundary is assumed to be no-slip wall and the top boundary is assumed to be free-slip boundary [5].

Constitutive Relations

Previous experimental studies have concluded that viscoelasticity played a vital role in effective transport of mucus. In this study, an Oldroyd-B model is used as the constitutive equation for mucus. In this model, the stress tensor σ can be decomposed into two parts:

${\sigma }_M={\sigma }_{\mathrm{M,N}}+{\sigma }_{\mathrm{M,E}}$ (2)

σ_M,N is related to Newtonian part of stress tensor and the second term ( σ_M,E) is related to the elastic contribution of it. The Newtonian solvent contribution can be calculated as::

${\sigma }_{\mathrm{M,E}}={\mathrm{2\eta }}_{\mathrm{M,N}}D$(3)

And the elastic contribution is derived based on the Upper Convected Maxwell model (UCM) as follows:

${\sigma }_{\mathrm{M,E}}+\lambda {\sigma }_{M,E}^{\nabla }={\mathrm{2\eta }}_{\mathrm{M,E}}D$ (4)

In equation (4), λ is the relaxation time, which gives an indication of the magnitude of the elastic nature of fluid. The viscosity of mucus also decomposes into Newtonian (η_M,N) and elastic (η_M,E) viscosities as follows:

${\eta }_{\mathrm{M}}={\eta }_{\mathrm{M,N}}+{\eta }_{\mathrm{M,E}},\beta =\frac{{\eta }_{\mathrm{M,E}}}{{\eta }_{\mathrm{M}}}\mathrm{(5)}$

And the upper convected derivative of σ_M,E is defined as:

${\sigma }_{M,E}^{\nabla }=\frac{\partial {\sigma }_{\mathrm{M,E}}}{\partial \stackrel{\sim }{t}}+\overrightarrow{u}.\nabla {\sigma }_{\mathrm{M,E}}-{\sigma }_{\mathrm{M,E}}.\nabla \overrightarrow{u}-\nabla {\overrightarrow{u}}^T.{\sigma }_{\mathrm{M,E}}$ (6)

In Eqs. (3) and (4), D is the rate of deformation which is defined as:

$D=\frac{1}{2}(\mathrm{\nabla V}+{\mathrm{\nabla V}}^{\mathrm{T}})$ (7)

The Oldroyd-B constitutive equation can be derived from a molecular model in which the polymer molecule is idealized as an infinitely extensible Hookean spring connecting two Brownian beads [23]. This model has specially been used for simple shear prediction flows that are in qualitative agreement with measurements for some Boger fluids [24].

Numerical Simulation

In this part, a 2D numerical model based on immersed boundary-lattice Boltzmann method has been used for the simulation of muco-ciliary clearance problem (Figure 1). This method uses a fixed Cartesian mesh to represent fluid phase which is composed of Eulerian points. For the boundary immersed in the fluid, a set of Lagrangian points is used to represent it [25].

At the beginning of this part to simulate real rheology properties of the mucus layer and also the real dimension of the geometry, transformation coefficients form the physical domain to the lattice Boltzmann domain are introduced as:

$C_{h_x}=\frac{\Delta X^{\mathrm{phy}}}{\Delta X^{\mathrm{lb}}},C_{h_y}=\frac{\Delta Y^{\mathrm{phy}}}{\Delta Y^{\mathrm{lb}}},C_t=\frac{\Delta t^{\mathrm{phy}}}{\Delta t^{\mathrm{lb}}},C_{\rho }=\frac{{\rho }^{\mathrm{phy}}}{{\rho }_0^{\mathrm{lb}}}$ (8)

In equation (8), Δx^phy and Δy^phy are grid spacing in x and y directions, Δt^phy is time spacing and ρphy is density for physical domain. Additionally, Δx^lb and Δy^lb are grid spacing, Δt^lb is time spacing and ρ₀^lb is referenced density in LBM domain. In addition, C_hx ,C_hy , C_t and C_ρ are related to space in x and y directions, time and density transformation coefficients, respectively. In this study, “lb” superscript is related to LBM variables and for simplicity; physical variables are shown without any superscript.

In equation (8), by considering Δx^lb = Δy^lb and Δx = Δy we can write C_hx =C_hy = C_h . The other transformation coefficients can be obtained as follows:

$C_u\frac{\overrightarrow{u}}{{\overrightarrow{u}}^{\mathrm{lb}}}=\frac{C_h}{C_t},C_v=\frac{v_N}{v^{\mathrm{lb}}}=\frac{C_h^2}{C_t},C_p=\frac{P}{P^{\mathrm{lb}}}=C_{\rho }(\frac{C_h}{C_t}{)}^2$ (9)

Where ν_N is the kinematic viscosity of Newtonian part of the fluid. C_u, C_ν and C_ρ are velocity, Newtonian kinematic viscosity and pressure transformation coefficients, respectively.

The lattice Boltzmann equations in fluid points can be shown as follows [26]:

$f_{\alpha }({\overrightarrow{x}}^{\mathrm{lb}}+{\overrightarrow{e}}_{\alpha }\Delta t^{\mathrm{lb}},t^{\mathrm{lb}}+\Delta t^{\mathrm{lb}})-f_{\alpha }\left({\overrightarrow{x}}^{\mathrm{lb}},t^{\mathrm{lb}}\right)=-\frac{1}{\tau }\left(f_{\alpha }\right({\overrightarrow{x}}^{\mathrm{lb}},t^{\mathrm{lb}})-f_{\alpha }^{\mathrm{eq}}({\overrightarrow{x}}^{\mathrm{lb}},t^{\mathrm{lb}}\left)\right)+{\overrightarrow{F}}_{\alpha }\Delta t^{\mathrm{lb}}$ (10a)

$F_{\alpha }={\omega }_{\alpha }(1-\frac{1}{2\tau })(\frac{{\overrightarrow{e}}_{\alpha }-{\overrightarrow{u}}^{\mathrm{lb}}}{C_s^2}+\frac{{\overrightarrow{e}}_{\alpha }.{\overrightarrow{u}}^{\mathrm{lb}}}{c_s^4}{\overrightarrow{e}}_{\alpha }).{\overrightarrow{f}}^{\mathrm{lb}}$ (10b)

${\rho }^{\mathrm{lb}}=\sum _{\alpha }{\overrightarrow{e}}_{\alpha }{f}_{\alpha }$ (10c)

${\rho }^{\mathrm{lb}}{\overrightarrow{u}}^{\mathrm{lb}}=\sum _{\alpha }{\overrightarrow{e}}_{\alpha }{f}_{\alpha }+\frac{{\rho }^{\mathrm{lb}}}{2}{\overrightarrow{f}}^{\mathrm{lb}}\Delta t^{\mathrm{lb}}$ (10d)

Where f_α is the distribution function, f_α^eq is its corresponding equilibrium distribution function for the discrete velocity ${\overrightarrow{e}}_{\alpha }$ , ${\overrightarrow{F}}_{\alpha }$ is the discrete force term, ${\overrightarrow{f}}^{\mathrm{lb}}$ is the force density action on the fluid field, ω_α is weighting coefficient which depends on the selected lattice velocity model , τ is the single relaxation time, ρ^lb is the density of fluid in LB domain, c_s = c/√3 is the sound speed and c = Δx^lb/Δt^lb is the lattice speed. f_α^eq is the equilibrium distribution function (EDF) defined as:

$f_{\alpha }^{\mathrm{eq}}={\rho }^{\mathrm{lb}}{\omega }_{\alpha }[1+\frac{3({\overrightarrow{e}}_{\alpha }.{\overrightarrow{u}}^{\mathrm{lb}})}{C^2}\frac{9({\overrightarrow{e}}_{\alpha }.{\overrightarrow{u}}^{\mathrm{lb}}{)}^2}{2C^4}-\frac{3|{\overrightarrow{u}}^{\mathrm{lb}}{|}^2}{2C^2}]$ (11)

Here, the two-dimensional nine velocity (D2Q9) model is used as shown in Figure 2. The particle velocity ${\overrightarrow{e}}_{\alpha }$ may be written as:

Figure2.

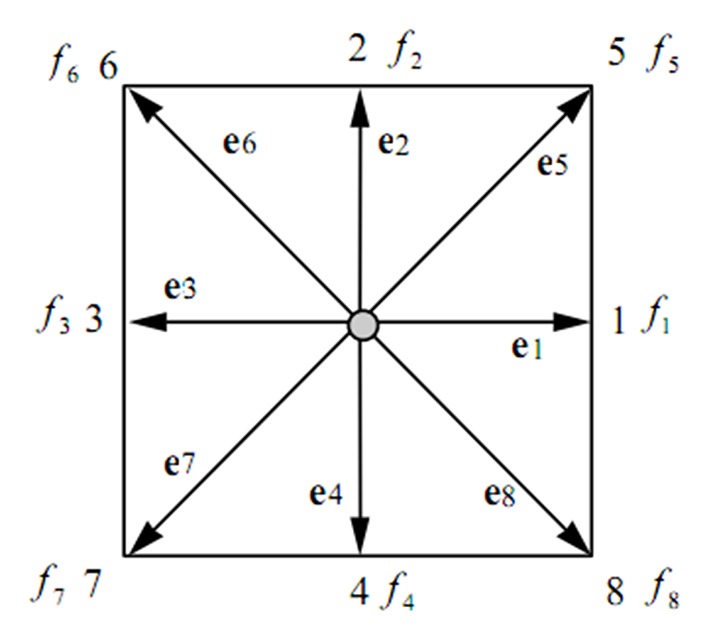
Lattice Arrangements for 2-D Problems, D₂Q₉

${\overrightarrow{e}}_{\alpha }=\{\begin{array}{cc}\left[0,0\right]\hfill & \mathrm{\alpha =0}\hfill \\ c\left[\cos \left(\frac{\left(\mathrm{\alpha -1}\right)\pi }{2}\right),\sin \left(\frac{\left(\mathrm{\alpha -1}\right)\pi }{2}\right)\right]\hfill & \mathrm{\alpha =1-4}\hfill \\ \surd 2c\left[\cos (\frac{\left(\mathrm{\alpha -5}\right)\pi }{2}+\frac{\pi }{4}),\sin (\frac{\left(\mathrm{\alpha -1}\right)\pi }{2}+\frac{\pi }{4})\right]\hfill & \mathrm{\alpha =5-8}\hfill \end{array}$ (12)

And the weighting coefficients ω_α are defined as:

${\omega }_{\alpha }=\{\begin{array}{cc}\frac{4}{9}& \mathrm{\alpha =0}\\ \frac{1}{9}& \mathrm{\alpha =1-4}\\ \frac{1}{36}& \mathrm{\alpha =5-8}\end{array}$ (13)

The single relaxation time in LB equations (τ) is calculated as:

$\tau =\frac{V^{\mathrm{lb}}}{C_s^2\Delta t^{\mathrm{lb}}}+0.5$ (14)

Where ν^lb is the kinematic viscosity in LBM domain.

In equation (10), f^lb consists of three different forces as follows:

${\overrightarrow{f}}^{\mathrm{lb}}={\overrightarrow{f}}_E^{\mathrm{lb}}+{\overrightarrow{f}}_{\mathrm{Cilia}}^{\mathrm{lb}}+{\overrightarrow{f}}_{\mathrm{Mem}}^{\mathrm{lb}}$ (15)

${\overrightarrow{f}}_E^{\mathrm{lb}}$ is related to the elastic part of the stress tensor in mucus layer, ${\overrightarrow{f}}_{\mathrm{Cilia}}^{\mathrm{lb}}$ is related to the force each cilium imposes to the fluid and ${\overrightarrow{f}}_{\mathrm{Mem}}^{\mathrm{lb}}$ is related to the elastic force on the interface between the mucus and PCL.

This is the first force which should be added to LB equations due to elastic part of the stress tensor of mucus. For calculating this force using the physical velocity field at the time level t = t_n and using finite difference method, the elastic part of the stress tensor (equation (4)) are solved and the value of σ_E in each time step is calculated. So, the elastic force of stress tensor can be calculated as:

${\overrightarrow{f}}_E=\frac{1}{\rho }\overrightarrow{\nabla }.{\sigma }_{\mathrm{M,E}}$ (16)

Since $\overrightarrow{f}$ is defined as a physical variable, it should be multiplied by force transformation coefficient to transform into LB force as follows:

${\overrightarrow{f}}_E^{\mathrm{lb}}={\overrightarrow{f}}_E\frac{C_t^2}{C_h}$ (17)

Immersed boundary method has been employed to simulate cilia forces. In this method, the interpolated velocity of fluid at cilia points is enforced to be equal to the velocity of the cilia at the same position at every evolution time step by a set of velocity correction $\delta {\overrightarrow{U}}^{\mathrm{lb}}$. For calculating this velocity correction, the following system of equations should be solved [25]:

$A\overrightarrow{X}=\overrightarrow{B}$ (18a)

$X=\{\delta {\overrightarrow{U}}_1^{\mathrm{lb}},\delta {\overrightarrow{U}}_2^{\mathrm{lb}},\mathrm{...},\delta {\overrightarrow{U}}_m^{\mathrm{lb}}{\}}^T$ (18b)

$A=\left[\begin{array}{cccccc}{\delta }_{11}& {\delta }_{12}& .& .& .& {\delta }_{\mathrm{1n}}\\ {\delta }_{21}& {\delta }_{22}& .& .& .& {\delta }_{\mathrm{2n}}\\ .& .& .& & & .\\ .& .& & .& & .\\ .& .& & & .& .\\ {\delta }_{\mathrm{m1}}& {\delta }_{\mathrm{m2}}& .& .& .& {\delta }_{\mathrm{mn}}\end{array}\right]\left[\begin{array}{cccccc}{\delta }_{11}^B& {\delta }_{11}^B& .& .& .& {\delta }_{\mathrm{1m}}^B\\ {\delta }_{21}^B& {\delta }_{22}^B& .& .& .& {\delta }_{\mathrm{2m}}^B\\ .& .& .& & & .\\ .& .& & .& & .\\ .& .& & & .& .\\ {\delta }_{\mathrm{n1}}^B& {\delta }_{\mathrm{n2}}^B& .& .& .& {\delta }_{\mathrm{nm}}^B\end{array}\right]$ (18c)

Here, m is the number of Lagrangian points on the cilia, and n is the number of Eulerian points. ${\overrightarrow{U}}_l^{\mathrm{lb}}(l=1,2,\mathrm{...},m)$ is the velocity vector of Lagrangian (cilia) points and $\delta {\overrightarrow{U}}_l^{\mathrm{lb}}(l=1,2,\mathrm{...},m)$ is the unknown velocity correction vector at the Lagrangian points. In equation (16) , δ_i,j^B=D_i,j(x_i,j^lb - X_l^lb)∆s^lb and δ_i,j=D_i,j(x_i,j^lb - X_l^lb)∆x^lb∆x^lb where ∆s_l^lb is the arc length of cilia elements and D_i,j(x_i,j^lb - X_l^lb) is Delta function which is defined as [5]:

$D_{\mathrm{ij}}(x_{\mathrm{ij}}^{\mathrm{lb}}-X_l^{\mathrm{lb}})=\delta (x_{\mathrm{ij}}^{\mathrm{lb}}-X_l^{\mathrm{lb}})\delta (y_{\mathrm{ij}}^{\mathrm{lb}}-Y_l^{\mathrm{lb}})$ (19a)

$\delta \left(r\right)=\{\begin{array}{cc}1-\left|r\right|,\hfill & \left|r\right|\le 2\hfill \\ 0,\hfill & \left|r\right|>2\hfill \end{array}$ (19b)

In this method, cilia forces at Lagrangian points ${\overrightarrow{U}}_{\mathrm{Cilia}}^{\mathrm{lb}}$ can be calculated as [25]:

${\overrightarrow{F}}_{\mathrm{Cilia}}^{\mathrm{lb}}=\frac{2\delta {\overrightarrow{U}}^{\mathrm{lb}}}{\delta t}$ (20)

By interpolating the value of cilia forces from Lagrangian (cilia) nodes to Eulerian (fluid) points, the cilia force on each node of fluid can be calculated as:

${\overrightarrow{f}}_{\mathrm{Cilia}}^{\mathrm{lb}}=\sum _l{\overrightarrow{F}}_{\mathrm{Cilia}}^{\mathrm{lb}}{D}_{\mathrm{ij}}(x_{\mathrm{ij}}^{\mathrm{lb}}-X_l^{\mathrm{lb}}∆s_l^{\mathrm{lb}})$ (21)

F_Mem is the elastic force exerted by the membrane interface of PCL and mucus to the fluid is calculated as [5]:

$F_{\mathrm{Mem}}=\frac{1}{\rho }\frac{\partial }{\mathrm{\partial S}}\left[T\right(s\left)\tau \right(s\left)\right]$ (22)

Where T(s) and τ(s) are defined as:

$T\left(s\right)=T_0(\frac{\partial X_{\mathrm{Mem}}}{\partial S_0}-1)$ (23a)

$\tau \left(s\right)=\frac{\partial X_{\mathrm{Mem}}}{\partial s}/\left|\frac{\partial X_{\mathrm{Mem}}}{\partial s}\right|$ (23b)

In equations (23), τ(s) is the unit tangential vector to the PCL-mucus membrane interface. The arc-lengths s and s0 are measured along the current and initial configuration of the membrane interface, respectively. The scalar T₀ is the stiffness constant which describes the elastic property of the flexible boundary.

Using force transformation coefficients ${\overrightarrow{F}}_{\mathrm{Mem}}$ can be transformed into LB force as follows:

$F_{\mathrm{Mem}}^{\mathrm{lb}}=F_{\mathrm{Mem}}\frac{C_t^2}{C_h}$ (24)

By interpolating the value of membrane force $\left({\overrightarrow{F}}_{\mathrm{Mem}}^{\mathrm{lb}}\right)$ from Lagrangian (membrane) nodes to Eulerian (fluid) points the membrane force on each node of fluid can be calculated as:

${\overrightarrow{f}}_{\mathrm{Mem}}^{\mathrm{lb}}=\sum _l{\overrightarrow{F}}_{\mathrm{Mem}}^{\mathrm{lb}}{D}_{\mathrm{ij}}(x_{\mathrm{ij}}^{\mathrm{lb}}-X_{\mathrm{Mem,l}}^{\mathrm{lb}}∆s_{\mathrm{Mem,l}}^{\mathrm{lb}})$ (25)

By computing these three forces, ${\overrightarrow{f}}^{\mathrm{lb}}$ can be calculated using equation (15). This force term should be used in equation (10b) and added to equation (10) as the extra force. mml:math> ${\overrightarrow{f}}^{\mathrm{lb}}$ is also used to modify fluid velocity using equation (10d). Finally, the membrane velocity U_Mem (X_Mem) is interpolated from the neighboring grid points. Subsequently, the location of the membrane interface is updated as:

$\frac{{\mathrm{\partial X}}_{\mathrm{Mem}}}{\mathrm{\partial t}}=U_{\mathrm{Mem}}$(26)

Results

In this section using the numerical scheme introduced in Section 2, 2D numerical simulation has been employed to study the CBF effects at various properties of mucus on the muco-ciliary clearance problem. The main feature of the present study is using an Oldroyd-B model for simulating mucus, in which the effect of mucus rheology can be considered more accurately. In addition, for simulating cilia forces and also mucus-PCL interface, an immerse boundary method is used. At the beginning of this section, the standard parameter set which we use for reference is defined as follows:

Length of cilia is L_Cilia = 6 μm, the spacing between any two neighboring cilia along the epithelium wall is chosen as d = 3 μm [5], the standard depth of PCL as L_PCL = 6 μm and the depth of the mucus layer as L_M = 4 μm [2], the density of the fluid is ρ = 1000 kg/m³ [2]. The stiffness constant of the virtual membrane is T₀ =32×10^-3 N/m [5], the cilia beat frequency is set f_s = 60 rad/s [5], the viscosity of PCL is η_PCL = 0.001 Pa.s [2] and the viscosity of mucus layer is η_M =0.0482 Pa.s [2]. As mentioned before, η_M is decomposed into viscous and elastic parts. Since a full viscoelastic characterization for mucus is not yet available, we assume that the standard viscosity of Newtonian part of mucus is the same as viscosity of PCL i.e. η_M,N =0.001 Pa.s and the elastic part of mucus viscosity is η_M,E = 0.0472 Pa.s. For the reference parameters, the viscosity ratio is β = η_M,E / η_M = 0.98. The standard value of relaxation time of mucus is about λ = 0.034 s [2].

The cilium beat pattern in our study is the cilium beat cycle reported in Folfurd and Blake [3] which is shown in Figure 3. In our numerical model, there are 13 cilia and each cilium has a cyclic motion. The cilia arrangements for t = 0, T_C / 13 and 8 T_C / 13 are plotted in Figure 4, here T_C is the consecutive beat cycle.

Figure3.

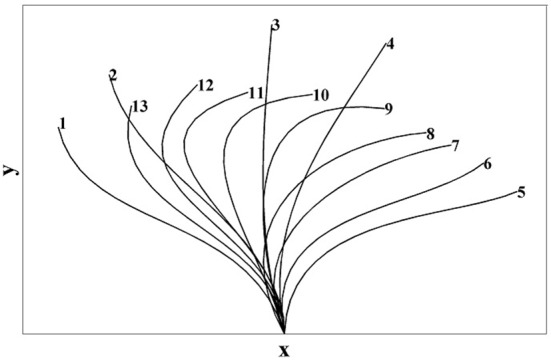
Beat Cycle Derived by Fulford and Blake [3]

Figure4.

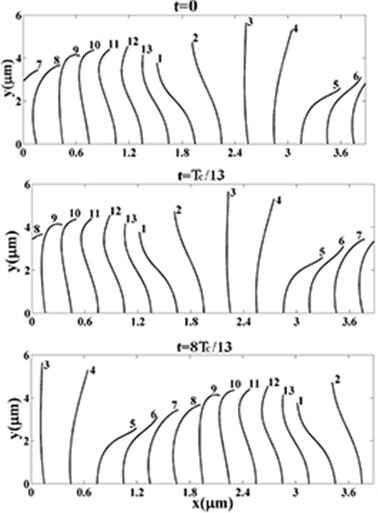
Arrangement of Cilia at Three Different Times in the Present Study

The computational mesh is chosen as 112×29 (∆x = ∆y = 3.5 × 10^-7), the number of control points along each cilium is 20 and along the interface membrane is 105. The time step is also ∆t = 8.5 × 10^-7. The time average mucus velocity at the outlet boundary of the domain can be calculated as:

$u_0=\frac{1}{T_C(L_t-L_{\mathrm{PCL}})}{\int }_0^{T_C}{\int }_{L_{\mathrm{PCL}}}^{L_t}{u}_M\mathrm{dydt}$ (27)

In equation (27), Lt is the total depth of ASL and T_C is the consecutive beat cycle.

The experimental investigation of Matsui et al. [22] showed a mean mucus transport of 39.2 µm/s. ICRP [27] reported a wide range of values depending upon disease, ambient conditions and other factors. For healthy subjects, values of 70 and 92 µm/s for tracheal transport and 40 µm/s for bronchial transport were reported. Smith et al. [2] showed a mean mucus velocity of 38.3 µm/s. Also numerical simulation of Lee et al. [5] predicts a mean mucus velocity of 44.38 µm/s using the standard parameter set. Our simulation using the standard parameter set predicts a time average mucus velocity of u₀ =44.07 µm/s which is in a reasonable agreement with the previous reported results. The velocity field and the beating cilia at t = 0 and 4T_C / 13 for the standard parameter set have been plotted in Figure 5. This figure shows a high forward velocity around the cilium at its effective stroke and the largest mucus velocity occurs close to the mucus-PCL interface.

Figure5.

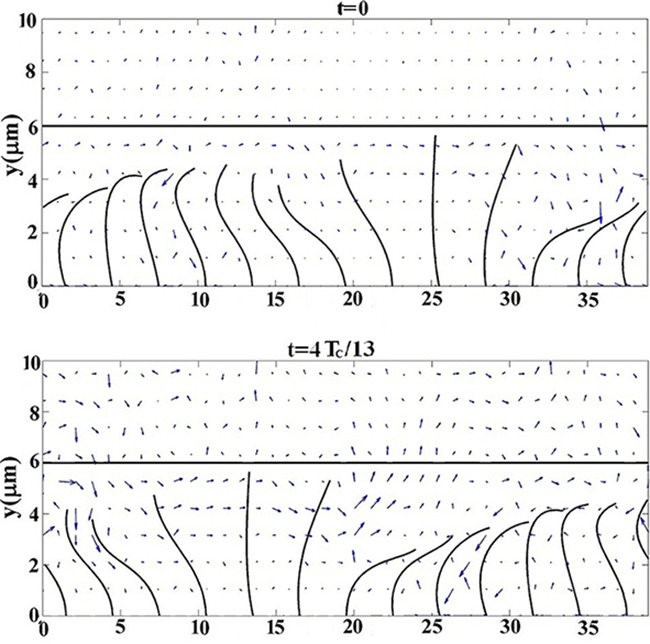
Velocity Field and Beating Cilia at t =0 and 4T_C / 13 for the Standard Parameter Set

Discussion

Table 1 demonstrates the variation of mean mucus velocity as a function of CBF. In this table, the numerical setting is equal to the standard setting, but with the cilia beat frequency set at 20, 40, 60, 80, 100, 120 and 140 rad/s. In this table, minus sign indicates a decrease in mucus velocity. This table indicates that CBF has great influence on mucus flow and increase in CBF as indicated in the literature leading to increase in mean mucus velocity. This table shows that when CBF increases to 140 rad/s, mean mucus velocity almost becomes twice.

Table 1.

Mean Mucus Velocity for Various amounts of Cilia Beat Frequency

fs (rad/s)	20	40	60	80	100	120	140
uM (µm/s)	21.59	33	44.07	55.52	66.69	77.99	90.22
% changes	-51.01	-25.12	0	25.98	51.32	76.97	104.71

Table 2 shows the effects of Newtonian and elastic contribution of the mucus viscosity on the mean mucus velocity for η_M = 0.0482 Pa.s. In this table, all parameters with the exception of Newtonian and elastic part of mucus viscosity are equal to the standard setting. Values of this table illustrate that increasing Newtonian part mucus viscosity has a greater effect than CBF on the mucus flow. When mucus viscosity is completely Newtonian (i.e. η_M = η_M,N = 0.0482 Pa.s and η_M,N = 0) mean mucus velocity becomes almost ten times the standard value (u₀ = 44.07 µm/s). This means that by increasing Newtonian part of mucus viscosity or decreasing elastic part of it, mucus flow increases significantly. This is possibly due to reducing in molecular weight of mucus by decreasing the elastic part of it.

Table 2.

Mean Mucus Velocity for Various amounts of Newtonian and Elastic Contributions of Mucus Viscosity for ηM = 0.0482 Pa.s

ηM,N (Pa.s)	0.001	0.005	0.01	0.015	0.02	0.025	0.03	0. 035	0. 04	0. 045	0. 0482
ηM,E (Pa.s)	0.047	0.043	0.038	0.033	0.028	0.023	0.018	0.013	0.008	0.003	0
uM (µm/s)	44.07	86.72	132.4	176.7	219.8	261.8	302.7	342.6	381.5	419.5	443.3
% change	0	96.8	200.4	300.9	398.7	494	586.9	677.4	765.7	851.9	905.9

To indicate the effect of CBF on the muco-ciliary transport process in detail, Table 3 shows the variation of mean mucus velocity as a function of CBF at various amounts of mucus properties. In this table, β is non-dimensional parameter called viscosity ratio, which is the ratio of elastic contribution of mucus viscosity to the total mucus viscosity (equation 5). As this table indicates, by increasing CBF or decreasing viscosity ratio mean mucus velocity intensifies. For better understanding, variation of non-dimensional mean mucus velocity as a function of CBF and viscosity ratio (β) has been plotted in Figure 6. As this figure indicates mean mucus velocity is affected by both viscosity ratio and CBF. This figure also shows that the variation of mean mucus velocity with respect to CBF in all values of β is similar and almost linear. This could be due to the linearity of fluid momentum equations at very low Reynolds numbers in which the fluid inertia can be neglected. This figure also illustrates that the maximum value of mean mucus velocity is related to β = 0 and f_s =140 rad/s in which mean mucus velocity is about 11.5 times the standard value of it.

Table 3.

Mean Mucus Velocity for Various amounts of CBF and Mucus Viscosity Ratio

fs (rad/s)	20	40	60	80	100	120	140
β
0	415.8	428.9	443.3	457.6	469.8	484	499.6
0.1	378.2	393.8	407.4	421.6	434.1	448.4	464
0. 3	303.3	318.5	332.6	346.7	359.7	374.2	389.9
0.5	225	239.2	254.3	268.6	281.9	296.1	312.2
0.7	143.2	158.2	172	186.3	199.9	214.4	229.8

Figure6.

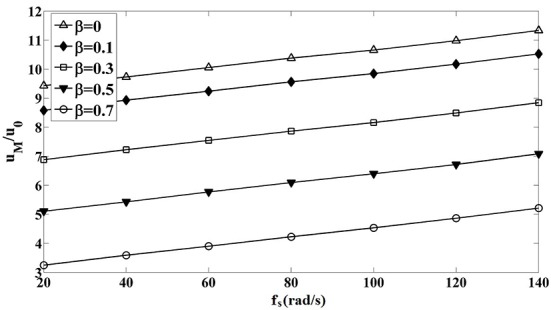
Variation of Non-dimensional Mean Mucus Velocity with respect to CBF for Different Values of Viscosity Ratio

Conclusion

In this study, we developed a 2D numerical simulation to study the effects of CBF at various amounts of mucus viscosity ratio on the mucu-ciliary clearance. Immersed boundary-lattice Boltzmann method has been employed to solve momentum equations. The main feature of the present investigation is considering mucus layer as a viscoelastic fluid and an Oldroyd-B model is used as the constitutive equation of it. Finite difference method is used to solve the constitutive equation of mucus. For simulating cilia forces and also updating accurate location of interface layer, an immersed boundary method is used. Results indicate that:

• 1- CBF and viscosity ratios of mucus are two parameters which play an important role in the muco-ciliary transport process. The effect of viscosity ratio is more significant.

• 2- For the standard parameter set decreasing in viscosity ratio has great effect on mucus flow. Reducing the viscosity ratio to zero leads to increase mean mucus velocity almost ten times the standard velocity.

• 3- For the standard configuration, increasing in CBF has a moderate effect on the mucus flow. By increasing CBF to 140 rad/s, mean mucus velocity becomes twice.

• 4- Variation of mean mucus velocity against CBF is almost linear and it has similar behavior for various amounts of viscosity ratio (β).