Dataset on the structure and thermodynamic and dynamic stability of Mo2ScAlC2 from experiments and first-principles calculations

Martin Dahlqvist; Rahele Meshkian; Johanna Rosen

doi:10.1016/j.dib.2016.12.046

. 2016 Dec 29;10:576–582. doi: 10.1016/j.dib.2016.12.046

Dataset on the structure and thermodynamic and dynamic stability of Mo₂ScAlC₂ from experiments and first-principles calculations

Martin Dahlqvist ^1,^⁎, Rahele Meshkian ¹, Johanna Rosen ¹

PMCID: PMC5219593 PMID: 28070549

Abstract

The data presented in this paper are related to the research article entitled “Theoretical stability and materials synthesis of a chemically ordered MAX phase, Mo₂ScAlC₂, and its two-dimensional derivate Mo₂ScC” (Meshkian et al. 2017) [1]. This paper describes theoretical phase stability calculations of the MAX phase alloy Mo_xSc_3-xAlC₂ (x=0, 1, 2, 3), including chemical disorder and out-of-plane order of Mo and Sc along with related phonon dispersion and Bader charges, and Rietveld refinement of Mo₂ScAlC₂. The data is made publicly available to enable critical or extended analyzes.

Specifications Table

Subject area	Physics, Materials science
More specific subject area	Phase stability predictions,
Type of data	Tables, Figures, Text file
How data was acquired	Density functional theory calculations using VASP 5.3.3, phonon dispersion using Phonopy 1.9.1, and atom charges using Bader charge analysis version 0.95a.
How data was acquired	θ-2θ X-ray diffraction (XRD) measurements were performed on the samples using a diffractometer (Rikagu Smartlab, Tokyo, Japan), with Cu-K_α radiation (40 kV and 44 mA). The scans were recorded between 3° and 120° with step size of 0.02° and a dwell time of 7 s.
Data format	Raw, Analyzed
Experimental factors	N/A
Experimental features	For synthesis of Mo₂ScAlC₂, elemental powders of Mo, Sc, Al and graphite were mixed in an agate mortar, put in an alumina crucible, and placed into a sintering furnace where it was heated up to 1700 °C and kept at that temperature for 30 min. Structural characterization was performed using X-ray diffraction (XRD), and for complementary structural and compositional analysis high-resolution scanning transmission electron microscopy (HRSTEM) measurement were carried out. See Ref. [1] for further information.
Data source location	Linköping, Sweden
Data accessibility	Data are available with this article.

Open in a new tab

Value of the data

•
This data allows other researchers to calculate and predict the phase stability of new compounds within the quaternary Mo-Sc-Al-C system and related subsystem.
•
The data presents refined/calculated structures that can be used as input for further theoretical evaluation of properties.
•
The structural information can also be used for interpretation and phase identification of, e.g., attained experimental XRD, (S)TEM, and electron diffraction data.

1. Data

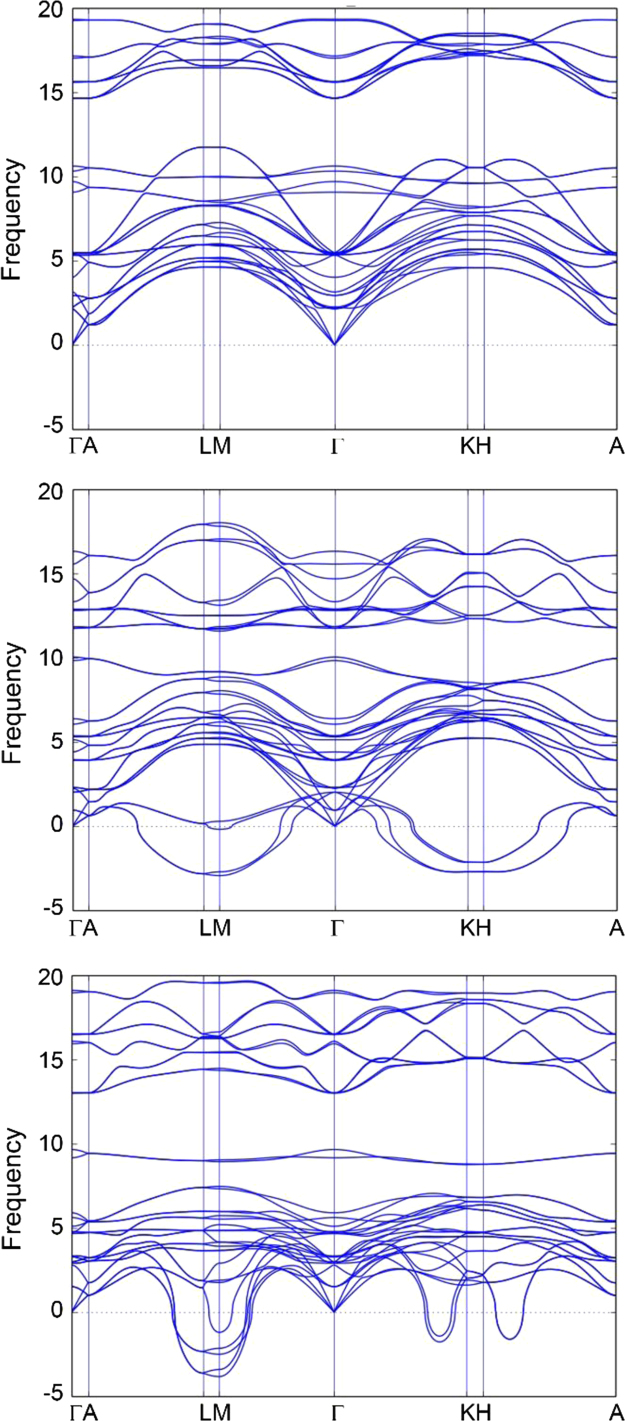
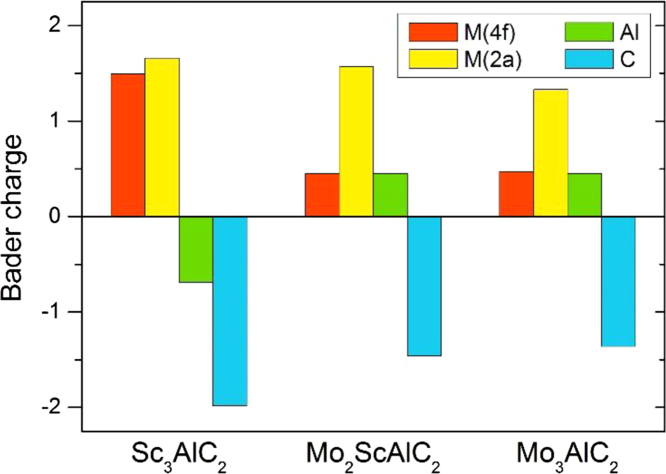
The dataset of this paper provides information for calculated phases within the quaternary Mo-Sc-Al-C system and data obtained from refinement of the XRD pattern. Table 1 provides calculated lattice parameters, formation enthalpy, and equilibrium simplex for the chemically ordered nanolaminates Mo₂ScAlC₂ and Sc₂MoAlC₂ with different atomic stacking sequences (described in detail in Fig. 7(a) in Ref. [2]). Table 2 provides information for all considered competing phases within the quaternary system. Fig. 1 show calculated phonon spectra for Mo₂ScAlC₂ of order A and its corresponding end members Sc₃AlC₂ and Mo₃AlC₂. Fig. 2 depicts calculated Bader charges of atoms in Mo_xSc_3-xAlC₂ (x=0, 2, 3). Table 3 shows the data obtained from refinement of the XRD pattern, see Ref. [1]; Lattice vectors a, b and c for the majority phase Mo₂ScAlC₂ are 3.033, 3.033 and 18.775 Å, respectively.

Table 1.

Calculated lattice parameters, equilibrium total energy E₀ in eV per formula unit, formation enthalpy ΔH_cp in meV per atom, and identified equilibrium simplex for Mo₂ScAlC₂ and Sc₂MoAlC₂. For comparison the corresponding end members Mo₃AlC₂ and Sc₃AlC₂ are also included.

Phase	Order	a (Å)	c (Å)	E₀ (eV/fu)	ΔH_cp (meV/atom)	Equilibrium simplex
Mo₃AlC₂		3.0716	18.541	−54.830	+141	C, Mo₃Al
Mo₂ScAlC₂	A	3.0619	19.072	−52.431	—24	(Mo_2/3Sc_1/3)₂AlC, MoC, ScC_0.875, Mo
Mo₂ScAlC₂	B	3.0774	19.252	−51.972	+53	(Mo_2/3Sc_1/3)₂AlC, MoC, ScC_0.875, Mo
Mo₂ScAlC₂	C	3.1622	18.789	−51.601	+114	(Mo_2/3Sc_1/3)₂AlC, MoC, ScC_0.875, Mo
Mo₂ScAlC₂	D	3.1771	18.865	−51.505	+130	(Mo_2/3Sc_1/3)₂AlC, MoC, ScC_0.875, Mo
Mo₂ScAlC₂	E	3.1271	19.054	−51.348	+157	(Mo_2/3Sc_1/3)₂AlC, MoC, ScC_0.875, Mo
Mo₂ScAlC₂	F	3.1221	19.109	−51.663	+104	(Mo_2/3Sc_1/3)₂AlC, MoC, ScC_0.875, Mo
Mo₂ScAlC₂	disorder	3.1252	18.861	−51.767	+87	(Mo_2/3Sc_1/3)₂AlC, MoC, ScC_0.875, Mo
Sc₂MoAlC₂	A	3.1798	19.819	−48.262	+28	(Mo_2/3Sc_1/3)₂AlC, Sc₃AlC, Sc₃C₄
Sc₂MoAlC₂	B	3.1808	19.845	−48.071	+60	(Mo_2/3Sc_1/3)₂AlC, Sc₃AlC, Sc₃C₄
Sc₂MoAlC₂	C	3.1886	19.696	−47.842	+98	(Mo_2/3Sc_1/3)₂AlC, Sc₃AlC, Sc₃C₄
Sc₂MoAlC₂	D	3.1892	19.770	−47.864	+94	(Mo_2/3Sc_1/3)₂AlC, Sc₃AlC, Sc₃C₄
Sc₂MoAlC₂	E	3.2279	19.802	−47.453	+162	(Mo_2/3Sc_1/3)₂AlC, Sc₃AlC, Sc₃C₄
Sc₂MoAlC₂	F	3.1898	19.700	−47.779	+108	(Mo_2/3Sc_1/3)₂AlC, Sc₃AlC, Sc₃C₄
Sc₂MoAlC₂	disorder	3.2251	19.335	−48.088	+57	(Mo_2/3Sc_1/3)₂AlC, Sc₃AlC, Sc₃C₄
Sc₃AlC₂		3.3170	20.885	−43.406	+155	Sc₃AlC, Sc₃C₄, ScAl₃C₃

Open in a new tab

Table 2.

Structural information and calculated total energy for competing phases considered within the quaternary Mo-Sc-Al-C system.

Phase	Prototype structure	Pearson symbol	Space group	V (Å³/uc)	a	b	c	E₀ (eV/fu)
Phase	Prototype structure	Pearson symbol	Space group	V (Å³/uc)	(Å)	(Å)	(Å)	E₀ (eV/fu)
Mo	W	cI2	Im-3m (229)	15.92	3.169			−10.850
Mo	Cu	cF4	Fm-3m (225)	16.15	4.012			−10.431
Mo	Mg	hP2	P6₃/mmc (194)	32.57	2.774		4.887	−10.414
Sc	Mg	hP2	P6₃/mmc (194)	49.25	3.321		5.157	−6.333
Sc	Sc	hP6	P6₁22 (178)	148.75	3.242		16.342	−6.201
Sc	Np	tP4	P4/nmm (129)	100.35	5.367		3.484	−6.223
Al	Cu	cF4	Fm-3m (225)	66.00	4.041			−3.745
Al	Mg	hP2	P6₃/mmc (194)	33.28	2.856		4.712	−3.712
Al	W	cI2	Im-3m (229)	16.93	3.235			−3.649
C	C (graphite)	hP4	P6₃/mmc (194)	38.14	2.464		7.250	−9.225
Al₄C₃	Al₄C₃	hR21	R-3m h (166)	245.00	3.355		25.129	−43.340
MoAl₁₂	WAl₁₂	cI26	Im-3 (204)	436.23	7.584			−57.303
MoAl₅	MoAl₅	hR36	R-3c h (167)	558.49	4.952		26.296	−31.001
Mo₄Al₁₇	Mo₄Al₁₇	mS84	C121 (5)	1305.85	9.187	4.939	28.974	−112.563
Mo₃Al₈	Mo₃Al₈	mS22	C12/m1 (12)	334.46	9.235	3.653	10.091	−66.170
Mo₃Al	Cr₃Si	cP8	Pm-3n (223)	123.48	4.980			−37.228
Sc₂Al	Ni₂In	hP6	P6₃/mmc (194)	128.50	4.902		6.176	−17.458
ScAl	CsCl	cP2	Pm-3m (221)	38.75	3.384			−10.973
ScAl	CrB	oC8	Cmcm (63)	81.00	3.338	11.101	4.371	−10.892
ScAl₂	MgCu₂	cF24	Fd-3m (227)	109.50	3.797			−15.277
ScAl₃	AuCu₃	cP4	Pm-3m (221)	69.25	4.107			−19.383
MoC	TiP	hP8	P6₃/mmc (194)	84.84	3.016		10.768	−19.821
MoC	NaCl	cF8	Fm-3m (225)	21.06	4.383			−19.640
MoC	η-MoC	hp12	P6₃/mmc (194)	126.16	3.074		15.401	−19.747
MoC	WC	hp2	P-6m2 (187)	21.00	2.928		2.829	−20.241
Mo₃C₂	Cr₃C₂	oP20	Pnma (62)	228.19	6.064	2.974	12.654	−50.938
Mo₂C	β׳׳-Mo₂C	hP3	P-3m1 (164)	38.06	3.068		4.669	−31.064
Mo₃C	Fe₃C	oP16	Pnma (62)	215.87	5.540	7.559	5.159	−40.423
Sc₂C	Ti₂C	cF48	Fd-3m (227)	852.33	9.481			−23.266
Sc₄C₃	P₄Th₃	cI28	I-43d (220)	188.75	7.227			−56.419
ScC_0.875	NaCl	cF8	Fm-3m (225)	208.70	4.708			−14.923
ScC	NaCl	cF8	Fm-3m (225)	25.70	4.685			−15.840
Sc₃C₄	Sc₃C₄	tP70	P4/mnc (128)	851.50	7.515		15.076	−58.764
Mo₃AlC	CaTiO₃	cP5	Pm-3m (221)	71.70	4.154			−45.341
Mo₃Al₂C	Mo₃Al₂C	cP24	P4₁32 (213)	327.20	6.891			−50.299
Mo₃Al₂C_0.9375	Mo₃Al₂C	cP24	P4₁32 (213)	1303.30	6.881			−49.691
Mo₃Al₂C_0.875	Mo₃Al₂C	cP24	P4₁32 (213)	648.29	6.869			−49.078
Mo₃Al₂C_0.875	Mo₃Al₂C	cP24	P4₁32 (213)	1296.87	6.870			−49.069
Mo₃Al₂C_0.75	Mo₃Al₂C	cP24	P4₁32 (213)	321.10	6.848			−47.844
Mo₂AlC	Cr₂AlC	hP8	P6₃/mmc (194)	107.46	3.031		13.505	−35.292
Mo₃AlC₂	Ti₃SiC₂	hP12	P6₃/mmc (194)	151.49	3.072		18.541	−54.830
Mo₄AlC₃	Ti₄AlN₃	hP16	P6₃/mmc (194)	196.50	3.117		23.358	−74.552
(Mo_2/3Sc_1/3)₂AlC	(Mo_2/3Sc_1/3)₂AlC	mS48	C2/c (15)	689.78	9.367	5.427	13.961	−33.308
ScAl₃C₃	ScAl₃C₃	hP14	P6₃/mmc (194)	164.34	3.362		16.789	−47.703
Sc₃AlC	CaTiO₃	cP5	Pm-3m (221)	84.90	4.395			−35.023
Sc₂AlC	Cr₂AlC	hP8	P6₃/mmc (194)	141.75	3.296		15.065	−27.385
Sc₃AlC₂	Ti₃SiC₂	hP12	P6₃/mmc (194)	199.00	3.317		20.885	−43.406
Sc₄AlC₃	Ti₄AlN₃	hP16	P6₃/mmc (194)	248.50	3.296		26.414	−59.294

Open in a new tab

Fig. 1 — Calculated phonon dispersion for (a) Mo₂ScAlC₂, (b) Sc₃AlC₂, and (c) Mo₃AlC₂.

Fig. 2 — Calculated charge for atoms in Sc₃AlC₂, Mo₂ScAlC₂, and Mo₃AlC₂ using Bader analysis.

Table 3.

Rietveld refinement of Mo₂ScAlC₂. The identified phases and their respective weight percentages according to the Rietveld refinement of the XRD pattern are: 1. Mo₂ScAlC₂ (73.9(0) wt.%), Mo₂C (14.1(8) wt.%), A1₂O₃ (7.4(0) wt.%), Mo₃Al₂C (3.5(0) wt.%) and, Mo₃Al (1.0(2) wt.%), the total χ² is 10.50.

Space group	P6₃/mmc (#194)
a (Å)	3.0334(8)
b (Å)	3.0334(8)
c (Å)	18.7750(0)
α	90.000
β	90.000
γ	120.000
Mo	4f (0.3333(3) 0.6666(7) 0.1363(2))
Mo	Occupancy of Mo=4.00(0) and Sc=0.00(0)
Sc	2a (0.0000 0.0000 0.0000)
Sc	Occupancy of Sc=1.83(4) and Mo=0.16(6)
Al	2b (0.0000 0.0000 0.2500) Occupancy of Al=2.00
C	4f (0.6666(7) 0.3333(3) 0.06825(5)) Occupancy of C=4.00

Open in a new tab

2. Experimental design, materials and methods

First-principles calculations were performed by means of density functional theory (DFT) and the projector augmented wave method [3], [4] as implemented within the Vienna ab-initio simulation package (VASP) 5.3.3 [5], [6], [7]. We adopted the non-spin polarized generalized gradient approximation (GGA) as parameterized by Perdew–Burke–Ernzerhof (PBE) [8] for treating electron exchange and correlation effects. A plane-wave energy cut-off of 400 eV was used and for sampling of the Brillouin zone we used the Monkhorst–Pack scheme [9]. The calculated total energy of all phases is converged to within 0.5 meV/atom with respect to k-point sampling and structurally optimized in terms of unit-cell volumes, c/a ratios (when necessary), and internal parameters to minimize the total energy.

Chemically disordered of Sc and Mo in Mo_xSc_3-xAlC₂ have been modelled using the special quasi-random structure (SQS) method [10], [11] on supercells of $4 \times 4 \times 1$ M₃AX₂ unit cells, with a total of 96 M-sites, respectively. Convergence tests with respect to total energy show that these sizes are appropriate to use, based on an energy of the $4 \times 4 \times 1$ unit cells being within 2 meV/atom compared to larger supercells.

Evaluation of phase stability was performed by identifying the set of most competing phases at a given composition, i.e. equilibrium simplex, using a linear optimization procedure [11], [12] including all competing phases in the system. A phase is considered thermodynamically stable when its energy is lower than the set of most competing phases, and when there is no imaginary frequencies in phonon spectra, i.e. an indicated dynamic stability. The approach has been proven successful to confirm already experimentally known MAX phases as well as to predict the existence of new ones [2], [13], [14].

Dynamical stability of the chemically ordered Mo_xSc_3-xAlC₂ (x=0, 2, 3) structures was evaluated by phonon calculations of $4 \times 4 \times 1$ supercells using density functional perturbation theory and as implemented in the PHONOPY code, version 1.9.1 [15], [16]. Calculated charges were obtained using Bader charge analysis, version 0.95a [17].

The synthesis of Mo2ScAlC2 were carried out by mixing elemental powders of Mo, Sc, Al and graphite in an agate mortar, put in an alumina crucible, and placed into a sintering furnace where it was heated up to 1700 °C and kept at that temperature for 30 min.

θ-2θ X-ray diffraction (XRD) measurements were performed on the samples using a diffractometer (Rikagu Smartlab, Tokyo, Japan), with Cu-K_α radiation (40 kV and 44 mA). The scans were recorded between 3° and 120° with step size of 0.02^° and a dwell time of 7 s. XRD pattern was analyzed by Rietveld refinement using FULLPROF code [18], where 5 backgrounds parameters, scale factors, X and Y profile parameters, lattice parameters, atomic positions, the overall B-factor and the occupancies for the main as well as the impurity phases were fitted.

Funding sources

J. R. acknowledges funding from the Swedish Research Council (VR) under Grant no. 621-2012-4425 and 642-2013-8020, from the Knut and Alice Wallenberg (KAW) Foundation, and from the Swedish Foundation for Strategic Research (SSF) through the synergy grant FUNCASE. All calculations were carried out using supercomputer resources provided by the Swedish National Infrastructure for Computing (SNIC) at the National Supercomputer Centre (NSC), the High Performance Computing Center North (HPC2N), and the PDC Center for High Performance Computing.

Footnotes

^{Transparency document}

Transparency document associated with this paper can be found in the online version at doi:10.1016/j.dib.2016.12.046.

^{Appendix A}

Supplementary material associated with this paper can be found in the online version at doi:10.1016/j.dib.2016.12.046.

Transparency document. Supplementary material

Supplementary material

mmc1.pdf^{(275.8KB, pdf)}

Appendix A. Supplementary material

Supplementary material

mmc2.zip^{(718B, zip)}

References

1.Meshkian R., Tao Q., Dahlqvist M., Lu J., Hultman L., Rosen J. Theoretical stability and materials synthesis of a chemically ordered MAX phase, Mo2ScAlC2, and its two-dimensional derivate Mo2ScC2 MXene. Acta Mater. 2016 [Google Scholar]
2.Anasori B., Dahlqvist M., Halim J., Moon E.J., Lu J., Hosler B.C., Caspi E.N., May S.J., Hultman L., Eklund P., Rosén J., Barsoum M.W. Experimental and theoretical characterization of ordered MAX phases Mo2TiAlC2 and Mo2Ti2AlC3. J. Appl. Phys. 2015;118:094304. [Google Scholar]
3.Blöchl P.E. Projector augmented-wave method. Phys. Rev. B. 1994;50:17953–17979. doi: 10.1103/physrevb.50.17953. [DOI] [PubMed] [Google Scholar]
4.Kresse G., Joubert D. From ultrasoft pseudopotentials to the projector augmented-wave method. Phys. Rev. B. 1999;59:1758–1775. [Google Scholar]
5.Kresse G., Hafner J. Ab initio molecular dynamics for liquid metals. Phys. Rev. B. 1993;47:558–561. doi: 10.1103/physrevb.47.558. [DOI] [PubMed] [Google Scholar]
6.Kresse G., Furthmüller J. Efficiency of ab-initio total energy calculations for metals and semiconductors using a plane-wave basis set. Comput. Mater. Sci. 1996;6:15–50. doi: 10.1103/physrevb.54.11169. [DOI] [PubMed] [Google Scholar]
7.Kresse G., Furthmüller J. Efficient iterative schemes for ab initio total-energy calculations using a plane-wave basis set. Phys. Rev. B. 1996;54:11169–11186. doi: 10.1103/physrevb.54.11169. [DOI] [PubMed] [Google Scholar]
8.Perdew J.P., Burke K., Ernzerhof M. Generalized gradient approximation made simple. Phys. Rev. Lett. 1996;77:3865–3868. doi: 10.1103/PhysRevLett.77.3865. [DOI] [PubMed] [Google Scholar]
9.Monkhorst H.J., Pack J.D. Special points for Brillouin-zone integrations. Phys. Rev. B. 1976;13:5188–5192. [Google Scholar]
10.Zunger A., Wei S.H., Ferreira L.G., Bernard J.E. Special quasirandom structures. Phys. Rev. Lett. 1990;65:353–356. doi: 10.1103/PhysRevLett.65.353. [DOI] [PubMed] [Google Scholar]
11.Dahlqvist M., Alling B., Abrikosov I.A., Rosén J. Phase stability of Ti2AlC upon oxygen incorporation: a first-principles investigation. Phys. Rev. B. 2010;81:024111–024118. [Google Scholar]
12.Dahlqvist M., Alling B., Rosén J. Stability trends of MAX phases from first principles. Phys. Rev. B. 2010;81:220102. [Google Scholar]
13.Eklund P., Dahlqvist M., Tengstrand O., Hultman L., Lu J., Nedfors N., Jansson U., Rosén J. Discovery of the ternary nanolaminated compound Nb2GeC by a systematic theoretical-experimental approach. Phys. Rev. Lett. 2012;109:035502. doi: 10.1103/PhysRevLett.109.035502. [DOI] [PubMed] [Google Scholar]
14.Ingason A.S., Mockute A., Dahlqvist M., Magnus F., Olafsson S., Arnalds U.B., Alling B., Abrikosov I.A., Hjörvarsson B., Persson P.O.Å., Rosen J. Magnetic self-organized atomic laminate from first principles and thin film synthesis. Phys. Rev. Lett. 2013;110:195502. doi: 10.1103/PhysRevLett.110.195502. [DOI] [PubMed] [Google Scholar]
15.Togo A., Oba F., Tanaka I. First-principles calculations of the ferroelastic transition between rutile-type and CaCl2-type SiO2 at high pressures. Phys. Rev. B. 2008;78:134106. [Google Scholar]
16.Togo A., Tanaka I. First principles phonon calculations in materials science. Scr. Mater. 2015;108:1–5. [Google Scholar]
17.Henkelman G., Arnaldsson A., Jónsson H. A fast and robust algorithm for Bader decomposition of charge density. Comput. Mater. Sci. 2006;36:354–360. [Google Scholar]
18.Rietveld H.M. A profile refinement method for nuclear and magnetic structures. J. Appl. Crystallogr. 1969;2:65–71. [Google Scholar]

Associated Data

This section collects any data citations, data availability statements, or supplementary materials included in this article.

Supplementary Materials

Supplementary material

mmc1.pdf^{(275.8KB, pdf)}

Supplementary material

mmc2.zip^{(718B, zip)}

[bib1] 1.Meshkian R., Tao Q., Dahlqvist M., Lu J., Hultman L., Rosen J. Theoretical stability and materials synthesis of a chemically ordered MAX phase, Mo2ScAlC2, and its two-dimensional derivate Mo2ScC2 MXene. Acta Mater. 2016 [Google Scholar]

[bib2] 2.Anasori B., Dahlqvist M., Halim J., Moon E.J., Lu J., Hosler B.C., Caspi E.N., May S.J., Hultman L., Eklund P., Rosén J., Barsoum M.W. Experimental and theoretical characterization of ordered MAX phases Mo2TiAlC2 and Mo2Ti2AlC3. J. Appl. Phys. 2015;118:094304. [Google Scholar]

[bib3] 3.Blöchl P.E. Projector augmented-wave method. Phys. Rev. B. 1994;50:17953–17979. doi: 10.1103/physrevb.50.17953. [DOI] [PubMed] [Google Scholar]

[bib4] 4.Kresse G., Joubert D. From ultrasoft pseudopotentials to the projector augmented-wave method. Phys. Rev. B. 1999;59:1758–1775. [Google Scholar]

[bib5] 5.Kresse G., Hafner J. Ab initio molecular dynamics for liquid metals. Phys. Rev. B. 1993;47:558–561. doi: 10.1103/physrevb.47.558. [DOI] [PubMed] [Google Scholar]

[bib6] 6.Kresse G., Furthmüller J. Efficiency of ab-initio total energy calculations for metals and semiconductors using a plane-wave basis set. Comput. Mater. Sci. 1996;6:15–50. doi: 10.1103/physrevb.54.11169. [DOI] [PubMed] [Google Scholar]

[bib7] 7.Kresse G., Furthmüller J. Efficient iterative schemes for ab initio total-energy calculations using a plane-wave basis set. Phys. Rev. B. 1996;54:11169–11186. doi: 10.1103/physrevb.54.11169. [DOI] [PubMed] [Google Scholar]

[bib8] 8.Perdew J.P., Burke K., Ernzerhof M. Generalized gradient approximation made simple. Phys. Rev. Lett. 1996;77:3865–3868. doi: 10.1103/PhysRevLett.77.3865. [DOI] [PubMed] [Google Scholar]

[bib9] 9.Monkhorst H.J., Pack J.D. Special points for Brillouin-zone integrations. Phys. Rev. B. 1976;13:5188–5192. [Google Scholar]

[bib10] 10.Zunger A., Wei S.H., Ferreira L.G., Bernard J.E. Special quasirandom structures. Phys. Rev. Lett. 1990;65:353–356. doi: 10.1103/PhysRevLett.65.353. [DOI] [PubMed] [Google Scholar]

[bib11] 11.Dahlqvist M., Alling B., Abrikosov I.A., Rosén J. Phase stability of Ti2AlC upon oxygen incorporation: a first-principles investigation. Phys. Rev. B. 2010;81:024111–024118. [Google Scholar]

[bib12] 12.Dahlqvist M., Alling B., Rosén J. Stability trends of MAX phases from first principles. Phys. Rev. B. 2010;81:220102. [Google Scholar]

[bib13] 13.Eklund P., Dahlqvist M., Tengstrand O., Hultman L., Lu J., Nedfors N., Jansson U., Rosén J. Discovery of the ternary nanolaminated compound Nb2GeC by a systematic theoretical-experimental approach. Phys. Rev. Lett. 2012;109:035502. doi: 10.1103/PhysRevLett.109.035502. [DOI] [PubMed] [Google Scholar]

[bib14] 14.Ingason A.S., Mockute A., Dahlqvist M., Magnus F., Olafsson S., Arnalds U.B., Alling B., Abrikosov I.A., Hjörvarsson B., Persson P.O.Å., Rosen J. Magnetic self-organized atomic laminate from first principles and thin film synthesis. Phys. Rev. Lett. 2013;110:195502. doi: 10.1103/PhysRevLett.110.195502. [DOI] [PubMed] [Google Scholar]

[bib15] 15.Togo A., Oba F., Tanaka I. First-principles calculations of the ferroelastic transition between rutile-type and CaCl2-type SiO2 at high pressures. Phys. Rev. B. 2008;78:134106. [Google Scholar]

[bib16] 16.Togo A., Tanaka I. First principles phonon calculations in materials science. Scr. Mater. 2015;108:1–5. [Google Scholar]

[bib17] 17.Henkelman G., Arnaldsson A., Jónsson H. A fast and robust algorithm for Bader decomposition of charge density. Comput. Mater. Sci. 2006;36:354–360. [Google Scholar]

[bib18] 18.Rietveld H.M. A profile refinement method for nuclear and magnetic structures. J. Appl. Crystallogr. 1969;2:65–71. [Google Scholar]

PERMALINK

Dataset on the structure and thermodynamic and dynamic stability of Mo₂ScAlC₂ from experiments and first-principles calculations

Martin Dahlqvist

Rahele Meshkian

Johanna Rosen

Abstract

1. Data

Table 1.

Table 2.

Fig. 1.

Fig. 2.

Table 3.

2. Experimental design, materials and methods

Funding sources

Footnotes

Transparency document. Supplementary material

Appendix A. Supplementary material

References

Associated Data

Supplementary Materials

ACTIONS

PERMALINK

RESOURCES

Cite

Add to Collections

PERMALINK

Dataset on the structure and thermodynamic and dynamic stability of Mo2ScAlC2 from experiments and first-principles calculations

Martin Dahlqvist

Rahele Meshkian

Johanna Rosen

Abstract

1. Data

Table 1.

Table 2.

Fig. 1.

Fig. 2.

Table 3.

2. Experimental design, materials and methods

Funding sources

Footnotes

Transparency document. Supplementary material

Appendix A. Supplementary material

References

Associated Data

Supplementary Materials

ACTIONS

PERMALINK

RESOURCES

Similar articles

Cited by other articles

Links to NCBI Databases

Dataset on the structure and thermodynamic and dynamic stability of Mo₂ScAlC₂ from experiments and first-principles calculations