Molecular dynamics studies of ground state and intermediate of the hyperthermophilic indole-3-glycerol phosphate synthase

Abstract

Indole-3-glycerol phosphate synthase catalyzes the terminal ring closure step in tryptophan biosynthesis. In this paper, we compare the results from molecular dynamics (MD) simulations of enzyme-bound substrate at 298, 333, 363, and 385 K and the enzyme-bound intermediate at 385 K, solvated in TIP3P water box with a charmm force field. Results from MD simulations agree with experimental studies supporting the observation that Lys-110 is the general acid. Based on its location in the active site during the MD simulations, Glu-210 warrants classification as the general base instead of the previously proposed Glu-159. We find that the relative population of the reactive enzyme-substrate Michaelis conformers [near attack conformers (NACs)] with temperature correlates well (correlation coefficient of 0.96) with the relative activity of this thermophilic enzyme. At higher temperature, the enzyme-substrate electrostatic interaction favors the binding of the substrate in NAC conformation, whereas, at lower temperature, the substrate is distorted and bound in a nonreactive conformation. This change is reflected in the ≈1,100-fold increase in population of NACs at 385 K relative to 298 K. The easily determined population of NACs at given temperature tells much about the thermophilic property of the enzyme. Thus, the hyperthermophilic enzyme has evolved to have optimum activity at high temperatures, and, with lowering of the temperature, the electrostatic interaction at the active site is enhanced and the structure is deformed. This model can be regarded as a general explanation for the activity of hyperthermophilic enzymes.

The reduced flexibility of hyperthermophilic enzymes is responsible for their stability at high temperature (1, 2). Hyperthermophilic enzymes do not denature at high temperatures because of an abundance of electrostatic interactions, such as increased number of salt bridges. The question commonly asked is how thermophilic enzyme achieves the balance between the need for increased stability at high temperatures and the need for sufficient flexibility to function properly. We address the problem of how a thermophilic enzyme achieves greater rate enhancement at higher temperature and the role of the ground state conformers in doing so.

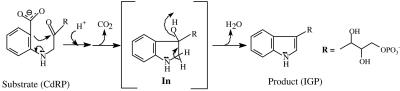
The enzyme chosen for this study is the monofunctional hyperthermophilic indole-3-glycerol phosphate (IGP) synthase (IGPS) from the archaeon Sulfolobus solfataricus and is a member of the family of enzymes having (βα)₈-fold barrel, commonly known as the TIM barrel (3). The natural habitat of S. solfataricus is sulfurous mud pools with temperatures ≈385 K. The IGPS is the terminal enzyme in the tryptophan biosynthesis pathway that catalyzes the ring closure of the substrate 1-(o-carboxyphenylamino) 1-deoxyribulose 5-phosphate (CdRP) to form the product IGP (Scheme 1) (4). Based on the available crystal structures and by modeling the intermediate in the enzyme active site (In), Kirschner and coworkers (5) provided useful insights into the catalytic mechanism of IGPS. The general acid and the general base for the reaction have been proposed to be Lys-110-NH₃⁺ and Glu-159-CO₂^-, respectively (6). However, in the x-ray crystal structures of IGPS bound to the substrate (CdRP) and substrate analogue, both ligands are bound in an extended, unproductive conformation, such that the two reactive carbon centers C1 and C2′ are separated by a distance that is too large to initiate bond formation. Also, the crystal structures were grown at room temperature, a condition in which the enzyme has very little activity (5).

Scheme 1.

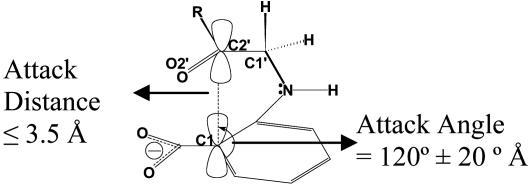
In covalent bond formation and regardless of the environment, nucleophilic and electrophilic atoms must come together at a van der Waals distance and at an angle approximating that in the transition state. We term such ground-state conformers near attack conformers (NACs) (7). The transition state can only be reached through a NAC. The NACs for the CdRP→IGP reaction are defined as those ground state conformers that have the two reacting moieties (C1 and C2′) within van der Waals contact distance (≤3.5 Å) at an approaching angle of 120 ± 20° (Fig. 1).†

Fig. 1.

Definition of NAC.

The aim of this study is to compare the ground state of substrate-bound IGPS at room temperature (298 K) and at higher temperatures (333, 363, and 385 K) and look for the possible structural differences that might contribute to the rate enhancement of reaction at higher temperature. To present a better understanding of the mechanism and the catalytic residues involved in the course of the reaction, we also explore the enzyme-bound In (see Scheme 1 for the structure of In) by means of a computational study. These five systems will be referred to as E·S298 (enzyme-substrate complex at 298 K), E·S333 (enzyme-substrate complex at 333 K), E·S363 (enzyme-substrate complex at 393 K), E·S385 (enzyme-substrate complex at S385), and E·In (enzyme-In substrate at 385 K).

Methods

The starting coordinates of the IGP-bound IGPS (enzyme-product) were taken from the x-ray structure published in the Protein Data Bank (PDB ID code 1A53, 2.00-Å resolution)(5). IGPS from the source S. solfataricus is a monomer and, therefore, was preferred for the current molecular dynamics (MD) studies.

MD simulations of E·S298, E·S333, E·S363, and E·S385 were carried out for 2,000 ps, and simulation of E·In was carried out for 1,500 ps by using the academic version of program charmm, Version c27b4 (10). The charmm 27 residue topology and parameter file were used for protein atoms and ligands. Periodic boundary condition was used to perform the MD simulations. The Verlet-Leapfrog algorithm was used to integrate the equations of motion by using a time step of 1.5 fs (11). The shake algorithm was used to constrain the bonds containing hydrogens to their equilibrium length (12). Images were generated by using the crystal module of charmm. Electrostatic interactions were treated with the partial mesh Ewald formalism (13, 14) as implemented (15) in the charmm program. Partial mesh Ewald calculations were performed by using a real space cutoff of 9 Å with Lennard-Jones interactions truncated at the same distance, at a convergence parameter (κ) of 0.36 Å^-1, and with a fifth-degree B-spline interpolation. The general acid Lys-110-NH₃⁺ was protonated in the MD simulations of E·S298, E·S333, E·S363 and E·S385. Lys-110-NH₂ was neutral in E·In to model the final step.‡ To neutralize the total charge of the system, three Na⁺ ions were added near the solvent-exposed carboxylate side chains of Asp and Glu.

Periodic boundary conditions were defined by using an orthorhombic box of dimensions 59.79 × 62.94 × 60.07 Å filled with TIP3P model water molecules (16). The water molecules in the box were minimized for 100 steps of steepest descent method. Two water boxes were generated for our purpose, namely box 1 and box 2. Box 1 was equilibrated for a period of 30 ps by using constant pressure-temperature dynamics at 300 K. This water box was used to solvate the E·S298 system. Box 1 was further heated and equilibrated for a period of 15 ps at 385 K by using constant pressure-temperature dynamics to generate box 2. Then, the water boxes (box 1 on E·S298, box 2 on E·S385 and E·In) were overlaid onto the enzyme-substrate complexes or enzyme-In with Na⁺ ions and crystal waters. Solvent water molecules with oxygen atoms within 2.8 Å of any non-hydrogen atoms were deleted. The total numbers of atoms were 21,930, 22,335, and, 22,326 for E·S298, E·S385, and E·In complexes, respectively.

During the equilibration of E·S298, the structure was relaxed in stages so that the most strained parts of the system could adjust without introducing artifacts. Initially, a harmonic constraint of force of 100 kcal·mol^-1·Å^-1 (1 cal = 4.184 J) was applied to atoms other than waters, and a 15-ps simulation was performed at 298 K. Then the constraints on ions were released and the system was heated gradually from 50 K to 298 K at 15-ps increments of 50 K. Next, all of the constraints were removed and the system was reequilibrated by heating the entire model at intervals of 50 K for 15 ps each from 0 K to 298 K. These stages were carried out in a constant pressure-temperature ensemble [with a temperature of 298 K and a pressure of 1 atm (1 atm = 101.3 kPa)] so that the water box could equilibrate in accordance with the number of water molecules. For subsequent simulations, the constant volume-temperature ensemble was used because it provides more stable trajectories (17). A 30-ps simulation was run at 298 K to equilibrate the system further at this temperature. The heating and equilibration phases of dynamics lasted 180 ps for the E·S298 system. The production simulation was then continued at an average temperature of 298 K.

The constrained MD simulations were performed for E·385 and E·In for the initial 15 ps at 385 K by applying a harmonic force constant of 100 kcal·mol^-1·Å^-1 to atoms other than waters. Then the constraints on ions were released and the system was heated gradually from 50 K to 385 K at 15-ps increments of 50 K. Finally, all of the constraints were removed, and the system was reequilibrated by heating the entire model from 50 K to 385 K in 15-ps intervals of 50 K. After the initial heating and equilibration phase, the systems were switched from a constant pressure-temperature ensemble to a constant volume-temperature ensemble. A 30-ps simulation was run at 385 K to equilibrate the system further at this temperature. The heating and equilibration phases of dynamics lasted 210 ps for the E·S385 system. The production simulation was then continued at an average temperature of 385 K. The E·S333 and E·S363 systems were generated by using the solvated E·S298 and E·S385 systems, respectively, as the starting structures (coordinates obtained before the systems were heated and equilibrated). The final dynamics for the E·S333 and E·S363 systems were performed at 333 K and 363 K, respectively, by using the protocol described above.

Models II and III were used to calculate the charge distribution of the indole and phosphate function (Fig. 7). The electrostatic potentials were obtained from the MP2/6-311+G(2d,p) optimized geometry of 1 and 2 by using the Merz-Kollman scheme implemented in gaussian98 (8, 18). resp fitting of the point charges to these electrostatic potentials was done to obtain the charges for the model compound (18, 19). (Table 2, which is published as supporting information on the PNAS web site).

Results and Discussion

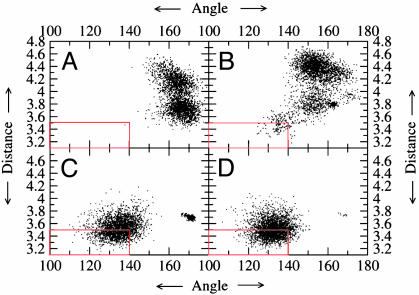
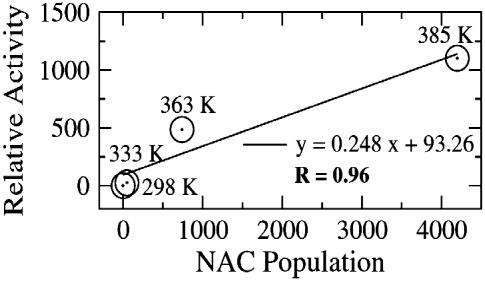
Results from the Enzyme-Substrate Dynamics at Various Temperatures. Contribution of NAC to the general acid catalyzed intramolecular ring formation. To compare the reactivity of enzyme-substrate complexes at different temperatures, we use the concept of the NACs, which are members of the Michaelis conformers ensemble. The NACs for the CdRP→IGP reaction are defined as ground state conformers that have the two reacting atoms (C1 and C2′) within van der Waals contact distance (≤3.5 Å) (9) at an attack angle of 120 ± 20° (Fig. 1). The structure of the NAC closely resembles the transition state calculated at the HF/6-31G. The major difference of kinetic interest is in the relative populations of the reactive Michaelis conformations in E·S333, E·S363, and E·S385 systems with respect to the E·S298 system. The relative populations of NACs at 298, 333, 363, and 385 K are 1, 25, 478, and 1,103, respectively (Fig. 2 and Table 1). The experimentally determined (20) increase in enzyme activity from 298 to 385 K is ≈4,200-fold (Fig. 3 and Table 1) (21). The increase in the mole percentage of NACs from 0.036% at 298 K to 40% at 385 K (≈1,100-fold increase) correlates well with the experimentally determined increase in enzyme activity. The relative population of NACs with temperature when plotted against the relative activity shows a linear relationship with a correlation coefficient of 0.96 (Fig. 3). Thus, increase in the time that the Michaelis complex exists as a NAC is linearly correlated to the change in enzymatic activity with increase in temperature.

Fig. 2.

Plot showing attack angle versus attack distance at 298 K (A), 333 K (B), 363 K (C), and 385 K (D). The red box encloses the NAC population. The populations of NACs at 298, 333, 363, and 385 K were 1, 25, 478, and 1,103, respectively.

Table 1. Relative specific activity.

Temperature, K	Relative activity	Population of NACs
298	1*	1
333	48	25
363	740	478
385	4,200*	1,103

^*Extrapolated from the experimental values by using Arrhenius equation logk = −4,797.7 (1/T) + 14.79.

Fig. 3.

Plot showing linear relationship between the relative specific activity and the NAC population. The correlation coefficient of 0.96 shows significant correlation between the two.

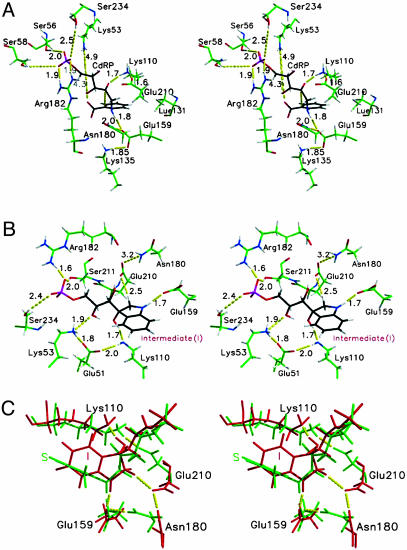
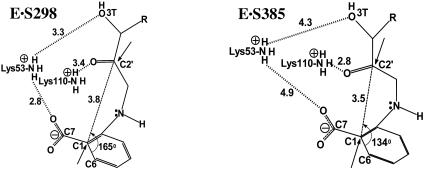
Taking a closer look at the active site, the higher population of NACs at elevated temperature can be attributed to the interplay between substrate and the residues Lys-53-NH₃⁺ and Lys-110-NH₃⁺, the latter playing the role of general acid. Both of these residues control the substrate conformation. The ε-amino group of Lys-110-NH₃⁺ is bridged to the ε-amino group of Lys-53-NH₃⁺ by the salt bridge interactions with carboxylate of the residue Glu-51-CO₂^- (Figs. 4A and 5C and D). The extent of electrostatic interactions between the positively charged Lys-53-NH₃⁺, Lys-110-NH₃⁺, and the substrate CdRP [carboxylate (O71 and O72) and the O3T hydroxyl of CdRP] are crucial in determining the geometry of reactants (Fig. 5). At 298 K, the Lys-53-NH₃⁺ interacts strongly with both carboxylate and O3T (Fig. 5B) of the CdRP, fixing them in the same plane. This conformation disfavors the bringing of the bond-forming centers C1 and C2′ into a correct orientation for the reaction. In other words, the angle at which C2′ approaches C1 is inappropriate at 298 K (Fig. 2 A). At 298 K, the average angle of approach (∠C2′-C1-C6) is 165 ± 20°. At 385 K, the average angle of approach is 135 ± 10° (Fig. 2D), which resembles the transition state calculated by HF/6-31G. It is worth pointing out that even though the reacting centers C1 and C2′ touch each other at van der Waals distance, the reaction is only favorable when they approach at the correct orientation, which again shows the importance of the angle dependence for NAC formation (22).

Fig. 4.

Stereoplot of the average structure from a MD simulation of E·S385 (A), E·In (B), and E·S385 (red) superimposed on E·In (green) (C). The carbon atoms of the substrate (CdRP) and In are shown in black for clarity. Note the hydrogen bond between Lys-110 and Glu-210 in A and the orientation of Glu-210 in B.

Fig. 5.

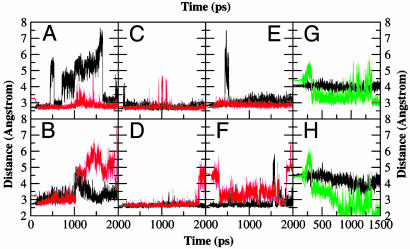
Plot showing important distances from MD simulations of E·S298, E·S385, and E·I. (A-F) Distance trajectories from the MD simulations of E·S298 (black) and E·S385 (red). The distances shown are between Lys-110-NH₃⁺ and CdRP-O2′ (A), Lys-53-NH₃⁺ and CdRP-O3T (B), Lys-110-NH₃⁺ and Glu-51-CO₂^- (C), Glu-51-CO₂^- and Lys-53-NH₃⁺ (D), Glu-159-CO₂^- and CdRP NH (E), and Arg-182 and CdRP-O1P (F). (G and H) The distance of the plausible general base candidates Glu-159-CO₂^- and Glu-210-CO₂^- from C1′ (black) and H1′ (green) of the In.

When the system is heated, Lys-53-NH₃⁺ exhibits more flexibility because of the weakening of electrostatic forces. Examination of Fig. 6 shows that loosening of electrostatic bonding at 385 K results in a distancing of Lys-53-NH₃⁺ from both the carboxylate and O3T of CdRP (see also Fig. 5B). This loosening of electrostatic interaction results in the substrate adopting the NAC conformation. However, it should be pointed out at this point that Lys-53-NH₃⁺ is needed for guiding the substrate to bind in the correct orientation at the active site. If this interaction is too strong, it results in trapping of the substrate in nonproductive conformer as with E·S298. In the case of E·S385, because of greater thermal flexibility at higher temperature, interaction with Lys-53-NH₃⁺ is moderate, which allows enough room for the substrate to form the reactive conformer. At the same time, the general acid Lys-110-NH₃⁺ migrates closer to the O2′ of the substrate, maintaining an average distance of 2.8 ± 0.2 Å at 385 K. The hydrogen bond between the amino group of the general acid Lys-110-NH₃⁺ and O2′ of CdRP is more stable in E·S385 than E·S298 (Fig. 5A). Thus, the interaction between the enzymatic general acid and the substrate is favored at high temperature, when the enzyme has optimum activity.

Fig. 6.

Structural alterations in E·S298 and E·S385. (Distances in angstroms from the average were generated from the last 200 ps of MD.)

Catalytic role of Glu-159. The amino group (NH) of CdRP is hydrogen-bonded to the carboxylate oxygen OE1 of Glu-159-CO₂^- with an average distance of 3.1 ± 0.2 Å and 2.9 ± 0.1 Å (R_OE1…NH) in E·S298 and E·S385 (Figs. 4A and 5E), respectively. The salt bridge with the positively charged Lys-135-NH₃⁺ and hydrogen bond to ND2 of Asn-180 holds Glu-159 in place (Fig. 4A). Glu-159-CO₂^- plays the important role of stabilizing the positive charge as it builds up on the NH group of the substrate. In our MD simulations of E·S298, E·S333, E·S363, and E·S385 the carboxylate of Glu-159-CO₂^- is strongly hydrogen-bonded to the NH of substrate. It acts as an electron sink that assists in the departure of the CO₂ group from CdRP. Apart from stabilizing the positive charge of the substrate, Glu-159-CO₂^- has been previously proposed to act as the general base that abstracts a proton from the C1′ atom. In our MD simulation studies on the ground states (E·S298, E·S333, E·S363, and E·S385), the carboxylate group of Glu-159-CO₂^- is in proximity to the C1′ of CdRP and can be a possible candidate for general base. Another possible candidate for the general acid is a nearby glutamate residue, Glu-210-CO₂^-, whose carboxylates are ≈4 Å from the C1′ of CdRP.

Binding of CdRP with polar and nonpolar interactions. The negatively charged phosphate group of CdRP is stabilized by electrostatic interactions with nearby polar amino acid side chains and hydrogen bonds to the solvent water molecules (Fig. 4A). These interactions were present in both E·S298 and E·S385 systems. The guanidium group of Arg-182 interacts with the phosphate oxygen by means of its NE and NH2 atoms. The positively charged Arg-182 is a part of a flexible loop region that orients itself when the substrate is docked to the active site of IGPS (Fig. 5F). Previously, the role of Arg-182 was attributed to stabilization of the negatively charged carboxylate of CdRP (23). From MD structures, it is evident that the catalytically crucial Arg-182 plays an important role in the stabilization of the negatively charged phosphate moiety of IGPS. Other residues that interact with the three electronegative phosphate oxygens of the substrate are Ser-211-OH, Ser-234-OH, and Ser-58-OH (Fig. 4A). Apart from these enzymatic groups, there are several water molecules that interact with the solvent-exposed phosphate oxygens (data not shown).

Throughout the MD simulation of E·S298, the benzene ring of the substrate CdRP is involved in interactions with the hydrophobic side chains of the surrounding enzymatic groups Leu-131, Lys-110, Leu-83, Phe-89, and Phe-112. The inactivity of the Leu-131-Phe mutant can be explained by our MD simulation results. Throughout the MD simulations of the ground state, the hydrophobic side chain of Leu-131 makes favorable contact with the bulky phenyl group of CdRP. The hydrophobic group of Leu-131 optimizes the packing of the hydrophobic core of IGPS, which is very important for the stability of an enzyme at high temperatures. It is also found to optimize the position of the catalytically important residues Lys-110 and Glu-159 by fitting itself in the cavity between them. The bulky Phe mutant of Leu-131 would occupy a larger volume and displace either of the two important residues Lys-110 and Glu-159 from their optimized location in the active site and thus impair the catalysis. The alkyl side chain of the general acid Lys-110-NH₃⁺ interacts with the bottom face of the benzene ring with an average distance of 4.0 ± 0.4 Å (R_CD…C4) at 385 K. The nonpolar side chains of Leu-131 and Leu-83 maintain a distance of 4.2 ± 0.6 Å (R_O2′…NZ) and 4.6 ± 0.9 Å (R_O2′…NZ), respectively, from the bottom face of the benzene ring throughout the MD simulation of E·S385. The phenyl ring of Phe-89 drifts away from the benzene ring of CdRP by ≈2 Å (7.9 ± 1.2 Å, R_CE2…C2), whereas the residue Phe-112 migrates closer to the substrate by ≈1.6 Å (3.8 ± 0.4 Å, R_CZ…C6) during the MD simulation of E·S385.

Reprotonation of the general acid (Scheme 2). The carboxylate oxygen of Glu-210-CO₂^- is hydrogen-bonded to the amino group of Lys-110-NH₃⁺ and maintains a distance of 2.7 ± 0.1 Å (R_OE1…NZ) throughout the MD simulation of E·S298 and E·S385. It is interesting to point out the hydrogen bond between the general acid Lys-110-NH₃⁺ and the Glu-210-CO₂^- carboxylate and its implication to the IGPS catalysis. In the ground state (E·S298 and E·S385), this interaction between the Lys-110-NH₃⁺ and Glu-210-CO₂^- orients the general acid in a position to donate a proton to the carbonyl group of the substrate (Fig. 4A). Also, it is conceivable that after picking up the C1′ proton the protonated Glu-210-COOH mediates the reprotonation of the ε-amino group of Lys-110-NH₂, which was deprotonated in the CdRP-to-In conversion (Scheme 2), thus restoring it to the general acid.

Scheme 2.

Results from the Enzyme-In Dynamics at 385 K (E·In). The MD simulation of the E·In complex highlights the mode of binding of the In to the active site of IGPS at 385 K (Scheme 1). The hydroxyl O2T of In is hydrogen-bonded to the ε-amino of Lys-110-NH₂ with an average distance of 2.8 ± 0.1 Å (R_O2′…NZ) (Fig. 4B). The residue Glu-51-CO₂^- bridges the ε-amino groups of Lys-110-NH₂ (R_OE1…NZ = 3.0 ± 0.4 Å) and Lys-53-NH₃⁺ (R_OE2…NZ = 2.7 ± 0.2 Å) through hydrogen bonding and salt bridges. The amino group of In displays strong hydrogen bonding interaction with the OE1 of Glu-159-CO₂^- throughout the MD simulation of E·In (R_OE1…NH = 2.8 ± 0.1 Å). This interaction is important in stabilizing the developing positive charge on the amino group of the In. The residue Asn-180 exhibits hydrogen bonding interaction with OE2 of Glu-210-CO₂^- with an average distance of 3.3 ± 0.6 Å, and it also interacts with OE1 of Glu-159-CO₂^- intermittently (R_OE1…ND2 = 4.8 ± 1.1 Å) (Fig. 4B). Such an interaction holds the catalytically viable residues Glu-159 and Glu-210 in place for catalysis.

Identifying the general base: Is it Glu-159-CO₂^- or Glu-210-CO₂^-? Based on the mutational analysis, Glu-159-CO₂^- has been previously proposed as the general base that abstracts a proton from the C1′ atom of In. In the x-ray crystal structure published by the Protein Data Bank (PDB ID code 1A53), the proposed general base Glu-159-CO₂^- is at a distance of 3.8 Å from the C1′ of the ligand. On a closer inspection of the active site from the x-ray crystal structure, we find that another Glu residue, Glu-210-CO₂^-, is also at a distance of 3.9 Å from the C1′ carbon of the ligand and, thus, can also be a possible candidate for general base. In our MD simulation studies on the ground states (E·S298 and E·S385), the carboxylate groups of both the residues Glu-159-CO₂^- and Glu-210-CO₂^- are in proximity to the C1′ of CdRP and the possibility of either of them acting as the general base cannot be ruled out. However, the MD simulation of E·In supports the possibility of Glu-210-CO₂^- as being the general base that abstracts the C1′ proton. In the intermediate state, Glu-210-CO₂^- carboxylate is in closer proximity to the C1′ protons of In compared with Glu-159-CO₂^- (Figs. 4B and 5G and H). Therefore, it is easier for Glu-210-CO₂^- to abstract the proton as compared with Glu-159-CO₂^-. It is also interesting to point out that not only Gu159 but also Glu-210 is a conserved residue across the species (Glu-214 in IGPS from Escherichia coli). Thus, Glu-210-CO₂^- warrants the classification as the general base. Experimental studies, such as mutational analysis of Glu-210, would be an interesting future project.

Correlation of motion. The correlation plots from the MD simulations of E·S298 and E·S385 are shown in Fig. 8, which is published as supporting information on the PNAS web site. It is clearly evident from these plots that the enzyme exhibits more motions (or flexibility) at 385 K than 298 K (higher coefficient of correlation). It is interesting to point out that the region of the graph marked by a circle has a high negative coefficient of correlation. This region includes two loops containing the residues 56-60 and 181-186. These loops interact with the phosphate of the substrate and might help in the entry-exit of the substrate from the active site. The coefficient of correlation between the two loops is higher at 385 K than 298 K, or, in other words, the correlated motion of these loops is damped at room temperature. Higher thermal motion of the substrate entry-exit loop at 385 K would increase the catalytic efficiency, thus favoring the reaction at 385 K.

Conclusion

IGPS catalyzes the terminal ring closure step in tryptophan biosynthesis (Scheme 1). The thermophilic enzyme has evolved to work at higher temperatures and undergo perfection at the temperature of its optimum activity. Robustness of these hyperthermophilic enzymes at higher temperatures is attributed to the increased electrostatic interactions by means of salt bridges and hydrogen bonds. In the evolution of the hyperthermophilic enzymes, electrostatic forces are optimized to allow creation of reactive Michaelis conformers. As the temperature is lowered there is an increase in the strength of the electrostatic interactions. In case of hyperthermophilic IGPS enzyme, increase in energies of electrostatic interactions is visible in the distortion of the Michaelis complex (Fig. 6). At room temperature, the two electrostatic bonds of Lys-53-NH₃⁺ with the substrate become shorter, twisting the substrate around a dihedral angle that sterically prevents the ring closure reaction. This motion also results in the distancing of the general acid catalyst Lys-110-NH₃⁺ from the substrate carbonyl (Fig. 6). These conformational change events are visible in the calculated fraction of time the Michaelis complex exists as reactive conformer (NAC) in the MD simulations of enzyme-bound substrate at 298 K (E·S298), 333 K (E·S333), 363 K (E·S363), and 385 K (E·S385) (Figs. 2 and 3 and Table 1). We use this observation as a probable determining factor in the temperature dependence of enzyme catalysis. The relative population of NACs exhibits a linear relationship with the relative activity at each temperature with a correlation coefficient of 0.96. It can be concluded that the increase in time that the Michaelis complex exists as a NAC is correlated to the change in activity of this enzyme with increase in temperature. This change is reflected in the ≈1,100-fold increase in population of NACs at 385 K relative to 298 K.

We also report our findings from the MD simulation of E·In. Based on its location in the active site during the MD simulations, Glu-210-CO₂^- warrants classification as the general base instead of the previously proposed Glu-159-CO₂^- (Fig. 4B). The hydrogen bond between Lys-110-NH₃⁺ and Glu-210-CO₂^- helps to orient the general acid in place in the ground state (E·S298 and E·S385). It is conceivable that because of this geometry, Glu-210-COOH (after picking up the C1′ proton) acts to reprotonate the ε-amino group of Lys-110-NH₂, the latter having been deprotonated in the CdRP-to-In conversion (Scheme 2) would restore Lys-110-NH₃⁺ and Glu-210-CO₂^- to their original state. The role of positively charged Arg-182 has, and thus, been assigned to the stabilization of the negatively charged phosphate of the substrate rather than the previously proposed role of stabilizing the substrate carboxylate.