Relationship of Leffler (Brønsted) α values and protein folding Φ values to position of transition-state structures on reaction coordinates

Abstract

The positions of transition states along reaction coordinates (r_‡) for simple chemical reactions are often estimated from Leffler α values, the slope of plots of ΔG^‡ (activation energy) versus ΔG⁰ (equilibrium free energy) for a series of structural variants. Protein folding is more complex than simple chemical reactions and has a multitude of reaction coordinates. Φ-Value analysis measures degree of structure formation at individual residues in folding transition states from the ratio ΔΔG^‡/ΔΔG⁰ for mutations. α values are now being used to analyze protein folding by lumping series of Φ values into single plots. But, there are discrepancies in the values of α for folding with more classical measures of the extent of structure formation, which I rationalize here. I show for chemical reactions with just a single reaction coordinate that α = r_‡ only for limiting cases, such as for reactants and products being in parabolic energy wells of identical curvature. Otherwise, α can differ radically from r_‡, with α being determined just by the angles of intersection of reactant and product energy surfaces. Φ is an index of the progress of a local, energy-based reaction coordinate at the global transition state: Φ <0.5 corresponds to <50% progress of the local coordinate at the global transition state and Φ >0.5 means >50%. Protein Leffler plots can force different local indexes to a single fit and give skewed underestimates of the extent of global structure formation in transition states that differ from other measures of structure formation.

A traditional way of estimating the position of transition states on reaction pathways is the use of kinetics and linear free energy relationships. A classical approach is the Leffler or Brønsted equation, which is applied to a reaction, as in Eq. 1,

1

in which the structures of the reactants S and P are systematically altered and the activation energy, ΔG^‡, of the reaction and its equilibrium free energy, ΔG⁰, are measured (1, 2). A plot of ΔG^‡ versus ΔG⁰ can be linear, and, if so, the slope (=∂ΔG^‡/∂ΔG⁰) is termed the Leffler α or Brønsted β. The value of α is often taken as the position of the transition state on the reaction coordinate, r_‡, relative to S and P. But, this is an oversimplification and there are documented anomalies (e.g., ref. 3 and references within).

Surprisingly, the Leffler equation applies to some noncovalent interactions in enzymic catalysis and in protein folding (4-6), despite the profound differences between the covalent and noncovalent reactions under study. The transition states of proteins can also move on reaction surfaces (7-10) and display Hammond (11) and anti-Hammond effects (12) that can be described in terms of More O'Ferrall-Albery-Jencks diagrams (13). In the analysis of covalent chemistry, we usually know the structures of the reagents well and follow just a few bond changes or movement of atoms or electrons and use linear free energy relationships (and simulation) to identify precisely the positions of those. There is little rearrangement in the rest of the molecule, and the reaction coordinate can be well defined. We generally deal with large changes in the energy of bonds that are subject to quantum theory, and we are concerned with potential energy surfaces. In the analysis of noncovalent reactions in protein folding, we examine the wholesale rearrangement of the structures of the reagents and attempt to define completely or largely unknown structures at sufficient atomic detail to reconstruct them by model building and simulation. The energetics is close to classical as each bond is comparable with kT. The energies are defined by a Maxwell-Boltzmann distribution where free energy is the crucial term because TΔS is comparable to ΔH and can often be the dominant energy term. The reaction coordinate for protein folding is difficult to define because so many parameters change simultaneously and there is not a unique reaction coordinate. A procedure in protein folding, Φ-value analysis, is similar to the Leffler approach, but differs from it in essential ways (14-17). Φ is defined by the changes in activation and equilibrium energies of protein folding, Φ = ΔΔG^‡/ΔΔG⁰, as a series of two-point linear free energy plots as residues in the protein are systematically mutated. Φ measures the relative strengths of noncovalent interaction energies in transition states and ground states. Φ values of 0 and 1 are interpreted as complete bond breaking and making, as for α. But the interpretation of Φ is more complex for fractional values and has complications from changes in structure of the denatured state of the protein. Importantly, each Φ value is a probe of an individual reaction coordinate, which is related to the movement of the target side chain.

Φ values are fed into computer simulation as experimental variables (18, 19) or benchmarks (20, 21) to determine the structure of transition states at atomic-level resolution. Φ-Value analysis and computer simulation of the folding of small domains are consistent with a transition state that is compact and a distorted form of the native structure (6, 21-24). On the other hand, Leffler plots appear to suggest that the transition state of folding is generally closer to that of the denatured state (6, 25-29). Here, I investigate the relationship between the Leffler α and r_‡ and show that the two are generally different and can differ radically for protein folding reactions, with α greatly underestimating the extent of structure formation.

Single-Reaction Coordinate and Harmonic Wells

As a simple starting point, consider the interconversion of two very similar conformational states of a protein and assume a single-reaction coordinate as the two states move in a completely concerted manner. The energy wells of each will be simple harmonic for small displacements. We can apply a simplified version of the treatment by Marcus of outer sphere electron transfer reactions (30), which has been extended to group transfer reactions (31) (Fig. 1). In the simplest case, the energy wells of each state are assumed to be parabolic of equal curvature. The transition state occurs where the two energy wells intersect at r_‡. It is easy to derive for this case that α = r_‡ (see below as a special case for the more general solution). Consider the more general case, which is less analyzed (32), where the two parabolic energy curves have different curvature. For the starting state S in Fig. 1:

2

Fig. 1.

Parabolic energy curves for a reaction of S to P.

For the product state P:

3

The point of intersection gives approximately the free energy of activation for the forward reaction:

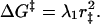4

And for the reverse:

5

Solving Eqs. 4 and 5 gives for r_‡:

6

We can relate α to r_‡ by taking the derivative of Eq. 4, with respect to ΔG⁰

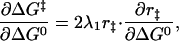7

and substituting the derivative of r_‡ with respect to ΔG⁰ from Eq. 6

8

to give:

9

Eq. 9 has some simplifying solutions. For symmetrical wells, λ₁ = λ₂, and α = r_‡. For S and P being isoenergetic, i.e., ΔG⁰ = 0,

10

Thus, if the two potential energy curves differ considerably in their distance dependence, then α differs greatly from r_‡.

The difference between α and r_‡, and how they depend on the shapes of the energy curves, is illustrated in Fig. 2, which shows S having either “steep” or “shallow” energy curves. The energy of S with the shallow curve intersects with the energy curve of P at a higher value of r_‡, indicating a later transition state than that for the S with the steep curve. But, it is obvious that the value of ΔΔG^‡ for a change in ΔΔG⁰ of P is smaller for the shallow curve than for the steep, and so S with the shallow curve has a smaller value of α, despite the later transition state.

Fig. 2.

Parabolic energy curves of widely differing curvature for S intersecting with energy curve for P. The shallower curve has a higher value of r_‡, corresponding to a later transition state, yet a lower value of ΔΔG^‡, which gives a lower value of α.

The simple harmonic energy wells may occur in practice in the reactions of enzymes such as the tyrosyl-tRNA synthetase, where the structure of the enzyme must accommodate the slightly different structures of substrates and products (33). As the reaction proceeds, the energy well for binding of the substrate must change as it proceeds to products, and small changes in a complex energy surface approximate to harmonic functions. Intersecting parabolas are suitable for allosteric changes (34, 35). However, the gross changes of protein folding take place on anharmonic surfaces, as in Fig. 3 (36). Along the previous lines of reasoning, we can expect α to underestimate r_‡. But, the situation for anharmonic surfaces can be analyzed in more depth.

Fig. 3.

Asymmetric wells for the folding of a denatured protein (D) to its native structure (N). The crossing of a shallow curve with a steep curve leads to a low value of α, despite a late transition state.

Single-Reaction Coordinate and Anharmonic Wells

The crucial factors in determining the value of α are the angles at which the free energy curves of S and P cross (Fig. 4). We can generalize this for asymmetric potential curves that are more complex than parabolas. The transition state moves on mutation through a distance δr_‡, as rationalized by Hammond (11). From the triangles in Fig. 4, ΔΔG^‡ = δr_‡tanθ₁ = δrtanθ₂, ΔΔG⁰ = (δr + δr_‡)tanθ₂. And so ΔΔG^‡/ΔΔG⁰ = δr/(δr + δr_‡) = tanθ₁/(tanθ₁ + tanθ₂). Accordingly,

11

Fig. 4.

Region of intersection of energy curves around the transition state. The broken line is the energy curve for a mutant that has been destabilized by ΔΔG⁰.

That is, in general α depends on the angles at which the energy curves cross, and so α is not necessarily equal to the reaction coordinate, r_‡. For example, the late transition state at the intersection of the shallow curve of D with the steep curve of N in Fig. 3, has θ₁ much lower than θ₂, which generates a low value of α that would be naively and incorrectly interpreted as implying an early transition state.

Eq. 11 may be written as:

12

Eq. 12 implies that different reaction coordinates can give different values of α if they are based on different properties of the protein.

Multiple-Reaction Coordinates and Protein Folding

Protein folding consists of the transition between a denatured D and the native conformation N. This can occur in an apparent two-state process, which is the simplest to analyze. The loosely defined denatured state has an ensemble of conformations of similar energy, but the energy rises as the conformations approach the structure of the transition state, ‡. The overall reaction coordinate for folding can be defined in a number of ways, three of the most common being: radius of gyration, r_g; β, the fraction of solvent-accessible surface area of the protein that is buried in any state, relative to D and N (7, 8, 37); and Q, the fraction of pairwise native-state contacts in any state relative to D and N (38, 39). Intuitively, we do not expect those three measures to give the same values of α or r_‡: to a crude approximation, surface area varies as radius² and volume as radius³ so that the position on a reaction coordinate on a scale of 0 to 1 will be the furthest advanced in terms of contraction of r_g, less so in terms of β (which is proportional to contraction of surface area), and least so in terms of Q (which is proportional to density or proximity of the atoms in a protein, i.e., contraction of volume).

Φ as an Index of Local Reaction Coordinates

The degree of folding at each residue can be considered as a local reaction coordinate. Each such coordinate can be probed by Φ, which = ΔΔG_‡-D/ΔΔG_N-D for a prescribed mutation of a side chain or even backbone moiety (40, 41). Φ effectively probes a local reaction coordinate based on Q_i. The relationship between the progress of a local reaction coordinate and the position of overall transition state can be analyzed by considering the two extreme mechanisms of folding, nucleation-condensation and framework as in Fig. 5 (6, 42, 43) and how individual reaction coordinates are coupled to the major transition state. [Hedberg and Oliveberg (10) have developed similar ideas and diagrams for analyzing Hammond effect movements in the transition state.] In nucleation-condensation (Fig. 5 Left), the formation of structure is highly cooperative with many elements formed simultaneously, being led by the formation of the nucleus. In the classical framework mechanism (Fig. 5 Right), elements of secondary structure form fully before the tertiary interactions are formed (44-46). It is clear in Fig. 5 that the transition states on the reaction coordinates for elements of structure that form mainly before or after the major transition state (i.e., those with very high and very low values of Φ) will not be coupled with the formation of the major transition state. Mutations with high and low Φ have the effect of altering the depths and surrounding regions of the energy wells of the D and N states without affecting the events at their crossover in the transition state. What is clear from Fig. 5 is that Φ measures the position of the transition state for an individual reaction coordinate relative to that for the overall reaction. If an individual reaction coordinate i in terms of Q_i is >50% formed at the overall transition state, then Φ_i will be >0.5. Conversely, if coordinate i is <50% formed at the overall transition state, then Φ_i will be <0.5.

Fig. 5.

Effects of coupling of individual reaction coordinates for nucleation-condensation (Left) and framework (Right) mechanisms of folding. (A) Individual values of Q_i for different elements of structure plotted against the overall value of Q, where Q is the fraction of native pairwise contacts relative to D (= 0) and N (= 1). For the pure framework mechanism, elements of secondary structure are completely formed before the main transition state. For nucleation-condensation, the formation of the nucleus leads, but is coupled with the main transition. (B) Sketch of frequency of Φ (n_Φ) against Φ for the two mechanisms.

A Leffler plot of ΔΔG_‡-D versus ΔΔG_N-D is the same as plotting all of the individual products of Φ_ix(ΔΔG_N-D)_i for each mutation against (ΔΔG_N-D)_i. The slope of such a curve is not the “average” position of the overall transition state on the reaction pathway but is instead the weighted average of the measured Φ values and their relative position to the degree of structure formation of the transition state. Such plots are biased by those values with the largest ΔΔG_N-D, which tend to be those for large mutations in the hydrophobic core of the protein, which is always formed late and hence has low values of Φ (17).

Experimental Observations

The position of the folding transition state on the reaction pathway in terms of accessible surface area may be measured experimentally from the effects of chemical denaturants on the kinetics and equilibria of folding, that is, the sensitivity of free energies of activation and equilibrium folding to the concentration of denaturant (usually urea or guanidinium chloride). Empirically, there are extrathermodynamic relationships due to Tanford (37):

13

14

where ΔG_D-N is the difference in free energy between folded and unfolded protein at a given denaturant concentration, ΔG_‡-N is the difference in free energy between the transition state and the folded protein at a given denaturant concentration, ΔG_D-N^H₂O and ΔG_‡-N^H₂O the values in water and m_D-N and m_‡-N are constants for a particular protein. m_‡-N and m_D-N are proportional to the change in exposure of amino acids as the structure of the native protein changes to that of the transition or denatured state. Eqs. 13 and 14 give ∂(ΔG_‡-N)/∂(ΔG_D-N) = m_‡-N/m_D-N = β_T, the Tanford β value (7, 8). β_T is an empirical reaction coordinate based on exposed surface area that is accessible to experimental observation.

Chymotrypsin inhibitor 2 (CI2) is a very good paradigm for testing the above equations because denaturation curves of most mutants fit precisely the simplest models for two-state folding, and its properties allow m_‡-N, m_D-N, ΔΔG_‡-N, and ΔΔG_‡-D to be measured with high accuracy (6, 47, 48). The Tanford β value for WT CI2 is 0.6, and the specific heat of activation relative to its equilibrium folding is 0.5, indicating that the transition state is 50-60% folded as measured by exposed surface area (49). Measurement by computer simulation of the radius of gyration gives the transition state as being at ≈80-90% of the distance between the denatured and native states, the compaction of surface-accessible area in the transition state is ≈50%, and Q is ≈40% realized (R. Day and V. Daggett, personal communication). A Leffler plot, on the other hand, gives a value of α of 0.2-0.3 for folding and 0.7-0.8 for unfolding, which we now see should not be taken as indicating a very early transition state for folding or its being diffuse (6). CI2 is the archetype of nucleation-condensation. Most of its Φ values cluster ≈0.3, with the nucleus in the N-terminal region of its helix being part of the nucleus. The low values of Φ dominate a Leffler plot.

β_T for structural subsets of mutants of CI2 varies as ΔΔG^‡ (8). This relationship is now justified in the analysis of Fig. 4, where it is seen that ∂r_‡/∂ΔG^‡ = 1/tanθ₁. Over the region where the energy curves are linear:

15

According to the Hedberg and Oliveberg (10) analysis, as in Fig. 5, movement of the transition state will be seen only for intermediate values of Φ. The values of β_T for CI2 are plotted in Fig. 6 versus ΔΔG_‡-N or ΔΔG_‡-D grouped into classes of 0.2 < Φ < 0.6 and 0.2 > Φ > 0.6: movement is not seen for high and low Φ but only for the intermediate values.

Fig. 6.

Movement of transition state for folding and unfolding of CI2 on mutation. The values of β_T for folding (A) and unfolding (B) are plotted against the changes in free energy of activation on mutation. The mutants are separated into classes of 0.2 < Φ < 0.6 (intermediate Φ) and 0.2 > Φ > 0.6 (low and high Φ). The former class has a significant slope, whereas the latter is much smaller or insignificant, as predicted (10). β_T was calculated from the ratios of m_‡-N/(m_‡-N + m_‡-D) and m_‡-D/(m_‡-N + m_‡-D) for folding and unfolding, respectively. Values of m_‡-N were measured under the same range of concentrations of guanidinium chloride (GdmCl) for all mutants (centered ≈4 M). Similarly, m_‡-D was measured under identical concentrations, beginning from 0 M GdmCl. All mutants shown have strictly linear dependences of free energies of activation on [GdmCl], and no mutant with any observed curvature was used (48) (collected data, this laboratory). The positions of low and significant slope are as described (14).

Engrailed homeodomain is the test case for a framework mechanism, the pathway being rigorously defined by experiment and simulation (50). A histogram of Φ values (data not shown) is clearly consistent with this mechanism (as sketched in Fig. 5). The Tanford β value is 0.8. A crude Leffler plot, however, gives an α value of 0.2-0.3 for engrailed homeodomain and its homologue cMyb (43), which is clearly inconsistent with a very compact state as found by experiment and simulation (43). The slope of the Leffler plot is again determined by the large energy changes caused by mutations in the core, and formation of the core is a major rate-determining process with lower Φ values.

Summary of Interpretation of Protein Folding Reaction Coordinates

As illustrated in Figs. 2 and 3 and quantified in Eqs. 11 and 12, the crossing from a shallow curve to a steep energy curve leads to a low value of α and vice versa. Values of β_T tend to be between 0.6 and 0.9 (51), which is usually interpreted as evidence for late transition states. This lateness may be so in terms of compaction but not necessarily so in terms of free energy: the high β_T values just show that the rate of change of energy with surface area compaction in the direction of folding at the transition state is greater than that of unfolding. Indeed, a small expansion of the folded protein will lead to only a small increase in surface area but a large change in energy. Consequently, β_T tends to be high and can lead to an overestimate of the actual degree of structure formation. The Leffler α, on the other hand, tends to underestimate the degree of structure formation because of the artefacts in lumping together different classes of mutations with different changes in equilibrium free energy. Φ is not a true measure of the position of a transition state and is unaffected by the relationship of α to a reaction coordinate. But Φ_i is a good estimate of Q_i for a particular moiety in a transition state. For the purposes of simulation of transition states, Φ values are divided into weak (<0.3), medium (0.3-0.6), and strong (>0.6) (16, 52). In practice, a medium value of Φ means that the region has close to native-like topology and strong means that it is very close to full native structure as is intuitively obvious and as shown by simulation (20, 53, 54).