Multi-Tissue Decomposition of Diffusion MRI Signals via ℓ₀ Sparse-Group Estimation

Abstract

Sparse estimation techniques are widely utilized in diffusion MRI (DMRI). In this paper, we present an algorithm for solving the ℓ₀ sparse-group estimation problem and apply it to the tissue signal separation problem in DMRI. Our algorithm solves the ℓ₀ problem directly, unlike existing approaches that often seek to solve its relaxed approximations. We include the mathematical proofs showing that the algorithm will converge to a solution satisfying the first-order optimality condition within a finite number of iterations. We apply this algorithm to DMRI data to tease apart signal contributions from white matter (WM), gray matter (GM), and cerebrospinal fluid (CSF) with the aim of improving the estimation of the fiber orientation distribution function (FODF). Unlike spherical deconvolution (SD) approaches that assume an invariant fiber response function (RF), our approach utilizes a response function group (RFG) to span the signal subspace of each tissue type, allowing greater flexibility in accounting for possible variations of the response function throughout space and within each voxel. Our ℓ₀ algorithm allows for the natural groupings of the RFs to be considered during signal decomposition. Experimental results confirm that our method yields estimates of FODFs and volume fractions of tissue compartments with improved robustness and accuracy. Our ℓ₀ algorithm is general and can be applied to sparse estimation problems beyond the scope of this paper.

I. Introduction

Brain tissue changes such as demyelination and axonal loss are common pathological features of many neurological diseases. Precise quantification of these changes can improve the accuracy of disease diagnosis and is essential for monitoring treatment response and effective patient management. Diffusion magnetic resonance imaging (DMRI) [1] is an ideal imaging modality for this purpose owing to its unique ability to extract microstructural information by utilizing restricted and hindered diffusion to probe compartments that are much smaller than the voxel size.

Sparse estimation techniques are widely utilized in DMRI [2]–[5]. However, most techniques to date are predominantly based on ℓ₁ regularization. This choice is partly due to the challenges involved in solving ℓ₀-regularized problems, which are in nature non-convex, non-smooth, and discontinuous. While iterative hard thresholding algorithms [6]–[8] and greedy algorithms such as matching pursuit [9], [10], orthogonal matching pursuit [11], and subspace pursuit [12] have been developed for solving ℓ₀-regularized least-squares problems, how they can be extended for solving more general ℓ₀ minimization problems, such as those involving grouping [13], [14], is not immediately apparent. We present in this paper an algorithm for solving the ℓ₀ sparse-group problem, which is the ℓ₀ counterpart of the ℓ₁ sparse-group LASSO problem presented in [14]. We include the mathematical proofs to show that our algorithm converges to a solution that satisfies the first order optimality condition within a finite number of iterations.

We apply our algorithm to the DMRI tissue signal separation problem. In DMRI, each imaging voxel is in the order of 10 mm³ in size and thus contains thousands of cells and tissue components. The diffusion of water molecules in each compartment (e.g., axons, dendrites, extracellular space, and cell soma) is affected by local viscosity, composition, geometry, and membrane permeability [15]. While the most commonly used diffusion tensor imaging (DTI) provides scalar indices such as fractional anisotropy (FA) and mean diffusivity (MD) for quantifying white matter integrity, they are limited by their non-specificity in identifying the exact causes of white matter changes [16], [17]. For example, the reduction in FA may be caused by any or a combination of the following factors that reduce the diffusion barriers: demyelination, fiber orientation variability, larger axon diameter, and lower packing density. For determining the more specific causes of changes, the signal contributions of the different white matter microstructural compartments need to be identified so that confounding information can be removed and information pertaining specifically to axonal injury and myelin damage can be teased out.

The general goal of diffusion compartment analysis is to identify signal contributions from constituent compartments and extract information that is most relevant to our problem at hand. Such approach increases specificity by removing confounding information. For example, it has been shown in [18] that by simply removing the diffusion signal that can be attributed to free diffusion [19], the sensitivity to the differences between stable and converting mild cognitive impairment (MCI) subjects can be significantly improved. In [20], the authors reported that by utilizing a model characterizing both intra- and extra-cellular diffusion, good estimations of neurite density and orientation dispersion can be obtained. It has been reported in [21] that by proper consideration of signal contributions from gray matter and cerebrospinal fluid, false positive local orientations can be significantly reduced. All these studies point to the importance of compartmentalized analysis of DMRI data.

We employ our ℓ₀ algorithm to tease apart, at each voxel, the signal contributions of white matter (WM), gray matter (GM), and cerebrospinal fluid (CSF) so that the fiber orientation distribution function (FODF) can be estimated with greater accuracy. The concept of FODF [4], [22]–[25] was first introduced by Tournier and his colleagues in [22]. Assuming that all WM fiber bundles in the brain share identical diffusion characteristics, the diffusion-attenuated signal can be expressed as the spherical convolution of a fiber response function (RF), i.e., the signal profile of a single coherent fiber bundle, with the FODF. The FODF, which represents the distribution of fiber orientations within the voxel, can therefore be recovered using spherical deconvolution (SD) [22]. The SD technique proposed in [22] was later improved in [23] by introducing constrained spherical deconvolution (CSD) for better conditioning of the inverse problem, greater robustness to noise, and less susceptibility to negative artifacts that are physically impossible. Unlike the multi-tensor approach [26], SD-based methods do not require one to specify the number of tensors to fit to the data. A discrete version of the formulation, coupled with sparse regularization, was investigated in [2], [3], [27]. Tracing FODFs across space allows one to gauge connectivity between brain regions [28] and provides in vivo information on white matter pathways for neuroscience studies involving development, aging, and disorders [29]–[34].

It has been recently reported that a mismatch between the kernel used in CSD and the actual fiber RF can cause spurious peaks in the estimated FODF [35]. Although CSD has been recently extended in [21] to include RFs of not only the white matter (WM) but also the gray matter (GM) and the cerebrospinal fluid (CSF), these RFs are still spatially fixed and similar shortcomings as reported in [35] remain a problem.

In this paper, we propose to estimate the WM, GM, and CSF volume fractions and the WM FODF by using response function groups (RFGs). Each RFG is a collection of exemplar RFs catering to the variations of the actual RFs. Unlike the conventional approach of using fixed RFs, the utilization of RFGs will allow tolerance to RF variations and hence minimize estimation error due to the mismatch between the RF and the data. The FODF and compartmental volume fractions for each voxel are estimated by solving the ℓ₀ sparse-group problem that takes into account the natural groupings of the RFs. Our work is an integration of concepts presented in [21], [36], [37] with a novel ℓ₀ estimation framework.

II. Related Works

Recently, Daducci et al. [38] linearize the fitting problem of microstructure estimation techniques, such ActiveAx [39] and NODDI [20], to drastically speed up axon diameter and density estimation by a few orders of magnitude. They achieve this by solving an ℓ₁ minimization problem with a dictionary containing instances of the respective biophysical models generated with a discrete sampling of the diffusion parameters. Their work was recently extended to account for crossing fibers [40], [41]. Similar to [38], we observed that by using RFGs containing RFs of varying parameters, the data can be explained with greater fidelity than by using RFs with a single fixed set of parameters. Dissimilar to [38], our work (i) solves a cardinality penalized problem instead of the ℓ₁ problem, and (ii) explicitly considers the natural coupling between RFGs via sparse-group estimation, which is similar but not identical to [14].

The use of ℓ₀ penalization is motivated by the observations reported in [42], where the authors show that the commonly used ℓ₁-norm penalization [27] conflicts with the unit sum requirement of the volume fractions and hence results in suboptimal solutions. To overcome this problem, the authors propose to employ a reweighted ℓ₁ minimization approached described by Candes et al. [43] to obtain solutions with enhanced sparsity, approximating solutions given by ℓ₀ minimization. However, despite giving improved results, this approach is still reliant on the suboptimal solution of the unweighted ℓ₁ minimization problem that has to be solved in the first iteration of the reweighted minimization scheme.

Another issue with ℓ₁ minimization is that it biases and attenuates coefficient magnitudes [44], resulting in the erosion of FODF peaks. While this can potentially be corrected by debiasing [44] — a post-processing approach where the coefficients are re-estimated without regularization using the support of the solution identified by ℓ₁ minimization — the desirable denoising effect of ℓ₁ penalization might be undone [44].

Besides ℓ₁-norm relaxation, other relaxation approaches have been proposed recently to substitute the ℓ₀-“norm”¹ by an ℓ_p-“norm” for some p ∈ (0, 1) (see for example [45]–[47]). In general, these approaches do not necessarily give high-quality solutions. See [48] for examples showing that, when p ∈ (0, 1], the solutions can deviate significantly from the true sparse solutions.

III. Contributions

In this work, we propose to directly minimize the ℓ₀ penalized problem instead of resorting to reweighted minimization. By doing so, we (i) overcome the suboptimality of reweighted minimization, and (ii) improve estimation speed greatly by avoiding solving the ℓ₁ minimization problem (especially the sparse-group problem [14]) multiple times to gradually improve sparsity. We will describe in this paper an algorithm based on iterative hard thresholding (IHT) [49] to effectively and efficiently solve the ℓ₀ penalized sparse-group problem.

The RFG framework affords the following advantages: (i) The exact RF does not need to be specified and can be determined automatically from the RFGs based on the data — this is akin to blind deconvolution for FODF estimation; (ii) The RF is allowed to vary across voxels as well as across fiber populations within each voxel; and (iii) The signal for each fiber population can be explained using a combination of RFs, making possible the modeling of signal with non-monoexponential decay.

Part of this work has been reported in our recently published conference paper [5]. Herein, we provide additional examples, results, derivations, and insights that are not part of the conference publication.

IV. Proposed Approach

In what follows, we will describe the concept of response function groups (RFGs), the estimation problem, the optimization framework, and some implementation issues.

A. Response Function Groups (RFGs)

DMRI acquires several diffusion-sensitized images, probing water diffusion in various directions and at various diffusion scales. At each voxel location, the diffusion-weighted signal S(b, ĝ), measured for diffusion weighting b and at gradient direction ĝ, can be represented as a mixture of N models:

$$S(b,\widehat{\mathbf{g}})=\sum _{i=1}^N{f}_i{S}_i(b,\widehat{\mathbf{g}})+\epsilon (b,\widehat{\mathbf{g}}),$$ (1)

where f_i is the volume fraction associated with the i-th model S_i and ε(b, ĝ) is the fitting residual. A wide variety of microstructural models described in [50] can be employed to capture the diffusion patterns of intra- and extra-axonal diffusion compartments. In the current work, we are interested in distinguishing signal contributions from WM, GM, and CSF and we choose to use the tensor model S_i(b, ĝ) = S_i(0) exp(−bĝ^TD_iĝ), where S_i(0, ĝ) = S_i(0) is the baseline signal with no diffusion weighting and D_i is a diffusion tensor. This model affords great flexibility in representing different compartments of the diffusion signal. Setting the diffusion tensor D = λI, the model represents isotropic diffusion with diffusivity λ. When λ = 0 and λ > 0 the model corresponds to the dot model and the ball model, respectively [50]. Setting D = (λ_|| − λ_⊥)v̂v̂^T + λ_⊥I, λ_|| > λ_⊥, the model represents anisotropic diffusion in principal direction v̂ with diffusivity λ_|| parallel to v̂ and diffusivity λ_⊥ perpendicular to v̂. When λ_⊥ = 0 and λ_⊥ > 0 the model corresponds to the stick model and the zeppelin model, respectively [50]. In our case, each RF is represented using the tensor model with a specific set of diffusion parameters.

Spherical deconvolution (SD) of the white matter (WM) diffusion-weighted signal with a fiber RF has been shown to yield high-quality estimates of FODFs [23]. According to [2], the solution to SD can be obtained in discretized form by including in the mixture model (1) a large number of anisotropic tensor models uniformly distributed on the unit sphere with fixed λ_|| and λ_⊥ and solving for {f_i} via minimizing the residual in the least-squares sense with some appropriate regularization, giving us the FODF. In this work, instead of fixing λ_|| and λ_⊥, we allow each of them to vary across a range of values. Therefore, each principal direction is now represented by a group of RFs, i.e., a RFG. Additional isotropic RFGs are included to account for signal contributions from GM and CSF. Formally, the representation can be expressed as

$$S(b,\widehat{\mathbf{g}})=\underset{\widehat{S}(b,\widehat{\mathbf{g}})}{\underbrace{\left[\sum _{i=1}^{N_{\text{WM}}}{S}_i^{\text{WM}}(b,\widehat{\mathbf{g}})\right]+S^{\text{GM}}(b,\widehat{\mathbf{g}})+S^{\text{CSF}}(b,\widehat{\mathbf{g}})}}+\epsilon (b,\widehat{\mathbf{g}}),$$ (2)

where we have N_WM WM RFGs, a GM RFG, and a CSF RFG with

$$\begin{array}{ll}{S}_i^{\text{WM}}(b,\widehat{\mathbf{g}})& =\sum _{j=1}^{K_{\text{WM}}}{f}_{i,j}^{\text{WM}}{S}_{i,j}^{\text{WM}}(0)exp(-b{\widehat{\mathbf{g}}}^{\mathrm{T}}{\mathbf{D}}_{i,j}^{\text{WM}}\widehat{\mathbf{g}}),\\ S^{\text{GM}}(b,\widehat{\mathbf{g}})& =\sum _{j=1}^{K_{\text{GM}}}{f}_j^{\text{GM}}{S}_j^{\text{GM}}(0)exp(-b{\widehat{\mathbf{g}}}^{\mathrm{T}}{\mathbf{D}}_j^{\text{GM}}\widehat{\mathbf{g}}),\\ S^{\text{CSF}}(b,\widehat{\mathbf{g}})& =\sum _{j=1}^{K_{\text{CSF}}}{f}_j^{\text{CSF}}{S}_j^{\text{CSF}}(0)exp(-b{\widehat{\mathbf{g}}}^{\mathrm{T}}{\mathbf{D}}_j^{\text{CSF}}\widehat{\mathbf{g}}),\end{array}$$ (3)

and

$$\begin{array}{ll}\hfill {\mathbf{D}}_{i,j}^{\text{WM}}& =({\lambda }_{\Vert ,j}^{\text{WM}}-{\lambda }_{\perp ,j}^{\text{WM}}){\widehat{\mathbf{v}}}_i{\widehat{\mathbf{v}}}_i^{\mathrm{T}}+{\lambda }_{\perp ,j}^{\text{WM}}\mathbf{I},\\ \hfill {\mathbf{D}}_j^{\text{GM}}& ={\lambda }_j^{\text{GM}}\mathbf{I},\\ \hfill {\mathbf{D}}_j^{\text{CSF}}& ={\lambda }_j^{\text{CSF}}\mathbf{I.}\end{array}$$ (4)

Given the signal S(b, ĝ), we need to estimate the volume fractions { $f_{i,j}^{\text{WM}}$}, { $f_j^{\text{GM}}$}, and { $f_j^{\text{CSF}}$}. If we take the Fourier transform of (2), it is easy to see that these volume fractions are in fact the weights that decompose the ensemble average propagator (EAP) of the overall signal into a weighted sum of the EAPs of the individual tensor models. The overall volume fractions associated with WM, GM, and CSF are respectively

$$f^{\text{MW}}=\sum _{i=1}^{N_{\text{WM}}}\underset{f^{{\text{WM}}_i}}{\underbrace{\sum _{j=1}^{K_{\text{WM}}}{f}_{i,j}^{\text{WM}}}},f^{\text{GM}}=\sum _{j=1}^{K_{\text{GM}}}{f}_j^{\text{GM}},f^{\text{CSF}}=\sum _{j=1}^{K_{\text{CSF}}}{f}_j^{\text{CSF}}.$$ (5)

The set {f^WM_i|i = 1, ..., N_WM} gives the WM FODF. For the sake of notational simplicity, we group the volume fractions into a vector

$$\mathbf{f}=\left[\begin{array}{c}{\mathbf{f}}^{{\text{WM}}_1}\\ ⋮\\ {\mathbf{f}}^{{\text{WM}}_{N_{\text{MW}}}}\\ {\mathbf{f}}^{\text{GM}}\\ {\mathbf{f}}^{\text{CSF}}\end{array}\right],$$ (6)

where

$$\begin{array}{ll}\hfill {\mathbf{f}}^{{\text{WM}}_i}& ={\left[f_{i,1}^{\text{WM}},\dots ,f_{i,K_{\text{WM}}}^{\text{WM}}\right]}^{\mathrm{T}},\hfill \\ \hfill {\mathbf{f}}^{\text{GM}}& ={\left[f_1^{\text{GM}},\dots ,f_{K_{\text{GM}}}^{\text{GM}}\right]}^{\mathrm{T}},\hfill \\ \hfill {\mathbf{f}}^{\text{CSF}}& ={\left[f_1^{\text{CSF}},\dots ,f_{K_{\text{CSF}}}^{\text{CSF}}\right]}^{\mathrm{T}}.\hfill \end{array}$$ (7)

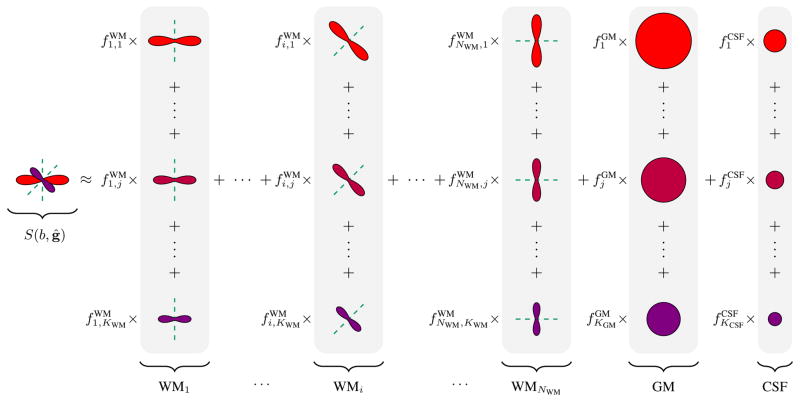
See Figure 1 for an illustration of how the signal can be represented using the RFGs. Note that N_WM is not the number of fiber populations, but is instead a sufficiently large number that results in a dense coverage of possible fiber directions. The fiber populations are unknown a priori and are automatically estimated by solving the sparse-group problem described next.

Fig. 1.

The signal, S(b, ĝ), can be represented using response function groups (RFGs) associated with white matter (WM), gray matter (GM), and cerebrospinal fluid (CSF). The volume fractions{ $f_{i,j}^{\text{WM}}$}, { $f_j^{\text{GM}}$}, and { $f_j^{\text{CSF}}$} are estimated using a sparse-group estimation framework. The groupings are shaded in gray. Note that each white matter RFG WM_i is associated with a direction v̂_i. See (2), (3), and (4) for the mathematical details.

B. Estimation of Volume Fractions

To estimate the volume fractions, we solve the following optimization problem:

$$\begin{gathered} \underset{\mathbf{f}\succcurlyeq 0}{min}\{\varphi (\mathbf{f})={\Vert S(b,\mathbf{g})-\widehat{S}(b,\mathbf{g})\Vert }_2^2+\alpha \gamma {\Vert \mathbf{f}\Vert }_0+(1-\alpha )\gamma \\ \left[\sum _{i=1}^{N_{\text{WM}}}\mathcal{I}({\Vert {\mathbf{f}}^{{\text{WM}}_i}\Vert }_2)+\mathcal{I}({\Vert {\mathbf{f}}^{\text{GM}}\Vert }_2)+\mathcal{I}({\Vert {\mathbf{f}}^{\text{CSF}}\Vert }_2)\right]\}, \end{gathered}$$ (8)

where ℐ(z) is an indicator function returning 1 if z ≠ 0 or 0 otherwise. The ℓ₀-“norm” gives the cardinality of the support, i.e., ||f||₀ = |supp(f)| = |{k : f_k ≠ 0}|. Parameters α ∈ [0, 1] and γ > 0 are for penalty tuning, analogous to those used in sparse-group LASSO [14]. Note that α = 1 gives the ℓ₀ fit, whereas α = 0 gives the group ℓ₀ fit. The problem can be written more succinctly in matrix form:

$$\underset{\mathbf{f}\succcurlyeq 0}{min}\left\{\varphi (\mathbf{f})={\Vert \mathbf{Af}-\mathbf{s}\Vert }_2^2+\alpha \gamma {\Vert \mathbf{f}\Vert }_0+(1-\alpha )\gamma \sum _{g\in \mathcal{G}}\mathcal{I}({\Vert {\mathbf{f}}_g\Vert }_2)\right\},$$ (9)

where f_g denotes the subvector containing the elements associated with group g ∈ 𝒢 = {WM₁, ..., WM_NWM, GM, CSF}. If the signal vector s is acquired at P (b, g)-points, A = [A^WM|A^GM|A^CSF] is a P × N matrix (N = N_WMK_WM + K_GM +K_CSF) with columns containing all the individual WM, GM, and CSF tensor models sampled at the corresponding P points. We describe next our algorithm for the solution to this problem.

C. Optimization

The problem we are interested in solving has the following form:

$$\underset{\mathbf{f}\succcurlyeq 0}{min}\left\{\varphi (\mathbf{f})=l(\mathbf{f})+r(\mathbf{f})\right\}.$$ (10)

In our case, the loss term $l(\mathbf{f})={\Vert \mathbf{Af}-\mathbf{s}\Vert }_2^2$ is smooth, convex, and has a gradient that is Lipschitz continuous. The regularization term r(f) = αγ||f||₀+(1 − α) γ Σ_g∈𝒢ℐ(||f_g||₂) is non-convex, non-smooth, and discontinuous. Note that the solution is trivial, i.e., f^* = 0, when $\gamma \ge {\Vert \mathbf{s}\Vert }_2^2$. We introduce here an algorithm called non-monotone iterative hard thresholding (NIHT), which we developed based on [6], [49], [51]–[53], to solve this problem. Proof of convergence is provided in the appendix.

1) Non-Monotone Iterative Hard Thresholding

The solution is outlined in Algorithm 1. The algorithm seeks the solution via gradient descent using a majorization-minimization (MM) [54] formulation of the problem. Step 1a minimizes the majorization of the objective function ϕ (·) at f^(k). The minimization involves a gradient descent step with step size 1/L^(k) (more on this in the next section). The parameters L_min and L_max constrain the step size so that it is neither too aggressive nor too conservative (Step 3). We choose the initial step size $1/L_0^{(k)}$ as proposed in [55], using a diagonal matrix $1/L_0^{(k)}\mathbf{I}$ to approximate the inverse of the Hessian matrix of l(f) at f^(k) (Step 3). A suitable step size is determined via backtracking line search, where the step size is progressively shrunk by a factor of 1/τ (Step 1c). Parameter η ensures that the line search leads to a sufficient change in the value of the objective function. Since the problem is non-monotone, i.e., the value of the objective function is not guaranteed to decrease at every iteration, we require the value of the objective function to be slightly smaller than the largest value of the objective function in M previous iterations (Step 1b). For M > 0, the algorithm may increase the value of the objective function occasionally but will eventually converge faster than the monotone case with M = 0 [52]. Parameter ε controls the stopping condition (Step 2). We divide |ϕ(f^(k+1)) − ϕ(f^(k))| by max(ϕ(f^(k+1)), 1) to compute the relative change or the absolute change of the value of the objective function, whichever is smaller. In this work, the following parameters were used: L_min = 1 × 10⁻⁹, L_max = 1 × 10⁹, η = 1 × 10⁻⁴, τ = 2, M = 10, and ε = 1 × 10⁻⁶.

Algorithm 1.

Non-Monotone Iterative Hard Thresholding (NIHT)

Data: Signal vector s; RF matrix A.

Parameters: Grouping 𝒢; sparsity γ; balance parameter α.

Parameters: Factor τ > 1; step size constants Lmin < Lmax; line search constant η > 0; stopping tolerance ε > 0; non-monotone parameter M.

Initialization: $L_0^{(0)}=1$; initial solution f(0).

Output: Volume fraction vector f.

/* Main Steps */ Set $L^{(k)}=L_0^{(k)}$. 1a) Solve subproblem (see Section IV-C2) $${\mathbf{f}}^{(k+1)}\in \underset{\mathbf{f}\ge 0}{\text{Arg}\text{min}}\left\{l({\mathbf{f}}^{(k)})+\nabla l{({\mathbf{f}}^{(k)})}^{\mathrm{T}}(\mathbf{f}-{\mathbf{f}}^{(k)})+\frac{L^{(k)}}{2}{\Vert \mathbf{f}-{\mathbf{f}}^{(k)}\Vert }_2^2+r(\mathbf{f})\right\}.$$ (11) 1b) If $$\varphi ({\mathbf{f}}^{(k+1)})\le \underset{{[k-M]}^{+}\le i\le k}{\text{max}}\varphi ({\mathbf{f}}^{(i)})-\frac{\eta }{2}{\Vert {\mathbf{f}}^{(k+1)}-{\mathbf{f}}^{(k)}\Vert }_2^2$$ (12) is satisfied, then go to Step 2. 1c)Set L(k) ← L(k) and go to Step 1a. If $$\frac{\mid \varphi ({\mathbf{f}}^{(k+1)})-\varphi ({\mathbf{f}}^{(k)})\mid }{max(\varphi ({\mathbf{f}}^{(k+1)}),1)}<\epsilon$$ is satisfied, then return f(k+1) as a solution. Otherwise, go to Step 3. Set $$L_0^{(k+1)}=max\left\{L_{min},min\left\{L_{max},\frac{\mathrm{\Delta }{l}^{\mathrm{T}}\mathrm{\Delta }\mathbf{f}}{{\Vert \mathrm{\Delta }\mathbf{f}\Vert }_2^2}\right\}\right\},$$ (13) where Δf = f(k+1) − f(k) and Δl = ∇l(f(k+1)) − ∇l(f(k)). Set k ← k + 1 and go to Step 1.

2) Solution to Subproblem

The subproblem is group separable and can be solved by tackling separately the problem associated with each group g ∈ 𝒢. With some algebra, the subproblem associated with group g can be shown to be

$${\mathbf{f}}_g^{(k+1)}\in \underset{{\mathbf{f}}_g\succcurlyeq 0}{\text{Arg}\text{min}}\left\{{\varphi }_g({\mathbf{f}}_g)={\Vert {\mathbf{f}}_g-{\mathbf{z}}_g^{(k)}\Vert }_2^2+\frac{2}{L^{(k)}}{r}_g({\mathbf{f}}_g)\right\},$$ (14)

where

$$\begin{array}{l}{\mathbf{z}}^{(k)}={\mathbf{f}}^{(k)}-\nabla l({\mathbf{f}}^{(k)})/L^{(k)}\\ ={\mathbf{f}}^{(k)}-2{\mathbf{A}}^{\mathrm{T}}(\mathbf{A}{\mathbf{f}}^{(k)}-\mathbf{s})/L^{(k)}\end{array}$$ (15)

and f_g and ${\mathbf{z}}_g^{(k)}$ are subvectors of f and z^(k) associated with group g. Note that (15) is a gradient descent with step size 1/L^(k). If we let ${\stackrel{\sim }{\gamma }}_1^{(k)}=2\alpha \gamma /L^{(k)}$, and ${\stackrel{\sim }{\gamma }}_2^{(k)}=2(1-\alpha )\gamma /L^{(k)}$, the solution to the problem can be obtained by hard thresholding [6]. That is, if ${\stackrel{\sim }{\mathbf{z}}}_g={\text{hard}}_{+}({\mathbf{z}}_g^{(k)},{\stackrel{\sim }{\gamma }}_1^{(k)})$,

where

$${[{\text{hard}}_{+}(\mathbf{z},\beta )]}_i=\{\begin{array}{ll}{z}_i\hfill & \text{if}{z}_i<\sqrt{\beta },\hfill \\ 0\hfill & \text{otherwise},\hfill \end{array}$$ (16)

the solution to the subproblem (14) is

$${\mathbf{f}}_g^{(k+1)}=\{\begin{array}{ll}{\stackrel{\sim }{\mathbf{z}}}_g\hfill & \text{if}{\Vert {\stackrel{\sim }{\mathbf{z}}}_g\Vert }_2^2>{\stackrel{\sim }{\gamma }}_1^{(k)}{\Vert {\stackrel{\sim }{\mathbf{z}}}_g\Vert }_0+{\stackrel{\sim }{\gamma }}_2^{(k)},\hfill \\ 0\hfill & \text{otherwise.}\hfill \end{array}$$ (17)

See the appendix for the proof. Note that the sparse-group LASSO [14] can be implemented in a similar fashion by replacing the above solution with a soft-thresholding version.

D. Implementation Issues

1) Normalization

The columns of A and the signal vector s are normalized to have unit ℓ₂-norm before solving (10). After obtaining the solution vector, it is rescaled back to the original range.

2) Tuning Parameter

If we replace r(f) = α γ||f||₁+(1 − α) γΣ_g∈𝒢||f_g||₂ in (10), the thresholding operation in (16) has to be replaced by soft-thresholding at level β/2. According to [56]–[58], in this case the parameter γ should be set according to the universal penalty level

$$\gamma =2\sigma \sqrt{2logN},$$ (18)

where σ is the noise standard deviation that can be measured from the background signal. To set the threshold in the case of hard-thresholding (see (16)) at the same level, we let

$$\gamma =2{\sigma }^{2}logN.$$ (19)

3) Initialization

To speed up computation, we warm start the optimization using the solution provided by a subspace pursuit algorithm [12], modified to use ℓ₁ sparse projection [59].

V. Experimental Results

We compared the proposed method (L200) with the following methods:

• L0 and L1: ℓ₀ and ℓ₁ minimization using a single RF each for WM, GM, and CSF [21]. The diffusion parameters of the WM, GM, and CSF RFs were determined respectively based on regions in the corpus callosum, cortex, and ventricles.

• L211: Sparse-group LASSO [14] using RFGs identical to the proposed method.

Similar to [42], and according to [43], we executed sparse-group LASSO multiple times for L1 and L211, each time reweighing the ℓ₂₁-norm and the ℓ₁-norm so that they eventually approximate their ℓ₀ counterparts. The tuning parameter γ was set according to Section IV-D2. We set α = 0.5 so that the effects for both group and individual sparsity are balanced. We will also report results of the above-mentioned methods with GM and CSF RFs removed, retaining only the WM RFs. In other words, single-tissue (ST) models are used. The ST variants are denoted respectively as L200-ST, L211-ST, L0-ST, and L1-ST.

The parameters of the RFGs were set to cover the typical values of the diffusivities of the WM, GM, and CSF voxels in the datasets described in the next sections: ${\lambda }_{\Vert }^{\text{WM}}=1\times {10}^{-3}{\text{mm}}^2/s,{\lambda }_{\perp }^{\text{WM}}=[0.2:0.05:0.3]\times {10}^{-3}{\text{mm}}^2/s$, λ^GM = [0.0 : 0.1 : 0.8] × 10⁻³ mm²/s, and λ^CSF = [1.3 : 0.1 : 1.5] × 10⁻³ mm²/s. The notation [a : s : b] denotes values from a to b, inclusive, with step s. Note that in practice, these ranges do not have to be exact but should however cover the range of parameter variation. We set, in (3), $S_{i,j}^{\text{WM}}(0)=S^{\text{WM}}(0),S_j^{\text{GM}}(0)=S^{\text{GM}}(0)$, and $S_j^{\text{CSF}}(0)=S^{\text{CSF}}(0)$, ∀i, j, according to the typical values of non-diffusion-weighted signals in the corpus callosum, cortex, and ventricles, respectively. The WM RFGs are distributed evenly on 321 points of a hemisphere, generated by subdivision of an icosahedron [60].

A. Synthetic Data

For quantitative evaluation, we generated a synthetic dataset using a mixture of four tensor models [26]. Two of which are anisotropic and represent two WM compartments that are at an angle of 45°, 60°, or 90° with each other. The other two are isotropic and represent the GM and CSF compartments. The generated diffusion-weighted signals therefore simulate the partial volume effects resulting from these compartments. The volume fractions and the diffusivities of the compartments were allowed to vary in ranges that mimic closely the real data discussed in the next section. The diffusion weightings and gradient directions were set according to the real data. Various levels of noise (SNR = 20, 30, 40, measured with respect to the signal value at b = 0 s/mm²) was added. The performance statistics (see next paragraph) for the data generated using a combination of WM/GM/CSF diffusivities and volume fractions were computed. The statistics over a set of combinations of diffusivities and volume fractions were then averaged and reported. This procedure was repeated 100 times.

We evaluated the accuracy of the estimated volume fractions and FODFs based on the ground truth data. The accuracy of the estimated volume fractions was evaluated by computing the root mean square (RMS) error between the estimated volume fractions (5) and the ground truth volume fractions. The accuracy of the estimated FODFs [22] was evaluated by comparing their peaks (local maxima) with respect to the directions of the WM tensor models used to generate the synthetic data. The orientational discrepancy (OD) measure defined in [61] was used as a metric for evaluating the accuracy of peak estimates. The peaks were estimated based on the method described in [4].

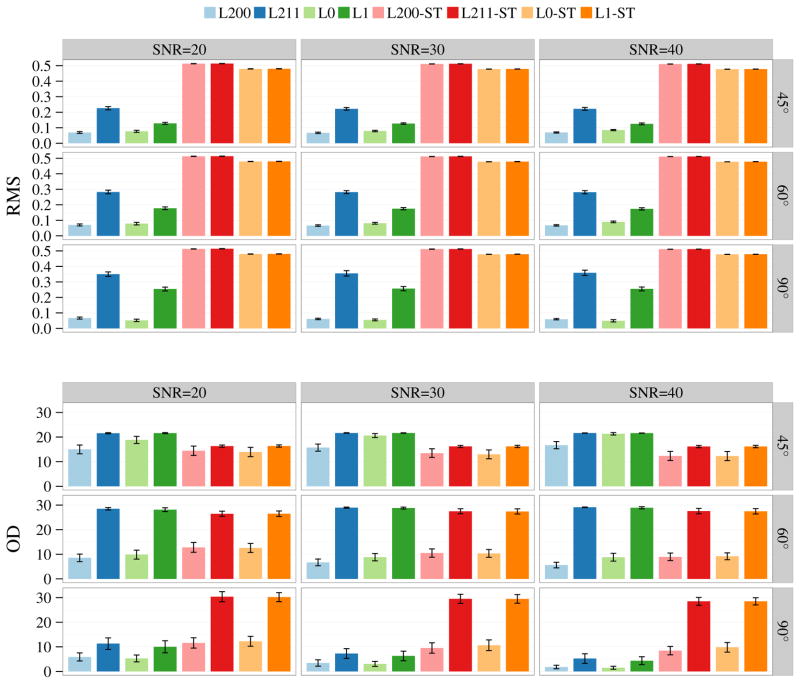
The results shown in Figure 2 indicate that, compared with the ℓ₁ methods, the ℓ₀ methods improve the estimation accuracy of both volume fractions and FODFs for different SNRs and crossing angles. For the ST methods, it is not surprising that the estimated volume fractions are incorrect. More important, without proper modeling of the different tissue compartments, errors are also introduced in the FODFs; see for examples the OD values for 90° crossing angle.

Fig. 2.

Estimation accuracy for volume fractions in terms of RMS error and FODFs in terms of OD. The bar plots show the mean performance statistics for SNR = 20, 30, 40 and crossing angle = 45°, 60°, 90°. The error bars indicate the standard deviations.

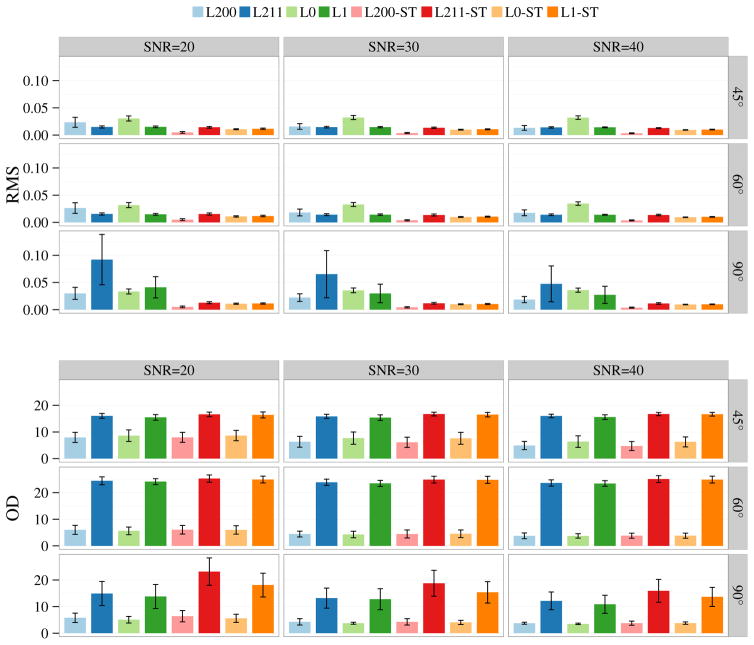
Figure 3 shows the results for synthetic data generated using only the WM compartments. In this case, the estimates of the ST methods are improved. The accuracy of the volume fraction estimates of the multi-tissue methods are slightly worse than the single-tissue methods, but the errors remain reasonably low. The FODF estimates of the ℓ₀ methods are consistently better than the ℓ₁ methods.

Fig. 3.

Estimation accuracy for volume fractions in terms of RMS error and FODFs in terms of OD. Only the WM compartments were used to generate the data. The bar plots show the mean performance statistics for SNR = 20, 30, 40 and crossing angle = 45°, 60°, 90°. The error bars indicate the standard deviations.

B. Real Data

For reproducibility, diffusion-weighted imaging data from the Human Connectome Project (HCP) [62] were used. The 1.25 × 1.25 × 1.25 mm³ data were acquired with diffusion weightings b = 1000, 2000, 3000 s/mm², each applied in 90 non-collinear directions. 18 baseline images with low diffusion weighting b = 5 s/mm² were also acquired. All images were acquired with reversed phase encoding for correction of EPI distortion.

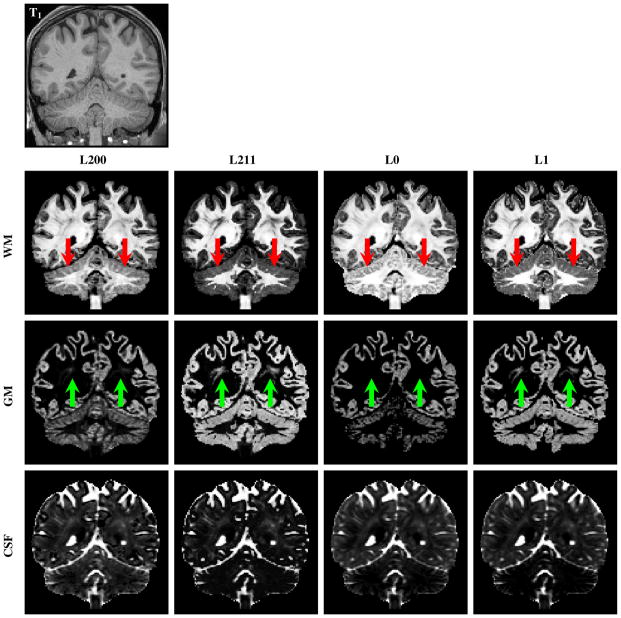
In this evaluation, we focus only on the multi-tissue methods. Figures 4 and 5 indicate that the WM, GM, and CSF volume fraction maps match quite well with the anatomy shown by the T₁-weighted image. Figure 4 indicates that L200 gives the best structural clarity in regions such as the cerebellum. L211 and L1 over-estimate the GM volume fractions in WM regions. Figure 5 confirms that L200 gives the best structural clarity and that in the brainstem L200 and L0 yield volume fraction estimates that are more spatially consistent. L200 also captures greater amount of cortical GM details. Figure 6 shows the WM FODF glyphs at two regions that contain a mixture of signals from WM and GM—the cortex and the deep GM. The left two columns of the figure show the WM FODF glyphs of the cortical region. In this region, the tissue type progressively transits from WM to GM and then CSF. The results indicate that for pure WM region, the results are relatively consistent across methods. Differences start to show up in regions with GM partial volume. The right two columns of the figure show results in deep GM with WM and GM partial voluming. At the cortex, the ℓ₀ methods are able to extract more directional information than the ℓ₁ methods, as indicated by the larger glyphs that penetrate deeper into the GM. In the deep GM, the larger glyphs yielded by the ℓ₀ methods again confirm that they are able to extract a greater amount of directional information. The ℓ₀ methods can therefore provide more information for tractography algorithms in studies that need to investigate neuronal connections associated with the cortex and the deep GM.

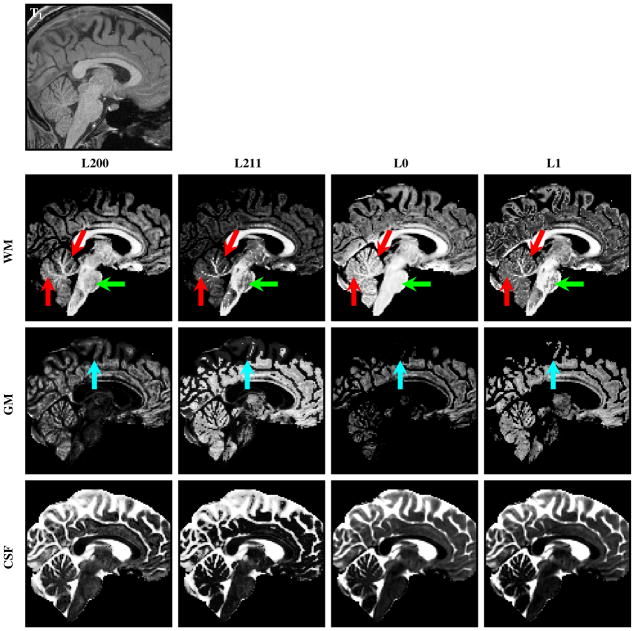
Fig. 4.

The WM, GM, and CSF volume fraction images obtained by L200, L211, L0, and L1. The T₁-weighted image at the top is shown for reference. L200 gives the best structural clarity in regions such as the cerebellum (red arrows). L211 and L1 over-estimate the GM volume fractions in WM regions (green arrows).

Fig. 5.

The WM, GM, and CSF volume fraction images obtained by L200, L211, L0, and L1. The T₁-weighted image at the top is shown for reference. L200 gives the best structural clarity in regions such as the cerebellum (red arrows). In the brainstem, L200 and L0 yield volume fraction estimates that are more spatially consistent (green arrows). L200 also captures greater amount of cortical GM details (cyan arrows).

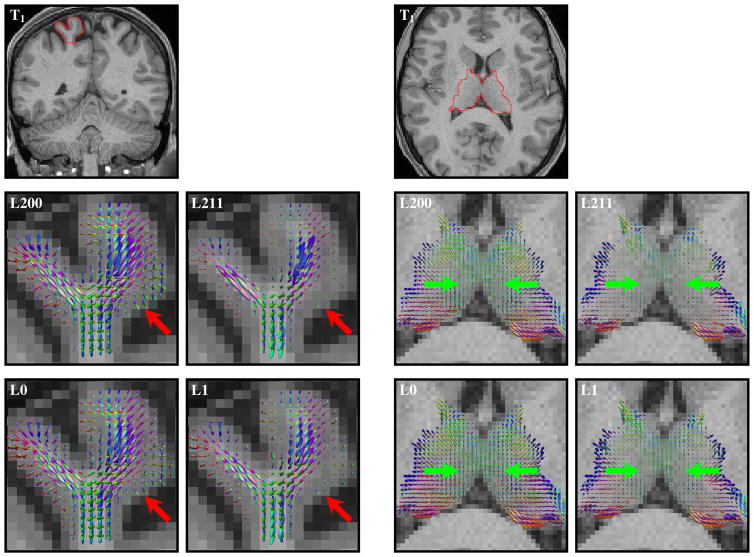
Fig. 6.

WM FODF glyphs, scaled according to the WM volume fractions, at (left) a cortical region and (right) a deep GM region. The red and green arrows mark regions where ℓ₀ methods yield a greater amount of WM directional information than the ℓ₁ methods.

C. Computation Speed

Our implementation of the ℓ₀ sparse-group solver is 8 times faster than the reweighted LASSO sparse-group solver implemented using a similar framework but by replacing hard thresholding with soft thresholding.

VI. DISCUSSION

Our method relies on a discrete dictionary consisting of RFs with parameters sampled discretely from the parameter space. When greater accuracy is needed, the parameter sampling density has to be increased. This increases the computational cost and when dictionary is large the computation can be intractable. This is especially the case when more sophisticated models, such as those used for microstructural estimation, need to be fitted to the data.

There are a number of remedies to this problem. First, we can use an iterative screening approach recently proposed in [59] to remove unrelated RFs during estimation. That is, during optimization of the ℓ₀ sparse-group problem, a subspace containing the solution can be estimated in each iteration and the minimization problem has to be solved only in this subspace, which is much smaller than the original space. This subspace is iteratively refined as better solution candidates are obtained. This approach can greatly reduce the computational load and at the same time promote robustness to local minima.

Alternatively, we can use a dictionary learning method to progressively refine the dictionary, as described in [63]. With such approach, the parameters of the RFs in the dictionary can be progressively refined in the continuous parameter space and hence obviates the need for including a large amount of RFs in the dictionary. Optimization is performed by alternating between solving the sparse problem and parameter adjustment.

Another approach is to use a Markov chain Monte Carlo (MCMC) based optimization technique, as reported in [64], [65]. This approach progressively narrows down the support of the solution with the goal of maximizing the posterior probability.

The estimation of the FODF can be further improved by imposing spatial regularity, similar to what was done in [66], [67]. The assumption is that the signals of neighboring voxels are highly correlated and, by encouraging spatially similar estimation outcomes, one can improve robustness to noise and yield greater estimation accuracy with a lesser number of samples [66], [67]. To account for larger changes at structural boundaries, regularization terms based on total variation (TV) [68] or wavelet [69] can be employed for edge preservation.

VII. CONCLUSION

We have shown that instead of restricting ourselves to one RF per compartment, it is possible to employ a group of RFs per compartment to cater to possible data variation across voxels. The use of ℓ₀ penalization is motivated by the following observations: (i) ℓ₁ penalization conflicts with the unit sum requirement of the volume fractions, as noted in [42]; (ii) ℓ₁ penalization is biased and attenuates coefficient magnitudes [52], resulting in the erosion of FODF peaks. Our results support that our ℓ₀ sparse-group estimation improves both volume fraction and FODF estimates.

Our method provides the flexibility of including different diffusion models in different groupings for robust microstructural estimation. Potential future work includes incorporating complex diffusion models [50] for estimation of subtle properties such as axonal diameter. We will also apply our method to the investigation of pathological conditions such as edema and also to applications such as tissue segmentation [70].

Biographies

Pew-Thian Yap is an Assistant Professor of Radiology and Biomedical Engineering at the University of North Carolina at Chapel Hill. He is also a faculty member of the Biomedical Research Imaging Center (BRIC). His research interest lies in diffusion MRI and its application to the characterization of brain white matter connectivity. He has made vital contributions to advancing innovative neurotechnologies for human brain mapping by developing novel algorithms for studying white matter pathways in the human brain. He has published more than 140 peer-reviewed papers in major international journals and conference proceedings. He is a senior member of IEEE.

Yong Zhang received his Ph.D. at Simon Fraser University in 2014. He then took up a postdoctoral research position at Stanford University. His major interests involve applying various optimization methods to solving problems arising in computer vision, machine learning, and medical image analysis. He has published more than 10 peer-reviewed papers in major international journals and conference proceedings.

Dinggang Shen is a Professor of Radiology, Biomedical Research Imaging Center (BRIC), Computer Science, and Biomedical Engineering at the University of North Carolina at Chapel Hill. He is currently directing the Center for Image Analysis and Informatics, the Image Display, Enhancement, and Analysis (IDEA) Lab in the Department of Radiology, and also the medical image analysis core in the BRIC. He was a tenure-track assistant professor at University of Pennsylvania and a faculty member at Johns Hopkins University. His research interests include medical image analysis, computer vision, and pattern recognition. He has published more than 700 papers in international journals and conference proceedings. He serves on the editorial boards of six international journals. He was on the Board of Directors of the Medical Image Computing and Computer Assisted Intervention (MICCAI) Society from 2012 to 2015.

APPENDIX

We provide here a detailed convergence analysis of the non-monotone iterative hard thresholding (NIHT) algorithm. We show in Theorem 1 that the number of iterations for the inner loop is bounded and in Theorem 2 that NIHT converges to a local minimizer of (10).

Theorem 1

For each k ≥ 0, the termination criterion of the inner loop (12) is satisfied after a finite number of iterations.

Proof

Since f^(k+1) is a minimizer of problem (14), we have

$$\nabla l{({\mathbf{f}}^{(k)})}^{\mathrm{T}}({\mathbf{f}}^{(k+1)}-{\mathbf{f}}^{(k)})+\frac{L^{(k)}}{2}{\Vert {\mathbf{f}}^{(k+1)}-{\mathbf{f}}^{(k)}\Vert }_2^2+r({\mathbf{f}}^{(k+1)})\le r({\mathbf{f}}^{(k)}).$$ (20)

Since ∇l is Lipschitz continuous with constant L_l, we have (from Proposition 12.60 in [71])

$$l({\mathbf{f}}^{(k+1)})\le l({\mathbf{f}}^{(k)})+\nabla l{({\mathbf{f}}^{(k)})}^{\mathrm{T}}({\mathbf{f}}^{(k+1)}-{\mathbf{f}}^{(k)})+\frac{L_l}{2}{\Vert {\mathbf{f}}^{(k+1)}-{\mathbf{f}}^{(k)}\Vert }_2^2.$$ (21)

Combining these two inequalities, we obtain

$$l({\mathbf{f}}^{(k+1)})+r({\mathbf{f}}^{(k+1)})\le l({\mathbf{f}}^{(k)})+r({\mathbf{f}}^{(k)})-\frac{L^{(k)}-L_l}{2}{\Vert {\mathbf{f}}^{(k+1)}-{\mathbf{f}}^{(k)}\Vert }_2^2$$ (22)

and hence

$$\varphi ({\mathbf{f}}^{(k+1)})\le \varphi ({\mathbf{f}}^{(k)})-\frac{L^{(k)}-L_l}{2}{\Vert {\mathbf{f}}^{(k+1)}-{\mathbf{f}}^{(k)}\Vert }_2^2.$$ (23)

It follows that

$$\varphi ({\mathbf{f}}^{(k+1)})\le \underset{{[k-M]}^{+}\le i\le k}{max}\varphi ({\mathbf{f}}^{(i)})-\frac{L^{(k)}-L_l}{2}{\Vert {\mathbf{f}}^{(k+1)}-{\mathbf{f}}^{(k)}\Vert }_2^2.$$ (24)

Hence, (12) holds whenever L^(k) ≥ L_l + η. This implies that L^(k) needs to be updated only a finite number of times and hence the conclusion holds.

Theorem 2

Let {f^(k)} be generated by NIHT when solving (10). Then these hold:

1. If the support set supp(f) = {i : f_i ≠ 0}, then supp(f^(k)) changes only finitely often.

2. f^(k) converges to local minimizer f^* of problem (10). Moreover, supp(f^(k)) → supp(f^*), r(f^(k)) → r(f^*), ϕ(f^(k)) → ϕ(f^*), and

$${\mathbf{f}}^{\ast }\in \underset{\mathbf{f}\succcurlyeq 0}{\text{Arg}min}\{l(\mathbf{f}):f_i\ne 0,i\in \mathit{supp}({\mathbf{f}}^{\ast })\}.$$ (25)

Proof

Let. L^(k) denote the final value of L^(k) at the kth iteration. From the proof of Theorem 1, we know that L̄^(k) ∈ [L_min, L̃), where L̃ = τ (L_l + η). Let {f^(k)} be the series of solutions to (14), then for all k ≥ 0,

$$\mid f_i^{(k+1)}\mid \ge \delta =\sqrt{2\alpha \gamma /\stackrel{\sim }{L}}>0,\text{if}{f}_i^{(k+1)}\ne 0.$$ (26)

Suppose supp(f^(k)) ≠ supp(f^(k+1)) for some k ≥ 1. Then some i exists such that ( $f_i^{(k)}\ne 0$ but $f_i^{(k+1)}=0$) or ( $f_i^{(k)}=0$ but $f_i^{(k+1)}\ne 0$), which together with (26) implies that $\mid f_i^{(k)}\mid \ge \delta$ or $\mid f_i^{(k+1)}\mid \ge \delta$ and we have

$${\Vert {\mathbf{f}}^{(k+1)}-{\mathbf{f}}^{(k)}\Vert }_2\ge \mid f_i^{(k+1)}-f_i^{(k)}\mid =max(\mid f_i^{(k+1)}\mid ,\mid f_i^{(k)}\mid )\ge \delta .$$ (27)

Since {ϕ(f^(k))} is bounded below and $\varphi ({\mathbf{f}}^{(k)})-\varphi ({\mathbf{f}}^{(k+1)})\ge \frac{\eta }{2}{\Vert {\mathbf{f}}^{(k+1)}-{\mathbf{f}}^{(k)}\Vert }_2^2$, {ϕ(f^(k))} converges to a finite value as k→∞ and

$$\underset{k\to \infty }{lim}{\Vert {\mathbf{f}}^{(k+1)}-{\mathbf{f}}^{(k)}\Vert }_2=0.$$ (28)

This contradicts (27) and implies that supp(f^(k)) does not change when k is sufficiently large.

(ii) It follows from (i) above that there exist some K ≥ 0 such that supp(f^(k)) stops changing and is fixed at a certain supp^* supp(f^(K)) for all k ≥ K. Then one can observe from (14) that ∀k > K,

$${\mathbf{f}}^{(k+1)}=\underset{\mathbf{f}\succcurlyeq 0}{argmin}\left\{l({\mathbf{f}}^{(k)})+\nabla l{({\mathbf{f}}^{(k)})}^T(\mathbf{f}-{\mathbf{f}}^{(k)})+\frac{{\overline{L}}^{(k)}}{2}{\Vert \mathbf{f}-{\mathbf{f}}^{(k)}\Vert }_2^2:f_i\ne 0,i\in {\text{supp}}^{\ast }\right\}.$$ (29)

Using $\varphi ({\mathbf{f}}^{(k)})-\varphi ({\mathbf{f}}^{(k+1)})\ge \frac{\eta }{2}{\Vert {\mathbf{f}}^{(k+1)}-{\mathbf{f}}^{(k)}\Vert }^2$ and the fact that r(f^(k)) = r(f^(k+1)) when k >K, we have

$$l({\mathbf{f}}^{(k)})-l({\mathbf{f}}^{(k+1)})\ge \frac{\eta }{2}{\Vert {\mathbf{f}}^{(k+1)}-{\mathbf{f}}^{(k)}\Vert }^2.$$ (30)

It follows from Theorem 1 in [72] that f^(k) → f^*, where

$${\mathbf{f}}^{\ast }\in \underset{\mathbf{f}\succcurlyeq 0}{\text{Arg}min}\left\{l(\mathbf{f}):f_i\ne 0,i\in {\text{supp}}^{\ast }\right\}.$$ (31)

Now consider a small perturbation vector Δf. By using (31) we have

$$l({\mathbf{f}}^{\ast })\le l({\stackrel{\sim }{\mathbf{f}}}^{\ast }),$$ (32)

where ${\stackrel{\sim }{f}}_i^{\ast }=0$ for i ∉ supp^* and ${\stackrel{\sim }{f}}_i^{\ast }=f_i^{\ast }+\mathrm{\Delta }{f}_i$ for i ∈ supp^*. In addition, based on the conclusion in part (i), we have l(f̃^*) ≤ l(f^*+Δf) (otherwise, supp(f^(k)) can change). Thus, f^* is a local minimizer of (10). In addition, we know from (26) that $f_i^{(k)}\ge \delta$ for k > K and i ∈ supp^*. This yields $f_i^{\ast }\ge \delta$ for i ∈ supp^* and $f_i^{\ast }=0$ for i ∉ supp^*. Hence, supp(f^(k)) = supp(f^*) = supp^* for all k > K, which clearly implies that r(f^(k)) = r(f^*) for every k > K. By continuity of l, we have l(f^(k)) → l(f^*). It then follows that

$$\varphi ({\mathbf{f}}^{(k)})=l({\mathbf{f}}^{(k)})+r({\mathbf{f}}^{(k)})\to l({\mathbf{f}}^{\ast })+r({\mathbf{f}}^{\ast })=\varphi ({\mathbf{f}}^{\ast }).$$ (33)

Finally, (25) holds due to (31) and the relation supp(f^*) = supp^*.

We show here the proof for the solution to subproblem (14).

Proof

The subproblem (14) can be written as

$${\mathbf{f}}_g^{(k+1)}\in \underset{{\mathbf{f}}_g\succcurlyeq 0}{\text{Arg}min}\left\{{\varphi }_g({\mathbf{f}}_g)={\Vert {\mathbf{f}}_g-{\mathbf{z}}_g^{(k)}\Vert }_2^2+{\stackrel{\sim }{\gamma }}_1^{(k)}{\Vert {\mathbf{f}}_g\Vert }_0+{\stackrel{\sim }{\gamma }}_2^{(k)}\mathcal{I}({\Vert {\mathbf{f}}_g\Vert }_2)\right\}.$$ (34)

Now let us consider the following two cases:

1. f_g = 0. Then the cost is ${\varphi }_g(0)={\Vert {\mathbf{z}}_g^{(k)}\Vert }_2^2$.

2. f_g ≠ 0, i.e., at least one entry of f_g is nonzero. Then we obviously have ${\stackrel{\sim }{\gamma }}_2^{(k)}\mathcal{I}({\Vert {\mathbf{f}}_g\Vert }_2)={\stackrel{\sim }{\gamma }}_2^{(k)}$. According to [6], we have

   $${\stackrel{\sim }{\mathbf{z}}}_g={\text{hard}}_{+}({\mathbf{z}}_g^{(k)},{\stackrel{\sim }{\gamma }}_1^{(k)})\in \underset{{\mathbf{f}}_g\succcurlyeq 0}{\text{Arg}min}\left\{{\varphi }_g({\mathbf{f}}_g)={\Vert {\mathbf{f}}_g-{\mathbf{z}}_g^{(k)}\Vert }_2^2+{\stackrel{\sim }{\gamma }}_1^{(k)}{\Vert {\mathbf{f}}_g\Vert }_0\right\},$$ (35)

   The cost for this solution is ${\Vert {\stackrel{\sim }{\mathbf{z}}}_g-{\mathbf{z}}_g^{(k)}\Vert }_2^2+{\stackrel{\sim }{\gamma }}_1^{(k)}{\Vert {\stackrel{\sim }{\mathbf{z}}}_g\Vert }_0+{\stackrel{\sim }{\gamma }}_2^{(k)}$.

Comparing the costs of the two cases above, the solution for problem (14) can be obtained as (17). That is, the solution is non-zero when

$${\Vert {\mathbf{z}}_g^{(k)}\Vert }_2^2>{\Vert {\stackrel{\sim }{\mathbf{z}}}_g-{\mathbf{z}}_g^{(k)}\Vert }_2^2+{\stackrel{\sim }{\gamma }}_1^{(k)}{\Vert \stackrel{\sim }{\mathbf{z}}\Vert }_0+{\stackrel{\sim }{\gamma }}_2^{(k)}$$ (36)

or equivalently

$${\Vert {\stackrel{\sim }{\mathbf{z}}}_g\Vert }_2^2>{\stackrel{\sim }{\gamma }}_1^{(k)}{\Vert {\stackrel{\sim }{\mathbf{z}}}_g\Vert }_0+{\stackrel{\sim }{\gamma }}_2^{(k)}.$$ (37)

In addition, from (9) we observe that if f = 0, $\varphi (0)={\Vert \mathbf{s}\Vert }_2^2$. Thus, the optimal solution is f^* = 0 when $\alpha \gamma +(1-\alpha )\gamma =\gamma \ge {\Vert \mathbf{s}\Vert }_2^2$.