Incorporation of Gradient Vector Flow Field in a Multimodal Graph-Theoretic Approach for Segmenting the Internal Limiting Membrane from Glaucomatous Optic Nerve Head-Centered SD-OCT Volumes

Abstract

The internal limiting membrane (ILM) separates the retina and optic nerve head (ONH) from the vitreous. In the optical coherence tomography volumes of glaucoma patients, while current approaches for the segmentation of the ILM in the peripapillary and macular regions are considered robust, current approaches commonly produce ILM segmentation errors at the ONH due to the presence of blood vessels and/or characteristic glaucomatous deep cupping. Because a precise segmentation of the ILM surface at the ONH is required for computing several newer structural measurements including Bruch's membrane opening-minimum rim width (BMO-MRW) and cup volume, in this study, we propose a multimodal multiresolution graph-based method to precisely segment the ILM surface within ONH-centered spectral-domain optical coherence tomography (SD-OCT) volumes. In particular, the gradient vector flow (GVF) field, which is computed from a multiresolution initial segmentation, is employed for calculating a set of non-overlapping GVF-based columns perpendicular to the initial segmentation. The GVF columns are utilized to resample the volume and also serve as the columns to the graph construction. The ILM surface in the resampled volume is fairly smooth and does not contain the steep slopes. This prior shape knowledge along with the blood vessel information, obtained from registered fundus photographs, are incorporated in a graph-theoretic approach in order to identify the location of the ILM surface. The proposed method is tested on the SD-OCT volumes of 44 subjects with various stages of glaucoma and significantly smaller segmentation errors were obtained than that of current approaches.

1. Introduction

The top surface of the retina and optic nerve head is called the internal limiting membrane (ILM) and is utilized for measuring several structural parameters such as Bruch's membrane opening-minimum rim width (BMO-MRW), total retinal thickness, and cup volume. The BMO-MRW, for instance, is measured as the minimum Euclidean distance between the BMO and the ILM surface, and has been shown to be superior to other conventional structural parameters for diagnosing open angle glaucoma [1]. Besides computing structural parameters from SD-OCT volumes, having a precise ILM surface segmentation is also necessary for extracting different features from SD-OCT volumes in approaches that utilize machine learning-techniques for segmenting different retinal structures such as retinal blood vessels, BMO points, optic disc, and optic cup [2, 3, 4, 5].

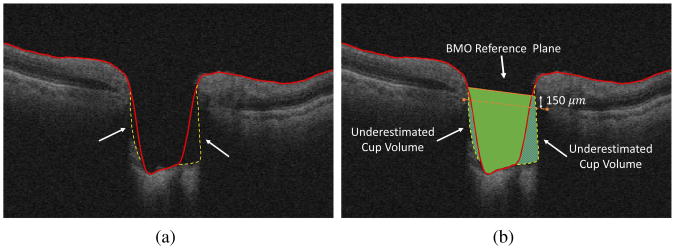
There has been a great deal of research in segmenting the intraretinal surfaces including machine-learning based approaches [6, 7, 8], model based approaches [9, 10], and graph-based approaches [2, 11, 12, 13, 14]. However, precisely segmenting the ILM surface in optic nerve head (ONH)-centered OCT, as needed for computing parameters such as the BMO-MRW of glaucoma patients, is more challenging than segmenting the ILM from a macular-centered OCT volume. The reason is that, due to the presence of deeper cups in glaucoma patients, the morphology of the ILM surface in the ONH region is very different from that of the macular region. Hence, many graph-based segmentation approaches [12, 2] initially designed to segment the intraretinal layers of the macula or the peripapillary region surrounding the ONH cannot catch the deep, steeply sloped cups which are characteristics of a glaucomatous ONH. This is due to the fact that the corresponding graph of the OCT volume is constructed such that each A-scan corresponds to a column in the graph and the ILM surface must intersect with each column only once. However, precise segmentation of the ILM surface inside the large and deep cups, present in glaucomatous OCT volumes, requires to intersect with each A-scan multiple times or to allow for sharp and large transitions (Fig. 1a). Shah et al. proposed a graph-theoretic segmentation method using the range expansion algorithm such that the sharp transitions were not penalized heavily [14]. More specifically, a truncated convex function was utilized for controlling the surface smoothness which allowed to preserve the discontinuity of the ILM surface while encouraging the smoothness. Even though this method improved the performance of its previous generations (i.e. [2, 12]) in segmenting the ILM surface within deeper cups, there is a trade-off between preserving discontinuity and obtaining a smooth ILM segmentation. Furthermore, the approach did not allow for multiple intersections with A-scans. Consequently, in the presence of steep slopes, many current ILM segmentation approaches would lead to underestimation of measurements such as cup volume (the volume between the ILM surface and the BMO reference plane) as shown in Fig. 1b and overestimation of measurements such as minimum-rim width.

Figure 1.

(a) ILM segmentation error due to the steep slopes as well as low signal strength. The red lines indicate segmentation results using the approach of Lee et al. [2] and the yellow dashed lines indicate the desired segmentation. (b) The resulting underestimated cup volume. The solid green region is the measure cup volume using automated ILM segmentation and the underestimated regions are shown with shaded patterns.

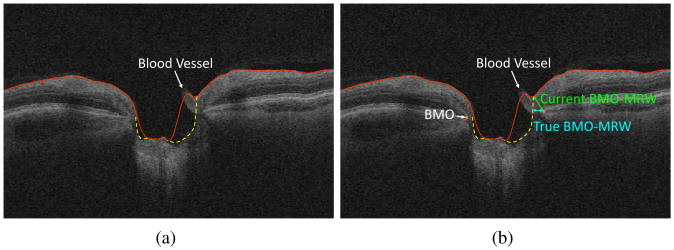
In addition to the presence of steep slopes, the presence of large retinal blood vessels, which is characteristic of the ONH region, causes the accurate segmentation of the ILM surface to be difficult. The large blood vessels located closer to the top surface of the retina are able to change the topology of the ILM surface. Since the current segmentation approaches include the retinal blood vessels as part of the ILM surface, as a result, the gaps surrounding the blood vessels may include as part of the ILM surface as well which leads to overestimating the BMO-MRW or underestimating the cup volume (Fig. 2b).

Figure 2.

(a) ILM segmentation error due to the presence of blood vessels. The red lines indicate segmentation results using the approach of Lee et al. [2] and the yellow dashed lines indicate the desired segmentation. (b) The resulting inaccuracy in computing the BMO-MRW structural parameter. Underestimating the cup volume because of including the blood vessel in the ILM segmentation is also observed.

In order to address the segmentation errors mentioned above, we incorporated the gradient vector flow (GVF) field [15] in a multimodal graph-theoretic approach to enable dealing with deep cupping as well as retinal blood vessels. In another application domain, Oguz et al. benefited from GVF field by proposing a graph-theoretic method for segmenting multiple objects and surfaces of the brain where in order to be able to segment the complex-topology surfaces of the brain, the columns in graph construction were obtained by computing the GVF field. Similarly, in order to allow for steep and deep cupping, we benefited from the direction of the GVF field to construct a new set of equally spaced columns along the normals of the ILM surface. Since the columns in the graph construction must be non-overlapping (otherwise it may lead to a self-intersecting surface segmentation) and GVF-based columns satisfy this condition, the OCT volume was resampled using the new GVF-based columns which also served as the columns in the graph construction.

In order to compute the GVF field, an initial ILM segmentation is required which was computed using a multiresolution method. Since the GVF-based columns are perpendicular at the initial ILM segmentation, the ILM surface in the resampled volume does not contain any steep slope or deep cupping, hence, we segment the ILM surface using a graph-theoretic approach by incorporating prior shape information [16]. The blood vessels are dealt with by correcting the initial segmentation as well as modifying the cost function that was used in the graph-based segmentation at the blood vessel locations. Since the blood vessels are more visible in fundus photographs (especially inside the ONH), they are segmented from registered fundus photographs. Based on the survey conducted by Kafieh et al. [17], the graph-theoretic approach proposed by Lee et al. is one of the best existing intraretinal approaches and will be used in this work for comparison purposes. A preliminary version of this work was presented in [18].

2. Methods

The flowchart of the proposed method is shown in Fig. 3. There are four major steps in the proposed method including: 1) preprocessing, 2) computing initialization and blood vessel correction, 3) computing GVF-based columns, and 4) identifying the ILM surface using a graph-theoretic method.

Figure 3.

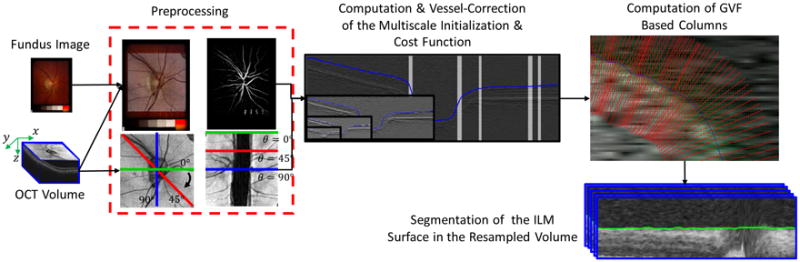
Flowchart of proposed algorithm.

2.1. Preprocessing

Due to better visibility of the retinal blood vessel inside ONH in fundus photographs than in SD-OCT projection images, the blood vessels are segmented from fundus photographs [19]. In order to be able to map the blood vessel mask to SD-OCT volumes, the fundus photographs need to be registered to their corresponding SD-OCT volumes. A 2D projection image is created from SD-OCT volume by segmenting the intraretinal layers and averaging the intensities within the retinal pigment epithelium (RPE)-complex subvolumes in the z-direction [2]. The fundus photographs are registered to the 2D projection images using an iterative closest point (ICP)-based approach [3].

Additionally, in order to obtain a more consistent shape of the ILM within the ONH region across all slices, the SD-OCT volume is transferred from the Cartesian domain (x×y×z) to the radial domain (r×θ×z) with angular resolution of one degree, which results in 180 radial B-scans. The computed retinal blood vessel mask is also transferred to the radial domain.

2.2. Initialization

During the initialization step, we obtain an initial ILM segmentation automatically through a multiresolution peak detection method (described in more detail in the subsequent paragraphs of this section). The result of peak detection in the highest resolution (i.e. original resolution) is considered as the initial ILM segmentation. The initial ILM segmentation is required only for computing the gradient vector flow (GVF) field. After computing the GVF field, the GVF-based columns are created by following the directions of gradient vectors (section 2.3) and the OCT volume is resampled using the GVF-based columns such that the ILM surface becomes a fairly smooth surface in the resampled volume (section 2.3). The final ILM segmentation is obtained from the resampled volume using the graph-theoretic algorithm. In particular, a sufficiently large band around the initial segmentation is resampled using the GVF-based columns which gives the graph-theoretic approach the opportunity to correct the errors that may exist in the initial segmentation. Therefore, it is not required that the initial segmentation to be very accurate.

More specifically, the multiresolution initial segmentation approach first involves downsampling the volume (by a factor of 2 each time) to three lower resolutions. The boundary of retina and vitreous body appears as a strong edge in OCT volumes and in order to capture this dark-to-bright transition, where the ILM surface generates a large response, the OCT volume at each level, I⁽ⁱ⁾, was convolved with an asymmetric 3D Gaussian derivative filter as follows:

$${ℰ}^{(i)}(r,\theta ,z)=\frac{\partial }{\partial z}\left[\frac{1}{2\pi {\sigma }_r^i{\sigma }_{\theta }^i{\sigma }_z^i}{e}^{-[{(\frac{r}{\sqrt{2}{\sigma }_r^i})}^2+{(\frac{\theta }{\sqrt{2}{\sigma }_{\theta }^i})}^2+{(\frac{z}{\sqrt{2}{\sigma }_z^i})}^2]}\right]\ast I^{(i)},i\in \{0,1,2,3\},$$ (1)

where ${\sigma }_r^i$, ${\sigma }_{\theta }^i$, and ${\sigma }_z^i$ are the standard deviation of the Gaussian filter in the i-th level in r, θ, and z, respectively. As it is depicted in Eq. 1, the derivative is performed only in z-direction, however, in order to incorporate the contextual information from surrounding regions and neighboring slices, the filter was designed in 3D. Since the first dominant high response from the top of each A-scan belongs to the ILM surface, the peak detector identifies the location of first peak at each A-scan within the lowest resolution, ℰ⁽³⁾(r, θ, z). While the entire A-scan was included for detecting the peaks in the lowest resolution, in the next resolution instead of the entire A-scan, the searching interval includes only a small portion of the A-scan relative to the location of the peak in the previous lower resolution. The response in the original (highest) resolution is considered as the ILM initial segmentation, 𝒮_i(r, θ). Besides allowing for the suppression of speckle noise, the other advantage of obtaining the initialization through a multiresolution process is that constraining the possible surface locations in the subsequent resolutions helps avoid finding edges produced by other surfaces.

Furthermore, before computing the GVF field, the ILM initial segmentation is corrected for the presence of retinal blood vessels. Since the presence of blood vessels may affect their surrounding regions as well, the radial blood vessel mask computed in section 2.1 was dilated by 2 pixels and mapped on the initial segmentation, 𝒮_i(r, θ), such that the surface segmentation at the A-scans containing blood vessel was ignored and a cubic interpolation was used to compute the new values at these locations. Therefore, the vessel-corrected initial segmentation, 𝒮_i–v(r, θ), is used in section 2.3 for computing the GVF field. Furthermore, the response of the 3D Gaussian filter in the original resolution, ℰ⁽⁰⁾(r, θ, z), is used as part of the cost function computation of the graph-theoretic approach in section 2.4.

2.3. Gradient Vector Flow Computation

In the cases of deep cupping, in order to be able to follow the steep slopes, we resample the volume using a set of equally spaced non-overlapping columns which are perpendicular to the initialization surface. Since the new columns are also used as the columns in the graph construction, these columns are computed by following the direction of the gradient vectors to assure non-overlapping columns. If an SD-OCT volume in the radial domain is represented by I(r, θ, z), GVF is the vector field V⃗(r, θ, z) = [u(r, θ, z), v(r, θ, z), w(r, θ, z)] that minimizes the energy function E [15]:

$$E=\int \int \int \mu {|\nabla \overrightarrow{V}|}^2+{|\nabla I|}^2{|\overrightarrow{V}-\nabla I|}^{2}drd\theta dz,$$ (2)

where μ is the regularization parameter. Due to the smooth shape of ONH, μ was not a sensitive parameter for computing GVF field and was set empirically to 0.02. The vector field in Eq. 2 can be found by solving the following Euler equations:

$$\begin{array}{c}\mu {\nabla }^{2}u-(u-I_r){|\nabla I|}^2=0,\\ \mu {\nabla }^{2}v-(v-I_{\theta }){|\nabla I|}^2=0,\\ \mu {\nabla }^{2}w-(w-I_z){|\nabla I|}^2=0,\end{array}$$ (3)

where ∇I = (I_r, I_θ, I_z) and I_r, I_θ, and I_z are the derivatives in r, θ, and z directions, respectively. Therefore, an initial vector field, ∇I, with high gradient at the initial segmentation is required in order to be able to compute the appropriate GVF field. The initial vector field, ∇I, is derived from the following 3D binary function I(r, θ, z):

$$I(r,\theta ,z)=\{\begin{array}{cc}0,& {\mathcal{S}}_{\mathrm{i}-\mathrm{v}}>z\\ 1,& {\mathcal{S}}_{\mathrm{i}-\mathrm{v}}<z\end{array}.$$ (4)

Constructing the GVF-based columns starts from a point on the initial surface 𝒮_i–v(r, θ), and continues by following the directions of the gradient flow on both sides of the initial surface. In order to find the next point on the column, the direction and the step size need to be determined. The direction of all normalized gradient vectors in the neighborhood of the current point (i.e. {V⃗_i/|V⃗_i| |i ∈ 𝒩_c} where 𝒩_c represents the neighborhood) are interpolated to find the resultant direction, V⃗_R. In order to avoid sampling artifacts, the step size, s, must be smaller than half of the distance between two voxels in the volume. Therefore, moving in the direction of V⃗_R with step size s indicates the next point on the column and assures obtaining non-overlapping columns. There is no limit on the length of the GVF-based column and the next points are obtained by continuously moving in the direction of the gradient flow at both sides of the initial surface. The length of the columns was set to 100 in this study (Fig. 4) (a value larger than the expected maximum error of the initial ILM segmentation) in order to assure the entire ILM surfaces appears in the resampled volume. This enables the graph-theoretic approach to correct any possible errors in the initialization.

Figure 4.

(a) A zoomed-in illustration of gradient vectors, for better illustration of the gradient vectors, a schematic image is provided where the larger and reddish vectors represents stronger gradient vectors. (b) The columns constructed by following the flow of the gradient vectors. The blue line shows the corrected initial segmentation.

2.4. Graph Construction and Cost Function Computation

The radial OCT volume is resampled using the GVF-based columns computed in section 2.3. When the OCT volume is transferred from the radial domain to the new space, the neighborhood relationships are retained (i.e., the 8-neighboring columns of a specific column in the radial volume and the resampled volume stay the same). Due to the fact that the GVF-based columns are along the normals at the initialization surface, and the columns are extended to the same length in both sides of the initial segmentation, it is expected that the ILM surface in the resampled volume appears as a smooth surface with minimal variation in the middle of the cube. We incorporate this prior shape information in the graph construction which helps with managing the presence of blood vessels.

Our graph-theoretic approach follows the methods proposed in [12, 16]. Consider a volumetric image in the resampled volume described as ℐ(i, j, k) with dimensions I×J×K, and the ILM surface 𝒮 can be defined as a function 𝒮(i, j) that maps each (i, j) pair to its corresponding k value. The surface 𝒮 has to intersect with one and only one voxel on each GVF-based column in the resampled domain, parallel to the k–axis and spans the entire i × j domain. In order to assure obtaining a smooth segmentation, the surface smoothness constraints in both i and j directions are enforced. The hard surface smoothness constraint represents the maximum allowed variation of 𝒮 between two adjacent columns in i–direction, Δ_i, and in j–direction, Δ_j. In other words, if ℐ(i, j, k₁) and ℐ(i + 1, j, k₂) are two adjacent voxels on the surface 𝒮 in the i–direction (k₁ = 𝒮(i, j) and k₂ = 𝒮(i + 1, j)), then |𝒮(i, j) − 𝒮(i + 1, j)| ≤ Δ_i. Similarly, for two adjacent voxels on the surface 𝒮 in the j–direction (ℐ(i, j, k₁) and ℐ(i, j + 1, k₂)) we have |𝒮(i, j) − 𝒮(i, j + 1)| ≤ Δ_j.

In order to incorporate the shape prior information, in addition to hard smoothness constraints, soft smoothness constraints, responsible for penalizing the deviation from the expected shape inside the allowed variations (hard smoothness constraints) is also enforced [16]. Therefore, the deviation of the surface 𝒮 from its expected shape is penalized via a convex function f(h). Specifically, for any pair of neighboring columns p = (i₁, j₁) and q = (i₂, j₂) on surface 𝒮(i, j), if the expected shape change of surface 𝒮 between (p, q) is m_{(i1, j1),(i2, j2)} the cost of the shape term can be written as:

$$C_{\mathit{\text{shape}}}=\sum _{\{(i_1,j_1),(i_2,j_2)\in {\mathcal{N}}_c\}}f(\mathcal{S}(i_1,j_1)-\mathcal{S}(i_2,j_2)-m_{(i_1,j_1),(i_2,j_2)}).$$ (5)

Here, 𝒩_c indicates the neighboring relationships. Due to the resampling of the volume along the normals of the initial segmentation, it is expected that the ILM surface appears as a smooth surface with minimal variation in the resampled volume, hence, m_{(i1, j1),(i2, j2)} = 0. Since the weights of those graph arcs that are responsible for enforcing the soft smoothness constraints are related to the second derivatives of the penalizing function f [16], and the arc weights need to be greater than or equal to zero, the penalizing function is required to be convex for which a quadratic function is employed in Eq. 5.

As part of the total cost function of the ILM surface, C_total, an edge-based cost function called the on-surface cost function is employed [12]. The on-surface cost function reflects the unlikelihood of a voxel being located on the ILM surface (i.e., it has lower values for the voxels located on the ILM surface). The strategy to deal with the blood vessels is relying more on the contextual information from adjacent slices, the shape prior knowledge, and the feasibility constraints than on the on-surface cost function values. Hence, the on-surface cost function at the blood vessel locations is modified to enable the graph-theoretic approach to cut through the blood vessels that change the shape of the ILM surface substantially. The blood vessel location is obtained by transferring the binary vessel map computed from the registered fundus photographs to the radial domain. The on-surface cost function can be expressed as:

$$\begin{array}{cc}{C}_{\mathit{\text{on}}-\mathit{\text{surface}}}=\sum _{\{(i,j,k)|k=\mathcal{S}(i,j)\}}w(i,j)\acute{ℰ}(i,j,k),& w(i,j)=\{\begin{array}{cc}1/3,& M_{\mathit{\text{vessel}}}(i,j)=1\\ 1,& M_{\mathit{\text{vessel}}}(i,j)=0\end{array}\end{array}$$ (6)

where w(i, j) controls the modification of the cost function at the blood vessel locations and M_vessel is the binary vessel map in the radial domain. The edge information, ℰ́(i, j, k), is computed by resampling the inverted response of the 3D Gaussian derivative filter (ℰ(r, θ, z) computed in section 2.2) using the GVF-based columns. The intensities of ℰ(r, θ, z) were normalized and inverted before resampling to reflect the unlikelihood of a voxel being located on the ILM surface. Therefore, the total cost of finding the ILM surface in the resampled volume can be written as follows:

$$C_{\mathit{\text{total}}}=C_{\mathit{\text{on}}-\mathit{\text{surface}}}+\alpha C_{\mathit{\text{shape}}}.$$ (7)

Here, the coefficient α was set to 0.85. As in [16], the optimal ILM surface (with respect to the cost function provided) can be found by computing the max–flow/min–cut in the arc-weighted graph. Once the ILM surface is obtained in the resampled volume, the segmentation is transferred back to the radial domain.

3. Experimental Methods

3.1. Data and Reference Standard

The dataset in this work includes optic nerve head (ONH)-centered SD-OCT volumes in one eye (per patient) of 44 open-angle glaucoma or glaucoma suspect patients acquired using a Cirrus HD-OCT device (Carl Zeiss Meditec, Inc., Dublin, CA) at the University of Iowa. The size of each scan was 200×200×1024 voxels (in the x-y-z direction, respectively) which corresponds to a voxel size of 30×30×2 μm, and the voxel depth was 8 bits in grayscale. Additionally, the color fundus photograph of the optic disc corresponding to each SD-OCT scan was taken as well. Twenty-four patients had stereo color fundus photographs taken using a stereo-base Nidek 3-Dx stereo retinal camera (3072×2048 pixels). The rest of the patients had color fundus photographs taken using a Topcon 50-DX camera (2392×2048 pixels). The pixel depth was 3 8-bit red, green and blue channels.

In order to obtain the reference standard, two radial slices were randomly chosen from each SD-OCT volume (i.e., for each volume the two radial B-scans were selected by computing two numbers between 1 and 180 using a random number generator that generates uniformly distributed numbers). One expert manually segmented the ILM surface from each slice twice (the time interval between manual delineations was more than one year) and the reference standard for each slice was computed by averaging the two manual delineations. Furthermore, a volumetric reference standard was obtained for one subject in the dataset such that the ILM surface was manually delineated on every five radial B-scans (every 5°).

3.2. Experiments

The performances of the following three methods were compared: 1) the initialization computed using a multiresolution process in section 2.2, 2) the ILM segmentation proposed by Lee et al. [2], and 3) the proposed graph-theoretic approach in this paper. The metrics used to evaluate the accuracy of the segmentation results consisted of the signed and unsigned border positioning errors calculated in the radial domain. The unsigned border positioning error was calculated by averaging the distances between all surface points (on two randomly selected slices) from the reference standard and the corresponding closest points from the segmentation result. The signed border positioning error was similarly calculated but the signs of the distances were retained. If the algorithm's surface point was above the surface point of the reference standard, the sign was considered positive.

Moreover, the signed and unsigned border position errors were also computed for the single subject with volumetric reference standard. The subject was selected such that it had the median unsigned border positioning error (computed from two randomly selected B-scans described in section 3.1) among the subjects in the dataset.

Additionally, in order to further assess the effectiveness of the proposed method in dealing with the presence of the retinal blood vessels and the steep slopes, the signed and unsigned border positioning errors were measured locally as well. Hence, for measuring the localized error at the blood vessel locations, only the A-scans intersecting with blood vessels were considered for measuring the border positioning errors. Similarly, the localized error of steep slope is computed at the A-scans containing steep slopes which were identified by computing the gradient of the ground truth. A paired t-test was utilized to compare the performances of three methods where p < 0.05 was considered significant.

Furthermore, the accuracy of the three segmentation approaches were evaluated using the cup volume. In order to compute the cup volume, the reference plane at each B-scan is defined as a straight line 150 μm (standard cup offset) above the straight line that connects the two BMO points [20] and the volume bounded between the ILM surface and the BMO reference plane was considered as the cup volume. The average of the cup volumes on the two B-scans with the manual segmentation was calculated for each subject.

4. Results

Two examples ILM surface segmentation are shown on a single radial B-scan in Fig. 5. The quantitative evaluations of border positioning errors for the entire ILM surface are provided in Table 1. The proposed method had significantly smaller signed and unsigned border positioning errors than the initialization and Lee et al. segmentations (p-value < 0.05). In addition, the proposed method improved the average unsigned border positioning error of Lee et al. method and the initialization by 51.95% and 71.06%, respectively.

Figure 5.

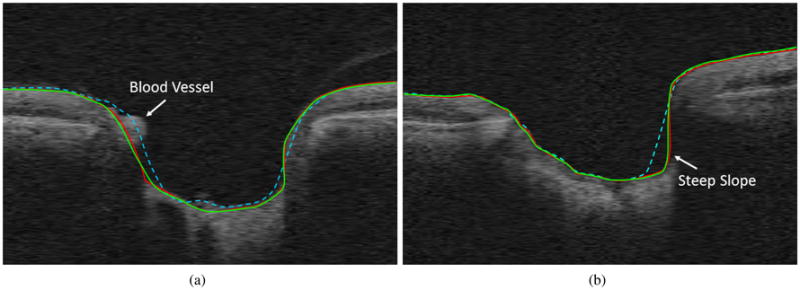
Example results on the ONH portion of two slices from two volumes (only the ONH portion shown for better visibility). Red is the reference standard, green is the proposed algorithm and dashed cyan is Lee et al. [2] results. (a) Shows the effect of the presence of blood vessels and (b) shows an example of deep cupping.

Table 1.

Average signed and unsigned border positioning error (Mean ± SD in μm).

Methods	Unsigned	Signed
Initialization	21.32 ± 11.02	7.95 ± 4.66
Lee et al. [2]	12.84 ± 7.45	5.84 ± 3.52
Proposed method	6.17 ± 3.19	-1.43 ± 1.54

The volumetric unsigned border positioning error for the initialization (19.45 μm), Lee et al. method (12.57 μm), and the proposed method (5.25 μm) was computed on the single subject. Moreover, the signed border positioning error for the initialization (7.04 μm), Lee et al. method (4.32), and the proposed method (-0.84 μm) was computed as well.

Furthermore, the localized border positioning errors at the blood vessel locations and steep slopes are reported in Table 2. The signed and unsigned border positioning errors (at the blood vessel locations) of the proposed method were significantly lower than the initialization and and Lee et al. segmentations (p-value < 0.05). The proposed method improved the average unsigned border positioning error (at the blood vessel locations) of Lee et al. method and the initialization by 64.65% and 78.88%, respectively.

Table 2.

Localized unsigned and signed border positioning error at blood vessel and steep slope locations (Mean ± SD in μm).

Error	Blood Vessel		Steep Slope
	Unsigned	Signed	Unsigned	Signed
Initialization	18.56±13.11	13.23±15.45	24.12±16.86	21.23±19.65
Lee et al. [2]	11.09± 9.68	10.34±12.24	14.35±10.11	13.44±13.11
Proposed method	3.92± 2.01	-1.23± 2.87	4.83± 3.25	3.56± 3.87

Similarly, the proposed method had significantly lower signed and unsigned border positioning errors (at the steep slopes) than the initialization and Lee et al. segmentations (p-value < 0.05). The proposed method improved the average unsigned border positioning error (at the steep slopes) of Lee et al. method and the initialization by 66.34% and 79.98%, respectively.

The cup volume measurements are reported in Table 3. Furthermore, the Bland-Altman graphs in the Fig. 6 clearly shows that initialization and the method in [2] underestimate the cup volume which resulted in the negative biases, whereas, the proposed method decreased the existing bias in the other approaches substantially. Additionally, the cup volume calculated using the manual segmentation and the automated approaches were compared using paired t-tests and the results showed that the cup volume computed using the initialization and the method in [2] are significantly different from that of the manual segmentation (p < 0.05). However, the cup volume computed using the proposed method was not significantly different from that of the manual segmentation (p > 0.05).

Table 3.

Cup volume measurements.

	Mean± SD in mm2	Pearson Correlation
Initialization	1.756±0.441	98.66
Lee et al. [2]	1.836±0.457	99.02
Proposed method	1.900±0.475	99.94
Reference standard	1.910±0.478	–

Figure 6.

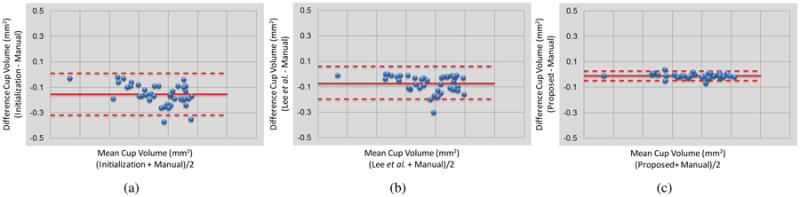
The Bland-Altman graphs of the cup volume measurement corresponding to (a) initialization, (b) Lee et al. [2], and (c) the proposed method in comparison with the manual tracing.

5. Discussion and Conclusion

In this work, we proposed a multimodal graph-theoretic approach for segmenting the internal limiting membrane surface from optic-nerve-head-centered SD-OCT volumes and the proposed method was tested on 44 glaucoma patients. The existing ILM segmentation approaches (e.g. the method in [2]) generate erroneous results inside the optic nerve head region due to the presence of retinal blood vessels and existing deep cupping and steep slopes in the ILM surface which are very typical in glaucomatous SD-OCT scans. These issues cause inaccurate measurements of ONH structural parameters such as Bruch's membrane opening-minimum rim width and cup volume. The proposed method deals with the issue of large blood vessels by modifying the cost function associated with the graph-theoretic approach and eliminates the steep slopes by resampling the OCT volumes using the gradient vector flow-based columns.

The large retinal blood vessels locating near the ILM surface, which are characteristics of ONH region, are able to change the morphology of the ILM surface. Current segmentation approaches include the blood vessels as part of the ILM surface which increase the possibility of inaccurate measurement of the structural parameters such as BMO-MRW. The correct way of dealing with retinal blood vessels is controversial [21], however, we currently argue that doing a better job of only including the non-vascular tissue can provide the most precise measurements of glaucoma parameters of interest such as BMO-MRW, where going around the vessels would lead to overestimating the MRW. Note that as BMO-MRW is measured as the shortest Euclidean distance from the BMO to the ILM surface, depending on the location of blood vessels, and the closest point on the ILM surface to BMO, the BMO-MRW parameter may or may not be affected by the presence of blood vessel. Hence, it is possible that BMO-MRW computed using the proposed ILM segmentation stays the same as that computed using the existing ILM segmentation approaches.

The proposed method also addresses the issue of segmenting ILM surface inside deep cups with steep slopes. In order to be able to accurately segment the ILM surface, the segmentation must be able to intersect with A-scans containing steep slopes more than once, therefore, those segmentation approaches [12, 2] that were initially designed to segment the intraretinal layers of the macula or the peripapillary region surrounding the ONH cannot catch the steep slopes inside the deeper cups. This issue results in inaccurate cup volume measurements [22], and the Bland-Altman graphs in Fig. 6 shows the negative bias of the method in [2] which is associated with the underestimating cup volumes. Resampling the volume using GVF-based columns which are along the normals of initial segmentation helps eliminate the steep slopes and transfers the ILM surface into a smooth surface with minimal variation. Therefore, the graph-theoretic approach incorporates this shape prior knowledge while segmenting the ILM surface in the resampled volume. The Bland-Altman graphs in Fig. 6 demonstrate that the proposed method successfully removed the negative bias existed in the initialization and Lee et al.'s method.

While Lang et al. [23] demonstrated that reformatting the OCT volume is beneficial for intraretinal layer segmentation in macular scans and GVF-based columns have been previously used in the graph-construction for segmenting complex-topology surfaces of the brain [24], we present a new framework for precise segmentation of the ILM surface by reformatting the OCT volumes using non-overlapping GVF-based columns. Additionally, use of multimodal information for the graph-construction and cost function design for use in the 3D graph-based approach that incorporates shape priors [16] is generally novel as well. In addition to allowing for a more precise ILM segmentation for ophthalmic applications, as in this work, it is expected that other application domains would also benefit from a multimodal graph-construction and cost-function design framework.

In summary, we proposed a method for accurate segmentation of the ILM surface within ONH region of OCT volumes where first, the blood vessels are segmented from the registered fundus photographs due to the higher visibility of ONH region in fundus photographs than OCT projection images. The vessel mask is transferred to the radial domain along with the OCT volumes and is utilized for two purposes 1) correcting the initial segmentation which is computed using a multiscale peak detection method and 2) modifying the cost function used in the graph-theoretic approach at the vessel locations. The radial volumes are resampled using non-overlapping GVF-based columns which are calculated by following the directions of gradient vector flow field of the initial segmentation. The optimal solution with respect to the edge-based and shape-based cost functions is obtained using a graph-theoretic approach in the resampled domain and finally the segmentation is transferred back to the original domain.

Highlights.

• We present a multimodal approach for segmenting the surface of the optic nerve head

• A graph-based approach is extended to utilize gradient-vector-flow-based columns

• Issues related to the presence of blood vessels and deep cups are overcome

• The approach will enable more accurate computation of glaucomatous measures