Local graph alignment and motif search in biological networks

Abstract

Interaction networks are of central importance in postgenomic molecular biology, with increasing amounts of data becoming available by high-throughput methods. Examples are gene regulatory networks or protein interaction maps. The main challenge in the analysis of these data is to read off biological functions from the topology of the network. Topological motifs, i.e., patterns occurring repeatedly at different positions in the network, have recently been identified as basic modules of molecular information processing. In this article, we discuss motifs derived from families of mutually similar but not necessarily identical patterns. We establish a statistical model for the occurrence of such motifs, from which we derive a scoring function for their statistical significance. Based on this scoring function, we develop a search algorithm for topological motifs called graph alignment, a procedure with some analogies to sequence alignment. The algorithm is applied to the gene regulation network of Escherichia coli.

The vast amount of sequence data collected over the past two decades is at the heart of quantitative molecular biology. Biological information is extracted from these data mainly by analyzing similarities between sequences. This approach is based on efficient sequence alignment algorithms and a statistical theory to assess the significance of the results (see ref. 1). Its ultimate goal is to infer functional relationships from correlations between sequences. Over the last few years, however, it has become clear that functions in many cases cannot be identified at the level of single genes. A given function may require the cooperative action of several genes, and conversely, a given gene may play a role in quite different functional contexts. The genome is thus a highly interactive system and the expression of a gene depends on the activity of other genes. The pathways of these interactions are encoded in so-called regulatory networks. Similarly complex networks govern signal transduction, that is, the influence of external signals on gene expression, or protein interactions, that is, the ability of two or more proteins to enter a bound state in a living cell.

A few exemplary cases of gene networks have been studied in much detail, such as the regulation of early development in the sea urchin Strongylocentrotus purpuratus (2) or in Drosophila (3). In some approximation, these structures can be understood as logical networks: the expression level of a gene is reduced to a binary variable (on or off) and is specified in terms of binary input data, i.e., the expression levels of its “upstream” genes.

On the other hand, a large amount of data on molecular interaction networks is now obtained by high-throughput experiments, for example protein interaction maps in yeast (4) or gene expression arrays (5). In these arrays, one probes the activity of an entire genome, rather than of just a few genes. However, the detailed logical connection of interaction pathways is typically lost. The information is reduced to a topological network, that is, a set of nodes (representing, e.g., genes or proteins) and links representing their pairwise interactions. These links can be directed as in the case of regulatory interactions or undirected as for protein–protein binding. The amount of topological data on molecular networks is expected to increase rapidly in the next few years, paralleling the earlier explosion of sequence data.

What can be learned from these data? Using the network topology alone, can we distinguish patterns of biological function from random background? The purpose of this article is to develop a “bioinformatics” approach to the search for local modules in networks. We discuss a heuristic search algorithm and its statistical grounding in a stochastic model of network evolution. This approach is designed to complement experiments in specific organisms by large-scale database searches.

Two seminal studies (6, 7) recently have shown that topological networks indeed contain statistically significant patterns indicative of biological functions. These motifs are patterns that occur more frequently in the observed network than expected in a suitable null ensemble. The motifs found so far have been identified because they occur identically at different positions in a network.

If network evolution is a stochastic process, however, functionally related motifs do not need to be topologically identical. Hence, the notion of a motif has to be generalized to a stochastic one as well. Variations arise because of uncertainties in the network data, or, more importantly, because some of the interactions can change without affecting the functionality of the motif. This “noise” is an important characteristic of biological systems, familiar from sequence analysis, where one searches for local sequence similarities blurred by mutations and insertions/deletions, rather than for identical subsequences. It leads us to the notion of a probabilistic motif in which each link occurs with a certain likelihood. Probabilistic motifs arise as consensus from finding a family of “sufficiently” similar subgraphs in a network. The search for mutually similar subgraphs and their probabilistic motifs is the central issue of this article.

The motifs of interest here are nonrandom in two ways: they have an enhanced number of internal links, associated, e.g., with feedback, and they appear in a significant number of subgraphs. Identifying these local deviations from randomness in networks requires a statistical theory of local graph structure, which we establish in this article. This is a complementary approach to the global statistics measured by the connectivity distribution (8) or connectivity correlations (9, 10) of a network.

Our approach leads to an algorithmic procedure termed local graph alignment, which is conceptually similar to sequence alignment. It is based on a scoring function measuring the statistical significance for families of mutually similar subgraphs. This scoring involves quantifying the significance of the individual subgraphs as well as their mutual similarity, and is thus considerably more complicated than for families of identical motifs. Our scoring function is derived from a stochastic model for network evolution. There is indeed evidence that network evolution can be described as a stochastic process. For example, the comparison of the regulatory networks for early development in several Drosophila species has revealed the continuous buildup and loss of gene interactions following an approximate molecular clock (11). Yet little is known about the specific pathways of network evolution. Our scoring function is compatible with divergent evolution of subgraphs but also with convergent evolution toward a common functional motif. These pathways can be illustrated by a comparison with sequence evolution. An example of convergent evolution is the formation of sequence motifs serving as binding sites of specific enzymes (12, 13). An example of divergent evolution is a set of sequences stemming from a common ancestor undergoing mutations independently. The probabilistic grounding of graph alignment allows us to infer optimal scoring parameters by a maximum-likelihood procedure (14).

As a computational problem, graph alignment is more challenging than sequence alignment. Sequences can be aligned in polynomial time by using dynamic programming algorithms. For graph alignment, a polynomial-time algorithm probably does not exist. Already simpler graph matching problems such as the subgraph isomorphism problem (deciding whether a graph contains a given subgraph) (15, 16) or finding the largest common subgraph of two graphs (17) are NP-complete and NP-hard, respectively. Thus, an important issue for graph alignment is the construction of efficient heuristic search algorithms. Here we solve this problem by mapping graph alignment onto a spin model familiar in statistical physics, which can be treated by simulated annealing.

This article is structured as follows. In the first part, we discuss the statistics of local subgraphs based on a probabilistic model. This is done in three steps: (i) an individual subgraph with an enhanced number of internal links, (ii) a subgraph in the presence of a template motif specifying the functional importance of each link, and (iii) correlated subgraphs, whose common pattern is to be inferred from the data instead of being given as a template. We then construct a scoring function designed to distinguish sets of statistically significant network motifs with an enhanced number of links from a background of other patterns. High-scoring motifs are found by an alignment algorithm, details of which are described in Supporting Text, which is published as supporting information on the PNAS web site. In the second part of the paper, we apply this method to the regulatory network of Escherichia coli and discuss the probabilistic motifs found. The statistics of these motifs is used to test the assumptions of our probabilistic model.

Graphs and Patterns

A topological network or graph is a set of nodes and links. Labeling the nodes by an index r = 1,..., N, the network is described by the adjacency matrix C, which has entries C_rr′ = 1 if there is a directed link from node r to node r′ and C_rr′ = 0 otherwise. Graphs with a generic adjacency matrix are called directed. The special case of a symmetric adjacency matrix can be used to describe undirected graphs. The in and out connectivities of a node, 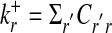and 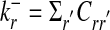, are defined as the number of in- and outgoing links, respectively. The total number of links is denoted by K = Σ_r,r′C_rr′. The networks considered here are sparse, i.e., their average connectivity K/N is of order 1.

A subgraph G is given by a subset of n vertices {r₁,..., r_n} and the resulting restriction of the adjacency matrix. More precisely, we define the matrix 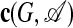with the entries c_ij = C_rirj (i, j = 1,..., n) specifying the internal links of the subgraph for a given order A of the nodes. This matrix c is called a pattern, which is contained in the subgraph. The definition of a pattern used here implies that two patterns are counted as separate if the matrices c and c′ are different. This assumes that nodes are distinguishable by their biochemical identity and their functional role even if they are at symmetric positions, i.e., if c and c′ differ only by the labeling of the nodes. An alternative definition would count two matrices c and c′ related by a relabeling as defining an identical pattern. Which definition is more appropriate depends on the particular biological application.

The most important characteristic of patterns for what follows is their number of internal links,

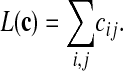[1]

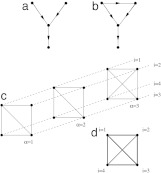
Fig. 1 shows two subgraphs that differ in the values of L.

Fig. 1.

Motifs and alignment in topological networks. (a) A randomly chosen connected subgraph is likely to be a tree; i.e., it has the number of internal links equal to its number of nodes minus 1. (b) Putatively functional subgraphs are distinguished by internal loops, i.e., by a higher number of internal links. (c) An alignment of three subgraphs with four nodes each. Each node carries an index α = 1, 2, 3 labeling its subgraph and an index i = 1, 2, 3, 4 given by the order of nodes within the subgraph. Nodes with the same index i are joined by dashed lines, defining a one-to-one mapping between any two subgraphs. Network links are shown as solid lines (with their arrows suppressed for clarity). (d) The consensus pattern of this alignment. Each link occurs with a likelihood c̄_ij indicated by the gray scale.

Graph Alignments and Motifs

A graph alignment is defined by a set of several subgraphs G^α (α = 1,..., p) and a specific order of the nodes 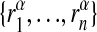in each subgraph; this joint order is again denoted by A. For simplicity, we assume here that the subgraphs are of the same size n, but it is not difficult to generalize our approach to include subgraphs of different size. For a given set of p mutually disjoint subgraphs, there are (n!)^p different alignments. An alignment associates each node in a subgraph with exactly one node in each of the other subgraphs. This association can be visualized by n “strings,” each connecting the p nodes with the same index i as shown in Fig. 1c.

A given alignment A specifies a pattern in each subgraph; we write 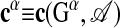. The consensus pattern of this alignment is given by the matrix

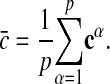[2]

This is a probabilistic pattern, the entry c̄_ij denoting the likelihood that a given link is present in the aligned subgraphs. For any two aligned subgraphs G^α and G^β, we can define the pairwise mismatch

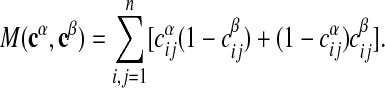[3]

The mismatch is 0 if and only if the matrices c^α and c^β are equal, and is positive otherwise. It can be considered as a Hamming distance for aligned subgraphs. The average mismatch over all pairs of aligned subgraphs, M̄ ≡ M(c̄, c̄), is termed the fuzziness of the consensus pattern c̄. Analogously, the average number of internal links is denoted by L̄ ≡ L(c̄).

We now define network motifs as statistically significant consensus patterns of graph alignments, which are distinguished by a high number of internal links and low fuzziness. Clearly, this definition is mathematically loose before we quantify the statistical significance. This quantification will be done in the next three sections.

Guided by the results of refs. 6 and 7, we take an enhanced number of internal links as a topological indicator of possible functional modules in networks. The additional links beyond a treelike topology can be associated with feedback or feed-forward loops in transcription networks, or clusters in protein interaction networks. For example, the triangle shown in Fig. 1b can be interpreted (6) as a low-frequency bandpass filter: the central node is activated if both top nodes are active. However, the right-hand node is activated by that on the left with a small delay, so the central node is activated provided the left node is active for a time longer than this delay. The nontreelike nature of this motif is crucial for its function. On the other hand, most randomly chosen connected subgraphs would be treelike. Clearly, an enhanced number of internal links is but the simplest topological indicator of putative functionality, and more detailed ways of identifying network motifs are likely to emerge in the future.

Statistics of Individual Subgraphs

To quantify the statistical significance of a given number of internal links, we first compute the relevant probability distribution in a suitable random graph ensemble, which is generated by an unbiased sum over all graphs with the same number of nodes and the same connectivities 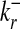, 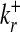(r = 1,..., N) as in the data set but randomly chosen links (10, 18). This null ensemble is appropriate for biological networks, whose connectivity distribution generally differs markedly from that of a random graph with uniformly distributed links. In the null ensemble, the probability of finding a directed link from node r_i to node r_j is in good approximation given by 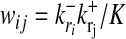(19). Hence, a given subset of nodes {r,..., r_n} forms a subgraph G with probability

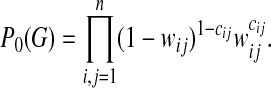[4]

This expression neglects double links, which can be included as in ref. 19. The probability P₀(G) depends on the pattern c(G) of the subgraph, as well as on its environment given by the connectivities 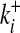, 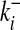(i = 1,..., n). In this ensemble, the expected number of internal links per node is small, 〈L〉₀/n ∼ n/N, where we denote the average over a given ensemble by 〈〉. Hence, most random subgraphs in a large and sparse graph are disconnected. Within the subset of connected subgraphs, most are treelike. (Later we will be interested in the subset of nontreelike subgraphs, and this will require a modification of the null ensemble.)

We now assume that subgraphs containing network motifs are generated by a different ensemble P_σ(G). The probability that a given pair of nodes carries a link is enhanced by a factor e^σ relative to the null ensemble 4, leading to

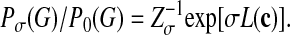[5]

Again the probability P_σ(G) that a given subset of nodes {r₁,..., r_n} forms a subgraph G depends on the matrix c(G). We have introduced the normalization factor Z_σ = Π_ijΣ_cij =0,1 exp[σL(c)]P₀(G), which ensures that P_σ(G) summed over all matrices c gives unity. The quantity σ, called the link reward, is multiplied by the total number L of internal links given by Eq. 1. The ensemble 5 is a statistically unbiased way to describe that functional motifs are distinguished by a large number of internal links. (Technically, it is the ensemble of maximal information entropy with a given average link number 〈L〉, which is determined by the value of σ.) This ensemble may be thought of as resulting from an evolutionary process favoring the formation of links due to selection pressure; such a process has recently been studied for regulatory networks (20). Here we focus on the detection of evolved motifs rather than on the reconstruction of evolutionary histories. Hence, we do not need to make assumptions on dynamical details of motif formation but only on its outcome, which is described by the ensemble P_σ(G). We have tested the form of this ensemble for the regulatory network of E. coli as discussed in Results and Discussion below. Moreover, the value of the link reward σ can be inferred from the data. One finds e^σ ∼ N/n, which results in a finite expected number 〈L〉/n of internal links per node within a motif.

Statistics in the Presence of a Template

The distribution 5 describes an ensemble with an enhanced number of links, which is appropriate for scoring individual subgraphs in the absence of further knowledge. Consider now an evolutionary process directed toward a given network motif represented by a template adjacency matrix t. An alignment A between the motif t and the subgraph G is specified by a given ordering of the nodes {r₁,..., r_n} in G. The outcome of this evolutionary process can be modeled by an ensemble 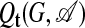with a bias against links that do not occur in the template,

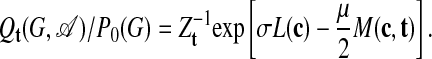[6]

This expression denotes the probability that a given subset of nodes {r₁,..., r_n} forms an aligned subgraph 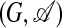, with the definition 3 of the pairwise mismatch of the subgraph G and the template t in a given alignment A. Again, Z_t is given by normalization. This is a hidden Markov model: the outcome of the stochastic process is an aligned subgraph 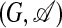, whereas only G is observed. The likelihood of observing G is then a sum over all alignments,

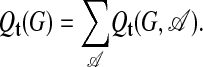[7]

This ensemble has two free parameters, the link reward σ and the mismatch penalty μ (with a factor 1/2 introduced for later convenience). It is conceptually similar to hidden Markov models for the alignment of sequences with gaps.

Statistics of Correlated Subgraphs

Now we turn to the case where a network motif is not given as a template but has to be inferred from a family of suitably aligned subgraphs. The underlying evolutionary process can be regarded as a biased link formation as in the previous section, with the consensus pattern c̄ as “template.” Assuming the link formation is independent for each subgraph, we obtain an ensemble given by

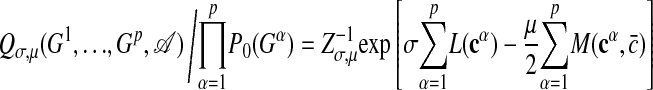[8]

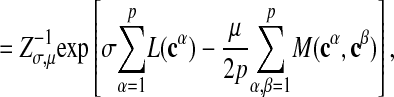where A specifies an alignment of all subgraphs and we have used the definition 2 of the consensus pattern. The normalization is given by

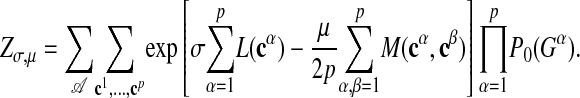[9]

The Scoring Function

We now construct a scoring function designed to select a set of (putatively) functional subgraphs, characterized by a consensus motif with a high number of internal links and low fuzziness, from the background of random subgraphs in a large network.

Based on the preceding discussion, we assume that the statistics of functional motifs is described by an ensemble 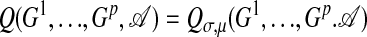, where the scoring parameters σ and μ remain to be determined from the data.

For the biological applications described above, where internal links are associated with feedback loops, it is clearly useful to restrict the motif search to the set of all connected subgraphs that contain internal loops, i.e., that are nontreelike. For connected subgraphs of size n, this set is given by the constraint L ≥ n on the internal link number. A large random graph typically contains a number of order one of such subgraphs, and these define the relevant null ensemble for motif search. We model these subgraphs by using the ensemble P_σ0 with an enhanced number of links defined in Eq. 5. The parameter σ₀ will be adjusted such that the average number of internal links in the null ensemble equals that found in the nontreelike subgraphs of a suitable randomized graph. Comparing with the ensemble P₀ of random subgraphs introduced earlier, it is clear that the constraint L ≥ n corresponds to a link reward σ₀ > 0.

Given these two ensembles, we define the log-likelihood score

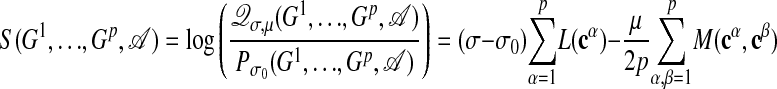[10]

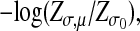which is positive if a set of subgraphs G¹,..., G^p and an alignment A between them is more likely to occur in the ensemble Q_σ,μ than in the null ensemble P_σ0. The term log(Z_σ,μ/Z_σ0) acts as a threshold assigning a negative score to alignments with too large fuzziness or a too small number of internal links.

As is clear from the form of the scoring function, graph alignment is a nontrivial optimization problem, the statistical weight of each subgraph G^α depending on the scoring parameters as well as on the other subgraphs included in the alignment. We address this problem in two steps. First we find the maximum-score alignment(s) for given score parameters, which is essentially an algorithmic search problem. Then we discuss the parameter dependence of high-scoring alignments and obtain the optimal values of σ and μ for a given data set from a maximum-likelihood procedure.

Maximum Score Alignments and Parametric Optimization

Finding the maximum score alignments involves a huge search space of possible alignments. The number of alignments is of order (np)^N for given p and the computational expense grows further when the optimization over p is performed. Here we use a heuristic algorithm, which can be described by a mapping to a discrete spin model. First we enumerate all nontreelike subgraphs of n nodes, which is feasible for modest values of n, and label them by the index α = 1,..., p_max. Next we evaluate the internal link numbers L^α = L(c^α) and the pairwise mismatches M^αβ, defined as the minimum of M(c^α, c^β) over all pairwise alignments of the subgraphs G^α and G^β. High-scoring multiple alignments are then found by a simulated annealing algorithm in the space (s¹,..., s^pmax), where each “spin” s^α takes the value 1 if G^α is included in the alignment and 0 otherwise. The resulting Hamiltonian H is

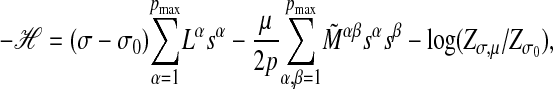[11]

where p = Σ_α s^α. The coupling between s^α and s^β is given by M̃ ^αβ, which is equal to the pairwise mismatch M^αβ if subgraphs α and β do not overlap, and a large positive constant if they do. (Two subgraphs overlap if they have more than one node in common. According to this definition, links in nonoverlapping subgraphs form independently as assumed in Eq. 8.) The threshold term log(Z_σ,μ/Z_σ0) is evaluated by saddle-point integration; details are given in Supporting Text. Simulated annealing using the Hamiltonian 11 will then yield high-scoring alignments of nonoverlapping subgraphs (22).

For fixed values of the scoring parameters, the algorithm is expected to produce well defined maximum-score alignments. This can be understood as follows. For a (hypothetical) alignment of subgraphs with equal number of internal links and equal pairwise mismatches, the score 10 scales linearly with p, the number of aligned subgraphs. This behavior is consistent with the interpretation of Eq. 10 as a log-likelihood score, because the aligned subgraphs occur independently. A high-scoring alignment in a realistic network may consist of a limited number of identical or very similar motifs. As we extend this alignment to include more subgraphs, subgraphs with increasing mutual mismatches are included. Hence, we expect the total mismatch to increase faster than linearly with p, leading to a maximum S*(σ, μ) of the total score at some intermediate value of p*(σ, μ).

The properties of the maximum-score alignments depend strongly on the parameters σ and μ. With increasing σ, the number of internal links L*(σ, μ) per subgraph is expected to increase. With increasing μ, both the number of graphs p*(σ, μ) and the fuzziness M̄ *(σ, μ) decrease. In this way, the maximum-score alignment varies between a set of independent subgraphs for μ = 0 and a set of identical subgraphs with identical motifs for μ → ∞.

A maximum-likelihood approach can be used to infer the optimal scoring parameters σ*, μ* for a given data set, which we obtain as the point of the global score maximum S* = max_σ,μS*(σ, μ).

Results and Discussion

In this section, we discuss the application of local graph alignment to motif search in the gene regulatory network of E. coli, taken from www.weizmann.ac.il/mcb/UriAlon/Network_motifs_in_coli/ColiNet-1.1/, containing 424 nodes and 577 directed links. Each labeled node in this network represents a gene. A directed link between two nodes signifies that the product of the gene represented by the first node acts as a transcription factor on the gene represented by the second. Throughout we consider motifs with a fixed number of nodes n = 5.

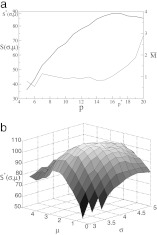
First we show that our algorithm indeed produces well defined alignments of maximal score (i.e., of maximal relative likelihood). For fixed parameters σ = 3.8 and μ = 4.0, this is illustrated by Fig. 2a, which shows the score S and the fuzziness M̄ for the highest-scoring alignment with a prescribed number p of subgraphs, plotted against p. As expected, the fuzziness increases with increasing p, and the total score reaches its global maximum S*(σ, μ) at an intermediate value p*(σ, μ). It is lower for p < p*(σ, μ) because the alignment contains fewer subgraphs and for p > p*(σ, μ) because the subgraphs have higher mutual mismatches. Fig. 2b shows the score S*(σ, μ) as a function of σ and μ. This function has a unique global maximum S*, which defines the maximum-likelihood point (σ* = 3.8, μ* = 2.25, p* = 24).

Fig. 2.

Maximum score alignment and parametric optimization. (a) Score optimization at fixed scoring parameters σ = 3.8 and μ = 4.0. The total score S (thick line) and the fuzziness M̄ (thin line) are shown for the highest-scoring alignment of p subgraphs, plotted as a function of p. (b) The score S*(σ, μ) plotted against the parameters μ and σ. The unique maximum S*defines the maximum-likelihood parameters σ* = 3.8 and μ* = 2.25.

The scoring parameter σ₀ of the null ensemble P_σ is determined as follows: the data set is randomized by generating a ⁰network with the same connectivities as in the data set but randomly chosen links (10, 18). Again, the nontreelike subgraphs are extracted and their average number of internal links is determined. The value of σ₀ is uniquely determined by the condition that the expected number of links in the null ensemble 5 equals the average number of internal links found in the nontreelike subgraphs. One obtains σ₀ = 2.45. As expected, σ₀ < σ*, which shows that the data set has an enhanced number of internal links relative to the randomized network.

At the maximum-likelihood scoring parameters, we can, moreover, verify the functional form of the ensembles used to construct the score function 10. To test the model 5 for individual subgraphs, we enumerate all subgraphs with n = 5 that have nontreelike patterns (i.e., a link number L ≥ 5). All ordered pairs of nodes i, j are then binned according to the probability w_ij of a directed link existing between them in the ensemble P₀(G). In Fig. 3a the fraction of these pairs i, j carrying a link is plotted against w (□). The expectation value of this fraction is given by Eq. 5 as e^σw/(1 – w + e^σw), shown as a solid line with a fit value σ* = 3.8.

Fig. 3.

Statistics of motif ensembles. (a) Testing the statistical model for single subgraphs (Eq. 5). Nontreelike subgraphs are enumerated and node pairs i, j are binned according to w_ij. The fraction of such pairs carrying a link is shown against w_ij. The solid line results from fitting the model with enhanced number of links (Eq. 5) to these data, giving σ = 3.8. (b) Testing the statistical model for alignments (Eq. 8). (Upper) The average value of 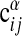over all α, i, j with a given expectation value of 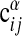according to Eq. 8 at σ = σ* = 3.8 and μ = μ* = 2.25 against the corresponding expectation value (□). For a perfect fit between model and data a straight line is expected (shown solid). (Lower) The same procedure is used averaging the two-point function 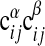over all α, β, i, j with a given expectation value .

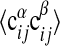Our model (Eq. 8) for generic alignments can be tested in a similar way. From this ensemble, the marginal probability that a given ordered pair of nodes specified by α, i, j is linked can be computed. We group all such pairs with the same expectation value 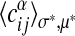according to Eq. 8 to build a histogram. For each group, the average of 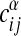over node pairs in the actual maximum-likelihood alignment is computed and plotted against the model prediction (see Fig. 3b). The same procedure is repeated for the two-point correlations 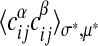between associated nodes in different subgraphs α and β as also shown in Fig. 3b. In both histograms, the data points cluster well around the straight line equating expectation values in the model 8 and averages in the actual alignment. The fluctuations seen reflect the limited size of the data set and the small number of fitting parameters in the model. For such data, more detailed models can hardly be tested because they would lead to overfitting.

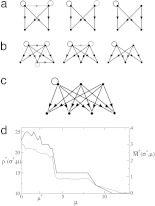
We now turn to the probabilistic consensus motifs found in the data for different number of nodes n = 4 and n = 5. Fig. 4a shows the n = 4 consensus motif c̄_ij at consecutive values of μ = μ* = 3.6, μ = 8, and μ = 15. The gray scale encodes the average number of links c̄_ij between a given pair of nodes. As expected, the fuzziness decreases with increasing values of the mismatch penalty μ and c̄_ij tends either to zero (no link present) or one (link present with certainty) as μ → ∞. The consensus motif is a layered structure, in this case with two input and two output nodes.

Fig. 4.

Probabilistic motifs in the E. coli transcription network. (a) Consensus motifs with n = 4 nodes at different values of μ. From left to right, μ = μ* = 3.6, μ = 8, and μ = 15. The gray scale of the links indicates the likelihood that a given link is present in the aligned subgraphs; the five gray values correspond to c̄ in the ranges 0.1–0.2, 0.2–0.4, 0.4–0.6, 0.6–0.8, and 0.8–0.9, and links with c̄ > 0.9 are shown black. The link reward is kept fixed at σ = σ* = 3.6 and σ₀ takes on the value 3.15. (b) Consensus motifs with n = 5 for different μ = μ* = 2.25, μ = 5, and μ = 12 (left to right) at σ = σ* = 3.8. (c) This pattern with n = 7 is found twice in the data set. From each such subgraph two nonoverlapping layered subgraphs with n = 4 and n = 5 can be generated. (d) The number p*(σ*, μ) of subgraphs in the maximum score alignment (thick line) and the fuzziness M̄ *(σ*, μ) (thin line) as a function of μ for n = 5.

A similar motif is found for n = 5. Fig. 4b shows the n = 5 consensus motif at consecutive values of μ = 2.25, 5, and 12. As in the case of n = 4, a layered structure is clearly discernible: the motif consistsof2 + 3 nodes forming an input and an output layer, with links largely going from the input to the output layer. The left node of the input layer has an average number of about 30 outgoing links. These connectivities are exceptional because the average out-connectivity of the network is 1.36.

Comparing the alignments of subgraphs of n = 4 nodes with those of n = 5 nodes in Fig. 4, one finds that many of the subgraphs found in the n = 4 alignments also are a part of the subgraphs found in the n = 5 alignments. This finding immediately leads to the question of how to identify larger patterns in the network from which the subgraphs at a given value of n are taken. Obviously any scoring scheme operating at a fixed number of nodes n will be blind to the combinatorial possibilities of selecting subgraphs from a larger pattern. The phenomenon is exemplified in Fig. 4c. From the 3-by-4 pattern two nonoverlapping layered subgraphs with n = 4 and n = 5 can be generated (nonoverlapping subgraphs have at most one node in common, see above). Larger patterns generate correspondingly more nonoverlapping subgraphs. In the supporting information, we discuss a simple scheme that allows one to identify larger patterns as in Fig. 4c from smaller subgraphs. The pattern of Fig. 4c is found twice in the data, contributing in total four nonoverlapping subgraphs to the alignments with n = 4 and n = 5. The statistics of these patterns at the level of identical patterns has recently been analyzed in ref. 23, their treatment using probabilistic patterns remains a future development.

Fig. 4d shows details of the alignments producing the consensus motifs at n = 5, namely, the number of subgraphs p*(σ = σ*, μ) and the fuzziness M̄ *(σ = σ*, μ) plotted as a function of μ. For μ > 12 the fuzziness reaches zero and the alignment contains 10 identical nonoverlapping motifs. This layered pattern has been found by the approach of ref. 6, which is based on counting identical motifs. However, the maximum-likelihood alignment occurs at μ* = 2.25 and contains a much larger number of p* = 24 nonoverlapping subgraphs, leading to the probabilistic consensus motif shown on the left in Fig. 4a. The same effect is found in the consensus motif of size n = 4. Furthermore, at arbitrary nonzero fuzziness the probability that a given pair of subgraphs have identical motifs decreases with subgraph size. As a result, counting identical motifs, rather than following a probabilistic approach as the one presented here, will miss a fraction of relevant subgraphs present in the data that increases with the size of the subgraph.

The probabilistic grounding of motif search is also indispensable for estimating the quantitative significance of the results obtained. Here we compare the maximum-likelihood alignment in the E. coli data set with suitable random graph ensembles. We do this in two steps, to disentangle the significance of the number of internal links and of the mutual similarity of patterns found in the data.

(i) To assess the significance of the number of internal links, we consider the ensemble of graphs with the same in- and out-connectivities as the data set but randomly chosen neighbors (18, 10) and compute the distribution of the score with scoring parameters σ = σ*, μ = 0. The null distribution of scores from the randomized graph has the average and standard deviation given by S* = 5.7 ± 2.1. The score S* = 73.1 found from the data is thus significantly higher, indicating an enhanced link number with respect to the random graph ensemble. (ii) The significance of the mutual similarity of the aligned patterns is assessed by comparing the data to mutually independent random subgraphs with the same average density of links. (This null ensemble is generated by randomizing the internal links of each subgraph independently.) We then compute the score with parameters σ = σ₀ = σ* and μ = μ* (thereby focusing only on the fuzziness of the data relative to that found in the ensemble of uncorrelated subgraphs). This null distribution of scores has average and standard deviation given by S* = 27.1 ± 6.3; the corresponding score S* = 50.1 found from the data is thus significantly higher. We note that the assessment of subgraph similarity is quite subtle. Subgraphs taken from a large but finite random graph may show a “spurious” mutual similarity with respect to independent random subgraphs because of a prevalence of internal loops. The statistical significance of the results can be formulated more precisely by using so-called p values, which involve the tail of the score distribution in the random graph ensemble. Fast and reliable p-value estimates are crucial for searching large databases, as is well known for sequence alignment (21). This approach can be carried over to the graph alignments discussed here.

The statistical framework presented is very flexible. For example, as large-scale data on the logic of gene regulation become available, the definition of the pairwise mismatch, Eq. 3, can be extended to reward aligning sets of nodes performing the same logical function. In this way, features of motifs going beyond their topology can be explored. Similarly, simple modifications of the mismatch score allow the analysis of undirected networks, networks whose links have a specific function (repressive or enhancing) or whose interaction strength is quantified by a real number.

The prospect of a sizable amount of new data on biological networks becoming available over the next few years through high-throughput methods opens exciting opportunities to identify the building blocks of molecular information processing in a wide range of organisms, and even build phylogenetic histories of regulation from transcription network data.