Broadband relaxation-optimized polarization transfer in magnetic resonance

Abstract

Many applications of magnetic resonance are limited by rapid loss of spin coherence caused by large transverse relaxation rates. In NMR of large proteins, increased relaxation losses lead to poor sensitivity of experiments and increased measurement time. In this article, we develop broadband relaxation-optimized pulse sequences that approach fundamental limits of coherence transfer efficiency in the presence of very general relaxation mechanisms that include cross-correlated relaxation. These broadband transfer schemes use techniques of chemical shift refocusing (specific trajectory adapted refocusing echoes) that are tailored to specific trajectories of coupled spin evolution. We present simulations and experimental data indicating significant enhancement in the sensitivity of multidimensional NMR experiments of large molecules through these methods.

The loss of signal because of spin relaxation (1) is a major problem in many practical applications of magnetic resonance. An important application is NMR spectroscopy of proteins (2, 3). Multidimensional coherence transfer experiments in protein NMR are characterized by large transverse relaxation rates. When these relaxation rates become comparable to the spin–spin couplings, the efficiency of coherence transfer is considerably reduced, leading to poor sensitivity and limiting the size of macromolecules that can be analyzed by NMR. Recent advances have made it possible to significantly extend the size limit of biological macromolecules amenable to study by liquidstate NMR (4–7). These techniques take advantage of the phenomenon of cross-correlation or interference between two different relaxation mechanisms (8–13). Until recently, it was not clear whether further improvements could be made and what the physical limit is for the coherence transfer efficiency between coupled spins in the presence of cross-correlated relaxation. In our recent work, using methods from optimal control theory, we derived fundamental limits on the efficiency of polarization transfer in the presence of general relaxation mechanisms (14–16). This work established that state-of-the-art experiments in NMR have the potential for significant improvement. We also provided relaxation-optimized pulse sequences that achieve the theoretical maximum transfer efficiency for a single spin pair. However, to apply these methods to practical NMR experiments, one needs to simultaneously address a family of coupled spin pairs with dispersion in their Larmor frequencies. In the limiting cases where cross-correlation rates are either much smaller or much larger than the spin–spin coupling, modifying the narrowband relaxation-optimized pulses into broadband transfer schemes is straightforward through conventional refocusing techniques. However, in experiments where both coupling and cross-correlation rates are comparable, the use of conventional refocusing methods for making relaxation-optimized sequences broadband significantly reduces the transfer efficiencies as these methods eliminate either the spin–spin couplings or the crosscorrelation effects. Finding broadband transfer schemes that can achieve the efficiency of relaxation-optimized sequences required the development of specific trajectory adapted refocusing (STAR) methods, where refocusing is performed in a moving coordinate system attached to an optimal trajectory. In this article, we present these methods and resulting broadband relaxation-optimized polarization transfer experiments.

Theory

We consider an isolated heteronuclear spin system consisting of two coupled spins 1/2, denoted I (e.g., ¹H) and S (e.g., ¹⁵N). We address the problem of selective population inversion of two energy levels (e.g., αβ and ββ) as shown in Fig. 1. This is a central step in high-resolution multidimensional NMR spectroscopy (17) and corresponds to the transfer of an initial density operator I_z, representing polarization on spin I, to the target state 2I_zS_z, representing two-spin order.

Fig. 1.

The broadband transfer of polarization I_z (A)to 2I_zS_z (B) corresponds to an offset-independent, but transition-selective, population inversion of the energy levels αβ and ββ.

For large molecules in the so-called spin diffusion limit (17), where longitudinal relaxation rates are negligible compared to transverse relaxation rates, both the initial term (I_z) and the final term (2I_zS_z) of the density operator are long-lived. However, the transfer between these two states requires the creation of coherences that in general are subject to transverse relaxation. The two principal transverse relaxation mechanisms are dipole–dipole (DD) relaxation and relaxation caused by chemical shift anisotropy (CSA) of spins I and S. The quantum mechanical equation of motion (Liouville–von Neumann equation) for the density operator ρ (17) is given by

[1]

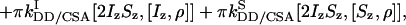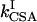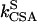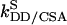where J is the heteronuclear coupling constant. The rates k_DD, , and represent autorelaxation rates caused by DD relaxation, CSA relaxation of spin I, and CSA relaxation of S, respectively. The rates and represent crosscorrelation rates of spin I and S caused by interference effects between DD and CSA relaxation. These relaxation rates depend on various physical parameters, such as the gyromagnetic ratios of the spins, internuclear distance, CSA tensors, strength of the magnetic field, and correlation time of the molecular tumbling (17). Let the initial density operator ρ(0) = A and ρ(t) denote the density operator at time t. The maximum efficiency of transfer between A and a target operator C is defined as the largest possible value of Trace{C^†ρ(t)} for any time t (18) (by convention operators A and C are normalized).

In our recent work (14) we showed that for a single spin pair IS, the maximum efficiency η of transfer between the operators I_z and 2I_zS_z depends only on the scalar coupling constant J and the net autocorrelated and cross-correlated relaxation rates of spin I, given by 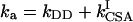and 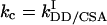, respectively. Here, the rates k_a and k_c are a factor of π smaller than in conventional definitions of the rates, e.g., k_a = 1/(πT₂), where T₂ is the transverse relaxation time in the absence of crosscorrelation effects (14, 15). The physical limit η of the transfer efficiency is given in ref. 14.

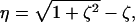[2]

where 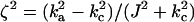. The optimal transfer scheme (cross-correlated relaxation-optimized pulse, CROP) has two constants of motion (see Fig. 2A). If l₁(t) and l₂(t) denote the 2D vectors (〈I_x〉(t), 〈I_y〉(t)) and (〈2I_xS_z〉(t), 〈2I_yS_z〉(t)), respectively, then throughout the optimal transfer process the ratio |l₂|/|l₁| of the magnitudes of the vectors l₂ and l₁ should be maintained constant at η. Furthermore, the angle γ between l₁ and l₂ is constant throughout. These two constants of motion depend on the transverse relaxation rates and the coupling constants and can be explicitly computed (14). These constants determine the amplitude and phase of the rf field at each point in time, and explicit expressions for the optimal pulse sequence can be derived. In Fig. 3 A and B, the optimal rf amplitude and phase of a CROP sequence is shown as a function of time for the case k_c/k_a = 0.75 and k_a = J.

Fig. 2.

The constants of motion of the CROP sequence. (A) Schematic representation of the magnetization vector r₁ = (〈I_x〉, 〈I_y〉, 〈I_z〉) and the antiphase vector r₂ = (〈2I_xS_z〉, 〈2I_yS_z〉, 〈2I_zS_z〉) in the common frame spanned by the standard Cartesian unit vectors i, j, and k. The vectors l₁ and l₂ are the projections of r₁ and r₂ into the transverse plane, and γ is the angle between l₁ and l₂. (B) For the optimal CROP trajectory (14), the unit vectors e₁ and e₂ in the direction of r₁ and r₂ are orthogonal and together with e₃ = e₁ × e₂ define a specific moving frame along the optimal trajectory. (C) The pulse element R₁(t) consists of a π rotation of spin I around e₁, which leaves r₁ invariant and inverts r₂ (dashed arrow) and a π rotation of spin S around an arbitrary axis in the transverse plane, which also leaves r₁ invariant and brings r₂ back to its initial position (solid arrow). Hence, R₁ neither changes the ratio |l₂|/|l₁| nor the angle γ, which are both constants of motion for the optimal CROP trajectory.

Fig. 3.

Ideal (A and B) and approximate (C and D) implementations of an on-resonance CROP sequence (14) for k_a = J and k_c/k_a = 0.75. (A) The ideal rf amplitude (where γ_I is the gyromagnetic ratio of spins I) in units of the coupling constant J. (C) A schematic representation of an approximate CROP sequence consisting of eight hard pulses of flip angle α = 21.5° is shown. (B and D) The phases ψ(t) of the ideal CROP sequence and its hard pulse approximation, respectively, are shown.

The transfer scheme as described assumes that the resonance frequencies of a single spin pair are known exactly. Therefore, the above methods cannot be directly used in spectroscopic applications with many spin pairs and a dispersion of Larmor frequencies. In this article, we develop methods to make the above principle of relaxation-optimized transfer applicable for a broad frequency range, making these methods suitable for spectroscopy of large proteins. A straightforward method of converting the smooth pulse shapes (as in Fig. 3A) into a broadband transfer scheme can be realized by the following steps.

1. Given the optimal amplitude A(t) and phase ϕ(t), of the on-resonance pulse (see Fig. 3 A and B), we can approximate the smooth pulse shape as a sequence of hard pulses with small flip angles α_k separated by evolution periods of duration Δ_k (compare Fig. 3C). These are DANTE (delays alternating with nutations for tailored excitation)-type sequences (19). The flip angle α_k at time t is just 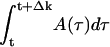, with the phase given by ϕ_k = ϕ(t) (compare Fig. 3D). The delays Δ_k could be chosen in many ways. For example, they all may be equal or can be chosen so that the flip angles α_k are equal (compare Fig. 3C).

2. Insertion of π pulses in the center of delays to refocus the transverse components of the spins makes the pulse sequence broadband (20) (see Fig. 4 A–C).

Fig. 4.

Different methods for refocusing chemical shifts. (A) Architecture of broadband relaxation-optimized pulse sequences, consisting of N periods of duration Δ_k (shown in B–D in more detail) and hard rf pulses with flip angles α_k and phases ϕ_k. (B) Chemical shift refocusing scheme preserving transfer through J coupling but eliminating transfer through the cross-correlated relaxation rate k_c. (C) Chemical shift refocusing scheme preserving transfer through k_c but eliminating transfer through J. (D) STAR echo scheme preserving transfer through both k_c and J. In B–D, filled bars represent 180° rotations around an axis in the x-y plane, and empty bars represent 180° rotations around tilted axes.

Note that this method of making relaxation-optimized pulses broadband is only applicable if one is using either just the couplings [as in insensitive nuclei enhanced by polarization transfer (INEPT) (21) or relaxation-optimized pulse element (15) transfer] or just the cross-correlation effects [as in standard cross relaxation-induced polarization transfer (CRIPT) (22, 23) or CROP transfer (14) for J = 0] as the transfer mechanism.

For example, the relaxation-optimized pulse elements (15), which only use transfer through couplings [special case of CROP (14) when k_c = 0] can be made broadband in a straightforward way as explained above. Simultaneous π rotations applied to spins I and S in the middle of the evolution periods refocus the chemical shift evolution while retaining the coupling terms (see Fig. 4B). Note, however, that such a pair of π rotations will eliminate any DD-CSA cross-correlation effects that might be present (7).

On the other hand, if J is very small or k_c is close to k_a (in which case transfer using cross-correlation effects is very efficient; compare Eq. 2), it is desirable to use relaxation-optimized sequences that use only cross-correlation effects for transfer [special case of CROP (14) when J = 0]. Such a relaxationoptimized transfer is characterized by a smooth rotation I_z → I_x and vice versa (–2I_xS_z → 2I_zS_z). Again, such a transfer can be made broadband as explained above. In this case the refocusing π pulses are applied only to spin I in the center of delays (see Fig. 4C). By such pulses, cross-correlation effects are retained but coupling evolution is eliminated (7).

Therefore, the advantage of the CROP sequence (which simultaneously uses both J couplings and cross-correlation effects) would be lost in using this conventional strategy to make these sequences broadband. The key observation for making CROP transfer broadband is that in the on-resonance CROP transfer scheme, the magnetization vector

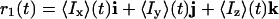always remains perpendicular (compare Fig. 2 A and B) to the net antiphase vector

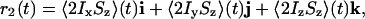where i, j, and k are the standard Cartesian unit vectors (for details see Supporting Text, which is published as supporting information on the PNAS web site). Let e₁, e₂ denote unit vectors in the direction of r₁ and r₂, and let e₃ = e₁ × e₂ denote the unit normal pointing out of the plane spanned by e₁ and e₂.

Let R₁(t) denote a π rotation of spin I around e₁(t) and a simultaneous π rotation of spin S around an arbitrary axis in the transverse plane. Observe that R₁(t) fixes the vectors r₁(t) and r₂(t) (see Fig. 2C). Similarly, let R₂(t) denote a π rotation around e₂(t) and a simultaneous π rotation of spin S around an arbitrary axis in the transverse plane. R₂(t) inverts r₁(t) and r₂(t), i.e., r₁(t) → –r₁(t) and r₂(t) → –r₂(t). We also define R₃(t) as a π rotation around e₃(t), which also results in r₁(t) → –r₁(t) and r₂(t) → –r₂(t). Note that these rotations are special because they change neither the ratio |l₂|/|l₁| nor the angle γ between the transverse components l₁ and l₂.

We now show how the rotations R₁ and R₃ can be used to produce a broadband CROP (BB-CROP) sequence. Given the implementation of the on-resonance CROP (Fig. 3 A and B) as a sequence of pulses and delays (Fig. 3 C and D), the chemical shift evolution during a delay Δ can be refocused by the sequence (compare Fig. 4D)

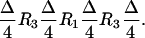The rotations R₁(t) and R₃(t) are defined by using the optimal trajectory and keep changing from one delay to another, as the vectors r₁(t) and r₂(t) evolve, which we refer to as STAR. To analyze how this refocusing works, at time instant t consider the coordinate system defined by e₁(t), e₂(t), and e₃(t) (compare Fig. 2B). The unit vector along z can be written as ae₁(t) + be₂(t) + ce₃(t). The chemical shift evolution generator I_z can be expressed as

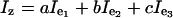[3]

and the evolution for time Δ/4 under the chemical shift takes the form exp{–i ω(aI_e1 + bI_e2 + cI_e3)Δ/4}. Assuming that the R₃ rotation is fast, so that there is negligible chemical shift evolution (and negligible relaxation) during the R₃, the sequence Δ/4 R₃ Δ/4 produces the net evolution

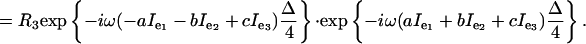For delays Δ « 1/ω, the effective evolution can be approximated by R₃ exp{–i ω cI_e3 Δ/2}. Now the rotation R₁ can be used to refocus the remaining chemical shift evolution caused by I_e by the complete STAR echo sequence Δ/4 R₃Δ/4 R₁ Δ/4 R₃ Δ/4. The effective evolution during the period Δ

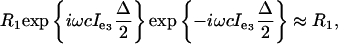i.e., chemical shift evolution, is eliminated. Note, we assume that the frame e₁, e₂, and e₃ does not evolve much during the four Δ/4 periods so that the two R₃ rotations are approximately the same. Under this STAR sequence, the general coupling evolution exp{–i2πJI_zS_z} and the general Liouvillian evolution (containing cross-correlation effects) is not completely preserved. In spite of this, the evolution of r₁(t) and r₂(t) for the CROP trajectory is unaltered, because, for this specific trajectory, the magnitude of the transverse components l₁(t) and l₂(t) and the angle γ between them is not changed by application of these tailored refocusing pulses. Because all evolution is confined to transverse operators, the efficiency of the BB-CROP is unaltered by application of STAR pulses.

Practical Considerations

Rotations of 180° around tilted axes as required by the operations (R₁ and R₃) of the STAR echo method can be realized in practice by off-resonance pulses. For example, a 180° rotation around an axis forming an angle θ with the x axis can be implemented by a pulse with an rf amplitude ν₁ and offset ν_off = ν₁ tan θ with a pulse duration τ_p = 1 (2ν_eff), where . At the start of the pulse, we assume both the on-resonance and off-resonance rotating frames are aligned. In the off-resonance rotating frame the axis of rotation does not move. After the pulse, the off-resonant rotating frame has acquired an angle of φ_off = 2πν_offτ relative to the on-resonance frame. For a pulse sequence specified in the on-resonance rotating frame, this can be taken into account by adding the phase φ_off acquired during a given off-resonant 180° pulse to the nominal phases of all following pulses on the same rf channel. Alternative implementations of rotations around tilted axes by composite on-resonance pulses would be longer and could result in larger relaxation losses during the pulses.

Under the assumption of ideal impulsive 180° rotations (with negligible pulse duration and negligible rf inhomogeneity), the STAR approach realizes a broadband transfer of polarization that achieves the optimal efficiency as given in ref. 14. However, spectrometers are limited in terms of their maximum rf amplitude and homogeneity of the rf field. Therefore, in practice, pulses have finite widths and hence evolution (especially relaxation) becomes important during the pulse duration. The effect becomes pronounced as the number of 180° pulses is increased to keep the refocusing periods Δ_k short for a better approximation to the on-resonance CROP. We observe that after a point the loss caused by relaxation during pulse periods overshadows the gain in efficiency one would expect by finer and finer approximations of the ideal CROP trajectory. Furthermore, dephasing caused by rf inhomogeneity increases as the number of 180° pulses is increased. Therefore, one is forced to find a compromise between loss caused by a large number of 180° pulses versus (i) loss of efficiency caused by a coarser discretization of the CROP, and (ii) reduced bandwidth of frequencies that can be refocused by an increased duration of the refocusing periods. When the number of refocusing periods becomes small, it is important to find a good way to discretize the CROP so as to maximize the efficiency of coherence transfer that can be achieved by a pulse sequence with a prescribed number of evolution periods. We have developed rigorous control theoretic methods based on the principle of dynamic programming (24) to efficiently achieve this discretization (see Supporting Text, Figs. 10 and 11, and Table 1, which are published as supporting information on the PNAS web site). This method helps us to compute optimal approximations of CROP sequences as a series of a small number of pulses and delays very efficiently.

Fig. 5A shows the buildup of antiphase vectors r₂ for 11 different offset frequencies of ±5 J (corresponding to ±1 kHz for J ≈ 200 Hz) during a CROP sequence consisting of 12 periods Δ_k without STAR echoes. As expected, the optimal transfer efficiency is achieved only for spins close to resonance. In contrast, a corresponding BB-CROP experiment with STAR produces efficient polarization transfer for a large range of offsets (compare Fig. 5B). Fig. 6 shows how the BB-CROP sequence “locks” the angle γ between l₂ and l₁ (compare Fig. 2) near its optimal value as given by on-resonance CROP.

Fig. 5.

The buildup of antiphase vectors r₂ is shown for 11 different offset frequencies ±5 J during a selective CROP (without STAR echoes) (A) and a corresponding BB-CROP (with STAR echoes) sequence consisting of 12 periods Δ_k (B). The sequence was optimized for k_a = J and k_c/k_a = 0.75 and a maximum rf amplitude of 67 J.

Fig. 6.

Evolution of the angle γ during the selective CROP (A) and BB-CROP (B) sequence as in Fig. 5 for the on-resonance case (red curves) and for an offset of –3 J. The optimal value of γ to be maintained during the CROP trajectory is indicated by dashed lines.

We have carried out extensive simulations to study the loss in efficiency caused by a large number of 180° pulses for realistic and hypothetical values of rf amplitudes. Fig. 7 illustrates how the offset dependence of the transfer efficiency η is effected by increasing the number of STAR echo periods both in the absence and presence of rf inhomogeneity. From Fig. 7 it is clear that one has to find an optimal number of evolution periods that gives the best performance for given system parameters like maximum rf amplitude, rf inhomogeneity, and the bandwidth one desires to cover.

Fig. 7.

Offset dependence of the transfer efficiency η for system parameters corresponding to the ¹³C-¹H moiety of ¹³C sodium formate in glycerol with k_a = J and k_c/k_a = 0.75 (14) (A and B) and corresponding to the ¹H-¹⁵N moiety of a protein with a rotational correlation time of 70 ns with k_a = 0.8 J and k_c/k_a = 0.73 (7) (C). A maximum rf amplitude on the I channel of 500 J (A), 67 J (B), and 550 J (C) is assumed, corresponding to a hypothetical 180° (¹³C) pulse duration of 5μs(A), realistic on-resonance 180° (¹³C) pulse duration of 39 μs(B), and a 180° (¹H) pulse duration of 10 μs(C) for a ¹H-¹⁵N coupling of J = 93 Hz. Blue, red, and green curves represent BB-CROP sequences with 4, 8, and 12 STAR echo periods Δ_k, respectively (for details, see Supporting Text). Solid and dashed curves correspond to simulations in the absence and presence of rf inhomogeneity, respectively, assuming a Gaussian rf distribution with a full width at a half-height of 10%. Dashed and dotted lines correspond to the maximum achievable efficiency of CROP and INEPT pulse sequences, respectively.

It is important to note that with high-resolution spectrometers, equipped with more rf power, relaxation losses during pulse periods can be made very small. This is illustrated in Fig. 7 A and B, assuming a maximum rf amplitude on the I channel of 500 and 67 J, respectively, corresponding to 180° pulse durations of 5 and 39 μs (typical value for ¹³C pulses) for the J ≈ 194 Hz coupling constant of the ¹³C-¹H spin pair of a model system (14, 15) (see below). For short 180^° pulses (large rf amplitude) during which relaxation losses become small, a larger number of refocusing pulses has the largest bandwidth and approaches the ideal CROP efficiency most closely (compare green curve in Fig. 7A).

The refocusing sequence Δ/4 R₃ Δ/4 R₁ Δ/4 R₃ Δ/4 as described in Theory is not the only STAR scheme for making CROP sequences broadband. For example, Δ/4 R₃ Δ/4 R₂ Δ/4 R₃ Δ/4 or Δ/4 R₂ Δ/4 R₁ Δ/4 R₂ Δ/4 also will perform STAR. However, as indicated above, in practice it may be necessary to have Δ as large as possible, in which case one should try to refocus the largest of the components a, b, and c of the chemical shift generator I_z (compare Eq. 3) more often during the refocusing cycle Δ. For example, the choice of the refocusing cycle presented here is optimal for the values of k_c/k_a = 0.75 and k_a/J = 1, in which case the vector e₃ is mostly in the x-y plane; hence, the magnitude of component c is smaller than the magnitude of a or b. Therefore, it is an advantage to refocus a and b more often by performing R₃ rotations (the R₃ rotation refocuses the a and b components), hence the choice of the sequence. Because there are no rotations of spin S during the application of R₃ pulses, the total number of pulses and the resulting effects caused by rf inhomogeneity are minimized. Dephasing losses caused by rf inhomogeneity of the 180° pulses (e.g., applied to spin S) can be further reduced by choosing appropriate phase cycling schemes (25–27).

In many cases it might also be possible to cut down relaxation losses by suitable implementation of the 180° pulses. For example, in the presence of a large contribution of the DD mechanism to the transverse relaxation rates, synchronization of I and S rotations can be used to create transverse bilinear operators such as I_xS_x, which commute with I_zS_z. This way some of the losses might be prevented when the antiphase magnetization is passed through the transverse plane during its inversion by R₃ pulses.

Experimental Results

To test the BB-CROP sequence, we chose an established model system (14, 15), consisting of a small molecule (¹³C-labeled sodium formate) dissolved in a highly viscous solvent [(²H₈) glycerol] to simulate the rotational correlation time of a large protein. Both the simplicity and sensitivity of the model system make it possible to quantitatively compare the transfer efficiency of pulse sequences and acquire detailed offset profiles in a reasonable time. Because of its large CSA and the resulting CSA-DD cross-correlation effects, we use the 13C spin of ¹³C-sodium formate to represent spin I and the attached ¹H spin to represent spin S with a heteronuclear scalar coupling constant of J = 193.6 Hz. At a temperature of 270.6 K and a magnetic field of 17.6 T, the experimentally determined auto-correlated and cross-correlated relaxation rates of spin I were k_a ≈ J and k_c ≈ 0.75 k_a [solvent: 99% (²H₈) glycerol]. For a given pulse sequence element, the achieved transfer efficiency of ¹³C polarization I_z to 2I_zS_z was measured by applying a hard proton pulse and recording the resulting proton antiphase signal (initial ¹H magnetization was dephased by applying a 90° proton pulse followed by a pulsed magnetic field gradient) (15).

Fig. 8 shows experimental on-resonance transfer efficiencies of the conventional INEPT (21) and CRIPT (22, 23) sequences as a function of the mixing time. Fig. 8 also shows the onresonance transfer efficiency of a CROP sequence consisting of four periods Δ_k (without refocusing), which shows a gain of 65% compared with the maximum INEPT efficiency. As expected (compare blue curve in Fig. 7B), the broadband version of this sequence (BB-CROP) with four STAR echoes has a reduced transfer efficiency because of relaxation losses during the additional 180° pulses, which in the current experiments had relatively long durations caused by the relatively small rf amplitude (13 kHz) of the I channel (¹³C) (the BB-CROP sequence is provided in Table 2, which is published as supporting information on the PNAS web site). Additional losses are caused by dephasing due to rf inhomogeneity, which is typically larger for the ¹³C channel (where most 180° pulses are given) compared to the ¹H channel. The experimentally determined on-resonance transfer efficiency of BB-CROP is 28% larger than the maximum INEPT transfer efficiency. In Fig. 9, the experimental offset profiles of the I_z → 2I_zS_z transfer efficiency of BB-CROP and INEPT are compared. A reasonable match is found between the experiments and the simulations shown in Fig. 7B. The parameters of the BB-CROP sequence used in the experiment are given in Table 2.

Fig. 8.

Experimental on-resonance transfer efficiencies of the CROP and corresponding BB-CROP sequence consisting of four periods Δ_k (without and with STAR echoes) and a total duration of 4.2 ms. For comparison, experimental on-resonance INEPT and CRIPT transfer efficiencies are shown as a function of the transfer time. In the experiments, spins I and S correspond to ¹³C and ¹H in ¹³C-sodium formate dissolved in (²H₈) glycerol.

Fig. 9.

Experimental offset dependence of the I_z → 2I_zS_z transfer efficiency for a BB-CROP sequence consisting of four periods with STAR echoes (red) and the INEPT sequence (black). The resulting two-spin order 2I_zS_z was converted to antiphase coherence 2I_zS_x by a hard 90° (S) pulse, and the resulting antiphase signals are shown for 11 offsets of spin I ±500 Hz.

Conclusion

In this article we introduce the principle of STAR, which was used to design BB-CROP sequence. We emphasize that with increasing rf amplitudes, the efficiency of the on-resonance CROP can be closely approached by the BB-CROP sequences. As future spectrometers are equipped with more rf power, we can significantly reduce the duration of 180° refocusing pulses, which are the major bottleneck in BB-CROP for achieving maximum efficiency. Increased rf amplitudes will also improve the offset performance of the BB-CROP sequence, by allowing for shorter refocusing periods, as discussed in detail above. Based on our simulations, we expect immediate gains in NMR spectroscopy of large proteins by use of the proposed BBCROPs. For example, in a heteronuclear single quantum correlation experiment involving ¹H and ¹⁵N, with maximum rf amplitudes corresponding to 12-μs ¹H 180° pulses and 40-μs ¹⁵N 180° pulses, we expect up to 70% enhancement in sensitivity over a reasonable bandwidth compared to state-of-the-art methods. With currently available rf amplitudes, in many applications it might even be advantageous to use broadband versions of relaxation-optimized pulse element or optimal CRIPT (special case of CROP where J = 0). In these cases, we use only 180° pulses in the center of each evolution period and hence reduce relaxation losses during the pulses (of course, as pointed out earlier, in these cases to do a broadband transfer we will necessarily eliminate either J couplings or crosscorrelation). In Figs. 8 and 9 we have not compared the sensitivity of BB-CROP with cross relaxation-enhanced polarization transfer (7) as the latter is not broadband for the transfer I_z → 2I_zS_z. Similar to the on-resonance CROP, we have found that the BB-CROP sequence is robust to variations in relaxation rates. Finally, the ability of the BB-CROP sequence to achieve the maximum possible transfer efficiency over a broad frequency range by use of high rf power provides a strong motivation for building high-resolution spectrometers with short 180° pulses.