Skip to main content
PMC home page
Scientific Reports logoLink to Scientific Reports
. 2017 Jan 9;7:40084. doi: 10.1038/srep40084

A new method for assessing the risk of infectious disease outbreak

Yilan Liao 1,2,a,*, Bing Xu 1,3,4,*, Jinfeng Wang 1,2, Xiaochi Liu 1,5
PMCID: PMC5220355  PMID: 28067258

Abstract

Over the past few years, emergent threats posed by infectious diseases and bioterrorism have become public health concerns that have increased the need for prompt disease outbreak warnings. In most of the existing disease surveillance systems, disease outbreak risk is assessed by the detection of disease outbreaks. However, this is a retrospective approach that impacts the timeliness of the warning. Some disease surveillance systems can predict the probabilities of infectious disease outbreaks in advance by determining the relationship between a disease outbreak and the risk factors. However, this process depends on the availability of risk factor data. In this article, we propose a Bayesian belief network (BBN) method to assess disease outbreak risks at different spatial scales based on cases or virus detection rates. Our experimental results show that this method is more accurate than traditional methods and can make uncertainty estimates, even when some data are unavailable.

With the appearance of a variety of new infectious diseases (e.g., H7N9, H5N1, and Ebola) and the renewed prevalence of existing diseases (e.g., dengue fever; hand, foot, and mouth disease; measles; and bacillary dysentery)1, the outbreak and prevalence of infectious diseases pose a serious threat to human health and life. Some infectious diseases have high mortality and fatality rates, and some of these diseases lack treatments or vaccines. Therefore, it is important to monitor disease occurrence and to give timely early warnings of potential disease outbreaks. These measures generate sufficient information on disease epidemics, reduce infectious disease outbreaks, and control the effects of the disease on specific populations2,3. To this end, the detection of abnormal disease distribution sand the accurate assessment of the risks of disease outbreaks are paramount.

Thus far, organizations at the national, state, and local level, including the American Centers for Disease Control and Prevention (CDC)4, Germany’s SurvNet@RKI5, and the University of Pittsburgh’s (USA) Real-time Outbreak and Disease Surveillance (RODS) Laboratory6, have developed various disease surveillance systems to improve public health. These surveillance systems generate a massive amount of data detailing the early detection of disease outbreaks. Generally, the early detection of disease outbreaks has two main goals: identifying the duration, locations, and shapes and sizes of potential disease clusters; and determining whether each of these potential clusters is due to a genuine outbreak or to chance fluctuations in case counts (see the Handbook of Bio-surveillance: “spatial and spatial-temporal”). To this end, many new techniques have been introduced over recent decades, including classical time-series models, as well as methods for detecting spatial and spatio-temporal clusters7,8. For example, since 2004, China’s CDC has established the China Infectious Disease Automated-alert and Response System(CIDARS)9. This system uses simple time-aggregation methods, such as control charts10, historical limits11, and SaTScan12 to estimate the risk of infectious disease outbreaks. However, these methods are all retrospective analyses that do not entail prospective studies. Multiple regression, What’s Strange About Recent Events (WSARE)8, and Hidden Markov models (HMMs)13 have been successfully used to predict further disease outbreaks based on multivariate records. An intelligent system proposed by Jiang et al.8 can even predict the size and duration of the outbreak and estimate how far the outbreak extends into a particular area. However, the accuracy of these methods is excessively dependent on the availability and quality of risk factor data. In practice, risk factor data are often not collected early enough during disease surveillance, especially in developing countries. Therefore, a Bayesian belief network (BBN)may be used to estimate the probability of infectious disease outbreaks in the case of missing risk factors.

BBNs use a combination of graph theory and probability theory based on Thomas Bayes’theorem14. They are graphical models of the probabilistic relationships among a set of variables that can express the mutual dependencies between variables in terms of quality and quantity15. As such, BBNs have been used in many fields because of their simplicity and soundness, especially in medical and industrial diagnosis16. For this paper, we used a BBN to assess the infectious disease outbreak risk on different spatial scales based on cases or virus detection rates. The experimental results showed that, once the relationship network among disease outbreak risks and factors has been determined, BBN accurately predicts the risk of further infectious disease out breaks even when some selected factors are missing. In addition, BBN is flexible for early warning of the infectious disease under different sceneries.

Methods

Bayesian Belief Network (BBN) Model

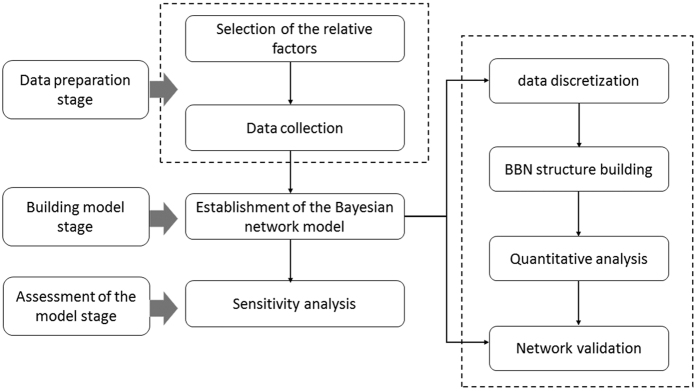
A BBN represents the hierarchical and mutual relationships among variables, in contrast to the regression model, which can only represent the outcome variables’ dependencies based on a predictor variable. With the BBN, the joint distribution of all variables is reflected in the directed acyclic graph(DAG), which is a finite directed graph with no directed cycles, where marginal and conditional probabilities can be computed for each node. Therefore, the BBN is more appropriate for prognostic and diagnostic applications. There are many BBN-based risk analysis applications, including analyses of risk in maritime transportation systems’ organizational factors17, workplace accidents caused by falls from heights18, safety risks for construction projects19, and assessing the risks of human neural tube defects20. A general framework for infectious disease risk assessment using BBN was designed as shown in Fig. 1. This method comprised three parts: (1) defining the risk level and selecting the risk factors; (2) building the BBN construct; and (3) calculating the joint probability of the target variable in the BBN and assessing the outbreak risk. In this study, the BBN software tool used was BN PowerSoft, which was developed by ChengJie21.

Figure 1. The framework for using Bayesian Belief Network to assess the disease outbreak risk.

Figure 1

Open in a new tab

Bayesian belief network construction

A BBN uses a directed acyclic graph (DAG)15 to represent the variables and probabilistic causal dependence among the variables. Each variable in the BBN is presented as a node with directed links. The information content of each variable is presented as one or multiple probability distributions. If a variable has no incoming arcs, it is not dependent on any other variables in the model universe, and, if it has parents, it has one probability distribution per combination of possible parent values. Therefore, a reliable relationship network is particularly important to predict disease outbreak risks using BBNs. During the process of Bayesian belief network construction, it is difficult to find a balance between the complexity of the network and the accuracy of probabilistic inference.

Generally, three methods — the expert knowledge method, the network structure learning algorithm, and an integration of these two methods — are applied to build the Bayesian belief network. The expert knowledge method involves building a network by setting nodes, ordering, giving constraints to the structure, and drawing the directed acyclic graph completely according to experts’ comments and the results of lecture review; however, the network structure learning algorithm is based on the independence test proposed by Cheng Jie21.

To introduce the approach, we first review the concept of d-separation, which plays an important role in our algorithm. For any three disjoint node sets X, Y, and Z in a belief network, X is said to be d-separated from Y by Z if there is no active undirected path bath between X and Y. A path between X and Y is active if the following conditions are met: (1) every node in the path has head-to-head arrows in Z or has a descendant in Z; and (2) every other node in the path is outside Z. To understand d-separation, we can use an analogy that is similar to the one suggested by (Waidyanatha 2010)3. We view a belief network as a network system of information channels. The information flow can pass through an active valve but not an inactive one. When all the valves (nodes) on one undirected path between two nodes are active, we say this path is open. If any valve in the path is inactive, we say the path is closed. When all paths between two nodes are closed given the status of a set of valves (nodes), we say the two nodes are d-separated by the set of nodes. The status of valves can be changed through the instantiation of a set of nodes. The amount of information flow between two nodes can be measured by using mutual information, when no nodes are instantiated, or conditional mutual information, when some other nodes are instantiated.

In information theory, the mutual information of two nodes Xi, Xj is defined as

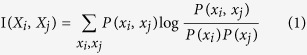graphic file with name srep40084-m1.jpg

and conditional mutual information is defined as

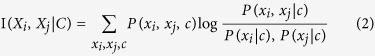graphic file with name srep40084-m2.jpg

where Xi, Xj are two nodes and C is a set of nodes. In our algorithm, we use conditional mutual information as CI tests to measure the average information between two nodes when the statuses of some valves are changed by the condition-set C. When I(Xi, Xj|C) is smaller than a certain threshold value ε, we say that Xi, Xj are d-separated by the condition-set C, and they are conditionally independent.

This algorithm also makes the following assumptions: (1) the database attributes have discrete values and there are no missing values in all the records; (2) the volume of data is large enough for reliable CI tests; and (3) the ordering of the attributes is available before the network construction, i.e., a node’s parents’ nodes should appear earlier in the order.

The algorithm has three phases: drafting, thickening, and thinning. In the first phase, the algorithm computes mutual information of each pair of nodes as a measure of closeness, and creates a draft based on this information. In the second phase, the algorithm adds arcs when the pairs of nodes cannot be d-separated. The result of phase II is an independence map (I-map) of the underlying dependency model. In the third phase, each arc of the I-map is examined using CI tests and will be removed if the two nodes of the arc can be d-separated. The result of Phase III is the minimal I-map.

Phase I: (Drafting)

1) Initialize the graph structure G < V, E> ; where V = nodes (i.e., all attribute fields of the data set), E = {} (E is a set of directed edges joining vertices. No loops of any length are allowed.), and S = Φ, R = Φ.

2) For each pair of nodes (vi, vj) where vi, vj ∈ V, compute mutual information I(vi, vj). For the pairs of nodes that have mutual information greater than a certain small value ε, sort them by their mutual information from large to small, and put them into an ordered set S.

3) Get the first two pairs of nodes in S and remove them from S. Add the corresponding arcs to E. (The direction of the arcs in this algorithm is determined by the previously available nodes ordering).

4) Get the first pair of nodes remaining in S and remove it from S. If there is no open path between the two nodes (these two nodes are d-separated given the empty set), add the corresponding arc to E. Otherwise, add the pair of nodes to the end of an ordered set R.

5) Repeat step 4 until S is empty.

Phase II: (Thickening)

6) Get the first pair of nodes in R and remove it from R.

7) Find a block set that blocks each open path between these two nodes by a set of minimum number of nodes. Conduct a CI test. If these two nodes are still dependent on each other given the block set, connect them by an arc.

8) Go to step 6 until R is empty.

Phase III: (Thinning)

9) For each edge in E, if an open path separate from the current edge remains, it will be brought from E. Then, the independence of the corresponding block set is tested. If the edge and corresponding block set are still correlated, the edge returns to E; otherwise, it is deleted.

Friedman proved theoretically that the method based on independence testing more closely resembles the semantics of the Bayesian networking principle, and it achieves effective results in practice22. In addition, for the integration method between the above methods, after constructing the network by the above automatic learning procedure, it is modified according to the experts’ comments and the results of the lecture review.

Quantitative analysis

After constructing a Bayesian belief network, a probabilistic inference is taken to elucidate the dependence relationships between variable nodes in the network. In our study, probabilistic inference was achieved by calculating the joint conditional probability distributions among variables based on their cause and consequence relationships. For each BBN node, a conditional probability formula or table, which represents the probabilities of each value of the node given the conditions of its parents, is supplied. In addition, the distributions of the parent nodes can be calculated given the values of their children. After the conditional probability table is obtained, the joint probability distributions can be decomposed into local probability distributions.

The joint probability distribution formula in BBN can be expressed as

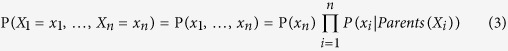graphic file with name srep40084-m3.jpg

where P(x1, …, xn) refers to the probability of a specificcombination of values x1, …, xn from the set of variables (X1, …, Xn), where Parent (Xi) refers to the set of 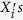Inline graphic immediateparent nodes. Thus, P(xi|Parents(Xi)) reflects the conditionalprobability, which is related to the node Xi based on its parent nodes.

According to the conditional probability table, the level of outbreak risk with the highest probability was considered the most probable potential risk. In contrast to other outbreak risk analysis methods, BBN provides an index of reliability (i.e., the joint probability distributions of the most probable potential risk).

Rough Set Method

The rough set method, proposed by Pawlak in 198223, offers mathematical tools to discover hidden patterns in data; therefore, its application in forewarning models needs to be investigated. Objects, which may be indiscernible due to the limited available information, can be expressed by the lower and upper approximations defined based on two extreme cases (full inclusion or nonempty overlay), regarding the relationships between an equivalence class and a target set. The main goal of the rough set-based analysis is to synthesize an approximation of concepts from the acquired data. Because of the novel and unique theory posed by rough set, it has become an important form of intelligence information processing technology that has been widely used in the fields of learning and knowledge discovery, data mining, and decision support and analysis. Rough set theory has also been used successfully in diagnosis and outcome prediction, which is discussed in a large number of articles. Su et al.24 (2006) used rough set theory to select the relevant features from data to predict diabetes. Wang et al.25 (2006) applied rough set theory to predict the malignancy degree of brain gliomas and achieved satisfactory results. Bai et al.40 (2010) utilized rough set to explore spatial decision rules in neural-tube birth defects and predict where high rates of the disease would occur.

Rough set theory is data-driven, and the advantage of this approach is that it does not require the user to make any a priori assumptions about the data. When using this method for epidemiological warnings, the whole analysis process can be divided into four steps: (1) data discretization, which, in this case, in order to ensure the comparability of different models, is the same as the data preparation which has been used in the Bayesian Network model; (2) find minimal reducts of conditional attributes, remove redundant attributes, and reduce system complexity; (3) generate rules according to the reducts, which can provide a rule base for inference and prediction; and (4) apply the rules to predict the epidemic outbreak risk level.

Linear Regression Model

As a comparison, a traditional linear regression model was used to estimate the HFMD outbreak risks. Regression analysis is a strong scientific method, which is an important branch of modern applied statistics. It has been widely used in many scientific fields. It can not only extract the information hidden in massive raw data groups and grasp the main characteristics of the population data to obtain the mathematical expression of the relationship between variables, but it can also use one or more variables to predict or forecast another dependent variable value. Regression forecasting method is the use of regression analysis method, through the statistical processing and analysis of a large number of observation data, to find out the relationship between the number of predictive objects and influencing factors. The theory of multiple linear regression requires data that generally follows a multivariate normal distribution with the same covariance, but it is usually difficult to meet such conditions with epidemiological data, where a lot of influence factors have 0/1 distribution. At this time, we can use a logistic regression model to predict the disease. For example, the most commonly used predictive method in the study of cancer epidemiology is the logistic regression method.

Model Evaluation

Model performance was evaluated with receiver operating characteristic (ROC) analysis, which has been widely useful for evaluating the performance of binary classifier. A typical ROC curve plots true positive rate (sensitivity) against false positive rate (1-specificity) for the entire range of possible thresholds, therefore providing a unified representation for assessing the overall model performance. The area under the curve (AUC) was used as a single performance measure to decide whether the model prediction was better than random (0.5). A perfect model would yield an AUC value of 1. Training AUC values were fairly high across models and higher than the testing AUC values, as anticipated (Phillips, 2010). The testing AUC values, which demonstrate the actual model predictive powers, suggest whether the model predictions are better than random.

Data preparation

The risk of disease outbreak is the probability or chance that a specified disease outbreak will occur. Existing outbreak definitions are composed of two components: (i) an endemic channel that aims to replicate historical trends of expected cases; and (ii) a set of criteria that determines what level of variation above this endemic frequency should be classified as an outbreak26. The methods used to define outbreak risk are closely linked to the targets of various disease surveillance methods and to the transmission characteristics of the specified diseases. One common method for defining further disease outbreak risk is to calculate the probability and extent that the current disease occurrence deviates from the historical baseline (i.e., the average value of historical data).

In the existing study, factors that affect the risks of disease outbreak in different areas have been classified as demographic, socioeconomic, and meteorological27,28. There are many statistical methods used to assess the relationship between risk factors and risks of disease outbreaks, such as principal component analysis and geo-detector29. In this study, we performed correlation analysis using SPSS software from IBM. The full dataset (both training and test set) was used to decide which risk factors were relevant.

Because BBNs are optimized for discrete variables, all continuous variables should be discretized before data is put into the network after determining risk factors. At present, there are three primary methods30 for discretizing continuous variables: equal intervals, equal frequencies, and entropy. The equal interval method is the simplest unsupervised discretization algorithm; it divides the continuous variable space into a series of average intervals based on the range of numerical attributes31. Similarly, the equal frequency method is based on equal numbers of data samples, and it divides the continuous variable space into a plurality of intervals based on the data frequency. The entropy method is supervised from beginning to end. It chooses the minimum entropy value in the numerical attribute as the split point and then classifies the interval results recursively, eventually resulting in layered discretization results. In this study, we used the entropy method to discretize continuous variables.

Results

To test the feasibility and effectiveness of BBN in assessing infectious disease outbreak risk, we respectively applied BBN to assess the hand, foot, and mouth disease (HFMD) and measles outbreak risks based on disease cases and symptoms at different spatial scales.

Case one: risk assessment of hand, foot and mouth disease (HFMD) outbreaks

In this case, a HFMD outbreak was defined as an abnormal increase in the severity and mortality of HFMD within the next month. BBN was used to assess HFMD outbreak risk in Hunan Province, China based on virus detection rate and demographic, socioeconomic and meteorological factors. It should be noted that the study period was during the peak months (April–July, Sep–Nov) of HFMD in Hunan32, and the study unit was the county.

Data sources

The disease data incorporated in the in BBN were the rate, severity, and mortality of HFMD and the rate of virus EV71 detection in mild cases. People older than five years were ignored in the study because HFMD mainly infects children under the age of 532. Considering that pre-kindergarten children and kindergarten students have different routes of exposure to virus EV71, we separately calculated the rates of virus EV71 detection in mild cases for children aged 0–3 and 3–5 years old. All HFMD cases and virus detection laboratory data were collected from the local CDC.

The environmental factors in this study were socioeconomic and meteorological factors. The socioeconomic factors included the density of the susceptible population (i.e., children under the age of 5) and urbanization levels. These data were extracted from the Hunan Statistical Yearbook33,34,35,36,37. The meteorological data were obtained from the China Meteorological Data Sharing Service System and included the average air pressure, maximum wind speed, average wind speed, average relative humidity, minimum relative humidity, and average temperature, temperature difference, rainfall, and sunshine.

In this study, the moving percentile method38, which has been used successfully in the China Infectious Disease Automated-alert and Response System (CIDARS), was applied to determine the risk levels of HFMD outbreaks. This method assesses the risk of HFMD outbreaks by comparing the reported severity and mortality rates of HFMD during the current observational period to that of the corresponding historical period at the county level. To account for the stability of the data, the current month was used as the current observation period, and the four months prior were used as the historical period. The severity and mortality rates of HFMD in the current observational period were the proportion of severe cases (i.e. cases sent to ICU) and of deaths, respectively, among all reported HFMD cases during the most recent month. We set the percentile of historical data, P50, P80, as the indicator of potential outbreak risks. When the severity and mortality rates of HFMD in the current observation period were less than P50, the risk level was set as level 0 (low risk). When the rate fell within [P50, P80], the risk level was level 1(moderate risk). If the rate was more than P80, outbreak risk was high, and the risk level was set as level 2. The current observation period and historical data block were dynamically shifted forward by month.

When all data were collected, discretization was performed prior to constructing the network. Table 1 shows each variable classification attribute in the BBN.

Table 1. Input variables in the BBN for estimating HFMD outbreak risk.

Variables name Corresponding categorical values Initial values Variables name Corresponding categorical values Initial values
The Risk Level of HFMD outbreak Low <P50 Average Relative Humidity (%) Low <70.850
Intermediate P50-P80 Lower Intermediate 70.850–73.994
High >P80 Intermediate 73.994–75.727
The rate of virus EV71 detection in mild case for children aged 0–5 years old (1/100) Low <0.057 Upper Intermediate 75.727–77.765
Lower Intermediate 0.057–0.151 High >77.765
Intermediate 0.151–0.267 Average Temperature (°C) Low <18.283
Upper Intermediate 0.267–0.407 Lower Intermediate 18.283–21.508
High >0.407 Intermediate 21.508–23.229
The rate of virus EV71 detection in mild case for children aged 0–3 years old (1/100) Low <0.050 Upper Intermediate 23.229–27.321
Lower Intermediate 0.050–0.155 High >27.321
Intermediate 0.155–0.263 Average Wind Speed (m/s) Low <1.658
Upper Intermediate 0.263–0.415 Lower Intermediate 1.658–1.797
High >0.415 Intermediate 1.797–1.958
The rate of virus EV71 detection in mild case for children aged 3–5 years old (1/100) Low <0.05 Upper Intermediate 1.958–2.194
Lower Intermediate 0.05–0.354 High >2.194
Upper Intermediate 0.354–0.9 Minimum Relative Humidity (%) Low <49.535
High >0.9 Lower Intermediate 49.535–53.342
The density of the susceptible population (ie., children under the age of 5) (pop/km2) Low <20.299 Intermediate 53.342–55.675
Lower Intermediate 20.299–21.081 Upper Intermediate 55.675–58.935
Intermediate 21.081–29.716 High >58.935
Upper Intermediate 29.716–33.449 Rainfall (mm) Low <3.017
High >33.449 Lower Intermediate 3.017–3.752
Average air pressure (hPa) Low <982.689 Intermediate 3.752–5.751
Lower Intermediate 982.689–987.763 Upper Intermediate 5.751–7.574
Intermediate 987.763–994.911 High >7.574
Upper Intermediate 994.911–1003.306 Sunshine Hours (h) Low <21.916
High >1003.306 Lower Intermediate 21.916–30.908
Urbanization Level (%) Low <42.815 Intermediate 30.908–41.319
Lower Intermediate 42.815–48.555 Upper Intermediate 41.319–52.896
Intermediate 48.555–56.825 High >52.896
Upper Intermediate 56.825–69.78 Temperature Difference (°C) Low <7.213
High >69.78 Lower Intermediate 7.213–7.547
Maximum Wind Speed (m/s) Low <3.934 Intermediate 7.547–8.029
Lower Intermediate 3.934–4.222 Upper Intermediate 8.029–8.544
Intermediate 4.222–4.499 High >8.544
Upper Intermediate 4.499–4.943      
High >4.943
Open in a new tab

The Application of BBN Model and Its Result

In this study, we used 70% of the data (98 samples) as the training data to build the network, and the remaining 42 samples were used as test data.

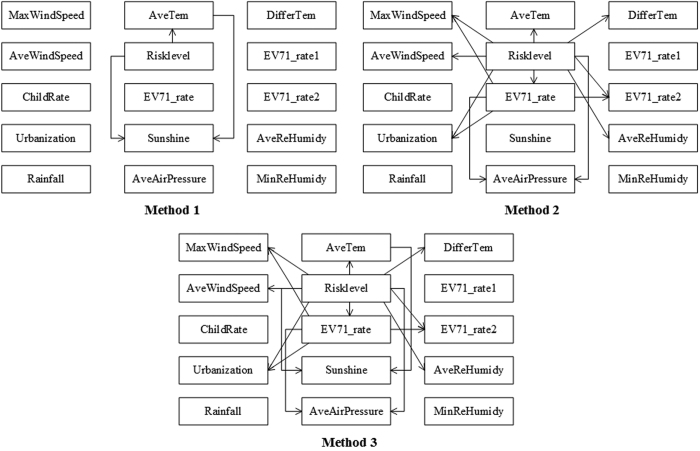
In this case, there were three different ways to construct the Bayesian belief network: (1) only the network structure learning algorithm proposed by Cheng Jie21 was used to determine the structure; (2) the network structure was first based on expert knowledge, and then the network structure learning algorithm was applied to modify the network; (3) the expert knowledge method followed the network structure learning algorithm in the course of network building. Figure 2 illustrates the Bayesian belief network construction via these three methods. In all networks, the variables are represented as nodes, and the arcs between the nodes indicate the relationships between variables. In addition, the arrows on the arcs extend from nodes to child nodes39.

Figure 2. The Bayesian Belief Network used to assess HFMD outbreak risk.

Figure 2

Open in a new tab

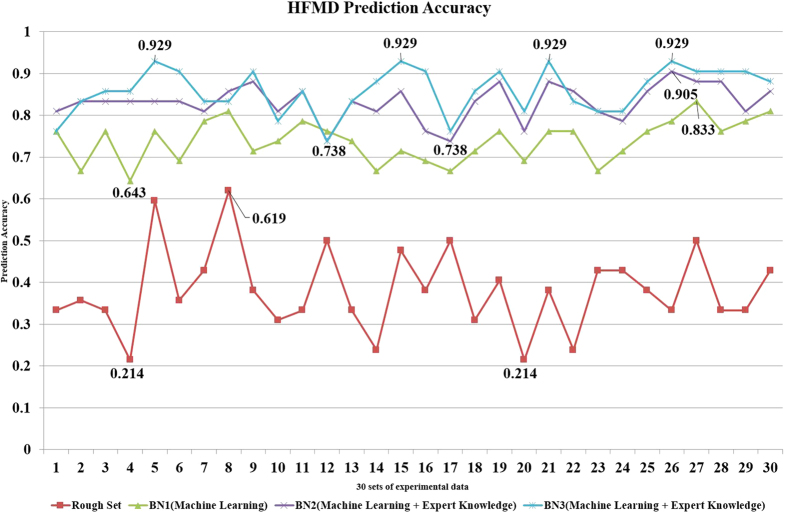
To evaluate the performances of different Bayesian belief networks, the percentage of samples correctly predicted from all test samples was taken as the index of the risk assessment accuracy. Figure 3 shows the risk assessment accuracy of these three networks. As seen in Fig. 3, all three networks performed well in assessing the HFMD outbreak risk. In addition, the risk assessment accuracy of the third method was highest. The highest accuracy value reached via the third method over the course of 30 experiments was 92.90 ± 4.61% at the 95% confidence level. Therefore, the networks constructed by the third method were finally applied to assess the HFMD outbreak risks in the study area. This network structure shows that the risk level was dependent on the rate of virus EV71 detection(r = 0.125, p = 0.009), urbanization levels(r = 0.275, p = 0.011), rate of virus EV71 detection in mild cases in children aged 3–5 years old(r = −0.119, p = 0.012), average air pressure(r = 0.098, p = 0.038), average relative humidity(r = 0.119, p = 0.011), average wind speed(r = −0.120, p = 0.000), maximum wind speed(r = −0.029, p = 0.037), average temperature(r = −0.268, p = 0.000), and temperature difference (r = 0.192, p = 0.000).

Figure 3. The accuracy of the BBN and rough set method used to assess HFMD outbreak risk.

Figure 3

Open in a new tab

As seen in the conditional probability table (Table 2), the effect of HFMD outbreak risk varied among the selected factors. Following the increase in the rate of virus EV71 detection, especially in mild cases in children aged 3–5 years old, the risk of HFMD outbreak appeared to increase. Some environmental factors also impacted the HFMD outbreak risk. When the average relative humidity was over 77.765%, the probability of risk level 0 suddenly decreased to 0.043, but the probability of risk level 2 remained at 0.25. The average temperature was found to have a negative effect on the HFMD outbreak risk; an HFMD outbreak was more likely to occur in lower temperatures.

Table 2. Conditional probability distribution table of the BBN for estimating HFMD outbreak risk.

Variables name Corresponding categorical values Probability of differentrisk levels
 Variables Corresponding categorical values Probability of different risk levels
0 1 2 0 1 2
The rate of virus EV71 detection in mild case for children aged 0–5 years old Low 0.348 0.214 0.1 Average Relative Humidity Low 0.13 0.214 0.2
Lower Intermediate 0.087 0.286 0.2 Lower Intermediate 0.261 0.143 0.2
Intermediate 0.174 0.071 0.15 Intermediate 0.261 0.071 0.1
Upper Intermediate 0.043 0.214 0.3 Upper Intermediate 0.304 0.286 0.25
High 0.348 0.214 0.25 High 0.043 0.286 0.25
The rate of virus EV71 detection in mild case for children aged 3–5 years old Low 0.426 0.335 0.278 Average Temperature Low 0.043 0.214 0.35
Lower Intermediate 0.288 0.244 0.253 Lower Intermediate 0.043 0.071 0.3
Upper Intermediate 0.158 0.208 0.318 Intermediate 0.261 0.357 0.15
High 0.129 0.213 0.151 Upper Intermediate 0.174 0.286 0.1
Average air pressure Low 0.226 0.274 0.146 High 0.478 0.071 0.1
Lower Intermediate 0.183 0.172 0.176 Average Wind Speed Low 0.043 0.214 0.15
Intermediate 0.161 0.172 0.272 Lower Intermediate 0.261 0.143 0.2
Upper Intermediate 0.241 0.172 0.26 Intermediate 0.087 0.286 0.25
High 0.19 0.208 0.146 Upper Intermediate 0.261 0.286 0.15
Urbanization Level Low 0.226 0.274 0.174 High 0.348 0.071 0.25
Lower Intermediate 0.212 0.208 0.198 Temperature Difference Low 0.217 0.143 0.2
Intermediate 0.248 0.203 0.291 Lower Intermediate 0.217 0.143 0.2
Upper Intermediate 0.154 0.142 0.217 Intermediate 0.304 0.214 0.25
High 0.161 0.172 0.121 Upper Intermediate 0.174 0.357 0.2
Maximum Wind Speed Low 0.226 0.274 0.174 High 0.087 0.143 0.15
Lower Intermediate 0.212 0.208 0.198  
Intermediate 0.248 0.203 0.291  
Upper Intermediate 0.154 0.142 0.217  
High 0.161 0.172 0.121  
Open in a new tab

The Application of Rough Set Method and Its Result

To compare with the risk assessment accuracy of the rough set method with BBN, we applied the rough set method in the HFMD and measles outbreak risks prediction experiments. Both the training data and the test sample data were input to each method. In the rough set method, we obtained 179 reducts from the decision system. The smallest set contains four attributes: the rate of virus EV71 detection in mild cases for children aged 0–5 years old, urbanization level, average temperature, and average wind speed. This means that at least four spatial attributes should be used to synthesize the decision rules. According to the 179 reducts, we next generated 17,165 rules. These rules, which discovered the relationship between the attributes and decision, are the decision rules. According to the decision rules, the risk levels of the HFMD outbreak were estimated. Figure 3 shows the accuracy of the BBN and the rough set method in 30 different experiments of the HFMD outbreak risk analysis. The prediction accuracy of the BBN, which fluctuated between 0.929 and 0.738, is markedly higher than that of the rough set method, which fluctuated between 0.619 and 0.214 in the experiments.

The Application of Linear Regression Model and Its Result

As a comparison, we also used a tradition linear regression model to estimate the HFMD outbreak risk. In this case, as the dependent variable is a discrete classification, we used the logistic regression model, which is the most commonly used method in epidemiological prediction research, to predict the HFMD outbreak risk level (0, 1, or 2). As was done before when constructing Bayesian Belief Networks and using Rough Set methods, the training data were input to build the logistic regression model, and the test data were criterion. The 30 experiments were carried out, and 30 fitting results were obtained. When we modelled each data set, we chose the optimal logistic model through the value of R2. In these statistic models, the general form was as follows:

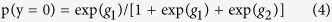graphic file with name srep40084-m5.jpg
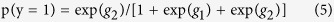graphic file with name srep40084-m6.jpg
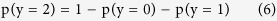graphic file with name srep40084-m7.jpg

Where

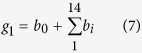graphic file with name srep40084-m8.jpg
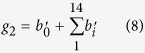graphic file with name srep40084-m9.jpg

Among them, p indicates the probability of the HFMD outbreak risk level; b0 and 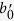Inline graphic are constant terms; bi and 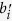Inline graphic are the coefficients, which correspond to different levels of various discrete risk factors xi.

Case two: Measles outbreak risk analysis

In this case, a measles outbreak was defined as an outbreak on the verge of happening. The goal of this case was to assess the measles outbreak risk in regions of China between December 1st, 2004 and June 30th, 2007, by BBN. The study area falls between 25°N–30°N and 105°E–115°E, China. The study unit in this case was the town.

Data sources

Data from 438 disease cases were used in this study and were provided by the China CDC. In addition to outbreak data, the disease data included records of measles cases at the specified regions in the study area, although no outbreak had been reported simultaneously.

According to the transmission characteristics of measles, the risk factors used here included residence environment factor and meteorological factors. The residence environment factor was whether there was a school or a factory in the town. The meteorological data came from the China Meteorological Data Sharing Service System and included diurnal barometric range, minimum daily temperature, daily amount of sunshine, minimum daily humidity, and maximum daily wind speed.

All meteorological data were calculated by the Inverse Distance Weighting (IDW) method based on values from 756 national meteorological stations. All continuous variables were discretized before being entered into the Bayesian network.

The Application of BBN Model and Its Result

In this case, the network structure learning algorithm was applied to construct the network, and then the network structure was modified based on expert knowledge. As seen in Fig. 4, the risk level of a measles outbreak was a father node of the residence environment factor, daily minimum temperature, diurnal barometric range, and daily amount of sunshine. The diurnal barometric range depended on the daily maximum wind speed. In addition, both the daily minimum temperature and daily amount of sunshine were child nodes of daily minimum humidity.

Figure 4. The Bayesian Belief Network used to assess measles outbreak risk.

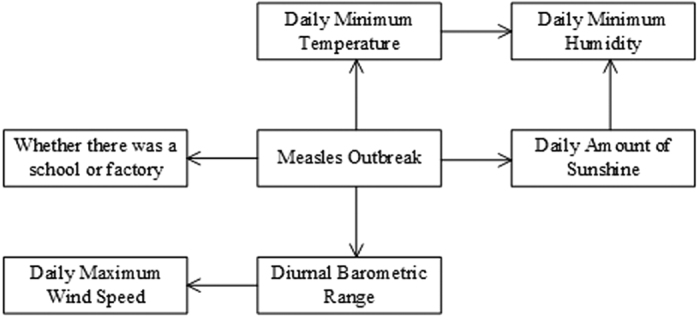
Figure 4

Open in a new tab

Table 3 shows the conditional probability distribution for the risk level of a measles outbreak based on seven factors. As seen in Table 3, measles outbreaks were more likely in crowded places, such as schools and factories, with a probability of 0.9469. When the minimum daily temperature was −2.675–8.65 °C, the outbreak probability was also high, occasionally reaching 0.9125. By contrast, when the minimum daily temperature was >19.975 °C, the outbreak probability was lowest, at 0.0255. The table also shows that the daily amount of sunshine had no influence on measles outbreaks; the probability fluctuated between 0.0745 and 0.1946. Researchers could use this impact factor data to make inferences about measles outbreak risk based on the table. For example, when the daily minimum temperature was 0.5 °C, the probability of a measles outbreak could be as high as 0.9125.

Table 3. The conditional probability distribution table of the BBN for estimating measles outbreak risk.

Variable name and value The probability of an outbreak
 Variable name and value The probability of an outbreak Variable name and value The probability ofan outbreak
Whether there is a school or a factory No Yes Daily maximum wind speed No Yes Daily sunshine time No Yes
No 0.9362 0.0639 Low 0.8811 0.1189 Low 0.8057 0.1946
Yes 0.0536 0.9469 Intermediate 0.4724 0.5276 Lower Intermediate 0.8986 0.1019
      High 0.5732 0.4268 Upper Intermediate 0.8722 0.1279
            High 0.9255 0.0745
Barometric diurnal range No Yes Daily minimum temperature No Yes Daily minimum humidity No Yes
Low 0.9152 0.0848 Low 0.4724 0.5276 Low 0.5417 0.4583
Lower Intermediate 0.6055 0.3945 Lower Intermediate 0.0875 0.9125 Lower Intermediate 0.9095 0.0905
Upper Intermediate 0.3092 0.6908 Upper Intermediate 0.4315 0.5685 Upper Intermediate 0.9030 0.0970
High 0.4724 0.5276 High 0.9745 0.0255 High 0.8501 0.1499
Open in a new tab

The Application of Rough Set Method and Its Result

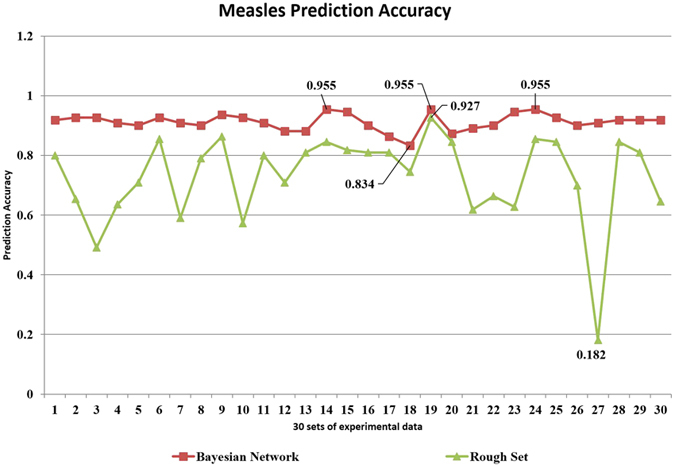
As a comparison, we also applied the rough set method to assess measles outbreak risk in the same area during the same period. In the BBN, linear regression model, and rough set method, 75% of the sample data (328) were randomly selected as the training data, and the remaining 110 samples served as the test data. To verify the accuracy and reliability of the method, we repeated the random sampling process 30 times, producing 30 sets of experimental data. The results (seen in Fig. 5) showed that the assessment accuracy of the measles outbreak risk for the BBN distributed at (1, 0.8). The highest accuracy value was 95.50 ± 3.50% at the 95% confidence level. In brief, the distance between the BBN and rough set method with regard to the accuracy of their assessments of measles outbreak risk was short. However, the fluctuations in the value of assessment accuracy of the rough set method reached large amplitudes. In 30 experiments, the highest accuracy of the rough set method reached 0.927, but the lowest accuracy was only 0.182. In the experiment with the highest accuracy, only one result containing all six attributes (daily minimum temperature, daily minimum humidity, daily amount of sunshine, diurnal barometric range, daily maximum wind speed, and whether there was a school or a factory in the town) was obtained. Then, 56 rules describing the relationship between the attributes and the decision were generated.

Figure 5. The accuracy of the BBN and the rough set method used to assess measles outbreak risk.

Figure 5

Open in a new tab

The Application of Linear Regression Model and Its Result

Similarly, we used logistic regression model to predict the measles outbreak risk level. The theory and procedure of how to use it were the same as the HFMD case before. The general form of models that be simulated from 30 sets experimental data was as follows:

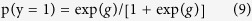graphic file with name srep40084-m12.jpg

Where

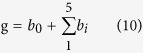graphic file with name srep40084-m13.jpg

Among them, p represents the probability of measles outbreak risk; b0 is a constant term; bi is the coefficient which corresponds to different levels of discrete various discrete risk factors xi.

The Evaluation of the BNN model, Rough Set Method and Linear regression model

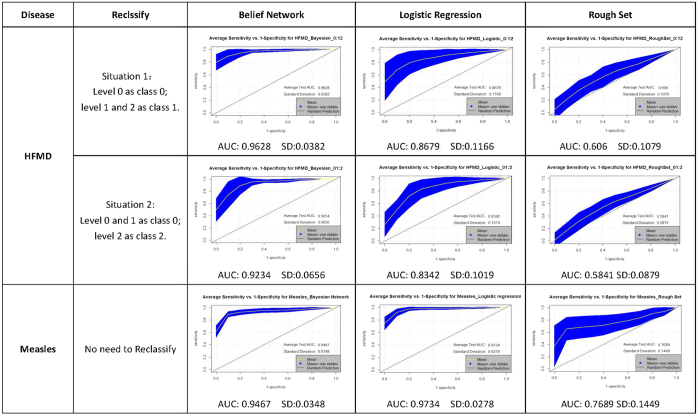
Because the ROC curve applies only to binary classifiers, we had to reclassify the HFMD outbreak risk level (0 or 1 or 2) into two classes. Situation 1: we defined level = 0 as the class that means there is no HFMD outbreak, and we merged level = 1 and level = 2 as the other class to represent the outbreak; Situation 2: we merged level = 0 and level = 1 to represent that the epidemic is not serious, and level = 2 as a representation of a very high HFMD outbreak risk. Meanwhile, for the measles dataset, due to the outbreak risk level (0 or 1) set as two values, reclassification was not needed. The ROC curves for each model’s average prediction of 30 replicate runs with a mean test AUC value and corresponding standard deviation are provided in Fig. 6.

Figure 6. ROC curve for Bayesian Belief Network model, Logistic Regression model and Rough Set method prediction averaged on each 30 replicate runs.

Figure 6

Open in a new tab

(The 1:1 line indicates the condition if the prediction is completely out of random chance (AUC = 0.5)).

In the lateral view, for the HFMD test dataset, no matter how to reclassify the risk level, the Bayesian network model achieved a very high performance evaluation (the average AUC test was 0.9628 for situation 1 and 0.9234 for situation 2), and better than the logistic regression model (average AUC test was 0.8679 for situation 1 and 0.8342 for situation 2) and rough set method (average AUC test was 0.606 for situation 1 and 0.5841 for situation 2). In the measles test dataset, the Bayesian network model (average test AUC was 0.9467) and logistic regression model (average test AUC is 0.9734) showed high prediction accuracy and were obviously superior to the rough set method (average AUC test was 0.7689). In the longitudinal view, the stability of the Bayesian network is good (standard deviation was 0.0382 for HFMD situation1, 0.0656 for HFMD situation2, and 0.0348 for measles), regardless of the classification of the disease, and the logistic regression model (standard deviation was 0.1166 for HFMD situation1, 0.1019 for HFMD situation2, and 0.0278 for measles) and rough set method (standard deviation was 0.1079 for HFMD situation1, 0.0879 for HFMD situation2, and 0.1449 for measles) do not have this advantage.

Discussion

In recent years, early warning systems have played an important role in preventing and controlling the spread of infectious diseases. However, the recent requirement for very early detection has shifted in the direction of research. An increasing number of studies focused on improving the speed and accuracy of outbreak risk assessment have been conducted. In this article, a general approach integrating the Bayesian network concept with infectious disease risk assessment was proposed and demonstrated. We first introduced the methodology for assessing the disease outbreak risk based on a BBN, and then detailed how to assess the outbreak risks of measles and HFMD using a BBN based on disease cases and symptoms at different spatial scales. Finally, we compared the accuracy and feasibility of the BBN and rough set methods. Our results showed that the BBN performed better than the rough set method, both in terms of accuracy and stability. Moreover, once the relationship network among disease outbreak risks and factors was determined, the BBN accurately predicted the further risk of infectious disease outbreaks without several selected factors.

There are many advantages to using a BBN to assess disease outbreak risk24. Firstly, a BBN describes the causal probability relationship between disease outbreak risk and risk factor variables, including variability, uncertainty, and subjectivity25. Therefore, the accuracy of risk assessment is not influenced by the missing variables. Secondly, because a BBN is a graph, it is easy to update and to understand the relationships among variables. In a BBN, the probabilistic causal dependencies among variables are expressed by arcs, and the strength of the dependencies are displayed in probability distribution tables. Lastly, according to the joint probability distributions of various disease outbreak risk levels, a BBN not only determines the most probable risk level, but also gives the probability that this risk level will appear and provides a detailed risk assessment to the public health department for disease surveillance. Although this study only applied a BBN to assess the outbreak risks of HFMD and measles, it can also be used to simultaneously assess the outbreak risk for other similar diseases.

Nevertheless, use of a BBN to assess infectious disease outbreak risks presents some limitations. Because a BBN is optimized to handle categorical variables, continuous data often must be discretized before modelling, which may result in information loss. Moreover, the accuracy of the method is closely related to the network structure. Although there are many network construction algorithms, it is difficult to update a proper Bayesian belief network in automatic and timely manner according to changes in the disease transmission process. This will affect the accuracy and sensitivity of disease outbreak risk assessment. In addition, the risk factors selected in this study were limited, and more related risk factors, such as symptom surveillance data and reported data from specified organizations, should be involved in future studies.

Additional Information

How to cite this article: Liao, Y. et al. A new method for assessing the risk of infectious disease outbreak. Sci. Rep. 7, 40084; doi: 10.1038/srep40084 (2017).

Publisher's note: Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.

Acknowledgments

This work was supported by the National Natural Science Foundation of China (no. 41101431, 41471377), and the Young Talent Fund of the Institute of Geographic Sciences and Natural Resources Research, CAS (no. 2012RC201).

Footnotes

Author Contributions Y.L. and B.X. contributed equally to this study. Y.L. and J.W. designed the study. Y.L. and B.X. wrote the first and subsequent drafts of the article. Y.L., B.X., and X.L. contributed to data analysis and drew the figures. All authors contributed to the writing. All authors have read and approved the article.

References

  1. Li L. T. et al. A patient-centered early warning system to prevent readmission after colorectal surgery: A national consensus using the Delphi method. J. Am. Coll. Surg. 216, 210–216 (2013). [DOI] [PubMed] [Google Scholar]
  2. Wagner M. M. et al. The emerging science of very early detection of disease outbreaks. J. Public Health Manag. Pract. 7, 51–59 (2001). [DOI] [PubMed] [Google Scholar]
  3. Waidyanatha N. Towards a typology of integrated functional early warning systems. International Journal of Criti. 6, 31–51 (2010). [Google Scholar]
  4. Lober W. B. et al. Roundtable on Bioterrorism Detection Information System–based Surveillance. J. Am. Med. Inform. Assoc. 9, 105–115 (2002). [DOI] [PMC free article] [PubMed] [Google Scholar]
  5. Faensen D. et al. SurvNet@ RKI-a multistate electronic reporting system for communicable diseases. EuroSurveill. 11, 100–3 (2006). [PubMed] [Google Scholar]
  6. Lawson A. B. & Cressie N. Spatial statistical methods for environmental epidemiology in Handbook of statistics (ed. Sen P. K. & Rao C. R.), 357–396 (Elsevier, 2000). [Google Scholar]
  7. Deng T. et al. Spatial-temporal clusters and risk factors of hand, foot, and mouth disease at the district level in Guangdong Province, China. PloS one 8, e56943 (2013). [DOI] [PMC free article] [PubMed] [Google Scholar]
  8. Jiang X. & Wallstrom G. L. A Bayesian network for outbreak detection and prediction in Proceedings of AAAI 2006 (ed. Gil Y. & Mooney R. J.), 1166–1160 (AAAI Press, 2006). [Google Scholar]
  9. Hanslik T., Boelle P. Y. & Flahault A. The control chart: an epidemiological tool for public health monitoring. Public Health 115, 277–281 (2001). [DOI] [PubMed] [Google Scholar]
  10. Yang W. Z. et al. A study on early detection for seven infectious diseases. Chin. J. Epidemiol. 25, 1039–1041 (2004). [PubMed] [Google Scholar]
  11. Hutwagner L. C., Thompson W. W., Seeman G. M. & Treadwell T. A simulation model for assessing aberration detection methods used in public health surveillance for systems with limited baselines. Stat. Med. 24, 543–550 (2005). [DOI] [PubMed] [Google Scholar]
  12. Huang L., Kulldorff M. & Gregorio D. A spatial scan statistic for survival data. Biometrics. 63, 109–118 (2007). [DOI] [PubMed] [Google Scholar]
  13. Rath T. M., Carreras M. & Sebastiani P. Automated detection of influenza epidemics with hidden Markov models in Advances in Intelligent data analysis V (ed. Berthold M. R. et al.), 521–532 (Springer, 2003). [Google Scholar]
  14. Dosso S. E., Nielsen P. L. & Harrison C. H. Bayesian inversion of reverberation and propagation data for geoacoustic and scattering parameters. J. Acoust. Soc. Am. 125, 2867–2880 (2009). [DOI] [PubMed] [Google Scholar]
  15. Holicky M., Marková J. & Sykora M. Forensic assessment of a bridge downfall using Bayesian networks. Eng. Fail. Anal. 30, 1–9 (2013). [Google Scholar]
  16. Smail L. Uniqueness of the Level Two Bayesian Network Representing a Probability Distribution. Internat. J. Math. Math. Sci. 2011, doi: 10.1155/2011/845398 (2010). [DOI] [Google Scholar]
  17. Trucco P., Cagno E., Ruggeri F. & Grande O. A Bayesian Belief Network modelling of organisational factors in risk analysis: A case study in maritime transportation. Reliab. Syst. Safe 93, 845–856 (2008). [Google Scholar]
  18. Martin J. E., Rivas T., Matías J. M., Taboada J. & Argüelles A. A Bayesian network analysis of workplace accidents caused by falls from a height. Saf. Sci. 47, 206–214 (2009). [Google Scholar]
  19. Zhang L., Wu X., Skibniewski M. J., Zhong J. & Lu Y. Bayesian-network-based safety risk analysis in construction projects. Reliab. Syst. Safe 131, 29–39 (2014). [Google Scholar]
  20. Liao Y., Wang J., Guo Y. & Zheng X. Risk assessment of human neural tube defects using a Bayesian belief network. Stoch. Environ. Res. Risk Assess. 24, 93–100 (2010). [Google Scholar]
  21. Cheng J. & Greiner R. Comparing Bayesian network classifiers in Proceedings of the fifteenth conference on uncertainty in artificial intelligence (ed. Laskey K. B. & Prade H.), 101–108, (Morgan Kaufmann Publishers, 1999). [Google Scholar]
  22. Bielza C. & Larranaga P. Discrete Bayesian network classifiers: a survey. ACM Computing Surveys (CSUR). 47, 5 (2014). [Google Scholar]
  23. Pawlak Z. Rough set. Int. J. Comput. Inf. Sci. 11(5), 341–356 (1982). [Google Scholar]
  24. Su C. T., Yang C. H., Hsu K. H. & Chiu W. K. Data mining for the diagnosis of Type II diabetes from three dimensional body surface anthropometrical scanning data. Computers & Mathematics with Applications. 51, 1075–1092 (2006). [Google Scholar]
  25. Wang X., Yang J., Jensen R. & Liu X. Rough set feature selection and rule induction for prediction of malignancy degree in brain glioma. Computer Methods and Programs in Biomedicine. 83, 147–156 (2006). [DOI] [PubMed] [Google Scholar]
  26. Brady O. J., Smith D. L., Scott T. W. & Hay S. I. Dengue disease outbreak definitions are implicitly variable. Epidemics 11, 92–102 (2015). [DOI] [PMC free article] [PubMed] [Google Scholar]
  27. Li W. Study on risk factors for severe hand, foot and mouth disease in china. PloS one 9, e87603 (2014). [DOI] [PMC free article] [PubMed] [Google Scholar]
  28. Kouadio I. K., Kamigaki T. & Oshitani H. Measles outbreaks in displaced populations: a review of transmission, morbidity and mortality associated factors. BMC Int. Health Hum. Rights 10, 5 (2010). [DOI] [PMC free article] [PubMed] [Google Scholar]
  29. Wang J. F. et al. Geographical detectors-based health risk assessment and its application in the neural tube defects study of the Heshun region, China. Int. J. Geogr. Inf. Sci. 24(1), 107–127 (2010). [Google Scholar]
  30. Friedman N. & Goldszmidt M. Discretizing continuous attributes while learning Bayesian networks. Proc Icml. 157–165 (1996). [Google Scholar]
  31. Hu K. Y. Research on concept lattice and rough set based data mining methods in Ph. D. thesis of Tsinghua University, 2–3 (Tsinghua University, 2001).
  32. Xing W. Hand, foot, and mouth disease in China, 2008–12: an epidemiological study. Lancet Infect. Dis. 14, 308–318 (2014). [DOI] [PMC free article] [PubMed] [Google Scholar]
  33. Hunan Provincial Bureau of Statistics. In Hunan Statistical Yearbook 2010 (ed. Dai L. P. et al.), 1–538, (China StatisticsPress, 2010). [Google Scholar]
  34. Hunan Provincial Bureau of Statistics. In Hunan Statistical Yearbook 2011 (ed. Dai L. P. et al.), 1–724, (China StatisticsPress, 2011). [Google Scholar]
  35. Hunan Provincial Bureau of Statistics. In Hunan Statistical Yearbook 2012 (ed. Li X. L. et al.), 1–741, (China StatisticsPress, 2012). [Google Scholar]
  36. Hunan Provincial Bureau of Statistics. In Hunan Statistical Yearbook 2013 (ed. Gao Y. et al.), 1–741, (China StatisticsPress, 2013). [Google Scholar]
  37. Hunan Provincial Bureau of Statistics. In Hunan Statistical Yearbook 2014 (ed. Zhang Z. et al.), 1–742, (China StatisticsPress, 2014). [Google Scholar]
  38. Yang W. Z. et al. Chinese outbreak automatic detection and quick response system based on internet. WPSAR. 2(1), doi: 10.5365/ wpsar.2010.1.1.009 (2011). [Google Scholar]
  39. Lin J. H. & Haug P. J. Exploiting missing clinical data in Bayesian network modeling for predicting medical problems. J. Biomed. Inform. 41(1), 1–14 (2008) [DOI] [PubMed] [Google Scholar]
  40. Bai H. X., Ge Y., Wang J. F. & Liao Y. L. Using rough set theory to identify villages affected by birth defects: the example of Heshun, Shanxi, China. International Journal of Geographical Information Science. 24, 559–576 (2010). [Google Scholar]

Articles from Scientific Reports are provided here courtesy of Nature Publishing Group

RESOURCES