Validating Whole-Airway CFD Predictions of DPI Aerosol Deposition at Multiple Flow Rates

Abstract

Background: The objective of this study was to compare aerosol deposition predictions of a new whole-airway CFD model with available in vivo data for a dry powder inhaler (DPI) considered across multiple inhalation waveforms, which affect both the particle size distribution (PSD) and particle deposition.

Methods: The Novolizer DPI with a budesonide formulation was selected based on the availability of 2D gamma scintigraphy data in humans for three different well-defined inhalation waveforms. Initial in vitro cascade impaction experiments were conducted at multiple constant (square-wave) particle sizing flow rates to characterize PSDs. The whole-airway CFD modeling approach implemented the experimentally determined PSDs at the point of aerosol formation in the inhaler. Complete characteristic airway geometries for an adult were evaluated through the lobar bronchi, followed by stochastic individual pathway (SIP) approximations through the tracheobronchial region and new acinar moving wall models of the alveolar region.

Results: It was determined that the PSD used for each inhalation waveform should be based on a constant particle sizing flow rate equal to the average of the inhalation waveform's peak inspiratory flow rate (PIFR) and mean flow rate [i.e., AVG(PIFR, Mean)]. Using this technique, agreement with the in vivo data was acceptable with <15% relative differences averaged across the three regions considered for all inhalation waveforms. Defining a peripheral to central deposition ratio (P/C) based on alveolar and tracheobronchial compartments, respectively, large flow-rate-dependent differences were observed, which were not evident in the original 2D in vivo data.

Conclusions: The agreement between the CFD predictions and in vivo data was dependent on accurate initial estimates of the PSD, emphasizing the need for a combination in vitro–in silico approach. Furthermore, use of the AVG(PIFR, Mean) value was identified as a potentially useful method for characterizing a DPI aerosol at a constant flow rate.

Introduction

Accurate predictions of pharmaceutical aerosol deposition and dosimetry in the respiratory airways has been a long-standing research goal. Applications of aerosol dosimetry models include new insights into the performance of existing inhalers,^(1,2) developing next-generation high efficiency aerosol delivery devices,^(3,4) and developing strategies that can target aerosol delivery to different regions of the lungs.^(5,6) One new application of accurate aerosol dosimetry models is the assessment of bioequivalence^(7,8) between innovator and generic inhalation drug products in order to assist with the regulatory and approval process.

Existing semi-empirical models have been shown to predict whole-airway deposition of pharmaceutical aerosols accurately.^(2,9,10) However, predicting regional and local aerosol deposition throughout the airways may require more advanced modeling techniques.^(11,12) It is expected that regional and local deposition patterns of drugs in the lungs will influence efficacy and treatment success.^(13,14) Furthermore, efficacy also depends on drug dissolution, absorption, and clearance.⁽¹³⁾

Computational fluid dynamics (CFD) models provide a potential method to predict regional and highly localized pharmaceutical aerosol drug deposition,⁽¹²⁾ as well as dissolution in airway surface liquid, absorption into lung tissue, and muco-ciliary clearance mechanics.⁽¹⁵⁾ The use of CFD whole-lung models to predict pharmaceutical aerosol deposition throughout the lungs is a new development,^(1,16–18) and validations with multiple in vivo studies are currently needed.

Existing airway deposition models can typically be classified as semi-empirical, whole-lung 1D (one dimensional), and computational fluid dynamics (CFD) 3D. These different modeling types were recently reviewed by Longest and Holbrook⁽¹²⁾ and are only briefly described here. Semi-empirical models provide correlations for whole-airway deposition or regional deposition based on fitting empirical data as a function of analytical parameters,⁽¹⁹⁾ as recently reviewed by Finlay and Martin.⁽²⁾ These models may be extended to capture factors that influence the mouth–throat deposition of pharmaceutical aerosols, such as the effect of a jet of air issuing from a dry powder inhaler (DPI), through the inclusion of addition correlations.^(9,20)

Whole-airway 1D models assume either a single path⁽²¹⁾ or stochastic⁽²²⁾ lung geometry and employ algebraic expressions for aerosol deposition by different physical mechanisms such as sedimentation, impaction, and diffusion.^(23,24) For nebulized droplets and environmental aerosols, these models often match available in vivo data in terms of total tracheobronchial (TB) and alveolar deposition relatively well.^(22,25–29)

Additional correlations can be included in 1D whole lung models to capture the effect of jet or spray momentum on deposition when dealing with pharmaceutical inhalers.⁽³⁰⁾ Katz et al.⁽³¹⁾ recently applied a whole-airway 1D model⁽²⁵⁾ to predict the deposition of nebulized droplets delivered through a relatively wide diameter mouthpiece and compared regional deposition results with the in vivo gamma scintigraphy study of Conway et al.⁽³²⁾ Limitations of the model's predictive capabilities for this pharmaceutical aerosol were identified in the mouth–throat and tracheobronchial regions. Similarly, previous applications of 1D models to capture in vivo deposition of nebulized polydisperse aerosols have revealed limitations in predictions of alveolar deposition and exhaled mass fraction.^(26,27,33)

CFD simulations seek to capture the delivery and deposition of pharmaceutical aerosols from a first principles approach. The relevant governing transport equations are solved in 3D models of the airways, which are discretized into interconnected small spatial elements (or control volumes) such as hexahedral, tetrahedral, or prism cells. Recent CFD studies of inhaled pharmaceutical aerosols have captured the effects of inhalers on transport and deposition in the mouth–throat region^(34–36) and have predicted aerosol deposition through numerous generations of the upper^(37–39) and lower TB airways.⁽⁴⁰⁾ However, prediction of aerosol transport and deposition throughout the lungs with CFD simulations (i.e., a CFD whole-lung model) remains challenging and requires simplifying techniques, which are actively being developed.^(41–44)

CFD predictions of pharmaceutical aerosol deposition in the upper airways have successfully resulted in correlations of deposition that are integrated into semi-empirical and 1D whole lung models.⁽²⁾ Compared with ambient aerosols, pharmaceutical aerosols often include the challenges of hygroscopic growth or droplet evaporation including two-way coupling, new patient interface devices not included in existing correlations, and electrostatic charge. Existing semi-empirical and 1D models can frequently be expanded to address these factors.^(45–47) However, use of a first-principles-based approach with 3D CFD simulations may be more direct, flexible, and accurate.

To simulate pharmaceutical aerosol deposition in the respiratory airways, our group has proposed a concurrent in vitro and CFD approach.^(1,16,17) A primary advantage of this approach is the flexibility to directly include new aspects of aerosol physics for developing new delivery strategies and inhalers. A disadvantage is that it remains difficult to implement due to the complexity of the underlying physics. In vitro experiments are employed to define the initial aerosol formed by the inhaler and to benchmark deposition in realistic upper airway models.^(34,48,49) In vitro experiments have also been used to benchmark deposition in lower airway bifurcations for the validation of CFD results.^(50–52) The CFD simulations then begin with the initial polydisperse aerosol size distribution and simulate flow dynamics within the inhaler-patient interface and respiratory airways. Aerosol physics are addressed on a first principles basis and include relevant particle forces, turbulent dispersion, size change, and nanoscale effects as needed. To predict deposition throughout the tracheobronchial airways, our group has developed the stochastic individual pathway (SIP) modeling approach.^(1,16,17) In this method, individual continuous pathways beyond the third bifurcation (B3) are generated extending into each lobe of the lung through the terminal bronchioles (B15). Along each pathway, one daughter branch of each bifurcation is continued and one is not, which is similar to the 1D whole lung Monte Carlo modeling technique of Koblinger and Hofmann.⁽²⁶⁾ A sufficient number of stochastically generated pathways are simulated until deposition results converge to an ensemble average.⁽¹⁶⁾ This approach is reported to reduce the required time to simulate the full TB region by a factor of 3 × 10⁵ with only an estimated minor loss in accuracy.⁽¹⁶⁾

Recently, we extended the SIP modeling approach to include the entire lung by developing correlations of aerosol deposition in representative models of complete acinar regions using inhalation profiles consistent with pharmaceutical inhalers.⁽⁵³⁾ Combining the SIP modeling approach with the new CFD predictions of alveolar deposition provides a CFD-based technique to simulate pharmaceutical aerosol delivery throughout the airways beginning with the site of aerosol formation.

Previous studies by our group have extensively compared pharmaceutical aerosol deposition in the mouth–throat (MT) and upper TB regions with concurrent in vitro experiments and found good agreement. Validation of the CFD predictions with in vitro data have been performed for metered dose inhalers (MDIs),^(1,34) DPIs,^(1,16,17,34) and softmist inhalers.^(34,48,49) These validation results highlight the ability of CFD to capture the effects of jet and spray momentum, hygroscopic size change including two-way coupling, effects of the mouthpiece on deposition, particle emission timing, and the complex interactions of turbulence and aerosol breakup.

In contrast with comparisons to in vitro data, validations of CFD model predictions using in vivo data for pharmaceutical aerosols are rare. Kleinstreuer et al.⁽⁵⁴⁾ and Vinchurkar et al.⁽⁵⁵⁾ reported successful CFD predictions of MT deposition and lung delivery compared with in vivo data sets for MDIs. However, the models only considered the MT and upper TB airways. Recent work in animal models has used upper airway CFD predictions to estimate lobar deposition for test aerosols successfully.^(56,57) While this work represents a significant advance, frequent complications associated with pharmaceutical aerosols were not included and the CFD simulations did not extend beyond the upper TB airways.

Recent studies of characteristic in vitro airway geometries and DPIs have established successful in vitro–in vivo correlations.^(58–60) For example, Delvadia et al.⁽⁵⁹⁾ showed that small, medium, and large characteristic in vitro geometries could predict MT and lung dose mean values and variability for a DPI at different flow rates. Similarly, a mean MT geometry was used to establish successful in vitro–in vivo correlations across a series of DPIs;⁽⁵⁸⁾ however, CFD predictions were not considered.

In a recent study, our group compared CFD model predictions of regional aerosol deposition throughout the lungs with in vivo data for multiple aerosols and inhalers.⁽⁶¹⁾ Good agreement was found between the whole-airway model predictions and in vivo data on a regional lung basis for a monodisperse aerosol, DPI, and softmist inhaler, each considered at one flow rate. Modifying the flow rate of a DPI presents a challenging scenario for CFD validation in which both the aerosol size profile and aerosol deposition pattern in the lungs can change. However, the effects of multiple flow rates were not considered in previous whole-airway validation studies.

The objective of this study is to compare CFD predictions of aerosol deposition from a commercial DPI implemented at multiple flow rates with existing in vivo data across multiple airway regions. CFD predictions are compared with the 2D gamma scintigraphy in vivo study of Newman et al.⁽⁶²⁾ employing the Novolizer DPI. As with previous studies, in vitro experiments are first used to characterize the initial aerosol size distribution at multiple inhalation flow rates. Two upper TB airway models with different degrees of physiological realism are evaluated to determine which model provides a better match to the regional in vivo data.

The SIP modeling approach is used to provide deposition profiles throughout the TB airways. New moving wall simulations of the alveolar region are performed to predict aerosol deposition correlations for the different inhalation profiles reported in the in vivo experiments. Comparisons are made between CFD predictions and gamma scintigraphy results in the MT, central, and peripheral airway regions. The ability to predict not only lung deposition but regional delivery is an important advantage of the CFD whole-airway approach.

Materials and Methods

Selection of the in vivo dataset and inhalation waveform

Previous studies have highlighted the importance of inhalation waveforms on the deposition of inhaled aerosols.^(63,64) The use of DPIs introduces an additional level of complexity in which the inhalation flow rate and waveform affect both the deposition profile and often the particle size distribution (PSD) of the aerosol emitted from the device.⁽¹⁾

To validate CFD model predictions throughout the airways, an in vivo case study was sought that considered use of a DPI expected to be flow rate dependent across multiple inhalation waveforms. The in vivo case study selected was that of Newman et al.⁽⁶²⁾ who considered 14 healthy subjects using a budesonide Novolizer DPI (200 μg; Meda, Pharmaceuticals, Somerset, NJ) with controlled and measured breathing conditions. Three separate experiments were conducted in which each of the 14 subjects used the Novolizer and targeted either slow, intermediate, or fast inhalation waveforms resulting in measured peak inspiratory flow rates (PIFR) of 99, 65, and 54 L/min (LPM), respectively. Lung deposition was quantified using a radiolabel drug and two-dimensional (2D) gamma scintigraphy imaging. Radiolabeling of the aerosol was proven to influence the mass median aerodynamic diameter (MMAD) negligibly, and images were acquired with minimal time delay to avoid inclusion of clearance effects. Regional lung deposition was determined by dividing the 2D planar image into boxes representing the central, intermediate, and peripheral lung. The imaging template used in the study of Newman et al.⁽⁶²⁾ was previously defined with an image provided in the study of Newman et al.⁽⁶⁵⁾ and compared to an anatomical drawing in Newman et al.⁽⁶⁶⁾ The regional deposition data reported by Newman et al.⁽⁶²⁾ are percentages of the metered dose (powder loaded in the inhaler) and therefore include the effect of drug retained in the inhaler and not aerosolized. This fraction of the dose was not simulated during the CFD studies. In order to determine the in vivo deposition as a percentage of the aerosolized dose, the % radioactivity on the device was subtracted from the total recovered radioactivity to determine the total aerosolized dose and the regional deposition values were scaled as a percentage of this value.

As described in several recent studies, the technique used for dividing 2D planar images to define regional lung deposition can have a significant impact on results.^(67,68) In the previous validation study of Tian et al.,⁽⁶¹⁾ acceptable agreement was found between the in vivo results of Newman et al.⁽⁶²⁾ and CFD computed airway predictions transferred to 2D planar images for the Novolizer inhaler, which was considered only at the PIFR of 99 LPM (fast inhalation), as well as a softmist inhaler also considered at a single flow rate. The methods established in the previous study of Tian et al.⁽⁶¹⁾ are repeated in the current study to evaluate the more challenging scenario of a single DPI evaluated at multiple flow rates generating different aerosol size distributions and tested in two separate airway geometries.

As described, subjects in the in vivo study of Newman et al.⁽⁶²⁾ were trained to inhale through the DPI at three different flow rates, resulting in measured mean PIFRs of 99, 65, and 54 LPM. For each of the three inhalation waveforms, spirometry recorded an inhalation volume of approximately 3 L. Following inhalation, subjects were instructed to perform a 10 s breath hold, which was verified by the spirometric data.

For the CFD calculations, the inhalation waveform metrics were converted to three DPI inhalation waveforms consistent with PIFRs of 99, 65, and 54 LPM (Fig. 1). The reproduced waveform shape is based on the profile described in Tian et al.⁽¹⁶⁾ for DPI use and quick-and-deep inhalation instructions. Based on the previous measurement studies of Delvadia⁽⁶⁹⁾ with a range of resistances including conditions identical to the Novolizer, the time to PIFR was selected as 0.5 s in all cases. The total inhalation time then varied based on the time required to inhale 3 L (Fig. 1). Characterizations of the three inhalation waveforms are provided in Table 1. The mean flow rates for the three inhalation profiles were calculated to be 61, 41, and 34 LPM.

FIG. 1.

Inhalation waveforms developed to match the inspiration conditions reported by Newman et al.⁽⁶²⁾ and labeled according to the peak inspiratory flow rate (PIFR).

Table 1.

Characteristics of Three Inhalation Waveform Cases

PIFR (LPM)	99	65	54
Mean flow rate (LPM)	61	41	34
Average of PIFR and Mean flow rate (LPM): AVG(PIFR, Mean)	80	53	44
Selected particle sizing flow rate (LPM)	80	45 (followed by 60)a	45
TPIFR (s)	0.5	0.5	0.5
T (s)	3.0	4.45	5.3
V (L)	3	3	3
Breath hold period (s)	10	10	10

^aRefined estimates were used to improve agreement with in vivo data.

PIFR, peak inspiratory flow rate; T_PIFR, time to PIFR; T, inhalation waveform period; V, inhaled volume.

Determination of initial aerosol size distribution

The CFD approach implemented in this study includes in vitro aerosol characterization experiments to determine the initial PSD emitted from the inhaler at multiple flow rates. Discrete element and multiphase flow techniques may someday enable the computation of powder breakup and estimation of PSDs emitted from DPIs.⁽⁷⁰⁾ However, the approach implemented in this study is intended to leverage the strengths of both in vitro and CFD methods to best determine pharmaceutical aerosol deposition throughout the airways. Currently, in vitro impactor-based experiments are the only available method to characterize drug emitted aerosol size distributions without the use of inhaler-specific correlations.⁽⁷¹⁾

With most DPIs, the inhalation flow rate has a significant influence on the PSD.^(72,73) For the Novolizer, a range of flow rates was selected to capture the inhalation profiles described in Table 1. The use of accurate inhalation profiles is also known to affect drug aerosol particle size and upper airway deposition.^(74,75) However, in vitro sizing of the drug aerosol using cascade impactor methods usually requires a steady state flow rate through the impactor. Methods of using a realistic inhalation waveform in combination with a cascade impactor are challenging and significantly complicates the experiments. A potential solution that avoids increasing the complexity of the experiments is to size the aerosol at an effective steady state flow, which captures its behavior in terms of airway deposition. Tian et al.⁽⁶¹⁾ previously found that sizing a DPI aerosol using the flow rate equivalent to the average of the waveform's PIFR and mean flow rate value [i.e., AVG(PIFR, Mean)], produced a PSD that lead to agreement between CFD predictions and in vivo airway deposition data. This technique of steady state sizing at an effective flow rate is applied in the current study and further evaluated. For the three inhalation waveforms, values of AVG(PIFR, Mean) are 80, 53, and 44 LPM, as shown in Table 1. To capture this range, impactor aerosol sizing flow rates of 100, 80, 60, and 45 LPM were initially selected. Future studies may require the assessment of aerosol size using the complete inhalation waveform. However, use of an effective flow rate for steady state aerosol sizing is evaluated in the current study as a potentially valuable alternative, which is consistent with the findings of Finlay and Gehmlich.⁽⁷⁶⁾

For sizing the Novolizer DPI aerosol, a Next Generation Impactor (NGI; MSP Corp., Shoreview, MN) was operated at multiple constant flow rates (i.e., square waveforms) of 100, 80, 60, and 45 LPM. The Novolizer DPI was connected directly to a pre-separator using a mouthpiece adaptor to ensure an airtight seal, and the flow was generated using a vacuum pump. A three-way solenoid valve downstream of the impactor was used to generate a square-wave inhalation profile at the four preselected flow rates for a time interval that drew a total 4 L of air through the system, based on standard DPI aerosol characterization protocols.

In the absence of the USP induction port, the impactor was positioned vertically to enable the inhaler to be oriented horizontally in the entrance to the pre-separator as it would be when used by a patient. Impactor stages and the pre-separator were coated to prevent particle bounce and re-entrainment. Drug deposition in the impactor was determined using a validated HPLC assay method for budesonide for four single dose experiments. Particle size distributions were reported as budesonide mass distribution recovered from the impactor. The mass median aerodynamic diameter (MMAD) of the impactor aerosol was defined as the particle size at the 50th percentile on a cumulative percent mass undersize distribution (D50) using linear interpolation.

Measured particle size distributions were translated to size bins in the numerical model using the midpoint cut-off diameters of the NGI stages determined using a standard extrapolation formula. Drug mass in the NGI pre-separator was assumed to have the pre-separator cut-off diameter, which was equal to or greater than 10.0 μm in all cases. It is expected that a fraction of this aerosol in the pre-separator is composed of larger diameter particles due to the presence of some drug remaining attached to lactose carrier particles. However, this underestimate of particle size in the pre-separator is of little significance with respect to lung deposition, as at these sizes they would all typically be retained in the MT region. As a result, MT and TB drug deposition predictions will be similar to the values that would occur from a more exact fractioning of sizes above the preseparator cutoff. The quality of this assumption will be evaluated with comparisons between the CFD predictions and in vivo estimates of drug deposition for the DPI.

Airway models

Airway model sections include the MT region, upper TB airways that extend through the lobar bronchi, SIP models extending into each lobe of the lung through the TB airways (approximately B15), and acinar regions extending from the respiratory bronchioles (B16) to the alveolar sacs. Development of these model segments have been previously described in detail.^(1,16,53,77)

Based on the healthy volunteer population of the Newman et al.⁽⁶²⁾ study, the airway geometry was created to be consistent with a characteristic adult having a functional residual capacity of 3 L.⁽²⁸⁾ The conducting airway model geometry was scaled to a total lung volume of 3.5 L to represent some size increase of the lungs (500 mL total) during inhalation and was held static. The alveolar model includes moving walls to drive the flow and varies between total lung volumes of 3 L and 6 L during inspiration. Previous validations of the SIP modeling approach provided good agreement in terms of regional deposition with in vivo results when a characteristic upper TB geometry (B1-B3) termed Model C was employed.⁽⁶¹⁾ However, the recent study of Walenga et al.⁽⁷⁸⁾ demonstrated that the more realistic upper TB model termed Model D (Fig. 2) has an effect on pharmaceutical aerosol deposition and distribution among the five lung lobes. In this study, CFD results based on Models C and D are compared with in vivo data to evaluate the merits of using the more complex upper airway geometry. Finally, a previous study by our group⁵³ has developed deposition correlations in a representative acinar model for two pharmaceutical inhalation waveforms with larger inhaled volumes and different profiles compared to those reported by Newman et al.⁽⁶²⁾ As a result, new simulations with the acinar moving wall model are needed to predict alveolar deposition for the three waveforms considered in this study. These individual airway segments, which complete the entire airway tract for orally inhaled products, are briefly reviewed below.

FIG. 2.

Mean adult airway model composed of the mouth–throat (MT), upper tracheobronchial (TB) airways extending from the trachea to the lobar bronchi (bifurcations B1–B3), and one stochastic individual pathway (SIP) model extending into the left lower lobe of the lung from B4 to the terminal bronchioles (outlets of B15).

The Novolizer inhaler was connected to a characteristic MT geometry based on the elliptical model originally proposed by Xi and Longest⁽⁷⁷⁾ (Fig. 2). This MT model was developed from the oral airway cast reported by Cheng et al.⁽⁷⁹⁾ and in-house CT data of the pharynx and larynx. The inhaler was directly connected to the MT geometry assuming an insertion depth of 0.5 cm and an angle of zero degrees with the horizontal plane.⁽³⁴⁾ This insertion creates a small difference from the previous in vitro and numerical studies of Delvadia et al.⁽⁵⁹⁾ and Longest and Hindle.⁽⁴⁸⁾ However, mouthpiece insertion only accounts for a small portion of the oral cavity length with these inhalers and is expected to have a very minor effect on the results. The studies of Delvadia et al.^(58,59) previously reported that this MT model was similar in dimensions to values of the mean adult population and, when used for in vitro studies, produced DPI deposition values consistent with averages from multiple in vivo experiments with a range of DPIs.

The whole-airway CFD model includes a complete geometry of the upper airways from the trachea through the third respiratory bifurcation (B3; Fig. 2). The first upper TB airway geometry extending through B3 was Model C described by Walenga et al.,⁽⁷⁸⁾ which was based on the anatomical cast dimensions reported by Yeh and Schum⁽⁸⁰⁾ and scaled to a total lung volume of 3.5 L (Fig. 3a). Walenga et al.⁽⁷⁸⁾ verified that this model provided airway dimensions consistent with mean values for an adult population. Anatomical features included in Model C are cartilaginous rings in the trachea, a D-shaped tracheal cross-section, asymmetrical bifurcations, and out-of-plane rotation of the bifurcations, all consistent with the Yeh and Schum⁽⁸⁰⁾ data.

FIG. 3.

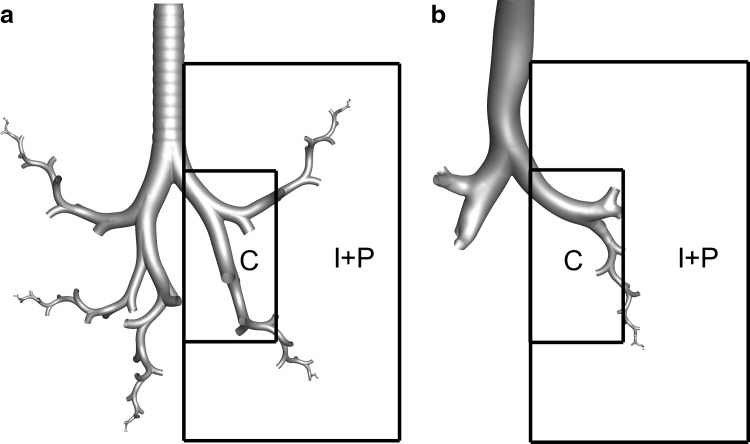
Conducting airway models beginning at the outlet of the MT region (outlet of larynx and start of trachea) with complete airways through B3, and SIP models extending from B4 to B15. The models considered include (a) the characteristic airway geometry developed by Tian et al.⁽⁶¹⁾ (Model C), and (b) the more realistic airway geometry developed by Walenga et al.⁽⁷⁸⁾ (Model D). Both models include characteristic SIP geometries extending from the lobar bifurcations (B3) through the terminal bronchioles (B15). The regional boxes were draw based on the methods employed by the in vivo study of Newman et al.⁽⁶²⁾ for 2D gamma scintigraphy analysis and segments bifurcations B1–B7 into the central (C) region with the remainder of the lung (B8 to B15 + alveolar region) captured by the combined intermediate and peripheral (I+P) regions.

For comparison to Model C, the more realistic upper TB model extending through B3 developed by Walenga et al.⁽⁷⁸⁾ and referred to as Model D is considered (Fig. 3b). This upper TB model was constructed from a CT scan selected to be consistent with medium-size adult male anatomy. Additional realistic details included in Model D are curvature of the trachea and main bronchi, noncircular cross sections extending beyond B3, and non-idealized bifurcation shapes. These additional geometric details were found to modify the overall predicted deposition of pharmaceutical aerosols in the region of B1-B3. Curvature of the trachea was also shown to alter the aerosol distribution pattern among the lung lobes, as previously reported by Lambert et al.⁽³⁷⁾ In both Models C and D, significant time was dedicated to constructing high quality hexahedral meshes, which were previously shown to be more efficient and more accurate compared with the tetrahedral or hybrid cell approach that is frequently employed.^(81,82)

Beyond the third bifurcation, stochastic individual path (SIP) models were considered extending into the lung lobes (Fig. 3). Bifurcations within the SIP models were constructed as physiologically realistic bifurcation units, as defined by Heistracher and Hofmann⁽⁸³⁾ with the airway dimensions reported by Yeh and Schum,⁽⁸⁰⁾ again scaled to be consistent with a total lung volume of 3.5 L. An advantage of the Yeh and Schum⁽⁸⁰⁾ data is that average dimensions are provided separately for each lung lobe. Continuation of the left or right branch of each bifurcation was considered to be consistent with the flow distribution, resulting in an equal probability for the symmetric outflow assumption in the SIP models starting at B4. However, if a selection led out of the general region of an initial lung lobe, the other branch was selected. Consecutive branches were rotated at 90^o to approximate physiological conditions.⁽⁸⁴⁾ Bifurcation 15 (B15) was assumed to end with the terminal bronchioles, based on existing anatomical data.⁽⁸⁰⁾

The previous study of Longest et al.⁽¹⁷⁾ on SIP model development verified that inter-lobe deposition for pharmaceutical aerosols varied significantly. However, deposition in the left lower (LL) lobe provided an average lobar deposition fraction value such that multiplying this value by 5 (for the five lung lobes) provided an adequate representation of total lobar deposition. The previous study of Tian et al.⁽⁶¹⁾ verified that this approach effectively predicted in vivo regional deposition when compared with 2D gamma scintigraphy results. Implementation of this approach will be considered again in this study in comparison with in vivo data.

Previous modeling approaches to simulate alveolar deposition of pharmaceutical aerosols have relied on empirically based estimates from in vivo studies⁽¹⁹⁾ or analytically-based estimates that employ particle deposition mechanisms in tubular geometries. The empirically-based estimates do not include breathing profiles used with pharmaceutical aerosols (e.g., deep inspiration with a breath-hold), whereas the analytically-based estimates neglect an accurate alveolar structure.

To improve the accuracy of predicted pharmaceutical aerosol deposition in the alveolar region, a recent study by our group⁽⁵³⁾ developed an approximate CFD model of the entire acinar region beginning with the respiratory bronchioles and extending to the alveolar sacs. In this previous study, it was determined that a multigenerational approximation of the acinar region could be used to predict deposition within the total region distal to the terminal bronchioles. CFD simulations were then used to develop correlations for alveolar deposition considering a range of particle sizes and two specific pharmaceutical inhalation waveforms as well as a breath-hold period. As with other aspects of the whole-airway CFD model, anatomical dimensions of the alveolar region are consistent with an average adult.⁽⁵³⁾ The approximate acinar geometry (model D3)⁽⁵³⁾ is implemented in the current study to develop correlations for alveolar particle deposition as a function of particle size and alveolar residence time for the three inhalation profiles of interest (Fig. 1).

CFD simulations

Based on the inhalation flow rate employed and resulting Reynolds numbers, turbulence is expected in the MT geometry through approximately bifurcation B3. Within this region, the LRN k-ω model was selected based on its ability to predict pressure drop, velocity profiles, and shear stress for transitional and turbulent flows effectively and accurately.^(85,86) Another significant advantage of the LRN k-ω model is numerical efficiency, which allows for the simulation of transient inhalation profiles. The conservation of mass and momentum equations used with the LRN k-ω model are available from Wilcox⁽⁸⁶⁾ and were previously reported by Longest and Xi.⁽⁸⁷⁾ Similarly, the equations governing turbulent kinetic energy (k) and specific dissipation rate (ω) were also reported by Longest and Xi.⁽⁸⁷⁾ The LRN k-ω model resolves the flow field through the buffer and viscous sublayers in transitional and turbulent boundary layer internal flows,⁽⁸⁶⁾ provided that the near-wall mesh spacing is sufficient.

Beyond B3, transition to laminar flow quickly occurs. As described by Tian et al.,⁽⁶¹⁾ difficulties associated with capturing this transitional region as airway diameter decreases may produce inaccurate results, whereas laminar simulations provide an acceptable approximation. In the current study, laminar simulations were conducted in the SIP airway models from B3 through B15 and also within the acinar geometry.

Airflow simulations in the acinar model involved moving wall algorithms to drive the flow in and out of the geometry, as previously described.⁽⁵³⁾ Briefly, expansion of the geometry followed the inhalation waveforms, and was based on uniform scaling in all three coordinate directions with the length scaling factor proportional to the one-third power of volume change. Therefore, the total inhaled volume of 3 L produced a linear scale factor of 1.44 at the end of each inhalation profile, which was maintained through the 10 s breath hold period. The equations describing scaling the geometry over time to match the three separate inhalation profiles are available in previous work.⁽⁵³⁾

Based on the aerosol size experiments, polydisperse size distributions of the drug were observed ranging from the submicrometer scale to 10 μm and larger. To address this broad range of particle sizes, a previously developed and optimized Lagrangian particle tracking method was employed.^(88,89)

To model the effects of turbulent fluctuations on particle trajectories, a random walk method was implemented.⁽⁹⁰⁾ The primary limitation of this eddy interaction model in conjunction with the Reynolds Averaged Navier Stokes equations is that it does not account for reduced turbulent fluctuations in the wall-normal direction, which results in an over-prediction of deposition.⁽⁹¹⁾ To better approximate turbulent effects on particle deposition, an anisotropic turbulence correction was applied for particle tracking.^(91,92) In this study, the exponential wall-normal damping function f_n was evaluated for n⁺ values ranging from 0 to a maximum of 60.

Based on the results of Tian et al.,⁽¹⁶⁾ transient simulations are required in the upper airways through approximately B3, whereas steady state approximations are acceptable in the SIP models. In this study, transient simulations are conducted for the inhalers, MT and upper TB airways for the complete inhalation waveforms. For the individual SIP models, steady state simulations are then performed at the mean flow rates (Table 1). In these steady state simulations, the inhaler and upper MT-TB models are included to generate approximate flow fields and particle conditions at the inlet to each of the SIP geometries. Tian et al.⁽¹⁶⁾ showed that this approach was accurate to within 5% of fully transient simulations in both the upper and lower airways, and provided a significant savings in solution time.

In performing the CFD simulations, previously established best-practices were implemented to provide a high quality solution. For the MT-TB model, including one SIP geometry, grid convergent results were found to occur with meshes consisting of approximately 1.8 million control volumes. Specifically, coarse, medium, and fine grids of approximately 850,000, 1,250,000, and 1,800,000 control volumes were considered. Maximum velocity values and deposition fractions varied by less than 2% between the two highest grid densities considered. As a result, the fine grid was implemented in this study. To improve the accuracy of particle deposition predictions in the turbulent flow fields, near-wall interpolation of the velocity profile was included, as described by Longest and Xi.⁽⁸⁹⁾ Both near-wall anisotropic turbulence corrections and near-wall velocity interpolation were included with user-defined functions.

For the Novolizer DPI generating a polydisperse drug aerosol, nine size bins consistent with the midpoint cut-off sizes of the Next Generation Impactor (NGI) stages at each respective flow rate were considered. To resolve deposition across all size bins, 450k particles were considered at the inlet of each model section. These values were determined as the number of required particles to reduce change in local deposition fractions to below 5% relative difference with the addition of 50k polydisperse particles. Based on experimental data, particles were delivered from the DPI over the first 0.5 s of inhalation as a first order approximation.⁽⁷²⁾

Whole-airway modeling considerations

In simulating aerosol deposition throughout the airways, a number of variable and sub-model selections were necessary. For these validation experiments, all variable and sub-model selections were determined a priori based on previous model development studies.^(1,16,17,61) Results and comparisons to in vivo data based on these initial selections are presented first in this study in order to determine the strength of the model in terms of predictive power without available in vivo data. Model refinements are then presented in order to increase model accuracy in terms of improving agreement with the in vivo data. Variable and sub-model selections for predicting aerosol deposition throughout the airways are provided in more detail below.

To facilitate the CFD solution of the complete airways, the respiratory tract was divided into three sections, which were the inhaler to B3 (including the complete asymmetrical upper TB region), B4–B7 (middle TB airways), and B8–B15 (lower TB airways). Division of the model into multiple sections may not be necessary; however, this division helps to match flow physics in each section with an appropriate CFD sub-model and reduces the number of particle trajectories required in the upper model regions. Based on previous studies, transport into the LL lobe was used as a representative average value of conditions in the five lung lobes.⁽¹⁷⁾

Transient simulations were implemented for the inhaler and upper airways through B3, whereas simulations in the SIP geometries implemented steady state conditions with velocity profiles interpolated at mean flow conditions. Particles were initialized at inlets of B4 and B8 using the polydisperse size distribution from the outlet of the respective upstream branches and using either a blunt or parabolic spatial profile, respectively. Polydisperse size distributions were implemented in all simulations.

Outflow boundary conditions in the upper TB model were based on estimates of ventilation to each lung lobe. Lobar ventilation approximations presented in the studies of Horsfield et al.,⁽⁹³⁾ Asgharian and Price,⁽⁹⁴⁾ and Yin et al.⁽⁹⁵⁾ were considered. Reasonable consistency among these studies led to the following distribution estimates for each of the five lung lobes: right upper 14%, right middle 7%, right lower 33%, left upper 15%, left lower 31%. The resulting right and left ventilation proportions were 54% and 46%, respectively. Beyond the lobar bronchi, symmetric outflow conditions were assumed at each bifurcation level (B4–B15). This assumption is not expected to largely influence the regional deposition characteristics of interest in this study.

As described above, steady state flow rates were used to determine the initial aerosol PSD. In vitro size evaluation was conducted at particle sizing flow rates of 100, 80, 60, and 45 LPM. For application in the CFD simulations, particle size distributions generated from the DPI at the average of the mean and peak flow rates of the inhalation waveforms [i.e., AVG (PIFR, Mean)], were required. Use of these effective DPI actuation flow rates is expected to capture conditions when a majority of the aerosol exits the inhaler. In contrast, sizing of the aerosol following actuation at mean or peak flow may over- or underestimate the MMAD, respectively. Average flow rates for aerosol sizing for the three waveforms were calculated to be 80, 53, and 44 LPM. As shown in Table 1, these average values were first approximated with available PSDs for constant flow rates of 80, 45, and 45 LPM, respectively. The quality of these approximations will be assessed based on comparisons with the experimental in vivo results.

Deposition fraction calculations and mapping

Deposition fractions (DFs) based on CFD predictions are defined as the ratio of regionally deposited drug mass to inhaled (or aerosolized) drug mass, and are frequently presented as a percentage. Values of DF are calculated in the regions of the MT, upper TB region (B1–B3), middle TB airways (B4–B7), lower TB airways (B8–B15), and alveolar region. Based on the nomenclature of some studies, the “small airways” can be assumed to start at B13, and are reported to have important implications in diagnosing and treating common respiratory diseases like asthma and COPD.⁽⁹⁶⁾

For the PSDs considered, deposition fractions are based on drug mass and not number concentration to be consistent with comparisons to the radiolabeled drugs used in the in vivo experiments. Calculation of DF from the inhaler through B3 is based on a transient simulation with the polydisperse aerosol measured in the in vitro experiments. As previously described, deposition efficiencies are then calculated in each SIP model employing the PSDs that exited the B1–B3 model outlets. Deposition efficiencies for each branch and TB region are then assembled to calculate DFs throughout the conducting airways as previously described.⁽¹⁶⁾ In addition, the fraction of aerosol remaining (FR) at the exit of B15 and entering the alveolar region is determined.

To predict deposition in the alveolar region, correlations are developed that take into account particle diameter, residence time, and changing geometric conditions. To capture these effects, particle release was considered at ten injection times (t_inject,i) for the three inhalation waveforms (Fig. 1), where i denotes the injection time index. The potential residence time in the geometry between the point of injection and the end of inhalation is calculated as

The deposition fraction for each injection time index i is then calculated as

Let f(t_i) denote the normalized fraction of aerosol entering the alveolar region at each time index i. The aerosol DF over a specific inhalation waveform (DF_w) is then

where n represents the total number of particle injections.

For the breath-hold (BH) period, no new particles enter the geometry. The DF during breath-hold (DF_BH) for each particle size bin is then

where t_BH is the time period of the BH phase.

The total DF combining deposition during the inhalation waveform and the BH period is then

for each particle size. Finally, alveolar deposition is dependent on deposition in the upper airways. Calculations from the SIP model define a fraction remaining (FR) entering the alveolar region based on the initially aerosolized dose. The alveolar deposition fraction taking into account upper airway deposition then becomes

for each particle size considered. To implement these correlations in combination with SIP model predictions, the time (t) that the particle enters the alveolar region (relative to the start of inhalation) is entered as the injection time in Eq. (1). As previously described,⁽⁵³⁾ the model acinar region is sufficiently large (i.e., contains a sufficient number of alveolar ducts) such that total alveolar deposition is not affected by gravity angle or the inclusion of additional alveolar branches.

CFD provides DF results in 3D space as they would occur in vivo. In contrast, 2D gamma scintigraphy produces forward projected planar images of the lung deposition profile. In order to validate the CFD data, a conversion or mapping to the 2D plane used in the in vivo experiments is required. In this study, mapping of the 3D CFD data was intended to mimic the procedure used in the selected in vivo case study⁶² to the extent possible. Specifically, the 3D CFD predictions were forward projected onto a 2D coronal plane. As with the experimental technique, contributions from the trachea were excluded from lung deposition estimates due to potential overlap with MT and esophageal deposition in vivo.

Based on the template provided by Newman et al.,⁽⁶⁵⁾ a rectangular box was drawn around the expected lung boundary for a characteristic adult that was determined from an in-house CT scan (Fig. 3). To match the template provided in the in vivo study, the height to width ratio of the lung boundary box was 2:1. Consistent with the in vivo study, the central region of the lung image was defined as 20% of the lung boundary area by scaling the boundary box by a factor of 0.45. The top of the central region was set equal to the approximate center of the main bifurcation (B1). Based on this mapping, Figure 3 indicates that the central region encloses, on average, the TB airways through approximately B7 in both airway models (Models C and D). As a result, central deposition is assumed to be B1–B7 (minus tracheal deposition) with intermediate (I) and peripheral (P) deposition combined defined as the region of B8–B15 plus the alveolar airways. An attempt was not made to match the intermediate region separately due to imprecision in this mapping approach.

As described, the method used to segment the 2D planar image can influence the predictions of regional lung deposition,⁽⁶⁷⁾ and a newly recommend method for dividing planar images was described⁽⁶⁸⁾ after the publication of Newman et al.⁽⁶²⁾ However, for validation purposes, the goal was to match the techniques used in the selected in vivo experiments as closely as possible. For the purpose of comparison, acceptable agreement between the CFD predictions and in vivo data will be determined based on the average relative error evaluated in the three regions of interest (MT, C, and I+P) having a value of 15% or less.

Results

Determination of aerosol PSD at different sizing flow rates

The aerosol PSDs determined at different constant particle sizing flow rates are presented in Figure 4 in terms of recovered drug mass fraction vs. midpoint aerodynamic diameter of each impactor stage. As described, cascade impaction with the NGI was used to determine the PSDs over a range of constant flow rates to define the initial aerosol conditions exiting the inhaler and entering the MT. For comparison, the MMADs of the aerosol determined using the USP data analysis method was employed. At the selected particle sizing flow rates of 100, 80, 60, and 45 LPM, the MMADs of the aerosol entering the impactor were 2.0, 2.2, 2.4, 2.6 μm, respectively. As expected, MMAD values increased as the flow rate through the inhaler decreased due to reduced aerodynamic energy to deaggregate the powder. It is important to recognize that the USP MMAD methods exclude the pre-separator mass fraction in their calculations. For the CFD calculations, it is important to include the pre-separator dose in the PSDs as shown (Fig. 4) as the whole of the aerosol cloud is presented to the airways. As illustrated in Figure 4, the pre-separator dose was assigned the diameter of the pre-separator cutoff aerodynamic diameter for each of the different particle sizing flow rates.

FIG. 4.

Aerodynamic particle size distributions (PSDs) measured using cascade impaction for the Novolizer DPI actuated with square waveform flow rates in the range of 45–100 LPM. The actuation flow rate is shown to alter the PSD and mass median aerodynamic diameter (MMAD) of the aerosol, based on the dose reaching the impactor.

Based on the results of Tian et al.,⁽⁶¹⁾ the PSD for each of the transient inhalation waveforms should be experimentally determined using the constant particle sizing flow rate value calculated as the average of each PIFR and mean flow rate [i.e., AVG(PIFR, Mean)]. These desired constant particle sizing flow rates are displayed in Table 1; however, these values were not matched exactly when the particle sizing experiments were conducted. As a result, PSDs were selected for each inspiratory waveform based on an estimated available particle sizing flow rate chosen from the options of 100, 80, 60, and 45 LPM. For the waveforms with PIFRs of 99, 65, and 54 LPM, the initially selected particle sizing flow rates were 80, 45, and 45 LPM, respectively. As shown in Table 1, the biggest difference between the desired AVG(PIFR, Mean) value and selected particle sizing flow rate was for the PIFR = 65 LPM waveform (desired 53 LPM vs. selected 45 LPM particle sizing flow rate; difference of 8 LPM). Given that in each case the difference between the desired and selected particle sizing flow rate was less than 10 LPM, this initial approach was expected to be adequate based on the findings of Finlay and Gehmlich.⁽⁷⁶⁾ For the 65 LPM waveform condition, the particle sizing flow rate of 45 LPM was initially selected over the 60 LPM value in order to minimize the amount of in vitro data that was required by the model to predict the in vivo lung deposition.

Comparison to in vivo data with Model C

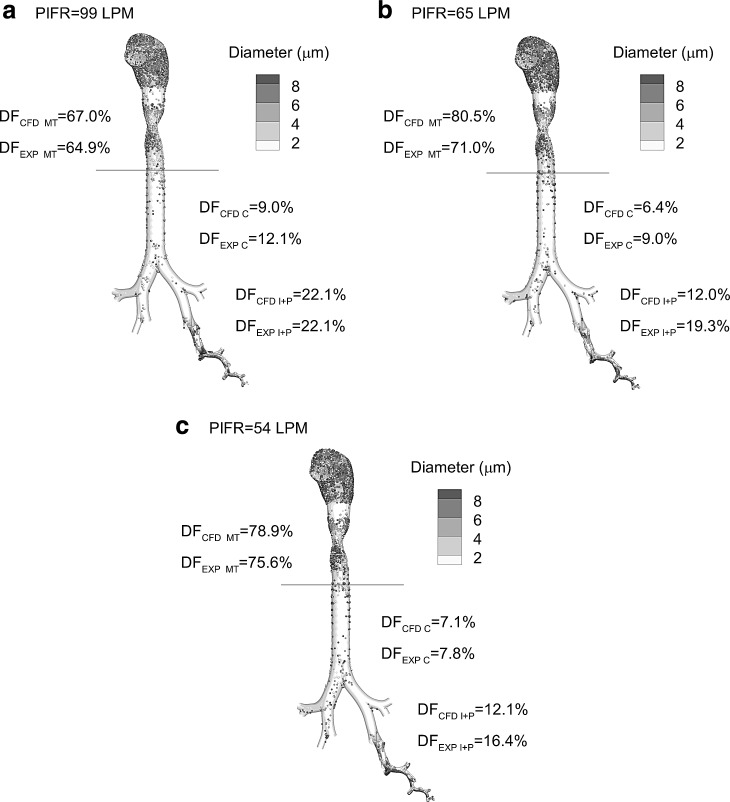
Comparisons of CFD model predictions of regional deposition fraction (DF) to the in vivo data of Newman et al.⁽⁶²⁾ are provided in Figure 5 for the PIFR waveform cases of 99, 65, and 54 LPM and the corresponding initial PSDs described in the previous section (refer to Table 1). In Figure 5, results for the 99 LPM waveform are repeated from Tian et al.⁽⁶¹⁾ for comparison with new data for PIFR waveforms of 65 and 54 LPM (as well as for comparison with Model D data in Fig. 8). As described by Tian et al.,⁽⁶¹⁾ agreement between the CFD and in vivo data is observed at 99 LPM with the largest relative difference of 25% occurring in the C region (DF = 9.0% CFD vs. 12.1% in vivo). Considering the 65 LPM waveform, there were some large differences observed between the CFD and in vivo data with the largest relative difference of 38% in the I + P region (DF = 12.0% CFD vs. 19.3% in vivo). For the 54 LPM waveform, the largest relative difference is in the I + P region with a value of 26% (DF = 12.1% CFD vs. 16.4% in vivo). Considering relative differences averaged across the three regions evaluated (MT, C, and I+P), the waveform cases of 99, 65, and 54 LPM produced values of 9.6%, 26.6%, and 13.2%, respectively. As a result, agreement between CFD and in vivo data is viewed as acceptable for the highest and lowest flow rate waveforms, with a need to improve predictions for the 65 LPM waveform. These predictions may be improved by considering the more realistic Model D geometry and reducing differences between the selected particle sizing flow rate and desired value of AVG(PIFR, Mean).

FIG. 5.

Comparison of CFD predicted and in vivo (EXP) reported regional deposition using the Model C airway geometry and SIP approach for different inspiratory waveforms characterized by PIFRs of (a) 99, (b) 65, and (c) 54 LPM.

FIG. 8.

Comparison of CFD predicted and in vivo (EXP) reported regional deposition using the Model D airway geometry and SIP approach for different inspiratory waveforms characterized by PIFRs of (a) 99, (b) 65, and (c) 54 LPM. Changing geometries from Model C to the more realistic Model D is not observed to improve agreement with the in vivo data for the case of I + P deposition with the 65 LPM waveform.

Predictions of alveolar deposition

New predictions of deposition in the alveolar region were made for the 99, 65, and 54 LPM waveforms using previously developed methods.⁽⁵³⁾ Figure 6 illustrates particle deposition in the complete acinar model for the case of the 54 LPM inhalation waveform at the end of inspiration (T = 5.3 s). Deposition fractions in the acinar model for each of the three inhalation waveforms evaluated across a range of particle sizes and injection time points are illustrated in Figure 7. In this figure, d_particle is the aerodynamic particle diameter and t is the particle residence time in the alveolar geometry, as described in Eq. (1). Presenting the alveolar data in terms of d_particle^α t ^β results in two distinct curves representing the importance of particle diameter (initial deposition phase) and alveolar geometry expansion (second phase), as previously described.⁽⁵³⁾ The resulting acinar DF correlations as a function of particle aerodynamic diameter and alveolar residence time for the three separate inspiratory waveforms are:

FIG. 6.

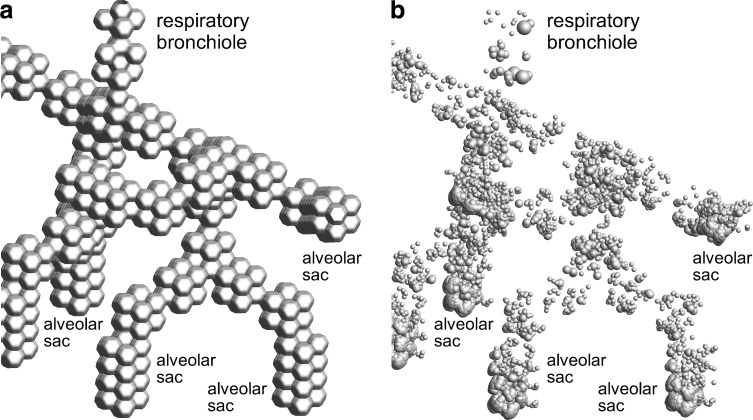
Depiction of aerosol deposition in the acinar model including (a) the acinar geometry extending from a respiratory bronchiole to the alveolar sacs, and (b) particle deposition locations for the 54 LPM PIFR waveform at the end of inspiration and breath hold. In Panel (a), the characteristic size of an alveolus is 300 μm. In Panel (b), the alveolar walls are removed for clarity and the size of the deposited particles is proportional to aerosol particle sizes in the range of 870 nm (smallest spheres) to 2.6 μm (largest spheres).

FIG. 7.

CFD predictions leading to new deposition fraction (DF) correlations for the different inspiratory waveforms with PIFRs of (a) 99, (b) 65, and (c) 54 LPM.

The correlation describing alveolar deposition during a breath-hold after a 3 L inspiration was previously developed⁽⁵³⁾ and implemented in this study to determine additional aerosol deposition during a period of 10 s. These correlations are used together with Equations 1–6, which account for the time dependence of particles entering the alveolar region and the fraction of the aerosol remaining at the exit of the terminal bronchioles, in order to predict the alveolar deposited dose. The new correlations presented as Equations 7–9 were implemented in the regional lung predictions for Model C illustrated in Figure 5 (previous section) as well as all remaining cases considered in this study.

Comparisons to in vivo data with Model D

Implementation of Model D in the CFD simulations had very little effect on regional deposition estimates and comparisons with the in vivo data as illustrated in Figure 8. All conditions for the Model D simulations (Fig. 8) were identical to the Model C simulations (Fig. 5) except for the change in the B1–B3 geometry (i.e., use of Model D). As with Model C, the maximum relative difference between CFD predictions and in vivo data occurred in the I + P region for the 65 LPM waveform with a value of approximately 41% (DF = 11.3% CFD vs. 19.3% in vivo). For the 99, 65, and 54 LPM waveforms, relative percent differences between the CFD and in vivo data averaged across the three regions of interest were 9.6, 25.4, and 13.6%, respectively. In summary, conversion to Model D provided acceptable agreement between the CFD and in vivo data for the waveform cases of 99 and 54 LPM, but little practical improvement compared with Model C.

Table 2 provides a summary of model parameters used in evaluating Model D (Fig. 8) together with CFD vs. in vivo regional comparisons and deposition based on dividing the airway into well defined anatomical sections. Using the SIP modeling approach, B1–B3 (trachea to lobar bronchi) is the upper TB region, B4–B7 is the middle TB region, and B8–B15 is the lower TB region, which leads to the alveolar airways. In comparison to ICRP,⁽²⁸⁾ B1–B7 represents the bronchi and B8–B15 represents the bronchioles. As illustrated in Table 2, relatively little aerosol deposition (<1%) is observed in the important lower TB airways (B8–B15). Deposition in the alveolar region varies by a factor of 2-fold depending on the inspiratory waveform used. Further comparisons among the waveform results are reserved for the following sections.

Table 2.

Comparison of CFD Predictions of Deposition Fraction (DF)^a as a Percentage of Aerosolized Dose to the In Vivo Data of Newman et al.⁽⁶²⁾ Normalized for the Aerosolized Dose from the Novolizer Inhaler Operated with Waveforms that have PIFRs of 99, 65, and 54 LPM

Model parameters
PIFR (LPM)	99	65	54
Inlet MMAD (μm)	2.2	2.6	2.6
Particle sizing flow rate (LPM)	80	45	45
DFs compared to in vivo data (%)
MT	66.0 (64.9)	79.2 (71.0)	78.2 (75.6)
Central lung with trachea excluded	9.0 (12.1)	6.9 (9.0)	6.9 (7.8)
Intermediate and peripheral lung	22.5 (22.1)	11.3 (19.3)	12.2 (16.4)
DFs using SIP approach lung division (%)
Trachea-B3	5.8	5.3	5.2
B4–B7	5.7	4.2	4.4
B8–B15	0.8	0.2	0.9
Alveolar	21.7	11.1	11.3

^aThe Model D upper airway geometry was used for these predictions. The in vivo data is shown in parentheses. Comparisons with the in vivo data are based on 2D planar projections of the CFD predictions. Deposition fractions based on the SIP approach for subdividing the lungs are also provided.

Improvements with properly selected sizing flow rate

For the 65 LPM waveform, Figure 9 evaluates regional particle deposition for an additional measured PSD. As described previously, the desired particle sizing flow rate of the 65 LPM waveform is AVG(PIFR, Mean) = 53 LPM, whereas a particle sizing flow rate of 45 LPM was initially selected as an available first approximation (Figs. 5 and 8). In Figure 9, the experimentally determined PSD evaluated at a particle sizing flow rate of 60 LPM was used. While only 7 LPM away from the ideal particle sizing flow rate, the PSD evaluated at 60 LPM provides significantly improved agreement with the in vivo data for the 65 LPM PIFR waveform (Fig. 9). Specifically, the relative difference in the MT and C regions were reduced to 6.7% and 7.7%, respectively. In addition, relative difference in the I + P region is reduced from 38% to 17.5% (DF = 15.9% CFD vs. 19.3% in vivo) and the relative difference averaged across the three regions considered is 10.6%.

FIG. 9.

Comparison of CFD predicted and in vivo (EXP) reported regional deposition using the Model C airway geometry and SIP approach for PSDs using a particle sizing flow rate of 60 LPM. Implementation of a 60 LPM particle sizing flow rate improved agreement with the in vivo data.

Table 3 provides model conditions and comparisons with in vivo data for the 65 LPM waveform and PSD from the particle sizing flow rate of 60 LPM (as shown in Figure 9). Also provided in Table 3 are DF values based on the SIP whole-airway simulation approach. The particle sizing flow rate of 60 LPM provided very good agreement with the in vivo data for all of the regional deposition predictions.

Table 3.

Comparison of CFD Predictions of Deposition Fraction (DF)^a as a Percentage of aerosolized Dose to the In Vivo Data of Newman et al.⁽⁶²⁾ Normalized for the Aerosolized Dose from the Novolizer Inhaler Operated with the PIFR = 65 LPM Inhalation Waveform and PSD Based on Particle Sizing Flow Rate of 60 LPM (Model C Upper Airway Geometry)

PIFR (LPM)	65
Inlet MMAD (μm)	2.4
Particle sizing flow rate (LPM)	60
MT	75.8 (71.0)
Central lung with trachea excluded	8.3 (9.0)
Intermediate and peripheral lung	15.9 (19.8)
Trachea–B3	6.6
B4–B7	4.4
B8–B15	1.9
Alveolar	14.0

^aThe in vivo data is shown in parentheses. Comparisons with the in vivo data are based on 2D planar projections of the CFD predictions. Deposition fractions based on the typical SIP approach for subdividing the lungs are also provided.

Discussion

A primary finding of this study is that the proposed combined in vitro and CFD whole lung simulation method can acceptably predict regional airway aerosol deposition from a modern DPI across multiple inhalation waveforms and PSDs compared with human in vivo 2D gamma scintigraphy data. The method consists of determining the initial PSD emitted from the inhaler, which is expected to be dependent on the inspiratory flow rate and waveform.^(1,73) These PSDs are then implemented at the point of aerosol formation in the inhaler and used as the starting point for CFD simulations throughout the airways.

In previous studies, concurrent in vitro predictions of MT and upper TB aerosol deposition with MDI,⁽¹⁾ DPI,^(1,16,17) and softmist^(48,49,97) devices were used to refine and validate CFD model predictions in identical geometries. In a series of developmental studies, different aspects of whole-airway CFD simulations were assessed leading to an emerging best-practice set of techniques.^(1,16,17) The previous in vivo validation study of Tian et al.⁽⁶¹⁾ demonstrated that the combined CFD and in vitro approach could predict the regional lung deposition of monodisperse aerosols as well as DPI and softmist aerosols considered at a single flow waveform for each inhaler.

In the current study, the combined approach employing whole-airway CFD SIP-based simulations is demonstrated to predict regional lung deposition accurately in comparison with in vivo data for multiple aerosols from a DPI. Through model refinement and reasonable estimates of the initial aerosol PSD, comparisons between the CFD predictions and available in vivo data resulted in relative differences that were <15% when averaged over the regions of interest for each of the three inhalation waveforms considered. With the final set of model parameters, absolute differences within individual regions were approximately 0 to 4.8%. This agreement is acceptable considering the variability associated with typical human subject inhaler testing, as with the study of Newman et al.,⁽⁶²⁾ together with the physical complexity of the aerosol drug delivery process. Specifically, factors increasing the variability in the human subjects study of Newman et al.⁽⁶²⁾ include the evaluation of multiple adult subjects with different airway geometries and inspiratory waveforms. The CFD simulations are complex due to the presence of transient and turbulent flow, multiple phases (air and particles), moving geometric boundaries, and the need for approximations that enable simulations of the vast respiratory system.

The process implemented in this study was to select all model parameters a priori and compare the model results with the available in vivo data. This approach was implemented in order to demonstrate the predictive power of the CFD SIP-based whole-airway simulations. In contrast, a study that varies multiple parameters to match the target data would be less convincing of model capabilities. During this process, it was determined that all model parameters described in the Methods were appropriate for matching the in vivo data except for the initial estimate of the particle sizing flow rate used for the 65 LPM waveform.

Based on agreement with in vivo data across the three considered inhalation waveforms, a second primary finding of this study is the use of constant flow rates to characterize the PSD exiting the inhaler and entering the CFD model at the MT. Our previous in vitro experiments and CFD simulations both demonstrated that a square-wave approximation of the time-averaged mean of an inhalation waveform under-predicts upper TB deposition compared with implementing the full inhalation waveform.^(16,17) The study of Finlay and Gehmlich⁽⁷⁶⁾ demonstrated that a steady state particle sizing flow rate that was representative of a full inhalation profile could be used with negligible changes to the predicted PSD for two different DPIs. These findings led Tian et al.⁽⁶¹⁾ to consider a constant particle sizing flow rate for a DPI equal to AVG(PIFR, Mean) of an inhalation waveform for determining the initial PSD entering the MT. This steady state average flow rate was previously reasoned by Kleinstreuer and co-workers⁽⁹⁸⁾ to provide an estimate of deposition by impaction that is very similar to considering a full transient inhalation waveform. Tian et al.⁽⁶¹⁾ demonstrated for the 99 LPM PIFR waveform that use of a particle sizing flow rate equal to AVG(PIFR, Mean) provided good agreement to the in vivo data of Newman et al.,⁽⁶²⁾ including an accurate prediction of MT deposition. In the current study, PSDs were initially implemented using particle sizing flow rates that were very close to the value of AVG(PIFR, Mean) for the 99 and 54 LPM waveforms, and approximately 8 LPM below the value of AVG(PIFR, Mean) for the 65 LPM waveform. Surprisingly, the model predictions matched the in vivo data to a high degree for the 99 and 54 LPM waveforms, with larger differences observed for the intermediate waveform case. In summary, the current study indicates that the best estimate for a constant particle sizing flow rate may be the value of AVG(PIFR, Mean), whereas values closer to the time-averaged mean may introduce inaccuracies in the model predictions. As described by Finlay and Gehmlich,⁽⁷⁶⁾ the selection of the best constant particle sizing flow rate may depend on the time course of inhaler emptying and therefore may be inhaler dependent, leading to the need for judicious selection.

As described, the current study provides evidence that a steady state flow rate can be used to approximate the PSD generated by a full inhalation profile. The fact that the resulting MT deposition matched the in vivo data and varied across waveforms (DF range of 66%–78%) implies that this constant flow approach may also be used to estimate airway deposition. Kleinstreuer and co-workers⁽⁹⁸⁾ reported that deposition by impaction in a bifurcating upper airway model during transient inspiratory flow could be approximated using an equivalent flow rate calculated as AVG(PIFR, Mean). Similarly, Finlay and Gehmlich⁽⁷⁶⁾ reported negligible differences in MT deposition determined using multiple inspiratory profiles compared with representative constant flow rates. For a DPI aerosol, Longest and co-workers^(16,17) illustrated that the use of the time-averaged mean flow rate under predicted upper TB deposition compared with estimates that simulated the full quick-and-deep inspiration profile for two inhalers, highlighting the need for a higher representative constant flow rate. Tian et al.⁽¹⁶⁾ also illustrated that constant square waveform simulations could not be replaced with steady state simulations for predicting MT deposition due to transient flow effects in the upper airways. Considered together, this evidence implies that both the PSD and MT aerosol deposition occurring with a DPI during realistic inspiratory conditions can be estimated using the corresponding AVG(PIFR, Mean) constant flow rate. This hypothesis was not tested in the current study and will require further assessment. In contrast, multiple other studies are pursuing an experimental approach that allows for reproduction of the full inspiratory profile together with constant flow through a cascade impactor using a mixing inlet arrangement.^(74,75,99) Additional studies are needed to evaluate the use of a constant representative flow rate calculated as AVG(PIFR, Mean) vs. reproducing different inspiratory profiles for in vitro aerosol size characterization and predictions of lung dose.

Future model improvements and further validations are needed to better estimate the whole-airway CFD approach. Due to the 10 s breath-hold, a large majority of the aerosol deposits in the alveolar region. Expansion of the SIP modeling approach is required to enable predictions of aerosol exhalation with shorter breath-hold periods. In the current study, comparisons were made to available 2D gamma scintigraphy data. The capture of a pulmonary fraction in the central lung region due to the coronal projection is a known limitation of this approach that was not taken into account with the model. Furthermore, the estimate of the central lung region including all bifurcations through B7 is made visually and is somewhat subjective.

Ideally, future model validations will consider patient-specific cases and/or 3D in vivo data.⁽³²⁾ Comparisons with 3D data will eliminate projection differences and will provide a more refined segmentation of the lungs. However, the accuracy of model predictions will be influenced by the degree to which a shell^(33,100) or similar 3D lung geometry mapping can capture bifurcating airway anatomy. The recent study by Conway et al.⁽³²⁾ provides an excellent 3D data set for future model validations that carefully reports particle size and breathing conditions for a nebulized aerosol. It is noted that Conway et al.⁽³²⁾ found segmenting the lung using a 2D or 3D approach produced large differences in predicted peripheral to central lung deposition ratios.

The study of Newman et al.⁽⁶²⁾ reports mean (and range) peripheral to central (P/C) ratios for the 99, 65, and 45 LPM inspiratory waveforms of 0.9 (0.6–1.3), 1.0 (0.8–1.3), and 1.0 (0.7–1.5). Based on the provided ranges and associated variability, these values are not statistically different and imply that the P/C ratio of the Novolizer DPI with a budesonide formulation is flow rate independent. This flow rate independence was described by Newman et al.⁽⁶²⁾ as being due to a higher flow rate producing the competing effects of a smaller aerosol and an increased potential for impaction for each particle size. The Newman et al.⁽⁶²⁾ study implies that the intermediate (I) region lung deposition values were not used in calculating the P/C ratios.

In the current study, intermediate deposition values were not determined explicitly. Therefore, it is not possible to calculate P/C ratios using the approach of Newman et al.⁽⁶²⁾ in order to further validate model performance. Instead, a different and potentially more meaningful P/C ratio can be calculated using the SIP model data and defining the P airways as the alveolar region and the C airways as the TB region. Based on the alveolar and TB data provided in Table 2, together with the refined data in Table 3, the CFD predicted P/C ratios for the 99, 65, and 54 LPM waveforms are 1.8, 1.1, and 1.1, respectively. Unfortunately, ranges of values are not available at each flow rate, but could be calculated using characteristic large, medium and small airways, as with Delvadia et al.⁽⁵⁹⁾ These predicted P/C ratios indicate a 1.6-fold higher value with the 99 LPM waveform compared with the 65 and 54 LPM waveforms. Therefore, it appears that the Novolizer DPI provides better deep lung penetration of the aerosol due to improved deaggregation as flow rate is increased to a value of 99 LPM. These results lead to the observation that the CFD whole-airway evaluation approach may enable a more sensitive and improved understating of aerosol deposition in the lungs compared with current 2D in vivo imaging techniques. Similarly, 3D SPECT imaging may provide significantly enhanced knowledge of lung aerosol distribution compared with 2D gamma scintigraphy. Furthermore, these CFD predictions may have important implications in predicting the efficacy of inhaled medications depositing in the intended targets of the TB or alveolar airways.

Two primary limitations of the current simulations include the use of a fixed upper airway geometry and an average fixed lung ventilation distribution estimated for healthy adults. While wall motion of the alveolar model was considered, the MT and TB airways were assumed rigid. In contrast, the glottis is expected to expand during inhalation, and Scheinherr et al.⁽¹⁰¹⁾ recently reported that dynamic change in glottic size occurred in approximately 50% of the population studied. The in vivo data set used for model comparisons was based on healthy individuals, motivating the application of a disease-free lung model in this study.

Future considerations of aerosol delivery to diseased lungs will need to account for the associated heterogeneous changes in lobar ventilation. Regional ventilation as a function of obstructive lung disease can be predicted using whole-lung 1D or lumped parameter models, as describe by Wongviriyawong et al.⁽¹⁰²⁾ Greenblatt et al.⁽¹⁰³⁾ recently used theoretical lung modeling to explain changes in lobar deposition of inhaled aerosols associated with bronchoconstriction. Using a different approach, Oakes et al.⁽⁵⁷⁾ implemented downstream resistance and compliance approximations to predict disease-associated heterogeneous lung ventilation in simulations of aerosol deposition in rat lungs. Coupling of the SIP approach with a whole-lung resistance and compliance model is needed to evaluate changes in heterogeneous lung ventilation associated with disease.

In conclusion, the developed whole-airway simulation approach was shown to match regional in vivo deposition results accurately across a range of inhalation flow rates for a DPI product. Accurate estimates of the initial PSDs were required as model inputs to enable matching the in vivo data. Specifically, it was determined that a constant particle sizing flow rate could be used to assess the PSD, which was calculated as the average of the inhalation waveform PIFR and time-averaged mean flow. Use of this constant sizing flow rate can simplify the in vitro experiments and can potentially be applied to simplify future MT deposition and lung delivery assessments. Considering that PSDs cannot currently be predicted from a first principles approach, results of this study stress that the whole-airway CFD approach is a combination method requiring good initial estimates of the aerosol PSD and well as initial in vitro benchmark deposition data in the upper airways. Results of the whole-airway CFD predictions highlight low delivered dose (<1%) in the lower TB airways at all inhalation waveforms considered. Furthermore, a P/C ratio defined based on the alveolar and TB airways displayed sensitivity and flow rate dependence that were not observed with the previous in vivo study. Future work remains to validate the model predictions with additional inhalers, evaluate model performance with 3D in vivo data, consider techniques to simplify and standardize the CFD simulations, expand the SIP approach to include disease-specific changes in lung ventilation, and apply the developed model techniques to predict the efficacy of inhaled medications.

Abbreviations Used

1-D

one dimensional

3-D

two dimensional

B#

airway bifurcation number

C

central

CFD

computational fluid dynamics

COPD

chronic obstructive pulmonary disease

CT

computed tomography

DF

deposition fraction

DPI

dry powder inhaler

EXP

experimental

FRC

functional residual capacity

HPLC

high performance liquid chromatography

I

intermediate

LL

left lower (lung lobe)

LRN

Low Reynolds Number

LPM

liters per minute

MDI

metered dose inhaler

MMAD

mass median aerodynamic diameter

MT

mouth–throat

NGI

Next Generation Impactor

P

peripheral

PIFR

peak inspiratory flow rate

PSD

polydisperse size distribution

QD

quick-and-deep

SD

slow-and-deep or standard deviation

SIP

stochastic individual pathway

SMI

softmist inhaler

SPECT

single-photon emission computed tomography

TB

tracheobronchial

Acknowledgments

Katharina Bormann and Xiangyin Wei are acknowledged for their assistance in measuring the initial size of the Novolizer DPI. The authors are grateful to Dr. Peter Byron for his review of the manuscript and useful discussions. This study was supported by Award U01 FD004570 from the US FDA and Award R01 HL107333 from the National Heart, Lung, and Blood Institute. The content is solely the responsibility of the authors and does not necessarily represent the official views of the US FDA, the National Heart, Lung, and Blood Institute or the National Institutes of Health.

Author Disclosure Statement

The authors declare there are no financial conflicts of interest.