Abstract
Three-dimensional density maps of biological specimens from cryo-electron microscopy (cryo-EM) can be interpreted in the form of atomic models that are modeled into the density, or they can be compared to known atomic structures. When the central axis of a helix is detectable in a cryo-EM density map, it is possible to quantify the agreement between this central axis and a central axis calculated from the atomic model or structure. We propose a novel arc-length association method to compare the two axes reliably. This method was applied to 79 helices in simulated density maps and six case studies using cryo-EM maps at 6.4–7.7 Å resolution. The arc-length association method is then compared to three existing measures that evaluate the separation of two helical axes: a two-way distance between point sets, the length difference between two axes, and the individual amino acid detection accuracy. The results show that our proposed method sensitively distinguishes lateral and longitudinal discrepancies between the two axes, which makes the method particularly suitable for the systematic investigation of cryo-EM map–model pairs.
Keywords: : axis, cryo-electron microscopy, fitting, helix, image, protein structure, secondary structure, spline
1. Introduction
The Electron Microscopy Data Bank (EMDB) archives three-dimensional (3D) density maps, also referred to as 3D images, which exhibit a wide range of spatial resolution levels, from about 2 Å to more than 80 Å. Density maps with better than 10 Å resolution are frequently linked to corresponding atomic models or structures deposited in the Protein Data Bank (PDB). In rare cases, corresponding atomic structures of the same specimen are solved at atomic resolution with complementary biophysical techniques. In most cases, atomic models are either derived directly from reliable near-atomic resolution maps at about 3 Å resolution or indirectly from a more challenging interpretation of lower resolution maps. Many atomic models derived from density maps at medium resolution of 4–8 Å are based on the fitting of known atomic structures (Rossmann, 2000; Wriggers and Birmanns, 2001; Schröder et al., 2007). In contrast, de novo modeling does not rely on a known atomic structure (Lindert et al., 2009; Al Nasr et al., 2010, 2012; Baker et al., 2011; Al Nasr et al., 2014; Al Nasr and He, 2016). However, despite active development of the de novo approach (Baker et al., 2011; Biswas et al., 2012, 2015, 2016; Lindert et al., 2012; Al Nasr et al., 2014; Al Nasr and He, 2016), no mature tool exists for deriving atomic models for medium-resolution density maps.
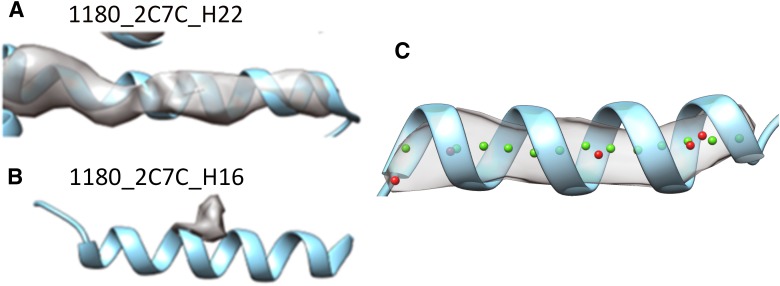
Due to diverse origins, reliability, and quality of the deposited cryo-electron microscopy (cryo-EM) map–model pairs, it is common to see local variations in maps when compared to atomic models or structures (Fig. 1). These variations can be due to conformational variability, map artifacts, modeling error, or other systematic differences (Wriggers and He, 2015). For example, the helix in Figure 1A has a strong cylinder characteristic, but the density in Figure 1B, at the same density threshold, does not resemble a cylinder despite being part of the same density map. A similar problem may occur in a β-sheet, a turn, or a loop. As more and more map–model pairs are being deposited in the databases, there is a need to quantify the level of local similarity of such structural features.
FIG. 1.
Local density variation at helix regions and the problem of evaluation between a set of points and the atomic model of a helix. The density (gray) at the helix location is superimposed with the atomic model (blue ribbon). The EMDB ID and the PDB ID are labeled for two cases in (A) and (B). (C) The set of points (red) in the approximate location of the helix axis is assigned to the density map. The location of the helix axis (green) was calculated from the atomic model (blue ribbon). EMDB, Electron Microscopy Data Bank; PDB, Protein Data Bank.
Secondary structure elements such as helices and β-sheets are the most striking structural features visible in medium-resolution images. In general, helices become visible in cryo-EM maps at resolution levels better than about 10 Å, whereas β-sheets begin to be visible at resolution levels better than about 8 Å (Baker et al., 2007). Various computational methods have been developed to detect helices and β-sheets (Jiang et al., 2001; Kong et al., 2004; Dal Palu et al., 2006; Baker et al., 2007; Zeyun and Bajaj, 2008), including recent methods SSEhunter, SSELearner, VolTrac, and SSETracer (Baker et al., 2007; Rusu and Wriggers, 2012b; Si et al., 2012; Si and He, 2013). As more methods become available to detect secondary structure elements from medium-resolution density maps, it becomes important to quantify the geometry of the detected features. As a first step toward this aim, we focus on helices in this article.
The accurate measurement of the discrepancy between an atomic representation of the helix and the corresponding cryo-EM density of the helix is needed for two purposes: (1) to validate the accuracy of secondary structure detection techniques for cryo-EM density maps and (2) to quantify the agreement of map–model pairs of a helix as part of a validation of the map or model (Wriggers and He, 2015). Since a helix appears as a cylinder in the density map, its axial line forms a natural fiducial marker for it. In numerical applications, this axis line is typically represented by a set of points with sub-Angstrom spacing that is centered in the cylindrical density (Wriggers and He, 2015). In this study, we investigate the problem of quantifying the agreement between a set of points located at the central axis of a helix (red points in Fig. 1C) and the atomic model of a helix (ribbon in Fig. 1C). This article compares four measures for estimating such agreement.
For helices from different biophysical origins where a structure is available to serve as a reference, it is straightforward to report the number of helices missed in the detection (false negatives) or incorrectly detected (false positives), but it is not trivial to provide a suitable geometric measurement of the structural discrepancy. Three methods have been previously used in the evaluation of helical similarity. The first one considers the length of the axial lines. If the length is within one turn difference from the length of the central axis of a helix model, the helix is considered a detected helix (Baker et al., 2007). This method evaluates the longitudinal difference between two lines, but it does not consider the lateral (cross-) displacement of the two axial lines. The second method evaluates individual amino acids and marks an amino acid as detected if its Cα atom is located within 2.5 Å distance from a designated helix voxel in the image (Kong et al., 2004). The sensitivity (proportion of true positives) and specificity (proportion of true negatives) can be calculated accordingly for each protein. There are two drawbacks to the counting of amino acids. One is that in the original form this method did not provide a measure of accuracy for individual helices (although we generalize it in Table 1 below to specific helices). The second is that the total protein accuracy is dependent on the radius threshold, and it is not clear if 2.5 Å is the best choice (we will test various thresholds shown in Table 1 and also provide a consensus radius for each helix). The third and more recently introduced method calculates the two-way distance between two sets of points (Si and He, 2014; He et al., 2015). One set is detected from the density map and the other is calculated from the atomic model or structure by averaging the geometric center of four consecutive amino acids. This method (see Section 2) mixes both lateral and longitudinal discrepancies between the axis lines in one parameter.
Table 1.
Averaged Radial Distance Between Backbone Centroids and the Helix Axis That Is Either Calculated From the PDB Structure or Assigned to the Simulated Density Map
| PDB | Sensitivity (%)f | ||||||
|---|---|---|---|---|---|---|---|
| Indexa | Helix IDb | r100c | r80d | Image r80e | S2.0 | S2.5 | S3.0 |
| 1 | 1FLP_1_4-19 | 1.99 | 1.98 | 2.40 | 53.33 | 86.67 | 100.00 |
| 2 | 1HZ4_6_107-123 | 1.96 | 1.95 | 1.86 | 93.75 | 100.00 | 100.00 |
| 3 | 3E46_7_160-171 | 2.02 | 1.96 | 2.24 | 63.64 | 100.00 | 100.00 |
| 4 | 1HZ4_4_67-83 | 1.97 | 1.96 | 2.08 | 81.25 | 100.00 | 100.00 |
| 5 | 1NG6_9_136-146 | 2.06 | 1.97 | 1.98 | 90.00 | 100.00 | 100.00 |
| 6 | 2OVJ_3_390-401 | 2.00 | 1.98 | 2.10 | 72.73 | 100.00 | 100.00 |
| 7 | 3E46_9_190-199 | 2.02 | 1.97 | 2.00 | 66.67 | 100.00 | 100.00 |
| 8 | 1NG6_1_3-16 | 1.99 | 1.96 | 2.24 | 69.23 | 100.00 | 100.00 |
| 9 | 2OVJ_9_493-504 | 2.08 | 2.06 | 2.50 | 45.45 | 90.91 | 100.00 |
| 10 | 1HZ4_12_209-225 | 1.97 | 1.96 | 2.39 | 62.50 | 93.75 | 100.00 |
| 11 | 2OVJ_10_514-533 | 2.08 | 1.95 | 2.28 | 63.16 | 94.74 | 100.00 |
| 12 | 3IEE_1_33-56 | 2.03 | 1.96 | 2.27 | 56.52 | 95.65 | 100.00 |
| 13 | 1NG6_3_47-71 | 2.08 | 1.97 | 2.03 | 75.00 | 100.00 | 100.00 |
| 14 | 3E46_4_106-118 | 2.10 | 1.96 | 2.13 | 75.00 | 100.00 | 100.00 |
| 15 | 1NG6_6_97-110 | 1.99 | 1.95 | 2.35 | 69.23 | 84.62 | 100.00 |
| 16 | 1LWB_2_17-28 | 2.07 | 1.96 | 2.17 | 72.73 | 100.00 | 100.00 |
| 17 | 3IEE_5_139-178 | 2.23 | 1.97 | 2.05 | 71.05 | 97.37 | 100.00 |
| 18 | 1HZ4_20_334-346 | 2.02 | 1.99 | 2.29 | 58.33 | 91.67 | 100.00 |
| 19 | 1FLP_2_21-35 | 2.05 | 2.00 | 2.50 | 64.29 | 85.71 | 85.71 |
| 20 | 3E46_8_176-185 | 2.10 | 1.95 | 2.25 | 44.44 | 100.00 | 100.00 |
| 21 | 1HG5_10_229-257 | 2.15 | 1.95 | 2.22 | 82.14 | 96.43 | 100.00 |
| 22 | 1HZ4_1_5-24 | 1.99 | 1.96 | 2.00 | 84.21 | 100.00 | 100.00 |
| 23 | 1NG6_4-5_74-90 | 2.04 | 1.95 | 1.92 | 87.50 | 100.00 | 100.00 |
| 24 | 1FLP_9-10_124-141 | 2.13 | 2.00 | 2.56 | 47.06 | 76.47 | 100.00 |
| 25 | 1NG6_2_20-39 | 2.00 | 1.95 | 2.13 | 73.68 | 94.74 | 100.00 |
| 26 | 3IEE_2_59-72 | 2.21 | 2.02 | 2.18 | 58.33 | 91.67 | 91.67 |
| 27 | 1FLP_6_82-97 | 2.00 | 1.94 | 2.32 | 53.33 | 100.00 | 100.00 |
| 28 | 1FLP_5_59-76 | 2.00 | 1.97 | 2.07 | 64.71 | 94.12 | 94.12 |
| 29 | 1UNF_7_125-138 | 2.05 | 1.98 | 2.28 | 84.62 | 100.00 | 100.00 |
| 30 | 1LWB_5_77-96 | 2.18 | 1.96 | 2.25 | 68.42 | 89.47 | 100.00 |
| 31 | 1HG5_9_191-221 | 2.06 | 1.97 | 1.93 | 86.67 | 96.67 | 100.00 |
| 32 | 1UNF_13_223-237 | 2.14 | 1.97 | 2.28 | 64.29 | 100.00 | 100.00 |
| 33 | 1HZ4_17_287-304 | 2.14 | 1.95 | 2.26 | 76.47 | 94.12 | 100.00 |
| 34 | 1HZ4_3_47-64 | 2.04 | 1.94 | 2.30 | 70.59 | 88.24 | 94.12 |
| 35 | 1FLP_7-8_103-120 | 2.04 | 1.97 | 2.22 | 70.59 | 94.12 | 100.00 |
| 36 | 1HZ4_11_188-202 | 1.98 | 1.94 | 2.01 | 71.43 | 92.86 | 100.00 |
| 37 | 1LWB_4_58-74 | 2.09 | 1.98 | 2.22 | 68.75 | 87.50 | 93.75 |
| 38 | 1HG5_3_56-66 | 2.00 | 1.97 | 1.96 | 90.00 | 100.00 | 100.00 |
| 39 | 2OVJ_7_451-463 | 2.06 | 1.97 | 2.30 | 66.67 | 83.33 | 100.00 |
| 40 | 3E46_1_3-18 | 2.15 | 1.97 | 2.26 | 60.00 | 93.33 | 100.00 |
| 41 | 2OVJ_2_364-376 | 2.14 | 2.03 | 2.28 | 66.67 | 91.67 | 100.00 |
| 42 | 1UNF_3-4_69-80 | 2.03 | 1.93 | 2.71 | 63.64 | 63.64 | 90.91 |
| 43 | 2OVJ_8_467-485 | 1.99 | 1.97 | 2.27 | 61.11 | 94.44 | 100.00 |
| 44 | 2OVJ_11-12_536-543 | 2.04 | 1.97 | 2.99 | 28.57 | 85.71 | 100.00 |
| 45 | 1HG5_5_91-99 | 2.05 | 2.00 | 4.10 | 62.50 | 87.50 | 87.50 |
| 46 | 1HZ4_16_267-283 | 1.98 | 1.96 | 2.02 | 81.25 | 87.50 | 100.00 |
| 47 | 1HZ4_8_149-162 | 2.00 | 1.94 | 2.02 | 84.62 | 100.00 | 100.00 |
| 48 | 1LWB_6_101-119 | 2.11 | 1.96 | 2.81 | 50.00 | 77.78 | 83.33 |
| 49 | 1HZ4_18_307-324 | 2.06 | 1.95 | 2.35 | 82.35 | 88.24 | 100.00 |
| 50 | 1NG6_7-8_116-130 | 2.13 | 2.03 | 2.66 | 42.86 | 78.57 | 92.86 |
| 51 | 1HG5_6_115-141 | 2.08 | 1.99 | 2.07 | 76.92 | 96.15 | 96.15 |
| 52 | 3E46_6_138-153 | 2.68 | 1.99 | 3.39 | 53.33 | 73.33 | 80.00 |
| 53 | 1UNF_12_209-219 | 2.14 | 1.99 | 2.62 | 50.00 | 80.00 | 90.00 |
| 54 | 3IEE_8_240-263 | 2.25 | 1.97 | 2.03 | 77.27 | 95.45 | 100.00 |
| 55 | 3E46_5_128-136 | 2.04 | 1.96 | 5.23 | 25.00 | 62.50 | 62.50 |
| 56 | 3IEE_9_271-284 | 2.24 | 1.96 | 4.66 | 41.67 | 58.33 | 58.33 |
| 57 | 3IEE_4_103-135 | 2.02 | 1.99 | 2.14 | 75.00 | 90.63 | 100.00 |
| 58 | 1HG5_2_39-49 | 2.00 | 1.94 | 1.93 | 90.00 | 100.00 | 100.00 |
| 59 | 1HZ4_9-10_168-185 | 2.10 | 1.97 | 2.52 | 64.71 | 76.47 | 100.00 |
| 60 | 1HG5_4_72-88 | 2.09 | 1.98 | 2.69 | 62.50 | 75.00 | 87.50 |
| 61 | 3IEE_6_185-205 | 2.27 | 2.20 | 2.31 | 58.82 | 88.24 | 100.00 |
| 62 | 3IEE_7_213-231 | 2.02 | 1.97 | 2.11 | 72.22 | 83.33 | 94.44 |
| 63 | 2OVJ_5_415-427 | 1.98 | 1.95 | 2.09 | 75.00 | 100.00 | 100.00 |
| 64 | 1LWB_1_5-11 | 2.02 | 1.95 | 1.96 | 100.00 | 100.00 | 100.00 |
| 65 | 1HG5_1_20-29 | 2.07 | 2.00 | 2.50 | 66.67 | 88.89 | 100.00 |
| 66 | 1HZ4_5_87-103 | 2.05 | 1.95 | 2.17 | 68.75 | 93.75 | 100.00 |
| 67 | 1FLP_3_37-41 | 2.11 | 2.06 | 2.13 | 75.00 | 100.00 | 100.00 |
| 68 | 1UNF_5_85-100 | 2.05 | 2.01 | 2.96 | 33.33 | 53.33 | 80.00 |
| 69 | 1UNF_2_47-58 | 2.00 | 1.97 | 2.31 | 63.64 | 100.00 | 100.00 |
| 70 | 1HG5_7_161-179 | 2.08 | 1.91 | 2.18 | 66.67 | 94.44 | 100.00 |
| 71 | 2OVJ_6_439-447 | 2.10 | 1.95 | 2.45 | 87.50 | 100.00 | 100.00 |
| Average values: | 2.07 | 1.97 | 2.37 | 67.40 | 90.97 | 96.66 | |
Results computed with SSETracer.
Index of the data as it appears in Figures 4 and 5. Sorted approximately by longitudinal discrepancy.
PDB ID, the chain ID in the PDB file, the helix ID, and the first and last amino acid index. Sequentially adjacent helices that share same direction are combined.
Averaged amino acid backbone centroid distance from the axis.
Radius for 80% of helix centroids to be within the radial distance from the axis calculated from PDB file.
Radius for 80% of helix centroids to be within the radial distance from the axis detected from the density image using SSETracer.
Sensitivity calculated as A/B using a specified radius threshold, where A is the number of detected AAs and B is the total number of AAs of the helix.
PDB, Protein Data Bank.
In this article, we propose a novel arc-length association method that distinguishes the lateral and longitudinal discrepancies. In Section 2, we introduce our new approach and the statistical validation techniques used in this article. Section 3 presents a comprehensive systematic comparison of the four helix distance measures on simulated and experimental density maps with associated atomic structures or models. Although each of the earlier methods captures a particular aspect of the distance measurement, there has not been a comprehensive evaluation of their performance. Finally, Section 4 summarizes the main advantages and disadvantages of the proposed arc-length association method.
2. Methodology
2.1. The detection of helices in cryo-EM density maps
In a medium-resolution density map, a helix appears as a cylinder, and various methods exist to detect the location of these helices. We applied SSETracer (Si and He, 2013) to detect the location of helices in a density map. SSETracer detects helices (and β-sheets) based on a characterization of local density features such as local structure tensor, local thickness, continuity of the skeleton, and density value. A detected helix is represented by a set of points located along the central axis of the helix (Fig. 1C). The current implementation of SSETracer contains a modified step in the axis extension to enhance the geometric characterization of the helix.
2.2. Representation of a helix in an atomic model
The actual axis of a helix was calculated from its atomic structure to compare it with the set of points detected from the density map. Given the backbone of a helix, the central axis was calculated by averaging four consecutive geometric centers of amino acids in the helix (Fig. 1C). Since the line formed by such points is expected to be shorter than the actual axis due to averaging, the end of the axis was determined by projecting the first/last Cα atom to the line of first/last segment of the axis, respectively. The DSSP annotation of secondary structures (as available at the PDB web site) was used to define the amino acid range of a helix in the atomic model or structure.
2.3. Splines of the axes
Each line is represented by a set of points. The number of points and the spacing among points often differ between the two sets. To measure the discrepancies between two sets of points, each set was first interpolated using a cubic Hermite spline.
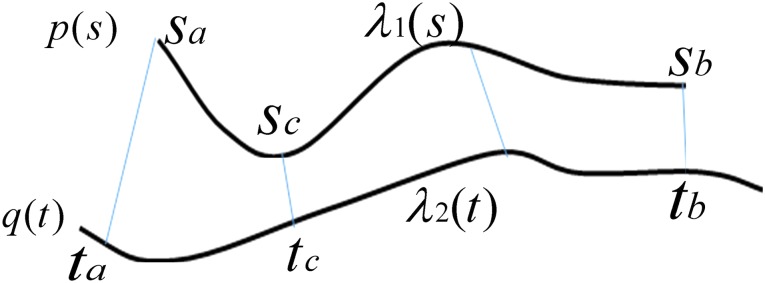
2.4. Arc-length association method for two splines
When comparing two splines, it is important to characterize both the lateral and the longitudinal discrepancies. Let the two lines be represented as splines, where N1 and N2 are the number of points, respectively (Fig. 2):
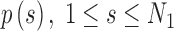 |
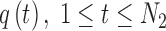 |
FIG. 2.
The arc-length association method to compare two splines.
An important question in the comparison is how to correspond a pair of points from the two splines. Our approach initially associated the closest pair of points. Let sc and tc be the closest points of the two lines. Two points correspond if they have the same arc length from sc and tc, respectively.
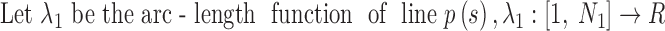 |
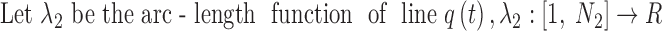 |
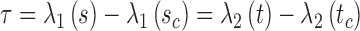 |
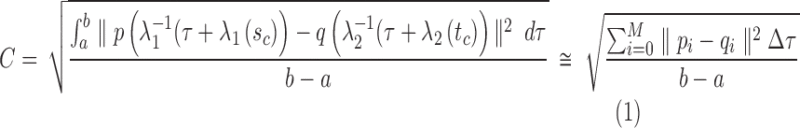 |
where  and
and  . sa is the point on p where
. sa is the point on p where  , and sb is the point on p where
, and sb is the point on p where 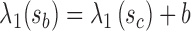 . Similarly, ta is the point on q where
. Similarly, ta is the point on q where 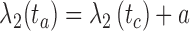 , and tb is the point on q where
, and tb is the point on q where 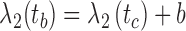 . C measures the lateral (cross-) discrepancy between two splines. In this case, pi and qi are the corresponding points of the two lines. They are determined based on the arc length from pi to
. C measures the lateral (cross-) discrepancy between two splines. In this case, pi and qi are the corresponding points of the two lines. They are determined based on the arc length from pi to 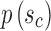 and qi to
and qi to 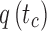 , respectively. M is the number of line segments between
, respectively. M is the number of line segments between 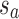 and sb. In addition to C, we introduce a measure of longitudinal discrepancy L (i.e., the non-overlapping arc length between the two splines).
and sb. In addition to C, we introduce a measure of longitudinal discrepancy L (i.e., the non-overlapping arc length between the two splines).
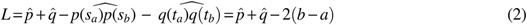
Here the arc length of a line l is represented as 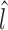 . L can result from a relative shift and/or a length difference.
. L can result from a relative shift and/or a length difference.
We also have a normalized measure P to characterize the proportion of L relative to the length of the union of both lines:
 |
2.5. Two-way distance between two splines
Given two axes of the helix, one detected in the image and one calculated from the atomic model, the distance between them can be calculated. Each axis is represented as a set of points along the line; the line is often not straight, particularly for long helices. In addition, the number of points on the two lines is often not the same. Let S be a set of points detected in a density map, and let 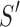 be the set of points calculated from the model. Every two consecutive points in each set define a line segment, and therefore, an axis can be thought of as having a set of line segments. The distance between two sets of points was estimated as in Equation 4. For each point
be the set of points calculated from the model. Every two consecutive points in each set define a line segment, and therefore, an axis can be thought of as having a set of line segments. The distance between two sets of points was estimated as in Equation 4. For each point 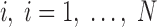 on S, we calculated
on S, we calculated 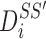 as the projection distance from i to the closest line segment of
as the projection distance from i to the closest line segment of 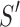 . If the projection of i was outside the line segment, the distance between i and the closest endpoint of the line segment was used as the projection distance. Similarly,
. If the projection of i was outside the line segment, the distance between i and the closest endpoint of the line segment was used as the projection distance. Similarly, 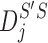 was calculated as the distance from each point
was calculated as the distance from each point 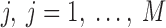 of
of 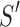 to the closest line segment of S.
to the closest line segment of S.
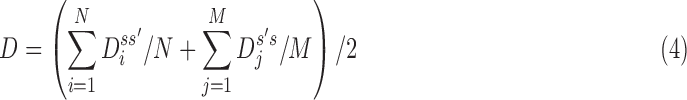 |
The distance as calculated in Equation 4 is a two-way distance. One way represents the distance from one line to the other, and the other represents the reverse. The larger the distance, the larger the misalignment is between the two lines. D is a mixture of lateral and longitudinal discrepancies.
2.6. Sensitivity and specificity for detecting amino acids
Instead of characterizing the geometry of helical axes, the detected amino acids can also be counted as a way to assess the accuracy of a helix. The backbone (N, Cα, C, and O) centroid was used as a representative position of the amino acid. If it lies within a certain threshold radius of the helix axis detected from the image, the amino acid was marked as detected. We reported the results using different thresholds: 2.0, 2.5, and 3 Å. (See Eq. 5 for the definition of the S2.5 value at radius 2.5 Å.) The sensitivity of each helix at the given radius was calculated as the ratio between the number of detected amino acids and the total number of amino acids. Since the sensitivity values differ between helices, and in some cases saturate at 100% for the fixed radius thresholds, we also included in Table 1 the helix-specific radii where the sensitivity reached 80% and 100% (denoted r80 and r100). We argue below that the r80 values provide a good indication of the positional accuracy afforded by the helical axis placement. The sensitivity values of all the helices can be averaged over the entire protein if a total value is required.
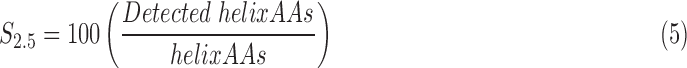 |
The specificity needs to take into account the number of nonhelix amino acids. A simple way to compute specificity is to consider the ratio between the number of incorrectly detected amino acids (Fp) and the total number of nonhelix amino acids for each protein (Eq. 6). We note that specificity values are not available for individual helices, and different proteins also have a different number of amino acids attributed to helices.
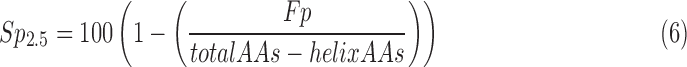 |
3. Results and Discussion
3.1. The data sets
We used nine proteins, for which the atomic structures were downloaded from the PDB, and their corresponding 3D density maps were simulated at 10 Å resolution using Chimera. Secondary structures were assigned to the atomic structures using DSSP at the PDB web site. The nine proteins include 87 helices comprising four or more amino acids. Eight of the 87 helices are short 310 helices, each of which is adjacent to another helix with a similar orientation. At medium resolution, two consecutive helices with similar orientations appear to be one long helix in the density map, so they were merged into one helix in the test. In addition to the simulated maps, six helix case studies were conducted using the cryo-EM density maps downloaded from the EMDB (Lawson et al., 2011). The cryo-EM density maps and their corresponding atomic structures are EMD-1733-3C91_H (6.8 Å), EMD-5352-3J0R_A (7.7 Å), and EMD-5030-4 V68_BR (6.4 Å). The cryo-EM density maps were aligned with their corresponding structures at download. The density maps of individual chains were extracted from the original density map of multiple chains using a mask of the chain derived from the PDB structure. SSETracer was applied to obtain the position of the helices from all the density maps (Si and He, 2013).
3.2. Lateral and longitudinal discrepancies
A helix can be approximated by a cylinder that is represented by its central axis. The geometric centers of backbone atoms N, C, Cα, and O of the amino acids on a helix lie consistently about 2.07 Å from the central axis (last row of column 3 in Table 1). An effective method to compare a helix in the density map with its atomic model is to compare the relative position of their central axes. We measured the lateral and longitudinal discrepancies of the axial lines to characterize the effect of length difference and positional shift. We noticed that the lateral discrepancies are generally small (column 6 of Table 2), within 1 Å for 62 of the 71 test cases and between 1 and 2 Å for the remaining nine helices. However, the longitudinal discrepancies (column 7 of Table 2) were more than 3 Å in most cases. These results suggest that helical axes are generally positioned in-line (providing confidence in the detection), but there are longitudinal discrepancies that may originate in systematic differences such as conformational variability, map artifacts, or modeling error (Wriggers and He, 2015). The specific longitudinal differences would need to be evaluated further on a case-by-case basis.
Table 2.
Helix Accuracy Measurement for Simulated Map-Structure Pairs Using Axis Length, the Two-Way Distance, the Arc Length, and the Sensitivity and Specificity of Detected Amino Acids
| Helix IDa | TLb | DLc | LDDd | 2-Waye | Cf | Lg(Å) | Ph | Fpior Sp2.5j | S2.5k |
|---|---|---|---|---|---|---|---|---|---|
| 1FLP_1_4-19 | 23.54 | 23.04 | Y | 0.76 | 0.88 | 0.04 | 0.00 | 1 | 86.67 |
| 1FLP_2_21-35 | 20.71 | 19.98 | Y | 0.75 | 0.91 | 1.84 | 0.09 | 0 | 85.71 |
| 1FLP_3_37-41 | 5.99 | 15.06 | N | 2.24 | 0.62 | 10.54 | 0.67 | 4 | 100.00 |
| 1FLP_5_59-76 | 26.84 | 29.43 | Y | 0.57 | 0.74 | 2.59 | 0.09 | 2 | 94.12 |
| 1FLP_6_82-97 | 23.18 | 23.34 | Y | 0.74 | 0.77 | 2.54 | 0.10 | 0 | 100.00 |
| 1FLP_7-8_103-120 | 28.54 | 24.47 | Y | 0.60 | 0.79 | 3.56 | 0.13 | 0 | 94.12 |
| 1FLP_9-10_124-141 | 27.19 | 24.13 | Y | 0.78 | 0.99 | 2.32 | 0.09 | 0 | 76.47 |
| 1FLP Summary: 142 total AAs, 109 helix AAs | 0.92 | 0.81 | 3.35 | 0.17 | 78.79 | 87.84 | |||
| 1HG5_1_20-29 | 14.02 | 17.18 | Y | 1.04 | 0.60 | 8.05 | 0.41 | 2 | 88.89 |
| 1HG5_2_39-49 | 15.89 | 20.82 | Y | 0.79 | 0.39 | 6.41 | 0.30 | 2 | 100.00 |
| 1HG5_3_56-66 | 15.93 | 18.40 | Y | 0.44 | 0.34 | 3.97 | 0.21 | 2 | 100.00 |
| 1HG5_4_72-88 | 24.83 | 20.67 | Y | 0.51 | 0.62 | 7.14 | 0.27 | 1 | 75.00 |
| 1HG5_5_91-99 | 12.82 | 11.30 | Y | 0.81 | 0.91 | 4.93 | 0.34 | 1 | 87.50 |
| 1HG5_6_115-141 | 41.70 | 35.76 | N | 0.37 | 0.54 | 5.38 | 0.13 | 0 | 96.15 |
| 1HG5_7_161-179 | 28.78 | 42.56 | N | 1.78 | 0.56 | 16.58 | 0.38 | 4 | 94.44 |
| 1HG5_9_191-221 | 46.59 | 48.69 | Y | 0.40 | 0.50 | 3.15 | 0.06 | 1 | 96.67 |
| 1HG5_10_229-257 | 44.29 | 41.59 | Y | 0.45 | 0.68 | 2.06 | 0.05 | 0 | 96.43 |
| 1HG5 Summary: 289 total AAs, 170 helix AAs | 0.73 | 0.57 | 6.41 | 0.24 | 86.02 | 90.85 | |||
| 1UNF_1_37-43 | 9.10 | N/A | N | N/A | N/A | N/A | N/A | 0 | 0.00 |
| 1UNF_2_47-58 | 17.39 | 26.80 | N | 1.86 | 0.64 | 13.76 | 0.48 | 1 | 100.00 |
| 1UNF_3-4_69-80 | 18.78 | 13.66 | Y | 0.77 | 0.90 | 4.45 | 0.25 | 0 | 63.64 |
| 1UNF_5_85-100 | 23.10 | 24.11 | Y | 1.63 | 1.30 | 12.35 | 0.42 | 3 | 53.33 |
| 1UNF_6_112-122 | 15.66 | N/A | N | N/A | N/A | N/A | N/A | 0 | 0.00 |
| 1UNF_7_125-138 | 20.12 | 16.73 | Y | 0.33 | 0.40 | 2.86 | 0.15 | 0 | 100.00 |
| 1UNF_12_209-219 | 15.46 | 21.33 | N | 1.38 | 1.22 | 5.88 | 0.28 | 3 | 80.00 |
| 1UNF_13_223-237 | 21.81 | 17.75 | Y | 0.48 | 0.57 | 3.34 | 0.16 | 0 | 100.00 |
| 1UNF Summary: 238 total AAs, 111 helix AAs | 1.08 | 0.84 | 7.11 | 0.29 | 92.23 | 68.37 | |||
| 2OVJ_2_364-376 | 18.85 | 16.45 | Y | 0.50 | 0.52 | 4.08 | 0.21 | 0 | 91.67 |
| 2OVJ_3_390-401 | 17.23 | 16.16 | Y | 0.50 | 0.69 | 0.65 | 0.04 | 0 | 100.00 |
| 2OVJ_5_415-427 | 18.84 | 23.23 | Y | 0.86 | 0.47 | 7.98 | 0.32 | 3 | 100.00 |
| 2OVJ_6_439-447 | 12.73 | 30.72 | N | 3.32 | 0.61 | 20.08 | 0.64 | 5 | 100.00 |
| 2OVJ_7_451-463 | 18.60 | 22.61 | Y | 0.76 | 0.79 | 4.01 | 0.18 | 1 | 83.33 |
| 2OVJ_8_467-485 | 27.74 | 32.53 | Y | 0.80 | 0.90 | 4.79 | 0.15 | 3 | 94.44 |
| 2OVJ_9_493-504 | 17.62 | 16.10 | Y | 0.65 | 0.77 | 1.11 | 0.06 | 1 | 90.91 |
| 2OVJ_10_514-533 | 30.84 | 29.02 | Y | 0.59 | 0.72 | 1.23 | 0.04 | 1 | 94.74 |
| 2OVJ_11-12_536-543 | 12.11 | 6.66 | N | 0.45 | 0.56 | 4.82 | 0.42 | 0 | 85.71 |
| 2OVJ Summary: 201 total AAs, 126 helix AAs | 0.94 | 0.67 | 5.41 | 0.23 | 84.00 | 88.24 | |||
| 3E46_1_3-18 | 22.98 | 23.71 | Y | 0.72 | 0.76 | 4.05 | 0.16 | 0 | 93.33 |
| 3E46_4_106-118 | 19.14 | 17.87 | Y | 0.32 | 0.37 | 1.35 | 0.07 | 1 | 100.00 |
| 3E46_5_128-136 | 12.26 | 5.80 | N | 1.15 | 1.53 | 5.92 | 0.51 | 0 | 62.50 |
| 3E46_6_138-153 | 22.25 | 22.92 | Y | 1.44 | 1.85 | 5.57 | 0.22 | 0 | 73.33 |
| 3E46_7_160-171 | 16.91 | 15.78 | Y | 0.52 | 0.58 | 0.47 | 0.03 | 0 | 100.00 |
| 3E46_8_176-185 | 13.77 | 14.15 | Y | 0.75 | 0.81 | 2.05 | 0.14 | 0 | 100.00 |
| 3E46_9_190-199 | 13.99 | 13.32 | Y | 0.30 | 0.35 | 0.67 | 0.05 | 0 | 100.00 |
| 3E46 Summary: 253 total AAs, 93 helix AAs | 0.74 | 0.89 | 2.87 | 0.17 | 99.08 | 84.88 | |||
| 1LWB_1_5-11 | 9.35 | 17.37 | N | 1.15 | 0.41 | 8.02 | 0.46 | 3 | 100.00 |
| 1LWB_2_17-28 | 17.16 | 15.05 | Y | 0.53 | 0.64 | 1.50 | 0.09 | 0 | 100.00 |
| 1LWB_3_30-36 | 10.94 | N/A | N | N/A | N/A | N/A | N/A | 0 | 0.00 |
| 1LWB_4_58-74 | 24.83 | 20.39 | Y | 0.50 | 0.60 | 3.85 | 0.16 | 0 | 87.50 |
| 1LWB_5_77-96 | 30.07 | 27.63 | Y | 0.46 | 0.54 | 3.04 | 0.10 | 0 | 89.47 |
| 1LWB_6_101-119 | 28.31 | 25.06 | Y | 0.99 | 1.24 | 5.09 | 0.17 | 0 | 77.78 |
| 1LWB Summary: 122 total AAs, 82 helix AAs | 0.73 | 0.69 | 4.30 | 0.20 | 92.50 | 80.49 | |||
| 1NG6_1_3-16 | 20.04 | 19.08 | Y | 0.52 | 0.60 | 0.92 | 0.05 | 1 | 100.00 |
| 1NG6_2_20-39 | 29.44 | 28.12 | Y | 0.36 | 0.41 | 2.42 | 0.08 | 0 | 94.74 |
| 1NG6_3_47-71 | 37.38 | 35.36 | Y | 0.32 | 0.51 | 1.28 | 0.03 | 1 | 100.00 |
| 1NG6_4-5_74-90 | 26.00 | 23.28 | Y | 0.25 | 0.43 | 2.18 | 0.09 | 0 | 100.00 |
| 1NG6_6_97-110 | 20.06 | 18.00 | Y | 0.46 | 0.54 | 1.45 | 0.07 | 1 | 84.62 |
| 1NG6_7-8_116-130 | 23.58 | 17.79 | N | 0.73 | 0.86 | 5.26 | 0.23 | 0 | 78.57 |
| 1NG6_9_136-146 | 15.70 | 14.52 | Y | 0.28 | 0.35 | 0.52 | 0.03 | 1 | 100.00 |
| 1NG6 Summary: 148 total AAs, 116 helix AAs | 0.42 | 0.53 | 2.00 | 0.08 | 87.50 | 92.24 | |||
| 3IEE_1_33-56 | 35.41 | 33.71 | Y | 0.53 | 0.67 | 1.25 | 0.04 | 1 | 95.65 |
| 3IEE_2_59-72 | 20.76 | 20.06 | Y | 0.76 | 0.91 | 2.45 | 0.11 | 0 | 91.67 |
| 3IEE_4_103-135 | 49.52 | 52.60 | Y | 0.68 | 0.79 | 6.13 | 0.11 | 2 | 90.63 |
| 3IEE_5_139-178 | 62.15 | 61.24 | Y | 0.47 | 1.25 | 1.61 | 0.03 | 1 | 97.37 |
| 3IEE_6_185-205 | 32.79 | 39.95 | N | 1.16 | 1.64 | 7.16 | 0.18 | 2 | 88.24 |
| 3IEE_7_213-231 | 28.08 | 29.62 | Y | 0.66 | 0.68 | 7.26 | 0.22 | 1 | 83.33 |
| 3IEE_8_240-263 | 36.41 | 42.32 | N | 0.84 | 1.07 | 5.91 | 0.14 | 3 | 95.45 |
| 3IEE_9_271-284 | 20.36 | 13.63 | N | 1.16 | 1.77 | 6.07 | 0.31 | 0 | 58.33 |
| 3IEE Summary: 270 total AAs, 193 helix AAs | 0.78 | 1.10 | 4.73 | 0.14 | 75.81 | 88.71 | |||
| 1HZ4_1_5-24 | 29.43 | 26.67 | Y | 0.42 | 0.62 | 2.14 | 0.07 | 0 | 100.00 |
| 1HZ4_2_28-40 | 18.58 | N/A | N | N/A | N/A | N/A | N/A | 0 | 0.00 |
| 1HZ4_3_47-64 | 26.49 | 22.25 | Y | 0.50 | 0.60 | 3.54 | 0.14 | 0 | 88.24 |
| 1HZ4_4_67-83 | 24.48 | 24.29 | Y | 0.33 | 0.43 | 0.51 | 0.02 | 0 | 100.00 |
| 1HZ4_5_87-103 | 24.74 | 33.38 | N | 0.94 | 0.75 | 8.64 | 0.26 | 2 | 93.75 |
| 1HZ4_6_107-123 | 24.85 | 24.62 | Y | 0.35 | 0.48 | 0.45 | 0.02 | 0 | 100.00 |
| 1HZ4_7_131-145 | 22.07 | N/A | N | N/A | N/A | N/A | N/A | 0 | 0.00 |
| 1HZ4_8_149-162 | 20.15 | 20.98 | Y | 0.44 | 0.38 | 5.07 | 0.22 | 1 | 100.00 |
| 1HZ4_9-10_168-185 | 28.19 | 28.99 | N | 1.01 | 0.79 | 7.05 | 0.24 | 1 | 76.47 |
| 1HZ4_11_188-202 | 21.45 | 20.44 | Y | 0.44 | 0.52 | 3.68 | 0.16 | 0 | 92.86 |
| 1HZ4_12_209-225 | 24.89 | 22.98 | Y | 0.59 | 0.72 | 1.19 | 0.05 | 0 | 93.75 |
| 1HZ4_13_229-238 | 14.16 | N/A | N | N/A | N/A | N/A | N/A | 0 | 0.00 |
| 1HZ4_14-15_248-263 | 24.62 | N/A | N | N/A | N/A | N/A | N/A | 0 | 0.00 |
| 1HZ4_16_267-283 | 24.66 | 19.16 | N | 0.24 | 0.29 | 4.94 | 0.21 | 0 | 87.50 |
| 1HZ4_17_287-304 | 25.97 | 24.27 | Y | 0.40 | 0.46 | 3.51 | 0.13 | 1 | 94.12 |
| 1HZ4_18_307-324 | 26.86 | 21.02 | N | 0.27 | 0.38 | 5.23 | 0.20 | 0 | 88.24 |
| 1HZ4_20_334-346 | 18.59 | 18.67 | Y | 0.79 | 0.88 | 1.70 | 0.09 | 1 | 91.67 |
| 1HZ4_21_352-365 | 20.32 | N/A | N | N/A | N/A | N/A | N/A | 0 | 0.00 |
| 1HZ4 Summary: 366 total AAs, 291 helix AAs | 0.52 | 0.56 | 3.67 | 0.14 | 92.00 | 68.99 | |||
Results computed with SSETracer.
PDB ID, the helix ID, and the first and last amino acid index for the helix. Sequentially adjacent helices that share the same direction are combined.
True length of the helix axis in the atomic model.
Detected length of the axis. N/A: Helix was not detected.
Length-difference detection. A helix is assumed to be detected when c-d ≤ 5.4 Å.
Averaged two-way distance (Eq. 4).
Lateral discrepancy C (Eq. 1).
Longitudinal discrepancy L (Eq. 2).
Proportion P of longitudinal discrepancy (Eq. 3).
Number of false-positive nonhelix AAs (Eq. 6) within a specified radius (sheet AA: radius = 3.0 Å, loop AA: radius = 2.0 Å) of the detected helix axis.
Amino acid detection specificity (Eq. 6).
Amino acid detection sensitivity (Eq. 5).
3.3. Results of arc-length association using simulated density maps
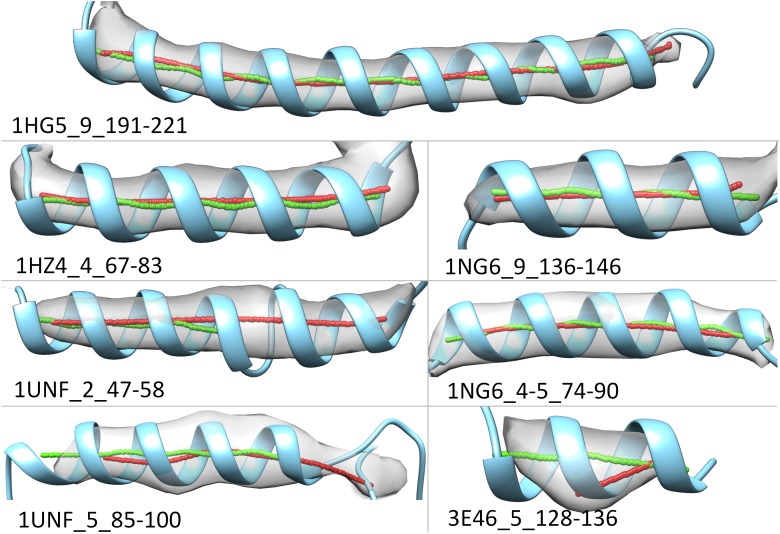
We evaluated map-structure pairs from simulated maps where the known atomic structures provide a known gold standard for comparison. One spline (red lines in Fig. 3) is derived from the set of points detected from the simulated map. The other spline (green lines in Fig. 3) is directly derived from the atomic structure. The arc-length method measures both lateral and longitudinal discrepancies. As an example, helix 1HZ4_4_67_83 is 17 amino acids in length (Fig. 3 and section of 1HZ4 of Table 2). The lateral discrepancy between the two splines is 0.43 Å, and the longitudinal discrepancy is 0.51 Å. The small lateral discrepancy is readily apparent by visual inspection (Fig. 3). The proportion of longitudinal discrepancy is 2% (column 8 of Table 2), which is also small. In general, very small discrepancies would be expected for simulated data, and the residual error is a lower bound for the experimental maps investigated below.
FIG. 3.
Comparison between two splines of a helix. The spline (red) generated from the 3D image (gray) is superimposed with the spline (green) that is calculated from the atomic structure of the helix (blue ribbon). The PDB ID, helix ID, and amino acid indexes are labeled for each helix. 3D, three-dimensional.
Interestingly, eight helices were not detected (N/A in Table 2). These undetected helices are generally shorter compared to the others. The proposed arc-length association only measures the discrepancy values for detected helices (true positives). We recommend that users report the number of any known undetected helices (false negatives) or wrongly detected helices (false positives) as part of their analysis.
The results show that the arc-length association method not only identifies misaligned helical axes but also distinguishes axes that have a slight discrepancy but are not visually obvious. In the case of a pair of obvious misalignment (1UNF_2_47-58, Fig. 3), the longitudinal discrepancy was measured as 13.76 Å (Table 2), which was the third largest among tested cases (Fig. 4). In this case, the detected axis is much longer than expected. Here, two helices that are almost consecutive in sequence appear as one longer helix. In two other cases (1NG6_9_136-146, and 1NG6_6_4-5_74-90, Fig. 3), a discrepancy is not visually obvious between two axes, but the arc-length method still measured longitudinal discrepancies of 2.18 and 0.52 Å, respectively (Table 2).
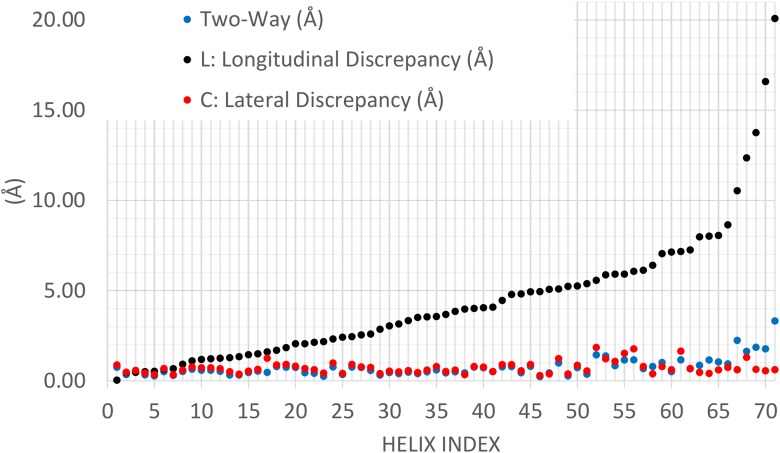
FIG. 4.
Helix accuracy evaluation using two methods. Arc-length association measures lateral (red dots) and longitudinal (black dots) discrepancy. Two-way distance (blue dots) measures the distance between two sets of points. The helix index corresponds to that in Table 1.
The sensitive measure of longitudinal discrepancy for the arc-length association can be potentially used to identify those complicated density maps where our current secondary structure detection methods do not detect well. In fact, our results show that 5 of the 71 test cases exhibit large longitudinal discrepancies (over 10 Å). These cases deserve more study and can be used for designing more accurate detection methods.
3.4. Comparison among four helix distance measures
We compared four helical distance measures: arc-length association, two-way distance, length difference, and amino acid sensitivity/specificity. Our data show that the two-way distance is similar to the lateral discrepancy and is only slightly affected by the longitudinal discrepancy (Fig. 4). This is expected since the calculation of the two-way distance primarily considers the projection distance, and longitudinal disagreement is only considered to a minor extent (Eq. 4). We observed in most cases that a higher two-way distance corresponded to higher lateral or longitudinal discrepancies (Table 2). However, arc-length association is more sensitive than two-way distance; it separates out the longitudinal discrepancy (inaccurate length determination) so that this is not eclipsed by the dominant lateral discrepancy. For example, the two-way distance values were 0.33 and 1.86 Å for 1HZ4_4_67-83 and 1UNF_2_47-58, respectively (Table 2 and Fig. 3), whereas their longitudinal discrepancy exhibited a significantly larger difference with values of 0.51 and 13.76 Å. The results in Table 2 suggest that when the two-way distance is over 1.3 Å, the lateral or longitudinal discrepancies need to be investigated in more detail.
One of the four measures investigates only the length difference between the two axes (Baker et al., 2007). If the length difference is within a turn (about 5.4 Å for a helix), the two axes are considered identical. The axial length difference is close to our definition of longitudinal discrepancy, but it misses the possibility of longitudinal shift. Our comparison shows that eight helices, such as 1HG5_1_20-29 and 1UNF_5_85-100, are marked detected (“Y” in Table 2) using the length difference criterion. According to the arc-length association, these cases exhibit significant longitudinal discrepancies of above 5.4 Å, a disagreement level that calls for further investigation being warranted. Arc-length association is more sensitive to longitudinal shift than the length difference method.
The direct comparison of axis lines as geometric fiducials is a common idea shared by the arc-length, two-way distance, and length difference methods. An alternative is to count individual amino acids that are in close proximity on the helix density region. There are two disadvantages to this approach. The first is that the result is dependent on the choice of the proximity radius threshold. We measured the sensitivity and specificity using radii of 2.0, 2.5, and 3.0 Å. As an example, the sensitivity of helix detection for 1NG6_2_20-39 is 73.68%, 94.74%, and 100% when the radius threshold is 2.0, 2.5, and 3.0 Å, respectively (row 25 of Table 1). This suggests that the choice of radius threshold is important if individual amino acids are used for measuring the accuracy of the helix assignment, which prompted us to propose a specific helix-dependent r value below (see Section 3.5).
The second drawback to using individual amino acids is that the specificity is dependent on the number of nonhelix amino acids in the protein. For example, the 1HG5 protein has 289 amino acids, of which 170 are on helices and 119 are not on helices (Table 2). However, for 1UNF, out of 238 amino acids, 111 are on helices and 127 are not on helices. Ideally, a measurement of a helix should be directly related to that helix and unbiased by other parts of the structure. In addition, the number of false-positive amino acids for each helix is usually small (Fig. 5) and is therefore not very robust (Eq. 6). By contrast, the arc-length association directly addresses the accuracy of individual helices on the basis of both lateral and longitudinal discrepancies. Consequently, the arc-length association is capable of identifying subtle discrepancies between the helix axis detected from a density map and that calculated from an atomic model.
FIG. 5.
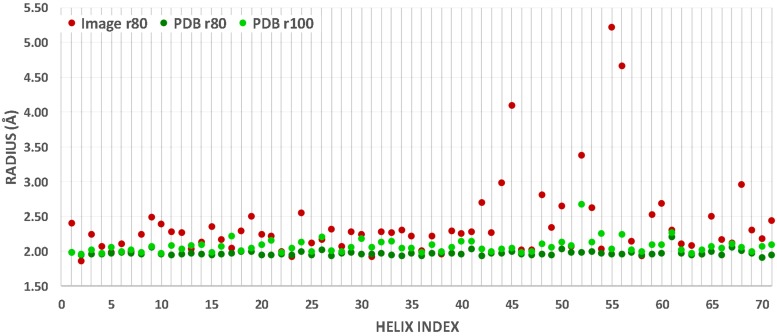
Backbone radial distance of helices. The distance between helix backbone centroids and the central axis, which is either calculated from the atomic model (green) or detected from the image (red), is shown for each helix. See Section 3 about r80 and r100. The helix index corresponds to that in Table 1.
3.5. Backbone radial distance of a helix
We measured the distance between the centroids of backbone atoms and the helix axis to understand the geometric relationship between a helix axis and its surrounding amino acids. For a helix axis calculated from the atomic structure of the protein, the average distance between the centroids and the axis is within 2.2 Å for 73 of the 79 helices of the data set. This suggests that the axis calculated from the atomic structure is quite accurate and that the backbone radial distance of a helix is consistent. Six helices have an average distance between 2.2 and 2.68 Å (Fig. 5 and Table 1). The average distance for the 71 test cases that include 79 helices is 2.07 Å. As mentioned in Section 2, we refer to this distance as r100, suggesting that 100% of centroids are within the radius of 2.07 Å from the axis if the axis is calculated accurately. Similarly derived is the r80 distance of 1.97 Å, indicating that 80% of centroids of a helix can be detected within a 1.97 Å radial distance from the axis. When a helix axis is detected from a density map at medium resolution, the axis generally is not as accurate as the one calculated from the atomic structure (Fig. 5). Using SSETracer-detected helix axes, the r80 value is 2.37 Å, suggesting that 80% of centroids can be detected within 2.37 Å from an axis detected from the density map. The sensitivity threshold is a heuristic parameter that allows the calculation of helix-specific radii. The 80% threshold was chosen because it is the sensitivity that can be achieved with state-of-the-art sequence-based secondary structure prediction methods.
This investigation addresses the question of how far a backbone centroid should be located from the helix axis in order for the amino acid to be considered to be a member of the helix. This radius threshold is needed when individual amino acids are used in the accuracy measurement of helix detection (Section 3.4). Previous studies of this parameter were limited in scope. Our results show that in idealized situations where the axis is determined accurately, a radius threshold of 2.07 Å can be used, since on average 100% of centroids are within this distance. However, for a detected helix axis that is not as accurate as that of a known structure, the r80 value of 2.37 Å can be considered. In general, we propose the use of the r80 value for a realistic estimation of the radius threshold when working with a detected helix axis from an experimental density map at medium resolution.
3.6. Case studies using experimental cryo-EM data
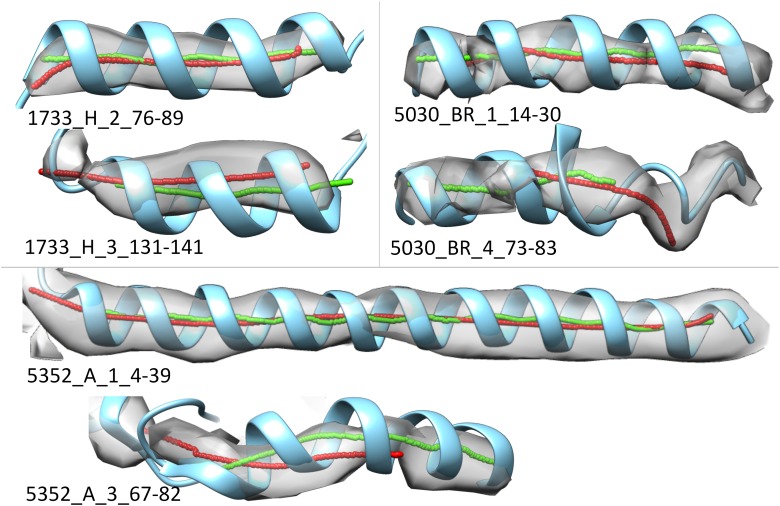
As an example of applications to experimental data, we show a range of helix discrepancies as identified by arc-length association (Fig. 6). In a visual inspection, three of the five cases show close agreement between the helical axes: 1733_H_2_76-89, 5030_BR_1_14-30, and 5352_A_1_4-39. The (lateral and longitudinal) discrepancies are (0.65, 2.78 Å), (1.01, 2.77 Å), and (0.84, 4.76 Å), respectively. Interestingly, the lateral displacement for 1733_H_3_131-141 is, at 1.16 Å, slightly larger than observed in the three similar map–model pairs. Visual inspection shows that the density in this case does not align with the atomic model as well (Fig. 6). Two challenging cases are 5030_BR_4_73-83 and 5352_A_367-82, where the density of a helix deviates from a cylinder and a coil that resembles a helix is adjacent to a helix, respectively. The (lateral and longitudinal) discrepancies are (1.13, 15.68 Å) and (1.47, 17.87 Å), respectively. In both cases, the arc-length method detected the disagreement between the two axes. Possible reasons for the disagreement include an error in the density map, an error in the atomic model, and an error in the detection of the helix axis from the density image.
FIG. 6.
Comparison of two splines calculated from a cryo-EM density map and the atomic model. The EMDB ID, chain ID, helix ID, and the first and last amino acid index are labeled. The annotation of the figure is the same as that used in Figure 3. cryo-EM, cryo-electron microscopy.
3.7. Helix axes detected using an alternative method, VolTrac
Although this article is predominantly focused on proposing a robust distance measure for helical axes, we expect that the arc-length association method will be applied to the comparison of secondary structure detection methods for cryo-EM maps in future work. With multiple methods available for helix detection, it is possible, in principle, to perform a meta-analysis of methods. (For example, when independent methods show large displacement between the density image and the atomic model, the cryo-EM density in that region needs to be studied further.) It will also be possible to improve the multistage secondary structure detection algorithms by assembling the best-performing stages from existing strategies.
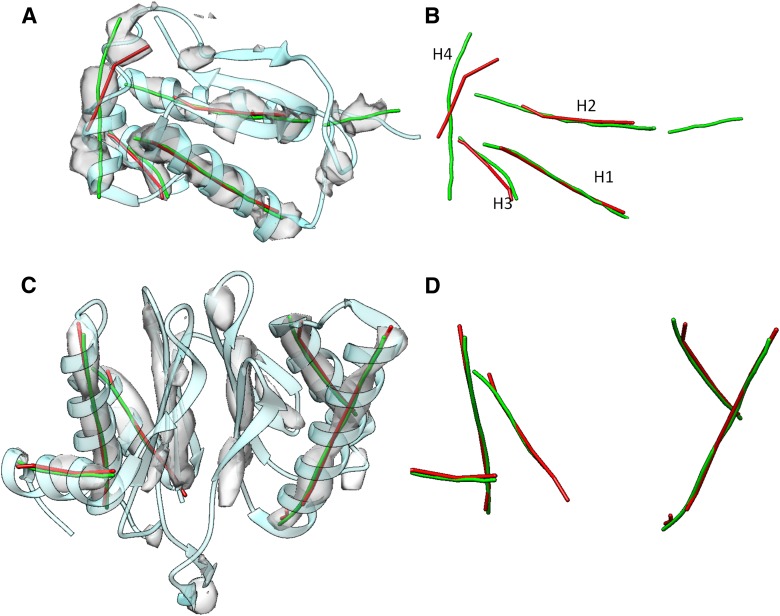
As a preliminary, limited example of such a meta-analysis, we performed two case studies with SSETracer and an alternative secondary structure detector, VolTrac (Fig. 7). VolTrac combines a template-based search with a genetic algorithm to detect the initial positions of a helix or other filamentous density (Rusu et al., 2012a; Rusu and Wriggers, 2012b). The axes detected by VolTrac are mostly similar to those detected by SSETracer, particularly for long helices. As an example, for EMD-1733, the two sets of axes (red and green lines in Fig. 7) align well for all five helices. Three of the four helices in EMD-5030-PDB-4V68_BR (Fig. 7A, B) also align well.
FIG. 7.
Axes of helices detected from cryo-EM images using SSETracer and VolTrac. Helix axes detected from cryo-EM density map EMD-5030 in (A) and (B) and EMD-1733 in (C) and (D) using SSETracer (Si and He, 2013) (red) and VolTrac (green) are superimposed with the image (gray) and the corresponding atomic model PDB-4V68_BR in (A) and PDB-3C91_H in (C) (blue ribbon).
Using the arc-length method, it is now possible to measure the displacements precisely. For instance, the largest displacement in the two test cases happens at the same helix (1733_H_3) for both methods. The (lateral and longitudinal) discrepancies of helix 1733_H_3 (Fig. 6) are (1.13, 2.69 Å) and (1.16, 9.39 Å) for VolTrac and SSETracer, respectively. When helices are correctly detected, VolTrac was actually more sensitive than SSETracer, as when the (lateral and longitudinal) discrepancies for the first and second helices of 1733_H are (0.75, 1.61 Å) and (0.50, 2.27 Å), respectively, for VolTrac but (0.75, 5.12 Å) and (0.65, 2.78 Å), respectively, for SSETracer. However, in EMD 5030, VolTrac incorrectly assigned one helix to a β-sheet region (Fig. 7B). A more comprehensive comparison of the advantages and limitations of each secondary structure prediction method will be the subject of future work, but our results suggest that the use of the arc-length association will be advantageous in such a comparison and in a meta-analysis of secondary structure detection methods.
4. Conclusion
We propose a new method to quantify the agreement between a set of points at the central axis of a helix and the atomic model of the helix. Due to the cylindrical nature of a helix, our proposed method directly compares the agreement between the set of points and the central axis of the helix model. Our results show that 80% accuracy can be achieved with a radius of 2.37 Å from backbone centroids. This work offers the potential to use the spline of a helix axis to accurately represent the helix's position.
One application of the arc-length association method is to measure the accuracy of a helix detected from cryo-EM at medium resolution. As more secondary structure detection methods become available, there is a need to accurately compare them. Current measures for helix detection have various strengths and weaknesses. Arc-length association was compared with three other methods that measure two-way distance, length difference, and the individual amino acid detection accuracy, respectively. This method was tested using 79 helices detected from simulated density maps at 10 Å resolution and six case studies involving cryo-EM density maps at 6.4–7.7 Å resolution. The results show a clear benefit in terms of measuring both the lateral and longitudinal discrepancies between the axis of the detected helix and that of the helix model. The comparison shows that the arc-length method is a more sensitive measure than the other three methods. With the availability of this method, we demonstrated various degrees of longitudinal discrepancy for the test cases, and the highlighted challenging cases can be used in the future to improve current secondary structure detection methods. To evaluate the accuracy of individual helix detection, we recommend reporting the number of false-negative and false-positive detections in addition to the lateral and longitudinal discrepancies. Another application of the proposed method is to quantify the agreement between the density at a helix and the atomic helix model from the perspective of the central axis. The assumption is that if the atomic model fits the density well, the central axes are expected to agree well. The arc-length method provides a sensitive measurement for the identification of potential regions of disagreement.
We believe that the current arc-length association is sufficiently complete for the purpose of detection of helices. However, other applications might require an additional and more detailed geometric characterization that is not offered by our approach. Quantities that might conceivably be of interest in 3D helix comparison, but which were not studied here, include measures of axis orientation and angular discrepancies, information as to whether the ends are systematically too short or too long, and a differentiation between longitudinal shift and length difference.
In future work, the method will be applied to the validation of map–model pairs, as proposed in a study by Wriggers and He (2015), and to the test and optimization of secondary structure detection methods. We note that a β-strand can also be represented as a set of points located near the central line of the strand (Si and He, 2014), so that an extension of the measuring separation of line-based fiducials to other secondary structure elements appears particularly promising.
Acknowledgments
The work in this article was supported, in part, by NSF DBI-1356621, NIH R01-GM062968, the Honors College of Old Dominion University, and a Virginia Space Grant Consortium Undergraduate Research Scholarship.
Authors' Contribution
All authors participated in the design of the method and the writing of the manuscript. S.Z. implemented the method. S.Z. and J.H. tested the method.
Author Disclosure Statement
No competing financial interests exist.
References
- Al Nasr K., Chen L., Si D., et al. 2012. Building the initial chain of the proteins through de novo modeling of the cryo-electron microscopy volume data at the medium resolutions. Proceedings of the ACM Conference on Bioinformatics, Computational Biology and Biomedicine. Orlando, FL, ACM: 490–497 [Google Scholar]
- Al Nasr K., and He J. 2016. Constrained cyclic coordinate descent for cryo-EM images at medium resolutions: Beyond the protein loop closure problem. Robotica 34, 1777–1790 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Al Nasr K., Ranjan D., Zubair M., et al. 2014. Sovling the secondary structure matching problem in cryo-EM de novo modeling using a constrained K-shortest path graph algorithm. IEEE/ACM Trans. Comput. Biol. Bioinform. 11, 419–429 [DOI] [PubMed] [Google Scholar]
- Al Nasr K., Sun W., and He J. 2010. Structure prediction for the helical skeletons detected from the low resolution protein density map. BMC Bioinform. 11(Suppl. 1), S44. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Baker M.L., Abeysinghe S.S., Schuh S., et al. 2011. Modeling protein structure at near atomic resolutions with Gorgon. J. Struct. Biol. 174, 360–373 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Baker M.L., Ju T., and Chiu W. 2007. Identification of secondary structure elements in intermediate-resolution density maps. Structure 15, 7–19 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Biswas A., Ranjan D., Zubair M., et al. 2015. A dynamic programming algorithm for finding the optimal placement of a secondary structure topology in Cryo-EM data. J. Comput. Biol. 22, 837–843 [DOI] [PubMed] [Google Scholar]
- Biswas A., Ranjan D., Zubair M., et al. 2016. An effective computational method incorporating multiple secondary structure predictions in topology determination for cryo-EM images. IEEE/ACM Trans. Comput. Biol. Bioinform. [Epub ahead of print]. DOI: 10.1109/TCBB.2016.2543721 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Biswas A., Si D., Al Nasr K., et al. 2012. Improved efficiency in cryo-EM secondary structure topology determination from inaccurate data. J. Bioinform. Comput. Biol. 10, 1242006. [DOI] [PubMed] [Google Scholar]
- Dal Palu A., He J., Pontelli E., et al. 2006. Identification of alpha-helices from low resolution protein density maps. Proc. Comput. Syst. Bioinform. Conf. 89–98 [PubMed] [Google Scholar]
- He J., Zeil S., Hallak H., et al. 2015. Comparison of an atomic model and its cryo-EM image at the central axis of a helix. Proceedings (IEEE Int. Conf. Bioinform. Biomed.) 2015:1253–1259 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Jiang W., Baker M.L., Ludtke S.J., et al. 2001. Bridging the information gap: Computational tools for intermediate resolution structure interpretation. J. Mol. Biol. 308, 1033–1044 [DOI] [PubMed] [Google Scholar]
- Kong Y., Zhang X., Baker T.S., et al. 2004. A structural-informatics approach for tracing beta-sheets: Building pseudo-C(alpha) traces for beta-strands in intermediate-resolution density maps. J. Mol. Biol. 339, 117–130 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Lawson C.L., Baker M.L., Best C., et al. 2011. EMDataBank.org: Unified data resource for CryoEM. Nucleic Acids Res 39(Suppl. 1), D456–D464 [DOI] [PMC free article] [PubMed]
- Lindert S., Alexander N., Wotzel N., et al. 2012. EM-fold: De novo atomic-detail protein structure determination from medium-resolution density maps. Structure 20, 464–478 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Lindert S., Staritzbichler R., Wötzel N., et al. 2009. EM-fold: De novo folding of alpha-helical proteins guided by intermediate-resolution electron microscopy density maps. Structure 17, 990–1003 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Rossmann M.G. 2000. Fitting atomic models into electron-microscopy maps. Acta Crystallogr. D Biol. Crystallogr. 56(Pt 10), 1341–1349 [DOI] [PubMed] [Google Scholar]
- Rusu M., Starosolski Z., Wahle M., et al. 2012a. Automated tracing of filaments in 3D electron tomography reconstructions using Sculptor and Situs. J. Struct. Biol. 178, 121–128 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Rusu M., and Wriggers W. 2012b. Evolutionary bidirectional expansion for the tracing of alpha helices in cryo-electron microscopy reconstructions. J. Struct. Biol. 177, 410–419 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Schröder G.F., Brunger A.T., and Levitt M. 2007. Combining efficient conformational sampling with a deformable elastic network model facilitates structure refinement at low resolution. Structure 15, 1630–1641 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Si D., and He J., 2013. Beta-sheet detection and representation from medium resolution cryo-EM density maps. BCB'13: Proceedings of ACM Conference on Bioinformatics, Computational Biology and Biomedical Informatics, Washington, DC, 764–770 [Google Scholar]
- Si D., and He J. 2014. Tracing beta-strands using strandtwister from cryo-EM density maps at medium resolutions. Structure 22, 1665–1676 [DOI] [PubMed] [Google Scholar]
- Si D., Ji S., Al Nasr K., et al. 2012. A machine learning approach for the identification of protein secondary structure elements from electron cryo-microscopy density maps. Biopolymers 97, 698–708 [DOI] [PubMed] [Google Scholar]
- Wriggers W., and Birmanns S. 2001. Using situs for flexible and rigid-body fitting of multiresolution single-molecule data. J. Struct. Biol. 133, 193–202 [DOI] [PubMed] [Google Scholar]
- Wriggers W., and He J. 2015. Numerical geometry of map and model assessment. J. Struct. Biol. 192, 255–261 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Zeyun Y., and Bajaj C. 2008. Computational approaches for automatic structural analysis of large biomolecular complexes. IEEE/ACM Trans. Comput. Biol. Bioinform. 5, 568–582 [DOI] [PubMed] [Google Scholar]