Summary
Working memory is thought to result from sustained neuron spiking. However, computational models suggest complex dynamics with discrete oscillatory bursts. We analyzed local field potential (LFP) and spiking from the prefrontal cortex (PFC) of monkeys performing a working memory task. There were brief bursts of narrow-band gamma oscillations (45-100 Hz), varied in time and frequency, accompanying encoding and re-activation of sensory information. They appeared at a minority of recording sites associated with spiking reflecting the to-be-remembered items. Beta oscillations (20-35 Hz) also occurred in brief, variable bursts but reflected a default state interrupted by encoding and decoding. Only activity of neurons reflecting encoding/decoding correlated with changes in gamma burst rate. Thus, gamma bursts could gate access to, and prevent sensory interference with, working memory. This supports the hypothesis that working memory is manifested by discrete oscillatory dynamics and spiking, not sustained activity.
Introduction
The ability to keep information “online” and available in the absence of sensory input is a key component of working memory (WM) and one of the most studied cognitive functions (Fuster and Alexander, 1971; Goldman-Rakic, 1995; Miller and Cohen, 2001). It is widely assumed to have a neural correlate in sustained neural activity in higher-order cortical areas such as the prefrontal cortex (PFC) (Fuster and Alexander, 1971; Funahashi et al., 1989; Goldman-Rakic, 1995; Miller et al., 1996; Pasternak and Greenlee, 2005). The mechanism, at first glance, seems straightforward: A sensory event elicits spiking activity that is maintained until that information is needed. This seemingly continuous “delay activity” may, however, reflect averaging across trials and/or neurons. Closer examination has suggested that the underlying dynamics are more complex (Rainer and Miller, 2001; Shafi et al., 2007; Stokes, 2015). For example, random sampling of neurons indicates that individual neurons bridging a multi-second memory delay is rare. Instead, most neurons show brief bouts of activity with variable onset latency and durations, sprinkled throughout the delay (Cromer et al., 2010; Shafi et al., 2007) suggesting highly dynamic activity (Durstewitz and Seamans, 2006; Stokes et al., 2013).
Continuous, persistent WM information can be simulated by attractor networks, originally serving as models for maintenance of saccade information (Amit and Brunel, 1997; Compte et al., 2000). In these models, information about saccade location is held in a persistent state without interruption. This state corresponds to a dynamic attractor and is supported by recurrent connections that sustain a pattern of activity. If this activity is disrupted, the information it was conveying is lost. By contrast, a related class of attractor models suggests that WM activity is non-stationary. Information is only expressed as spiking during short-lived attractor states. Between the active states, information is held by selective synaptic changes in the recurrent connections and therefore not lost with disrupted activity (Sandberg et al., 2003; Mongillo et al., 2008; Lundqvist et al., 2011; Lundqvist et al., 2012). The limited life-time of the attractor states has two advantages. First, less spiking is needed to store the information; energy is conserved during the silent states. Second, as information is not lost when activity is disrupted, attractors can hold multiple items in WM with minimal interference between them (or from sensory distractions). In these models, different items are serially encoded and read out, resulting in brief activations of spiking in the coding assemblies.
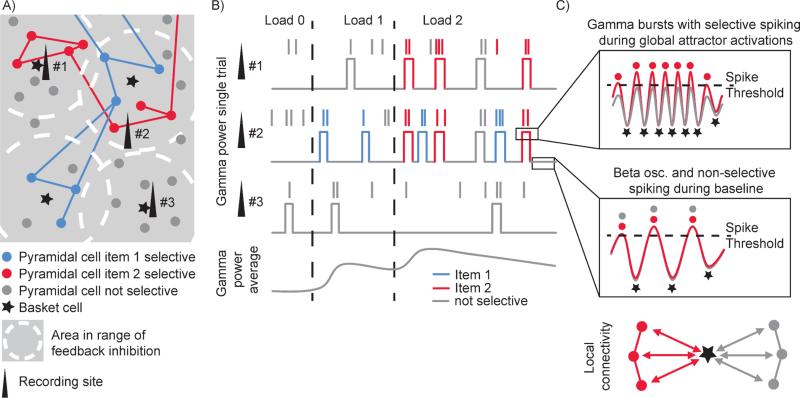
One of these models (Lundqvist et al., 2011; Figure 1A) implemented the functionality of short-lived attractor states using connectivity and synaptic plasticity constrained by known biology. The model predicts that a burst of gamma oscillations accompanies each attractor state (Figure 1B, C) and that the life-time of such bursts should correspond roughly to an alpha/theta cycle. The gamma oscillations result from fast, local feedback inhibition (Figure 1C), which has two chief consequences. First, firing rates are reduced during attractor retrieval. This state is otherwise characterized by runaway excitation but instead excitation and inhibition are dynamically balanced, leading to the low-rate irregular firing observed in biology (Lundqvist et al., 2010). Second, feedback inhibition normalizes firing rates in a winner-take-all dynamic, resulting in selective (informative) spiking in only a small subset of neurons (those that are part of the attractor; see Figure 1). This further predicts that there should be a close link between information in spiking and gamma power that goes beyond the broad-band increase in gamma power accompanying general increases in spiking activity. The model also predicts that as more items are stored in the network, they are replayed more and more often leading to a higher density of gamma bursts (Figure 1B) (Lundqvist et al., 2011). This could explain observed load-dependent power changes in gamma (Howard et al., 2003, Kornblith et al., 2015, Honkanen et al., 2014), beta (Kornblith et al., 2015, Honkanen et al., 2014) and theta/alpha (Jensen and Teshe, 2002; Palva et al., 2005) in primate cortex.
Figure 1.
Schematic view of the model and model predictions. A) Spatial organization of network. Locally, cells coding for the same stimulus are recurrently connected into local clusters. Several competing clusters share feedback inhibition from nearby inhibitory basket cells. Cell assemblies are formed by recurrent long-range connections connecting several spatially distributed local clusters, each receiving inhibition from a distinct pool of basket cells. B) The network displays non-linear attractor dynamics in which various cell assemblies are briefly activated. These activations are initially triggered by stimuli. Following a cell assembly activation, the synapses in the recurrent connections will be potentiated within a certain time window. This will cause the assembly to spontaneously reactivate once it has been triggered by an external stimulus. In this way information about multiple stimuli can be held in working memory with attractors, which code for various external stimuli, taking turns in a sequence of reactivations. In the LFP, these activations should be manifested as non-linear transitions into short-lived states with high narrow-band gamma power. These high power states should become more common in selective sites (but not in non-selective sites, compare site #1 and #2 with #3) as working memory load increases, leading to enhanced average gamma power with load. C) Oscillations (top) are created by local feedback inhibition (bottom) shared by several local clusters of pyramidal cells. During baseline the oscillations are in the beta range, and cells from all clusters spike at a similar rate. During attractor activations, there is a slight excitatory bias (from the recurrent connections and assembly specific synaptic potentiation) in one of the assemblies causing this group to consistently reach firing threshold first after each wave of feedback inhibition. As they spike, they activate a new wave of feedback inhibition, shutting down the rest of the cells. Computationally, this creates a winner-take-all dynamics with spiking only in the (temporarily) most excitable assembly coding for a stimulus. This selectivity in firing implies that the stimulus information conveyed by the corresponding neurons increases. The increased excitation in this state speeds up the oscillations to gamma range.
Non-stationary memory delay activity has also been suggested by observations that PFC activity and gamma oscillations show slow frequency modulation (Jensen and Teshe, 2002; Palva et al., 2005; Watrous et al., 2013; Axmacher et al., 2010). However, the model makes more specific predictions. On a single trial, there should be no prolonged baseline shift in gamma power following stimulus encoding. Gamma power should instead make sharp transitions into the high-power attractor state and repeatedly fall back to pre-stimulus baseline levels throughout the WM delay (thus manifesting what Stokes, 2015, refers to as active-silent states) (Figure 1B). As a result, on a trial-by-trial basis, PFC activity is not modulated at slower frequencies in a highly periodic fashion. Instead gamma bursts occur irregularly and the slow periodicity previously observed is instead due to the life-span of the gamma bursts. The power modulation only appears as periodic when averaging across trials.
We sought to test model predictions in local field potential (LFP) and spike data from the PFC of monkeys performing a multi-item memory task. We did so by performing a unique trial-by-trial analysis of neural activity. This avoided the cross-trial averaging that would obscure the complex temporal dynamics predicted by the model.
Results
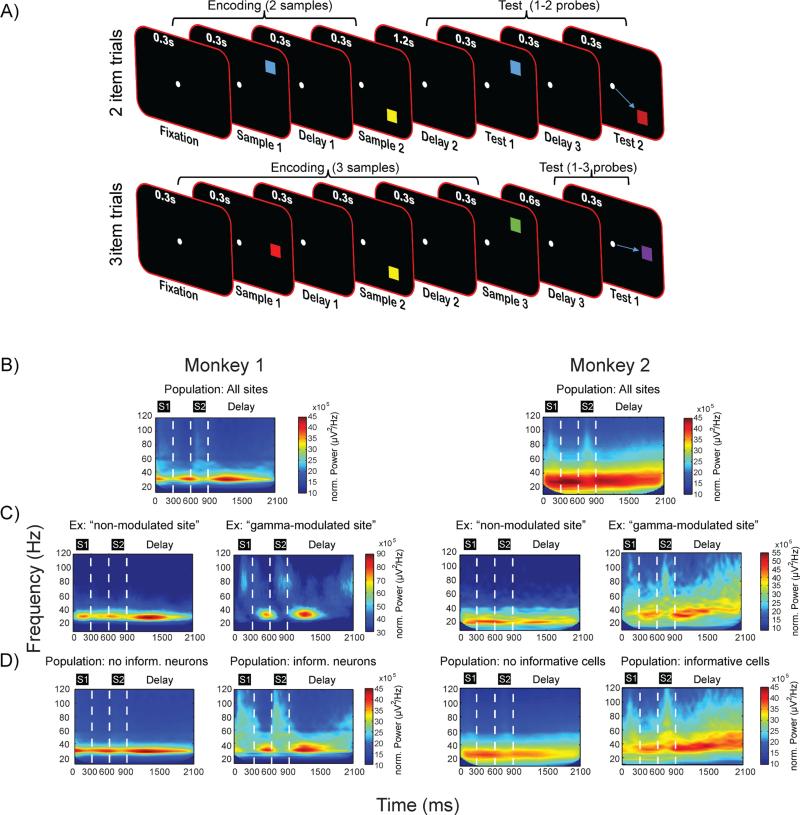
We trained two monkeys to retain multiple colored squares over a short memory delay period (Figure 2A). Each trial began with an encoding phase, where two or three squares appeared in a sequence, each in a unique location. After a memory delay (1.2 or 0.6 sec), there was a test phase in which a new sequence of squares appeared in the same locations as during the encoding phase. However, one of the squares in the test sequence had a different color. The monkey had to respond by making a saccade (Figure S1) to the changed square to receive a reward. Performance was 73% correct on two-item trials and 56% correct on three-item trials, comparable to performance previously reported in monkeys (Buschman and Miller, 2011). Using multiple acute electrodes in lateral PFC (lPFC) and frontal eye-field (FEF), we recorded LFPs and spikes from 321 electrodes with isolatable neurons, which were kept for LFP analysis. Out of the isolatable units we analyzed those with at least 4 spikes per trial (n=293).
Fig. 2.
Experimental setup and LFP spectral power. A) Each trial consisted of three phases: encoding, delay and test. Following fixation on a white dot in the center of the screen, two (top) or three (bottom) colored squares were sequentially presented to the monkeys. Following a delay period, the stimulus sequence was repeated with the color of one square changed. The monkeys were rewarded for a saccade to the changed square. B-D) Spectrograms, not normalized to baseline, of raw LFPs for monkey M1 (left) and M2 (right). The following is displayed for each monkey: B) Average spectrogram from all electrodes and correct trials during encoding (time 0 refers to the onset of the first stimulus) and delay in 2 item trials. S1-S2 refers to sample 1-2, respectively. C) Example of spectrograms from single electrodes, recorded the same day, that display non-modulated (left) or gamma-modulated profiles (right). D) Average spectrograms from all electrodes in two-item trials including (right) or excluding (left) neurons that carry information about the presented squares. Power in all spectrograms estimated using multi-taper time-frequency analysis (Experimental Procedures). See also Figure S1, S2 and S3.
Prediction 1: Gamma oscillations are tied to neural encoding of information
The tested model predicts specific roles for gamma and beta oscillations. Encoding or decoding a stimulus triggers a gamma oscillatory attractor state and suppresses a default beta oscillatory state (Figure 1C). This was superficially supported by the average time-frequency evolution for all electrodes (Figure 2B); beta power was suppressed and weak gamma power increases were observed during stimulus presentations. These beta and gamma oscillations were induced (not phase-locked to stimuli, Figure S2A, B). By contrast, stimulus presentation also evoked lower-frequency (3-10 Hz) activity that was phase-locked to stimulus and not present during memory delays (Figure S2A, B).
Because of its posited role in gating encoding, gamma should only occur where local neuron populations convey stimulus information. Thus, the model predicts that at sites where the gamma state is not triggered, spiking is not informative. We first tested this by determining whether gamma was present at some recording sites and not others. Indeed, there was a dramatic difference. The majority of sites (195/321, 61%) showed beta oscillations throughout the trial and no significant increase of gamma in response to stimuli (Figure 2C, referred to as “non-modulated sites”). However, for the other sites (126/321, 39%; 42.2% monkey M1, 37.5% monkey M2) gamma power significantly increased following stimulus presentations (Figure 2C, referred to as “gamma-modulated sites”). A comparison revealed that the largest difference between the gamma-modulated and non-modulated sites was between 45-100 Hz (Figure S2C), indicating that gamma power changes indeed reflected oscillations and not the spectral consequences of spiking (investigated in more detail below). In addition, modulated sites also showed a stronger beta suppression during stimulus presentations and stronger stimulus-locked 3-10 Hz power (Figure S2C). The latter difference was evident in the evoked potentials (Figure S3), suggesting differences in the processing of bottom-up inputs. Next, we determined whether firing in gamma-modulated sites selectively conveyed information about the stimulus.
First, we analyzed the spiking of all recorded neurons. To quantify information they carried about stimuli, we estimated the percentage explained variance (PEV; Olejnik and Algina, 2003, see Experimental Procedures), which measured for each cell the proportion of variance in firing rate that could be explained by stimulus identity (color and location, see Experimental Procedures). About ¼ of the neurons (24.2%, 71 out of 293; see Experimental Procedures for criteria) carried information about the location of the square, its color, or both (Figure S4; average PEV based on color and location combined for informative group was 0.063, PEV based on location only was 0.046). Remarkably, all of these informative neurons (71/71) were recorded at the less common gamma-modulated sites (Fisher's exact test for contingency, p<10−24). The more common non-modulated sites produced spiking activity that did not convey any significant information about stimuli. To further demonstrate this, we recalculated the spectrograms separately for the recording sites that contained any neuron whose spiking conveyed stimulus information (Figure 2D, “Population: informative cells”) and those that did not (Figure 2D, “Population: no informative cells”). This yielded virtually identical results to the spectrograms sorted by the presence or absence of stimulus induced gamma power.
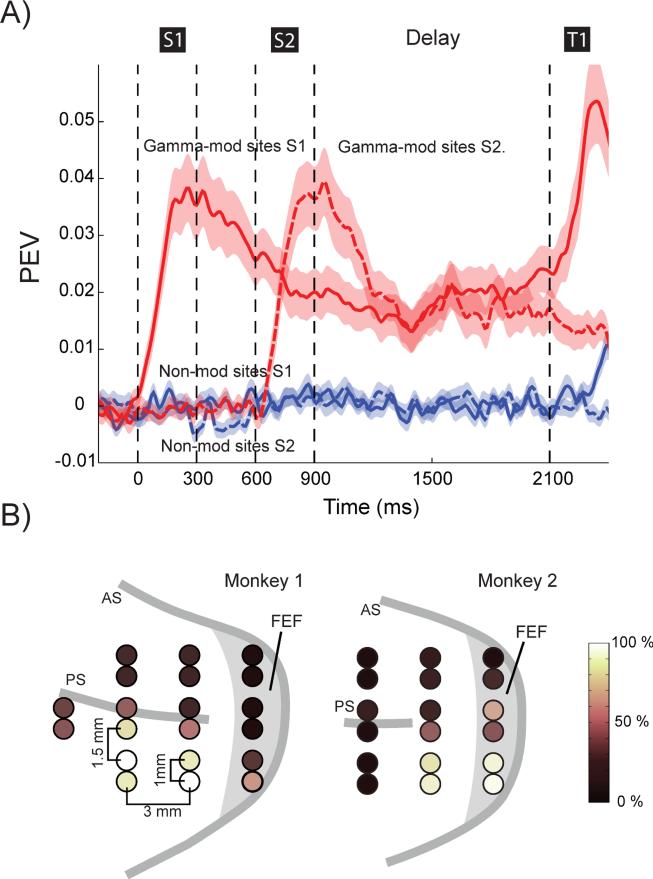
To illustrate this yet further, we plotted the average information from spiking on gamma-modulated vs non-modulated sites (Figure 3A). Neurons from the non-modulated sites had virtually no average stimulus information. They only showed weak information after the test stimulus when the animal made a saccade to the target. By contrast, spiking from gamma-modulated sites showed significant stimulus information starting from sample stimulus onset and continuing throughout trial (Figure 3A). Thus, induced gamma oscillations and beta-band suppressions at stimulus presentation were strongly co-localized with stimulus information in spiking. This is consistent with the model prediction that stimulus/encoding depends on triggering a gamma attractor state (Figure 1B, A) that disrupts the default beta state. If the local neurons do not carry stimulus information, gamma is not triggered and that population stays in the default beta state.
Fig. 3.
Anatomical location and information on gamma-modulated sites. A) The average information measured using PEV from all cells recorded from gamma-modulated (red) or non-modulated (blue) sites at the time of stimulus presentations (time 0 refers to the onset of the first stimulus). S1-S2 refers to sample 1-2. B) The layout of the grid used for inserting the electrodes for monkey M1 (left) and M2 (right). Circles denote recording locations and color code describes the across-session likelihood that an electrode at that particular site displayed increased gamma power during stimulus presentations (gamma-modulated site). See also Figure S4 and S5.
This difference between stimulus information from gamma-modulated vs non-modulated sites was not simply due to better quality recordings from the gamma-modulated sites. The average number of isolatable neurons was not higher in the gamma modulated vs the non-modulated sites (1.41 vs 1.43, p=0.81). The average spiking rate from gamma-modulated sites were only slightly higher than those on non-modulated sites (8.3 vs 6.5 spikes/s; Figure S5). But to ensure that the differences were not merely due to increased spiking, we gradually removed the neurons with the highest spike rates from gamma-modulated sites until the mean spike rate was the same on the gamma-modulated and non-modulated sites (removing 10% of the most active units was sufficient; Figure S5). This did not change the average information (PEV across all neurons and the entire trial) for the gamma-modulated sites (0.031 vs 0.031, p=0.87) and the information in non-modulated sites remained significantly lower (mean PEV=0.0006) than in gamma-modulated sites. Similarly, taking 80% of the most active neurons from non-modulated sites resulted in equating average spiking rates between the two types of sites (8.3 spikes/s) but the mean PEV nonetheless remained significantly lower on the non-modulated sites (0.0008; not significantly higher than in the original group, p=0.91). Finally, the gamma-modulated sites were clustered (Figure 3B) in the cortex. As they were sampled with new electrodes each day, the difference between gamma-modulated and non-modulated sites were not due to the electrodes. Instead, there seemed to be an anatomical clustering of working memory information where gamma-modulated sites contained a mix of informative and non-informative neurons while non-modulated sites contained only non-informative neurons (as suggested by the model, compare recording site #2 and #3 in schematic Figure 1A of the model).
Prediction 2: Gamma and beta occur in brief, narrow-band bursts
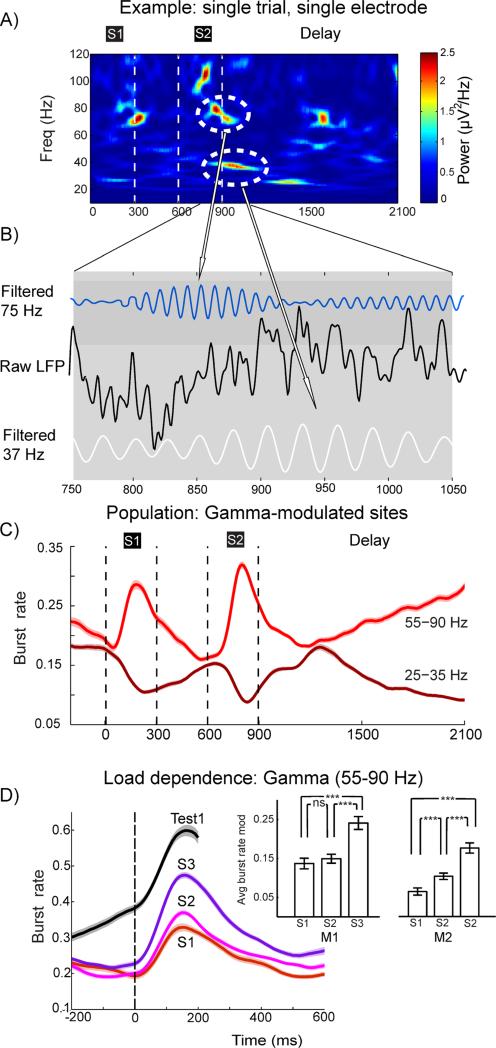
The model predicts that on single trials, beta and gamma power increases should occur in brief, irregular, bursts (Figure 1). Each burst should be narrow-band and well-defined in frequency, but widely scattered in frequency because it reflects a transient attractor state where the exact frequency is set by the instantaneous level of excitation in the local microcircuit. The average spectrograms in Figure 2 seem to suggest the opposite (broad-band, long-lasting signals), but this was an artifact of averaging across trials. Further, the model predicts that as working memory load increases, the number of coding assemblies taking turn being active will increase, leading to more gamma bursts per trial (and consequently higher trial-averaged gamma power; Figure 1). Below, we demonstrate that, as predicted, on individual trials both gamma and beta oscillations occurred in brief bursts that were narrow and variable in frequency, like high-power “bubbles” against low tonic background activity. Examples from a single trial are shown in Figures 4A (spectrogram) and 4B (raw LFP).
Fig. 4.
Oscillatory gamma and beta bursts. A) Example of spectrogram from a single two-item trial. B) Zoom-in on the raw LFP (black) around the time of the encircled gamma and beta bursts seen in the top right spectrogram. Blue curve is shows the LFP filtered at 75 Hz (center of the encircled gamma burst), white curve show LFP filtered at 37 Hz (center of the encircled beta burst. C) Estimated burst rate for two-item trials in gamma (light red) and beta (dark red) frequency bands for gamma-modulated sites (both monkeys combined). Burst rate is the time-dependent portion of trials exhibiting a burst at a given time point. D) Gamma burst rate in three-item trials around the time of the presentations of each item (S1-S3) and the first test item for the same electrodes as in C). Inset displays the average size of the gamma burst rate modulation effects in monkey M1 and M2 (three stars denote significance at level p<0.01; error bars denote the standard error of the mean). See also Figure S6, S7 and S8.
To quantify this “bubbling”, we defined a gamma or beta burst as an increase in power of two standard deviations above the mean spectral power in that band, lasting at least three cycles (see Experimental Procedures). The gamma bursting predominantly ranged from 45-100 Hz. Each burst on average lasted 67 ms (std. dev. 19 ms) and was narrow in frequency (on average power dropped to 50% relative to the power of the central frequency of the burst within 9.5 Hz, std. dev. 2.9 Hz, see Experimental Procedures). Beta bursting occurred predominately in the 20-35 Hz range, each burst on average lasting 130 ms (std. dev. 37 ms) and also narrow in frequency (mean 5.1, std. dev. 1.7 Hz). To investigate the bursts’ relation to trial-averaged power, we calculated burst rate on gamma-modulated sites (Experimental Procedures) by measuring the across-trial density of bursts in each time point (Figure 4C). Both the gamma and beta burst rates were indeed highly correlated with the across-trial power (mean correlation over electrodes: r=0.93, std. err.=0.01 for gamma and r=0.91, std. err.=0.01 for beta; for all correlations p<10−8. Figure S7). This suggests that the broad-band long-lasting increases in beta and gamma power seen in the average spectrograms were due to gamma and beta bursts of short duration and narrow frequency on a trial-by-trial basis. We confirmed that a bubbling pattern of gamma and beta bursts on single trials gradually turns into smooth continuous broad-band pattern when averaged over an increasing number of trials (Figure S6).
To test the prediction that gamma bursting increases with WM load (Figure 1B), we studied trials with three item presentations focusing on the time of each sequential stimulus presentation and the first 300 ms of each following delay. Each subsequent stimulus presentation (increase in load; Figure 2A) seemed to result in higher gamma burst rates (Fig 4D). This was tested by quantifying the burst rate over a 150 ms window centered on the peak in average burst rate for each stimulus presentation. Pairwise comparisons between all combinations of stimulus load (i.e., 1 vs 2, 2 vs 3, 1 vs 3) demonstrated significantly higher burst rates for higher loads (p<10−8, Friedman test; pairwise post hoc comparisons with Bonferroni correction at the overall significance α=0.05; see inset for statistics on each monkey separately). Importantly, as also predicted (Figure 1), this was due to an increased number of bursts (burst count during the presentation and delay combined (600 ms) for each load condition progressively increased, p<10−12, testing procedure as above), and not due to load-dependent changes in burst length (p>0.31, Kruskal-Wallis test).
The gamma bursting allowed us to study the relation between gamma bursts and spiking at a single trial level. The model predicts that gamma, but not beta, bursts should correspond to states with higher spiking rates (Figure 1C). Indeed, spike rates were significantly higher inside than outside gamma bursts (p<10−12, permutation test on the largest cluster based statistics) (Figure S8A). There was no significant difference between spikes rates inside and outside of beta bursts (Figure S8B, C; p=0.98).
The relatively long duration and narrow frequency range of individual bursts quantified above (see also Figure 4A) suggest they are not simply spectral byproducts of spiking. Spike-shape bleeding would have created gamma events with the opposite profile: broad in frequency and even briefer (around 1 ms) (Ray and Maunsell, 2011). In addition, the gamma and beta bursts were visible in raw LFPs (Figure 4B). We further tested whether the gamma oscillations corresponded to rhythmic population activity rather than spike-shape bleeding by looking at spike-gamma burst interactions as above. Early network models (Brunel and Wang, 2003) with the same pyramidal-interneuron interaction as in the tested model (Figure 1C) suggest that both gamma frequency and spike rates are co-modulated by excitation. We therefore divided gamma into two non-overlapping sub-bands (low: 40-65 Hz vs high: 70-100 Hz). As predicted, the spike rate modulation by gamma bursts was higher in the high gamma than in the low gamma band (p<10−8, Wilcoxon signed-rank test). Thus, higher spike rates are associated with the higher frequency gamma bursts. This would not have been expected if gamma power was due to spike-shape bleeding as spike rate then would have had no effect on the spectral component.
Prediction 3: Beta and gamma underlie different network states
The model further predicts that because gamma and beta bursting correspond to different states of the network (stimulus coding vs default states, respectively) they should be anti-correlated. The average spectrogram shown in Figure 2D and the plots of burst rates for gamma-modulated sites (Figure 4C and Figure S7) suggest this. Indeed, most of the gamma-modulated sites (112/126) showed a significant negative correlation between gamma and beta power across the trial (p<0.05: r=−0.41, SE=0.04). However, looking into beta (20-25 and 25-35 Hz) and gamma (46-60, 60-75 and 75-90 Hz) power in small 50 ms time bins, we could not find evidence that power in any beta sub-band correlated with power in any gamma sub-band in the same trial and time bin. Thus, there was no apparent instantaneous connection between the two frequencies on a single trial level.
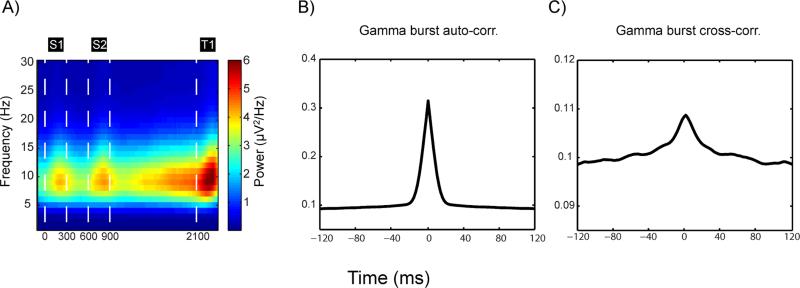
Prediction 4: Gamma bursts are not periodic
Several studies (Palva et al., 2005; Axmacher et al., 2010) as well as the model suggest that gamma power should be modulated by slower frequency oscillations. The model explains this low frequency modulation, not by periodic occurrence of gamma bursts, but by consistency in the duration of the gamma burst per se. In order to examine this, we analyzed the spectral content of the gamma power envelope. This showed a pronounced peak at 8-10 Hz, which was stronger for gamma modulated sites and during elevations in gamma burst rate (Figure 5A, compare with Figure 4C). As predicted, this peak was related to the life-time of gamma bursts rather than their periodic occurrence, as evidenced by the burst auto-correlogram (Figure 5B; Experimental Procedures), which only had a central peak and no side-peaks (as would have been expected from a periodic occurrence). In addition, the coefficient of variance for inter-burst intervals was close to 1 (mean CV2 for delay = 0.997, std. dev. 0.028, mean CV2 full trial = 0.993, std. dev. 0.018; see Experimental Procedures), indicating a highly variable generation, not periodic appearance. The cross-correlograms also showed a central (albeit much smaller, compare scales) peak (Figure 5C), demonstrating a weak spatial coordination in the timing of bursts across sites.
Fig. 5.
Slow modulation of gamma power. A) The difference between spectrograms of the envelopes of the gamma-band (45-100 Hz) oscillations in gamma-modulated versus non-modulated sites. B) Auto-correlogram of gamma (45-100 Hz) bursts for gamma-modulated sites during the delay period. C) Cross-correlogram of gamma bursts calculated between all simultaneously recorded gamma-modulated sites. S1-S2 refers to sample 1-2, and T1 to the first test item.
Prediction 5: Gamma bursts are associated with stimulus decoding
The model predicts that gamma bursts not only encode stimuli but also the bursts “replay” (and beta pauses) when information is read out of working memory as spiking. This was supported by our observation that gamma burst rate increased late in the memory delay in two-item (Figure 2C, gamma-modulated sites; Figure 4C) and three-item trials (Figure S7C), accompanied by a drop in beta bursting. This could reflect a replay of stored attractor memories (Lundqvist et al., 2011; Figure 1B) in anticipation of the need to compare them to the test item. This increase in gamma bursting was not related to the anticipation of just any stimulus. Presentations of to-be-encoded sample stimuli at the start of the trial were predictable, but there was no anticipatory increase in gamma bursting (Figure 4D).
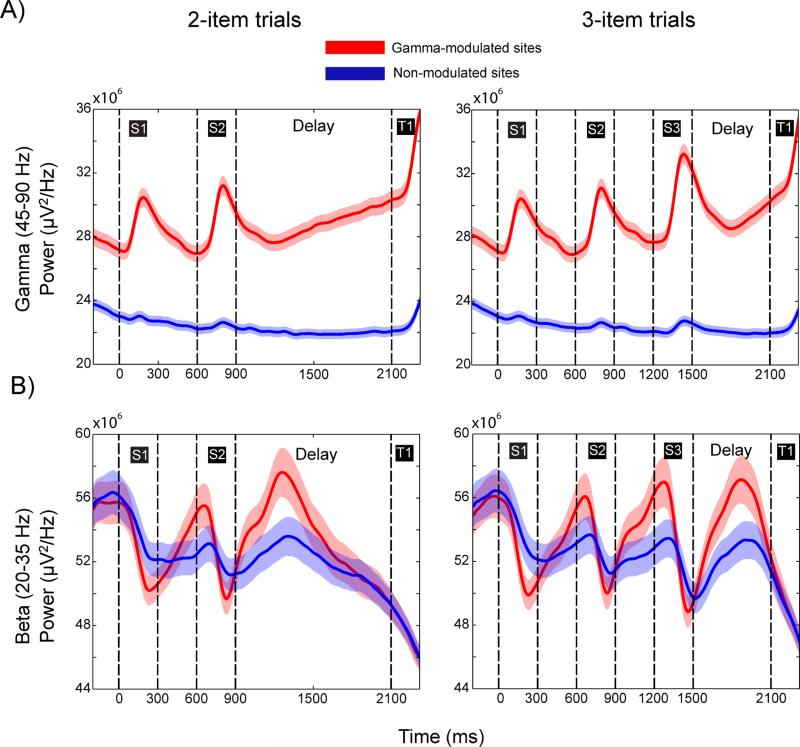
To investigate this further, we examined the gamma power evolution on the gamma-modulated sites (with informative spikes; Figure 3A, red lines) versus non-modulated sites (with non-informative spikes). We used spectral band power rather than a burst rate as the latter measure was inherently normalized across recording sites (Experimental Procedures). The results are illustrated in Figure 6A for both two-item (left panel) and three-item (right panel) trials. In both cases, the gamma power from the gamma-modulated sites (red lines) increased in anticipation of the end of the delay. By contrast, non-modulated sites (without informative spikes, Figure 3A, blue lines) did not show any anticipatory increase. At these sites, the only increase in gamma power occurred at the end of the trial when the animals made their choice, likely due to the saccade. This was also the only period when neurons from the non-modulated sites showed elevated spiking (Figure S5) and carried stimulus information (Figure 3A).
Fig. 6.
Power in gamma-modulated and non-modulated sites. A) Gamma band power in two-(left) and three- (right) item trials averaged for gamma-modulated (red) and non-modulated (blue) sites. B) Same as A), but for beta-band power. Shaded regions represent standard errors.
In contrast to gamma, beta-band power in two-item trials dropped at the end of the delay (prior to T1 relative to early delay in Figure 6B) regardless of the site type (gamma-modulated or non-modulated site, p<10−18 for both, Wilcoxon signed-rank test for the average band power between the first and second half of the delay). Towards the end of delay and during test stimulus, average beta power was not different between gamma-modulated and non-modulated sites (p=0.51, Wilcoxon signed-rank test). This was in contrast to sample presentation when beta was globally suppressed, but more strongly in gamma-modulated sites (Figure 6B and Figure S2; especially relative to the pre-stimulus levels).
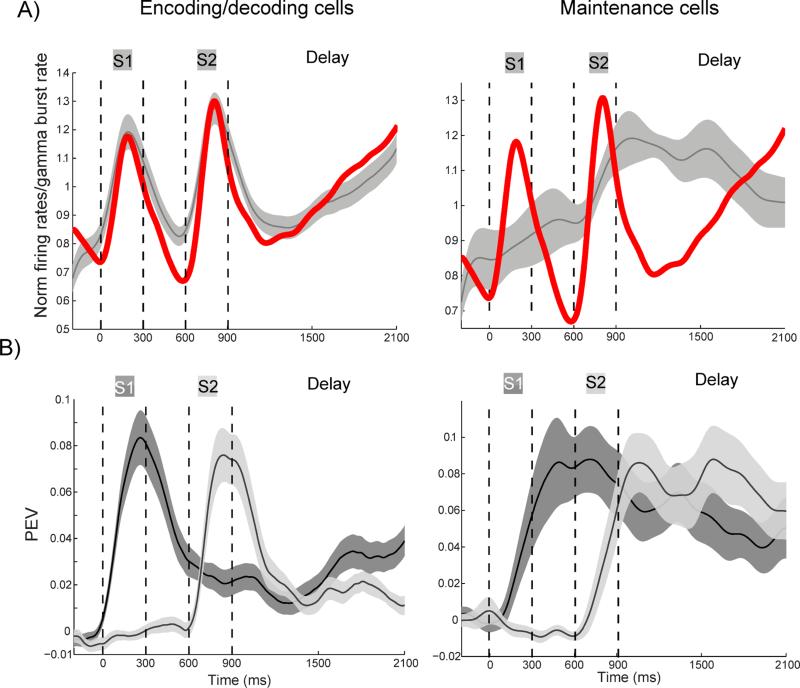
To further investigate the role of gamma in encoding and decoding, we examined neurons that carried information about the sample stimuli. There were two subgroups, selected by when in the trial their peak firing rates occurred. For one group of neurons the peak in firing rates took place during stimulus presentation (the “encoding group”; Figure 7A left panel). The other group of neurons showed a peak of spiking during the memory delay (the “maintenance group”; Figure 7A right panel). Importantly, the encoding neurons were suppressed at the onset of delay but ramped up activity during the second half of the delay, a property they were not selected for. Trial-averaged activity of the encoding group therefore exhibited a similar trend to the gamma burst rate (Figure 7A, left, red line, gamma-modulated sites). Activity of the maintenance group, by contrast, showed a different temporal profile than the average gamma burst rate (Figure 7A, right, red line). Thus, one group of neurons fired during encoding and decoding epochs, closely following the gamma burst rate, while the other fired when the information needed to be maintained but not accessed. As expected, the time course of neural information in these two groups (PEV, see Experimental Procedures) was strongly correlated with their spiking rate (Figure 7B). Thus, late in the delay gamma bursting increased (p<10−14) as did spike rate (p<10−3) and information (PEV, p<10−3) in the encoding/decoding group (first 300 ms of the delay vs last 600 ms, Wilcoxon signed-rank test).
Fig. 7.
Information and firing rates in two-item trials. A) The average normalized firing rates of all informative early (encoding/decoding, left, N=50) and late (maintenance, right, N=21) responding cells. The red curve is the normalized gamma-band (55-90 Hz) burst rate as a reference. B) The average PEV based on first (dark) and second (light) stimuli for informative early (encoding/decoding, left) and late (maintenance, right) responding cells. Shaded areas represent standard errors.
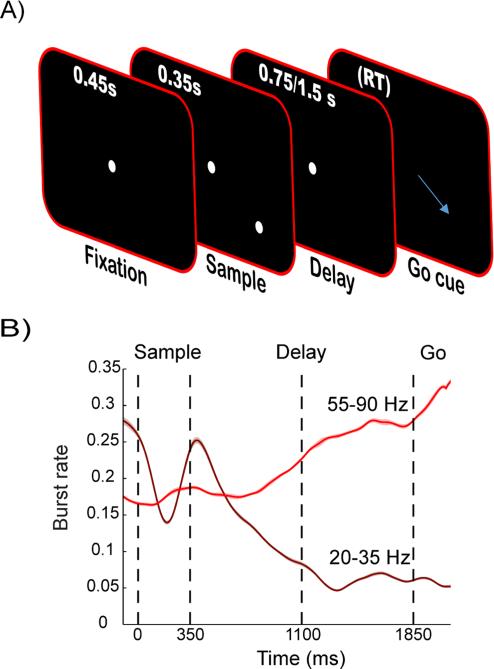
It was possible that the increases in gamma bursting and information in the encoding neurons could reflect anticipation of encoding of the test stimulus rather than decoding information from working memory per se. To test this, we needed a task in which the monkeys could anticipate the end of a memory delay (and thus the need to decode) without anticipation of a (test) stimulus. To this end, we trained two new monkeys on a spatial delayed response task (Funahashi et al., 1989; Pesaran et al., 2002; Goldman-Rakic, 1995). The monkeys had to fixate at a dot in the middle of the screen while a target location was flashed (Figure 8A). After a delay period, signaled by the removal of the fixation dot, the animals were to saccade to the location of the previously flashed target. While this task also involved short-term memory maintenance, it was markedly different from the main task. It was less complex and more related to the maintenance of a motor plan rather than the maintenance of two or more stimuli. Critically, at the end of delay there was no new stimulus as in our original working memory task, but instead the cue to use the working memory information was the disappearance of the fixation dot. These differences allowed us to test the generality of the anticipatory effects found in the main task.
Fig. 8.
Bursts in a delayed saccade task. A) Schematic of the task. The monkeys were to maintain fixation until the fixation dot disappeared and then saccade to the earlier flashed target location. B) Burst rate in gamma (light) and beta (dark) frequency ranges averaged across monkeys and areas (FEF and PFC). Time 0 corresponds to the onset of the sample presentation. Displayed is the subset of trials (1/7) where the delay time was doubled (1500 ms) relative to the standard delay of 750 ms (marked with dashed line 1100 ms into trial). Shaded areas (hardly visible) represent the standard error (N=124).
To more directly verify the hypothesis that gamma bursts are induced as the animal anticipates the need to decode information from working memory, we used two different lengths of memory delay. In 6/7 trials the delay was 750 ms, while in 1/7 of the trials the delay was 1500 ms. This setup was inspired by the observation that gamma bursts seemed to occur earlier in two-item trials, which contained a longer delay interval and were also less common than the three-item trials. We predicted increased gamma and reduced beta burst rates at the end of the delays, and that these effects should be particularly strong in the second half of the unexpectedly long delays. This is indeed what we found (Figure 8B; results pooled across all electrodes in lPFC and FEF of both monkeys). The increase in gamma burst rate towards the end of the 750 ms delay was maintained throughout the entire second half of the 1500 ms delay (1100-1850 ms in Figure 8B), and was accompanied by a decrease in beta burst rate.
Discussion
Model predictions were borne out by trial-by-trial analysis of PFC activity during a multi-item working memory task. There was an interplay between spiking activity and induced oscillations in two main frequency bands, beta (20-35 Hz) and gamma (45-100 Hz). Rather than an overall change in the activity state, there were discrete bursts of beta and gamma LFP oscillations, each brief in duration and narrow in frequency range, like small “bubbles” of oscillatory events. It was only by averaging across trials and recording sites that we observed the broad-band, smoothly varying oscillatory power that has been previously reported (Sederberg et al., 2003; Howard et al., 2003; Roux et al., 2012; Roux and Uhlhaas, 2014; Honkanen et al., 2014; Kornblith et al., 2015). The distinction that the gamma oscillations were narrow-band on a single trial level is of interest as narrow-band gamma in visual cortex is related to sensory processing (Gray and Singer, 1989; Ray and Maunsell, 2011; Lachaux et al., 2005; Fisch et al., 2009) and has been shown to occur in bursts (Tallon-Baudry and Bertrand, 1999; Kucewicz et al., 2014).
Previous studies reported various different oscillatory correlates of WM (Tallon-Baudry and Bertrand, 1999; Howard et al., 2003; Palva et al., 2005; Jensen and Tische, 2002; Kornblith et al., 2015). Here we examined spiking and LFPs in tandem. This revealed a close link between informative spiking and gamma bursts. Spiking that conveyed stimulus information was only found at the minority of recording sites that showed increased gamma bursts to stimuli. Given their length (average 67 ms) and narrow within-burst frequency range, the gamma bursts were not the result of spike shape bleeding into the high-frequency spectral content but instead reflected true oscillatory events (Nir et al., 2007). The gamma bursts and related spiking were induced during encoding and then spontaneously re-appeared throughout the trial, particularly in anticipation of decoding of working memory content.
These results are consistent with the tested multi-item working memory model (Figure 1). In this model, a brief gamma burst accompany the coordinated activation of an ensemble coding a specific memory item. In particular, the gamma bursts are manifestations of attractor states that correspond to different memory items. Due to the brief life-time and synaptic foundation of these attractor states, information about distinct items is not retrieved simultaneously, preventing unwanted interference when more than one object is stored (Figure 1). Our findings thus provide support for the discrete coding and periodic replay hypothesis (Sandberg et al., 2003; Lundqvist et al., 2011; Fuentemilla et al., 2011). In this view, WM information is only present in brief bursts of spiking and maintained in synaptic changes between such events (Sandberg et al., 2003; Mongillo et al., 2008; Lundqvist et al., 2011; 2012; Stokes, 2015).
The tested model further predicted that increasing working memory load should result in a greater rate, but not length, of gamma bursts (Lundqvist et al., 2011), as more items take turn being active. This prediction is opposite to the main conjecture of a related model (Lisman and Idiart, 1995), where the duration of bursts, but not their number, should increase with load. Both sets of predictions could potentially explain reported increases in mid-range gamma-band power with stimulus load (Howard et al., 2003; Roux et al., 2012; Honkanen et al., 2014; Kornblith et al., 2015). These earlier reports displayed broad-band and relatively long-lasting effects, but our observations suggest that they were likely to be the result of trial averaging. Our trial-by-trial analysis revealed that increased memory load was linked to the increased rate, but not length, of brief narrow-band gamma bursts. The consistent life-time of bursts also accounted for the slow modulation of average gamma-band power at 8-10 Hz. It was not a continuous periodic modulation, but rather the result of irregular occurrences of bursts of stereotyped length, as predicted by the model. There was no evidence for low frequency oscillations during the memory delay. This does not preclude a role for slower oscillations, especially in other brain areas (Jensen and Teshe, 2002; Palva et al., 2005; Axmacher et al., 2010; Watrous et al., 2013).
We found that the heterogeneous population of spiking neurons carrying stimulus information could be reduced to two principal populations with different relationships to oscillatory dynamics. One population was mainly active at stimulus encoding and decoding. Its spiking activity profile closely followed the gamma burst rate recorded at the gamma-modulated sites with informative spiking. A second population of informative spiking neurons were active mainly during memory delays when instead average beta burst rate was higher. Thus, different modes of working memory could be reflected by a shift in the balance of beta and gamma burst rates. Activation or suppression of gamma bursting (which was anti-correlated with beta bursting) could activate or suppress spiking of encoding/decoding neurons and thus gate access to working memory or protect working memory from interference from new sensory inputs.
These gamma and beta dynamics may play similar roles in other behaviors and other cortical areas. We observed the same relationship between gamma and beta (and encoding/decoding vs maintenance) in a simpler working memory task that involved planning a delayed saccade (Funahashi et al., 1989) and, hence, a motor plan. This is consistent with observations of increased gamma power in monkey LIP during the encoding and decoding epochs of a delayed saccade task (Pesaran et al., 2002). Fast gamma-like oscillations also appear just prior to the onset of movements in M1 (Donoghue et al., 1998). Gamma oscillations have often been associated with stimulus processing (Fries, 2009) and visual attention in sensory cortex (Gregoriou et al., 2009). Further, general beta power suppression, together with specific patterns of increased gamma power (Lachaux et al., 2005; Fisch et al., 2009) or gamma bursting (Tallon-Baudry and Bertrand, 1999; Kucewicz et al., 2014) have been tied to object and category recognition. Indeed, the working memory model tested here is an adaptation of a perceptual model (Lundqvist et al., 2006). In that model, partial and noisy inputs activate an internal time-limited attractor state representing the likely external stimulus. These non-linear activations are coupled with induced, stimulus-specific patterns of gamma and suppressed beta power (Lundqvist et al., 2010). It is the addition of synaptic potentiation (Wang et al., 2006) to this network that makes it capable of storing and replaying stimulus-induced attractor states and thus useful for working memory (Mongillo et al., 2008; Lundqvist et al., 2011). Therefore, the beta and gamma dynamics observed here seem to be a reoccurring theme, reflecting similar mechanisms that have been adapted across the cortex.
Experimental Procedures
Experimental setup
Two monkeys were trained on a serial working memory task. In order to obtain a liquid reward (apple juice) monkeys had to memorize a series of two or three colored squares. Each side of the square was 1 degree visual angle (DVA) in length and placed either 4 or 6 (for horizontal squares only) DVA lateral of the central fixation, either at the horizontal meridian or 75° above or below the meridian. Stimuli were only shown on the visual hemifield contralateral to the recording site. All behavioral procedures were controlled using MonkeyLogic, a Matlab-based software tool for control of behavioral experiments (Asaad and Eskandar, 2008) interfacing through digital IO cards (NI-PCI6221, National Instruments). Eye movements were controlled using a video-based tracking system (Eyelink 1000, SR Research).
Data collection
For each recording, a new set of acute electrode pairs (tungsten, epoxy-coated, FHC) was lowered through a grid (19 mm diameter, custom design grid and microdrives) that was always oriented in the same direction. A total of 18 (M1) and 20 (M2) prefrontal electrodes were recorded from simultaneously on each session (14 sessions for M1, 16 session for M2) but only the ones containing isolatable units were kept for further analysis. The recordings were performed on a Blackrock Cerebus system and Plexon unity-gain headstages. The LFPs were recorded at a sampling rate of 30 kHz.
Signal processing
We first removed apparent noise sources to the signal. In particular, a notch filter was applied to remove 60 Hz line noise with constant phase across a session. In addition, we removed periodic deflections seen in the evoked potentials (every 47 millisecond, lasting 1 ms, on a subset of electrodes, phase-locked to stimulus onset). The signal was filtered and downsampled to 1 kHz. We applied and compared 3 different methods for time-dependent spectral estimation of the signal: Morlet wavelet analysis (Tallon-Baudry et al., 1996) as well as multi-taper analysis (with a family of orthogonal tapers produced by Slepian functions; Slepian, 1978; Thomson, 1982; Jarvis and Mitra, 2001) and bandpass filtering techniques (Butterworth filter of order 4-6 applied in the forward and reverse directions to obtain the effect of zero-phase filtering, followed by Hilbert transform to extract analytic representation of the signals). They all yielded very similar results in terms of qualitative time-frequency content. They also led to comparable burst extraction outcomes. For all the presented spectrograms (except Figure S6 and S2 in which a large frequency range was scanned and Morlet wavelets used; number of waves = 6, number of octaves = 6 and a step size of 0.05 octaves) and for all burst extraction the multi-taper approach was adopted with frequency-dependent window lengths corresponding to 6-8 oscillatory cycles and frequency smoothing corresponding to 0.2-0.3 of the central freq, f0, i.e. f0±0.2f0, where f0 were sampled with the resolution of 1 Hz (this configuration implies that 2-3 tapers were used). The spectrograms were estimated with the temporal resolution of 1 ms.
Typically we present total power of raw LFPs (after removal of noise), without subtracting any baseline or estimated evoked content. Evoked (Figure S2B) power, in contrast, was calculated by averaging the LFPs across trials for each electrode, and estimating power on the averaged signal.
Selection of gamma modulated sites
Spectral power in correct trials was estimated for each electrode. Electrodes with obvious artifacts (N=14) were removed. These artifacts manifested themselves as persistent narrow-band patterns within either 6-8 Hz or 20-22 Hz (N=6), and apparent bleeding of spikes into the upper frequency ranges of the spectral power estimations (above 50 Hz, N=8 in M2). Each of the remaining 321 electrodes was categorized either as a so-called “gamma-modulated” or “non-modulated” site. Gamma-modulated sites were defined as those that displayed a significant increase in gamma band power during all presentations for either two- or three-item trials (comparing the last 200 ms of the 300 ms presentation window to the 200 ms interval preceding the presentation; Wilcoxon signed-rank test at α=0.05).
Burst extraction
In the first step of the oscillatory burst identification a temporal profile of the LFP spectral content within a frequency band of interest was estimated. We used two alternative methods of spectral quantification (see above). We either narrow-band filtered LFP trials and extracted the analytic amplitudes (envelope) or we used single-trial spectrograms, obtained with the multi-taper approach, to calculate smooth estimates of time-varying band power (all presented results were obtained with the multi-taper approach; the results for the two methods were very similar). Next we defined oscillatory bursts as intervals during individual trials when the respective measure of instantaneous spectral power exceeded the threshold set as 2 standard deviations above the trial mean value for that particular frequency, and with the duration of at least 3 cycles. Further, we extracted the time-frequency representation of the signal in the spectro-temporal neighborhood of each burst using the multi-taper approach, and averaged the power density across the local spectral range to obtain its local temporal profile. We resorted to fitting two-dimensional Gaussian function to the local time-frequency map to specify the aforementioned neighborhood. Finally, we defined the burst length as a time subinterval where the average instantaneous power was higher than half of the local maximum (half-power point).
Having the burst intervals extracted for the beta band (20-35 Hz) and three gamma sub-band oscillations (40-65, 55-90 and 70-100 Hz) from each trial, we defined a trial-average measure – a so-called burst rate for each spectral band. This quantity corresponds to the chance of a burst occurrence on an individual electrode at a particular time in the trial (a proportion of trials where a given electrode displays burst-like oscillatory dynamics around the time point of interest sliding over the trial length).
To estimate how narrow in frequency the burst events were, we defined their frequency span analogously as their temporal length, i.e. in terms of the half-power point (3dB drop). Hence, similarly as in the burst length estimation, we averaged the time-frequency representation of the signal in the local neighborhood of the burst, this time along the temporal dimension, and identified the frequency range where this average spectral power component did not fall below 50% of the local maximum (epicenter of the burst's power).
Burst auto and cross correlation
To describe the temporal characteristics of the burst occurrence we estimated their auto- and cross-correlation function. We first extracted a binary string for each electrode in each trial where only the middle time point of every burst was set to 1. Then for all electrodes we evaluated the trial-average auto-correlation using this binary representation. Analogously, we averaged cross-correlation between the binary representations of burst occurrences at all pairs of electrodes. In the case of both auto- and cross-correlation, the estimates were corrected for the lag-dependent size of overlap between the two binary strings, i.e. raw correlations were scaled by the length of the strings minus the size of lag.
We also estimated the coefficient of variance, CV2, for inter-burst intervals (Holt et al., 1996) using the binary string representation of burst occurrences at each electrode according to the following formula:
where Ii is the time interval between the i-th consecutive pair of burst events (middle time points) (i=1,..,n) across the concatenated binary strings of all trials.
Burst-spike interactions
To calculate the trial-average firing rates within and outside bursts, the instantaneous firing rates were first estimated for each unit by convolving spike trains with a Gaussian kernel (20 ms wide). Then, with a sliding window we averaged normalized firing rates across trials where the matching electrode was either engaged in an oscillatory burst (within-burst firing) or it was not (outside-burst firing). The aforementioned normalization of firing rates was performed independently for each trial and unit by calculating the relative firing rate change with respect to the trial mean value (within trial modulation).
Selection of informative cells
The bias-corrected PEV (Olejnik and Algina, 2003; Buschman et al., 2011) was estimated from average firing rates in 50 ms bins across trials with different stimulus dependent conditions. We performed 2-way ANOVA where trials were either grouped by the location (Figure S4 only) or combination of location and color of the presented items. All correct trials were used, as the groups were well balanced each session. The bias-correction was used as it avoids the problem of non-zero mean PEV (ω2) for small sample sizes.
where MSE is the mean squared error, df the degrees of freedom, SSTotal the total variance and SSBetween groups the variance between groups. As a result, (bias-corrected) PEV allowed for the quantification of information carried by the modulation of firing rates of individual units accounting for the location or combination of color and position of the presented stimulus object. A unit was defined as informative if its PEV for the combination of color and location exceeded the threshold of 0.05 in two consecutive time bins anywhere in the trial after the relevant stimulus had been presented. Normalization of firing rates for each cell amounted to the scaling by its total intra- (across time) and inter-trial average firing rate.
Statistical methods
The majority of tests performed in this study were nonparametric due to insufficient evidence for model data distributions. To address the multi-comparisons problem we employed Kruskal-Wallis, Friedman's and Wilcoxon's signed-rank tests where appropriate. In addition, for the comparison between temporal profiles of the normalized firing rates within versus outside oscillatory bursts we resorted to a permutation test on the largest cluster based statistics (Maris and Oostenveld, 2007), originally proposed to increase the test sensitivity based on the known properties of the data (here: temporal dependency). Finally, some attention should be given to the way we report correlations between the measures of time-varying spectral band content and burst rate statistics. The correlation analyses were performed on individual electrodes and only the summary statistics (mean and SE) for the electrode-wise significant effects (p<0.01) were presented.
Additional analysis
We also performed spike-field coupling, cross-frequency coupling and behavioral analyses, which were omitted from the main manuscript. The motivation and more details are described in Supplemental Experimental Procedures.
Supplementary Material
Highlights.
Working memory information in neuronal spiking was linked to brief gamma bursts
The narrow-band gamma bursts increased during encoding, decoding and with WM load
Beta bursting reflected a default network state interrupted by gamma
Support for a model of WM based on discrete dynamics and not sustained activity
Acknowledgements
We like to thank Jefferson Roy, Simon J. Kornblith, Jacob Donoghue, Matthew Silver, Andre Bastos, Robert Schmidt, Roman Loonis and Alik Widge for valuable suggestions and comments.
This work was supported by the NIMH (5R01MH091174-05), The MIT Picower Innovation Fund, Human Brain Project for P.H., JFDP Fellowship for M.L., DFG RO 3864/2-1 to J.R.
Footnotes
Publisher's Disclaimer: This is a PDF file of an unedited manuscript that has been accepted for publication. As a service to our customers we are providing this early version of the manuscript. The manuscript will undergo copyediting, typesetting, and review of the resulting proof before it is published in its final citable form. Please note that during the production process errors may be discovered which could affect the content, and all legal disclaimers that apply to the journal pertain.
Author contributions
CRediT taxonomy: Conceptualization, E.K.M., J.R., M.L., P.H. and T.J.B; Investigation, J.R. (main), T.J.B., M.L., and S.L.B.; Formal analysis, M.L. and P.H.; Validation, P.H.; Data curation, J.R., S.L.B., M.L. and P.H.; Software, P.H. and M.L.; Writing – Original Draft, M.L., and E.K.M.; Writing – Review & Editing, M. L., E.K.M., P.H. and J.R.; Visualization, M.L., P.H. and J.R.; Funding Acquisition, E.K.M., J.R., M.L., and P.H.; Resources, E.K.M.; Supervision, E.K.M.
References and Notes
- Amit DJ, Brunel N. Model of global spontaneous activity and local structured activity during delay periods in the cerebral cortex. Cereb. Cortex. 1997;7:237–252. doi: 10.1093/cercor/7.3.237. [DOI] [PubMed] [Google Scholar]
- Asaad WF, Eskandar EN. A flexible software tool for temporally-precise behavioral control in Matlab. J Neurosci. Meth. 2008;174(2):245–258. doi: 10.1016/j.jneumeth.2008.07.014. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Axmacher N, Henseler MM, Jensen O, Weinreich I, Elger CE, Fell J. Cross-frequency coupling supports multi-item working memory in the human hippocampus. Proc. Natl. Acad. Sci. 2010;107(7):3228–3233. doi: 10.1073/pnas.0911531107. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Brunel N, Wang XJ. What determines the frequency of fast network oscillations with irregular neural discharges? I. Synaptic dynamics and excitation-inhibition balance. J. Neurophysiol. 2003;90:415–430. doi: 10.1152/jn.01095.2002. [DOI] [PubMed] [Google Scholar]
- Buschman TJ, Siegel M, Roy JE, Miller EK. Neural substrates of cognitive capacity limitations. Proc. Natl. Acad. Sci. 2011;108(27):11252–11255. doi: 10.1073/pnas.1104666108. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Compte A, Brunel N, Goldman-Rakic PS, Wang XJ. Synaptic mechanisms and network dynamics underlying spatial working memory in a cortical network model. Cerebral Cortex. 2000;10(9):910–923. doi: 10.1093/cercor/10.9.910. [DOI] [PubMed] [Google Scholar]
- Cromer JA, Roy JE, Miller EK. Representation of multiple, independent categories in the primate prefrontal cortex. Neuron. 2010;66:796–807. doi: 10.1016/j.neuron.2010.05.005. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Donoghue JP, Sanes JN, Hatsopoulos NG, Gaál G. Neural discharge and local field potential oscillations in primate motor cortex during voluntary movements. J Neurophysiol. 1998;79(1):159–173. doi: 10.1152/jn.1998.79.1.159. [DOI] [PubMed] [Google Scholar]
- Durstewitz D, Seamans JK. Beyond bistability: biophysics and temporal dynamics of working memory. Neuroscience. 2006;139(1):119–133. doi: 10.1016/j.neuroscience.2005.06.094. [DOI] [PubMed] [Google Scholar]
- Fisch L, Privman E, Ramot M, Harel M, Nir Y, Kipervasser S, Andelman F, Neufeld MY, Kramer U, Fried I, Malach R. Neural “ignition”: enhanced activation linked to perceptual awareness in human ventral stream visual cortex. Neuron. 2009;64(4):562–574. doi: 10.1016/j.neuron.2009.11.001. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Fries P. Neuronal gamma-band synchronization as a fundamental process in cortical computation. Annu Rev Neurosci. 2009;32:209–224. doi: 10.1146/annurev.neuro.051508.135603. [DOI] [PubMed] [Google Scholar]
- Fuentemilla L, Penny WD, Cashdollar N, Bunzeck N, Duzel E. Theta-coupled periodic replay in working memory. Curr. Biol. 2010;20:606–612. doi: 10.1016/j.cub.2010.01.057. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Funahashi S, Bruce CJ, Goldman-Rakic PS. Mnemonic coding of visual space in the monkey's dorsolateral prefrontal cortex. J Neurophysiol. 1989;61(2):331–349. doi: 10.1152/jn.1989.61.2.331. [DOI] [PubMed] [Google Scholar]
- Fuster JM, Alexander GE. Neuron activity related to short-term memory. Science. 1971;173:652–654. doi: 10.1126/science.173.3997.652. [DOI] [PubMed] [Google Scholar]
- Gray CM, Singer W. Stimulus-specific neuronal oscillations in orientation columns of cat visual cortex. Proc. Natl. Acad. Sci. 1989;86:1698–1702. doi: 10.1073/pnas.86.5.1698. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Goldman-Rakic PS. Cellular basis of working memory. Neuron. 1995;14:477–485. doi: 10.1016/0896-6273(95)90304-6. [DOI] [PubMed] [Google Scholar]
- Gregoriou GG, Gotts SJ, Zhou H, Desimone R. High-frequency, long-range coupling between prefrontal and visual cortex during attention. Science. 2009;324(5931):1207–1210. doi: 10.1126/science.1171402. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Holt GR, Softky WR, Koch C, Douglas RJ. Comparison of discharge variability in vitro and in vivo in cat visual cortex neurons. J Neurophysiol. 1996;75:1806–1814. doi: 10.1152/jn.1996.75.5.1806. [DOI] [PubMed] [Google Scholar]
- Honkanen R, Rouhinen S, Wang SH, Palva JM, Palva S. Gamma Oscillations Underlie the Maintenance of Feature-Specific Information and the Contents of Visual Working Memory. Cerebral Cortex. 2014:bhu263. doi: 10.1093/cercor/bhu263. [DOI] [PubMed] [Google Scholar]
- Howard MW, Rizzuto DS, Caplan JB, Madsen JR, Lisman J, Aschenbrenner-Scheibe R, Schulze-Bonhage A, Kahana MJ. Gamma oscillations correlate with working memory load in humans. Cerebral cortex. 2003;13(12):1369–1374. doi: 10.1093/cercor/bhg084. [DOI] [PubMed] [Google Scholar]
- Jarvis MR, Mitra PP. Sampling Properties of the Spectrum and Coherency of Sequences of Action Potentials. Neural Computation. 2001;13(4):717–749. doi: 10.1162/089976601300014312. [DOI] [PubMed] [Google Scholar]
- Jensen O, Tesche CD. Frontal theta activity in humans increases with memory load in a working memory task. Eur J Neurosc. 2002;15(8):1395–1399. doi: 10.1046/j.1460-9568.2002.01975.x. [DOI] [PubMed] [Google Scholar]
- Kornblith S, Buschman TJ, Miller EK. Stimulus Load and Oscillatory Activity in Higher Cortex. 2015Cerebral Cortex:bhv182. doi: 10.1093/cercor/bhv182. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Kucewicz MT, Cimbalnik J, Matsumoto JY, Brinkmann BH, Bower MR, Vasoli V, Sulc V, Meyer F, Marsh WR, Stead SM, Worrell GA. High frequency oscillations are associated with cognitive processing in human recognition memory. Brain. 2014:awu149. doi: 10.1093/brain/awu149. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Lachaux JP, George N, Tallon-Baudry C, Martinerie J, Hugueville L, Minotti L, Kahane P, Renault B. The many faces of the gamma band response to complex visual stimuli. Neuroimage. 2005;25(2):491–501. doi: 10.1016/j.neuroimage.2004.11.052. [DOI] [PubMed] [Google Scholar]
- Lisman JE, Idiart MA. Storage of 7+/−2 short-term memories in oscillatory subcycles. Science. 1995;267(5203):1512–1515. doi: 10.1126/science.7878473. [DOI] [PubMed] [Google Scholar]
- Lundqvist M, Rehn M, Djurfeldt M, Lansner A. Attractor dynamics in a modular network model of neocortex. Network. 2006;17:253–276. doi: 10.1080/09548980600774619. [DOI] [PubMed] [Google Scholar]
- Lundqvist M, Compte A, Lansner A. Bistable, Irregular Firing and Population Oscillations in a Modular Attractor Memory Network. PLoS Comput. Biol. 2010;6:e1000803. doi: 10.1371/journal.pcbi.1000803. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Lundqvist M, Herman P, Lansner A. Theta and gamma power increases and alpha/beta power decreases with memory load in an attractor network model. J. Cogn. Neurosci. 2011;23:3008–3020. doi: 10.1162/jocn_a_00029. [DOI] [PubMed] [Google Scholar]
- Lundqvist M, Herman P, Lansner A. Variability of spike firing during theta-coupled replay of memories in a simulated attractor network. Brain Res. 2012;1434:152–61. doi: 10.1016/j.brainres.2011.07.055. [DOI] [PubMed] [Google Scholar]
- Maris E, Oostenveld R. Nonparametric statistical testing of EEG- and MEG-data. J Neurosci. Meth. 2007;164:177–190. doi: 10.1016/j.jneumeth.2007.03.024. [DOI] [PubMed] [Google Scholar]
- Mongillo G, Barak O, Tsodyks M. Synaptic theory of working memory. Science. 2008;319:1543–1546. doi: 10.1126/science.1150769. [DOI] [PubMed] [Google Scholar]
- Miller EK, Erickson CA, Desimone R. Neural mechanisms of visual working memory in prefrontal cortex of the macaque. J Neurosci. 1996;16(16):5154–5167. doi: 10.1523/JNEUROSCI.16-16-05154.1996. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Miller EK, Cohen JD. An integrative theory of prefrontal cortex function. Annu Rev Neurosci. 2001;24:167–202. doi: 10.1146/annurev.neuro.24.1.167. [DOI] [PubMed] [Google Scholar]
- Nir Y, Fisch L, Mukamel R, Gelbard-Sagiv H, Arieli A, Fried I, Malach R. Coupling between neuronal firing rate, gamma LFP, and BOLD fMRI is related to interneuronal correlations. Curr Biol. 2007;17(15):1275–1285. doi: 10.1016/j.cub.2007.06.066. [DOI] [PubMed] [Google Scholar]
- Olejnik S, Algina J. Generalized eta and omega squared statistics: measures of effect size for some common research designs. Psychological methods. 2003;8(4):434. doi: 10.1037/1082-989X.8.4.434. [DOI] [PubMed] [Google Scholar]
- Palva JM, Palva S, Kaila K. Phase Synchrony among Neuronal Oscillations in the Human Cortex. J Neurosci. 2005;25(15):3962–3972. doi: 10.1523/JNEUROSCI.4250-04.2005. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Pasternak T, Greenlee MW. Working memory in primate sensory systems. Nat Rev Neurosci. 2005;6(2):97–107. doi: 10.1038/nrn1603. [DOI] [PubMed] [Google Scholar]
- Pesaran B, Pezaris JS, Sahani M, Mitra PP, Andersen RA. Temporal structure in neuronal activity during working memory in macaque parietal cortex. Nat Neurosci. 2002;5(8):805–811. doi: 10.1038/nn890. [DOI] [PubMed] [Google Scholar]
- Rainer G, Miller EK. Timecourse of object-related activity in the primate prefrontal cortex during a short-term memory task. Eur J Neurosci. 2002;15:1244–1254. doi: 10.1046/j.1460-9568.2002.01958.x. [DOI] [PubMed] [Google Scholar]
- Ray S, Maunsell JH. Different origins of gamma rhythm and high-gamma activity in macaque visual cortex. PLoS Biol. 2011;9(4):e1000610. doi: 10.1371/journal.pbio.1000610. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Roux F, Wibral M, Mohr HM, Singer W, Uhlhaas PJ. Gamma-band activity in human prefrontal cortex codes for the number of relevant items maintained in working memory. J Neurosci. 2012;32:12411–12420. doi: 10.1523/JNEUROSCI.0421-12.2012. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Roux F, Uhlhaas PJ. Working memory and neural oscillations: alpha–gamma versus theta–gamma codes for distinct WM information?. Trends Cogn Sci. 2014;18(1):16–25. doi: 10.1016/j.tics.2013.10.010. [DOI] [PubMed] [Google Scholar]
- Sandberg A, Tegnér J, Lansner A. A working memory model based on fast Hebbian learning. Net: Comp. Neur. Sys. 2003;14(4):789–802. [PubMed] [Google Scholar]
- Sederberg PB, Kahana MJ, Howard MW, Donner EJ, Madsen JR. Theta and gamma oscillations during encoding predict subsequent recall. J Neurosci. 2003;23(34):10809–10814. doi: 10.1523/JNEUROSCI.23-34-10809.2003. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Shafi M, Zhou Y, Quintana J, Chow C, Fuster J, Bodner M. Variability in neuronal activity in primate cortex during working memory tasks. Neuroscience. 2007;146(3):1082–1108. doi: 10.1016/j.neuroscience.2006.12.072. [DOI] [PubMed] [Google Scholar]
- Slepian D. Prolate spheroidal wave functions, Fourier analysis, and uncertainty. V-The discrete case. AT&T Technical Journal. 1978;57:1371–1430. [Google Scholar]
- Stokes MG, Kusunoki M, Sigala N, Nili H, Gaffan D, Duncan J. Dynamic coding for cognitive control in prefrontal cortex. Neuron. 2013;78(2):364–375. doi: 10.1016/j.neuron.2013.01.039. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Stokes MG. ‘Activity-silent’ working memory in prefrontal cortex: a dynamic coding framework. TINS. 2015;19(7):394–405. doi: 10.1016/j.tics.2015.05.004. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Tallon-Baudry C, Bertrand O, Delpuech C, Pernier J. Stimulus specificity of phase-locked and non-phase-locked 40 Hz visual responses in human. J Neurosci. 1996;16(13):4240–4249. doi: 10.1523/JNEUROSCI.16-13-04240.1996. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Tallon-Baudry C, Bertrand O. Oscillatory gamma activity in humans and its role in object representation. TINS. 1999;3(4):151–162. doi: 10.1016/s1364-6613(99)01299-1. [DOI] [PubMed] [Google Scholar]
- Thomson D. Spectrum estimation and harmonic analysis. Proceedings of the IEEE. 1982;70:1055–1096. [Google Scholar]
- Wang Y, Markram H, Goodman PH, Berger TK, Ma J, Goldman-Rakic PS. Heterogeneity in the pyramidal network of the medial prefrontal cortex. Nat Neurosci. 2006;9:534–542. doi: 10.1038/nn1670. [DOI] [PubMed] [Google Scholar]
- Watrous AJ, Tandon N, Conner CR, Pieters T, Ekstrom AD. Frequency-specific network connectivity increases underlie accurate spatiotemporal memory retrieval. Nat Neurosci. 2013;16(3):349–356. doi: 10.1038/nn.3315. [DOI] [PMC free article] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.