Fully automated quantitative cephalometry using convolutional neural networks

Abstract.

Quantitative cephalometry plays an essential role in clinical diagnosis, treatment, and surgery. Development of fully automated techniques for these procedures is important to enable consistently accurate computerized analyses. We study the application of deep convolutional neural networks (CNNs) for fully automated quantitative cephalometry for the first time. The proposed framework utilizes CNNs for detection of landmarks that describe the anatomy of the depicted patient and yield quantitative estimation of pathologies in the jaws and skull base regions. We use a publicly available cephalometric x-ray image dataset to train CNNs for recognition of landmark appearance patterns. CNNs are trained to output probabilistic estimations of different landmark locations, which are combined using a shape-based model. We evaluate the overall framework on the test set and compare with other proposed techniques. We use the estimated landmark locations to assess anatomically relevant measurements and classify them into different anatomical types. Overall, our results demonstrate high anatomical landmark detection accuracy ($\sim 1\%$ to 2% higher success detection rate for a 2-mm range compared with the top benchmarks in the literature) and high anatomical type classification accuracy ($\sim 76\%$ average classification accuracy for test set). We demonstrate that CNNs, which merely input raw image patches, are promising for accurate quantitative cephalometry.

1. Introduction

Quantitative morphometry of the human skull and analyses of the spatial relationships among teeth, mandible, maxilla, and cranial base are crucial in orthodontics, orthognathic treatment, and maxillofacial surgeries.^1–7 Such analyses are usually performed using two-dimensional (2-D) x-ray images of the human head, i.e., cephalograms, because of the high resolution enabled by modern x-ray imaging devices and the superior distinguishability of the bony structure boundaries in x-ray images. A standard cephalometric analysis procedure involves identification of anatomically relevant anchor points, i.e., landmarks, measurement of various angles and distances between these landmarks, and qualitative assessment of pathologies from these angles and distances. Manual cephalometric analyses by medical experts are typically very time-consuming.^3,6,7 Moreover, significant interobserver variability can be observed.⁶ Since pathology identification and further treatment procedures are highly sensitive to correct estimation of the landmark locations, inaccurate manual cephalometric analysis can potentially have severe consequences. It is highly desired to construct a fully automated framework that can accurately detect landmarks, perform required measurements, and assess pathologies.

During the last decades, various automated techniques for detection of anatomical landmarks and tissue boundaries have been studied. Cardillo and Sid-Ahmed⁸ used template matching and gray-scale morphological operators for automated identification of landmarks from cephalograms. Grau et al.⁹ demonstrated that the detection performance can be improved when template matching is additionally augmented with image edge detection and contour segmentation operators. Davis et al.^10,11 used rough and fine image features for detecting a limited set of candidate points that are likely to represent the landmarks and exploited the spatial relationships among landmarks for selecting the optimal candidate points. Yue et al.² combined statistical gray-level image patches with a principal component analysis-based shape model for cephalometric landmark detection. Feghi et al.¹² used machine learning techniques based on neuro-fuzzy systems and $k$-means clustering for automated cephalometric analysis. Mohseni and Kasaei¹³ initially estimated landmark positions using affine registration and further refined these positions using a histogram-based boundary search. Kaur and Singh⁵ demonstrated high landmark detection accuracy by combining rotation-invariant template matching and Zernike moments. Recently, Wang et al.^6,7 organized two public challenges on automated cephalometry and summarized the performance of the state-of-the-art landmark detection algorithms. Top algorithms from these challenges are based on random forests for classification of the intensity appearance patterns of individual landmarks and statistical shape analysis for exploiting the spatial relationships among landmarks. Pei et al.¹⁴ recently explored bimodal deep Boltzmann machines for anatomical structure detection and annotation and demonstrated the potential of deep architectures. Despite the variety of techniques studied, it is still an open question as to how fully automated landmark detection can achieve the performance target that all landmarks can be detected within the clinically accepted 2-mm range.

In this paper, we propose the first fully automated framework for cephalogram analysis using one of the rapidly developing deep learning techniques—convolutional neural networks (CNNs). CNNs are biologically inspired variants of multilayer perceptron type of deep machine learning techniques.^15–17 They are in particular well-suited for image processing and recognition applications because they exploit spatially local correlation by imposing local connectivity patterns. CNNs have been successfully demonstrated for a wide range of applications, including image classification,^18–20 image segmentation,^21,22 image alignment,²³ facial landmark detection,^24,25 human pose estimation,²⁶ and lane detection.²⁷ In some of these applications, the performance of CNNs has even surpassed human performance. However, successful demonstrations have been mostly restricted to the areas where there is abundance of data available for training. Adaptation of the successful CNN techniques to medical imaging is very challenging, in particular, because of the small size of the medical image datasets available for training. In this paper, we utilize CNNs for accurate detection of anatomical landmarks merely from raw image patches. We use CNNs to model the consistent intensity appearance patterns of individual landmarks and use the trained networks for recognition of the same patterns in previously unseen target images. To ensure the objective assessment of CNN performance on computerized cephalometry, we use a publicly available database with 400 manually annotated x-ray images and compare the obtained results against the state-of-the-art approaches.⁷ We also combine CNNs with the shape model from one of the best-performing cephalometric landmark detection algorithms.²⁸ Finally, we use the estimated landmark locations to quantitatively assess craniofacial pathologies and compare the overall results with benchmarks from the literature.

2. Methodology

In this section, we describe the methodological foundations of using deep learning in automated cephalometry. Section 2.1 focuses on the main concepts of CNNs, the overall architecture, and explaining the significance of various operations at different layers. Section 2.2 introduces the cephalometric landmark detection problem and describes how CNNs can be used to detect such landmarks. Section 2.3 gives details about using different data augmentation approaches for enriching the training phase of the framework.

2.1. Convolutional Neural Networks

Performance of the automated cephalometric analysis very much depends on its capability to recognize particular appearance patterns that correspond to the location of anatomical landmarks. In a typical medical image analysis application, a training set is used to extract the models that capture such appearance patterns of the reference landmark locations, which are commonly generated by clinical experts. The representativeness of these models and the ability to detect the landmarks in a previously unseen target image is determined by (a) the amount and diversity of information that can be learned from the training set and (b) the success of the particular model and the learning procedure in generalizing these patterns, i.e., not “overfitting” the training set.

In our proposed approach, the landmark appearance is modeled based on deep learning, which processes candidate neighborhoods in a multilayer architecture. Compared with other machine learning approaches, the fundamental strength of deep learning is its capability to extract how to represent the raw image in an optimal way such that the end-to-end estimation procedure is flexible, accurate, and robust. Previous approaches in medical image analysis applications were based on generating hand-crafted features from raw data (such as Haar-like,²⁹ scale-invariant feature transform,³⁰ speeded up robust features,³¹ Sobel-filtered,³² and so on) and building machine learning models (such as random forests,²⁸ $k$-means clustering,⁴ latent semantic analysis,³⁰ and so on) based on these features. However, these approaches are restricted to a specified raw image representation and cannot be well-generalized for challenging image recognition tasks with complex patterns.

As one of the strongest deep learning techniques, CNNs employ a hierarchical structure to propagate information of the salient features to subsequent layers while exploiting the spatially local correlation between them.^15–17 As inputs to CNNs, image patches are used at the first layer. A typical CNN architecture consists of repetitive application of three layers: (a) convolution, (b) nonlinear activation, and (c) pooling. At convolution layers, a 2-D convolution operation is employed using learnable filters. Intuitively, the convolution operation outputs a measure of the spatial similarity of the input with the filter. CNNs learn the filters that activate when they see a particular image pattern at some spatial position of the output of the preceding layer. To improve the learning rate and to avoid internal covariate shift, batch normalization is applied before 2-D convolution layers. Nonlinear activation layer applies a nonlinear function elementwise to increase the predictive strength of CNN layers. Choice of the nonlinear function depends on the desired output range, gradient computation considerations, and computational complexity. Commonly used nonlinear activations are rectified linear unit [ReLU, $f(x)=\max (x,0)$], sigmoid [$f(x)=1/(1+{\mathrm{e}}^{-x})$], and hyperbolic tangent [$f(x)=({\mathrm{e}}^{2x}-1)/({\mathrm{e}}^{2x}+1)$] functions. The pooling layer is applied to downsample the resulting outputs and to avoid progressive growth of the number of parameters. A common choice for pooling operation is maximum pooling, which is based on taking the maximum value pixels in a small window. (For example, $2\times 2$ maximum pooling outputs the maximum of four values in each $2\times 2$ block.) Outputs of the last layer are fully connected to a set of neurons that can classify the input to the network. Despite the large parameter space and nonconvexity of the objective functions, efficient training of CNNs is enabled by first-order gradient methods. Because of the layerwise structure, gradients can be computed recursively using chain rule—the technique commonly known as backpropagation.

2.2. Cephalometric Landmark Detection

To detect the landmark $l$ (where $1\le l\le L$ and $L$ is the total number of landmarks) in a previously unseen target image, the intensity appearance patterns around landmark $l$ should be learned from the images in the training set. Let ${\mathbf{I}}_{(x_i,y_i)}$ denote the $N\times N$ image patch centered at landmark $l$ in a training image, where $N$ is sufficiently large to visually recognize that pixel $(x_i,y_i)$ represents the landmark. Although a large $N$ value yields more information from farther locations, the higher dimensionality comes at the expense of a higher required number of parameters to map it to an output, i.e., potential overfitting problems and higher computational complexity. Our goal is to find $L$ functions $g_l:{[\mathrm{0,255}]}^N\times {[\mathrm{0,255}]}^N\mapsto [\mathrm{0,1}]$ [for $1\le l\le L$, assuming pixel values in the range (0, 255)] such that $g_l({\mathbf{I}}_{(x_i,y_i)})$ is an estimate of the probability that the pixel $(x_i,y_i)$ is the landmark. Ideally, this should yield 1 only when the pixel $i$ is the landmark $l$, and it should yield 0 for all other pixels. Thus, to determine $g_l()$ functions, CNNs are trained with binary-labeled data points, as described in Sec. 2.3.

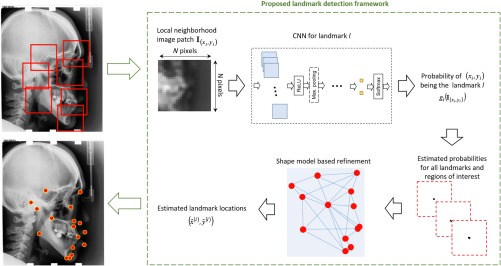
After estimating the probability of a pixel being one of the anatomical landmarks in the target image, i.e., computing $g_l({\mathbf{I}}_{(x_i,y_i)})$ values, a straightforward approach for landmark location estimation would be assigning the locations based on weighted spatial averaging $({\widehat{x}}^{(l)},{\widehat{y}}^{(l)})=\sum _i(x_i,y_i)·h_l\{g_l[\mathbf{I}(x_i,y_i)]\}$, where $h_l()$ is a heuristic weight function. However, these approaches do not consider the relative spatial relationships between all $L$ landmarks. The overall estimation can be further improved by refining the likelihood estimations by a probabilistic shape-based model to consider the relative spatial arrangements of the candidate estimations. For shape-based refinement, we consider the approach of modeling the spatial relationships by Gaussian kernel density estimation problems and applying random forests in a multilandmark environment that demonstrated good performance on cephalometric analysis^33–35 (we refer the readers to the original publications^33–35 for more detailed descriptions of these techniques). The overall landmark detection framework is summarized in Fig. 1. Eventually, as the outputs of shape-based refinement, the landmark location estimates $({\widehat{x}}^{(l)},{\widehat{y}}^{(l)})$ are used to quantitatively assess craniofacial pathologies.

Fig. 1.

Schematics of the proposed cephalometric landmark detection framework.

2.3. Constructing the Training Set

In the proposed cephalometric landmark detection framework, CNNs are used to estimate the probability of each pixel being a particular anatomical landmark, for which they are trained with binary-labeled data points—whether a pixel is a true landmark or false landmark.

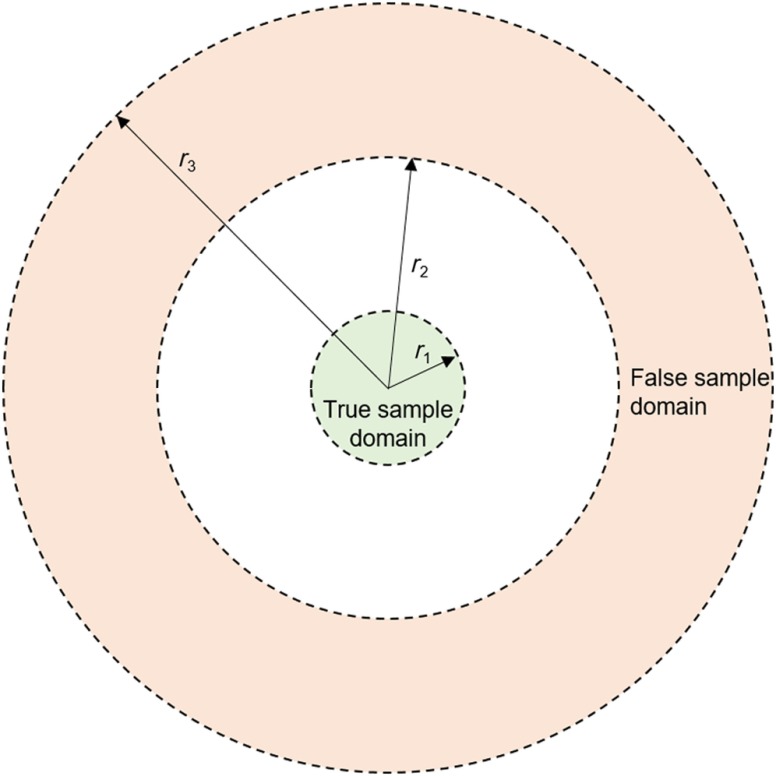
One common challenge in medical image analysis is the small size of the training dataset because obtaining ground-truth labeling by clinical experts is time-consuming. Typically, training datasets indicate only one pixel as the true location for each anatomical landmark. However, it should be noted that a typical value for the pixel width in an x-ray image is $\sim 0.1\mathrm{mm}$,^6,7 whereas the desired estimation accuracy can be around 1 to 2 mm. Thus, to increase the amount of diversity in training, an efficient strategy is to use the neighboring pixels as additional true landmarks. This approach can also be considered in the context of bias-variance trade-off in machine learning. Although the fitting error for the actual single pixel can be increased (higher bias), the sensitivity of estimation can be decreased (lower variance). To represent a false landmark location, any pixel that is sufficiently far from the true landmark location can be used. However, trivial false landmark points chosen from unrelated regions would not contribute to learning, so false landmark points should be within a reasonable neighborhood. Figure 2 shows the domains (parameterized by the radii $r_1$, $r_2$, and $r_3$), from which true and false landmarks are sampled.

Fig. 2.

Domains of true and false landmark samples for training.

3. Implementation and Results

3.1. Description of the Dataset

In this study, we focus on the cephalometric x-ray image dataset,^6,7 which includes 19 anatomical landmarks as listed in Table 1. The ground truth locations of the anatomical landmarks are generated by two experts.⁷ The mean intraobserver variability is 1.73 and 0.90 mm for two different experts, whereas the mean interobserver variability is 1.38 mm⁷ (which suggest a reasonable accuracy target for an automated landmark detection technique). To be consistent with the previous studies, we use 150 images for training and 250 images for testing (which is partitioned into different datasets similar to previous benchmarks, such as IEEE ISBI 2014 Challenge Test Set, IEEE ISBI 2015 Challenge Test Set 1, and IEEE ISBI 2015 Challenge Test Set 2^6,7). Original image sizes are $2400\times 1935\text{pixels}$, and the resolution is $0.1\mathrm{mm}/\text{pixel}$ along both directions. The images are downsampled by 3 (by taking the average of each $3\times 3$ patch) for dimensionality reduction purposes, which significantly reduces the computational complexity while not losing significant information.

Table 1.

List of anatomical landmarks.

Landmark number	Anatomical name
L1	Sella
L2	Nasion
L3	Orbitale
L4	Porion
L5	Subspinale
L6	Supramentale
L7	Pogonion
L8	Menton
L9	Gnathion
L10	Gonion
L11	Lower incisal incision
L12	Upper incisal incision
L13	Upper lip
L14	Lower lip
L15	Subnasale
L16	Soft tissue pogonion
L17	Posterior nasal spine
L18	Anterior nasal spine
L19	Articulate

Pathological assessment of the craniofacial structure is based on the classification of particular clinical measurement methods (see Table 2). These methods can be formulated as geometrical functions of the landmark locations, such as the angle or the distance between them. The ground truth anatomical types are determined using the ground truth landmark locations for the test sets.

Table 2.

Classification of anatomical types based on eight standard clinical measurement sets.^6,7

Methods	Type 1	Type 2	Type 3
(1) The angle between L5, L2, and L6 A point–nasion–B point angle (ANB)	3.2 deg to 5.7 deg	$>5.7$	$<3.2$
	Class I (normal)	Class II	Class III
(2) The angle between L1, L2, and L6 sella–nasion–B point angle (SNB)	74.6 deg to 78.7 deg	$<74.6\mathrm{deg}$	$>78.7\mathrm{deg}$
	Normal mandible	Retrognathic mandible	Prognathic mandible
(3) The angle between L1, L2, and L5 sella–nasion–A point angle (SNA)	79.4 deg to 83.2 deg	$>83.2\mathrm{deg}$	$<79.4\mathrm{deg}$
	Normal maxilla	Prognathic maxilla	Retrognathic maxilla
(4) ODI	68.4 deg to 80.5 deg	$>80.5\mathrm{deg}$	$<68.4\mathrm{deg}$
	Normal	Deep bite tendency	Open bite tendency
(5) APDI	77.6 deg to 85.2 deg	$<77.6\mathrm{deg}$	$>85.2\mathrm{deg}$
	Normal	Class II tendency	Class III tendency
(6) The ratio of posterior face height to anterior face height facial height index (FHI)	0.65 deg to 0.75 deg	$>0.75$	$<0.65$
	Normal	Short face tendency	Long face tendency
(7) The angle between L1, L2, and L9 frankfurt-mandibular plane angle (FMA)	26.8 deg to 31.4 deg	$>31.4\mathrm{deg}$	$<26.8\mathrm{deg}$
	Normal	Mandible high angle tendency	Mandible low angle tendency
(8) The distance between L12 and L11 modify-wits (MW)	2 mm to 4.5 mm	0 mm	$>4.5\mathrm{mm}$
	Normal	Edge to edge	Large over jet
		$<0\mathrm{mm}$
		Anterior cross bite

3.2. Convolutional Neural Networks Architecture and Training

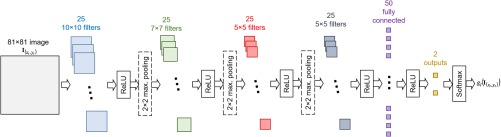
Figure 3 shows the overall CNN architecture used for each of the 19 landmarks. The image patch size $N$ is chosen as 81. There are four stages of 2-D convolutions, each followed by rectified linear units. After the first three stages of 2-D convolutions, a $2\times 2$ maximum pooling is applied to reduce the number of parameters. The first two stages of 2-D convolution operations have a stride of 1 (i.e., different outputs are calculated for regions only 1 pixel apart), and the last two stages of 2-D convolution operations have a stride of 2 (i.e., different outputs are calculated for regions 2 pixels apart). The last stage of 2-D convolution is followed by a fully connected layer. Convolution of the fully connected layer is followed by an ReLU layer, and the two neurons at the last layer are obtained. Their outputs are combined using the sigmoid function, and a scalar output in the interval (0, 1) is obtained. Overall, from $81\times 81\text{pixels}$, the data size is progressively reduced to $72\times 72$, $36\times 36$, $30\times 30$, $15\times 15$, $11\times 11$, $5\times 5$, and $1\times 1\text{pixels}$, as it propagates toward the output of the network.

Fig. 3.

CNN architecture for local information based probability mapping.

For each landmark, the cephalometric dataset indicates only one pixel as the true landmark location. A binary-labeled training set is constructed as described in Sec. 2.3. To determine the domains of true and false landmarks, the three parameters $r_1$, $r_2$, and $r_3$ in Fig. 2 are chosen as 0.67, 2, and 40 mm, respectively. The exact radii values are relatively flexible, for example, increasing $r_3$ from 40 to 41 mm will increase the number of pixels that can be potentially selected for training by $\sim 4\%$. From each training image, 25 positive and 500 negative samples are randomly chosen to construct the training set of size 78,750 images for each landmark. The batch size is chosen as 500 for training. Initial network weights are independently sampled from a Gaussian distribution with mean 0 and standard deviation 0.1. Weight regularization is applied with a weight decay coefficient of 0.001. The learning rate is initially chosen as 0.001. Backpropagation is applied with a momentum coefficient of 0.9. Thirty five epochs are used while training as no significant error reduction is observed beyond. For implementation, we use the CNN toolbox.³⁶

3.3. Landmark Location Results

The overall cephalometric analysis framework (see Fig. 1) is tested for the 250 test images that are not used while training and developing models.

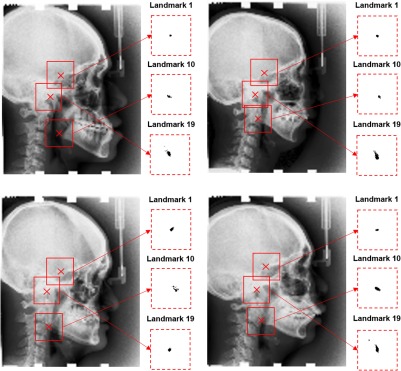
As the outputs of the CNNs, probability values for each pixel that is one of the landmarks are computed. Figure 4 exemplifies the corresponding estimations for landmarks L1, L10, and L19. It is observed that CNNs are highly successful in detecting the appearance patterns to assign accurate probability measures, as the highest probabilities are concentrated around the ground truth landmark locations. The location estimation accuracy and confidence varies among different landmarks. For example, it is observed that high probability values for L10 occur in regions farther from the center compared with L1, and high probability values L19 location occur in a wider region compared with L1.

Fig. 4.

Four test images and corresponding estimations of the probability of candidate location being the landmark. The estimations are shown for three example landmarks: L1, L10, and L19. Red crosses in test images denote the ground truth locations of L1 (top), L10 (bottom), and L19 (middle). Inside each red dashed box, the probability of each point being the corresponding landmark is shown by the grayscale color map such that the white corresponds to 0 and black corresponds to 1. The red dashed boxes are centered at ground-truth landmark locations and have a size of $4\times 4{\mathrm{cm}}^2$.

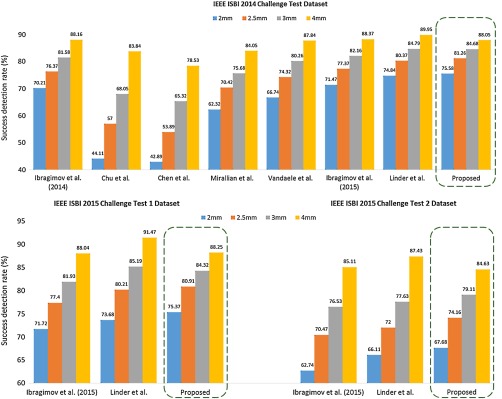
The outputs of the CNNs are combined with the shape model described in Sec. 2.2, and location estimations for the landmarks are obtained for each test image. Figure 5 shows the success detection rate of our technique versus other techniques in the literature for predefined test subsets.^6,7 The success detection rate is defined as the ratio of the corresponding landmarks within the proximity of the precision range from the ground truth location. For the clinically accepted success detection range of 2 mm, our overall framework achieves 75.58%, 75.37%, and 67.68% accuracy for the three test subsets and outperforms all other published techniques.

Fig. 5.

Success detection rates of the technique proposed in this article versus other benchmarks for test sets from IEEE ISBI 2014 Challenge and IEEE ISBI 2015 Challenge Datasets.⁷

3.4. Pathology Classification Results

Based on the classification schemes described in Table 2, pathological assessment is performed using the estimated landmark locations. Tables 3 and 4 show the accuracy results for the two predefined test subsets. Overall, an average classification accuracy of 75.92% and 76.75% are obtained. The results are slightly worse than the technique by Lindner and Coates mostly because of a few outliers despite the better accuracy obtained for a majority of the landmarks.

Table 3.

Accuracy results for classification of anatomical types for IEEE ISBI 2015 Challenge Dataset 1.⁷

Reference	IEEE ISBI 2015 Challenge Dataset 1
	Confusion matrix (proposed)				Diagonal average (proposed, %)	Diagonal average28,33–35 (%)	Diagonal average37 (%)
ANB		Type 1 (%)	Type 2 (%)	Type 3 (%)	61.47	59.42	64.99
	Type 1	46.15	10.26	43.59
	Type 2	40.00	51.43	8.57
	Type 3	11.84	1.32	86.84
SNB		Type 1	Type 2	Type 3	70.11	71.09	84.52
	Type 1	71.43	14.29	14.29
	Type 2	33.33	58.33	8.33
	Type 3	17.47	1.94	80.58
SNA		Type 1	Type 2	Type 3	63.57	59.00	68.45
	Type 1	60.00	10.00	30.00
	Type 2	34.94	56.63	8.43
	Type 3	18.52	7.41	74.07
ODI		Type 1	Type 2	Type 3	75.04	78.04	84.64
	Type 1	70.97	17.74	11.29
	Type 2	26.67	73.33	0.00
	Type 3	19.18	0.00	80.82
APDI		Type 1	Type 2	Type 3	82.38	80.16	82.14
	Type 1	72.5	15.00	12.50
	Type 2	15.79	81.58	2.63
	Type 3	6.94	0.00	93.06
FHI		Type 1	Type 2	Type 3	65.92	58.97	67.92
	Type 1	87.88	6.06	6.06
	Type 2	66.67	33.33	0.00
	Type 3	23.46	0.00	76.54
FMA		Type 1	Type 2	Type 3	73.90	77.03	75.54
	Type 1	61.76	26.47	11.76
	Type 2	10.75	86.02	3.23
	Type 3	21.74	4.35	73.91
MW		Type 1	Type 2	Type 3	81.31	83.94	82.19
	Type 1	77.78	11.11	11.11
	Type 2	11.29	87.10	1.61
	Type 3	9.30	11.63	79.07

Table 4.

Accuracy results for classification of anatomical types for IEEE ISBI 2015 Challenge Dataset 2.⁷

Reference	IEEE ISBI 2015 Challenge Dataset 2
	Confusion matrix (proposed)				Diagonal average (proposed, %)	Diagonal average28,33–35 (%)	Diagonal average37 (%)
ANB		Type 1 (%)	Type 2 (%)	Type 3 (%)	77.31	76.64	75.83
	Type 1	61.29	3.23	35.48
	Type 2	18.52	77.78	3.70
	Type 3	7.14	0.00	92.86
SNB		Type 1	Type 2	Type 3	69.81	75.24	81.92
	Type 1	58.06	12.90	29.03
	Type 2	23.08	69.23	7.69
	Type 3	16.07	1.79	82.14
SNA		Type 1	Type 2	Type 3	66.72	70.24	77.97
	Type 1	60.47	20.93	18.60
	Type 2	22.50	75.00	2.50
	Type 3	29.41	5.88	64.70
ODI		Type 1	Type 2	Type 3	72.28	63.71	71.26
	Type 1	72.22	7.41	20.37
	Type 2	35.00	60.00	5.00
	Type 3	11.54	3.85	84.62
APDI		Type 1	Type 2	Type 3	87.18	79.93	87.25
	Type 1	76.19	14.29	9.52
	Type 2	4.55	90.91	4.55
	Type 3	5.56	0.00	94.44
FHI		Type 1	Type 2	Type 3	69.16	86.74	90.90
	Type 1	82. 98	2.13	14.89
	Type 2	0.00	50.00	50.00
	Type 3	23.53	1.96	74.51
FMA		Type 1	Type 2	Type 3	78.01	78.90	80.66
	Type 1	60.71	35.71	3.57
	Type 2	8.33	90.00	1.67
	Type 3	8.33	8.33	83.33
MW		Type 1	Type 2	Type 3	77.45	77.53	82.11
	Type 1	78.05	9.76	12.20
	Type 2	15.38	84.62	0.00
	Type 3	21.21	9.09	69.70

4. Discussions

In this work, we demonstrated a fully automated cephalometric analysis framework that yields highly accurate automated landmark location and pathology detection. Since the same shape model as that in the approach of Ibragimov et al.^33–35 was used in this work, we can conclude that CNNs outperform random forests in cephalometric analysis and yield higher success detection rates for 2-, 3-, and 3.5-mm ranges. On the other hand, CNNs yield a lower success detection rate for the 4-mm range, which suggests that outliers cannot be avoided for certain cases. Consequently, CNNs demonstrate a better accuracy in pathology assessment of ANB, SNA, overbite depth indicator (ODI), and anteroposterior dysplasia indicator (APDI) but a worse accuracy for SNB, FHI, FMA, and MW measurements in comparison with the random forest-based approach. It is important to note that different pathology grades have very narrow intervals so even a slight shift in landmark location can change the pathology assessment result. As another random-forest based approach, the method approached by Lindner et al.,³⁷ yields a slightly higher success detection range for high ranges and consequently a better performance in pathology assessment. It should be noted that they combined a random forest-based intensity model with a different shape model, hence it is hard to assess whether the performance difference is due to the intensity appearance model or the shape model. Overall, it is important to emphasize that the proposed framework outperforms all alternative methods in clinically acceptable detection, i.e., locating landmarks in a 2-mm range. This metric is generally considered to be the key indicator for estimating the quality of automated cephalometry (some paper referenced by Wang). Indeed, an automatically detected landmark will require manual repositioning if the amount of dispositioning is above a certain threshold, for example, 3 mm. Thus, in combination with manual repositioning, the proposed framework will estimate the pathologies from cephalograms with a much higher accuracy.

The proposed framework is a synergy of CNNs that detect candidate points for each landmark and the statistical shape model that can identify optimal candidate points. The overall performance is mostly dominated by the CNN outputs. For example, a naïve technique, such as spatially averaging the highest CNN outputs without the statistical shape model, yields 67.22%, 79.14%, and 83.20% success detection rates for 2-, 3-, and 3.5-mm ranges, respectively. On the other hand, inclusion of the statistical shape model further improves the accuracy by incorporating joint spatial information and by correcting CNNs when they are stuck at local optimum locations. Consequently, high accuracy of the overall framework should still rely on the statistical shape model.

There are fundamental limitations on the achievable accuracy of out-of-sample landmark detection because a landmark cannot be uniquely positioned due to the x-ray imaging imperfections. In addition to, interobserver accuracy between expert clinicians determines a reasonable accuracy target since the training sets are generated by expert clinicians. The accuracy of the proposed framework is very close to the interobserver accuracy between expert clinicians and has an important potential to assist in cephalometric analysis based on anatomical landmarks. In addition, the framework can be generalized to detect other anatomical landmarks by simply modifying the training procedure to learn their intensity appearance patterns. The major limitation of the proposed technique is observed to be the occurrence of outliers, which is possibly due to the considerable dissimilarity of the training and test images. We expect the accuracy of the proposed technique to improve with the increase in the size and diversity of the training set. A promising future direction for deep-learning based automated cephalometric analysis is landmark-free pathology assessment that can potentially improve cephalometric analysis.

5. Conclusions

We study the application of deep CNNs for fully automated quantitative cephalometry for the first time. Our proposed framework is based on CNNs for detection of anatomical landmarks, which takes the raw image patches as inputs without any feature engineering. CNNs are trained to output probabilistic estimations of different landmark locations, which are combined using a shape-based model. The estimated landmark locations are used to assess anatomically relevant measurements and classify them into different anatomical types. Overall, our framework demonstrates high anatomical landmark detection accuracy ($\sim 1\%$ to 2% higher success detection rate for a 2-mm range compared with the top benchmarks in the literature) and high anatomical type classification accuracy ($\sim 76\%$ average classification accuracy for test set). The results are expected to further improve with the increase in the amount of training dataset. Our end-to-end framework is highly flexible, and does not require specially designed features. Thus, it may be generalized to numerous anatomical landmark detection problems beyond cephalometry.

Biographies

Sercan Ö Arık received his BS degree from Bilkent University, Ankara, Turkey, in 2011, his MS degree from Stanford University, Stanford, California, USA, in electrical engineering in 2013, and his PhD from Stanford University, California, USA, in electrical engineering in 2016. He is a research scientist at Baidu USA. He has (co-)authored more than 25 journal and conference papers. His main current research interests include applications of signal processing, machine learning, optimization, and statistics.

Bulat Ibragimov received his BS degree from Kazan Federal University, Kazan, Russia, in 2010, and his PhD from the University of Ljubljana, Ljubljana, Slovenia, in 2014. He is a postdoctoral researcher at Stanford University. He has (co-)authored more than 20 journal and conference papers and won three public image analysis competitions. His research interests are machine learning and shape modeling in medical image analysis.

Lei Xing received his PhD in physics from Johns Hopkins University, Baltimore, Maryland, USA, in 1992. He is currently the Jacob Haimson professor of medical physics and director of medical physics, Division of Radiation Oncology Department at Stanford University. He is an author on more than 250 peer-reviewed publications, a coinventor on many issued and pending patents, and a coinvestigator or principal investigator on numerous NIH, DOD, NSF, and ACS grants.

Disclosures

The authors have no competing or other conflict of interest to disclose.