Iterative error correction of long sequencing reads maximizes accuracy and improves contig assembly

Abstract

Next-generation sequencers such as Illumina can now produce reads up to 300 bp with high throughput, which is attractive for genome assembly. A first step in genome assembly is to computationally correct sequencing errors. However, correcting all errors in these longer reads is challenging. Here, we show that reads with remaining errors after correction often overlap repeats, where short erroneous k-mers occur in other copies of the repeat. We developed an iterative error correction pipeline that runs the previously published String Graph Assembler (SGA) in multiple rounds of k-mer-based correction with an increasing k-mer size, followed by a final round of overlap-based correction. By combining the advantages of small and large k-mers, this approach corrects more errors in repeats and minimizes the total amount of erroneous reads. We show that higher read accuracy increases contig lengths two to three times. We provide SGA-Iteratively Correcting Errors (https://github.com/hillerlab/IterativeErrorCorrection/) that implements iterative error correction by using modules from SGA.

Introduction

The use of high-throughput sequencing techniques has increased greatly over the past decade. Different sequencing platforms are available, such as Illumina, PacBio, 454, IonTorrent and Nanopore; Illumina is most widely used to date. While being limited to relatively short read lengths in the past, a single run on an Illumina MiSeq machine can now produce 15 gigabases (GB) of paired-end reads as long as 300 bp. The latest Illumina HiSeq 2500 machine can even produce up to 300 GB of paired-end 250 bp reads. This high throughput of long reads is attractive for genome assembly. Although Illumina data already contain relatively few errors at a rate of <1% [1], the probability that reads are completely error-free is low, especially for longer 250 or 300 bp reads.

For genome assembly, it is desirable to use reads that are as accurate as possible. Therefore, correction of sequencing errors is an essential preprocessing step. Many tools for error correction of short read sequencing data exist: BFC [2], BLESS [3], Coral [4], ECHO [5], EULER [6, 7], Fiona [8], Hammer [9], HiTEC [10], Karect [11], Lighter [12], Musket [13], MyHybrid [14], Quake [15], RACER [16], Reptile [17], SGA [18] and SHREC [19], among others. All rely on errors being infrequent and sequencing coverage being sufficiently high so that errors can be corrected using other reads covering the same genomic locus. Most of these tools can be divided into two categories according to how they approach the correction of sequencing reads: k-mer-based correction, which deals primarily with base substitutions, and overlap-based correction, which can also correct insertions and deletions. A detailed overview of each approach and the existing tools is given by Laehnemann et al. [1].

The idea behind k-mer-based correction is that a sequencing error will result in a k bp long substring of the read (k-mer) that does not occur in the genome and thus has a low count in the input data. Such infrequent k-mers can be detected, and the erroneous base can be corrected if substituting it to another base results in a k-mer that occurs more frequently (solid k-mer). K-mer-based correction depends on a parameter choice for the k-mer size, as well as for the count threshold of infrequent and solid k-mers. The idea behind overlap-based correction is to build a multiple sequence alignment of similar reads that probably come from the same genomic locus. Then, sequencing errors are detected as rare differences in alignment columns and are corrected with the alignment column consensus. Overlap-based correction depends on parameters for the minimum read similarity, count thresholds for rare differences and the minimum number of reads supporting the consensus base.

Previous studies have addressed the performance of some of the error correction tools [20, 21]. Most tools perform well on the tested data sets, and almost all reads can be corrected for smaller genomes [20]. However, for complex repeat-rich genomes, such as the human genome, a substantial proportion of the reads still have errors after correction. For example, errors remain in 15–20% of human 100 bp HiSeq reads after correcting with the top-performing tool (Table 2 in [20]). This performance is even worse for longer reads. Errors remain in more than half of 250 bp MiSeq reads from the small Escherichia coli genome (Table 3 in [20]).

There are several possible reasons why sequencing errors may remain uncorrected. First, reads with many errors are more difficult to correct because they are not similar to other reads from the same locus. However, such reads are easy to discard because of many infrequent k-mers present in them. Second, reads coming from a genomic locus with a low sequencing coverage might not be corrected because of the lack of solid k-mers in other reads from the same locus. Third, sequencing errors might remain undetected if the error results in a k-mer found elsewhere in the genome, which frequently occurs in repeat regions. While the first two cases are harder to address computationally, correction of errors in repeats can be improved for longer 250 or 300 bp reads.

Here, we show that many reads with uncorrected sequencing errors after standard correction overlap repeats. In these reads, short erroneous k-mers occur identically in another repeat copy, and are thus mistakenly considered correct. To improve error correction of long Illumina reads, we used modules from the String Graph Assembler and developed an iterative error correction pipeline that runs multiple rounds of k-mer-based correction with an increasing k-mer size, followed by a final round of overlap-based correction. We show that this iterative strategy effectively corrects errors in repeats and reduces the total amount of erroneous reads. We further show that this higher read accuracy translates into two to three times longer contig assemblies.

Methods

Simulated data sets

To investigate why sequencing errors remain after standard error correction and to test if iterative error correction improves read accuracy, we first simulated reads from known genomes. Simulated data have the advantage that we know the true sequence of every sampled read before errors were introduced. This allows us to accurately measure whether a read is error-free after each round of error correction.

Our analyses are based on the human chromosome 11 (135 Mb), Anolis carolinensis chromosome 4 (156 Mb) and chicken chromosome 14 (15 Mb). We first filled assembly gaps and ambiguous bases (N’s) with random sequences. We then created a second haplotype by introducing heterozygosity at the known rate for each species [single nucleotide polymorphism (SNP) rate 0.001 for human, 0.003 for lizard and 0.0006 for chicken, according to [22]; default indel rate 0.0001; no structural variation] using pirs [23]. Last, we used ART [24] and a MiSeq 2 × 300 bp specific error profile to simulate reads from the three chromosomes at 30X coverage each (parameters: 15X coverage for each haplotype, 550 ± 55 bp fragment size). All simulated data sets and the error-profile are available at http://bds.mpi-cbg.de/hillerlab/IterativeErrorCorrection/.

Real data

To test our error correction strategy on real data sets, we downloaded 2 × 250 bp MiSeq reads for the rice strains IR64, DJ123 and Nipponbare (SRX180591, SRX186093 and SRX179262, respectively; http://schatzlab.cshl.edu/data/rice/). We also downloaded a human 2 × 100 bp HiSeq read data set (Library 1 from http://gage.cbcb.umd.edu/data/). To be consistent with our simulations, we down-sampled all data sets to 30X coverage.

Overlap of reads with repeats

We obtained coordinates of interspersed and tandem repeats for all three chromosomes from the UCSC genome browser ‘rmsk' tables [25]. All repeats that are at most 10% diverged from the repeat consensus were downloaded. This set covers 9.5% of human chromosome 11, 2.3% of lizard chromosome 4 and 1% of chicken chromosome 14. For completeness, we also analyzed overlap with all repeats regardless of divergence rate (Supplementary Table 1).

Error correction strategy

In our iterative error correction pipeline, base substitutions are corrected in subsequent rounds of k-mer-based correction with an increasing k-mer size. To also correct remaining small insertions and deletions, we run a final round of overlap-based correction.

We tested our strategy using the String Graph Assembler [18], because (i) the SGA code is open source; (ii) it implements both the k-mer-based and overlap-based correction approaches; (iii) SGA is modular, allowing us to run only selected steps in the genome assembly workflow; (iv) SGA works with reads of different lengths and uses efficient data structures to handle large amounts of data [26]; and, most importantly, (v) it is one of the best correction methods for complex repeat-rich genomes [21].

The SGA error correction modules were not designed to work with large k-mer sizes, where at certain loci only a few reads might overlap by k bp or more. To avoid mis-corrections in these regions, for example, by mis-correcting one infrequent k-mer to a k-mer that has an only slightly higher frequency, we added the following parameters to SGA:

K-mer-based correction:

• – count-offset = N (default 1): When correcting a k-mer, require the count of the new k-mer to be at least N higher than the count of the old k-mer.

• Overlap-based correction:

• – base-threshold = N (default 2): Attempt to correct bases in a read that are seen less than N times in a specific column of the multiple sequence alignment.

• – min-count-max-base = N (default 4): When correcting a base, require the count of the new consensus base to be at least N.

We used these parameters: –count-offset 2, –min-overlap 40, –error-rate 0.01 and defaults otherwise.

Measuring read accuracy for the simulated data sets

Because we aim at maximizing the number of error-free reads, we distinguish between ‘correct' and ‘erroneous' reads. A read is considered correct, if its sequence is identical to the genomic locus of the haplotype where it was sampled from. In contrast, a read is considered erroneous, if it has at least one mismatch or insertion/deletion. We also consider a read as erroneous, if its sequence is identical to the alternative haplotype, which can occur by mistaking a SNP for an error and correcting it to the other allele. Our approach is thus more stringent than considering a read as correct if it is found identically anywhere in the diploid genome. In addition to counting how many reads are correct, we determined (i) the total number of sequencing errors by aligning the sequence of a read to the sequence of the correct read, and (ii) the percent of the genome covered by ≥ 10/20/30 correct reads from the genomic coordinates where the read was sampled from.

Measuring read accuracy for the real data sets

We determined the number of error-free reads by counting the number of reads that map exactly to the reference genome. Specifically, we ran bowtie2 [27] with default parameters and counted the number of occurrences of the flag ‘MD:Z:', followed by the exact read length in the resulting sam files. It should be noted that the rice reference genome has assembly gaps, ambiguous bases (N’s) and only one haplotype, which implies that not all reads can map exactly, even if they are error-free.

Genome assembly

We used SGA to assemble error-corrected reads into contigs. In total, six contig sets were separately assembled for (i) reads after the single best k-mer-based correction, and (ii) reads after correction with our iterative strategy. Potentially erroneous reads were filtered out with ‘sga filter' (parameters: –kmer-threshold 2, –homopolymer-check, –low-complexity-check; defaults otherwise), and an overlap-based string graph was generated with ‘sga overlap' (parameters: –min-overlap 75; defaults otherwise). Contigs were assembled with ‘sga assemble', and the minimum overlap between sequences in the string graph was optimized for each contig set (parameters: –min-overlap ranging from 75 to 200, –resolve-small 10; defaults otherwise).

We assessed assembly quality by testing how many of the assembled ≥400 bp contigs map back to a single continuous genomic region by using Blat with the parameters -tileSize=18 -minMatch=4 -maxIntron=10. Then, we counted every contig where at least 98% of its sequence matches with at least 98% identity to the genome and where the alignment span in the genome is at most 102% of the contig length. Manual inspection of several contigs that did not fulfill these criteria showed that these are short, <1000 bp sequences and match better to the other chromosome haplotype, which was not used for Blat. To assess the coverage of complete genes, we used BUSCO [28] in genome mode with the vertebrate gene set.

Iterative error correction using other methods

For RACER, we set the genome size to the size of human chromosome 11 (135006516bp). Lighter was run with -K kmer_ length genome_size (-K 32 135006516). For BFC and Musket, we specified the k-mer size with the -k parameter. All other parameters were the default values.

Results

Most uncorrected 300 bp reads overlap repeats

We started by using simulated reads to investigate why error correction does not correct all errors. Before any correction, 87% of all reads were erroneous. After k = 40 correction, 12.9, 9.6 and 5% of the human, lizard and chicken reads that became correct overlap repeats, whereas 64.8, 24.2 and 10.5% of the reads that still contained errors overlap repeats, which is 2- to 5-fold higher.

These numbers show that errors in repeat regions are particularly problematic and often remain uncorrected. Because repeats have many similar copies in the genome, a sequencing error in a repeat-overlapping read has a higher probability to result in an erroneous k-mer that occurs identically in another repeat copy. K-mer correction with a small k will fail to detect this erroneous k-mer as infrequent (not solid) because it is found in reads that come from the other repeat copy. Consequently, the error will not be corrected. Figure 1 shows an example from our simulated data set.

Figure 1.

Example of a sequencing error in a repeat region that remains undetected during correction with a small k-mer. Forty-mers containing a sequencing error (arrow) overlap a SINE repeat and are found identically elsewhere on human chromosome 11. Consequently, this k-mer is considered solid, and the error is not corrected in the corresponding read. However, increasing k to 50 or more would recognize this region as infrequent. Thus, longer sequence contexts, which 300 bp reads provide, allow detecting and correcting such errors in highly similar repeats.

Iterative error correction corrects repeat-overlapping reads

Based on the example in Figure 1, we reasoned that additional correction rounds with larger k-mer sizes could correct additional reads. To test this, we subjected the simulated data sets after k = 40 correction to additional rounds of correction, with k increasing up to two-third of the read length (k = 75/100/125/150/175/200) and measured the percentage of erroneous reads. Consistently, for all three species, additional correction rounds substantially decreased the amount of erroneous reads (lines in Figure 2A; Supplementary Table 2). No single correction round achieved the accuracy of iterative correction, regardless of whether we used k-mer-based correction with varying ks or overlap-based correction (crosses in Figure 2A). For example, while 3.4% of the human reads have errors after the single best k = 75 correction, only 0.82% have errors after iterative correction until k = 200. In agreement with the observed decrease in the percentage of erroneous reads, subsequent correction rounds also steadily decrease the total number of errors and increase the percentage of the genome covered by 10, 20 or 30 correct reads (Supplementary Tables 3 and 4).

Figure 2.

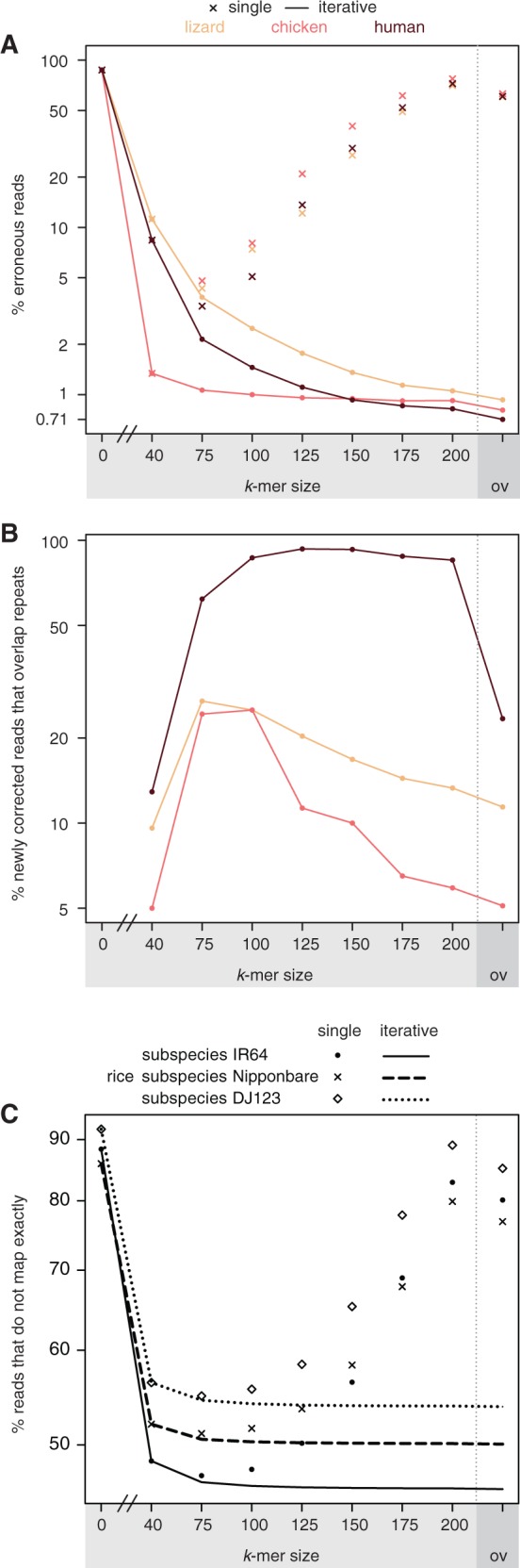
Iterative error correction corrects more errors than any single correction round and particularly corrects repeat-overlapping reads. (A) The percentage of erroneous reads decreases when correcting errors in iterative rounds (lines). The final achieved percentage is substantially lower than any single correction round (crosses), irrespective of which k-mer size is used. The final overlap-based correction is shown on the right. The human, lizard and chicken data are simulated 300 bp MiSeq reads. (B) The Y-axis shows the percentage of newly corrected reads after each iteration of k-mer correction that overlap repeats. Subsequent rounds correct more repeat-overlapping reads than the first k = 40 round. (C) The percentage of 250 bp MiSeq reads from three rice subspecies that do not map exactly to the reference genome decreases when correcting errors in iterative rounds.

We next explored whether iterative error correction helps to correct errors in repeat-overlapping reads. After each correction round, we extracted newly corrected reads that were erroneous in the previous round, and checked for overlap with repeats. We found that the percentage of repeat-overlapping reads is substantially higher in each subsequent round compared with the first k = 40 correction round (Figure 2B; Supplementary Table 1). For the repeat-rich human genome, this percentage reaches 93% after k = 125 correction. Taken together, these results show that iterative error correction can correct substantially more reads than any single correction round, and that subsequent rounds with a higher k increasingly correct errors in repeat regions.

A final round of overlap-based correction corrects insertion and deletion errors

While iterative k-mer-based correction minimized substitution errors, it alone cannot correct the errors that result from small insertion and deletions. Indeed, 20, 16 and 19% of the erroneous human, lizard and chicken reads contained insertion and deletion errors after k = 200 correction. We therefore ran a final round of overlap-based correction, which reduced the percentage of erroneous reads with insertions and deletions to 9, 7 and 8%. After this final step of the error correction pipeline, only 0.71, 0.93 and 0.81% of the human, lizard and chicken reads are still erroneous (right-most data points in Figure 2A; Supplementary Table 2).

Iterative error correction minimizes errors in real 250 bp reads

To test if iterative error correction also improves read accuracy in real sequencing reads, we applied this strategy to 2 × 250 bp MiSeq data from three different rice subspecies. After each iteration, we determined the percentage of reads that map exactly to the reference genome. As shown in Figure 2C, iterative error correction consistently improved the percentage of exactly mapped reads (Supplementary Table 2). We conclude that iterative error correction using multiple k-mer-based and a final overlap-based correction minimizes the total number of erroneous reads in both simulated and real data.

Reducing the number of erroneous reads substantially improves contig assembly

Next, we tested if the reduction in the number of erroneous reads translates into improved contig assembly for the human, lizard and chicken data. We applied SGA to assemble contigs from (i) reads after the single best k-mer-based correction (k = 75 for human and lizard; k = 40 for chicken), and (ii) reads after our iterative error correction strategy. Figure 3 shows the corresponding NG50 values, where half of the respective chromosome consists of contigs of at least that length. NG50 values improve 2.1-fold for human, 2.2-fold for lizard and 2.9-fold for chicken. Thus, the reduction in the number of erroneous reads, even if just from 3.4 to 0.7% as for human, results in substantially longer contigs.

Figure 3.

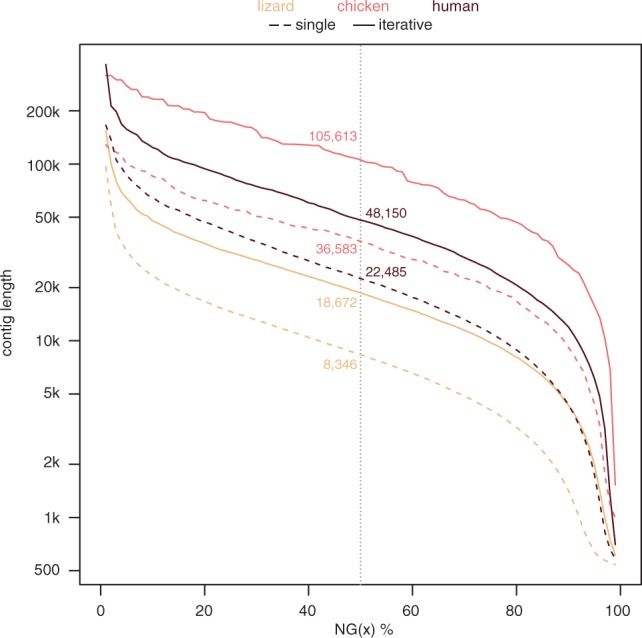
Contig sizes improve 2- to 3-fold after iterative error correction. NG(x)% graph shows the contig size (Y-axis), where x% of the chromosome consists of contigs of at least that size. Contigs assembled from simulated reads after iterative error correction and after the single-best correction round are shown by solid and dashed lines, respectively. The vertical dotted line depicts NG50; corresponding numbers are stated alongside.

To evaluate assembly accuracy and to rule out that the longer contigs are because of mis-assemblies joining nonadjacent genomic regions, we aligned the contigs to the genome from which we sampled the raw reads. We found that virtually all contigs assembled from iteratively corrected reads map to a single continuous genomic region (99.71% for human, 99.89% for lizard and 100% for chicken). We also used BUSCO [28] to assess assembly correctness by counting the number of complete single-copy genes found in each assembly. BUSCO found more complete single-copy genes in the assemblies from iteratively corrected reads (17 versus 15 genes for human, 67 versus 44 genes for lizard and 27 versus 23 for chicken). Together, this shows that the increase in contig lengths is not because of assembly errors and that the assembly accuracy is high.

Fewer correction rounds reduce runtime while preserving correction accuracy

While iterative error correction minimizes the number of erroneous reads and substantially improves contig assembly, it clearly requires additional runtime. Compared with the runtime of the best single k-mer correction, seven iterative k-mer correction rounds and a final overlap correction run 6–8 times as long (Supplementary Table 5). Overlap correction, which computes multiple sequence alignments of reads, takes up to 40% of the total runtime and needs 1.5 times as much memory compared with k-mer correction.

For practical considerations, we looked for ways to reduce runtime while preserving correction performance. We tested fewer correction rounds with larger step-sizes for k: three rounds with k = 40/125/200 instead of seven rounds with k = 40/75/100/125/150/175/200, both followed by a final overlap-based correction round. We found that fewer rounds run ∼5 times as long as the best single k-mer correction (Supplementary Table 5) and increase the percentage of erroneous reads by only 0.18, 0.27 and 0.04% for human, lizard and chicken (Figure 4, Supplementary Table 2). This shows that the final achieved read accuracy is highly similar, irrespective of the k-mer step-size. Omitting the computationally expensive overlap correction step further reduces the runtime to just 1.8, 1.9 and 3.4 times at the cost of an increase of 0.31, 0.42 and 0.16% erroneous reads for human, lizard and chicken.

Figure 4.

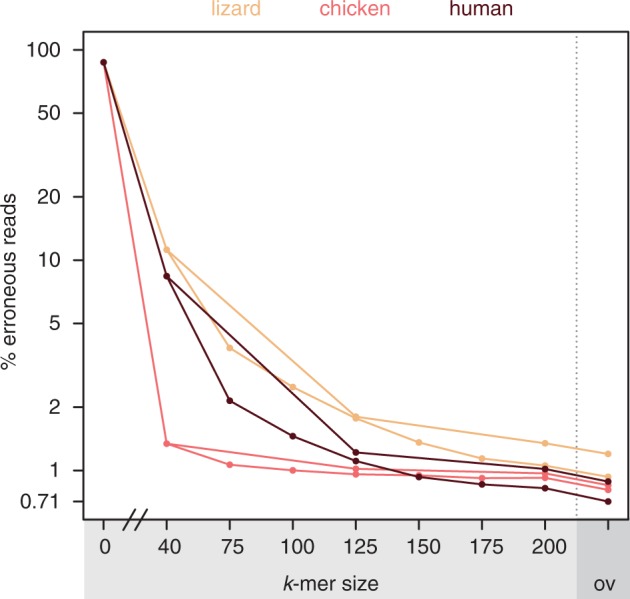
Fewer iterative correction rounds preserve correction accuracy. Three instead of seven rounds of k-mer based correction, both followed by overlap-based correction, achieve a similar percentage of erroneous reads.

K-mers larger than two-third of the read length can correct errors if sequencing coverage is high

In principle, the higher the sequencing coverage, the larger the k-mer size that can be used for error correction. To explore if this is indeed the case, we sampled reads with 60X and 100X coverage from our human simulated genome, in addition to the 30X data set described above. Iterative error correction was run as before, with the addition of k = 225 and k = 250 correction rounds. After each round, we measured the ratio of correct to erroneous reads; a ratio > 1 corresponds to more corrections than mis-corrections.

As shown in Figure 5A, correction with k = 225 and k = 250 further decreases the percentage of erroneous reads in the 60X and 100X data sets (dashed and dotted lines), but not in the 30X data set (solid line; see also Supplementary Table 2). In agreement with this result, we consistently observed more corrections than mis-corrections in the 60X and 100X data sets (Figure 5B). In fact, not a single base was mis-corrected for k ≤ 150 in the 100X data set. In contrast, more mis-corrections than corrections were observed for k ≥ 225 in the 30X data set.

Figure 5.

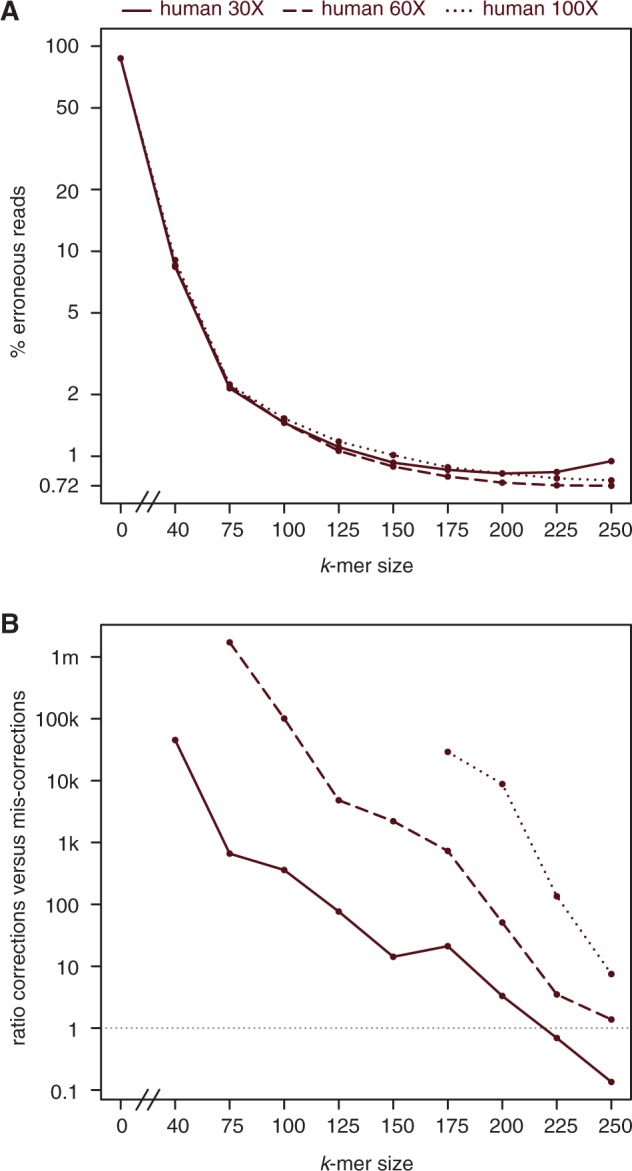
K-mers larger than two-third of the read length can correct errors if sequencing coverage is high. (A) The percentage of erroneous reads in the human 30X data set (solid line) starts to increase again with k = 225 and k = 250 correction. In contrast, the percentage consistently decreases in the 60X (dashed line) and 100X (dotted line) data set. (B) In agreement with A, we start to observe more mis-corrections than corrections after k = 225 and k = 250 correction in the human 30X data set (ratio below 1), but not in the 60X and 100X data sets (ratio > 1 irrespective of the k-mer size).

As mis-corrections in the 30X data set with higher k-mer sizes are unexpected and unwanted, we explored potential reasons and found that they almost exclusively represent ‘haplotype conversions'. Ninety-six per cent of the reads mis-corrected after k = 250 correction perfectly aligned to the respective alternative haplotype, that is, the haplotype from which the read did not originate. These haplotype conversions can occur if sequencing coverage is low and uneven for the two haplotypes, such that SNPs are mistakenly considered as errors. It should be noted that we strictly consider haplotype conversions as mis-corrections, even though removing heterozygosity is likely advantageous for genome assembly. Taken together, increasing k beyond two-third of the read length is beneficial for data sets with high sequencing coverage, even if the further reduction in erroneous reads is marginal.

Iterative error correction of 120 bp reads improves read accuracy but not consistently contig assembly

Because many genome assemblies are based on shorter read data, we also simulated 2 × 120 bp reads from all three chromosomes at 30X coverage each, and used real human 2 × 100 bp sequencing data to test iterative error correction. Indeed, as for 300 bp reads, iterative error correction consistently reduced the percentage of erroneous reads (Supplementary Figures 1 and 2). However, in contrast to 300 bp reads, iterative correction of 120 bp reads improved contig assembly only for chicken, but not for human and lizard (Supplementary Figure 1B). Two reasons likely contribute to this. First, shorter 120 bp reads span less repeats. For example, given 30X coverage, only 0.6% of the human Alu repeats are spanned by at least one 120 bp read, while 14.8% are spanned by at least one 300 bp read. Second, the length of the reads limits the length of the overlap between reads during assembly. In principle, longer read overlaps can help to resolve assembly ambiguities caused by repeats. We compared the minimum exact read overlap that resulted in the best assembly with regard to NG50. For both single and iteratively corrected 120 bp reads, the best human and lizard assembly was achieved with a minimum read overlap of 80 bp. In contrast, a larger minimum read overlap resulted in the best assembly of iteratively corrected 300 bp reads (single versus iterative correction: minimum overlap of 80 versus 100 bp for human and 100 versus 130 bp for lizard). Overall, iterative error correction consistently improves contig assembly only for longer sequencing reads.

Other methods also benefit from iterative error correction

To test if other error correction tools correct more errors if they are used in an iterative fashion, we applied musket [13] and BFC [2] to the human 30X data set. As shown in Figure 6, subsequent correction rounds decrease the percentage of erroneous reads for both methods. While Musket and BFC are faster than SGA (Supplementary Table 5), they do not achieve the accuracy of SGA. We also tested two other methods that cannot be run iteratively because their maximum k-mer size is restricted to small ks (Lighter [12]) or because k is automatically determined from the genome size (RACER [16]). We found that both methods are outperformed by iterative correction with Musket or SGA (Figure 6). These results show that iterative error correction is not specific to SGA but rather a general strategy for many error correction tools.

Figure 6.

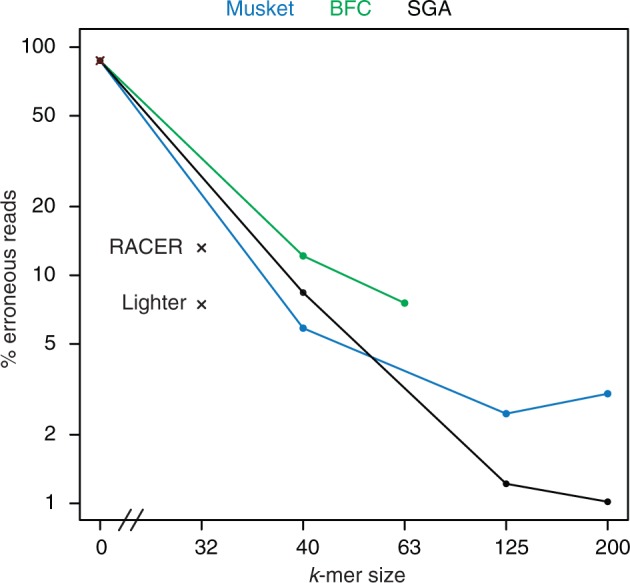
The percentage of erroneous reads also decreases if other error correction methods are used with an iterative error correction strategy. Three correction rounds with Musket [13] and k = 40/125/200 and two correction rounds with BFC [2] and k = 40/63 also reduce the percentage of erroneous 300 bp reads in the human 30X data set. The SGA curve is reproduced from Figure 4 for comparison. For BFC, we ran only two rounds because BFC requires k to be at most 63. Please note that for Musket, the percentage of erroneous reads increases from 2.5% (k = 125) to 3% (k = 200). For comparison, we also tested RACER [16] and Lighter [12]. We ran Lighter only once because it requires k to be at most 32. RACER was run only once because it automatically determines the optimal k, given the genome size (135006516bp) as input. Because RACER does not output the chosen value for k, we plot the performance (13.18% erroneous reads) arbitrarily at k = 32.

Discussion

As sequencing technologies advance, longer reads will likely be the first choice for genome assembly projects. Genome assembly from next-generation sequencing data requires sequencing of a short insert library for contig building. In the past, short insert libraries were often sequenced with 2 × 100 bp reads from Illumina HiSeq sequencers. Illumina technology now offers to sequence 2 × 250 or even 2 × 300 bp reads. Given a short insert library with a mean fragment size of around 450 bp, these reads are able to span some classes of repeats. For example, longer reads will span the up to 300 bp long short interspersed elements that make up 15% of the human genome and represent a significant challenge for assembly because of 1.8 million present copies [29]. However, longer Illumina reads have the disadvantage of being less accurate. Even if the sequencing error rate is the same, the longer the reads are, the lower is the probability that reads are completely error-free. Given that error-free read data are desirable for genome assembly, computational error correction is essential. Therefore, we developed a strategy for improving error correction that maximizes accuracy of long sequencing reads, especially of repeat-overlapping reads.

Existing error-correction tools typically use a single and relatively small k-mer size of <30 bp to correct as many errors as possible in a single round [1]. Some of the tools determine the optimal k-mer size as the one that results in the greatest number of corrections, while other tools let the user chose k. However, there is an inherent trade-off to the choice of a single, fixed k-mer size: while a small k allows for more corrections, because reads have to overlap only by k bp, it can fail to detect errors if the erroneous k is found elsewhere in the genome [15] (see also Figure 1). On the other hand, a large k allows for correcting errors in repeats (Figure 1), but fails to detect errors in low coverage regions and to correct errors in reads with many errors. Here, we show that iterative error correction combines the advantages of small and large k-mers to minimize the number of erroneous reads (Figure 2).

While iterative error correction requires longer runtimes, by far, more time is spent on genome assembly, subsequent genome annotation and finally the analysis of the new genome. Importantly, annotation and analysis critically depend on the quality of the genome assembly. As shown in Figure 3, improving the accuracy of long Illumina reads helps to obtain better assemblies. Hence, read accuracy should be the main consideration. Iterative error correction likely helps genome assembly in two ways. First, although assemblers like SGA try to discard erroneous reads, some of these reads will escape filtering and will be used for assembly. Indeed, SGA did not discard 34% (155 812 of 456 827) of the erroneous human reads after the single best k = 75 correction, and 62% (97 006 of 155 812) of these non-discarded reads overlapped repeats. These erroneous reads add spurious branchings in assembly graphs and hamper assembly contiguity. As shown in Figure 2B, iterative error correction corrects more errors in repeats and thus alleviates the problem of adding branchings because of sequencing errors in parts of the assembly graph that are already hard to resolve. Second, iterative error correction increases the number of correct reads in our data sets by 2.7% for human, 3.4% for lizard and 0.5% for chicken. While these additional reads may have little effect for loci with high read coverage, they will help to build contigs spanning loci with low coverage.

We used SGA to test iterative error correction, because it is one of the best performing error correction methods for large genomes [21] and also outperforms other methods. However, as shown in Figure 6, other tools can benefit from an iterative error correction strategy. Thus, future error correction tool development and benchmarking is likely to benefit from iterative correction in general.

Practical guidance to the users

To facilitate application of the proposed iterative error correction by the community, we provide a wrapper script called SGA-Iteratively Correcting Errors (SGA-ICE) that implements the pipeline by repeatedly using SGA modules. Just given an input directory with the fastq files containing the sequencing reads, SGA-ICE produces an executable shell script that contains all commands for iterative error correction. By default, SGA-ICE runs three rounds of k-mer-based correction with a k between 40 and two-third the read length (which SGA-ICE will determine automatically), followed by a final round of overlap-based correction. Thus, SGA-ICE eliminates the need for the user to choose a single k-mer value. Alternatively, the user can specify which ks to use and whether to run a final overlap-based correction round.

For Illumina sequencing data of large genomes, such as vertebrate genomes, we recommend the SGA-ICE default strategy of three k-mer correction rounds, which reduces runtime while preserving most of the correction accuracy, as shown in Figure 4. Omitting overlap correction would reduce the runtime further; however, small insertion and deletion errors would remain in the reads. If runtime considerations are not important or if the genome is smaller, we recommend running more than three rounds to maximize read accuracy, for example, with k = 40/75/100/125/150/175/200. As suggested by Figure 5, the sequencing coverage determines the largest k-mer that can be used. For a coverage of ∼30X, which should be sufficient to build contigs from long Illumina reads, we do not recommend using k-mers larger than two-third the read length. However, for high sequencing coverage of 60X or more, it will be advantageous to use these large k-mers, as they are able to correct errors in extremely similar genomic repeats that are difficult to bridge during contig assembly.

SGA-ICE is available at https://github.com/hillerlab/Iterative ErrorCorrection/.

Key Points

• Sequencing errors in reads that overlap highly similar genomic repeats are hard to correct by k-mer-based approaches.

• Long 250 or 300 bp Illumina reads provide an opportunity to correct such errors by using longer k-mers.

• Iterative error correction running multiple correction rounds with an increasing k-mer size corrects more errors, particularly in repeats.

• The reduction in the number of erroneous reads improves contig assembly for long Illumina reads.

• Iterative correction eliminates the need for the user to choose a single k-mer value.

Supplementary data

Supplementary data are available online at http://bib.oxfordjournals.org/.

Funding

This work was supported by the Max Planck Society and fellowship 2012/01319-8 from Fundação de Amparo à Pesquisa do Estado de São Paulo (FAPESP) (to J.G.R.).

Katrin Sameith has a PhD in Bioinformatics. She is a postdoctoral researcher with an interest in bioinformatics and functional genomics.

Juliana Roscito has a PhD in developmental biology. She is a postdoctoral researcher interested in developmental and evolutionary biology and genomics.

Michael Hiller has a PhD in Bioinformatics. He is the head of a research group that works on computational genomics approaches to study phenotype–genotype associations.