Abstract
The uneven distribution of wealth and individual economic capacities are among the main forces, which shape modern societies and arguably bias the emerging social structures. However, the study of correlations between the social network and economic status of individuals is difficult due to the lack of large-scale multimodal data disclosing both the social ties and economic indicators of the same population. Here, we close this gap through the analysis of coupled datasets recording the mobile phone communications and bank transaction history of one million anonymized individuals living in a Latin American country. We show that wealth and debt are unevenly distributed among people in agreement with the Pareto principle; the observed social structure is strongly stratified, with people being better connected to others of their own socioeconomic class rather than to others of different classes; the social network appears to have assortative socioeconomic correlations and tightly connected ‘rich clubs’; and that individuals from the same class live closer to each other but commute further if they are wealthier. These results are based on a representative, society-large population, and empirically demonstrate some long-lasting hypotheses on socioeconomic correlations, which potentially lay behind social segregation, and induce differences in human mobility.
Keywords: socioeconomic status, social networks, stratification, rich clubs, human mobility
1. Introduction
Socioeconomic imbalances, which universally characterize all modern societies [1,2], are partially induced by the uneven distribution of economic power between individuals. Such disparities are among the key forces behind the emergence of social inequalities [2,3], which in turn leads to social stratification and spatial segregation in social structures characterized by correlations between the social network, living environment and socioeconomic status of people. Although this hypothesis was drawn a long time ago [4], the empirical observation of spatial, socioeconomic and structural correlations in large social systems has been difficult as it requires simultaneous access to multimodal characters for a large number of individuals. Our aim in this study is to find evidence of social stratification through the analysis of a combined large-scale anonymized dataset that discloses simultaneously the social interactions, frequent locations and the economic status of millions of individuals.
The identification of socioeconomic classes is among the historical questions in the social sciences with several competing hypothesis proposed on their structure and dynamics [5]. One broadly accepted definition identifies lower, middle and upper classes [6–10] based on the socioeconomic status of individuals. These classes can be further used to indicate correlations characterizing the social system. People who live in the same neighbourhood may belong to the same class, and may have similar levels of education, jobs, income, ethnic background, and may even share common political views. These similarities together with homophily, i.e. the tendency of people to build social ties with similar others [11,12], strongly influence the structure of social interactions and also have indisputable consequences on the global social network. The coexistence of social classes and homophily may lead to a strongly stratified social structure where people of the same social class tend to be better connected among each other, while connections between different classes are less frequent than one would expect from structural characteristics only [4,13,14]. These correlations may further determine the living environment and mobility of people leading to spatial segregation and specific commuting patterns characterizing people from similar social classes [15–17].
The observation of such correlations should be possible through the analysis of the social structure [18]. Research on social networks has recently been accelerated through the advent of new technologies which allow the collection of detailed digital footprints of interactions of large numbers of people [19,20]. These advancements have allowed us to observe that social networks appear with heterogeneous connection patterns, are structurally, spatially and temporally correlated [21,22], and to identify various social mechanisms driving their evolution [23,24]. However, although such datasets may contain some information about individual characteristics, they commonly miss one important dimension: they do not provide any direct estimator of the economic status of people, which could strongly influence their connection preferences and may determine the social position of an individual in the global social network. Coarse-grained information details about people's economic status are typically provided as statistical census measures without disclosing the underlying social structure, or by social surveys [25] covering a small and less representative population.
In this paper, we aim to close this gap through the analysis of a combined dataset collecting the social interactions, proxy location and economic situation of a large set of individuals. More precisely, we analyse the transaction and purchase history coupled with time-resolved, spatially detailed mobile phone interactions of millions of anonymized inhabitants of a Latin American country over eight months (for a detailed data description, see Data and material). After introducing precise indicators of economic status, we show that not only individual income but also debt is distributed unevenly in accordance with the Pareto principle. Through the detection of homophilic correlations in the social structure, we provide strong empirical evidence of the stratified intra- and inter-class structure of the social network, and the existence of assortative socioeconomic correlations and ‘rich clubs’. Finally, we present quantitative results about the relative spatial distribution and typical commuting distances of people from different socioeconomic classes.
2. Results
The full description of one's socioeconomic status is rather difficult as it is characterized not only by quantitative features but also related to one's social or cultural capital [26], reputation or professional skills. However, we can estimate socioeconomic status by assuming a correlation between one's social position and economic status, which can be approximated by following the network position and financial development of people. This approach in turn not only gives us a measure of an individual's socioeconomic status but can also help us to draw conclusions about the overall distribution of socioeconomic potential in the larger society.
2.1. Economic status indicators
Our estimation of an individual's economic status is based on the measurement of consumption power. We use a dataset which contains the amount and type of daily debit/credit card purchases, monthly loan amounts and some personal attributes such as age, gender and zip code of billing address of approximately six million anonymized customers of a bank in the studied country over eight months (for further details see Data and material). In addition, for a smaller subset of clients, the data provide the precise salary and total monthly income that we use for verification purposes as explained later.
By following the purchase history of each individual, we estimate their economic position from their average amount of debit card purchases. More precisely, for an individual u who spent a total amount of Pu(t) in month t, we estimate his/her average monthly purchase (AMP) as
| 2.1 |
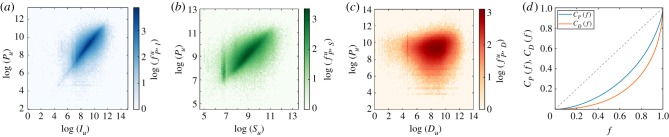
where |T|u corresponds to the number of active months of the user (with at least one purchase). In order to verify this individual economic indicator, we check its correlations with other indicators, such as the salary Su (defined as the average monthly salary of individual u over the observation period T) and the income Iu (defined as the average total monthly income including salary and other incoming bank transfers). We find strong correlations between individual AMP Pu and income Iu with a Pearson correlation coefficient r ≈ 0.758 (p < 0.001, s.e. = 7.33 × 10−4) (for correlation heat map, see figure 1a), and also between Pu and salary Su with r ≈ 0.691 (p < 0.001, s.e. = 9.695 × 10−4) (figure 1b). Note that direct economic indicators, such as Iu and Su, are available only for a smaller subset of users (for exact numbers, see figure 1), thus for this study we decided to use Pu because this measure is available for the whole set of users.
Figure 1.
Correlations and distributions of individual economic indicators. The heat maps show correlations between the AMP Pu and (a) average income Iu, (b) average salary Su and (c) average monthly debt Du for (a) 625 412 (b) 389 567 and (c) 339 288 customers who have (accordingly) both corresponding measures available. Colours in panels (a–c) depict the logarithm of the fraction of customers with the given measures. (d) Cumulative distributions of Pu (blue line) and Du (orange line) as functions of sorted fraction f of individuals. Distributions were measured for 6 002 192 (resp.339 288) individuals from whom AMP (resp. AMD) values were available. Dashed line shows the case of perfectly balanced distribution.
At the same time, we are interested in an equivalent indicator, which estimates the financial commitments of individuals. We define the average monthly debt (AMD) of an individual u by measuring
| 2.2 |
where du(t) indicates the debt of individual u in month 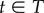 and |T|u is the number of active months where the user had debt. Arguably, individual debt could depend on the average income and thus on the AMP of a person due to the loaning policy of the bank. Interestingly, as demonstrated in figure 1c, we found weak correlations between AMP and AMD with a small coefficient r ≈ 0.104 (p < 0.001, s.e. = 2.48 × 10−3), which suggests that it is worth studying these two indicators independently.
and |T|u is the number of active months where the user had debt. Arguably, individual debt could depend on the average income and thus on the AMP of a person due to the loaning policy of the bank. Interestingly, as demonstrated in figure 1c, we found weak correlations between AMP and AMD with a small coefficient r ≈ 0.104 (p < 0.001, s.e. = 2.48 × 10−3), which suggests that it is worth studying these two indicators independently.
2.2. Overall socioeconomic imbalances
The distribution of an individual economic indicator may disclose signs of socioeconomic imbalances at the population level. This hypothesis was first suggested by V. Pareto and later became widely known as the law named after him [27]. The present data provide a straightforward way to verify this hypothesis through the distribution of individual AMP. We measured the normalized cumulative function of AMP for f fraction of people sorted by Pu in an increasing order
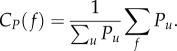 |
2.3 |
We computed this distribution for the 6 002 192 individuals assigned with AMP values. This function shows (figure 1d blue line) that AMP is distributed with a large variance, i.e. indicating large economical imbalances just as suggested by Pareto's law. A conventional way to quantify the variation of this distribution is provided by the Gini coefficient G [28], which characterizes the deviation of the CP(f) function from a perfectly balanced situation, where wealth is evenly distributed among all individuals (diagonal dashed line in figure 1d). In our case, we found GP ≈ 0.461, which is relatively close to the World Bank reported value G = 0.481 for the studied country [29], and corresponds to a Pareto index [30] of α = 1.315. This observation indicates a 0.73 : 0.27 ratio characterizing the uneven distribution of wealth, i.e. 27% of people are responsible for 73% of the total monthly purchases in the observed population. Note that these values are close to the values G = 0.6 and 80 : 20, which were suggested by Pareto.
At the same time, we have characterized the distribution of individual AMD by measuring the corresponding CD(f) function as shown in figure 1d (orange line) for 339 288 individuals for whom AMD values were available. It indicates even larger imbalances in the case of debt with a Gini coefficient GD ≈ 0.627 and α = 1.140 indicating 19% of the population to be actually responsible for 81% of the overall debt in the country. This observation suggests that Pareto's hypothesis holds not only for the distribution of purchases but also for debt. Note that a similar distribution of debt of bankrupt companies has been reported [31].
2.3. Class definition and demographic characters
The economic capacity of individuals arguably correlates with their professional occupation, education level and housing, which in turn determine their social status and environment. At the same time, status homophily [11,12], i.e. people's tendency to associate with others of similar social status, has been argued to be an important mechanism that drives the creation of social ties. Our hypothesis is that these two effects, diverse socioeconomic status and status homophily, potentially lead to the emergence of a stratified structure in the social network where people of the same social class tend to be better connected among themselves than with people from other classes. A similar hypothesis had been suggested earlier [32] but its empirical verification had been impossible until now as this would require detailed knowledge about the social structure and precise estimators of individual economic status. In the following, our main contribution is to clearly identify signatures of social stratification in a representative society-level dataset, which contains information on both the social network structure and the economic status of people.
In order to investigate signatures of social stratification, we combine the bank transaction data with data disclosing the social connections between the bank's customers. To identify social ties, we use a mobile communication dataset, provided by one mobile phone operator in the country, with a customer set that partially overlaps with the user set found in the bank data (for details on data matching policy, see Data and material). To best estimate the social network, we connect people who communicated with each other at least once via calling or SMS during the observation period of 21 months between January 2014 and September 2015, but we remove non-human actors, such as call centres and commercial communicators by using a recursive filtering method. For the purpose of our study, we select all mobile phone users who appear as customers in the bank dataset and take the largest connected component of the intersection graph. After this procedure, we obtain a social network with |E| = 1 960 239 links and N = 992 538 nodes, each corresponding to an individual with a valid non-zero AMP value Pu. For further details about the datasets, their combinations, filtering and network construction, see Data and material.
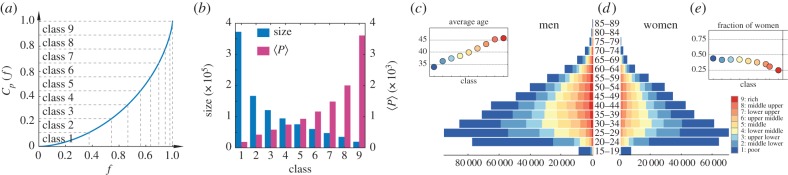
Taking each individual in the selected social network, we assign each of them to one of n = 9 socioeconomic classes based on their individual AMP values. This classification is defined by sorting individuals by their AMP, taking the cumulative function CP(f) of AMP and cutting it into n segments such that the sum of AMP in each class is equal to 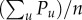 (as shown in figure 2a). Our selection of nine distinct classes is based on the common three-stratum model [6,7], which identifies three main social classes (lower, middle and upper), and three sub-classes for each of them [14]. More importantly, this way of classification relies merely on individual economic estimators, Pu, and naturally partitions individuals into classes with decreasing sizes, and increasing 〈P〉 per capita average AMP values for richer groups (for exact values, see figure 2b). (To assign purchase values in USD, we used the daily average currency rate (17.90 MXN/USD) on 2 March 2016.) To explore the demographic structure of the classes, we used data on the age and gender of customers. We have drawn the population pyramids for men and women in figure 2d with coloured bars indicating the number of people in a given social class at a given age. We found a positive correlation between social class and average age, suggesting that people in higher classes are also older on average (figure 2c). In addition, our data verify the presence of gender imbalance as the fraction of women varies from 0.45 to 0.25 going from lower to upper socioeconomic classes (figure 2e).
(as shown in figure 2a). Our selection of nine distinct classes is based on the common three-stratum model [6,7], which identifies three main social classes (lower, middle and upper), and three sub-classes for each of them [14]. More importantly, this way of classification relies merely on individual economic estimators, Pu, and naturally partitions individuals into classes with decreasing sizes, and increasing 〈P〉 per capita average AMP values for richer groups (for exact values, see figure 2b). (To assign purchase values in USD, we used the daily average currency rate (17.90 MXN/USD) on 2 March 2016.) To explore the demographic structure of the classes, we used data on the age and gender of customers. We have drawn the population pyramids for men and women in figure 2d with coloured bars indicating the number of people in a given social class at a given age. We found a positive correlation between social class and average age, suggesting that people in higher classes are also older on average (figure 2c). In addition, our data verify the presence of gender imbalance as the fraction of women varies from 0.45 to 0.25 going from lower to upper socioeconomic classes (figure 2e).
Figure 2.
Social class characteristics (a) schematic demonstration of user partitions into nine socioeconomic classes by using the cumulative AMP function CP(f). Fraction of individuals belonging to a given class (x-axis) has the same sum of AMP 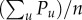 (y axis) for each class. (b) Number of individuals (blue), and the average AMP 〈P〉 (to assign purchase values in USD we used the daily average currency rate (17.90 MXN/USD) on the 2nd March 2016) per individual (pink) in different classes. (c) Average age of different classes. (d) Age pyramids for men and women with colours indicating the corresponding socioeconomic groups and with bars proportional to absolute numbers. (e) Fraction of women in different classes.
(y axis) for each class. (b) Number of individuals (blue), and the average AMP 〈P〉 (to assign purchase values in USD we used the daily average currency rate (17.90 MXN/USD) on the 2nd March 2016) per individual (pink) in different classes. (c) Average age of different classes. (d) Age pyramids for men and women with colours indicating the corresponding socioeconomic groups and with bars proportional to absolute numbers. (e) Fraction of women in different classes.
2.4. Structural correlations and social stratification
Using the above-defined socioeconomic classes and the social network structure, we turn to look for correlations in the inter-connected class structure. To highlight structural correlations, such as the probability of connectedness, we use a randomized reference system. It is defined as the corresponding configuration network model structure where we take the original social network, select random pairs of links and swap them without allowing multiple links and self-loops. Hence, the degree of each of the four nodes involved in the swap remains unchanged. In order to remove any residual correlations, we repeated this procedure 5 × |E| times. This degree-preserving randomization keeps the number of links, individual degrees (and hence any degree–wealth correlations), individual economic indicators Pu, and the assigned class of people unchanged, but destroys any higher-order structural correlations in the social structure and consequently also between socioeconomic layers. In each case, we repeat this procedure 100 times and present results averaged over the independent random realizations. Taking the original (resp. randomized) network, we count the number of links |E(si, sj)| (resp. |Ern(si, sj)|) connecting people in different classes si and sj. After repeating this procedure for each pair of classes in both networks, we take the fraction
| 2.4 |
which gives us how many times more (or less) links are present between classes in the original structure when compared with the randomized one. Note that in the randomized structure the probability that two people from given classes are connected depends only on the number of social ties of the individuals and the size of the corresponding classes, but is independent of the effect of potential structural correlations. This way the comparison of the original and random structures highlights structural patterns induced by anything other than node degrees. Such patterns could emerge due to status homophily, degree–degree correlations (as we study later here and in the electronic supplementary material), or due to triadic closure, communities, motifs and any other structural correlations that one could think of.
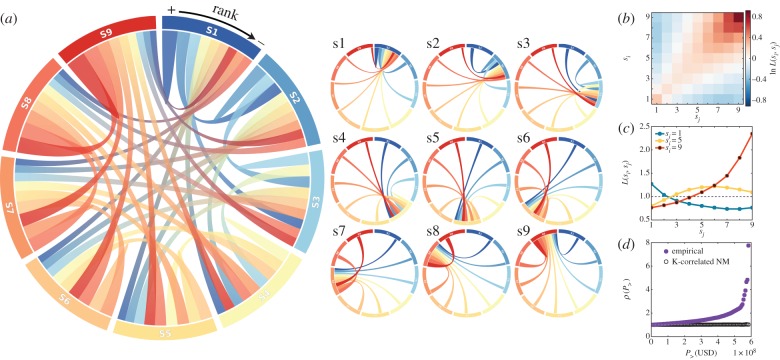
From the chord diagram visualization of this measure in figure 3a, we can draw several conclusions. Note that for better visual presentation in figure 3a, we have normalized L(si, sj) and thus chord width indicates relative values 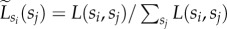 when compared with the origin class sj (as also explained in the figure caption). First, after sorting the chords of a given class si in a decreasing L(si, sj) order, chords connecting a class to itself (self-links) always appear at top (or top second) positions of the ranks. At the same time, other top positions are always occupied by chords connecting to neighbouring social classes. These two observations (better visible in figure 3a insets) indicate strong effects of status homophily and the existence of stratified social structure where people from a given class are the most connected with similar others from their own or from neighbouring classes, while connections with individuals from remote classes are least frequent. A second conclusion can be drawn by looking at the sorting of links in the middle and lower upper classes (S4–S8). As demonstrated in the inset of figure 3a, people prefer to connect upward and tend to hold social ties with others from higher social classes rather than with people from lower classes.
when compared with the origin class sj (as also explained in the figure caption). First, after sorting the chords of a given class si in a decreasing L(si, sj) order, chords connecting a class to itself (self-links) always appear at top (or top second) positions of the ranks. At the same time, other top positions are always occupied by chords connecting to neighbouring social classes. These two observations (better visible in figure 3a insets) indicate strong effects of status homophily and the existence of stratified social structure where people from a given class are the most connected with similar others from their own or from neighbouring classes, while connections with individuals from remote classes are least frequent. A second conclusion can be drawn by looking at the sorting of links in the middle and lower upper classes (S4–S8). As demonstrated in the inset of figure 3a, people prefer to connect upward and tend to hold social ties with others from higher social classes rather than with people from lower classes.
Figure 3.
Structural correlations in the socioeconomic network. (a) Chord diagram of connectedness of socioeconomic classes si, where each segment represents a social class si connected by chords with width proportional to the corresponding inter-class link fraction 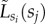 , and using gradient colours matched with opposite ends sj. Note that the
, and using gradient colours matched with opposite ends sj. Note that the 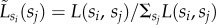 normalized fraction of L(si, sj)
normalized fraction of L(si, sj)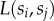 (in equation (2.4)) was introduced here to assign equal segments for each class for better visualization. Chords for each class are sorted in decreasing width order in the direction shown above the main panel. On the minor chord diagrams of panel (a), graphs corresponding to each class are shown with non-gradient link colours matching the opposite end other than the selected class. (b) Matrix representation of L(si, sj) (for definition see equation (2.4)) with logarithmic colour scale. (c) The L(si, sj) function extracted for three selected classes (1 (blue), 5 (yellow) and 9 (red)). Panels (a–d) provide quantitative evidence on the stratified structure of the social network and the upward-biased connections of middle classes. (d) ‘Rich-club’ coefficient ρ(P>) (definition see equation (2.6)) based on the empirical (purple), and a degree-correlated null model (black) networks. On the individual level, the richest people of the population appear to be eight times more densely connected than expected randomly.
(in equation (2.4)) was introduced here to assign equal segments for each class for better visualization. Chords for each class are sorted in decreasing width order in the direction shown above the main panel. On the minor chord diagrams of panel (a), graphs corresponding to each class are shown with non-gradient link colours matching the opposite end other than the selected class. (b) Matrix representation of L(si, sj) (for definition see equation (2.4)) with logarithmic colour scale. (c) The L(si, sj) function extracted for three selected classes (1 (blue), 5 (yellow) and 9 (red)). Panels (a–d) provide quantitative evidence on the stratified structure of the social network and the upward-biased connections of middle classes. (d) ‘Rich-club’ coefficient ρ(P>) (definition see equation (2.6)) based on the empirical (purple), and a degree-correlated null model (black) networks. On the individual level, the richest people of the population appear to be eight times more densely connected than expected randomly.
These conclusions can be further verified by looking at other representations of the same measure. First, we show a heat map matrix representation of equation (2.4) (figure 3b), where L(si, sj) values are shown with logarithmic colour scales. This matrix has a strong diagonal component verifying that people of a given class are always better connected among themselves (red) and with others from neighbouring groups, while social ties with people from remote classes are largely under-represented (blue) when compared with the expected value provided by the random reference model. This again indicates the presence of homophily and the stratified structure of the socioeconomic network. The upward-biased inter-class connectivity can also be concluded here from the increase of the red area around the diagonal by going towards richer classes. These conclusions are even more straightforward from figure 3c where the L(si, sj) is shown for three selected classes (1, poor; 5, middle and 9, rich). These curves clearly indicate the connection preferences of the selected classes. Moreover, they show that the richest people appear with the strongest homophilic preferences as their class is approximately 2.25 times better connected among each other than expected by chance, on the expense of weaker connectivity to remote classes. This effect is somewhat weaker for middle classes, which function as bridges between poor and rich classes, but apparently upward-biased towards richer classes. This set of results directly verifies our earlier conjectures that the structure of the socioeconomic network is strongly stratified and builds up from social ties, whose creation is potentially driven by status homophily, and determined by the socioeconomic characteristics of individuals.
However, one can argue that the observed stratified structure can be simply the consequence of simultaneously present degree–degree and degree–wealth correlations. More precisely, if the degree of an individual is highly correlated with its economic status and at the same time the network is strongly assortative (i.e. people prefer to connect to other people with similar degrees), we may observe similar effects as in figure 3a–c. To rule out this possibility, we completed an extensive correlation analysis, which showed us that no strong effects of degree–degree correlations can be detected and that the degree and wealth of individuals are very weakly correlated. To further clarify the effects of these correlations, we defined another null model similar to the configuration network model, but where degree–degree correlations were preserved. In this model, instead of selecting link pairs randomly for swapping, we select a link and one of its ends randomly, and choose another link randomly where the degree of one of the ending nodes is equal to the degree of the selected end of the first link. Swapping the other ends of the links (with potentially different degrees) will result in two other links between nodes of the original degrees but connected randomly otherwise (for further details, see the electronic supplementary material). Using this null model, we demonstrated that simultaneously present degree–degree and degree–wealth correlations cannot explain the observed stratified structure (for results, see the electronic supplementary material).
The above observations further suggest that the social structure may show assortative correlations in terms of socioeconomic status at the individual level. In other words, richer people may be better connected among themselves than one would expect them by chance and this way they form tightly connected ‘rich clubs’ in a structure similar to the suggestion of Mills [33]. This can be verified by measuring the rich-club coefficient [34,35], after we adjust its definition to our system as follows. We take the original social network structure, sort individuals by their AMP value Pu and remove them in an increasing order from the network (together with their connected links). At the same time, we keep track of the density of the remaining network defined as
| 2.5 |
where 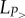 and
and 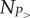 are the number of links and nodes remaining in the network after removing nodes with Pu smaller than a given value P>. In our case, we consider P> as a cumulative quantity going from 0 to ∑uPu with values determined just as in the case of CP(f) in figure 2a but now using 100 segments. At the same time, we randomize the structure using a configuration network model and by removing nodes in the same order, we calculate an equivalent measure ϕrn(P>) as defined in equation (2.5) but in the uncorrelated structure. For each randomization process, we used the same parameters as earlier and calculated the average density 〈ϕrn〉(P>) of the networks over 100 independent realizations. Using the two density functions, we define the ‘rich-club’ coefficient as
are the number of links and nodes remaining in the network after removing nodes with Pu smaller than a given value P>. In our case, we consider P> as a cumulative quantity going from 0 to ∑uPu with values determined just as in the case of CP(f) in figure 2a but now using 100 segments. At the same time, we randomize the structure using a configuration network model and by removing nodes in the same order, we calculate an equivalent measure ϕrn(P>) as defined in equation (2.5) but in the uncorrelated structure. For each randomization process, we used the same parameters as earlier and calculated the average density 〈ϕrn〉(P>) of the networks over 100 independent realizations. Using the two density functions, we define the ‘rich-club’ coefficient as
| 2.6 |
which indicates how many times the remaining network of richer people is denser connected than expected from the reference model. In our case (figure 3d purple symbols), the rich-club coefficient increases monotonously with P> and grows rapidly once only the richer people remain in the network. At its maximum, it shows that the richest people are approximately eight times more connected in the original structure than in the uncorrelated case. This provides direct evidence about the existence of tightly connected ‘rich clubs’ [33], and the presence of strong assortative correlations in the social structure on the level of individuals in terms of their socioeconomic status. Note that this measure also suggests that the observed ‘rich clubs’ were not induced by degree–wealth correlations. The connectedness of nodes in the randomized structure were actually determined merely by their degrees, and because we kept wealth–degree correlations, the wealth-sorted removal process shows exactly the expected density of remaining richer nodes assuming only their original degree but no other correlations. This way the fraction of the two network density curves, i.e. the rich-club coefficient, actually characterizes exactly the effect of status homophily when compared with the randomized case where only degrees and degree–wealth correlations determined the connectedness of the network.
In addition, to rule out the possibility that our observation was induced by positive degree–degree correlations, we performed another randomization of the network, where we kept node degrees, degree–degree and degree–wealth correlations but removed any other structural correlations. This randomization procedure preserving degree–degree correlations is identical to the one we defined earlier and in the electronic supplementary material. To measure the corresponding rich-club coefficient function, we substituted in the numerator of equation (2.6) the residual network density function measured in this new degree-correlated null model using the same wealth-sorted removal sequence as earlier. Results in figure 3d (black symbols) show that the obtained rich-club coefficient appears approximately as a constant function around one. This way it demonstrates that the entangled effects of degree–degree and degree–wealth correlations cannot explain the emergence of ‘rich clubs’ observed in the empirical case. The network, which conserves degrees and these two correlations, emerges with a structure just as the network, which conserves degrees and degree–wealth correlations only. Consequently, the observed increasing rich-club coefficient in the case of the empirical structure is induced by status homophily or other tie creation mechanisms and not by degree–degree or degree–wealth correlations.
2.5. Spatial correlations between socioeconomic classes
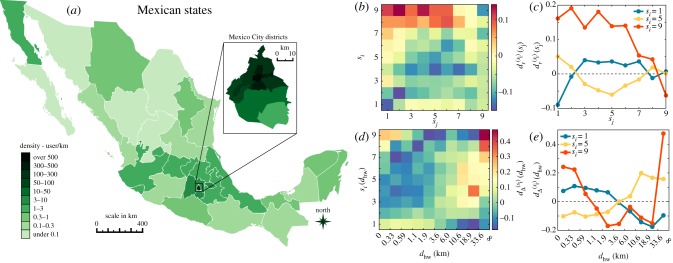
As we discussed earlier, the economic capacity of an individual strongly determines the possible places he/she can afford to live, arguably leading to somewhat homogeneous neighbourhoods, districts, towns and regions occupied by people from similar socioeconomic classes. This effect may translate to correlations in the spatial distribution of socioeconomic classes in relation with each other. To study such correlations, we use three different types of geographical information extracted for individuals from the data: the zip code of the reported billing address; the home; and work locations estimated from call activity logs (for details, see Data and material). To give an overall image about the spatial distribution of the investigated users, we use their zip location and assign them in different states of the country as shown in figure 4a. Importantly, the observed population distribution correlates well with census data [36] with coefficient r = 0.861 (p < 0.001) on the state level, which indicates that our data record a fairly unbiased sample of the population in terms of distribution in space.
Figure 4.
Spatial socioeconomic correlations. (a) State level population distribution of individuals based on their zip locations. Inset depicts a zoom on the capital district. Information details depicted here were entirely obtained from the used dataset. The map representation was generated by using an open source code available at https://gist.github.com/diegovalle/5843688github.com/diegovalle (no copyright reserved) and shape files openly available at http://www.inegi.org.mxwww.inegi.org.mx (no copyright reserved). (b) Relative average geodesic distances for different classes using the measure 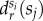 defined in equation (2.8). (c) The same
defined in equation (2.8). (c) The same 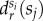 functions as on panel (b) shown for a selected set of classes (1-poor (blue), 5-middle (yellow), 9-rich (red)). (d)
functions as on panel (b) shown for a selected set of classes (1-poor (blue), 5-middle (yellow), 9-rich (red)). (d) 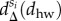 differences between commuting distance distributions calculated for different classes and for the whole population. x-scale depicts in logarithmic values of dhw commuting distances. (e) The same
differences between commuting distance distributions calculated for different classes and for the whole population. x-scale depicts in logarithmic values of dhw commuting distances. (e) The same 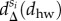 functions as on panel (d) shown for a selected set of classes (1-poor (blue), 5-middle (yellow), 9-rich (red)).
functions as on panel (d) shown for a selected set of classes (1-poor (blue), 5-middle (yellow), 9-rich (red)).
To quantify spatio-socioeconomic correlations, we measure the relative average geodesic distance between classes. More precisely, we take all connected individuals 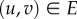 belonging to classes
belonging to classes 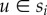 and
and 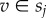 , respectively and measure the geodesic distance
, respectively and measure the geodesic distance 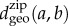 between their zip locations. Using these values, we calculate the average geodesic distance between any pairs of socioeconomic classes as
between their zip locations. Using these values, we calculate the average geodesic distance between any pairs of socioeconomic classes as
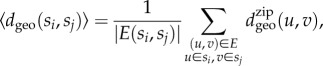 |
2.7 |
where |E(si, sj)| assigns the number of links between nodes in classes si and sj. Note that because the social network is undirected the measure defined in equation (2.7) is symmetric, i.e. 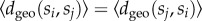 . Subsequently, we calculate the average distance between nodes from class si and any of their neighbours
. Subsequently, we calculate the average distance between nodes from class si and any of their neighbours 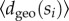 to derive
to derive
| 2.8 |
This measure is not symmetric anymore and gives us the relative average geodesic distance between individuals in si to individuals in other classes sj when compared with the average distance of individuals si from any of their connected peers. Results are presented as a heat map matrix in figure 4b where the diagonal component suggests a peculiar correlation. It shows that the relative average distance is always minimal (and negative) between individuals of the same class si. This means that people tend to live relatively the closest to similar others from their own socioeconomic class as to individuals from different classes, independently in which class they belong to. This is even more visible in figure 4c after extracting the 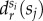 curves (corresponding to rows in figure 4b) for three selected classes. It highlights that while people of the poorest class live relatively the closest to each other, rich people tend to leave relatively the furthest from anyone from lower socioeconomic classes. These correlations are very similar to ones we already observed in the social structure suggesting that the stratified structure and spatial segregation may have similar roots. They are determined by the entangled effects of economic status and status homophily, together with other factors such as ethnicity or other environmental effects, which we cannot consider here.
curves (corresponding to rows in figure 4b) for three selected classes. It highlights that while people of the poorest class live relatively the closest to each other, rich people tend to leave relatively the furthest from anyone from lower socioeconomic classes. These correlations are very similar to ones we already observed in the social structure suggesting that the stratified structure and spatial segregation may have similar roots. They are determined by the entangled effects of economic status and status homophily, together with other factors such as ethnicity or other environmental effects, which we cannot consider here.
The socioeconomic status of people may also correlate with their typical commuting distances (between home and work), a question that has been studied thoroughly during the last few decades. Some of these studies suggest a positive correlation between economical status (income) and the distance people travel every day between their home and work locations [37–39]. Such correlations were partially explained by the positive payoff between commuting farther for better jobs, while keeping better housing conditions. On the other hand, recent studies suggest that such trends may change nowadays as in central metropolitan areas, where the better job opportunities are concentrated, became more expensive to live and thus occupied by people from richer classes [40,41]. Without going into detail, we looked for overall signs of such correlations by using the estimated home (ℓh) and work (ℓw) locations of individuals from different classes. For each individual, we measure a commuting distances as dhw = |ℓh − ℓw| and compute the 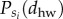 distributions for everyone in a given si class, together with the Pall (dhw) distribution considering all individuals. For each class, we are interested in
distributions for everyone in a given si class, together with the Pall (dhw) distribution considering all individuals. For each class, we are interested in
| 2.9 |
i.e. the difference between the corresponding distributions at each distance dhw. This measure is positive (resp. negative) if more (resp. less) people commute at a distance dhw when compared with the overall distribution, thus indicating whether people of a given class are over (under)represented at a given distance. Interestingly, our data are in agreement with both of the above-mentioned hypotheses, as seen in figure 4d where we show 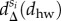 for each class as a heat map. There, poorer people are over represented in shorter distances while this trend is shifted towards larger distances (see right skewed yellow component in figure 4d) as going up in the class hierarchy. This continues until we reach the richest classes (8 and 9) where the distance function becomes bimodal assigning that more people of these classes tend to live very far or very close to their work places when compared with expectations considering the whole population. This is even more visible in figure 4e where selected
for each class as a heat map. There, poorer people are over represented in shorter distances while this trend is shifted towards larger distances (see right skewed yellow component in figure 4d) as going up in the class hierarchy. This continues until we reach the richest classes (8 and 9) where the distance function becomes bimodal assigning that more people of these classes tend to live very far or very close to their work places when compared with expectations considering the whole population. This is even more visible in figure 4e where selected 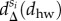 functions are depicted for selected classes.
functions are depicted for selected classes.
3. Discussion
In this paper, we have investigated socioeconomic correlations through the analysis of a coupled dataset of mobile phone communication records and bank transaction history for millions of individuals over eight months. After mapping the social structure and estimating individual economic capacities, we addressed four different aspects of their correlations: (i) we showed that individual economic indicators such as AMPs and also debts are unevenly distributed in the population in agreement with the Pareto principle; (ii) after grouping people into nine socioeconomic classes, we detected effects of status homophily and showed that the socioeconomic network is stratified as people most frequently maintain social ties with people from their own or neighbouring social classes; (iii) we observed that the social structure is upward-biased towards wealthier classes and show that assortative correlations give rise to strongly connected ‘rich clubs’ in the network; (iv) finally, we demonstrated that people of the same socioeconomic class tend to live closer to each other when compared with people from other classes, and found a positive correlation between their economic capacities and the typical distance they use to commute.
Even though our study is built on large and detailed data, the used data cover only partially the population of the investigated country. However, as we demonstrated above, for population-level measures, such as the Gini coefficient and spatial distribution, we obtained values close to independently reported cases, and thus our observations may generalize in this sense. In addition, the question remains how well mobile phone call networks approximate real social structure. A recent study [42] demonstrated that real social ties can be effectively mapped from mobile call interactions with precision up to 95%. However, it is important to keep in mind that the poorest social class of the society is probably under-represented in the data as they may have no access to bank services and/or do not hold mobile phones. Datasets simultaneously disclosing the social structure and the socioeconomic indicators of a large number of individuals are still very rare. However, several promising directions have been proposed lately to estimate socioeconomic status from communication behaviour on regional level [43–45] or even for individuals [46], just to mention a few. In future works, these methods could be used to generalize our results to other countries using mobile communication datasets. Here, our aim was to report some general observations in this direction using directly estimated individual economic indicators. Our overall motivation was to empirically verify some long-standing hypotheses and to explore a common ground between hypothesis-driven and data-driven research addressing social phenomena.
4. Data and material
4.1. Mobile communication data
Communication data used in our study record the temporal sequence of 7 945 240 548 call and SMS interactions of 111 719 360 anonymized mobile phone users for 21 months (between January 2014 and September 2015) in Mexico. Each call detailed record contains the time, unique caller and callee IDs, the direction and duration of the interaction, and the cell tower location of the client(s) involved in the interaction. Other mobile phone users, who are not clients of the actual provider also appear in the dataset with unique IDs. All unique IDs are anonymized as explained below, thus individual identification of any person is impossible from the data. Using this dataset, we constructed a large social network where nodes were users (whether clients or not of the actual provider), while links were drawn between them if they interacted (via call or SMS) at least once during the observation period. In order to filter out call services and other non-human actors from the social network, after construction we recursively removed all nodes (and connected links) who appeared with either in-degree kin = 0 or out-degree kout = 0. We repeated this procedure recursively until we received a network where each user had kin, kout > 0, i.e. made at least one outgoing and received at least one incoming communication events during the nearly 2 years of observation. After construction and filtering the network remained with 82 453 814 users connected by 1 002 833 289 links, which were considered to be undirected after this point.
4.2. Credit and purchase data
To estimate individual economic indicators, we used a dataset provided by a single bank in the studied country. These data record financial details of 6 002 192 of people assigned with unique anonymized identifiers over eight months from November 2014 to June 2015. The data provide time varying customer variables as the amount and type of their daily debit/credit card purchases, their monthly loan measures, and static user attributes as their billing postal code (zip code), their age, and gender. In addition, for a subset of clients we have the records of monthly salary (38.9% of users) and income (62.5% of users) defined as the sum of their salaries and any incoming bank transactions. Note that the observation period of the bank credit information falls within the observation period of the mobile communication dataset, this way ensuring the largest possible overlap between the sets of bank and mobile phone customers.
4.3. Location data
We used two types of location data for a set of customers. We used the zip code of billing address of bank customers (also called zip location). We also estimated the work and home locations for a set of users using geo-localized mobile communication events. To determine home (resp. work) locations, we looked for the most frequented locations during nights and weekends (resp. during daylight at working days). From the total 992 538 individuals, we found 990 173 with correct zip codes, and 94 355 with detectable home and work locations (with at least 10 appearances at each location). Each method has some advantages and disadvantages. While frequency-dependent locations are more precise, they strongly depend on the activity and regularity of users in terms of mobility. On the other hand, zip codes provide a more coarse-grained information about the location of individuals but they are assumed to be more reliable due to reporting constraints to the bank and because they do not depend on the call activity of individuals.
4.4. Combined datasets and security policies
A subset of IDs of the anonymized bank and mobile phone customers were matched. The matching, data hashing and anonymization procedure were carried out through direct communication between the two providers (bank and mobile provider) and were approved by the national banking commission of the country. This procedure was done without the involvement of the scientific partners. After this procedure only anonymized hashed IDs were shared disallowing the direct identification of individuals in any of the datasets. Owing to the signed non-disclosure agreements and the sensitive nature of the datasets, it is impossible to share them publicly.
This way of combining of the datasets allowed us to simultaneously observe the social structure and estimated economic status of the connected individuals. The combined dataset contained 999 456 IDs, which appeared in both corpuses. However, for the purpose of our study we considered only the largest connected component of this graph containing IDs valid in both data corpuses. This way we operate with a connected social graph of 992 538 people connected by 1 960 242 links, for all of them with communication events and detailed bank records available.
Supplementary Material
Acknowledgements
We thank M. Fixman and J. Brea for assistance with the dataset, J. Saramäki and J. P. Chevrot for useful discussions and the anonymous reviewers for their constructive comments.
Authors' contributions
All authors participated in the design of the project and the writing of the manuscript. Y.L., M.K. and E.F. designed the measures; Y.L. and M.K. performed the data analysis. All authors reviewed the manuscript.
Competing interests
We have no competing interests.
Funding
We acknowledge the support from the SticAmSud UCOOL project, INRIA,and the CODDDE (ANR-13-CORD-0017-01) and SoSweet (ANR-15-CE38-0011-01) ANR projects.
References
- 1.Piketti T. 2014. Capital in the twenty-first century Cambridge, MA: Harvard University Press. [Google Scholar]
- 2.Sernau S. 2013. Social inequality in a global age. Beverley Hills, CA: SAGE Publications. [Google Scholar]
- 3.Hurst CE. 2015. Social inequality, 8th edn London, UK: Pearson Education. [Google Scholar]
- 4.Grusky DB. 2011. Theories of stratification and inequality. In The concise encyclopedia of sociology (eds G Ritzer, JM Ryan) pp. 622–624. Oxford, UK: Wiley-Blackwell. [Google Scholar]
- 5.Giddens A, Ociepka F, Zujewicz W. 1973. The class structure of the advanced societies. London, UK: Hutchinson. [Google Scholar]
- 6.Akhbar-Williams T. 2010. Class structure. In Encyclopedia of African American popular culture, vol. 1 (ed Smith JC.), pp. 320–323. Westport, CT: Greenwood. [Google Scholar]
- 7.Brown DF. 2009. Social class and status. In Concise encyclopedia of pragmatics (ed. Mey JL.), 953 Amsterdam, The Netherlands: Elsevier. [Google Scholar]
- 8.Stark R. 2007. Sociology. Belmont, CA: Thompson/Wadsworth. [Google Scholar]
- 9.Gilbert D. 2002. The American class structure: in an age of growing inequality. Beverley Hills, CA: Pine Forge Press. [Google Scholar]
- 10.Stiglitz J. 2012. The price of inequality. New York, NY: Norton. [Google Scholar]
- 11.McPherson M, Smith-Lovin L, Cook JM. 2001. Birds of a feather: homophily in social networks. Annu. Rev. Sociol. 27, 415–444. ( 10.1146/annurev.soc.27.1.415) [DOI] [Google Scholar]
- 12.Lazarsfeld PF, Merton RK. 1954. Friendship as a social process: a substantive and methodological analysis. In Freedom and control in modern society, vol. 18 (eds M Berger, T Abel, CH Page), pp. 18–66. Van Nostrand series in sociology. New York, NY: Van Nostrand. [Google Scholar]
- 13.Doob CB. 2016. Social inequality and social stratification in US society. London, UK: Routledge. [Google Scholar]
- 14.Saunders P. 1990. Social class and stratification. London, UK: Routledge. [Google Scholar]
- 15.Carra G, Mulalic I, Fosgerau M, Barthelemy M. 2016. Modelling the relation between income and commuting distance. J. R. Soc. Interface 13, 119 ( 10.1098/rsif.2015.0315) [DOI] [PMC free article] [PubMed] [Google Scholar]
- 16.Sim A, Yaliraki SN, Barahona M, Stumpf MPH. 2015. Great cities look small. J. R. Soc. Interface 12, 20150315 ( 10.1098/rsif.2016.0306) [DOI] [PMC free article] [PubMed] [Google Scholar]
- 17.Iceland J, Wilkes R. 2006. Does socioeconomic status matter? Race, class, and residential segregation. Soc. Probl. 53, 248–273. ( 10.1525/sp.2006.53.2.248) [DOI] [Google Scholar]
- 18.Wasserman S, Faust K. 1994. Social network analysis: methods and applications. Cambridge, UK: Cambridge University Press. [Google Scholar]
- 19.Lohr S. 2012. The age of big data. New York, NY: New York Times.
- 20.Lazer D, et al. 2009. Computational social science. Science 323, 721–723. ( 10.1126/science.1167742) [DOI] [PMC free article] [PubMed] [Google Scholar]
- 21.Abraham A, Hassanien AE, Smasel V. 2010. Computational social network analysis: trends, tools and research advances. New York, NY: Springer. [Google Scholar]
- 22.Newman MEJ. 2003. The structure and function of complex networks. SIAM Rev. 45, 167–256. ( 10.1137/S003614450342480) [DOI] [Google Scholar]
- 23.Hedström P, Swedberg R. 1998. Social mechanisms, an analytical approach to social theory. Cambridge, UK: Cambridge University Press. [Google Scholar]
- 24.Holme P, Liljeros F. 2015. Mechanistic models in computational social science. Front. Phys. 3, 78 ( 10.3389/fphy.2015.00078) [DOI] [Google Scholar]
- 25.Campbell KE, Marsden PV, Hurlbert JS. 1986. Social resources and socioeconomic status. Soc. Netw. 8, 97–117. ( 10.1016/S0378-8733(86)80017-X) [DOI] [Google Scholar]
- 26.Bourdieu P. 1984. Distinction: a social critique of the judgement of taste. London, UK: Routledge. [Google Scholar]
- 27.Pareto V. 1971. Manual of political economy. London, UK: Oxford University Press. [Google Scholar]
- 28.Gastwirth JL. 1972. The estimation of the Lorenz curve and Gini index. Rev. Econ. Stat. 54, 306–316. ( 10.2307/1937992) [DOI] [Google Scholar]
- 29.The World Bank. GINI index (World Bank estimate) http://data.worldbank.org/indicator/SI.POV.GINI (accessed 1/2/2016).
- 30.Souma W. 2000. Physics of personal income. In Empirical science of financial fluctuations: the advent of econophysics (ed. Takayasu H.), pp. 343–352. Tokyo, Japan: Springer. [Google Scholar]
- 31.Aoyama H. 2000. Pareto's law for income of individuals and debt of bankrupt companies. Fractals 8, 293–300. [Google Scholar]
- 32.Bottero W. 2005. Stratification: social division and inequality. London, UK: Routledge. [Google Scholar]
- 33.Mills CW. 1956. The power elite. London, UK: Oxford University Press. [Google Scholar]
- 34.Zhou S, Mondragón RJ. 2004. The rich-club phenomenon in the internet topology. IEEE Commun. Lett. 8, 180–182. ( 10.1109/LCOMM.2004.823426) [DOI] [Google Scholar]
- 35.Colizza V, Flammini A, Serrano MA, Vespignani A. 2006. Detecting rich-club ordering in complex networks. Nat. Phys. 2, 110–115. ( 10.1038/nphys209) [DOI] [Google Scholar]
- 36.Instituto Nacional de Estadística y Geografía. (http://www.inegi.org.mx) 2015 census (accessed 22 February 2016).
- 37.Wheeler JO. 1967. Occupational status and work-trips: a minimum distance approach. Soc. Forces 45, 508–515. ( 10.1093/sf/45.4.508) [DOI] [Google Scholar]
- 38.Wheeler JO. 1967. Some effects of occupational status and work trips. J. Reg. Sci. 9, 69–77. ( 10.1111/j.1467-9787.1969.tb01442.x) [DOI] [Google Scholar]
- 39.Poston DL. 1972. Socioeconomic status and work-residence separation in metropolitan America. Pac. Sociol. Rev. 15, 367–380. ( 10.2307/1388353) [DOI] [Google Scholar]
- 40.LeRoy S, Sonstelie J. 1983. Paradise lost and regained: transportation innovation, income, and residential location. J. Urban Econ. 13, 67–89. ( 10.1016/0094-1190(83)90046-3) [DOI] [Google Scholar]
- 41.Rosenthal SS, Ross SL. 2015. Change and persistence in the economic status of neighborhoods and cities. In Handbook of regional and urban economics, vol. 5 (eds Duranton G, Henderson JV, Strange WC), pp. 1047–1120. Amsterdam, The Netherlands: Elsevier. [Google Scholar]
- 42.Eagle N, Pentland AS, Lazer D. 2009. Inferring friendship network structure by using mobile phone data. Proc. Natl Acad. Sci. USA 106, 15 274–15 278. ( 10.1073/pnas.0900282106) [DOI] [PMC free article] [PubMed] [Google Scholar]
- 43.Šćepanović S, Mishkovski I, Hui P, Nurminen JK, Ylä-Jääski A. 2015. Mobile phone call data as a regional socio-economic proxy indicator. PLoS ONE 10, e0124160 ( 10.1371/journal.pone.0124160) [DOI] [PMC free article] [PubMed] [Google Scholar]
- 44.Blumenstock J, Eagle N. 2010. Mobile divides: gender, socioeconomic status, and mobile phone use in Rwanda. ICTD 2010 (ACM) 6, 1–10. ( 10.1145/2369220.2369225) [DOI] [Google Scholar]
- 45.Mao H, Shuai X, Ahn YY, Bollen J. 2015. Quantifying socio-economic indicators in developing countries from mobile phone communication data: applications to Côte d'Ivoire. EPJ Data Sci. 4, 15 ( 10.1140/epjds/s13688-015-0053-1) [DOI] [Google Scholar]
- 46.Blumenstock J, Cadamuro G, On R. 2015. Predicting poverty and wealth from mobile phone metadata. Science 350, 1073–1076. ( 10.1126/science.aac4420) [DOI] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.