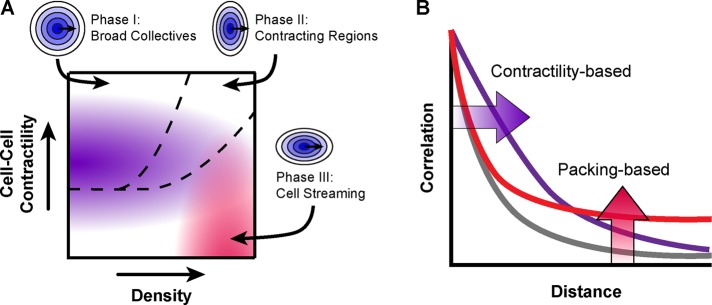
Cell density and actomyosin contractility control the organization of migrating collectives within an epithelium

Cell density organizes collective migration within an epithelium. Computational models predict the regulation of collective migration in an in vivo epithelium and demonstrate how commonly altered cellular properties can prime groups of cells to adopt migration patterns that may be harnessed in health or exploited in disease.

Abstract

The mechanisms underlying collective migration are important for understanding development, wound healing, and tumor invasion. Here we focus on cell density to determine its role in collective migration. Our findings show that increasing cell density, as might be seen in cancer, transforms groups from broad collectives to small, narrow streams. Conversely, diminishing cell density, as might occur at a wound front, leads to large, broad collectives with a distinct leader–follower structure. Simulations identify force-sensitive contractility as a mediator of how density affects collectives, and guided by this prediction, we find that the baseline state of contractility can enhance or reduce organization. Finally, we test predictions from these data in an in vivo epithelium by using genetic manipulations to drive collective motion between predicted migratory phases. This work demonstrates how commonly altered cellular properties can prime groups of cells to adopt migration patterns that may be harnessed in health or exploited in disease.

INTRODUCTION

Collective migration of cells underlies embryonic development, tissue regeneration, and tumor invasion (Krawczyk, 1971; Ewald et al., 2008; Friedl and Gilmour, 2009). In these processes, cells coordinate their individual motions to productively migrate in groups, giving rise to intricate branching structures (e.g., breast development), covering injured areas while retaining tissue integrity (e.g., skin wound healing), or invading into surrounding tissue (e.g., cancer metastasis).

To understand the complex behaviors of groups of cells, parallels have been made to other crowded physical systems, including solids, liquids, and amorphous glasses (Angelini et al., 2011; Puliafito et al., 2012; Nnetu et al., 2013; Sadati et al., 2013; Deforet et al., 2014; Bi et al., 2015, 2016; Garcia et al., 2015). These studies find similarities but also highlight that unlike standard physical systems, cellular tissues fall into a class of materials known as active matter (Angelini et al., 2011), meaning that cells internally generate their own migratory forces. Furthermore, cells are mechanosensitive and mechanoresponsive and can be physically coupled to one another, allowing cells to directly affect their neighbors (Chen et al., 2004; Das et al., 2015). The types of collective motion that can form in these force-generating systems and the properties that control organization and motion are only partially understood.

Cell density has been implicated as an important property influencing the behavior of groups of cells, but how collective migration is specifically affected and through which mechanisms are not completely known (Angelini et al., 2011; Nnetu et al., 2013; Vedel et al., 2013). Understanding this effect is of broad importance because shifts in cell density underlie many biological processes in which collective migration occurs. In development and early cancer, for example, the level of cell proliferation is high (Cooper, 2000; Hanahan and Weinberg, 2011). In the former, it is closely regulated to maintain normal tissue growth and homeostasis, whereas in the latter, this proliferation is dysregulated, leading to abnormal expansion of cells within tissues. In both instances, cell proliferation may increase cell density within a tissue and thereby influence the migratory dynamics of constituent cells. A wound to an epithelial surface creates free space and the stimulus for directed migration to repair the denuded surface (Poujade et al., 2007). In contrast to development and cancer, this wound additionally produces a local drop in cell density extending multiple rows back from the site of injury (Krawczyk, 1971). This decrease in cell density therefore may affect the organization and collective migration of cells at the leading edge. A more complete understanding of the role of cell density in collective migration may allow for predictions as to how changes in tissue states generate the migratory behaviors that emerge.

In this study, we asked how cell density affects the collective organization and movement of cells within a model epithelium. The express purpose was to develop a quantitative model of collective cell migration, and through experiment and simulation, we identify force-sensitive contractility as a mediator of the response of collective migration to increasing density. This iterative approach led to the development of a phase diagram of cell migration summarizing changes in collective behavior in response to changes in cell density and cell–cell contractility. We then tested the predictive value of this phase diagram in an in vivo epithelium. Through genetic manipulations altering cell density and contractility, we were able to drive the Drosophila ovarian follicular epithelium from one predicted migratory phase to another.

RESULTS

Collective cell migration within an epithelium exhibits two distinct responses to increasing cell density

To develop a quantitative model describing how cells organize into collective groups within an epithelium, we asked how changing cell density within a confluent epithelial monolayer affected collective migration. Human breast epithelial cells (MCF10A) were plated in confluent monolayers, and time-lapse videos spanning 2.3 mm² were acquired across a range of cell densities. Cell density was measured for each field of view using a nuclear label (Supplemental Figure S1A). Density was varied by plating a constant number of cells and taking measurements at progressively longer times; however, measurements made at the same time on more densely plated cells yielded similar results (Supplemental Figure S1, B–E).

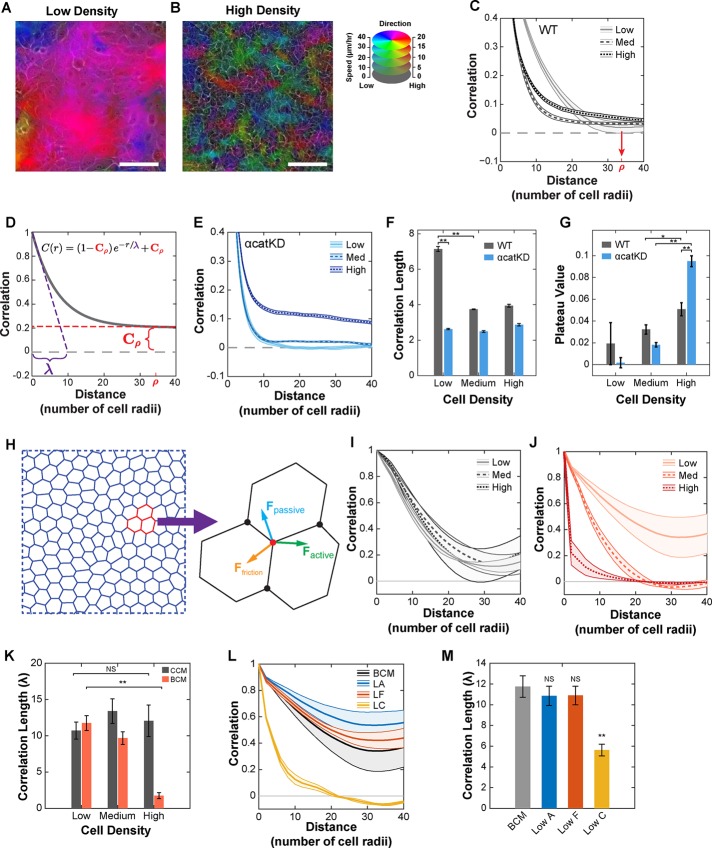
Qualitatively, motion within the monolayer was highly organized at low density, with large groups of cells moving together in similar directions (Figure 1A and Supplemental Video S1). At high density, cell movement was more heterogeneous, and groups of similarly moving cells appeared smaller (Figure 1B and Supplemental Video S2). Although mobility decreased with increasing density, migration remained superdiffusive across the range in cell density (Supplemental Figure S1, H–K). To quantify organization while adjusting for changes in cell size, we computed a radial spatial autocorrelation function for the measured velocity field (see the Supplemental Experimental Procedures) with distance normalized by mean cell radius. This function has a value of 1 when motion is aligned and 0 when motion is random and is referred to here as radial correlation because correlations are computed only as a function of radial distance between observations. At low density, radial correlation decayed to ∼0 at a distance of 34 cell radii (red arrow, Figure 1C). This value, ρ, served as a reference distance over which organization turned to random motion in low-density epithelia. Increasing density led to a faster early decay in radial correlation; however, the curve then plateaued, remaining >0 at the reference distance of ρ = 34 cell radii (Figure 1C and Supplemental Figure S1G).

FIGURE 1:

Local and regional organization of collective migration within an epithelium. (A) Heatmap overlay of cell velocity for low-density WT cells with migration direction and speed encoded with color hue and intensity, respectively. (B) Same as A for high-density WT cells. Scale bars, 100 μm (A, B). (C) Radial correlation for WT cells across a range of densities. Red arrow denotes ρ, the distance over which radial correlation decayed to zero for low-density WT cells. (D) Fitting function used to measure correlation length (purple, λ) and plateau value (red, C_ρ). (E) Radial correlation for αcatKD cells across a range of densities. (F) Value of correlation length (λ) obtained by fitting curves to Eq. 1. (G) Value of plateau value (C_ρ) obtained by fitting curves to Eq. 1. (H) Diagram of the vertex model and vertex force balance used to simulate epithelial migration. (I) Radial correlation curves for simulated epithelial migration using the constant contractility model. (J) Radial correlation curves for simulated epithelial migration using the biomechanical contractility model. (K) Value of correlation length (λ) obtained by fitting constant contractility (CCM) and biomechanical contractility (BCM) correlation curves. (L) Radial correlations for simulated epithelial migration at low density for the biomechanical contractility model (BCM) and variations of the model: low adhesion (LA), low friction (LF), and low contractility coupling (LC). (M) Value of correlation length (λ) for the various models in L. Error bars and envelopes are SEM. For C and E–G, each density is the mean of 14 (WT) or 6 (αcatKD) 2.3-mm² regions (four 10× fields per region). For I–M, data are mean values from three simulations. See Supplemental Tables S2 and S3 for simulated cell type parameters. Student’s t test was used to assess significance. NS, not significant; *p < 0.05; **p < 0.01. See also Supplemental Videos S1 and S2.

These results suggested the presence of two length scales of organization. To determine this, we measured the initial decay rate and the correlation plateau value by fitting each correlation curve to the following function:

(1)

where C is the correlation at distance r, C_ρ is the correlation plateau value evaluated at a distance of ρ = 34 cell radii, and λ is the correlation decay length (Figure 1D). The two variables λ and C_ρ identify two scales of organization. The parameter λ is a measure of local organization, and C_ρ is a measure of broader regional organization describing how local groups are organized relative to each other. Higher values of both λ and C_ρ correspond to increased order. Correlation curves were fitted using data out to 40 cell radii, where the form of the fitting function remained valid; however, fitting to a mixed exponential-linear decay model, which matches data out to 100 cell radii, produced results in close agreement (Supplemental Figure S2, E–I).

We found that epithelia exhibited two distinct responses to increasing cell density that differentially affected these two length scales. First, local organization (λ) decreased with increasing density, indicating a paradoxical decrease in local collective cell organization with increasing density. Second, regional organization (C_ρ) increased with increasing density (Figure 1, F and G).

The observed effects at high density could involve specific cell–cell adhesion contacts (e.g., E-cadherin mediated) or a more general phenomenon involving cell packing (Huttenlocher et al., 1998; Trappe et al., 2001). To distinguish between these possibilities, we depleted α-catenin using a specific small hairpin RNA (shRNAi; Supplemental Figure S1F; Bajpai et al., 2008). α-Catenin is a key component linking cadherin bonds to the actin cytoskeleton and as such is required for strong epithelial cell–cell adhesion (Nagafuchi et al., 1994). In α-catenin–depleted cells, local organization (λ) remained low across all densities, but regional organization (C_ρ) dramatically increased with increasing density (Figure 1E). Therefore cell–cell adhesion appeared necessary to produce the high local organization seen in wild-type (WT) epithelia at low density, and the increase in regional organization seen in WT epithelia at high density was enhanced by a reduction of functional cell–cell adhesion.

To facilitate determining the underlying physical cause(s) of this density response, we formulated a two-dimensional (2D) vertex model of monolayer migration (Figure 1H). Vertex models are advantageous for simulating epithelial cell migration because they incorporate the connected nature of epithelia, cell shape changes, neighbor rearrangements, and a range of forces driving cell motion (Fletcher et al., 2014). For a detailed description of the model and the values of parameters used, see the Supplemental Experimental Procedures and Supplemental Tables S2 and S3. Briefly, each cell is represented as a polygon with shared vertices and edges. Migration is governed by motion of their vertices and arises from passive (elastic and adhesive), frictional, and active (protrusive and contractile) forces.

On the basis of previous modeling of cell sheets confined to circular regions (Li and Sun, 2014), we simulated the migration of 1000 cells under conditions of constant protrusive and contractile forces, referred to as the constant contractility model. These simulations captured low-density WT behavior (Figure 1I); however, organization was not responsive to changes in density (Figure 1K). We therefore modified the vertex model to incorporate dynamic signaling of Rho-ROCK-myosin II activation sensitive to the physical environment of each cell, referred to as the biomechanical contractility model (see the Supplemental Experimental Procedures and Supplemental Figure S2K). This model is based on the observation that cells actively respond to externally applied mechanical forces by increasing myosin activation (Koride et al., 2014). The biomechanical contractility model predicted local organization across all densities, including the paradoxical decrease in local organization with increasing density (Figure 1, J and K). The experimental trend in regional organization was not observed, however. This reflects a limitation of the periodic boundary conditions used in the simulation, which influence long-distance correlations. Performing simulations of larger size reduced this effect but still showed influence of the periodic boundary conditions (Supplemental Figure S1, L and M). For this reason, we focused the simulation on examining local organization.

Given the requirement of α-catenin for local organization at low density, we asked whether the simulation could inform how it does so. Reducing α-catenin may affect a number of model parameters, including cell–cell adhesion and cell–cell friction. Reducing cell–cell adhesion or cell–cell friction alone did not reduce local organization (λ) at low density (Figure 1, L and M); however, it is unlikely these properties can be modified in isolation in cells. Beyond reducing adhesion, depletion of α-catenin likely reduced the coupling of contractile forces between cells. Reducing the parameter governing contractile force coupling diminished local organization at low density (Figure 1, L and M), consistent with experimental observations (Figure 1E).

In summary, simulations identified a critical role for active contractility in organizing collective motion within an epithelium in response to changing cell density.

Regulated actomyosin contractility drives collective migration

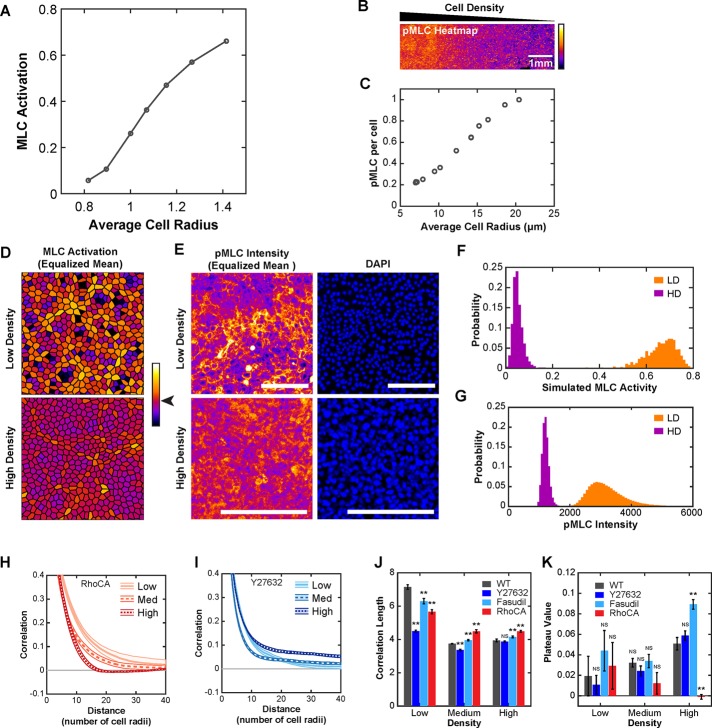
Migration in the biomechanical model is driven by the state of the active contractility signaling system, providing experimentally testable predictions regarding activation of the Rho-ROCK-myosin II pathway. Mean simulated cell–cell contractile activity was found to decrease with increasing density (Figure 2A). To test this prediction experimentally, we plated cells in a density gradient spanning 8 to 20 μm in mean cell radius across a distance of 1 cm (Figure 2B). As a measure for actomyosin contractility, we measured the phosphorylated myosin light chain (pMLC) staining intensity per cell by quantitative immunofluorescence and found it to decrease with increasing cell density (Figure 2C). Supporting these data, measurement of pMLC intensity per cell with the same methods used to control density in migration experiments produced equivalent results (Supplemental Figure S2D).

FIGURE 2:

Actomyosin contractility drives collective behavior. (A) Mean level of simulated MLC activity across a range of densities. (B) Intensity of pMLC immunofluorescence staining across a gradual density gradient of WT cells (high, left; low, right). (C) Quantification of mean pMLC immunofluorescence signal per cell, normalized to the lowest density measurement. (D) Simulated MLC activity for 500 individual cells at low and high density scaled such that mean activity levels are equal (mean value color denoted by arrowhead on color bar). (E) Intensity of pMLC immunofluorescence staining of regions of ∼500 cells at low and high density (magnified from B) and scaled such that mean pMLC intensity levels are equal. Scale bars, 100 μm. (F) Histogram of absolute (without equalizing means) MLC activity for cells from D. (G) Histogram of absolute pMLC immunofluorescence intensity for the regions in E. (H) Radial correlation curves for RhoCA cells. (I) Radial correlation curves for Y27632-treated WT cells. (J) Correlation length (λ) for WT, RhoCA, and ROCK inhibition. (K) Plateau value (C_ρ) for WT, RhoCA, and ROCK inhibition. Each density is the mean value from 14 (WT), 6 (Y27632), 6 (Fasudil), or 8 (RhoCA) 2.3-mm² regions (four 10× fields per region). Error bars and envelopes are SEM. Student’s t test was used to assess significance. NS, not significant; **p < 0.01.

The biomechanical contractility model also predicted the presence of contractile domains, defined as regions of high contractile activity surrounded by regions with lower contractile activity (Figure 2D). In simulation, contractile domains were more evident at low density than high density (Figure 2, D and F). Experimentally, clusters of cells with high pMLC levels surrounded by regions with low pMLC levels were also more evident at low density (Figure 2, E and G). Therefore two density-dependent features predicted by the biomechanical contractility model, namely mean contractility and the presence of contractile domains, were found experimentally.

Given the identified important role of cell–cell contractility in regulating collective migration in response to cell density, we hypothesized that changing baseline levels of actomyosin contractility would alter how cells responded to changes in density. Actomyosin contractility was reduced by treating cells with ROCK inhibitor Y27632 or Fasudil (Supplemental Figure S2B) or increased by stably expressing constitutively active Rho (RhoCA) (Supplemental Figure S2C). At low density, both decreasing and increasing actomyosin contractility diminished local organization (λ) without affecting regional organization (C_ρ; Figure 2, H–K). At high density, decreasing or increasing contractility led to small differences in local organization relative to WT (Figure 2J). In contrast, regional organization showed larger differences relative to WT, increasing in cells with reduced contractility and decreasing in cells with increased contractility (Figure 2K).

In summary, these experiments indicated that the baseline state of actomyosin contractility altered the effect of cell density on collective migration.

Directional correlations reveal transitions in collective shape

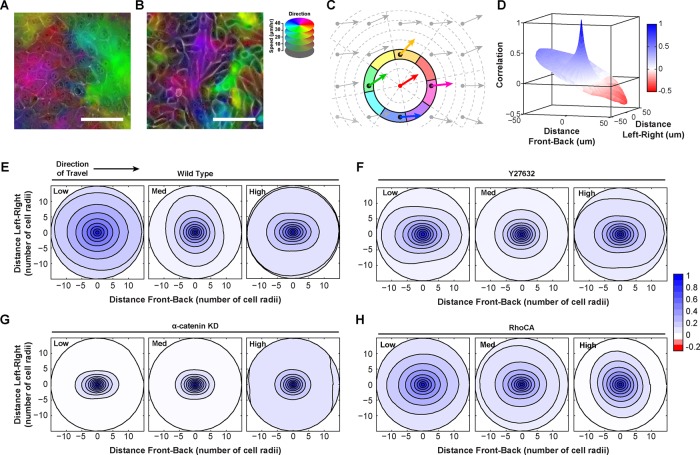
Inspection of time-lapse videos suggested that changes in the shape or pattern of collective groups accompanied changes in collective size (Supplemental Videos S3 and S4) and that measuring radial correlation alone masked these patterns. For example, in contracting regions (i.e., cells converging on a point), correlations in the direction of travel may be low or negative, whereas correlations in the reverse direction of travel may be high (Figure 3A and Supplemental Figure S3). These values are combined in the measurement of radial correlation, and thus this difference would not be apparent. In the case of streaming motions (i.e., follow-the-leader), the average correlation in the direction of travel remains higher than correlations perpendicular to the direction of travel (Figure 3B and Supplemental Figure S3). Again, these two disparate values would be averaged in radial correlation.

FIGURE 3:

Cell density and contractility control transitions in collective shape. (A) Contracting region in WT cells at low density (migration direction and speed correspond to color hue and intensity, respectively). Magenta and green regions are converging. (B) Streaming motion in α-catenin–depleted (αcatKD) cells at low density. Purple region is elongated in the direction of cell migration. (C) Diagram of directional correlation. (D) Representative directional correlation from a single field of view for low-density WT epithelial cells. (E–H) Experimental polar correlation function at low, medium, and high density for WT, αcatKD, Y27632, and RhoCA epithelial cells, respectively. Each density is the mean value from 14 (WT), 6 (Y27632), or 8 (RhoCA) regions (four fields of view per region). See also Supplemental Videos S3 and S4.

To measure the shape of collectively migrating groups, we defined a polar spatial correlation function using a mathematical approach related to previous methods (Szabo et al., 2010; Kabla, 2012; Kuriyama et al., 2014; see the Supplemental Experimental Procedures), referred to here as directional correlation. In this analysis, correlations were assigned both a distance and a direction relative to the index vector (Figure 3C). In WT cells at low density, directional correlations from a single field of view often exhibited dramatic asymmetries relative to the direction of travel, suggesting the presence of large contracting, stretching, or rotating domains (Figure 3D). When multiple tiled fields of view were combined, directional correlation lost front-to-back asymmetry due to the averaging of many contracting and expanding regions, but additional features remained. At low density, WT cells displayed a high degree of organization in the direction of travel and perpendicular to it, indicating that collectives were broad (Figure 3E). At medium density, directional correlation decayed more slowly perpendicular to the direction of travel, also consistent with broad collective groups (Figure 3E). At high density, directional correlation was highest in the direction of travel, indicating a transition to streaming motion in which cells moved in a follow-the-leader manner and slid past lateral neighbors (Figure 3E).

In contrast, αcatKD cells exhibited streaming motions at all densities, with greater correlation parallel to the direction of travel (Figure 3G). Decreasing actomyosin contractility with Y27632 mimicked α-catenin depletion, producing streaming behavior even at low densities (Figure 3F). Increasing contractility with RhoCA resulted in directional correlations consistent with broad collectives even at high density (Figure 3H). These data indicated that actomyosin contractility is important for organizing broad collectives. Reducing cell–cell contractility (either pharmacologically, by increasing density, or by uncoupling via α-catenin depletion) led to streaming type motions.

Flow of information within an epithelial sheet

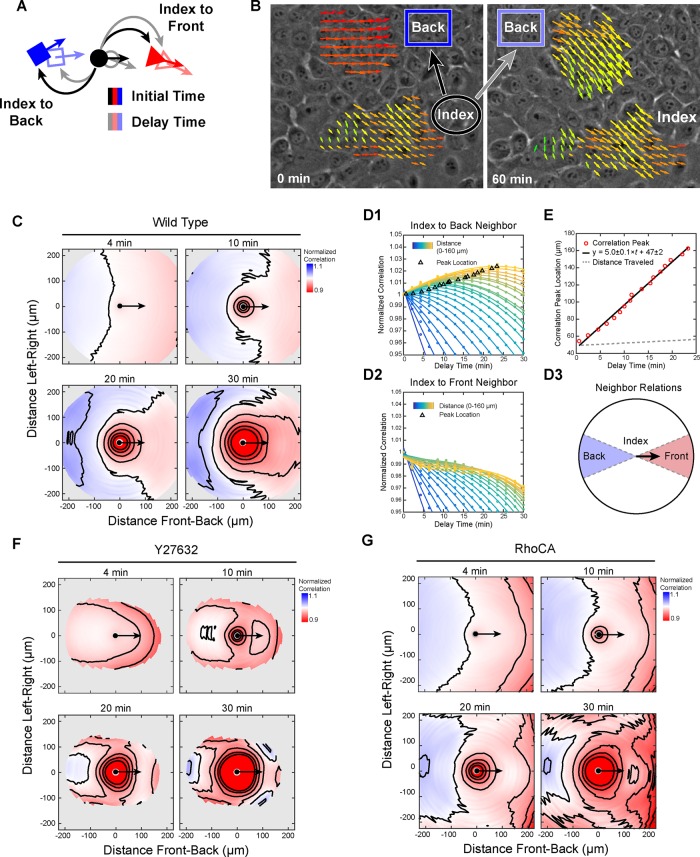
Low-density WT epithelia displayed the greatest degree of local organization. To determine how these large and broad collective groups might form, we generalized the directional correlation function to include time correlations, referred to here as spatiotemporal correlation (see the Supplemental Experimental Procedures). In this measurement, the velocity of an index position at an initial time is compared with the velocities of neighboring positions as they evolve through time, where the difference between the two time points is referred to as delay time (Figure 4A).

FIGURE 4:

Dynamics of collective migration: directional transfer of information from leaders to followers. (A) Diagram of spatiotemporal correlation. Neighbors are defined by distance and direction from an index position (solid shapes). Correlations are computed at the initial time (black arrows) and as a function of delay time (gray arrows) as the neighbor positions migrate (outlined shapes). (B) Representative leader–follower relationship. Neighbors (dark blue box) positioned behind an index group are initially not aligned (black arrow) to the index group but increase alignment (gray arrow) over time. (C) Spatiotemporal correlation normalized to zero-delay-time values for WT low-density cells at increasing delay times. (D1) Normalized spatiotemporal correlation as a function of delay time for index-to-back neighbors of increasing distance from the index point (points) with cubic fit (lines). (D2) Same as D1 for index-to-front neighbors. (D3) Diagram of index-to-back and index-to front neighbors. (E) Delay time for peak normalized correlation vs. neighbor distance, linear fit (black line), and mean distance traveled (dashed gray line). (F) Same as C for Y27632-treated low-density WT cells. (G) Same as C for low-density RhoCA cells. Correlations for each cell type are the mean value from seven (WT), six (Y27632), or eight (RhoCA) 2.3-mm² regions (four 10× fields per region).

Spatiotemporal correlations provided information on how the motion of a cell at a given time may affect the motion of neighboring cells at later times. Consider two groups of cells in which the neighboring group is behind an index group relative to the index group direction of travel (Figure 4B). The neighboring group has a certain degree of correlation with the index group at an initial reference time. As time passes, correlation between the neighboring group and initial state of the reference group may change. If the correlation increases, this means that the migration of the neighboring group aligned to the index group over the delay time (Figure 4B). Using this analysis, we found that neighboring cells behind and beside aligned their motion to the direction of migration of an index cell.

For low-density WT cells, spatiotemporal correlations normalized to values at zero delay time were used to assess changes in organization. At a delay of 4 min, neighboring positions behind the index position in an arc of ∼145° were more correlated with the index position than at 0 min, whereas positions in front were not (Figure 4C). At later times, the region of enhanced correlation grew to include lateral neighboring positions in an arc of ∼240°. This asymmetry in spatiotemporal correlation shows that information flows from front to back even within a confluent epithelium, by which the current migration of a given cell provides information on the future migration of neighbors in back or beside but not those in front (where front and back are defined by the index cell migration direction).

As delay time increased, the peak in spatiotemporal correlation appeared to shift to distances further behind the index point. This peak represents the response time of the system (Katz et al., 2011), and a shift of the peak to increasing distances at longer delay times provides the rate at which this response propagates. To measure this, we used two 45° sectors in front of and behind the index point to define index-to-back neighbors and index-to-front neighbors (Figure 4D3). For index-to-back neighbors, the peak in normalized correlation occurred at later times for neighboring positions farther from the index position, indicating that the response indeed propagated rearward (Figure 4D1). In contrast, no peaks were observed for index-to-front neighbors (Figure 4D2), consistent with the previously determined direction of information flow. Plotting neighbor distance versus time delay for each peak produced a linear trend (slope of 5.0 ± 0.1 μm/min, intercept of 47 ± 2 μm; Figure 4E). The slope of this line is the propagation rate of cellular response, and, of note, it is significantly greater than the mean cell speed (0.29 μm/min). The difference in propagation rate and migration speed means that the relative alignment was not due to neighboring cells migrating in a similar direction once they reached the position of an index cell.

This transfer of information depended on the Rho-ROCK-myosin II signaling axis. Inhibiting contractility using Y27632 largely prevented trailing neighbors from aligning to the heading of an index position (Figure 4F). In epithelia with increased contractility, alignment occurred but did not include as many lateral neighbors (Figure 4G). The correlation peak for RhoCA cells propagated rearward at a rate similar to that of WT cells of 4.4 ± 0.3 μm/min. Furthermore, the alignment of neighbor cells to an index cell was dependent on cell density, with no detectable alignment response at medium or high density (Supplemental Figure S4).

These results demonstrated that the formation of broad collectives depends on actomyosin contractility, which serves to direct the migration of neighboring cells behind and beside an index cell.

Cell density and actomyosin contractility define phases of collective migration

Taken together, these data indicated that epithelial collective migration can be described in terms of size (radial correlation) and shape (directional correlation) in a phase diagram based on two parameters: cell density and functional cell–cell contractility (i.e., contractility contingent on cell–cell adhesion; Figure 5A). Cell density and cell–cell contractility differentially affect collective size at two length scales: local and regional organization. Local organization was greatest for low-density epithelia with WT levels of cell–cell contractility (Figure 5, A and B, purple shading) and decreased with increasing density or manipulations of actomyosin contractility. Regional organization was greatest for high-density cells with low levels of functional cell–cell contractility (Figure 5, A and B, red shading).

FIGURE 5:

Phases of collective migration as a function of cell density and contractility. (A) Phase diagram depicting collective size in terms of local organization (purple) and regional organization (red), as well as collective shape (dashed black lines). (B) Diagram of radial correlation for local organization (purple) and regional organization (red).

Three general shapes of collective migration were observed through the directional correlation analysis (Figure 5A, dashed black lines). In the first region (I), correlation was high in all directions relative to the direction of travel. In the second region (II), directional correlation was greatest perpendicular to the migration heading of a given cell, consistent with a mixture of contracting and stretching regions: cells are likely to be moving with lateral neighbors whether converging to or diverging from a point but may be migrating in the opposite direction of neighbors ahead (contracting) or behind (stretching). In the third region, directional correlation was low perpendicular to the migration heading of an index cell, consistent with streaming motions.

Contractility and cell density drive in vivo changes in collective migration

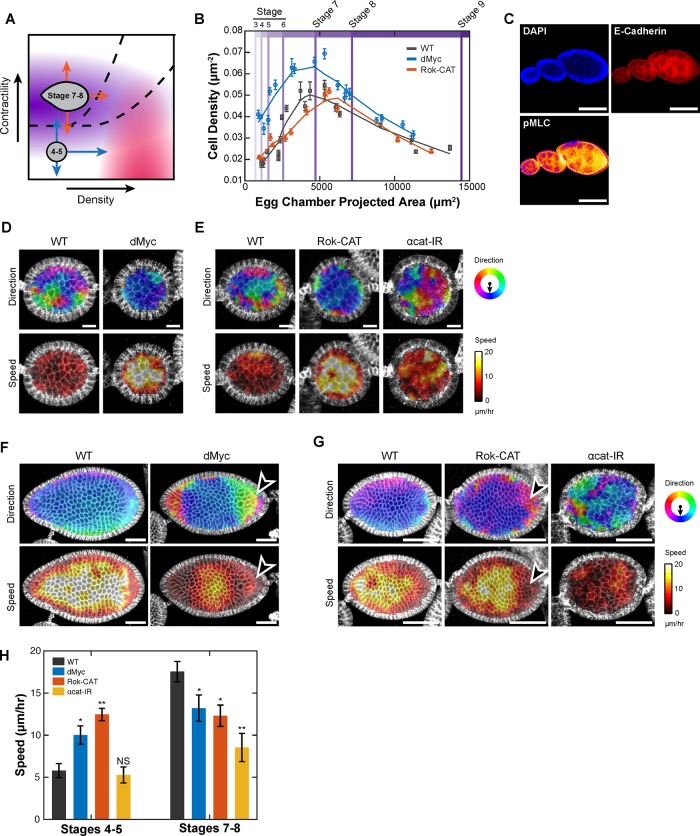
To test these predictions in an in vivo epithelium with three-dimensional (3D) geometry, we turned to the Drosophila ovarian follicular epithelium. The developing Drosophila egg chamber has a basement membrane and apical-basal–polarized epithelium surrounding an oocyte and supporting nurse cells. During the course of egg development, the epithelial layer undergoes a migratory transition (Haigo and Bilder, 2011; Cetera et al., 2014; Cetera and Horne-Badovinac, 2015). In early stages (1–5), cells exhibit random jostling motions with slow drift in the future direction of organized migration. At stage 6, the follicular epithelium transitions to fast and highly organized collective motion. This organized migration is believed to be essential for egg chamber elongation allowing for efficient egg extrusion (Horne-Badovinac, 2014), yet the mechanisms that initiate and accelerate rotation are not fully understood. The proposed phase diagram predicts that both cell density and contractility must be tightly regulated for the onset and maintenance of rapid collective migration.

We first tested predictions regarding the initiation of organized collective motion, focusing on stages 4 and 5 when egg chambers were large enough to measure velocity fields but had not yet begun rapid rotation. Stage 4 and 5 ovarian follicular epithelia were low density, had low levels of basolateral actomyosin contractility, and displayed a low degree of organized motion, consistent with a phase in the bottom left of the diagram (Figure 6, A–D). A confluent monolayer and the spheroidal layer of ovarian follicle cells may both be considered to be edgeless epithelia; however, an important distinction between the two affects the ability to separate local versus regional organization. Moving radially outward from a given cell in a monolayer leads only to neighboring cells of greater absolute distance from a given cell. Moving radially outward from a given cell within a circularly connected epithelium, such as the follicular epithelium, eventually leads back to the same cell. Because of this connected nature, regional organization has the potential to directly influence local organization (i.e., the “region” may include the local group itself). For this reason, we hypothesized that manipulations that affected either type of organization in 2D monolayers might lead to overall increases in collectivity.

FIGURE 6:

Prediction of in vivo collective migration. (A) Phase diagram showing hypothesized states of early (stage 4 and 5) and late (stage 7 and 8) follicular epithelium. Predicted phase transitions are denoted by blue and orange arrows. (B) Cell density as a function of projected egg chamber area and stage for developing WT, dMyc, and Rok-CAT Drosophila eggs. (C) Fixed WT egg chambers at three stages of development (5, 7, and 8 from left to right) stained for DAPI, anti–E-cadherin, and anti-pMLC. (D) Migration direction (top) and speed (bottom) of WT vs. dMyc stage 5 egg chambers. Measurements show speed and direction of migration over a 5-min interval. (E) Migration direction (top) and speed (bottom) of WT vs. Rok-CAT and αcat-IR–expressing stage 5 egg chambers. (F) Migration direction (top) and speed (bottom) of WT and dMyc–expressing stage 8 egg chambers. Arrowhead denotes region of decreased speed and organization for Myc follicular epithelium. (G) Migration direction (top) and speed (bottom) for WT vs. Rok-CAT and αcat-IR expressing stage 7 egg chambers. Arrowhead denotes region of decreased speed and organization in Rok-CAT follicular epithelium. (H) Mean migration speed of follicular epithelial cells. Student’s t test was used to assess significance. NS, not significant; *p < 0.05; **p < 0.01.

Our findings predict that increasing either contractility or cell density would lead to the early onset of organized collective migration, whereas decreasing functional contractility by disrupting cell–cell adhesion would increase disorganization (Figure 6A, blue arrows). To increase contractility, a constitutively active Drosophila ROCK allele (Rok-CAT) was expressed specifically in the follicular epithelium using the traffic jam-Gal4 promoter (tj-Gal4; Supplemental Figure S5A). To increase cell density, we overexpressed Drosophila Myc (dMyc) using tj-Gal4. Myc is a proto-oncogene that increases cell proliferation through induction of cyclin D2 (Bouchard et al., 1999). Expression of dMyc increased cell density compared with stage-matched WT egg chambers, leading to smaller cells (equivalently, more per unit area) for any given stage (Figure 6B). Consistent with predictions, highly organized motion of stage 4 and 5 egg chambers emerged by increasing either contractility or density (Figure 6, D, E, and H, and Supplemental Video S5). Reducing functional cell–cell contractility through α-catenin RNAi expression (αcat-IR) increased the degree of disorganization in WT stage 5 follicular epithelia, leading to extensive neighbor exchange (Figure 6E and Supplemental Video S5). In summary, increasing density or contractility drove stage 4 and 5 ovarian follicular epithelium to a state of highly organized collective rotation while depleting α-catenin to reduce cell–cell adhesion and functional cell–cell contractility drove the epithelium into a state of greater disorder.

We next tested predictions regarding the maintenance of collective migration for stage 7 and 8 egg chambers, which exhibit highly uniform collective migration. Contractility of stage 7 and 8 egg chambers was greater than in earlier stages, as measured by pMLC staining, especially on the basolateral surfaces, consistent with published findings (Figure 6C; Wang and Riechmann, 2007). Cell density peaked during stage 6 and lowered again for stage 7 and 8 egg chambers (Figure 6B). Therefore we hypothesized that this epithelium was in a phase corresponding to midlevel contractility and slightly higher density than stage 4 and 5 egg chambers, offering multiple predictions. Increasing contractility, increasing cell density, or decreasing contractility should drive this epithelium from a state in which maximal order is produced to one with disorder (orange arrows in Figure 6A). Increasing cell density by tj-Gal4 Myc overexpression decreased organization and speed of stage 7 and 8 follicular epithelia (Figure 6, F and H, and Supplemental Video S6). Increasing contractility by expressing Rok-CAT showed the predicted reduction in organization, with regions of cells undergoing swirling motions that led to decreased order and regions with slower speed (Figure 6, G and H, and Supplemental Video S7). Reducing cell–cell contractility through expression of α-catenin RNAi in stage 7 and 8 egg chambers dramatically disrupted organization (Figure 6, G and H, and Supplemental Video S7). We controlled for disparities between morphological staging and developmental progression by measuring the size of egg chambers undergoing a border cell delamination and saw no difference (Supplemental Figure S5, B and C).

In summary, these data demonstrated that the state of collective migration in an in vivo epithelium could be predictably transformed by controlling cell density and cell–cell contractility.

DISCUSSION

In this study, we took a multifaceted approach to determine the fundamental physical and biological mechanisms underlying how cells within an epithelium organize to collectively migrate. Focusing on the response of collective migration to changes in cell density revealed that increasing cell density drove changes in actomyosin contractility that reduced local organization, increased regional organization, and changed the shape of collective motion from large, broad groups to small, narrow streams. By defining these phases of collective migration and the parameters governing transitions among them, we were able to predictably alter collective migration in an in vivo epithelium.

The observation that local organization decreased while regional order increased with increasing cell density suggests that multiple length scales of coordination exist within an epithelium. Absolute local organization has been observed to decrease with increasing cell density (Angelini et al., 2010), and here we confirm that this reflects a true reduction in local group size by normalizing to cell radius. Of interest, as local group organization decreased, the relative organization between these local groups increased. A potential explanation is that at high density, cells generate motile forces but are no longer able to align their motions to neighboring cells via a system of active contractility, leading cells to slide past each other and reduce local organization. This is not to say that these motions are uncoordinated: at high density, cells are less deformable, and individual rearrangements cannot occur in isolation and may be coupled (Sadati et al., 2013), leading to an increase in regional organization. This two-level structure of organization bridges reports of decreases in correlation length with those that describe increases in the size of clusters of fast motion, termed dynamic heterogeneities, in the migration of cells at high-density (Trepat and Fredberg, 2011). Of note, increasing contractility prevented increases in regional organization, whereas diminishing contractility increased regional organization, supporting the idea that cell–cell contractility may prevent the growth of regional organization by organizing local motions at high density.

Contact inhibition of locomotion (CIL) is a process by which cells alter their motion in response to interactions with neighbors (Abercrombie, 1970) and has been suggested to explain, in part, how collectives prioritize migration toward a free edge (Mayor and Carmona-Fontaine, 2010). CIL could, in principle, contribute to the observed alterations in local organization and motility with changing density. Cell–cell contacts and signal transduction of this event are critical for CIL, but the types of cell–cell contacts that form between two cells or groups of cells are likely context dependent. In a confluent epithelium, contacts are ubiquitous and dynamic, but rather than general inhibition or redirection of motions, collective behavior emerges. Indeed, it has been proposed that cell–cell adhesions within a chain of cells signal differently from newly formed adhesions, which are believed to induce CIL (Desai et al., 2013). Similarly, contacts within epithelial sheets may be different from nascent contacts that mediate CIL upon collision and act to mediate cohesion rather than repulsion. The leader–follower structure we observed through spatiotemporal analysis suggests that there is prioritization among these contacts and that cell–cell tension may be a mediator. We also find that increasing cell density within an already confluent sheet reduces local collective organization, suggesting that signaling from cell–cell contacts may change as cell density increases.

Beyond demonstrating the effect of cell density and contractility on collective size, we find that these variables control transitions between specific shapes of collective migration. We observed a key transition between broad collectives and streaming collectives that occurs with increasing density or loss of functional cell–cell contractility. This change in collective shape may have important implications for collective invasion. Kuriyama et al. (2014) demonstrated that a reduction in N-cadherin was essential for collectives of neural crest cells to productively migrate during Xenopus development. Their correlation analyses show that the effect of N-cadherin reduction is consistent with a collective shape change from broad collectives to streaming motions, enabling collectives to reshape and migrate through geometrically constrained regions. α-Catenin and other components linking cell adhesion to actomyosin contractility are commonly altered in cancers (Shiozaki et al., 1994; Hiscox and Jiang, 1996), and our results suggest that these losses could enhance invasion by changing collective group shape to streaming patterns.

Spatiotemporal analyses of cell migration revealed that broad collectives arise through information transfer by which cells align to neighbors that they are behind or beside. Monolayer stress microscopy demonstrates that cells within epithelial sheets are under tension, and migration direction tends to align with the principal direction of normal stress. Our data give a dynamic view of cellular response to this picture of forces, demonstrating that the migration of a given cell can initiate changes in the migration of specific neighboring cells at low density. In the context of wound healing, the presence of a free edge may initially bias the migration direction of the first row of cells, reducing local cell density and putting the rest of the sheet in the “front-to-back” neighbor category. This directional signal can then propagate rearward, leading to a cycle of density reduction, neighbor response, and directed migration.

The propagation speed of the alignment response is significantly faster than the speed of cell migration, suggesting that cellular communication rather than external cues may be involved. This may be related to previously identified waves of contractility (Serra-Picamal et al., 2012). Although these waves propagated at 1 μm/min, they were computed from the time required to reach maximum response, and significant changes in cellular strain and stress appear earlier. In addition, the observed propagation rate predicts the average cellular response time to be ∼6 min (5 μm/min, 32-μm diameter), similar to the estimated time of 5 min required for cells to change direction in galvanotactic studies (Cohen et al., 2014). Recent data on Rho GTPase polarization provide a potential molecular mechanism for this response. Mechanical tension, as may be generated between an index cell and trailing neighbor, can polarize Cdc42 activity in a P-cadherin– and β-Pix–dependent manner and Rac1 activity due to relocalization of Merlin (Das et al., 2015; Plutoni et al., 2016). Supporting this mechanism, cells with constitutively active Rho or inhibited ROCK show a poorer alignment response, potentially reflecting a decreased ability to generate polarized RhoGTPase activity. Furthermore, we find that the alignment response extends to encompass lateral positions. This indicates that whereas front-to-back polarization is likely a dominant component in organizing collective migration, lateral cell–cell associations may be important in maximizing the organization of large collectives.

Previous hypothesized cell migration phase diagrams have included three axes: cell density, cell force production, and cell–cell adhesion (Sadati et al., 2013). These data indicate that two of these axes—cell force production and cell–cell adhesion—might be highly coupled in epithelial systems, as α-catenin depletion and ROCK inhibition had similar effects on both collective size and shape. We furthermore find that phases are not simply defined by a single parameter. The studied cell types have similar local organization at high density, yet this motion differs in both regional and directional organization. This phase diagram still represents a simplified model of cell behavior. Many more cell-intrinsic and extrinsic properties play a role in governing collective migration, including chemokines, extracellular matrix (ECM) proteins, and physical properties, as well as cell–ECM adhesion (Haas and Gilmour, 2006; Nguyen-Ngoc et al., 2012). It is likely that these features may affect how cells respond to increasing density or changes in contractility. In addition, it is almost certain that alterations to an important component of one of these general cellular properties (e.g., an alteration to ROCK to affect cell–cell contractility) will influence another (e.g., cell–ECM force generation) and that these additional effects may be of importance for an observed phenotype. Indeed, here we see that the WT response of collective migration to changes in density is itself driven by changes in contractility signaling.

The Drosophila egg-chamber follicular epithelium provided an opportunity to test these predictions in a system with 3D geometry and native ECM structure. Using this system, we demonstrated that basic cell migration studies can be used to provide insight into in vivo migratory processes and found that although many factors govern cell migration, cell density and contractility are two major influences. Increasing contractility or cell density led to high-speed collective rotational migration of the early follicular epithelium. It is likely that this represents an enhancement of underlying emerging collective rotation rather than initiation of collective motion. The follicular epithelium in stage 4 and 5 egg chambers has been shown to drift slowly in the direction of future rapid rotation (Cetera et al., 2014), but migration is not yet fast and uniform. Increasing contractility or cell–cell density may serve to better couple local and regional motions, respectively, until the entire egg chamber begins rotating. Although the connected nature of both the egg chambers and simulation provide coupling of local and regional motions, it is worth noting an important difference between migration on a spheroidal surface and the surface of a torus to which the periodic boundary conditions apply. Whereas it is possible to have uniform migration on the surface of a torus, no such velocity field can exist on a sphere, which must contain at least one stationary point or “cowlick” (Milnor, 1978). The formation and maintenance of these stationary points, especially when the egg chamber is approximately spherical, presents an interesting avenue for further exploration.

In a developmental context, these predictions suggest that both cell density and cell–cell contractility may be endogenously regulated to control the onset of collective motion. The observed levels of actomyosin contractility and cell density in the development of WT egg chambers in fact follow a trajectory consistent with the onset of rotation at stage 6: at this stage, WT egg chambers reach a peak in cell density and have increased levels of actomyosin contractility (Figure 6, B and C). Once rotating, however, an excess of contractile force generation or cell density may disrupt communication, leading to disorganized motion.

Overall these data demonstrate how fundamental properties of individual cells affect the migratory properties of entire tissues, controlling the size and structure of collective groups. In development and wound healing, transitions in density and contractility can be harnessed for productive migration. However, in cancer, these same systems may be exploited to enhance invasion.

MATERIALS AND METHODS

Cell culture and density control

Density variation was achieved by plating 6 × 10⁵ cells per 30-mm dish and making measurements at 24, 48, and 72 h (low, medium, and high density, respectively). The values for each density condition are listed in Supplemental Table S1. Medium was replaced each day, and cell density was measured using Hoechst 33342 (Thermo Fisher, Waltham, MA) dye. Separate plates were used for each density to avoid phototoxicity. Distance values were normalized by cell size in each field of view before combination into a single density bin. Gradients in cell density were generated by swirling the culture dish for 30 s immediately after plating a uniform suspension of cells, increasing the relative concentration of cells in the center of the dish. To deplete α-catenin, the lentiviral pFLRu vector containing anti–α-catenin shRNA and puromycin resistance was used as described previously (Bajpai et al., 2008). MCF10A cells expressing constitutively active Rho were generated in the same manner using a QL activating mutant Rho (Coso et al., 1995) subcloned into a pFLRu vector. Puromycin (Sigma-Aldrich, St. Louis, MO) was used in cell selection and maintenance at a concentration of 1.5 μg/ml. Fasudil (Sigma-Aldrich) and Y27632 (Sigma-Aldrich) were both used at a concentration of 30 μM for 5 h for ROCK inhibition.

Drosophila lines, staging, and dissections

All crosses and staging were performed at 25°C. Stocks are described in FlyBase (http://flybase.org/). UAS-Myc (dm; B#9675) and UAS-Rok-CAT-3.1 (B#6669) were provided by the Bloomington Drosophila Stock Center (Indiana University, Bloomington, IN). En-Gal4, UAS-GFP was provided by J. Skeath (Washington University in St. Louis, St. Louis, MO). Nrg-GFP; TJ-Gal4; Indy-GFP was provided by S. Horne-Badovinac (University of Chicago, Chicago, IL). Epithelial cells were staged according to morphological features described by Cummings and King (1969) by matching the z-stack projected area of each epithelial cell to the expected areas across stages. For ovariole experiments, 1- to 3-d-old females were aged on yeast for 1–3 d before dissection. Ovaries were dissected as described in Prasad et al. (2007) in live-imaging medium (Schneider’s S2 Medium, 0.6× penicillin/streptomycin, 15% [vol/vol] fetal bovine serum [FBS], 0.2 mg/ml insulin) and stained for 10 min with CellMask Deep Red Plasma Membrane Stain (Thermo Fisher) at 1:1000 dilution in live-imaging medium. Cell size measurements were made at the basal surface. Border cell delamination was defined as the time point at which a distinct cluster of cells emerged from the surrounding single-layered follicular epithelium.

Immunofluorescence

Cells were fixed in 4% paraformaldehyde (PFA; VWR, Radnor, PA) in phosphate-buffered saline (PBS), permeabilized with 0.5% Triton X-100 (Sigma-Aldrich) in PBS, blocked in 1% bovine serum albumin (BSA; Sigma-Aldrich) and PBS overnight at 4°C, incubated with primary antibodies overnight at 4°C, and incubated with secondary bodies for 2 h at room temperature with 5-min washes in PBS in between. Ovarioles were fixed for 40 min in 4% PFA in PBS, followed by a 5-min wash in PBX (PBS with 0.1% Triton X-100), two 20-min washes in PAXD (PBS with 1% BSA, 0.3% Triton X-100, and 0.3% deoxycholate), and one-20 min wash in PAXDG (PAXD with 5% normal goat serum). The mean level of pMLC staining intensity per cell within the density gradient was calculated by normalizing the total intensity of pMLC signal within a region by the number of cells within that region at 13 points along the density gradient. All regions contained at least 200 cells. Ovarioles were incubated overnight at 4°C in primary antibody diluted in PAXDG and washed three times in PBX at room temperature. Ovarioles were then incubated overnight at 4°C in secondary antibody diluted in PAXDG and washed twice in PBX and once in PBS, all at room temperature. Prepared tissues were mounted in Vectashield mounting medium with or without 4′,6-diamidino-2-phenylindole (DAPI; Vector Laboratories, Burlingame, CA). See the Supplemental Experimental Procedures for antibodies and concentrations.

Imaging

For cells, live-cell and fixed epifluorescence imaging was performed on a Nikon Ti-E microscope with a humidity- and temperature-controlled incubation chamber (LiveCell Imaging, Seoul, Korea). Data were collected from 2.3-mm² regions by tiling four 10× regions of view. Time-lapse imaging was performed with 60-min duration and 2-min frame intervals. Reference images of the dish surface were taken at each frame and field of view to correct for stage drift. For Drosophila, time-lapse imaging was performed on either an inverted Zeiss LSM510 or an upright LSM700 confocal microscope over 3.5 h with 5-min frame intervals. See also the Supplemental Experimental Procedures.

Imaging analysis and statistics

Image analysis was performed using Matlab (MathWorks, Natick, MA) and ImageJ (National Institutes of Health, Bethesda, MD). Cellular motion was measured with particle image velocimetry for monolayers (Thielicke and Stamhuis, 2014) and optical flow for Drosophila (Vig et al., 2016). Mean cell radius was computed for each field of view using custom software to segment Hoechst 33342–stained nuclei and is defined as the radius of a circle with area equivalent to the mean cell area. Correlation computations were performed using custom Matlab software. Curve fitting was performed using Matlab software, and data beyond a distance of 40 cell radii were not used to fit Eq. 1 due to departure from the form of the fitting function beyond this distance. See also the Supplemental Experimental Procedures.

Abbreviations used:

αcatKD

α-catenin knockdown

αcatIR

α-catenin RNAi

BCM

biochemical contractility model

CCM

constant contractility model

CIL

contact inhibition of locomotion

ECM

extracellular matrix

LA

low adhesion

LC

low contractility

LF

low friction

pMLC

phosphorylated myosin light chain

RhoCA

constitutively active rho

WT

wild type.