GDP-to-GTP exchange on the microtubule end can contribute to the frequency of catastrophe

The mechanisms that lead to microtubule catastrophe are poorly understood. Computational simulations and experiments show that GDP-to-GTP exchange on the microtubule end can contribute to the initiation of catastrophe. This reaction does not figure into the current understanding, and so the results complement more mechanochemical models.

Abstract

Microtubules are dynamic polymers of αβ-tubulin that have essential roles in chromosome segregation and organization of the cytoplasm. Catastrophe—the switch from growing to shrinking—occurs when a microtubule loses its stabilizing GTP cap. Recent evidence indicates that the nucleotide on the microtubule end controls how tightly an incoming subunit will be bound (trans-acting GTP), but most current models do not incorporate this information. We implemented trans-acting GTP into a computational model for microtubule dynamics. In simulations, growing microtubules often exposed terminal GDP-bound subunits without undergoing catastrophe. Transient GDP exposure on the growing plus end slowed elongation by reducing the number of favorable binding sites on the microtubule end. Slower elongation led to erosion of the GTP cap and an increase in the frequency of catastrophe. Allowing GDP-to-GTP exchange on terminal subunits in simulations mitigated these effects. Using mutant αβ-tubulin or modified GTP, we showed experimentally that a more readily exchangeable nucleotide led to less frequent catastrophe. Current models for microtubule dynamics do not account for GDP-to-GTP exchange on the growing microtubule end, so our findings provide a new way of thinking about the molecular events that initiate catastrophe.

INTRODUCTION

Microtubules (MTs) are hollow, cylindrical polymers of αβ-tubulin that have essential roles in organizing the cytoplasm and segregating chromosomes during cell division (reviewed in Desai and Mitchison, 1997; Howard and Hyman, 2003). Microtubules switch between phases of growing and shrinking, a hallmark property called dynamic instability that is directly targeted by some antimitotic drugs. Dynamic instability results from the biochemical and structural properties of the polymerizing αβ-tubulin subunits and how they interact with the microtubule lattice. Unpolymerized, GTP-bound αβ-tubulin subunits assemble into microtubules, where their GTPase activity is greatly accelerated (Nogales et al., 1998). This assembly-dependent GTPase activity results in a “stabilizing cap” of GTP- or GDP⋅Pi-bound αβ-tubulin at the end of growing microtubules. Loss of this stabilizing cap triggers catastrophe—the switch from growing to shrinking—by exposing the more labile GDP lattice.

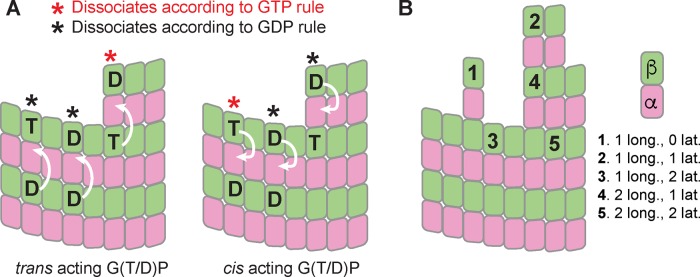
The microtubule-stabilizing role of GTP is widely appreciated, but there are conflicting views about the molecular mechanisms by which GTP stabilizes microtubules. Indeed, recent years have seen a change in thinking about the role of nucleotides in microtubule assembly and dynamics. Initially, a cis-acting view of nucleotide action dominated (Melki et al., 1989; Wang and Nogales, 2005; Nogales and Wang, 2006). This cis-acting view postulated that nucleotide state dictated the conformation of unpolymerized αβ-tubulin, with GTP favoring a straighter, microtubule-compatible conformation and GDP favoring a curved, microtubule-incompatible conformation. This cis-acting nucleotide provided an appealing structural rationale to explain why microtubule polymerization requires GTP and why GTP hydrolysis leads to catastrophe. However, numerous biochemical and structural studies failed to detect nucleotide state–dependent conformational changes in unpolymerized αβ-tubulin that the cis-acting model predicts should occur (Honnappa et al., 2003; Rice et al., 2008; Barbier et al., 2010; Nawrotek et al., 2011; Ayaz et al., 2012; Pecqueur et al., 2012). Based on these and other studies, an alternative model for the role of GTP has gained favor (Buey et al., 2006; Rice et al., 2008). This “lattice” or trans-acting model postulates that the effect of nucleotide state acts across the longitudinal interface, on a different αβ-tubulin than the one to which the nucleotide is bound. In a trans-acting model, the nucleotide does not affect the conformation/curvature of the unpolymerized αβ-tubulin to which it is bound. The difference between cis and trans models is most apparent when considering the terminal αβ-tubulin subunits at the growing end of the microtubule (Figure 1): in a cis-acting model, the nucleotide bound to the terminal subunit controls the strength of lattice contacts, but in a trans-acting model, it is the nucleotide underneath (i.e., bound to a different αβ-tubulin) the terminal subunit that controls how tightly that terminal subunit associates with the lattice.

FIGURE 1:

Cis- and trans-acting nucleotides in microtubule dynamics. (A) In the trans-acting model (left), the effect of nucleotide state is relayed across the longitudinal interface (arrows pointing from one αβ-tubulin to the one above). In the cis-acting model (right), the effect of nucleotide state is expressed on the subunit to which the nucleotide is bound (arrows pointing inside the same αβ-tubulin). T and D indicate nucleotide state, and red and black asterisks indicate which subunits make tighter lattice contacts. These different models made different predictions for how tightly terminal subunits will be bound. (B) In our model, the strength with which a given subunit is bound is determined by how many longitudinal and lateral interactions it makes, with more interactions giving tighter binding and slower dissociation. The effect of GDP is implemented as a multiplicative correction X such that subunits dissociating according to the “GDP rule” will dissociate X-fold faster than their “GTP rule” equivalents.

Most models for microtubule dynamics do not incorporate a trans-acting nucleotide because these models were formulated when the exchangeable nucleotide was believed to act in-cis. Indeed, early models from Chen and Hill (Chen and Hill, 1983, 1985), later models from Martin and Bayley (Bayley et al., 1989, 1990; Martin et al., 1993), more recent models from Odde and colleagues (VanBuren et al., 2002, 2005; Coombes et al., 2013), and others (Zakharov et al., 2015) all share some version of a cis-acting nucleotide. A more recent model (Margolin et al., 2012) began to explore how a trans-acting nucleotide might affect polymerization dynamics but also invoked a protofilament cracking reaction that is difficult to validate experimentally. In the present study, we sought to investigate potential functional consequences of trans-acting GTP by incorporating it into a computational model for microtubule dynamics, using only parameters that should be amenable to experimental perturbation. Following an approach adopted by a number of other groups, we developed a Monte Carlo–based algorithm that translates assumed biochemical properties of αβ-tubulin subunits into predictions of microtubule dynamics by simulating biochemical reactions—association, dissociation, and GTP hydrolysis—one at a time. For simplicity, we did not incorporate assumptions about αβ-tubulin mechanochemistry as in other models (VanBuren et al., 2002; Coombes et al., 2013; Zakharov et al., 2015). Whether they incorporate mechanochemistry or not, these kinds of simulations provide a link between subunit biochemistry and the more “mesoscale” parameters of microtubule dynamics: growing and shrinking rates and the frequencies of catastrophe and rescue. Besides incorporating a trans-acting role for the nucleotide, our model is conceptually most similar to an earlier model developed using a predominantly cis-acting mechanism for GTP/GDP (VanBuren et al., 2002; Supplemental Figure S1).

Our simulations with a trans-acting nucleotide revealed that transient exposure of GDP-bound αβ-tubulin on the microtubule plus end caused a slowing of elongation during which the stabilizing GTP cap eroded, increasing the propensity for catastrophe. This GTPase-dependent slowdown is not a unique consequence of trans-acting GTP, because we also observed it in a model using a cis-acting nucleotide. We hypothesized that if GDP exposure led to catastrophe by reducing the rate of microtubule elongation, then GDP-to-GTP exchange on terminal subunits might mitigate the catastrophe-promoting effect of terminal GDP exposure. Our model calculations support this idea by showing that increased rates of GDP to GTP exchange on terminal subunits reduce the predicted frequency of catastrophe. We also performed experiments to perturb nucleotide-binding affinity (using mutant αβ-tubulin or modified nucleotides) with the goal of selectively increasing the rate of GDP-to-GTP exchange, and we observed that weaker nucleotide binding led to less frequent catastrophe. Thus our simulations and experiments together support a model in which the rate of terminal nucleotide exchange can affect the frequency of catastrophe. These findings provide new ways of thinking about the molecular events that lead to catastrophe.

RESULTS

A model for microtubule dynamics that incorporates trans-acting nucleotide

We developed a kinetic Monte Carlo model to simulate MT polymerization dynamics one biochemical event (association, dissociation, GTP hydrolysis) at a time (part of the model was described in Ayaz et al., 2014). Our model uses a two-dimensional representation of the microtubule lattice to capture different kinds of binding environments (Figure 1A); it was inspired by one developed by VanBuren et al. (2002). Our algorithm is constructed in a way that makes it easy to implement different biochemical assumptions. Here we use our simulator with two different versions of the biochemical “rules” governing polymerization and depolymerization: one set implements cis-acting GTP (Figure 1B) as described previously by others (VanBuren et al., 2002; Supplemental Figure S1), and the other set implements trans-acting GTP (Buey et al., 2006; Rice et al., 2008; Nawrotek et al., 2011; Margolin et al., 2012; Figure 1B). For simplicity, we adopted a minimal parameterization that does not attempt to describe “mechanical” properties of αβ-tubulin and microtubules such as spring-like conformational strain. This strain is believed to increase as αβ-tubulin changes from its curved, unpolymerized conformation to the straight conformation found in the polymer.

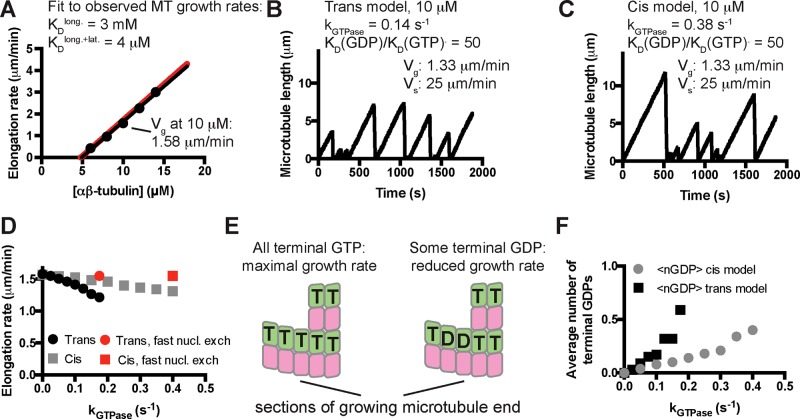
To obtain model parameters that could recapitulate MT elongation and shrinking rates and approximate the frequency of catastrophe, we followed the divide-and-conquer approach outlined in VanBuren et al. (2002; Materials and Methods). To compare our model parameters more easily to prior work, we trained our model on the same benchmark observations that were used in other computational studies (Walker et al., 1988). First, we used “GTP-only” simulations to search for parameters that recapitulated MT growth rates over a range of αβ-tubulin concentrations (Walker et al., 1988; Figure 2A). With those parameters fixed, we optimized the weakening effect of GDP on the longitudinal interface by tuning it to make “all-GDP” microtubules depolymerize at the observed average rate of rapid, postcatastrophe shrinking. Because the growing and shrinking are taken to be “all-GTP” and “all-GDP” behaviors, the parameters that determine growing and shrinking rates are shared between simulations implementing cis- and trans-acting nucleotides. Finally, keeping the prior parameters fixed, we separately optimized the GTPase rate constant to obtain the observed catastrophe frequency at 10 μM αβ-tubulin for cis and trans models (Figure 2, B and C). The parameters we obtained are comparable to those identified previously for the same data, with our model showing less rescue (VanBuren et al., 2002). The longitudinal affinity we obtained (3 mM) is weaker that the one reported in Gardner et al. (2011a; 75 μM); that study used different data as the fitting target. Compared to the cis-acting rules, the trans-acting ones require a slower GTPase rate to achieve the same frequency of catastrophe. Like the earlier study (VanBuren et al., 2002) that inspired ours, our model predicts a concentration dependence of catastrophe that is steeper than the one measured in vitro and does not recapitulate “age-dependent” catastrophe. Nevertheless, our model provides a useful framework for investigating the possible effects of different biochemical assumptions.

FIGURE 2:

Kinetic Monte Carlo simulations of microtubule dynamics. (A) Simulations with “GTP-only” parameters recapitulate experimentally observed microtubule elongation rates over a range of mammalian αβ-tubulin concentrations (dots: simulated elongation rates; black line: linear fit to the simulated elongation rates; red line: concentration-dependent elongation rates from Walker et al., 1988). (B) After optimizing the GTPase rate constant and the affinity- weakening effect of GDP, the trans model can recapitulate the experimentally observed frequency of catastrophe and rate of shrinking at 10 μM αβ-tubulin. Note that the elongation rate obtained here (1.33 μm/min) is slower than in the GTP only simulations (1.58 μm/min). (C) Same as B, but using a version of cis-acting GTP (Supplemental Figure S1). Compared to the trans model, a faster rate of GTPase activity was required to obtain the measured frequency of catastrophe. A similar GTPase-induced “slowdown” in elongation was observed. (D) Simulations show that for both trans and cis models, the magnitude of the GTPase-induced slowdown increases with the GTPase rate. Red dots indicate growth rates in simulations in which terminal GDP-to-GTP exchange was instantaneous. (E) Exposure of terminal GDP-bound αβ-tubulins might provide an explanation for the GTPase-induced decrease in elongation rates. (F) In both trans and cis simulations, microtubules expose approximately one terminal GDP subunit every three end configurations sampled during a growth phase.

In simulations, GDP exposure on the microtubule plus end reduces microtubule elongation rate; GDP-to-GTP exchange mitigates this slowdown

When a nonzero GTPase rate constant was used in simulations, the elongation rates decreased from their “GTP-only” values for both cis and trans models (e.g., by 15% in Figure 2, B and C). To our knowledge, such a GTPase-induced “slowdown” has not previously been reported. Simulations using a range of GTPase rate constants revealed that for both cis and trans models, the rate of microtubule elongation decreased monotonically from its “GTP-only” value as the GTPase rate increased (Figure 2D). We speculated that the GTPase-induced slowdown occurred because GDP-tubulin was being exposed on the microtubule end, creating low-affinity binding sites that antagonized elongation enough to reduce average growth rates without triggering catastrophe (Figure 2E). If this is true, then the microtubules in our simulations should have increasing amounts of GDP-bound terminal subunits as the GTPase rate constant is increased. Counting the terminal GDP-bound subunits during growth revealed that the simulated microtubules do indeed expose GDP-bound terminal subunits and that the frequency of exposure increases with increasing GTPase rate (Figure 2F). Using the parameters from Figure 2, B and C, shows that “cis” and “trans” microtubules on average each expose one terminal GDP subunit ∼33% of the time during a growth phase. In other words, on average, every third configuration sampled during growth contained one terminal GDP. To confirm that the GTPase-induced slowdown did in fact result from exposing GDP-bound terminal subunits, we modified our simulation code to instantaneously convert terminal GDP-tubulin subunits back to the GTP state. This modification resulted in elongation rates indistinguishable from those obtained in the absence of GTPase (red points in Figure 2D).

The computational experiments just described indicate that 1) GDP-bound terminal subunits can be exposed on the end of growing microtubules, 2) this exposure slows elongation rates, and 3) the GTPase-induced slowdown is abrogated when GDP-to-GTP exchange on terminal subunits occurs instantaneously. We hypothesized that a finite rate of GDP-to-GTP exchange on terminal subunits might affect the frequency of catastrophe by modulating the GTPase-induced slowdown in our simulations (Figure 3A). To test this, we added a terminal GDP-to-GTP exchange reaction to our algorithm (Figure 3B), assuming that GDP release is rate limiting for exchange. The rate of terminal GDP-to-GTP exchange markedly affected the predicted frequency of catastrophe in simulations, with faster rates reducing the frequency of catastrophe (Figure 3B). At very fast rates of terminal nucleotide exchange, the catastrophe frequency approached zero in the trans model, and at very slow rates of exchange, the catastrophe frequency approached a maximum value. At intermediate rates of nucleotide exchange, the predicted catastrophe frequency depends sensitively on the rate of exchange (Figure 3B).

FIGURE 3:

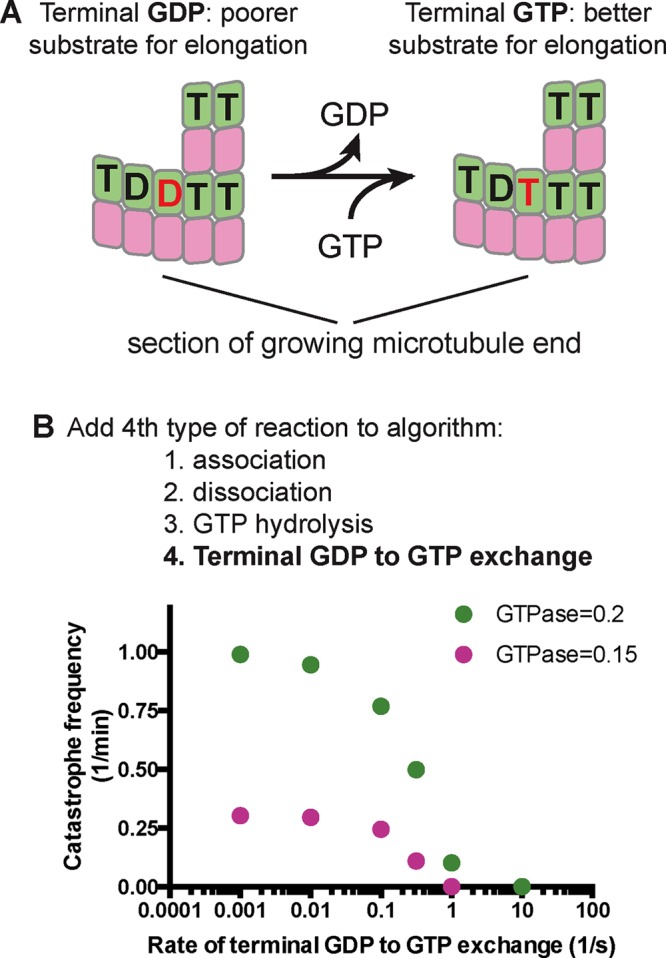
A possible role for terminal GDP-to-GTP exchange in microtubule catastrophe. (A) GDP-to-GTP exchange on a terminal subunit. (B) To investigate in simulations the possible relevance of terminal GDP-to-GTP exchange, we added it as another possible event in our simulation algorithm. Varying the rate of terminal GDP-to-GTP exchange in simulations with two different GTPase rate constants (green, 0.2 s⁻¹; pink, 0.15 s⁻¹) yielded a marked effect on the predicted frequency of catastrophe, with faster rates of exchange giving less frequent catastrophe.

Observing a GDP-induced “slowdown” in simulations led us to speculate that actual microtubules regularly expose GDP-bound subunits on their growing plus ends and that terminal nucleotide exchange might affect their frequency of catastrophe. In what follows, we use two complementary perturbations of nucleotide binding to explore whether GDP-to-GTP exchange on the growing microtubule end affects the frequency of catastrophe in vitro, using yeast αβ-tubulin as a model system because it has allowed in vitro studies using site-directed mutants (Davis et al., 1994; Sage et al., 1995; Dougherty et al., 1998, 2001; Gupta et al., 2002; Uchimura et al., 2010; Johnson et al., 2011; Geyer et al., 2015).

In experiments, weaker nucleotide binding correlates with less frequent catastrophe

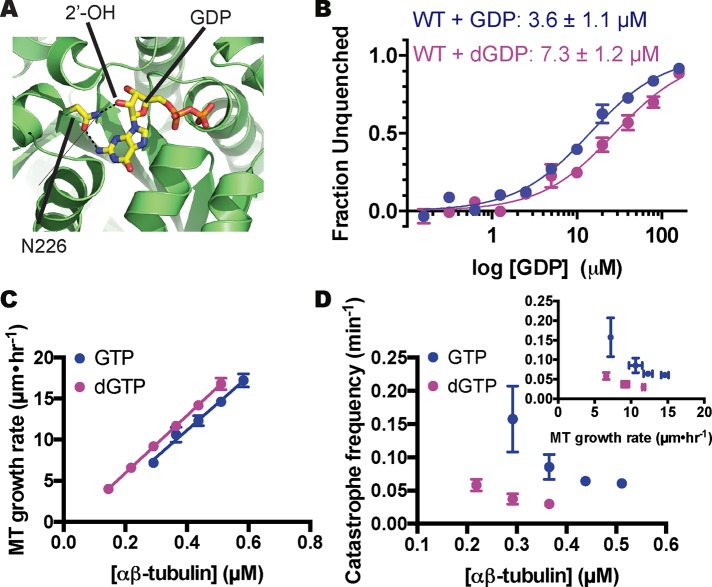
An αβ-tubulin mutant that exchanges nucleotide faster but that is otherwise normal could provide a way to test the prediction that faster terminal exchange reduces the frequency of catastrophe. Although directly measuring the rate of nucleotide exchange on the MT end is not yet possible, we reasoned that faster exchange would likely result from a decrease in αβ-tubulin GTP/GDP binding affinity, which is easily measured. To affect nucleotide binding as selectively as possible, we sought to mutate GTP-interacting residues that do not also participate in polymerization contacts or GTPase activity. The conserved β-tubulin residue C12 fits these criteria: the side chain packs underneath the guanosine base of the exchangeable nucleotide, does not contact neighboring αβ-tubulins, and has not been implicated in catalysis (Figure 4A). We therefore overexpressed and purified (Johnson et al., 2011) C12A yeast αβ-tubulin in order to study its GTP-binding and polymerization dynamics.

FIGURE 4:

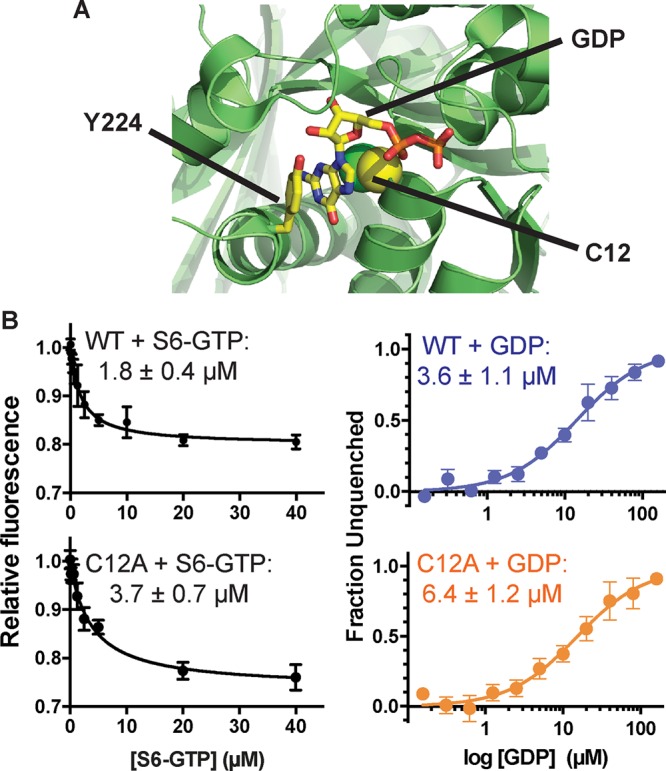
Nucleotide-binding properties of β:C12A αβ-tubulin. (A) β:C12 (side chain represented as spheres) is a conserved residue that contacts the exchangeable GTP but does not participate in polymerization contacts. The view, which is approximately of the plus end of β-tubulin, shows part of the surface that would be contacted by another αβ-tubulin; Y224 shields the guanosine from polymerization contacts by stacking on top of it. PDB 4I4T (Prota et al., 2013) was used for this illustration. (B) The β:C12A mutation reduces the nucleotide-binding affinity of αβ-tubulin. Left, affinities of wild-type and β:C12A αβ-tubulin for S⁶-GTP measured by monitoring quenching of αβ-tubulin intrinsic fluorescence by S⁶-GTP. Each data point represents the mean fraction of signal quenched at a particular concentration of S⁶-GTP (n = 4; error bars represent the SEM). Right, affinities of wild-type and β:C12A αβ-tubulin for GDP measured using a fluorescence unquenching assay. Each data point represents mean fraction of signal restored at a particular concentration of GDP (n = 6; error bars represent SEM).

We first measured the nucleotide-binding affinity of C12A yeast αβ-tubulin using a fluorescence-quenching assay (Fishback and Yarbrough, 1984; Amayed et al., 2000). This assay takes advantage of the fact that 6-thio-GTP (S⁶-GTP) quenches the intrinsic fluorescence of αβ-tubulin when bound. We first determined the affinity of wild-type and C12A αβ-tubulin for S⁶-GTP, obtaining values of 1.8 and 3.7 μM, respectively (Figure 4B). We next used a competition assay to obtain their affinity for GDP. Wild-type αβ-tubulin binds GDP with K_D = 3.6 μM; C12A binds GDP less tightly, with K_D = 6.4 μM (Figure 4B). A prior measurement of GTP binding to yeast αβ-tubulin showed higher affinity (∼50 nM; Davis et al., 1993); this discrepancy might be explained by the glycerol-free conditions we used (glycerol has been observed to increase the nucleotide-binding affinity of αβ-tubulin; Yarbrough and Fishback, 1985). Whatever the reason, our measurements showed that the β:C12A mutation caused a decrease in the affinity of GTP/GDP binding.

To determine whether the β:C12A mutation also affected the apparent biochemistry of microtubule elongation and/or the frequency of catastrophe, we used time-lapse differential interference contrast (DIC) microscopy to measure the polymerization dynamics of wild-type and β:C12A αβ-tubulin. Yeast microtubules elongate robustly at lower concentrations than their vertebrate counterparts (Gupta et al., 2002; Bode et al., 2003; Geyer et al., 2015). The β:C12A and wild-type microtubules showed similar concentration-dependent growth rates. This similarity suggests that the mutation had little effect on the affinity of the interactions that drive elongation (estimated from extrapolation to the x-axis, 51 and 42 nM for wild type and β:C12A, respectively) or on the apparent rate constant for subunit addition (estimated from the slope/concentration dependence of elongation rates, 14.9 and 12.2 μM⁻¹ s⁻¹ for wild type and β:C12A, respectively; Figure 5A). Despite the somewhat slower growth rates at a given concentration, β:C12A MTs underwent catastrophe substantially less frequently than did wild type, showing a sixfold difference at concentrations around 0.3 μM (Figure 5B).

FIGURE 5:

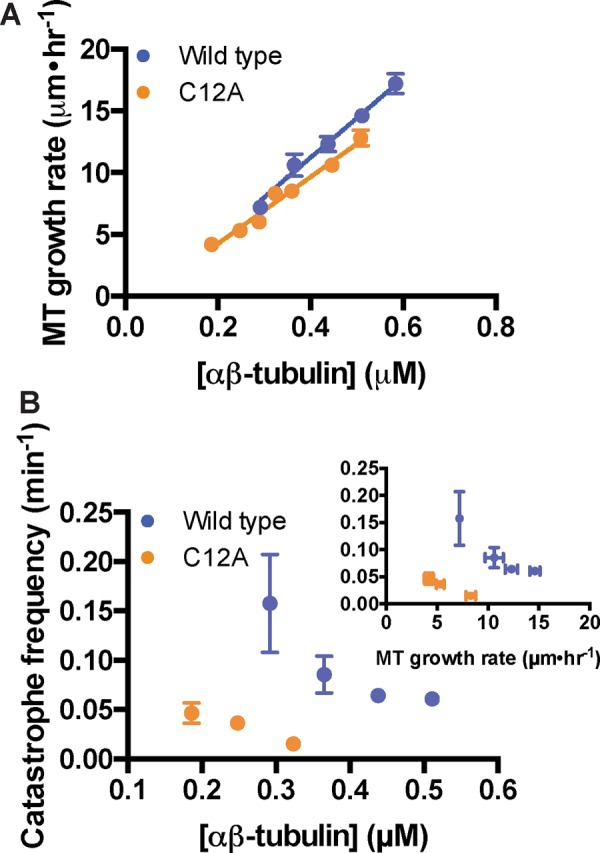
β:C12A microtubules undergo catastrophe less frequently than does wild type. (A) β:C12A microtubules show comparable concentration-dependent elongation rates as wild type (four microtubules per data point, error bars show SD). Parameters slope and y-intercept from the linear regressions are, respectively, for wild type, 14.9 ± 0.9 μM⁻¹ s⁻¹ and −0.9 ± 0.4 s⁻¹, and for β:C12A, 12.2 ± 0.3 μM⁻¹ s⁻¹ and −0.5 ± 0.3 s⁻¹. (B) β:C12A microtubules undergo catastrophe approximately sevenfold less frequently than does wild type. Inset, plot of catastrophe frequency vs. MT growth velocity. The small changes in growth rate do not explain the change in catastrophe frequency. Each data point represents the catastrophe frequency measured at a particular concentration of αβ-tubulin. From left to right, for wild type (blue), n = 10, 21, 75, and 75; and for β:C12A (orange), n = 20, 90, and 63. Error bars represent SD.

To further probe a potential link between the rate of terminal GDP-to-GTP exchange and the frequency of microtubule catastrophe, we sought an alternative way to perturb nucleotide-binding affinity that would be free of the complications associated with mutations. Earlier work showed that deoxy analogues of GTP promote MT assembly and bind less tightly to the exchangeable site (Hamel et al., 1984). Structures of αβ-tubulin (for a recent high-resolution example, see Prota et al., 2013) further show that the 2′ hydroxyl group of the guanine nucleotide does not make polymerization contacts (Figure 6A). Thus measuring microtubule dynamics in the presence of dGTP should provide an alternative to site-directed mutants. Using the competition assay described earlier, we determined that yeast αβ-tubulin binds dGDP about twofold less tightly than GDP (7.3 vs. 3.6 μM; Figure 6B), a change in affinity consistent with prior measurements using mammalian αβ-tubulin (Hamel et al., 1984). Measured MT elongation rates changed little with dGTP compared with GTP (concentration dependence for elongation rates, 15.8 vs. 14.9 μM⁻¹ s⁻¹ for wild type; extrapolation to the x-axis: 30 vs. 61 nM for wild type; Figure 6C), indicating that the removal of the 2′-OH did not substantially perturb the strength of lattice contacts. Even accounting for the slightly faster elongation, however, the catastrophe frequency decreased markedly in the presence of the weaker-binding dGTP (greater than fourfold decrease at 0.3 μM; Figure 6D).

FIGURE 6:

αβ-Tubulin binds less tightly to, and undergoes catastrophe less frequently with, 2′-deoxy guanine nucleotides. (A) The 2′ hydroxyl of GTP, which is absent in dGTP, makes a hydrogen bond with a conserved asparagine (N202). PDB 4I4T (Prota et al., 2013) was used for this illustration. (B) Affinities of yeast αβ-tubulin for GDP and dGDP measured using a fluorescence-based competition assay (see Materials and Methods). αβ-Tubulin binds to dGDP about twofold less tightly than to GDP. Each data point represents the mean fraction of signal restored measured at a particular concentration of GDP or dGDP (n = 6 for GDP, blue; n = 4 for dGDP, purple; error bars represent SEM). (C) MTs polymerizing with dGTP show comparable concentration-dependent elongation rates to those growing with GTP MTs (four MTs per data point; error bars show SD). Parameters slope and y-intercept from the linear regression for elongation in the presence of dGTP are, respectively, 15.8 ± 0.06 μM⁻¹ s⁻¹ and −0.5 ± 0.02 s⁻¹. (D) MTs assembled with dGTP undergo catastrophe approximately fourfold less frequently than with GTP. Inset, plot of catastrophe frequency vs. MT growth velocity showing that the small increase in growth rate cannot explain the change in catastrophe frequency. Each data point represents the catastrophe frequency measured at a particular concentration of αβ-tubulin From left to right, for wild type + GTP (blue), n = 10, 21, 75, and 75; and for wild type + dGTP (purple), n = 43, 23, and 18. Error bars represent SD.

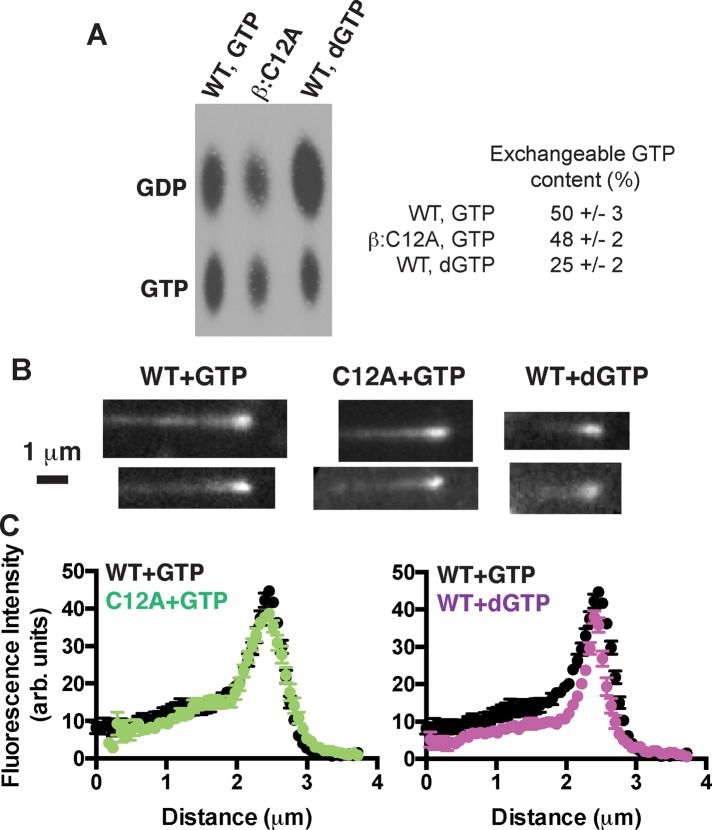
A decreased frequency of catastrophe for two different perturbations that reduce nucleotide-binding affinity is consistent with our proposal that the rate of terminal nucleotide exchange can contribute to the frequency of catastrophe. However, the experiments described do not rule out an alternative mechanism in which reduced GTPase activity (as a result of the mutation and/or the use of dGTP) is responsible for the reduced frequency of catastrophe. We used two approaches to investigate the possibility that the β:C12A mutation or the use of dGTP affected GTPase activity. We first performed experiments with ³²P-GTP to compare the nucleotide content of wild-type microtubules (polymerizing with GTP) to β:C12A microtubules (with GTP) and to wild-type microtubules polymerizing with dGTP. These data show that wild-type and β:C12A microtubules contain comparable amounts of exchangeable GTP (50 and 48%, respectively) and that when polymerizing with dGTP, wild-type microtubules contain less GTP (25%; Figure 7A). These data indicate that the β:C12A mutation has little if any effect on GTPase in the microtubule and that dGTP appears to somewhat increase GTPase rates. These GTP contents are higher than expected, and the temporal resolution of the GTPase assay is limited. We therefore used Bim1 (Schwartz et al., 1997), an EB1-family protein that reports on features of the microtubule lattice believed to be related to nucleotide state (Maurer et al., 2012; Zhang et al., 2015), as an alternative readout that permits more instantaneous visualization of the stabilizing cap (Maurer et al., 2014). Wild-type and β:C12A microtubules have Bim1 caps of very similar size and maximal intensity, and Bim1 binds comparably to the noncap lattice of wild-type and mutant microtubules (Figure 7, B and C). The lack of substantial differences in the binding of Bim1 to wild-type and β:C12A microtubules suggests that any differences in the distribution of GTP must be small. These data also argue against a potential allosteric effect of the mutation like the one we recently described for β:T238A αβ-tubulin (Geyer et al., 2015). In contrast, wild-type microtubules growing with dGTP show narrower and less intense Bim1 caps, which suggests that the dGTP is either more rapidly hydrolyzed or perturbs microtubule structure in a way that reduces Bim1 binding. Taken together, the ³²P-GTP and Bim1 experiments argue against an alternative model in which a GTPase defect is responsible for the reduced catastrophe frequency of β:C12A or wild-type (dGTP) microtubules.

FIGURE 7:

Exchangeable GTP content of microtubules probed with ³²P-GTP and with an EB1 protein. (A) Image shows ³²P nucleotide content of wild-type (grown with GTP or dGTP) or β:C12A mutant microtubules (grown with GTP) analyzed by TLC. Data from four independent trials. Wild-type and β:C12A microtubules growing with GTP show comparable ³²P-GTP content; wild-type microtubules growing with dGTP show reduced ³²P-GTP content. (B) Representative images of microtubules growing in the presence of Bim1-GFP. Scale bar, 1 μm. (C) Plots of average Bim1-GFP intensity (n = 10) on microtubules. Wild-type and β:C12A microtubules growing with GTP show very similar Bim1 comets, whereas wild-type microtubules growing with dGTP show a narrower comet.

Terminal GDP exposure–induced slowing of microtubule elongation leads to erosion of the stabilizing cap

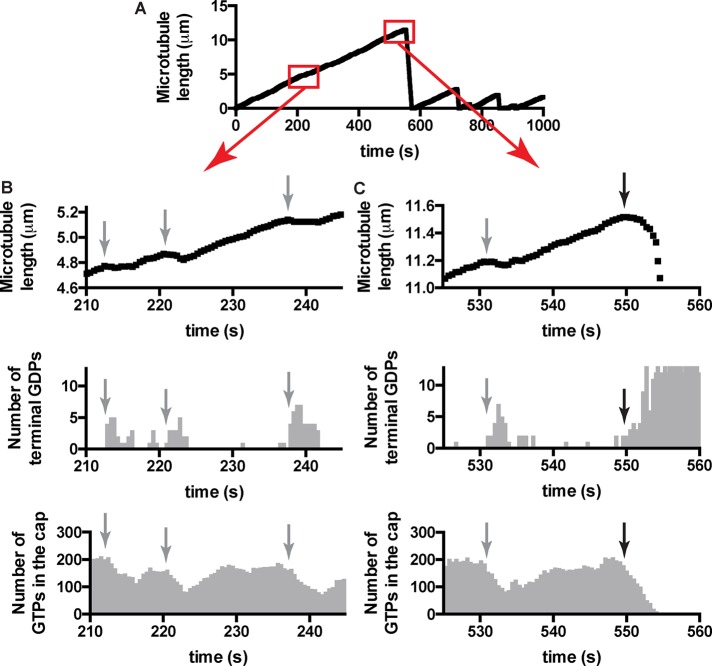
To better understand how terminal GDP exposure could contribute to microtubule catastrophe and elongation rate, we examined simulated growth phases more closely (Figure 8). We extracted the length of the microtubule (as determined by the total number of αβ-tubulin subunits incorporated), the size of the GTP cap (number of incorporated subunits bound to GTP; the remainder are bound to GDP), and the number of GDP-bound subunits exposed on the growing end. A representative plot of simulated microtubule length versus time is shown in Figure 8A; the two boxed regions are shown with higher temporal and spatial resolution in Figure 8, B and C. The simulations show transient pauses (sometimes involving net loss of subunits) in the rate of microtubule elongation (Figure 8, B and C, top; the time at which pauses begin is indicated by gray arrow) that are associated with the exposure of a small number of terminal GDP-bound subunits (Figure 8, B and C, middle). The stabilizing GTP cap—which fluctuates around a steady-state value of ∼200 GTP-bound αβ-tubulins under the conditions of our simulations—erodes as a consequence of the pausing. In our simulations, the pausing and erosion of the GTP cap that are induced by exposure of terminal GDP-bound subunits can sometimes lead to catastrophe (black arrow in Figure 8C) but not always. Indeed, elongating microtubules can “recover” normal elongation rates and GTP caps by eliminating the terminal GDP-bound subunits (Figure 8, B and C). GDP-to-GTP exchange on terminal subunits is one of the biochemical pathways that allow recovery from pausing and its attendant erosion of the GTP cap.

FIGURE 8:

Insights into catastrophe from the model. (A) Length history plot from a simulation using model parameters (from Figure 2B) and 10 μM αβ-tubulin. Boxed regions are shown in greater detail below. (B) Top, transient reductions in the elongation rate (indicated by gray arrows) are apparent when the growth phase is plotted with greater temporal and spatial resolution. Middle, the pausing occurs when GDP-bound subunits are exposed on the microtubule end, consistent with the model advanced in Figure 2. Bottom, when microtubule elongation slows, the GTP cap erodes. Elimination/reduction of GDP-bound subunits on the microtubule end, which can occur through multiple mechanisms, including terminal GDP- to-GTP exchange, restores more normal growth rates, which allow the GTP cap to recover. The GTP cap fluctuates around its steady-state value of ∼190 under these conditions. Faster nucleotide exchange on the microtubule end contributes to increase the likelihood of these “minirescues,” which occur as a consequence of terminal GDP exposure. (C) Top, catastrophes in our simulations are also preceded by a reduction in elongation rate (black arrow marks the onset of the slowdown). This slowing before catastrophe is reminiscent of that seen in a recent study of EB1. Middle, as with the transient pausing, the slowing before catastrophe is associated with the exposure of GDP-bound terminal αβ-tubulin subunits. Bottom, the disappearance of the GTP cap occurs over the course of several seconds. The microtubule can have all terminal subunits bound to GDP before the cap has been completely lost.

DISCUSSION

We began this study using a computational model to investigate the consequences of trans-acting nucleotide for microtubule dynamics. Our simulations with trans-acting nucleotide revealed that GDP-terminated protofilaments were frequently exposed during sustained growth without necessarily causing catastrophe. This apparently contrasts with a common assumption associated with cis-acting GTP—that the exposure of GDP-bound αβ-tubulin “poisons” the protofilament (VanBuren et al., 2005). Our computational simulations further revealed that transient exposure of GDP-bound αβ-tubulins on the microtubule end reduces the rate of elongation and this in turn erodes the GTP cap and increases the likelihood of MT catastrophe. GDP-to-GTP exchange on terminal GDP-bound subunits can modulate the frequency of catastrophe by mitigating the effects of GDP exposure on growing microtubule ends.

Current thinking about catastrophe is dominated by considerations about the size of the microtubule’s stabilizing GTP cap and the release of strain from the resulting GDP lattice (Bowne-Anderson et al., 2013; Maurer et al., 2014). However, the molecular events that cause loss of the cap during otherwise steady-state growth are poorly understood (Gardner et al., 2013; Bowne-Anderson et al., 2015; Brouhard, 2015). GDP-to-GTP exchange on the growing microtubule end represents a simple biochemical mechanism that is spatially segregated from GTP hydrolysis and provides a new way of thinking about how catastrophe might be initiated. That terminal nucleotide exchange could be relevant to catastrophe is not a new idea. Indeed, GDP-to-GTP exchange on the growing microtubule end figured in some of the earliest computational models for microtubule dynamics (Chen and Hill, 1983, 1985). Early in vitro studies also showed that the terminal nucleotide was exchangeable (Mitchison, 1993; Caplow and Shanks, 1995) and that modulating the amount of terminal GDP exposure could alter the frequency of catastrophe (Caplow and Shanks, 1995; Vandecandelaere et al., 1995). Our experiments with mutant αβ-tubulin and deoxy-GTP sought to perturb nucleotide binding without affecting other aspects of αβ-tubulin biochemistry. Those experiments showed that reduced GTP/GDP-binding affinity results in a lower frequency of microtubule catastrophe, providing support for the idea that the rate of GDP-to-GTP exchange on the growing microtubule end contributes to catastrophe. The GDP exposure–induced slowing of elongation and ensuing erosion of the GTP cap that we observed in simulations is reminiscent of a recent study of the end-binding protein EB1 in which microtubule growth was observed to slow down before the EB1-marked stabilizing cap began to shrink (Maurer et al., 2014). We speculate that exposure of terminal GDP-bound subunits contributes to that slowdown.

Our goal was to explore a simple model incorporating a trans-acting nucleotide. A surprising observation from the simulations led to the ideas about terminal GDP exposure and the role of terminal GDP-to-GTP exchange. Terminal nucleotide exchange can occur only at the microtubule plus end, and this end-specific biochemical difference may contribute to the differing dynamic properties of microtubule plus and minus ends. The minimal model that we developed does not capture the concentration or age dependence of microtubule catastrophe (Gardner et al., 2011b, 2013) and also does not attempt to model allosteric/mechanochemical properties that are likely to have important roles in catastrophe (VanBuren et al., 2005; Zanic et al., 2013; Coombes et al., 2013; Geyer et al., 2015; Zakharov et al., 2015). It seems that to successfully recapitulate the full spectrum of catastrophe and place terminal nucleotide exchange into the broader context of allostery and mechanochemistry, future models will need to incorporate aspects from several current models: trans-acting nucleotide, GDP-to-GTP exchange on the microtubule end, multiple conformations and “spring-like” mechanical properties of αβ-tubulin, and perhaps also neighbor-state specific rates of GTP hydrolysis and/or exchange. We expect that progress on this challenging goal will accelerate in light of recently developed methods that enable in vitro work with site-directed αβ-tubulin mutants (des Georges et al., 2008; Johnson et al., 2011; Widlund et al., 2012; Minoura et al., 2013) and because experimental observations of catastrophe are being extended to higher spatial and temporal resolution (Gardner et al., 2011b; Maurer et al., 2014).

MATERIALS AND METHODS

Kinetic modeling

We wrote a computer program to perform kinetic Monte Carlo simulations (Gillespie, 1976) of MT dynamics, implementing an algorithm similar to one described previously (VanBuren et al., 2002). Part of our implementation has been described elsewhere (Ayaz et al., 2014). Briefly, the microtubule lattice is represented by a two-dimensional grid to account for the different kinds of binding sites on the microtubule end and with a staggered periodic boundary condition to mimic the cylindrical microtubule structure (Ayaz et al., 2014). A portion of the lattice is treated as permanently occupied to provide a seed for elongation. The program simulates MT dynamics one biochemical reaction (subunit addition or dissociation, GTP hydrolysis, or GDP-to-GTP exchange) at a time. Our parameterization assumes that the nucleotide (GTP or GDP) acts in-trans to affect the strength of longitudinal contacts such that GTP contacts are stronger than GDP ones (Figure 1A, and see later discussion). This assumption is consistent with recent high-resolution electron microscopy studies of microtubule structure (Alushin et al., 2014; Zhang et al., 2015). With the notable exception of the work of Margolin et al. (2012), prior models assumed cis-acting GTP (Bayley et al., 1989; VanBuren et al., 2002, 2005; Brun et al., 2009; Gardner et al., 2011a; Coombes et al., 2013; Zakharov et al., 2015). The rate of subunit addition into any available site is given by k_on*[αβ-tubulin]. Occupied sites—including GTP-bound terminal subunits—can dissociate at a rate given by k_on*K_D^site, where K_D^site is the affinity of interaction at a particular site, which is determined by the neighbor state (number and type of lattice contacts) and obtained from longitudinal and corner affinities through thermodynamic coupling (Erickson and Pantaloni, 1981; VanBuren et al., 2002). The fitted parameters of 3 mM for the longitudinal affinity and 4 μM for the longitudinal plus lateral affinity indicate that each lateral interface increases affinity by ∼750-fold. GTP hydrolysis is modeled for all nonterminal subunits with rate constant k_GTPase. The weakening effect of GDP on the longitudinal interface is modeled as a multiplicative scaling of the longitudinal contribution—this is equivalent to a loss of favorable free energy of association. Because of the high concentration of GTP in our assays (1 mM), we assume that GDP release is rate limiting for GDP-to-GTP exchange. Accordingly, we model exchange on terminal subunits with rate constant k_exchange. Simulations begin with only 13 possible events (associations onto the end of each protofilament). Execution times for each event are determined by sampling a random number x between 0 and 1 and then calculating the time as −(1/rate) ln(x), where rate gives the appropriate rate constant as described earlier. At each step, the event with the shortest execution time is implemented, the simulation time is advanced accordingly, and the list of possible events and their associated rates is updated to account for changes in subunit neighbor state. To obtain the length (in micrometers) of a simulated microtubule at a given time, we divide the number of subunits by 1625 (one αβ-tubulin is 8 nm in length).

Parameter optimization

To recapitulate experimentally observed, concentration-dependent rates of MT elongation, and as described previously (Ayaz et al., 2014), we performed a manual grid search using “GTP-only” (negligible GTPase rate constant) simulations to obtain longitudinal and corner (longitudinal plus lateral) affinities, initially ignoring GDP-to-GTP exchange on the MT end. With these parameters fixed, we next searched for the “GDP-weakening” factor that would yield the experimentally observed concentration-independent rate of rapid microtubule shrinking. Finally, we searched for a GTPase rate constant that would give the appropriate frequency of catastrophe (Figure 2B). This procedure essentially followed the approach outlined in VanBuren et al. (2002) and yielded similar values for the parameters in common between the two models. For an assumed on-rate constant of 4 × 10⁶ M⁻¹ s⁻¹, we obtained K_longitudinal = 3 mM, K_{longitudinal+lateral} = 4 μM, 50-fold weakening effect of GDP at the longitudinal interface, and k_GTPase = 0.14 s⁻¹.

Protein expression and purification

Plasmids to express wild-type yeast αβ-tubulin have been described previously (Johnson et al., 2011; Ayaz et al., 2012) and were used without further modification. Plasmids encoding the β:C12A and β:C12S mutants were generated by site-directed mutagenesis. The integrity of constructs was confirmed by sequencing.

Wild-type and mutant yeast αβ-tubulin were overexpressed in Saccharomyces cerevisiae (Johnson et al., 2011). All proteins were purified using Ni-affinity and anion exchange chromatography as described previously (Johnson et al., 2011; Ayaz et al., 2012) and dialyzed into storage buffer (10 mM 1,4-piperazinediethanesulfonic acid [PIPES], pH 6.9, 1 mM MgSO₄, 1 mM ethylene glycol tetraacetic acid [EGTA]) containing 50 μM GTP (for polymerization measurements) or 50 μM GDP (for binding assays). Chemicals were obtained from Sigma-Aldrich (St. Louis, MO). Nucleotides were obtained from Jena Bioscience (Jena, Germany).

Binding assays

Wild-type or mutant yeast αβ-tubulin in 50 μM GDP was taken from −80°C, rapidly thawed, and filtered (0.1-μm centrifugal filter; Millipore, Billerica, MA) at 4°C to remove aggregates. To remove free GDP and GDP bound to αβ-tubulin, filtrate was exchanged into binding buffer (10 mM PIPES, 1 mM EGTA, and 1 mM MgSO₄) using a Nick Sephadex G-50 gravity desalting column (GE Healthcare, Piscataway, NJ). A control experiment in which ion exchange chromatography was used to quantify the nucleotide content of thusly treated tubulin showed that this procedure removes ∼90% of the exchangeable nucleotide (unpublished data). The concentration of αβ-tubulin in the filtrate was measured by ultraviolet (UV) absorbance using an extinction coefficient of 106,835 M⁻¹ cm⁻¹ (assuming all of the exchangeable GDP was removed).

To measure the affinity of S⁶-GTP for αβ-tubulin, we prepared 220-μl samples containing either 0.16 μM wild-type or mutant αβ-tubulin in binding buffer with 0.5% Tween-20 and a variable concentration of S⁶-GTP. We used a competition assay to measure the affinity of GDP or dGDP for αβ-tubulin: samples were prepared as described but with 5 μM S⁶-GTP, and variable concentrations of competing nucleotide (GDP or dGDP) were added. All samples were kept in Eppendorf (Hauppauge, NY) Protein LoBind tubes and allowed to equilibrate to room temperature before measurement.

Measurements of fluorescence quenching by S⁶-GTP and unquenching by GDP or dGDP were made in 96-well flat-bottom black polystyrene plates using a Thermo Scientific (Waltham, MA) Varioskan FLASH plate fluorimeter. Samples were loaded at 200 μl (including a blank) per well. Tryptophan fluorescence from αβ-tubulin was excited at 296 nm using a 12-nm slit width. Emission was monitored at 329 nm, with dynamic range set to medium high and a measurement time of 80 ms. Each sample was measured 100 times, and mean fluorescence intensities were calculated. Replicate experiments were repeated multiple times on different days.

Because S⁶-GTP absorbs strongly at tryptophan’s emission peak and both GDP and dGDP absorb at the excitation wavelength, it was necessary to correct our experiments for inner filter effects (Fishback and Yarbrough, 1984). To accomplish this, we measured fluorescence from control samples consisting of ∼50 μg/ml bovine serum albumin (BSA) in the assay buffer and a variable concentration of S⁶-GTP or GDP (GDP and dGDP have the same UV absorbance). The concentration of BSA was chosen to give about the same fluorescence intensity as 0.16 μM αβ-tubulin. Each sample was measured as described, and mean fluorescence and SE values were calculated. An exponential decay function was fitted to the mean fluorescence intensity values of each titration series (S⁶-GTP or GDP) and used to calculate correction factors that were later applied to the raw intensities recorded in quenching and unquenching experiments. For S⁶-GTP quenching experiments, we corrected fluorescence emission data using the expression F_corrected = F_observed × EM_correction([S6-GTP]), where EM_correction denotes the inner filter correction for emission determined at different concentrations of S6-GTP. For GDP or dGDP competition experiments, we corrected fluorescence emission data using the F_corrected = F_observed × EM_correction(5 μM S6-GTP) × EX_correction([GDP]), where EX_correction is the inner filter correction for excitation determined at various concentrations of GDP.

Direct binding measurements were fitted to a single-site saturation binding curve accounting for ligand depletion and weighted by the SEs (GraphPad Prism, version 6; San Diego, CA). Competition binding measurements were fitted to a single-site competition binding model, weighted by standard errors (GraphPad Prism, version 6).

GTPase activity assay

Wild-type or mutant yeast αβ-tubulin in 50 μM GTP was taken from −80ºC, rapidly thawed, and filtered (0.1-μm centrifugal filter; Millipore) at 4ºC to remove aggregates. The concentration of αβ-tubulin in the filtrate was measured by UV absorbance using an extinction coefficient of 115,000 M⁻¹ cm⁻¹ to account for two bound guanine nucleotides. We polymerized 1 μM αβ-tubulin of each species in assembly buffer (100 mM K⋅PIPES, 2 mM MgSO₄, 1 mM EGTA, pH 6.9) containing 1 mM GTP, 66 nM α-³²P-GTP, 2 μM epothilone, and 10% glycerol at 30ºC. After 1 h, the reactions were centrifuged at 128,000 × g and 30ºC for 10 min. The short centrifugation time was chosen to achieve a time resolution that was comparable to the microtubule growth lifetimes in the DIC assays. Pellets were washed rapidly four times with assembly buffer to remove free nucleotide and unpolymerized αβ-tubulin. Pelleted MTs were denatured in 6 M guanidine HCl before being analyzed for nucleotide content by TLC. Nucleotide content was visualized by exposing x-ray film to the TLC plate.

Time-lapse measurements of microtubule dynamics

Flow chambers were prepared as described previously (Gell et al., 2010). Sea urchin axonemes (Waterman-Storer, 2001) were adsorbed directly to treated coverglass before the blocking step to provide seeds for microtubule growth.

For dynamics assays, wild-type or mutant yeast αβ-tubulin in 50 μM GTP was thawed, filtered, and measured for concentration as described. Protein was kept on wet ice for no more than 30 min before use in a MT dynamics assay. MT dynamics reactions were imaged by DIC microscopy (using an Olympus IX81 microscope (Olympus Optical, Tokyo, Japan) with a Plan Apo N 60×/1.42 numerical aperture objective lens and DIC prisms with illumination at 550 nm. Temperature was maintained at 30°C by a WeatherStation temperature controller fitted to the microscope’s body. The microscope was controlled by Micro-Manager 1.4.16 (Edelstein et al., 2010) and images recorded with an ORCA-Flash2.8 complementary metal-oxide semiconductor camera (Hamamatsu, Hamamatsu City, Japan). Images were recorded every 500 ms for 1–2 h. At the end of each movie, a set of out-of-focus background images was taken for background subtraction (see later description). To improve signal to noise, batches of 10 raw images were averaged using ImageJ (Schneider et al., 2012). The averaged images were opened as a stack, and their intensities were normalized to the average image intensity before background subtraction. MT length was measured manually using the PointPicker plug-in for ImageJ. Rates of MT elongation and catastrophe frequencies were determined as described previously (Walker et al., 1988).

Dynamic assays with Bim1–green fluorescent protein

Samples containing either wild-type or β:C12A αβ-tubulin in the presence of 1 mM GTP or 2′dGTP, along with 50 nM Bim1–green fluorescent protein (GFP) in imaging buffer (BRB80, 0.1 mg/ml BSA, 0.1% methylcellulose, and antifade reagents [glucose, glucose oxidase, catalase], without the addition of β-mercaptoethanol; Gell et al., 2010), were introduced into the flow chambers and imaged at 30°C by total internal reflection fluorescence microscopy as described previously (Geyer et al., 2015). Images of MTs were taken every 5 s for 15–20 min. Bim1-GFP fluorescence intensity along microtubules and extending beyond their growing ends was obtained using the PlotProfile function in ImageJ (Schneider et al., 2012). The peak position of Bim1-GFP fluorescence was determined by fitting a Gaussian to the intensity profile, and the line scans were shifted to align the peaks to the nearest pixel. The background intensity (as determined from the fluorescence in the line scan beyond the end of the MT) was subtracted before averaging of the individual profiles.

Abbreviations used:

dGDP

2’-deoxyguanosine 5’-diphosphate

GDP

guanosine 5’-diphosphate

GTP

guanosine 5’-triphosphate

MT

microtubule

S6-GTP

6-thioguanisone 5’-triphosphate

WT

wild type.