Microtubule aging probed by microfluidics-assisted tubulin washout

Microtubule aging—the decrease of stability with age—is an interesting but mechanistically not understood property of microtubules. It constrains possible mechanisms of catastrophe induction and is believed to be crucial for length regulation. New in vitro experiments and model fits provide insight into the origin of microtubule aging.

Abstract

Microtubules switch stochastically between phases of growth and shrinkage. The molecular mechanism responsible for the end of a growth phase, an event called catastrophe, is still not understood. The probability for a catastrophe to occur increases with microtubule age, putting constraints on the possible molecular mechanism of catastrophe induction. Here we used microfluidics-assisted fast tubulin washout experiments to induce microtubule depolymerization in a controlled manner at different times after the start of growth. We found that aging can also be observed in this assay, providing valuable new constraints against which theoretical models of catastrophe induction can be tested. We found that the data can be quantitatively well explained by a simple kinetic threshold model that assumes an age-dependent broadening of the protective cap at the microtubule end as a result of an evolving tapered end structure; this leads to a decrease of the cap density and its stability. This analysis suggests an intuitive picture of the role of morphological changes of the protective cap for the age dependence of microtubule stability.

INTRODUCTION

Microtubules are structurally polar polymers consisting of 13 protofilaments arranged into a tube and are found in all eukaryotic cells. Microtubule plus ends switch between phases of continuous growth and shrinkage (Mitchison and Kirschner, 1984; Horio and Hotani, 1986; Cassimeris et al., 1988). This property, termed dynamic instability, is crucial for microtubule functions in living cells—for example, for exploring intracellular space to capture chromosomes in preparation for cell division or for dynamic cytoskeleton reorganizations, as needed during mitosis and differentiation (Kumar and Wittmann, 2012; Akhmanova and Steinmetz, 2015).

Dynamic instability is a consequence of GTP-tubulin addition to growing microtubule ends followed by GTP hydrolysis; this leads to the establishment of a protective “GTP cap” at the growing microtubule ends preceding the GDP lattice that is prone to depolymerization when unprotected. Loss of the GTP cap or parts of it or other GTP hydrolysis-dependent processes are believed to induce the transition from growth to shrinkage, called a catastrophe (Carlier, 1991; Desai and Mitchison, 1997; Howard and Hyman, 2009). However, the exact condition leading to catastrophe is still under debate.

An interesting feature of catastrophes, as revealed by in vitro experiments with purified tubulin, is that the likelihood of catastrophe increases with the growth duration of individual microtubules, that is, with microtubule age (Odde et al., 1995; Gardner et al., 2011b; Mohan et al., 2013). This leads to a microtubule lifetime distribution with a distinct maximum, in contrast to a continuously decaying monoexponential distribution as expected for a simple one-step process with a constant, age-independent catastrophe probability (Odde et al., 1995). Microtubule aging has attracted attention because this property has been suggested to allow cells to keep microtubule length in a “useful” range (Gardner et al., 2011b). Furthermore, the phenomenon of microtubule aging strongly constrains catastrophe models.

A large variety of theoretical models of microtubule dynamic instability have been proposed considering various degrees of detail (for a historical overview, see Bowne-Anderson et al., 2013). The range extends from simple phenomenological kinetic models (for recent examples, see Brun et al., 2009; Bowne-Anderson et al., 2013; Duellberg et al., 2016) to elaborate microscopic models that consider the energetics of individual tubulin–tubulin interactions in the three-dimensional lattice of a microtubule (for recent examples, see Margolin et al., 2012; Coombes et al., 2013; Zakharov et al., 2015). Whereas simpler models assume some specific element as a catastrophe criterion, catastrophe is an emergent property of microscopic models. Roughly two classes of recent kinetic models can be distinguished that have been proposed to explain the mechanism underlying microtubule aging at steady state. In the first class of models, induction of catastrophe is assumed to be a consequence of a kinetic multiple-step process, with each step having a constant probability. Either individual kinetic steps are assumed to lead to short-lived states characterized, for example, by the transient presence of GDP tubulins at microtubule ends, requiring the additional condition of local and temporal coincidence of such states (Brun et al., 2009), or the kinetic steps are assumed to lead to long-lived states, for example, permanently end-exposed GDP tubulin blocking further elongation of a protofilament, previously also called “defects.” Such long-lived states introduce an element of “memory,” and catastrophe induction has been proposed to require the additional condition of accumulation of a distinct number of such defects (Gardner et al., 2011b; Bowne-Anderson et al., 2013, 2015). A conceptually quite different, microscopic model proposed a different mechanism for aging: it predicts an increasingly tapered microtubule end structure with microtubule age, which leads to a decrease in microtubule stability over time (Coombes et al., 2013). A change of the microtubule end structure with time had been observed experimentally by electron microscopy of growing microtubule ends; these experiments show a sheet-like or rugged appearance, often called a taper, indicating that not all protofilaments have the same lengths (Mandelkow et al., 1991; Chretien et al., 1995; Coombes et al., 2013). It is unclear which of these quite different proposed mechanisms is responsible for microtubule aging, mostly because the postulated conditions inducing catastrophe cannot be directly observed experimentally before catastrophe actually occurs.

We recently demonstrated that fast tubulin washout experiments can provide valuable additional information about the condition leading to catastrophe (Duellberg et al., 2016). We used a microfluidics-assisted in vitro assay to measure how microtubule stability depends on microtubule growth speed. In these experiments, sudden tubulin removal instantaneously caused microtubule growth to stop, followed by a delay of several seconds before microtubules underwent catastrophe, as observed earlier (Walker et al., 1991). We observed that this delay time, a measure of microtubule stability at the moment of tubulin removal, tended to increase with the instantaneous microtubule growth speed at tubulin removal. This stability increase correlated with an increasing size of the binding region of end binding 1 (EB1) proteins, supporting the notion that these proteins recognize the protective cap in the microtubule end region. The delay times and their dependence on the microtubule growth speed could be explained by considering that the protective cap was gradually lost after tubulin washout by 1) microtubule maturation (i.e., GTP hydrolysis/phosphate release) and 2) slow microtubule shrinkage between tubulin washout and catastrophe. A simple kinetic threshold model suggested that a minimal density of cap sites in the highest-density region of the protective cap—that is, close to the microtubule end—was required to keep the microtubule stable; this defined the condition for catastrophe induction in tubulin washout experiments (Duellberg et al., 2016).

In our previous study, however, the question remained unexplored of whether microtubule aging can also be observed in tubulin washout experiments. Aging probed by tubulin washout might provide additional information, allowing us to decide which of the current ideas best describes the mechanism responsible for microtubule aging.

Here we performed microfluidics-assisted fast tubulin washout experiments at different microtubule growth times to test whether aging affects the momentary microtubule stability in this assay. We measured delay times under conditions of different overall microtubule stability. We found that aging indeed reduces the momentary microtubule stability after sudden tubulin removal. This reduction of stability with age was observed robustly at all conditions tested. Multistep catastrophe models in their current form fail to explain the measured delay times between tubulin washout and catastrophe; however, the delay times are well explained by a kinetic threshold model that considers an age-dependent change of the shape of the protective cap induced by a tapered end structure elongating with microtubule growth time.

RESULTS

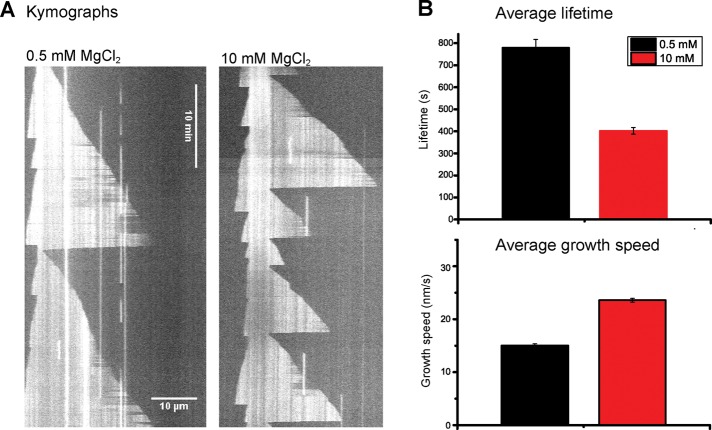
To explore microtubule stability under different conditions, we used the magnesium ion concentration as a control parameter for setting different stability levels because it is well established that it affects microtubule dynamic instability parameters (Heusele et al., 1987; Schilstra et al., 1991). As controls, we first performed experiments in simple flow chambers with dynamic microtubules growing in the presence of 10 μM purified Alexa 568–tubulin from surface-immobilized, guanylyl 5′-α,β-methylene­diphosphonate (GMPCPP)-stabilized microtubule seeds (Bieling et al., 2007). Movies were acquired using total internal reflection fluorescence (TIRF) microscopy (example kymographs are shown in Figure 1A). We observed that the mean lifetime of microtubules decreased from 779 to 402 s when the magnesium concentration was increased from 0.5 to 10 mM (Figure 1B, top). At the same time, the growth speed increased from 15.0 to 23.6 nm/s (Figure 1B, bottom). This agrees with trends reported previously (Heusele et al., 1987; O’Brien et al., 1990; Schilstra et al., 1991). For both magnesium concentrations, we observed nonmonoexponential lifetime distributions (Supplemental Figure S1A), as reported for other in vitro conditions (Odde et al., 1995; Gardner et al., 2011b; Mohan et al., 2013), indicative of aging at steady-state conditions.

FIGURE 1:

Magnesium ions destabilize dynamic microtubule plus ends. (A) Representative TIRF microscopy kymographs of microtubule growth at 10 μM Alexa 568–tubulin under steady-state conditions in the presence of 0.5 (left) or 10 mM (right) MgCl₂. Microtubule plus ends point toward the right. (B) Average lifetime of growth episodes (top; n > 228) and average growth speed (bottom, n > 148) of microtubule plus ends. Error bars are SEM.

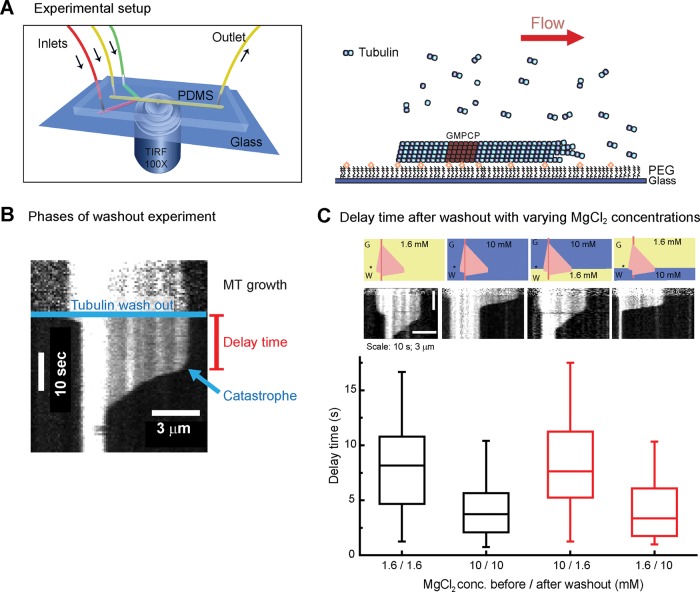
Next we performed microfluidics-assisted sudden tubulin washout experiments, as described recently (Duellberg et al., 2016), at different magnesium concentrations (Figure 2A). Microtubules grow first in the presence of 20 μM purified Alexa 568–tubulin, followed by rapid buffer exchange 160 s after the start of tubulin growth, removing the tubulin and keeping all other concentrations constant (Materials and Methods). Microtubules immediately stopped growing at the moment of washout and underwent catastrophe with a delay of typically several seconds after tubulin removal (Figure 2B and Supplemental Figure S2; Walker et al., 1991). The average delay time was halved from ∼8 to 4 s when the magnesium concentration was increased from 1.6 to 10 mM (Figure 2C, two left columns), confirming a trend observed previously (Duellberg et al., 2016). We also noted that the rapid depolymerization of the microtubules after catastrophe was faster at higher magnesium concentration (Supplemental Figure S3), as reported for microtubules undergoing catastrophes at steady state (O’Brien et al., 1990). Taken together, these data demonstrate that increased magnesium concentrations make microtubules more dynamic but overall less stable, as shown by their reduced steady-state lifetimes, as well as by their reduced delay times after tubulin washout.

FIGURE 2:

Tubulin washout assay. (A) Microfluidics-assisted tubulin washout setup (left). Microtubules grow from surface-immobilized, GMPCPP-stabilized seeds under constant flow; changing solution allows fast tubulin removal (right). (B) Representative kymograph of a tubulin washout experiment. The microtubule elongates in the presence of 20 μM tubulin (MT growth) until tubulin is washed out (blue line). A delay time of several seconds (red) is observed until catastrophe occurs, followed by fast depolymerization. For clarity, background subtraction was applied using ImageJ (National Institutes of Health, Bethesda, MD). For the definition of the catastrophe criterion, see Supplemental Figure S2. (C) Average delay times of microtubule plus ends after tubulin washout in the presence of varying magnesium concentrations as indicated. Top, schematic drawings with the idealized kymographs illustrating the sequence of magnesium concentrations used; asterisk indicates time of washout. Tubulin washout was performed at 160 s after the start of growth. Middle, representative kymographs for each condition. Bottom, box plot showing the measured average delay times. Tubulin washout was performed in the constant presence of 1.6 (first column) or 10 mM (second column) MgCl₂ or the MgCl₂ concentration was changed at tubulin washout as indicated (third and fourth columns). n > 51 per condition.

In tubulin washout experiments, microtubule stability can in principle be influenced by events before and after washout—in other words by both growth history and subsequent response to tubulin removal, eventually leading to loss of stability. To test directly the relative importance of the kinetic process during these two phases before catastrophe, we suddenly changed the magnesium concentration at the same time as we removed the tubulin. We observed that the microtubule stability responded quickly to the change in magnesium concentration and that the buffer after tubulin washout had a strong effect on the observed delay times (Figure 2C, two right columns). This can be explained in terms of the higher magnesium concentrations previously observed to accelerate tubulin dissociations from microtubule ends after tubulin removal and to increase the critical cap density required for stability (Duellberg et al., 2016). Therefore the question arises of whether microtubule aging, which depends on events before tubulin removal, is detectable at all in tubulin washout experiments.

To test this directly, we allowed microtubules to grow for different times before tubulin was removed. We chose two time points for tubulin washout, 35 and 160 s, which were mostly determined by technical reasons. At 35 s, microtubules are still “young” but already long enough for reliable catastrophe detection, which requires the measurement of an extended episode of fast depolymerization. At 160 s, microtubules are ∼4.5 times “older,” and the growth trajectories can still be conveniently quantified (at much later times, microtubules increasingly grow out of the field of view, terminating their measurable trajectory). We measured the corresponding delay times for these washout time pairs for 1.6, 4, and 10 mM MgCl₂, always keeping the buffer composition unchanged at the moment of tubulin washout. We observed that at all three magnesium concentrations, the microtubule stability was significantly reduced when tubulin was removed at the later growth time (Figure 3). This demonstrates that the effect of microtubule aging, although comparatively small, can be robustly measured in tubulin washout experiments under conditions of different overall stability (set by the magnesium concentration). This challenges multistep models of aging that do not have an element of memory (Brun et al., 2009), which are expected to predict that delay times are independent of the time of tubulin washout.

FIGURE 3:

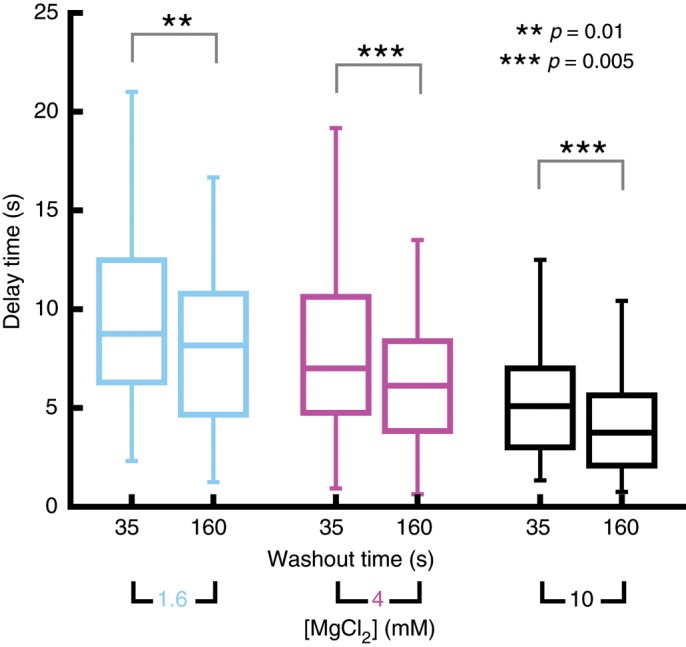
Microtubule age–dependent delay times after tubulin washout. Box plots showing the means and distribution characteristics of delay times measured for two tubulin washout times (35 and 160 s) and three MgCl₂ concentrations (1.6, 4, and 10 mM) as indicated. Tubulin concentration was 20 μM. Significance levels for the differences between mean values are denoted by asterisks. n > 67 per condition. The 160-s data sets for 1.6 and 10 mM MgCl₂ are identical to data presented in Figure 2C in the two left columns of the bar graph.

Both defect accumulation and an elongating tapered microtubule end structure can qualitatively explain microtubule aging in washout experiments (Bowne-Anderson et al., 2013; Coombes et al., 2013). To be able to distinguish between these two models, we quantitatively compared theoretical predictions to our experimental data.

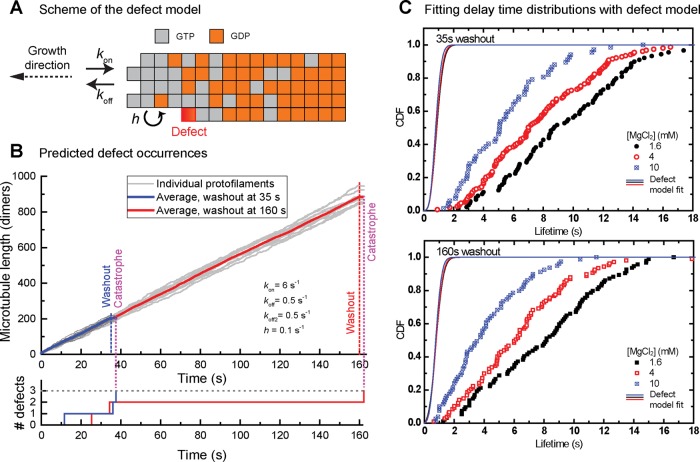
In the multistep defect model, a defect corresponds to an end-exposed GDP-tubulin. This defect occurs when GTP in the penultimate tubulin is hydrolyzed to GDP and subsequently the terminal GTP tubulin is lost by dissociation. Such defects are assumed to be permanent. Steady-state lifetime distributions were well explained assuming that three defects induce catastrophe, defining the catastrophe criterion in this model. We extended the existing model (Bowne-Anderson et al., 2013) by calculating the expression for the delay time distributions after tubulin washout: assuming that the condition for catastrophe is unaffected by tubulin removal, we considered that defects can first accumulate before washout and then with accelerated kinetics also after washout (see Materials and Methods and Figure 4). The obtained analytical expression describing the delay time distribution depends on the four parameters of the steady-state model: the number of defects causing catastrophe to occur, the tubulin association and dissociation rates during growth, and the GTP hydrolysis rate. It also contains the tubulin washout time and the dissociation rate after washout, which we allow to be different from that before washout (Figure 4, A and B, and Supplemental Table S1). Using this expression, we made a global fit to all six measured delay time distributions, assuming that the accumulation of three defects triggers catastrophe, as previously proposed (Gardner et al., 2011b; Bowne-Anderson et al., 2013). The initial tubulin association and dissociation rates were constrained by the measured growth speeds and the postwashout dissociation rates by the previously measured shrinkage speed after washout (Duellberg et al., 2016). The GTP hydrolysis rate was first assumed to be identical to the microtubule maturation rate (Maurer et al., 2014), which we measured in independent experiments by comet analysis of Mal3–green fluorescent protein (GFP) added at low concentrations to growing microtubules (summarized in Supplemental Table S1).

FIGURE 4:

The multistep defect model fails to explain the age-dependent delay times after tubulin washout. (A) Schematic of the multistep defect model, illustrating the kinetic steps (with association rate k_on, dissociation rate k_off, and hydrolysis rate h) and the nucleotide states that tubulin subunits (gray boxes for GTP, orange for GDP) can adopt. Permanent defects occur when the exposed terminal dimer of a protofilament is in a GDP state (red). For details, see Bowne-Anderson et al. (2013) and Material and Methods. (B) Kinetics of defect occurrence. Top, average length of a simulated microtubule with washout at 35 (dashed blue) and 160 s (solid red). Light gray curves show the 13 individual protofilaments in each microtubule. Simulated growth parameters are shown. Bottom, accumulation of defects with time for two example simulations. In this model, a catastrophe occurs after a set number of defects (here three) have accumulated. (C) Cumulative distributions of measured delay times after tubulin washout for the three different MgCl₂ concentration data sets (colored symbols), with a washout time of 35 (top) and 160 s (bottom). Same data as in Figure 3. Solid lines are fits to the data using the theoretical CDF for the multistep defect model (Materials and Methods). Fitting parameters are given in Supplemental Table S1.

Under these constraints, the model failed to explain the data, predicting delay times that were an order of magnitude too short (Figure 4C). When we allowed the fitting to increase the hydrolysis above the maturation rate (to allow for the possibility that maturation might correspond to phosphate release and not GTP hydrolysis; Maurer et al., 2011; Zhang et al., 2015), the poor fit remained unchanged, keeping the hydrolysis rate equal to the maturation rate (Supplemental Table S1). When we removed the constraint on the GTP hydrolysis rate entirely, the model predicted delay times in a reasonable range; however, this required the hydrolysis rate to be in the range of 10⁻³ s⁻¹ (Supplemental Table S2), two orders of magnitude slower than the measured maturation rate. This slow hydrolysis rate would be equivalent to GTP caps with lengths of ∼20 μm, that is, longer than the typical length of microtubules in vitro (∼10 μm for the conditions in Figure 1) and in living cells (Yu and Baas, 1994; Srayko et al., 2006). Changing the defect number criterion for catastrophe from three also did not explain the data (Supplemental Table S1). Therefore we conclude that the defect model in its current form fails to explain the delay times as measured after tubulin washout.

Recent simulations based on a different model suggested that microtubule aging at steady state could be explained as a consequence of an increase in microtubule end taper length with microtubule growth time (Coombes et al., 2013). This model accounted for different nucleotide state–dependent interaction energies of the different tubulin–tubulin binding interfaces in a microtubule, resulting in tubulin binding/unbinding kinetics depending on the ruggedness of the microtubule end structure. Catastrophe occurred as an emergent property of the model when the overall microtubule end stability became too low.

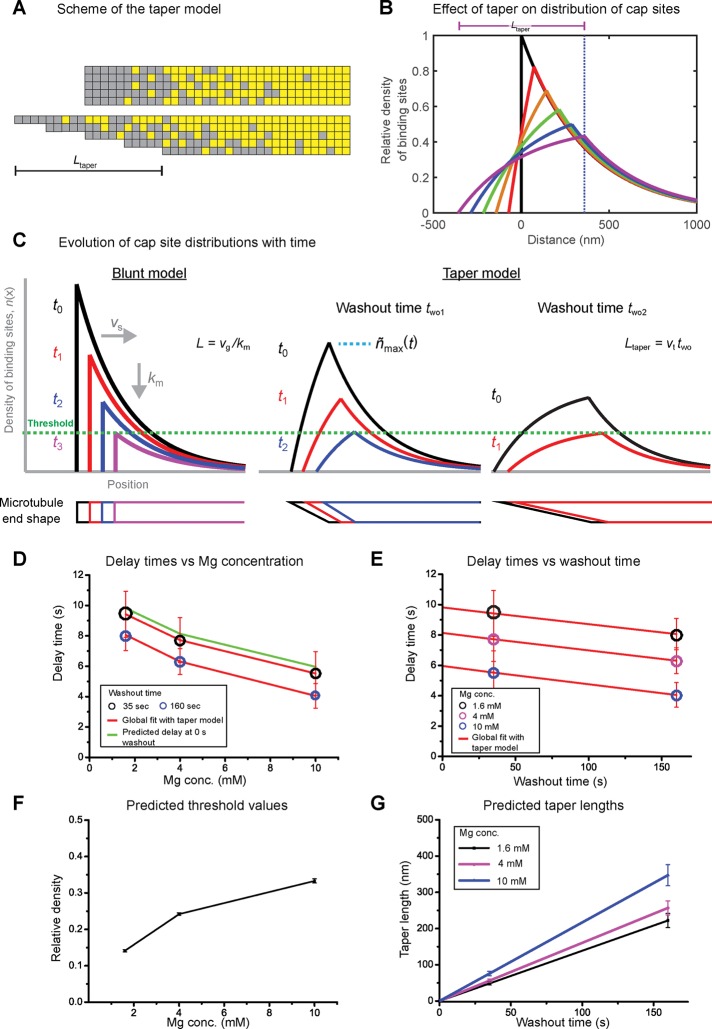
Here we consider the consequence of such taper elongation with time in a more phenomenological model and propose that it affects the shape of the protective cap. In a previous kinetic threshold model (Duellberg et al., 2016), we approximated this shape by a monoexponential distribution of cap sites, in agreement with the observed comet-like shape of the EB-binding region (Bieling et al., 2007; Dixit et al., 2009; Seetapun et al., 2012; Bechstedt et al., 2014; Ettinger et al., 2016) and random hydrolysis GTP cap models (Mitchison and Kirschner, 1984; Carlier, 1991). The cap length is given by the growth rate of the microtubule and its maturation rate (Bieling et al., 2007). After tubulin washout, protective cap sites are then lost as a consequence of continued microtubule maturation and slow depolymerization (shrinkage), and catastrophe occurs when a critical density is reached (Duellberg et al., 2016). In the previous model, the density of the decaying cap is always highest at the very end of the nontapered (blunt) microtubule. To account for aging effects, we now assume in addition that the protective cap changes shape during microtubule growth as a consequence of a growing taper structure, broadening the region of starting positions of the cap (Figure 5, A and B). This causes a deformation of the monoexponential cap site distribution, continuously reducing the maximum steady-state density with time of microtubule growth as the taper length increases (Figure 5B). This means that after tubulin washout, the time it takes to reach the critical maximum density that triggers catastrophe decreases with microtubule age (Figure 5C and Supplemental Figure S5, A and B). For simplicity, we assume that the taper length increases linearly with growth time of the microtubule (Materials and Methods), as suggested by electron microscopy observations (Coombes et al., 2013). The assumption of a different taper shape had a negligible effect on our model (Supplemental Figure S5, C and D).

FIGURE 5:

The taper-cap density threshold model explains age-dependent delay times. (A) Schematic of a blunt (top) and tapered (bottom) microtubule end with taper length L_taper. Each microtubule is composed of 13 protofilaments, with the squares representing EB1 binding (gray) or nonbinding (yellow) states for each tubulin dimer. (B) Spatial profile of the density of binding sites at the end of a microtubule with increasing length of linear taper. For a blunt end (black line) the binding sites are distributed approximately exponentially along the microtubule. This distribution is smeared out with increasing taper length (colored lines). (C) Schematic showing the spatial profile of the density of binding sites at the end of a microtubule with increasing times after washout, t, for our previous (blunt end) model (left) and the current taper-cap density model (right) at two different washout times, t_wo. Corresponding time points after washout are shown by the same colored curves. The bottom row of shapes indicates the microtubule end profile. After washout, the microtubule end shrinks at a speed v_s, while binding sites continue to mature at a rate k_m. Later tubulin washout, t_wo2, corresponds to a longer taper length, as the taper is assumed to elongate while microtubules grow. The longer the taper is at washout, the faster the critical threshold density is reached that triggers catastrophe (green dashed line); therefore older microtubules show shorter delay times. For details, see Materials and Methods. (D, E) Global fit using the taper-cap density threshold model (red lines) to the measured delay times (colored circles) for the two tubulin washout times and the three MgCl₂ concentrations, plotted as a function of magnesium concentration (D) and tubulin washout time (E). Same data as in Figure 3. The diameter of the circles indicates the measured SE; the error of the predicted delay times (red error bars) has been determined by error propagation (see Materials and Methods). The green line in D indicates the predicted hypothetical delay times for microtubules at the washout time of 0 s (no taper), representing their theoretical maximum stability. (F, G) Predicted parameter values. The model had four free fit parameters: one threshold density (at which catastrophe is induced) per data set as defined by the magnesium concentration (F); one proportionality factor linking the taper growth speed to the microtubule growth speed, which is shared for all conditions and allows the prediction of the mean taper lengths at the moment of washout (G). Error bars are fit errors (F) or were obtained from error propagation (G). Fitting parameters are given in Supplemental Table S2.

This “taper-cap density” threshold model is essentially mathematically identical to the previous threshold model, with the difference that the cap density threshold is replaced by the product of the threshold and an age-dependent factor that captures the effect of taper elongation on the shape of the protective cap (Materials and Methods). As in the earlier version of the model (Duellberg et al., 2016), the delay times also depend on the microtubule growth speed before tubulin washout, the slow shrinkage speed between washout and catastrophe, and the microtubule maturation rate.

We used this modified model to perform a global fit to the six mean delay times measured at the different washout times and different magnesium concentrations (Figure 5, D and E). All kinetic rates were fixed to experimentally determined values (Materials and Methods and Supplemental Table S2). For simplicity and to reduce the number of free parameters, we assumed in addition that all taper growth speeds were proportional to the microtubule growth speeds. This left us as free fit parameters with one density threshold value for each magnesium concentration and a single proportionality factor linking microtubule and taper growth speeds. We found that this model well explained the aging data at the three magnesium ion concentrations (Figure 5, D and E). The global fit predicts first that increasing the magnesium concentration from 1.6 to 10 mM increases the maximum cap density threshold from ∼15% to ∼30%, that is, lowered the microtubule stability, consistent with a previous observation (Figure 5F in Duellberg et al., 2016). Second, it provided estimates for taper growth velocities and consequently the taper lengths at tubulin washout (Figure 5G). Despite the simplicity of the model, the predicted taper lengths of <100 nm at 35 s of growth and in the range of several hundred nanometers at 160 s of growth are well within the range of reported lengths determined by electron microscopy (Chretien et al., 1995; Austin et al., 2005; Zovko et al., 2008; Coombes et al., 2013) and simulations (Gardner et al., 2011a; Castle and Odde, 2013; see Discussion).

In summary, these results show that a broadening protective cap as a consequence of taper elongation, combined with a stability threshold defined by a critical maximum cap density, can account for the microtubule age dependence of momentary microtubule stabilities as measured after tubulin washout.

DISCUSSION

We showed here for the first time that microtubule stability probed by sudden tubulin removal decreases with microtubule age (Figure 3). Age-dependent processes that take place before tubulin washout can reliably be detected, although the measured delay times in the assay used here are strongly affected by kinetic processes taking place after washout (Figure 2). The measured age-dependent delay times provide novel constraints for models of age-dependent microtubule stability. Models in which catastrophe is not (or not strongly) expected to depend on growth history (Brun et al., 2009; Zakharov et al., 2015) are challenged by the observation of age-dependent delay times in tubulin washout experiments, although they successfully explain steady-state data.

We focused here mostly on testing two other prominent ideas that can explain microtubule age-dependent catastrophes at steady state and could, in principle, also explain delay times after tubulin washout: one model is based on a multistep process that leads to catastrophe (Gardner et al., 2011b; Bowne-Anderson et al., 2013), and the other assumes a gradual structural change at growing microtubule ends effectively causing a continuously increasing catastrophe probability over time (Coombes et al., 2013). We find that the current form of the multistep defect accumulation model fails to explain the observed age-dependent delay times after tubulin washout under the constraints of the experimental data. In contrast, a kinetic model assuming that an increasingly tapered end structure reduces the maximum density of the protective microtubule cap and that microtubule stability requires a distinct critical density of cap sites can quantitatively account for the measured delay times.

The multistep defect accumulation model was previously proposed to correctly predict delay times after tubulin washout, on the basis, however, of the assumption that microtubule slow depolymerization (shrinkage) between tubulin washout and catastrophe is much slower than recently measured (Duellberg et al., 2016). When measured constraints are used for this shrinkage rate and the GTP hydrolysis rate, the model fails because it either predicts delay times that are an order of magnitude too short or, when the constraint on the hydrolysis rate is relaxed, it predicts a very slow hydrolysis rate that would be very different from the value of the steady-state model (Bowne-Anderson et al., 2013) and would mean that the length of the protective cap is longer than typical microtubules in cells (Yu and Baas, 1994; Srayko et al., 2006; Figure 4).

Several other observations might also argue against catastrophe-inducing defects as the main mechanism for catastrophe induction. Defects have been postulated to correspond to the irreversible loss of a protofilament during growth as a consequence of a permanently exposed GDP-tubulin (Bowne-Anderson et al., 2013). However, it has been shown that free tubulin can incorporate into lateral cracks in a GDP microtubule lattice that were induced by mechanical strain (Schaedel et al., 2015). This argues against the idea that GTP tubulin cannot bind to exposed GDP-tubulins. Furthermore, the observation that GDP tubulin incorporations at growing microtubule ends do not necessarily lead to microtubule catastrophe (Valiron et al., 2010), suggests that growth can continue despite temporarily end-exposed GDP-tubulins. Finally, protofilament number switches are observed both toward lower and higher protofilament numbers by electron microscopy (Chretien et al., 1992), arguing also against an obligatory irreversible loss of protofilaments over time. Alternatively, the catastrophe-promoting feature in the multistep defect model has been hypothesized to be a structural dislocation of a protofilament relative to its neighbors, which might be retained as the microtubule grows (Gardner et al., 2011b). However, such dislocations, similar to other proposed destabilizing structural events, such as cracks within the GTP cap (Flyvbjerg et al., 1996), have not been directly observed in the context of catastrophes.

Tapered or sheet-like microtubule end structures, however, have been directly and repeatedly observed by electron microscopy in vitro with purified proteins (Mandelkow et al., 1991; Chretien et al., 1995; Coombes et al., 2013), Xenopus egg extract (Arnal et al., 2000), mammalian cells (Zovko et al., 2008), and plant cells (Austin et al., 2005). In in vitro experiments, microtubule age was shown to correlate with both microtubule end taper length and the probability of catastrophe induction, making it a plausible mechanism for microtubule aging (Coombes et al., 2013).

An increasing taper length corresponds to a shift of protofilament ends relative to each other. Therefore a tapered end structure is expected to effectively smear out the distribution of the protective GTP (and/or GDP+Pi) cap sites, thereby reducing the density of protective sites at steady state (Figure 5). Consistent with the idea of an increasing taper length being responsible for aging, the maximum density of EB sites, corresponding to the protective cap (Maurer et al., 2012, 2014; Duellberg et al., 2016), has been observed to decrease over time (Coombes et al., 2013; Mohan et al., 2013).

We added the consideration of the effect of a growing taper length on the shape of the protective cap to our recent maximum density threshold model developed to explain delay times in tubulin washout experiments. This modified threshold model with a single additional factor capturing age (see Materials and Methods) can quantitatively explain the age dependence of the measured delay times after tubulin washout. The model predicts that the maximum density threshold leading to catastrophe is reached earlier by older microtubules because they already show an age-dependent reduction of the maximum protective cap density at the moment of tubulin washout. In comparison to the previous version of the threshold model, which did not consider aging (Duellberg et al., 2016), the taper-cap density model predicts ∼30% lower threshold values (for washout times of ∼100 s). This means thresholds of 1.8–4.3 tubulins per ring of tubulins (corresponding to cap densities of 0.14–0.33; Supplemental Table S2) instead of 2.4–5.6 tubulins per ring if no aging is considered for the range of magnesium concentrations studied here.

The critical cap density in our kinetic model provides an intuitive coarse-grained picture for the condition of catastrophe that is an emergent property of more microscopic models. The two types of model do not necessarily need to be considered as mutually exclusive. We note that the existing microscopic model predicting taper length growth with time and aging under steady state has not yet been tested against data sets reporting aging as measured by tubulin washout.

Of interest, our simple kinetic model makes quantitative predictions for the range of taper lengths at the moment of tubulin washout that can be compared with previous electron microscopy observations. Mean taper lengths in the range of 200 and 300 nm were observed for microtubules growing at 1 mM MgCl₂ in the presence of 13 and 19.5 μM tubulin, respectively (see Table IV in Chretien et al., 1995), very similar to the values predicted by our analysis for tubulin washout at 160 s and 1.6 mM MgCl₂ (Figure 5G). A later study determined the dependence of the taper length on the microtubule length (see Figure 3B in Coombes et al., 2013), which, together with the measured microtubule growth speed of 7 nm/s in that study, gives an estimate of taper growth speed of 0.3 nm/s or a proportionality factor of 0.04, which compares well to the predicted factor of 0.047 predicted by our analysis (Supplemental Table S2).

Although some previous simulations and experimental data (Coombes et al., 2013) suggest a linear increase of the taper length with growth time, as also assumed for simplicity in our simple kinetic model here, other simulations and experimental data seem to suggest that the taper growth speed might slow down after some time or reach a steady-state length (Chretien et al., 1995; Zakharov et al., 2015). The dependence of taper length and growth time might also vary among experimental conditions (Mandelkow et al., 1991; Chretien et al., 1995; Vitre et al., 2008; Coombes et al., 2013). Although it is likely that taking a more complex taper growth behavior into account will change the detailed values of the predicted density thresholds and taper growth speeds to some extent, the range of the predicted values may be only little affected as long as the density distribution of the protective cap changes on a similar time scale as assumed here.

Taken together, the analysis of our data supports the idea of tapering being a main source for microtubule aging, consistent with other data (Odde et al., 1995; Kerssemakers et al., 2006; Schek et al., 2007; Gardner et al., 2011a; Coombes et al., 2013; Duellberg et al., 2016). The next challenge will be to measure directly how the taper length evolves in real time at individual growing microtubule ends; this is not convincingly achievable with current fluorescence microscopy techniques essentially because the predicted taper lengths are in the range of the size of the microscope’s point spread function (Maurer et al., 2014; Bohner et al., 2015), and superresolution methods are extremely challenging for moving objects such as a growing microtubule end. Further technological developments will be needed to allow precise real-time observations of the microtubule end taper. Together with real-time observations of the shape of the protective cap and its fluctuations, they should provide important additional experimental information for further refinement of quantitative models that can comprehensively explain the underlying nature of catastrophe induction not only after tubulin washout, but also at steady state.

MATERIALS AND METHODS

Proteins

Tubulin was purified from porcine brain as described (Castoldi and Popov, 2003). Tubulin was labeled with NHS-biotin (Thermo Fisher, Waltham, MA) or NHS–Alexa 568 (Life Technologies, Waltham, MA) using standard procedures (Hyman et al., 1991). Mal3-GFP was expressed in Escherichia coli BL21 RIL and purified as described (Maurer et al., 2011).

Measurement of microtubule lifetimes at steady state

To measure how microtubule lifetimes depend on the magnesium concentration at steady state, we performed TIRF microscopy experiments in simple flow chambers, as described earlier (Bieling et al., 2010; Gardner et al., 2011b), in the presence of 10 μM Alexa 568–tubulin (12.5% labeled), 0.5 or 10 mM MgCl₂, and otherwise the same concentrations as used for microfluidics experiments (see later description). Microtubule lifetimes were determined from kymographs as the times from start of growth (or occasionally rescue) until catastrophe. Experiments were performed at 30°C. Frame rate was 0.25 Hz, and other imaging conditions were as described for washout experiments (see later description). Data are averages from at least three experiments.

Microfluidics-assisted tubulin washout experiments

Microfluidics-assisted tubulin washout experiments were performed essentially as described previously, using TIRF microscopy (Duellberg et al., 2016). In brief, microtubules were grown from immobilized biotin-labeled GMPCPP seeds in a microfluidics chamber at 20 μM Alexa 568–tubulin (12.5% labeled). The final solution during growth was 80 mM K–1,4-piperazinediethanesulfonic acid, pH 6.85 (Sigma-Aldrich, Dorset, UK), 90 mM KCl (Fisher, Leicestershire, UK), 1 mM ethylene glycol tetraacetic acid (Sigma-Aldrich), 1.6, 4, or 10 mM MgCl₂ (Fisher) as stated in the text, 5 mM 2-mercaptoethanol (Sigma-Aldrich), 50 μg/ml β-casein (Sigma-Aldrich), 2 mM GTP (Fermentas, Waltham, MA), 0.1% methylcellulose (Sigma-Aldrich), 20 mM glucose (Fisher), 1 mg/ml glucose oxidase (Serva, Heidelberg, Germany), and 0.5 mg/ml catalase (Sigma-Aldrich). Microtubules were grown for 35 or 160 s as indicated under constant flow of 15 μl/min until tubulin was suddenly removed by solution exchange, keeping all other concentrations constant (Figures 3–5). Only microtubules that were aligned with the direction of the flow were analyzed. Small deviations from that alignment do not alter microtubule stability, as previously demonstrated (see Figure 1–figure supplement 2, in Duellberg et al., 2016). In two experiments, we also changed the magnesium concentration at washout (Figure 2C). Experiments were performed at 30°C. Presented data for each condition are averaged from at least four washout experiments performed on different days. Microtubule growth was observed by TIRF microscopy at 2 Hz with an exposure time of 100 ms per image.

Kymograph analysis

To increase throughput compared with a previous study (Duellberg et al., 2016), we used higher microtubule densities on the surface. This meant that automated microtubule end tracking as used before (Duellberg et al., 2016) was not possible because microtubule “crossing” caused our tracking program to lose track (Maurer et al., 2014). Therefore growth speeds before tubulin washout, the tubulin washout times, and the catastrophe times were determined from kymographs. The washout time was manually detected based on the strong decrease of background intensity (Supplemental Figure S2). The catastrophe time was defined as the time when the microtubule had been in a fast shrinkage phase for a distance corresponding to 3 pixels (360 nm) relative to its position at the time point of tubulin washout. We verified that this catastrophe criterion led to very similar delay times as the previously used criterion of a 25% shrinkage-speed change, which requires automated end tracking (Supplemental Figure S2). The delay time was defined as the difference between washout time and catastrophe time.

Measurement of EB-site maturation rates

To test whether the maturation rate depends on the magnesium concentration, we performed comet analysis experiments in simple flow chambers as described earlier (Bieling et al., 2010; Maurer et al., 2014) at the same concentrations used for microfluidics experiments, in the additional presence, however, of low concentrations of Mal3-GFP (to be able to visualize the fluorescent Mal3-GFP comet). In initial experiments, we noticed that magnesium reduced the affinity of Mal3-GFP for microtubule binding (for both the end region and the lattice; unpublished data). We therefore adjusted the Mal3-GFP concentration to have similar Mal3 binding, resulting in similar GFP end intensities for the different magnesium concentrations tested: Mal3-GFP was present at 1.6, 4, and 10 nM for experiments performed with 1.6, 4, and 10 mM MgCl₂, respectively. Maturation rates and their SEs were then determined as described (Maurer et al., 2014). The maturation rates were found to be independent of the MgCl₂ concentration in the buffer.

Multistep-defect model for delay-time distributions after tubulin washout

Steady-state solution.

Previously, a multistep “defect” model with coupled-random hydrolysis was presented for the description of microtubule lifetime distributions at steady state (Bowne-Anderson et al., 2013). Here we further develop this model to describe delay time distributions after fast tubulin washout.

During steady-state growth, a 13-protofilament microtubule is modeled as a collection of 13 independent protofilaments, each of which has GTP-tubulin dimer association and disassociation rate constants of k_on and k_off, respectively. GTP-to-GDP hydrolysis occurs randomly at rate h for all dimers except the terminal subunit, as shown in Figure 4. A permanent modification to an individual protofilament, here called a “defect,” occurs when the terminal subunit is in a GDP state. Furthermore, a catastrophe occurs after a threshold number n = 3 of these destabilizing events occurs for the whole microtubule (Gardner et al., 2011b; Figure 4).

The average growth speed is v_g = 8nm(k_on − k_off), and the steady-state probability that a protofilament has a subterminal dimer in a GDP state is defined as f(k_off, k_on, h) (Bowne-Anderson et al., 2013). The rate at which defects occur in a single protofilament is thus

If X is a continuous random variable representing the time until a defect occurs, then the distribution function of waiting times for a defect is

and the survival function (the probability of a defect occurring after time t) is

The survival function can be shown to be

For a microtubule of 13 protofilaments, the probabilities that there are a total of 0, 1, or 2 defects at time t are, respectively,

where [13,2] is 13!/(2! 11!) combinations. The total probability of a microtubule surviving until t is thus p_tot(t) = p₀ + p₁ + p₂.

This gives the steady-state probability distribution as derived in Bowne-Anderson et al. (2013).

Tubulin washout.

We now consider the case in which all free tubulin is removed during washout at t_wo. After washout, k_on = 0, we assume that the hydrolysis rate remains constant (Duellberg et al., 2016) but the dissociation rate can change to k_off2. We define the postwashout probability that a protofilament has a subterminal subunit in a GDP state as f ′(k_off2, 0, h).

At a time t ′ after washout, the time evolution of f ′ can be approximated by df ′/dt ′ = h(1 − f ′).

Solving this with the boundary constraint at washout (t ′ = 0), f ′ = f, gives

The rate at which defects occur in a single protofilament is now

and we define γ′ = ∫λ′(t′) dt′ .

Because we consider only microtubules that have not had a catastrophe before washout, the probabilities that there are a total of 0, 1, or 2 defects at washout are normalized to give

The distribution and survival functions after washout are now 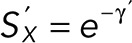and 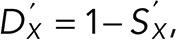respectively, and the probability of a single defect happening at exactly t’ is .

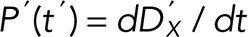By considering the different combinations of defects that can occur before and after washout that result in a catastrophe at t’, we obtain the total postwashout probability density function (PDF) for waiting times:

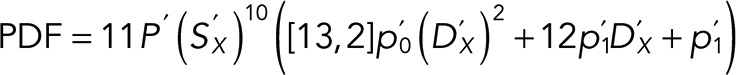The corresponding cumulative distribution function (CDF) is

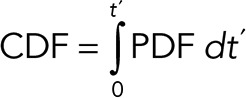An explicit expression for the PDF was found by using the assumption 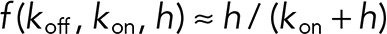(Bowne-Anderson et al., 2013).

To investigate the effect of the number of defects required for catastrophe, solutions were also derived for thresholds of 2 and 4 defects and used to fit the experimental data (Supplemental Table S2).

Stochastic simulations.

To check the validity of the assumptions made in the postdilution theory developed here, the model was implemented in Mathematica (Wolfram, Oxfordshire, UK) by creating a matrix representing the hydrolysis state of the subunits in 13 independent protofilaments. For each protofilament, association, dissociation, and hydrolysis events were modeled as exponentially distributed random variables, using the supplied rate constants.

Steady-state (pre-washout) simulations gave lifetime distributions in agreement with the theory developed in Bowne-Anderson et al. (2013). Furthermore, extending the simulation to include a dilution time point gave lifetime distributions in agreement with the foregoing theory (Supplemental Figure S4).

Data fitting.

To fit the experimental data, we implemented the explicit expression for the CDF after washout derived here in Origin (OriginPro 2016; OriginLab, Northampton, MA). Fitting parameters were fixed to experimental values for each condition, where known (Supplemental Table S1): the predilution association and dissociation rates were coupled to the measured growth speed, v_g, but otherwise free; the postdilution disassociation rate was fixed by the measured shrinkage speed, v_s; the hydrolysis rate was free to take any value greater (= faster) than or equal to the measured maturation rate, k_m.

Fits were also done assuming that the predilution and postdilution dissociation rates were equal and set by the shrinkage speed and with the hydrolysis rate free to take any value (not limited by the measured k_m; Supplemental Table S1).

Taper-cap density model for delay times after tubulin washout

We showed recently that the delay time after tubulin washout can be estimated based on the kinetics of the loss of EB cap sites after washout (Duellberg et al., 2016). In this previous kinetic model, we assumed that at the moment of tubulin washout (t′ = 0), a microtubule with growth velocity v_g and maturation rate k_m has an approximately monoexponential profile of EB binding sites in space (the “comet”), starting at the microtubule end (x = 0):

where n(x) is the linear cap density and n_x0 = 13/8 nm is the maximum end density. After tubulin washout but before a catastrophe, the loss of the EB cap is due to continued maturation at rate k_m and slow shrinkage of the microtubule from its end with speed v_s. This gives a spatial profile of binding sites at time t’ after washout and position x′ from the shrinking end:

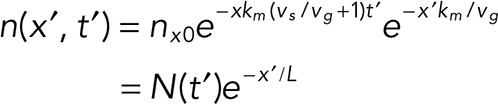where L = v_g/k_m is defined as the comet length.

In addition, we consider here that the microtubule end structure can be tapered at the moment of washout: we assume that this leads to different starting positions of the cap regions for each protofilament in the microtubule, resulting in a smearing of the overall binding-site profile (Figure 5A). Using a continuous approximation of a linear taper, we obtain the linear cap density for a microtubule with a taper length L_taper = 2a by convolving n(x′, t′) with a rectangular pulse

yielding

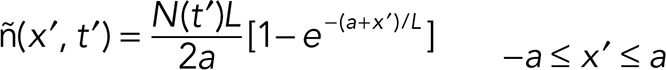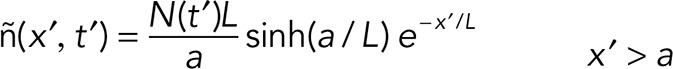For simplicity, we assumed that the taper length stays constant during slow shrinkage.

Of interest is the maximum linear cap density, which is found at :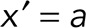

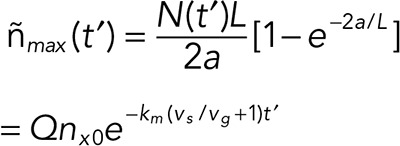where the factor 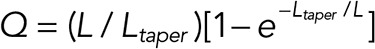depends only on the ratio of the taper and comet lengths.

Assuming that catastrophe occurs when the maximum linear cap density (equivalent to the end density in the previous version of the model; Duellberg et al., 2016) has reached a critical threshold value, , the delay time is given by

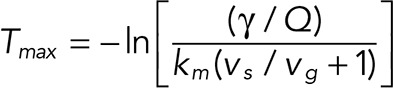with a fractional threshold 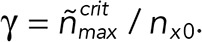By setting Q = 1 (absence of taper), one finds the expression for the delay time of our previous model (Duellberg et al., 2016).

To calculate the dependence of the delay time on the washout time, t_wo (i.e., microtubule growth time/age), we assume that the taper length grows with time (Coombes et al., 2013) with constant taper growth speed v_t. Hence, L_taper = v_tt_wo and

Furthermore, to reduce the number of free parameters for the global fit to the delay time data at three different Mg concentrations in Figure 5, we assume that the taper growth speed is proportional to the microtubule growth speed, v_t = f_tv_g, with the proportionality factor f_t shared for all Mg concentrations. Insertion leads to the aging factor Q being expressed in a growth speed–independent form:

Data fitting.

We performed a global fit to all six delay times using Matlab (Figure 5). For the three Mg concentrations, v_g, v_s and k_m were fixed to known values, leaving four free parameters: the three threshold values for the three Mg concentration and one shared proportionality factor, f_t. The errors of the predicted delay times and taper lengths were estimated by SE propagation using experimental SEs and fit errors as input. All values are summarized in Supplemental Table S1.

Abbreviations used:

CDF

cumulative distribution function

EB

end binding

GDP

guanosine diphosphate

GFP

green fluorescent protein

GMPCPP

guanylyl 5′-α,β-methylenediphosphonate

GTP

guanosine triphosphate

PDF

probability density function

PDMS

polydimethylsiloxane

PEG

polyethylene glycol

TIRF

total internal reflection fluorescence.